Competing Manufacturers Adopt Blockchain for Tracing Power Batteries: Is There a Win-Win Zone?

Abstract

Blockchain-based battery tracking offers solutions to issues like information asymmetry, counterfeit battery risk, and technical barriers in assessing battery condition. This paper aims to identify the drivers behind manufacturers adopting blockchain for battery tracking and assess whether a mutually beneficial outcome exists. We develop a game model featuring two competing manufacturers, and extend it to include asymmetric competition and battery quality considerations. Equilibrium solutions reveal two main incentives for manufacturers to adopt blockchain: reverse profit compensation and enhancement of battery quality. Blockchain traceability facilitates retired battery recovery in a large-scale market, even when adoption costs outweigh reuse savings and collection prices are low. If one manufacturer implements blockchain, reducing blockchain costs or expanding the market can lead to a “win-win” outcome for competitors. Our findings offer novel managerial insights into manufacturers’ blockchain adoption decisions.

1. Introduction

Lithium-ion batteries (LIBs) have become a critical component of electric vehicles (EVs), particularly plug-in hybrid electric vehicles (HEVs) and battery electric vehicles (BEVs). Improper disposal of LIBs can damage the environment and human health [1]. Recycling high-value materials such as lithium, cobalt and nickel helps relieve environmental pressure [2,3], improve resource utilization [4], reduce production costs [5] and carbon emissions [6,7]. Echelon utilization of retired batteries through peak shaving and energy arbitrage enables maximum economic benefits to develop a circular economy [8,9,10]. Under Extended Producer Responsibility (EPR), EV manufacturers are responsible for battery recycling. Thus, the power battery supply chain is a closed-loop supply chain integrating forward sales and reverse recycling.

Information sharing in competitive supply chains often focuses on retailers sharing information with manufacturers. Previous research suggests information sharing can increase sales [11,12] and reduce inventory and shortage costs [13]. However, information sharing is only optimal given low sharing investment and economical production [14]. Emerging technologies like big data, blockchain, and cloud computing have increased supply chain transparency and allowed new formats of information sharing. This provides an opportunity for manufacturers to participate directly. For example, BMW, Ford, Renault and General Motors co-founded the Mobility Open Blockchain Initiative (MOBI) to reduce used car fraud by creating a digital vehicle identity. Volkswagen partners with blockchain company Minespider to track battery materials from origin to factory. Therefore, studying manufacturer competition under emerging forms of information sharing is necessary.

There are three main reasons that make tracking batteries important. First, asymmetric information between upstream and downstream parties leads to retired batteries flowing to informal recyclers. The improper processing causes additional environmental impacts. Second, counterfeit batteries pose quality and safety risks. The pursuit of profit makes counterfeit batteries an emerging issue. Concerns about adulterated batteries in clandestine markets could reduce battery prices and impede sales of original products [15]. Using counterfeit batteries also poses safety risks to consumers. Moreover, tampering with battery data can cause secondary use and recycling to fail [16,17]. Finally, the lack of information creates technical barriers in assessing battery status, hindering secondary battery use [8]. Key technologies like battery screening and performance evaluation impact environmental and economic benefits [18]. Therefore, providing information through battery tracking is extremely urgent.

Blockchain is decentralized and provides immutable data storage with limited privacy [19,20]. Blockchain-based battery tracking has several advantages: (1) Complete information facilitates detecting battery status. The blockchain can store usage data like maximum charge/discharge times, state of charge, and energy, in addition to basic information [21]. Battery life information assists in assessing health and reducing unnecessary testing [22]. This helps identify second-life duration with less environmental impact. (2) Transparent and immutable information enhances security. Blockchain improves supply chain transparency [23]. Assigning a unique ID allows accessing production, use and disposal data. Traceability locates responsible parties for improper disposal. This eases consumer concerns about safety and environment, expanding market potential [24]. (3) Blockchain ensures data integrity and prevents counterfeiting. Battery health depends on thousands of parameters [25]. Data integrity decreases with more transmission links, increasing errors. Blockchain prevents unilateral changes, misuse, emissions, and clandestine markets [15].

Despite the potential benefits, many manufacturers hesitate to adopt blockchain due to significant adoption costs [26], including high computational power and electricity consumption [27], and increases energy and storage requirements for adding network nodes [28]. Motivated by these observations, our study delves into EV manufacturers’ attitudes toward blockchain adoption, exploring the following questions: (1) What motivates EV manufacturers to embrace blockchain for battery tracking? (2) Does blockchain truly enhance the efficiency of battery recycling? (3) Is there a “win-win” outcome for competing EV manufacturers through blockchain implementation?

In this paper, we develop a game model for the power battery supply chain involving two competing EV manufacturers. We investigate two scenarios to assess whether manufacturers can achieve greater profitability by adopting blockchain: (1) Scenario N, where the manufacturer opts out of blockchain, facing reduced market potential and higher reuse costs; (2) Scenario B, where the manufacturer engages in blockchain, enjoying an expanded market and reduced reuse costs. By comparing profits in Scenarios N and B, we aim to identify the driving factors behind blockchain implementation.

The work contributions to three main areas. First, a game model is extended by incorporating blockchain adoption decisions into both forward and reverse supply chains. While prior studies on blockchain adoption have focused on implementation technology [21,29], this study explores the strategic decision-making process of EV manufacturers for battery tracking. By leveraging the advantages of blockchain in battery recycling, the understanding of its potential within the EV battery supply chain is deepened.

Second, the research reveals the motivations driving battery manufacturers to adopt blockchain. Although existing studies demonstrate the feasibility and security of utilizing blockchain technology for battery tracking [15,30,31,32,33], insufficient attention has been given to manufacturers’ motivations. Two key drivers for blockchain adoption are identified: reverse profit compensation and improvements in battery quality. These findings provide valuable decision-making insights for managers.

Finally, the paper identifies a “win-win” scenario for competing manufacturers who adopt blockchain. While several studies highlight reasons why manufacturers may hesitant to adopt blockchain, such as high adoption costs [26,27,28], the discussion suggests that by reducing blockchain costs or expanding the market, a mutually beneficial outcome can be achieved.

The remainder of the paper is organized as follows. Section 2 reviews related literature. Section 3 presents the model and equilibrium solutions under two scenarios. Section 4 discusses the results and manufacturers’ blockchain adoption preferences. Section 5 explores the impact of asymmetric competition and battery quality. Finally, Section 6 concludes our findings and provides managerial insights.

2. Literature Review

Our work relates closely to the literature on information sharing within supply chains. Previous studies indicate that information sharing between retailers and manufacturers can increase sales [12] and reduce inventory and shortage costs [13]. However, information sharing is only optimal given low investment and economical production [14]. Emerging technologies have profoundly transformed information sharing. Blockchain plays a significant role in improving efficiency [34,35], transparency [23,26,32,36], and traceability [33,37]. Most blockchain-based supply chain literature examines the overall impact. Micro-level research involves pricing decisions [38], risk appetite [39], and financing benefits [40].

Tracking enables transparency in supply chain operations. Sunny et al. [33] overview blockchain-based traceability solutions that increase transparency. A major application is anti-counterfeiting, observed in medicines [41,42], diamonds [40], and personal protection [43]. In food, it ensures safety. In automotive/battery sectors, feasibility studies use literature analysis. Antônio Rufino Júnior et al. [15] show blockchain can track batteries. Kim et al. [30] find blockchain in battery management systems ensures safety, reliability and performance. Raj Kumar Reddy et al. [32] explore blockchain for automotive supply chain visibility. Zhou et al. [35] find traceability reduces product quality in competitive markets.

The above literature provides a theoretical basis for blockchain operational management in supply chains, but detailed discussion with battery supply chains is still insufficient:

(1)

Existing research on battery manufacturer decisions to adopt blockchain is inadequate. A comprehensive view should consider the closed-loop battery supply chain integrating sales and recycling. Specifically, blockchain’s role in the reverse recycling supply chain requires discussion.

(2)

Asymmetric competition between manufacturers and battery quality influence decisions, yet current research does not account for these factors.

We model the supply chain of two competing battery manufacturers, setting up scenarios with and without blockchain. Further, we consider asymmetric competition between manufacturers and incorporate battery quality. By calculating optimal solutions, we obtain conclusions and recommendations to fill this research gap. Our approach to validating the effectiveness of the proposed game model encompasses rigorous formulation, parameter calibration, simulation-based analysis, and sensitivity analysis. Through these comprehensive steps, we aim to demonstrate the reliability and utility of our model in informing strategic decision-making in the EV battery supply chain.

3. Model and Equilibrium Analysis

We consider a closed-loop supply chain for power battery, consisting of two competing EVs manufacturers (denoted I and E respectively) and consumers (see Figure 1). Manufacturers sell new batteries at a price $p_i$ to consumers, which is often sold in bundles with EVs. Retired batteries, no longer suitable for EVs, are collected by manufacturers at a price $h_i$ and are utilized by laddering and recycling for revenue $A$. Follow Heydari et al. [44], the consumers’ willing-to-return is noted as $r_i=h_i/h_{max}$ ($i=I,E$), where $h_{max}$ denotes the maximum price to get all retired batteries collected. EV manufacturers, according to the extended producer responsibility (EPR), are responsible for providing all information on power batteries. The information relates to production, consumption, and recycling, contributing to the establishment of a traceability management system for power batteries.

The adoption of blockchain by manufacturers can provide the following enhancements.

(1)

Expanding market potential.

Through blockchain traceability management, consumers will have access to comprehensive and efficient information and their concerns about battery safety will be reduced. In line with the findings of the literature [45], the application of blockchain in supply chain management will increase consumer trust. As a result, manufacturers embedded in the blockchain are supported by a wider range of consumers, which expands the market potential. We use $\rho \in (0,1)$ to represent the manufacturer’s disadvantage in market potential without the adoption of blockchain.

(2)

Reducing retired batteries reuse cost.

Determining the health status of retired power batteries has been a key issue impeding recycling. Adopting blockchain throughout the life cycle of a power battery will improve the accuracy of battery health status determination, thereby reducing reuse cost such as testing and sorting of retired batteries [46,47]. We use $k\in (0,1)$ to represent the manufacturer’s disadvantage in battery reuse cost in the absence of blockchain.

However, the manufacturer’s profits may be affected as there are costs associated with blockchain adoption. We therefore consider two contrasting scenarios to investigate the drivers for EV manufacturers to embrace the blockchain. They are: Scenario B, where two competing manufacturers both choose to adopt blockchain, and incur a unit cost $c$. Blockchain expands the market potential for new batteries and reduces the cost of reusing retired batteries; Scenario N, where manufacturers are choosing not to adopt blockchain. Accordingly, manufacturers have a disadvantage in market potential and battery recycling cost. For ease of reference, we summarize the notations of this paper as follows.

Decision variables:

${p_i}^j$: retail price for party $i$ in Scenario $j$. $i\in \{I,E\}$ and $j\in \{N,B\}$;

${h_i}^j$: collection price of retired battery for party $i$ in Scenario $j$. $i\in \{I,E\}$ and $j\in \{N,B\}$;

${H_i}^j$: quality level of battery for party $i$ in Scenario $j$. $i\in \{I,E\}$ and $j\in \{N,B\}$.

Parameters:

$a$: market potential of power battery in EVs;

$b$: competition intensity degree between the two manufacturers, $b\in [0,1]$;

$c$: blockchain adoption cost of manufacturer;

$\rho$: manufacturer’s disadvantage in market potential without blockchain, $\rho \in [0,1]$;

$A$: manufacturer benefits from retired battery recycling;

$k$: manufacturer’s disadvantage in recycling cost without blockchain, $k\in [0,1]$;

${r_i}^j$: consumers’ willing-to-return of party $i$ in Scenario $j$. $i\in \{I,E\}$ and $j\in \{N,B\}$;

${{\pi }_i}^j$: profit of supply chain party $i$ in Scenario $j$. $i\in \{I,E\}$ and $j\in \{N,B\}$.

Followed Niu et al. [48], we formulate the competition between two manufacturers. The superscript N and B denote Scenario N and Scenario B, respectively.

In Scenario N, the demand functions are:

$${q_I}^N=\rho a-{p_I}^N-b{p_E}^N, {q_E}^N=\rho a-{p_E}^N-b{p_I}^N$$

where $\rho \in [0,1]$ represents the manufacturer’s disadvantage in market potential without adoption of blockchain, and $b\in [0,1]$ is the competition intensity.

The profit functions of manufacturers are:

$${{\pi }_i}^N={p_i}^N{q_i}^N+\left(kA-{h_i}^N\right){r_i}^N{q_i}^N i\in \{I,E\}$$

In Scenario B, with blockchain adoption, consumer concerns about battery safety will be alleviated, resulting in a greater willingness to purchase EVs. Thus, the demand functions become:

$${q_I}^B=a-{p_I}^B-b{p_E}^B, {q_E}^B=a-{p_E}^B-b{p_I}^B$$

The profit functions of manufacturers are:

$${{\pi }_i}^B=({p_i}^B-c){q_i}^B+(A-{h_i}^B-c){r_i}^B{q_i}^B i\in \{I,E\}$$

The sequence of events unfolds as follows. In stage 1, the manufacturers determine whether to adopt blockchain technology. In stage 2, they set the new battery prices $p_i$ simultaneously. In stage 3, two manufacturers simultaneously determine the retired power battery collection prices $h_i$.

We employ backward induction to solve the games, with the outcomes summarized in Table S1 (see Supplementary Material). To ensure positive outputs and eliminate trivial cases, we impose the conditions $a\ge \frac{A^2{k}^2}{4\rho h_{max}}$, $A>c$ and $\frac{{(A-c)}^2}{4(a+c)}<h_{max}\le \frac{{(A-c)}^2}{4c}$.

4. Discussion

4.1. Analysis of Forward Supply Chain

Before investigating how the manufacturers’ blockchain adoption affects the supply chain parties’ profits, we first compare the retail prices and sales amount of a new battery with and without blockchain adoption. We have Lemma 1 and Corollary 1.

Lemma 1.

The manufacturers determine a higher retail price for a new battery in Scenario B than that in Scenario N if one of the following conditions occurs. i.e., ${p_i}^B>{p_i}^N$ for

(i) 

$c<A\left(1-k\right), and h_{max}>\frac{{(A-c)}^2-A^2{k}^2}{4(a+c-a\rho )}$, or

(ii) 

$c\ge A\left(1-k\right), and h_{max}\ge 0.$

Proofs of all Lemmas, Corollaries and Propositions are provided in the Appendix A.

Lemma 1 indicates that when the cost of blockchain adoption is greater than the reuse cost savings (i.e., $c\ge A(1-k$)), the manufacturers set a higher retail price in Scenario B. Otherwise, the maximum collection price has to satisfy certain conditions. One possible reason for this decision is that taking the blockchain is costly and manufacturers expect to reduce the cost of recycling detection rely on blockchain. If the blockchain adoption cost is not covered by the reuse cost savings, they have to compensate lost profits by raising retail prices. On the contrary, low collection rates due to low consumers’ willing-to-return (i.e., high $h_{max}$) also forces manufacturers to increase the retail price of new batteries.

Corollary 1.

The total sales amount in Scenario B is higher than that in Scenario N if maximum collection price exceeds the threshold $\frac{{(A-c)}^2+A^2{k}^2(1+b)}{4(a+c-a\rho )}$ (i.e., ${q_i}^B>{q_i}^N$ for $h_{max}>\frac{{(A-c)}^2+A^2{k}^2(1+b)}{4(a+c-a\rho )}$).

Corollary 1 shows that manufacturers’ blockchain adoption has the opportunity to improve sales amount, depending on the maximum collection price $h_{max}$. Low consumer willingness to return (i.e., high $h_{max}$) leads to high retail prices (see Lemma 1). A significant sales quantity in Scenario B highlights the value of blockchain in sales amount promotion.

4.2. Analysis of Reverse Supply Chain

Then we consider the collection prices and retired battery amount with and without blockchain adoption. We have Lemma 2 and Corollary 2.

Lemma 2.

The manufacturers establish a higher collection price for retired battery in Scenario B than that in Scenario N when the cost of blockchain adoption less than the threshold $A(1-k)$ (i.e., ${h_i}^B>{h_i}^N$ for $c<A(1-k)$).

Lemma 2 indicates that if blockchain adoption cost is smaller than the reuse cost savings (i.e., $c<A(1-k$)), manufacturers set a higher collection price in Scenario B. Recall that under the same condition, manufacturers decide on a higher retail price in Scenario B for low willing-to-return (i.e., ${p_i}^B>{p_i}^N$ for a high $h_{max}$) to recover lost profits (see Lemma 1). Accordingly, raising collection prices responds to a desire for low returns.

Corollary 2.

The total collection amount in Scenario B is higher than that in Scenario N if one of the following conditions occurs, i.e., ${l_i}^B>{l_i}^N$ for

(i) 

$c<A\left(1-k\right),\left\{\begin{array}{c}a>\frac{\left(1+b\right) [A^3{k}^3-{\left(A-c\right)}^3+4c{h}_{max}\left(A-c\right)]}{4h_{max} [A\left(1-k\rho \right)-c]} and h_{max}>\frac{{\left(A-c\right)}^3-A^3{k}^3}{4c(A-c)}\\ a>0 and h_{max}\le \frac{{\left(A-c\right)}^3-A^3{k}^3}{4c\left(A-c\right)}\end{array}\right.$, or

(ii) 

$c\ge A(1-k), a>\frac{\left(1+b\right) [A^3{k}^3-{\left(A-c\right)}^3+4c{h}_{max}\left(A-c\right)]}{4h_{max} [A\left(1-k\rho \right)-c]} and 0<\rho <\frac{A-c}{Ak}.$

Corollary 2 suggests that high collection prices induce high collection amount holds only under certain conditions. Apart from blockchain cost, collection amount is affected by the consumers’ willing-to-return and the market scale. Specifically, if blockchain adoption cost is smaller than reuse cost savings (i.e., $c<A(1-k$)), manufacturers are able to obtain more retired batteries in Scenario B under a high consumers’ willing-to-return, or a low willing-to-return but in the large-scale market. Under these conditions, manufacturers set higher recycling prices (see Lemma 2). And if the blockchain adoption cost is greater than the saved reuse cost (i.e., $c\ge A(1-k)$), only a large-scale market can facilitate the above conclusion holds, as manufacturers lose the high collection price advantage. This hints at the blockchain advantage to boost collection amount in a large-scale market.

Proposition 1.

The total profits of reverse supply chain in Scenario B is higher than that in Scenario N if one of the following conditions occurs, i.e., ${{RV}_i}^B>{{RV}_i}^N$ for:

(i) 

$c<A(1-k), and \left\{\begin{array}{c}a>0 and h_{max}\le \frac{{\left(A-c\right)}^4-A^4{k}^4}{4c{\left(A-c\right)}^2}\\ a>\frac{\left(1+b\right) [{\left(A-c\right)}^4-A^4{k}^4-4c{h}_{max}{\left(A-c\right)}^2]}{4h_{max} [A^2{k}^2\rho -{\left(A-c\right)}^2]} and h_{max}>\frac{{\left(A-c\right)}^4-A^4{k}^4}{4c{\left(A-c\right)}^2} \end{array}\right.$, or

(ii) 

$c\ge A(1-k), a>\frac{\left(1+b\right)\left[{\left(A-c\right)}^4-A^4{k}^4-4c{h}_{max}{\left(A-c\right)}^2\right]}{4h_{max}\left[A^2{k}^2\rho -{\left(A-c\right)}^2\right]}, and 0<\rho <\frac{{(A-c)}^2}{A^2{k}^2}.$

Proposition 1 shows that the profitability of the reverse supply chain is related to the blockchain cost, the market scale, and the consumers’ willing-to-return. This is similar to the results for collection amount, while the collection price is only affected by the blockchain cost. We combine Proposition 1 with Lemma 2 and Corollary 2 to explore the correlation behind it. For a small blockchain cost (i.e., $c<A(1-k$)), manufacturer selects a higher collection price in Scenario B. This enables a higher collection amount with a high willing-to-return, or a large-scale market with a low willing-to-return. Accordingly, the reverse supply chain profit is also higher in scenario B. And if blockchain adoption cost is large (i.e., $c\ge A(1-k)$), only a large-scale market can afford high collection prices and amount. Thus, the disadvantage of collection price and amount induce the reverse supply chain with blockchain adoption more profitable in a large-scale market.

4.3. Preference of Manufacturers

We examine the total profits of manufacturers with and without blockchain to understand the motivation of blockchain adoption. We obtained Proposition 2 and Figure 2.

Proposition 2.

The total profits of supply chain in Scenario B is higher than that in Scenario N if one of the following conditions occurs, i.e., ${{\pi }_i}^B>{{\pi }_i}^N$ if

(i) 

$c<A(1-k),\left\{\begin{array}{c}a>0,h_{max}\le \frac{{(A-c)}^2-A^2{k}^2}{4c} \\ a>\frac{(1+b) [{\left(A-c\right)}^2-A^2{k}^2+4c{h}_{max}]}{4h_{max}(1-\rho )}, \frac{{(A-c)}^2-A^2{k}^2}{4c}\le h_{max}\le \frac{{(A-c)}^2+A^2{k}^2}{4c} \end{array}\right.$, or

(ii) 

$c\ge A(1-k), a>\frac{\left(1+b\right)\left[{\left(A-c\right)}^2-A^2{k}^2+4c{h}_{max}\right]}{4h_{max}\left(1-\rho \right)}, and h_{max}\le \frac{{(A-c)}^2+A^2{k}^2}{4c}.$

Proposition 2 presents the conditions under which the manufacturer with blockchain adoption is more profitable. To intuitively present the conditions, we have conducted numerical experiments and the results are shown in Figure 1. A small blockchain cost for Figure 2a and a large blockchain cost for Figure 2b.

Observation 1.

For a small blockchain cost (i.e., $c<A(1-k)$), manufacturers prefer to adopt blockchain if consumers have a high willing-to-return; For a large blockchain cost (i.e., $c\ge A(1-k)$), manufacturers prefer to adopt blockchain if consumers have a high willing-to-return in a large-scale market.

Observation 1 illustrate that one of the key determinants of blockchain adoption by manufacturers is the consumers’ willingness to return. This is because high willingness consumers are more concerned about the environmental benefits of battery recycling. They may be attracted by the comprehensive and valid traceability information with blockchain, thus expanding the market potential. For a small blockchain cost, we use the colored regions in Figure 2a to denote the decision area for manufacturer preference Scenario B. And if blockchain cost is large (i.e., $c\ge A(1-k)$), only a large-scale market with high willing-to-return ensures that the formula ${{\pi }_i}^B>{{\pi }_i}^N$ holds, which is represented by the color region in Figure 2b.

Combining Proposition 1 and 2, we identify a driver for manufacturers to adopt blockchain: reverse profit compensation. We notice that in the forward supply chain, both retail price and sales amount are higher in Scenario N than that in Scenario B, if consumer willing-to-return is high (see Lemma 1 and Corollary 1). However, manufacturers’ profits in Scenario B is always higher than that of Scenario N under the high willing-to-return. It indicates a significant contribution of the reverse supply chain to total profits. Recall that in the small-scale market with low blockchain cost or in the large-scale market with high blockchain cost, the collection amount and the reverse supply chain profit outperform in Scenario B (see Corollary 2 and Proposition 1). The expanded market attract more consumers with high willing-to-return to participate in retired batteries recycling. It in turn boost reverse profits to offset the blockchain spending. And the profit compensation mechanism is equally applicable in the case of a high blockchain cost (i.e., $c\ge A(1-k)$).

5. Extension of the Models

5.1. Model Extension 1—Asymmetric Competition (Model E1)

We assume that one of the manufacturers has implemented blockchain (suppose manufacturer I), what will be the impact on the decision of the other new entrant (suppose manufacturer E)? Is there a win-win zone with asymmetric competition? Again, we consider two scenarios. The objective functions in Scenario N and Scenario B are as follows, respectively.

In Scenario N:

$${{\pi }_I}^N=({p_I}^N-c){q_I}^N+(A-{h_I}^N-c){r_I}^N{q_I}^N$$

$${{\pi }_E}^N={p_E}^N{q_I}^N+(kA-{h_E}^N){r_E}^N{q_E}^N$$

In Scenario B:

$${{\pi }_I}^B=({p_I}^B-c){q_I}^B+(A-{h_I}^B-c){r_I}^B{q_I}^B$$

$${{\pi }_E}^B=({p_E}^B-c){q_E}^B+(A-{h_E}^B-c){r_E}^B{q_E}^B$$

We use backward induction to solve the games. The solutions are summarized in Table S2 (see Supplementary Material). We require $a>\frac{2{(A-c)}^2-b{A}^2{k}^2-8c{h}_{max}}{4\rho h_{max}(2-b)}$, $A>c$ and $\frac{{(A-c)}^2}{4(a+c)}<h_{max}\le \frac{b{(A-c)}^2-2A^2{k}^2}{4bc}$ to ensure positive outputs and rule out trivial cases.

5.2. Model Extension 2—Considering Battery Quality (Model E2)

Scholars have verified that battery quality has a significant impact on the sales of new batteries and the recycling of retired batteries [48,49]. On the basis of an asymmetric competition model, how the battery quality will affect the manufacturer’s blockchain adoption decision, and whether there is also a win-win zone. We assume that manufacturer I has implemented blockchain, and that manufacturer E needs to decide whether to adopt blockchain.

Consumers’ willing-to-return is noted with reference to Genc and Giovanni [50] as ${r_i}^j=\frac{\eta {h_i}^j}{{H_i}^j},i=\{I,E\}$, where ${h_i}^j$ is collection price paid by manufacturer, ${H_i}^j$ represents battery quality level, and $\eta$ is recycling scale factor. The retail price is also related to the battery quality, denoted as ${p_i}^j=\omega {H_i}^j$, where $\omega \in [0,1]$ is a positive constant. With reference to the literature [51], battery sales are determined by the retail price and the quality level. Thus, in Scenario N, the demand functions become:

$${q_I}^N=\rho a-{p_I}^N-b{p_E}^N+\theta {H_I}^N, {q_E}^N=\rho a-{p_E}^N-b{p_I}^N+\theta {H_E}^N$$

In Scenario B, the demand functions become:

$${q_I}^B=a-{p_I}^B-b{p_E}^B+\theta {H_I}^B, {q_E}^B=a-{p_E}^B-b{p_I}^B+\theta {H_E}^B$$

where $\theta \in [0,1]$ is the consumer quality sensitivity.

The objective functions in Scenario N and Scenario B are as follows, respectively.

In Scenario N:

$${{\pi }_I}^N=({p_I}^N-c){q_I}^N+(A-{h_I}^N-c){r_I}^N{H_I}^B{q_I}^N$$

$${{\pi }_E}^N={p_E}^N{q_I}^N+(kA-{h_E}^N){r_E}^N{H_E}^B{q_E}^N$$

In Scenario B:

$${{\pi }_I}^B=({p_I}^B-c){q_I}^B+(A-{h_I}^B-c){r_I}^B{H_I}^B{q_I}^B$$

$${{\pi }_E}^B=({p_E}^B-c){q_E}^B+(A-{h_E}^B-c){r_E}^B{H_E}^B{q_E}^B$$

We use backward induction to solve the games. The outcomes are summarized in Table S3 (see Supplementary Material). We require $a\ge a_0$, $A>c$ and $\omega \ge 2\theta$ to ensure positive outputs and rule out trivial cases.

5.3. Preference of Manufacturers in Extensions

5.3.1. Model E1

Considering that manufacturers’ decisions are directly influenced by the market scale, we simulated two market scale parameters. Figure 3a represents the manufacturers’ profits in a small-scale market, while Figure 3b is for a large-scale market. To focus on the decision of the new entrant, we have represented the variation of manufacturer E with a red line and manufacturer I with a black line. We have Observation 2.

Observation 2.

There exists a “win-win” zone for manufacturers with asymmetric competition. In the small-scale market, lower blockchain cost result in higher revenue for both parties in Scenario B (see Figure 3a); In the large-scale market, adopting blockchain is the optimal decision for both manufacturers, even if the cost is increasing (see Figure 3b).

Figure 3 shows that the advantages of blockchain for both manufacturers weaken as cost increases, and manufacturer E is more significant. Regarding Observation 2, it is intuitive that manufacturer E with blockchain is more profitable. However, we observe that in the small-scale market, a “win-win” zone exists only when blockchain cost is low, allowing both manufacturers to outperform in Scenario B. This is consistent with the findings in the basic model. Recall that manufacturers prefer to blockchain adoption on the condition that the cost is not higher than the reuse savings in a small-scale market. Similarly, if blockchain adoption cost exceeds the reuse savings, a large-scale market is required for the formula ${{\pi }_i}^B>{{\pi }_i}^N$ to hold (see Proposition 2). As Figure 3b demonstrates, if a is large, Scenario B has an absolute advantage. This suggests two ways to encourage manufacturers to participate in blockchain: reducing blockchain adoption cost or expanding the market scale.

5.3.2. Model E2

Before profits comparison, we wonder whether there is also a “win-win” zone at the equilibrium quality level. Therefore, we conducted numerical experiments for different market scale and obtained Figure 4 and Observation 3. We use $\mathsf{\Delta }{H}_E$ and $\mathsf{\Delta }{H}_I$ represent the reward advantage of manufacturer E and manufacturer I under Scenario B, respectively.

Observation 3.

There exists a “win-win” zone for manufacturers’ quality in model E2. In the small-scale market, small blockchain cost allows manufacturers to have a higher quality in Scenario B (see Figure 4a); while in the large-scale market, the condition for a higher quality in Scenario B is significant blockchain cost (see Figure 4b).

Observation 3 describes the manufacturer’s best quality decisions under different scenarios. We notice that as blockchain cost rises, the quality advantage of the manufacturer I in Scenario B gradually degrade, while the quality advantage of manufacturer E becomes more significant. This is shown in Figure 4 as $\mathsf{\Delta }{H}_I$ decreasing monotonically with respect to blockchain cost, and $\mathsf{\Delta }{H}_E$ increasing monotonically with respect to blockchain cost. The possible reason for this phenomenon is that the adoption of blockchain (Scenario B) by manufacturer E increases information transparency on battery quality and enhances the competitive advantage. Even though blockchain cost is boosting up, manufacturer E chooses to produce higher-quality batteries. Manufacturer I, in response to competition from manufacturer E’s blockchain adoption, has improved the quality of batteries, compared to Scenario N. As cost increases, manufacturer E’s competitive advantage fades and, accordingly, manufacturer I’s improvement in battery quality diminishes.

Moreover, we have identified another driver to spur manufacturers’ blockchain adoption: improving battery quality. This is consistent with the findings of the literature [45,46] that blockchain enhances product quality. Specifically, in the small-scale market, manufacturer E has absolutely high quality under Scenario B, while the quality advantage of manufacturer I fades away as the blockchain cost rises. If blockchain adoption cost exceeds the threshold, manufacturer I believes that the high cost will weaken the advantage of the rival and no further battery quality improvement is needed. As shown in Figure 4a, the “win-win” zone (i.e., $\mathsf{\Delta }{H}_i>0,i=\{I,E\}$) emerges in low blockchain cost area. In the large-scale market, manufacturer I has absolutely high quality under Scenario B, and manufacturer E gradually improves battery quality as blockchain cost increases. The “win-win” zone appears in high blockchain cost area, as shown in Figure 4b. Therefore, regardless of market scale, manufacturer E always has a higher quality in Scenario B within the “win-win” zone.

Next, we analyze whether there is a “win-win” zone in the manufacturers’ profits and how it is influenced by the relevant parameters. Similarly, two market scale parameters are considered, Figure 5a for a small-scale, and Figure 5b for a large-scale. We have Observation 4.

Observation 4.

There exists a “win-win” zone for manufacturers’ profits in model E2. In the small-scale market, lower blockchain cost result in higher revenue for both parties in Scenario B (see Figure 5a); In the large-scale market, blockchain adoption is the optimal decision for both manufacturers, even if the adoption cost is increasing (see Figure 5b).

Observation 4 illustrates the impact of battery quality on manufacturers’ decisions. Consistent with model E1, the advantage of blockchain for both manufacturers diminishes as blockchain cost rises. It is more pronounced for manufacturer E. The existence of a “win-win” zone requires a low blockchain cost to be in a small-scale market. In the large-scale market, the decision to adopt blockchain takes a significant advantage.

6. Conclusions

Recycling and reusing retired power batteries is critical to reducing environmental impact and improving resource utilization. However, asymmetric information, counterfeit battery risks, and technical barriers in assessing battery status pose challenges for an efficient supply chain. Blockchain enables manufacturers to directly participate in information sharing. In practice, EV manufacturers must fulfill Extended Producer Responsibility (EPR) and provide battery information. However, manufacturers hesitate due to high costs. Therefore, we examine whether blockchain adoption is rewarding for manufacturers.

Unlike existing studies that focus on blockchain implementation technology or feasibility, this work constructs a game model for blockchain adoption decisions by battery manufacturers. We consider two competing EV manufacturers dominating new battery sales and retired battery recycling. With blockchain, manufacturers benefit from an expanded market and reduced reuse costs, although adoption is costly. We distinguish scenarios with and without manufacturer blockchain adoption.

By solving and comparing equilibrium solutions, we conclude: (1) Blockchain boosts retired battery recovery even when adoption costs exceed reuse savings and collection prices are low. (2) Manufacturers adopt blockchain given high consumer return willingness in small markets with low costs, or large markets with high costs. (3) If one manufacturer implements blockchain, reducing costs or expanding the market creates a “win-win” for competitors. (4) With battery quality, results also support a “win-win” in small, low-cost markets or large, high-cost markets. (5) Two drivers for blockchain adoption are reverse profit compensation and improving battery quality.

Our work provides new managerial insights for manufacturers when they decide whether to adopt blockchain for tracking batteries. These insights are summarized as follows.

(1)

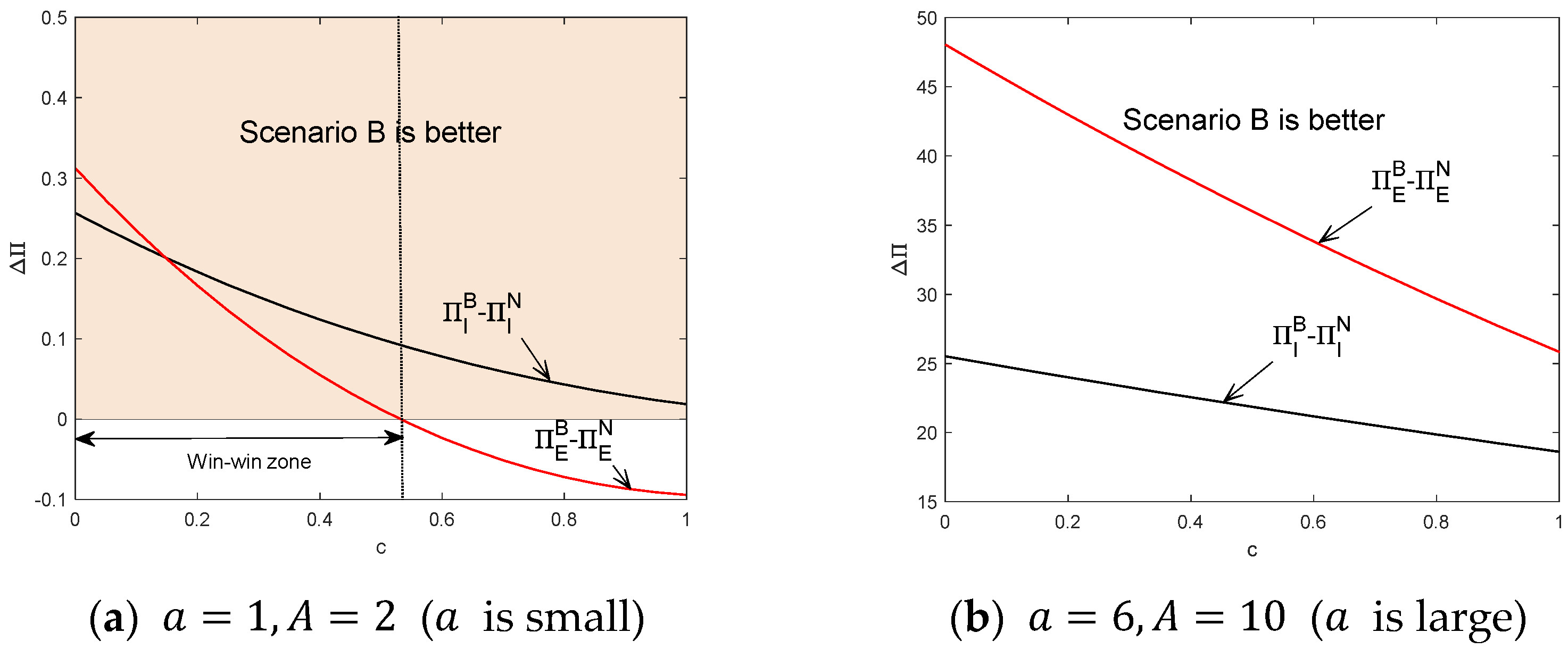
When the market scale is large, blockchain-based tracking can enhance the recycling amount of retired batteries as well as reverse supply chain profits to fend off competition risks. Therefore, an appropriately expanded market is more conducive to the recycling of retired batteries.

(2)

There is a “win-win” zone of battery quality in the small-scale market with low cost or the large-scale market with high cost. Blockchain-based tracking to improve battery quality could be achieved by reducing blockchain costs or expanding the market.

We discuss two future research directions. First, manufacturers may face competition from retailers and other informal recyclers to recycle retired batteries. In this case, whether blockchain adoption manufacturers enjoy a competitive advantage is debatable. Second, competing manufacturers may source power batteries from the common supplier. In this case, it becomes a one-to-two supply chain, optimal pricing, and recycling decisions will both change.