Abstract
The long-standing, unrestrained utilization of energy resources by China’s manufacturing sector has created irreversible obstacles to regional sustainable development. Consequently, the Chinese government has implemented a water resource tax policy in certain regions, with the aim of compelling manufacturing enterprises to adopt green and energy-saving innovations. This study used panel data from Chinese manufacturing companies listed on the A-share market from 2009 to 2020 and employed a double machine learning model to explore whether the water resource fee-to-tax reform can compel enterprises to enhance their tripartite green energy-saving innovation drive. These innovations consist of vision-driven and mission-driven green energy-saving technological innovations and green management energy-saving innovations. Following a quasi-natural experiment, our findings revealed the following: (1) The water resource fee-to-tax policy promoted the internal coupling coordination of the triple-driven system. (2) The policy compelled progress in mission-driven green energy-saving technological innovations and green energy-saving management innovations but hindered vision-driven green energy-saving technological innovations. (3) Within the internal systems of manufacturing enterprises, green energy-saving management innovations play a positive mediating role between the water resource fee-to-tax policy and the mission-driven green energy-saving technology innovation subsystem, but they lack a similar positive mediating mechanism for the vision-driven green energy-saving technology innovation subsystem. (4) The counterfactual framework verified that the mechanistic pathway “water resource fee-to-tax → green energy-saving management innovation → mission-driven/vision-driven green energy-saving technological innovation” could be further extended to other manufacturing enterprises not currently under policy compulsion. (5) In the interaction system between manufacturing enterprises and external markets, the development of marketization and financial technology positively regulated the promoting effect of the water resource fee-to-tax policy on mission-driven green energy-saving technological innovations and green energy-saving management innovations, but it did not have a similar effect on vision-driven green energy-saving technological innovations.
1. Introduction
In the face of severe environmental challenges and resource constraints, forging a sustainable development path for the new era has become a global responsibility. In September 2020, Chinese President Xi Jinping announced China’s dual carbon goals (carbon peak and carbon neutrality) at the United Nations General Assembly. In October 2021, the Chinese government issued the “Opinions of the CPC Central Committee and the State Council on Fully, Accurately, and Comprehensively Implementing the New Development Philosophy to Achieve Peak Carbon Dioxide Emissions and Carbon Neutrality” and the “Action Plan for Carbon Peak Before 2030”, two essential documents providing a top-level design and policy guidance for achieving the dual carbon goals. The urgency of worsening environmental and climate conditions, combined with the stringent constraints of the dual carbon goals, highlights the need to promote green development. Therefore, for China’s economy is to achieve high-quality growth, it must consider both ecological efficiency and the coordinated and unified development of green sustainability.
From an international perspective, India, Russia, and the United Kingdom serve as microcosms of manufacturing transformation, collectively highlighting the universal challenges faced in resource utilization and environmental protection across the global manufacturing sector, while also showcasing unique strategies and outcomes specific to each nation.
India’s case illuminates the significant contribution of the informal manufacturing sector to the country’s carbon footprint, particularly in terms of CO2 emissions within key supply chains. This not only underscores the urgency for emissions reduction in the informal sector but also indirectly emphasizes the importance of water resource management, given the intimate connection between carbon emissions and water usage in manufacturing, especially in water-intensive industries such as textiles and leather [1].
Russia’s efforts to transform its heavy industry, though hindered by a resource-intensive development model, draw attention to the prudent use and conservation of water resources. With vast water resources but also facing pollution issues, the country’s focus turns to reducing unsustainable water exploitation through industrial upgrading and technological innovation, presenting an urgent environmental agenda.
In contrast, the United Kingdom, having recognized early on the necessity for industrial restructuring, demonstrates advanced practices in environmental protection and resource efficiency within its manufacturing sector. Stringent environmental regulations and the promotion of a circular economy have effectively facilitated the widespread adoption of green technologies, elevating the industry’s environmental standards and asserting the UK’s leadership in global climate action. Nonetheless, a detailed analysis of the UK’s total production carbon footprint revealed that in 2019, 54% of greenhouse gas emissions linked to national production activities originated from four core sectors: fossil fuel extraction and processing, manufacturing and electricity generation, animal-based food production, and aviation [2]. This finding underscores how, even in countries with relatively commendable environmental records, emissions from specific sectors dominate, posing challenges to comprehensive climate mitigation efforts.
Drawing from these three experiences, propelling manufacturing towards a green, low-carbon, and circular economy necessitates not only a focus on carbon emissions reduction but also a concurrent reinforcement of water conservation and recycling, ensuring manufacturing activities coexist harmoniously with natural ecosystems and fostering environmentally friendly development in the truest sense.
Studies on the critical factors driving corporate green energy-saving innovation have also been actively explored by scholars in the past, including digital transformation [3], green financial instruments [4], green subsidies [5], corporate size [6], financing constraints [7], and executives’ environmental awareness [8], with most scholars focusing on the impact of policy and regulatory systems on green energy-saving innovation based on China’s current situation and political system [9,10]. As the “visible hand” in economic development, government policies profoundly impact corporate operations and strategic decision making [11]. In promoting green energy-saving innovation, a series of measures taken by the government—including but not limited to environmental tax reforms, green subsidy policies, and energy-saving and emissions reduction regulations—directly or indirectly stimulate corporate green energy-saving innovation activities [12].
In the internal development of manufacturing enterprises, green energy-saving innovations can be subdivided into two main areas: green energy-saving management innovations and green energy-saving technological innovations [13]. Green energy-saving management innovation focuses on the strategic renewal of the internal management system and organizational structure to pursue sustainable development [14], while energy-saving technological innovation emphasizes breakthroughs and progress at the technological level [15]. Corporate green energy-saving technological innovations can be broadly divided into mission-driven and vision-driven innovations [16]. The water resource fee-to-tax policy is a significant initiative by the Chinese government to address the issues of water resource overuse and environmental pollution. The policy aims to transition from the previous water resource fee system to a water resource tax, thereby increasing the cost of water usage to encourage high-water-consuming enterprises to optimize their water use and implement water-saving measures.
The analysis above indicates that the water resources’ tax policy, green energy-saving management innovations, and green energy-saving technological innovations are closely related, yet the existing research still has room for further improvement. On the one hand, the current literature on the policy effects of transitioning from water resource fees to taxes focuses on the macro-level, and it lacks an in-depth analysis of how this policy impacts micro-level corporate behaviors. On the other hand, scholars have not sufficiently detailed their exploration of corporate green energy-saving innovation behaviors, and more meticulous and systematic research is needed on how policies affect the internal mechanisms of green energy-saving innovations.
Therefore, based on a double machine learning model, this research focuses on discussing the specific impact mechanisms of the water resource fee-to-tax policy on corporate green energy-saving innovations. The main marginal contributions of this work are as follows: First, this study assessed, from a micro-perspective, whether the water resource fee-to-tax policy promoted the “triple drive” of corporate green energy-saving innovation systems. Second, it analyzed and empirically tested the mediating effect of green energy-saving management innovations on the impact of the water resource fee-to-tax policy on corporate green energy-saving technological innovation behavior. Third, it further analyzed the influence of two external mechanisms, financial technology and the marketization process, on the policy effects of the water resource fee-to-tax reform, including a heterogeneity analysis at the regional and corporate levels. Through an empirical analysis, this research not only provides robust support for the scientific nature of the water resource fee-to-tax policy but also offers suggestions for the government’s subsequent in-depth implementation and the green transformation faced by manufacturing enterprises.
2. Theoretical Foundation
2.1. Water Resource Fee-to-Tax Policy
The “water-defined development” ecological strategy aims to strengthen the rigid constraints on water resources, promote the intensive and economical use of water re-sources, and ensure that urban development, land use, population distribution, and industrial layout match the carrying capacity of water resources. In response to this strategic objective, the Chinese government initiated a pilot program in 2016 to transition from a water resource fee to a tax system. As a vital means for the government to regulate the supply and demand contradiction of water resources, and address the negative externalities of water resource development, this policy centers on the principle of “clearing fees to establish taxes”. It aims to ensure a seamless transition from a “water resource fee” to a “water resource tax”. It has already been implemented in nine provinces and municipalities, including Beijing, Tianjin, Shanxi, Inner Mongolia, Henan, Shandong, Sichuan, Shaanxi, and Ningxia.
The fee-to-tax reform for water resources is not only a crucial means of environmental protection but also a key driver for promoting corporate green energy-saving innovation [17]. Based on the theory of resource externalities, the “fee-to-tax” reform raises the cost of water use and production for manufacturing enterprises, forcing companies to proactively engage in green energy-saving innovations and change their production processes [18]. The double dividend hypothesis suggests that a water resource tax can motivate manufacturing enterprises [19], especially those with a high-water consumption, through tax leverage to pursue the blue and green dividends brought by green energy-saving innovations, thus promoting the green transformation of manufacturing enterprises while considering water-saving and efficiency enhancements [20]. Furthermore, the transition from water resource fees to taxes can promote corporate green energy-saving innovations by increasing the cost of environmental non-compliance and encouraging research and development investments.
In the traditionally water-intensive industries such as mining and metallurgy, where technology limitations and management practices have historically led to inefficient wastewater discharge and tailings handling—often accompanied by environmental pollution risks—the implementation of water resource fee-to-tax reforms has imposed new legal constraints and introduced economic incentives. These changes have compelled enterprises to recalibrate their strategies, steering them towards a path of green innovations. Throughout this transformative journey, companies have not only enhanced the efficiency of water utilization in production processes but have also delved into the realms of wastewater recycling and tailings treatment innovations, striving for maximum water conservation and minimal environmental footprint.
2.2. Mission-Driven Energy-Saving Technological Innovations
Mission-driven energy-saving technological innovations typically originate from a direct response to current environmental issues and focus more on improving existing operations and processes to reduce negative environmental impacts and meet regulations and standards. These types of innovations often have a shorter time horizon and aim to achieve specific and immediate environmental benefits. For instance, high-water-consuming industries such as mining and metallurgy are focusing on future market development trends and global economic transformations by investing in cutting-edge green technology research. For example, these companies are developing intelligent water resource management systems based on the Internet of Things (IoT) and big data analytics to monitor, control, and optimize the allocation and consumption of water resources in real-time. Additionally, vacuum water-saving technology has become a strategic investment area, aiming to reduce water consumption while achieving efficient and environmentally friendly production. Furthermore, some pioneering companies are pursuing the goal of “zero liquid discharge”, striving to achieve the highest standards of wastewater purification and completely eliminate environmental pollution, setting a green benchmark within the industry.
2.3. Vision-Driven Energy-Saving Technological Innovations
In contrast, vision-driven innovations take a more forward-looking approach, based on long-term sustainable development goals and the company’s predictions about future markets. They seek significant technological breakthroughs and are dedicated to developing new business models and market opportunities to maintain a leading position in the future green economy. For example, mining and metallurgy companies are adopting advanced water-saving technologies and equipment in response to current environmental challenges and regulatory requirements. For instance, they have implemented high-pressure atomization cooling systems to replace traditional water-cooling systems, significantly reducing the demand for fresh water. These companies have also built advanced wastewater treatment and reuse facilities, utilizing technologies such as reverse osmosis, membrane filtration, and biological treatment to ensure that wastewater is purified and returned to the production cycle. Additionally, the promotion of dry stacking techniques for tailings and the development of tailings resource recovery technologies have enabled these industries to reduce water consumption while achieving resource recycling. These measures not only help companies comply with environmental regulations but also enhance production efficiency and resource utilization.
2.4. Green Energy-Saving Management Innovations
The three modes of corporate green energy-saving innovations have diverse emphases, but they complement each other and, together, constitute a triple drive system towards achieving corporate green sustainability. In this triadic green energy-saving innovation system, green energy-saving management innovations occupy a unique position. They not only provide a solid management foundation and organizational support for directly promoting the green transformation of manufacturing enterprises but also indirectly contribute to sustainable development by inspiring technological-level green changes. Although they do not directly involve breakthroughs or transformations in industrial technology, they can profoundly impact internal production and R&D activities through crucial links, such as by optimizing planning, reorganizing production organization, adjusting factor allocation, improving process management, and reasonably deploying talents.
On the management front of mining and metallurgy firms, a robust environmental management system has been put in place, clarifying environmental responsibilities and integrating water resource management performance into the appraisal system. Innovative practices are incentivized through reward mechanisms. Collaboration with research institutions and the cultivation of ecological partnerships facilitate the continuous introduction and dissemination of cutting-edge green technologies. By enhancing transparency, proactively disclosing progress in water management, and assuming social responsibilities, these enterprises are bolstering their societal image, shaping a model of practice that spans from technological innovations to management overhaul, and comprehensively driving green transitions. Such initiatives align with policy directives while fostering long-term sustainable development for the companies, thereby making substantial contributions to the construction of an eco-friendly society.
3. Research Hypotheses and Mechanism Analysis
3.1. The Corporate Green Energy-Saving Innovation “Triple Drive” System under the Water Resource Fee-to-Tax Policy
The water resource fee-to-tax policy aims to promote sustainable ecological development. It follows the essential “tax-for-fee shift” principle and uses a volume-based taxation method. The policy imposes high tax standards on areas with the severe over-extraction of groundwater and water resources, over-planned water extraction, or special industry water use. Under the pressure of high taxes, companies are inevitably driven towards green energy-saving innovations to reduce costs [21].
From a corporate management perspective, the transition from water resource fees to taxes creates an inclination towards green production management within manufacturing enterprises.
As mentioned, the water resource fee-to-tax policy subjects high-water-consumption manufacturing enterprises to significant tax pressures. Consequently, companies will be compelled to innovate in the allocation ratio and management forms of human resources, intangible assets, raw materials, and other factors to reduce costs [22]. By establishing a green management energy-saving system, manufacturing enterprises can achieve the scale and integration of green production, effectively reducing the over-exploitation of water resources and improving their water use efficiency [23]. Moreover, the water resource fee-to-tax policy will also impact corporate culture. In China, where the government exerts a significant influence on the market, government policies significantly impact corporate actions [24]. The introduction of the water resource fee-to-tax policy underscores the importance of environmental and low-carbon awareness [25]. Consequently, driven by the policy, manufacturing enterprises will inevitably integrate this awareness into their corporate culture, forming a new collective value orientation. At the same time, management will widely promote a green corporate culture, encouraging full participation in green actions to advance green energy-saving management innovations from a cultural perspective [26]. Thus, it will establish a management model for green production and operations.
From the perspective of a corporate-level analysis, green energy-saving innovations in corporations encompass both green energy-saving management and technological innovations. The latter can be categorized as mission-driven or vision-driven innovations [27].
With respect to mission-driven green energy-saving technological innovations, manufacturing enterprises will inevitably pursue green energy-saving technological innovations under the pressure of taxes to ensure their current development [28]. The water resource fee-to-tax policy not only taxes and regulates manufacturing enterprises’ water use that exceeds rigid constraints but also strengthens the tax collection and management of wastewater treatment. As a market-based regulatory tool, this policy will produce external shocks, leading to a “survival of the fittest” effect in the short term [29]. Therefore, to avoid penalties from local governments and to reduce operating costs for survival in the current environment, manufacturing enterprises will adopt advanced environmental protection equipment, thereby quickly reducing wastewater discharge and achieving the efficient use of water resources [30].
From the vision-driven green energy-saving technological innovations perspective, manufacturing enterprises will also innovate in green technology while being guided by policy to realize mid-to-long-term development. On the one hand, local governments in pilot areas have been tasked by the central government with the responsibility of using governmental power to intervene and guide key manufacturing industries towards green, water-saving transformations [31]. In China, the government has a significant impact on determining the success of a company’s development, and manufacturing enterprises aiming for long-term development must consider their social responsibility and corporate image [32]. Therefore, companies must align with policy directions by reducing inefficient water waste, taking on environmental and social responsibilities, and establishing a responsible corporate image. On the other hand, considering external environmental pressures (such as institutional and stakeholder pressures) [33] and the objective requirements of reducing production costs caused by tax burdens, their costs remain high if companies rely solely on importing equipment to improve water resource efficiency. Therefore, manufacturing enterprises must independently research and develop green technologies to achieve sustainable development.
However, the independent innovations of green technologies face challenges such as significant capital investment, long project payback periods, high investment risks, and the inability to obtain a short-term return [34,35,36,37]. Moreover, implementing the water resource fee-to-tax policy has already increased the tax burden costs in the short term, creating greater financial pressure on companies. This has led to a lack of motivation for manufacturing enterprises to invest in potential green technology research and development, as they view its value as highly uncertain. During the implementation of the water resource fee-to-tax policy, most local governments in the pilot areas have yet to establish a clear timetable for industrial water-saving transformation and transition [38]. Local government decisions are still influenced by a “race-to-the-bottom competition” triggered by the “promotion tournament” [39], believing that supporting manufacturing enterprises in short-term, limited-return, vision-driven green energy-saving technological innovations would consume vast social resources and government finances. As a result, they will no longer compel manufacturing enterprises to invest additional resources into more visionary industrial technological transformations, leaving both manufacturing enterprises and governments without the motivation to devote effort and action towards long-term industrial water-saving and greening transformations. Based on the above analysis, the following hypothesis was proposed:
Hypothesis 1 (H1).
The water resource fee-to-tax policy can promote mission-driven green energy-saving technological innovations and management innovations, but its impact on vision-driven green energy-saving technological innovations is still being determined.
3.2. The Coupling and Coordination of the Corporate Tripartite Green Energy-Saving Innovation under the Water Resource Fee-to-Tax Policy
With the formal implementation of the water resource fee-to-tax policy, manufacturing enterprises are faced with a direct increase in their costs and a severe test of their existing business models and industrial structures. Additionally, this policy also conveys a clear message that protecting water resources and the ecological environment is an inescapable social responsibility in corporate development. Therefore, this policy compels manufacturing enterprises to undertake self-renewal, significantly stimulating green energy-saving management innovations [40].
Green energy-saving management innovations will inevitably drive the development of green energy-saving technological innovations within manufacturing enterprises. First, green energy-saving management innovations can reduce the cost of energy-saving technological innovations for manufacturing enterprises [41]. Strong support from management, a well-developed green management energy-saving system, and the scale and integration of green production can all efficiently help manufacturing enterprises in green technology research and development in the short term, thereby reducing tax pressures and achieving current development [42]. Secondly, green energy-saving management innovation implies that the manufacturing enterprise management has initiated reforms towards green development, which will encourage deep collaboration and exchange with innovation entities such as universities, reducing the risk and pressure of R&D and making these innovation entities more willing to engage in vision-driven green energy-saving technological innovations [43]. Finally, green energy-saving management innovations embody a corporate culture of environmentally friendly and high-quality development that focuses on the medium- to long-term development of the companies and emphasizes the importance of R&D and the application of green technology among employees [44]. Therefore, green energy-saving management innovations create a conducive environment for green energy-saving technological innovations, thus accelerating the process of green energy-saving technological innovations within manufacturing enterprises.
At the same time, mission-driven and vision-driven green energy-saving technological innovations complement each other. On the one hand, mission-driven green energy-saving technological innovations can provide technical accumulation for vision-driven green energy-saving technological innovations; on the other hand, although vision-driven green energy-saving technological innovations may not demonstrate technological effects in the short term, it can provide technical direction and prospects for mission-driven green energy-saving technological innovations. From the analysis above, the following hypothesis was formulated:
Hypothesis 2 (H2).
The water resource fee-to-tax policy can promote the synergistic development of corporate green energy-saving management innovations, mission-driven green energy-saving technological innovations, and vision-driven green energy-saving technological innovations.
The synergistic dynamics of the triadic green energy-saving innovation are portrayed in Figure 1. This diagram serves as a conceptual map, offering a clear view of how these components foster each other’s growth, shaping a “triple-drive system for corporate green energy-saving innovations”. The gray wireframes represent counterclockwise relationships, while the black wireframes represent clockwise relationships.
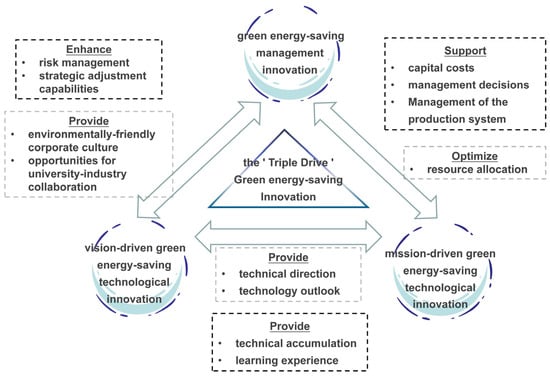
Figure 1.
Synergistic triad of corporate green energy-saving innovations.
3.3. The Mediating Effect of Corporate Green Energy-Saving Management Innovation
As discussed earlier, following the water resource fee-to-tax policy implementation, companies inevitably need to consider engaging in green energy-saving management innovations to respond to policy requirements, adapt to conceptual trends, and balance operational goals with economic benefits. This involves shifting from traditional modes of production that are high in energy consumption, water use, and pollution to management and organizational adjustments that are more environmentally friendly and sustainable. Furthermore, through adjustments or reorganizations in management models and organizational forms, green energy-saving management innovations can effectively reduce the R&D costs for companies, mitigate the risks associated with autonomous upgrading, and deeply instill a culture of sustainable development. Then, it impacts critical internal aspects such as planning optimization, production organization, the input of elements, process management, and talent deployment, accelerating the pace of mission-driven and vision-driven green energy-saving technological innovations in manufacturing enterprises [30]. Based on the analysis above, the following hypothesis was proposed:
Hypothesis 3 (H3).
Green energy-saving management innovations play a positive mediating role between the water resource fee-to-tax policy and both mission-driven and vision-driven green energy-saving technological innovations.
3.4. Counterfactual Framework Analysis of the Mediating Effect of Corporate Green Energy-Saving Management Innovations
The causal inference under a counterfactual analysis framework currently represents a leading direction in the field of empirical economics. Improving the water resource utilization efficiency and achieving economic green development are essential not only in pilot areas where the water resource fee-to-tax policy has been implemented, but also in other regions of China. Therefore, this paper focuses on whether the policy could be extended to non-pilot areas and whether it would similarly promote green energy-saving technological innovations in these areas.
In recent years, China has continuously emphasized sustainable development, and achieving green development has become a nationwide consensus. Therefore, by considering factors such as the national direction and market competition, manufacturing enterprises in non-pilot areas are not only basing their actions on the current situation but are also considering the future, actively increasing their investment in mission-driven and vision-driven green energy-saving technological innovations in their strategic planning [45]. This approach is not only aimed at enhancing the competitiveness of manufacturing enterprises and adapting to potential future policy changes but is also a commitment to social and environmental responsibilities. Thus, manufacturing enterprises would also respond to water resource conservation and sustainable use demands by developing water-saving technologies, optimizing production processes, and improving water recycling rates [46].
Based on such analyses, we can reasonably speculate that, once the water resource fee-to-tax policy is implemented in a broader area, it will stimulate more manufacturing enterprises to engage in green energy-saving management innovations and promote both mission-driven and vision-driven green energy-saving technological innovations. From the above analysis, the following hypothesis was proposed:
Hypothesis 4 (H4).
In non-pilot areas, the water resource fee-to-tax policy will promote mission-driven and vision-driven green energy-saving technological innovations by encouraging green energy-saving management innovations.
3.5. The Moderating Effect of Financial Technology
Financial technology, an organic integration of finance and technology, leverages cutting-edge technologies such as big data and blockchains to innovate traditional financial markets and services, making financial services more efficient, secure, and convenient. With the deepening development of financial technology, a series of emerging services and products have continuously evolved. These products and services, integrated with technologies such as big data, can help manufacturing enterprises improve their financing efficiency, broaden their financing channels, and optimize risk assessment tools, thereby facilitating their development and transformation [47,48].
The transition from water resource fees to taxes creates significant tax pressure on high-water-consumption manufacturing enterprises. Under this pressure, manufacturing enterprises will inevitably seek changes through green energy-saving management innovations and mission-driven green energy-saving technological innovations [49]. However, the main challenge they face in this transformation is financial. Financial technology can provide security for both manufacturing enterprises and bank loans [50], enabling manufacturing enterprises to acquire more costs for innovations in the short-term [51].
For vision-driven green energy-saving technological innovations, although financial technology can make it easier for manufacturing enterprises to obtain financing for innovations and support long-term R&D investments and innovation cooperation, this type of innovation often involves a higher uncertainty and longer return cycles. It also relies more on the support of the entire ecosystem, including guidance from government policies, knowledge contributions from research institutions, and market acceptance. As a result, the moderating effect of financial technology on the impact of the water resource fee-to-tax policy on vision-driven green energy-saving technological innovations is relatively limited. Based on the analysis above, the following hypothesis was proposed:
Hypothesis 5 (H5).
Financial technology positively moderates the effect of the water resource fee-to-tax policy in promoting green energy-saving management innovations and mission-driven green energy-saving technological innovations but does not significantly moderate the pathway between the policy and vision-driven green energy-saving technological innovations.
3.6. The Moderating Effect of the Marketization Process
The marketization process represents a transition in the market system, involving dynamic changes across economic, social, legal, and political landscapes [52].
As the marketization process progresses, the price mechanism usually conveys the signals of resource scarcity and environmental cost increases more accurately following the water resource fee-to-tax reform. This clearer price signaling will undoubtedly prompt both manufacturing enterprises and consumers to treat water resources more sensitively and cautiously. Meanwhile, under the influence of marketization, the external environment for manufacturing enterprises can be significantly optimized, especially regarding the completeness of laws and systems and the fairness of market competition [53,54]. This optimization ensures the smooth and effective implementation of the water resource fee-to-tax policy. Moreover, it allows manufacturing enterprises to enjoy stable policy support and a solid environmental backing, thereby boldly engaging in green energy-saving innovations and practices.
In the process of marketization, the capital and resources tend to flow towards areas that can quickly generate returns, resulting in a relative lack of necessary support for long-term, high-risk, vision-driven innovations. Moreover, the coherence and predictability of policies are crucial for incentivizing long-term investments. If the policy signals are unclear or lack sustained incentive measures, this may limit manufacturing enterprises’ investments and innovations in vision-driven green technology [54]. While the water resource fee-to-tax policy promotes environmentally friendly behaviors among manufacturing enterprises through economic means, it has not yet established a more explicit and stable policy support and incentive mechanism. Hence, the marketization process is unlikely to strengthen the relationship between the water resource fee-to-tax policy and vision-driven green energy-saving technological innovations. Based on the analysis above, the following hypothesis was proposed:
Hypothesis 6 (H6).
The development of the marketization process has a positive moderating effect on the promotion of green energy-saving management innovations and mission-driven green energy-saving technological innovations through the water resource fee-to-tax policy, but it cannot significantly moderate the pathway between the policy and vision-driven green energy-saving technological innovations.
Based on the above theoretical analysis, the theoretical framework of this article was constructed, as shown in Figure 2. It served to guide the empirical analysis and assisted in interpreting rigid water resource constraints in the corporate green energy-saving innovation research system.
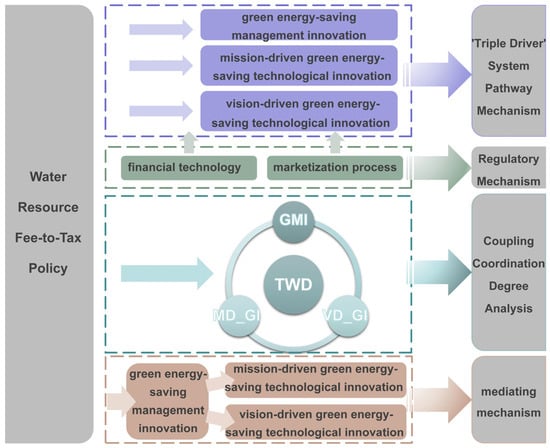
Figure 2.
Rigid water resource constraints—corporate green energy-saving innovations research system.
4. Experimental Process
To verify the series of mechanism hypotheses proposed earlier, this study has designed a comprehensive experimental process, including baseline regression analysis, mediation effect testing, and counterfactual framework analysis. This study selects data from A-share-listed companies on the Shanghai and Shenzhen Stock Exchanges and from various prefecture-level cities in China, covering the period from 2009 to 2022.
To test Hypotheses 1 and 2, this study first conducts baseline regression analysis using a double machine learning model, which provides unbiased estimates of policy effects by controlling for high-dimensional variables. The purpose of the baseline regression is to evaluate the direct impact of the water resource fee-to-tax policy on mission-driven green energy-saving technological innovations, vision-driven green energy-saving technological innovations, and green energy-saving management innovations. For Hypothesis 3, this study employs a mediation effect model to test whether green energy-saving management innovations mediate the impact of the water resource fee-to-tax policy on mission-driven and vision-driven green energy-saving technological innovations. The specific steps include estimating the impact of the policy on green energy-saving management innovations, estimating the impact of green energy-saving management innovations on mission-driven and vision-driven green energy-saving technological innovations, and testing the indirect impact of the policy on these innovations through green energy-saving management innovations.
To further validate Hypothesis 4, a counterfactual framework analysis is adopted to explore the potential effects of the water resource fee-to-tax policy in non-pilot areas. The specific steps include constructing a counterfactual framework assuming the policy was not implemented in the pilot areas, estimating the green energy-saving innovation performance of enterprises in non-pilot areas post-policy implementation, and comparing the results between actual pilot areas and non-pilot areas under the counterfactual framework. To test Hypotheses 5 and 6, models are constructed to examine the moderating effects of financial technology and marketization on the policy outcomes. The specific steps include constructing regression models with interaction terms between the policy and financial technology to test their moderating effects on green energy-saving management innovations and mission-driven green energy-saving technological innovations, and constructing regression models with interaction terms between the policy and marketization to test their moderating effects on these innovations.
5. Research Design
5.1. Quasi-Natural Experimental Design and Model Construction
This paper aims to explore the impact mechanism of the water resource fee-to-tax policy pilot on mission-driven green energy-saving technological innovations, vision-driven green energy-saving technological innovations, green energy-saving management innovations, and the synergistic development of these three types of green energy-saving innovations in manufacturing enterprises. It employs a double machine learning model for causal inference. The double machine learning model excels in handling high-dimensional data for prediction more adeptly than traditional statistical methods (like linear regression and OLS), but it is not employed directly for prediction; rather, its significance lies in fitting and generalizing over high-dimensional control variables to achieve unbiased estimation of the coefficients associated with the core variables. And it does not impose strict assumptions on the data-generating process. Instead, it learns the functional form of variables from the existing data, thereby avoiding model specification bias.
Since its formal introduction by Chernozhukov et al. in 2018 [55], research on the double machine learning (DML) method has primarily bifurcated into two directions. One stream of research focuses on leveraging DML to evaluate economic causal relationships. For instance, Yang et al. (2020) [56] employed Gradient Boosting to assess the effects of audit firms, demonstrating the superiority of their approach over propensity score matching. Zhang et al. (2022) [57] analyzed the multifaceted impacts of nocturnal subway services on London’s economy, while Farbmacher et al. (2022) [58] combined causal mediation analysis to explore the role of health insurance in youth health. Conversely, another line of inquiry prioritizes methodological innovations, such as Chiang et al.’s (2022) [59] multidirectional cross-fitting technique, which bolsters the robustness of high-dimensional data analysis, and Bodory et al.’s (2022) [60] integration of dynamic analysis, broadening the model’s applicability in dynamic contexts.
Compared to conventional causal inference models, DML offers unique advantages in variable selection and model estimation, making it particularly suitable for the research question at hand. On the one hand, corporate green management energy saving and technological innovation are composite indicators influenced by myriad factors within the socioeconomic context. To ensure an accurate estimation of policy effects, it is essential to comprehensively account for the potential confounding effects of other factors. Traditional regression models, however, may grapple with the “curse of dimensionality” and multicollinearity when dealing with high-dimensional control variables. DML, utilizing various machine learning algorithms and regularization techniques, automatically selects an effective subset of control variables from a preselected high-dimensional set, enhancing prediction accuracy. This process alleviates the “curse of dimensionality” associated with redundant controls and mitigates bias from restricting to a limited set of primary controls. Furthermore, nonlinear relationships among variables are prevalent, and linear regression models can introduce specification biases with less robust estimates. DML harnesses the strengths of machine learning algorithms in handling nonlinear data, effectively averting model misspecification issues, as highlighted by Yang et al. (2020) [56]. Additionally, through the use of instrumental variable functions, two-step prediction error regressions, and sample splitting fitting strategies, DML addresses the “regularization bias” inherent in machine learning estimations, ensuring an unbiased estimation of treatment effects even in small samples.
Based on the foundational principles of constructing and utilizing double machine learning models, this paper constructs Model (1) as follows:
Model (1):
where is the core explanatory variable of interest, representing the treatment variable of the water resource fee-to-tax policy pilot, making the estimation parameter of interest and the basis for inference in this study. denotes a series of high-dimensional control variables, which relate to the dependent variable of the corporate green energy-saving innovation “triple drive” system () and in a high-dimensional complex nonlinear form. To investigate the differential impacts of the water resource fee-to-tax policy on the three types of green energy-saving innovation, mission-driven green energy-saving technological innovation (), vision-driven green energy-saving technological innovation (), and green energy-saving management innovation () are set as dependent variables for partial linear regression. denotes the error term with a conditional mean of zero. The direct estimation of Equation (1) yields the estimator for the treatment effect:
where n denotes the sample size.
Based on these estimators, further examination of their estimation bias can be conducted:
In this context, follows a normal distribution with a mean of zero, and , where it is noteworthy that the double machine learning approach employs machine learning and regularization algorithms to estimate the specific functional form , inevitably introducing “regularization bias”. While this prevents excessive variance in the estimator, it also renders it unbiased, characterized by a slow convergence rate of towards , with . Consequently, as n approaches infinity, b also tends towards infinity, impeding the convergence of to .
To expedite the convergence and ensure unbiasedness of the treatment effect estimator under small-sample conditions, an auxiliary regression is constructed as Equation (2) of Model (1).
Here, denotes the regression function of the treatment variable on high-dimensional control variables, also requiring machine learning algorithms for estimating its form , with being the error term with a conditional mean of zero.
The operational procedure involves the following: initially, estimating the auxiliary regression and obtaining residuals ; secondly, applying machine learning algorithms to estimate and modifying the main regression equation to ; finally, using as an instrumental variable for and attaining the unbiased coefficient estimator:
Similarly, Equation (6) can be approximated as
where adheres to a normal distribution with a mean of zero. Given the application of machine learning twice, the overall convergence rate of depends on the rates at which approaches and approaches , specifically . Compared to Equation (4), converges to zero at a faster pace, thereby enabling the attainment of an unbiased estimator for the treatment effect coefficient.
Next, this study aimed to explore the mechanism pathways of “water resource fee-to-tax → green energy-saving management innovations → mission-driven green energy-saving technological innovations” and “water resource fee-to-tax → green management energy-saving innovations → vision-driven green energy-saving technological innovations”. Therefore, a mediating effect model was first constructed based on a double machine learning stepwise regression method (Model (2)):
Model (2):
The first equation was designed to estimate the total effect of the policy treatment variable on the dependent variables to evaluate the overall impact of the water resource fee-to-tax policy on green energy-saving technological innovations. The second and third equations aimed to estimate the direct and indirect effects along the pathways “→→” and “→→”, respectively. These equations measure the extent to which green energy-saving management innovations mediate the relationship between the policy and both mission-driven and vision-driven green energy-saving technological innovations.
To address the potential issues in parameter estimation that may arise with the three-step mediation effect model and to explore the effectiveness and scalability of the water resource fee-to-tax policy within a counterfactual framework, a causal mediation effect model (Model (3)) was constructed in this study. This model further investigated the aforementioned mechanism pathways as follows:
Model (3):
where Y represents the outcome variable ( and ), which is influenced by both the policy treatment variable and the mechanism variable . Since is also affected by , this leads to four equations. and represent the direct effects for the treatment group and control group, respectively. The former indicates the difference between the actual situation of the treatment group () and the scenario where the treatment group individuals are not subjected to the policy intervention but the mechanism variable is still influenced by the policy (). The latter represents the difference between the scenario where the control group individuals are introduced to the policy intervention, but the mechanism variable is not affected by the policy () or the actual situation of the control group (). The magnitude of this result determines whether the water resource fee-to-tax policy can bypass the mechanism variable (green energy-saving management innovations) and directly affect the outcome variables (mission-driven and vision-driven green energy-saving technological innovations) without indirectly going through the mechanism variable. This result also indicates whether this effect will remain when the water resource fee-to-tax policy is extended to non-pilot areas. Similarly, and explain the indirect effects for the treatment and control groups.
Lastly, to verify the external mechanisms, namely whether financial technology () and the level of marketization can regulate the policy effects of the water resource fee-to-tax, this study constructed Models (4) and (5).
Model (4):
Model (5):
and represent the coefficients of the interaction terms between the policy and the moderating variables. The direction of the moderating effect can be determined by comparing the signs of and with the sign of from Model (1). Specifically, if is significantly different from 0, and the signs of and are the same as that of , it indicates that the moderating variables have a positive moderating effect on the original policy impact. Conversely, if the signs of and are opposite to , it suggests a negative moderating effect.
This study, excluding causal mediation effect analysis, employed Stata 17.0 interfacing with Python 3.11 for the processing of panel data, including training, generalization, and parameter estimation. The software offers various base learning algorithms such as LassoIC, LassoCV, Random Forest, Neural Networks, and Gradient Boosting. These algorithms play distinctive roles within the double machine learning (DML) framework, each designed with specific principles and implementation steps:
LassoIC and LassoCV are integral parts of the DML workflow, primarily for variable selection in high-dimensional datasets. Both leverage Lasso’s L1 regularization for sparsity, encouraging insignificant coefficients to approach zero. LassoIC chooses the regularization parameter based on information criteria like AIC or BIC, while LassoCV employs cross-validation for automatic tuning. In DML, LassoIC helps identify influential control variables, and LassoCV ensures robustness with a data-driven approach, though both can be sensitive to criterion choice or computationally demanding.
Random Forest (RF) bolsters prediction accuracy and model stability by combining multiple decision trees. Under DML, RF constructs trees from random data and feature subsets, aggregating their outcomes for predictions. RF excels in nonlinear modeling and interaction detection, crucial for complex causality. Its advantages are strong nonlinearity handling, stability, parallel computing support, and feature importance indication, but it can be less interpretable and computationally intensive with large datasets.
Neural Networks (NNets) within DML span preprocessing to final effect estimation, involving data cleaning, architecture design for capturing nonlinearity, and optimization through backpropagation with regularization. In the DML first stage, NNet predicts control variable impacts, producing purified proxies for unbiased estimation in the next phase. While offering high flexibility and accuracy, NNet requires substantial data and tuning, along with considerable computational resources.
Gradient Boosting Machine (GradBoost) in DML iteratively builds decision trees to minimize prediction errors. In the DML first phase, it estimates control variable effects, improving predictions via iterative learning. It effectively captures linear and nonlinear relationships and interactions, enhancing the analysis of complex data. However, GradBoost may overfit with overly complex models or insufficient data and lacks straightforward interpretability.
Ultimately, Random Forest was chosen as the primary algorithm for the DML framework examining the water resource fee-to-tax policy’s impact on corporate green innovations. This decision rested on its superior nonlinear modeling capabilities, robustness through ensemble trees, suitability for parallel computation, and provision of interpretable feature importance measures, offering a balanced combination of prediction accuracy, computational efficiency, and interpretability for this study’s requirements.
5.2. Core Dependent Variables
5.2.1. Mission-Driven Green Energy-Saving Technological Innovations (MD_GI)
Mission-driven green energy-saving technological innovations refer to green energy-saving technological innovations within a manufacturing enterprise’s existing technological framework that aim to achieve some of the manufacturing enterprise’s current mission needs. They emphasize how to use existing resources, processes, and product designs more efficiently and more environmentally friendly to reduce costs, decrease emissions, and improve the recycling rate of resources. For example, in water-saving processes, a manufacturing enterprise might remodel its existing production lines, introduce water-saving equipment, or optimize the production processes to reduce water resource waste. From the perspective of the nature of energy-saving technological innovations, this type carries a lower risk because it involves modifications and finetuning based on known technologies and market demands, which helps manufacturing enterprises consolidate and expand their market share in green products and manufacturing.
In terms of measurement, this study utilized the Wingo data platform to search for the green patent situation of A-share-listed manufacturing enterprises from 2009 to 2020. A green patent was considered a mission-driven green energy-saving technological innovation for the company if over 80% of the patents referenced by a green patent had the same IPC4 classification number as the existing company’s patent portfolio IPC4 (which includes all the patents applied for by the company and all the patents referenced by the company in the past five years). This approach allows for a focused analysis of how companies innovate within their existing technological frameworks to address immediate challenges, reflecting the mission-driven aspect of their green energy-saving technological innovation efforts.
5.2.2. Vision-Driven Green Energy-Saving Technological Innovations (VD_GI)
Vision-driven green energy-saving technological innovations originate from a manufacturing enterprise’s forward-looking observations of the future market development trends and global economic transformations. It involves bold attempts and cutting-edge research in unknown or emerging green technology fields. These types of innovations may include entirely new environmental concepts, immature technological solutions, or markets that have not been fully developed. For example, in the field of water-saving, manufacturing enterprises might invest in the R&D of intelligent water-saving management systems based on IoT technology and a big data analysis to monitor, control, and optimize the allocation and consumption of water resources in real-time. In recent years, vacuum water-saving technology has also become an essential green energy-saving technological innovation that many manufacturing enterprises have strategically invested in ahead of time. For an individual manufacturing enterprise, vision-driven green energy-saving technological innovations lack a technical foundation and precedents to follow, thus carrying greater risk and uncertainty. However, once thriving, they can fundamentally change the manufacturing enterprise’s production pattern, bringing significant competitive advantages and new avenues for sustainable growth.
In terms of measurements, this study also used the Wingo data platform to search for the green patent situation of A-share-listed manufacturing enterprises from 2009 to 2020. A green patent is considered a vision-driven green energy-saving technological innovation for the company if over 80% of the patents referenced by the green patent have IPC4 classification numbers different from those of the existing company’s patent portfolio IPC4 (which includes all the patents applied for by the company, as well as all the patents referenced by the company in the past five years).
5.2.3. Green Energy-Saving Management Innovations (GMI)
Green energy-saving management innovations in manufacturing enterprises refer to the innovative practice of actively integrating concepts of environmental protection and resource conservation into all manufacturing enterprise management activities in response to sustainable development, thereby improving and optimizing management models. Unlike green energy-saving technological innovations, green energy-saving management innovations are a form of institutional innovation within the manufacturing enterprise, but they have a profound impact on the resource efficiency and environmentally friendly development of the manufacturing enterprise’s production and operational activities.
To measure green energy-saving management innovations, this study referred to the work of Xi and Zhao [61], based on the CSMAR platform’s environmental database. It considers whether A-share-listed companies have passed the ISO14001 [62] certification, whether they have passed the ISO9001 [63] certification, and the companies’ environmental management system, environmental education and training, and particular environmental actions from the corporate environmental regulation and human dispute disclosure information. The sum of these five indicators serves as a proxy indicator for corporate green energy-saving management innovations.
5.2.4. Coupling Coordination Degree of the “Triple-Drive” System of Green Energy-Saving Innovations
To investigate the degree of the synergistic development of mission-driven green energy-saving technological innovations, vision-driven green energy-saving technological innovations, and green energy-saving management innovations—referred to as the “triple drive” system within manufacturing enterprises—this study constructed a coupling coordination degree model for the above three green energy-saving innovation systems, which can measure the level of synergistic development of the three green energy-saving innovation systems within manufacturing enterprises.
In this formulation, i represents the region; t represents time; C_it denotes the coupling degree; T_it is the coordination degree; and TWD_it is the coupling coordination degree among the manufacturing enterprise’s vision-driven green energy-saving technological innovation (VD_GI), mission-driven green technological (MD_GI), and green energy-saving management innovation (GMI). The weights α, β, and γ represent the respective weights of each system, which were obtained through the entropy weight method in this study.
Figure 3 illustrates the changes in four key variables across various provinces in China from 2009 to 2020. These variables include Green Management Innovation (GMI), Mission-Driven Green Innovation (lnMD_GI), Vision-Driven Green Innovation (lnVD_GI), and the Three-Wheel Coupling Coordination Degree (TWD). The radar charts provide a visual representation of the temporal trends and regional differences in these aspects. The charts show the average values of these indicators, highlighting the progressive improvements in green management and technological innovations, as well as the variations in the coupling coordination degree, showcasing the disparities and developments among different provinces over the years.
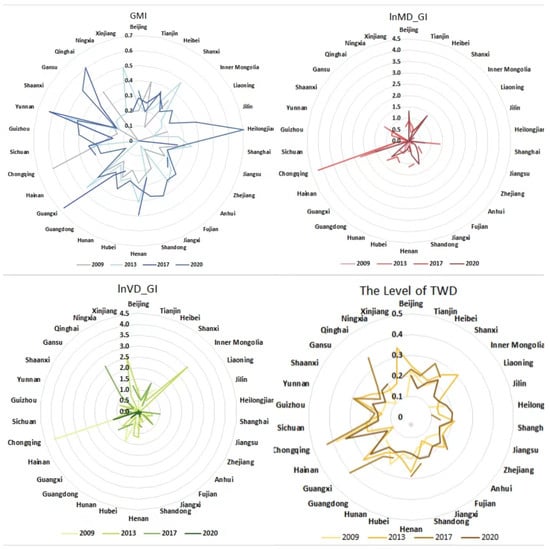
Figure 3.
Trends of variables.
This study analyzed the changes in green energy-saving innovations indicators across Chinese regions from 2009 to 2020, producing the distribution maps shown in Figure 4. It was observed that the eastern coastal regions usually exhibited higher values in these indicators, which is consistent with their economic development, energy-saving technological innovation capabilities, and robust environmental policies. By 2020, the areas with high values expanded spatially, indicating the promotion and deepening of green energy-saving management innovations nationwide. In particular, the decrease in high-value areas and the expansion of medium-value areas for mission-driven green energy-saving technological innovations may suggest that, while some regions have slowed down in terms of short-term energy-saving technological innovations, others may have achieved rapid improvements through policy incentives and investments. The spatial distribution changes in vision-driven green energy-saving technological innovations in 2020 may indicate a nationwide focus on long-term environmental investments and planning. As indicated by the overall coupling and coordination degree of the “three-wheel drive”, the eastern regions dominated the high-value positions in 2009, while the central and western inland regions were low-value. By 2020, the significant expansion of high-value areas reflected the vigorous support and promotion of green energy-saving innovations in the central and western regions by the state. These regions have shown remarkable progress made by the government in promoting green energy-saving innovations across different regions.
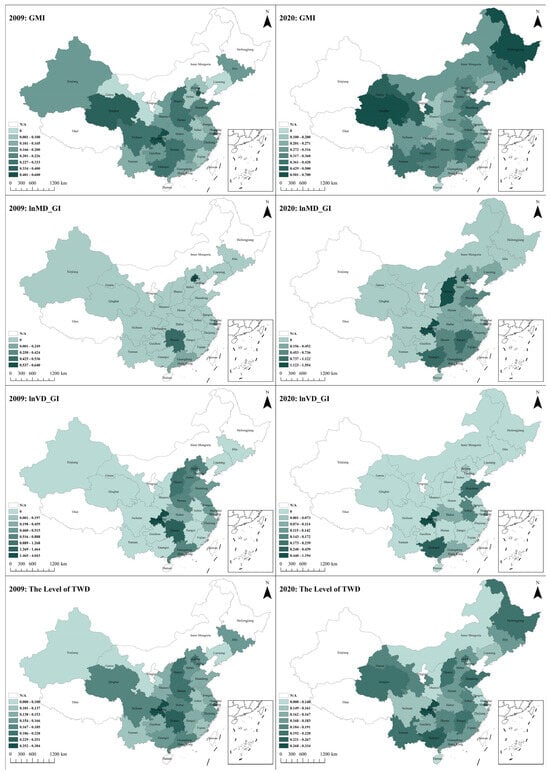
Figure 4.
Distribution maps.
5.3. Explanatory Variable/Experimental Treatment Variable: Water Resource Fee-to-Tax Policy (DID)
The transition from water resource fees to taxes is a significant tax reform measure that has been implemented in some areas of China to strengthen water resource management and conservation and to promote the rational allocation, preservation, and effective protection of water resources. Essentially, the fee-to-tax reform is an integral part of China’s implementation of a rigid water resource constraint system. This system advocates for mandatory management measures for the utilization of water resources, strictly limiting socioeconomic activities within the capacity of water resources to prevent the overexploitation and misuse of water. The fee-to-tax reform is part of the rigid water resource constraint system and uses economic leverage and the Pigovian tax effect to encourage manufacturing enterprises and individuals to consciously conserve water and reduce unnecessary water usage. This is aligned with the goal of controlling the total water usage within the system.
In 2016, China piloted the water resource tax reform in Hebei Province; by 2017, this pilot policy expanded to nine provinces, including Beijing, Tianjin, the Inner Mongolia Autonomous Region, Shandong Province, Henan Province, Sichuan Province, Shaanxi Province, Shanxi Province, and the Ningxia Hui Autonomous Region. These regions are either along the Yellow River Basin, in the arid areas of China’s temperate continental climate, or in high-water-consuming areas due to the concentration of manufacturing and heavy industries. This study matched the experimental treatment variable to the manufacturing enterprise panel data according to the location of the manufacturing enterprise samples studied, which were represented by a dummy variable. Manufacturing enterprises entering the pilot areas were assigned a value of 1 for this variable, while other samples were assigned a value of 0.
5.4. Moderating Variables
5.4.1. City-Level Financial Technology Development (Fintech)
This study refers to Li Chuntao et al. [64], in selecting 48 keywords related to financial technology, including EB-level storage, NFC payments, differential privacy technology, big data, third-party payments, etc. These keywords were matched with all the cities in China, and the combination of city + keyword was searched for each year on Baidu News, a Chinese news search engine platform. For example, searching for “Beijing + blockchain” yielded the number of news pages that contained both “Beijing” and “blockchain” from 2009 to 2020. Using web crawler technology, this study examined the web page source code of the Baidu News advanced search results and extracted the number of search results, summing the search results for all the keywords at the city level to obtain the total search volume. That city’s financial technology development level was then matched to the panel data of manufacturing enterprises according to the manufacturing enterprises’ locations, so the moderating variable for the manufacturing enterprises from the same city in the same year was the city’s financial technology development level for that year.
5.4.2. Marketization Level (Market)
This study used the city marketization index values from the “China Annual Provincial Marketization Index Report” published by Fan Gang and Wang Xiaolu [65], the most authoritative source in China, as the moderating variable (market) for this research. These values were also matched to the manufacturing enterprise panel data according to the location of the manufacturing enterprises.
5.5. Control Variables
The following control variables were used in this study, and all were matched to the panel data of the Chinese A-share-listed companies from 2009 to 2020:
At the manufacturing enterprise level: the manufacturing enterprise size, measured as the natural logarithm of the total assets at the end of the year; the listing duration, measured from the year of listing to the year of variable selection; the debt-to-assets ratio, measured as the total liabilities/total assets; the ESG rating, measured using the China Securities ESG score; the cash flow level, measured as the net cash flow from operating activities/total assets; the growth potential, measured as (current period revenue-previous period revenue)/previous period revenue; the profitability, measured as the net profit/total assets; the market power, measured as ln(revenue/cost of goods sold + 1); the capital intensity, measured as ln(total fixed assets/number of employees); the shareholding concentration, measured as the shareholding percentage of the largest shareholder; the board size, measured as the number of board members; the board independence, measured as the number of independent directors/total number of board members; and the ownership structure, which was assigned as 1 if the company was state-owned and -controlled, and was otherwise assigned as 0.
At the city level: the population density, measured as the population/city area; the per-capita GDP in real terms, measured as the real GDP/population; and the urbanization level, measured as the rate of urbanization.
This study employed Python web scraping techniques to extract keywords related to urban policy and science and technology talent from the government work reports of Chinese cities from 2009 to 2020. The keywords included “basic research”, “scientific research”, “applied basic research”, “core technology”, “basic science”, “cutting-edge technology”, “original innovation”, “key technology”, “social welfare technology”, “talent resources”, “overseas high-level talents”, “returnees”, “talent team construction”, “science and technology system reform”, “talent-power strategy”, “strategy for invigorating China through science and education”, “scientific and technological achievements”, “intellectual property”, “scientific and energy-saving technological innovations”, “high-level talents”, “leading talents”, “innovations team”, “talent team”, “innovations and entrepreneurship”, “scientific researchers”, “double innovations”, and “innovation-driven”. The frequency of these keywords and the total word count in the government work reports were calculated after removing stop words for segmentation. The ratio of the keyword frequency to the total word count served as a proxy variable for the city’s policy focus on basic research and talent attention.
Referencing Zhao and Zhang [66], this study evaluated the development level of the digital economy in Chinese cities using the entropy method. This method combines five indicators: internet users per hundred people, the proportion of computer service and software personnel, per-capita telecommunications business volume, per-capita postal business, and mobile phone users per hundred people.
5.6. Sample Selection and Data Sources
This study selected panel data from prefecture-level cities in China and A-share-listed companies on the Shanghai and Shenzhen stock exchanges from 2009 to 2022 as the initial sample for empirical testing. It investigated the changes in the tripartite green energy-saving innovation system of manufacturing enterprises before and after the implementation of the water resource fee-to-tax policy. The city-level data were obtained from the “China City Statistical Yearbook” and the statistical yearbooks and bulletins of prefecture-level cities; the listed company data were sourced from the CSMAR and WIND databases; and the ESG ratings were based on the Huazheng ESG scores. This study processed the original data by excluding the companies listed as ST or *ST during the sample period; eliminating observations with obvious anomalies in the debt-to-asset ratios, net profits, etc.; and controlling the impact of extreme values by trimming 1% from the top and bottom of the continuous variables.
6. Empirical Results Analysis
6.1. Baseline Regression Analysis
6.1.1. Baseline Regression Analysis of the Water Resource Fee-to-Tax Policy and the “Triple Drive” of Corporate Green Energy-Saving Innovation
This study estimates the policy effects of the water resource fee-to-tax policy on mission-driven green energy-saving technological innovations, vision-driven green energy-saving technological innovations, and green energy-saving management innovations in manufacturing enterprises, using a double machine learning model based on the lasso regression algorithm. The sample split ratio is set at 1:4, and the regression results are presented in Table 1.

Table 1.
Baseline regression results.
Model (1), controlling for city-fixed and time-fixed effects across the entire sample interval, shows that the regression coefficient for the water resource fee-to-tax policy on mission-driven green energy-saving technological innovations is positive and equals 0.336, significant at the 1% level. As proposed in Hypothesis H1, this indicates that the water resource fee-to-tax policy can promote mission-driven green energy-saving technological innovations in manufacturing enterprises. This may be because, as a tax policy with more robust enforcement, the water resource tax policy increases the cost of water use and business risk for manufacturing enterprises, thereby forcing manufacturing enterprises to engage in mission-driven green energy-saving technological innovations [67].
Model (3) shows that the regression coefficient for the water resource fee-to-tax policy is 0.0228, also significant at the 10% level, suggesting that the water resource fee-to-tax policy, as an ecological policy aimed at achieving sustainable development, can also force manufacturing enterprises to innovate in green management from destructive ecological operation. This finding supports Hypothesis H1, which suggested that the policy would transform environmentally harmful operational and management models into resource-saving ones. The implementation of the water resource fee-to-tax policy often leads local governments to introduce corresponding constraints on enterprises to comply with environmental trends, guiding them to achieve water resource constraints through green management energy-saving innovations. This mechanism aligns with our earlier theoretical analysis, which proposed that regulatory pressure would drive management-level changes in pursuit of sustainability.
In contrast, in Model (2), the regression result for the water resource fee-to-tax policy on vision-driven green energy-saving technological innovations is not significant. This may be because the motivation for innovations in vision-driven green energy-saving technological innovations generally comes from the company’s sense of social responsibility and considerations of long-term sustainable development, requiring specific innate attributes. However, the water resource fee-to-tax policy limits manufacturing enterprises’ use of water as an ecological resource, increases production costs in the short-term, strengthens financial constraints, and thus crowds out vision-driven green energy-saving technological innovations. This finding suggests that the policy effect on vision-driven green technological energy-saving innovations is not clear-cut, supporting our earlier discussion that such innovations rely more on long-term strategic planning and intrinsic motivation rather than immediate cost pressures.
Thus, Hypothesis H1 is confirmed by these findings. The empirical results support our theoretical assumptions by demonstrating that the water resource fee-to-tax policy promotes mission-driven green technological energy-saving innovations and green management energy-saving innovations, but its effect on vision-driven green technological energy-saving innovations is less pronounced due to the different motivational factors involved.
6.1.2. Baseline Regression Analysis of the Synergistic Effect of the Water Resource Fee-to-Tax Policy on the “Triple drive” System of Corporate Green Energy-Saving Innovation
Table 2 reports the regression results of the impact of the implementation of the water resource fee-to-tax policy on the synergistic effect of the “triple drive” system of corporate green energy-saving innovation. Models (1) and (2) are the regression results with and without including year-fixed and city-fixed effects. It can be observed that the coefficients of the coupling coordination degree of the “triple drive” system of green energy-saving innovation are 0.0172 and 0.0202, both significant at the 1% level. This indicates that the water resource fee-to-tax policy can promote the coupling coordination degree of the “triple drive” system of green energy-saving innovation, confirming Hypothesis H2. This is because the water resource fee-to-tax policy, by increasing tax pressure, affects the cost structure of manufacturing enterprises, raises industry green standards to intensify market competition, and integrates environmental concepts to strengthen social responsibility, thereby motivating manufacturing enterprises on multiple levels and promoting the synergistic development of technological and management green energy-saving innovation.

Table 2.
Baseline regression results for synergistic effect.
Model (3) shows that the coefficient of the degree of coupling of the “triple drive” system of green energy-saving innovation is 0.00930, which does not reject the null hypothesis, indicating that the water resource fee-to-tax policy cannot promote the coupling degree of the “triple drive” system of green energy-saving innovation. Due to the high cost of green technology R&D, especially long-term investment projects lacking short-term returns, manufacturing enterprise resources are limited. Under cost pressures, manufacturing enterprises may focus more on short-term profits than long-term sustainable development. In such cases, high-cost green technology investments are unlikely to be prioritized, leading to a substitution effect between mission-driven and vision-driven green energy-saving technological innovations, with a bias towards mission-driven green energy-saving technological innovations.
Model (4) shows that the coefficient of the coordination degree of the “triple drive” system of green energy-saving innovation is significantly positive at 0.0207, passing the 1% significance test. This result indicates that the water resource fee-to-tax policy can also promote the coordination degree of the “triple drive” system of green energy-saving innovation, effectively validating Hypothesis H2. These findings suggest that while the water resource fee-to-tax policy has a robust positive effect on the synergistic development of green innovations, the distribution of resources between different types of green technological energy-saving innovations (mission-driven and vision-driven) may vary due to differing cost structures and priorities.
6.2. Robustness Test
This paper conducts robustness tests on the baseline regression of the “triple drive” system from the following four aspects: first, by changing the regression algorithm from the lasso regression algorithm to the Support Vector Machine (SVM) algorithm and re-estimating the parameters; second, by changing the sample split ratio from the original 1:4 to 1:7; third, by adjusting the sample split ratio to 1:3; and fourth, by excluding the first year of policy implementation. The robustness test results, as shown in Table 3, indicate that after altering the regression algorithm and sample split ratios, and excluding the first year of policy implementation data, the regression coefficients for the water resource fee-to-tax policy on mission-driven green energy-saving technological innovation and green energy-saving management innovations remain significantly positive. In contrast, the coefficients for vision-driven green energy-saving technological innovations are not significant. Compared to the baseline regression results, although there are changes in the coefficients and significance levels, the significance remains unchanged, and the results are consistent with the main regression, demonstrating the robustness of this study’s research.

Table 3.
Robustness test results.
6.3. Mechanism of Action Test
6.3.1. Ordinary Mediation Mechanism Test
This paper, based on a double machine learning model, employs a stepwise regression approach to validate the mediation mechanism paths of “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Mission-Driven Green Energy-Saving Technological Innovations” and “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Vision-Driven Green Energy-Saving Technological Innovations”. It uses Sobel, Aroian, and Goodman tests to verify the mediation effect pathway analysis results, as shown in Table 4.

Table 4.
Ordinary mediation effect regression results.
From Table 4, it is observed that in the mechanism pathway “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Mission-Driven Green Energy-Saving Technological Innovations”, the effect of the water resource fee-to-tax policy on green energy-saving management innovations and mission-driven green energy-saving technological innovations, as well as the impact of green energy-saving management innovations on mission-driven green energy-saving technological innovations, is all significantly positive. This indicates that the mediation effect along this pathway is valid and represents a partial mediation effect with a mediation proportion of 4.2%. The Sobel, Aroian, and Goodman tests all pass, suggesting that green energy-saving management innovations can significantly mediate between the water resource fee-to-tax policy and mission-driven green energy-saving technological innovations in manufacturing enterprises. This is because the green tax system can suppress high-pollution and high-energy-consumption behaviors of manufacturing enterprises through the internalization of environmental costs and positive green incentives [68], guiding them towards management mechanism innovations for green transformation. Such a transformation would provide resource support for the manufacturing enterprise’s mission-driven green energy-saving technological innovations, aligning with the first part of Hypothesis H3.
In the pathway “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Vision-Driven Green Energy-Saving Technological Innovations”, although the effect of green energy-saving management innovations on vision-driven green energy-saving technological innovations is significantly positive with a coefficient of 0.339, the overall pathway coefficient of 0.0157 is not significant, indicating the absence of a mediation effect along this pathway. This contradicts the latter part of Hypothesis H3. This is because, although green energy-saving management innovations can provide intrinsic motivation for vision-driven green energy-saving technological innovations at the strategic level and ensure the stability and continuity of innovations in terms of institutional perfection, the financial pressure and resource limitations brought by the implementation of the water resource fee-to-tax policy for manufacturing enterprises lacking resources and technological endowments can severely distort this positive effect, ultimately leading to insignificant regression results.
6.3.2. Counterfactual Framework
To further investigate the causal mediation pathways within the “triple drive” system mechanism of the water resource fee-to-tax policy, this study conducts counterfactual framework tests on the “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Mission-Driven Green Energy-Saving Technological Innovations” and “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Vision-Driven Green Energy-Saving Technological Innovations” pathways. The regression results are shown in Table 5 and Table 6.

Table 5.
Counterfactual framework 1.

Table 6.
Counterfactual framework 2.
Table 5 reveals that in the pathway “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Mission-Driven Green Energy-Saving Technological Innovations”, both the treatment and control groups show significant positive direct and indirect effects. This not only demonstrates through a counterfactual framework that the water resource fee-to-tax policy can indirectly promote mission-driven green energy-saving technological innovations by promoting green energy-saving management innovations but also indicates that if this policy were expanded nationally (to the manufacturing enterprises in the control group), the pathway “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Mission-Driven Green Energy-Saving Technological Innovations” would still be valid.
Table 6 shows that in the pathway test for “Water Resource Fee-to-Tax Policy → Green Energy-Saving Management Innovations → Vision-Driven Green Energy-Saving Technological Innovations”, the direct effects in both the treatment and control groups are significantly negative. This indicates that the water resource fee-to-tax policy directly suppresses manufacturing enterprises’ vision-driven green energy-saving technological innovations. Moreover, if this policy were expanded to areas of the control group (where the water resource fee-to-tax policy has not been implemented), it would also suppress the vision-driven green energy-saving innovations of manufacturing enterprises. Secondly, the indirect effect in the treatment group is not significant, but it is significantly positive in the control group. This is because, under this policy, manufacturing enterprises in the treatment group are mainly located in areas with tight water resources and excessive water-saving pressure, so even with good green energy-saving management innovations, it is not possible to effectively promote vision-driven green energy-saving technological innovations in manufacturing enterprises. In contrast, manufacturing enterprises in the control group are mostly in areas with abundant water resources, where manufacturing enterprises face relatively less environmental and cost pressures regarding water carrying capacity and water costs, and they have better technological conditions and financial endowments. If the water resource fee-to-tax policy were expanded to these areas, even under rigid water constraints, improved green energy-saving management innovations could promote vision-driven green energy-saving technological innovations in these manufacturing enterprises. Thus, there exists a masking effect in the ordinary mediation pathway, and the specific pathways are not clear, but they can be clarified through a counterfactual framework. This analysis verifies Hypothesis H4.
6.4. Testing the Moderating Mechanism
6.4.1. External Mechanism I: The Moderating Effect of Financial Technology
As previously analyzed, the implementation of the water resource fee-to-tax policy can promote mission-driven green energy-saving technological innovations and green energy-saving management innovations in manufacturing enterprises, but it does not have a significant effect on vision-driven green energy-saving technological innovations. To further test whether financial technology has a significant external moderating effect on these three pathways driven by the water resource fee-to-tax policy, this paper constructs a moderating effect model for testing, with regression results shown in Table 7.

Table 7.
Regression results for the moderating effect of financial technology.
Model (1) shows that the interaction term (Water Resource Fee-to-Tax Policy × Financial Technology) is not significantly related to manufacturing enterprises’ vision-driven green energy-saving technological innovations. This indicates that financial technology does not moderate the relationship between the water resource fee-to-tax policy and vision-driven green energy-saving technological innovations. The reason is that although financial technology can play a role in alleviating financing constraints, manufacturing enterprises’ subjective financing intentions are not inclined towards vision-driven green energy-saving technological innovations. Furthermore, the development of financial technology can alleviate the asymmetry of information between investors and manufacturing enterprises. If investors and financial institutions detect through big data that manufacturing enterprises are allocating funds to riskier, more uncertain vision-driven green energy-saving technological innovations, they may choose to avoid risk. Thus, Hypothesis H5 regarding vision-driven green technological energy-saving innovations is supported.
Results from Models (2) and (3) show that the regression coefficients of Water Resource Fee-to-Tax Policy × Financial Technology are 0.0611 and 0.00447, respectively, both significant and positive. This suggests that FinTech can enhance the positive effects of the water resource fee-to-tax policy on mission-driven green technological energy-saving innovations and green management energy-saving innovations. As hypothesized, financial technology can alleviate financing constraints [69], and it enables manufacturing enterprises facing resource constraints and increased costs to have sufficient funds for green energy-saving technological innovations with market potential and promising prospects in the short-term, achieving short-term economic benefits while coping with the pressure of “allocating production based on water availability”. Green energy-saving management innovations also require substantial funds and financial technology can accelerate capital flows and promote capital inflow to manufacturing enterprises. Hypothesis H5 is validated.
6.4.2. External Mechanism II: The Moderating Effect of the Marketization Process
Using the same method, the moderating effect of the marketization process on the “triple drive” system of the water resource fee-to-tax policy was tested, with results shown in Table 8.

Table 8.
Regression results for the moderating effect of the marketization process.
In Model (1), the interaction term of the water resource fee-to-tax policy × marketization on vision-driven green energy-saving technological innovations had a coefficient of 0.00218, which did not pass the test. This is because the advancement of marketization inevitably intensifies market competition and raises investors’ expectations for corporate profitability. This dual pressure often forces manufacturing enterprises to shift their strategic focus towards pursuing short-term economic returns, indicating that under the influence of the marketization level, there is still no significant relationship between the water resource fee-to-tax policy and vision-driven green energy-saving technological innovations. This finding aligns with our earlier discussion that emphasized the high-risk and long-term nature of vision-driven innovations, which is less appealing to firms under competitive and profitability pressures, thereby supporting Hypothesis H6 for vision-driven innovations.
The coefficient in Model (2) is 0.0241, significantly positive at the 1% level, indicating that the marketization process has a positive moderating effect between the water resource fee-to-tax policy and mission-driven green energy-saving technological innovations. This is because the development of the marketization process can improve the price mechanism and promote market competition. The improvement in knowledge and data factor markets can especially encourage manufacturing enterprises to carry out mission-driven green energy-saving technological innovations. Furthermore, market competition pressure will further compel manufacturing enterprises to engage in mission-driven green energy-saving technological innovations, confirming Hypothesis H6 for mission-driven innovations.
The interaction term in Model (3) with green energy-saving management innovations has a regression coefficient of 0.00169, which is significant at the 10% level. The marketization process can enhance manufacturing enterprises’ sensitivity to managerial systemic responses to the water resource fee-to-tax policy, enabling them to adjust their management strategies more effectively according to rigid water constraints. Therefore, the marketization process can also strengthen the positive relationship between the water resource fee-to-tax policy and green energy-saving management innovations. This finding supports Hypothesis H6, suggesting that marketization facilitates enterprises’ responsiveness to environmental regulations, thereby enhancing their green management energy-saving innovations.
These expanded explanations further integrate the empirical findings with our theoretical hypotheses. Hypothesis H6 suggested that marketization would moderate the relationship between the water resource fee-to-tax policy and different types of green innovations. The results from models (2) and (3) confirm this by demonstrating the significant positive moderating effects of marketization on mission-driven green technological innovations and green management energy-saving innovations, while model (1) illustrates why this effect does not extend to vision-driven innovations.
6.5. Heterogeneity Analysis
6.5.1. ESG Rating Heterogeneity Analysis
On the level of manufacturing enterprise heterogeneity analysis, a company’s ESG (Environmental, Social, and Governance) performance may lead to heterogeneity in policy effects. To explore whether the promotion effect of the water resource fee-to-tax policy on the coupling coordination degree of the “triple drive” system of green energy-saving innovations varies among companies with different ESG ratings, this study divides the entire sample based on an ESG rating of 4 as the median value. Companies with an ESG rating of 4 or higher are classified as high-ESG companies and the rest as low-ESG companies. The analysis is then performed separately for these groups, as shown in Table 9.

Table 9.
Regression results for ESG rating heterogeneity analysis.
Model (1) presents the regression results for the impact of the water resource fee-to-tax policy on the coupling coordination degree of the green energy-saving innovation “triple drive” system among high-ESG companies, while Model (2) shows the impact on low-ESG companies. The results indicate that in the high-ESG sample, the coefficient of the water resource fee-to-tax policy on the coupling coordination degree of the “triple drive” system of green energy-saving innovation is 0.0175, significant at the 5% level. This result suggests that the situation for high-ESG-sample companies is consistent with the conclusions obtained for the entire sample. These companies, which comprise a large portion of all manufacturing enterprises in the sample, have a more mature internal governance structure and a more prominent contribution to society and positive externalities. Under the water resource fee-to-tax policy regulation, they can further deepen the “triple drive” system based on their existing management mechanisms and technological foundations.
However, in the low-ESG sample, the coefficient of the water resource fee-to-tax policy is not significant, indicating that the policy does not have a significant promotional effect on the coupling coordination degree of the “triple drive” system of green energy-saving innovation in low-ESG companies. These companies make up a smaller portion of all manufacturing enterprise samples, with relatively backward existing management mechanisms and lacking technology and financial endowments, so the water resource fee-to-tax policy cannot force them to transform and may even impose a burden on these manufacturing enterprises.
These findings suggest that the effectiveness of the water resource fee-to-tax policy is heterogeneous across enterprises with different ESG ratings. High-ESG enterprises, with their advanced governance and robust resources, can leverage the policy to enhance their green innovations. In contrast, low-ESG enterprises struggle to respond positively to the policy due to inherent deficiencies.
6.5.2. Regional Heterogeneity Analysis
On the regional level of heterogeneity analysis, the “Interim Measures for Water Resource Tax Reform Pilot” and “Measures for Expanding the Pilot Implementation of Water Resource Tax Reform” stipulate that double taxation is applied to areas within pilot provinces that are overburdened with water resources. Therefore, the impact of the fee-to-tax policy on green energy-saving innovations may vary between overburdened and non-overburdened areas. To explore whether the implementation of the water resource fee-to-tax policy on the coupling coordination degree of the “triple drive” system of green energy-saving innovations exhibits regional heterogeneity, this study divides manufacturing enterprises subject to the water resource fee-to-tax policy into two regional samples based on geographic location, resource distribution, and endowment differences: the eastern and central regions versus the western region. The relationship between policy implementation and the degree of coupling coordination of manufacturing enterprise green energy-saving innovation (“triple drive”) in these regions is shown in Table 10.

Table 10.
Regression results for regional heterogeneity analysis.
This study finds significant heterogeneity in the impact of the water resource fee-to-tax policy implementation on the coupling coordination degree of the manufacturing enterprise green energy-saving innovation “triple drive” system across different regions. Model (1) shows a regression coefficient of 0.0240 in the eastern and central regions, significant at the 1% level; Model (2) shows a regression coefficient of −0.0450 in the western region, significantly negative at the 5% level. Furthermore, considering the absolute value of the regression coefficients of the water resource fee-to-tax policy, the impact on the coupling coordination degree of the “triple drive” system of green energy-saving innovation is greater in the western region compared to the eastern and central regions. This indicates that not only does the impact of the water resource fee-to-tax policy on the coupling coordination degree of the green energy-saving innovation “triple drive” system exhibit directional heterogeneity but also demonstrates asymmetric characteristics in terms of impact magnitude across different regions.
The reasons for this heterogeneity are multifaceted. The manufacturing enterprise samples in the eastern and central regions, where the market is developed, manufacturing development is positive, and financial and technological conditions are advanced, make up a large portion of all manufacturing enterprises. Additionally, these regions have abundant water resources; even under rigid water constraints, the threshold is relatively high, which drives manufacturing enterprises towards green energy-saving innovations and transformation and exerts less pressure on production. Therefore, the water resource fee-to-tax policy can promote the development of the “triple drive” system coupling coordination.
In contrast, the western regions face opposite conditions. The negative significant impact of the policy on the coupling coordination degree of green innovation in these regions is due to the less developed market conditions, lower financial and technical endowments, and more severe water scarcity. The implementation of the water resource fee-to-tax policy in these regions imposes significant financial and operational burdens on enterprises, making it challenging for them to engage in green innovations and transformations. Thus, the policy’s impact is directionally negative and more pronounced in these regions, highlighting the regional heterogeneity in its effectiveness.
After an in-depth analysis of the empirical data, we present a summarizing view of the policy’s impact on various dimensions of corporate green energy-saving innovation, depicted in Figure 5. This visual tool helps to clarify the subtle interplay among types of innovations and the overarching role of financial technology and marketization processes. *, **, *** indicate significance at the 10%, 5%, and 1% levels, respectively, with t-statistics in parentheses. And n.s. stands for no relevance.
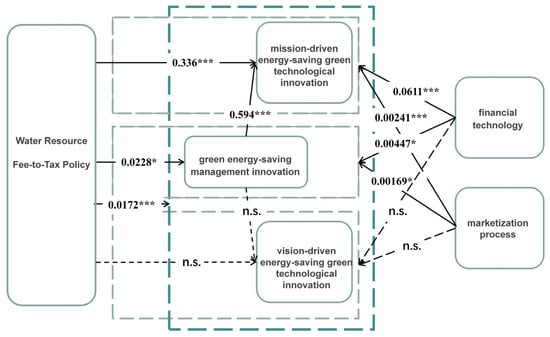
Figure 5.
Impact matrix of water resource policy on green energy-saving innovation.
7. Discussion
This study highlights the significant impact of the water resource fee-to-tax policy on promoting green energy-saving innovations in Chinese manufacturing enterprises. The policy effectively incentivizes enterprises to implement immediate, practical innovations aimed at reducing water consumption and improving operational efficiency. These mission-driven innovations are crucial for complying with regulatory requirements and addressing immediate environmental challenges. However, the increased cost pressures and regulatory demands can hinder the ability of enterprises to invest in long-term, high-risk vision-driven innovations, which require substantial resources and time to develop.
The findings of this study add to the growing body of literature emphasizing the role of regulatory policies in promoting green innovations. For instance, studies by Yin et al. (2023) [9] and Liu et al. (2023) [10] have similarly found that government policies can drive corporate behavior towards more sustainable practices. However, our research extends these findings by highlighting the differential impact of the water resource fee-to-tax policy on different types of green innovations. While previous studies have primarily focused on the overall promotion of green practices, this study reveals that mission-driven innovations receive a significant boost from such policies, whereas vision-driven innovations face constraints. This nuanced understanding underscores the need for tailored support mechanisms to ensure comprehensive green innovation across different domains.
Firstly, it is crucial to leverage big data and other technologies, along with regional conditions, to set resource constraint standards compatible with local industries. Advanced hydrological models and Geographic Information Systems (GISs) can be used to map the availability, quality, and distribution of water resources, allowing for tailored standards. Additionally, water quality analysis should identify pollution sources and levels, utilizing remote sensing technologies to monitor changes in water bodies and aquifers. Implementing a dynamic adjustment mechanism ensures that enterprises gradually transition towards efficient resource use and environmental friendliness while pursuing economic benefits. Governments can establish an information-sharing platform to provide enterprises with real-time data on resource use efficiency, environmental impact assessments, and best-practice cases, encouraging companies to innovate technologically and exceed these standards rather than just meet them.
Secondly, governments should introduce a series of incentive measures, such as green tax incentives, research and development subsidies, green credit, and green bonds. Special support should be given to enterprises dedicated to vision-driven green technological innovations (e.g., developing renewable energy, circular economy solutions) and mission-driven green technological innovations (e.g., pollution control technologies). Encouraging companies to set up dedicated green technology research funds and guiding social capital towards green projects through policy incentives can reduce the initial costs and risks of green innovation for enterprises. For instance, funding programs could support the development of advanced water purification technologies, desalination plants, and water recycling systems.
Moreover, promoting and implementing the ISO 14001 environmental management system certification can help enterprises systematically identify, control, and improve their environmental performance. Governments can organize training and consulting services to enhance the awareness of the importance of green management among enterprise leaders, integrating green concepts into strategic planning, supply chain management, and product design to reduce resource consumption and environmental pollution from the source. Implementing technologies such as real-time water quality monitoring systems, automated irrigation systems, and water-efficient manufacturing processes can be part of these green management practices.
In addition, constructing a collaborative mechanism with multi-stakeholder participation is essential. Governments should facilitate industry–university–research collaboration platforms, encouraging deep cooperation between universities, research institutions, and enterprises to tackle green technology innovation challenges. Through technology transfer and joint research projects, technological achievements can be accelerated into practical productivity, effectively linking innovation chains with industrial chains. Collaborative projects could focus on developing smart water management systems, advanced hydrological forecasting models, and integrated watershed management practices.
This study has several limitations. First, the analysis is based on data from Chinese manufacturing enterprises, which may limit the generalizability of the findings to other contexts. Second, this study focuses on the short- to medium-term impacts of the policy, and the long-term effects remain to be explored. Finally, the use of patent data as a proxy for innovation may not capture all aspects of green innovation activities.
Future research should explore the long-term impacts of the water resource fee-to-tax policy on green innovations. Comparative studies in different regional and international contexts can provide insights into the adaptability and scalability of the policy. Additionally, investigating the interactions between policy measures, financial incentives, and technological advancements will offer a more comprehensive understanding of how to optimize water resource management.
8. Research Conclusions and Policy Recommendations
Using the implementation of the water resource tax as a quasi-natural experiment, this study utilized a double machine learning model to explore the relationship between the water resource fee-to-tax policy and the “triple-drive” system of corporate green energy-saving innovations. The following conclusions were made:
Firstly, the enactment of the water resource fee-to-tax policy significantly promoted corporate green energy-saving management innovations and mission-driven green energy-saving technological innovations. This could be attributed to the rigid constraints of the water resource tax leading to increased costs, prompting manufacturing enterprises to undertake short-term energy-saving technological innovations to absorb green compensations and balance financial pressures. Furthermore, the catalytic effect of the water resource fee-to-tax policy could lead to the development of a more comprehensive green policy mechanism locally, compelling manufacturing enterprises to adjust and reform their green management energy-saving models. However, the policy effect of the water resource fee-to-tax policy on vision-driven green energy-saving technological innovations remains uncertain. Under this policy, manufacturing enterprises’ financial and technological endowments may not match the requirements for vision-driven green energy-saving technological innovations, often leading to a crowding-out effect that surpasses the anticipated promotional effect of the policy.
Secondly, implementing the water resource fee-to-tax policy significantly improved the coupling coordination degree of the “triple-drive” system of corporate green energy-saving innovations. This was because the policy not only stimulated the motivation for innovation at the technological level but also promoted green transformations at the management level, achieving the efficient and harmonious development of tripartite innovative behaviors.
Thirdly, green energy-saving management innovations can act as an influencing mechanism, positively mediating the pathway through which the water resource fee-to-tax policy promotes mission-driven green energy-saving technological innovations in manufacturing enterprises. Additionally, this study utilized a counterfactual framework to verify that, if the policy were expanded to non-pilot areas, green energy-saving management innovations could mitigate the negative effects of the water resource fee-to-tax policy on vision-driven green energy-saving technological innovations.
Fourth, the development of financial technology and the advancement of marketization processes can synergize with the water resource fee-to-tax policy to enhance its promotional effects on corporate management and mission-driven green energy-saving technological innovations. However, they do not have a significant moderating effect on vision-driven green energy-saving technological innovations.
Fifth, compared to companies with lower ESG ratings, the water resource fee-to-tax policy had a more substantial positive impact on the coupling coordination degree of the “triple-drive” system of green energy-saving innovations in companies with an ESG advantage. There was also heterogeneity in its impact across regions with significant water resource conditions, particularly in areas such as the west, which faces significant water-saving pressures. In such regions, the water resource fee-to-tax policy may not promote the coordinated development of local green energy-saving innovations and poses a challenge to the green transformation of local manufacturing enterprises.
Based on the above conclusions, this study proposes the following specific policy recommendations:
Firstly, the long-term stability of the water resource fee-to-tax policy should be optimized and a comprehensive supporting policy system should be constructed. The empirical analysis indicated that vision-driven green energy-saving technological innovations receive limited policy incentives, primarily due to the high risk associated with their longtime horizon, the difficulty of technological development, and the mismatch between investments and return. This finding suggests that the water resource fee-to-tax policy needs to ensure long-term stability and predictability, allowing businesses to plan and invest over the long-term in a stable policy environment. Specific measures include clarifying and publishing a clear policy timetable and roadmap, including mid- to long-term goals, pilot scopes, and subsequent water resource fee-to-tax implementation steps, which would enable manufacturing enterprises to make corresponding long-term R&D plans. For green energy-saving innovation projects with long-term ecological benefits but lacking in short-term economic returns, the government could support long-term R&D subsidies or tax incentives to ease the financial pressures on companies. Establishing a risk assessment mechanism for the regular supervision and evaluation of subsidized projects can increase the controllability of project risks. Promoting collaboration across multiple platforms, such as the government, manufacturing enterprises, academia, and other social organizations, can concentrate wisdom and resources while dispersing risks.
Secondly, the marketization process should be accelerated and green financial technology policies should be improved. Empirical analysis shows that the development of financial technology can promote the flow of financial resources to green energy-saving innovations, and the advancement of marketization levels creates a healthier and more transparent market environment for corporate green energy-saving innovations. Based on this finding, policies should focus on perfecting green financial technology and accelerating marketization construction. By utilizing big data, artificial intelligence, and other technological means to better identify and support potential green energy-saving innovation projects, the leveraging of intelligent algorithms and blockchain technology to optimize the process of green subsidies and credit issuance can significantly enhance the efficiency and accuracy of fund distribution. A high marketization means a higher market-based allocation of factors, where the “invisible hand” of the market becomes the dominant force, guiding the efficient flow and optimal allocation of resources. To achieve this goal, the government must perfect legal frameworks and regulatory systems that are compatible with the market economy, including protecting intellectual property rights, combating unfair competition, etc., to create a fair and transparent market environment.
Thirdly, help should be provided to companies to improve their ESG scores and encourage them to adopt regionally differentiated support measures. Based on the heterogeneity analysis of companies, the water resource fee-to-tax policy is more advantageous in promoting the coordinated development of green energy-saving innovations among companies with high ESG ratings but has a suppressive effect on the coordinated development of green energy-saving innovations in companies in the western region. Given this result, the government could encourage companies to enhance their data management levels and efficiently improve their ESG management by embedding ESG information management tools in their internal control systems through IT means. Additionally, adopting differentiated and refined fiscal and tax policies based on companies’ ESG scores can compel companies to improve their ESG performance. For the western region, special development funds or tax rebates could be established to support local companies’ construction of green energy-saving innovation infrastructure. At the same time, empirical research suggests that improving cross-regional cooperation mechanisms, actively promoting cooperation and knowledge exchange between manufacturing enterprises in the eastern and western regions, sharing resources and technology, and achieving complementary advantages can promote the coordinated development of green energy-saving innovations among manufacturing enterprises in the western region.
Emerging markets and developing economies, such as India, Indonesia, and Mexico, face similar developmental challenges and contradictions as China. These countries experience rapid industrialization, increasing environmental degradation and the urgent need for sustainable resource management. Common issues include water scarcity, pollution, and inefficient resource utilization, which hinder sustainable development and environmental conservation efforts. Given the success of the water resource fee-to-tax policy in China, there are promising prospects for implementing similar strategies in these countries. Future research should focus on adapting this policy framework to different regional contexts, considering local environmental conditions, economic structures, and regulatory landscapes. Comparative studies between regions can help identify best practices and tailor policy measures to maximize their effectiveness.
To address water scarcity and pollution, these countries should enhance their regulatory frameworks to enforce stricter controls on industrial discharges and agricultural runoff. Investing in advanced wastewater treatment technologies can significantly reduce pollution levels and improve water quality. Developing comprehensive water management plans that incorporate the latest scientific data and technological innovations can ensure more efficient water use and allocation.
Addressing the issue of inefficient resource utilization requires the promotion of water-efficient technologies and practices across industries and agriculture. Governments should incentivize the adoption of modern irrigation techniques and water-saving industrial processes through subsidies and tax incentives. Public–private partnerships can play a crucial role in funding and disseminating these technologies.
To overcome the lack of technological innovation, it is essential to foster an environment conducive to research and development. Governments should establish innovation hubs and provide grants to support research in water management technologies. Collaboration between academic institutions, industry stakeholders, and government agencies can drive the development and implementation of cutting-edge solutions. Furthermore, creating a favorable regulatory environment for patenting and commercializing new technologies can encourage innovation and investment in sustainable water management practices.
By addressing these common challenges through targeted measures, emerging markets and developing economies can achieve sustainable water resource management. These efforts will not only mitigate water scarcity and pollution but also promote overall environmental sustainability and economic resilience.
Author Contributions
Conceptualization, L.K.; methodology, L.K. and J.L.; data curation, L.K.; writing—original draft preparation, L.K. and H.Z.; writing—review and editing, L.K., J.L. and H.Z.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Fund Program of China—Research on the reconstruction of the governance model of food safety problems based on blockchain technology (Grant No. 22CGL040).
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Acknowledgments
We sincerely thank the editors and reviewers for their valuable comments during the review process of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mitoma, H. Carbon footprint analysis considering production activities of informal sector: The case of manufacturing industries of India. Energy Econ. 2023, 125, 106809. [Google Scholar] [CrossRef]
- Ivanova, D.; Wieland, H. Tracing carbon footprints to intermediate industries in the United Kingdom. Ecol. Econ. 2023, 214, 107996. [Google Scholar] [CrossRef]
- Xu, C.; Sun, G.; Kong, T. The impact of digital transformation on enterprise green innovation. Int. Rev. Econ. Financ. 2024, 90, 1–12. [Google Scholar] [CrossRef]
- Tan, X.; Dong, H.; Liu, Y.; Su, X.; Li, Z. Green bonds and corporate performance: A potential way to achieve green recovery. Renew. Energy 2022, 200, 59–68. [Google Scholar] [CrossRef]
- Han, F.; Mao, X.; Yu, X.; Yang, L. Government environmental protection subsidies and corporate green innovation: Evidence from Chinese microenterprises. J. Innov. Knowl. 2024, 9, 100458. [Google Scholar] [CrossRef]
- Asni, N.; Agustia, D. Does corporate governance induce green innovation? An emerging market evidence. Corp. Gov. Int. J. Bus. Soc. 2022, 22, 1375–1389. [Google Scholar] [CrossRef]
- Yu, C.-H.; Wu, X.; Zhang, D.; Chen, S.; Zhao, J. Demand for green finance: Resolving financing constraints on green innovation in China. Energy Policy 2021, 153, 112255. [Google Scholar] [CrossRef]
- Liu, T.; Cao, X. Going Green: How Executive Environmental Awareness and Green Innovation Drive Corporate Sustainable Development. J. Knowl. Econ. 2024, 1–28. [Google Scholar] [CrossRef]
- Yin, X.; Wang, D.; Lu, J.; Liu, L. Does green credit policy promote corporate green innovation? Evidence from China. Econ. Chang. Restruct. 2023, 56, 3187–3215. [Google Scholar] [CrossRef]
- Liu, B.; Cifuentes-Faura, J.; Ding, C.J.; Liu, X. Toward carbon neutrality: How will environmental regulatory policies affect corporate green innovation? Econ. Anal. Policy 2023, 80, 1006–1020. [Google Scholar] [CrossRef]
- Wu, H.; Liu, S.; Hu, S. Visible hand: Do government subsidies promote green innovation performance moderating effect of ownership concentration. Pol. J. Environ. Stud. 2021, 30, 881–892. [Google Scholar] [CrossRef]
- Jin, H.; Yang, J.; Chen, Y. Energy saving and emission reduction fiscal policy and corporate green technology innovation. Front. Psychol. 2022, 13, 1056038. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.W.; Abbas, J.; Sial, M.S.; Alvarez-Otero, S.; Cioca, L.I. Achieving green innovation and sustainable development goals through green knowledge management: Moderating role of organizational green culture. J. Innov. Knowl. 2022, 7, 100272. [Google Scholar] [CrossRef]
- Fernandes Rodrigues Alves, M.; Vasconcelos Ribeiro Galina, S.; Dobelin, S. Literature on organizational innovation: Past and future. Innov. Manag. Rev. 2018, 15, 2–19. [Google Scholar] [CrossRef]
- Guinot, J.; Barghouti, Z.; Chiva, R. Understanding Green Innovation: A Conceptual Framework. Sustainability 2022, 14, 5787. [Google Scholar] [CrossRef]
- Chen, Y.S.; Chang, C.H.; Wu, F.S. Origins of green innovations: The differences between proactive and reactive green innovations. Manag. Decis. 2012, 50, 368–398. [Google Scholar] [CrossRef]
- Xu, C.; Gao, Y.; Hua, W.; Feng, B. Does the Water Resource Tax Reform Bring Positive Effects to Green Innovation and Productivity in High Water-Consuming Enterprises? Water 2024, 16, 725. [Google Scholar] [CrossRef]
- Chen, Z.-R.; Yuan, Y.; Xiao, X. Analysis of the fee-to-tax reform on water resources in China. Front. Energy Res. 2021, 9, 752592. [Google Scholar] [CrossRef]
- Shang, S.; Chen, Z.; Shen, Z.; Shabbir, M.S.; Bokhari, A.; Han, N.; Klemeš, J.J. The effect of cleaner and sustainable sewage fee-to-tax on business innovation. J. Clean. Prod. 2022, 361, 132287. [Google Scholar] [CrossRef]
- Speck, S. Environmental tax reform and the potential implications of tax base erosions in the context of emission reduction targets and demographic change. Econ. Politica 2017, 34, 407–423. [Google Scholar] [CrossRef]
- Jia, Z.; Wen, S.; Sun, Z. Current relationship between coal consumption and the economic development and China’s future carbon mitigation policies. Energy Policy 2022, 162, 112812. [Google Scholar] [CrossRef]
- Berbel, J.; Borrego-Marin, M.M.; Exposito, A.; Giannoccaro, G.; Montilla-Lopez, N.M.; Roseta-Palma, C. Analysis of irrigation water tariffs and taxes in Europe. Water Policy 2019, 21, 806–825. [Google Scholar] [CrossRef]
- Su, Y.; Cheng, Z.H. The impact of water resource taxes on total factor water efficiency. Water Policy 2023, 25, 200–217. [Google Scholar] [CrossRef]
- Wang, R.X.; Wijen, F.; Heugens, P. Government’s green grip: Multifaceted state influence on corporate environmental actions in China. Strateg. Manag. J. 2018, 39, 403–428. [Google Scholar] [CrossRef]
- Huang, B. An exhaustible resources model in a dynamic input–output framework: A possible reconciliation between Ricardo and Hotelling. J. Econ. Struct. 2018, 7, 8. [Google Scholar] [CrossRef]
- Güerlek, M.; Tuna, M. Reinforcing competitive advantage through green organizational culture and green innovation. Serv. Ind. J. 2018, 38, 467–491. [Google Scholar] [CrossRef]
- Bouncken, R.B.; Fredrich, V.; Ritala, P.; Kraus, S. Coopetition in new product development alliances: Advantages and tensions for incremental and radical innovation. Br. J. Manag. 2018, 29, 391–410. [Google Scholar] [CrossRef]
- Zhao, K.J.; Yao, P.; Liu, J.X. The Impact of Water Resource Tax on the Sustainable Development in Water-Intensive Industries: Evidence from Listed Companies. Sustainability 2024, 16, 912. [Google Scholar] [CrossRef]
- Kirsanova, N.; Lenkovets, O.; Hafeez, M. Issue of accumulation and redistribution of oil and gas rental income in the context of exhaustible natural resources in arctic zone of russian federation. J. Mar. Sci. Eng. 2020, 8, 1006. [Google Scholar] [CrossRef]
- Wang, L.; Muniba; Lakner, Z.; Popp, J. The impact of water resources tax policy on water saving behavior. Water 2023, 15, 916. [Google Scholar] [CrossRef]
- Ing, J. Adverse selection, commitment and exhaustible resource taxation. Resour. Energy Econ. 2020, 61, 101161. [Google Scholar] [CrossRef]
- Ohori, S. Environmental tax and public ownership in vertically related markets. J. Ind. Compet. Trade 2012, 12, 169–176. [Google Scholar] [CrossRef]
- Lu, N.; Zhou, W. The impact of green taxes on green innovation of enterprises: A quasi-natural experiment based on the levy of environmental protection taxes. Environ. Sci. Pollut. Res. 2023, 30, 92568–92580. [Google Scholar] [CrossRef] [PubMed]
- Du, G.; Zhou, C.M.; Ma, Y.N. Impact mechanism of environmental protection tax policy on enterprises’ green technology innovation with quantity and quality from the micro-enterprise perspective. Environ. Sci. Pollut. Res. 2023, 30, 80713–80731. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.; Zhang, K.; Dou, J. Energy saving and emission reduction effects of economic agglomeration: Theory and Chinese experience. Manag. World 2019, 35, 36–60. [Google Scholar]
- Xia, S.; You, D.; Tang, Z.; Yang, B. Analysis of the spatial effect of fiscal decentralization and environmental decentralization on carbon emissions under the pressure of officials’ promotion. Energies 2021, 14, 1878. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, J.; Cui, X. Fiscal decentralization and environmental pollution: From the perspective of carbon emission. China Ind. Econ 2011, 10, 65–75. [Google Scholar]
- Chen, M.; Hu, X.H.; Zhang, J.J.; Xu, Z.; Yang, G.; Sun, Z.A. Are Firms More Willing to Seek Green Technology Innovation in the Context of Economic Policy Uncertainty? -Evidence from China. Sustainability 2023, 15, 14188. [Google Scholar] [CrossRef]
- Feng, T.T.; Wu, X.H.; Guo, J. Racing to the bottom or the top? Strategic interaction of environmental protection expenditure among prefecture-level cities in China. J. Clean. Prod. 2023, 384, 135565. [Google Scholar] [CrossRef]
- Seman, N.A.A.; Govindan, K.; Mardani, A.; Zakuan, N.; Saman, M.Z.M.; Hooker, R.E.; Ozkul, S. The mediating effect of green innovation on the relationship between green supply chain management and environmental performance. J. Clean. Prod. 2019, 229, 115–127. [Google Scholar] [CrossRef]
- Wu, H.; Hu, S. The impact of synergy effect between government subsidies and slack resources on green technology innovation. J. Clean. Prod. 2020, 274, 122682. [Google Scholar] [CrossRef]
- Yan, Y.; Guan, J. Social capital, exploitative and exploratory innovations: The mediating roles of ego-network dynamics. Technol. Forecast. Soc. Chang. 2018, 126, 244–258. [Google Scholar] [CrossRef]
- Gunasekaran, A.; Subramanian, N.; Rahman, S. Green supply chain collaboration and incentives: Current trends and future directions. Transp. Res. Part E Logist. Transp. Rev. 2015, 74, 1–10. [Google Scholar] [CrossRef]
- Dube, A.S.; Gawande, R.S. Analysis of green supply chain barriers using integrated ISM-fuzzy MICMAC approach. Benchmarking Int. J. 2016, 23, 1558–1578. [Google Scholar] [CrossRef]
- Fan, T. Research on the reform and perfection of resource Tax system. Open J. Soc. Sci. 2021, 9, 316. [Google Scholar] [CrossRef]
- He, L.; Chen, K. Can China’s “tax-for-fee” reform improve water performance–evidence from Hebei province. Sustainability 2021, 13, 13854. [Google Scholar] [CrossRef]
- Chiu, Y.-B.; Lee, C.-C. Effects of financial development on energy consumption: The role of country risks. Energy Econ. 2020, 90, 104833. [Google Scholar] [CrossRef]
- Tang, D.C.; Chen, W.Y.; Zhang, Q.; Zhang, J.Q. Impact of Digital Finance on Green Technology Innovation: The Mediating Effect of Financial Constraints. Sustainability 2023, 15, 3393. [Google Scholar] [CrossRef]
- Sun, C. Digital finance, technology innovation, and marine ecological efficiency. J. Coast. Res. 2020, 108, 109–112. [Google Scholar] [CrossRef]
- Psarrakis, D.; Kaili, E. Funding innovation in the era of weak financial intermediation: Crowdfunding and ICOs for SMEs in the context of the capital markets union. New Models Financ. Financ. Report. Eur. SMEs A Pract. View 2019, 71–82. [Google Scholar] [CrossRef]
- Lv, C.C.; Shao, C.H.; Lee, C.C. Green technology innovation and financial development: Do environmental regulation and innovation output matter? Energy Econ. 2021, 98, 105237. [Google Scholar] [CrossRef]
- Lin, C.; Ma, Y.; Su, D. Corporate governance and firm efficiency: Evidence from China’s publicly listed firms. Manag. Decis. Econ. 2009, 30, 193–209. [Google Scholar] [CrossRef]
- Zeng, W.; Li, L.; Huang, Y. Industrial collaborative agglomeration, marketization, and green innovation: Evidence from China’s provincial panel data. J. Clean. Prod. 2021, 279, 123598. [Google Scholar] [CrossRef]
- Sun, B.; Ruan, A.; Peng, B.; Liu, S. Pay disparities within top management teams, marketization and firms’ innovation: Evidence from China. J. Asia Pac. Econ. 2022, 27, 715–735. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Chetverikov, D.; Demirer, M.; Duflo, E.; Hansen, C.; Newey, W.; Robins, J. Double/Debiased Machine Learning for Treatment and Structural Parameters; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Yang, J.-C.; Chuang, H.-C.; Kuan, C.-M. Double machine learning with gradient boosting and its application to the Big N audit quality effect. J. Econom. 2020, 216, 268–283. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Ren, G. Quantifying the social impacts of the London Night Tube with a double/debiased machine learning based difference-in-differences approach. Transp. Res. Part A Policy Pract. 2022, 163, 288–303. [Google Scholar] [CrossRef]
- Farbmacher, H.; Huber, M.; Lafférs, L.; Langen, H.; Spindler, M. Causal mediation analysis with double machine learning. Econom. J. 2022, 25, 277–300. [Google Scholar] [CrossRef]
- Chiang, H.D.; Kato, K.; Ma, Y.; Sasaki, Y. Multiway cluster robust double/debiased machine learning. J. Bus. Econ. Stat. 2022, 40, 1046–1056. [Google Scholar] [CrossRef]
- Bodory, H.; Huber, M.; Lafférs, L. Evaluating (weighted) dynamic treatment effects by double machine learning. Econom. J. 2022, 25, 628–648. [Google Scholar] [CrossRef]
- Xi, L.; Zhao, H. The influence mechanism and data test of enterprise ESG performance on earnings sustainability. Manag. Rev. 2022, 34, 313–326. [Google Scholar]
- ISO 14001:2015; Environmental Management Systems—Requirements with Guidance for Use. ISO: Geneva, Switzerland, 2015.
- ISO 9001:2015; Quality Management Systems—Requirements. ISO: Geneva, Switzerland, 2015.
- Li, C.; Yan, X.; Song, M.; Yang, W. Financial innovation, technology and enterprises new three board listed company evidence. China Ind. Econ. 2020, 2020, 81–98. [Google Scholar]
- Gang, F.; Xiaolu, W.; Ma, G. The contribution of marketization to China’s economic growth. China Econ. 2012, 7, 4–14. [Google Scholar]
- Tao, Z.; Zhang, Z.; Liang, S. Digital economy, entrepreneurship, and high-quality economic development: Empirical evidence from urban China. Front. Econ. China 2022, 17, 393–426. [Google Scholar]
- Zhang, C.; Huang, L.Y.; Long, H.Y. Environmental regulations and green innovation of enterprises: Quasi-experimental evidence from China. Environ. Sci. Pollut. Res. 2023, 30, 60590–60606. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wen, C.; He, J. The influence of China Environmental Protection Tax Law on firm performance–evidence from stock markets. Appl. Econ. Lett. 2020, 27, 1044–1047. [Google Scholar] [CrossRef]
- Zeng, Q.; Tong, Y.J.; Yang, Y.Y. Can green finance promote green technology innovation in enterprises: Empirical evidence from China. Environ. Sci. Pollut. Res. 2023, 30, 87628–87644. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).