Quasi-Wireless Capacitive Power Transfer for Wire-Free Robotic Joints †
Abstract
1. Introduction
2. Materials and Methods
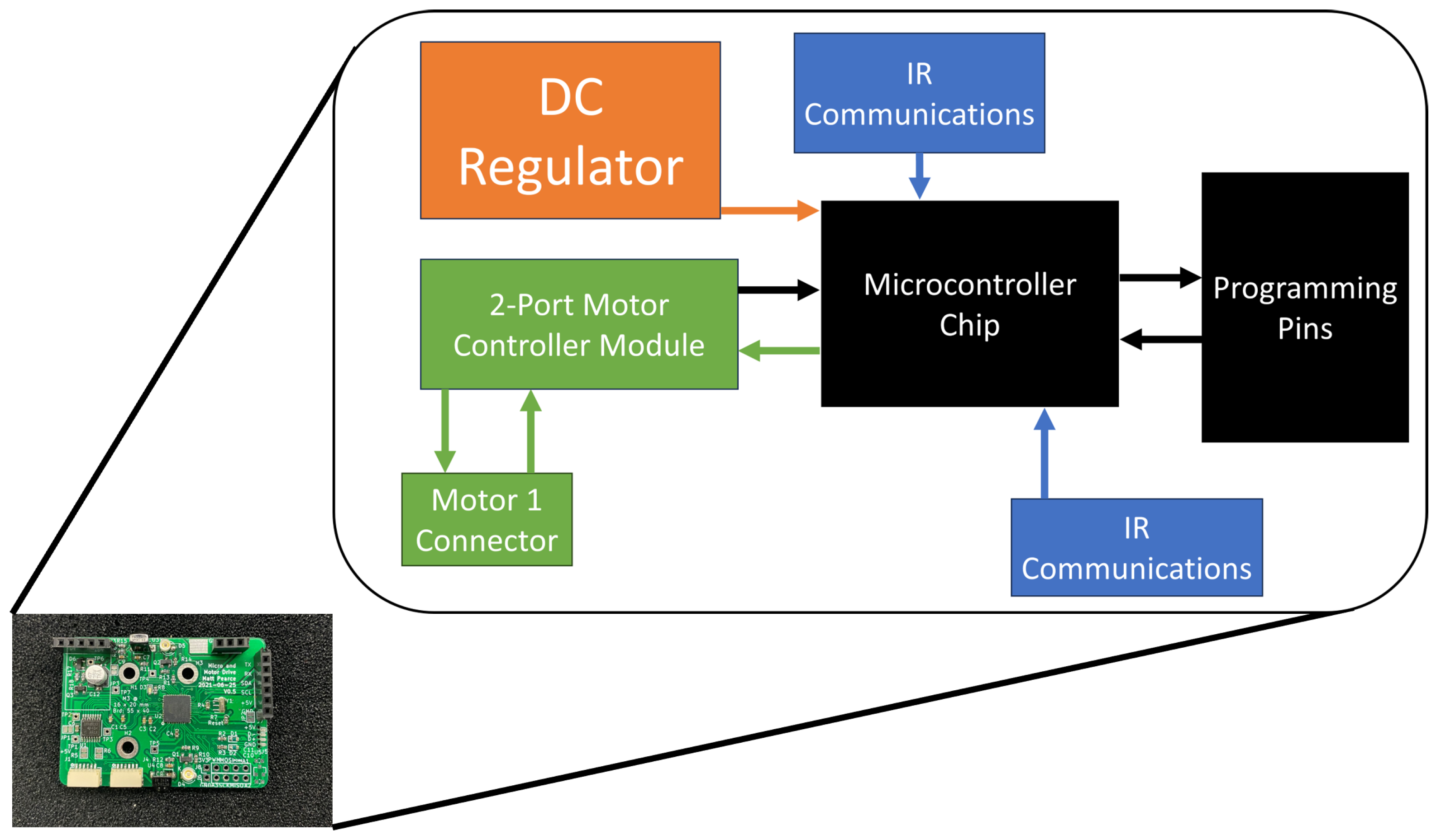
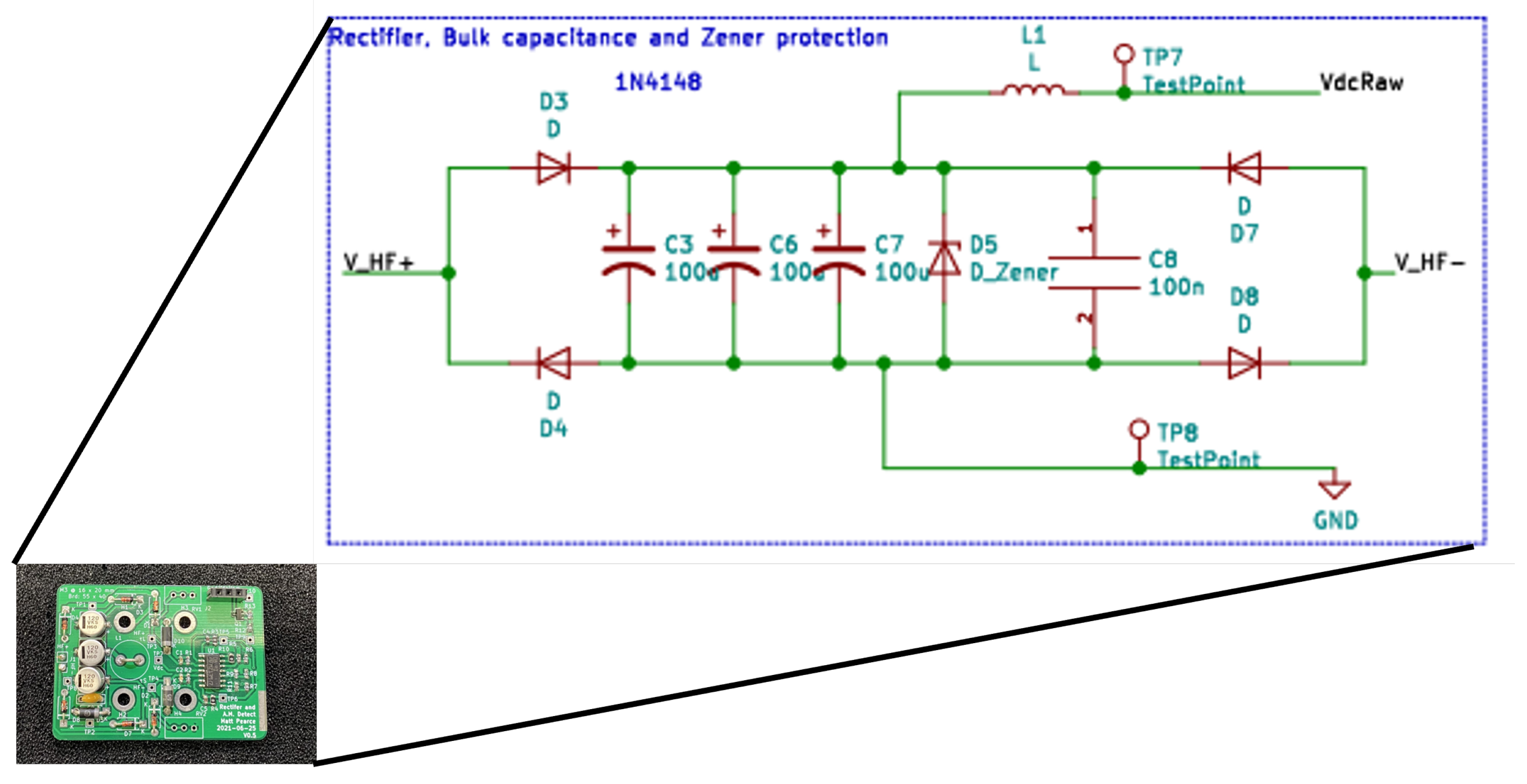
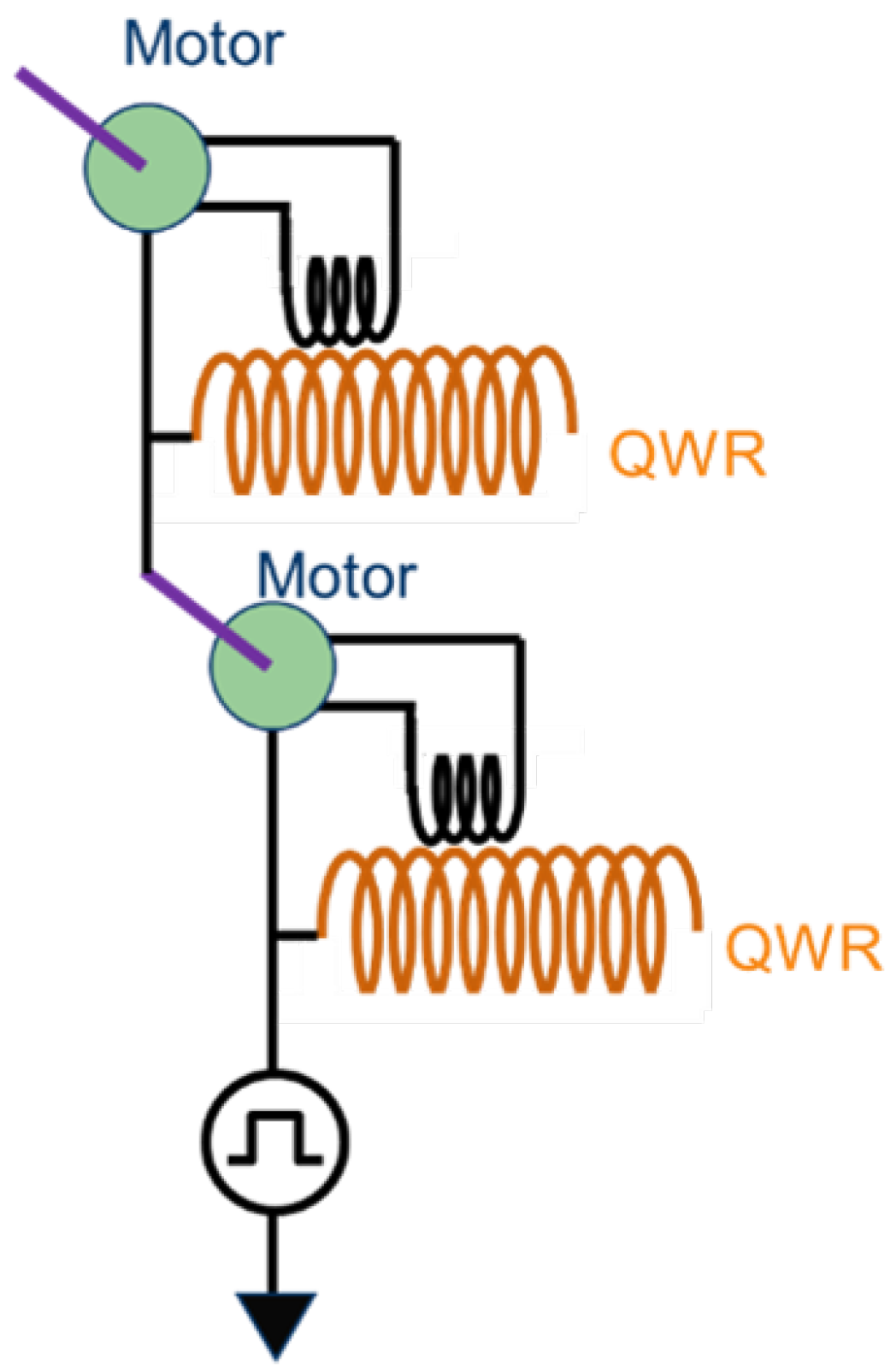
2.1. Experimental Setup
2.2. Control Scheme
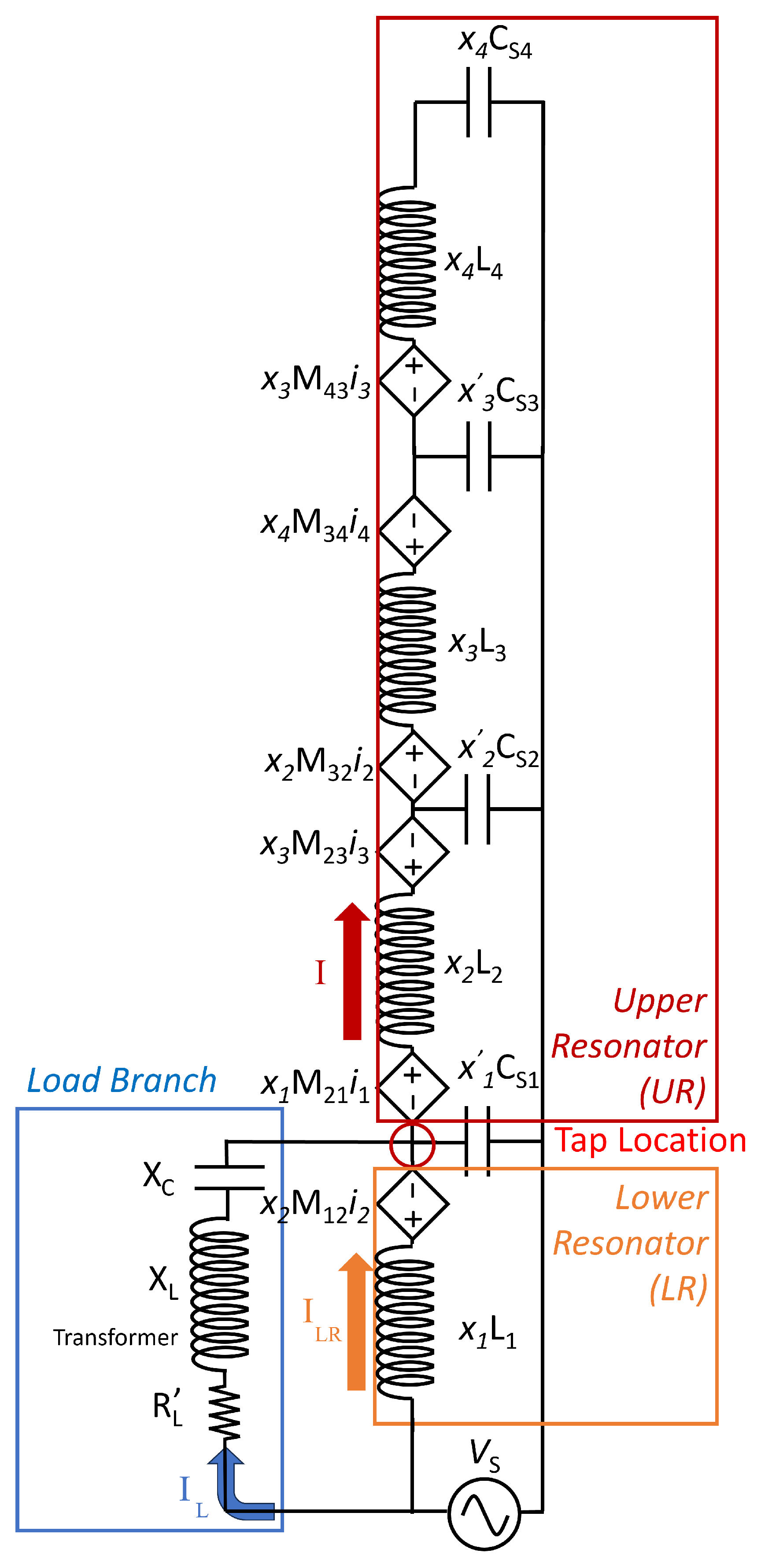
2.3. Unilateral Wiring Current Path
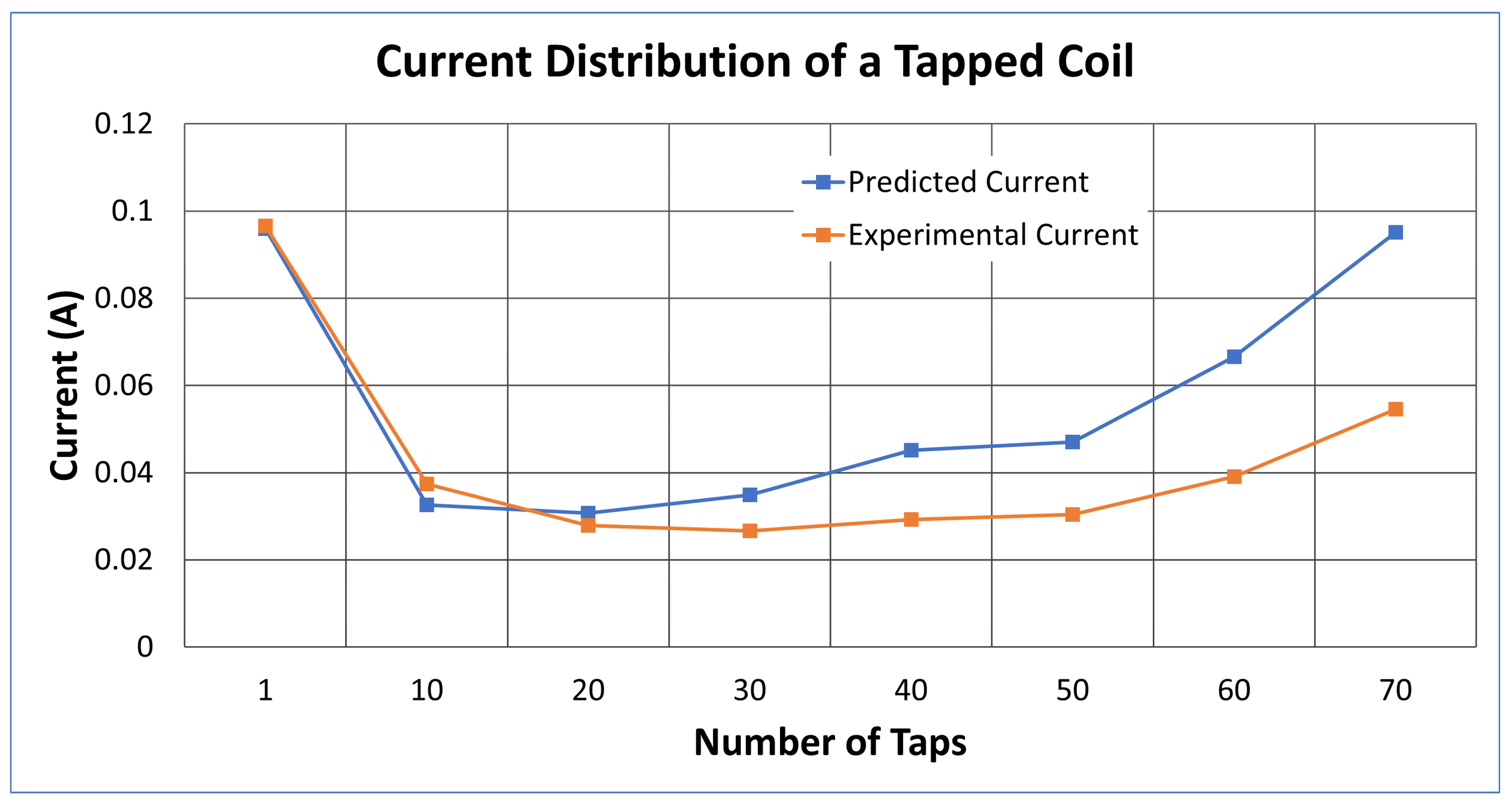
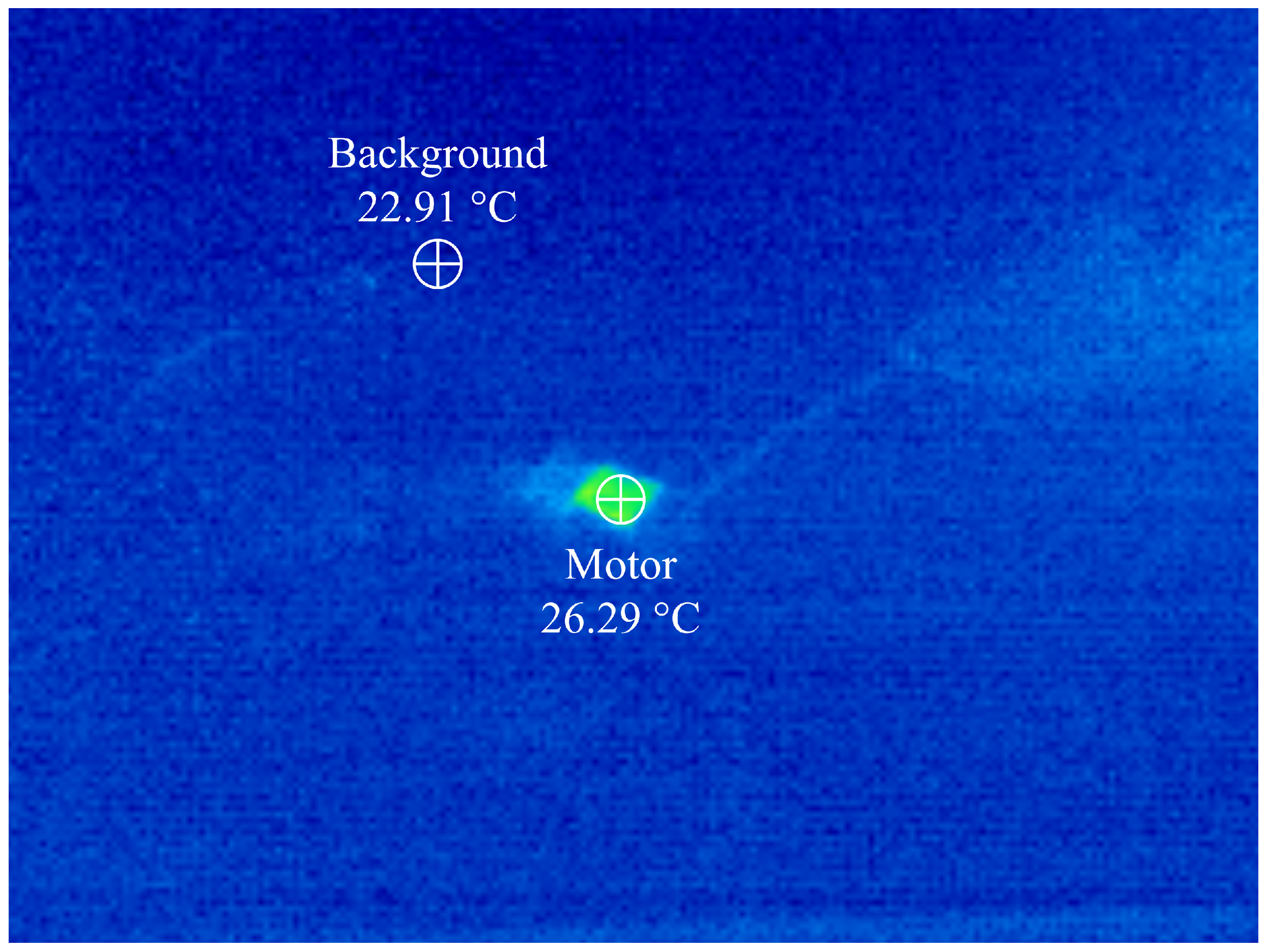
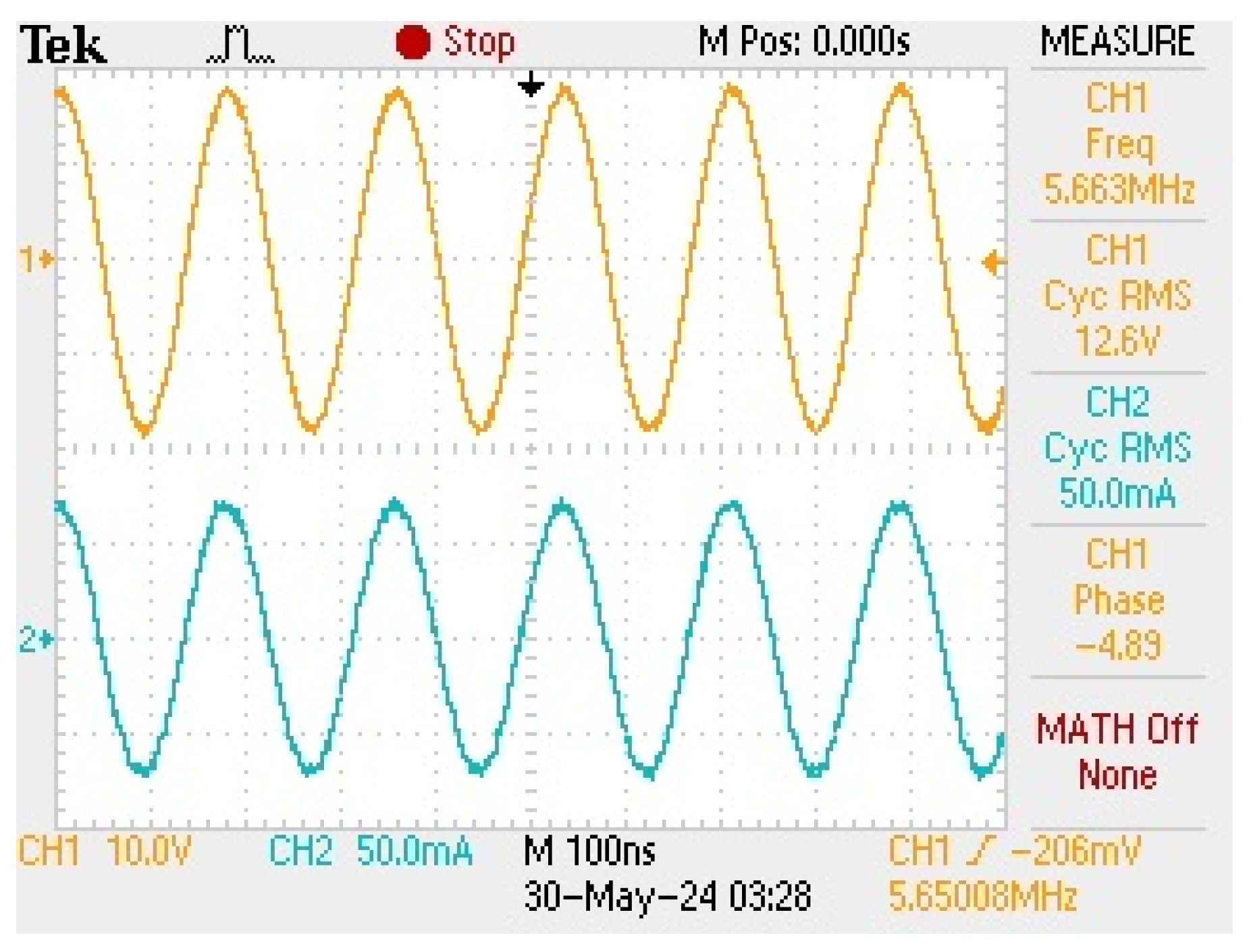
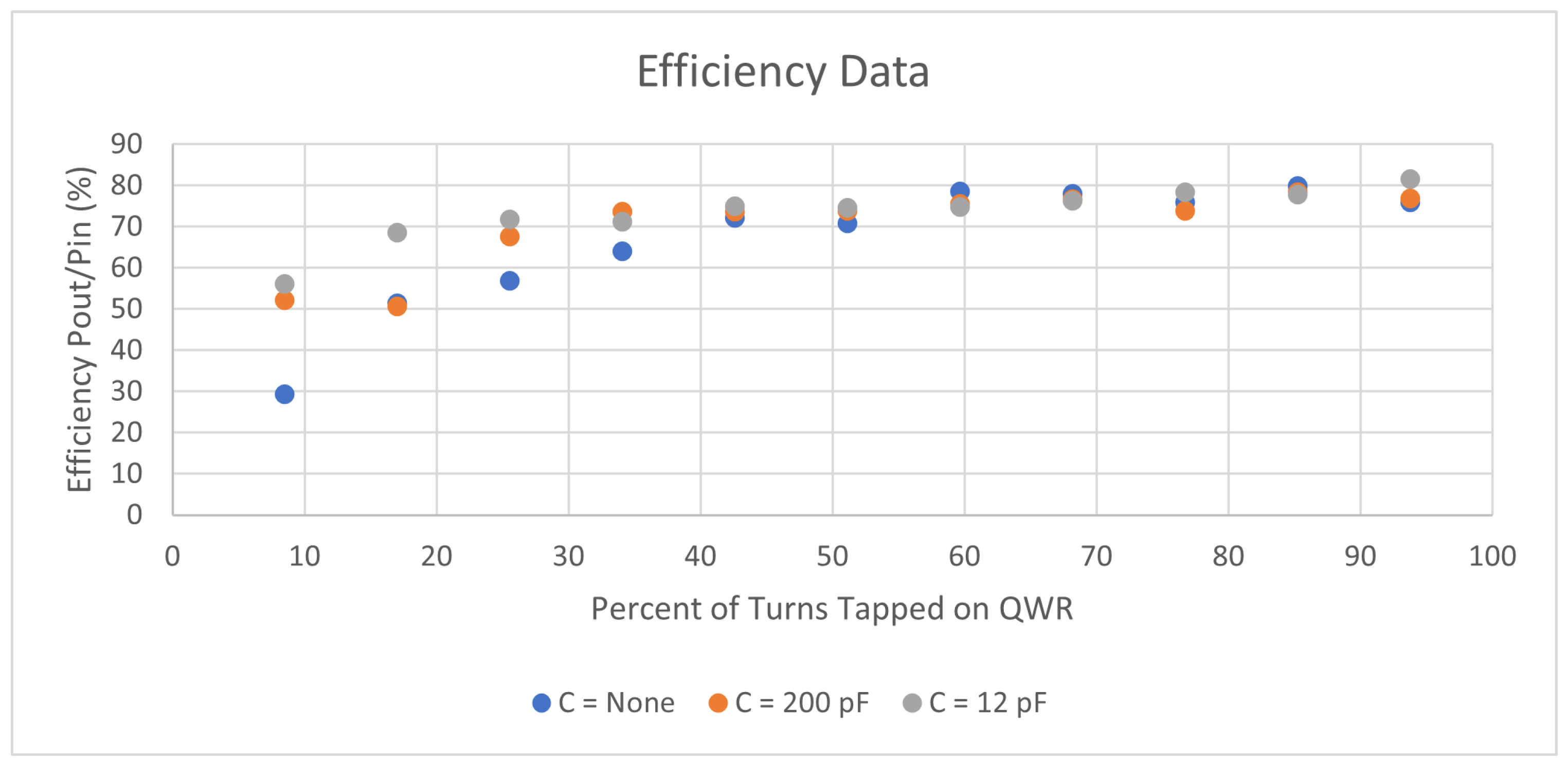
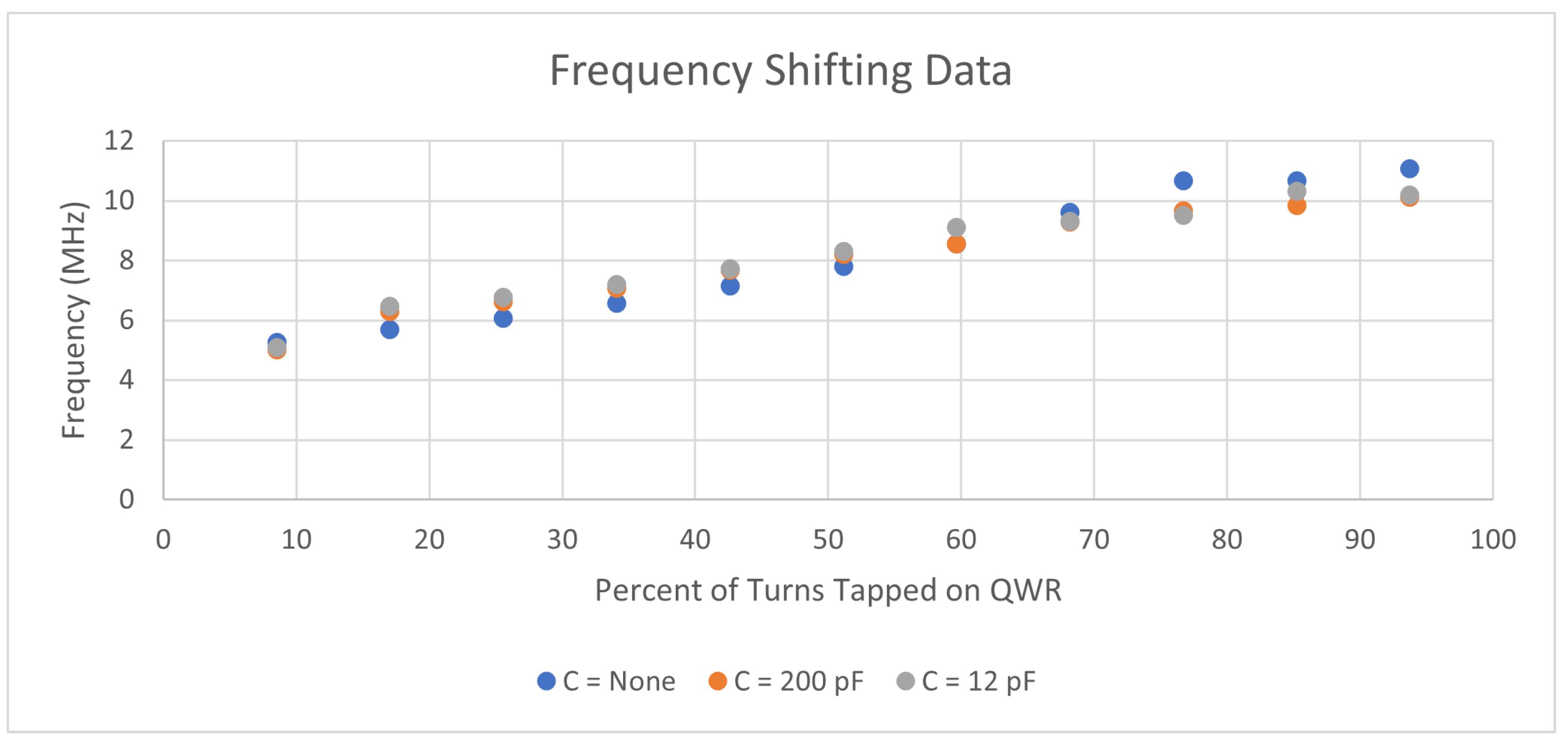
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marcrum, T.; Williams, J.; Johnson, C.; Pearce, M.; Vaughan, C.; Boyd, D. Impedance Matching a Quarter Wave Resonant Receiver to Improve Efficiency in Unipolar Capacitive Wireless Power Transfer. In Proceedings of the 2023 IEEE Wireless Power Technology Conference and Expo (WPTCE), San Diego, CA, USA, 4–8 June 2023; p. 4. [Google Scholar]
- Vital de Campos de Freitas, S.; Cezar Domingos, F.; Mirzavand, R.; Mousavi, P. Capacitive Resonant System to Charge Devices with Metallic Embodiments. In Proceedings of the 2019 IEEE Wireless Power Transfer Conference (WPTC), London, UK, 18–21 June 2019; pp. 347–350, ISSN 2573-7651. [Google Scholar] [CrossRef]
- Dai, J.; Ludois, D.C. A Survey of Wireless Power Transfer and a Critical Comparison of Inductive and Capacitive Coupling for Small Gap Applications. IEEE Trans. Power Electron. 2015, 30, 6017–6029. [Google Scholar] [CrossRef]
- Wallin, T.J.; Pikul, J.; Shepherd, R.F. 3D printing of soft robotic systems. Nat. Rev. Mater. 2018, 3, 84–100. [Google Scholar] [CrossRef]
- Slyper, R.; Hodgins, J. Prototyping robot appearance, movement, and interactions using flexible 3D printing and air pressure sensors. In Proceedings of the 2012 IEEE RO-MAN: The 21st IEEE International Symposium on Robot and Human Interactive Communication, Paris, France, 9–13 September 2012; pp. 6–11, ISSN 1944-9437. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Lang, Z.; Qi, C.; Jin, X.; Chen, X.; Xu, D. Analysis and Design of Rotary Wireless Power Transfer System with Dual-Coupled XLC/S Compensation Topology. IEEE Trans. Ind. Appl. 2023, 59, 2639–2649. [Google Scholar] [CrossRef]
- Stuhne, D.; Hoang, V.D.; Vasiljevic, G.; Bogdan, S.; Kovacic, Z.; Ollero, A.; Ebeid, E.S.M. Design of a Wireless Drone Recharging Station and a Special Robot End Effector for Installation on a Power Line. IEEE Access 2022, 10, 88719–88737. [Google Scholar] [CrossRef]
- Sun, Z.J.; Ye, B.; Qiu, Y.; Cheng, X.G.; Zhang, H.H.; Liu, S. Preliminary Study of a Legged Capsule Robot Actuated Wirelessly by Magnetic Torque. IEEE Trans. Magn. 2014, 50, 1–6. [Google Scholar] [CrossRef]
- Lee, J.; Ha, J.I. Wirelessly Powered Coil-Type Robot with 1D Self-Actuation Capability. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 2382–2388. [Google Scholar] [CrossRef]
- Lee, J.; Ha, J.I. Wirelessly Powered Coil-Type Robot with 2D Translational and 1D Rotational Self-Actuation Ability. In Proceedings of the 2018 15th International Conference on Ubiquitous Robots (UR), Honolulu, HI, USA, 26–30 June 2018; pp. 214–219. [Google Scholar] [CrossRef]
- Fiorillo, F.; Beatrice, C.; Bottauscio, O.; Manzin, A.; Chiampi, M. Approach to magnetic losses and their frequency dependence in Mn–Zn ferrites. Appl. Phys. Lett. 2006, 89, 122513. [Google Scholar] [CrossRef]
- Pasquale, M.; Fiorillo, F.; Coisson, M.; Beatrice, C. Magnetic permeability, losses and ferromagnetic resonance in ferrites under magnetic field bias from DC to the microwave regime. In Proceedings of the 2008 Conference on Precision Electromagnetic Measurements Digest, Broomfield, CO, USA, 8–13 June 2008; pp. 524–525, ISSN 2160-0171. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Hofmann, H.; Mei, Y.; Mi, C. A dynamic capacitive power transfer system with reduced power pulsation. In Proceedings of the 2016 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Knoxville, TN, USA, 4–6 October 2016; pp. 60–64. [Google Scholar] [CrossRef]
- Muharam, A.; Mostafa, T.M.; Nugroho, A.; Hapid, A.; Hattori, R. A Single-Wire Method of Coupling Interface in Capacitive Power Transfer for Electric Vehicle Wireless Charging System. In Proceedings of the 2018 International Conference on Sustainable Energy Engineering and Application (ICSEEA), Tangerang, Indonesia, 1–2 November 2018; pp. 39–43. [Google Scholar] [CrossRef]
- Sedehi, R.; Budgett, D.; Hu, A.P.; McCormick, D. Effects of Conductive Tissue on Capacitive Wireless Power Transfer. In Proceedings of the 2018 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (Wow), Montreal, QC, Canada, 3–7 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Funato, H.; Kobayashi, H.; Kitabayashi, T. Analysis of transfer power of capacitive power transfer system. In Proceedings of the 2013 IEEE 10th International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 22–25 April 2013; pp. 1015–1020, ISSN 2164-5264. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Mi, C. A Review on the Recent Development of Capacitive Wireless Power Transfer Technology. Energies 2017, 10, 1752. [Google Scholar] [CrossRef]
- Cheah, W.C.; Watson, S.A.; Lennox, B. Limitations of Wireless Power Transfer Technologies for Mobile Robots. Wirel. Power Transf. 2019, 6, 175–189. [Google Scholar] [CrossRef]
- Jin, K.; Zhou, W. Wireless Laser Power Transmission: A Review of Recent Progess. IEEE Trans. Power Electron. 2018, 34, 3842–3859. [Google Scholar] [CrossRef]
- Detka, K.; Gorecki, K. Wireless Power Transfer—A Review. Energies 2022, 15, 7236. [Google Scholar] [CrossRef]
- Faiz, M.I.S.; Awal, M.R.; Basar, M.R.; Latiff, N.A.A.; Yahya, M.S.; Saat, S. A Comparative Review on Acoustic and Inductive Power Transfer. J. Adv. Res. Appl. Sci. Eng. Technol. 2025, 44, 188–224. [Google Scholar] [CrossRef]
- Makhdoom, R.; Maji, S.; Sinha, S.; Etta, D.; Afridi, K. Multi-MHz In-Motion Capacitive Wireless Power Transfer System for Mobile Robots. In Proceedings of the 2022 Wireless Power Week (WPW), Bordeaux, France, 5–8 July 2022. [Google Scholar] [CrossRef]
- Yousuf, M.A.; Das, T.K.; Khallil, M.E.; Aziz, N.A.A.; Rana, M.J.; Hossain, S. Comparison Study of Inductive Coupling and Magnetic Resonant Coupling Method for Wireless Power Transmission of Electric Vehicles. In Proceedings of the 2021 2nd International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 5–7 January 2021. [Google Scholar] [CrossRef]
- Zhao, W.; Qu, X.; Lian, J.; Tse, C.K. A Family of Hybrid IPT Couplers With High Tolerance to Pad Misalignment. IEEE Trans. Power Electron. 2022, 37, 3617–3625. [Google Scholar] [CrossRef]
- Robinson, C.A.; Pearce, M.G.S.; Lu, H.; Van Neste, C.W. Capacitive Omnidirectional Position Sensor Using a Quarter Wave Resonator. IEEE Sens. J. 2022, 22, 15817–15824. [Google Scholar] [CrossRef]
- Van Neste, C.W.; Phani, A.; Larocque, A.; Hawk, J.E.; Kalra, R.; Banaag, M.J.; Wu, M.; Thundat, T. Quarter wavelength resonators for use in wireless capacitive power transfer. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017; pp. 229–234. [Google Scholar] [CrossRef]
- Pickering, A.K.; Hull, R.; Hawk, J.E.; Phani, A.; Neste, C.W.V.; Thundat, T. Quasi-wireless surface power and control for battery-free robotics. Wirel. Power Transf. 2015, 2, 134–142. [Google Scholar] [CrossRef]



| IPT | MRPT | CPT | APT | |
|---|---|---|---|---|
| Pros | Most commonly used WPT technique [18] Capable of high power transmission level (kW) [19] High power transfer efficiency [19,20] Low sensitivity to environmental factors (pollutants and weather) [21] | Employs resonance frequency matching of Tx and Rx, which allows for less reliance on alignment [18,19] Range can be extended using intermediate coils that are tuned to the same system’s resonant frequency [22,23] | Transfer power through metallic materials without significant eddy current losses [19,20,22] Less reliance on Tx and Rx alignment [18] Implementation is often more cost efficient than with IPT systems [20] | Most secure WPT methodology due to the safe transmission of sound waves in the required frequency band [21] Resistivity to electromagnetic interference due to the transfer of energy occurring through sound waves [18] |
| Cons | Potential of significant eddy current losses [19] Potential for cross-talk due to inductance leakage [23] Challenging to transmit power through objects such as walls [21] | Complex systems, potentially consisting of additional matching networks [18] High sensitivity to frequency shifts due to resonance frequency aligned Tx and Rx [18] | Bipolar CPT requires many capacitive plates for transmission [18] Single-Wire CPT requires a large counterpoise [14] Normally, lower transmission efficiency and distance than IPT [18,20] | Relatively low power transmission levels (mW), often being used in bio-medical devices [18] Hardly explored in robotics due to low transmission efficiency [18] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcrum, T.; Williams, J.-C.; Johnson, C.S.; Pearce, M.; Pope, C.; Van Neste, C.W.; Vaughan, C.; Boyd, D. Quasi-Wireless Capacitive Power Transfer for Wire-Free Robotic Joints. Energies 2024, 17, 2858. https://doi.org/10.3390/en17122858
Marcrum T, Williams J-C, Johnson CS, Pearce M, Pope C, Van Neste CW, Vaughan C, Boyd D. Quasi-Wireless Capacitive Power Transfer for Wire-Free Robotic Joints. Energies. 2024; 17(12):2858. https://doi.org/10.3390/en17122858
Chicago/Turabian StyleMarcrum, Tyler, John-Caleb Williams, Christopher S. Johnson, Matthew Pearce, Carson Pope, C. W. Van Neste, Charles Vaughan, and Darren Boyd. 2024. "Quasi-Wireless Capacitive Power Transfer for Wire-Free Robotic Joints" Energies 17, no. 12: 2858. https://doi.org/10.3390/en17122858
APA StyleMarcrum, T., Williams, J.-C., Johnson, C. S., Pearce, M., Pope, C., Van Neste, C. W., Vaughan, C., & Boyd, D. (2024). Quasi-Wireless Capacitive Power Transfer for Wire-Free Robotic Joints. Energies, 17(12), 2858. https://doi.org/10.3390/en17122858







