Non-Linear Phenomena in Voltage and Frequency Converters Supplying Non-Thermal Plasma Reactors
Abstract
1. Introduction
2. Plasma Reactors as Electrical Energy Receivers
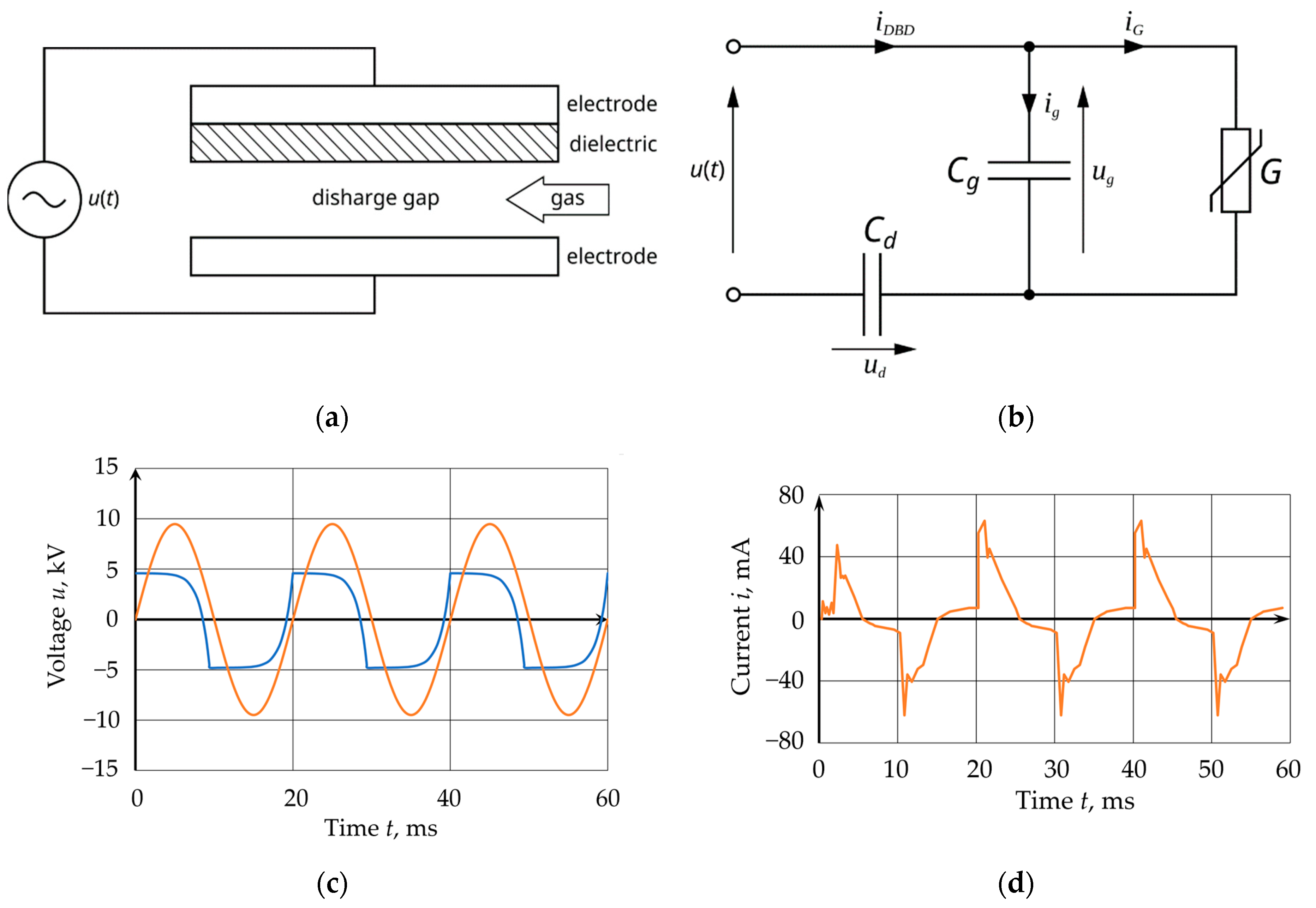
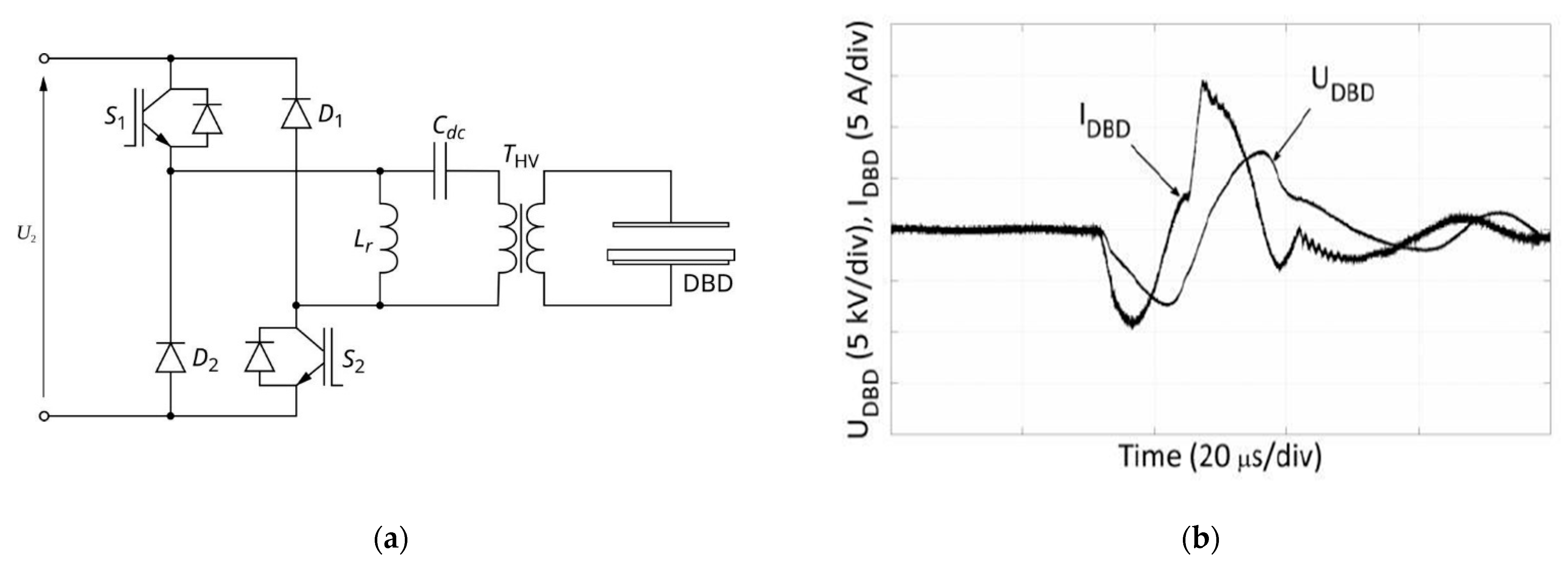
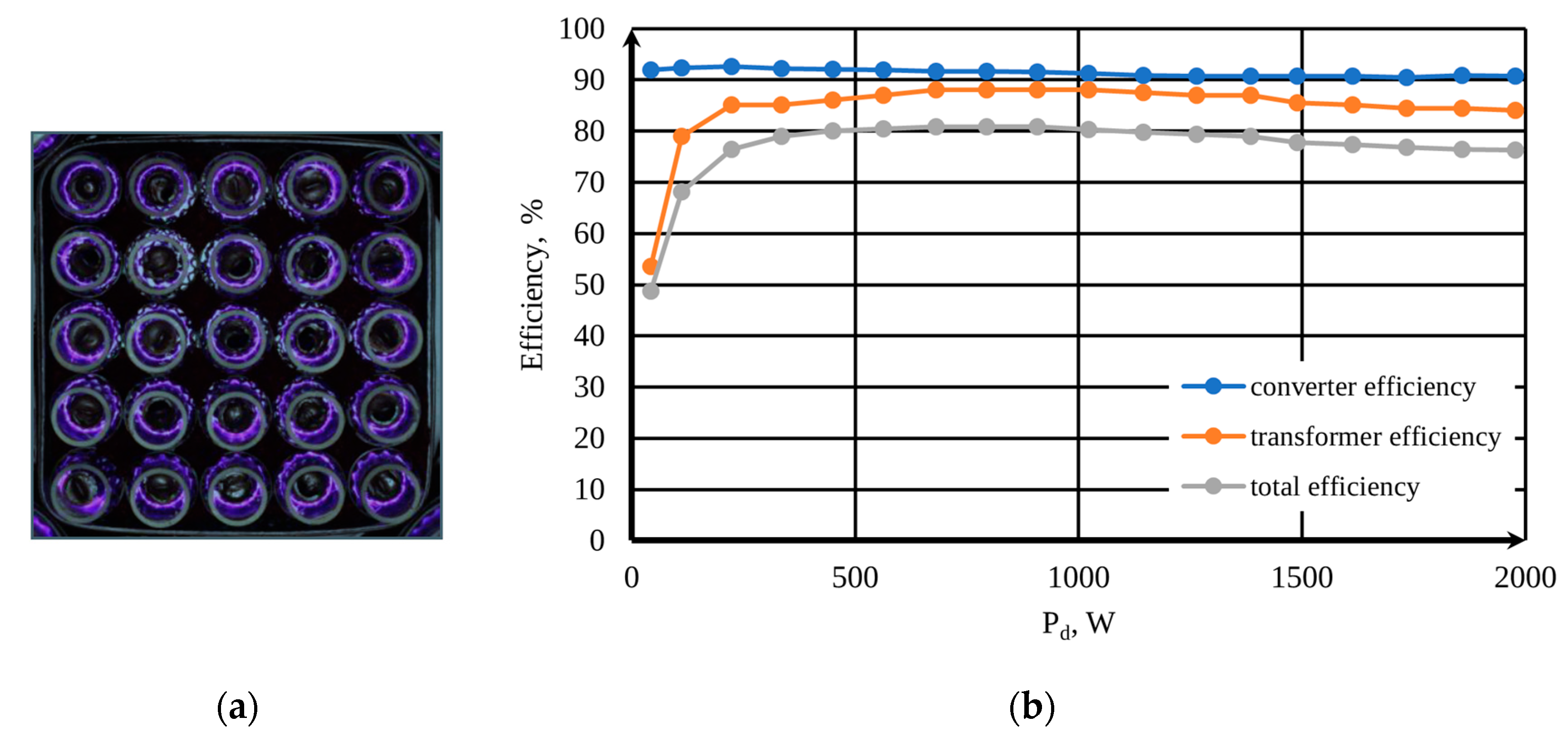
2.1. Plasma Reactor with DBD
- -
- Geometric parameters of the discharge elements (shape, dimensions and surface Quality of electrodes, type and thickness of dielectric);
- -
- Physical and chemical parameters of the input gas (type and composition of gas, presence of impurities, temperature, humidity);
- -
- Electrical parameters of the power supply system (voltage value, frequency and shape, internal impedance).
2.2. GAD Plasma Reactor
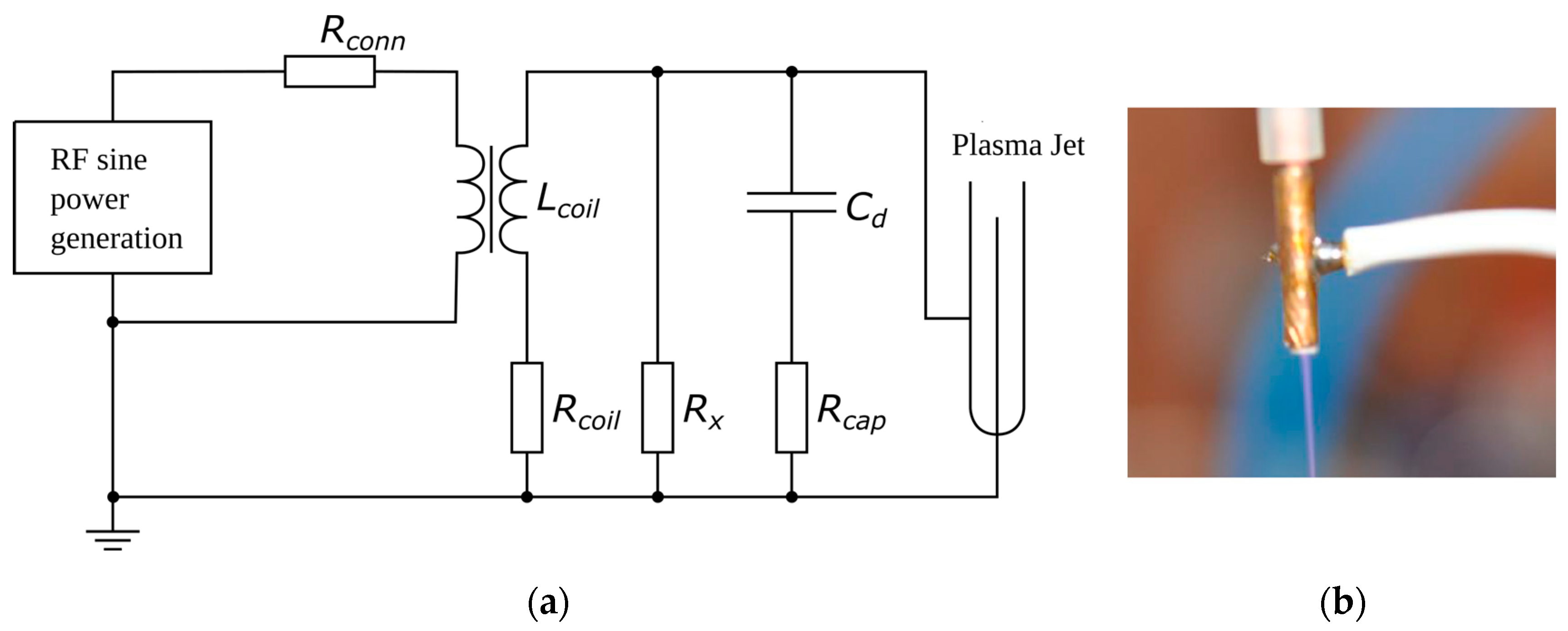
2.3. Atmospheric Pressure Plasma Jets
3. Non-Linear Phenomena in PSS of PR Producing APCP
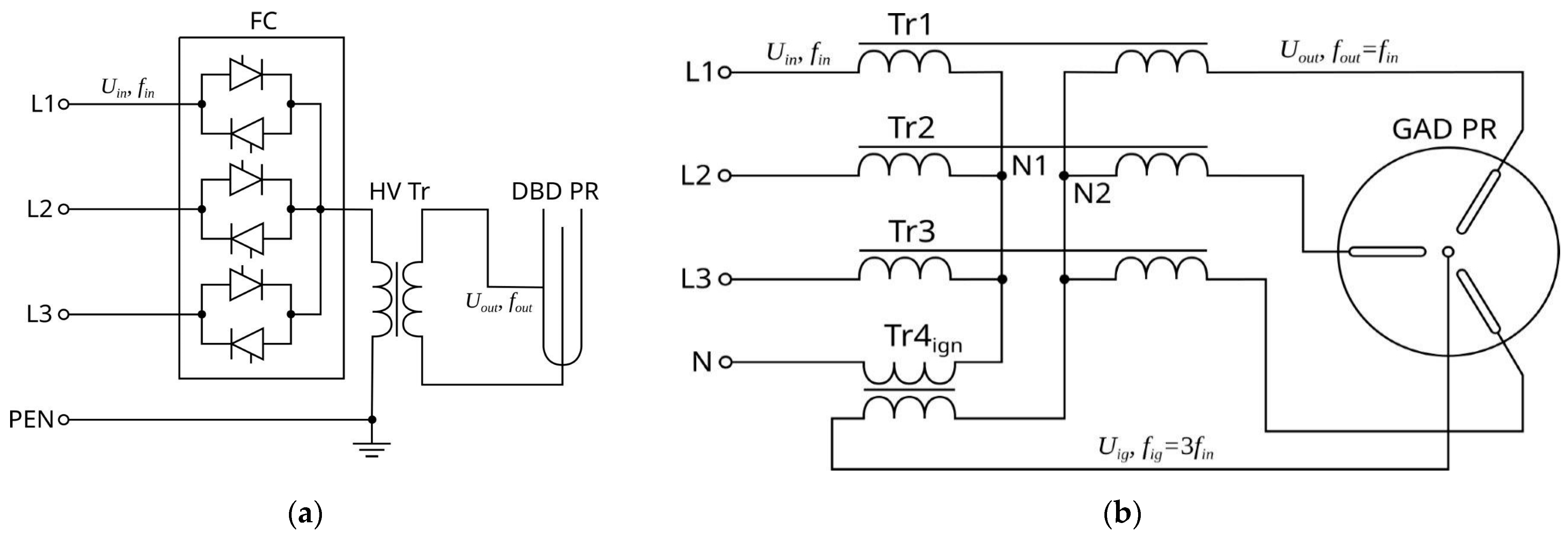
3.1. Generation of Higher Harmonics
- -
- In each phase, one magnetic or thyristor switch is in the conducting state, , Figure 7a,
- -
- Magnetic or thyristor switches in two phases are in the conducting state for part of period Figure 7b,
- -
- In each phase of the three-phase circuit, three thyristors (magnetic switches) are conducting for part of the period equal to π/6, Figure 7c.
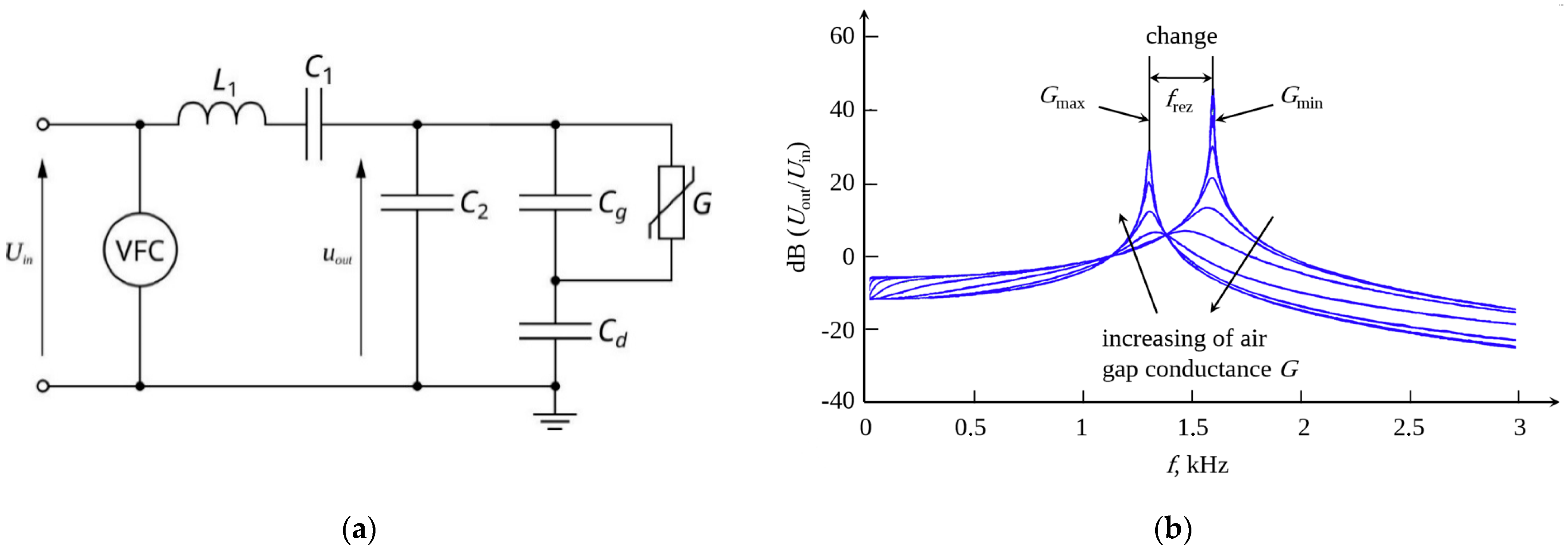
3.2. Resonance Phenomenon
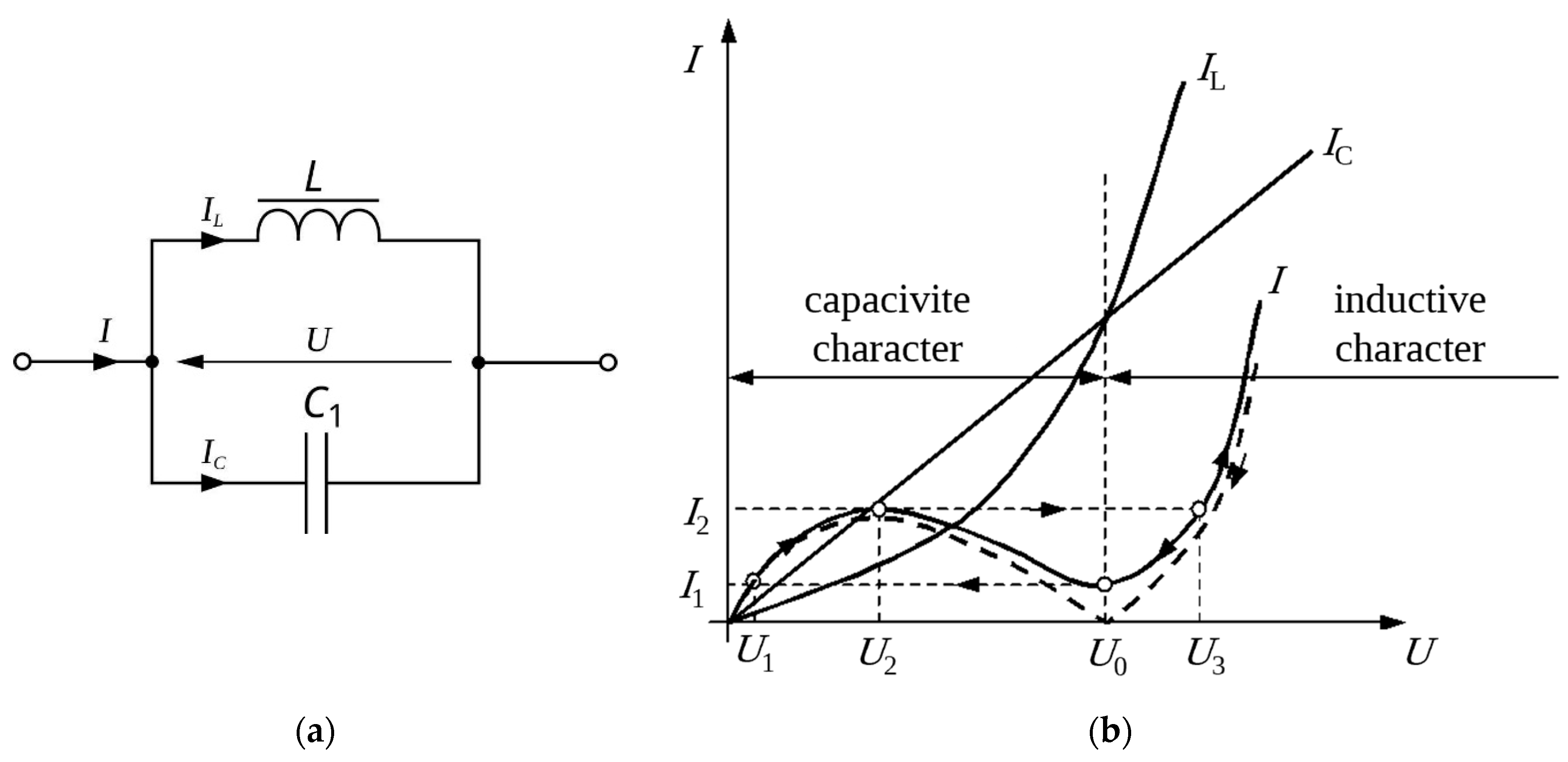
3.3. Phenomena of Ferroresonance
3.4. Pulsed Power Energy and the Phenomenon of SOs in PPS
4. Examples of APCP Reactor Power Supply Systems
4.1. PSS of PR Using Higher Harmonics
4.2. PSS of PR Using Resonance Phenomena
4.3. PSS of PR Using IFR and UFR Phenomena
4.4. PSS of PR Using Pulsed Power and the Phenomenon of SOs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stryczewska, H.D.; Boiko, O.; Stępień, M.A.; Lasek, P.; Yamazato, M.; Higa, A. Selected Materials and Technologies for Electrical Energy Sector. Energies 2023, 16, 4543. [Google Scholar] [CrossRef]
- Li, S.R.; Ongis, M.; Manzolin, G.; Gallucci, F. Non-thermal plasma-assisted capture and conversion of CO2. Chem. Eng. J. 2021, 410, 128335. [Google Scholar] [CrossRef]
- Barkhordari, A.; Karimian, S.; Rodero, A.; Krawczyk, D.A.; Iman Mirzaei, S.I.; Falahat, A. Carbon Dioxide Decomposition by a Parallel-Plate Plasma Reactor: Experiments and 2-D Modelling. Appl. Sci. 2021, 11, 10047. [Google Scholar] [CrossRef]
- Bárdos, L.; Baránková, H. Cold atmospheric plasma: Sources, processes, and applications. Thin Solid Films 2010, 518, 6705–6713. [Google Scholar] [CrossRef]
- Cretu, D.; Burlică, R.; Astanei, D.; Dirlău, J.-D.; Beniugă, O. Energy efficiency evaluation of HV power supplies for non-thermal plasma generation. In Proceedings of the 8th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 21–23 May 2019. [Google Scholar]
- Fanellia, F.; Fracassi, F. Atmospheric pressure non-equilibrium plasma jet technology: General features, specificities and applications in surface processing of materials. Surf. Coat. Technol. 2017, 322, 174–201. [Google Scholar] [CrossRef]
- Mohapatro, S.; Rajanikanth, B.S. A core study on NOx removal in diesel exhaust by pulsed/AC/DC electric discharge plasma. In Proceedings of the IEEE 2011 International Conference on Power and Energy Systems (ICPS), Chennai, India, 22–24 December 2011; IEEE Explore Digital Library: New York, NY, USA, 2011; pp. 1–6. [Google Scholar]
- Massines, F.; Sarra-Bournet, C.; Fanelli, F.; Naudé, N.; Gherardi, N. Atmospheric pressure low temperature direct plasma technology: Status and challenges for thin film deposition. Plasma Process. Polym. 2012, 9, 1041–1073. [Google Scholar] [CrossRef]
- Wedaa, H.; Abdel-Salam, M.; Ahmed, A.; Mizuno, A. NO removal using dielectric barrier discharges in a multirod reactor stressed by AC and pulsed high voltages. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1743–1751. [Google Scholar] [CrossRef]
- Eliasson, B.; Hirth, M.; Kogelschatz, U. Ozone synthesis from oxygen in dielectric barrier discharges. J. Phys. D Appl. Phys. 1987, 20, 1421. [Google Scholar] [CrossRef]
- Eliasson, B.; Kogelschatz, U. Modelling and applications of silent discharge plasmas. IEEE Trans. Plasma Sci. 1991, 19, 309–323. [Google Scholar] [CrossRef]
- Matsumoto, T.; Wang, D.; Namihira, T.; Akiyama, H. Performances of 2 nanoseconds pulsed discharge plasma. Jpn. J. Appl. Phys. 2011, 50, 08JF14. [Google Scholar] [CrossRef]
- Akiyama, H.; Sakugawa, T.; Namihira, T.; Takaki, K.; Minamitani, Y.; Shimomura, N. Industrial applications of pulsed power technology. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1051–1064. [Google Scholar] [CrossRef]
- Mohapatro, S.; Allamsetty, S.; Madhukar, A.; Sharma, N.K. Nanosecond pulse discharge based nitrogen oxides treatment using different electrode configurations. High Voltage 2017, 2, 60–68. [Google Scholar] [CrossRef]
- Liguori, A.; Pollicino, A.; Stancampiano, A.; Tarterini, F.; Focarete, M.L.; Colombo, V.; Gherardi, M. Deposition of plasma-polymerized polyacrylic acid coatings by a nonequilibrium atmospheric pressure nanopulsed plasma jet. Plasma Process. Polym. 2016, 13, 375–386. [Google Scholar] [CrossRef]
- Huiskamp, T.; Takamura, N.; Namihira, T.; Pemen, A.J.M. Matching a Nanosecond Pulse Source to a Streamer Corona Plasma Reactor with a DC Bias. IEEE Trans. Plasma Sci. 2015, 43, 617–624. [Google Scholar] [CrossRef]
- Młotek, M.; Reda, E.; Reszke, E.; Ulejczyk, B.; Krawczyk, K. A gliding discharge reactor supplied by a ferro-resonance system for liquid toluene decomposition. Chem. Eng. Res. Des. 2016, 111, 277–283. [Google Scholar] [CrossRef]
- Brasov Felea, I.C.; Hnatiuc, E.; Astanei, D. Characterization of cold plasma glidarc reactors. In Proceedings of the International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 2–3 September 2021. [Google Scholar]
- Komarzyniec, G.; Aftyka, M. Cooperation of the Plasma Reactor with a Converter Power Supply Equipped with a Transformer with Special Design. Energies 2023, 16, 6825. [Google Scholar] [CrossRef]
- Stryczewska, H.D. Supply Systems of Non-Thermal Plasma Reactors. Construction Review with Examples of Applications. Appl. Sci. 2020, 10, 3242. [Google Scholar] [CrossRef]
- Winter, J.; Brandenburg, R.; Weltmann, K.D. Atmospheric pressure plasma jets: An overview of devices and new directions. Plasma Sources Sci. Technol. 2015, 24, 064001. [Google Scholar] [CrossRef]
- Lu, X.; Laroussi, M.; Puech, V. On atmospheric-pressure non-equilibrium plasma jets and plasma bullets. Plasma Sources Sci. Technol. 2012, 21, 034005. [Google Scholar] [CrossRef]
- Chen, F.; Liu, S.; Liu, J.; Huang, S.; Xia, G.; Song, J.; Xu, W.; Sun, J.; Liu, X. Surface modification of tube inner wall by transferred atmospheric pressure plasma. Appl. Surf. Sci. 2016, 389, 967–976. [Google Scholar] [CrossRef]
- Guaitella, O.; Sobota, A. The impingement of a kHz helium atmospheric pressure plasma jet on a dielectric surface. J. Phys. D Appl. Phys. 2015, 48, 255202. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Z.; Huang, Q.; Tan, X.; Lu, X.; Ostrikov, K. Atmospheric-pressure plasma jets: Effect of gas flow, active species, and snake-like bullet propagation. Phys. Plasmas 2013, 20, 023503. [Google Scholar] [CrossRef]
- Laroussi, M.; Akan, T. Arc-free atmospheric pressure cold plasma jets: A review. Plasma Process. Polym. 2007, 4, 777–788. [Google Scholar] [CrossRef]
- Stryczewska, H.D.; Stępień, M.A.; Boiko, O. Plasma and Superconductivity for the Sustainable Development of Energy and the Environment. Energies 2022, 15, 4092. [Google Scholar] [CrossRef]
- Foest, R.; Schmidt, M.; Becker, K. Microplasmas, an emerging field of low-temperature plasma science and technology. Int. J. Mass Spectrom. 2006, 248, 87–102. [Google Scholar] [CrossRef]
- Mariotti, D.; Sankaran, R.M. Microplasmas for nanomaterials synthesis. J. Phys. D Appl. Phys. 2010, 43, 323001. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Q. Microplasma: A new generation of technology for functional nanomaterial synthesis. Plasma Chem. Plasma Process. 2015, 35, 925–962. [Google Scholar] [CrossRef]
- Fanelli, F.; Fracassi, F. Aerosol-assisted atmospheric pressure cold plasma deposition of organic–inorganic nanocomposite coatings. Plasma Chem. Plasma Process. 2014, 34, 473–487. [Google Scholar] [CrossRef]
- Mariotti, D.; Belmonte, T.; Benedikt, J.; Velusamy, T.; Jain, G.; Švrček, V. Low temperature atmospheric pressure plasma processes for ‘‘green’’ third generation photovoltaics. Plasma Process. Polym. 2016, 13, 70–90. [Google Scholar] [CrossRef]
- Babaeva, N.Y.; Kushner, M.J. Interaction of multiple atmospheric-pressure microplasma jets in small arrays: He/O2 into humid air. Plasma Sources Sci. Technol. 2014, 23, 015007. [Google Scholar] [CrossRef]
- Penkov, O.V.; Khadem, M.; Lim, W.S.; Kim, D.E. A review of recent applications of atmospheric pressure plasma jets for materials processing. J. Coat. Technol. Res. 2015, 12, 225–235. [Google Scholar] [CrossRef]
- Malik, M.A.; Schoenbach, K.H.; Abdel-Fattah, T.M.; Heller, R.; Jiang, C. Low Cost Compact Nanosecond Pulsed Plasma System for Environmental and Biomedical Applications. Plasma Chem. Plasma Process. 2017, 37, 59–76. [Google Scholar] [CrossRef]
- Koliadimas, A.; Apostolopoulos, D.; Svarnas, P.; Sklias, K.; Athanasopoulos, D.K.; Mitronikas, E.D. Micro-Processor Based Modular Pulsed High Voltage Power Supply for Driving Atmospheric-Pressure DBD Plasmas. IEEE Trans. Plasma Sci. 2019, 47, 1621–1628. [Google Scholar] [CrossRef]
- Tsai, M.T.; Ke, C.W. Design and implementation a high-voltage high-frequency pulse power generation system for plasma applications. In Proceedings of the 14th Power Electronic and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 1556–1560. [Google Scholar]
- Yong-Nong, C.; Chih-Ming, K. Design of Plasma Generator Driven by High-frequency High-voltage Power Supply. J. Appl. Res. Technol. 2013, 11, 225–234. [Google Scholar] [CrossRef]
- Sánchez-Trujillo, A.B.; Martínez-Méndez, R.; Portillo-Rodríguez, O.; Vázquez-Guzman, G. Prototype of a Plasma Generator for Electrosurgery. In Proceedings of the 13th International Conference on Power Electronics (CIEP), Guanajuato, Mexico, 20–23 June 2016; pp. 188–191. [Google Scholar]
- Aftyka, M. Analiza Porównawcza Zasilaczy Wieloelektrodowych Reaktorów Nietermicznej Plazmy Generowanej Ślizgajacym sie Wyładowaniem Łukowym (Comparative Analysis of Power Supplies for Multi-Electrode Reactors Generating Non-Thermal Plasma with a Gliding Arc Discharge). Ph.D. Thesis, Lublin University of Technology, Lublin, Poland, 2023. (In Polish). [Google Scholar]
- Jakubowski, T. Rezonansowy Przekształtnik Tranzystorowy do Zasilania Reaktora Plazmy Nietermicznej (Resonant Transistor Converter for Powering a Non-Thermal Plasma Reactor). Ph.D. Thesis, West Pomeranian University of Technology ZUT, Szczecin, Poland, 2012. (In Polish). [Google Scholar]
- Kalisiak, S.; Holub, M.; Jakubowski, T. Resonant inverter with output voltage pulse-phase-shift control for DBD plasma reactor supply. In Proceedings of the 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–9. [Google Scholar]
- Mućko, J. Corona treatment system with resonant inverter selected properties. In Proceedings of the 13th Power Electronic and Motion Control Conference, Poznań, Poland, 1–3 September 2008; pp. 1316–1320. [Google Scholar]
- Pacheco-Sotelo, J.; Valdivia-Barrientos, R.; Pacheco-Pacheco, M.; Ramos-Flores, F.; Soria-Arguello, G.; Ibañez-Olvera, M. Impulse Three Phase Power Supply Used for a Gliding Plasma Discharge. J. Phys. Conf. Ser. 2015, 591, 012062. [Google Scholar]
- Krupski, P.; Stryczewska, H.D. A Gliding Arc Microreactor Power Supply System Based on Push–Pull Converter Topology. Appl. Sci. 2020, 10, 3989. [Google Scholar] [CrossRef]









| Quantity | Unit of Measure | Value |
|---|---|---|
| V | 2200 | |
| V/m | 10,000 | |
| W | 200 | |
| W/m | 2000 | |
| rad | 0.261 | |
| m/s | 5, 10, 15, 20, 25 | |
| m | 10−2 | |
| Um | V | 4000, 5000, 6000, 7000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komarzyniec, G.K.; Stryczewska, H.D.; Boiko, O. Non-Linear Phenomena in Voltage and Frequency Converters Supplying Non-Thermal Plasma Reactors. Energies 2024, 17, 2846. https://doi.org/10.3390/en17122846
Komarzyniec GK, Stryczewska HD, Boiko O. Non-Linear Phenomena in Voltage and Frequency Converters Supplying Non-Thermal Plasma Reactors. Energies. 2024; 17(12):2846. https://doi.org/10.3390/en17122846
Chicago/Turabian StyleKomarzyniec, Grzegorz Karol, Henryka Danuta Stryczewska, and Oleksandr Boiko. 2024. "Non-Linear Phenomena in Voltage and Frequency Converters Supplying Non-Thermal Plasma Reactors" Energies 17, no. 12: 2846. https://doi.org/10.3390/en17122846
APA StyleKomarzyniec, G. K., Stryczewska, H. D., & Boiko, O. (2024). Non-Linear Phenomena in Voltage and Frequency Converters Supplying Non-Thermal Plasma Reactors. Energies, 17(12), 2846. https://doi.org/10.3390/en17122846








