A New Tailored Approach to Calculate the Optimal Number of Outdoor Air Changes in School Building HVAC Systems in the Post-COVID-19 Era
Abstract
1. Introduction
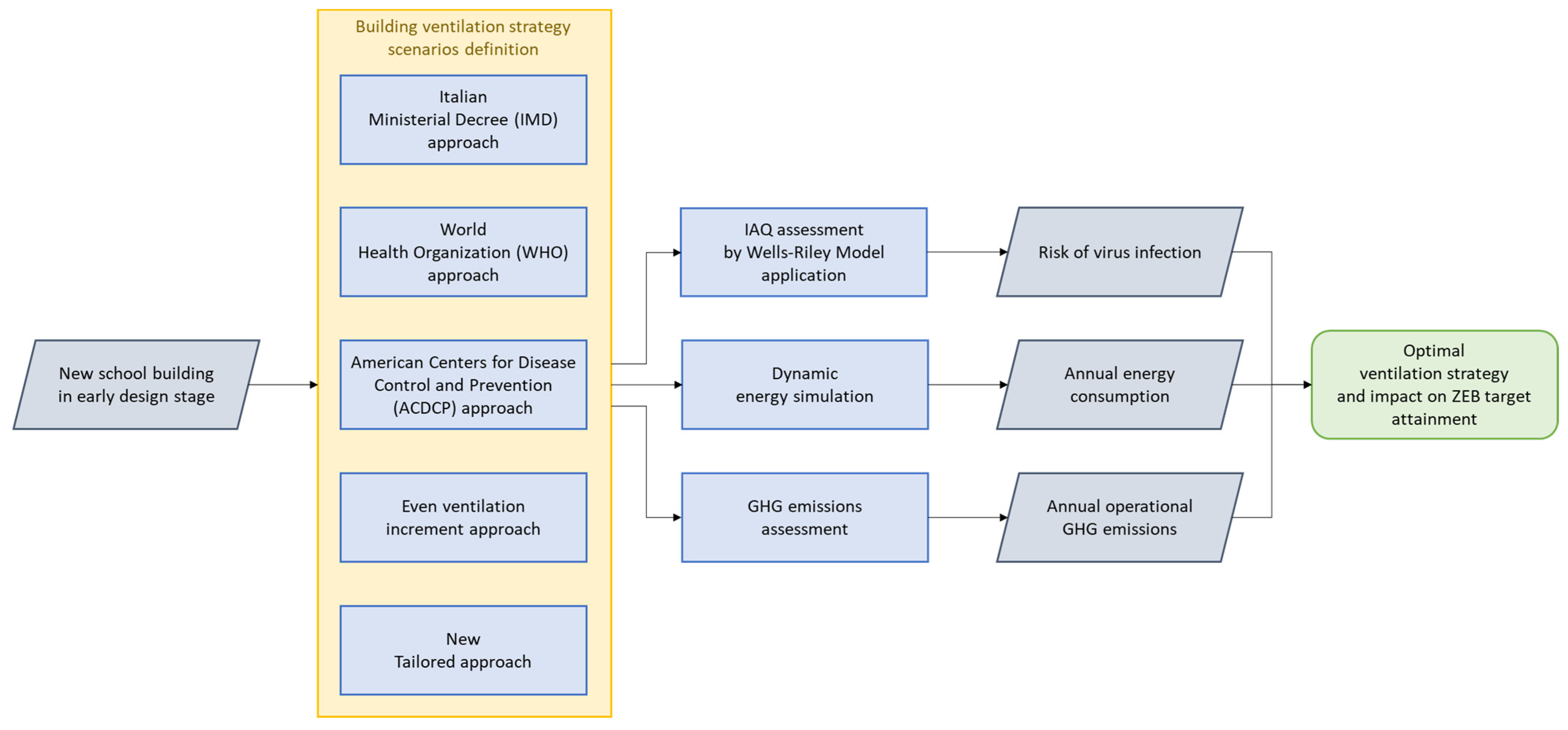
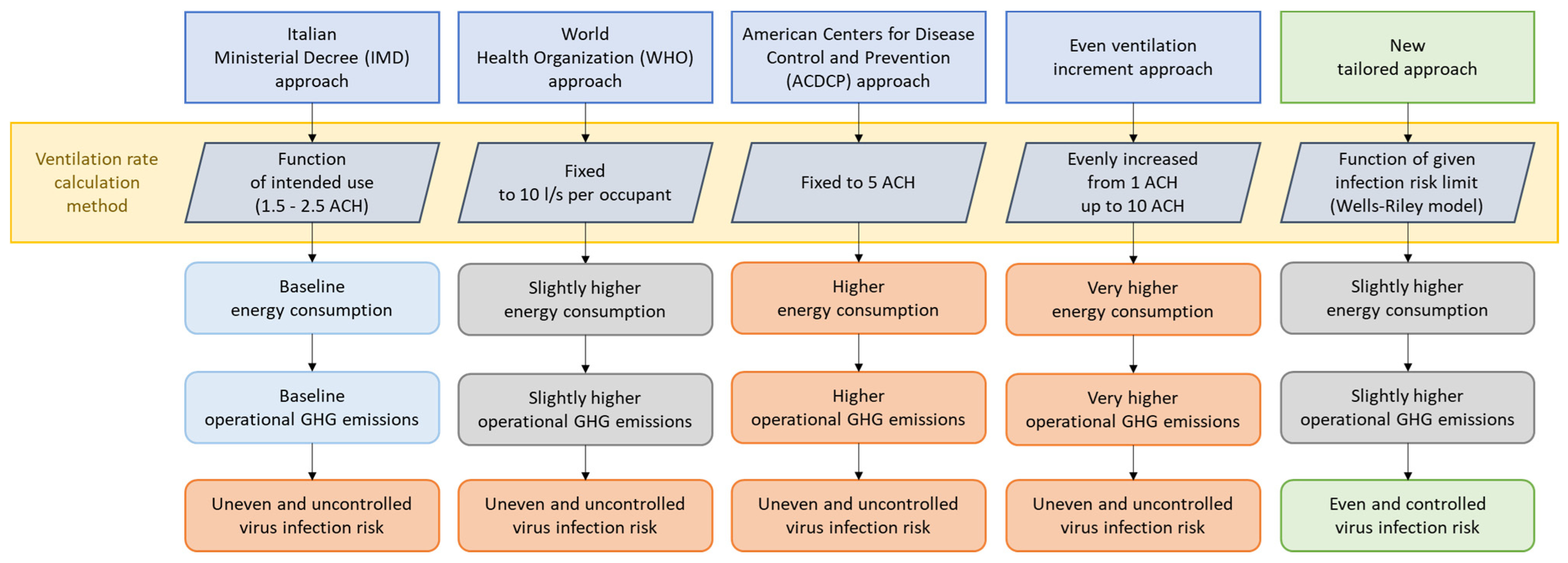
Aims and Innovations of This Study
- Four known approaches and one novel approach for the design of ventilation rates in buildings are analysed using the Wells–Riley method and the dynamic energy simulation to highlight the relationship between outdoor ACH values, risk of virus infection for occupants, building energy consumption, and GHG emissions. The four known approaches are:
- A novel tailored approach for the design of ventilation rates in buildings is proposed to provide the low, controlled, and even risk of virus infection with limited increases in operational energy consumption and GHG emissions.
- This proposed approach can be used for the assessment of the optimal number of hourly outdoor air changes and the risk of virus infection but also to redefine regulatory requirements in post-pandemic era.
- The financial impact of the analysed strategies on the attainment of the ZEB target is assessed by considering the costs of a PV system designed to 100% compensate GHG emissions due to the different ventilation approaches, mainly in post-pandemic conditions.
2. Literature Review
3. Methodology
3.1. Building Energy Modelling
3.2. The Wells–Riley Model
- assessment of the quantum emission rate;
- assessment of the quantum concentration exposure in the microenvironment;
- assessment of the quantum dose received by an exposed susceptible subject;
- estimation of the probability of infection based on a dose–response model.
- the term represents the dose of “quanta” inhaled by a susceptible subject [86];
- : pulmonary respiration rate [m3/h];
- : instantaneous concentration of infective doses in the room [quanta/m3];
- : exposure time [h].
- : emission of infectious doses by an asymptomatic subject [quanta∗h−1];
- : number of asymptomatic infected individuals;
- : volume of the room [m3];
- = initial number of infective doses [quanta];
- : time [h];
- : overall removal factor in the environment [h−1];
- : removal factor due to inactivation of the virus in the environment [h−1];
- : removal factor for deposition in the environment [h−1];
- : ventilation rate [h−1].
- I: number of asymptomatic infected individuals;
- q: number of quanta produced by an infected person in 1 h [h−1];
- : average air flow rate per person’s breathing, set at 0.6 [m3/h];
- T: time [h].
- P = probability of infection;
- Ns = number of people.
3.3. Ventilation Rate Scenarios
3.4. Zero-Emission Building (ZEB) Target Attainment
- : size of the PV system [kWp];
- : annual operational GHG emissions of the building–plant system [kgCO2-eq];
- : annual compensated GHG emissions by PV renewable energy generated in loco with a system of unitary power (1 kWp) [kgCO2-eq/kWp].
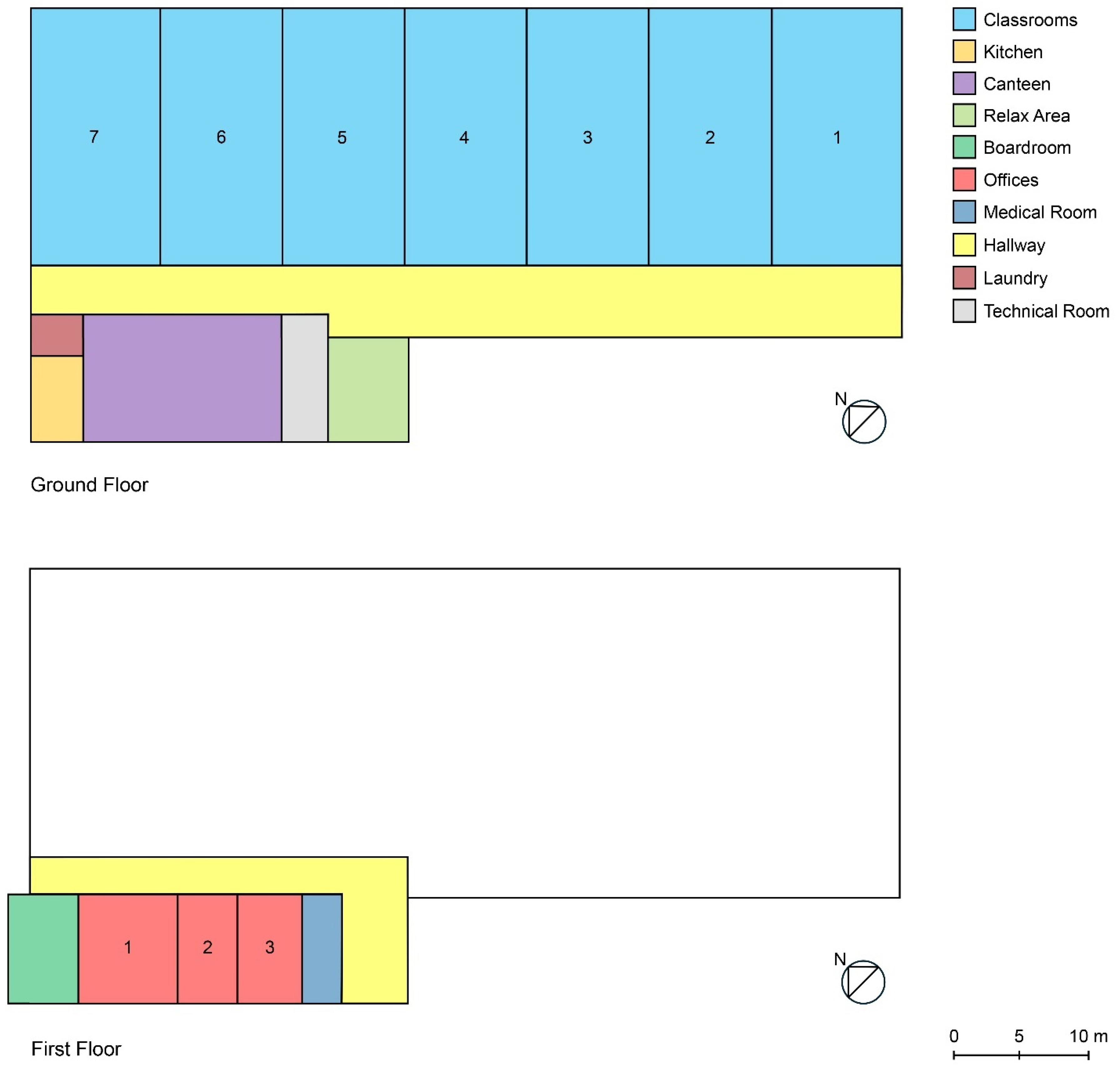
4. Case Study
4.1. Locality and Climate
4.2. Building Characteristics and Energy Model
4.3. Characteristics of the PV System for the ZEB Target Attainment
5. Results and Discussion
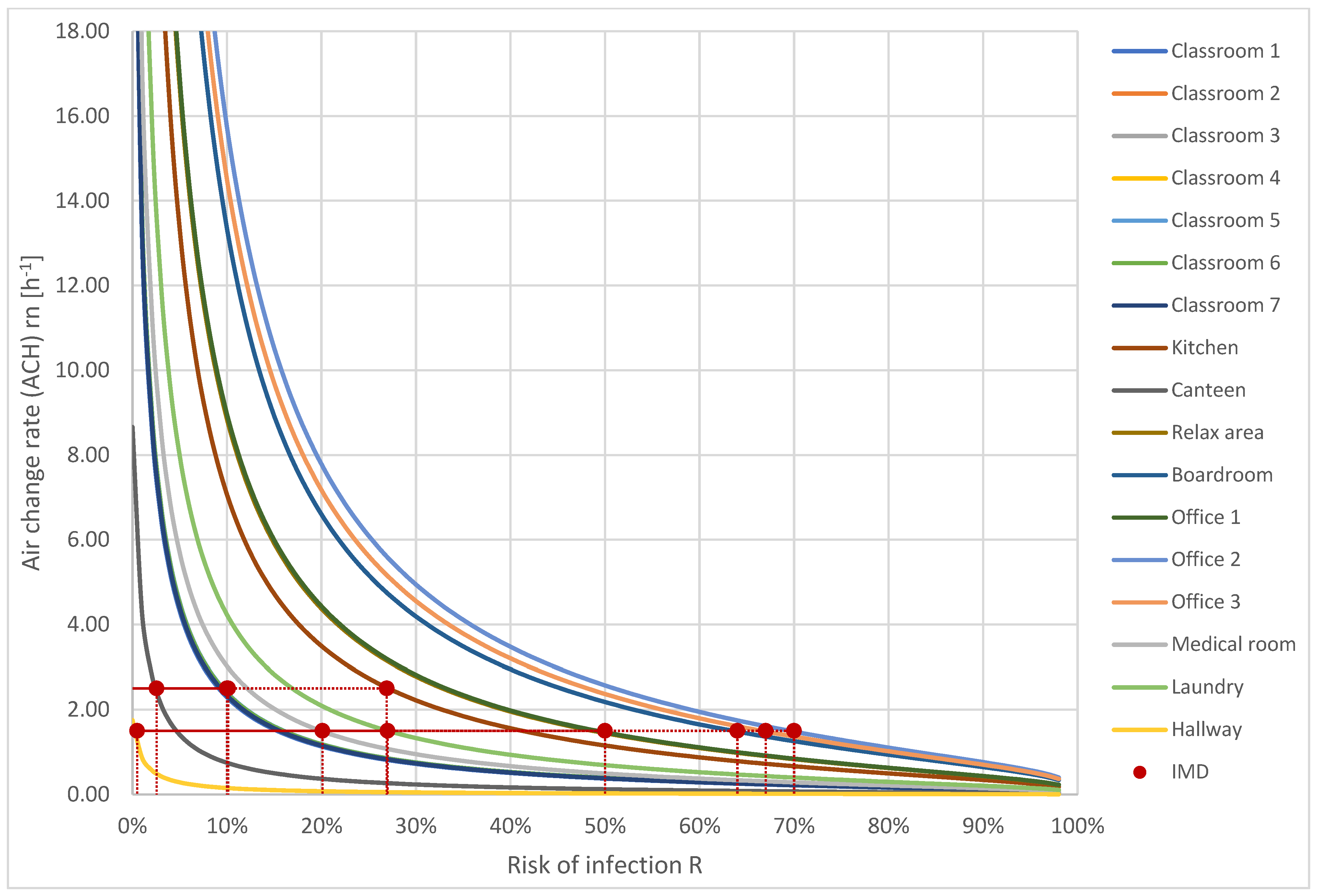
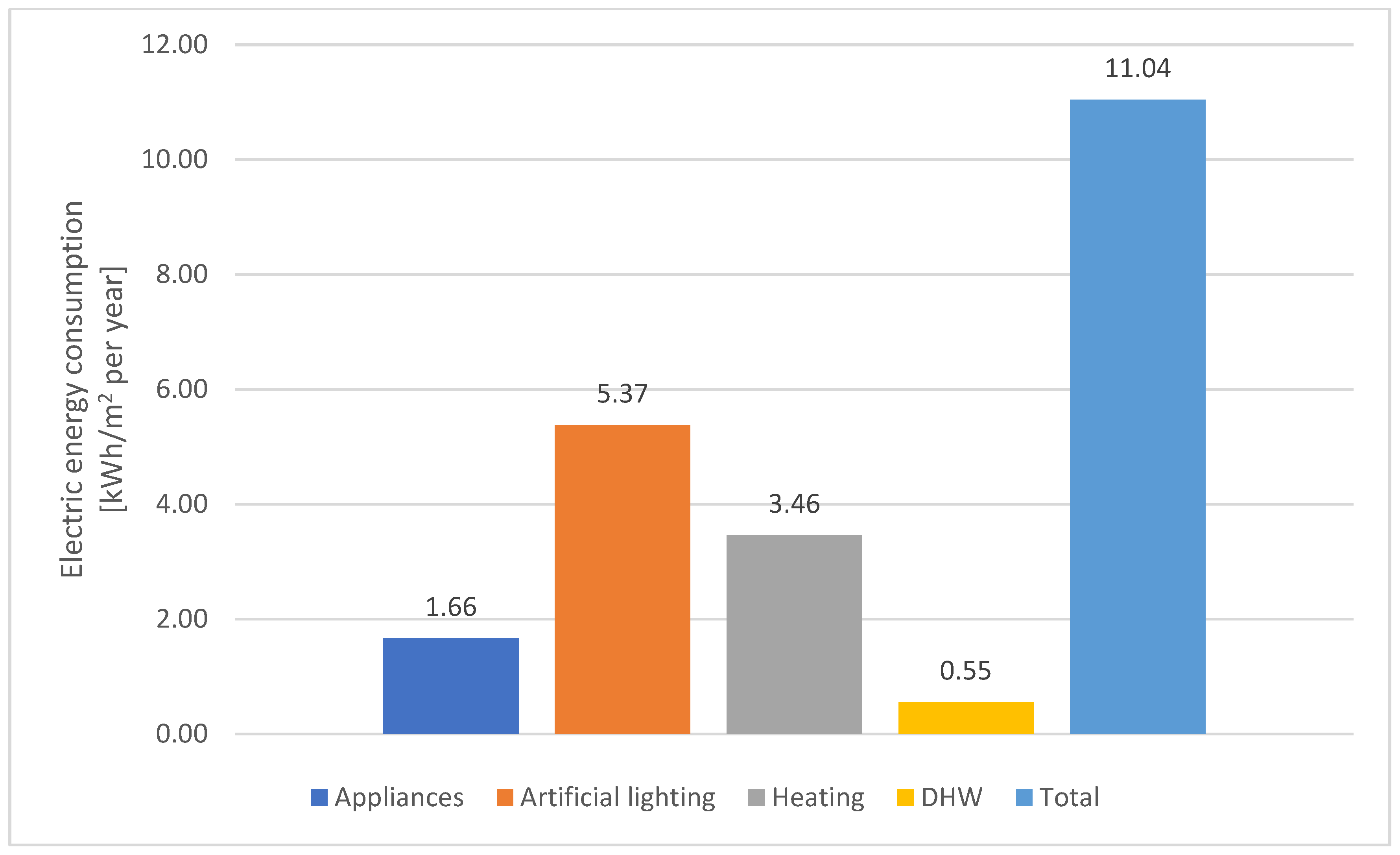
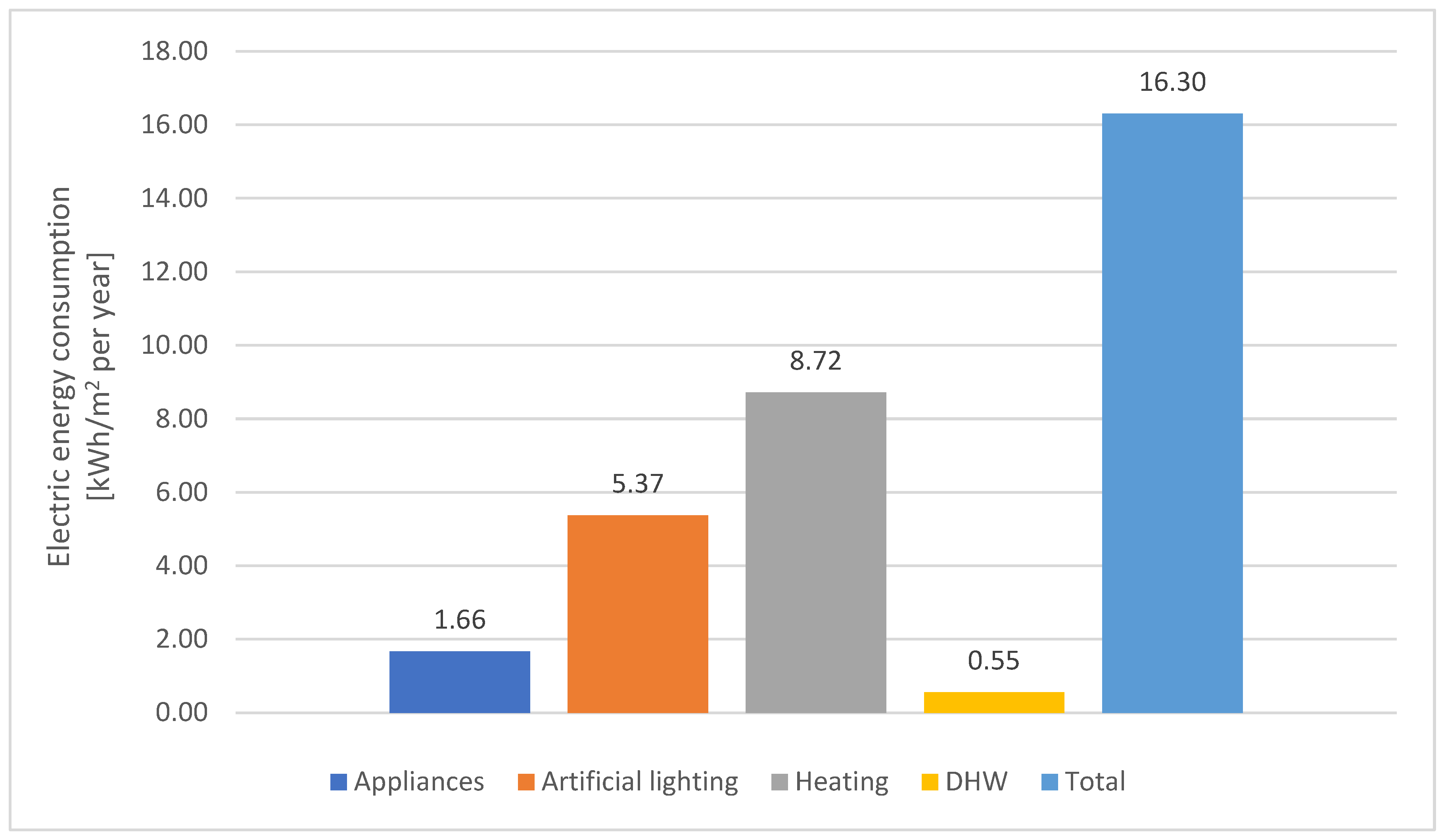
5.1. Italian Ministerial Decree Approach (IMD Approach)
- -
- building appliances: 3023 kWh per year or 1.66 kWh/m2 per year;
- -
- artificial lighting: 9774 kWh per year or 5.37 kWh/m2 per year;
- -
- DHW: 1000 kWh per year or 0.55 kWh/m2 per year;
- -
- heating + mechanical ventilation: 6289 kWh per year or 3.46 kWh/m2 per year.
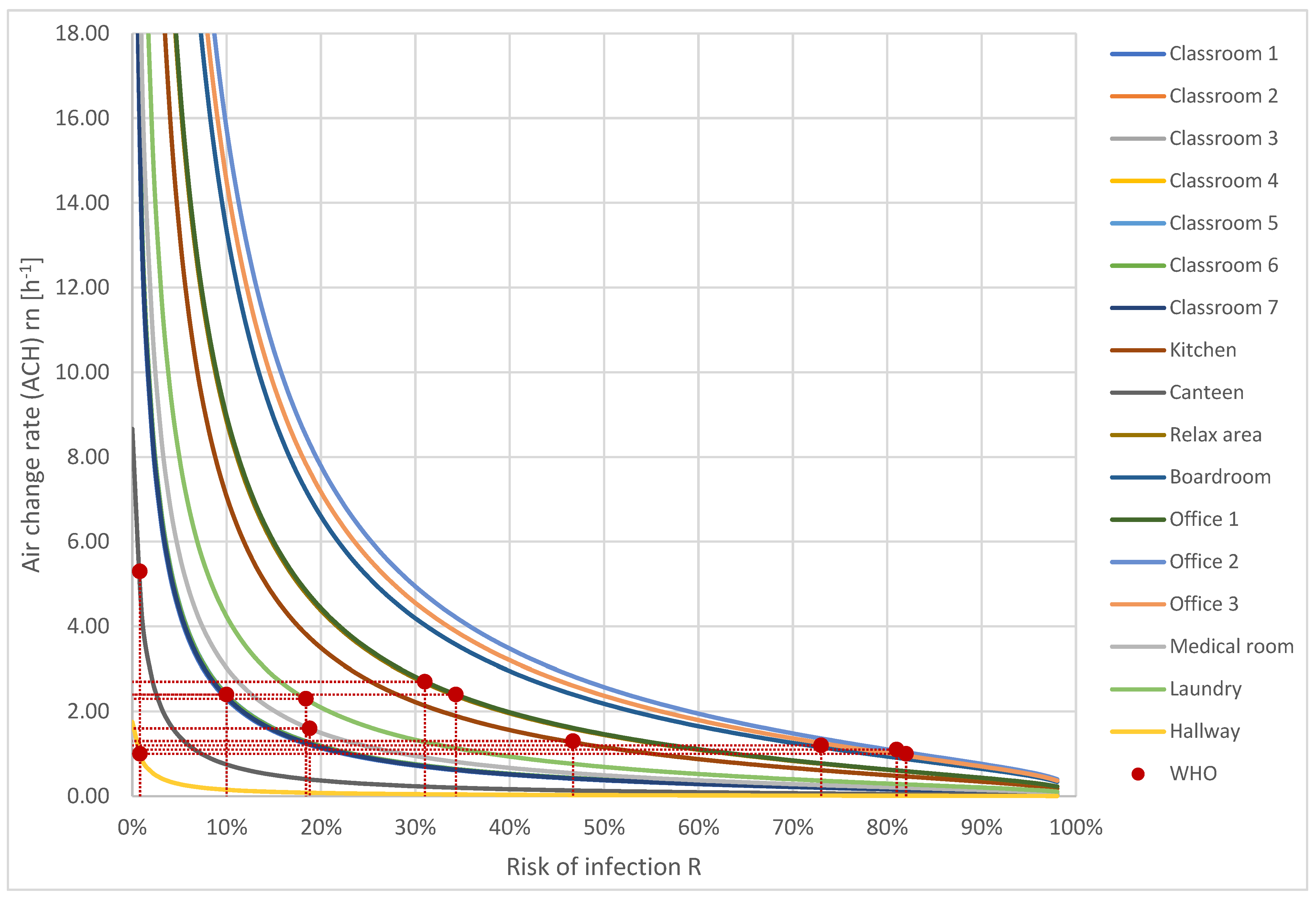
5.2. World Health Organization Approach (WHO Approach)
5.3. American Centers for Disease Control and Prevention Approach (ACDCP Approach)
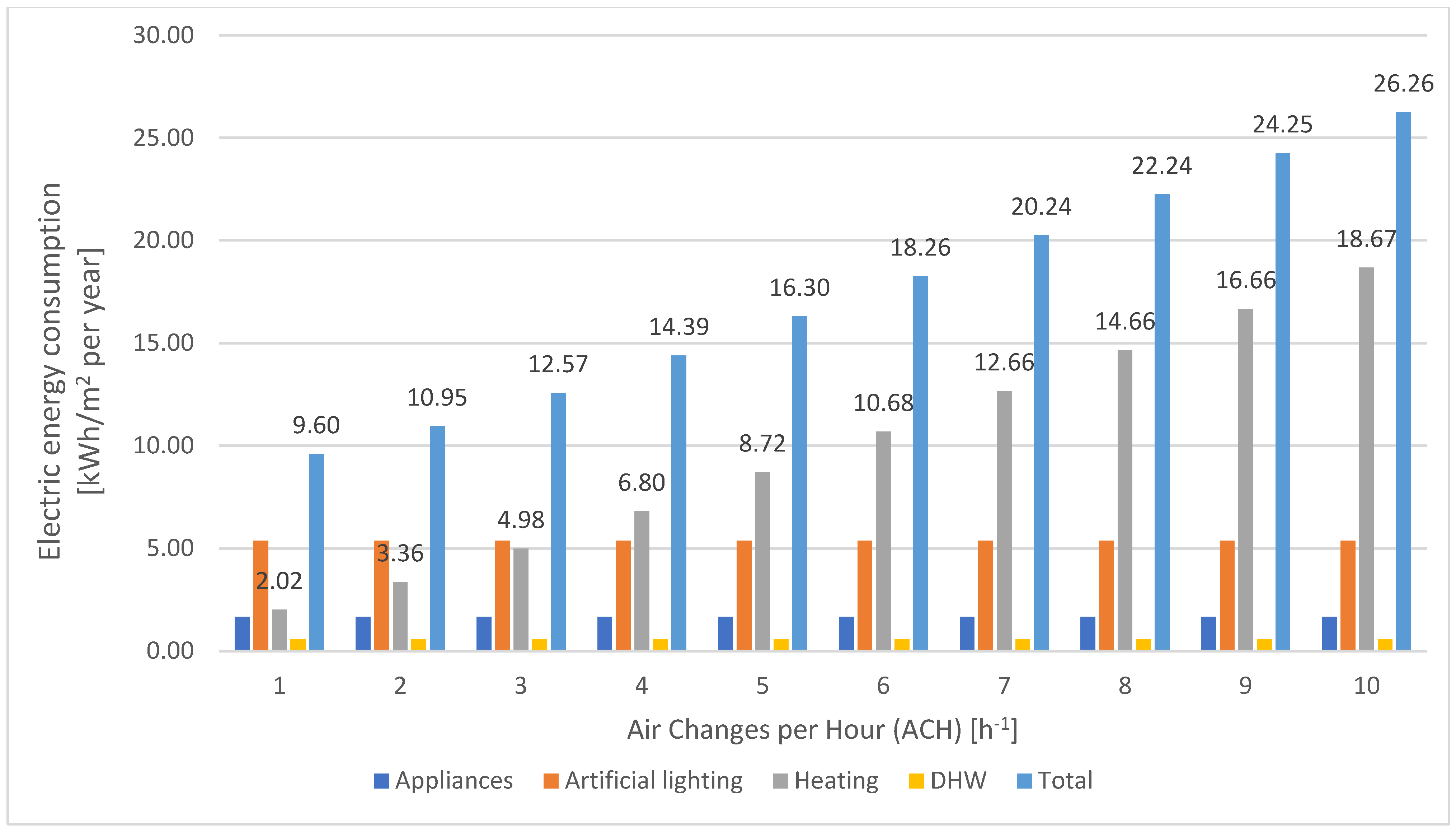
5.4. Gradual Increase in Ventilation Approach (Parametric Analysis)
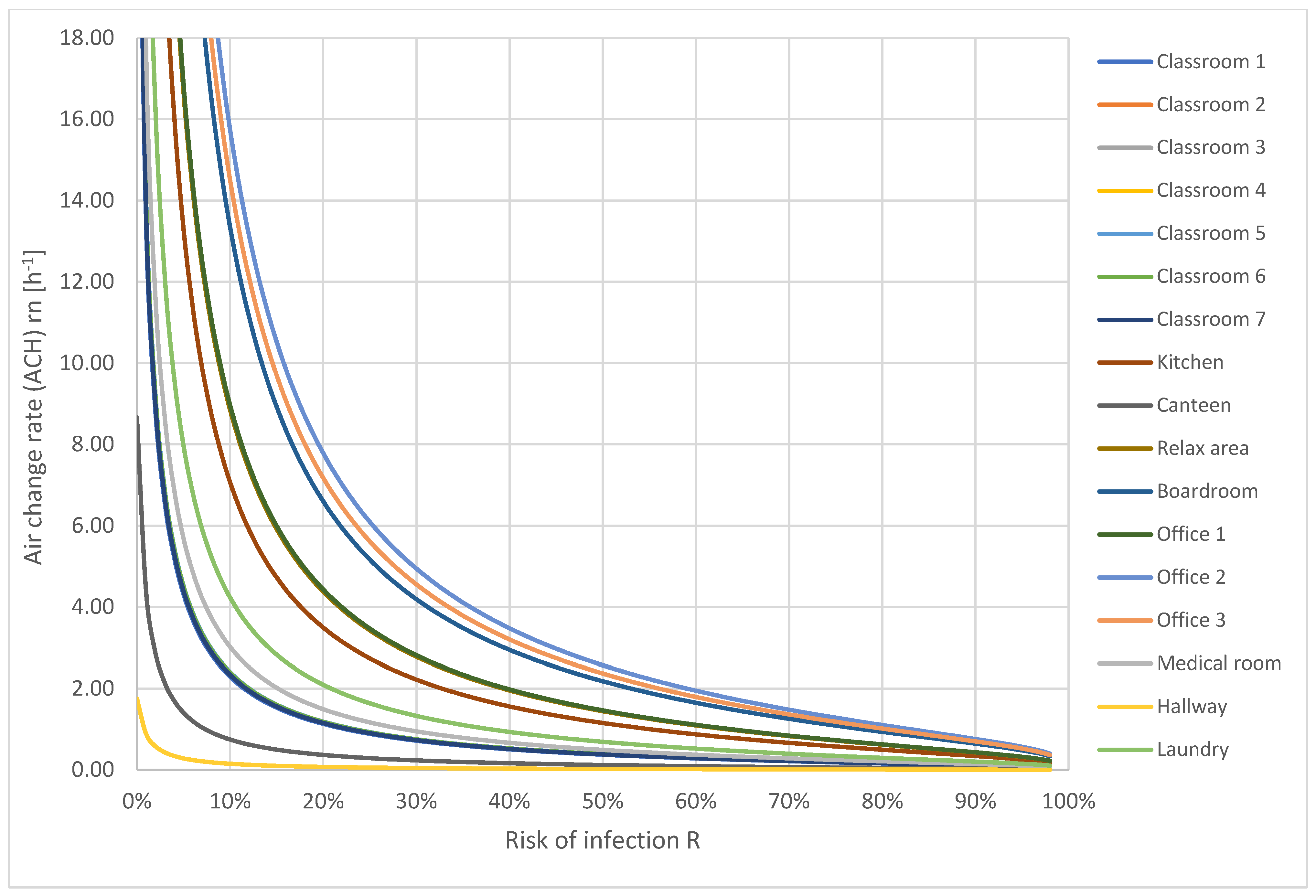
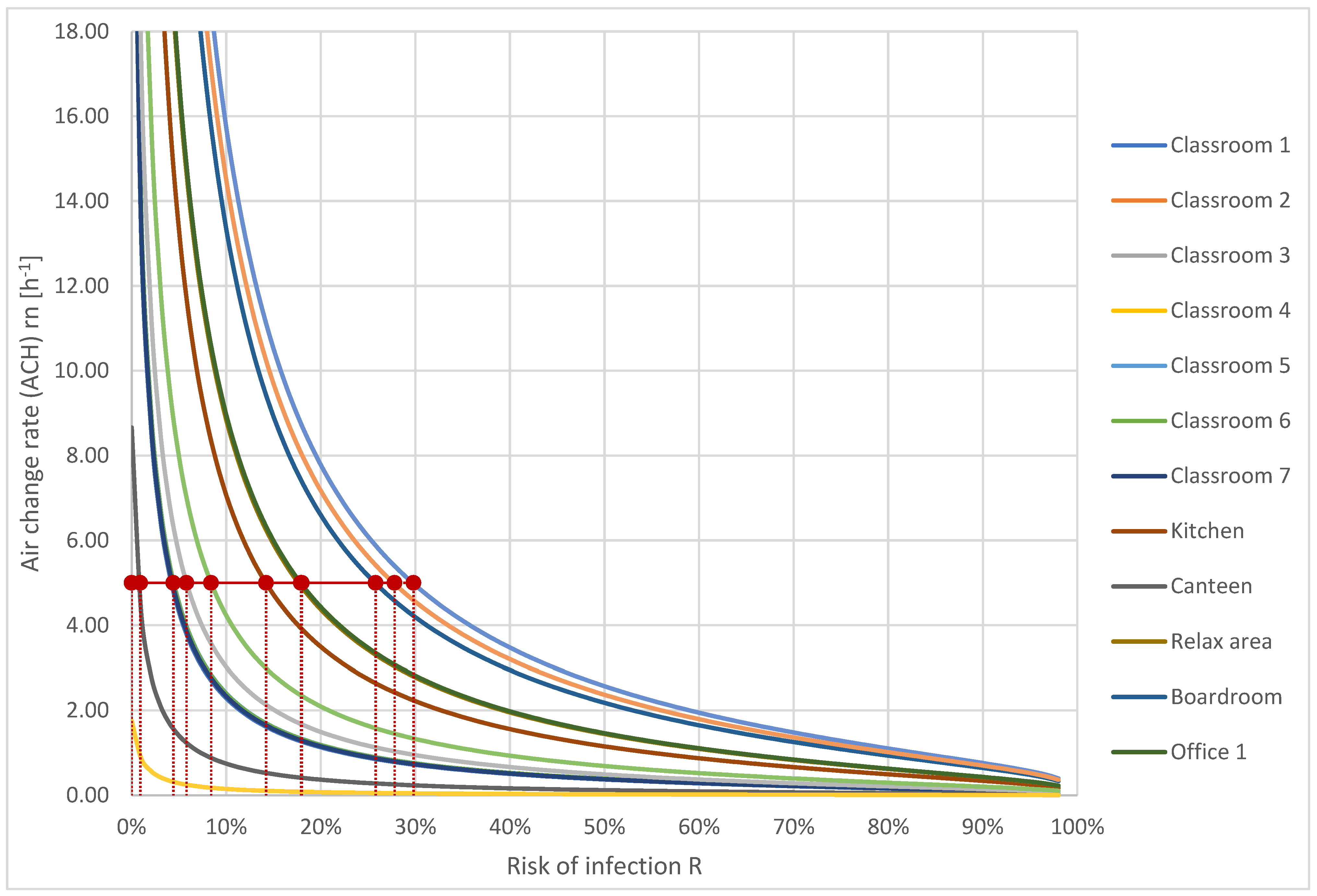
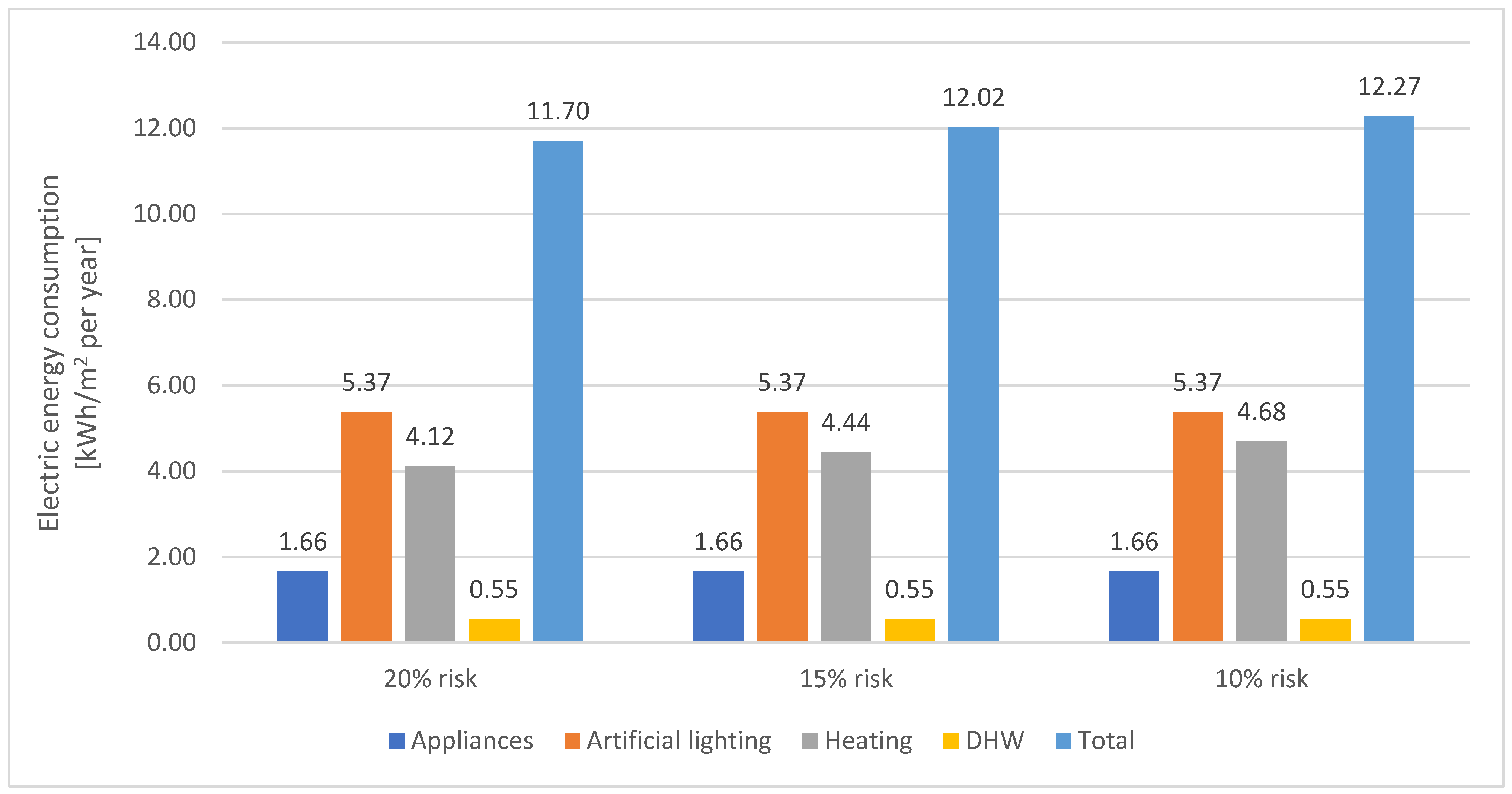
5.5. New Tailored Approach (Controlled Maximum Infection Risk in All Rooms)
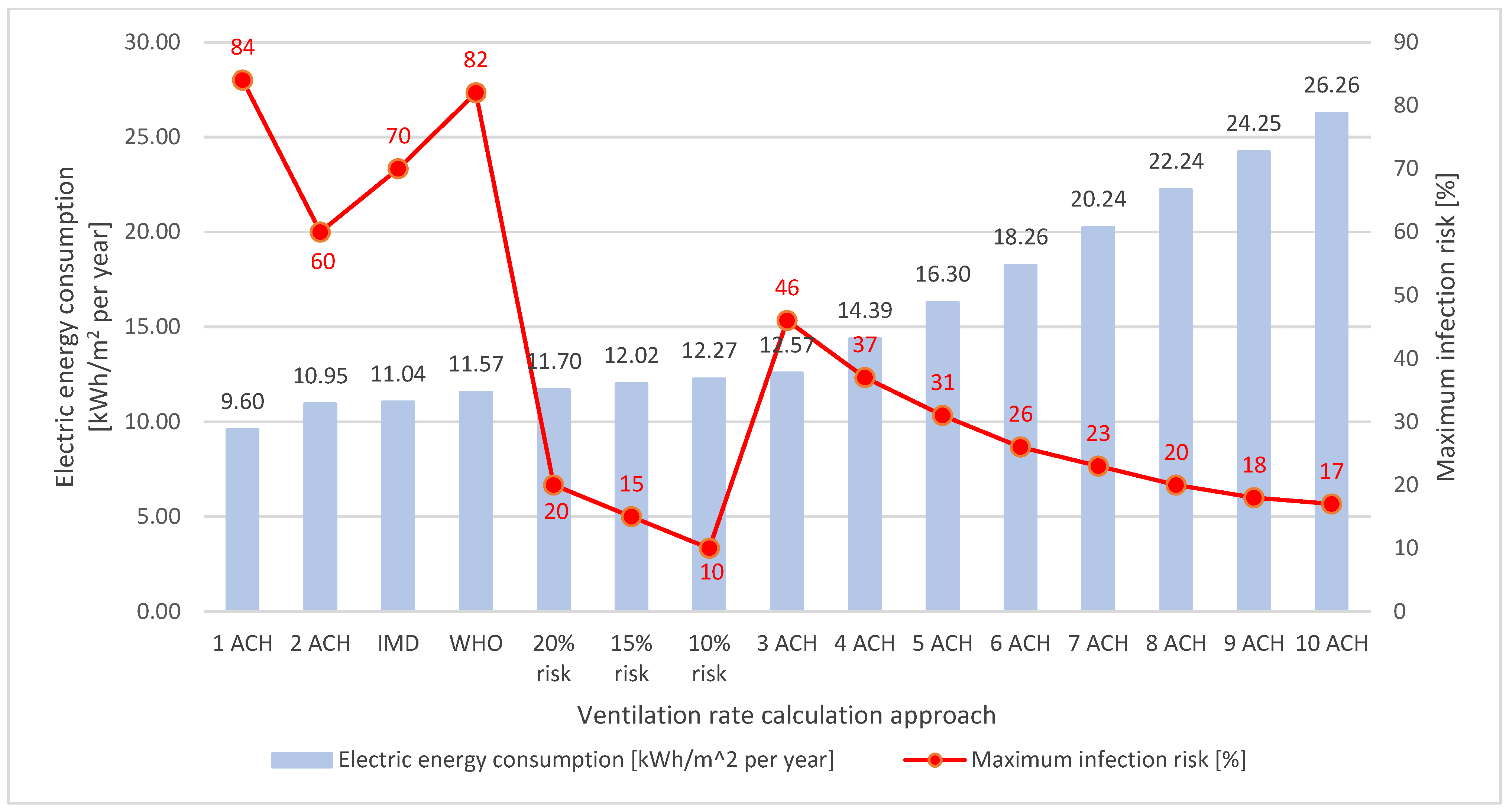
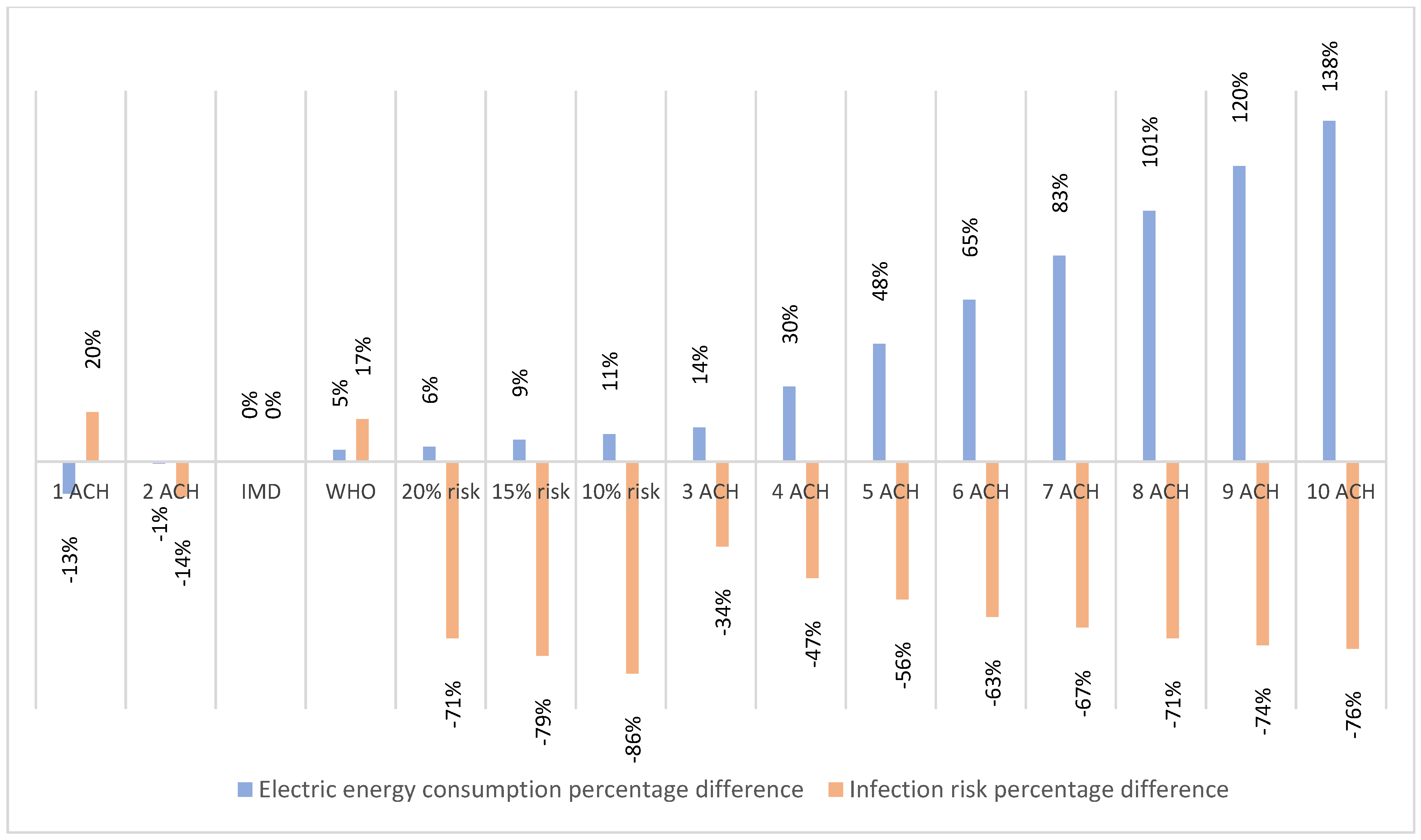
5.6. Comparison of the Analysed Approaches
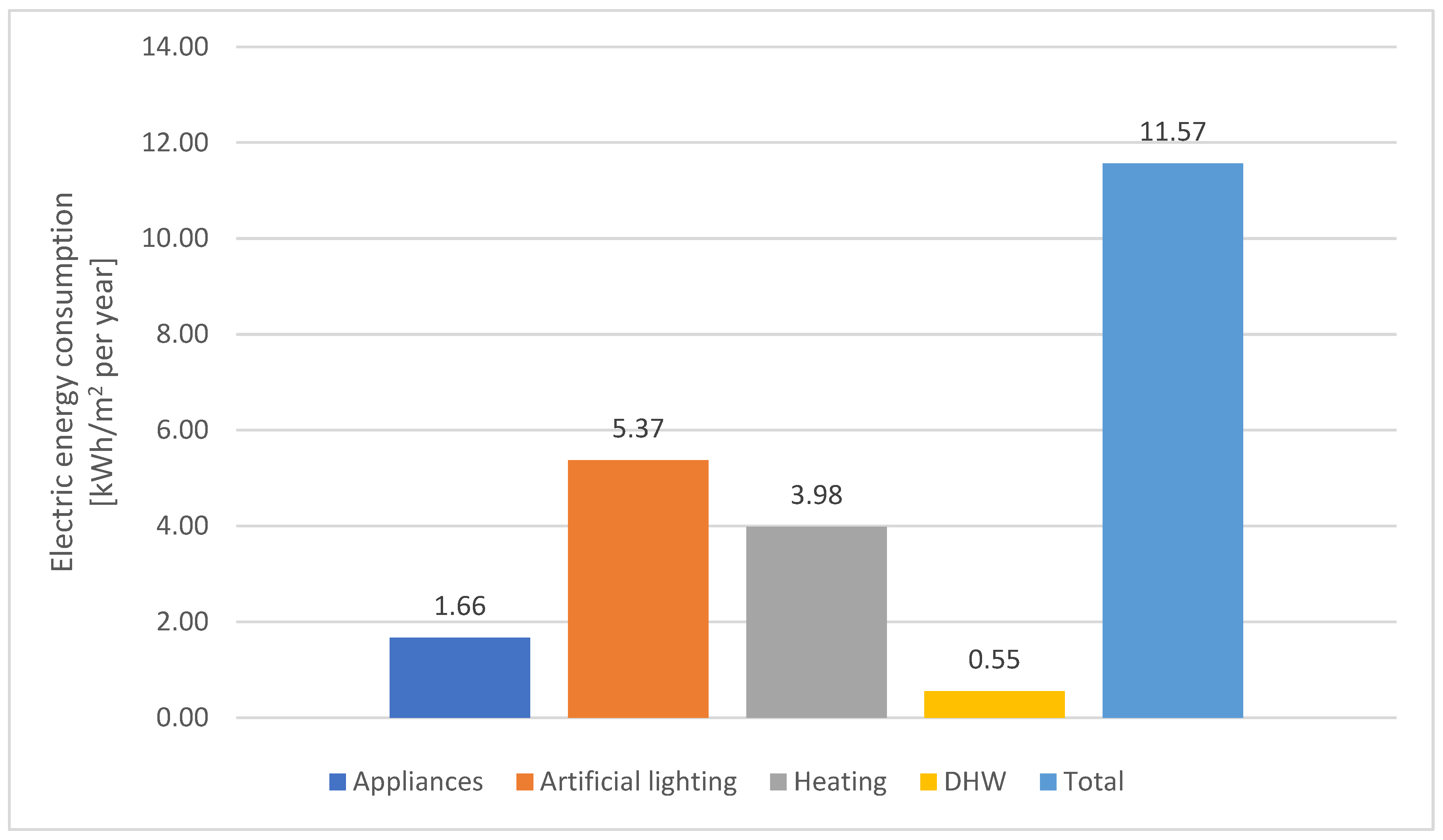
5.7. ZEB Target Attainment
5.8. Application, Challenges, and Costs
- -
- The increase in the outdoor ACH (and therefore the increase in the size of the air handling units and air distribution systems) and related energy consumption, but this barrier is common to all the approaches that rely on the increasing of outdoor ACH in the post-COVID-19 era;
- -
- The development and implementation of a specific commercial software for practitioners.
6. Conclusions
7. Main Limitations of the Study and Future Developments
- -
- The Wells–Riley model assumes steady-state conditions and the perfect mixing of air. This means that it assumes the distribution of pathogen-laden aerosols is spatially and temporally uniform, i.e., ideal conditions. Therefore, although several studies have demonstrated the suitability of this method for evaluating the effectiveness of outdoor air changes in reducing the risk of contagion, the airborne infection risk could be under- or overestimated using these ideal conditions.
- -
- Moreover, there are several COVID-19 strains as well as other various airborne respiratory infections. Based on this, the proposed study (to evaluate the optimal outdoor airflow rate in each room using only the infection risk-based ventilation airflow calculations) could be extended to also consider these factors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pejović, B.; Karadžić, V.; Dragašević, Z.; Backović, T. Economic Growth, Energy Consumption and CO2 Emissions in the Countries of the European Union and the Western Balkans. Energy Rep. 2021, 7, 2775–2783. [Google Scholar] [CrossRef]
- Lin, Y.; Zhong, S.; Yang, W.; Hao, X.; Li, C.Q. Towards Zero-Energy Buildings in China: A Systematic Literature Review. J. Clean. Prod. 2020, 276, 123297. [Google Scholar] [CrossRef]
- Chalgynbayeva, A.; Gabnai, Z.; Lengyel, P.; Pestisha, A.; Bai, A. Worldwide Research Trends in Agrivoltaic Systems—A Bibliometric Review. Energies 2023, 16, 611. [Google Scholar] [CrossRef]
- Shaikh, S.; Katyara, S.; Majeed, A.; Khand, Z.H.; Staszewski, L.; Shah, M.; Shaikh, M.F.; Bhan, V.; Memon, Q.; Majeed, U.; et al. Holistic and Scientific Perspectives of Energy Sector in Pakistan: Progression, Challenges and Opportunities. IEEE Access 2020, 8, 227232–227246. [Google Scholar] [CrossRef]
- European Commission. The European Green Deal; European Commission: Brussels, Belgium, 2019. [Google Scholar]
- Buckley, N.; Mills, G.; Reinhart, C.; Berzolla, Z.M. Using Urban Building Energy Modelling (UBEM) to Support the New European Union’s Green Deal: Case Study of Dublin Ireland. Energy Build. 2021, 247, 111115. [Google Scholar] [CrossRef]
- Reddy, V.J.; Hariram, N.P.; Maity, R.; Ghazali, M.F. Sustainable Vehicles for Decarbonizing the Transport Sector: A Comparison of Biofuel, Electric, Fuel Cell and Solar-Powered Vehicles. World Electr. Veh. J. 2024, 15, 93. [Google Scholar] [CrossRef]
- Belussi, L.; Barozzi, B.; Bellazzi, A.; Danza, L.; Devitofrancesco, A.; Fanciulli, C.; Ghellere, M.; Guazzi, G.; Meroni, I.; Salamone, F.; et al. A Review of Performance of Zero Energy Buildings and Energy Efficiency Solutions. J. Build. Eng. 2019, 25, 100772. [Google Scholar] [CrossRef]
- Charani Shandiz, S.; Rismanchi, B.; Foliente, G. Energy Master Planning for Net-Zero Emission Communities: State of the Art and Research Challenges. Renew. Sustain. Energy Rev. 2021, 137, 110600. [Google Scholar] [CrossRef]
- Izadi, M.; Taghavi, S.F.; Neshat Safavi, S.H.; Afsharpanah, F.; Yaïci, W. Thermal Management of Shelter Building Walls by PCM Macro-Encapsulation in Commercial Hollow Bricks. Case Stud. Therm. Eng. 2023, 47, 103081. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Mikulcic, H.; Kalogirou, S. Sustainable Development Using Renewable Energy Technology. Renew. Energy 2020, 146, 2430–2437. [Google Scholar] [CrossRef]
- Agostinelli, S.; Neshat, M.; Majidi Nezhad, M.; Piras, G.; Astiaso Garcia, D. Integrating Renewable Energy Sources in Italian Port Areas towards Renewable Energy Communities. Sustainability 2022, 14, 13720. [Google Scholar] [CrossRef]
- Mohammed, B.U.; Wiysahnyuy, Y.S.; Ashraf, N.; Mempouo, B.; Mengata, G.M. Pathways for Efficient Transition into Net Zero Energy Buildings (NZEB) in Sub-Sahara Africa. Case Study: Cameroon, Senegal, and Côte d’Ivoire. Energy Build. 2023, 296, 113422. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S.A. Recent Advances in Renewable Energy Technology for the Energy Transition. Renew. Energy 2021, 179, 877–884. [Google Scholar] [CrossRef]
- Minelli, F.; Ciriello, I.; Minichiello, F.; D’Agostino, D. From Net Zero Energy Buildings to an Energy Sharing Model—The Role of NZEBs in Renewable Energy Communities. Renew. Energy 2024, 223, 120110. [Google Scholar] [CrossRef]
- Carpino, C.; Austin, M.C.; Mora, D.; Arcuri, N. Retrofit Measures for Achieving NZE Single-Family Houses in a Tropical Climate via Multi-Objective Optimization. Buildings 2024, 14, 566. [Google Scholar] [CrossRef]
- Maduta, C.; Melica, G.; D’Agostino, D.; Bertoldi, P. Towards a Decarbonised Building Stock by 2050: The Meaning and the Role of Zero Emission Buildings (ZEBs) in Europe. Energy Strategy Rev. 2022, 44, 101009. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S. Renewable Energy for Sustainable Development. Renew. Energy 2022, 199, 1145–1152. [Google Scholar] [CrossRef]
- Skandalos, N.; Wang, M.; Kapsalis, V.; D’Agostino, D.; Parker, D.; Bhuvad, S.S.; Udayraj; Peng, J.; Karamanis, D. Building PV Integration According to Regional Climate Conditions: BIPV Regional Adaptability Extending Köppen-Geiger Climate Classification against Urban and Climate-Related Temperature Increases. Renew. Sustain. Energy Rev. 2022, 169, 112950. [Google Scholar] [CrossRef]
- Coban, H.H. Hydropower Planning in Combination with Batteries and Solar Energy. Sustainability 2023, 15, 10002. [Google Scholar] [CrossRef]
- Kırant-Mitić, T.; Voss, K. Energy Flexibility Analysis of a University Building Using Rule Based Control and Model Predictive Control. In Proceedings of the BauSim 2022: 9th Conference of IBPSA-Germany and Austria, Weimar, Germany, 20–22 September 2022; Volume 9. [Google Scholar] [CrossRef]
- Coban, H.H.; Lewicki, W. Flexibility in Power Systems of Integrating Variable Renewable Energy Sources. J. Adv. Res. Nat. Appl. Sci. 2023, 9, 190–204. [Google Scholar] [CrossRef]
- Khan, S.; Sudhakar, K.; bin Yusof, M.H. Building Integrated Photovoltaics Powered Electric Vehicle Charging with Energy Storage for Residential Building: Design, Simulation, and Assessment. J. Energy Storage 2023, 63, 107050. [Google Scholar] [CrossRef]
- Thorvaldsen, K.E.; Korpås, M.; Lindberg, K.B.; Farahmand, H. A Stochastic Operational Planning Model for a Zero Emission Building with Emission Compensation. Appl. Energy 2021, 302, 117415. [Google Scholar] [CrossRef]
- Liang, X.; Chen, K.; Chen, S.; Zhu, X.; Jin, X.; Du, Z. IoT-Based Intelligent Energy Management System for Optimal Planning of HVAC Devices in Net-Zero Emissions PV-Battery Building Considering Demand Compliance. Energy Convers. Manag. 2023, 292, 117369. [Google Scholar] [CrossRef]
- Coban, H.H. How Is COVID-19 Affecting the Renewable Energy Sector and the Electric Power Grid? Eur. J. Sci. Technol. 2021, 27, 484–494. [Google Scholar] [CrossRef]
- D’Agostino, D.; Minelli, F.; Minichiello, F.; Musella, M. Improving the Indoor Air Quality of Office Buildings in the Post-Pandemic Era—Impact on Energy Consumption and Costs. Energies 2024, 17, 855. [Google Scholar] [CrossRef]
- Zheng, W.; Hu, J.; Wang, Z.; Li, J.; Fu, Z.; Li, H.; Jurasz, J.; Chou, S.K.; Yan, J. COVID-19 Impact on Operation and Energy Consumption of Heating, Ventilation and Air-Conditioning (HVAC) Systems. Adv. Appl. Energy 2021, 3, 100040. [Google Scholar] [CrossRef]
- Acosta, I.; Campano, M.Á.; Bellia, L.; Fragliasso, F.; Diglio, F.; Bustamante, P. Impact of Daylighting on Visual Comfort and on the Biological Clock for Teleworkers in Residential Buildings. Buildings 2023, 13, 2562. [Google Scholar] [CrossRef]
- Pirouz, B.; Palermo, S.A.; Naghib, S.N.; Mazzeo, D.; Turco, M.; Piro, P. The Role of HVAC Design and Windows on the Indoor Airflow Pattern and ACH. Sustainability 2021, 13, 7931. [Google Scholar] [CrossRef]
- Pérez-Urrestarazu, L.; Kaltsidi, M.P.; Nektarios, P.A.; Markakis, G.; Loges, V.; Perini, K.; Fernández-Cañero, R. Particularities of Having Plants at Home during the Confinement Due to the COVID-19 Pandemic. Urban For. Urban Green. 2021, 59, 126919. [Google Scholar] [CrossRef]
- Moghadam, T.T.; Ochoa Morales, C.E.; Lopez Zambrano, M.J.; Bruton, K.; O’Sullivan, D.T.J. Energy Efficient Ventilation and Indoor Air Quality in the Context of COVID-19—A Systematic Review. Renew. Sustain. Energy Rev. 2023, 182, 113356. [Google Scholar] [CrossRef]
- Bellia, L.; Błaszczak, U.; Diglio, F.; Fragliasso, F. Light-Environment Interactions and Integrative Lighting Design: Connecting Visual, Non-Visual and Energy Requirements in a Case Study Experiment. Build. Environ. 2024, 253, 111323. [Google Scholar] [CrossRef]
- Liu, P.; Justo Alonso, M.; Mathisen, H.M. Global Sensitivity Analysis and Optimal Design of Heat Recovery Ventilation for Zero Emission Buildings. Appl. Energy 2023, 329, 120237. [Google Scholar] [CrossRef]
- Stamatellou, A.M.; Zogou, O.; Stamatelos, A. Energy Cost Assessment and Optimization of Post-COVID-19 Building Ventilation Strategies. Sustainability 2023, 15, 3422. [Google Scholar] [CrossRef]
- Faulkner, C.A.; Castellini, J.E.; Lou, Y.; Zuo, W.; Lorenzetti, D.M.; Sohn, M.D. Tradeoffs among Indoor Air Quality, Financial Costs, and CO2 Emissions for HVAC Operation Strategies to Mitigate Indoor Virus in U.S. Office Buildings. Build. Environ. 2022, 221, 109282. [Google Scholar] [CrossRef] [PubMed]
- Lo Verso, V.R.M.; Giuliani, F.; Caffaro, F.; Basile, F.; Peron, F.; Dalla Mora, T.; Bellia, L.; Fragliasso, F.; Beccali, M.; Bonomolo, M.; et al. Questionnaires and Simulations to Assess Daylighting in Italian University Classrooms for IEQ and Energy Issues. Energy Build. 2021, 252, 111433. [Google Scholar] [CrossRef]
- Monge-Barrio, A.; Bes-Rastrollo, M.; Dorregaray-Oyaregui, S.; González-Martínez, P.; Martin-Calvo, N.; López-Hernández, D.; Arriazu-Ramos, A.; Sánchez-Ostiz, A. Encouraging Natural Ventilation to Improve Indoor Environmental Conditions at Schools. Case Studies in the North of Spain before and during COVID. Energy Build. 2022, 254, 111567. [Google Scholar] [CrossRef]
- Miao, S.; Gangolells, M.; Tejedor, B. A Comprehensive Assessment of Indoor Air Quality and Thermal Comfort in Educational Buildings in the Mediterranean Climate. Indoor Air 2023, 2023, 6649829. [Google Scholar] [CrossRef]
- Gaspar, K.; Gangolells, M.; Casals, M.; Pujadas, P.; Forcada, N.; Macarulla, M.; Tejedor, B. Assessing the Impact of the COVID-19 Lockdown on the Energy Consumption of University Buildings. Energy Build. 2022, 257, 111783. [Google Scholar] [CrossRef] [PubMed]
- Batterman, S. Review and Extension of CO2-Based Methods to Determine Ventilation Rates with Application to School Classrooms. Int. J. Environ. Res. Public Health 2017, 14, 145. [Google Scholar] [CrossRef]
- Arpino, F.; Cortellessa, G.; D’Alicandro, A.C.; Grossi, G.; Massarotti, N.; Mauro, A. CFD Analysis of the Air Supply Rate Influence on the Aerosol Dispersion in a University Lecture Room Air Change per Hour. Build. Environ. 2023, 235, 110257. [Google Scholar] [CrossRef]
- D’Alicandro, A.C.; Mauro, A. Experimental and Numerical Analysis of CO2 Transport inside a University Classroom: Effects of Turbulent Models. J. Build. Perform. Simul. 2023, 16, 434–459. [Google Scholar] [CrossRef]
- Kurnitski, J.; Kiil, M.; Mikola, A.; Võsa, K.V.; Aganovic, A.; Schild, P.; Seppänen, O. Post-COVID Ventilation Design: Infection Risk-Based Target Ventilation Rates and Point Source Ventilation Effectiveness. Energy Build. 2023, 296, 113386. [Google Scholar] [CrossRef]
- EN 16798-1:2019; Energy Performance of Buildings—Ventilation of Buildings—Part 1: Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acou. European Committee for Standardization (CEN): Brussels, Belgium, 2019.
- ISO 17772-1:2017; Energy Performance of Buildings—Indoor Environmental Quality—Part 1: Indoor Environmental Input Parameters for the Design and Assessment of Energy Performance of Buildings. International Organization for Standardization (ISO): Geneva, Switzerland, 2017.
- The Minister for Public Works in concert with the Minister for Public Education Decreto Ministeriale 18 Dicembre 1975, n.29—Norme Tecniche Aggiornate Relative All’edilizia Scolastica, Ivi Compresi Gli Indici Di Funzionalità Didattica, Edilizia Ed Urbanistica, Da Osservarsi Nella Esecuzione Di Opere Di Edilizia Scolastica (in Italia; Gazzetta Ufficiale della Repubblica Italiana 2 febbraio 1976 n. 29. 1975. Available online: https://www.indicenormativa.it/norma/urn%3Anir%3Aministero.lavori.pubblici%3Adecreto%3A1975-12-18#:~:text=Norme%20tecniche%20aggiornate%20relative%20all,di%20opere%20di%20edilizia%20scolastica (accessed on 27 May 2023).
- Centers for Disease Control and Prevention Improving Ventilation in Buildings. Available online: https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/improving-ventilation-in-buildings.html (accessed on 22 November 2023).
- DesignBuilder. DesignBuilder Software, v 6 2019, imited Clarendon Court 1st Floor 54/56 London Rd Stroud, Gloucestershire GL5 2AD (UK). 2019. Available online: http://www.designbuilder.co.uk/i (accessed on 10 May 2024).
- EnergyPlus Testing with Building Thermal Envelope and Fabric Load Tests from ANSI/ASHRAE Standard 140-2007; EnergyPlus Version 6.0.0.023; U.S. Department of Energy: Washington, DC, USA, 2010.
- Shaikh, S.A.; Shaikh, A.M.; Shaikh, M.F.; Jiskani, S.A.; Memon, Q.A.; Ahmed, I. Technical and Economical Evaluation of Solar PV System for Domestic Load in Pakistan: An Overlook Contributor to High Tariff and Load Shedding. Sir Syed Univ. Res. J. Eng. Technol. 2022, 12, 23–30. [Google Scholar] [CrossRef]
- Istituto Superiore di Sanità—Gruppo di Lavoro ISS Ambiente e Qualità dell’Aria Indoor Indicazioni Ad Interim per La Prevenzione e Gestione Degli Ambienti Indoor in Relazione Alla Trasmissione Dell’infezione Da Virus SARS-CoV-2; 2021; Volume ii. Available online: https://www.iss.it/rapporti-covid-19/-/asset_publisher/btw1J82wtYzH/content/rapporto-iss-covid-19-n.-11-2021-indicazioni-ad-interim-per-la-prevenzione-e-gestione-degli-ambienti-indoor-in-relazione-alla-trasmissione-dell-infezione-da-virus-sars-cov-2.-aggiornamento-del-rapporto-iss-covid-19-n.-5-2020-rev.-2.-versione-del-18-aprile (accessed on 27 May 2024). (In Italian).
- Mikszewski, A.; Stabile, L.; Buonanno, G.; Morawska, L. The Airborne Contagiousness of Respiratory Viruses: A Comparative Analysis and Implications for Mitigation. Geosci. Front. 2022, 13, 101285. [Google Scholar] [CrossRef] [PubMed]
- Judson, S.D.; Munster, V.J. Nosocomial Transmission of Emerging Viruses via Aerosol-Generating Medical Procedures. Viruses 2019, 11, 940. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Huang, X.; Yu, I.T.S.; Wong, T.W.; Qian, H. Role of Air Distribution in SARS Transmission during the Largest Nosocomial Outbreak in Hong Kong. Indoor Air 2004, 15, 83–95. [Google Scholar] [CrossRef] [PubMed]
- Megahed, N.A.; Ghoneim, E.M. Indoor Air Quality: Rethinking Rules of Building Design Strategies in Post-Pandemic Architecture. Environ. Res. 2021, 193, 110471. [Google Scholar] [CrossRef] [PubMed]
- Sodiq, A.; Khan, M.A.; Naas, M.; Amhamed, A. Addressing COVID-19 Contagion through the HVAC Systems by Reviewing Indoor Airborne Nature of Infectious Microbes: Will an Innovative Air Recirculation Concept Provide a Practical Solution? Environ. Res. 2021, 199, 111329. [Google Scholar] [CrossRef] [PubMed]
- Luongo, J.C.; Fennelly, K.P.; Keen, J.A.; Zhai, Z.J.; Jones, B.W.; Miller, S.L. Role of Mechanical Ventilation in the Airborne Transmission of Infectious Agents in Buildings. Indoor Air 2016, 26, 666–678. [Google Scholar] [CrossRef]
- Ye, J.; Lin, C.; Liu, J.; Ai, Z.; Zhang, G. Systematic Summary and Analysis of Chinese HVAC Guidelines Coping with COVID-19. Indoor Built Environ. 2022, 31, 1176–1192. [Google Scholar] [CrossRef]
- Bonadonna, L.; La Rosa, G.; Settimo, G.; Sorrentino, E.; Veschetti, E.; Bertinato, L. Rapporto ISS COVID-19 n.33/2020: Indicazioni Sugli Impianti Di Ventilazione/Climatizzazione in Strutture Comunitarie Non Sanitarie e in Ambienti Domestici in Relazione Alla Diffusione Del Virus SARS-CoV-2. 2020. Available online: https://www.iss.it/rapporti-covid-19/-/asset_publisher/btw1J82wtYzH/content/rapporto-iss-covid-19-n.-33-2020-indicazioni-sugli-impianti-di-ventilazione-climatizzazione-in-strutture-comunitarie-non-sanitarie-e-in-ambienti-domestici-in-relazione-alla-diffusione-del-virus-sars-cov-2.-versione-del-25-maggio-2020 (accessed on 27 May 2024). (In Italian).
- REHVA COVID-19 Guidance Document. How to Operate and Use Building Services in Order to Prevent the Spread of the Coronavirus Disease (COVID-19) Virus (SARS-CoV-2) in Workplaces; REHVA: Brussels, Belgium, 2020. [Google Scholar]
- Shamim, J.A.; Hsu, W.; Daiguji, H. Review of Component Designs for Post-COVID-19 HVAC Systems: Possibilities and Challenges. Heliyon 2022, 8, e09001. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Du, C.; Fu, Z.; Fu, M. Re-Thinking of Engineering Operation Solutions to HVAC Systems under the Emerging COVID-19 Pandemic. J. Build. Eng. 2021, 43, 102889. [Google Scholar] [CrossRef]
- D’Alicandro, A.C.; Massarotti, N.; Mauro, A. Aerosol Hazards in Operating Rooms: A Review of Numerical and Experimental Studies. J. Aerosol Sci. 2021, 158, 105823. [Google Scholar] [CrossRef]
- D’Alicandro, A.C.; Mauro, A. Effects of Operating Room Layout and Ventilation System on Ultrafine Particle Transport and Deposition. Atmos. Environ. 2022, 270, 118901. [Google Scholar] [CrossRef]
- Rodríguez, D.; Urbieta, I.R.; Velasco, Á.; Campano-Laborda, M.Á.; Jiménez, E. Assessment of Indoor Air Quality and Risk of COVID-19 Infection in Spanish Secondary School and University Classrooms. Build. Environ. 2022, 226, 109717. [Google Scholar] [CrossRef] [PubMed]
- Faulkner, C.A.; Castellini, J.E.; Zuo, W.; Sohn, M.D. Comprehensive Analysis of Model Parameter Uncertainty Influence on Evaluation of HVAC Operation to Mitigate Indoor Virus: A Case Study for an Office Building in a Cold and Dry Climate. Build. Environ. 2023, 238, 110314. [Google Scholar] [CrossRef]
- Elsaid, A.M.; Mohamed, H.A.; Abdelaziz, G.B.; Ahmed, M.S. A Critical Review of Heating, Ventilation, and Air Conditioning (HVAC) Systems within the Context of a Global SARS-CoV-2 Epidemic. Process Saf. Environ. Prot. 2021, 155, 230–261. [Google Scholar] [CrossRef] [PubMed]
- Yu, I.T.S.; Li, Y.; Wong, T.W.; Tam, W.; Chan, A.T.; Lee, J.H.W.; Leung, D.Y.C.; Ho, T. Evidence of Airborne Transmission of the Severe Acute Respiratory Syndrome Virus. N. Engl. J. Med. 2004, 350, 1731–1739. [Google Scholar] [CrossRef] [PubMed]
- Ferrara, M.; Peretti, C.; Fabrizio, E.; Corgnati, S.P. On the Multi-Domain Impacts of Coupling Mechanical Ventilation to Radiant Systems in Residential Buildings. Energies 2023, 16, 4870. [Google Scholar] [CrossRef]
- Quijada, M.C.; Solano, T.; Austin, M.C. Optimal Hybrid Ventilation Strategy to Assure Adequate Indoor Thermal Comfort and Air Quality in Educational Spaces under a Tropical Climate. J. Phys. Conf. Ser. 2022, 2385, 012095. [Google Scholar] [CrossRef]
- Sun, C.; Chen, J.; Hong, S.; Zhang, Y.; Kan, H.; Zhao, Z.; Deng, F.; Zeng, X.; Sun, Y.; Qian, H.; et al. Indoor Air Quality and Its Health Effects in Offices and School Buildings in the Yangtze River Delta. Air Qual. Atmos. Health 2023, 16, 1571–1586. [Google Scholar] [CrossRef]
- Knibbs, L.D.; Morawska, L.; Bell, S.C.; Grzybowski, P. Room Ventilation and the Risk of Airborne Infection Transmission in 3 Health Care Settings within a Large Teaching Hospital. Am. J. Infect. Control 2011, 39, 866–872. [Google Scholar] [CrossRef] [PubMed]
- Cavallini, A.; Busato, F.; Pregliasco, F. Remarks on the Air Recirculation in HVAC Systems during the SARS-CoV-2 Outbreak: The Case of All-Air Ducted Plants. AiCARR J. 2020, 63, 50–55. [Google Scholar]
- Ding, E.; Zhang, D.; Bluyssen, P.M. Ventilation Regimes of School Classrooms against Airborne Transmission of Infectious Respiratory Droplets: A Review. Build. Environ. 2022, 207, 108484. [Google Scholar] [CrossRef]
- Franceschini, P.B.; Neves, L.O. A Critical Review on Occupant Behaviour Modelling for Building Performance Simulation of Naturally Ventilated School Buildings and Potential Changes Due to the COVID-19 Pandemic. Energy Build. 2022, 258, 111831. [Google Scholar] [CrossRef]
- Buonanno, G.; Morawska, L.; Stabile, L. Quantitative Assessment of the Risk of Airborne Transmission of SARS-CoV-2 Infection: Prospective and Retrospective Applications. Environ. Int. 2020, 145, 106112. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Qian, H.; Sun, Z.; Cao, J.; Liu, F.; Luo, X.; Ling, R.; Weschler, L.B.; Mo, J.; Zhang, Y. Assessing and Controlling Infection Risk with Wells-Riley Model and Spatial Flow Impact Factor (SFIF). Sustain. Cities Soc. 2021, 67, 102719. [Google Scholar] [CrossRef] [PubMed]
- Elmalky, A.M.; Araji, M.T. Computational Fluid Dynamics Using Finite Volume Method: A Numerical Model for Double Skin Façades with Renewable Energy Source in Cold Climates. J. Build. Eng. 2022, 60, 105231. [Google Scholar] [CrossRef]
- Pirouz, B.; Mazzeo, D.; Palermo, S.A.; Naghib, S.N.; Turco, M.; Piro, P. CFD Investigation of Vehicle’s Ventilation Systems and Analysis of ACH in Typical Airplanes, Cars, and Buses. Sustainability 2021, 13, 6799. [Google Scholar] [CrossRef]
- Choudhary, B. Udayraj A Coupled CFD-Thermoregulation Model for Air Ventilation Clothing. Energy Build. 2022, 268, 112206. [Google Scholar] [CrossRef]
- Boutera, Y.; Boultif, N.; Moummi, N.; Arıcı, M.; SM Saleh, M.; Rouag, A.; Kethiri, M.A.; Beldjani, C. Evaluation of the Earth-Air Heat Exchanger’s Performance in Improving the Indoor Conditions of an Industrial Poultry House Using Computational Fluid Dynamics Verified with Field Tests. J. Clean. Prod. 2024, 434, 140218. [Google Scholar] [CrossRef]
- D’Alicandro, A.C.; Capozzoli, A.; Mauro, A. Thermofluid Dynamics and Droplets Transport inside a Large University Classroom: Effects of Occupancy Rate and Volumetric Airflow. J. Aerosol Sci. 2024, 175, 106285. [Google Scholar] [CrossRef]
- D’Alicandro, A.C.; Mauro, A. Air Change per Hour and Inlet Area: Effects on Ultrafine Particle Concentration and Thermal Comfort in an Operating Room. J. Aerosol Sci. 2023, 171, 106183. [Google Scholar] [CrossRef]
- Szczepanik, N.; Schnotale, J. CFD Simulations and Measurements of Carbon Dioxide Transport in a Passive House. In Proceedings of the ICR, The 24th IIR International Congress of Refrigeration: Improving Quality of Life, Preserving the Earth, Yokohama, Japan, 16–22 August 2015. [Google Scholar]
- Gammaitoni, L.; Nucci, M.C. Using a Mathematical Model to Evaluate the Efficacy of TB Control Measures. Emerg. Infect. Dis. 1997, 3, 335–342. [Google Scholar] [CrossRef] [PubMed]
- Riley, E.C.; Murphy, G.; Riley, R.L. Airborne Spread of Measles in a Suburban Elementary School. Am. J. Epidemiol. 1978, 107, 421–432. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Tang, H. Study on Ventilation Rates and Assessment of Infection Risks of COVID-19 in an Outpatient Building. J. Build. Eng. 2021, 42, 103090. [Google Scholar] [CrossRef]
- Yan, Y.; Li, X.; Fang, X.; Tao, Y.; Tu, J. A Spatiotemporal Assessment of Occupants’ Infection Risks in a Multi-Occupants Space Using Modified Wells–Riley Model. Build. Environ. 2023, 230, 110007. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Lin, Z. Dilution-Based Evaluation of Airborne Infection Risk—Thorough Expansion of Wells-Riley Model. Build. Environ. 2021, 194, 107674. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Ji, Y.; Fei, F.; Zhu, M.; Jin, T.; Xue, P.; Zhang, N. Optimization of COVID-19 Prevention and Control with Low Building Energy Consumption. Build. Environ. 2022, 219, 109233. [Google Scholar] [CrossRef]
- Li, B.; Cai, W. A Novel CO2-Based Demand-Controlled Ventilation Strategy to Limit the Spread of COVID-19 in the Indoor Environment. Build. Environ. 2022, 219, 109232. [Google Scholar] [CrossRef]
- Aviv, D.; Chen, K.W.; Teitelbaum, E.; Sheppard, D.; Pantelic, J.; Rysanek, A.; Meggers, F. A Fresh (Air) Look at Ventilation for COVID-19: Estimating the Global Energy Savings Potential of Coupling Natural Ventilation with Novel Radiant Cooling Strategies. Appl. Energy 2021, 292, 116848. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhang, N.; Hu, T.; Wang, Z.; Zhang, Y. Optimization of Energy Efficiency and COVID-19 Pandemic Control in Different Indoor Environments. Energy Build. 2022, 261, 111954. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik-Ścisło, N.; Flaga-Maryańczyk, A. Indoor Air Quality Modelling and Measurements of a Studio Apartment with a Mechanical Exhaust System. E3S Web Conf. 2018, 44, 00171. [Google Scholar] [CrossRef]
- Szczepanik-Scislo, N. Improving Household Safety via a Dynamic Air Terminal Device in Order to Decrease Carbon Monoxide Migration from a Gas Furnace. Int. J. Environ. Res. Public Health 2022, 19, 1676. [Google Scholar] [CrossRef] [PubMed]
- Mantesi, E.; Chmutina, K.; Goodier, C. The Office of the Future: Operational Energy Consumption in the Post-Pandemic Era. Energy Res. Soc. Sci. 2022, 87, 102472. [Google Scholar] [CrossRef] [PubMed]
- Chalgynbayeva, A.; Bai, A. The Most Relevant Factors and Trends in Energy Cooperation between Kazakhstan and China, Focused on Renewable Energy Sources (RES). Appl. Stud. Agribus. Commer. 2022, 15, 65–76. [Google Scholar] [CrossRef]
- Akbari, V.; Naghashzadegan, M.; Kouhikamali, R.; Afsharpanah, F.; Yaïci, W. Multi-Objective Optimization of a Small Horizontal-Axis Wind Turbine Blade for Generating the Maximum Startup Torque at Low Wind Speeds. Machines 2022, 10, 785. [Google Scholar] [CrossRef]
- Chalgynbayeva, A.; Mizik, T.; Bai, A. Cost–Benefit Analysis of Kaposvár Solar Photovoltaic Park Considering Agrivoltaic Systems. Clean Technol. 2022, 4, 1054–1070. [Google Scholar] [CrossRef]
- Afsharpanah, F.; Sheshpoli, A.Z.; Pakzad, K.; Ajarostaghi, S.S.M. Numerical Investigation of Non-Uniform Heat Transfer Enhancement in Parabolic Trough Solar Collectors Using Dual Modified Twisted-Tape Inserts. J. Therm. Eng. 2021, 7, 133–147. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Goswami, A.; Sadhu, P.K. Design, Development and Performance Analysis of FSPV System for Powering Sustainable Energy Based Mini Micro-Grid. Microsyst. Technol. 2023, 29, 1465–1478. [Google Scholar] [CrossRef]
- Maity, R.; Sudhakar, K.; Abdul Razak, A.; Karthick, A.; Barbulescu, D. Agrivoltaic: A Strategic Assessment Using SWOT and TOWS Matrix. Energies 2023, 16, 3313. [Google Scholar] [CrossRef]
- Elmalky, A.M.; Araji, M.T. Computational Procedure of Solar Irradiation: A New Approach for High Performance Façades with Experimental Validation. Energy Build. 2023, 298, 113491. [Google Scholar] [CrossRef]
- Elmalky, A.M.; Araji, M.T. A New Trigonometric Model for Solar Radiation and Shading Factor: Varying Profiles of Building Façades and Urban Eccentricities. Energy Build. 2023, 282, 112803. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Sadhu, P.K.; Sarkar, D. Performance Evaluation of Building Integrated Photovoltaic System Arrays (SP, TT, QT, and TCT) to Improve Maximum Power with Low Mismatch Loss under Partial Shading. Microsyst. Technol. 2023, 30, 583–597. [Google Scholar] [CrossRef]
- Rai, R.; Jamali, S.; Ahmed, K.; Zaidi, A.A.; Ali, M.; Memon, A.H. Development of a Small Scale Photovoltaic Thermal Hybrid (PV/T) System for Domestic Applications in Pakistan. Clean Energy Technol. J. 2023, 1, 60–70. [Google Scholar] [CrossRef]
- EnergyPlus Input Output Reference. The Encyclopedic Reference to EnergyPlus Input and Output; USA, Department of Energy: Washington, DC, USA, 2010; pp. 1996–2016.
- Sze To, G.N.; Chao, C.Y.H. Review and Comparison between the Wells-Riley and Dose-Response Approaches to Risk Assessment of Infectious Respiratory Diseases. Indoor Air 2010, 20, 2–16. [Google Scholar] [CrossRef]
- Buonanno, G.; Stabile, L.; Morawska, L. Estimation of Airborne Viral Emission: Quanta Emission Rate of SARS-CoV-2 for Infection Risk Assessment. Environ. Int. 2020, 141, 105794. [Google Scholar] [CrossRef]
- Maity, R.; Mathew, M.; Hossain, J. Increase in Power Production of Rooftop Solar Photovoltaic System Using Tracking. In Proceedings of the 2018 International Conference on Power Energy, Environment and Intelligent Control, Greater Noida, India, 13–14 April 2018; pp. 415–419. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Kambezidis, H.D.; Kaskaoutis, D.G.; Karagiannis, D.; Polo, J.M. Comparison between MRM Simulations, CAMS and PVGIS Databases with Measured Solar Radiation Components at the Methoni Station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Martinez-de-Pison, F.J.; Sanz-Garcia, A. Sources of Uncertainty in Annual Global Horizontal Irradiance Data. Sol. Energy 2018, 170, 873–884. [Google Scholar] [CrossRef]
- Chen, D.; Chen, H.W. Using the Köppen Classification to Quantify Climate Variation and Change: An Example for 1901-2010. Environ. Dev. 2013, 6, 69–79. [Google Scholar] [CrossRef]
- President of the Italian Republic DPR 26 Agosto 1993 n.412. Regolamento Recante Norme per La Progettazione, l’installazione, l’esercizio e La Manutenzione Degli Impianti Termici Degli Edifici Ai Fini Del Contenimento Dei Consumi Di Energia; Gazzetta Ufficiale della Repubblica Italiana. 1993. Available online: https://www.bosettiegatti.eu/info/norme/statali/1993_0412.htm (accessed on 27 May 2024). (In Italian).
- Italian Ministry of Economic Development—Applicazione Delle Metodologie Di Calcolo Delle Prestazioni Energetiche e Definizione Delle Prescrizioni e Dei Requisiti Minimi Degli Edifici; Gazzetta Ufficiale della Repubblica Italiana. 2015. Available online: https://www.mimit.gov.it/index.php/it/normativa/decreti-interministeriali/decreto-interministeriale-26-giugno-2015-applicazione-delle-metodologie-di-calcolo-delle-prestazioni-energetiche-e-definizione-delle-prescrizioni-e-dei-requisiti-minimi-degli-edifici (accessed on 27 May 2024). (In Italian)
- Vio, M. Gli Impianti Di Climatizzazione e Il Rischio Di Contagio. AiCARR J. 2020, 34–40. (In Italian) [Google Scholar]

| Description | Value | Measure Unit |
|---|---|---|
| Altitude | 8 | m |
| Latitude | 41°21′00′′ N | - |
| Longitude | 13°25′00′′ E | - |
| Koppen classification | C | - |
| Italian climatic zone (DPR 412/93 [115]) | C | - |
| Heating degree days | 1089 | HDD |
| Description | Value | Measure Unit |
|---|---|---|
| Total number of floors | 2 | - |
| Net floor area | 1820 | m2 |
| Net volume | 6150 | m3 |
| External wall area | 750 | m2 |
| Window area | 490 | m2 |
| Air infiltration, 50 Pa | 0.05 | h−1 |
| Window-to-wall ratio (WWR) | 40 | % |
| Building Envelope Component | Thermal Transmittance | Thermal Transmittance Limit Value |
|---|---|---|
| W/(m2K) | W/(m2K) | |
| Floor | 0.27 | 0.38 |
| Roof | 0.26 | 0.33 |
| Wall | 0.19 | 0.34 |
| Windows | 1.70 | 2.20 |
| Service | Description | Value | Measure Unit |
|---|---|---|---|
| Heating | System | Hydronic radiant panels | - |
| System type | Hydronic | - | |
| Generation | Two electric air-to-water heat pumps | - | |
| Heating capacity (rating conditions) | 160 | kW | |
| COP (rating conditions) | 3.80 | - | |
| Distribution | Centralised | - | |
| Distribution efficiency | 0.98 | - | |
| Emission | Radiant floor | - | |
| Emission efficiency | 0.99 | - | |
| Control system | Modulating | - | |
| Indoor air temperature/RH set-point | 20/50 | °C/% | |
| System availability | 07:00–17:00 Monday–Friday 15 November–31 March | - | |
| Cooling | Not present | ||
| DHW | System | Dedicated electric air-to-water heat pump with 300 L storage tank | - |
| Generation | Dedicated electric air-to-water heat pump | - | |
| Capacity (rating conditions) | 12 | kW | |
| COP (rating conditions) | 3.50 | - | |
| Distribution | Centralised | - | |
| Distribution efficiency | 0.99 | - | |
| System availability | 07:00–17:00 Monday–Friday All year | - | |
| Mechanical Ventilation | Supply external air flow rate | Variable | L/s or h−1 |
| Fan power | 10 | kW | |
| SFP (specific fan power) | 832 | W/(m3/s) | |
| Heat recovery | Crossflow | - | |
| Heat recovery efficiency | 0.85 | - | |
| System availability | 07:00–17:00 Monday–Friday All year | - | |
| # | Room | Volume | Number of Occupants | Outdoor Air Volume | Risk of Infection | ||
|---|---|---|---|---|---|---|---|
| m3 | L/s | m3/h | h−1 | % | |||
| 1 | Classroom 1 | 472.9 | 36 | 333 | 1200 | 2.5 | 10 |
| 2 | Classroom 2 | 453.3 | 34 | 315 | 1133 | 2.5 | 10 |
| 3 | Classroom 3 | 453.3 | 34 | 315 | 1133 | 2.5 | 10 |
| 4 | Classroom 4 | 453.3 | 34 | 315 | 1133 | 2.5 | 10 |
| 5 | Classroom 5 | 451.1 | 34 | 315 | 1133 | 2.5 | 10 |
| 6 | Classroom 6 | 453.3 | 34 | 315 | 1133 | 2.5 | 10 |
| 7 | Classroom 7 | 464.2 | 35 | 324 | 1167 | 2.5 | 10 |
| 8 | Kitchen | 57.5 | 2 | 38 | 138 | 2.5 | 28 |
| 9 | Canteen | 362.6 | 53 | 252 | 907 | 2.5 | 3 |
| 10 | Relaxing area | 122.4 | 8 | 51 | 184 | 1.5 | 50 |
| 11 | Boardroom | 81.2 | 6 | 33 | 120 | 1.5 | 64 |
| 12 | Office 1 | 120.9 | 4 | 50 | 180 | 1.5 | 50 |
| 13 | Office 2 | 68.8 | 2 | 27 | 98 | 1.5 | 70 |
| 14 | Office 3 | 74.7 | 2 | 30 | 108 | 1.5 | 67 |
| 15 | Medical room | 44.8 | 2 | 19 | 68 | 1.5 | 21 |
| 16 | Hallway | 895.5 | 25 | 373 | 1343 | 1.5 | 1 |
| 17 | Laundry | 32 | 2 | 13 | 48 | 1.5 | 28 |
| # | Room | Volume | Number of Occupants | Outdoor Airflow Volume | Risk of Infection | ||
|---|---|---|---|---|---|---|---|
| m3 | L/s | m3/h | h−1 | % | |||
| 1 | Classroom 1 | 472.9 | 36 | 360 | 1296 | 2.7 | 10 |
| 2 | Classroom 2 | 453.3 | 34 | 340 | 1224 | 2.7 | 10 |
| 3 | Classroom 3 | 453.3 | 34 | 340 | 1224 | 2.7 | 10 |
| 4 | Classroom 4 | 453.3 | 34 | 340 | 1224 | 2.7 | 10 |
| 5 | Classroom 5 | 451.1 | 34 | 340 | 1224 | 2.7 | 10 |
| 6 | Classroom 6 | 453.3 | 34 | 340 | 1224 | 2.7 | 10 |
| 7 | Classroom 7 | 464.2 | 35 | 350 | 1260 | 2.7 | 10 |
| 8 | Kitchen | 57.5 | 2 | 20 | 72 | 1.3 | 47 |
| 9 | Canteen | 362.6 | 53 | 530 | 1908 | 5.3 | 2 |
| 10 | Relaxing area | 122.4 | 8 | 80 | 288 | 2.4 | 35 |
| 11 | Boardroom | 81.2 | 6 | 60 | 216 | 2.7 | 32 |
| 12 | Office 1 | 120.9 | 4 | 40 | 144 | 1.2 | 73 |
| 13 | Office 2 | 68.8 | 2 | 20 | 72 | 1.1 | 81 |
| 14 | Office 3 | 74.7 | 2 | 20 | 72 | 1.0 | 82 |
| 15 | Medical room | 44.8 | 2 | 20 | 72 | 1.6 | 20 |
| 16 | Hallway | 895.5 | 25 | 250 | 900 | 1.0 | 2 |
| 17 | Laundry | 32 | 2 | 20 | 72 | 2.3 | 19 |
| # | Room | Volume | Number of Occupants | Outdoor Airflow Volume | Risk of Infection | ||
|---|---|---|---|---|---|---|---|
| m3 | L/s | m3/h | h−1 | % | |||
| 1 | Classroom 1 | 472.9 | 36 | 657 | 2365 | 5 | 5 |
| 2 | Classroom 2 | 453.3 | 34 | 629 | 2266 | 5 | 5 |
| 3 | Classroom 3 | 453.3 | 34 | 629 | 2266 | 5 | 5 |
| 4 | Classroom 4 | 453.3 | 34 | 629 | 2266 | 5 | 5 |
| 5 | Classroom 5 | 451.1 | 34 | 629 | 2256 | 5 | 5 |
| 6 | Classroom 6 | 453.3 | 34 | 629 | 2266 | 5 | 5 |
| 7 | Classroom 7 | 464.2 | 35 | 645 | 2321 | 5 | 5 |
| 8 | Kitchen | 57.5 | 2 | 80 | 287 | 5 | 15 |
| 9 | Canteen | 362.6 | 53 | 504 | 1813 | 5 | 2 |
| 10 | Relaxing area | 122.4 | 8 | 170 | 612 | 5 | 19 |
| 11 | Boardroom | 81.2 | 6 | 113 | 406 | 5 | 26 |
| 12 | Office 1 | 120.9 | 4 | 168 | 604 | 5 | 19 |
| 13 | Office 2 | 68.8 | 2 | 96 | 344 | 5 | 30 |
| 14 | Office 3 | 74.7 | 2 | 104 | 373 | 5 | 28 |
| 15 | Medical room | 44.8 | 2 | 62 | 224 | 5 | 7 |
| 16 | Hallway | 895.5 | 25 | 1244 | 4478 | 5 | ~ 0 |
| 17 | Laundry | 32 | 2 | 44 | 160 | 5 | 9 |
| # | Room | Volume | Number of Occupants | 1 ACH | 2 ACH | 3 ACH | 4 ACH | 5 ACH | 6 ACH | 7 ACH | 8 ACH | 9 ACH | 10 ACH | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | A | B | A | B | A | B | A | B | A | B | A | B | A | B | A | B | A | B | ||||
| m3 | m3/h | % | m3/h | % | m3/h | % | m3/h | % | m3/h | % | m3/h | % | m3/h | % | m3/h | % | m3/h | % | m3/h | % | |||
| 1 | Classroom 1 | 472.9 | 36 | 473 | 23 | 946 | 12 | 1419 | 9 | 1892 | 6 | 2365 | 5 | 2838 | 4 | 3310 | 4 | 3783 | 3 | 4256 | 3 | 4729 | 3 |
| 2 | Classroom 2 | 453.3 | 34 | 453 | 24 | 907 | 13 | 1360 | 9 | 1813 | 7 | 2266 | 5 | 2720 | 5 | 3173 | 4 | 3626 | 3 | 4079 | 3 | 4533 | 3 |
| 3 | Classroom 3 | 453.3 | 34 | 453 | 24 | 907 | 13 | 1360 | 9 | 1813 | 7 | 2266 | 5 | 2720 | 5 | 3173 | 4 | 3626 | 3 | 4079 | 3 | 4533 | 3 |
| 4 | Classroom 4 | 453.3 | 34 | 453 | 24 | 907 | 13 | 1360 | 9 | 1813 | 7 | 2266 | 5 | 2720 | 5 | 3173 | 4 | 3626 | 3 | 4079 | 3 | 4533 | 3 |
| 5 | Classroom 5 | 451.1 | 34 | 451 | 24 | 902 | 13 | 1354 | 9 | 1805 | 7 | 2256 | 5 | 2707 | 5 | 3158 | 4 | 3610 | 3 | 4061 | 3 | 4512 | 3 |
| 6 | Classroom 6 | 453.3 | 34 | 453 | 24 | 907 | 13 | 1360 | 9 | 1813 | 7 | 2266 | 5 | 2720 | 5 | 3173 | 4 | 3626 | 3 | 4079 | 3 | 4533 | 3 |
| 7 | Classroom 7 | 464.2 | 35 | 464 | 24 | 928 | 13 | 1393 | 9 | 1857 | 7 | 2321 | 5 | 2785 | 4 | 3250 | 4 | 3714 | 3 | 4178 | 3 | 4642 | 3 |
| 8 | Kitchen | 57.5 | 2 | 57 | 56 | 115 | 34 | 172 | 24 | 230 | 19 | 287 | 15 | 345 | 13 | 402 | 11 | 460 | 10 | 517 | 9 | 575 | 8 |
| 9 | Canteen | 362.6 | 53 | 363 | 8 | 725 | 4 | 1088 | 3 | 1450 | 2 | 1813 | 2 | 2176 | 1 | 2538 | 1 | 2901 | 1 | 3263 | 1 | 3626 | 1 |
| 10 | Relaxing area | 122.4 | 8 | 122 | 64 | 245 | 40 | 367 | 29 | 490 | 23 | 612 | 19 | 734 | 16 | 857 | 14 | 979 | 12 | 1102 | 11 | 1224 | 10 |
| 11 | Boardroom | 81.2 | 6 | 81 | 79 | 162 | 54 | 244 | 40 | 325 | 32 | 406 | 26 | 487 | 23 | 568 | 20 | 649 | 18 | 731 | 16 | 812 | 14 |
| 12 | Office 1 | 120.9 | 4 | 121 | 65 | 242 | 41 | 363 | 29 | 483 | 23 | 604 | 19 | 725 | 16 | 846 | 14 | 967 | 12 | 1088 | 11 | 1209 | 10 |
| 13 | Office 2 | 68.8 | 2 | 69 | 84 | 138 | 60 | 206 | 46 | 275 | 37 | 344 | 30 | 413 | 26 | 482 | 23 | 551 | 20 | 619 | 18 | 688 | 17 |
| 14 | Office 3 | 74.7 | 2 | 75 | 82 | 149 | 57 | 224 | 43 | 299 | 34 | 373 | 28 | 448 | 25 | 523 | 21 | 598 | 19 | 672 | 17 | 747 | 16 |
| 15 | Medical room | 44.8 | 2 | 45 | 30 | 90 | 16 | 134 | 11 | 179 | 8 | 224 | 7 | 269 | 6 | 314 | 5 | 359 | 4 | 403 | 4 | 448 | 3 |
| 16 | Hallway | 895.5 | 25 | 896 | 2 | 1791 | 1 | 2687 | 1 | 3582 | ~0 | 4478 | ~0 | 5373 | ~0 | 6269 | ~0 | 7164 | ~0 | 8060 | ~0 | 8955 | ~0 |
| 17 | Laundry | 32 | 2 | 32 | 39 | 64 | 22 | 96 | 15 | 128 | 12 | 160 | 9 | 192 | 8 | 224 | 7 | 256 | 6 | 288 | 5 | 320 | 5 |
| # | Room | Volume | Number of Occupants | Outdoor Airflow Volume | Risk of Infection | ||
|---|---|---|---|---|---|---|---|
| m3 | L/s | m3/h | h−1 | % | |||
| 1 | Classroom 1 | 472.9 | 36 | 157 | 567 | 1.2 | 20 |
| 2 | Classroom 2 | 453.3 | 34 | 151 | 544 | 1.2 | 20 |
| 3 | Classroom 3 | 453.3 | 34 | 151 | 544 | 1.2 | 20 |
| 4 | Classroom 4 | 453.3 | 34 | 151 | 544 | 1.2 | 20 |
| 5 | Classroom 5 | 451.1 | 34 | 151 | 544 | 1.2 | 20 |
| 6 | Classroom 6 | 453.3 | 34 | 151 | 544 | 1.2 | 20 |
| 7 | Classroom 7 | 464.2 | 35 | 155 | 557 | 1.2 | 20 |
| 8 | Kitchen | 57.5 | 2 | 56 | 201 | 3.5 | 20 |
| 9 | Canteen | 362.6 | 53 | 40 | 145 | 0.4 | 20 |
| 10 | Relaxing area | 122.4 | 8 | 156 | 563 | 4.5 | 20 |
| 11 | Boardroom | 81.2 | 6 | 149 | 536 | 6.6 | 20 |
| 12 | Office 1 | 120.9 | 4 | 151 | 544 | 4.6 | 20 |
| 13 | Office 2 | 68.8 | 2 | 149 | 537 | 7.8 | 20 |
| 14 | Office 3 | 74.7 | 2 | 149 | 538 | 7.2 | 20 |
| 15 | Medical room | 44.8 | 2 | 19 | 67 | 1.5 | 20 |
| 16 | Hallway | 895.5 | 25 | 25 | 90 | 0.1 | 20 |
| 17 | Laundry | 32 | 2 | 19 | 70 | 2.2 | 20 |
| # | Room | Volume | Number of Occupants | Outdoor Airflow Volume | Risk of Infection | ||
|---|---|---|---|---|---|---|---|
| m3 | L/s | m3/h | h−1 | % | |||
| 1 | Classroom 1 | 472.9 | 36 | 197 | 709 | 1.5 | 15 |
| 2 | Classroom 2 | 453.3 | 34 | 189 | 680 | 1.5 | 15 |
| 3 | Classroom 3 | 453.3 | 34 | 189 | 680 | 1.5 | 15 |
| 4 | Classroom 4 | 453.3 | 34 | 189 | 680 | 1.5 | 15 |
| 5 | Classroom 5 | 451.1 | 34 | 189 | 680 | 1.5 | 15 |
| 6 | Classroom 6 | 453.3 | 34 | 189 | 680 | 1.5 | 15 |
| 7 | Classroom 7 | 464.2 | 35 | 193 | 696 | 1.5 | 15 |
| 8 | Kitchen | 57.5 | 2 | 75 | 270 | 4.8 | 15 |
| 9 | Canteen | 362.6 | 53 | 50 | 181 | 0.5 | 15 |
| 10 | Relaxing area | 122.4 | 8 | 214 | 771 | 6.0 | 15 |
| 11 | Boardroom | 81.2 | 6 | 216 | 788 | 9.8 | 15 |
| 12 | Office 1 | 120.9 | 4 | 201 | 725 | 6.1 | 15 |
| 13 | Office 2 | 68.8 | 2 | 216 | 777 | 10.6 | 15 |
| 14 | Office 3 | 74.7 | 2 | 199 | 717 | 9.0 | 15 |
| 15 | Medical room | 44.8 | 2 | 25 | 90 | 2.0 | 15 |
| 16 | Hallway | 895.5 | 25 | 25 | 90 | 0.1 | 15 |
| 17 | Laundry | 32 | 2 | 27 | 96 | 2.8 | 15 |
| # | Room | Volume | Number of Occupants | Outdoor Airflow Volume | Risk of Infection | ||
|---|---|---|---|---|---|---|---|
| m3 | L/s | m3/h | h−1 | % | |||
| 1 | Classroom 1 | 472.9 | 36 | 302 | 1088 | 2.3 | 10 |
| 2 | Classroom 2 | 453.3 | 34 | 290 | 1043 | 2.3 | 10 |
| 3 | Classroom 3 | 453.3 | 34 | 290 | 1043 | 2.3 | 10 |
| 4 | Classroom 4 | 453.3 | 34 | 290 | 1043 | 2.3 | 10 |
| 5 | Classroom 5 | 451.1 | 34 | 288 | 1038 | 2.3 | 10 |
| 6 | Classroom 6 | 453.3 | 34 | 290 | 1043 | 2.3 | 10 |
| 7 | Classroom 7 | 464.2 | 35 | 290 | 1043 | 2.3 | 10 |
| 8 | Kitchen | 57.5 | 2 | 117 | 420 | 7.3 | 10 |
| 9 | Canteen | 362.6 | 53 | 81 | 290 | 0.8 | 10 |
| 10 | Relaxing area | 122.4 | 8 | 333 | 1200 | 9.0 | 10 |
| 11 | Boardroom | 81.2 | 6 | 334 | 1202 | 13.5 | 10 |
| 12 | Office 1 | 120.9 | 4 | 312 | 1124 | 9.1 | 10 |
| 13 | Office 2 | 68.8 | 2 | 332 | 1197 | 16.0 | 10 |
| 14 | Office 3 | 74.7 | 2 | 332 | 1195 | 14.8 | 10 |
| 15 | Medical room | 44.8 | 2 | 39 | 139 | 3.1 | 10 |
| 16 | Hallway | 895.5 | 25 | 50 | 179 | 0.2 | 10 |
| 17 | Laundry | 32 | 2 | 19 | 70 | 4.3 | 10 |
| Ventilation Rate | Compensated GHG Emission | PV System Power | System Components | Cost | Total Cost |
|---|---|---|---|---|---|
| kgCO2-eq per Year | kWp | EUR | EUR | ||
| IMD approach | 8938 | 13.6 | N°34 modules | 8500 | 22,680 |
| Inverter | 3300 | ||||
| Support structure (68 m2) | 4080 | ||||
| Design and installation | 6800 | ||||
| WHO approach | 9361 | 14.0 | N°35 modules | 8750 | 23,250 |
| Inverter | 3300 | ||||
| Support structure (70 m2) | 4200 | ||||
| Design and installation | 7000 | ||||
| ACDCP approach | 13,194 | 20.0 | N°50 modules | 12,500 | 32,700 |
| Inverter | 4200 | ||||
| Support structure (100 m2) | 6000 | ||||
| Design and installation | 10,000 | ||||
| Gradual ventilation increment (case of 10 ACH) | 21,252 | 32.0 | N°80 modules | 20,000 | 51,400 |
| Inverter | 4800 | ||||
| Support structure (160 m2) | 9600 | ||||
| Design and installation | 17,000 | ||||
| Tailored approach (case of 10% risk) | 9937 | 15.2 | N°38 modules | 9500 | 25,260 |
| Inverter | 3600 | ||||
| Support structure (76 m2) | 4560 | ||||
| Design and installation | 7600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Agostino, D.; Di Mascolo, M.; Minelli, F.; Minichiello, F. A New Tailored Approach to Calculate the Optimal Number of Outdoor Air Changes in School Building HVAC Systems in the Post-COVID-19 Era. Energies 2024, 17, 2769. https://doi.org/10.3390/en17112769
D’Agostino D, Di Mascolo M, Minelli F, Minichiello F. A New Tailored Approach to Calculate the Optimal Number of Outdoor Air Changes in School Building HVAC Systems in the Post-COVID-19 Era. Energies. 2024; 17(11):2769. https://doi.org/10.3390/en17112769
Chicago/Turabian StyleD’Agostino, Diana, Martina Di Mascolo, Federico Minelli, and Francesco Minichiello. 2024. "A New Tailored Approach to Calculate the Optimal Number of Outdoor Air Changes in School Building HVAC Systems in the Post-COVID-19 Era" Energies 17, no. 11: 2769. https://doi.org/10.3390/en17112769
APA StyleD’Agostino, D., Di Mascolo, M., Minelli, F., & Minichiello, F. (2024). A New Tailored Approach to Calculate the Optimal Number of Outdoor Air Changes in School Building HVAC Systems in the Post-COVID-19 Era. Energies, 17(11), 2769. https://doi.org/10.3390/en17112769









