The Effects of a Seagull Airfoil on the Aerodynamic Performance of a Small Wind Turbine
Abstract
1. Introduction
2. Methodology
2.1. Geometry and Conditions
2.2. Turbulence Model
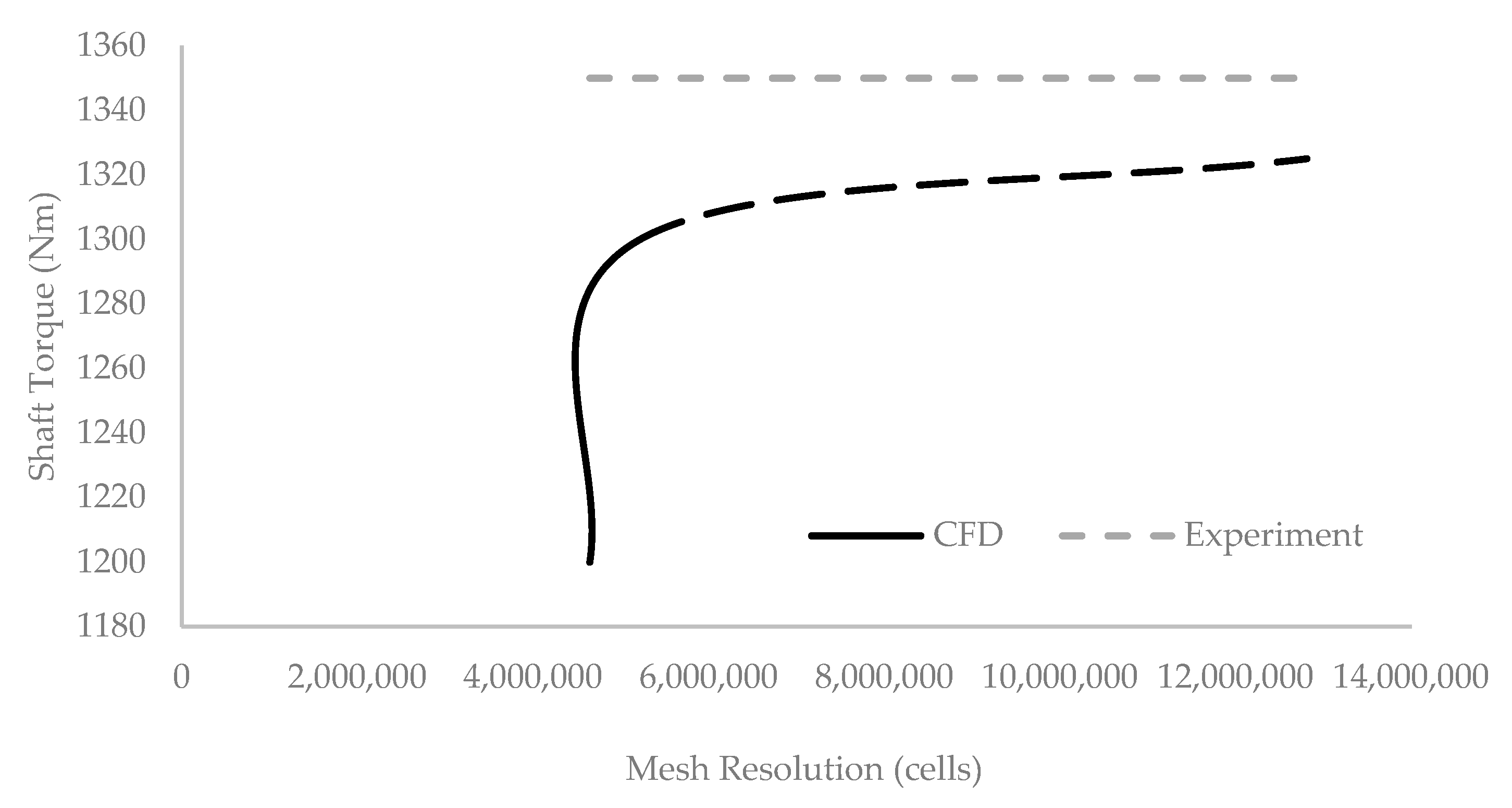
2.3. Meshing Strategy
3. Results and Discussion
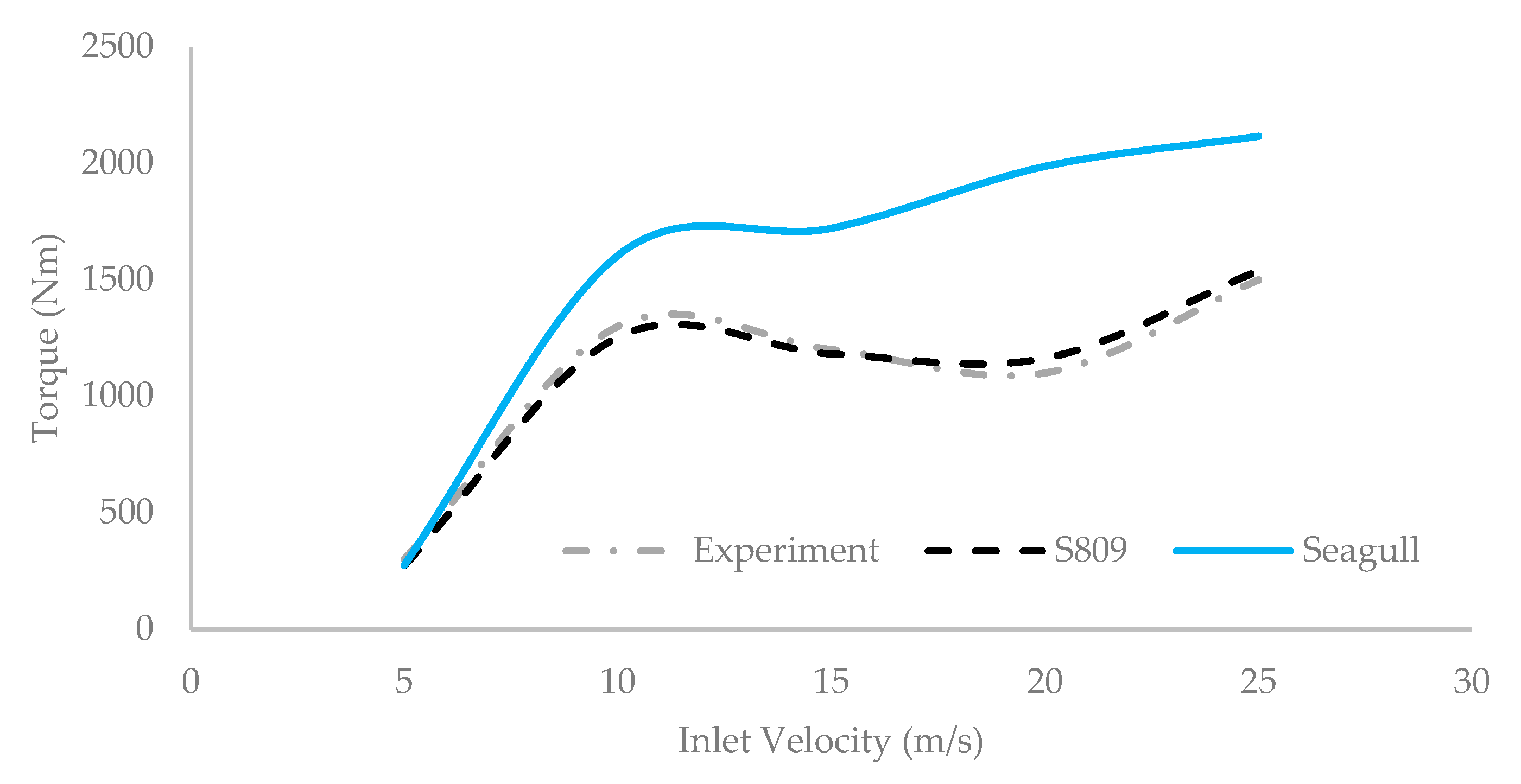
3.1. Torque Outputs
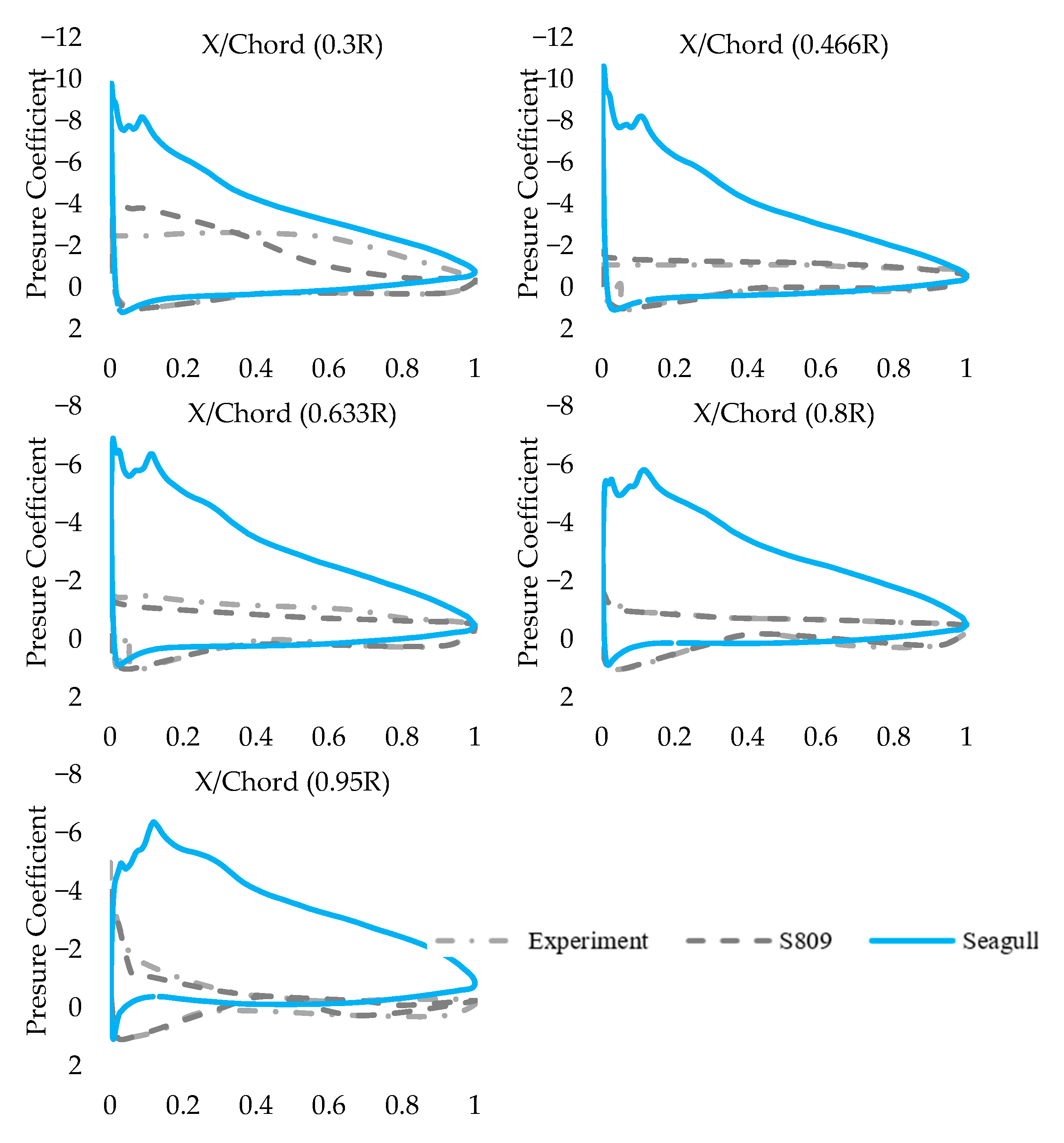
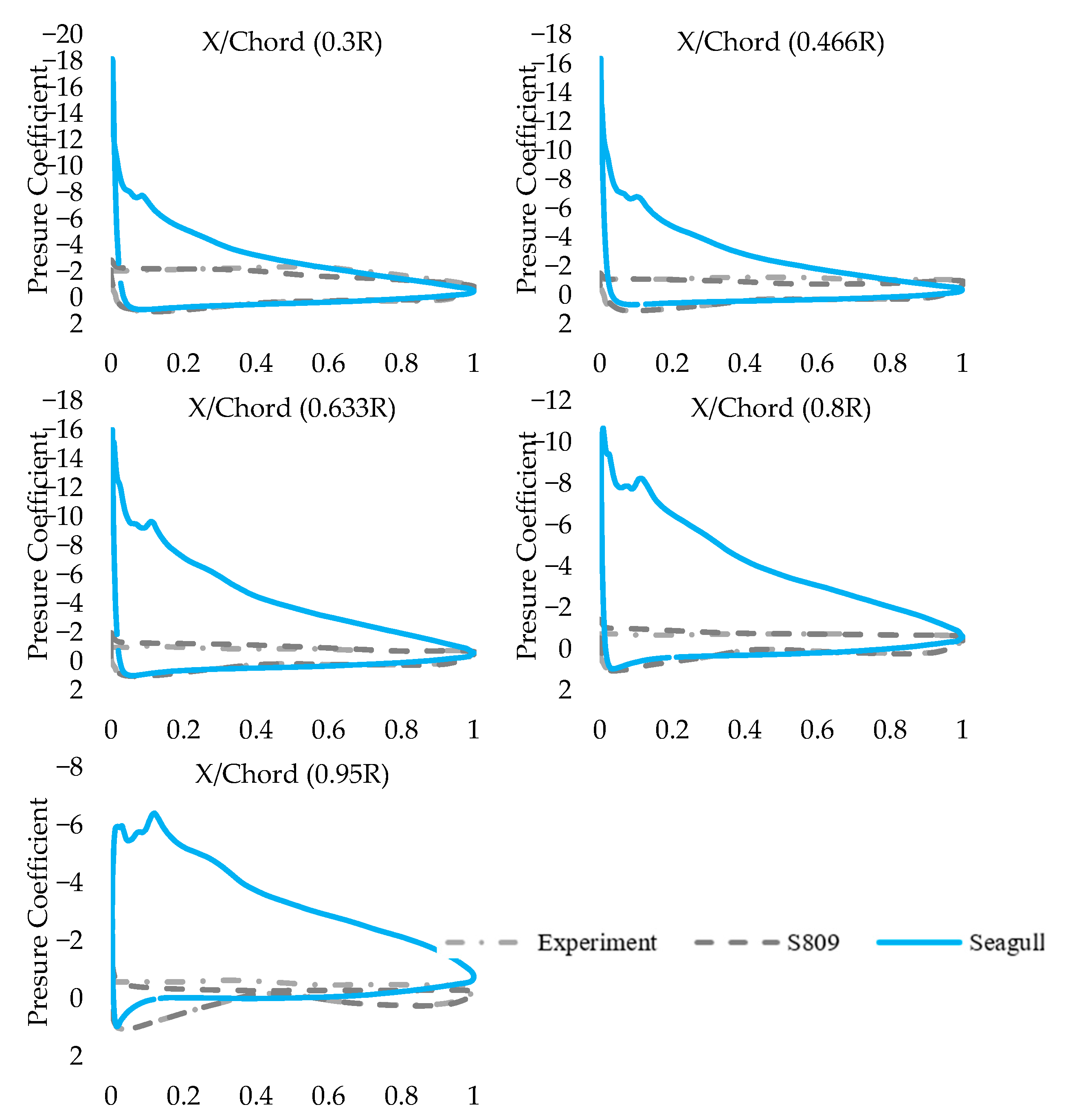
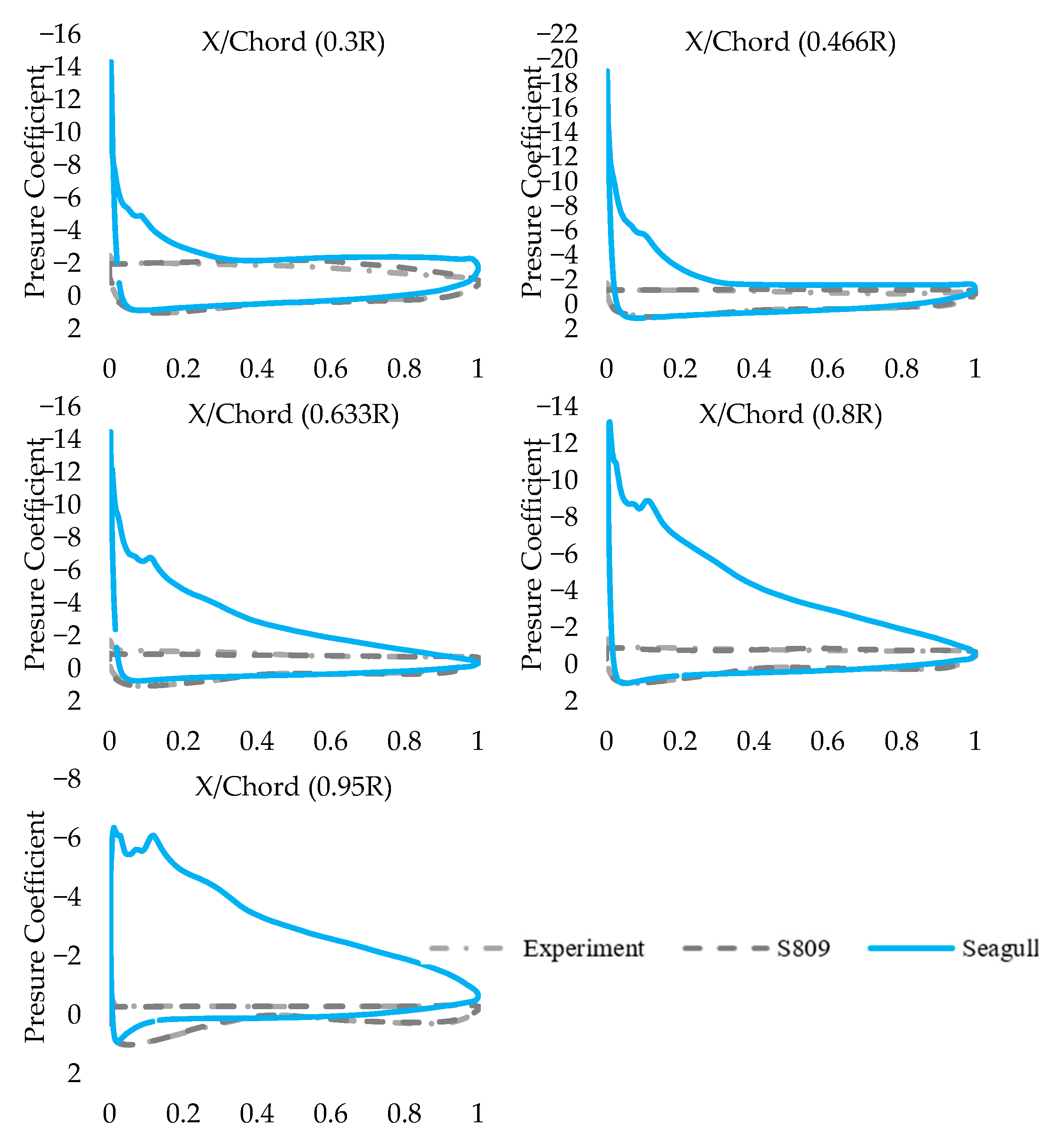
3.2. Pressure Distributions
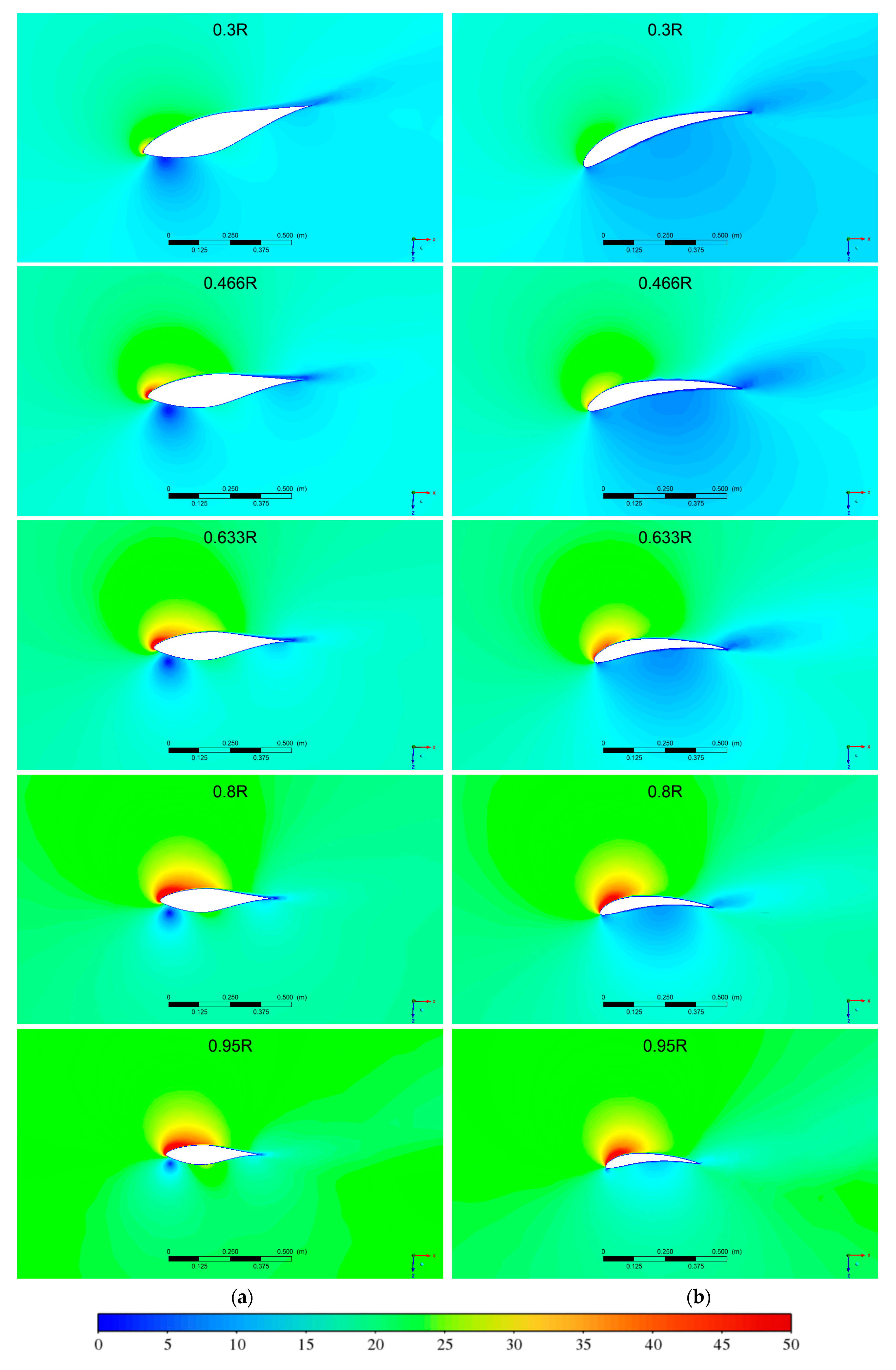
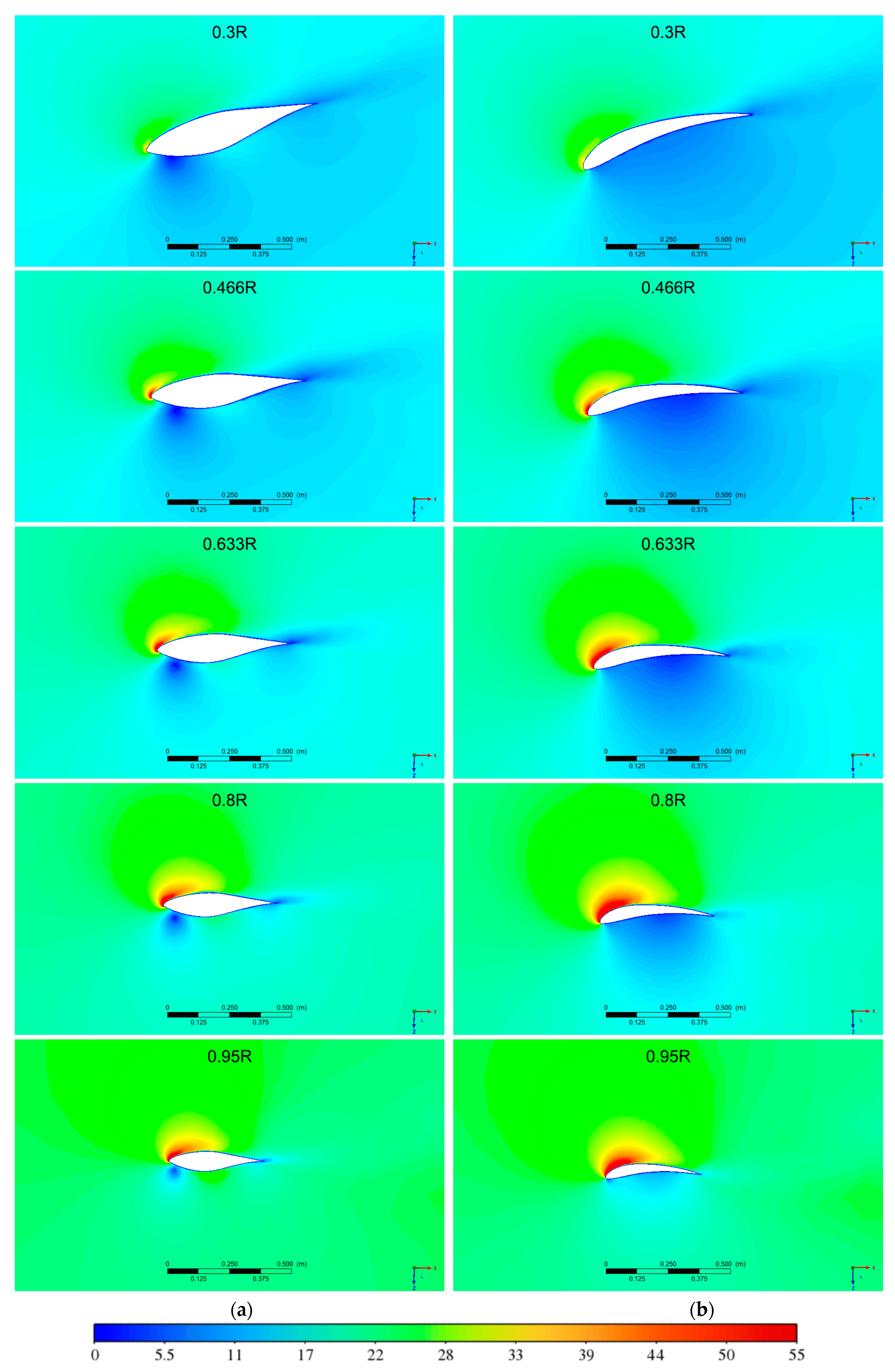
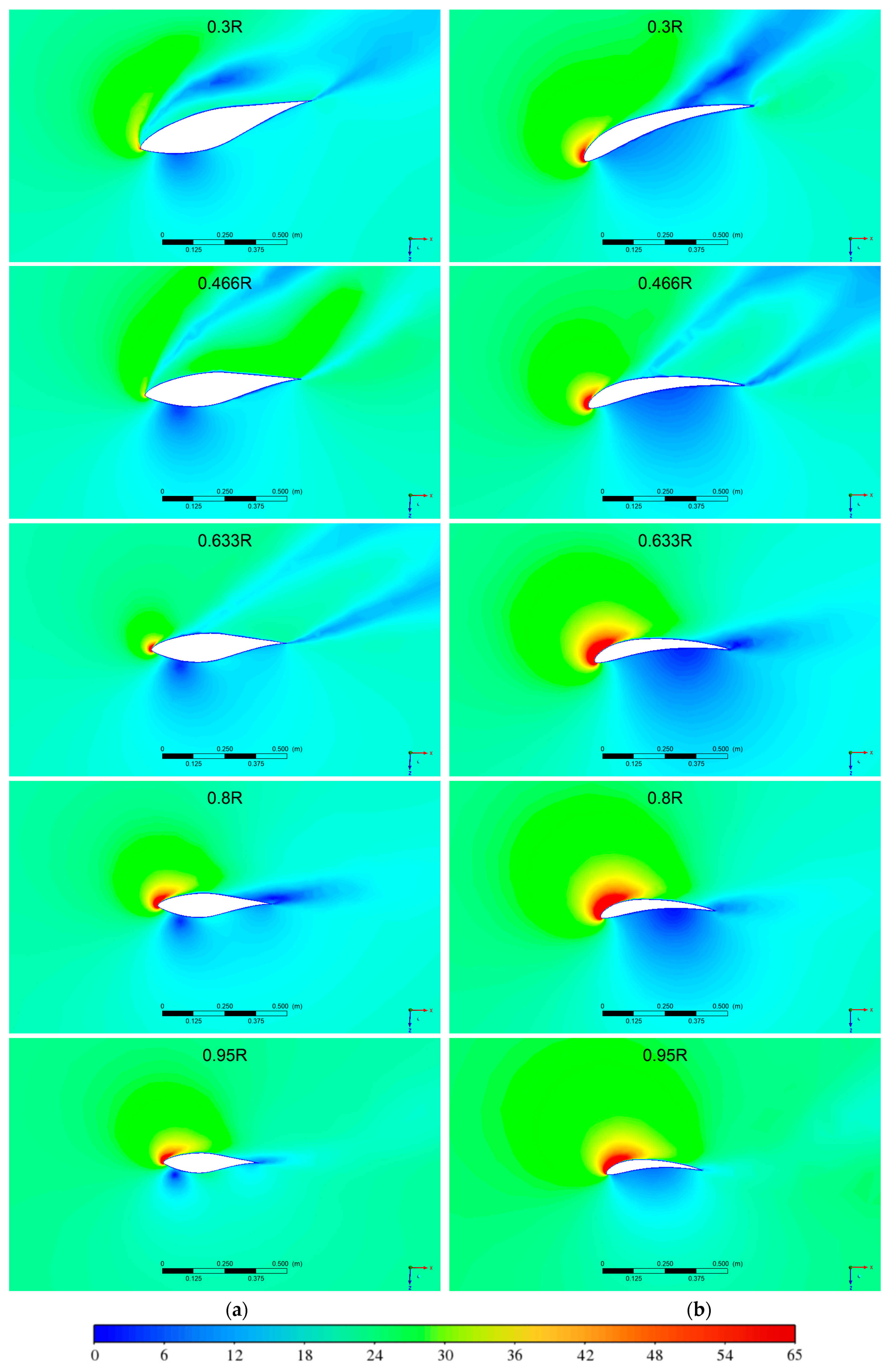
3.3. Local Velocities
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- March, A.I.; Bradley, C.W.; Garcia, E. Aerodynamic Properties of Avian Flight as a Function of Wing Shape. In Proceedings of the ASME International Mechanical Engineering Congress & Expositio, Orlando, FL, USA, 5–11 November 2005. [Google Scholar]
- Lees, J.J.; Dimitriadis, G.; Nudds, R.L. The influence of flight style on the aerodynamic properties of avian wings as fixed lifting surfaces. PeerJ 2016, 4, e2495. [Google Scholar] [CrossRef] [PubMed]
- Bourton, J. Supercharged Swifts Take Flight Speed Record; BBC News: London, UK, 2010. [Google Scholar]
- Grolier. The New Book of Knowledge; Scholastic Corporation: New York, NY, USA, 2003; p. 278. [Google Scholar]
- Tucker, V.A. Gliding Birds: Reduction of Induced Drag by Wing Tip Slots Between the Primary Feathers. J. Exp. Biol. 1993, 180, 285–310. [Google Scholar] [CrossRef]
- Weimerskirch, H.; Guionnet, T.; Martin, J.; Shaffer, S.; Costa, D. Fast and fuel efficient? Optimal use of wind by flying albatrosses. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2000, 267, 1869–1874. [Google Scholar] [CrossRef] [PubMed]
- Günther Pfeifhofer, H.T. The Flight of Albatross—How to Transform It into Aerodynamic Engineering? Engineering 2014, 6, 427–438. [Google Scholar] [CrossRef]
- Robles, G.E.; Luna, E.C.R.; Tayactac, R.G.; Honra, J.P.; Calderon, A.D. Design and Aerodynamic Analysis of a Bio-inspired HAWT with Albatross and Stork Airfoil for Low Wind Velocity using CFD. In Proceedings of the 6th International Conference on Power and Energy Engineering, Shanghai, China, 25–27 November 2022. [Google Scholar]
- Anderson, J.D. Fundamental of Aerodynamics; McGraw-Hill: Boston, MA, USA, 2001. [Google Scholar]
- Buhl, M. Wind Turbine Airfoil Families. National Renewable Energy Laboratory. 6 July 2012. Available online: https://wind.nrel.gov/airfoils/AirfoilFamilies.html (accessed on 11 July 2021).
- Yossri, W.; Ayed, S.B.; Abdelkefi, A. Evaluation of the efficiency of bioinspired blade designs for low-speed small-scale wind turbines with the presence of inflow turbulence effects. Energy 2023, 273, 127210. [Google Scholar] [CrossRef]
- Coxworth, B. Seagull-Inspired Blades Could Give Small-Scale Wind Turbines a Power Boost. 24 June 2019. Available online: https://newatlas.com/seagull-wing-wind-turbine-blades/60277/ (accessed on 13 July 2021).
- Seagull-Wing-Inspired Small-Scaled Wind Turbine to Deliver 15% More Power. 5 July 2019. Available online: https://www.energytrend.com/news/20190705-14345.html (accessed on 13 July 2021).
- Liu, T.; Kuykendoll, K.; Rhew, R.; Jones, S. Avian Wing Geometry and Kinematics. AIAA J. 2016, 44, 954–963. [Google Scholar] [CrossRef]
- Song, Y.; Perot, J.B. CFD Simulation of the NREL Phase VI Rotor. Wind Eng. 2015, 39, 299–310. [Google Scholar] [CrossRef]
- Yelmule, M.M.; Vsj, E.A. CFD predictions of NREL Phase VI Rotor Experiments in NASA/AMES Wind tunnel. Int. J. Renew. Energy Res.-IJRER 2013, 3, 261–269. [Google Scholar]
- Suárez, J.M.; Doerffer, P.; Szulc, O. CFD Validated Technique for Prediction of Aerodynamic Characteristics on Horizontal Axis Wind Energy Turbines; EWEA Offshore: Copenhagen, Denmark, 2015. [Google Scholar]
- Elfarra, M.A.; Sezer-Uzol, N.; Akmandor, I.S. NREL VI rotor blade: Numerical investigation and winglet design and optimization using CFD. Wind Energy 2014, 17, 605–626. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Zhou, X.; Zhang, Z.; Yang, X. Cross-wind dynamic response of concrete-filled double-skin wind turbine towers: Theoretical modelling and experimental investigation. J. Vib. Control. 2023, 10775463231186708. [Google Scholar] [CrossRef]
- WebPlotDigitizer. Available online: https://apps.automeris.io/wpd/ (accessed on 15 January 2023).
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [Google Scholar]
- Sorensen, N.N.; Michelsen, J.A.; Schreck, S. Navier–Stokes predictions of the NREL phase-VI rotor in the NASA Ames 80ft x 120ft wind tunnel. Wind Energy 2002, 7476, 151–169. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Detached-eddy simulation of flow around the NREL Phase VI blade. Wind Energy 2002, 5, 185–197. [Google Scholar] [CrossRef]
- Chao, D.D.; Van Dam, C.P. Computational aerodynamic analysis of a blunt trailing-edge airfoil modification to the NREL Phase VI rotor. Wind Energy 2007, 10, 529–550. [Google Scholar] [CrossRef]
- Hsu, M.C.; Akkerman, I.; Bazilevs, Y. Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment. Wind Energy 2014, 17, 461–481. [Google Scholar] [CrossRef]
- Simms, D.; Schreck, S.; Hand, M.; Fingersh, L.J. NREL Unsteady Aerodynamics Experiment in the NASA-Ames Wind Tunnel: A Comparison of Predictions to Measurements; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [Google Scholar]
- 40-BY 80-/80-BY 120-Foot Wind Tunnels. NASA Ames Research Center. Available online: https://rotorcraft.arc.nasa.gov/Research/Facilities/windtunnels.html (accessed on 15 January 2023).
- Sihag, S.; Kumar, M.; Tiwari, A.K. CFD Validation and Aerodynamic Behaviour of NREL Phase VI Wind Turbine. In Proceedings of the International Conference on Materials Science and Engineering, Paris, France, 19–20 October 2022. [Google Scholar]
- Betz, A. Introduction to the Theory of Flow Machines; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Burton, T. Wind Energy Handbook; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]





| Upper Surface | Lower Surface |
|---|---|
| x/c | x/c |
| y/c | y/c |
| 1 | 0 |
| 0.92993 | 0.031035 |
| 0.7997 | 0.070418 |
| 0.66972 | 0.098108 |
| 0.6155 | 0.1068 |
| 0.5633 | 0.11494 |
| 0.50037 | 0.123 |
| 0.42815 | 0.129 |
| 0.37163 | 0.13169 |
| 0.30726 | 0.133 |
| 0.2563 | 0.12993 |
| 0.19 | 0.12 |
| 0.13778 | 0.10657 |
| 0.11539 | 0.0985 |
| 0.099293 | 0.090545 |
| 0.084438 | 0.08282 |
| 0.070202 | 0.075298 |
| 0.05968 | 0.068284 |
| 0.047301 | 0.060253 |
| 0.036159 | 0.052121 |
| 0.027494 | 0.045717 |
| 0.018829 | 0.037076 |
| 0.011401 | 0.028537 |
| 0.0044444 | 0.018978 |
| 0 | 0 |
| 0.0023234 | −0.0064312 |
| 0.01037 | −0.013139 |
| 0.025185 | −0.016058 |
| 0.08 | −0.013 |
| 0.13767 | −0.0038977 |
| 0.17687 | 0.004 |
| 0.2257 | 0.013222 |
| 0.3085 | 0.027596 |
| 0.36489 | 0.035043 |
| 0.4261 | 0.040955 |
| 0.49047 | 0.045365 |
| 0.55419 | 0.046196 |
| 0.61921 | 0.045693 |
| 0.68358 | 0.042362 |
| 0.74177 | 0.037599 |
| 0.8633 | 0.023534 |
| 1 | 0 |
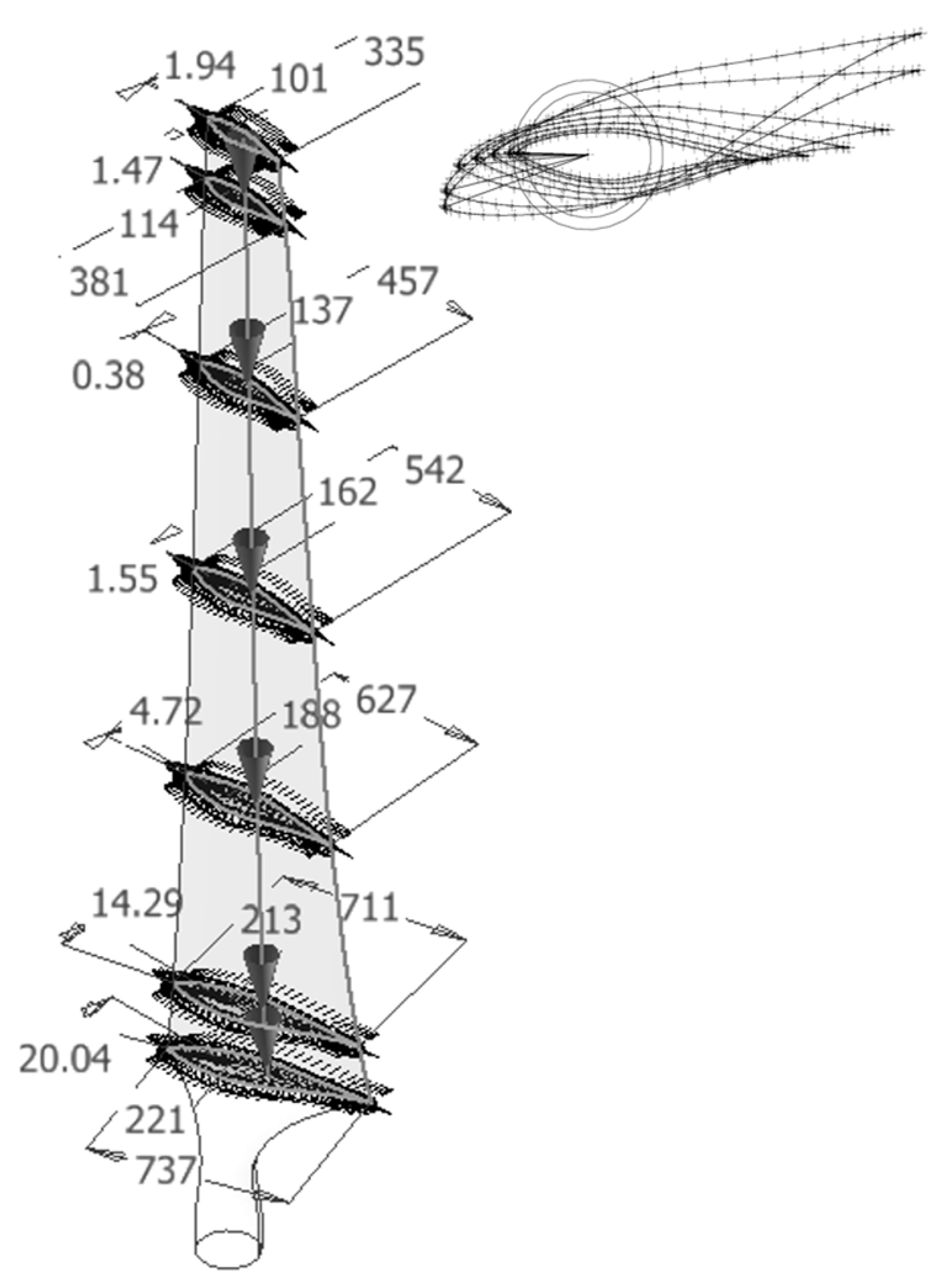
| Radial Distance R (m) | Span Station (R/5.029) | Chord Length (m) | Twist (Degrees) | Thickness (m) (20.95% Chord) | Twist Axis (% Chord), (m) |
|---|---|---|---|---|---|
| 0.0 | 0.0 | Hub center of rotation | Hub center of rotation | Hub center of rotation | Hub center of rotation |
| 0.508 | 0.101 | 218 (root hub adapter) | 0.0 (root hub adapter) | 0.218 (root hub adapter) | 50 (root hub adapter) |
| 0.660 | 0.131 | 0.218 | 0.0 | 0.218 | 50 |
| 0.883 | 0.176 | 0.183 | 0.0 | 0.183 | 50 |
| 1.257 | 0.250 | 0.737 | 20.040 | 0.154 | 30, (0.221) |
| 1.343 | 0.267 | 0.728 | 18.074 | 0.152 | 30, (0.218) |
| 1.510 | 0.300 | 0.711 | 14.292 | 0.149 | 30, (0.213) |
| 1.648 | 0.328 | 0.697 | 11.909 | 0.146 | 30, (0.209) |
| 1.952 | 0.388 | 0.666 | 7.979 | 0.139 | 30, (0.199) |
| 2.257 | 0.449 | 0.636 | 5.308 | 0.133 | 30, (0.190) |
| 2.343 | 0.466 | 0.627 | 4.715 | 0.131 | 30, (0.188) |
| 2.562 | 0.509 | 0.605 | 3.425 | 0.126 | 30, (0.181) |
| 2.867 | 0.570 | 0.574 | 2.083 | 0.120 | 30, (0.172) |
| 3.172 | 0.631 | 0.543 | 1.150 | 0.113 | 30, (0.162) |
| 3.185 | 0.633 | 0.542 | 1.115 | 0.113 | 30, (0.162) |
| 3.476 | 0.691 | 0.512 | 0.494 | 0.107 | 30, (0.153) |
| 3.781 | 0.752 | 0.482 | −0.015 | 0.100 | 30, (0.144) |
| 4.023 | 0.800 | 0.457 | −0.381 | 0.095 | 30, (0.137) |
| 4.086 | 0.812 | 0.451 | −0.475 | 0.094 | 30, (0.135) |
| 4.391 | 0.873 | 0.420 | −0.920 | 0.088 | 30, (0.162) |
| 4.696 | 0.934 | 0.389 | −1.352 | 0.081 | 30, (0.116) |
| 4.780 | 0.950 | 0.381 | −1.469 | 0.079 | 30, (0.114) |
| 5.000 | 0.994 | 0.358 | −1.775 | 0.075 | 30, (0.107) |
| 5.029 | 1 | 0.335 | −1.944 | 0.075 | 30, (0.101) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sesalim, D.; Naser, J. The Effects of a Seagull Airfoil on the Aerodynamic Performance of a Small Wind Turbine. Energies 2024, 17, 2768. https://doi.org/10.3390/en17112768
Sesalim D, Naser J. The Effects of a Seagull Airfoil on the Aerodynamic Performance of a Small Wind Turbine. Energies. 2024; 17(11):2768. https://doi.org/10.3390/en17112768
Chicago/Turabian StyleSesalim, Dean, and Jamal Naser. 2024. "The Effects of a Seagull Airfoil on the Aerodynamic Performance of a Small Wind Turbine" Energies 17, no. 11: 2768. https://doi.org/10.3390/en17112768
APA StyleSesalim, D., & Naser, J. (2024). The Effects of a Seagull Airfoil on the Aerodynamic Performance of a Small Wind Turbine. Energies, 17(11), 2768. https://doi.org/10.3390/en17112768






