Optimal Scheduling of a Cascade Hydropower Energy Storage System for Solar and Wind Energy Accommodation
Abstract
1. Introduction
2. Cascade Hydropower Energy Storage System Optimal Scheduling Model
2.1. Operational Modeling
- 1.
- Maximizing total power generation
- 2.
- Minimizing wind and solar energy curtailment
- 3.
- Minimizing net load fluctuation
2.2. Models for Calculating the Hybrid System
2.2.1. Wind and Solar Power Model
2.2.2. Hydropower Model
2.2.3. Pumping Station Model
2.3. Constraints
2.3.1. The Power Balance Constraint
2.3.2. Wind and Solar Power Constraint
2.3.3. Cascade Hydropower Constraints
- 1.
- Water balance constraints
- 2.
- Cascade hydropower plant reservoir hydraulic connection
- 3.
- Reservoir forebay water level constraints
- 4.
- Forebay water level constraints
- 5.
- Total discharge constraints
- 6.
- Hydropower output constraints
- 7.
- Relationship between capacity and reservoir water level
- 8.
- Relationship between tailwater level and discharge flow
2.3.4. Hydropower Individual Unit Constraints
- 1.
- Unit output constraints
- 2.
- Hydropower unit generation flow constraints
- 3.
- Constraints on vibration zones
- 4.
- Constraints on online and offline duration
- 5.
- Power climbing constraint of hydropower unit
- 6.
- Power fluctuation constraint of hydropower unit
- 7.
- Hydropower unit generating head constraints
- 8.
- Head loss function
2.3.5. Pumping Station Constraints
- 1.
- Pump power constraints
- 2.
- Pump flow constraints
- 3.
- Pump operating head constraints
2.4. Linearization of Nonlinear Constraints
3. Case Study
4. Results and Discussion
- The simulation results of WSH and WSHPS systems without pumping station and with pumping station are compared in Section 4.1. The response of different systems to the reservoir inflows of cascade hydropower station is analyzed to demonstrate the advancement of the presented model.
- The performance of the WSHPS system is compared and analyzed by taking the solar and wind power generation scenarios in summer and winter as reference terms in Section 4.2.
- The impact of pumping station installation capacity configuration on the complementary scheduling operation of the WSHPS system is studied in Section 4.3.
4.1. Impact of Reservoir Inflows on the Performance for Different Hybrid Systems
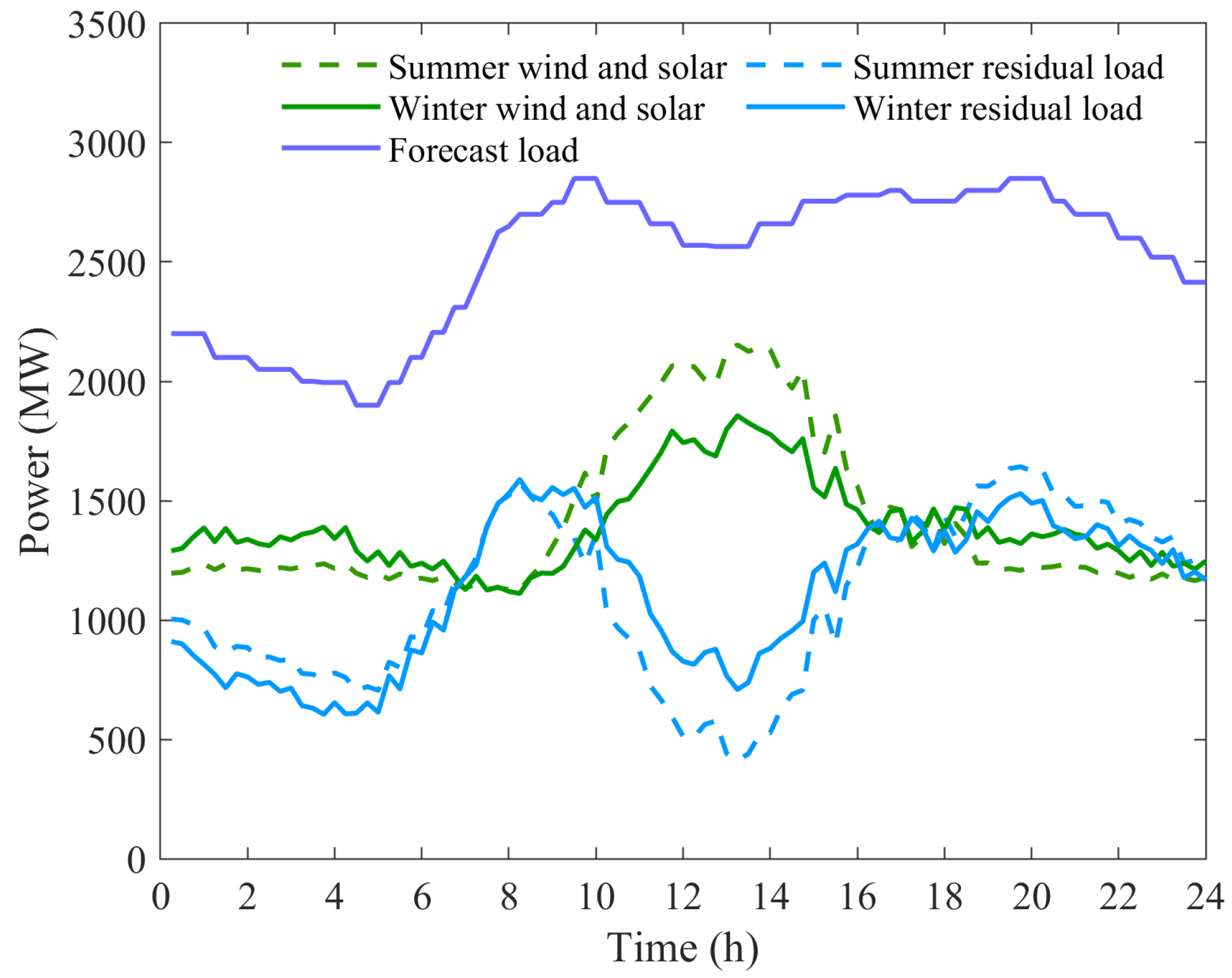
4.2. Optimal Scheduling of WSHPS System under Different Scenarios
4.3. Influence of Installed Capacity Configuration of Pumping Station
5. Conclusions
- The WSHPS system improves total power production and wind–solar energy consumption under different inflow scenarios. Compared with the WSH system, the total power production of WSHPS systems increased by 10.69%, 11.40%, and 11.27% in dry, normal, and wet years, respectively. The solar curtailment decreased by 68.97%, 61.61%, and 48.43%, respectively, and the wind curtailment decreased by 76.14%, 58.48%, and 50.91% respectively.
- Compared to the scheduling results in winter, the higher proportion of wind and solar integration in summer leads to higher net load fluctuations and serious energy curtailment in summer.
- As the installed capacity configuration of the pumping stations increases, the total power generation of the WSHPS system increases, while the curtailment of wind and solar energy decreases. However, the energy consumption of the storage pumping stations increases, along with the need for higher construction costs for pumping stations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sets and indices | |
| I | Total number of hydropower plants |
| i | Index of hydropower plants |
| , , | Weights associated with each optimization objective |
| M | Total number of units in the pumping station |
| m | Index of units in the pumping station |
| N | Total number of units in the hydropower plant |
| n | Index of units in the hydropower plant |
| T | Total number of time periods |
| t | Index of time periods |
| Parameters and coefficient | |
| Latitude of the PV module | |
| Optimal tilt angle of the PV module | |
| Climbing capacity of unit n in plant i [MW] | |
| Duration of time period t, which is set to 15 min in this paper | |
| Water level deviation at the end of the dispatching period [m] | |
| Temperature coefficient | |
| Air density [kg/m3] | |
| Declination angle of the sun | |
| A | Area swept by the wind turbine blade [m2] |
| Maximum startup times of the unit n in plant i during the scheduling period | |
| Rated power of the solar energy [MW] | |
| Maximum power output of solar power station [MW] | |
| Maximum power output of the wind farm [MW] | |
| Load demand of the system in time period t [MW] | |
| Upper bound of the k prohibited operating zone of unit n in plant i [MW] | |
| Lower bound of the k prohibited operating zone of unit n in plant i [MW] | |
| Maximum power output of unit n in plant i [MW] | |
| Minimum power output of unit n in plant i [MW] | |
| Maximum power output of plant i [MW] | |
| Minimum power output of plant i [MW] | |
| Rated power of unit m [MW] | |
| Maximum turbine discharge of unit n in plant i [m3/s] | |
| Minimum turbine discharge of unit n in plant i [m3/s] | |
| Maximum total water discharge of plant i [m3/s] | |
| Minimum total water discharge of plant i [m3/s] | |
| Maximum pumped flow of unit m in the pumping station [m3/s] | |
| Minimum pumped flow of unit m in the pumping station [m3/s] | |
| Solar radiation intensity [W/m2] | |
| Minimum number of continuous periods of the unit n | |
| Temperature under standard test conditions (25 °C) | |
| Minimum required offline duration of unit n in plant i [15 min] | |
| Minimum required online duration of unit n in plant i [15 min] | |
| Initial water level of reservoir i [m] | |
| Target water level of reservoir i at the end of the scheduling horizon [m] | |
| Upper bound of the forebay water level of reservoir i [m] | |
| Lower bound of the forebay water level of reservoir i [m] | |
| Wind energy utilization coefficient | |
| Rated power of wind farms [MW] | |
| Forecasted local reservoir inflow of plant i in time period t [m3/s] | |
| , , | Cut-in, rated, and cut-off wind speeds [m/s] |
| Variables | |
| Tailwater level of reservoir i in time period t [m] | |
| Binary variable that is equal to 1 if unit n is online in time period t, but is otherwise equal to 0 | |
| Binary variable that is equal to 1 if unit m is online in time period t, but is otherwise equal to 0 | |
| , , | Objective functions |
| Head loss of the unit n in plant i in time period t [m] | |
| Net water head of unit n in plant i in time period t [m] | |
| Pumping head of unit m in time period t [m] | |
| Power output of the hydropower plant in time period t [MW] | |
| Energy curtailment of the solar power station in time period t [MW] | |
| Power output of solar power station in time period t [MW] | |
| Energy curtailment of the wind farm in time period t [MW] | |
| Power output of the wind farm in time period t [MW] | |
| Net load average value of the scheduling period [MW] | |
| Power output of unit n in plant i in time period t [MW] | |
| Power output of hydropower plant i in time period t [MW] | |
| Power consumption of pump unit m in time period t [MW] | |
| Net load of the system in time period t [MW] | |
| Power consumption of the pumping station in time period t [MW] | |
| Total pumping flow of the pumping station in time period t [m3/s] | |
| Generating water flow of unit n in plant i in time period t [m3/s] | |
| Total water spillage of plant i in time period t [m3/s] | |
| Generating water flow of plant i in time period t [m3/s] | |
| Pumping flow of pump unit m in time period t [m3/s] | |
| Actual temperature of the cell in the period [°C] | |
| Binary variable that equals 1 if unit n is shut down in time period t, but otherwise equals 0 | |
| Binary variable that equals 1 if unit n is started up in time period t, but otherwise equals 0 | |
| Forebay water level of reservoir i in time period t [m] | |
| Reservoir total inflow of plant i in time period t [m3/s] | |
| Total outflow of plant i in time period t [m3/s] | |
| Actual wind speed [m/s] | |
| Reservoir water storage of plant i at the end of time period t [m3] | |
| Functions | |
| Relation function between the tailwater level and total water discharge of plant i | |
| Relation function between head loss and turbine flow of unit n in plant i | |
| Relation function between the forebay water level and water storage of plant i | |
| Relation function between the power consumption, net water head, and pumped flow of unit m | |
| Relation function between the power production, net water head, and generating water flow of unit n in plant i | |
References
- Wang, C.; Liu, C.; Chen, J.; Zhang, G. Cooperative planning of renewable energy generation and multi-timescale flexible resources in active distribution networks. Appl. Energy 2024, 356, 122429. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Y.; Wang, R.; Ma, R. Assessing the national synergy potential of onshore and offshore renewable energy from the perspective of resources dynamic and complementarity. Energy 2023, 279, 128106. [Google Scholar] [CrossRef]
- Yu, S.; Wan, K.; Cai, C.; Xu, L.; Zhao, T. Resource curse and green growth in China: Role of energy transitions under COP26 declarations. Resour. Policy 2023, 85, 103768. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Xiao, Y.; Zhu, F.; Ding, L.; Yang, F. Power Generation Scheduling for a Hydro-Wind-Solar Hybrid System: A Systematic Survey and Prospect. Energies 2022, 15, 8747. [Google Scholar] [CrossRef]
- Javed, M.S.; Ma, T.; Jurasz, J.; Amin, M.Y. Solar and wind power generation systems with pumped hydro storage: Review and future perspectives. Renew. Energy 2020, 148, 176–192. [Google Scholar] [CrossRef]
- Schmidt, J.; Cancella, R.; Junior, A.O.P. The effect of windpower on long-term variability of combined hydro-wind resources: The case of Brazil. Renew. Sust. Energy Rev. 2016, 55, 131–141. [Google Scholar] [CrossRef]
- Weschenfelder, F.; Leite, G.D.N.P.; Costa, A.C.A.D.; Vilela, O.D.C.; Ribeiro, C.M.; Ochoa, A.A.V.; Araújo, A.M. A review on the complementarity between grid-connected solar and wind power systems. J. Clean. Prod. 2020, 257, 120617. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Z.; Hu, W.; Wang, Y.; Dong, L.; Zhang, J.T. Coordinated optimal operation of hydro–wind–solar integrated systems. Appl. Energy 2019, 242, 883–896. [Google Scholar] [CrossRef]
- Lu, N.; Wang, G.; Su, C.; Ren, Z.; Peng, X.; Sui, Q. Medium-and long-term interval optimal scheduling of cascade hydropower-photovoltaic complementary systems considering multiple uncertainties. Appl. Energy 2024, 353, 122085. [Google Scholar] [CrossRef]
- Jin, X.; Liu, B.; Liao, S.; Cheng, C.; Li, G.; Liu, L. Impacts of different wind and solar power penetrations on cascade hydroplants operation. Renew. Energy 2022, 182, 227–244. [Google Scholar] [CrossRef]
- Tan, Q.; Nie, Z.; Wen, X.; Su, H.; Fang, G.; Zhang, Z. Complementary scheduling rules for hybrid pumped storage hydropower-photovoltaic power system reconstructing from conventional cascade hydropower stations. Appl. Energy 2024, 355, 122250. [Google Scholar] [CrossRef]
- Li, H.; Zhang, R.; Mahmud, M.A.; Hredzak, B. A novel coordinated optimization strategy for high utilization of renewable energy sources and reduction of coal costs and emissions in hybrid hydro-thermal-wind power systems. Appl. Energy 2022, 320, 119019. [Google Scholar] [CrossRef]
- Yuan, W.; Zhang, S.; Su, C.; Wu, Y.; Yan, D.; Wu, Z. Optimal scheduling of cascade hydropower plants in a portfolio electricity market considering the dynamic water delay. Energy 2022, 252, 124025. [Google Scholar] [CrossRef]
- Su, C.; Wang, P.; Yuan, W.; Wu, Y.; Jiang, F.; Wu, Z.; Yan, D. Short-term optimal scheduling of cascade hydropower plants with reverse-regulating effects. Renew. Energy 2022, 199, 395–406. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, C.T.; Cai, H.; Jin, X.; Jia, Z.B.; Wu, X.; Su, H.; Yang, T. Long-term stochastic model predictive control and efficiency assessment for hydro-wind-solar renewable energy supply system. Appl. Energy 2022, 316, 119134. [Google Scholar] [CrossRef]
- Guo, Y.; Ming, B.; Huang, Q.; Wang, Y.; Zheng, X.; Zhang, W. Risk-averse day-ahead generation scheduling of hydro-wind-photovoltaic complementary systems considering the steady requirement of power delivery. Appl. Energy 2022, 309, 118467. [Google Scholar] [CrossRef]
- Ren, Y.; Yao, X.; Liu, D.; Qiao, R.; Zhang, L.; Zhang, K.; Jin, K.; Li, H.; Ran, Y.; Li, F. Optimal design of hydro-wind-PV multi-energy complementary systems considering smooth power output. Sustain. Energy Technol. Assess. 2022, 50, 101832. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Li, J.; Liu, Y.; Yao, L.; Wang, Y.; Wang, C.; Pei, S.; Zhou, J.Z. Short-term optimal operation of wind-solar-hydro hybrid system considering uncertainties. Energy Convers. Manag. 2020, 205, 112405. [Google Scholar] [CrossRef]
- Tan, Q.; Wen, X.; Sun, Y.; Lei, X.; Wang, Z.; Qin, G. Evaluation of the risk and benefit of the complementary operation of the large wind-photovoltaic-hydropower system considering forecast uncertainty. Appl. Energy 2021, 285, 116442. [Google Scholar] [CrossRef]
- Shi, X.; Jia, R.; Huang, Q.; Huang, G.; Lei, X.; Li, J.; Ming, B.; Zhao, Z.; Li, L. Day-ahead complementary operation for wind-hydro-thermal system considering the multi-dimensional uncertainty. Csee J. Power Energy Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Liao, S.; Liu, H.; Liu, B.; Zhao, H.; Wang, M. An information gap decision theory-based decision-making model for complementary operation of hydro-wind-solar system considering wind and solar output uncertainties. J. Clean. Prod. 2022, 348, 131382. [Google Scholar] [CrossRef]
- Huang, K.; Liu, P.; Kim, J.S.; Xu, W.; Gong, Y.; Cheng, Q.; Zhou, Y. A model coupling current non-adjustable, coming adjustable and remaining stages for daily generation scheduling of a wind-solar-hydro complementary system. Energy 2023, 263, 125737. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, Y.; Fang, G.; Ding, Z. Research on short-term optimal scheduling of hydro-wind-solar multi-energy power system based on deep reinforcement learning. J. Clean. Prod. 2023, 385, 135704. [Google Scholar] [CrossRef]
- Xie, J.; Zheng, Y.; Pan, X.; Zheng, Y.; Zhang, L.; Zhan, Y. A short-term optimal scheduling model for wind-solar-hydro hybrid generation system with Cascade hydropower considering regulation reserve and spinning reserve requirements. IEEE Access 2021, 9, 10765–10777. [Google Scholar] [CrossRef]
- Huang, K.; Liu, P.; Ming, B.; Kim, J.S.; Gong, Y. Economic operation of a wind-solar-hydro complementary system considering risks of output shortage, power curtailment and spilled water. Appl. Energy 2021, 290, 116805. [Google Scholar] [CrossRef]
- Shu, S.; Mo, L.; Wang, Y. Peak shaving strategy of wind-solar-hydro hybrid generation system based on modified differential evolution algorithm. Energy Procedia 2019, 158, 3500–3505. [Google Scholar] [CrossRef]
- Li, J.; Lu, J.; Yao, L.; Cheng, L.; Qin, H. Wind-solar-hydro power optimal scheduling model based on multi-objective dragonfly algorithm. Energy Procedia 2019, 158, 6217–6224. [Google Scholar] [CrossRef]
- Zhang, Q.; Xie, J.; Pan, X.; Zhang, L.; Fu, D. A short-term optimal scheduling model for wind-solar-hydro-thermal complementary generation system considering dynamic frequency response. IEEE Access 2021, 9, 142768–142781. [Google Scholar] [CrossRef]
- Liu, B.; Liu, T.; Liao, S.; Lu, J.; Cheng, C.T. Short-term coordinated hybrid hydro-wind-solar optimal scheduling model considering multistage section restrictions. Renew. Energy 2023, 217, 119160. [Google Scholar] [CrossRef]
- Tan, S.; Wang, X.; Jiang, C. Optimal scheduling of hydro–PV–wind hybrid system considering CHP and BESS coordination. Appl. Sci. 2019, 9, 892. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, X.; Gong, N.; Ma, H. Day-ahead optimal dispatching of wind-solar-hydro-thermal combined power system with pumped-storage hydropower integration. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 430–434. [Google Scholar]
- Zhang, T.; Huang, W.; Chen, S.; Zhu, Y.; Kang, F.; Zhou, Y.; Ma, G. The scheduling research of a wind-solar-hydro hybrid system based on a sand-table deduction model at ultra-short-term scales. Energies 2023, 16, 3280. [Google Scholar] [CrossRef]
- Guo, S.; Zheng, K.; He, Y.; Kurban, A. The artificial intelligence-assisted short-term optimal scheduling of cascade hydro-photovoltaic complementary system with hybrid time steps. Renew. Energy 2023, 202, 1169–1189. [Google Scholar] [CrossRef]
- Ak, M.; Kentel, E.; Savasaneril, S. Quantifying the revenue gain of operating a cascade hydropower plant system as a pumped-storage hydropower system. Renew. Energy 2019, 139, 739–752. [Google Scholar] [CrossRef]
- Jurasz, J.; Mikulik, J.; Krzywda, M.; Ciapała, B.; Janowski, M. Integrating a wind- and solar-powered hybrid to the power system by coupling it with a hydroelectric power station with pumping installation. Energy 2018, 144, 549–563. [Google Scholar] [CrossRef]
- Xu, X.; Hu, W.; Cao, D.; Huang, Q.; Chen, C.; Chen, Z. Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system. Renew. Energy 2020, 147, 1418–1431. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, C.; Yu, S.; Shen, J.; Wu, X.; Su, H. Preliminary feasibility analysis for remaking the function of cascade hydropower stations to enhance hydropower flexibility: A case study in China. Energy 2022, 260, 125163. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, G.; Wen, X.; Tan, Q.; Zhang, P.; Liu, Z. Coordinated operation of conventional hydropower plants as hybrid pumped storage hydropower with wind and photovoltaic plants. Energy Convers. Manag. 2023, 277, 16654. [Google Scholar] [CrossRef]
- Ju, C.; Ding, T.; Jia, W.; Mu, C.; Zhang, H.; Sun, Y. Two-stage robust unit commitment with the cascade hydropower stations retrofitted with pump stations. Appl. Energy 2023, 334, 120675. [Google Scholar] [CrossRef]
- Tang, Y.; Fang, G.; Tan, Q.; Wen, X.; Lei, X.; Ding, Z. Optimizing the sizes of wind and photovoltaic power plants integrated into a hydropower station based on power output complementarity. Energy Convers. Manag. 2020, 206, 112465. [Google Scholar] [CrossRef]
- Su, C.; Cheng, C.; Wang, P.; Shen, J.; Wu, X. Optimization model for long-distance integrated transmission of wind farms and pumped-storage hydropower plants. Appl. Energy 2019, 242, 285–293. [Google Scholar] [CrossRef]
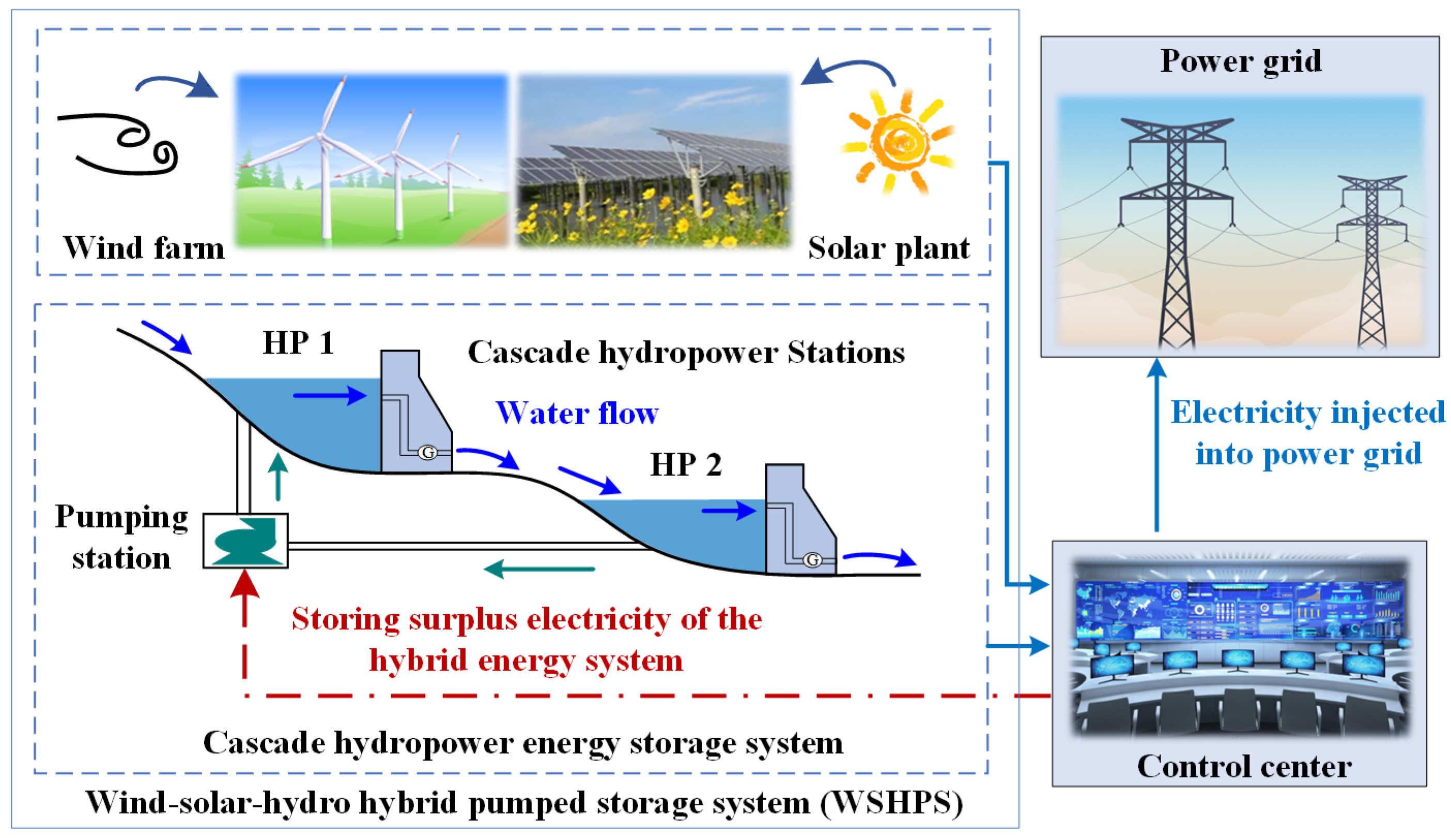











| Parameters | HP 1 | HP 2 |
|---|---|---|
| Regulating reservoir volume (108 m3) | 35 | 7.2 |
| Dead water level (m) | 1071 | 936 |
| Normal water level (m) | 1140 | 970 |
| Beginning and end water level (m) | 1076 | 950 |
| Beginning and end water level deviation (m) | 0.5 | 0.1 |
| Maximum reservoir release (m3/s) | 6866 | 12,142 |
| Minimum reservoir release (m3/s) | 180 | 355 |
| Installed capacity (MW) | 900 | 900 |
| Regulation ability | Multi-year | Daily |
| Plant | Unit | (m3/s) | (MW) | (MW) | Range of POZs (MW) | / (h) | (h) |
|---|---|---|---|---|---|---|---|
| HP 1 | 632.2 | 250 | 100 | [80 130] | 2 | 1 | |
| 632.2 | 200 | 80 | [70 120] | 2 | 1 | ||
| HP 2 | #1–3 | 490.5 | 300 | 150 | [130 180] | 2 | 1 |
| Item | Dry Year | Normal Year | Wet Year | |
|---|---|---|---|---|
| Total power generation (MWh) | WSH | 60,321.25 | 60,321.25 | 60,321.25 |
| WSHPS | 66,771.25 | 67,196.25 | 67,121.25 | |
| Increase | 10.69% | 11.40% | 11.27% | |
| Wind curtailment (MWh) | WSH | 2201 | 2502.12 | 4419.95 |
| WSHPS | 525.16 | 1038.96 | 2169.63 | |
| Decrease | 76.14 % | 58.48% | 50.91% | |
| Solar curtailment (MWh) | WSH | 474 | 554.08 | 897.89 |
| WSHPS | 147.08 | 212.74 | 463.03 | |
| Decrease | 68.97 % | 61.61% | 48.43% | |
| Net load fluctuation (MW) | WSH | 167.32 | 153.20 | 98.19 |
| WSHPS | 257.15 | 235.49 | 174.89 | |
| Electricity consumption (MWh) | WSHPS | 6450 | 6875 | 6800 |
| Item | Summer | Winter |
|---|---|---|
| Total electricity generation (MWh) | 66,996.25 | 67,196.25 |
| Wind curtailment (MWh) | 857.21 (3.05%) | 1038.96 (3.52%) |
| Solar curtailment (MWh) | 747.99 (12.77%) | 212.74 (5.45%) |
| Net load fluctuation (MW) | 264.88 | 235.49 |
| Electricity consumption (MWh) | 6675 | 6875 |
| Item | 225 (MW) | 300 (MW) | 375 (MW) |
|---|---|---|---|
| Total electricity generation (MWh) | 65,646.25 | 67,196.25 | 68,665 |
| Wind curtailment (MWh) | 1265.01 (4.28%) | 1038.96 (3.52%) | 792.05 (2.68%) |
| Solar curtailment (MWh) | 259.21 (6.64%) | 212.74 (5.45%) | 181.30 (4.64%) |
| Net load fluctuation (MW) | 219.63 | 235.49 | 253.93 |
| Electricity consumption (MWh) | 5325 | 6875 | 8343.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, H.; Guo, P.; Li, C.; Wu, S. Optimal Scheduling of a Cascade Hydropower Energy Storage System for Solar and Wind Energy Accommodation. Energies 2024, 17, 2734. https://doi.org/10.3390/en17112734
Liu Y, Zhang H, Guo P, Li C, Wu S. Optimal Scheduling of a Cascade Hydropower Energy Storage System for Solar and Wind Energy Accommodation. Energies. 2024; 17(11):2734. https://doi.org/10.3390/en17112734
Chicago/Turabian StyleLiu, Yuanyuan, Hao Zhang, Pengcheng Guo, Chenxi Li, and Shuai Wu. 2024. "Optimal Scheduling of a Cascade Hydropower Energy Storage System for Solar and Wind Energy Accommodation" Energies 17, no. 11: 2734. https://doi.org/10.3390/en17112734
APA StyleLiu, Y., Zhang, H., Guo, P., Li, C., & Wu, S. (2024). Optimal Scheduling of a Cascade Hydropower Energy Storage System for Solar and Wind Energy Accommodation. Energies, 17(11), 2734. https://doi.org/10.3390/en17112734







