An Energy Flow Control Algorithm of Regenerative Braking for Trams Based on Pontryagin’s Minimum Principle
Abstract
:1. Introduction
2. Regenerative Braking System and Algorithm Requirements
2.1. Regenerative Braking System Requirements
2.2. Algorithm Requirements
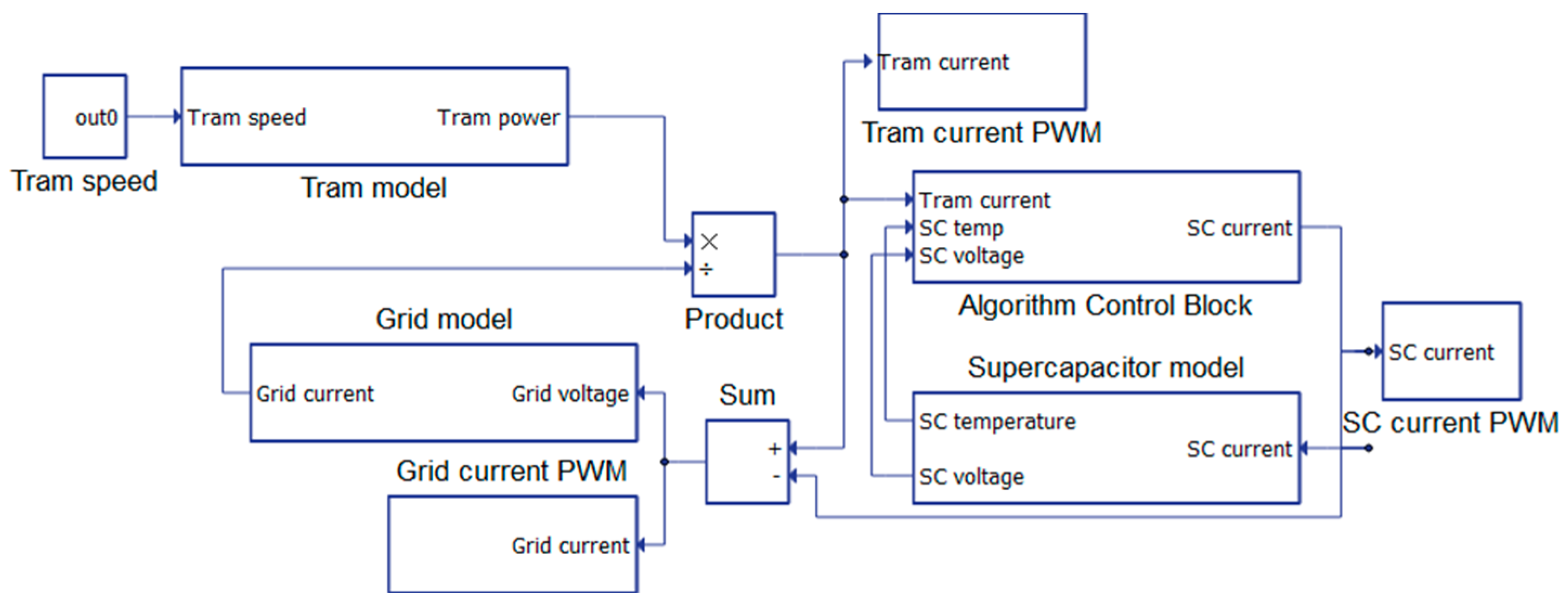
3. Regenerative Braking System Model
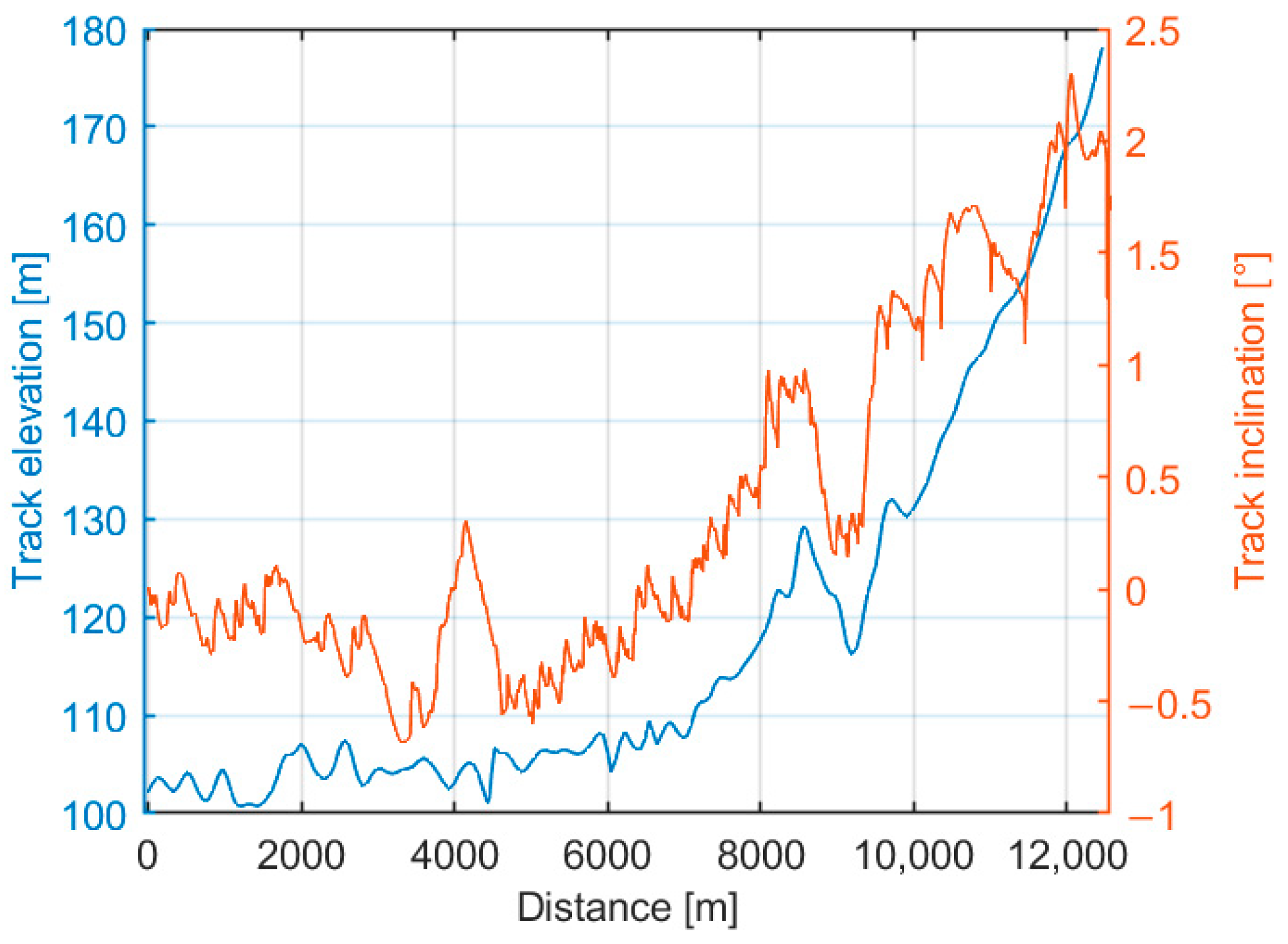
3.1. Tram and Track Inclination Model
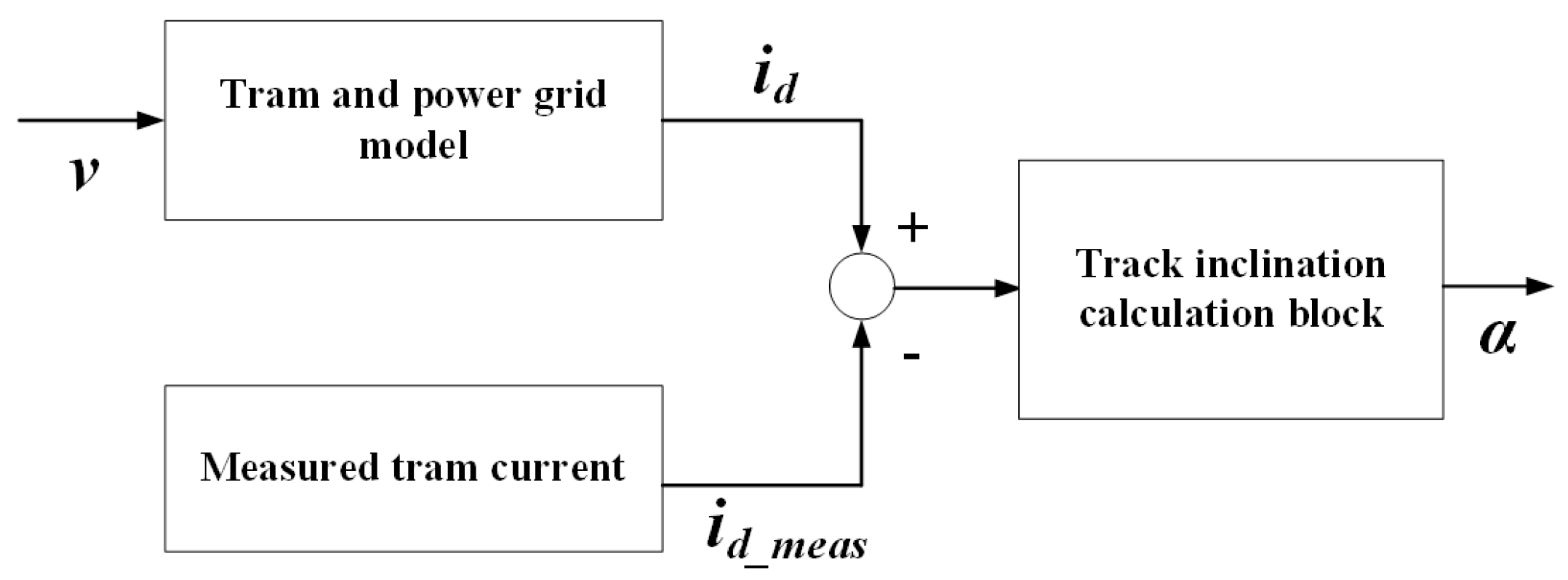
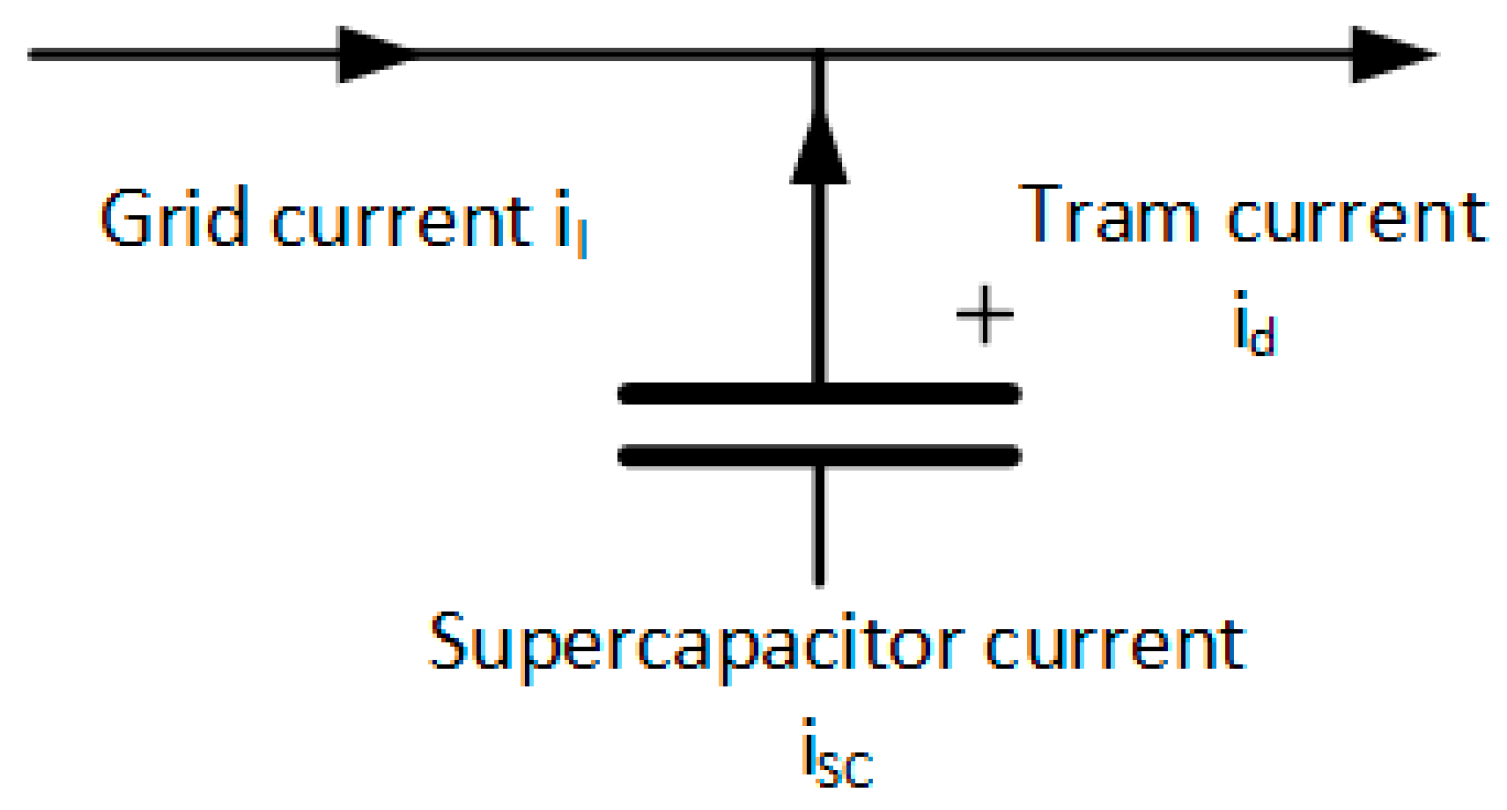
3.2. Power Grid Model
3.3. Supercapacitor Electrothermal Model
4. Supercapacitor Reference Current Calculation
4.1. Supercapcacitor Reference Current Calculation during Incline Stops
- Given that the tram stopped by regenerative braking, it is assumed that the SC ESS already has a significant amount of energy stored; so, no excessive recharging current is required.
- The use of excessive recharging current indirectly affects the voltage of the power grid, which negatively affects other trams running on the same grid sector. A current of 100 A causes a voltage drop in the power grid sector of fewer than 5 V, which is less than 15% of the average current load on the power grid sector from operating a tram on the observed power grid sector. By choosing such a recharging current, it is possible to recharge a larger number of vehicles at the same time without significantly stressing the power grid.
4.2. Supercapacitor Reference Current Calculation during Acceleration and Braking
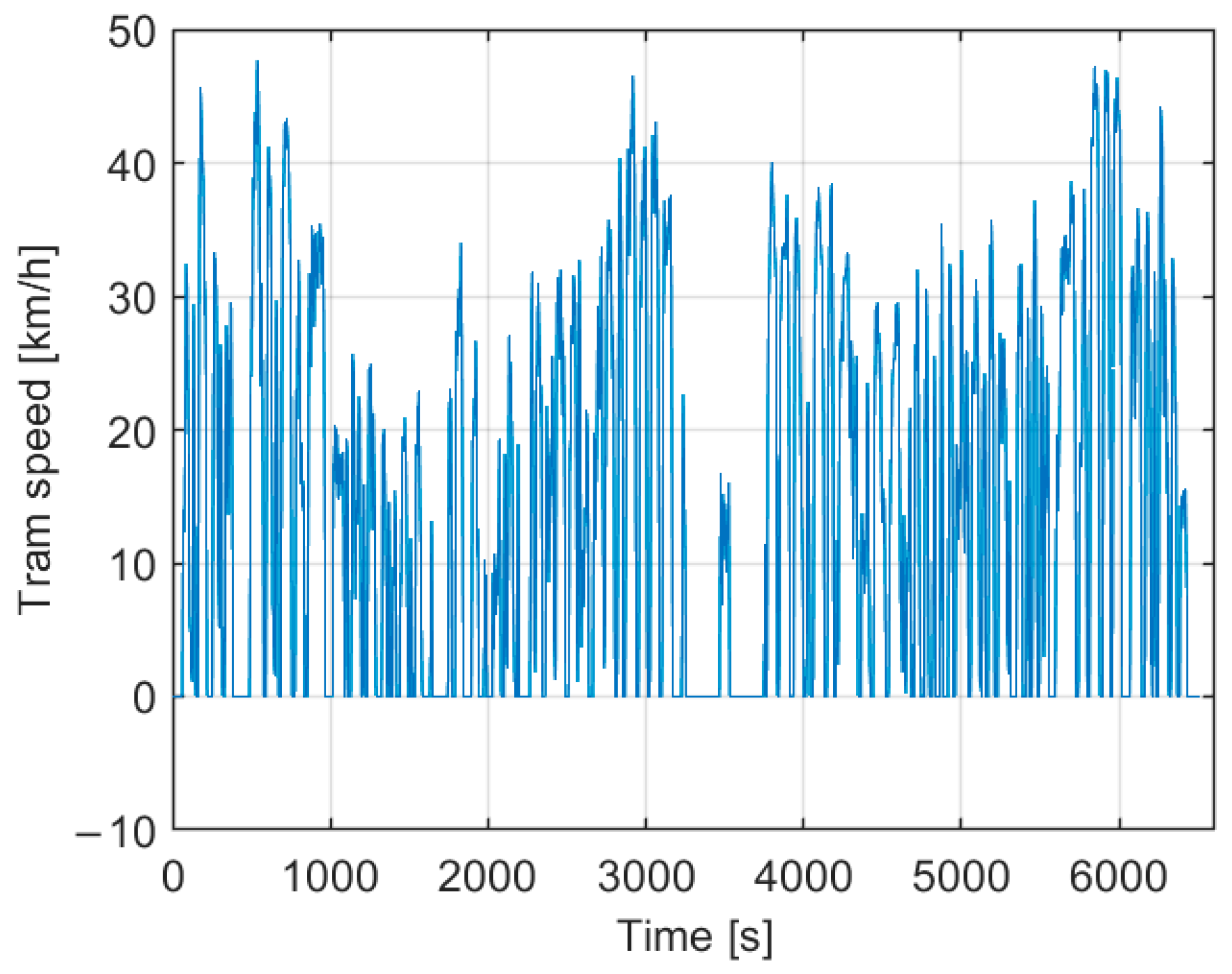
5. Simulation Experiments
5.1. Offline Simulation Experiment
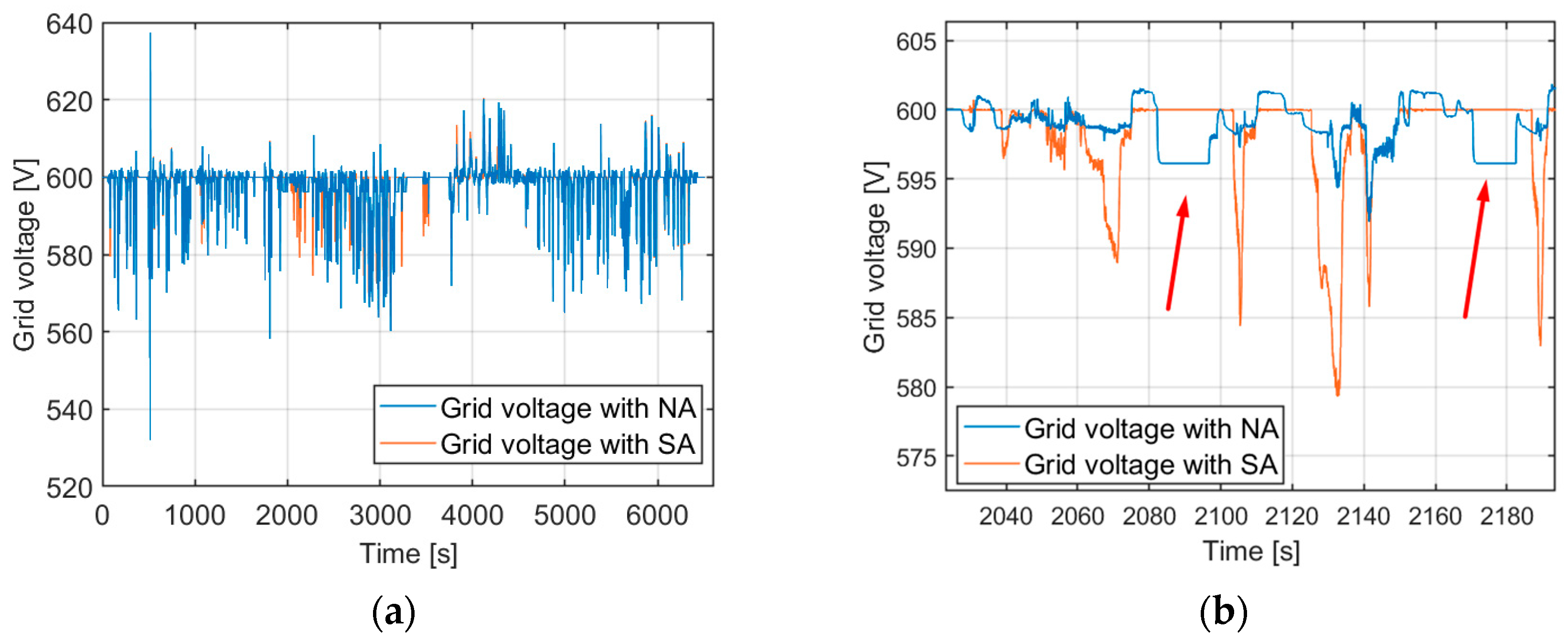
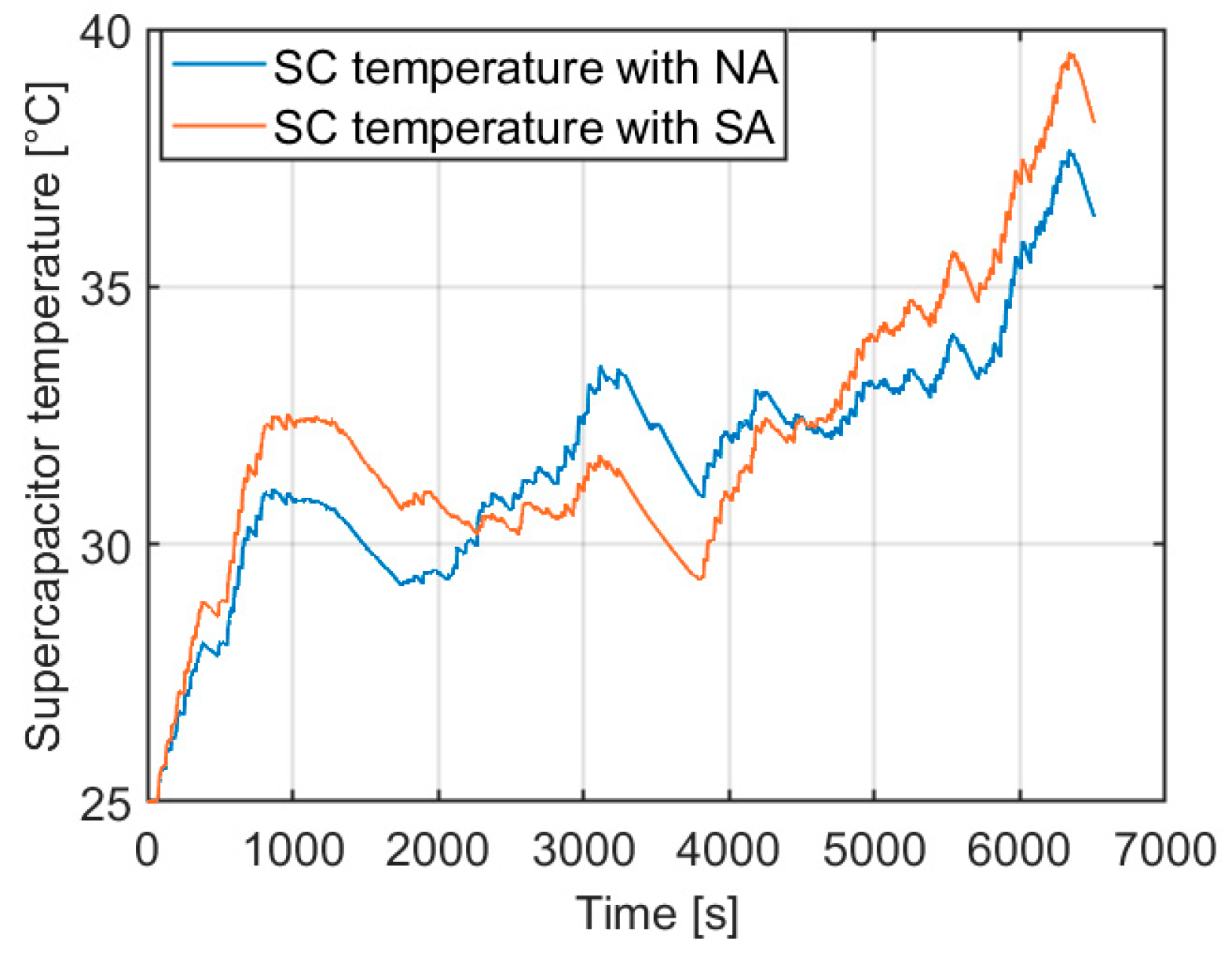
5.1.1. Offline Simulation Experiment Results
5.2. HIL Simulation Experiment
HIL Simulation Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ESS | Energy storage system | SC capacitance | |
| SC | Supercapacitor | SC equivalent series resistance | |
| HIL | Hardware In the Loop | Thermal capacitance | |
| Tram speed | Thermal resistance | ||
| Tram power | Ambient temperature | ||
| Grid voltage | SC heat loss | ||
| Tram current | Criterion function | ||
| SC voltage | Temperature criterion scaling coefficient | ||
| SC temperature | Hamiltonian | ||
| SC reference current | Optimal value | ||
| Grid current | Lagrange multiplier | ||
| Total traction force | Normal cone vector | ||
| Tram mass | Differential equation coefficient | ||
| Tram acceleration | Tangent cone, normal cone | ||
| Gravitational constant | Set | ||
| Track inclination | Optimal SC current | ||
| Davis formula coefficient | Parabola coefficients | ||
| Tram current difference | Nominal minimum, maximum SC current | ||
| DC voltage source value | SC current scaling coefficient | ||
| Grid resistance | NA | New algorithm | |
| Grid inductance | SA | Simple algorithm |
Appendix A. Optimal Control Using Pontryagin’s Minimum Principle [32]
References
- González-Gil, A.; Palacin, R.; Batty, P. Sustainable urban rail systems: Strategies and technologies for optimal management of regenerative braking energy. Energy Convers. Manag. 2013, 75, 374–388. [Google Scholar] [CrossRef]
- Hamada, A.T.; Orhan, M.F. An overview of regenerative braking systems. J. Energy Storage 2022, 52, 105033. [Google Scholar] [CrossRef]
- Xing, L.; Li, X. Review of Regenerative Braking Energy Storage and Utilization Technology in Urban Rail Transit. In The Proceedings of the 9th Frontier Academic Forum of Electrical Engineering; Ma, W., Rong, M., Liu, W., Wang, S., Li, G., Eds.; Springer: Singapore, 2021; Volume 742, pp. 775–783. [Google Scholar]
- Belay Kebede, A.; Worku, G.B. A research on regenerative braking energy recovery: A case of Addis Ababa light rail transit. eTransportation 2021, 8, 100117. [Google Scholar] [CrossRef]
- Fournier, D.; Fages, F.; Mulard, D. A Greedy Heuristic for Optimizing Metro Regenerative Energy Usage; Civil-Comp Press: Stirlingshire, UK. [CrossRef]
- Tian, Z.; Weston, P.; Zhao, N.; Hillmansen, S.; Roberts, C.; Chen, L. System energy optimisation strategies for metros with regeneration. Transp. Res. Part C Emerg. Technol. 2017, 75, 120–135. [Google Scholar] [CrossRef]
- Zhao, N.; Tian, Z.; Hillmansen, S.; Chen, L.; Roberts, C.; Gao, S. Timetable Optimization and Trial Test for Regenerative Braking Energy Utilization in Rapid Transit Systems. Energies 2022, 15, 4879. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, C.; Jin, B.; Wang, Q.; Geng, H. Timetable optimization for maximization of regenerative braking energy utilization in traction network of urban rail transit. Comput. Ind. Eng. 2023, 183, 109448. [Google Scholar] [CrossRef]
- Cipolletta, G.; Delle Femine, A.; Gallo, D.; Luiso, M.; Landi, C. Design of a Stationary Energy Recovery System in Rail Transport. Energies 2021, 14, 2560. [Google Scholar] [CrossRef]
- Zhao, S.; Feng, Q.; Yang, H.; Zhang, Y. Control strategy of hybrid energy storage in regenerative braking energy of high-speed railway. Energy Rep. 2022, 8, 1330–1338. [Google Scholar] [CrossRef]
- Che, C.; Wang, Y.; Lu, Q.; Peng, J.; Liu, X.; Chen, Y.; He, B. An effective utilization scheme for regenerative braking energy based on power regulation with a genetic algorithm. IET Power Electron. 2022, 15, 1392–1408. [Google Scholar] [CrossRef]
- Sengor, I.; Kilickiran, H.C.; Akdemir, H.; Kekezoglu, B.; Erdinc, O.; Catalao, J.P.S. Energy Management of a Smart Railway Station Considering Regenerative Braking and Stochastic Behaviour of ESS and PV Generation. IEEE Trans. Sustain. Energy 2018, 9, 1041–1050. [Google Scholar] [CrossRef]
- Akbari, S.; Fazel, S.S.; Jadid, S. Optimal operation of a smart railway station based on a multi-energy hub structure considering environmental perspective and regenerative braking utilization. Energy Sci. Eng. 2021, 9, 1614–1631. [Google Scholar] [CrossRef]
- Chen, J.; Hu, H.; Ge, Y.; Wang, K.; Huang, W.; He, Z. An Energy Storage System for Recycling Regenerative Braking Energy in High-Speed Railway. IEEE Trans. Power Deliv. 2021, 36, 320–330. [Google Scholar] [CrossRef]
- Cicek, A.; Şengör, I.; Guner, S.; Karakus, F.; Erenoglu, A.K.; Erdinc, O.; Shafie-Khah, M.; Catalao, J.P.S. Integrated Rail System and EV Parking Lot Operation With Regenerative Braking Energy, Energy Storage System and PV Availability. IEEE Trans. Smart Grid 2022, 13, 3049–3058. [Google Scholar] [CrossRef]
- Cutrignelli, F.; Saponaro, G.; Stefanizzi, M.; Torresi, M.; Camporeale, S.M. Study of the Effects of Regenerative Braking System on a Hybrid Diagnostic Train. Energies 2023, 16, 874. [Google Scholar] [CrossRef]
- Sumpavakup, C.; Ratniyomchai, T.; Kulworawanichpong, T. Optimal energy saving in DC railway system with on-board energy storage system by using peak demand cutting strategy. J. Mod. Transp. 2017, 25, 223–235. [Google Scholar] [CrossRef]
- Liu, W.; Xu, J.; Tang, J. Study on control strategy of urban rail train with on-board regenerative braking energy storage system. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3924–3929. [Google Scholar] [CrossRef]
- Pavlović, T.; Župan, I.; Šunde, V.; Ban, Ž. HIL Simulation of a Tram Regenerative Braking System. Electronics 2021, 10, 1379. [Google Scholar] [CrossRef]
- Radu, P.; Szelag, A.; Steczek, M. On-Board Energy Storage Devices with Supercapacitors for Metro Trains—Case Study Analysis of Application Effectiveness. Energies 2019, 12, 1291. [Google Scholar] [CrossRef]
- Liu, X.; Li, K. Energy storage devices in electrified railway systems: A review. Transp. Saf. Environ. 2020, 2, 183–201. [Google Scholar] [CrossRef]
- Zhao, J.; Burke, A.F. Review on supercapacitors: Technologies and performance evaluation. J. Energy Chem. 2021, 59, 276–291. [Google Scholar] [CrossRef]
- Yassine, M.; Fabris, D. Performance of Commercially Available Supercapacitors. Energies 2017, 10, 1340. [Google Scholar] [CrossRef]
- Zheng, F.; Li, Y.; Wang, X. Study on effects of applied current and voltage on the ageing of supercapacitors. Electrochim. Acta 2018, 276, 343–351. [Google Scholar] [CrossRef]
- Kreczanik, P.; Venet, P.; Hijazi, A.; Clerc, G. Study of Supercapacitor Aging and Lifetime Estimation according to Voltage, Temperature, and RMS Current. IEEE Trans. Ind. Electron. 2014, 61, 4895–4902. [Google Scholar] [CrossRef]
- Negroiu, R.; Ionescu, C.; Svasta, P.; Vasile, A. Influence of temperature on supercapacitors behavior in series/parallel connections. In Proceedings of the 2017 IEEE 23rd International Symposium for Design and Technology in Electronic Packaging (SIITME), Constanta, Romania, 26–29 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 367–370. [Google Scholar] [CrossRef]
- Reichbach, N.; Mellincovsky, M.; Peretz, M.M.; Kuperman, A. Long-Term Wide-Temperature Supercapacitor Ragone Plot Based on Manufacturer Datasheet. IEEE Trans. Energy Convers. 2016, 31, 404–406. [Google Scholar] [CrossRef]
- Hoo, D.S.; Chua, K.H.; Hau, L.C.; Chong, K.Y.; Lim, Y.S.; Chua, X.R.; Wang, L. An Investigation on Recuperation of Regenerative Braking Energy in DC Railway Electrification System. In Proceedings of the 2022 IEEE International Conference in Power Engineering Application (ICPEA), Shah Alam, Malaysia, 7–8 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Huang, K.; Tasiu, I.A.; Lu, B.; Meng, X.; Liu, Z.; Sun, W. Modeling of Regenerative Braking Energy for Electric Multiple Units Passing Long Downhill Section. IEEE Trans. Transp. Electrific. 2022, 8, 3742–3758. [Google Scholar] [CrossRef]
- Župan, I.; Šunde, V.; Ban, Ž.; Krušelj, D. Algorithm with temperature-dependent maximum charging current of a supercapacitor module in a tram regenerative braking system. J. Energy Storage 2021, 36, 102378. [Google Scholar] [CrossRef]
- Sengor, I.; Kilickiran, H.C.; Akdemir, H.; Kilic, B. Determination of Potential Regenerative Braking Energy in Railway Systems: A Case Study for Istanbul M1A Light Metro Line. JOACE 2017, 5, 21–25. [Google Scholar] [CrossRef]
- Geering, H.P. Optimal Control with Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Župan, I.; Lelas, M.; Ban, Ž.; Šunde, V. Optimizing braking energy flow through charging status surface expansion. Eng. Rev. 2020, 41, 129–140. [Google Scholar] [CrossRef]








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 17.965 | 0.04 °C/W | ||
| 34.536 | 33,000 J/°C | ||
| 7827.249 | 25 °C | ||
| 600 V | 500 V | ||
| 0.0387 | 2864 | ||
| 0.0023 H | 3780 | ||
| 0.018 | 2887 | ||
| 63 F | 77.999 |
| Total Stored Braking Energy | Max/Average Temperature | SC Lifetime Reduction | |
|---|---|---|---|
| SA algorithm | |||
| NA algorithm | |||
| NA algorithm () | |||
| NA algorithm () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Župan, I.; Šunde, V.; Ban, Ž.; Novoselnik, B. An Energy Flow Control Algorithm of Regenerative Braking for Trams Based on Pontryagin’s Minimum Principle. Energies 2023, 16, 7346. https://doi.org/10.3390/en16217346
Župan I, Šunde V, Ban Ž, Novoselnik B. An Energy Flow Control Algorithm of Regenerative Braking for Trams Based on Pontryagin’s Minimum Principle. Energies. 2023; 16(21):7346. https://doi.org/10.3390/en16217346
Chicago/Turabian StyleŽupan, Ivan, Viktor Šunde, Željko Ban, and Branimir Novoselnik. 2023. "An Energy Flow Control Algorithm of Regenerative Braking for Trams Based on Pontryagin’s Minimum Principle" Energies 16, no. 21: 7346. https://doi.org/10.3390/en16217346
APA StyleŽupan, I., Šunde, V., Ban, Ž., & Novoselnik, B. (2023). An Energy Flow Control Algorithm of Regenerative Braking for Trams Based on Pontryagin’s Minimum Principle. Energies, 16(21), 7346. https://doi.org/10.3390/en16217346






