A Fuzzy OLTC Controller: Applicability in the Transition Stage of the Energy System Transformation
Abstract
1. Introduction
2. OLTC Control Methods
2.1. Basic Methods
2.2. Advanced Methods
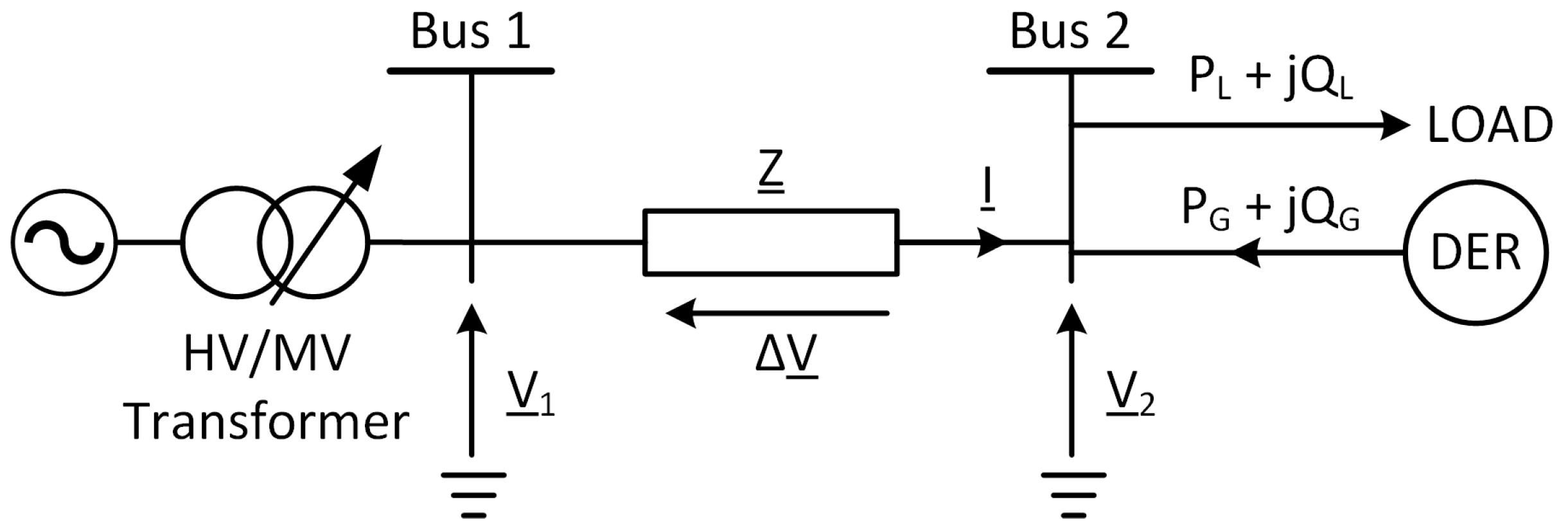
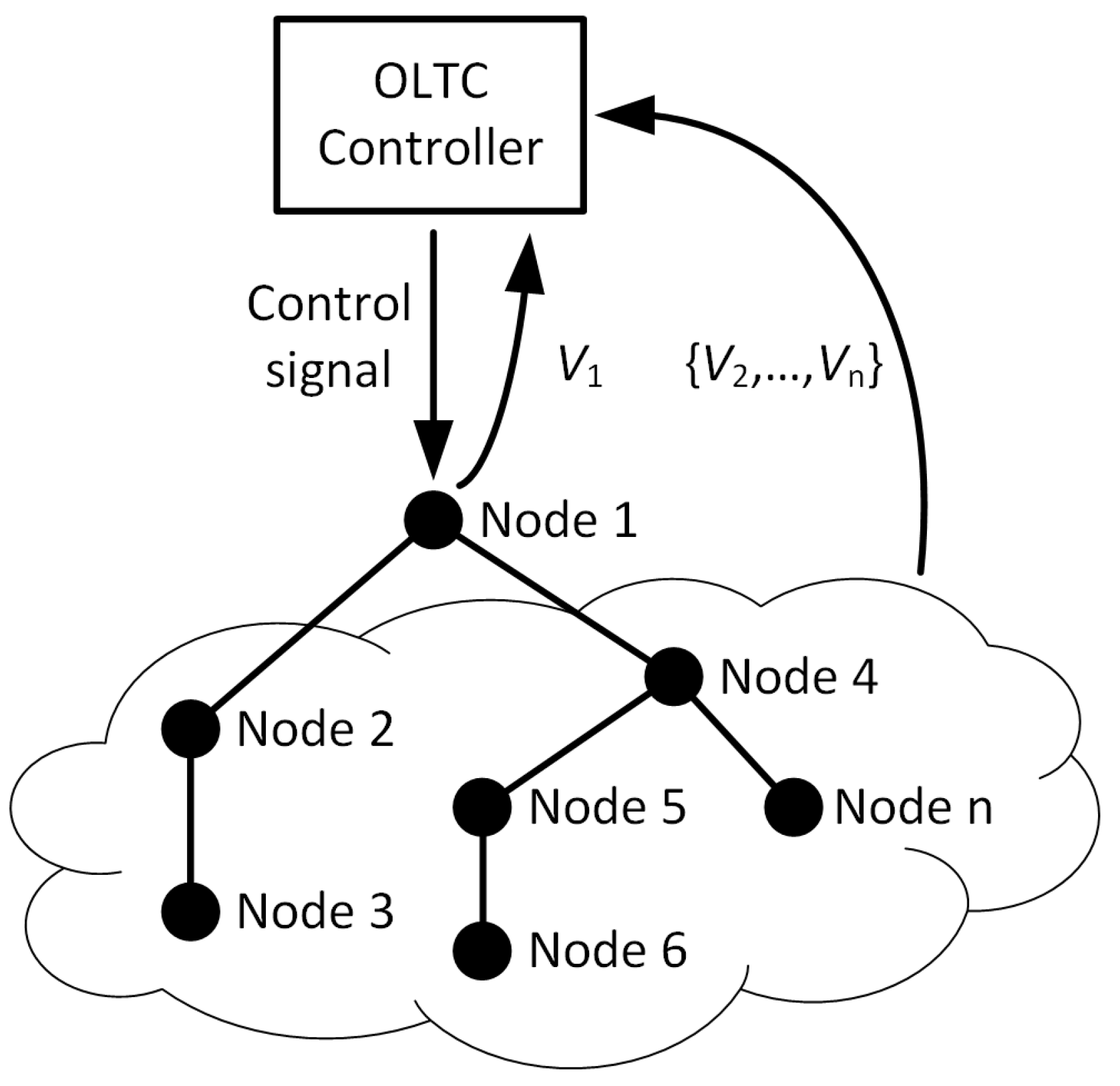
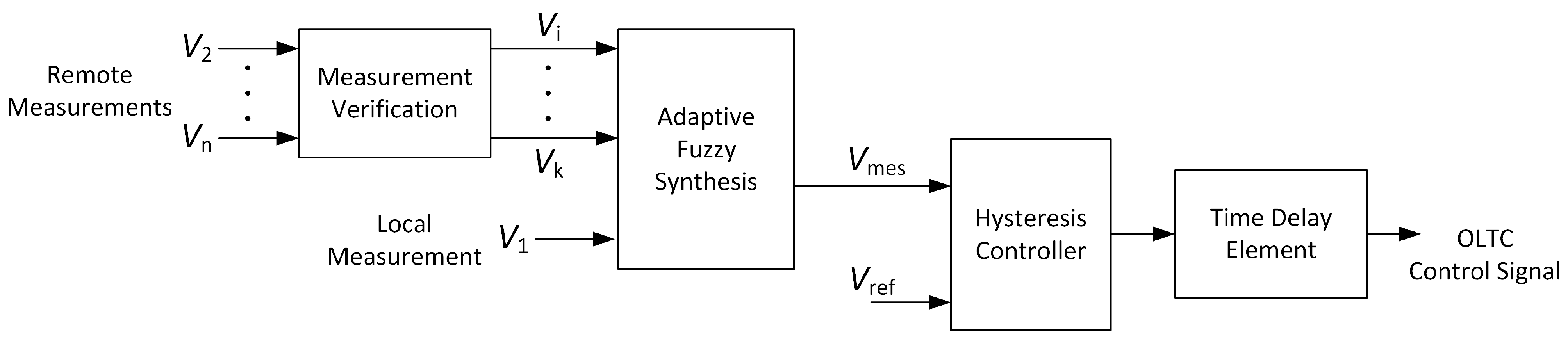
3. Proposed OLTC Controller Algorithm
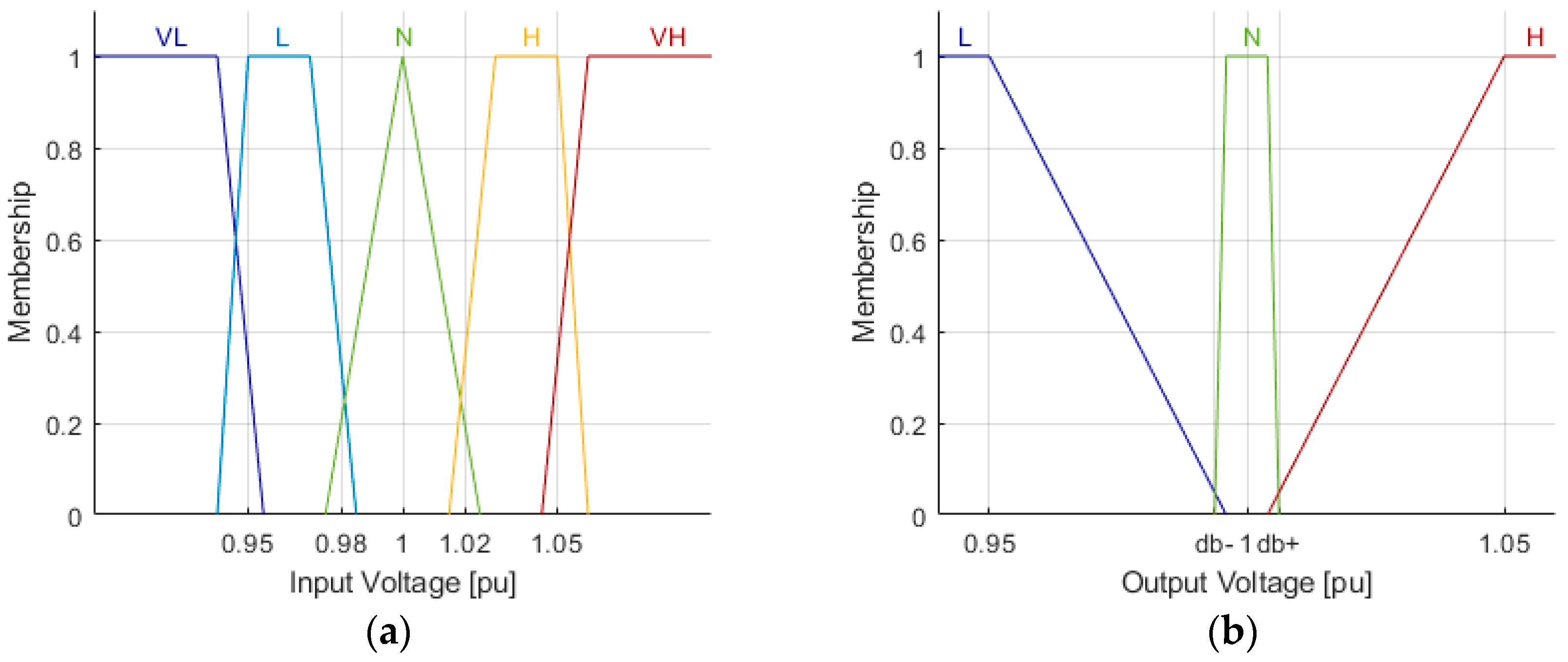
Adaptive Fuzzy Synthesis
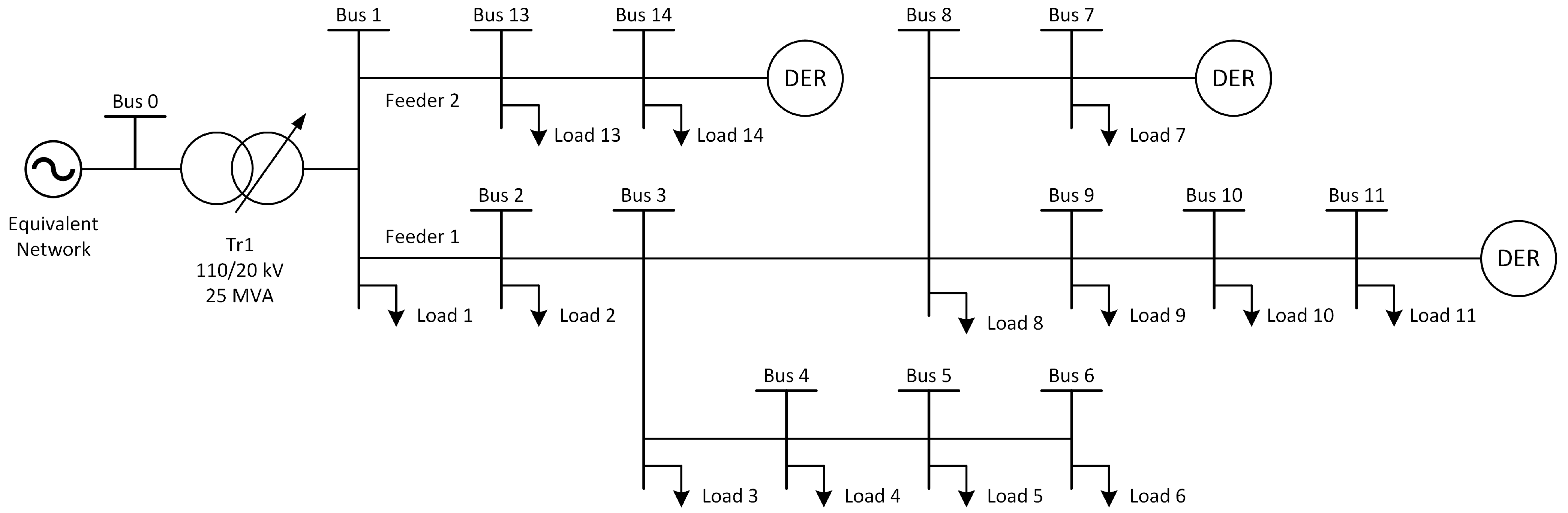
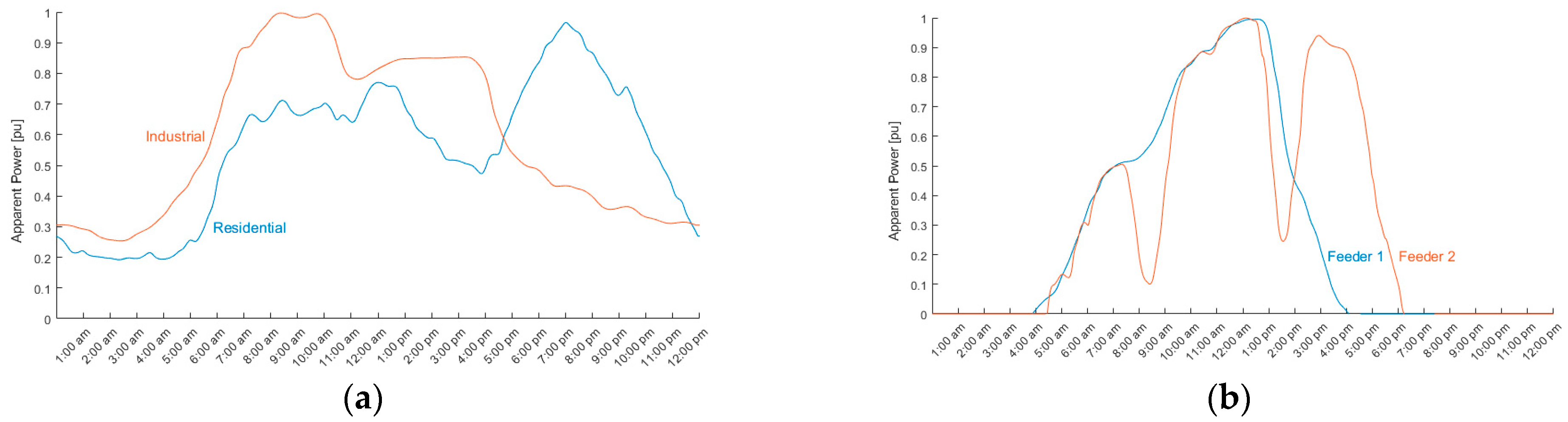
4. Methods and Experiments
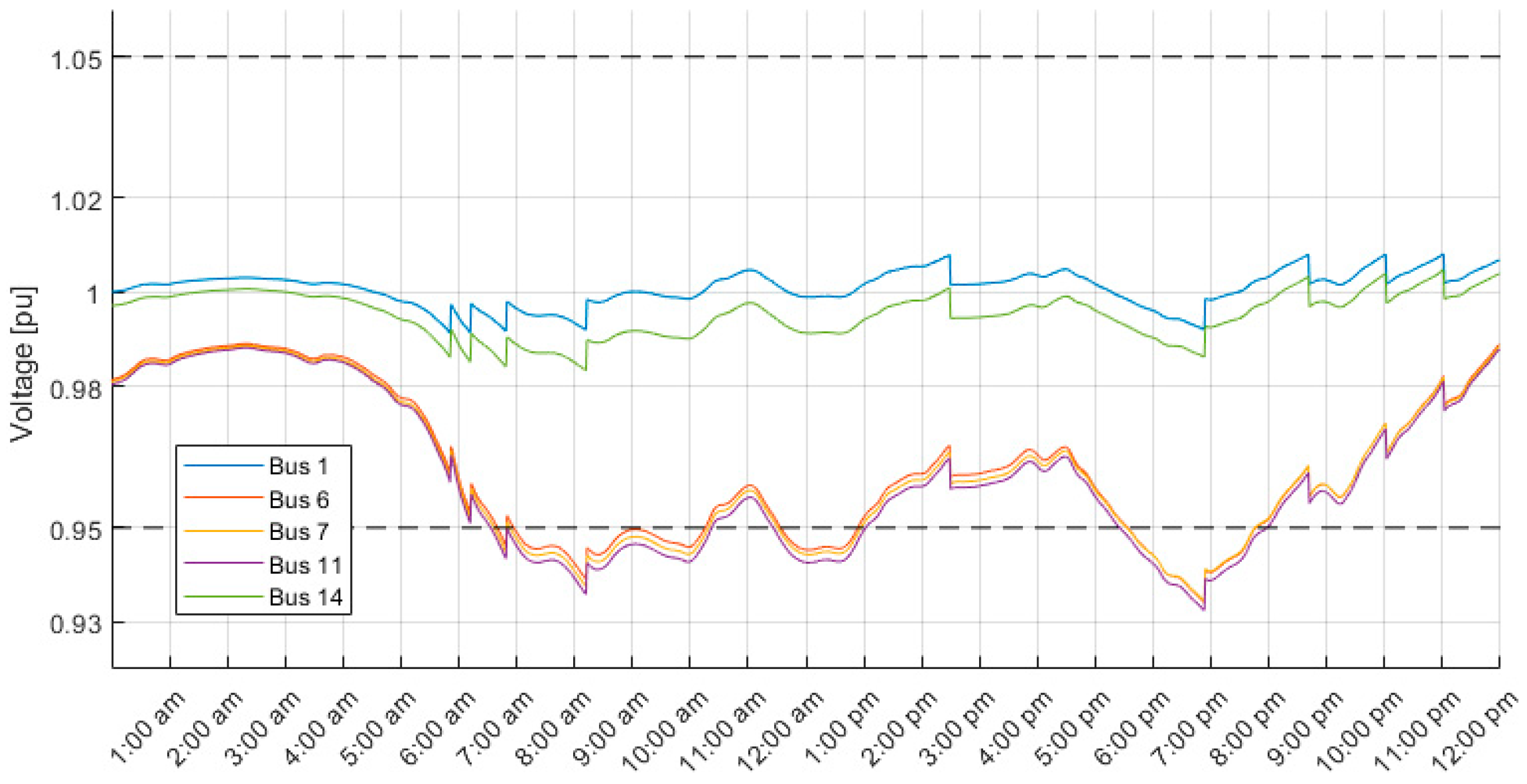
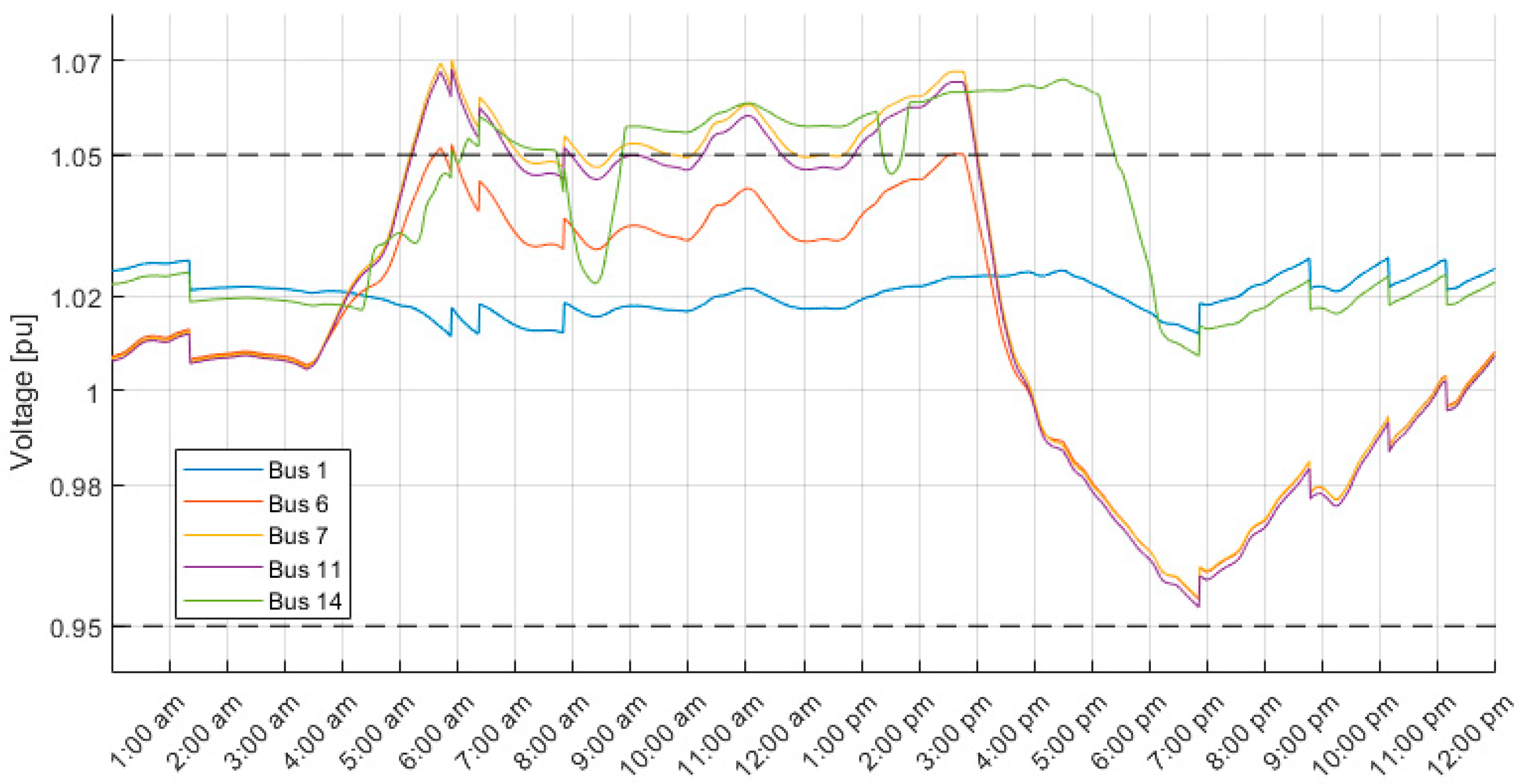
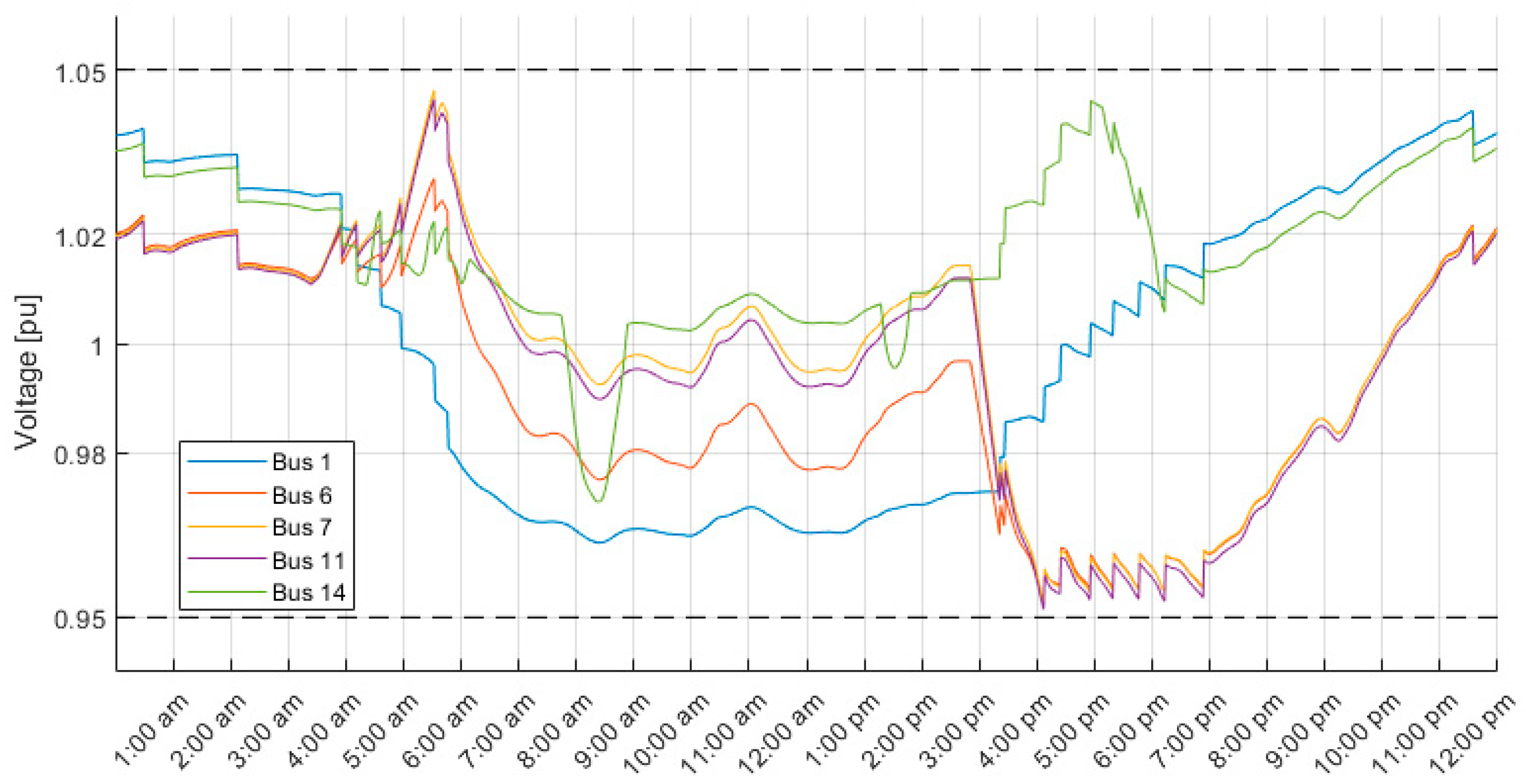
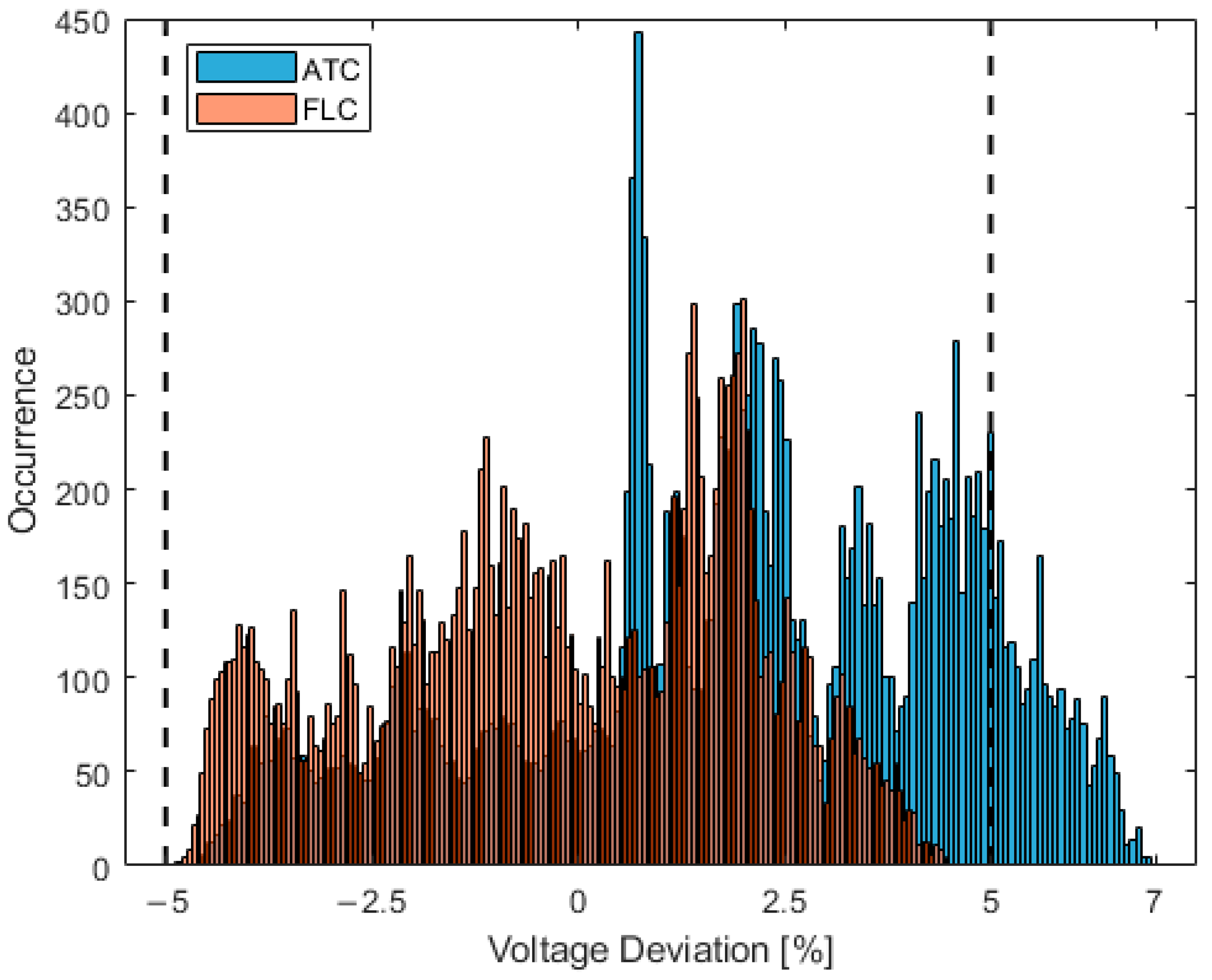
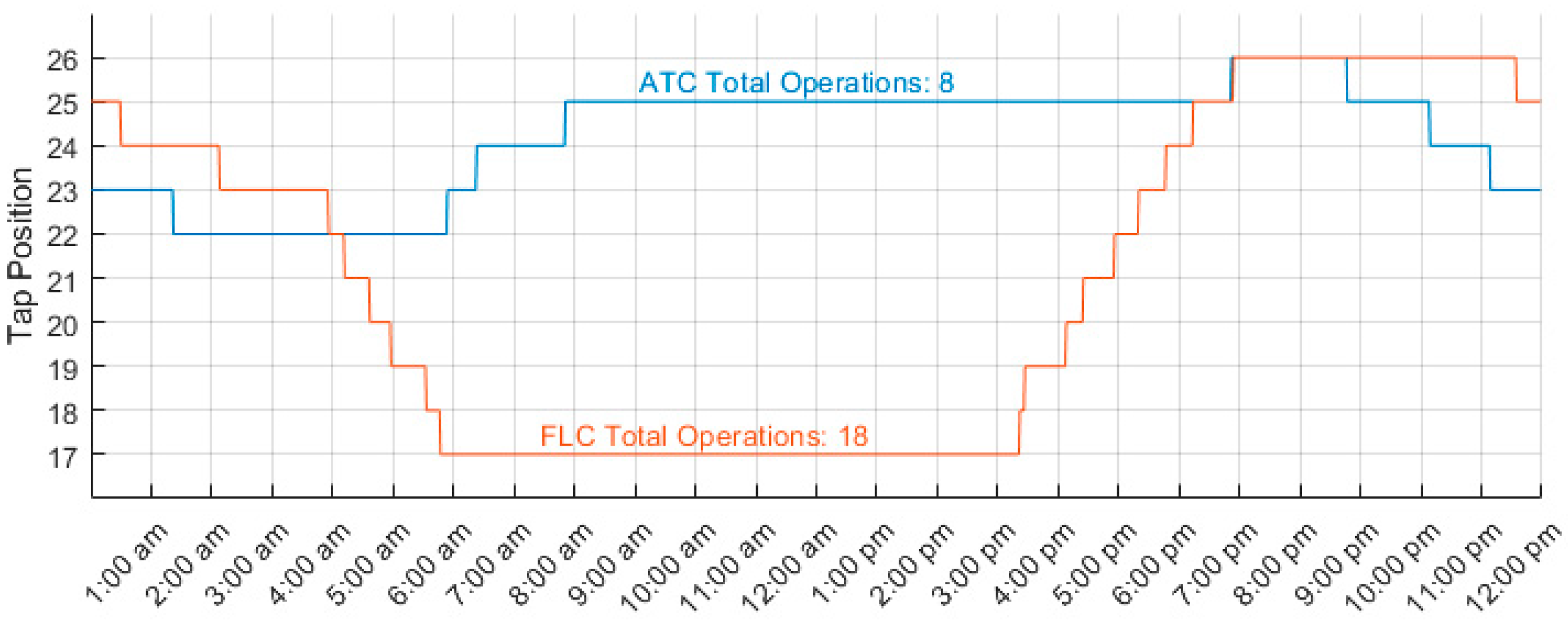
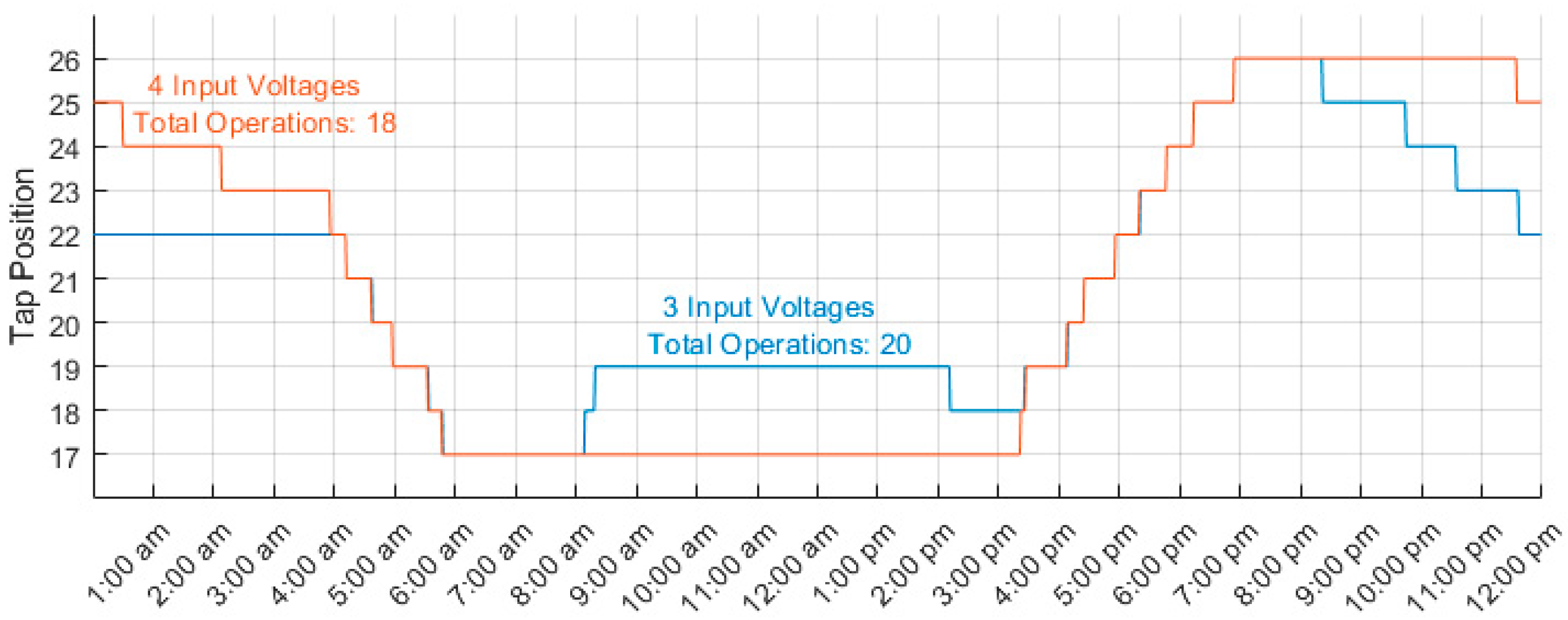
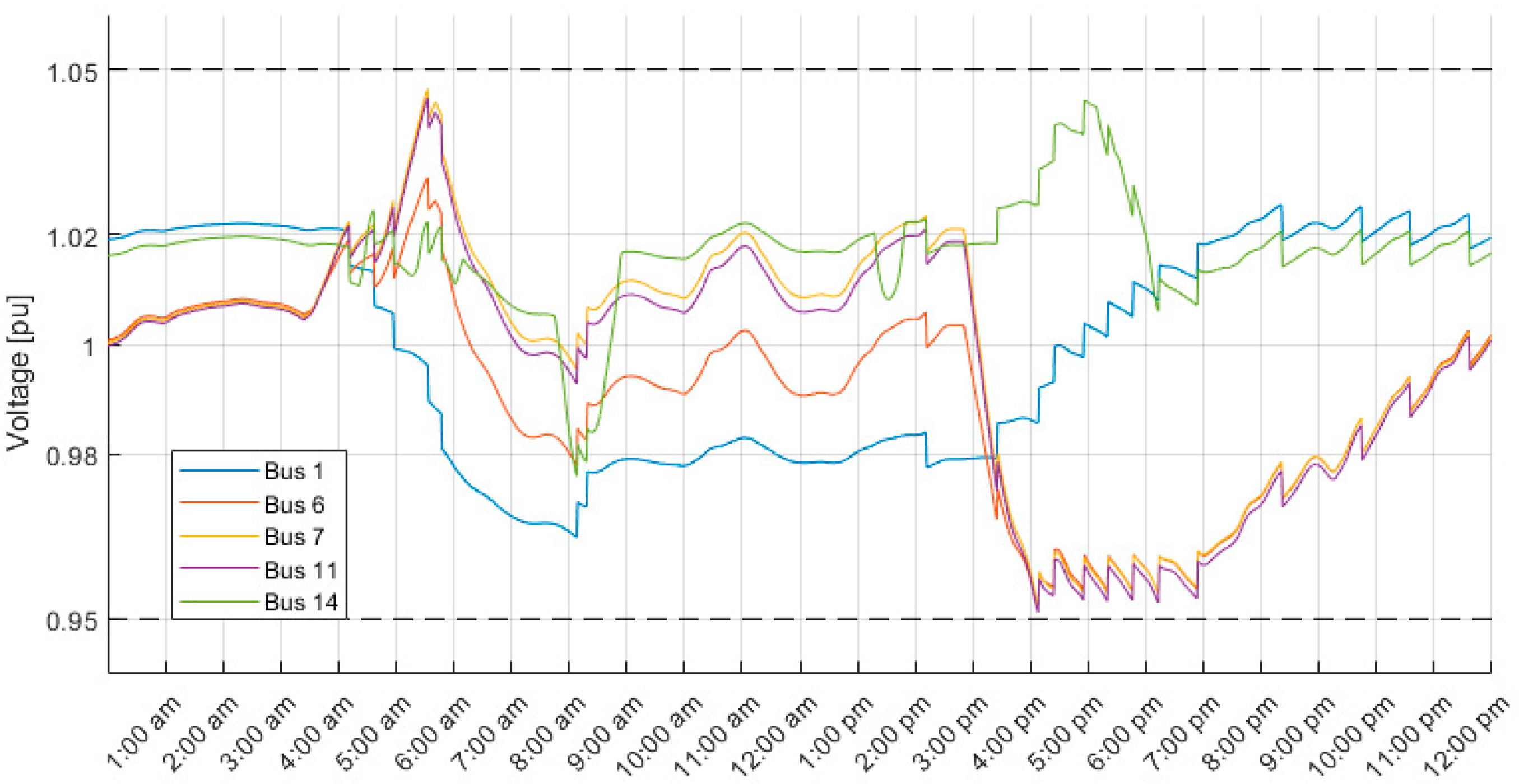
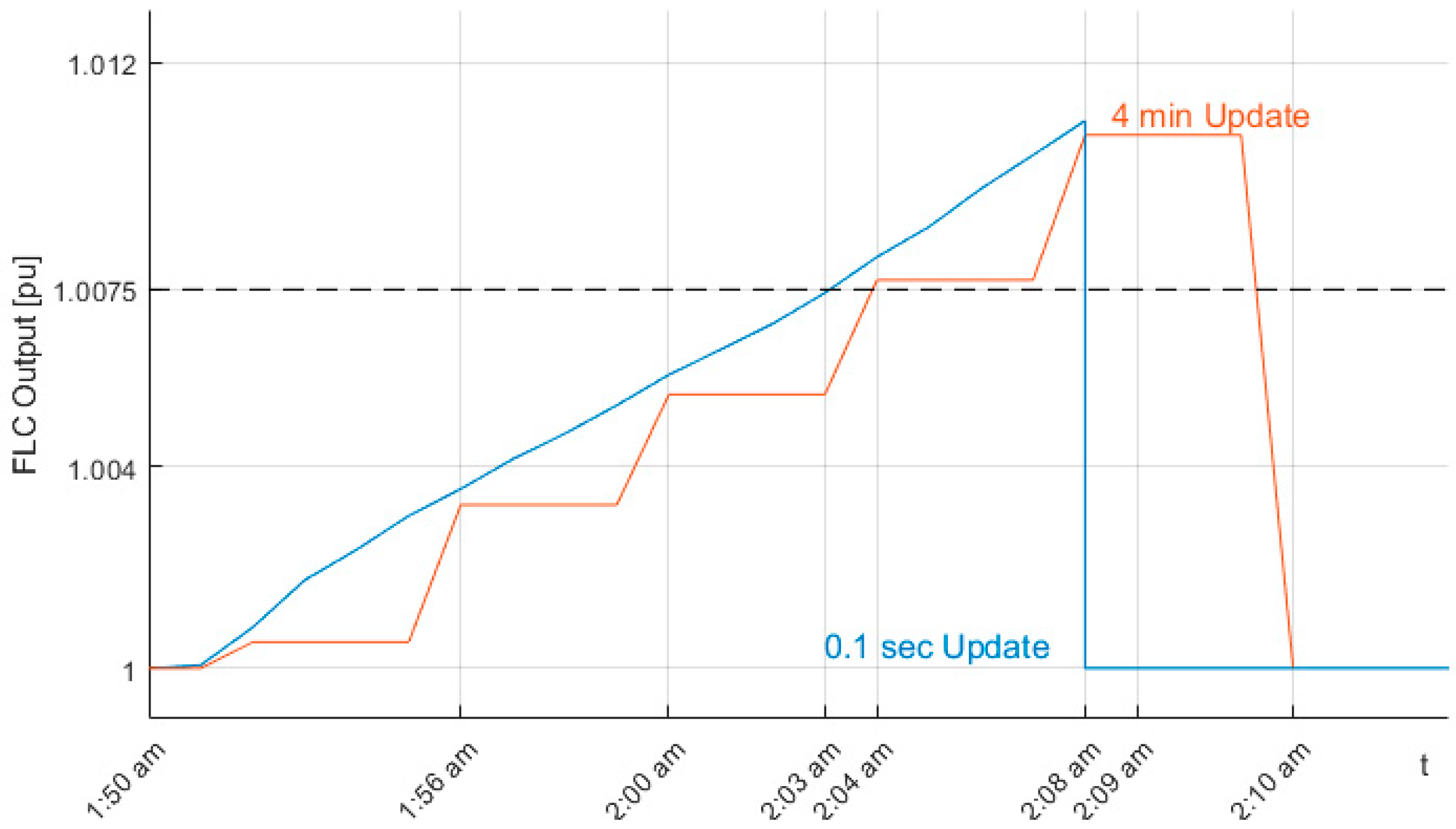
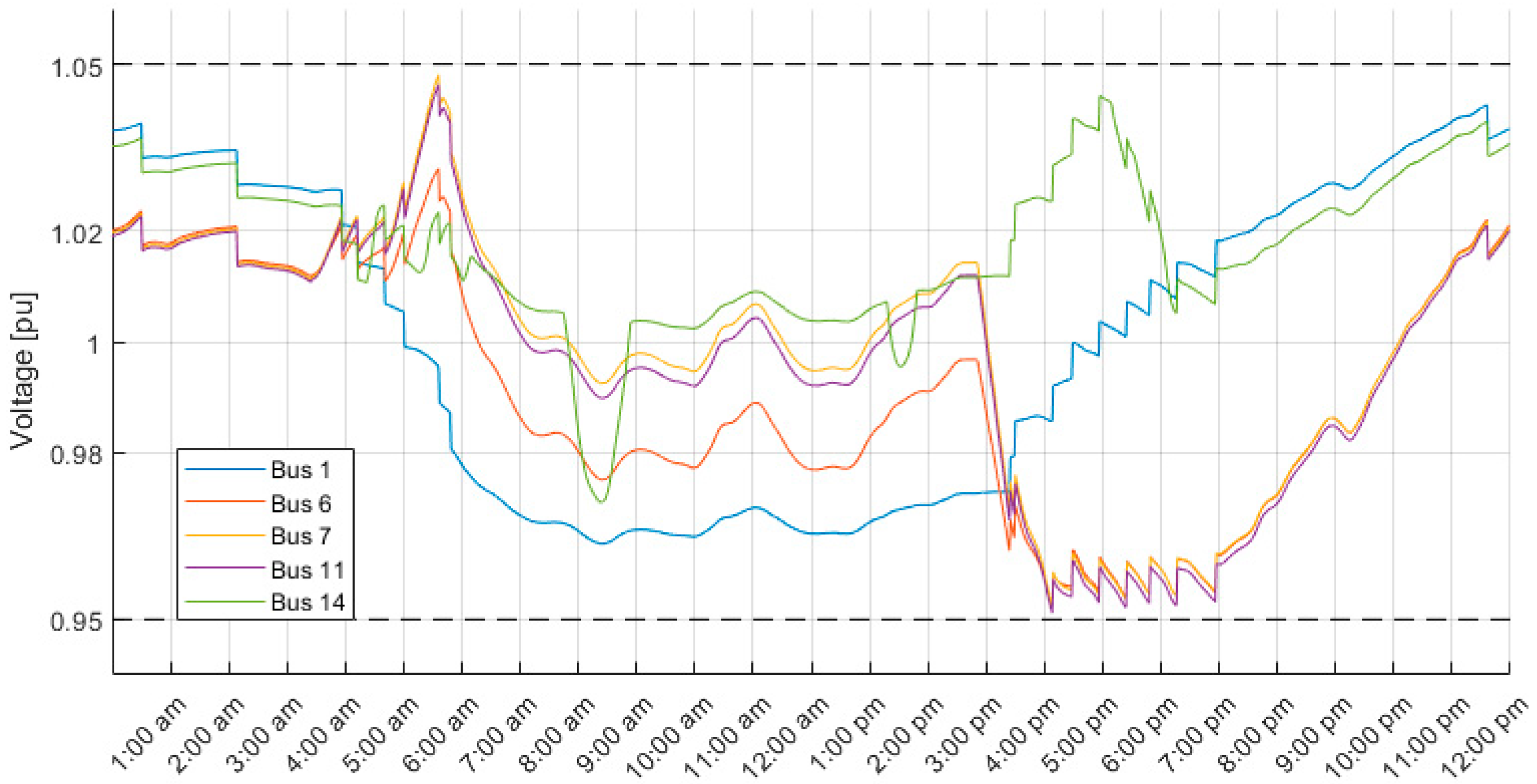
5. Results and Discussion
5.1. Comparison of FLC with ATC
5.2. Impact of Input Voltage Quantity
5.3. Impact of Data-Receiving Time Step
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hidalgo, R.; Abbey, C.; Joós, G. A review of active distribution networks enabling technologies. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar] [CrossRef]
- Sarimuthu, C.R.; Ramachandaramurthy, V.K.; Agileswari, K.R.; Mokhlis, H. A review on voltage control methods using on-load tap changer transformers for networks with renewable energy sources. Renew. Sustain. Energy Rev. 2016, 62, 1154–1161. [Google Scholar] [CrossRef]
- Gao, C.; Redfern, M.A. A review of voltage control techniques of networks with distributed generations using On-Load Tap Changer transformers. In Proceedings of the 45th International Universities Power Engineering Conference UPEC2010, Cardiff, UK, 31 August–3 September 2010. [Google Scholar]
- Murray, W.; Adonis, M.; Raji, A. Voltage control in future electrical distribution networks. Renew. Sustain. Energy Rev. 2021, 146, 111100. [Google Scholar] [CrossRef]
- Razavi, S.-E.; Rahimi, E.; Sadegh, M.; Nezhad, A.E.; Lotfi, M.; Shafie-khah, M.; Catalão, J.P.S. Impact of distributed generation on protection and voltage regulation of distribution systems: A review. Renew. Sustain. Energy Rev. 2019, 105, 157–167. [Google Scholar] [CrossRef]
- Ismail, F.B.; Mazwan, M.; Al-Faiz, H.; Marsadek, M.; Hasini, H.; Al-Bazi, A.; Yang Ghazali, Y.Z. An Offline and Online Approach to the OLTC Condition Monitoring: A Review. Energies 2022, 15, 6435. [Google Scholar] [CrossRef]
- Ghosh, S.; Rahman, S.; Pipattanasomporn, M. Distribution Voltage Regulation Through Active Power Curtailment With PV Inverters and Solar Generation Forecasts. IEEE Trans. Sustain. Energy 2017, 8, 13–22. [Google Scholar] [CrossRef]
- Maataoui, Y.; Chekenbah, H.; Boutfarjoute, O.; Puig, V.; Lasri, R. A Coordinated Voltage Regulation Algorithm of a Power Distribution Grid with Multiple Photovoltaic Distributed Generators Based on Active Power Curtailment and On-Line Tap Changer. Energies 2023, 16, 5279. [Google Scholar] [CrossRef]
- Ma, W.; Wang, W.; Chen, Z.; Wu, X.; Hu, R.; Tang, F.; Zhang, W. Voltage regulation methods for active distribution networks considering the reactive power optimization of substations. Appl. Energy 2021, 284, 116347. [Google Scholar] [CrossRef]
- Salih, S.N.; Chen, P. On Coordinated Control of OLTC and Reactive Power Compensation for Voltage Regulation in Distribution Systems With Wind Power. IEEE Trans. Power Syst. 2016, 31, 4026–4035. [Google Scholar] [CrossRef]
- Jafari, M.R.; Parniani, M.; Ravanji, M.H. Decentralized Control of OLTC and PV Inverters for Voltage Regulation in Radial Distribution Networks With High PV Penetration. IEEE Trans. Power Deliv. 2022, 37, 4827–4837. [Google Scholar] [CrossRef]
- Yao, E.; Samadi, P.; Wong, V.W.S.; Schober, R. Residential Demand Side Management Under High Penetration of Rooftop Photovoltaic Units. IEEE Trans. Smart Grid 2016, 7, 1597–1608. [Google Scholar] [CrossRef]
- Ponnaganti, P.; Pillay, J.R.; Bak-Jensen, B. Opportunities and challenges of demand response in active distribution networks: Opportunities and challenges of demand response. WIREs Energy Environ. 2018, 7, e271. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Kim, C.; Kim, S.; Kim, E.; Kim, D.; Mehmood, K.K.; Khan, S.U. Coordinated Control Algorithm for Distributed Battery Energy Storage Systems for Mitigating Voltage and Frequency Deviations. IEEE Trans. Smart Grid 2016, 7, 1713–1722. [Google Scholar] [CrossRef]
- Ahmad Khan, H.; Zuhaib, M.; Rihan, M. Voltage fluctuation mitigation with coordinated OLTC and energy storage control in high PV penetrating distribution network. Electr. Power Syst. Res. 2022, 208, 107924. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Y.; Liu, T.; Lei, S.; Hill, D.J. A New Formulation of Distribution Network Reconfiguration for Reducing the Voltage Volatility Induced by Distributed Generation. IEEE Trans. Power Syst. 2020, 35, 496–507. [Google Scholar] [CrossRef]
- Caldon, R.; Coppa, M.; Sgarbossa, R.; Turri, R. A simplified algorithm for OLTC control in active distribution MV networks. In Proceedings of the AEIT Annual Conference, Mondello, Palermo, Italy, 3–5 October 2013. [Google Scholar] [CrossRef]
- Yoon, K.-H.; Shin, J.-W.; Nam, T.-Y.; Kim, J.-C.; Moon, W.-S. Operation Method of On-Load Tap Changer on Main Transformer Considering Reverse Power Flow in Distribution System Connected with High Penetration on Photovoltaic System. Energies 2022, 15, 6473. [Google Scholar] [CrossRef]
- Kasztenny, B.; Rosolowski, E.; Izykowski, J.; Saha, M.M.; Hillstrom, B. Fuzzy logic controller for on-load transformer tap changer. IEEE Trans. Power Deliv. 1998, 13, 164–170. [Google Scholar] [CrossRef]
- Choukri, L.; Chekenbah, H.; Lasri, R.; Bouhorma, M.; Maataoui, Y. On-Load Tap-Changer Control by a Fuzzy Logic Controller. In Proceedings of the 2019 4th World Conference on Complex Systems (WCCS), Quarzazate, Marocco, 22–25 April 2019. [Google Scholar] [CrossRef]
- Azzouz, M.A.; Farag, H.E.; El-Saadany, E.F. Fuzzy-based control of on-load tap changers under high penetration of distributed generators. In Proceedings of the 2013 3rd International Conference on Electric Power and Energy Conversion Systems, Istanbul, Turkey, 2–4 October 2013. [Google Scholar] [CrossRef]
- Stifter, M.; Bletterie, B.; Brunner, H.; Burnier, D.; Sawsan, H.; Andrén, F.; Schwalbe, R.; Abart, A.; Nenning, R.; Herb, F.; et al. DG DemoNet validation: Voltage control from simulation to field test. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, UK, 5–7 December 2011. [Google Scholar] [CrossRef]
- Herb, F.; Bletterie, B.; Abart, A.; Schwalbe, R.; Pointer, R.; Stifter, M. DG DemoNet: Impact of volt/VAR control on increasing the voltage band reserve—Results from field trial validations. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013. [Google Scholar] [CrossRef]
- Li, C.; Disfani, V.R.; Pecenak, Z.K.; Mohajeryami, S.; Kleissl, J. Optimal OLTC voltage control scheme to enable high solar penetrations. Electr. Power Syst. Res. 2018, 160, 318–326. [Google Scholar] [CrossRef]
- Tasnim, S.; Sarimuthu, C.R.; Lan, B.L.; Tan, C.P. A game theory approach for OLTC voltage control operation in an active distribution network. Electr. Power Syst. Res. 2023, 214, 108861. [Google Scholar] [CrossRef]
- Daratha, N.; Das, B.; Sharma, J. Coordination between OLTC and SVC for Voltage Regulation in Unbalanced Distribution System Distributed Generation. IEEE Trans. Power Syst. 2014, 29, 289–299. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Chuang, Y.-S.; Lai, J.-W. A novel STATCOM control scheme for the coordination with OLTC on voltage regulation. Int. J. Smart Grid Clean Energy 2014, 3, 161–167. [Google Scholar] [CrossRef][Green Version]
- Bakhshideh Zad, B.; Lobry, J.; Vallee, F. Coordinated control of on-load tap changer and D-STATCOM for voltage regulation of radial distribution systems with DG units. In Proceedings of the 2013 3rd International Conference on Electric Power and Energy Conversion Systems, Istanbul, Turkey, 2–4 October 2013. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, S.; Sidhu, T.; Siva, A.K. Smart meters for enhancing protection and monitoring functions in emerging distribution systems. Int. J. Electr. Power Energy Syst. 2021, 27, 106626. [Google Scholar] [CrossRef]
- Yahya, S.; Ndyetabura, H.; Mvungi, N.; Lujara, S. Low Cost Data Acquisition System for Electrical Secondary Distribution Network. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunisia, 13–16 April 2020. [Google Scholar] [CrossRef]
- Dusabimana, E.; Yoon, S.-G. A Survey on the Micro-Phasor Measurement Unit in Distribution Networks. Electronics 2020, 9, 305. [Google Scholar] [CrossRef]
- Guerrero, C.A.V.; Da Silveira, P.M.; Carvalho, J.M.; Bonatto, B.D.; Oliveira, D.Q.; Santos, M.; Marujo, D.; Zambroni, A.C.; Felver, L.A.; Oliveira, J.A.; et al. A new software-in-the-loop strategy for real-time testing of a coordinated Volt/Var Control. In Proceedings of the 2016 IEEE PES PowerAfrica, Livingstone, Zambia, 28 June–2 July 2016. [Google Scholar] [CrossRef]
- Tuominen, V.; Reponen, H.; Kulmala, A.; Lu, S.; Repo, S. Real-time hardware- and software-in-the-loop simulation of decentralised distribution network control architecture. IET Gener. Transm. Distrib. 2017, 11, 3057–3064. [Google Scholar] [CrossRef]
- Andrén, F.; Henein, S.; Stifter, M. Development and validation of a coordinated voltage controller using real-time simulation. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011. [Google Scholar] [CrossRef]
- Strunz, K. Benchmark Systems for Network Integration of Renewable and Distributed Energy Resources. CIGRE Task Force C6.04.02; Electra; CIGRE: Paris, France, 2014; Volume 575, ISBN 978-285-873-270-8. Available online: https://www.e-cigre.org/publications/detail/elt-273-8-benchmark-systems-for-network-integration-of-renewable-and-distributed-energy-resources.html (accessed on 24 May 2024).
- IEC TR 61850-1:2013; Communication Networks and Systems for Power Utility Automation—Part 1: Introduction and Overview. IEC: Geneva, Switzerland, 2013.
- IEEE Std 1815-2012; IEEE Standard for Electric Power Systems Communications-Distribiuted Network Protocol (DNP3). IEEE: Piscataway, NJ, USA, 2012.
- IEC 60870-5-104; Transmission Protocols–Network Access for IEC 60870-5-101 Using Standard Transport Profiles. IEC: Geneva, Switzerland, 2006.


| Rule Number | Input Voltage 1 | Input Voltage 2 | Input Voltage 3 | Output Voltage |
|---|---|---|---|---|
| 1 | VL | 1 | 1 | L |
| 2 | 1 | VL | 1 | L |
| 3 | 1 | 1 | VL | L |
| 4 | L | L | 1 | L |
| 5 | 1 | L | L | L |
| 6 | L | 1 | L | L |
| 7 | N | N | 1 | N |
| 8 | 1 | N | N | N |
| 9 | N | 1 | N | N |
| 10 | VL | VH | 1 | N |
| 11 | VL | 1 | VH | N |
| 12 | VH | VL | 1 | N |
| 13 | 1 | VL | VH | N |
| 14 | 1 | 1 | VL | N |
| 15 | 1 | 1 | VL | N |
| 16 | L | N | H | N |
| 17 | L | H | N | N |
| 18 | N | L | H | N |
| 19 | H | L | N | N |
| 20 | N | H | L | N |
| 21 | H | N | L | N |
| 22 | H | H | 1 | H |
| 23 | 1 | H | H | H |
| 24 | H | 1 | H | H |
| 25 | VH | 1 | 1 | H |
| 26 | 1 | VH | 1 | H |
| 27 | 1 | 1 | VH | H |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wróblewski, W.; Kowalik, R.; Januszewski, M.; Kurek, K. A Fuzzy OLTC Controller: Applicability in the Transition Stage of the Energy System Transformation. Energies 2024, 17, 2716. https://doi.org/10.3390/en17112716
Wróblewski W, Kowalik R, Januszewski M, Kurek K. A Fuzzy OLTC Controller: Applicability in the Transition Stage of the Energy System Transformation. Energies. 2024; 17(11):2716. https://doi.org/10.3390/en17112716
Chicago/Turabian StyleWróblewski, Wiktor, Ryszard Kowalik, Marcin Januszewski, and Karol Kurek. 2024. "A Fuzzy OLTC Controller: Applicability in the Transition Stage of the Energy System Transformation" Energies 17, no. 11: 2716. https://doi.org/10.3390/en17112716
APA StyleWróblewski, W., Kowalik, R., Januszewski, M., & Kurek, K. (2024). A Fuzzy OLTC Controller: Applicability in the Transition Stage of the Energy System Transformation. Energies, 17(11), 2716. https://doi.org/10.3390/en17112716






