Well Logging Reconstruction Based on a Temporal Convolutional Network and Bidirectional Gated Recurrent Unit Network with Attention Mechanism Optimized by Improved Sand Cat Swarm Optimization
Abstract
1. Introduction
- (1)
- A TCN-BiGRU-AM initially takes advantage of a TCN’s superior parallel processing capabilities. Secondly, it takes advantage of a BiGRU’s capacity to extract the contextual correlation between characteristics. Furthermore, it makes use of an AM’s capability to extract internal self-correlation.
- (2)
- The variable spiral strategy and sparrow warning mechanism are first introduced to enhance the SCSO’s optimization capability. The ISCSO is used to optimize the hyperparameters of TCN-BiGRU-AM, thereby improving the prediction performance.
- (3)
- In engineering practice, ISCSO-TCN-BiGRU-AM significantly outperforms the competing models in missing logging reconstruction. The proposed model has effective practical implications and can successfully handle real industry needs.
2. Principles and Methods
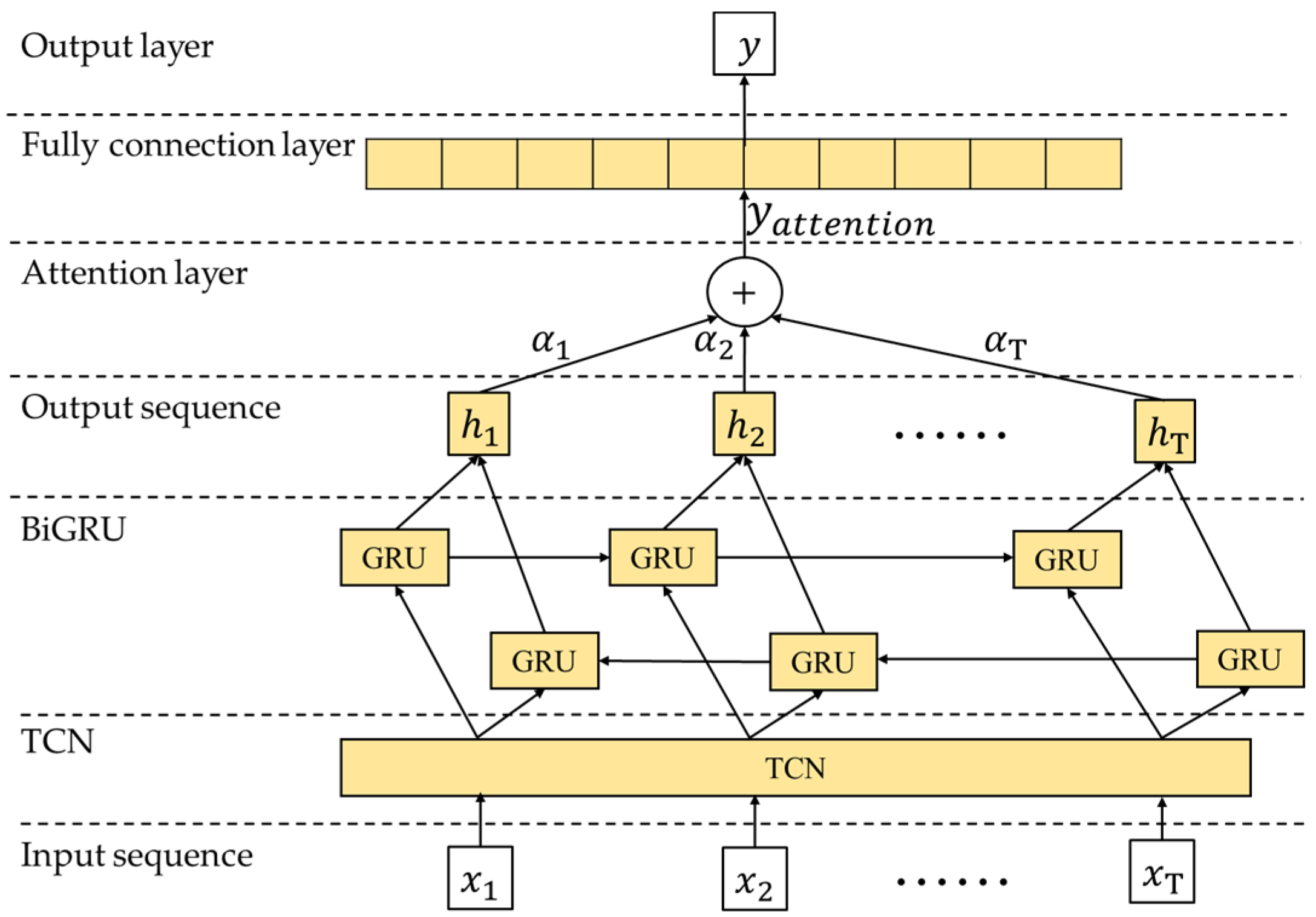
2.1. TCN-BiGRU-AM
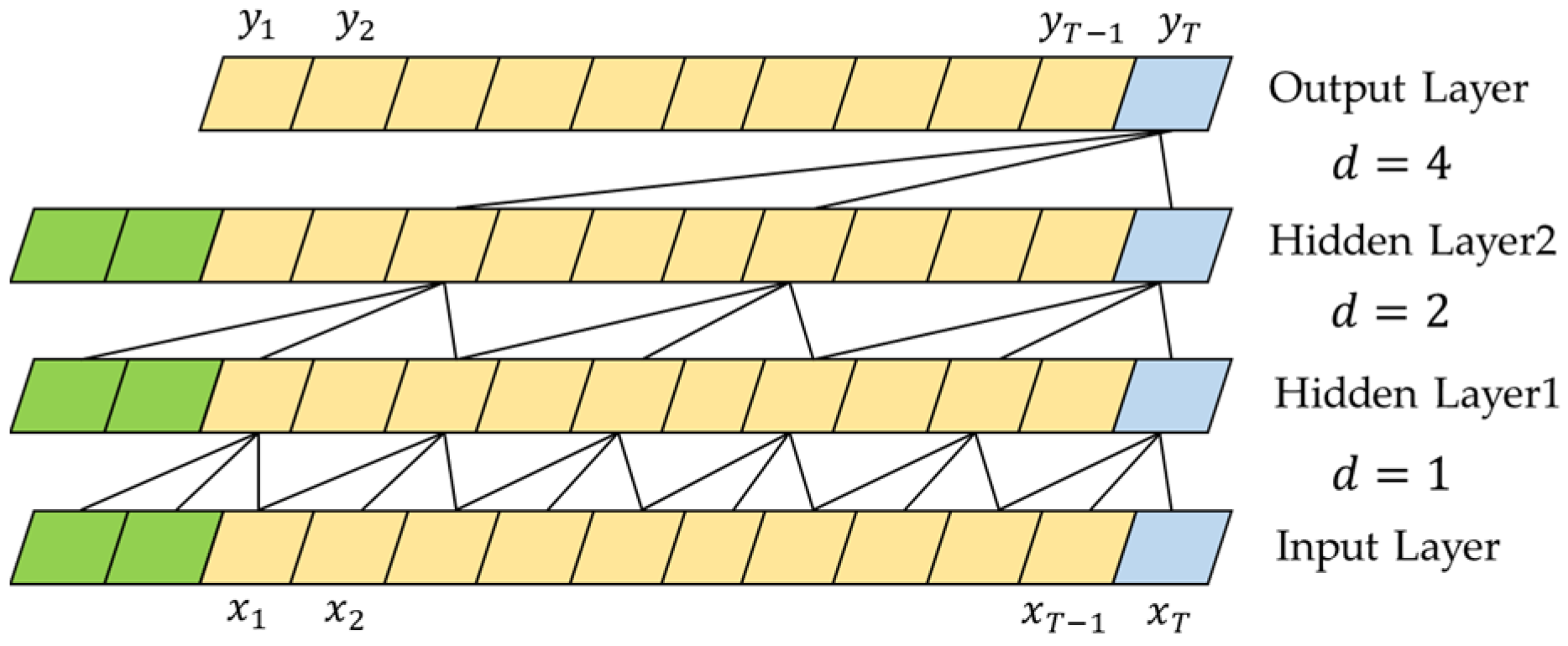
2.1.1. TCN
- (1)
- Causal convolution
- (2)
- Dilated convolution
- (3)
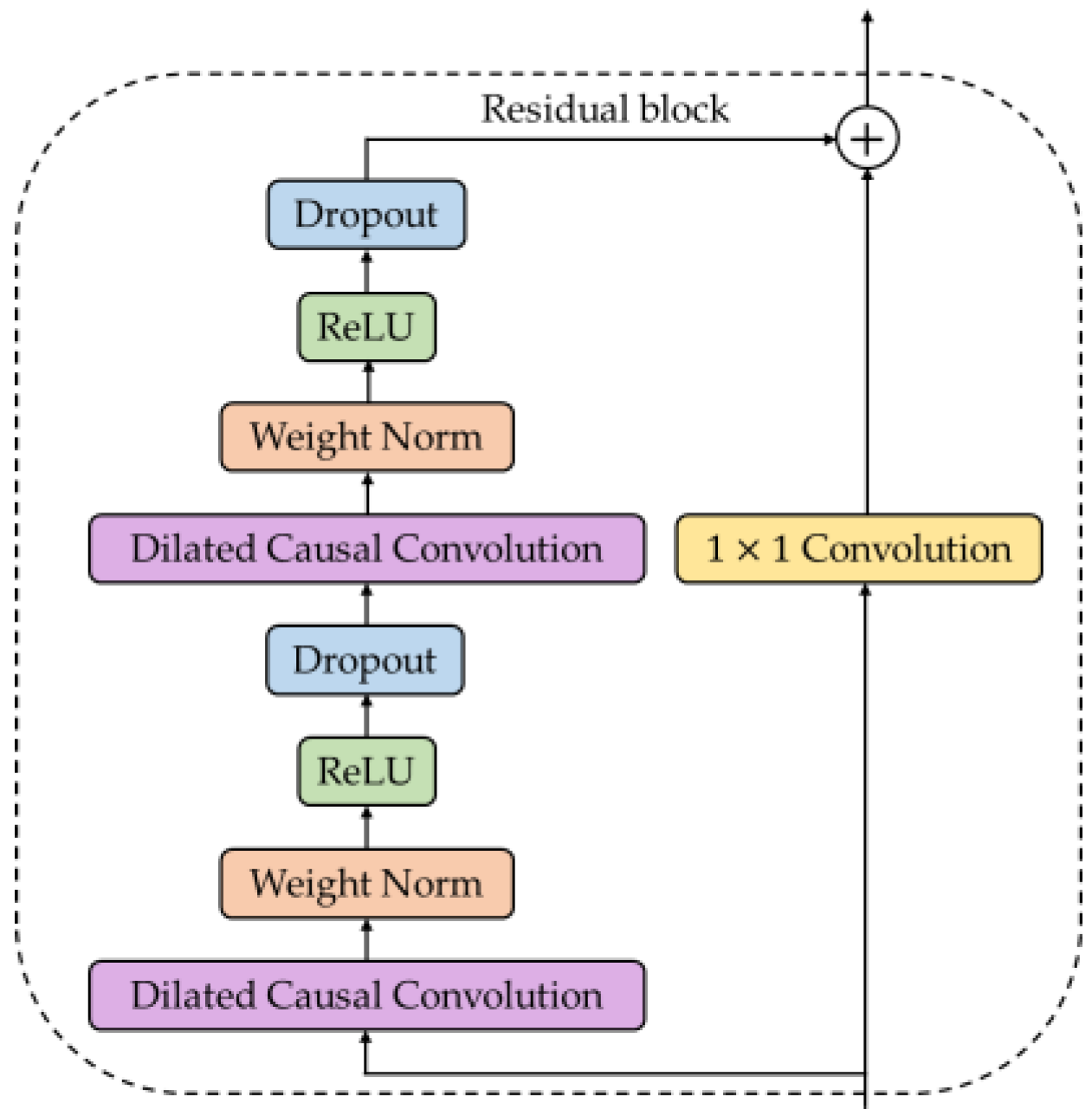
- Residual module
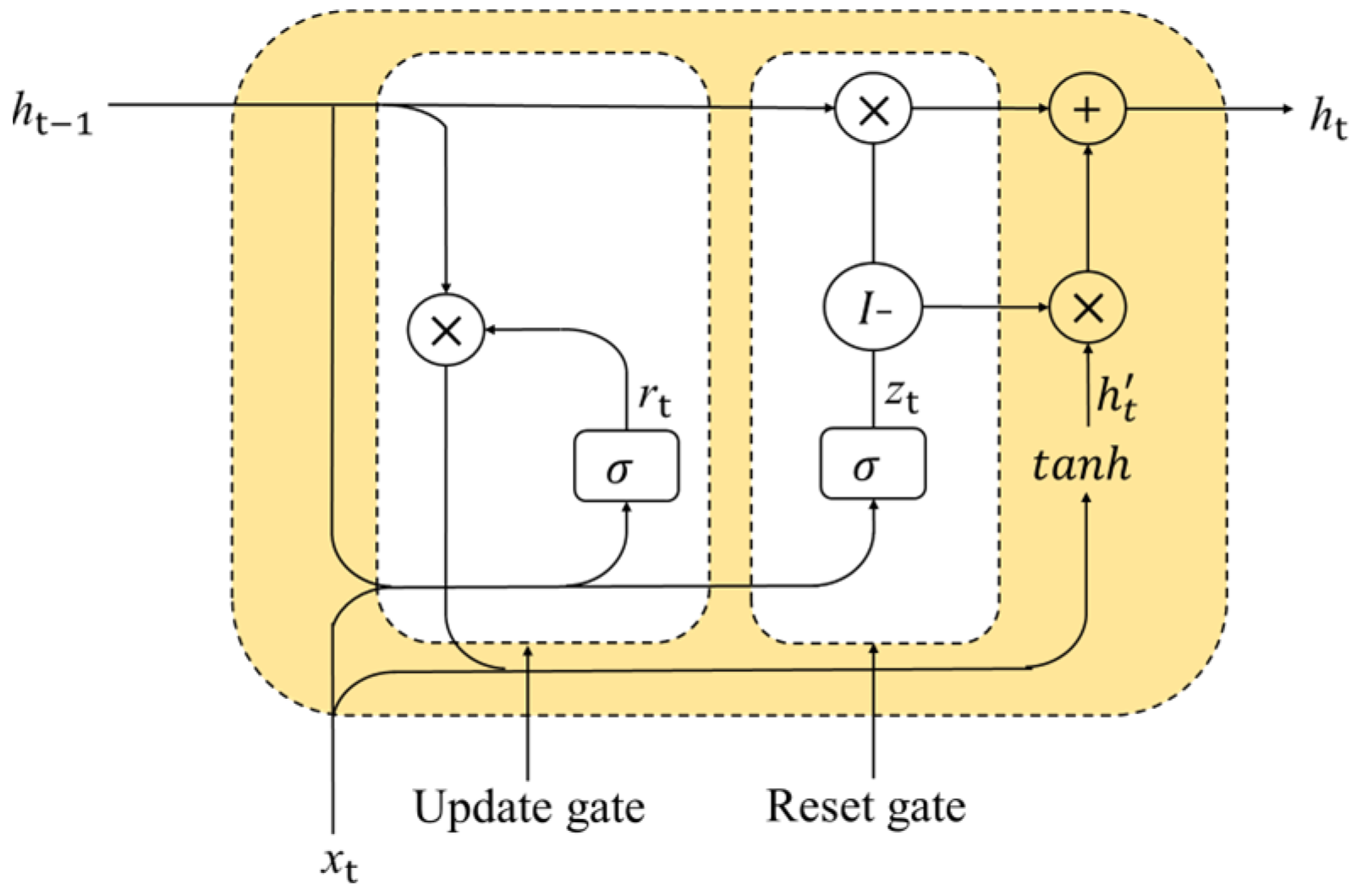
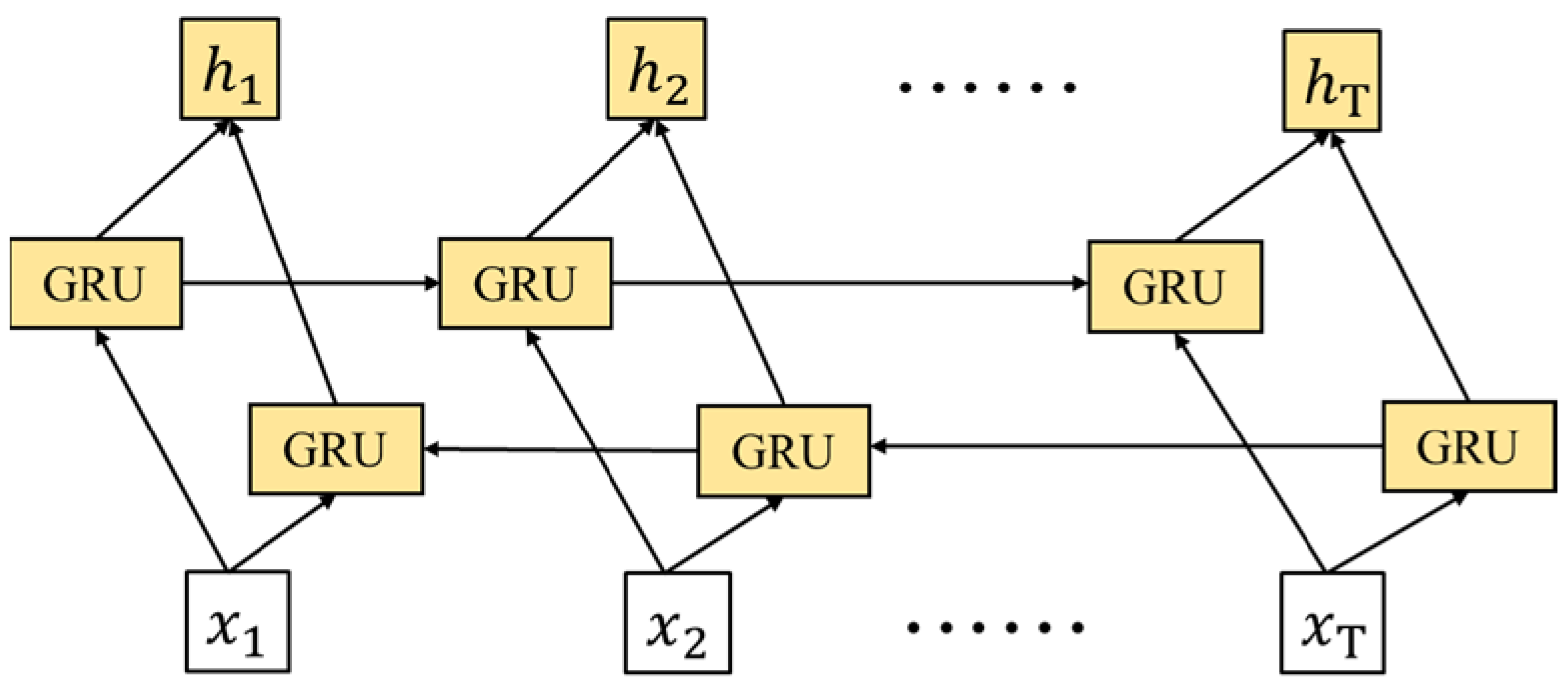
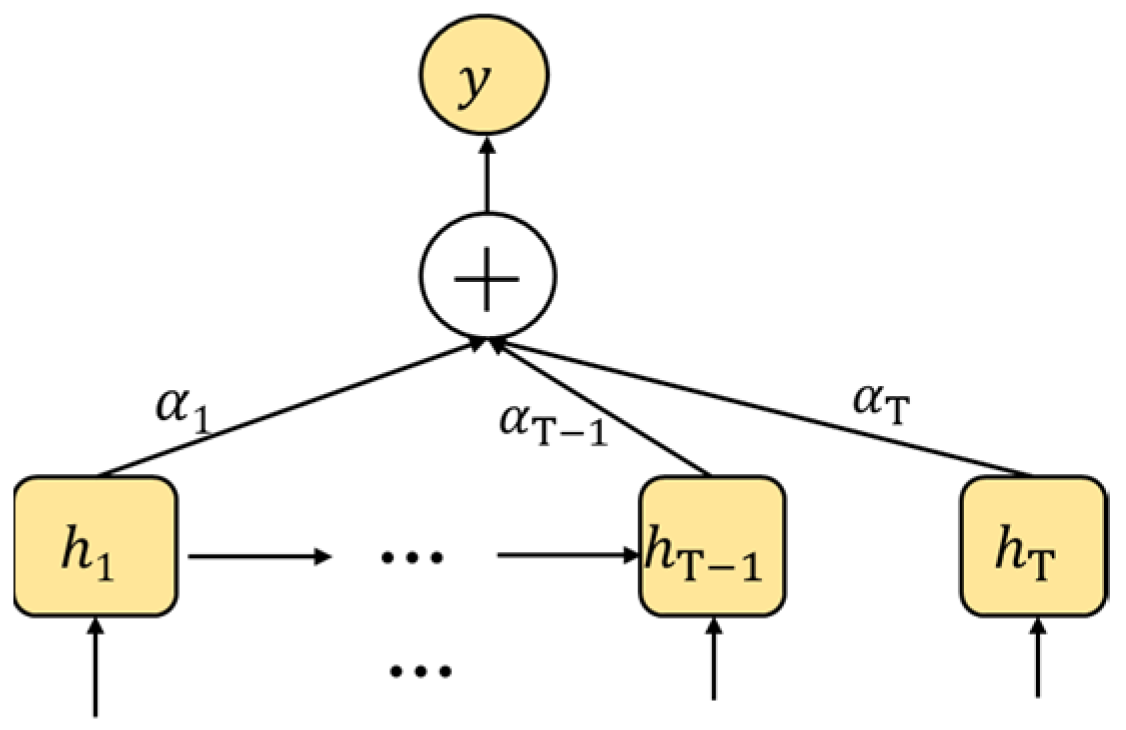
2.1.2. BiGRU-AM
2.1.3. TCN-BiGRU-AM Flow Chart
2.2. SCSO
2.3. Improvement of SCSO
2.3.1. Variable Spiral Strategy
2.3.2. Sparrow Warning Mechanism
2.3.3. ISCSO Flow
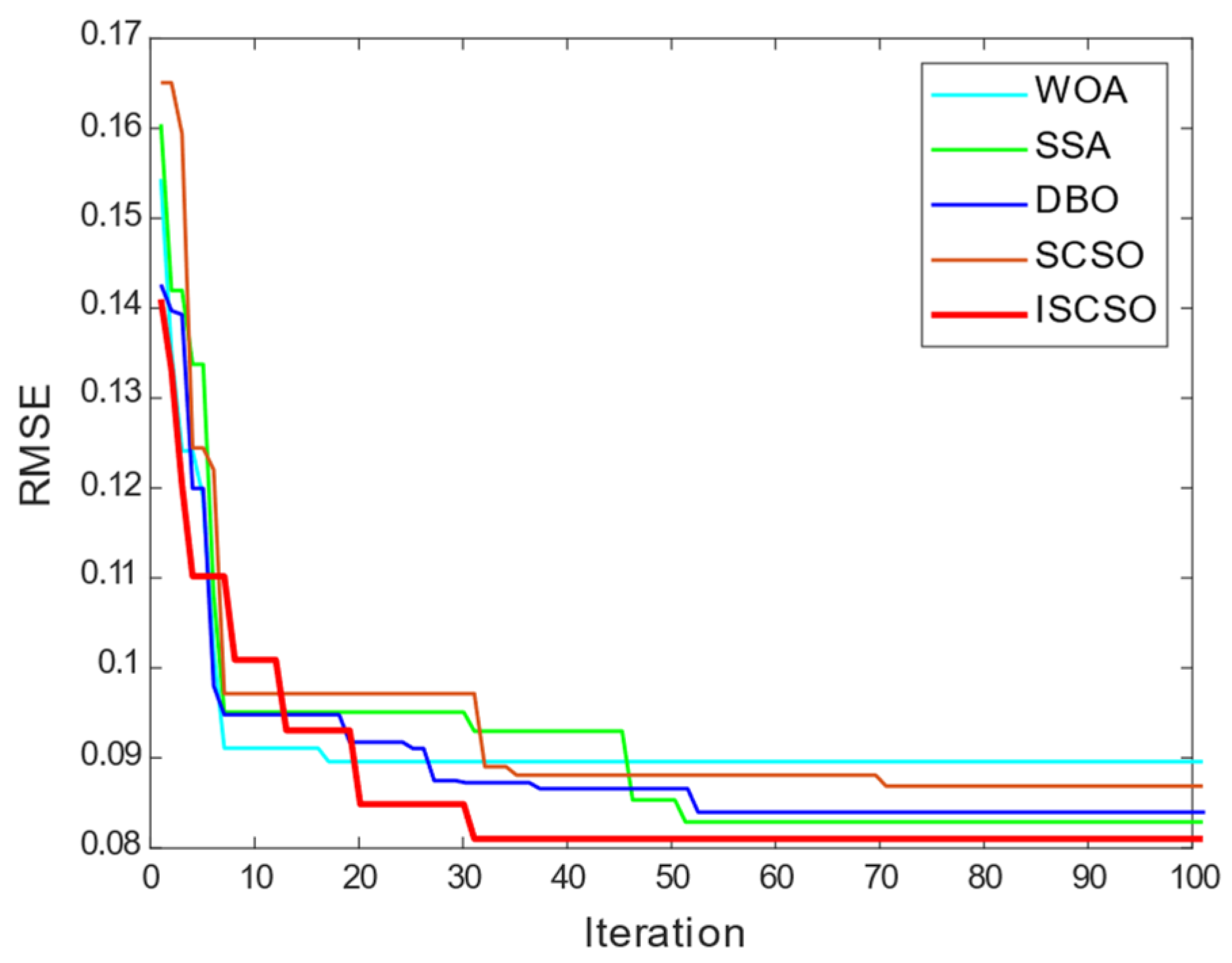
3. ISCSO Performance Test
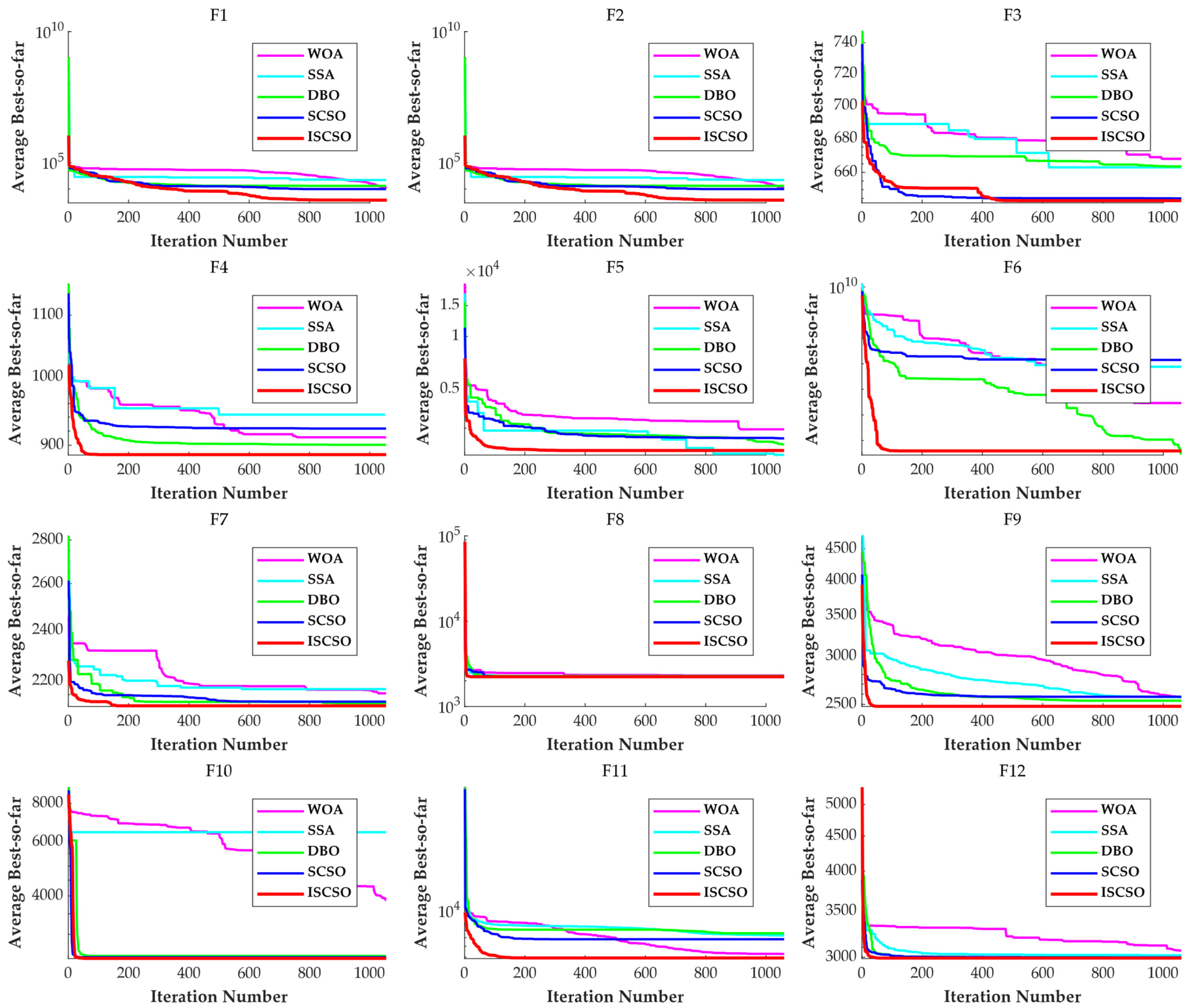
3.1. Analysis of CEC–2022 Functions
3.2. Analysis of Rank Sum Test
4. Practical Application and Analysis
4.1. ISCSO-TCN-BiGRU-AM Prediction Flow
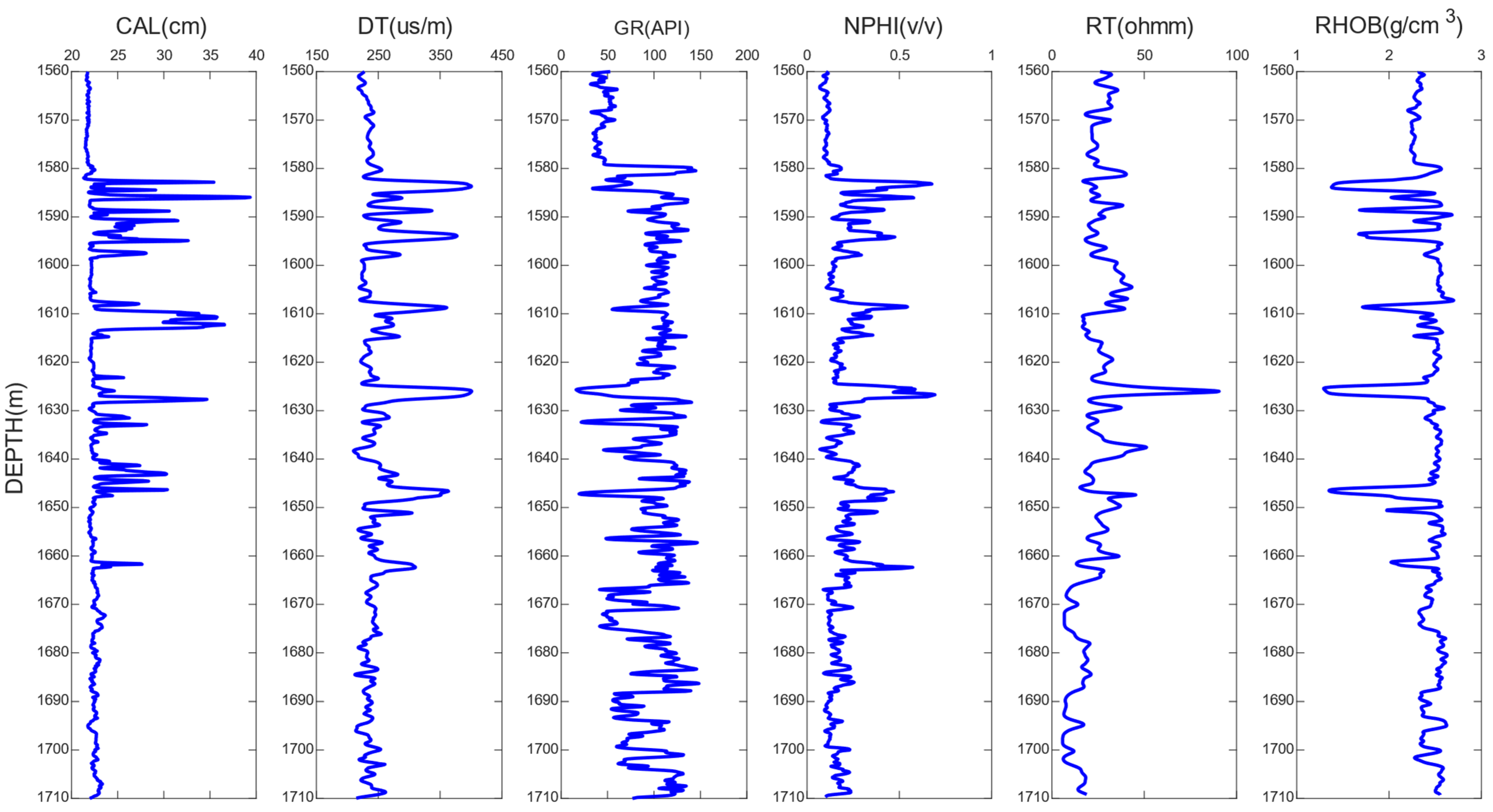
4.2. Data Preparation
4.3. Model Parameter Setting
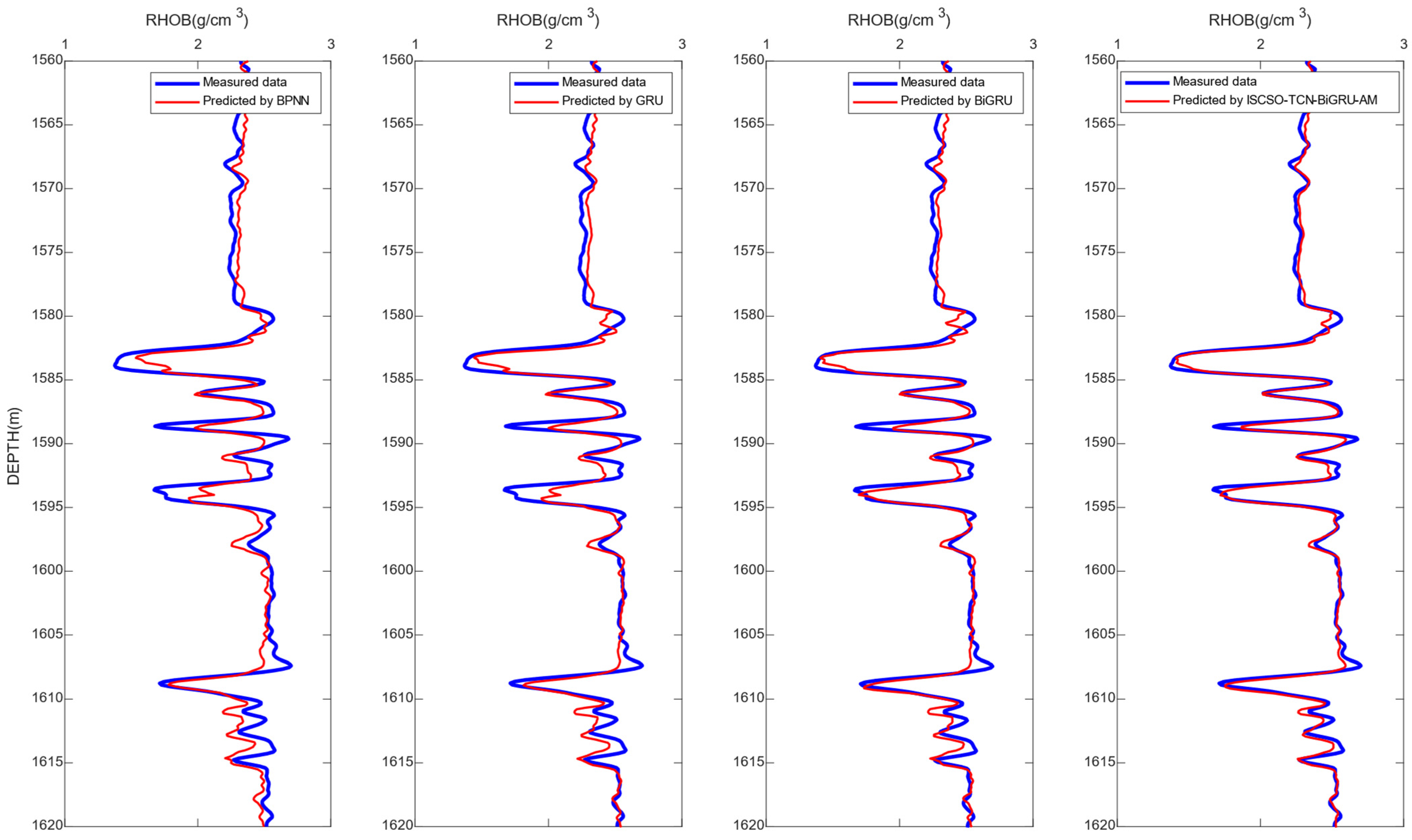
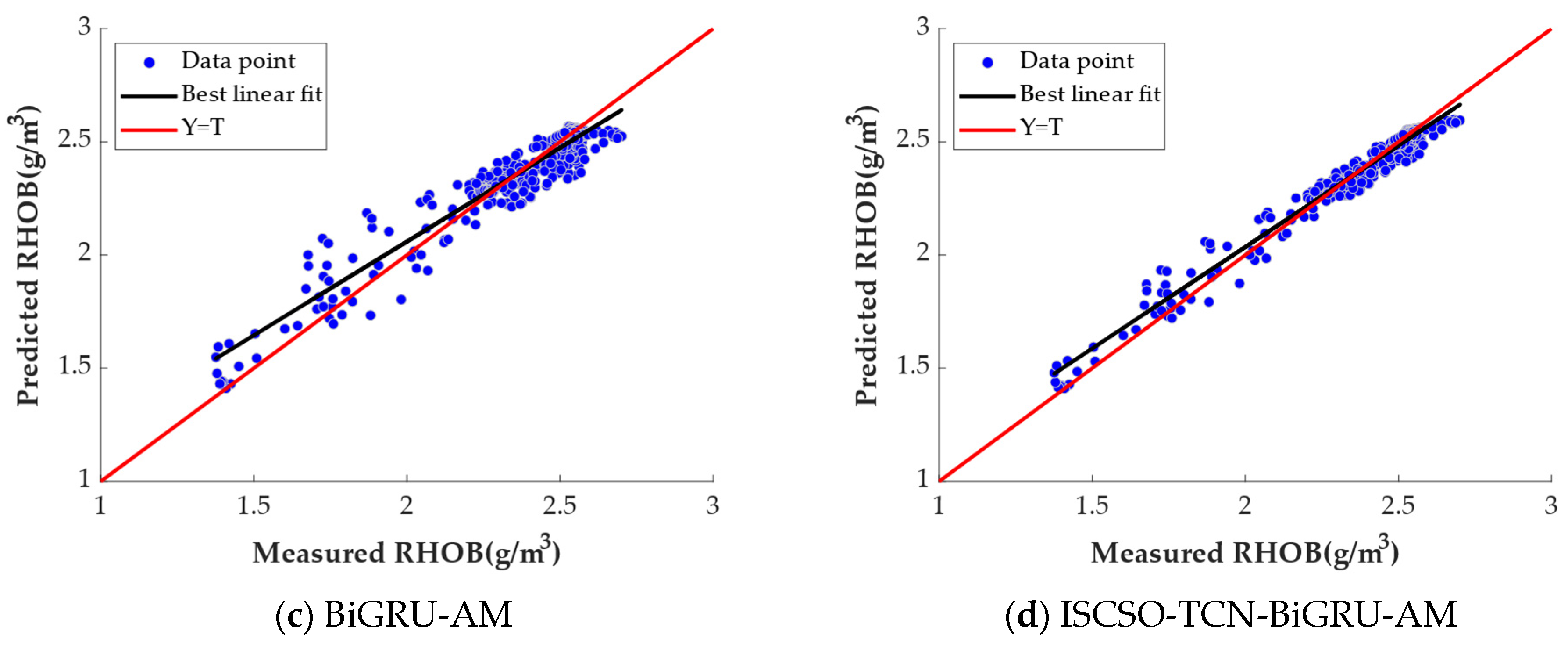
4.4. Analysis of Prediction Results
5. Conclusions
- (1)
- The ISCSO with variable spiral strategy and sparrow warning mechanism enhances population diversity, boosts the average search efficiency, and lessens the tendency to quickly settle into the local optimum during the search process.
- (2)
- The TCN-BiGRU-AM integrates the network architectures of a TCN and BiGRU-AM. This hybrid architecture can not only deal with complex time dependence but can also improve processing adaptability to the dynamic characteristics of the time series.
- (3)
- The ISCSO can enhance the prediction performance by optimizing the hyperparameters. Compared with the competing models, the ISCSO-TCN-BiGRU-AM can more effectively make an accurate prediction. It has high utilization and practical application values.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sarhan, M.A. Geophysical assessment and hydrocarbon potential of the Cenomanian Bahariya reservoir in the Abu Gharadig Field, Western Desert, Egypt. J. Pet. Explor. Prod. Technol. 2021, 11, 3963–3993. [Google Scholar] [CrossRef]
- Qiao, L.; He, N.; Cui, Y.; Zhu, J.; Xiao, K. Reservoir Porosity Prediction Based on BiLSTM-AM Optimized by Improved Pelican Optimization Algorithm. Energies 2024, 17, 1479. [Google Scholar] [CrossRef]
- Qiao, L.; Cui, Y.; Jia, Z.; Xiao, K.; Su, H. Missing Well Logs Prediction Based on Hybrid Kernel Extreme Learning Machine Optimized by Bayesian Optimization. Appl. Sci. 2022, 12, 7838. [Google Scholar] [CrossRef]
- Farouk, S.; Sen, S.; Belal, N.; Omran, M.A.; Assal, E.M.; Sarhan, M.A. Assessment of the petrophysical properties and hydrocarbon potential of the lower Miocene Nukhul formation in the Abu Rudeis-Sidri Field, Gulf of Suez Basin, Egypt. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 9, 36. [Google Scholar] [CrossRef]
- Smith, J.H. A Method for Calculating Pseudo Sonics from E-Logs in a Clastic Geologic Setting. GCAGS Trans. 2007, 57, 1–4. [Google Scholar]
- Wang, J.; Liang, L.; Qiang, D.; Tian, P.; Tan, W. Research and application of reconstructing logging curve based on multi-source regression model. Lithol. Reserv. 2016, 28, 113–120. [Google Scholar]
- Liao, H.M. Multivariate regression method for correcting the influence of expanding diameter on acoustic curve of density curve. Geophys. Geochem. Explor. 2014, 38, 174–179. [Google Scholar]
- He, X.H.; Li, K.S.; Xu, J.C.; Fu, M.Y.; Yang, Y.F.; Sun, J.Q. Application of Log Lithofacies Classification Model Based on Clustering-Support Vector Classification Method. Well Logging Technol. 2023, 47, 129–137. [Google Scholar]
- Ramachandram, D.; Taylor, G.W. Deep Multimodal Learning: A Survey on Recent Advances and Trends. IEEE Signal Process. Mag. 2017, 34, 96–108. [Google Scholar] [CrossRef]
- Rolon, L.; Mohaghegh, S.D.; Ameri, S. Using artificial neural networks to generate synthetic well logs. J. Nat. Gas Sci. Eng. 2009, 1, 118–133. [Google Scholar] [CrossRef]
- Duan, Y.X.; Xu, D.S.; Sun, Q.F.; Li, Y. Research and Application on DBN for Well Log Interpretation. J. Appl. Sci. 2018, 36, 689–697. [Google Scholar]
- Rahman, A.; Srikumar, V.; Smith, A.D. Predicting electricity consumption for commercial and residential buildings using deep recurrent neural networks. Appl. Energy 2018, 212, 372–385. [Google Scholar] [CrossRef]
- Zhang, Y.; Ai, Q.; Lin, L.; Yuan, S.; Li, Z. A very short-term load forecasting method based on deep LSTM RNN at zone leve. Power Syst. Technol. 2019, 43, 1884–1892. [Google Scholar]
- Niu, D.; Yu, M.; Sun, L.J.; Gao, T.; Wang, K.K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Yang, W.B.; Xia, K.W.; Fan, S.R. Oil Logging Reservoir Recognition Based on TCN and SA-BiLSTM Deep Learning Method. Eng. Appl. Artif. Intell. 2023, 121, 105950. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 39, 2627–2651. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Seyedali, M.; Andrew, L. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar]
- Vaferi, B.; Eslamloueyan, R.; Ayatollahi, S. Automatic recognition of oil reservoir models from well testing data by using multi-layer perceptron networks. J. Pet. Sci. Eng. 2011, 77, 254–262. [Google Scholar] [CrossRef]
- Zeng, L.; Ren, W.; Shan, L. Attention-based bidirectional gated recurrent unit neural networks for well logs prediction and lithology identification. Neurocomputing 2020, 414, 153–171. [Google Scholar] [CrossRef]
- Bensoltane, R.; Zaki, T. Combining BERT with TCN-BiGRU for enhancing Arabic aspect category detection. J. Intell. Fuzzy Syst. 2023, 44, 4123–4136. [Google Scholar] [CrossRef]


| Function | ISCSO | SCSO | DBO | SSA | WOA |
|---|---|---|---|---|---|
| F1 | 3.00 × 102 | 2.08 × 103 | 7.69 × 102 | 4.99 × 103 | 1.14 × 103 |
| (1.55 × 102) | (2.33 × 103) | (9.13 × 102) | (2.45 × 103) | (5.45 × 102) | |
| F2 | 4.12 × 102 | 4.41 × 102 | 4.34 × 102 | 4.46 × 102 | 4.64 × 102 |
| (2.10 × 101) | (3.43 × 101) | (3.43 × 101) | (3.02 × 101) | (4.45 × 101) | |
| F3 | 6.18 × 102 | 6.23 × 102 | 6.21 × 102 | 6.20 × 102 | 6.41 × 102 |
| (9.06 × 100) | (9.66 × 100) | (1.15 × 101) | (1.04 × 101) | (1.30 × 101) | |
| F4 | 8.20 × 102 | 8.27 × 102 | 8.23 × 102 | 8.48 × 102 | 8.26 × 102 |
| (7.06 × 100) | (6.78 × 100) | (5.19 × 100) | (6.6 × 100) | (9.18 × 100) | |
| F5 | 9.88 × 102 | 1.11 × 103 | 1.10 × 103 | 9.79 × 102 | 1.45 × 103 |
| (2.85 × 101) | (1.25 × 102) | (1.10 × 102) | (4.80 × 101) | (1.76 × 102) | |
| F6 | 3.15 × 103 | 4.54 × 103 | 3.02 × 103 | 5.76 × 104 | 7.70 × 103 |
| (1.56 × 103) | (2.15 × 103) | (1.82 × 103) | (3.51 × 104) | (6.59 × 103) | |
| F7 | 2.01 × 103 | 2.05 × 103 | 2.04 × 103 | 2.08 × 103 | 2.08 × 103) |
| (1.38 × 101) | (2.97 × 101) | (1.55 × 101) | (3.38 × 101) | (2.92 × 101) | |
| F8 | 2.21 × 103 | 2.23 × 103 | 2.22 × 103 | 2.26 × 103 | 2.24 × 103 |
| (3.66 × 101) | (5.90 × 100) | (8.34 × 100) | (3.27 × 101) | (1.39 × 101) | |
| F9 | 2.52 × 103 | 2.58 × 103 | 2.55 × 103 | 2.65 × 103 | 2.61 × 103 |
| (3.05 × 101) | (4.28 × 101) | (3.89 × 101) | (4.68 × 101) | (4.32 × 101) | |
| F10 | 2.51 × 103 | 2.56 × 103 | 2.56 × 103 | 2.63 × 103 | 2.59 × 103 |
| (3.09 × 101) | (6.68 × 101) | (6.33 × 101) | (4.45 × 101) | (6.86 × 101) | |
| F11 | 2.82 × 103 | 2.80 × 103 | 2.83 × 103 | 3.22 × 103 | 2.84 × 103 |
| (1.16 × 102) | (1.54 × 102) | (1.87 × 102) | (2.24 × 102) | (1.32 × 102) | |
| F12 | 2.87 × 103 | 2.87 × 103 | 2.87 × 103 | 2.88 × 103 | 2.95 × 103 |
| (7.06 × 100) | (1.69 × 101) | (8.01 × 100) | (2.06 × 101) | (8.41 × 101) |
| Function | ISCSO vs. SCSO | ISCSO vs. DBO | ISCSO vs. SSA | ISCSO vs. WOA |
|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F2 | 1.77 × 10−4 | 7.23 × 10−3 | 3.58 × 10−8 | 1.84 × 10−6 |
| F3 | 1.41 × 10−3 | 5.30 × 10−3 | 7.24 × 10−3 | 2.15 × 10−6 |
| F4 | 1.98 × 10−3 | 3.91 × 10−3 | 4.44 × 10−4 | 2.17 × 10−3 |
| F5 | 2.78 × 10−7 | 3.26 × 10−7 | 1.07 × 10−9 | 3.04 × 10−1 |
| F6 | 2.50 × 10−3 | 8.24 × 10−3 | 3.34 × 10−11 | 1.11 × 10−6 |
| F7 | 5.79 × 10−3 | 6.97 × 10−3 | 1.12 × 10−3 | 7.98 × 10−3 |
| F8 | 4.35 × 10−5 | 3.78 × 10−3 | 8.35 × 10−8 | 8.20 × 10−7 |
| F9 | 2.75 × 10−5 | 2.75 × 10−5 | 5.31 × 10−7 | 1.21 × 10−5 |
| F10 | 1.29 × 10−6 | 1.49 × 10−4 | 9.92 × 10−11 | 5.07 × 10−10 |
| F11 | 6.18 × 10−2 | 2.61 × 10−1 | 1.49 × 10−8 | 2.61 × 10−1 |
| F12 | 4.92 × 10−1 | 2.17 × 10−1 | 5.60 × 10−7 | 6.72 × 10−10 |
| Model | RMSE | MAE | Time (s) |
|---|---|---|---|
| BPNN | 0.1020 | 0.0815 | 15.6341 |
| GRU | 0.0956 | 0.0712 | 25.1322 |
| BiGRU-AM | 0.0755 | 0.0574 | 31.2581 |
| ISCSO-TCN-BiGRU-AM | 0.0614 | 0.0457 | 42.2412 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Teng, H.; Qiao, L.; Yu, H.; Cui, Y.; Xiao, K. Well Logging Reconstruction Based on a Temporal Convolutional Network and Bidirectional Gated Recurrent Unit Network with Attention Mechanism Optimized by Improved Sand Cat Swarm Optimization. Energies 2024, 17, 2710. https://doi.org/10.3390/en17112710
Wang G, Teng H, Qiao L, Yu H, Cui Y, Xiao K. Well Logging Reconstruction Based on a Temporal Convolutional Network and Bidirectional Gated Recurrent Unit Network with Attention Mechanism Optimized by Improved Sand Cat Swarm Optimization. Energies. 2024; 17(11):2710. https://doi.org/10.3390/en17112710
Chicago/Turabian StyleWang, Guanqun, Haibo Teng, Lei Qiao, Hongtao Yu, You Cui, and Kun Xiao. 2024. "Well Logging Reconstruction Based on a Temporal Convolutional Network and Bidirectional Gated Recurrent Unit Network with Attention Mechanism Optimized by Improved Sand Cat Swarm Optimization" Energies 17, no. 11: 2710. https://doi.org/10.3390/en17112710
APA StyleWang, G., Teng, H., Qiao, L., Yu, H., Cui, Y., & Xiao, K. (2024). Well Logging Reconstruction Based on a Temporal Convolutional Network and Bidirectional Gated Recurrent Unit Network with Attention Mechanism Optimized by Improved Sand Cat Swarm Optimization. Energies, 17(11), 2710. https://doi.org/10.3390/en17112710





