Comparative Analysis of Deep Learning Methods for Fault Avoidance and Predicting Demand in Electrical Distribution

Abstract

In recent years, the distribution network in Chile has undergone various modifications to meet new demands and integrate new technologies. However, these improvements often do not last as long as expected due to inaccurate forecasting, resulting in frequent equipment changes and service interruptions. These issues affect project investment, unsold energy, and penalties for poor quality of supply. Understanding the electricity market, especially in distribution, is crucial and requires linking technical quality standards with service quality factors, such as the frequency and duration of interruptions, to understand their impact on regulated distribution to customers. In this context, a comparative study will be carried out between Long Short-Term Memory (LSTM) and transformer architectures, with the aim of improving the sizing of distribution transformers and preventing failures when determining the nominal power of the transformer to be installed. Variables such as voltages and operating currents of transformers installed between 2020 and 2021 in the Valparaíso region, Chile, along with the type and number of connected customers, maximum and minimum temperatures of the sectors of interest, and seasonality considerations will be used. The compilation of previous studies and the identification of key variables will help to propose solutions based on error percentages to optimise the accuracy of transformer sizing.

1. Introduction

Efficient sizing of electrical distribution transformers is a critical element of the electrical infrastructure as it directly affects the stability, reliability, and quality of the power supply. The ability to accurately predict power demand and size transformers accordingly is essential to avoid service interruptions, optimise network performance, and reduce operating and maintenance costs [1,2,3].

In this context, various techniques and approaches have emerged to improve accuracy in transformer sizing, particularly in the use of tools based on artificial intelligence and machine learning [4]. Two of the most prominent architectures in this field are Long Short-Term Memory (LSTM) neural networks and transformer models.

LSTM neural networks have excelled in capturing temporal dependencies in data sequences, which is especially relevant in applications where behaviour over time is crucial [5]. On the other hand, transformer models, driven by attention mechanisms, have demonstrated excellent results in natural language processing tasks and have also been successfully applied to sequential problems in other domains [6,7,8,9].

This article focuses on comparing and analysing the performance of these two techniques, LSTM and transformers, specifically applied to the sizing of electrical distribution transformers. The selection of these techniques is based on their demonstrated ability to capture complex patterns in sequential data and their potential to effectively model the dynamic behaviour of transformers in real-world settings [10,11,12,13].

Moreover, the scalability of these models is a crucial aspect of their practical implementation. These techniques can be adapted to various scales of power prediction, ranging from household consumption to the sizing of distribution elements, and even to the generation of energy. This adaptability allows for a comprehensive approach to transformer sizing, addressing both small-scale and large-scale power demands. By extending the application of these models to include scenarios like power generation from electric generators and considering additional factors such as water demand, the complexity and robustness of the predictive models are further enhanced [14,15,16].

Working with real world data is crucial as it ensures that the models are tested and validated under realistic conditions, enhancing their reliability and applicability in practical scenarios, as in [17,18] where they use real data from electric vehicles to evaluate the future scenario.

The main contributions of this study can be summarised as follows:

• The study demonstrates the potential of deep learning models to accurately predict electricity consumption. The work includes an analysis of the use of two different methods and the considerations that need to be taken into account when applying deep learning techniques in the context of a real operating environment. The use of such techniques could help electrical distribution companies to improve the estimation of the required capacity of electrical transformers.
• Insights generated into the effectiveness and suitability of LSTM and transformer techniques in sizing electrical distribution transformers. The study aims to delineate the strengths and limitations of each technique.
• This work uses real data from electrical distribution transformers, encompassing variables like voltages, operating currents, connected customer types and quantities, and ambient temperatures, among others. This data was collected from transformers installed between 2020 and 2021 in the Valparaíso region, Chile. The incorporation of real data strengthens the validity and relevance of the results obtained, facilitating a precise evaluation of the compared techniques’ performance in an operational real-world setting.

The article is structured as follows: Section 2 provides a comprehensive review of the literature related to transformer sizing and the use of machine learning techniques in this context. Section 3 describes in detail the methodology used, including the configuration of LSTM and transformer models. In Section 4, data processing is extensively addressed, delving into the details of how to manage and prepare the data for analysis. Section 5 presents the results of the comparison between LSTM and transformer techniques, including performance metrics and qualitative analysis. Finally, Section 6 presents the conclusions of the study, discusses the implications of the results, and suggests areas for future research and practical applications in the electrical distribution domain.

2. Related Works

Between 2017 and 2019, distributors in the region faced a number of significant challenges according to data collected in the novelty book [19]. In 2017, there was a notable frequency of failures primarily caused by tree-related problems, totalling 1177 incidents, followed by self-produced failures at 1092 and maintenance at 1013. Accidents ranked fourth with 907 cases, followed by overloads at 587. In the following year, 2018, there was a decrease in the overall frequency of failures, although tree-related failures remained the main cause with 1019 cases, followed by maintenance at 976 and accidents at 873. However, overloads experienced a notable increase, with 727 cases recorded. Lastly, in 2019, the data showed a general decrease in the frequency of failures, highlighting maintenance as the main cause with 648 cases, followed by accidents at 498 and self-produced failures at 481. These findings can largely be attributed to the durability of transformers and issues related to their sizing. The decrease in failure frequency over these years suggests an improvement in the management and maintenance of this critical equipment. However, the observed increase in overloads between 2017 and 2018 indicates the need to review load and discharge protocols as well as preventive maintenance practices to mitigate such problems in the future. Overall, these data underscore the importance of a comprehensive approach to managing electrical assets to ensure a reliable and safe supply of electrical power.

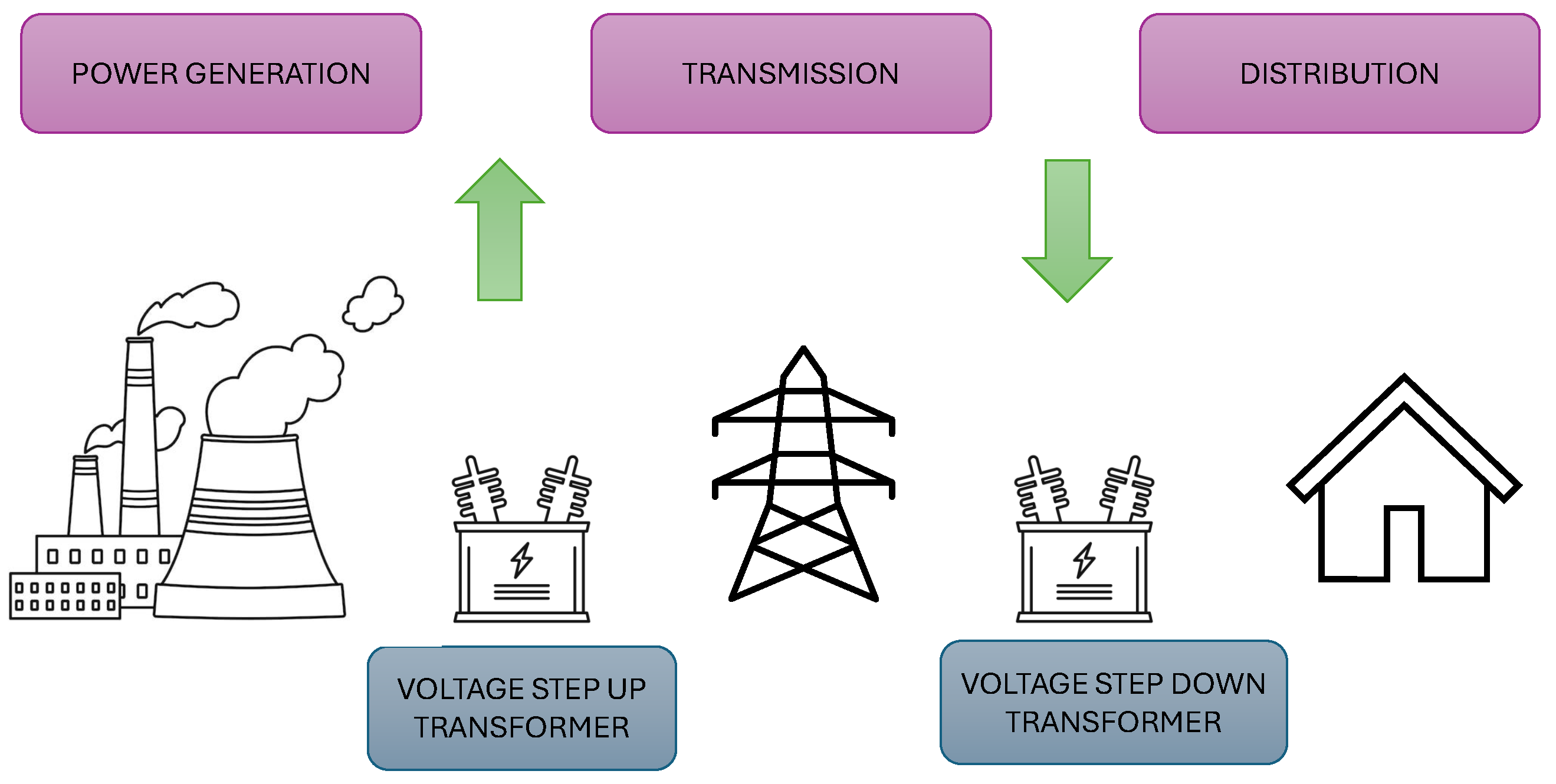
In Figure 1, it is possible to appreciate the power system, where if the voltage-reducing transformer experiences any complications, it produces immediate effects on the service quality for both residential and industrial customers.

Various techniques have been used to estimate the value of transformers, such as in the year 2018 [20], where a statistical power estimation model based on linear regression was implemented. Subsequently, another technique used in 2019 [21] involved generating a model based on the analysis of power response from different modules to the climatic behaviour of an area over a year. In 2020, a forecast model based on Monte Carlo simulation was used [22]. These mentioned models allowed for obtaining a power estimation that yielded better results than those obtained by the distributor, considering the factor mechanism used for sizing.

The accurate estimation of electrical consumption is crucial for efficient energy management and decision-making in the electrical sector. Time series analysis, which involves studying electrical data over time, is a fundamental tool for understanding variability and trends in electrical energy consumption. In [23,24], a detailed overview of modern techniques for time series analysis is presented, including advanced modelling and forecasting approaches that are essential for understanding and predicting electrical consumption behaviour over time.

The use of neural networks, particularly Long Short-Term Memory (LSTM) networks and transformer models, has emerged as an effective strategy in electrical consumption estimation. In [25], the effectiveness of LSTMs in capturing complex temporal patterns in electrical data is highlighted. Additionally, transformer models have shown great potential in sequence processing, as discussed in [26], making them valuable tools for accurate electrical consumption prediction and energy management optimization.

Although in this study, the historical data may be synthetic and not derived from real records, the use of synthetic data remains relevant for evaluating and comparing the performance of different electrical consumption estimation techniques. In [27], the importance of synthetic data in evaluating machine learning models is discussed, especially when real data may be limited or unavailable.

The application of machine learning techniques, such as LSTMs and transformers, in electrical consumption estimation represents a significant advancement in energy management optimization and informed decision-making. These techniques offer greater adaptability to the complexity and variability of electrical data, resulting in more precise estimation and overall improvement in energy efficiency and strategic resource planning.

3. Neural Networks

In the field of electrical distribution transformer sizing, the use of neural networks, especially Long Short-Term Memory (LSTM) networks and transformer models, has gained prominence due to their ability to capture complex patterns in sequential data and adapt to temporal changes. Below, we delve deeper into the role and functioning of these neural networks in accurately estimating electrical consumption and optimizing transformer sizing.

3.1. LSTM

Neural networks are a set of algorithms inspired by the functioning of the human brain, designed to recognize patterns in data and perform machine learning tasks. These networks are composed of basic units called artificial neurons that are interconnected in layers. Each neuron takes inputs, performs weighted calculations, and produces an output that is transmitted to the subsequent layers. As neural networks are trained with data, they adjust their weights and connections to learn and improve their ability to perform specific tasks such as classification, pattern recognition, or content generation [28].

Within neural networks, there are various types, and one of the most commonly used is Recurrent Neural Networks (RNNs). RNNs are well suited for handling sequences of data, as they allow information to flow through neurons in loops, giving them a kind of short-term memory. However, traditional RNNs struggle to maintain long-term information due to the vanishing gradient problem.

To address this problem, Long Short-Term Memory (LSTM) neural networks were developed. LSTMs are a variant of RNNs that include specialized memory units, allowing the network to learn and retain long-term information. Each LSTM unit has three gates (input, output, and forget) that regulate the flow of information, giving them the ability to remember and process sequences more effectively. LSTMs are widely used in tasks such as natural language processing, automatic translation, and text generation, where a deep contextual understanding of data sequences is required. In summary, LSTM neural networks are a powerful extension of recurrent neural networks that have revolutionized machines’ ability to effectively understand and generate sequential data [29].

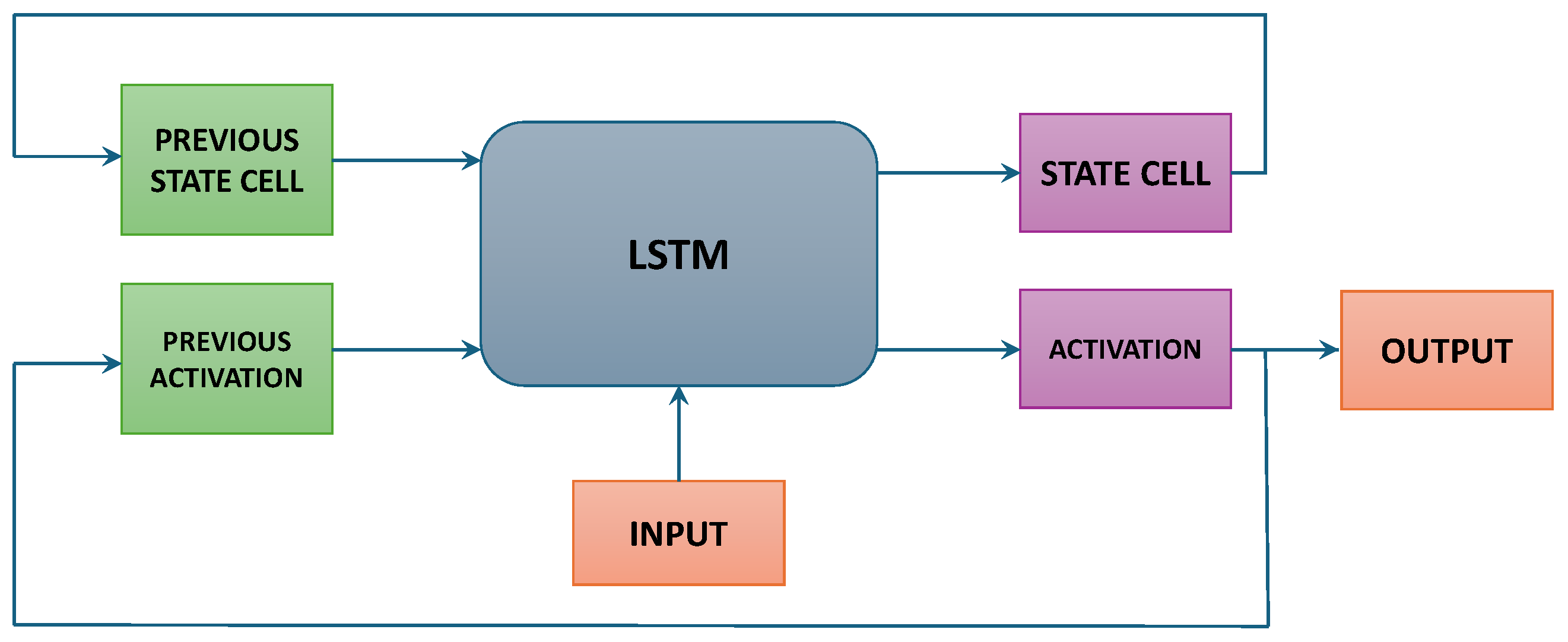
In a Long Short-Term Memory (LSTM) neuron, the fundamental structure consists of a memory unit that enables the retention of long-term information, setting it apart from neurons in traditional Recurrent Neural Networks (RNNs). Each LSTM unit has three main gates: the input gate, the output gate, and the forget gate, as visualized in Figure 2. These gates are essential for regulating the flow of information within the neuron. The input gate controls how much new information should be stored in the cell’s memory, the output gate regulates how much information is sent as the neuron’s output, and the forget gate determines how much prior information should be deleted or “forgotten” from the memory. This gate and internal memory structure allows LSTMs to learn and retain relevant information across temporal sequences, making them particularly suitable for tasks involving long-term dependencies in sequential data, such as natural language processing or speech recognition.

LSTM (Long Short-Term Memory) networks are equipped with specialized units called cells that enable them to capture and remember long-term dependencies in sequential data. One of the key equations in the LSTM cell is the update equation for the cell state ($c_t$) at time step (t), which is given by [30]:

$$c_t=f_t·c_{t-1}+i_t·{\tilde{c}}_t,$$

(1)

where:

• $c_t$ is the cell state at the time step (t);
• $f_t$ is the forget gate at time step (t), which determines how much of the previous state ($c_{t-1}$) to forget;
• $i_t$ is the input gate at time step (t), which determines how much of the new candidate state ${\tilde{c}}_t$ to incorporate into the current cell state;
• ${\tilde{c}}_t$ is the new candidate state at time step (t), which is calculated using the tanh activation function and input values at that moment.

This equation illustrates the core of the long-term memory and information control process in an LSTM cell, making it an excellent choice for explaining the operation of these models.

3.2. Transformers

Transformers are a type of neural network architecture that has gained significant traction in the field of natural language processing and sequence modelling [31,32]. Unlike traditional recurrent neural networks (RNNs) and their variants like LSTM, which process sequences in a sequential manner, transformers operate using an attention mechanism that allows them to consider relationships between all elements in a sequence simultaneously, as visualized in Figure 3. This attention mechanism enables transformers to capture long-range dependencies and contextual information effectively, making them highly suitable for tasks requiring a deep understanding of sequential data, such as language translation, text generation, and sentiment analysis [33,34].

At the core of transformers are self-attention layers, which allow the network to weigh the importance of each element in the input sequence when generating an output. This mechanism enables transformers to process inputs in parallel, significantly improving their efficiency compared to traditional sequential processing in RNNs. Additionally, transformers incorporate positional encoding to retain information about the order of elements in the input sequence, addressing one of the limitations of traditional attention mechanisms.

One of the key innovations introduced by transformers is the transformer architecture, which consists of encoder and decoder layers. The encoder processes the input sequence and generates a representation that captures the contextual information, while the decoder uses this representation to generate the output sequence. This modular architecture, along with the attention mechanism, allows transformers to achieve state-of-the-art performance in various natural language processing tasks, surpassing previous limitations in handling long-range dependencies and contextual information in sequential data.

Transformers are a type of neural network architecture that has gained prominence in natural language processing and sequence modelling tasks. Unlike traditional recurrent neural networks (RNNs) and their variants like LSTMs, which process sequences sequentially, transformers operate using a mechanism called attention that allows them to consider relationships between all elements of a sequence simultaneously.

One of the key components of a transformer model is the multi-head attention mechanism, which is used to compute attention scores between input tokens. The simplified equation for multi-head attention can be expressed as [35]:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V,$$

(2)

where:

• Q is the query matrix;
• K is the key matrix;
• V is the value matrix;
• $d_k$ is the dimension of the key vectors.

This equation illustrates how attention scores are calculated by taking the dot product of the query and key matrices, followed by applying the softmax function to obtain attention weights, and finally multiplying by the value matrix to obtain the weighted sum of values.

The multi-head attention mechanism in transformers allows them to capture long-range dependencies and contextual information effectively, making them suitable for tasks that require a deep understanding of sequential data.

4. Data Processing

In this section, the data were derived from equipment located at Valparaíso between July 2020 and June 2021, with a temporal resolution of 10 min. The variables considered in this study are the following: operational voltage and current, customer type, customer count, customer consumption, daily variability, and maximum and minimum temperatures in the location areas.

To ensure confidentiality, the data has been normalized on a scale from 0 to 1. This means that real values have been transformed to preserve the privacy of the original data.

Atmospheric information from the Agrometeorology Service [36] was used to complement the transformer operation data. It is important to note that, to simplify the presentation and analysis, 20 transformers were selected in a representative manner from the total sample.

One of the challenges encountered when working with this real data was the presence of gaps in the measurements. These gaps were addressed using interpolation techniques. Interpolation is a mathematical technique used to estimate values within a range of known data points. For this study, linear interpolation was applied, which is a simple and commonly used method. The formula for linear interpolation is as follows [37,38]:

$$y=y_1+\frac{(x-x_1)·(y_2-y_1)}{(x_2-x_1)},$$

(3)

where:

• x is the value for which interpolation is desired;
• $x_1$ and $x_2$ are the known data points on either side of x;
• $y_1$ and $y_2$ are the values corresponding to $x_1$ and $x_2$, respectively;
• y is the estimated value at x.

Although linear interpolation provides a basic estimation, it is acknowledged that more sophisticated techniques such as Markov processes can offer more accurate results by considering dependencies and sequential patterns in the data.

For better understanding,

Table 1. Example of normalized data from selected transformers.

ID	V (Normalized)	I (Normalized)	Customer Consumption	T (°C)	…
T1	0.75	0.68	120 kWh	20	…
…	…	…	…	…	…
T20	0.70	0.55	110 kWh	21	…

presents a sample of the normalized data from the selected transformers. This table provides an overview of the data used in the study, highlighting the normalization of values and relevant information for each selected transformer.

The properties of the computer where the training and subsequent testing of both techniques will be carried out are specified in

Table 2. Computer Specifications.

Component	Specifications
CPU	Intel(R) Xeon(R) CPU @ 2.30 GHz
	Cores: 1 per processor, 2 in total
	Cache Memory: 46,080 KB
	Architecture: 46 bits physical, 48 bits virtual
RAM	Capacity: 13.6 GB
GPU	Model: Tesla T4
	Memory: 15,360 MiB
	CUDA Driver: Version 12.2

.

5. Result and Analysis

For this study, data from 111 distribution transformers located in the Valparaíso region between the years 2020 and 2021 were utilized. However, for this work, the results of 20 randomly selected transformers will be presented. The focus of this analysis is on predicting the nominal power of these transformers based on real data collected between July 2020 and June 2021 at 10-min intervals. This dataset includes a range of parameters, specifically operational voltage and current, types of customers, customer count, consumption patterns, daily fluctuations, as well as the maximum and minimum temperatures in the region.

5.1. LSTM

The model uses a recurrent neural network (LSTM) to process data sequences, such as time series. The LSTM layer with 100 units and ‘ReLU’ activation allows capturing patterns over time and handling long-term dependencies in the data. After the LSTM layer, dense layers are applied for prediction. The model is trained using the RMSprop optimizer in Python [39], which evaluates its performance with metrics such as mean squared error (MSE). In summary, the LSTM model learns complex temporal relationships to predict future steps in time series data. The parameters of the model are found in

Table 3. Parameters of the LSTM model.

Parameter	Value
input_shape	(12, 8)
output_dim	1
activation function	ReLU
optimizer	RMSprop
loss function	MSE
metrics	MSE, MAE
batch_size	72
epochs	1000

.

The analysis of the training results in

Table 4. Twenty Training Results with LSTM.

ID	Time (s)	Train RMSE	Val RMSE	Test RMSE
1	399.58	0.0718	1.0155	0.6224
2	398.72	0.0728	0.8266	0.4336
3	395.44	0.0735	0.8464	0.4517
4	274.65	0.0748	0.8236	0.4437
5	391.44	0.0739	0.8334	0.4535
6	391.89	0.0742	0.8293	0.4418
7	390.58	0.0746	0.8268	0.4440
8	396.89	0.0842	0.8399	0.4479
9	392.27	0.1310	0.8283	0.4537
10	391.48	0.0793	0.8321	0.4436
11	394.01	0.1506	0.8198	0.4548
12	397.98	0.0857	0.8291	0.4680
13	396.87	0.0779	0.8780	0.4734
14	393.84	0.0747	0.8163	0.4386
15	400.09	0.0738	0.8307	0.4560
16	398.10	0.0742	0.8553	0.4572
20	397.57	0.0767	0.8189	0.4438
21	397.40	0.0785	0.8357	0.4563
22	396.35	0.0810	0.9594	0.5207
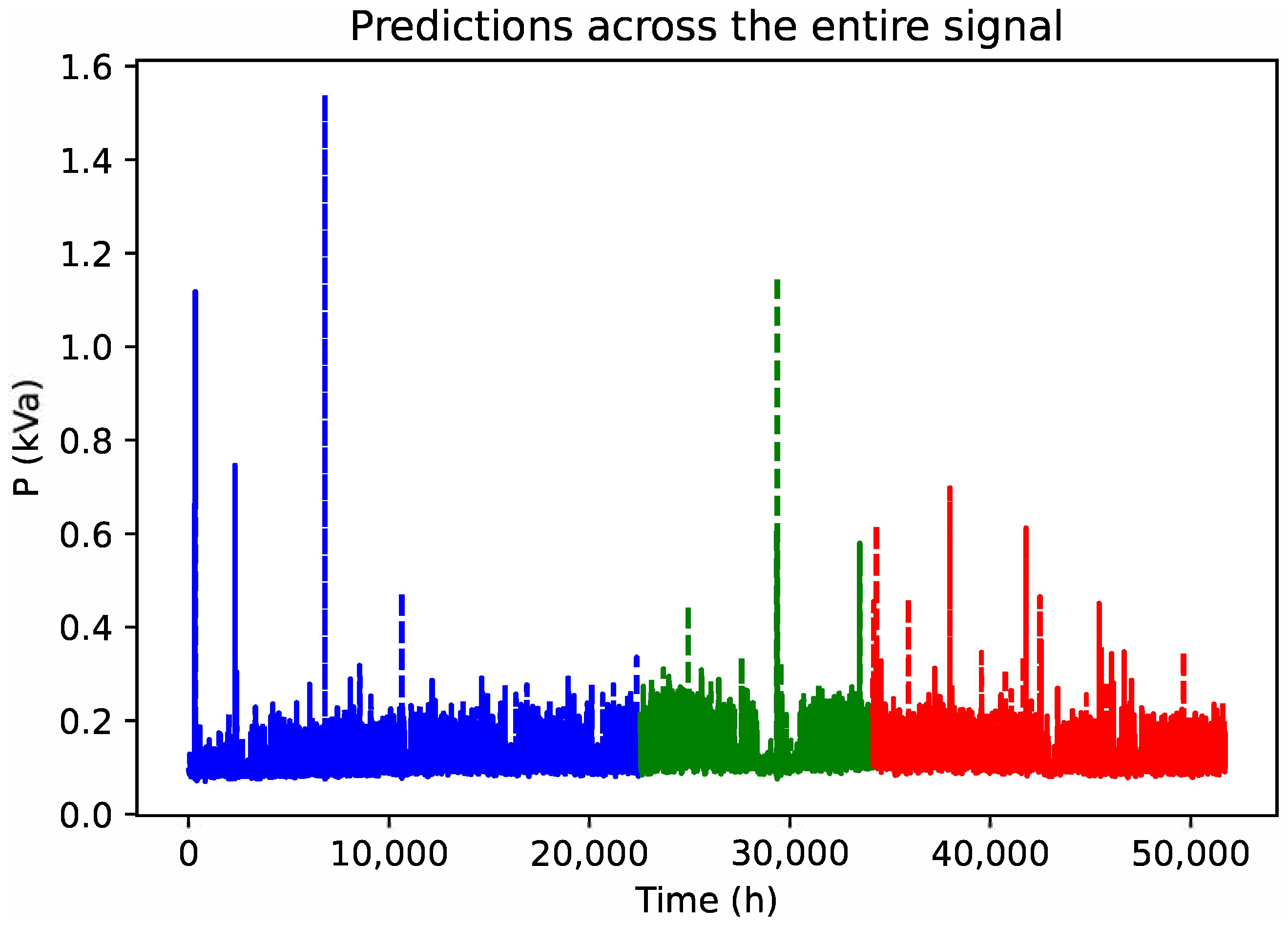
23	396.11	0.0768	0.8447	0.4418

reveals that the recurrent neural network (LSTM) model demonstrates strong performance on the training set with low RMSE values. However, concerns arise regarding its generalization ability, as the metrics on the validation and test sets are significantly higher, as shown in Figure 4. This suggests the presence of potential overfitting, especially given that the standard deviations for these metrics are also higher in the validation and test sets compared to the training set. The model architecture, comprising an LSTM layer followed by dense layers, appears to lack regularization techniques such as Dropout, which could contribute to this disparity among the data sets. Additionally, the use of the MSE metrics during training provides detailed insight into the model’s learning process. In summary, it is recommended to explore additional strategies, such as incorporating regularization and adjusting the model architecture, to enhance its generalization capability and mitigate the observed potential overfitting in the validation and test data.

5.2. Transformers

This model is a transformer in Python [39] that uses multi-head attention and convolutions to learn patterns in input sequences of 12 steps with 8 features each. Each layer of the model comprises a multi-head attention followed by a convolution layer and normalization, allowing the model to capture complex relationships in the data. After several layers, a Global Average Pooling layer is used to obtain an aggregated representation of the sequence, followed by dense layers with ReLU activations and a linear output layer for regression. The model is trained using the Adam optimizer and MSE loss function with the option to save the model for later use. The parameters of the model are found in

Table 5. Parameters of the Transformers Model.

Parameter	Value
input_shape	(12, 8)
d_model	1
nhead	4
num_layers	4
ff_dim	4
Optimizer	Adam
Learning_rate	0.001
Loss	MSE
Epochs	10
Batch_size	72
Validation_split	0.33

.

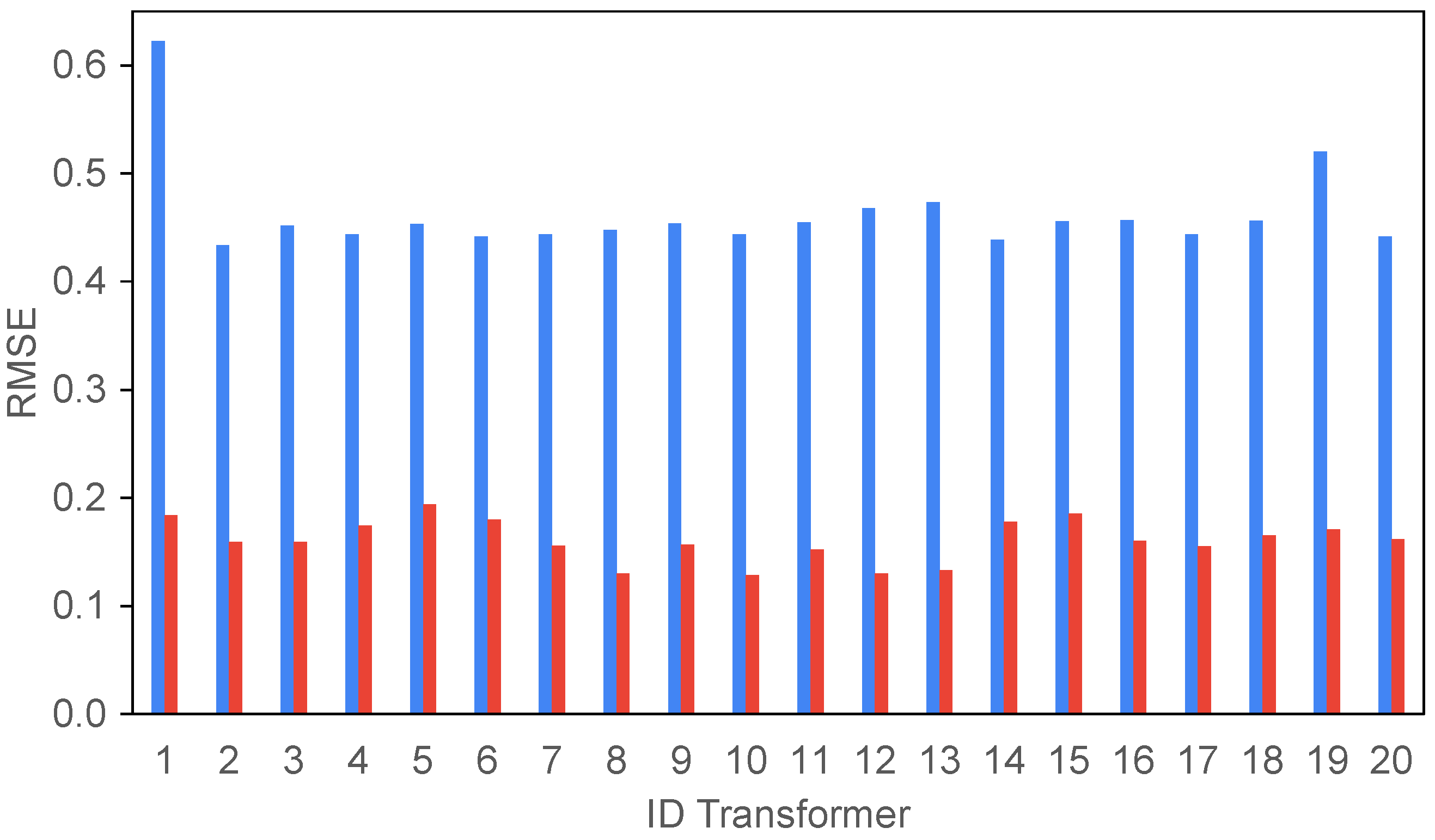
The analysis of the results in this table showcases the model’s performance across three datasets in

Table 6. Twenty Training Results with Transformers.

ID	Time (s)	Train RMSE	Val RMSE	Test RMSE
1	27.20	0.2118	0.2202	0.1840
2	21.55	0.2177	0.2071	0.1589
3	26.40	0.2179	0.2072	0.1592
4	21.02	0.2350	0.2161	0.1745
5	21.07	0.2166	0.2457	0.1942
6	21.07	0.2382	0.2187	0.1799
7	20.07	0.1979	0.1826	0.1555
8	25.92	0.1863	0.1736	0.1300
9	22.59	0.1991	0.2155	0.1569
10	26.01	0.1848	0.1740	0.1284
11	21.35	0.1993	0.2102	0.1523
12	26.62	0.1863	0.1755	0.1298
13	21.29	0.1886	0.1810	0.1332
14	22.20	0.2074	0.2356	0.1776
15	26.97	0.2116	0.2424	0.1855
16	21.98	0.1988	0.2046	0.1602
20	23.00	0.2124	0.2059	0.1550
21	18.87	0.2244	0.2116	0.1654
22	21.93	0.2313	0.2137	0.1709
23	26.13	0.2158	0.1962	0.1617

for different transformers identified by their ID. The metrics used to evaluate the model’s performance are root mean squared error (RMSE).

We observe significant variations in RMSE values among different transformers. For instance, the transformer with ID 1 has an RMSE of 0.2118 in the training set, while the transformer with ID 10 has an RMSE of 0.1848 in the same set. This indicates that the model’s performance varies depending on the specific transformer. It can be inferred that if the metrics are consistent across all three sets, it suggests good generalization capability, as shown in Figure 5.

Finally, the analysis conducted in the previous LSTM table and the current transformer table reveals some key differences in the performance and generalization of the models.

In the LSTM table, it can be observed that the model exhibits solid performance on the training set with low RMSE values. However, the metrics on the validation and test sets are higher, indicating possible errors, which are visualized in Figure 4. This is further verified by the higher standard deviations in the validation and test sets compared to the training set.

On the other hand, in the transformer table, we see that the RMSE metrics vary considerably among different transformers. This suggests that the model’s performance varies depending on the specific transformer. Additionally, comparing the training, validation, and test metrics provides insights into the model’s generalization capability.

The analysis of RMSE test values in the two techniques reveals a significant difference: when using transformers, errors remain below 0.2, as opposed to LSTM, where they can easily exceed 0.4. These findings suggest that the choice of technique can substantially influence accuracy, with a potential $50\%$ reduction in RMSE by changing the technique, as illustrated in Figure 6.

6. Conclusions

In summary, this study reveals that the LSTM model performs well on the training set but faces challenges in generalization on the validation and test sets, suggesting possible overfitting issues. On the other hand, the transformer model shows significant variability in its performance depending on the specific transformer used, implying a differential adaptability of the model to different contexts. A key contribution of this work lies in comparing these two models in a specific prediction context, providing valuable insights into their strengths and weaknesses. Additionally, it is important to note that this study was conducted using real transformer distribution data, adding relevance and practical applicability to the obtained results.

The analysis of RMSE values in the test set for both techniques reveals a significant difference when using transformers. These findings suggest that the choice of technique can substantially influence accuracy, with a potential $50\%$ reduction in RMSE by changing the technique. For future work, exploring regularization strategies to improve the generalization of both models and delving into the transformer model’s adaptability to different data configurations is recommended.

This work demonstrates the potential of deep learning models to accurately predict electricity consumption in the context of a real operating environment. The use of such techniques could help electrical distribution companies improve the estimation of the required capacity of electrical transformers. Additionally, it is crucial to consider electromobility and net billing in future work due to their significant impact on power consumption in distribution transformers.