The Impact of Energy Efficiency on Economic Growth: Application of the MARCO Model to the Portuguese Economy 1960–2014
Abstract
1. Introduction
2. Background and Motivation
2.1. Neoclassical Growth Theory—Ignoring the Role of Efficient Energy Use
2.2. Ecological Economics—Energy’s Potential to Perform Work as a Driver of Growth
2.3. Energy–Economy Models at the Macro Level and Their Limitations
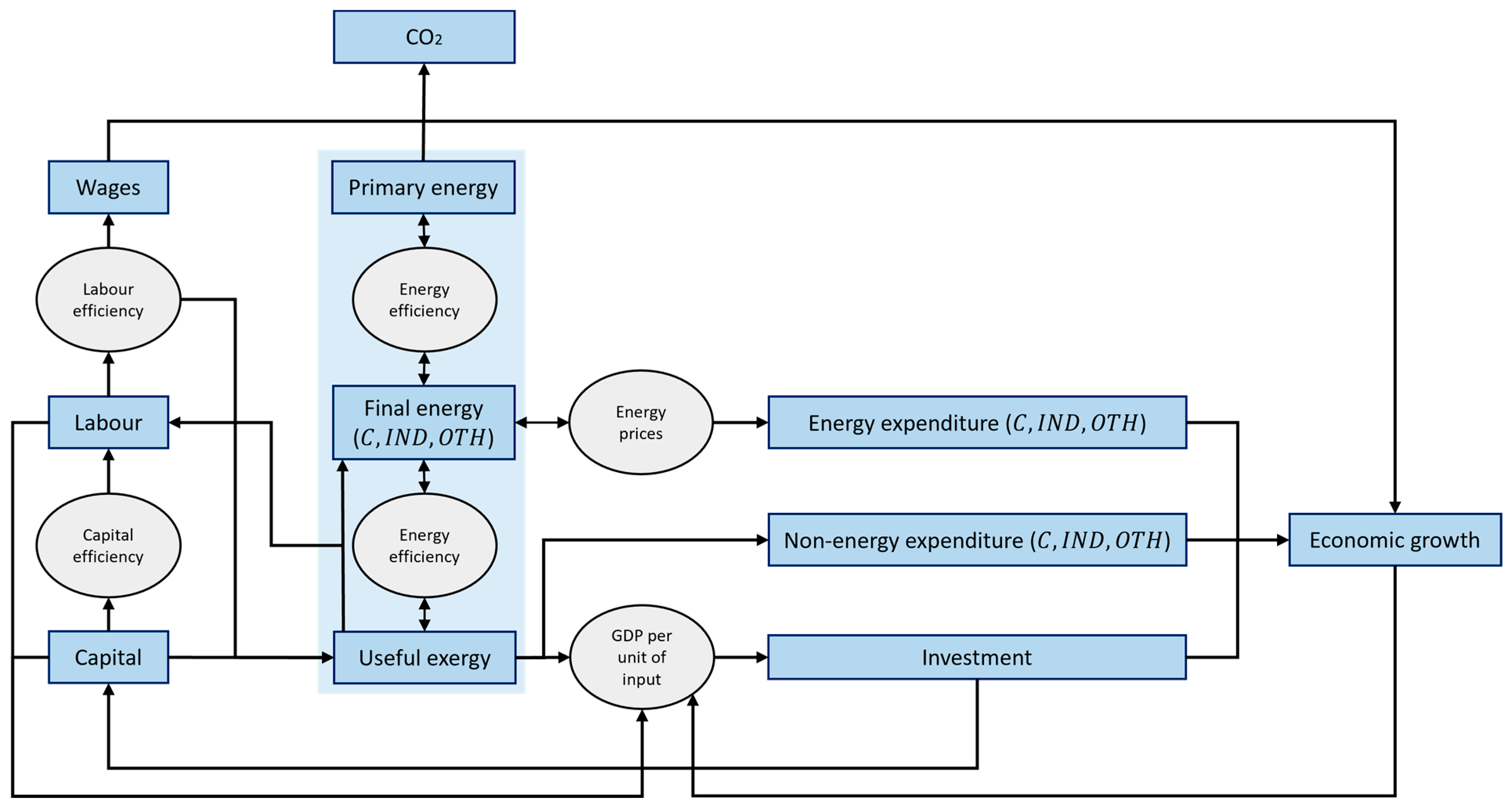
2.4. The Thermodynamically Consistent MARCO Model
3. Materials and Methods
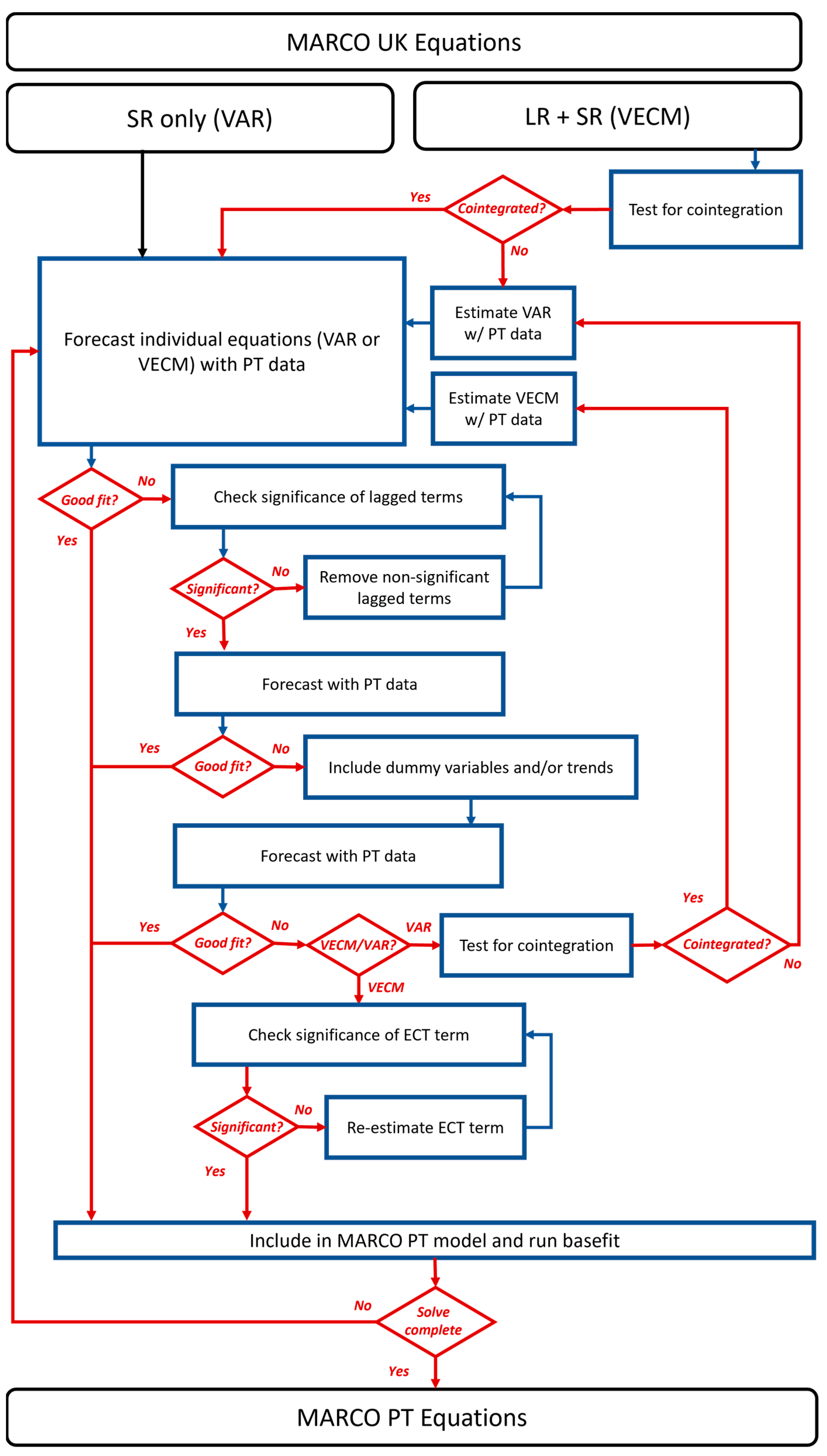
3.1. Model Equations
3.2. Data
3.3. Basefit Model and Validation
3.4. Counterfactual Simulations and Output Elasticities
- Thermodynamic final-to-useful aggregate exergy efficiency ().
- Total final energy use (sum of households , industry , and other ).
- Investment expenditure ().
- Labor supply (in number of employees ).
- Energy prices (paid by households , industry , and others ).
- Total useful exergy ().
4. Results and Discussion
4.1. Econometric Test Results
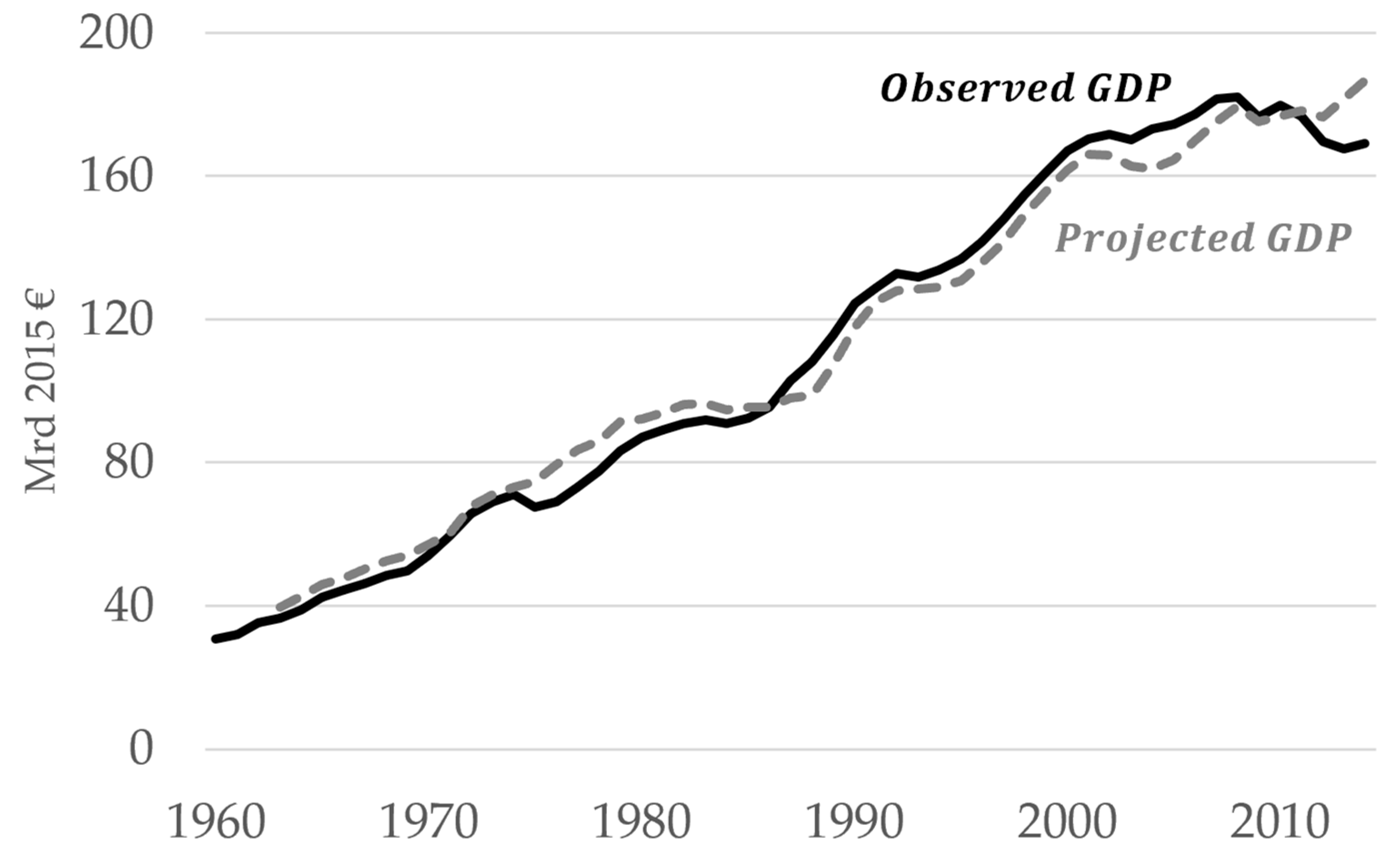
4.2. Basefit Solution
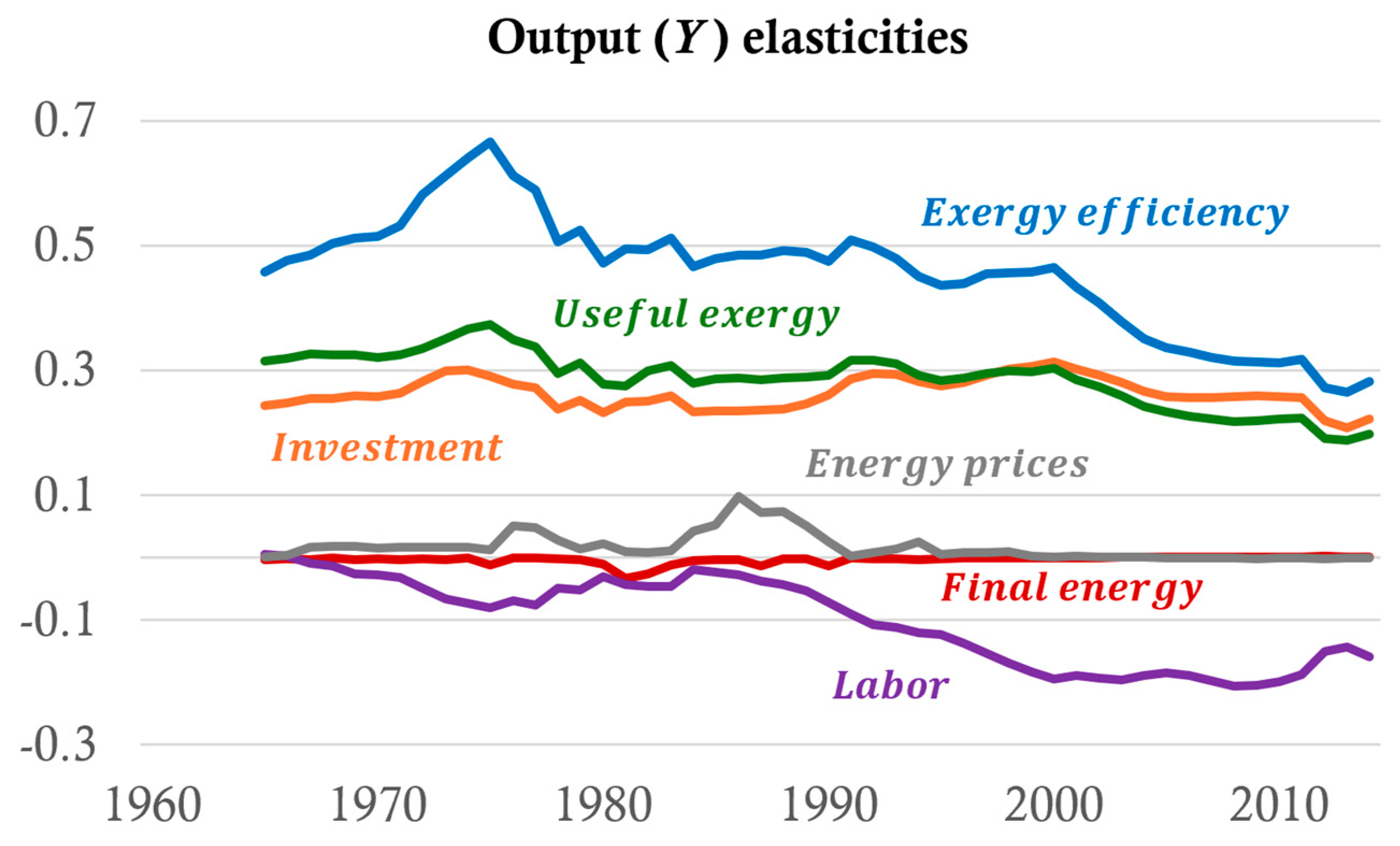
4.3. Simulation Results and Output Elasticities
4.3.1. The Historical Impact of Energy Efficiency
4.3.2. Divergent Influences of Capital and Labor
4.4. Insights into the Role of Efficiency Energy Use on Economic Growth
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Capturing the Multiple Benefits of Energy Efficiency; IEA: Paris, France, 2015; Available online: https://www.iea.org/reports/capturing-the-multiple-benefits-of-energy-efficiency (accessed on 14 September 2023).
- Dean, E.; Harper, M. The BLS productivity measurement program. In New Developments in Productivity Analysis; University of Chicago Press: Chicago, IL, USA, 2001; pp. 55–84. [Google Scholar]
- Feenstra, R.C.; Inklaar, R.; Timmer, M.P. The Next Generation of the Penn World Table. Am. Econ. Rev. 2015, 105, 3150–3182. [Google Scholar] [CrossRef]
- Schreyer, P.; Pilat, D. Measuring productivity. OECD Econ. Stud. 2001, 33, 127–170. [Google Scholar]
- Timmer, M.P.; O’Mahony, M.; Van Ark, B. EU KLEMS growth and productivity accounts: An overview. Int. Product. Monit. 2007, 14, 74–85. [Google Scholar] [CrossRef]
- Easterly, W.; Levine, R. What have we learned from a decade of empirical research on growth? It’s Not Factor Accumulation: Stylized Facts and Growth Models. World Bank Econ. Rev. 2001, 15, 177–219. [Google Scholar] [CrossRef]
- Acs, Z.J.; Estrin, S.; Mickiewicz, T.; Szerb, L. The Continued Search for the Solow Residual: The Role of National Entrepreneurial Ecosystem (No. 8652). IZA Discussion Papers. 2014. Available online: https://www.iza.org/publications/dp/8652/the-continued-search-for-the-solow-residual-the-role-of-national-entrepreneurial-ecosystem (accessed on 17 April 2023).
- Solow, R.M. Technical progress, capital formation, and economic growth. Am. Econ. Rev. 1962, 52, 76–86. [Google Scholar]
- Denison, E.F. Education, economic growth, and gaps in information. J. Political Econ. 1962, 70, 124–128. [Google Scholar] [CrossRef]
- Denison, E.F. Sources of postwar growth in nine western countries. Am. Econ. Rev. 1967, 57, 325–332. [Google Scholar]
- Jorgenson, D.W.; Griliches, Z. The explanation of productivity change. Rev. Econ. Stud. 1967, 34, 249–283. [Google Scholar] [CrossRef]
- Acemoglu, D.; Dell, M. Productivity differences between and within countries. Am. Econ. J. Macroecon. 2010, 2, 169–188. [Google Scholar] [CrossRef]
- Oulton, N. The Mystery of TFP; CFM Discussion Paper Series (CFM-DP2017-06); Centre For Macroeconomics: London, UK, 2016; p. 31. [Google Scholar]
- O’Mahony, M.; Castaldi, C.; Los, B.; Bartelsman, E.; Maimaiti, Y.; Peng, F. EUKLEMS-Linked Data: Sources and Methods; University of Birmingham: Birmingham, UK, 2008. [Google Scholar]
- Koszerek, D.; Havik, K.; Mc Morrow, K.; Röger, W.; Schönborn, F. An Overview of the EU KLEMS Growth and Productivity Accounts. European Economy-Economic Papers 2008–2015 Number 290. 2007. Available online: https://ec.europa.eu/economy_finance/publications/pages/publication9467_en.pdf (accessed on 2 November 2023).
- Van Ark, B. Total Factor Productivity: Lessons from the Past and Directions for the Future (No. 271). NBB Working Paper. 2014. Available online: https://www.nbb.be/doc/ts/publications/wp/wp271en.pdf (accessed on 24 May 2023).
- Felipe, J.; McCombie, J.S. How sound are the foundations of the aggregate production function? East. Econ. J. 2005, 31, 467–488. [Google Scholar]
- Felipe, J.; McCombie, J.S. The aggregate production function: “Not even wrong”. Rev. Political Econ. 2014, 26, 60–84. [Google Scholar] [CrossRef]
- McCombie, J.S. What does the aggregate production function show? Further thoughts on Solow’s “second thoughts on growth theory”. J. Post Keynes. Econ. 2001, 23, 589–615. [Google Scholar] [CrossRef]
- Sraffa, P. Production of commodities by means of commodities. In What Are the Questions and Other Essays; Routledge: London, UK, 2016; pp. 144–150. [Google Scholar]
- Robinson, J. The production function and the theory of capital. Rev. Econ. Stud. 1953, 21, 81–106. [Google Scholar] [CrossRef]
- King, J.E. A History of Post Keynesian Economics Since 1936; Edward Elgar Publishing: Cheltenham, UK, 2002. [Google Scholar]
- Kim, Y.E.; Loayza, N. Productivity growth: Patterns and determinants across the world. In World Bank Policy Research Working Paper 8852; World Bank: Washington, DC, USA, 2019. [Google Scholar]
- Stanton, E.A.; Ackerman, F.; Kartha, S. Inside the integrated assessment models: Four issues in climate economics. Clim. Dev. 2009, 1, 166–184. [Google Scholar] [CrossRef]
- Millner, A.; McDermott, T.K. Model confirmation in climate economics. Proc. Natl. Acad. Sci. USA 2016, 113, 8675–8680. [Google Scholar] [CrossRef] [PubMed]
- Daly, H.E. When smart people make dumb mistakes. Ecol. Econ. 2000, 34, 1–3. [Google Scholar] [CrossRef]
- Solow, R.M. Intergenerational equity and exhaustible resources. Rev. Econ. Stud. 1974, 41, 29–45. [Google Scholar] [CrossRef]
- Stiglitz, J. Growth with exhaustible natural resources: Efficient and optimal growth paths. Rev. Econ. Stud. 1974, 41, 123–137. [Google Scholar] [CrossRef]
- Hudson, E.A.; Jorgenson, D.W. Energy policy and US economic growth. Am. Econ. Rev. 1978, 68, 118–123. [Google Scholar]
- Allen, E.L.; Cooper, C.L.; Edmonds, F.C.; Edmonds, J.A.; Reister, D.B.; Weinberg, A.M.; Whittle, C.E.; Zelby, L.W. US Energy and Economic Growth, 1975–2010; No. ORAU/IEA-76-7; Institute for Energy Analysis: Oak Ridge, TN, USA, 1976. [Google Scholar] [CrossRef]
- Jorgenson, D.W. The role of energy in the US economy. Natl. Tax J. 1978, 31, 209–220. [Google Scholar] [CrossRef]
- Koetse, M.J.; De Groot, H.L.; Florax, R.J. Capital-energy substitution and shifts in factor demand: A meta-analysis. Energy Econ. 2008, 30, 2236–2251. [Google Scholar] [CrossRef]
- Fiorito, G.; van den Bergh, J.C. Capital-energy substitution in manufacturing for seven OECD countries: Learning about potential effects of climate policy and peak oil. Energy Effic. 2016, 9, 49–65. [Google Scholar] [CrossRef]
- d’Arge, R.C.; Kogiku, K.C. Economic growth and the environment. Rev. Econ. Stud. 1973, 40, 61–77. [Google Scholar] [CrossRef]
- Kümmel, R. Energy as a factor of production and entropy as a pollution indicator in macroeconomic modelling. Ecol. Econ. 1989, 1, 161–180. [Google Scholar] [CrossRef]
- Gross, L.S.; Veendorp, E.C.H. Growth with Exhaustible Resources and a Materials-Balance Production Function. Nat. Resour. Model. 1990, 4, 77–94. [Google Scholar] [CrossRef]
- Lindenberger, D.; Kümmel, R. Energy and the state of nations. Energy 2011, 36, 6010–6018. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Exergy: Energy, Environment and Sustainable Development; Newnes: Oxford, UK, 2012. [Google Scholar]
- Reistad, G.M. Available energy conversion and utilization in the United States. ASME J. Eng. Power 1975, 97, 429–434. [Google Scholar] [CrossRef]
- APS. Energy Future: Think Efficiency: How America Can Look within to Achieve; American Physical Society: Washington, DC, USA, 2008. [Google Scholar]
- Cullen, J.M.; Allwood, J.M.; Borgstein, E.H. Reducing energy demand: What are the practical limits? Environ. Sci. Technol. 2011, 45, 1711–1718. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.; Borges, A.S.; Domingos, T. Exploring the links between total factor productivity and energy efficiency: Portugal, 1960–2014. Energy Econ. 2021, 101, 105407. [Google Scholar] [CrossRef]
- Serrenho, A.C.; Sousa, T.; Warr, B.; Ayres, R.U.; Domingos, T. Decomposition of useful work intensity: The EU (European Union)-15 countries from 1960 to 2009. Energy 2014, 76, 704–715. [Google Scholar] [CrossRef]
- Serrenho, A.C.; Warr, B.; Sousa, T.; Ayres, R.U.; Domingos, T. Structure and dynamics of useful work along the agriculture-industry-services transition: Portugal from 1856 to 2009. Struct. Chang. Econ. Dyn. 2016, 36, 1–21. [Google Scholar] [CrossRef]
- Sousa, T.; Brockway, P.E.; Cullen, J.M.; Henriques, S.T.; Miller, J.; Serrenho, A.C.; Domingos, T. The need for robust, consistent methods in societal exergy accounting. Ecol. Econ. 2017, 141, 11–21. [Google Scholar] [CrossRef]
- Warr, B.; Ayres, R. REXS: A forecasting model for assessing the impact of natural resource consumption and technological change on economic growth. Struct. Chang. Econ. Dyn. 2006, 17, 329–378. [Google Scholar] [CrossRef]
- Warr, B.S.; Ayres, R.U. Evidence of causality between the quantity and quality of energy consumption and economic growth. Energy 2010, 35, 1688–1693. [Google Scholar] [CrossRef]
- Warr, B.; Ayres, R.U. Useful work and information as drivers of economic growth. Ecol. Econ. 2012, 73, 93–102. [Google Scholar] [CrossRef]
- Santos, J.; Domingos, T.; Sousa, T.; Aubyn, M.S. Useful exergy is key in obtaining plausible aggregate production functions and recognizing the role of energy in economic growth: Portugal 1960–2009. Ecol. Econ. 2018, 148, 103–120. [Google Scholar] [CrossRef]
- Sakai, M.; Brockway, P.E.; Barrett, J.R.; Taylor, P.G. Thermodynamic efficiency gains and their role as a key ‘engine of economic growth’. Energies 2019, 12, 110. [Google Scholar] [CrossRef]
- Wall, G. Exergy conversion in the Swedish society. Resour. Energy 1987, 9, 55–73. [Google Scholar] [CrossRef]
- Sciubba, E. Beyond thermoeconomics? The concept of extended exergy accounting and its application to the analysis and design of thermal systems. Exergy Int. J. 2001, 1, 68–84. [Google Scholar] [CrossRef]
- Heun, M.K.; Brockway, P.E. Meeting 2030 primary energy and economic growth goals: Mission impossible? Appl. Energy 2019, 251, 112697. [Google Scholar] [CrossRef]
- European Commission. Assessing the Employment and Social Impact of Energy Efficiency, Report Submitted to the European Commission (DG ENER) by Cambridge Econometrics, E3MLab, ICF International and Warwick Institute for Employment Research. 2015. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/CE_EE_Jobs_main18Nov2015.pdf (accessed on 30 July 2023).
- European Commission. A Spatial Computable General Equilibrium Model for EU Regions and Sectors. 2016. Available online: https://ec.europa.eu/jrc/en/publication/rhomolo-v2-model-description-spatial-computable-general-equilibrium-model-eu-regions-and-sectors (accessed on 1 December 2023).
- HRMC. Technical Documents and Research Based on HM Revenue & Customs (HRMC) CGE Model. 2013. Available online: https://www.gov.uk/government/publications/computable-general-equilibrium-cge-modelling (accessed on 22 February 2023).
- OBR. The Macroeconomic Model. Briefing Paper No. 5. 2013. Available online: https://budgetresponsibility.org.uk/topics/obr-macroeconomic-model/ (accessed on 1 April 2023).
- Geanakoplos, J. Arrow-Debreu Model of General Equilibrium; Palgrave Macmillan: London, UK, 1989; pp. 43–61. [Google Scholar]
- Babatunde, K.A.; Begum, R.A.; Said, F.F. Application of computable general equilibrium (CGE) to climate change mitigation policy: A systematic review. Renew. Sustain. Energy Rev. 2017, 78, 61–71. [Google Scholar] [CrossRef]
- Sterman, J.; Fiddaman, T.; Franck, T.; Jones, A.; McCauley, S.; Rice, P.; Sawin, E.; Siegel, L. Climate interactive: The C-ROADS climate policy model. Syst. Dyn. Rev. 2012, 28, 295–305. [Google Scholar] [CrossRef]
- ENE (Environment Northeast). Energy Efficiency: Engine of Economic Growth in Eastern Canada. A Macroeconomic Modeling & Tax Revenue Impact Assessment, ENE Ottawa. 2012. Available online: www.env-ne.org/public/resources/ENE_EnergyEfficiencyEngineofEconomicGrowth_EarternCanada_EN_2012_0611_FINAL.pdf (accessed on 8 January 2023).
- Pollitt, H.; Lewney, R.; Mercure, J.F. Conceptual differences between macro-econometric and CGE models. In Proceedings of the 27th International Input-Output Association Conference, Glasgow, UK, 30 June–5 July 2019. [Google Scholar]
- Barker, T.; Anger, A.; Chewpreecha, U.; Pollitt, H. A new economics approach to modelling policies to achieve global 2020 targets for climate stabilisation. Int. Rev. Appl. Econ. 2012, 26, 205–221. [Google Scholar] [CrossRef]
- Lavoie, M. Post-Keynesian Economics: New Foundations; Edward Elgar Publishing: Cheltenham, UK, 2022. [Google Scholar]
- Scrieciu, S.; Rezai, A.; Mechler, R. On the economic foundations of green growth discourses: The case of climate change mitigation and macroeconomic dynamics in economic modeling. Wiley Interdiscip. Rev. Energy Environ. 2013, 2, 251–268. [Google Scholar] [CrossRef]
- Patterson, M.G. What is energy efficiency?: Concepts, indicators and methodological issues. Energy Policy 1996, 24, 377–390. [Google Scholar] [CrossRef]
- Madlener, R.; Alcott, B. Energy rebound and economic growth: A review of the main issues and research needs. Energy 2009, 34, 370–376. [Google Scholar] [CrossRef]
- Van der Werf, E. Production functions for climate policy modeling: An empirical analysis. Energy Econ. 2008, 30, 2964–2979. [Google Scholar] [CrossRef]
- Mundaca, L.; Neij, L.; Worrell, E.; McNeil, M. Evaluating energy efficiency policies with energy-economy models. Annu. Rev. Environ. Resour. 2010, 35, 305–344. [Google Scholar] [CrossRef]
- E3ME Technical Manual; Version 6; Cambridge Econometrics: Cambridge, UK, 2014.
- Sijm, J.; Lehmann, P.; Chewpreecha, U.; Gawel, E.; Mercure, J.F.; Pollitt, H.; Strunz, S. EU Climate and Energy Policy beyond 2020: Are Additional Targets and Instruments for Renewables Economically Reasonable? In The European Dimension of Germany’s Energy Transition; (No. 3/2014), UFZ Discussion Paper; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Ertesvåg, I.S. Society exergy analysis: A comparison of different societies. Energy 2001, 26, 253–270. [Google Scholar] [CrossRef]
- Ayres, R.U.; Warr, B. Accounting for growth: The role of physical work. Struct. Chang. Econ. Dyn. 2005, 16, 181–209. [Google Scholar] [CrossRef]
- Stresing, R.; Lindenberger, D.; Kümmel, R. Cointegration of output, capital, labor, and energy. Eur. Phys. J. B 2008, 66, 279–287. [Google Scholar] [CrossRef]
- Guevara, Z.; Sousa, T.; Domingos, T. Insights on energy transitions in Mexico from the analysis of useful exergy 1971–2009. Energies 2016, 9, 488. [Google Scholar] [CrossRef]
- Felício, L.; Henriques, S.T.; Serrenho, A.; Domingos, T.; Sousa, T. Insights from past trends in exergy efficiency and carbon intensity of electricity: Portugal, 1900–2014. Energies 2019, 12, 534. [Google Scholar] [CrossRef]
- Brillet, J.L. Structural Econometric Modelling: Methodology and Tools with Applications under EViews; IHS Global Inc.: Englewood, CO, USA, 2016. [Google Scholar]
- Johansen, S. Statistical analysis of cointegration vectors. J. Econ. Dyn. Control 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econom. J. Econom. Soc. 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Phillips, P.C.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- [database] AMECO. Annual Macro-Economic Database of the European Commission’s Directorate General for Economic and Financial Affairs. 2022. Available online: https://economy-finance.ec.europa.eu/economic-research-and-databases/economic-databases/ameco-database_en (accessed on 13 January 2023).
- [database] DGEG. Direção-Geral de Energia e Geologia. Estatísticas e Preços—Estatística da Energia. 2023. Available online: http://www.dgeg.gov.pt/ (accessed on 13 January 2023).
- [database] Banco de Portugal. Novas Séries Longas Para A Economia Portuguesa—SLEP2020. Portal de estatísticas do Banco de Portugal. 2020. Available online: https://bpstat.bportugal.pt/conteudos/noticias/1498/ (accessed on 13 January 2023).
- [database] EuroStat. European Statistics Database. 2023. Available online: https://ec.europa.eu/eurostat/data/database (accessed on 13 January 2023).
- [database] World Bank. World Development Indicator. World Bank National Accounts Data, and OECD National Accounts Data Files. 2023. Available online: https://data.worldbank.org/indicator/ (accessed on 13 January 2023).
- [database] Global Carbon Atlas. Portugal—Territorial (MtCO2). 2018. Available online: http://www.globalcarbonatlas.org/en/CO2-emissions (accessed on 13 January 2023).
- da Silva, E.G.; Lains, P. Capital Formation and Long-Run Growth: Evidence from Portuguese Data, 1910–2011; IBEROMETRICS VI; Facultad de Economía y Empresa: Zaragoza, Spain, 2013; pp. 16–17. [Google Scholar]
- Varga, R.S. Basic Iterative Methods and Comparison Theorems. In Matrix Iterative Analysis; Springer: Berlin/Heidelberg, Germany, 2009; pp. 63–110. [Google Scholar]
- Koesler, S.; Swales, K.; Turner, K. International spillover and rebound effects from increased energy efficiency in Germany. Energy Econ. 2016, 54, 444–452. [Google Scholar] [CrossRef]
- Allan, G.; Gilmartin, M.; Turner, K.; McGregor, P.G.; Swales, J.K. UKERC Review of Evidence for the Rebound Effect: Technical Report 4: Computable General Equilibrium Modelling Studies. 2007. Available online: https://ukerc.ac.uk/publications/ukerc-review-of-evidence-for-the-rebound-effect-technical-report-4-computable-general-equilibrium-modelling-studies/ (accessed on 14 September 2023).
- Froot, K.A.; Rogoff, K. Perspectives on PPP and long-run real exchange rates. Handb. Int. Econ. 1995, 3, 1647–1688. [Google Scholar]
- Sercu, P.; Uppal, R.; Van Hulle, C. The exchange rate in the presence of transaction costs: Implications for tests of purchasing power parity. J. Financ. 1995, 50, 1309–1319. [Google Scholar] [CrossRef]
- Brockway, P.E.; Barrett, J.R.; Foxon, T.J.; Steinberger, J.K. Divergence of trends in US and UK aggregate exergy efficiencies 1960–2010. Environ. Sci. Technol. 2014, 48, 9874–9881. [Google Scholar] [CrossRef]
- Brockway, P.; Sorrell, S.; Foxon, T.; Miller, J. Exergy economics: New insights into energy consumption and economic growth. In Transitions in Energy Efficiency and Demand; Routledge: London, UK, 2018; pp. 133–155. [Google Scholar]
- Keen, S.; Ayres, R.U.; Standish, R. A Note on the Role of Energy in Production. Ecol. Econ. 2019, 157, 40–46. [Google Scholar] [CrossRef]
- Voudouris, V.; Ayres, R.; Serrenho, A.C.; Kiose, D. The economic growth enigma revisited: The EU-15 since the 1970s. Energy Policy 2015, 86, 812–832. [Google Scholar] [CrossRef]
- Kümmel, R.; Lindenberger, D.; Weiser, F. The economic power of energy and the need to integrate it with energy policy. Energy Policy 2015, 86, 833–843. [Google Scholar] [CrossRef]
- Kümmel, R.; Ayres, R.U.; Lindenberger, D. Thermodynamic laws, economic methods and the productive power of energy. J. Non-Equilibrium Thermodyn. 2010, 35, 145–179. [Google Scholar] [CrossRef]
- Heun, M.K.; Santos, J.; Brockway, P.E.; Pruim, R.; Domingos, T.; Sakai, M. From theory to econometrics to energy policy: Cautionary tales for policymaking using aggregate production functions. Energies 2017, 10, 203. [Google Scholar] [CrossRef]
- Semieniuk, G.; Taylor, L.; Rezai, A.; Foley, D.K. Plausible energy demand patterns in a growing global economy with climate policy. Nat. Clim. Chang. 2021, 11, 313–318. [Google Scholar] [CrossRef]
- Brockway, P.E.; Sorrell, S.; Semieniuk, G.; Heun, M.K.; Court, V. Energy efficiency and economy-wide rebound effects: A review of the evidence and its implications. Renew. Sustain. Energy Rev. 2021, 141, 110781. [Google Scholar] [CrossRef]
- Nieto, J.; Pollitt, H.; Brockway, P.E.; Clements, L.; Sakai, M.; Barrett, J. Socio-macroeconomic impacts of implementing different post-Brexit UK energy reduction targets to 2030. Energy Policy 2021, 158, 112556. [Google Scholar] [CrossRef]
- FRED. Federal Reserve Bank of St. Louis. Consumer Price Index: Energy for Portugal [PRTCPIENGAINMEI]. 2019. Available online: https://fred.stlouisfed.org/series/PRTCPIENGAINMEI (accessed on 13 January 2023).


| Scenario | Variable | Average Output Elasticity | |||||
|---|---|---|---|---|---|---|---|
| 1965–1975 | 1976–1985 | 1986–1995 | 1996–2005 | 2006–2014 | 1965–2014 | ||
| Scenario 1 | Exergy efficiency | 0.5434 | 0.5145 | 0.4797 | 0.4177 | 0.3028 | 0.4564 |
| Scenario 2 | Final energy | −0.0035 | −0.0098 | −0.0045 | −0.0002 | 0.0006 | −0.0036 |
| Scenario 3 | Investment | 0.2683 | 0.2496 | 0.2648 | 0.2892 | 0.2435 | 0.2636 |
| Scenario 4 | Labor supply | −0.0339 | −0.0457 | −0.0792 | −0.1792 | −0.1822 | −0.1011 |
| Scenario 5 | Energy prices | 0.0135 | 0.0284 | 0.0372 | 0.0030 | −0.0011 | 0.0165 |
| Scenario 6 | Useful exergy | 0.3345 | 0.3019 | 0.2959 | 0.2775 | 0.2118 | 0.2868 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, J.; Viana, M.; Nieto, J.; Brockway, P.E.; Sakai, M.; Domingos, T. The Impact of Energy Efficiency on Economic Growth: Application of the MARCO Model to the Portuguese Economy 1960–2014. Energies 2024, 17, 2688. https://doi.org/10.3390/en17112688
Santos J, Viana M, Nieto J, Brockway PE, Sakai M, Domingos T. The Impact of Energy Efficiency on Economic Growth: Application of the MARCO Model to the Portuguese Economy 1960–2014. Energies. 2024; 17(11):2688. https://doi.org/10.3390/en17112688
Chicago/Turabian StyleSantos, João, Miguel Viana, Jaime Nieto, Paul E. Brockway, Marco Sakai, and Tiago Domingos. 2024. "The Impact of Energy Efficiency on Economic Growth: Application of the MARCO Model to the Portuguese Economy 1960–2014" Energies 17, no. 11: 2688. https://doi.org/10.3390/en17112688
APA StyleSantos, J., Viana, M., Nieto, J., Brockway, P. E., Sakai, M., & Domingos, T. (2024). The Impact of Energy Efficiency on Economic Growth: Application of the MARCO Model to the Portuguese Economy 1960–2014. Energies, 17(11), 2688. https://doi.org/10.3390/en17112688









