Enhanced Day-Ahead Electricity Price Forecasting Using a Convolutional Neural Network–Long Short-Term Memory Ensemble Learning Approach with Multimodal Data Integration
Abstract
1. Introduction
1.1. The Necessity of Day-Ahead Electricity Price Forecasting
1.2. Day-Ahead Electricity Price Forecasting Models
1.3. Day-Ahead Electricity Prices: Negative Trends in the US and EU and Non-Negative Limitations in Japan
1.4. Paper Contributions and Organization
2. Methodology
2.1. LSTM and CNN–LSTM Forecasting Models
2.2. Ensemble Learning Strategy
| Algorithm 1 Ensemble Learning Procedure |
|
2.3. “Policy-Versus-Policy” Zero Prices Forecasting Strategy
2.4. Performance Evaluation
3. Data Preparation
3.1. Electricity Data
3.1.1. Day-Ahead Electricity Price
3.1.2. Actual Power Generation
3.2. Meteorological Forecast Data
3.3. Calendar Forecast Data
3.3.1. Cyclic Features
3.3.2. Holiday Features
3.4. Multiple Feature Sets
3.5. Prediction Methods
3.6. Model Training Platform
4. Results and Discussion
4.1. Ensemble Learning Prediction Results
- Using all features, the ensemble learning prediction with the CNN–LSTM model achieved the highest performance metrics, underscoring the efficacy and validity of the proposed features in enhancing DAEPF accuracy.
- Applying the natural logarithm transformation to the target day-ahead electricity price significantly improved performance.
- The CNN–LSTM model (30 iterations ensemble) outperformed the LSTM model (15 iterations ensemble, special case for comparison), requiring less than the training time of the LSTM model.
- Using the same ensemble learning of 30 iterations, the CNN–LSTM model outperformed the LSTM model in terms of and RMSE, though slightly weaker in MAE, requiring less than half of the training time of the LSTM model.
4.2. Day-by-Day Prediction Result
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DAEPF | Day-ahead electricity price forecasting |
| RES | Renewable energy sources |
| OCCTO | Organization for Cross-regional Coordination of Transmission Operators, Japan |
| JMBSC | Japan Meteorological Business Support Center |
| JEPX | Japan Electric Power Exchange |
| ASHRAE | American Society of Heating, Refrigerating and Air-conditioning Engineers |
| PV | Photovoltaic |
| ARMA | Autoregressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| RF | Random Forest |
| SVR | Support Vector Regression |
| MLP | Multilayer Perceptron |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| CNN–LSTM | Convolutional Neural Network6-Long Short-Term Memory |
| FC | Fully-connected |
| ReLU | Rectified Linear Unit |
| MAE | Mean absolute error |
| RMSE | Root mean squared error |
| Coefficient of determination | |
| MSM-GPV | Mesoscale Model Grid Point Value |
| UGRD | U-Component of Wind |
| VGRD | V-Component of Wind |
| TMP | Temperature |
| RH | Relative humidity |
| LCDC | Low Cloud Cover |
| MCDC | Middle Cloud Cover |
| HCDC | High Cloud Cover |
| TCDC | Total Cloud Cover |
| APCP | Accumulated Precipitation |
| DSWRF | Downward Shortwave Radiation Flux |
| Symbols | |
| e | Natural logarithm |
| Minimum value of the day-ahead electricity price over a rolling window | |
| Maximum value of the day-ahead electricity price over a rolling window | |
| Mean value of the day-ahead electricity price over a rolling window | |
| Standard deviation of the day-ahead electricity price over a rolling window | |
| y | Target variable |
| Predicted target variable | |
| Ensemble prediction of the target variable | |
| n | Sequence length of the target variable |
| N | Total training times of the model |
| t | t-th value in a variable sequence |
| i | i-th value in a variable sequence |
| k | k-th individual prediction after k-th training of the model |
| w | Rolling window length |
References
- Abdelilah, Y.; Bahar, H.; Criswell, T.; Bojek, P.; Briens, F.; Le Feuvre, P. Renewables 2020: Analysis and Forecast to 2025; IEA: Paris, France, 2020. [Google Scholar]
- Weitemeyer, S.; Kleinhans, D.; Vogt, T.; Agert, C. Integration of Renewable Energy Sources in future power systems: The role of storage. Renew. Energy 2015, 75, 14–20. [Google Scholar] [CrossRef]
- Asiaban, S.; Kayedpour, N.; Samani, A.E.; Bozalakov, D.; De Kooning, J.D.M.; Crevecoeur, G.; Vandevelde, L. Wind and Solar Intermittency and the Associated Integration Challenges: A Comprehensive Review Including the Status in the Belgian Power System. Energies 2021, 14, 2630. [Google Scholar] [CrossRef]
- Huang, S.; Xiong, L.; Zhou, Y.; Gao, F.; Jia, Q.; Li, X.; Li, X.; Wang, Z.; Khan, M.W. Distributed Predefined-Time Control for Power System with Time Delay and Input Saturation. IEEE Trans. Power Syst. 2024, 1–14. [Google Scholar] [CrossRef]
- Özen, K.; Yıldırım, D. Application of bagging in day-ahead electricity price forecasting and factor augmentation. Energy Econ. 2021, 103, 105573. [Google Scholar] [CrossRef]
- Wang, K.; Yu, M.; Niu, D.; Liang, Y.; Peng, S.; Xu, X. Short-term electricity price forecasting based on similarity day screening, two-layer decomposition technique and Bi-LSTM neural network. Appl. Soft Comput. 2023, 136, 110018. [Google Scholar] [CrossRef]
- Li, W.; Becker, D.M. Day-ahead electricity price prediction applying hybrid models of LSTM-based deep learning methods and feature selection algorithms under consideration of market coupling. Energy 2021, 237, 121543. [Google Scholar] [CrossRef]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead electricity price forecasting via the application of artificial neural network based models. Appl. Energy 2016, 172, 132–151. [Google Scholar] [CrossRef]
- He, K.; Xu, Y.; Zou, Y.; Tang, L. Electricity price forecasts using a Curvelet denoising based approach. Physica A Stat. Mech. Its Appl. 2015, 425, 1–9. [Google Scholar] [CrossRef]
- Yang, Z.; Ce, L.; Lian, L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA and kernel-based extreme learning machine methods. Appl. Energy 2017, 190, 291–305. [Google Scholar] [CrossRef]
- Chaâbane, N. A hybrid ARFIMA and neural network model for electricity price prediction. Int. J. Electr. Power Energy Syst. 2014, 55, 187–194. [Google Scholar] [CrossRef]
- Conejo, A.J.; Plazas, M.A.; Espinola, R.; Molina, A.B. Day-ahead electricity price forecasting using the wavelet transform and ARIMA models. IEEE Trans. Power Syst. 2005, 20, 1035–1042. [Google Scholar] [CrossRef]
- Girish, G.P. Spot electricity price forecasting in Indian electricity market using autoregressive-GARCH models. Energy Strategy Rev. 2016, 11–12, 52–57. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J. Energy futures price prediction and evaluation model with deep bidirectional gated recurrent unit neural network and RIF-based algorithm. Energy 2021, 216, 119299. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Ma, J.; Jin, Q. BRIM: An Accurate Electricity Spot Price Prediction Scheme-Based Bidirectional Recurrent Neural Network and Integrated Market. Energies 2019, 12, 2241. [Google Scholar] [CrossRef]
- Swapna, G.; Soman, K.P.; Vinayakumar, R. Automated detection of diabetes using CNN and CNN-LSTM network and heart rate signals. Procedia Comput. Sci. 2018, 132, 1253–1262. [Google Scholar] [CrossRef]
- Qiu, D.; Dong, Z.; Ruan, G.; Zhong, H.; Strbac, G.; Kang, C. Strategic retail pricing and demand bidding of retailers in electricity market: A data-driven chance-constrained programming. Adv. Appl. Energy 2022, 7, 100100. [Google Scholar] [CrossRef]
- Lu, W.; Li, J.; Li, Y.; Sun, A.; Wang, J. A CNN-LSTM-Based Model to Forecast Stock Prices. Complexity 2020, 2020. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; Houm, Y.E.; Ou Ali, I.H. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Power Syst. Res. 2022, 208, 107908. [Google Scholar] [CrossRef]
- Li, Y.; Garg, A.; Shevya, S.; Li, W.; Gao, L.; Lee Lam, J.S. A Hybrid Convolutional Neural Network-Long Short Term Memory for Discharge Capacity Estimation of Lithium-Ion Batteries. J. Electrochem. Energy Convers. Storage 2021, 19, 030901. [Google Scholar] [CrossRef]
- Li, T.; Hua, M.; Wu, X. A Hybrid CNN-LSTM Model for Forecasting Particulate Matter (PM2.5). IEEE Access 2020, 8, 26933–26940. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Alhussein, M.; Aurangzeb, K.; Haider, S.I. Hybrid CNN-LSTM Model for Short-Term Individual Household Load Forecasting. IEEE Access 2020, 8, 180544–180557. [Google Scholar] [CrossRef]
- Cordoni, F. A comparison of modern deep neural network architectures for energy spot price forecasting. Digit. Financ. 2020, 2, 189–210. [Google Scholar] [CrossRef]
- Neupane, B.; Woon, W.L.; Aung, Z. Ensemble Prediction Model with Expert Selection for Electricity Price Forecasting. Energies 2017, 10, 77. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy 2019, 187, 115804. [Google Scholar] [CrossRef]
- Seel, J.; Millstein, D.; Mills, A.; Bolinger, M.; Wiser, R. Plentiful electricity turns wholesale prices negative. Adv. Appl. Energy 2021, 4, 100073. [Google Scholar] [CrossRef]
- Shiri, A.; Afshar, M.; Rahimi-Kian, A.; Maham, B. Electricity price forecasting using Support Vector Machines by considering oil and natural gas price impacts. In Proceedings of the 2015 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 17–19 August 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Barbour, E.; Wilson, G.; Hall, P.; Radcliffe, J. Can negative electricity prices encourage inefficient electrical energy storage devices? Int. J. Environ. Stud. 2014, 71, 862–876. [Google Scholar] [CrossRef]
- Marqusee, J.; Becker, W.; Ericson, S. Resilience and economics of microgrids with PV, battery storage, and networked diesel generators. Adv. Appl. Energy 2021, 3, 100049. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chen, J.; Zeng, G.Q.; Zhou, W.; Du, W.; Lu, K.D. Wind speed forecasting using nonlinear-learning ensemble of deep learning time series prediction and extremal optimization. Energy Convers. Manag. 2018, 165, 681–695. [Google Scholar] [CrossRef]
- Japan Electric Power Exchange. Day Ahead Market. 2023. Available online: https://www.jepx.jp/en/electricpower/market-data/spot/ (accessed on 19 August 2023).
- Organization for Cross-Regional Coordination of Transmission Operators, Japan. Menu. 2023. Available online: https://occtonet3.occto.or.jp/public/dfw/RP11/OCCTO/SD/LOGIN_login (accessed on 1 August 2023).
- Japan Meteorological Business Support Center. Numerical Weather Prediction Model GPV-MSM. 2023. Available online: http://www.jmbsc.or.jp/jp/online/file/f-online10200.html (accessed on 15 July 2023).
- Google Maps. Available online: https://www.google.com/maps/@36.2932467,137.3408308,6z?entry=ttu (accessed on 3 May 2024).
- OpenCV Team. OpenCV Library. 2023. Available online: https://opencv.org/ (accessed on 19 August 2023).
- ANSI/ASHRAE Standard 55-2017; Thermal Environmental Conditions for Human Occupancy. ASHRAE Inc.: Peachtree Corners, GA, USA, 2017.
- Wang, Z.; Matsuhashi, R.; Onodera, H. Towards wearable thermal comfort assessment framework by analysis of heart rate variability. Build. Environ. 2022, 223, 109504. [Google Scholar] [CrossRef]
- Wang, Z.; Matsuhashi, R.; Onodera, H. Intrusive and non-intrusive early warning systems for thermal discomfort by analysis of body surface temperature. Appl. Energy 2023, 329, 120283. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J.; Grosse, E. Regression by local fitting: Methods, properties, and computational algorithms. J. Econ. 1988, 37, 87–114. [Google Scholar] [CrossRef]
- Korenberg, M.J. A robust orthogonal algorithm for system identification and time-series analysis. Biol. Cybern. 1989, 60, 267–276. [Google Scholar] [CrossRef] [PubMed]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
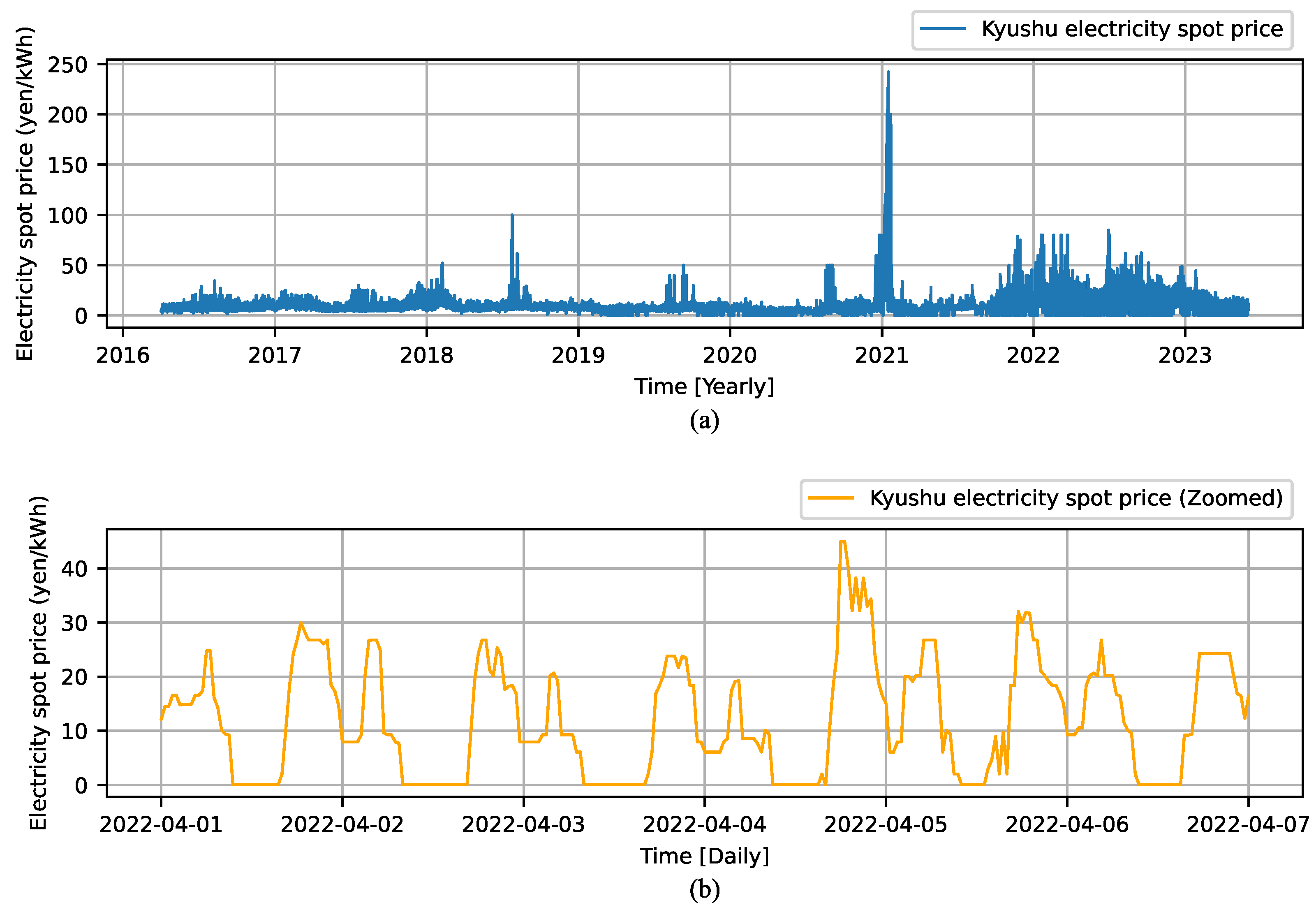


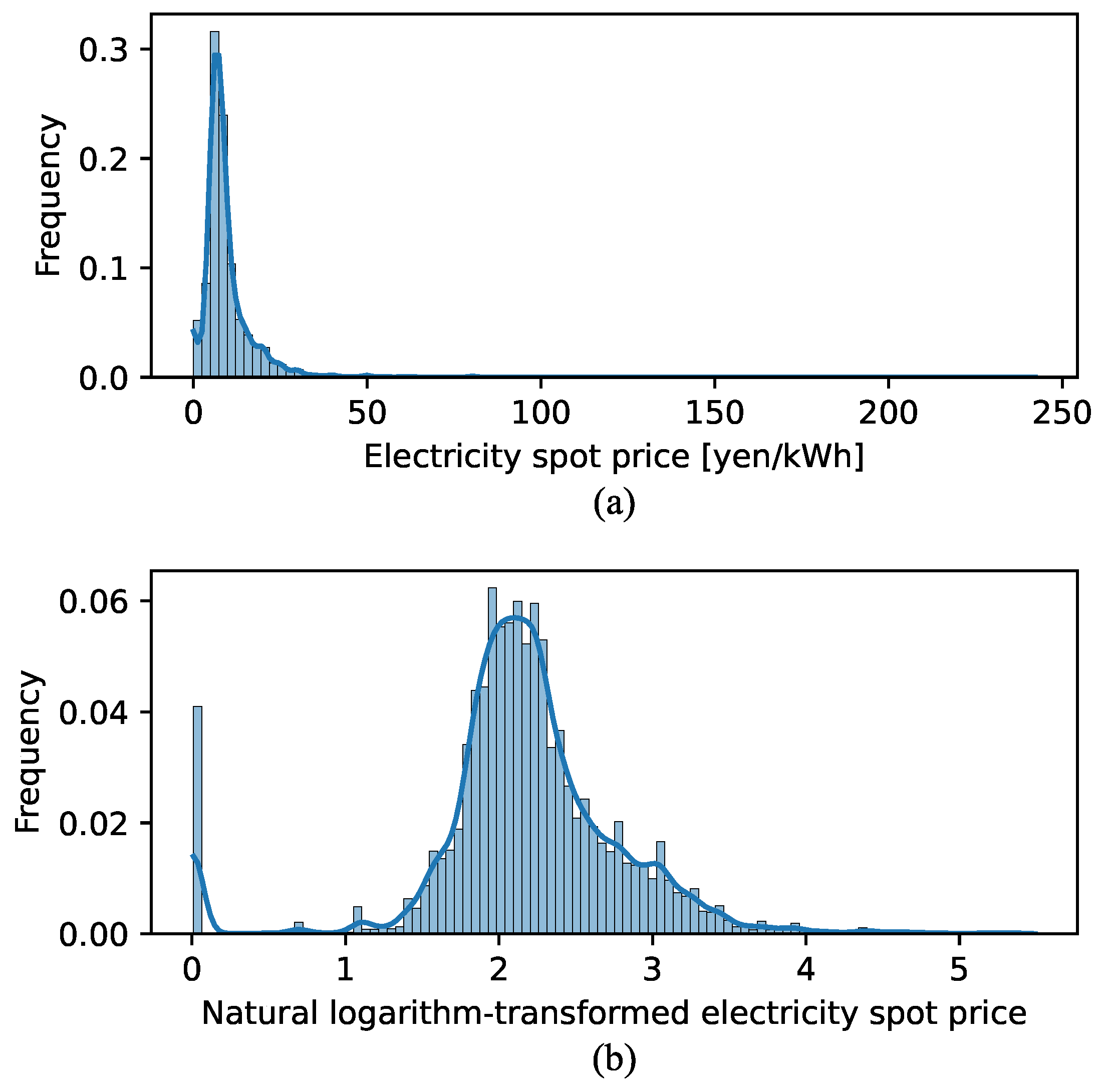

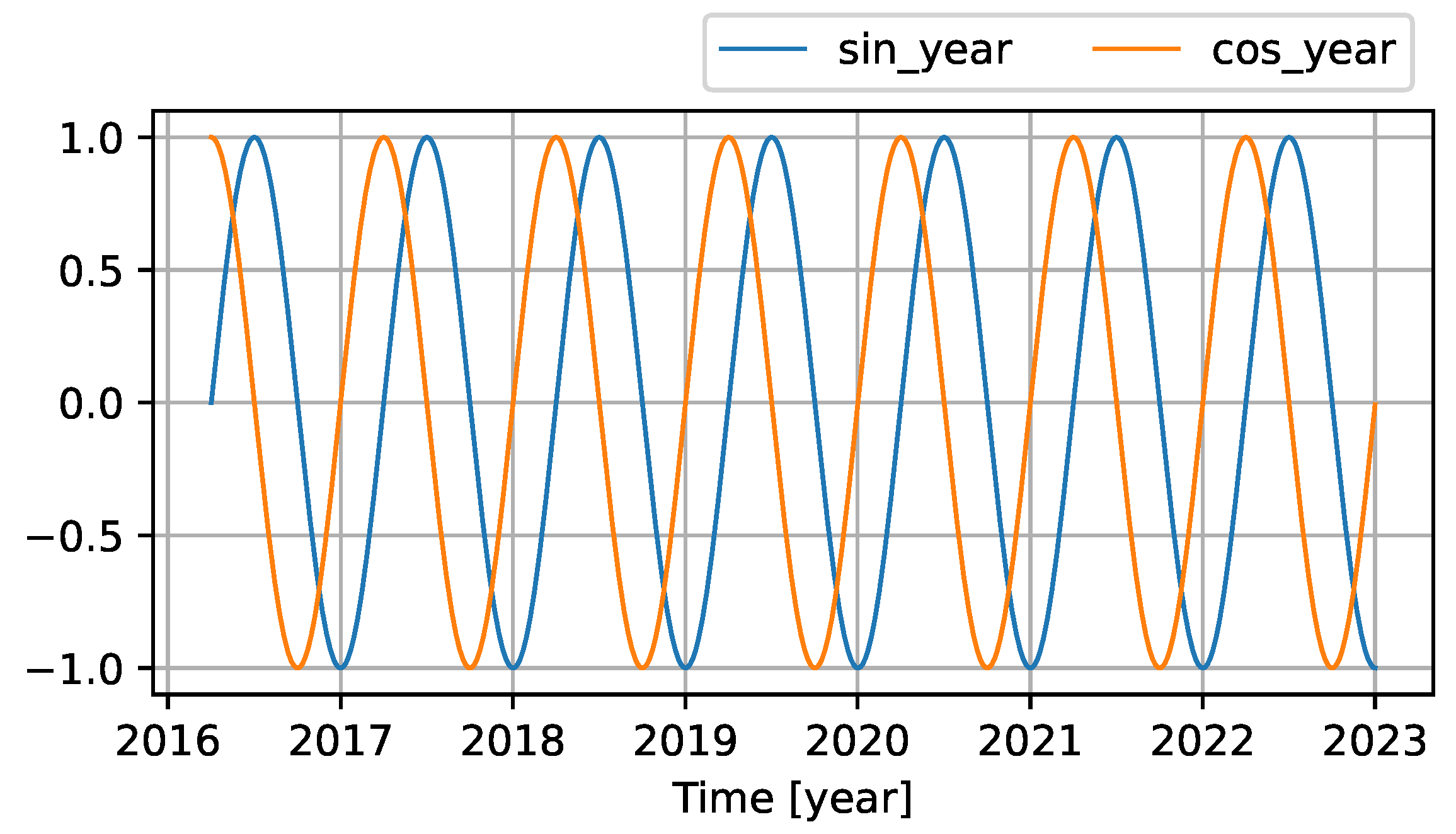


| Original | Log-Transformed | |
|---|---|---|
| Skewness | 8.77 | −0.68 |
| Kurtosis | 123.00 | 3.81 |
| Feature Set | Model | Prediction Method | Log Transformation | Ensemble Times | Training Time | MAE [JPY/kWh] | RMSE [JPY/kWh] | |
|---|---|---|---|---|---|---|---|---|
| All | CNN-LSTM | (a) | Yes | 30 | 52 min | 0.592 | 5.112 | 6.941 |
| No actual power generation | CNN-LSTM | (a) | Yes | 30 | 50 min | 0.583 | 5.216 | 7.020 |
| No holidays | CNN-LSTM | (a) | Yes | 30 | 51 min | 0.575 | 5.231 | 7.088 |
| No meteorological data | CNN-LSTM | (a) | Yes | 30 | 40 min | 0.572 | 5.200 | 7.117 |
| No rolling features | CNN-LSTM | (a) | Yes | 30 | 46 min | 0.561 | 5.328 | 7.207 |
| No cyclic features | CNN-LSTM | (a) | Yes | 30 | 42 min | 0.530 | 5.489 | 7.457 |
| No system price | CNN-LSTM | (a) | Yes | 30 | 51 min | 0.558 | 5.233 | 7.226 |
| All | CNN-LSTM | (a) | No | 30 | 53 min | 0.535 | 5.490 | 7.411 |
| All | LSTM | (a) | Yes | 15 | 58 min | 0.581 | 5.112 | 7.034 |
| All | LSTM | (a) | Yes | 30 | 117 min | 0.587 | 5.070 | 6.986 |
| Feature Set | Model | Prediction Method | Test Period | Log Transformation | Ensemble Times | MAE | RMSE | |
|---|---|---|---|---|---|---|---|---|
| All | CNN-LSTM | (a) | 1 March 2023–31 March 2023 | Yes | 30 | 0.750 | 2.197 | 2.851 |
| All | CNN-LSTM | (b) | 1 March 2023–31 March 2023 | Yes | 30 | 0.787 | 1.936 | 2.630 |
| No. | CNN-LSTM | LSTM | ||||
|---|---|---|---|---|---|---|
| MAE [JPY/kWh] | RMSE [JPY/kWh] | MAE [JPY/kWh] | RMSE [JPY/kWh] | |||
| 1 | 0.501 | 5.569 | 7.677 | 0.496 | 5.507 | 7.720 |
| 2 | 0.554 | 5.360 | 7.261 | 0.463 | 5.661 | 7.967 |
| 3 | 0.437 | 5.996 | 8.159 | 0.462 | 5.691 | 7.978 |
| 4 | 0.529 | 5.455 | 7.463 | 0.510 | 5.483 | 7.614 |
| 5 | 0.529 | 5.442 | 7.460 | 0.522 | 5.401 | 7.514 |
| 6 | 0.530 | 5.541 | 7.454 | 0.447 | 5.760 | 8.084 |
| 7 | 0.538 | 5.420 | 7.388 | 0.490 | 5.582 | 7.761 |
| 8 | 0.565 | 5.284 | 7.170 | 0.544 | 5.269 | 7.343 |
| 9 | 0.538 | 5.421 | 7.389 | 0.447 | 5.776 | 8.086 |
| 10 | 0.554 | 5.365 | 7.260 | 0.487 | 5.629 | 7.787 |
| 11 | 0.525 | 5.486 | 7.493 | 0.518 | 5.492 | 7.549 |
| 12 | 0.545 | 5.329 | 7.334 | 0.500 | 5.570 | 7.687 |
| 13 | 0.517 | 5.533 | 7.557 | 0.501 | 5.634 | 7.677 |
| 14 | 0.504 | 5.575 | 7.657 | 0.518 | 5.498 | 7.551 |
| 15 | 0.525 | 5.441 | 7.495 | 0.534 | 5.446 | 7.419 |
| 16 | 0.499 | 5.452 | 7.698 | 0.495 | 5.543 | 7.722 |
| 17 | 0.529 | 5.343 | 7.463 | 0.497 | 5.501 | 7.713 |
| 18 | 0.517 | 5.605 | 7.554 | 0.493 | 5.527 | 7.743 |
| 19 | 0.531 | 5.390 | 7.448 | 0.473 | 5.652 | 7.896 |
| 20 | 0.544 | 5.349 | 7.341 | 0.494 | 5.591 | 7.737 |
| 21 | 0.547 | 5.320 | 7.315 | 0.527 | 5.390 | 7.474 |
| 22 | 0.530 | 5.437 | 7.451 | 0.522 | 5.356 | 7.514 |
| 23 | 0.550 | 5.436 | 7.290 | 0.502 | 5.595 | 7.671 |
| 24 | 0.547 | 5.388 | 7.317 | 0.514 | 5.433 | 7.583 |
| 25 | 0.477 | 5.680 | 7.866 | 0.500 | 5.521 | 7.686 |
| 26 | 0.544 | 5.347 | 7.340 | 0.485 | 5.599 | 7.799 |
| 27 | 0.519 | 5.505 | 7.537 | 0.513 | 5.469 | 7.584 |
| 28 | 0.497 | 5.547 | 7.711 | 0.519 | 5.543 | 7.541 |
| 29 | 0.546 | 5.404 | 7.327 | 0.495 | 5.533 | 7.723 |
| 30 | 0.548 | 5.384 | 7.309 | 0.544 | 5.402 | 7.340 |
| Min | 0.437 | 5.284 | 7.170 | 0.447 | 5.269 | 7.340 |
| Max | 0.565 | 5.996 | 8.159 | 0.544 | 5.776 | 8.086 |
| Average | 0.527 | 5.460 | 7.473 | 0.500 | 5.535 | 7.682 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Mae, M.; Yamane, T.; Ajisaka, M.; Nakata, T.; Matsuhashi, R. Enhanced Day-Ahead Electricity Price Forecasting Using a Convolutional Neural Network–Long Short-Term Memory Ensemble Learning Approach with Multimodal Data Integration. Energies 2024, 17, 2687. https://doi.org/10.3390/en17112687
Wang Z, Mae M, Yamane T, Ajisaka M, Nakata T, Matsuhashi R. Enhanced Day-Ahead Electricity Price Forecasting Using a Convolutional Neural Network–Long Short-Term Memory Ensemble Learning Approach with Multimodal Data Integration. Energies. 2024; 17(11):2687. https://doi.org/10.3390/en17112687
Chicago/Turabian StyleWang, Ziyang, Masahiro Mae, Takeshi Yamane, Masato Ajisaka, Tatsuya Nakata, and Ryuji Matsuhashi. 2024. "Enhanced Day-Ahead Electricity Price Forecasting Using a Convolutional Neural Network–Long Short-Term Memory Ensemble Learning Approach with Multimodal Data Integration" Energies 17, no. 11: 2687. https://doi.org/10.3390/en17112687
APA StyleWang, Z., Mae, M., Yamane, T., Ajisaka, M., Nakata, T., & Matsuhashi, R. (2024). Enhanced Day-Ahead Electricity Price Forecasting Using a Convolutional Neural Network–Long Short-Term Memory Ensemble Learning Approach with Multimodal Data Integration. Energies, 17(11), 2687. https://doi.org/10.3390/en17112687






