Combined Geometrical Optimisation of a Square Microchannel with Smoothed Corners
Abstract
1. Introduction
2. Mathematical Model
2.1. Performance Evaluation Criteria
2.2. Entropy Generation Number
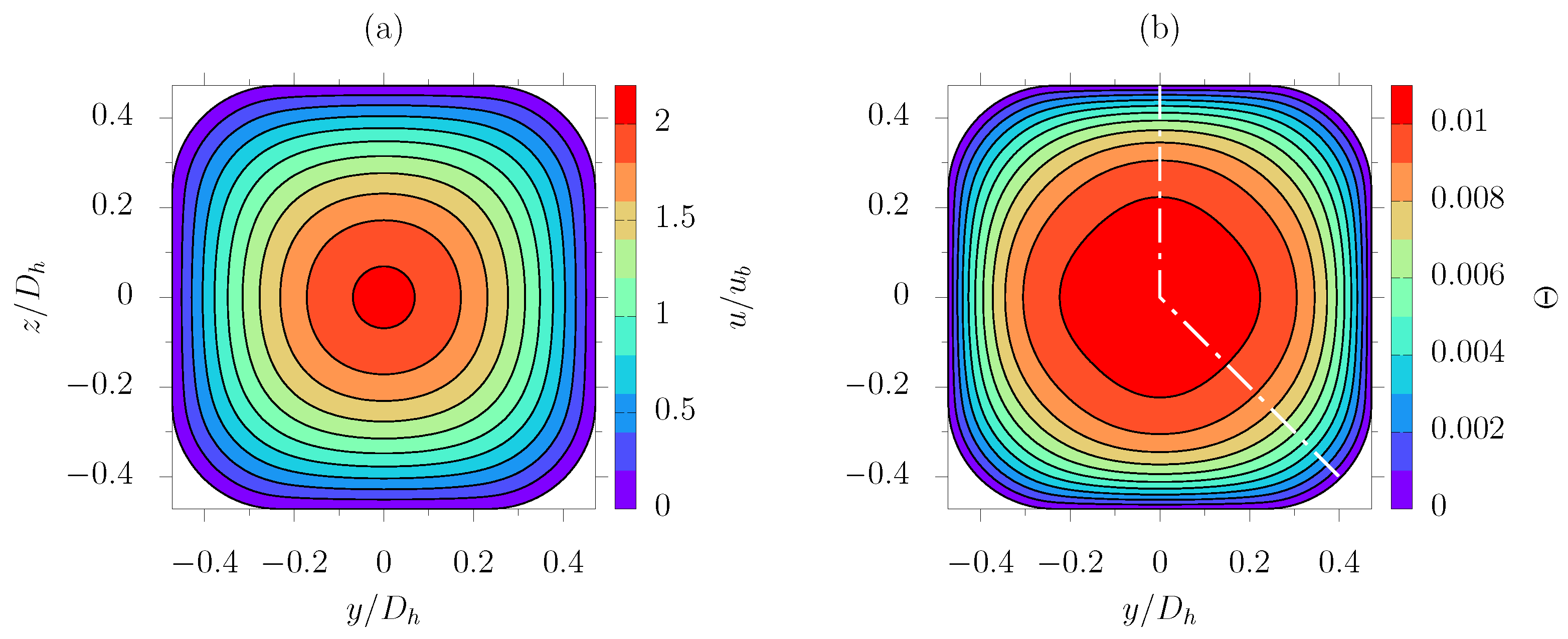
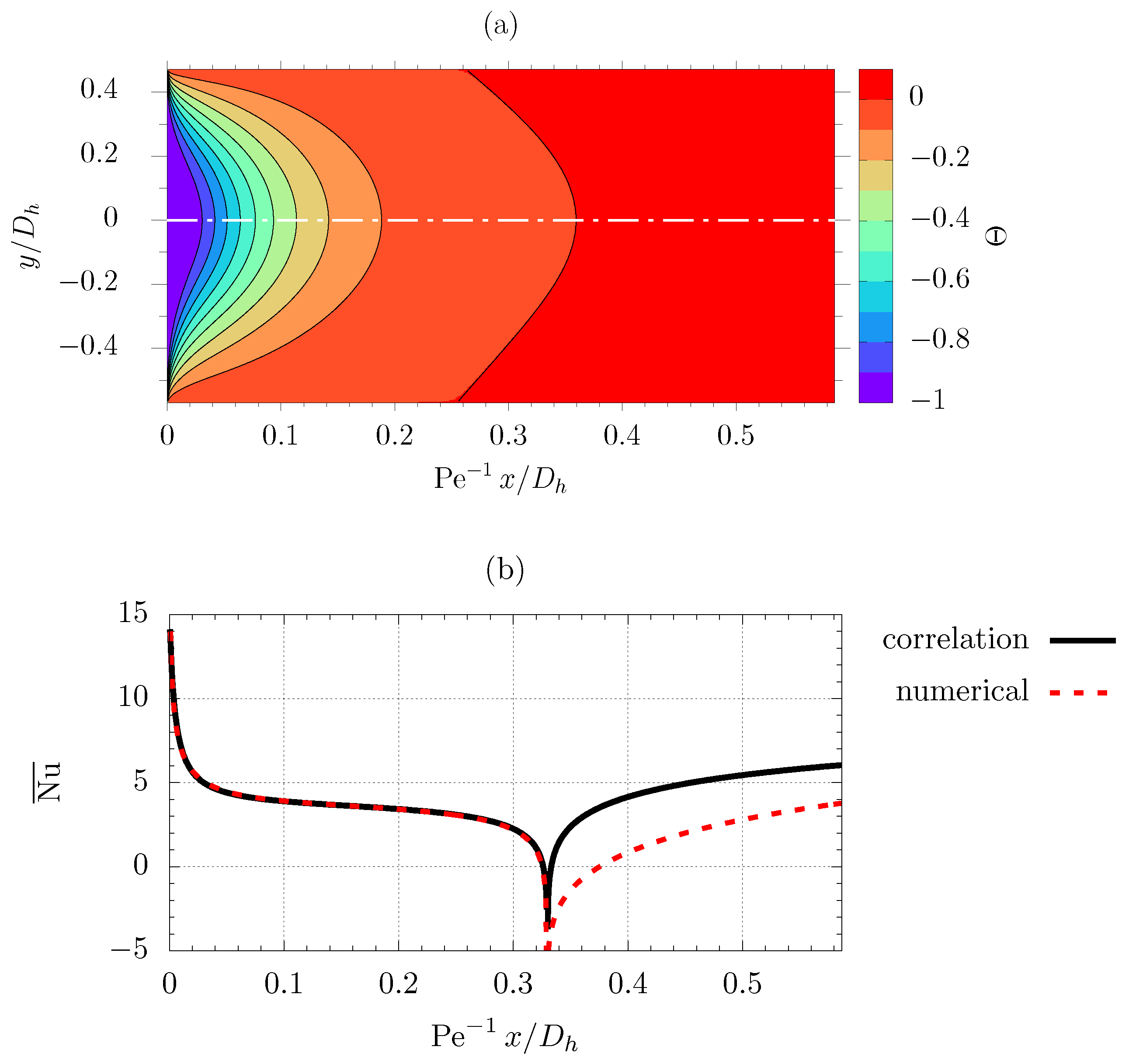
2.3. Graetz–Brinkman Problem
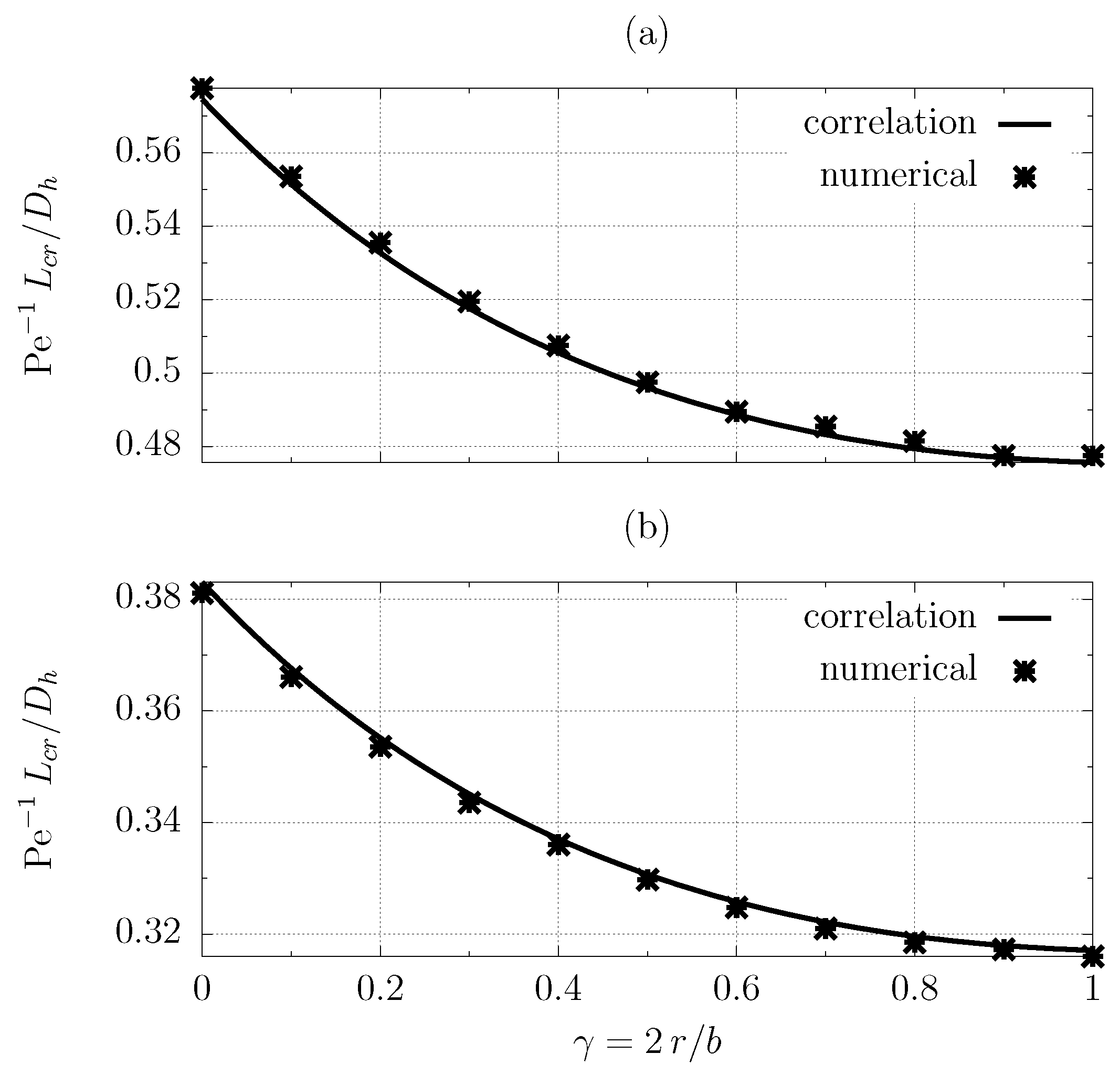
3. Results
3.1. Nusselt Number Correlation
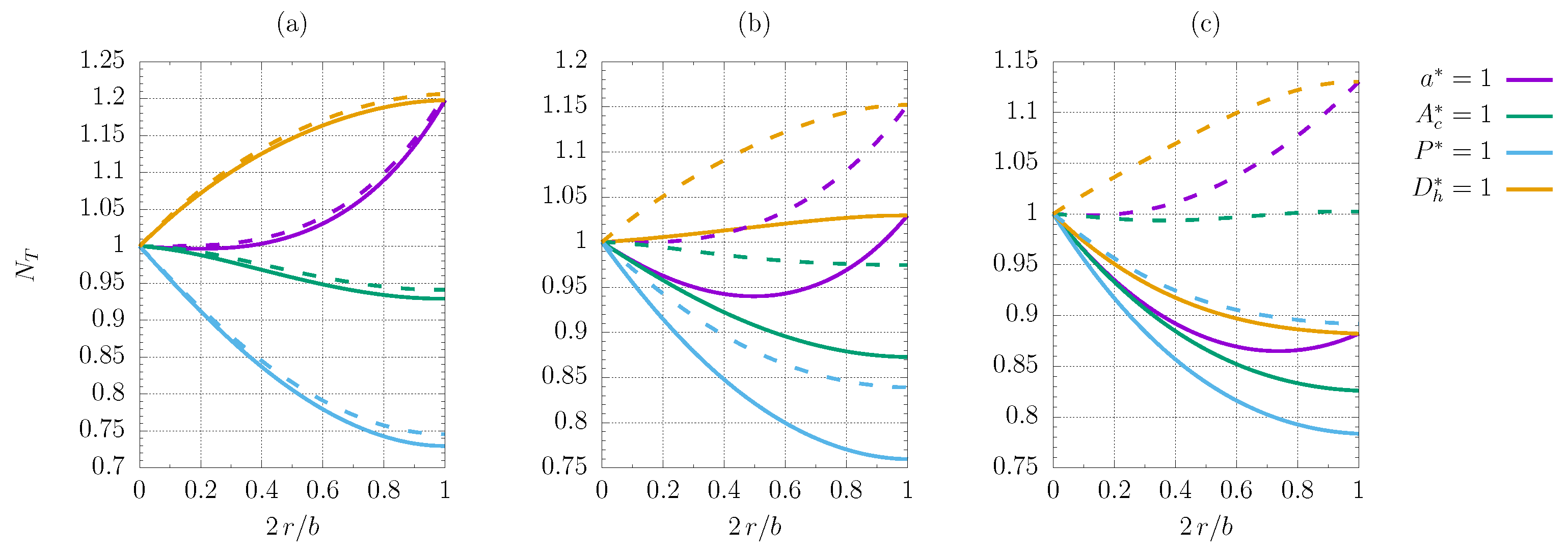
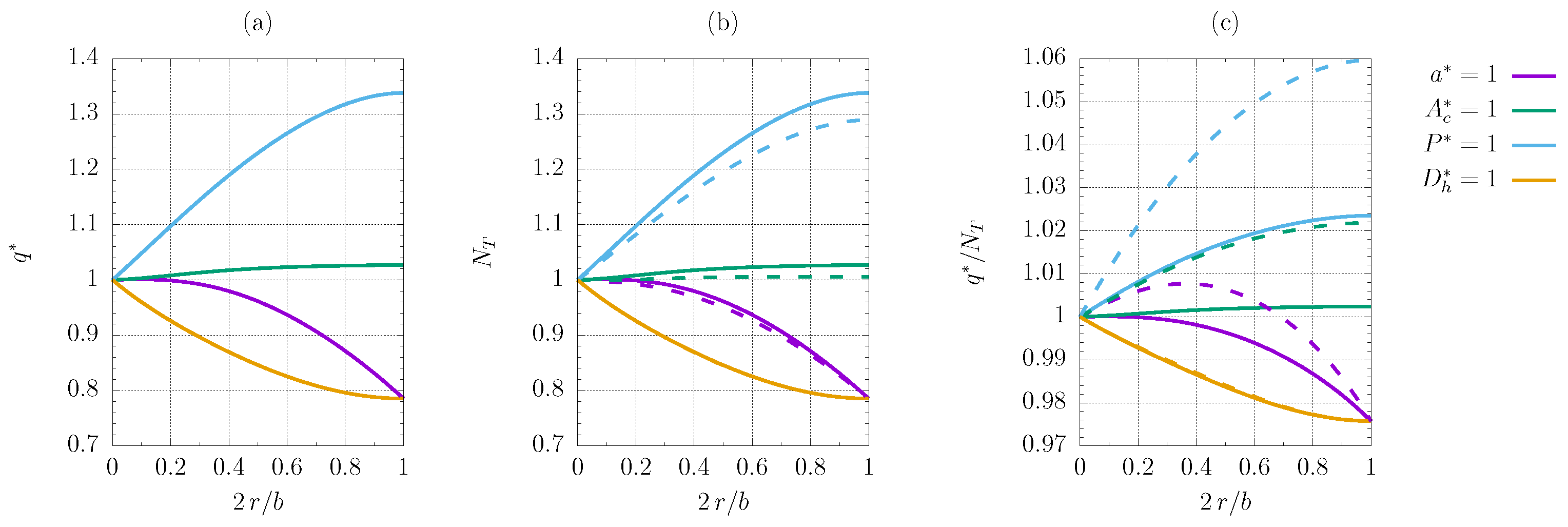
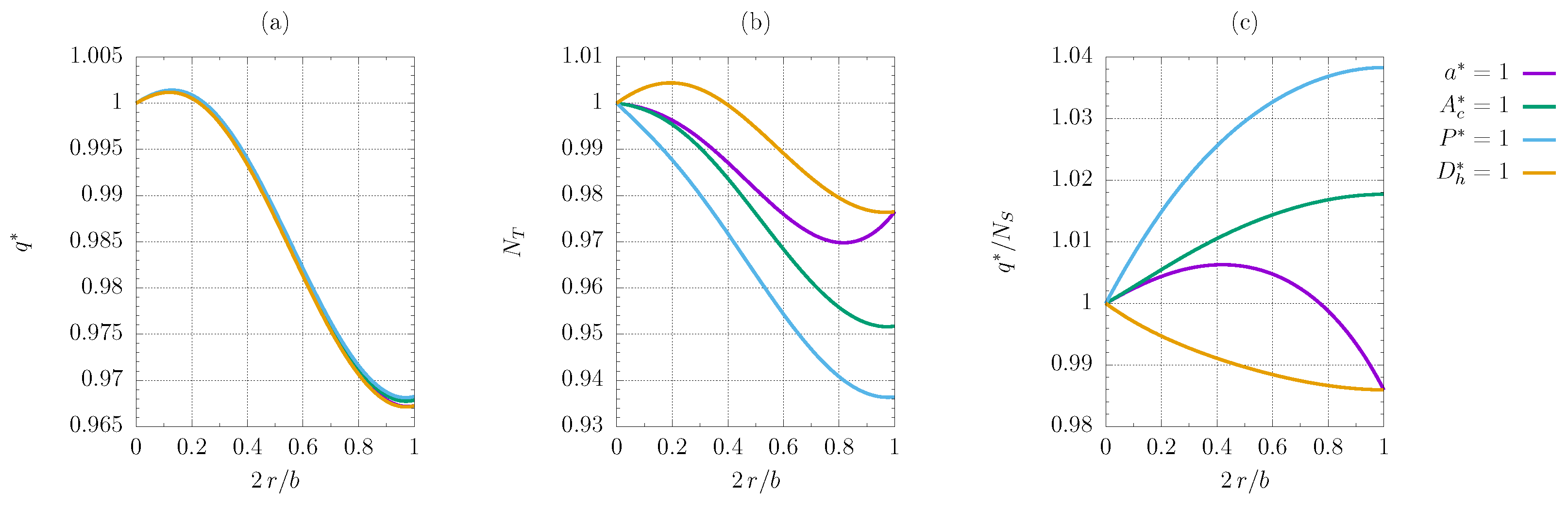
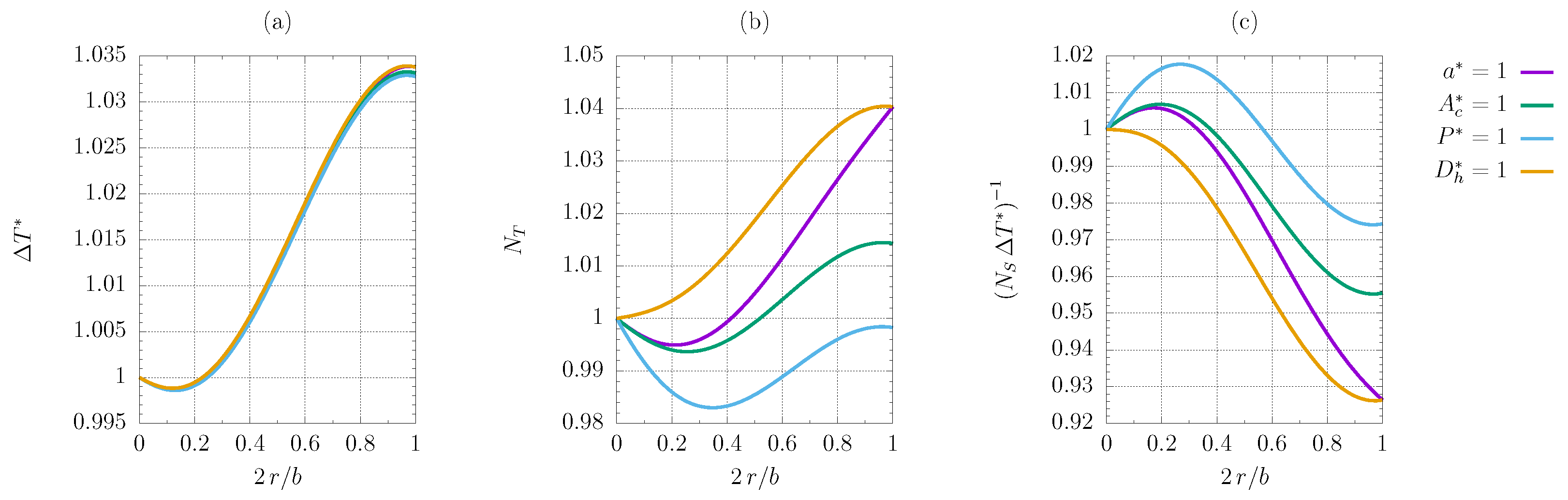
3.2. Microchannel Geometry Optimisation
3.2.1. FG1a Criterion
3.2.2. FG1b Criterion
3.2.3. FG2a Criterion
3.2.4. FG2b Criterion
3.2.5. VG2a Criterion
3.2.6. VG2b Criterion
4. Conclusions
- -
- The constrained heated perimeter and cross-sectional area almost invariably exhibit an improvement from the reference configuration when the corners are smoothed. The sole exception is criterion FG1b. The comparison with a standard modelisation in the case of the VG2a criterion proves that viscous heating plays a crucial role, showing that the increase in the objective function is more substantial when viscous dissipation is present, if the constrained heated perimeter and cross-sectional area are are considered.
- -
- The constrained characteristic length and hydraulic diameter never yield better results if the corners are smoothed, the FG2a criterion being the only exception; for the FG1a and VG2a criteria, there is a local maximum for in-between values of the smoothing parameter corresponding to a minimum improvement of F when the characteristic length is fixed, albeit limited to about ;
- -
- Some plots exhibit maxima and minima for some in-between values of the smoothing radius, but the trend is primarily monotonous.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EGM | Entropy generation minimisation |
| EGN | Entropy generation number |
| FG | Fixed Geometry |
| MFD | Micro-flow device |
| PEC | Performance evaluation criteria |
| VG | Variable Geometry |
References
- Ohadi, M.; Choo, K.; Dessiatoun, S.; Cetegen, E. Next Generation Microchannel Heat Exchangers; Springer Briefs in Applied Sciences and Technology; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y.; Li, M.; Huang, J. A review of development of micro-channel heat exchanger applied in air-conditioning system. Energy Proc. 2012, 14, 148–153. [Google Scholar] [CrossRef]
- Tuckerman, D.; Pease, R.; Guo, Z.; Hu, J.; Yildirim, O.; Deane, G.; Wood, L. Microchannel heat transfer: Early history, commercial applications, and emerging opportunities. In Proceedings of the International Conference on Nanochannels, Microchannels, and Minichannels, Edmonton, AB, Canada, 19–22 June 2011; Volume 2, pp. 739–756. [Google Scholar] [CrossRef]
- Yu, Z.Q.; Li, M.T.; Cao, B.Y. A comprehensive review on microchannel heat sinks for electronics cooling. Int. J. Extrem. Manuf. 2024, 6, 022005. [Google Scholar] [CrossRef]
- Xiong, X.; Li, Y.; Zhao, C.; Yu, W. Recent progress on heat transfer performance and influencing factors of different microchannel heat sinks. J. Enhanc. Heat Transf. 2023, 30, 71–120. [Google Scholar] [CrossRef]
- Li, H.; Zou, Z.; Li, H.; Chen, Y.; Fu, C. Thermal performance of a microchannel primary surface recuperator for portable microturbine generators: Design and experimental study. Appl. Therm. Eng. 2022, 206, 118103. [Google Scholar] [CrossRef]
- Aydin, O.; Avci, M. Laminar forced convective slip flow in a microduct with a sinusoidally varying heat flux in axial direction. Int. J. Heat Mass Transf. 2015, 89, 606–612. [Google Scholar] [CrossRef]
- Lorenzini, M.; Fabbri, G.; Salvigni, S. Performance evaluation of a wavy-fin heat sink for power electronics. Appl. Therm. Eng. 2007, 27, 969–975. [Google Scholar] [CrossRef]
- Vishnu, R.; Selvakumar, R.D.; Alkaabi, A.K.; Vengadesan, S. Active vortex generation and enhanced heat transfer in a 3D minichannel by Onsager-Wien effect. Appl. Therm. Eng. 2023, 233, 121064. [Google Scholar] [CrossRef]
- Morini, G.L. Viscous heating in liquid flows in micro-channels. Int. J. Heat Mass Transf. 2005, 48, 3637–3647. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Liquid flow in microchannels: Experimental observations and computational analyses of microfluidics effects. J. Micromech. Microeng. 2003, 13, 568–579. [Google Scholar] [CrossRef]
- Henning, T.; Brandner, J.; Schubert, K.; Lorenzini, M.; Morini, G. Low-frequency instabilities in the operation of metallic multi-microchannel evaporators. Heat Transf. Eng. 2007, 28, 834–841. [Google Scholar] [CrossRef]
- Baek, S.; Bradley, P.E.; Radebaugh, R. Heat transfer coefficient measurement of LN2 and GN2 in a microchannel at low Reynolds flow. Int. J. Heat Mass Transf. 2018, 127, 222–233. [Google Scholar] [CrossRef]
- Yang, Y.; Chalabi, H.; Lorenzini, M.; Morini, G. The effect on the nusselt number of the nonlinear axial temperature distribution of gas flows through microtubes. Heat Transf. Eng. 2014, 35, 159–170. [Google Scholar] [CrossRef]
- Manda, U.; Mazumdar, S.; Peles, Y. Effects of cross-sectional shape on flow and heat transfer of the laminar flow of supercritical carbon dioxide inside horizontal microchannels. Int. J. Therm. Sci. 2024, 201, 108992. [Google Scholar] [CrossRef]
- Asim, M.; Mohammad, S.; Kanwal, A.; Uddin, G.M.; Khan, A.A.; Mujtaba, M.; Veza, I.; Kalam, M.; Almomani, F. Comparative study of the parameters affecting the performance of microchannels’ heat exchangers: Latest advances review. Energy Sci. Eng. 2023, 11, 3869–3887. [Google Scholar] [CrossRef]
- Suzzi, N.; Lorenzini, M. Viscous heating of a laminar flow in the thermal entrance region of a rectangular channel with rounded corners and uniform wall temperature. Int. J. Therm. Sci. 2019, 145, 106032. [Google Scholar] [CrossRef]
- Suzzi, N.; Lorenzini, M. Numerical Investigation of Thermally Developing and Fully Developed Electro-Osmotic Flow in Channels with Rounded Corners. Fluids 2021, 6, 22. [Google Scholar] [CrossRef]
- Herwig, H.; Hausner, O. Critical view on “new results in micro-fluid mechanics”: An example. Int. J. Heat Mass Transf. 2003, 46, 935–937. [Google Scholar] [CrossRef]
- Morini, G.L.; Lorenzini, M.; Colin, S.; Geoffroy, S. Experimental investigation of the compressibility effects on the friction factor of gas flows in microtubes. In Proceedings of the 4th International Conference on Nanochannels, Microchannels and Minichannels, ICNMM2006, Limerick, Ireland, 19–21 June 2006; Volume 2006 A, pp. 411–418. [Google Scholar] [CrossRef]
- Çetin, B.; Yazıcıoğlu, A.G.; Kakaç, S. Slip-flow heat transfer in microtubes with axial conduction and viscous dissipation—An extended Graetz problem. Int. J. Therm. Sci. 2009, 48, 1673–1678. [Google Scholar] [CrossRef]
- Vocale, P.; Morini, G.L.; Spiga, M. Dilute gas flows through elliptic microchannels under H2 boundary conditions. Int. J. Heat Mass Transf. 2014, 71, 376–385. [Google Scholar] [CrossRef]
- Barletta, A.; Magyari, E. The Graetz–Brinkman problem in a plane-parallel channel with adiabatic-to-isothermal entrance. Int. Commun. Heat Mass Transf. 2006, 33, 677–685. [Google Scholar] [CrossRef]
- Dong, X.; Liu, X. Multi-objective optimization of heat transfer in microchannel for non-Newtonian fluid. Chem. Eng. J. 2021, 412, 128594. [Google Scholar] [CrossRef]
- Lorenzini, M.; Daprá, I.; Scarpi, G. Heat Transfer for a Giesekus Fluid in a Rotating Concentric Annulus. Appl. Therm. Eng. 2017, 122, 118–125. [Google Scholar] [CrossRef]
- Kiyasatfar, M. Convective heat transfer and entropy generation analysis of non-Newtonian power-law fluid flows in parallel-plate and circular microchannels under slip boundary conditions. Int. J. Therm. Sci. 2018, 128, 15–27. [Google Scholar] [CrossRef]
- Bayareh, M. An overview of non-Newtonian nanofluid flow in macro- and micro-channels using two-phase schemes. Eng. Anal. Bound. Elem. 2023, 148, 165–175. [Google Scholar] [CrossRef]
- Colin, S.; Lalonde, P.; Caen, R. Validation of a second-order slip flow model in rectangular microchannels. Heat Transf. Eng. 2004, 25, 23–30. [Google Scholar] [CrossRef]
- Su, L.; Yang, Y. Convective Heat Transfer and Entropy Generation Analysis in Elliptic Microchannels. ASME J. Heat Mass Transf. 2024, 146, 021004. [Google Scholar] [CrossRef]
- Sadr, R.; Yoda, M.; Zheng, Z.; Conlisk, A. An experimental study of electro-osmotic flow in rectangular microchannels. J. Fluid Mech. 2004, 506, 357–367. [Google Scholar] [CrossRef]
- Geri, M.; Lorenzini, M.; Morini, G. Effects of the Channel Geometry and of the Fluid Composition on the Performance of DC Electro-osmotic Pumps. Int. J. Therm. Sci. 2012, 55, 114–121. [Google Scholar] [CrossRef]
- Shamshiri, M.; Khazaeli, R.; Ashrafizaadeh, M.; Mortazavi, S. Electroviscous and thermal effects on non-Newtonian liquid flows through microchannels. ASME J. Non–Newton. Fluid Mech. 2012, 173–174, 1–12. [Google Scholar] [CrossRef]
- Shit, G.; Mondal, A.; Sinha, A.; Kundu, P. Electro-osmotic flow of power-law fluid and heat transfer in a micro-channel with effects of Joule heating and thermal radiation. Phys. A Stat. Mech. Its Appl. 2016, 462, 1040–1057. [Google Scholar] [CrossRef]
- Al-Rjoub, M.; Roy, A.; Ganguli, S.; Banerjee, R. Assessment of an active-cooling micro-channel heat sink device, using electro-osmotic flow. Int. J. Heat Mass Transf. 2011, 54, 4560–4569. [Google Scholar] [CrossRef]
- Al-Rjoub, M.; Roy, A.; Ganguli, S.; Banerjee, R. Improved flow rate in electro-osmotic micropumps for combinations of substrates and different liquids with and without nanoparticles. J. Electron. Packag. Trans. 2015, 137, 021001. [Google Scholar] [CrossRef]
- Michelsen, M.L.; Villadsen, J. The Graetz problem with axial heat conduction. Int. J. Heat Mass Transf. 1974, 17, 1391–1402. [Google Scholar] [CrossRef]
- Basu, T.; Roy, D.N. Laminar heat transfer in a tube with viscous dissipation. Int. J. Heat Mass Transf. 1985, 28, 699–701. [Google Scholar] [CrossRef]
- Aparecido, J.B.; Cotta, R.M. Thermally developing laminar flow inside rectangular ducts. Int. J. Heat Mass Transf. 1990, 33, 341–347. [Google Scholar] [CrossRef]
- Lee, P.S.; Garimella, S.V. Thermally developing flow and heat transfer in rectangular microchannels of different aspect ratios. Int. J. Heat Mass Transf. 2006, 49, 3060–3067. [Google Scholar] [CrossRef]
- Filali, A.; Khezzar, L.; Siginer, D.; Nemouchi, Z. Graetz problem with non-linear viscoelastic fluids in non-circular tubes. Int. J. Therm. Sci. 2012, 61, 50–60. [Google Scholar] [CrossRef]
- Barışık, M.; Yazıcıoğlu, A.G.; Çetin, B.; Kakaç, S. Analytical solution of thermally developing microtube heat transfer including axial conduction, viscous dissipation, and rarefaction effects. Int. Commun. Heat Mass Transf. 2015, 67, 81–88. [Google Scholar] [CrossRef]
- Webb, R.L.; Kim, N.H. Principles of Enhanced Heat Transfer; Taylor and Francis: New York, NY, USA, 2004. [Google Scholar]
- Webb, R.; Eckert, E. Application of rough surfaces to heat exchanger design. Int. J. Heat Mass Transf. 1972, 15, 1647–1658. [Google Scholar] [CrossRef]
- Bergles, A.; Blumenkrantz, A.; Taborek, J. Performance Evaluation Criteria for enhanced heat transfer surfaces. In Proceedings of the International Heat Transfer Conference 5, Tokyo, Japan, 3–7 September 1974. [Google Scholar]
- Bejan, A. The concept of irreversibility in heat exchanger design: Counterflow heat exchangers for gas-to-gas applications. J. Heat Transf. 1977, 99, 374–380. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. Thermodynamic optimization of geometry in engineering flow systems. Exergy Int. J. 2001, 1, 269–277. [Google Scholar] [CrossRef]
- Yilmaz, M.; Sara, O.N.; Karsli, S. Performance evaluation criteria for heat exchangers based on second law analysis. Exergy Int. J. 2001, 1, 278–294. [Google Scholar] [CrossRef]
- Saenen, T.; Baelmans, M. Size effects of a portable two-phase electronics cooling loop. Appl. Therm. Eng. 2013, 50, 1174–1185. [Google Scholar] [CrossRef]
- Stevens, T.; Baelmans, M. Optimal pressure drop ratio for micro recuperators in small sized gas turbines. Appl. Therm. Eng. 2008, 28, 2353–2359. [Google Scholar] [CrossRef]
- Karathanassis, I.K.; Papanicolaou, E.; Belessiotis, V.; Bergeles, G.C. Multi-objective design optimization of a micro heat sink for Concentrating Photovoltaic/Thermal (CPVT) systems using a genetic algorithm. Appl. Therm. Eng. 2013, 59, 733–744. [Google Scholar] [CrossRef]
- Zimparov, V. Extended performance evaluation criteria for enhanced heat transfer surfaces: Heat transfer through ducts with constant wall temperature. Int. J. Heat Mass Transf. 2000, 43, 3137–3155. [Google Scholar] [CrossRef]
- Zimparov, V. Extended performance evaluation criteria for enhanced heat transfer surfaces: Heat transfer through ducts with constant heat flux. Int. J. Heat Mass Transf. 2001, 44, 169–180. [Google Scholar] [CrossRef]
- Zimparov, V.; Vulchanov, N. Performance evaluation criteria for enhanced heat transfer surfaces. Int. J. Heat Mass Transf. 1994, 37, 1807–1816. [Google Scholar] [CrossRef]
- Petkov, V.; Zimparov, V.; Bergles, A. Performance evaluation of ducts with non-circular shapes and laminar fully developed flow. Int. Rev. Chem. Eng. 2012, 4, 379–391. [Google Scholar]
- Petkov, V.; Zimparov, V.; Bergles, A. Performance evaluation of ducts with non-circular shapes: Laminar fully developed flow and constant wall temperature. Int. J. Therm. Sci. 2014, 79, 220–228. [Google Scholar] [CrossRef]
- Ray, S.; Misra, D. Laminar fully developed flow through square and equilateral triangular ducts with rounded corners subjected to H1 and H2 boundary conditions. Int. J. Therm. Sci. 2010, 49, 1763–1775. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ray, S. Performance optimisation of laminar fully developed flow through square ducts with rounded corners. Int. J. Therm. Sci. 2011, 50, 2522–2535. [Google Scholar] [CrossRef]
- Lorenzini, M.; Morini, G. Single-phase, Laminar Forced Convection in Microchannels with Rounded Corners. Heat Transf. Eng. 2011, 32, 1108–1116. [Google Scholar] [CrossRef]
- Lorenzini, M.; Suzzi, N. The Influence of Geometry on the Thermal Performance of Microchannel Heat Sinks with Viscous Dissipation. Heat Transf. Eng. 2016, 37, 1096–1104. [Google Scholar] [CrossRef]
- Suzzi, N.; Lorenzini, M. Performance assessment of electro-osmotic flowof rectangular microchannels with smoothedcorners. Phys. Fluids Conf. Ser. 2023, 2648, 012069. [Google Scholar] [CrossRef]
- Wibulswas, P. Laminar Flow Heat Transfer in Non-Circular Ducts. Ph.D. Thesis, University College London, London, UK, 1966. [Google Scholar]

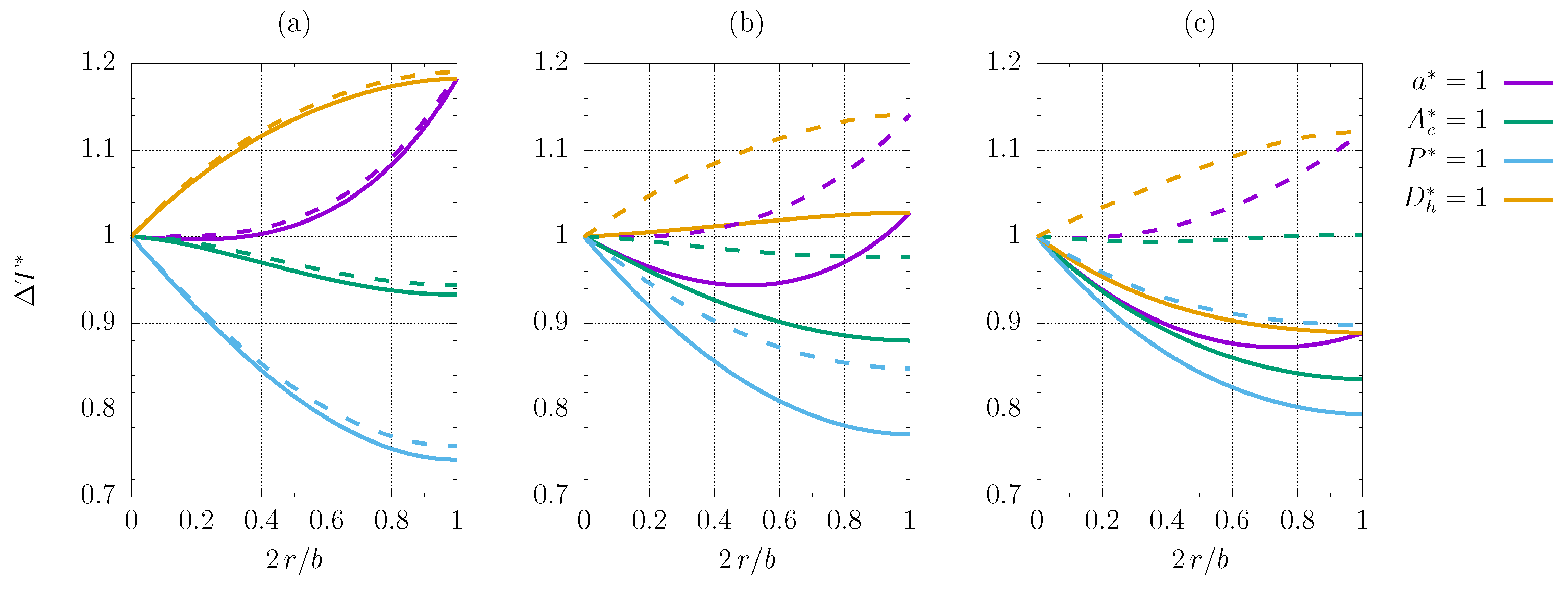
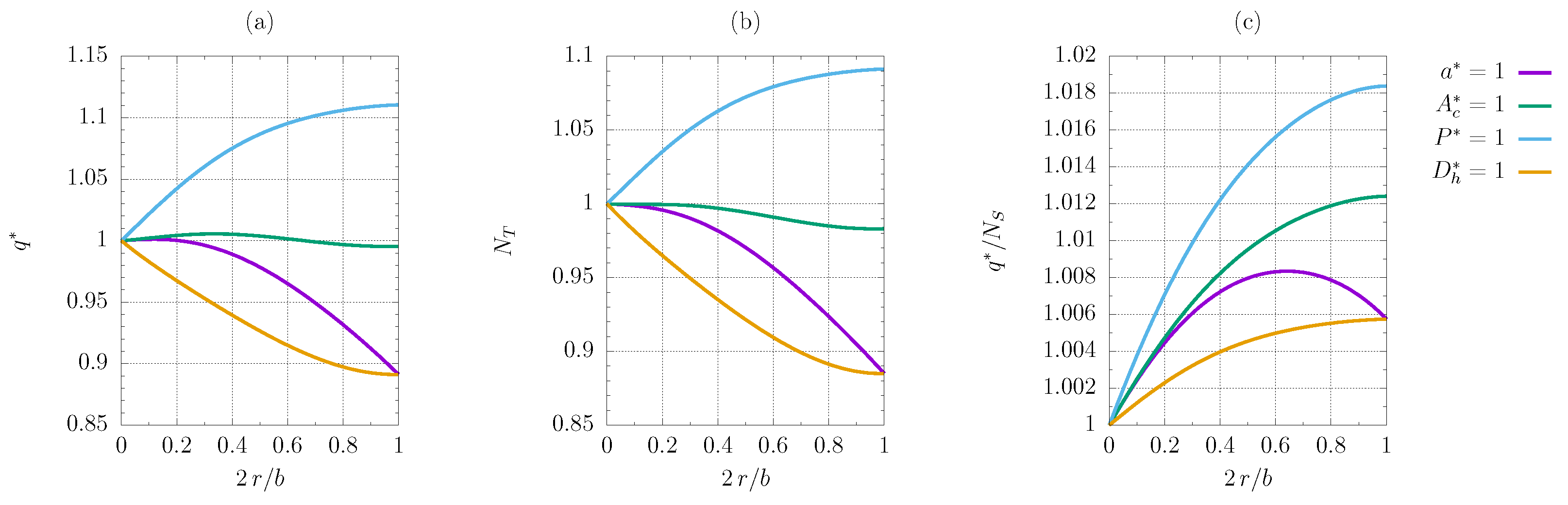
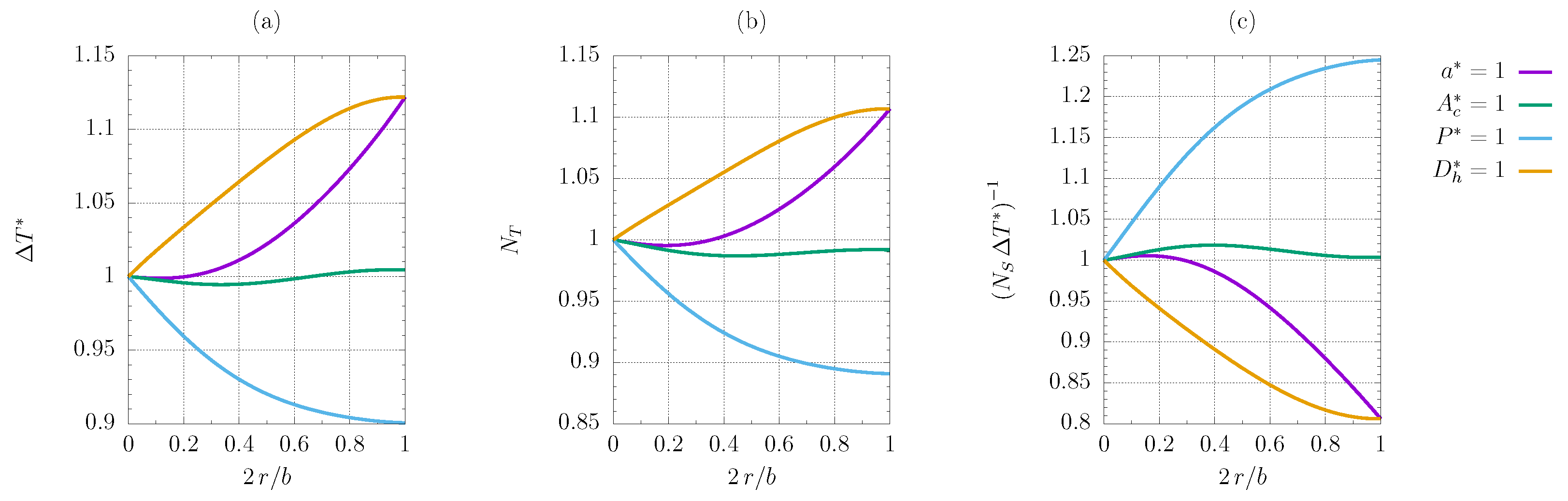

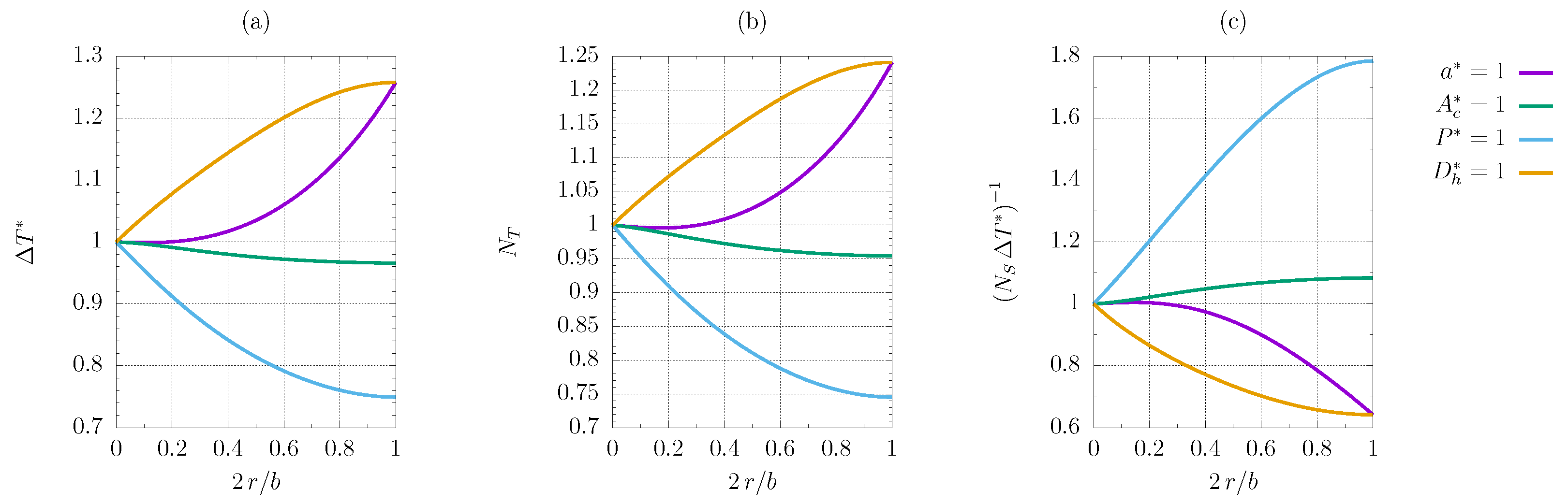
| Criteria | |||||
|---|---|---|---|---|---|
| FG1a | ↑ | 1 | 1 | 1 | |
| FG1b | 1 | ↓ | 1 | 1 | |
| FG2a | ↑ | 1 | 1 | 1 | |
| FG2b | 1 | ↓ | 1 | 1 | |
| VG2a | ↑ | 1 | 1 | 1 | |
| VG2b | 1 | ↓ | 1 | 1 |
| Constraint | |
|---|---|
| b | |||||||
|---|---|---|---|---|---|---|---|
| 0 | 0 | ||||||
| Test Case | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (a) | 1 | 0 | 10 | 35 | 15 | ||||
| (b) | 1 | 0 | 10 | 35 | 15 | ||||
| (c) | 1 | 0 | 10 | 1 | 35 | 15 | 1375 |
| 1 | 0 | 60 | 30 | 1900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lorenzini, M.; Suzzi, N. Combined Geometrical Optimisation of a Square Microchannel with Smoothed Corners. Energies 2024, 17, 2666. https://doi.org/10.3390/en17112666
Lorenzini M, Suzzi N. Combined Geometrical Optimisation of a Square Microchannel with Smoothed Corners. Energies. 2024; 17(11):2666. https://doi.org/10.3390/en17112666
Chicago/Turabian StyleLorenzini, Marco, and Nicola Suzzi. 2024. "Combined Geometrical Optimisation of a Square Microchannel with Smoothed Corners" Energies 17, no. 11: 2666. https://doi.org/10.3390/en17112666
APA StyleLorenzini, M., & Suzzi, N. (2024). Combined Geometrical Optimisation of a Square Microchannel with Smoothed Corners. Energies, 17(11), 2666. https://doi.org/10.3390/en17112666







