Abstract
Ocean energy sources are a promising source of energy. However, simulating a hydrokinetic farm with multiple units requires significant computational resources, while physical experimentation on site is expensive. Therefore, the scientific challenge is to develop analytical and experimental tools that consider real aspects of areas with generation potential in a controlled laboratory environment. This paper presents a theoretical and experimental tool for analysing the interconnection of a hydrokinetic energy farm comprising 20 generation units. The test bench is a Power Hardware in the Loop type, consisting of one physical prototype generator to scale and 19 discrete averaged models operating in real-time. The system allows generators to interact through an amplifier, emulating the impact of power injection in a small electrical network. This is based on the variability of the marine resource, specifically the current velocities in the Cozumel-Mexico channel. Unlike other publications, the most significant contribution of this work is a complete feasible emulation of a marine current plant interconnected to an electrical grid, where the objective is to have a global analysis of the operation of each generation unit and the impact of the interconnection as a whole, considering that such information is of utmost importance for the execution of future projects of power generation from the sea.
1. Introduction
Ocean energy is currently seen as a promising source of energy for local power generation and microgrids. Viable options have been formulated for medium- and long-term solutions to electrify remote areas, creating economic growth opportunities to combat energy poverty [1,2]. Different technologies that are focused on the extraction of energy have been published in the state of the art. Ocean currents are the most promising renewable energy, due to their semi-permanent nature [3]. The efficiency of these devices depends on extensive multidisciplinary research and development. This includes measuring current velocities, designing turbines and their structural support, designing electrical generators and power electronic converters with their own regulations, and assessing the impact on the voltage stability of the electrical grid to determine compatibility and interconnection levels [4].
Real-time simulation has provided research benefits in various scientific fields, including aeronautics, robotics, and renewable energy systems [5].
HIL (Hardware in the Loop) is a real-time plant model interfaced to a piece of hardware under test. It typically employs low-power signal interfaces from sensors and actuators, enabling comprehensive closed-loop testing without the need for testing on real systems.
In contrast, PHIL (Power Hardware in the Loop) simulation involves the integration of one or more real-time plant models with physical devices, such as power electronics converters, motors, generators, and/or renewable energy sources. This interaction is facilitated through control and monitoring signals, as well as power exchange from bidirectional amplifiers.
PHIL simulation offers a distinct advantage over HIL in that it enables the real-time comparison of the intricate and dynamic behaviour of a physical component with its mathematical representation. This approach allows for a more comprehensive technical and scientific analysis of the phenomena under investigation [6].
In the field of marine energy, detailed simulation of marine turbines may involve complex techniques such as finite element analysis or frequency response. Similarly, detailed simulation of power electronic converters requires integration steps on the order of 10−6 s or 10−7 s to represent switching frequencies.
The simulation of hydrokinetic generator systems is computationally expensive, while large-scale experiments require significant economic and time investment [7].
The accuracy of these experiments is ultimately limited by scaling rules that cannot be satisfied simultaneously.
Although there are several non-detailed modelling techniques, such as phasor models, small models, linearized models, and simple algebraic models [8], that can represent generation systems interconnected to the power grid using less computational load, the technical and scientific challenge is to obtain sufficiently accurate models to capture the dynamics of power converters without requiring a large number of computational resources to simulate several systems in parallel [6].
This paper presents the optimal development of small-signal models for an ocean current power plant to be implemented and tested on real-time simulators. Tests can be conducted in the early stages of the design process [9] by using a set of scaled experiments and mathematical models of the system components under strictly controlled conditions. This allows for the analysis of different approaches. The given information allows for a more precise understanding of component behaviour in realistic operational scenarios while keeping computational and monetary costs low [9,10].
The need to accurately represent the interconnection of a marine current generation plant to a distribution network lies in the importance of comprehensively understanding the interactions of a new project in order to minimize calculation and installation errors prior to its commissioning. It is believed that research tools such as those illustrated here have a direct impact on the national and international objectives of the future utilization of the potential for energy generation by means of the sea. Therefore, it is essential to have as much information as possible to facilitate this process. It is important to note that all evaluations presented are objective and unbiased. Table 1 reviews previous studies on ocean energy harnessing using Hardware-in-the-Loop (HIL), Software-in-the-Loop (SIL), and Power-Hardware-in-the-Loop (PHIL).

Table 1.
State of the art applicable to HIL simulation of ocean current power generation.
1.1. State of the Art
In [11], SIL simulation has been implemented using a low real-time controller method. The energy conversion involves controlling a DC machine, piston, hooks, and counterweights, with the machine programming imitating the ocean currents in real-time. This research places greater emphasis on the mechanical part, without considering the electrical conversion process.
In [12], a hybrid simulation called “Real-time Hybrid Modelling for Ocean Wave Energy Converters” was conducted to address problems such as physical implementation difficulties and high computational cost. The study demonstrates the feasibility of emulating wave movement using a stepper motor and piston actuator. Additionally, the researchers conducted measurements and characterised the swell.
The method described in [13] involves the implementation of a real-time controller to predict wave force excitation and its impact on energy absorption in the near future. The study presents the predicted effect of wave intensity on the energy absorption of a Wave Energy Converter (WEC) that simulates a buoy with a radius of 5 m, a spring, and a damper. The results are used to compare force, linear velocity, and power with and without error prediction. Despite the facts, it is important to note that the work does not provide an in-depth discussion of electric conversion.
In [14], a maximum power point tracking (MPPT) strategy is introduced to maximize energy conversion in a real-wave environment. The approach utilizes a WEC-based linear generator with a power of 10 kW, a linear test bench to replicate ocean wave movements in the laboratory, and a 30 kW power system for real-time data acquisition. The primary contribution of this study is the MPPT achieved by utilizing the phase resistance of a grinding machine and a DC/DC frequency converter controlled by the real-time system OPAL-RT. It is important to note that this research does not cover the interconnection of the linear generator to the electrical grid.
In [15], a simulation of an Oscillating Water Column (OWC) was conducted on the Basque Coast in Spain using the MIL and SIL frameworks. The simulation included a Wells Turbine and a Double-Fed Induction Generator (DFIG) for wave energy conversion. The power and torque results obtained through simulation, based on two-meter-high waves with ten-second periods, were applied to a PMSG generator.
In [16], the authors present a prototype based on real data collection and emulation of a 22 kW turbine. The study shows velocity graphs and torque obtained from the generator, but the electrical power conditioner for interconnecting to the grid is not considered.
At different conferences, the authors of [17,18,19] have presented their work on converting ocean energy into electrical energy using a two-machine system, one as an emulator and the other as a generator. The informatics subsystem consists of a computational unit that implements the characteristics of a marine turbine and control algorithms for the universal emulator. The results include velocity graphs and torque simulation. Instead, only a small part of the electric system stages was presented.
In [20], waveforms were simulated in real-time over the stages of the electricity grid interconnection using the same emulator as in [19]. The simulation includes the process of active power injection into the electric grid using a back-to-back converter.
Recent research that covers all the ocean energy conversion process is presented in [21], where the authors focus on the implementation of wells within an oscillating water column. They utilize a hydrokinetic generator prototype that employs a turbine emulator connected by an axis to a PMSG machine. Energy is harvested using a PFC boost rectifier followed by a VSC converter for interconnection to the electrical grid. Nevertheless, although the study is comprehensive, the authors do not thoroughly examine the stages of energy conversion in the phases of power converters. Additionally, the tension variations exhibited in the grid are not attributed to generating fluctuations caused by ocean energy. Based on the analysed research and the information presented in Table 1, it is evident that technological development begins with the measurement process, followed by the survey of mechanical collectors, implementation of the electric power conversion process, and finally, interconnection to the electrical grid. Instead, investigations into interconnected generators as averaged models are necessary due to the current state of technology development. It is important to consider the effects of the generated voltage resulting from natural variability in oceans.
1.2. Paper Contribution
Based on Figure 1, this paper presents the operation of a marine power generation farm using Power-Hardware-in-the-Loop. The farm comprises 20 generating units, out of which 19 are simulated with real-time averaged models and one is a physical prototype.
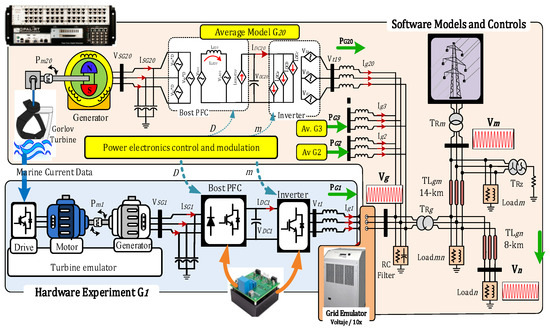
Figure 1.
Power-Hardware-in-the-Loop experiment for 0.5 MW hydrokinetic energy farm interconnection in microgrid.
The authors used measured data from the Cozumel [22,23] channel to closely represent the behaviour of the variations and intermittencies of the marine currents. This research also presents detailed results of the electrical energy acquisition system, including voltage variations machine’s output. Results demonstrate the voltage stability as it passes through different power electronics topologies.
The scheme outlines the steps required to achieve the objective based on the current state of the art. The research can be used for academic and industrial purposes.
2. Mathematical Model
This section describes the mathematical fundamentals of the operation of the hydrokinetic system, showing the governing equations of each component.
2.1. Gorlov Turbine
The Gorlov turbine is a vertical axis hydrokinetic turbine with helicoidal blades, developed by Alexander Gorlov, based on the Darrieus turbine (Figure 2). In a study conducted by BK. Kirke, it was found that modifying the pitch angles of the helical blades of the Gorlov turbine resulted in an improvement of the initial torque and power coefficient by up to 40% [24,25].

Figure 2.
Physical structure of the Gorlov turbine.
The power coefficient for the NACA0014 turbine, as presented in [26], was utilised in this study. The maximum value, depicted in Figure 3, was 38%. The circular tank used in the experiment had dimensions of 10.5 m × 3.2 m. The turbine had a diameter of 0.3 m, a blade chord length of 0.1 m, a height of 0.45 m, and a blade pitch angle of 43.63°. With a fluid velocity of 1.5 m/s, the obtained output value was 84 W.
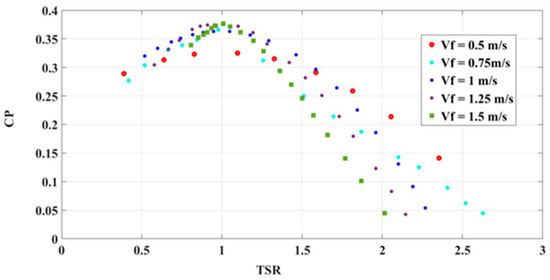
Figure 3.
Power coefficient and TSR curves [26].
The present research utilised the flow velocities from the Cozumel Channel, which range between 0.5 m/s and 1.5 m/s. These values were recorded in situ by [22,23]. As the values closely match those used in the experiment by [26], it is possible to scale the 84 W Gorlov turbine to a 25 kW Gorlov turbine.
The geometry and the maximum power point tracking (MPPT) curve of the 25 kW turbine is computed with Equation (1):
Equation (1) yields an area of 39.26 m2. Then, we propose a turbine height of 1.5 times larger than the diameter of the base in the area obtained; this consideration results in a diameter of 5.1 m. The height of the turbine is achieved by having the cross-sectional area and diameter giving a result of 7.7 m. The next step is to calculate the rotational velocity, to obtain its maximum values. For this we used Equation (2):
where is the flow velocity, is the turbine radius and . The maximum torques are then obtained using Equation (3):
Once the maximum torques and maximum rotational speeds are obtained, the maximum powers are estimated with Equation (4):
The MPPT curve for the 25 kW turbine is displayed in Figure 4.
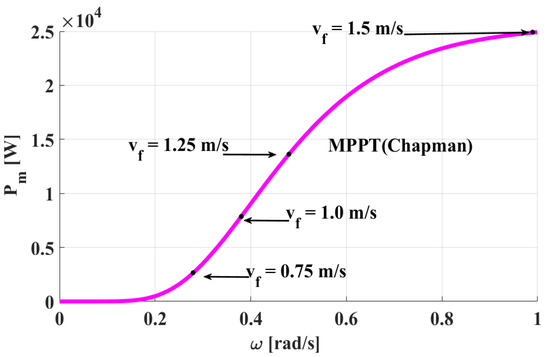
Figure 4.
MPPT for the 25 kW Gorlov turbine.
Theoretical analysis of the turbine operation is conducted using a 1:63 ratio for rotational speed. This is because the maximum speed in our research is 1 rad/s, while the simulation uses 63 rad/s, as stated in [26]. There, the power output of the turbine is approximately 100 W, whereas for our research it is 25 kW. To increase the scale, a gearbox is used.
2.2. PMSG Generator
Assuming that the three-phase armature of the permanent magnet synchronous generator is symmetrically distributed, and that the mutual inductance is zero, the voltage is calculated as presented in (5) [27,28]. Core-generator saturation, eddy currents, and hysteresis losses are neglected.
where is the phase voltage of the generator; is the current phase of the generator; is the winding resistance of the generator stator; is the inductance from the generator stator winding; is the force, With each other, is the number of the poles of a generator, is the rotor speed generator, is the permanent magnet flux. In the system of the rotating coordinate system d-q [27,28], the models for voltage generation on PMSG are
and are the components in the voltage of the axle generator stator in the axis d and axis q, respectively; and are the components of the generator stator current in the axis d and axis q, severally; and are the components of induction in the axis d and axis q, each to each. The equation of electromagnetic torque of the generator can be expressed as
Considering the PMSG including surface assembly structure, given the fact that = = , the electromagnetic torque can be simplified. Finally, the PMSG dynamic is governed by the relationship between the mechanical torque () and electromagnetic torque () as
where represents the system inertia and B is the friction coefficient. The six-poles PMSG physical structure and the main variables diagram of the generator are shown in Figure 5a,b.
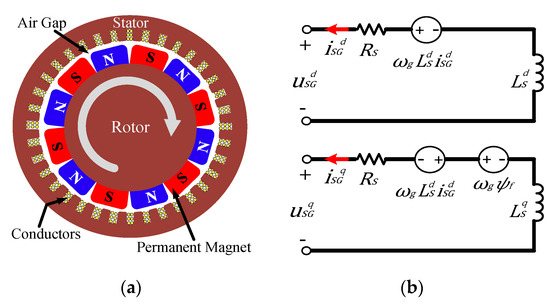
Figure 5.
Physical diagram of the PMSG machine. (a) Physical diagram. (b) Phase diagram.
2.3. PFC DC/DC Boost Converter
In this section, the alternating voltages obtained from the PMSG generator is converted to direct voltage () using a three-phase PFC boost converter consisting of an uncontrolled diode rectifier and a DC-DC boost converter with high frequency operation, as shown in Figure 6 The rectified voltage can be defined as the peak magnitude of the three-phase line-to-line voltage obtained from the PSMG, so it can be represented as
where and have been described in (6) and (7).
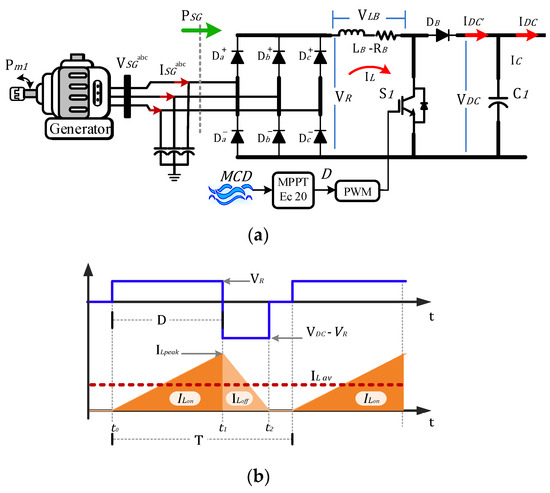
Figure 6.
Three-phase boost PFC rectifier. (a) Topology. (b) Waveforms.
The PFC boost converter is controlled by a duty cycle signal D as the ratio between the on and off times [29]. Thus, from and and , it is possible obtain an average current value considering the waveforms of a boost converter for a discontinuous conduction mode as shown in Figure 6b. Initially, it is observed that the maximum peak current is given by
The current value storage in the inductor between can be defined as
Consider the time period as
The value of discharge current in capacitor can be defined as
Finally, an average current value in the boost converter can be defined as:
The PFC-Boost output current is equivalent to discharge current; therefore, it can be deduced that .
The MPPT PFC-Boost control has the function of obtaining the highest power of each linear speed from the PMSG, obtained through the iterations of and each marine speed to acquire the optimal values such as mechanical power, rotational speed, and torque. [30]. Using the polynomial of (18), it is possible to operate always at the optimal power extraction values of the system, avoiding power losses or deceleration of the turbine-PMSG system. A duty cycle dependent on the marine current speed is obtained by
2.4. VSC Model
Figure 7 shows a three-phase VSC connected to the mains voltage through the impedance , it can produce the phase current which flows to the grid. is the voltage capacitor that depends on , and is the final AC voltage in the VSC ruled by the modulation. Assuming that the switching frequency, , is ten times higher than the linear frequency, , it means ; the average model is valid based on the variable modulation index defined as a sinusoidal variation in the continuous stability [–1, 1]. It can be used to represent the average relationship between the current and voltage of the three-phase VSC rectifier [31], where
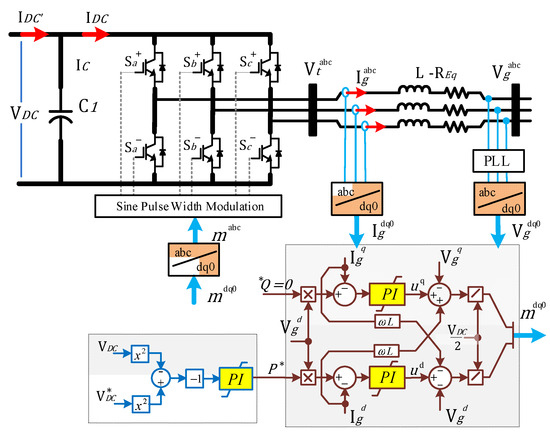
Figure 7.
Three-phase VSC inverter with dq0-Frame control.
The relationship in the time domain to AC side of the three-phase VSC rectifier is established through
The sum of currents entering to the capacitor is
The relationship in the time domain of the DC side of the rectifier is expressed as
The power transfer function between the and voltages with along can be analysed using the dq0-Frame control applying equivalent equations based on the Clarke and Park transformations as [31], where the main purpose is to simplify three variables into two variables, transforming them into invariant signals in time. Finally, a dq0 model derived from AC converter (21) can be described as
The presence of in (24) and (25) indicates the coupled dynamic and . Considering that and , based on the dq0-Frame, it is possible to obtain
where and are two control inputs, replacing (26) and (27) in (24) and (25), respectively; a first order linear system is formed, described in (26) and (27) in the time and frequency domains, as shown in [31].
From this point on, once the information of the modulating variables is available, it is possible to define the power delivered by the VSC converter to the grid interconnection point, considering
Finally, the mathematical models that were analysed allow for a reduced algebraic representation of the mechanical and electrical energy conversion elements. This representation is used as a lightweight model for real-time implementation. It is then validated with a dynamic model and later with a laboratory-scale prototype.
3. Numerical Simulation and Experimental Results
In order to validate the correct operation of a hydrokinetic farm, it is necessary to implement a scaled prototype and real-time model and establish a relationship between the 0.25 kW scaled results (Section 2.1) and the 25 kW software model. The data for both scenarios can be found in Table 2. As previously mentioned, implementing a detailed real-time model can be computationally demanding. Therefore, it is preferable to use reduced models that accurately represent the desired conversion processes at a lower computational cost.

Table 2.
Scale ratio 1:100 between the experimental system and real-time averaged model.
3.1. Real-Time Simulation Models
This research presents a detailed simulation process for the implementation of a hydrokinetic real-time (RT) model. The simulation process highlights the selection of the most significant equations of the system and the use of the parameters listed in Table 2.
A test is carried out to observe the behaviour of both systems for a theoretical step in the velocity of the marine resource (), ranging from 0.9 to 1.5.m/s.
As shown in Figure 8b, the duty cycle increases as the power transfer increases, according to the MPPT points defined by Equation (18).
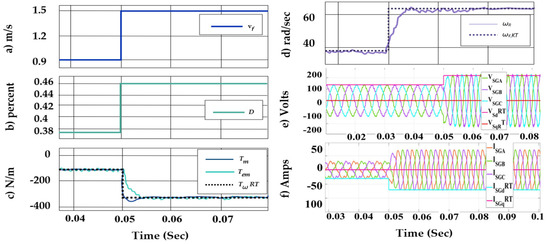
Figure 8.
Gorlov turbine and PMSG models validation. (a) Marine current step. (b) Duty cycle. (c) Torques. (d) PMSG speeds. (e) PMSG abc and dq0 voltages. (f) PMSG abc and dq0 currents.
The behaviour of the mechanical () and electromagnetic () torques and mechanical speed () of the detailed model are contrasted with those obtained by the RT model, obtained from Equation (5), showing an adequate steady-state behaviour of both systems. Finally, in Figure 8e,f, there is an increase in the magnitude and frequency of the voltages VSGabc and currents ISGabc of the PMSG. These are represented in the dq-frame RT model, obtained from (6) and (7).
The DC voltage rectified by the diode bridge is obtained from (12), which is shown in Figure 9a in the detailed model and in the RT model.
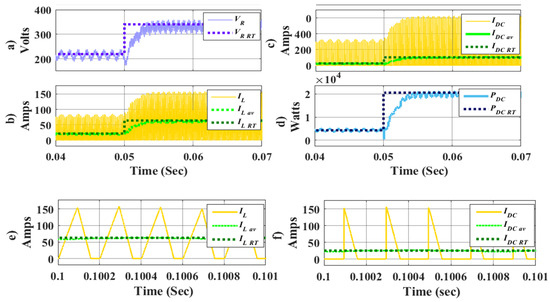
Figure 9.
AC/DC PFC boost model validation. (a) Rectification voltage of PMSG. (b) Input boost currents (IL). (c) Output boost currents (IDC). (d) Power in DC port (PDC). (e) Zoom in IL waveform. (f) Zoom in IDC waveform.
Subsequently, the boost converter’s input current () is observed. This is shown averaged and compared to the current obtained in the RT model () from Equation (17). Additionally, the output current obtained in Equation (16) is shown. The voltage VDC is considered constant in steady state due to the regulation action of the VSC converter, with . The power at the DC port in the RT model is . Finally, Figure 9e,f display a zoomed view of the input and output waveforms of the PFC-Boost, which is consistent with the analysis in Figure 6b.
From the same theoretical step as , it can be observed in Figure 10a that the injected current to capacitor , coming from the boost converter in Figure 10b, generates a transient error of 1.8% on as shown in Figure 10c, in the detailed model. This error has a period of 0.02 s, which is not significant data for a steady-state RT model.
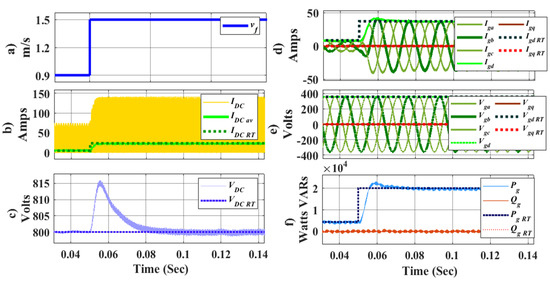
Figure 10.
DC/AC Inverter VSC model validation. (a) Marine current step; (b) Output Boost currents (IL); (c) ; (d) Currents in the grid; (e) Voltages in the grids; (f) Active and reactive powers.
Figure 10d shows the currents from the inverter VSC to the grid at , which are compared with the values from the detailed model and , demonstrating an equivalent steady-state result.
The voltage at the interconnection point is shown with respect to and values on Figure 10e, where the analysed power value has no significant effect on its magnitude. The response of active and reactive power injected into the network is shown in Figure 10f.
Finally, it is possible to represent the conversion process of a hydrokinetic generator in a computationally light form for real-time implementation. The next step is to reproduce the behaviour of 19 of these RT models and operate them in conjunction with a scaled prototype in a PHIL environment, as shown below.
3.2. Experimental Results
The PHIL validation of hydrokinetic generation interconnected to the distribution electrical networks is carried out using hardware conversion stages and controlled by Opal-RT Technologies® with the OP-5600. Nineteen models operate in real time in parallel to a 250 W prototype, as shown in Figure 11, verifying the robustness and correct operation of the scheme in Figure 1. The main implementation’s equipment are shown in Table 3.

Figure 11.
Physical electrical energy acquisition system. (a) Variable frequency drive. (b) PMSM generator. (c) Induction motor. (d) Boost circuit (e) VSC inverter. (f) OP5600 HIL module. (g) Three-phase electrical grid.

Table 3.
Main equipment for marine current PHIL emulation.
Figure 11a,b show a driver used to control the speed of an induction motor in order to emulate the operation of the Gorlov turbomachine. The speed data are provided by an analogue via OPAL RT. Figure 11b shows the PMSG generator, which provides variable magnitude and frequency AC voltage. The detailed simulation of the PMSG generator is shown in Figure 12, and the experimental waveforms are presented later.
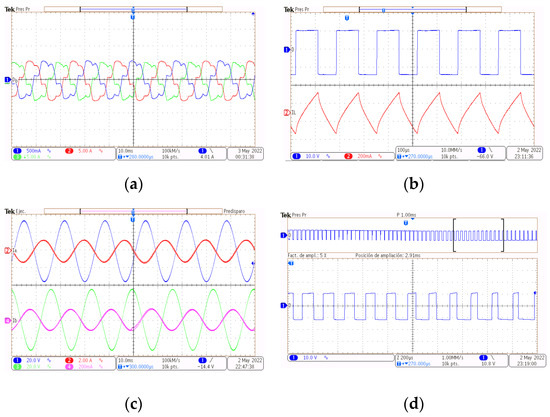
Figure 12.
The experimental variables waveform in scaled-down prototype. (a) Currents on PMSG. (b) Duty cycle and current in PFC boost converter. (c) PWM modulation variables. (d) Grid current and voltage interconnection.
Figure 11d shows the AC/DC PFC-Boost converter that rectifies and extracts the electrical power from the PMSG based on the MPPT polynomial relationship described in Equation (18). Figure 11e shows the VSC converter that performs the interconnection stage to the electrical grid. It operates in inverter mode from the dq0 control scheme seen in Figure 7.
The waveforms in the simulation and experiment are shown next. The function of the VSC is to inject the power from the DC port into the electrical microgrid. This power comes from the previous mechanical and electrical conversion of the VSC to inject the power from the DC port into the electrical microgrid. This power comes from the previous mechanical and electrical conversion stages. Real-time operation is based on the OPAL RT simulator (Figure 11f). The simulator executes control rules for the physical power electronics converters and communicates with the software models of generators and the electrical microgrid.
The power variables communicate with each other through the California Instruments network emulator, as shown in Figure 11g. This emulator is controlled by the OPAL RT simulator to physically represent an interconnection node at scale.
This section presents the oscilloscope-captured experiment waveforms, following the scaled parameters in Table 2 and the test-bench construction described above. Figure 12a shows the currents of the 250 W PMSG, which operate with a total harmonic distortion (THD) of approximately 16% for the experiment and 12% for the simulation. The difference in impedance between a 250 W PMSG and the simulation on a 25 kW machine can be attributed to this variation.
Figure 12b presents the duty cycle and IL waveform in the PFC-boost converter. The current waveforms in this DC/DC power conversion stage are similar to the theoretical waveforms presented in Figure 6b and the detailed simulation in Figure 9.
The VSC variable modulation waveforms are shown in Figure 12c as a pulse train under SPWM modulation to operate the power switches.
The voltage and current of the electrical grid are manifested in reverse phase, which refers to the active power injected into the grid. The laboratory tests results are shown in Figure 12d for a current magnitude of nearly 7.3 A and 44 VLL, showing a peak sine at 36 V. The simulation waveform in Figure 12d shows a current of 73 A and 440 VLL voltage with a peak at 360 V.
3.3. Power-Hardware-in-the-Loop Integrations
To fully emulate the integration of a hydrokinetic generation farm, a grid equivalent is necessary.
For this small farm, a three-node distribution network, with two sections of short distribution lines attached to loads and transformers, is implemented. This allows for a voltage variability analysis regarding the injection of generated power. Table 4 lists the parameters of the implemented network.

Table 4.
Electrical grid parameters.
The interconnection behaviour of the PHIL system and the hydrokinetic power farm interconnection is shown in Figure 13. This is the result of the whole system from the energy source to the electric grid.
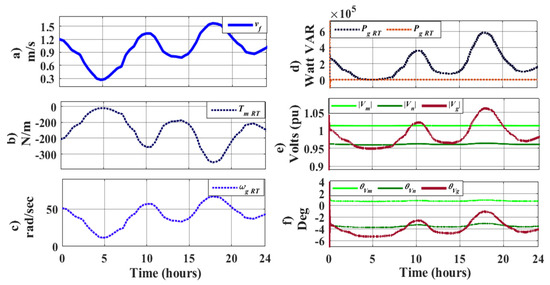
Figure 13.
Measurements of PHIL scenery for hydrokinetic farm.
The input data, i.e., ocean current velocity, are drawn in Figure 13a. The torque and angular velocity for each generation unit are shown in Figure 13b,c, respectively. The total injected active and reactive power generated are shown in Figure 13d, demonstrating the effect of voltage and angle variation at each power grid node in Figure 13e, and Figure 13f respectively.
Based on the given characteristics, the simulation and experiment demonstrate optimal power extraction from the generators until the injection of active power into the microgrid.
On the other hand, the waveforms in the simulation and experiment demonstrate the equivalent process in real-time between the 250 W prototype systems and the 25 kW software models. Therefore, it is possible to define that this type of analysis is feasible through communication with a power amplifier.
This approach enables the analysis of the effects of voltage variations and losses in the main components of an electrical network, which is one of the primary contributions of this article.
Table 5 presents a summary of voltage variabilities at different levels of active power penetration.

Table 5.
Main variables conversion process with respect to marine current in the hydrokinetic 0.5 mw farm interconnection.
4. Conclusions
The majority of the publications found in the state of the art address the efficiency and behaviour of different marine turbo-machines. It has been found that the papers that involve the stages of power electronics conversion in order to analyse the processes and effects of mechanical to electrical energy conversion, such as [19,20,21], only analyse the interconnection of a generation unit interconnected to an infinite bus. In contrast, the most significant contribution of this work is a complete emulation of a farm interconnected to a three-node distribution power grid. This allows for a comprehensive analysis of the operation of each unit and the impact of interconnection as a whole.
This paper describes the implementation of a PHIL marine power generation system based on a Gorlov turbine and PMSG generator in a laboratory setting. The system was also simulated in real-time. The simulation model was created using the turbine curves, PMSG machine model, and the averaged behaviour of the AC/DC and DC/AC conversion stages. The PHIL system has been designed to implement 19 software generators and a scaled physical prototype. It aims to emulate the generation of a 0.5 MW marine power farm, which is interconnected to a three-node power grid.
The validation results demonstrate a reliable correlation between the marine generation software and hardware systems. The software successfully reproduces various states of generation based on actual measurements of marine resources. This emulation allows for the assessment of the impact of voltage variability on the interconnection node of a network and its neighbouring nodes resulting from marine generation.
The effectiveness of the PHIL system in verifying control strategies and considering design iterations in the mechanical, electromagnetic, and control parts of a marine generation farm has been verified. Structural changes generate low or no monetary costs in the analysed tests and case studies.
5. Future Works
5.1. Volt/Var Regulation
For future research, the proposed PHIL system can be expanded to carry out studies on the optimal Volt/Var voltage regulation at the interconnection point. Using the same marine current profile, Figure 14 shows the injection of reactive power, where the voltage Vg = 1 pu is maintained.
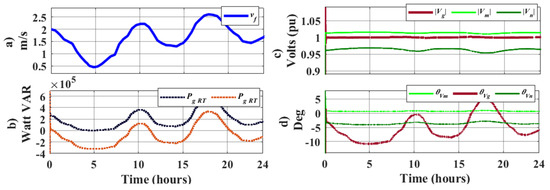
Figure 14.
Effect of Volt/Var regulation control in Vg; (a) Aleatory Marine current; (b) Active and reactive powers (c) Nodal voltages (d) Angle Voltages.
5.2. BESS Integration
In this context, it is necessary to analyse the optimal sizing and the cost/benefit. of the system according to the generation, expansion, and electrical parameters profiles. Figure 15 shows the effect of adding a BESS where it is possible to reduce the generation variability in a range and improve the voltage regulation at the interconnect point.
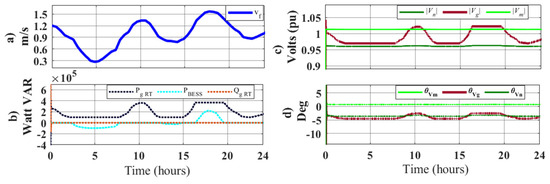
Figure 15.
Effect of BESS integration; (a) Aleatory Marine current; (b) Active and reactive powers (c) Nodal voltages (d) Angle Voltages.
Author Contributions
Conceptualization, U.J.-R. and J.R.R.-R.; Formal analysis turbomachine, C.E.; Project administration and funding acquisition, E.M.; Experiment, N.M.S.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Fondo Sectorial CONACYT-SENER-Sustentabilidad energética, project 249795 “Centro Mexicano de Innovación en Energía del Océano (CEMIE-Océano)”, and in part by the Programa de Apoyos para la Superación del Personal Académico de la UNAM (PASPA) 2023.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Nomenclature | Abbreviation |
| At | Transversal Area |
| DC | Direct Current |
| Cpmax | Maximum Power Coefficient |
| DFIG | Double Fed Induction Generator |
| Fc | Commutation Frequency |
| HIL | Hardware in the Loop |
| MIL | Model in the Loop |
| MPPT | Maximum Power Point Tracking |
| Np | PMSG Poles par Number |
| OWC | Oscillating Water Column |
| OWEC | Ocean Wave Energy Converters |
| PHIL | Power Hardware in The Loop |
| Pm | Mechanical Power |
| PMSG | Permanent Magnet Synchronous Generator |
| SIL | Software in the Loop |
| Electromagnetic torque | |
| Tmax | Maximum Torque |
| Tm | Mechanic Torque |
| TSR | Tip Speed Ratio |
| Vf | Flow Velocity |
| Vr | Boost Input Voltage |
| VSC | Voltage Source Converters |
| WEC | Wave Hardware in the Energy Converter |
| Symbols | |
| Φ | Inclination angle |
| b | Friction coefficient |
| D | Service cycle |
| fcom | Commutation VSC |
| fline | Line frequency |
| Esg | PMSG induced voltage |
| The phase current of VSC | |
| ILavmod | Average current |
| ILpeak | Peak current |
| Isg | PMSG generator current |
| J | Inertial momentum |
| LB | Boost inductance |
| y | The components of induction in the axis d and axis q. |
| L-Req | Impedance of VSC |
| Modulation index | |
| Rs | The winding resistance of the generator stator |
| T | Period |
| The permanent magnet flux | |
| The component in the voltage of the axle generator stator axe d | |
| The component in the voltage of the generator stator in axe q | |
| VDC | Boost output voltage |
| Mains voltage of VSC | |
| Vsg | PMSG terminal voltage |
| The final AC voltage | |
| ωg | Mechanical speed |
| ωmax | Maximum rotational speed |
References
- Gorr Pozzi, E. Wave energy Resource Harnessing assessment in a subtropical costal Region of the pacific. J. Mar. Sci. Eng. 2021, 9, 1264. [Google Scholar] [CrossRef]
- Khan, J.; Leon, D.; Moshref, A.; Arabi, S.; Bhuyan, G. Network Security Assessments for Integrating Large-Scale Tidal Current and Ocean Wave Resources into Future Electrical Grids. Proc. IEEE 2013, 101, 956–977. [Google Scholar] [CrossRef]
- Couch, S.J.; Wallace, A.R.; Bryden, I.G. Overview of the SUPERGEN Marine Energy Research Program. In Proceedings of the 2007 International Conference on Clean Electrical Power, Capri, Italy, 21–23 May 2007; pp. 312–314. [Google Scholar]
- Rahman, S.; Saha, S.; Islam, S.N.; Arif, M.T.; Mosadeghy, M.; Haque, M.E.; Oo, A.M. Analysis of Power Grid Voltage Stability with High Penetration of Solar PV Systems. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–8. [Google Scholar]
- Cao, S.; Lin, N.; Dinavahi, V. Faster-than-real-time hardware emulation of transients and dynamics of a grid of microgrids. IEEE Open Access J. Power Energy 2023, 10, 36–47. [Google Scholar] [CrossRef]
- Opal-RT Corporate Headquarters. Power hil (p-hil): A Revolution in the Industry. Available online: https://blob.opal-rt.com/medias/L00161_0439.pdf (accessed on 1 May 2024).
- Chen, H.; Tang, T.; Aït-Ahmed, N.; Benbouzid, M.E.H.; Machmoum, M.; Zaïm, M.E.-H. Attraction, Challenge and Current Status of Marine Current Energy. IEEE Access 2018, 6, 12665–12685. [Google Scholar] [CrossRef]
- VLacerda, A.; Araujo, E.P.; Cheah-Mañe, M.; Gomis-Bellmunt, O. Phasor Modeling Approaches and Simulation Guidelines of Voltage-Source Converters in Grid-Integration Studies. IEEE Access 2022, 10, 51826–51838. [Google Scholar] [CrossRef]
- Baracho, F.R.A.C.; Coelho, A.M.L.; Pereira, F.C.S.; Silveira, P.M. A theoretical and practical approach for under excitation protection and control studies of large hydrogenerators in a real-time environment. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–11. [Google Scholar]
- Prabakar, K.; Pratt, A.; Krishnamurthy, D.; Maitra, A. Hardware-in-the-Loop Test Bed and Test Methodology for Microgrid Controller Evaluation. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, USA, 16–19 April 2018; pp. 1–9. [Google Scholar]
- Chen, C.-A.; Li, X.; Zuo, L.; Ngo, K.D.T. An innovative generic platform to simulate real-time PTO for ocean energy converters based on SIL method. IEEE Trans. Ind. Electron. 2018, 68, 3262–3272. [Google Scholar] [CrossRef]
- Borner, T. Real Time Hybrid Modeling for Ocean Wave Energy Converters; University of California: Berkeley, CA, USA, 2015. [Google Scholar]
- Li, L.; Yuan, Z.; Gao, Y.; Zhang, X. Wave Force Prediction Effect on the Energy Absorption of a Wave Energy Converter with Real-Time Control. IEEE Trans. Suwithn. Energy 2019, 10, 615–624. [Google Scholar] [CrossRef]
- Amon, E.A.; Brekken, T.K.A.; Schacher, A.A. Maximum Power Point Tracking for Ocean Wave Energy Conversion. IEEE Trans. Ind. Appl. 2012, 48, 1071086. [Google Scholar] [CrossRef]
- M’zoughi, F.; Bouallègue, S.; Ayadi, M. Modeling and SIL simulation of an oscillating water column for ocean energy conversion. In Proceedings of the IREC2015 The Sixth International Renewable Energy Congress, Sousse, Tunisia, 24–26 March 2015; pp. 1–6. [Google Scholar]
- Kelly, J.F.; Christie, R. Applying Hardware-in-the-Loop capabilities to an ocean renewable energy device emulator. In Proceedings of the 2017 Twelfth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 11–13 April 2017; pp. 1–7. [Google Scholar]
- Erdogan, N.; Murray, D.B.; Giebhardt, J.; Wecker, M.; Donegan, J. Real-Time Hardware Emulation of a Power Take-Off Model for Grid-Connected Tidal Energy Systems. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 11–15 May 2019; pp. 1368–1372. [Google Scholar]
- Caraiman, G.; Nichita, C.; Mînzu, V.; Dakyo, B.; Joen, C.H. Study of a real time emulator for marine current energy conversion. In Proceedings of the XIX International Conference on Electrical Machines IC-EM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar]
- Caraiman, G.; Nichita, C.; Mînzu, V.; Dakyo, B.; Jo, C.H. Real time marine current turbine emulator: Design, development and control strategies. In Proceedings of the 2012 International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2145–2150. [Google Scholar]
- Caraiman, G.; Nichita, C.; Mînzu, V.; Dakyo, B. Marine current turbine emulator design based on hardware in the loop simulator structure. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010; pp. T12-101–T12-107. [Google Scholar]
- Ramirez, D.; Bartolome, J.P.; Martinez, S.; Herrero, L.C.; Blanco, M. Emulation of an OWC Ocean Energy Plant with PMSG and Irregular Wave Model. IEEE Trans. Sustain. Energy 2015, 6, 1515–1523. [Google Scholar] [CrossRef]
- Athié, G.; Jiménez, T.R.; De la Miyar-Loza, M.; Enríquez, C.; Sheinbaum, J.; Marín, M.; Mariño, I. Variability of the Yucatan current in the Mexican Caribbean and its effect, on the upwelling of Yucatán. In Proceedings of the 2021 First International Congress of Cemie-Ocean, Online, 2–4 June 2021. [Google Scholar]
- Fontes, J.H.; Félix, A.; Mendoza, E. On the Marine Energy Resource of México. J. Mar. Sci. Eng. 2019, 7, 191. [Google Scholar] [CrossRef]
- Gorlov, A.M. Unidirectional Helical Reaction Turbine Operable under Reversible Fluid Flow for Power Systems. U.S. Patent 5,451,137, 19 September 1995. [Google Scholar]
- Jayaram, V.; Bavanish, B. A brief study of the influence of the index revolution on the performance of Gorlov Helical Turbine. Int. J. Renew. Energy Res. 2022, 12, 827–845. [Google Scholar]
- Yang, B.; Shu, X.W. Hydrofoil optimization and experimental validation in helical vertical axis turbine for power generation from marine current. Ocean Eng. 2012, 42, 35–46. [Google Scholar] [CrossRef]
- Mejia-Ruiz, G.E.; Guerrero, J.M.R.; Paternina, M.R.A.; de la Cruz, J.; Mendez, A.Z.; Sandoval, A.P.P. Enhancing Grid Integration and Design of Low Speed PMSGs by Exploiting SRF-PLL -Based Sensorless Control and Holistic Modeling. IEEE Trans. Energy Convers. 2022, 37, 2962–2973. [Google Scholar] [CrossRef]
- Chowdhury, M.M.; Haque, M.E.; Saha, S.; Mahmud, M.A.; Gargoom, A.; Oo, A.M.T. An Enhanced Control Scheme for an IPM Synchronous Generator Based wind Turbine with MTPA Trajectory and Maximum Power Extraction. IEEE Trans. Energy Convers. 2018, 33, 556–566. [Google Scholar] [CrossRef]
- Luo, F.L.; Ye, H. Ordinary DC/DC Converters, Fundamental Converters, Boost Converter. In Power Electronics, Advanced Conversion Technologies; CRC Press: Boca Raton, FL, USA, 2010; pp. 146–149. [Google Scholar]
- Zhao, Y.; Kong, S.; Liu, D.; Guo, D. Modeling and simulation of maximum wind energy capture by segmented slope duty-cycle perturbation method. In Proceedings of the 2021 33rd, Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 564–568. [Google Scholar]
- Yazdani, A.; Iravani, R. Grid-Imposed Frequency VSC System: Control in αβ-Frame. In Voltage-Sourced Converters in Power Systems, Modeling, Control and Applications; Wiley: Toronto, ON, Canada, 2010; pp. 160–203. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).