A Dynamic Reserve Evaluation Method for an Ultra-Deep Fractured Tight Sandstone Gas Reservoir
Abstract
1. Introduction
2. Literature Review
3. Model Introduction
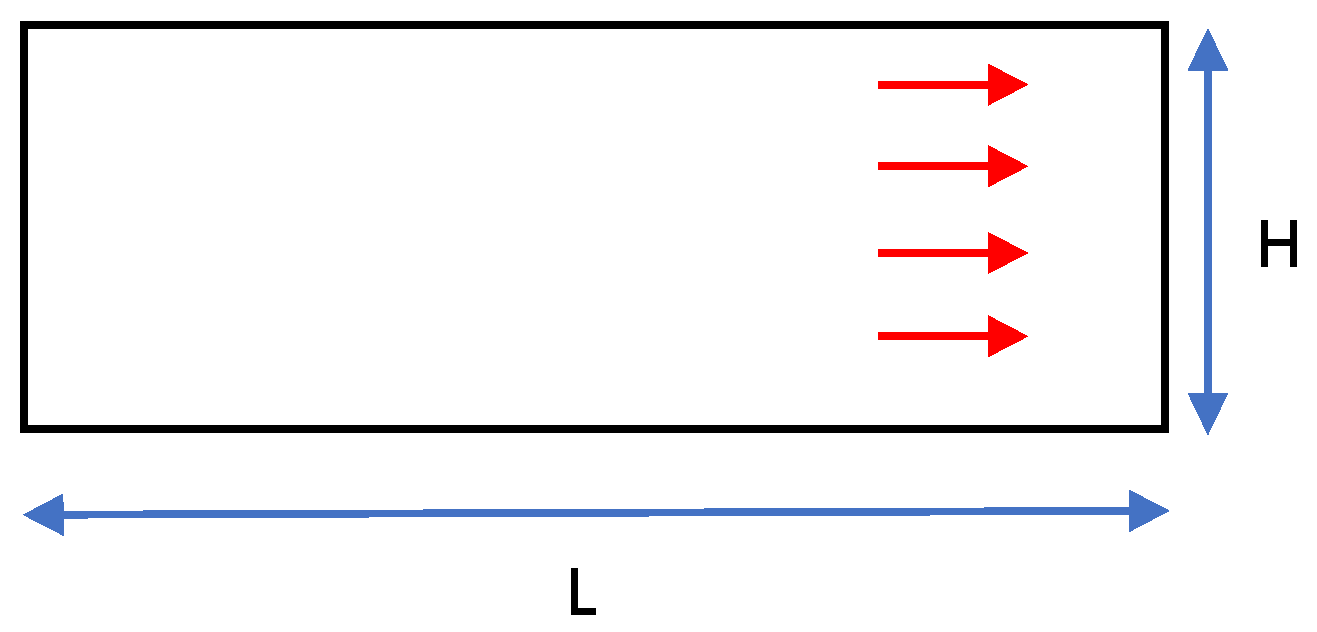
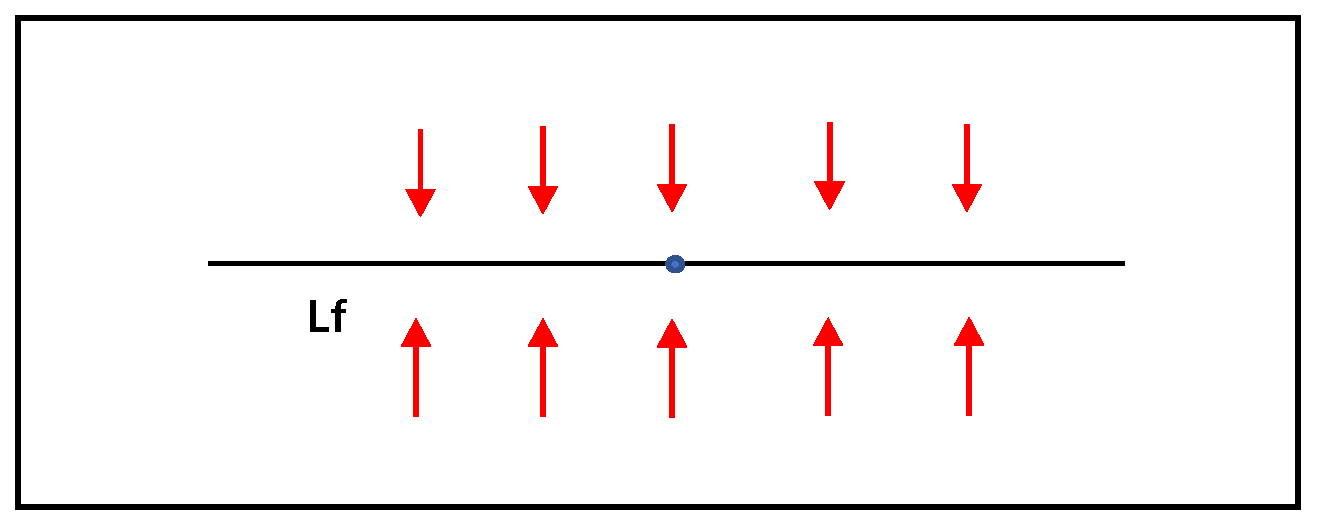
3.1. Gas Flow Theory
3.2. Pressure Change Rate Theorem
3.3. The Proposed Model
4. Results and Discussions
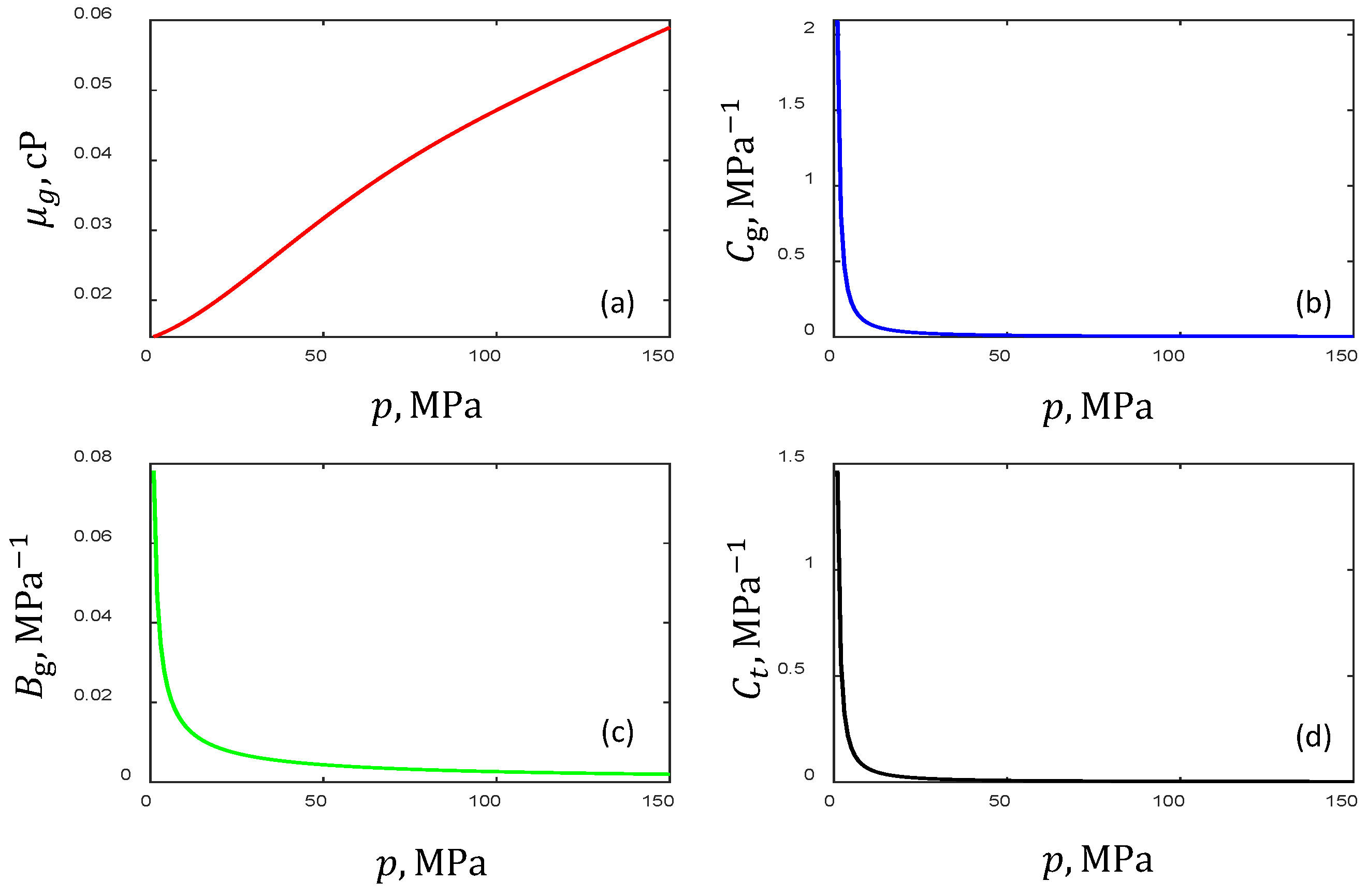
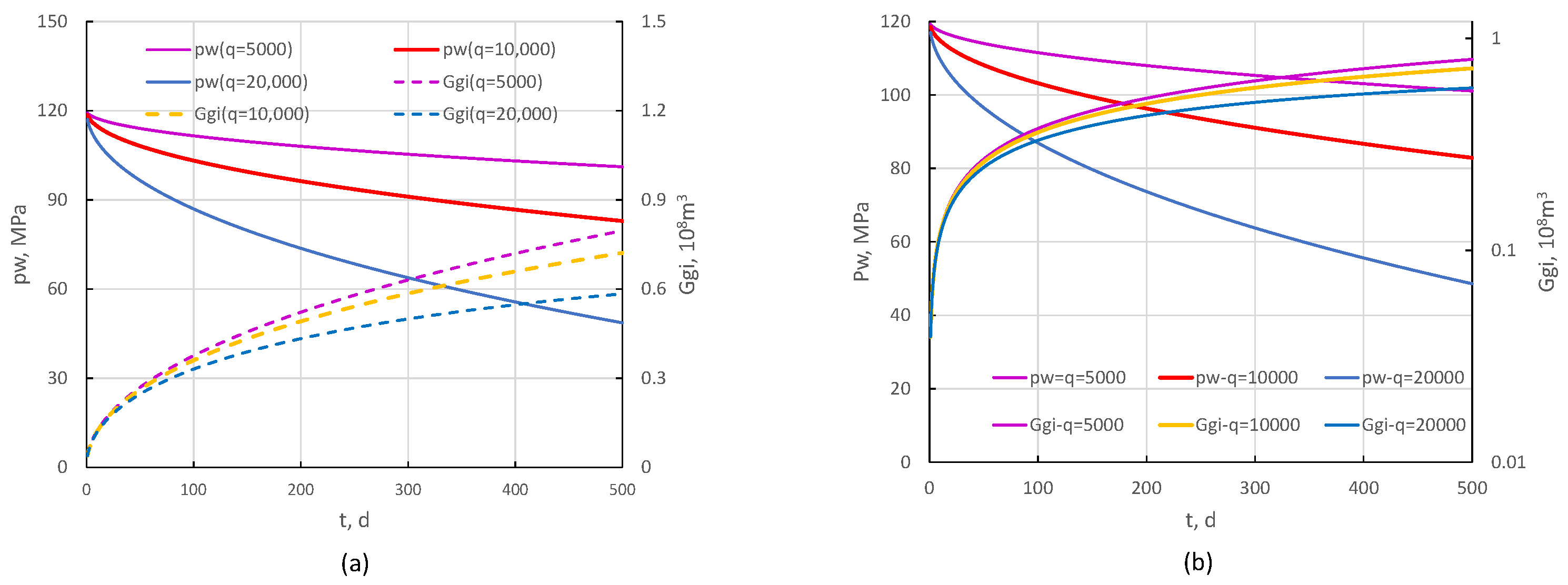
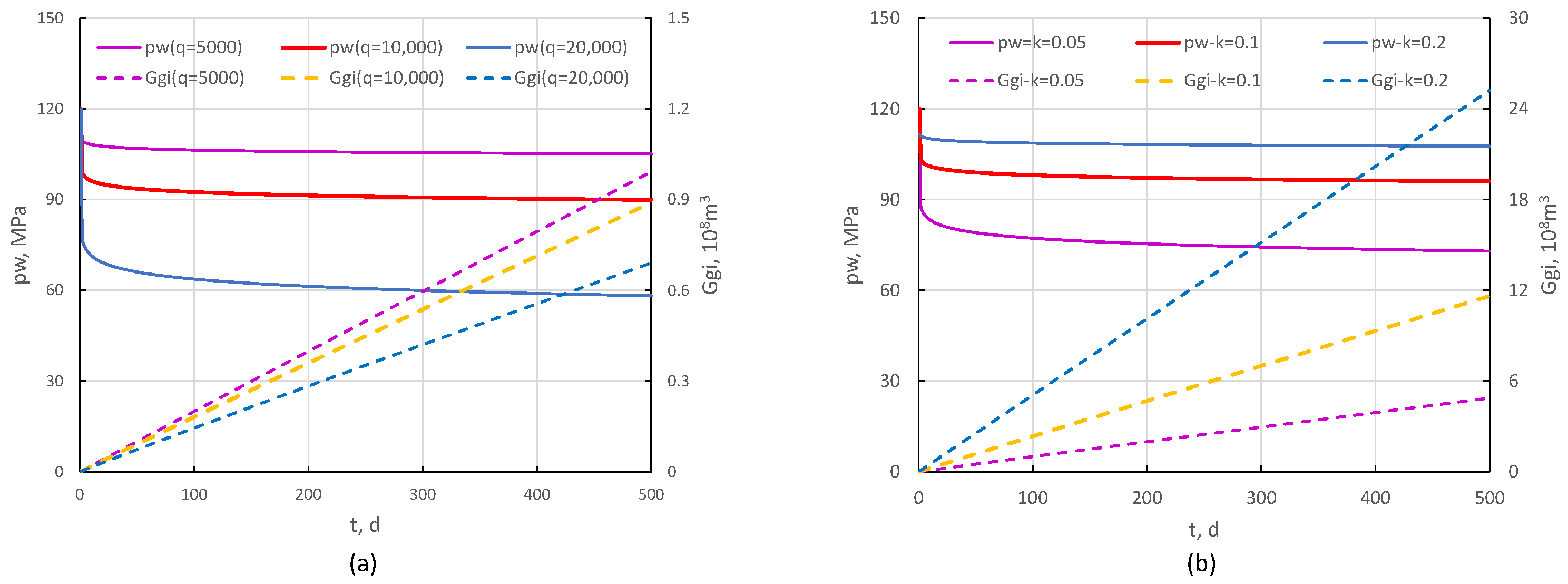
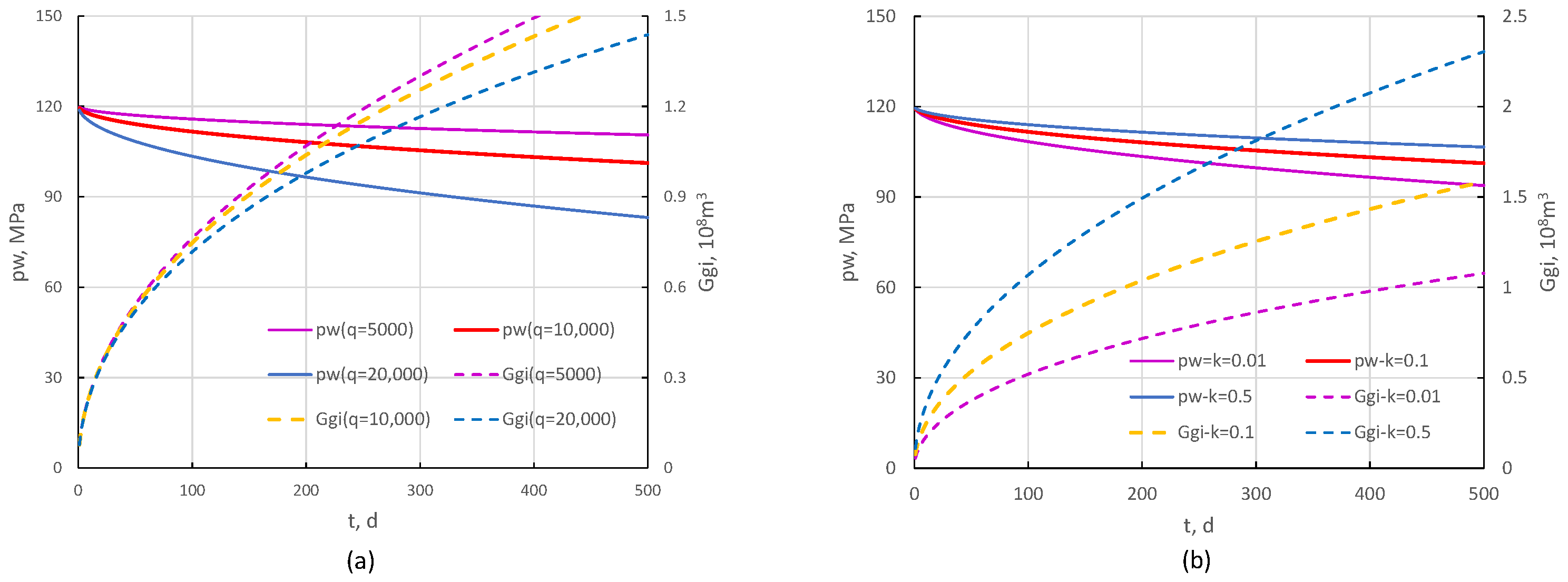
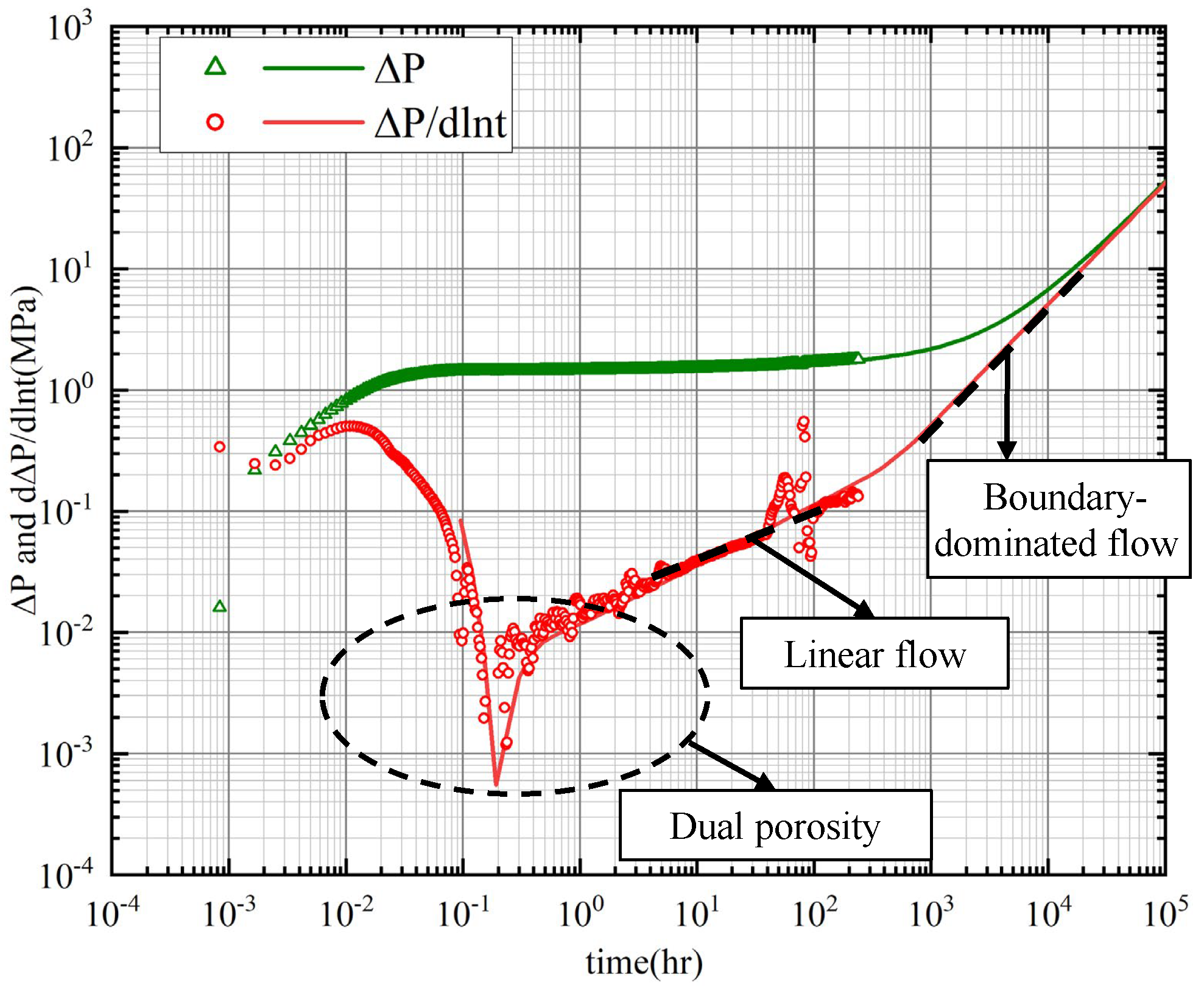
4.1. Pressure Change Characteristics of the Gas Parameters
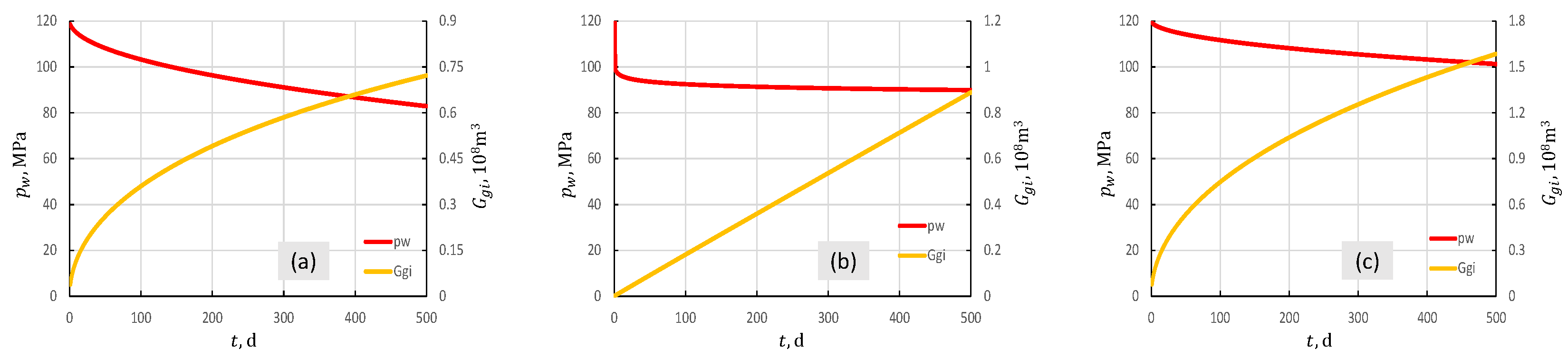
4.2. Sensitivity Analysis
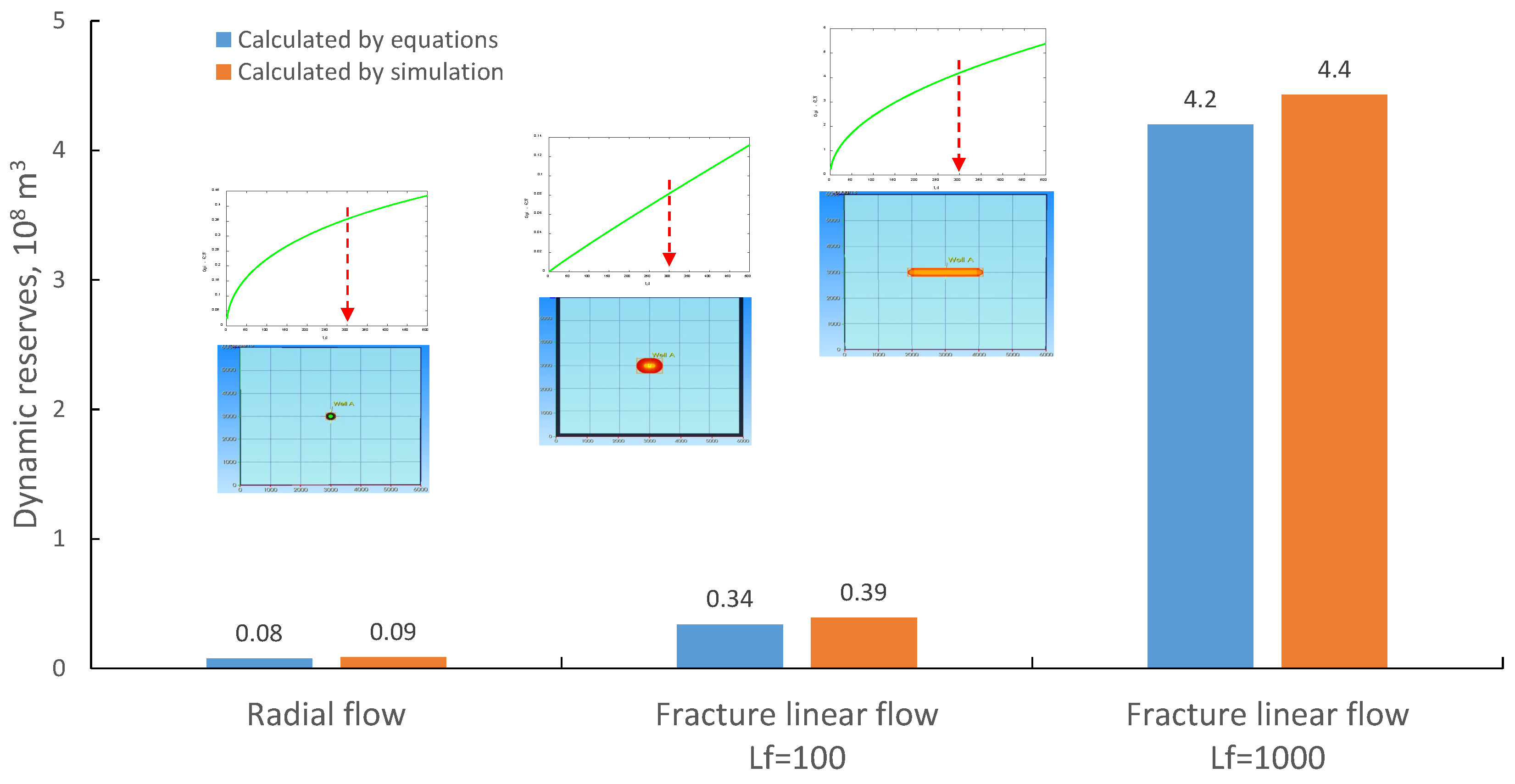
4.3. Applications to Real Field Cases
4.3.1. Brief Introduction to the Gas Reservoirs
4.3.2. Results and Discussions of the Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, T.; Sun, X. Development of Keshen ultra-deep and ultra-high pressure gas reservoirs in the Kuqa foreland basin, Tarim Basin: Understanding and technical countermeasures. Nat. Gas Ind. B 2019, 6, 16–24. [Google Scholar] [CrossRef]
- Guo, J.; Qi, X.; Hou, L.; Hao, A.; Zeng, X.; Lin, S.; Pu, X.; Xie, Z.; Wang, Y.; Wang, X.; et al. Origin and accumulation models of ultra-low permeability-tight sandstone (gravel) gas in Bohai Bay Basin, China. J. Nat. Gas Geosci. 2022, 7, 211–223. [Google Scholar] [CrossRef]
- Tian, J.; Liu, H.; Wang, L.; Sima, L.; Liu, S.; Liu, X. Identification of fractures in tight-oil reservoirs: A case study of the Da’anzhai member in the central Sichuan Basin, SW China. Sci. Rep. 2021, 11, 23846. [Google Scholar] [CrossRef] [PubMed]
- Lei, Q.; Xu, Y.; Yang, Z.; Cai, B.; Wang, X.; Zhou, L.; Liu, H.; Xu, M.; Wang, L.; Li, S. Progress and development directions of stimulation techniques for ultra-deep oil and gas reservoirs. Pet. Explor. Dev. 2021, 48, 221–231. [Google Scholar] [CrossRef]
- Xu, K.; Yang, H.; Zhang, H.; Ju, W.; Li, C.; Fang, L.; Wang, Z.; Wang, H.; Yuan, F.; Zhao, B.; et al. Fracture effectiveness evaluation in ultra-deep reservoirs based on geomechanical method, Kuqa Depression, Tarim Basin, NW China. J. Pet. Sci. Eng. 2022, 215, 110604. [Google Scholar] [CrossRef]
- Yao, J.; Huang, Z.Q.; Liu, W.Z.; Zhang, Y.; Zeng, Q.D.; Yan, X. Key mechanical problems in the development of deep oil and gas reservoirs. Sci. Sin. Phys. Mech. Astron. 2018, 48, 044701. [Google Scholar] [CrossRef]
- The Ministry of Natural Resources of People’s Republic of China. Regulation of Petroleum Reserves Estimation. 2020. Available online: https://www.nssi.org.cn/nssi/front/111560820.html (accessed on 25 May 2024).
- Medeiros, F.; Ozkan, E.; Kazemi, H. Productivity and Drainage Area of Fractured Horizontal Wells in Tight Gas Reservoirs. SPE Reserv. Eval. Eng. 2007, 11, 902–911. [Google Scholar] [CrossRef]
- Fang, J.; Peng, X.; Liu, L.; Ye, L. Comprehensive limits of the movable reserves in fractured-porous sandstone. J. Southwest Pet. Univ. 2017, 39, 93. [Google Scholar]
- Fetkovich, M. Decline Curve Analysis Using Type Curves. J. Pet. Technol. 1980, 32, 1065–1077. [Google Scholar] [CrossRef]
- Sun, H. Fundamentals of Advanced Production Decline Analysis; Gulf Professional Publishing: Houston, TX, USA, 2015; pp. 1–29. [Google Scholar] [CrossRef]
- Chu, W.C.; Scott, K.D.; Flumerfelt, R.; Chen, C.; Zuber, M.D. A New Technique for Quantifying Pressure Interference in Fractured Horizontal Shale Wells. SPE Reserv. Eval. Eng. 2020, 23, 143–157. [Google Scholar] [CrossRef]
- Luo, R.; Yu, J.; Wan, Y.; Liu, X.; Zhang, L.; Mei, Q.; Zhao, Y.; Chen, Y. Evaluation of Dynamic Reserves in Ultra-Deep Naturally Fractured Tight Sandstone Gas Reservoirs; OnePetro: Richardson, TX, USA, 2019. [Google Scholar] [CrossRef]
- He, J.; Guo, X.; Cui, H.; Lei, K.; Lei, Y.; Zhou, L.; Liu, Q.; Zhu, Y.; Liu, L. Modification of the Calculation Method for Dynamic Reserves in Tight Sandstone Gas Reservoirs. ACS Omega 2021, 6, 29955–29964. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; He, Y.; Guo, C.; Yu, Y. Dynamic Material Balance Method for Estimating Gas in Place of Abnormally High-Pressure Gas Reservoirs. Lithosphere 2021, 2021, 6669012. [Google Scholar] [CrossRef]
- Arps, J.J. Analysis of Decline Curves. Trans. AIME 1945, 160, 228–247. [Google Scholar] [CrossRef]
- Mathews, C.; Russell, D. Pressure Buildup and Flow Tests in Wells. SPE Monogr. Ser. 1967, 1, 27. [Google Scholar]
- Spivey, J.P.; Lee, W.J. Applied Well Test Interpretation; Society of Petroleum Engineers: Dallas, TX, USA, 2013. [Google Scholar] [CrossRef]
- Whittle, T.; Gringarten, A. The Determination of Minimum Tested Volume from the Deconvolution of Well Test Pressure Transients. Proc.-SPE Annu. Tech. Conf. Exhib. 2008, 6, 4112–4120. [Google Scholar] [CrossRef]
- Mattar, L.; McNeil, R. The Flowing Material Balance Procedure; OnePetro: Richardson, TX, USA, 1995; Volume 6. [Google Scholar] [CrossRef]
- Mattar, L.; McNeil, R. The “flowing” gas material balance. J. Can. Pet. Technol. 1998, 37, 52–55. [Google Scholar] [CrossRef]
- Mattar, L.; Anderson, D.; Stotts, G. Dynamic material balance - Oil-or gas-in-place without shut-ins. J. Can. Pet. Technol. 2006, 45, 7–10. [Google Scholar] [CrossRef]
- Stumpf, T.N.; Ayala, L.F. Rigorous and Explicit Determination of Reserves and Hyperbolic Exponents in Gas-Well Decline Analysis. SPE J. 2016, 21, 1843–1857. [Google Scholar] [CrossRef]
- Blasingame, T.A.; McCray, T.L.; Lee, W.J. Decline Curve Analysis for Variable Pressure Drop/Variable Flowrate Systems; OnePetro: Richardson, TX, USA, 1991; Volume 1. [Google Scholar] [CrossRef]
- Marhaendrajana, T.; Blasingame, T.A. Decline Curve Analysis Using Type Curves—Evaluation of Well Performance Behavior in a Multiwell Reservoir System; OnePetro: Richardson, TX, USA, 2001; Volume 9, pp. 1647–1661. [Google Scholar] [CrossRef]
- Orozco, D.; Aguilera, R. Use of Dynamic Data and a New Material-Balance Equation for Estimating Average Reservoir Pressure, Original Gas in Place, and Optimal Well Spacing in Shale Gas Reservoirs. SPE Reserv. Eval. Eng. 2018, 21, 1035–1044. [Google Scholar] [CrossRef]
- Tabatabaie, S.H.; Behmanesh, H.; Mattar, L. Using the Flowing Material Balance Model to Determine Which Wells Out of a Group of Wells belong to the Same Common Pool. SPE Reserv. Eval. Eng. 2022, 25, 719–729. [Google Scholar] [CrossRef]
- He, J.; Ling, K.; Pei, P.; Ni, X. Calculation of rock compressibility by using the characteristics of downstream pressure change in permeability experiment. J. Pet. Sci. Eng. 2016, 143, 121–127. [Google Scholar] [CrossRef]
- Cheng, Y.; Luo, X.; Lu, T.; Guo, C.; Tan, C. Well-Controlled Dynamic Reserves Calculation of Abnormally High-Pressured Gas Reservoirs Developed with Edge and Bottom Aquifers. Processes 2023, 11, 938. [Google Scholar] [CrossRef]
- Wang, C.; Jia, A.; Guo, Z.; Huang, S.; Shi, X.; Cui, F. An Improved Correlation of Compressibility Factor Prediction of Variable CO2-Content Condensate Gases. Energies 2022, 16, 105. [Google Scholar] [CrossRef]
- Al-Hussainy, R.; Ramey, J.A.H.J. Application of Real Gas Flow Theory to Well Testing and Deliverability Forecasting. J. Pet. Technol. 1966, 18, 637–642. [Google Scholar] [CrossRef]
- Russell, D.; Goodrich, J.; Perry, G.; Bruskotter, J. Methods for Predicting Gas Well Performance. J. Pet. Technol. 1966, 18, 99–108. [Google Scholar] [CrossRef]
- George, S. Well Test Design and Analysis; PennWell Books: Tulsa, OK, USA, 2011. [Google Scholar]
- Zhang, L.; Guo, C.; He, Y.; Yu, Y.; Liu, C. Determination of gas in place for abnormally pressured gas reservoirs from production data. Nat. Gas Geosci. 2021, 32, 703–717. [Google Scholar]
- Spivey, J.P.; Lee, W.J.; Sheikh, H.M.U.D. Transient Volume of Investigation: Definition, Theory, and Applications. In Proceedings-SPE Annual Technical Conference and Exhibition; OnePetro: Richardson, TX, USA, 2020. [Google Scholar] [CrossRef]
- Hale, B.W.; Evers, J.F. Elliptical Flow Equations for Vertically Fractured Gas Wells. J. Pet. Technol. 1981, 33, 2489–2497. [Google Scholar] [CrossRef]
- Londono, F.E.; Archer, R.A.; Blasingame, T.A. Simplified Correlations for Hydrocarbon Gas Viscosity and Gas Density—Validation and Correlation of Behavior Using a Large-Scale Database; OnePetro: Richardson, TX, USA, 2002; Volume 4. [Google Scholar] [CrossRef]
- Londono, F.E.; Archer, R.A.; Blasingame, T.A. Correlations for Hydrocarbon-Gas Viscosity and Gas Density—Validation and Correlation of Behavior Using a Large-Scale Database. SPE Reserv. Eval. Eng. 2005, 8, 561–572. [Google Scholar] [CrossRef]
- Dranchuk, P.M.; Abou-Kassem, J.H. Calculation of Z Factor for Natural Gases Using Equation of State. J. Can. Pet. Technol. 1975, 14, 34–36. [Google Scholar] [CrossRef]


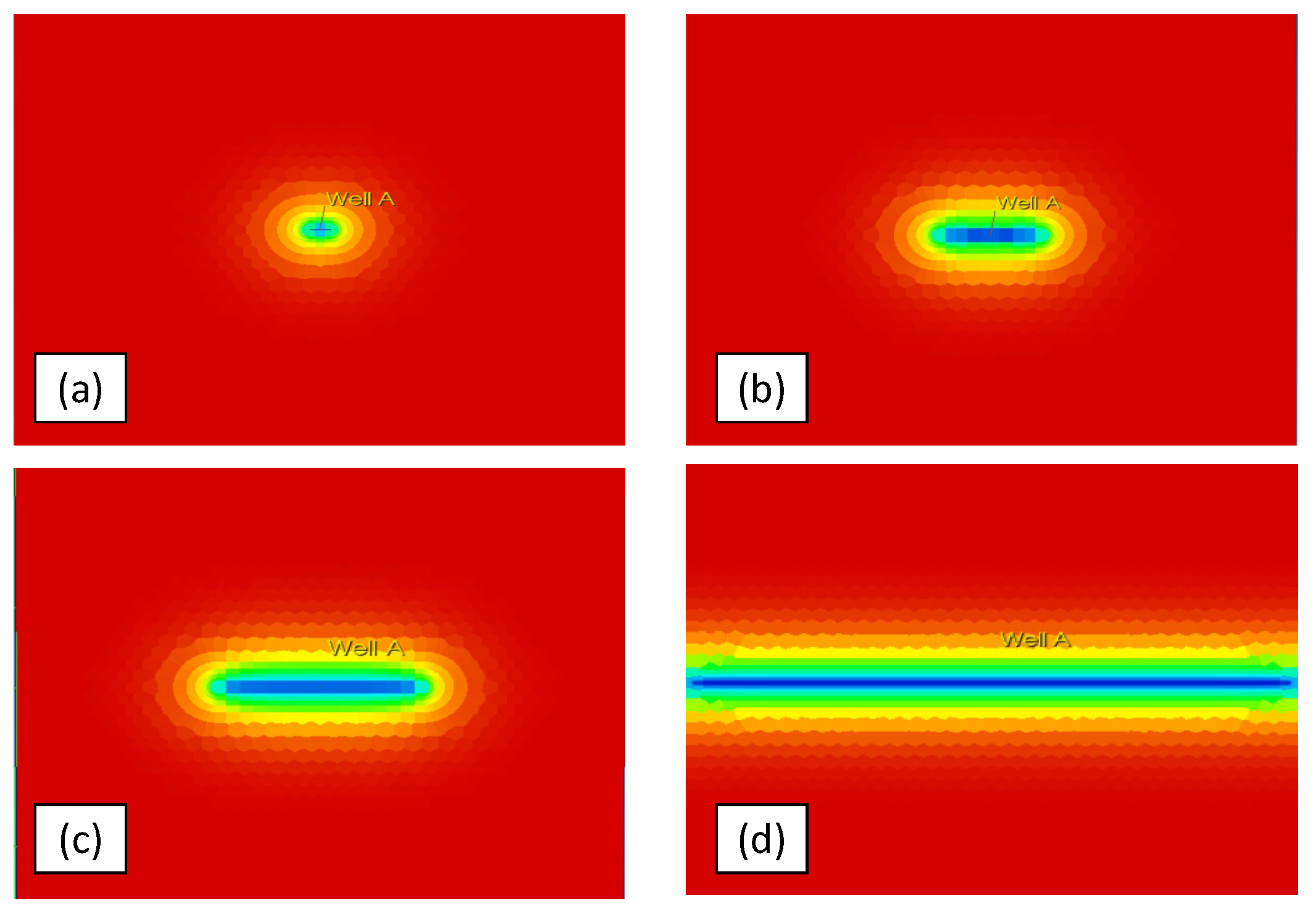
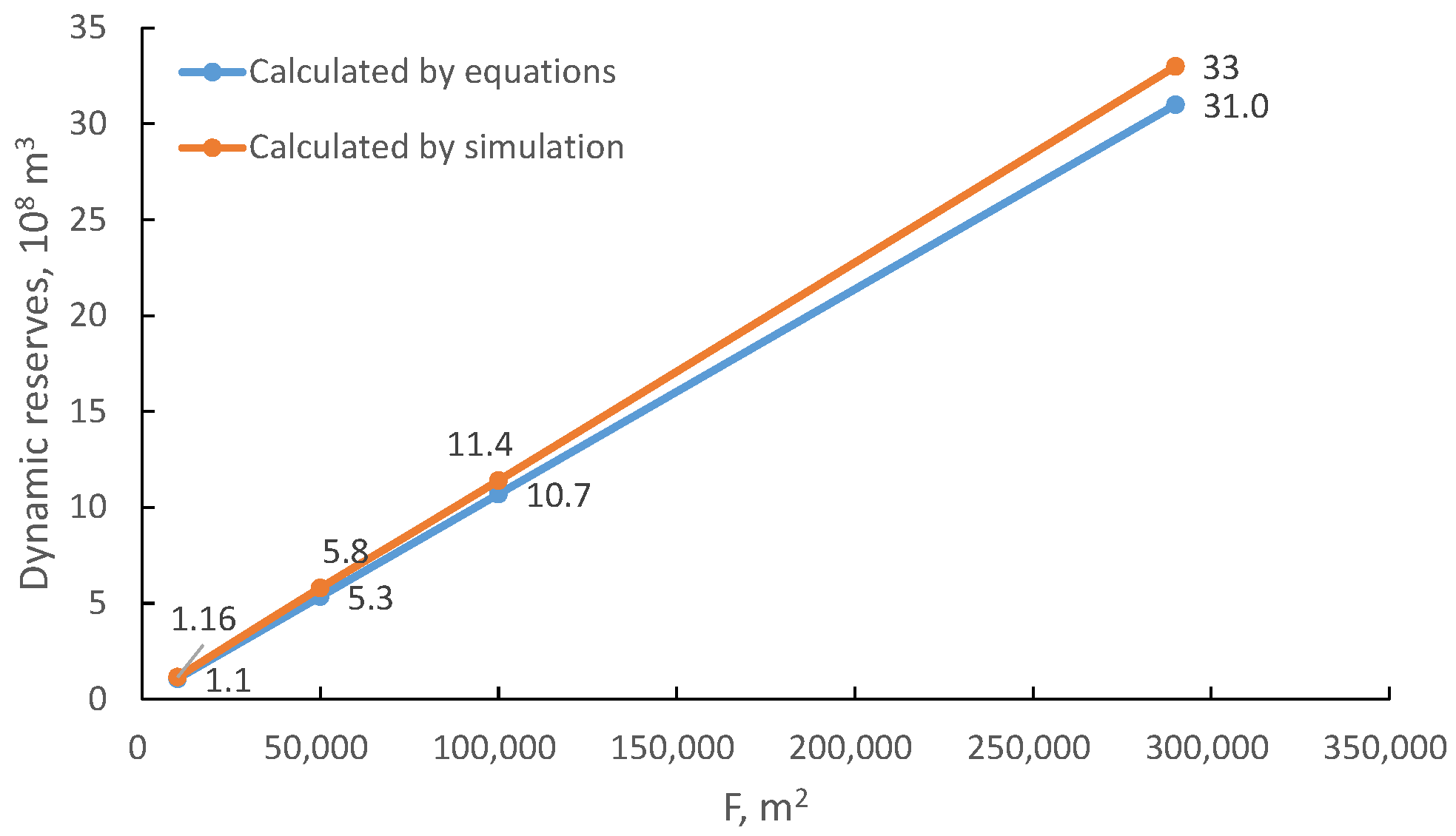
| No. | Parameter | Value | No. | Parameter | Value |
|---|---|---|---|---|---|
| 1 | Permeability k | mD | 6 | Water compressibility | MPa−1 |
| 2 | Matrix porosity | 5% | 7 | Rock compressibility | MPa−1 |
| 3 | Water saturation | 30% | 8 | Skin factor S | 0.1 |
| 4 | Net pay h | 100 m | 9 | Fracture half-length | 100 m |
| 5 | Width w | 100 m | 10 | Initial reservoir pressure | 120 MPa |
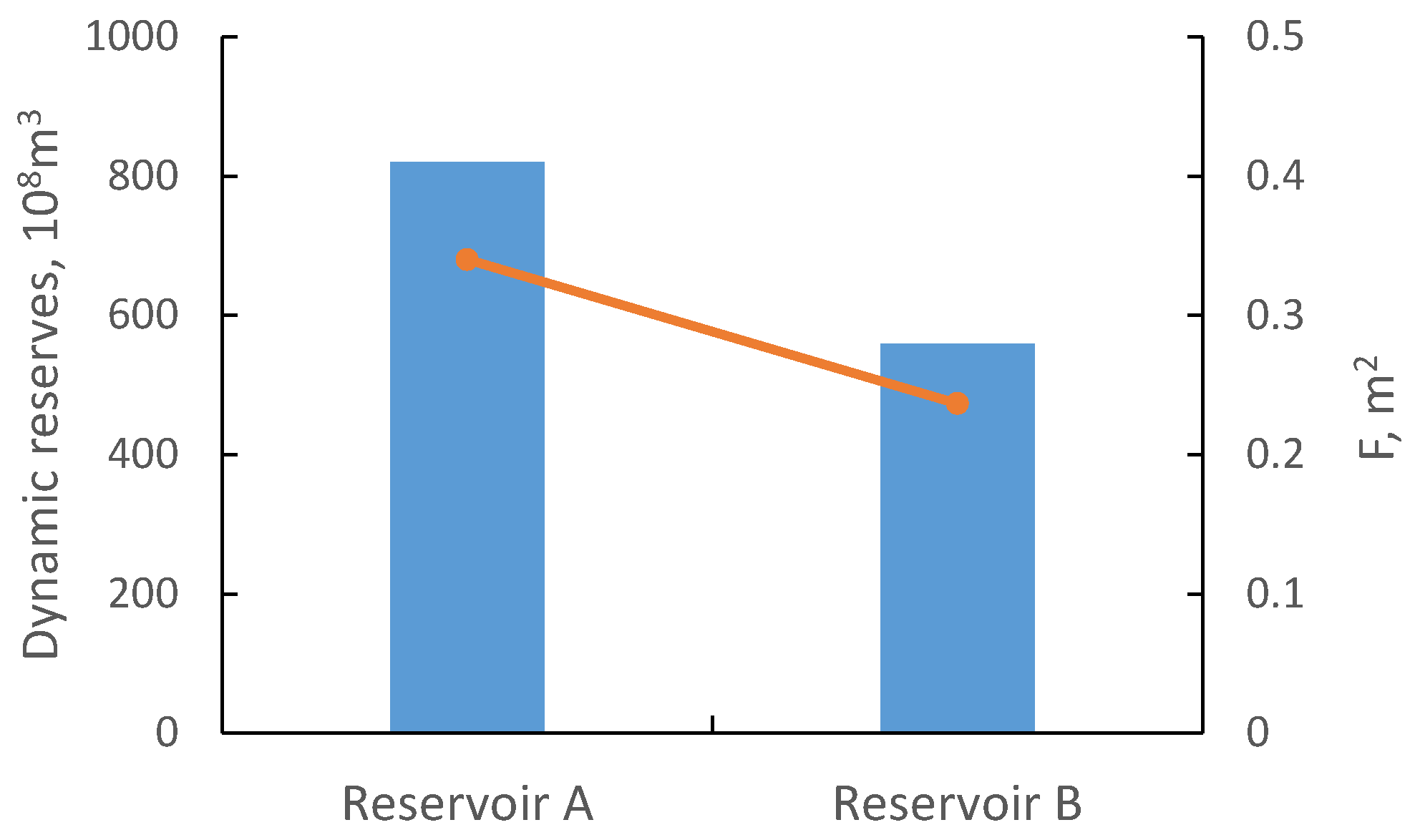
| Reservoir | Dynamic Reserve | k | ||||||
|---|---|---|---|---|---|---|---|---|
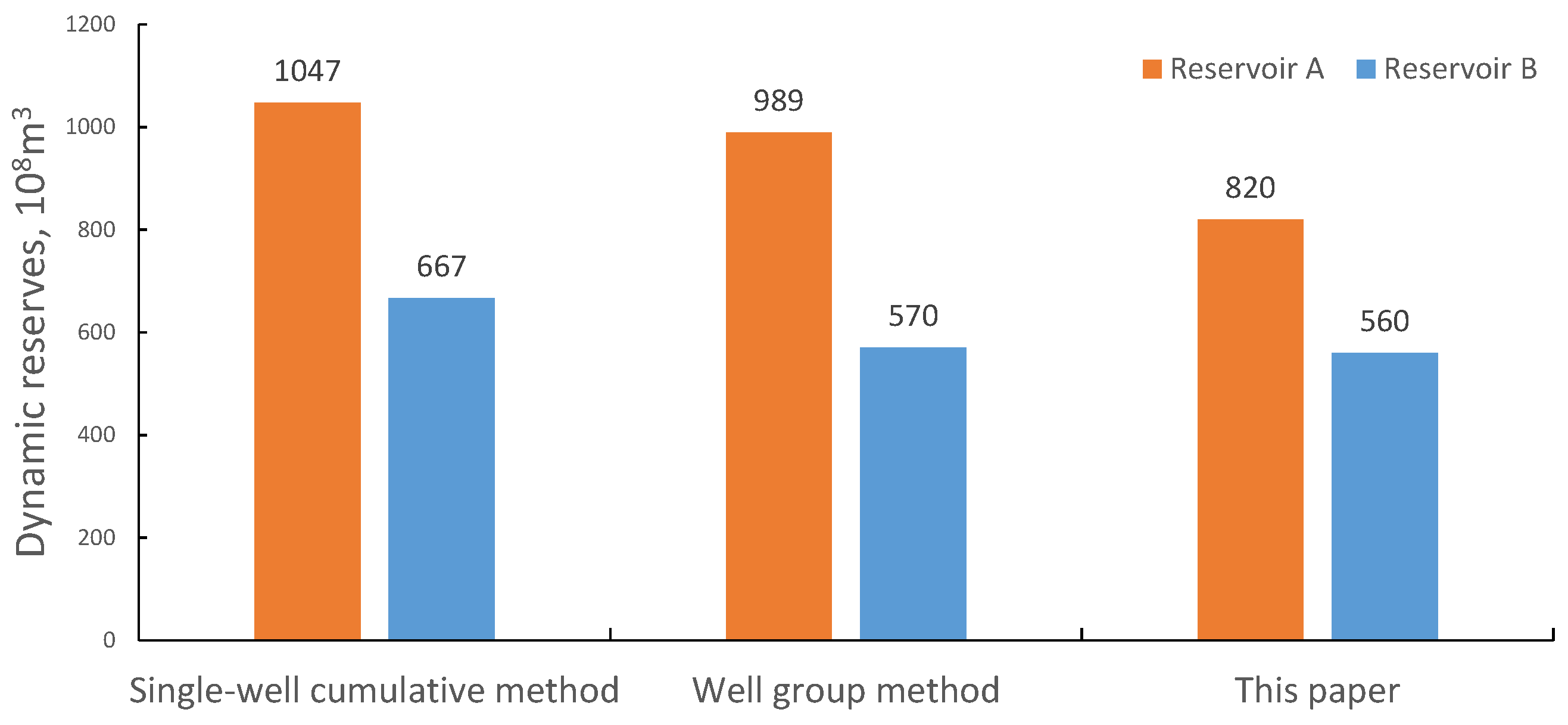
| A | 820 | 0.1 | 0.06 | 0.3 | 0.0474 | 0.0058 | 0.0030 | 34,010,554 |
| B | 560 | 0.1 | 0.06 | 0.3 | 0.0460 | 0.0063 | 0.0032 | 23,671,205 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Wang, C.; Chang, B.; Cao, Z.; Tang, H. A Dynamic Reserve Evaluation Method for an Ultra-Deep Fractured Tight Sandstone Gas Reservoir. Energies 2024, 17, 2648. https://doi.org/10.3390/en17112648
He X, Wang C, Chang B, Cao Z, Tang H. A Dynamic Reserve Evaluation Method for an Ultra-Deep Fractured Tight Sandstone Gas Reservoir. Energies. 2024; 17(11):2648. https://doi.org/10.3390/en17112648
Chicago/Turabian StyleHe, Xinxing, Chenhui Wang, Baohua Chang, Zhenglin Cao, and Haifa Tang. 2024. "A Dynamic Reserve Evaluation Method for an Ultra-Deep Fractured Tight Sandstone Gas Reservoir" Energies 17, no. 11: 2648. https://doi.org/10.3390/en17112648
APA StyleHe, X., Wang, C., Chang, B., Cao, Z., & Tang, H. (2024). A Dynamic Reserve Evaluation Method for an Ultra-Deep Fractured Tight Sandstone Gas Reservoir. Energies, 17(11), 2648. https://doi.org/10.3390/en17112648






