Optimization Design and Performance Study of a Heat Exchanger for an Oil and Gas Recovery System in an Oil Depot
Abstract
1. Introduction
2. Methodology
2.1. Optimization of Heat Exchanger Type
2.2. Preliminary Design
2.3. Detailed Design
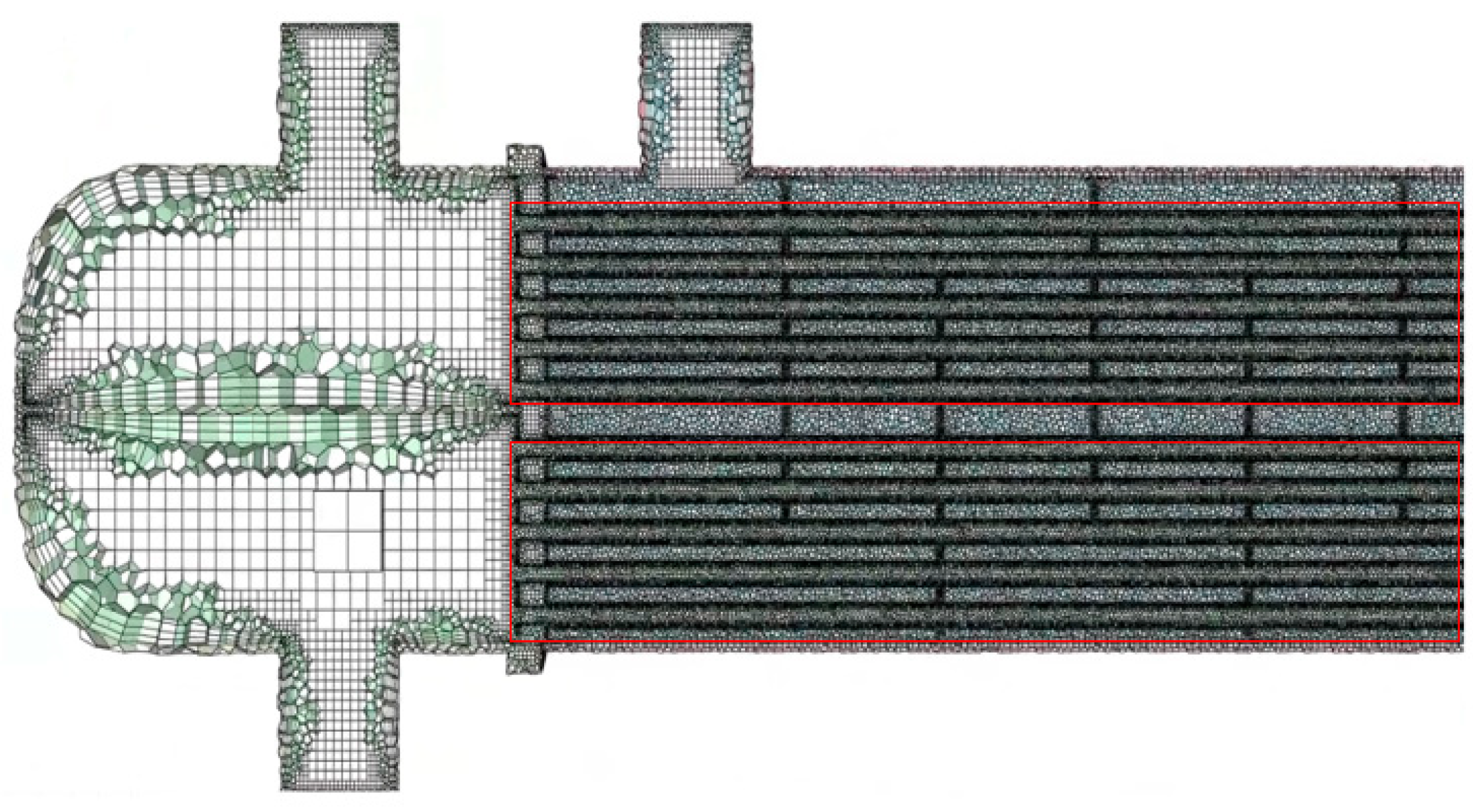
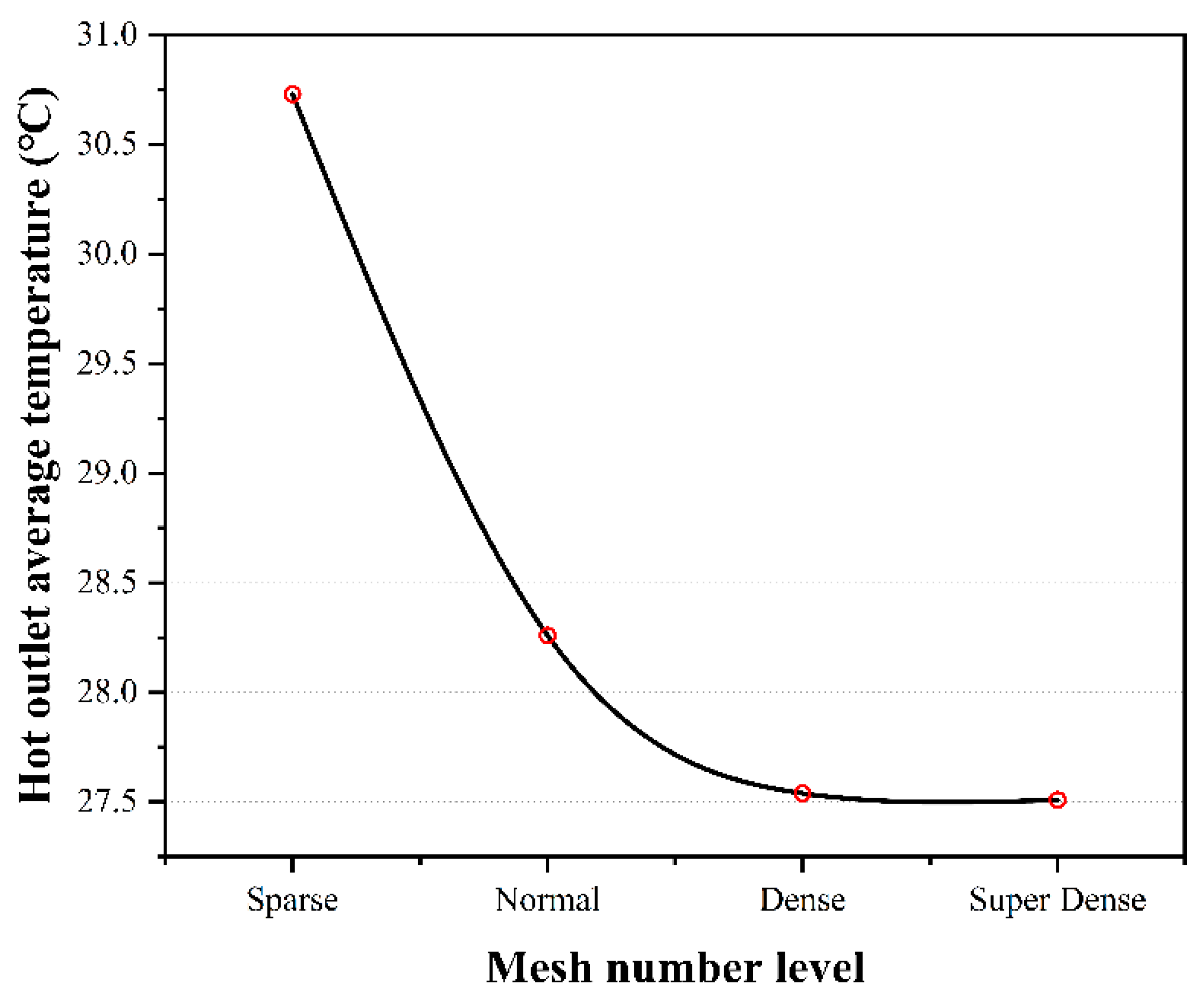
2.4. CFD Numerical Simulation
3. Case Study
3.1. Basic Data
3.2. Preliminary Design
3.3. Detailed Design
3.4. CFD Simulation
3.4.1. Physical Structure
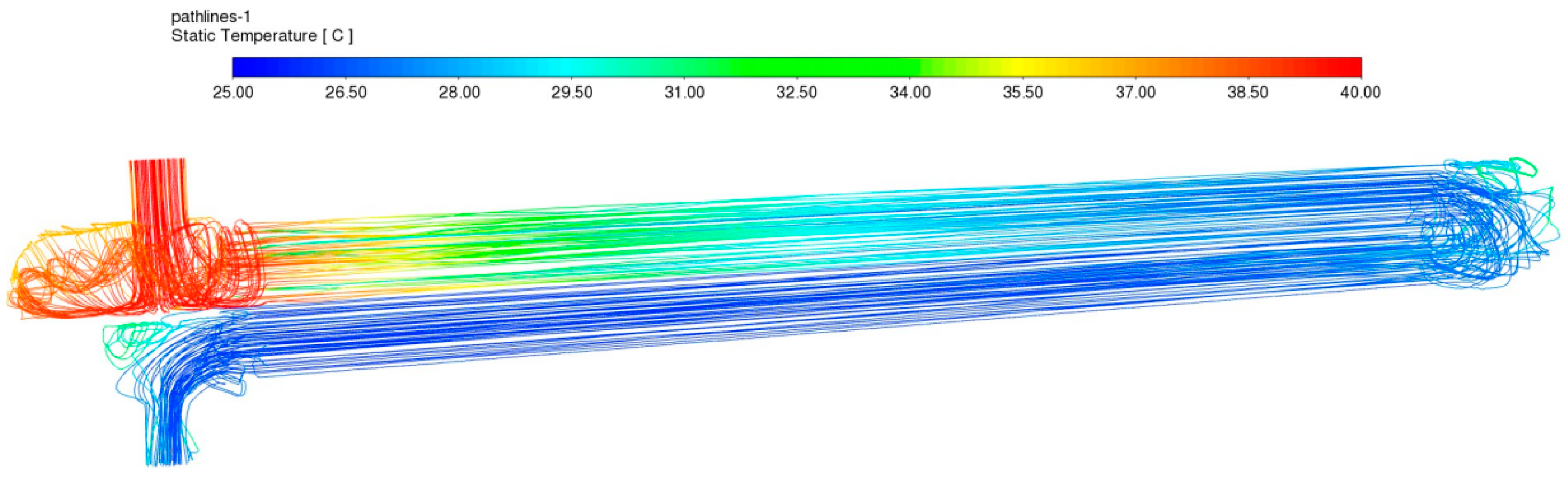
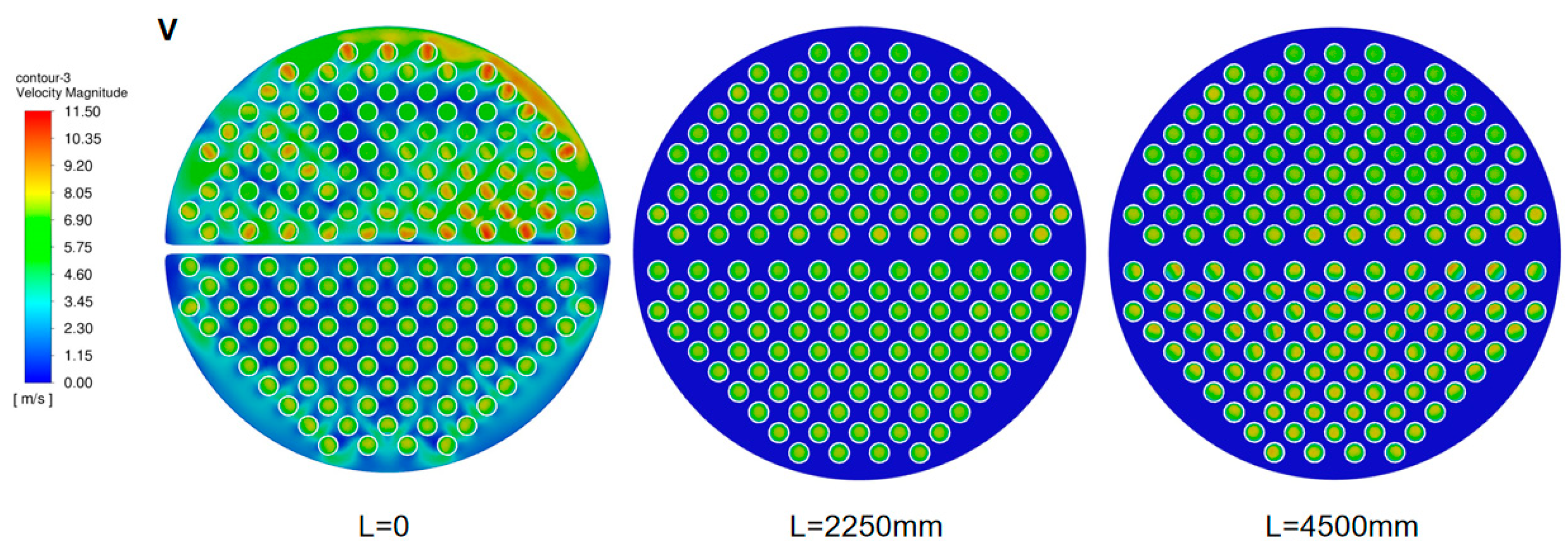
3.4.2. Results and Analysis of Flow Field and Thermodynamic Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Q | Heat load, W |
| mc | The mass flow rate of the cold fluid, kg/s |
| mh | The mass flow rate of hot fluid, kg/s |
| cp,c | The constant pressure specific heat of cold fluid, J/(kg·K) |
| cp,h | The constant pressure specific heat of hot fluid, J/(kg·K) |
| Tc,i | The inlet temperature of cold fluid, K |
| Tc,o | The outlet temperature of cold fluid, K |
| Th,i | The inlet temperature of hot fluid, K |
| Th,o | The outlet temperature of hot fluid, K |
| R | Ideal gas constant, J/(mol·K); |
| p | Pressure, kPa |
| T | The absolute temperature, K |
| V | The molar volume, m3 |
| a | The energy parameter related to temperature |
| b | The temperature dependent volume parameter. |
| K | The overall heat transfer coefficient, W/(m2·K) |
| A | The heat exchanger area, m2 |
| Δtm | The mean temperature difference between cold and hot fluids, K |
| Δtm’ | The logarithmic mean temperature difference, K |
| FT | A correction factor used to account for the logarithmic mean temperature difference |
| Am | The area margin |
| Ao | The actual surface area of the heat exchanger, m2 |
| Areq | The heat transfer area required, m2 |
| ρ | The fluid density |
| w | The fluid velocity, m/s |
| ui | The velocity in the direction i, m/s |
| Fi | The mass force in the direction i, N |
| E | The conservation of energy |
| h | The sensible heat enthalpy |
| Gb | The kinetic energy generated by buoyancy effects |
| Gk | The kinetic energy produced by the mean velocity gradient |
| YM | The impact of compressible turbulent pulsation expansion on the overall dissipation rate |
| αk | The inverse Prandtl numbers for |
| ∂ε | The inverse Prandtl numbers for |
| Sε | Source terms |
| μt | Turbulent viscosity |
References
- Hong, B.; Shao, B.; Zhou, M.; Qian, J.; Guo, J.; Li, C.; Xu, Y.; Zhu, B. Evaluation of Disaster-Bearing Capacity for Natural Gas Pipeline under Third-Party Damage Based on Optimized Probabilistic Neural Network. J. Clean. Prod. 2023, 428, 139247. [Google Scholar] [CrossRef]
- Li, Y.; Dai, G. Energy Saving and Emission Reduction of Fossil Energy Based on Low Carbon Economy and Its Consumption Structure Optimization. Int. J. Low-Carbon Technol. 2019, 14, 381–385. [Google Scholar] [CrossRef]
- Hua, L.-Y.; Cui, T.; Li, J.-X.; Zou, B.-D.; Yang, Y.-Y.; Cheng, G. VOCs Removal and Emission Monitoring of Beijing Bulk Gasoline Terminals in 2012–2019. Huan Jing Ke Xue 2021, 42, 1328–1332. [Google Scholar] [PubMed]
- Guo, T.; Jiao, Y.; Tang, Y.; Lu, D.; Kong, X.; Shen, J.; Jiang, Q. Marking the Status and Development of Marine VOCs Recovery Technology. E3S Web Conf. 2021, 248, 01010. [Google Scholar]
- Zhou, J.Y.; Wang, B.F.; Nie, L.H.; Lu, J.X.; Hao, Y.J.; Xu, R.R. Experimental Study on Emission of VOCs from Tanker Using Hollow Fiber Membrane Absorption Method with Different Absorbents. IOP Conf. Ser. Mater. Sci. Eng. 2018, 292, 012113. [Google Scholar] [CrossRef]
- Vlasenko, V.S.; Karakozov, A.A.; Perveev, A.A. Vapor Recovery Unit of Gasoline from the Tanks of Filling Stations with Gas-Dynamic Cooling. IOP Conf. Ser. Earth Environ. Sci. 2020, 459, 032043. [Google Scholar] [CrossRef]
- Fetisov, V.; Mohammadi, A.H.; Pshenin, V.; Kupavykh, K.; Artyukh, D. Improving the Economic Efficiency of Vapor Recovery Units at Hydrocarbon Loading Terminals. Oil Gas Sci. Technol.–Rev. IFP Energ. Nouv. 2021, 76, 38. [Google Scholar] [CrossRef]
- Wang, J.; Nan, J.; Wang, Y. CFD-Based Optimization of a Shell-and-Tube Heat Exchanger. Fluid Dyn. Mater. Process. 2023, 19, 2761–2775. [Google Scholar] [CrossRef]
- Aydin, A.; Yaşsar, H.; Engin, T.; Buyukkaya, E. Optimization and CFD Analysis of a Shell-and-Tube Heat Exchanger with a Multi Segmental Baffle. Therm. Sci. 2022, 26, 1–12. [Google Scholar] [CrossRef]
- Abushammala, O.; Hreiz, R.; Lemaître, C.; Favre, É. Optimal Design of Helical Heat/Mass Exchangers under Laminar Flow: CFD Investigation and Correlations for Maximal Transfer Efficiency and Process Intensification Performances. Int. J. Heat Mass Transf. 2020, 153, 119610. [Google Scholar] [CrossRef]
- Cavazzuti, M.; Agnani, E.; Corticelli, M.A. Optimization of a Finned Concentric Pipes Heat Exchanger for Industrial Recuperative Burners. Appl. Therm. Eng. 2015, 84, 110–117. [Google Scholar] [CrossRef]
- Dvořák, V.; Vít, T. CAE Methods for Plate Heat Exchanger Design. Energy Procedia 2017, 134, 234–243. [Google Scholar] [CrossRef]
- Khail, A.A.; Erisen, A. A Review: CFD Approaches of Plate Heat Exchangers. Arch. Comput. Method Eng. 2023, 30, 1157–1165. [Google Scholar] [CrossRef]
- Afgan, I.; Kahil, Y.; Benhamadouche, S.; Ali, M.; Alkaabi, A.; Berrouk, A.S.; Sagaut, P. Cross Flow over Two Heated Cylinders in Tandem Arrangements at Subcritical Reynolds Number Using Large Eddy Simulations. Int. J. Heat Fluid Flow 2023, 100, 109115. [Google Scholar] [CrossRef]
- Bhandurge, S.; Wankhade, A.M.; Jadhao, P.K. Analysis and experimentation of shell and tube heat exchanger with different orientation of baffles. Int. J. Res. Sci. Eng. Technol. 2016, 3, 7–14. [Google Scholar]
- Mellal, M.; Benzeguir, R.; Sahel, D.; Ameur, H. Hydro-Thermal Shell-Side Performance Evaluation of a Shell and Tube Heat Exchanger under Different Baffle Arrangement and Orientation. Int. J. Therm. Sci. 2017, 121, 138–149. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, X.; Huang, X.; Jia, J.; Tong, J. Optimization of High-Pressure Shell-and-Tube Heat Exchanger for Syngas Cooling in an IGCC. Int. J. Heat Mass Transf. 2010, 53, 4543–4551. [Google Scholar] [CrossRef]
- Bashtani, I.; Esfahani, J.A.; Kim, K.C. Hybrid CFD-ANN Approach for Evaluation of Bio-Inspired Dolphins Dorsal Fin Turbulators of Heat Exchanger in Turbulent Flow. Appl. Therm. Eng. 2023, 219, 119422. [Google Scholar] [CrossRef]
- AL-Khaffajy, M.; Mossad, R. Optimization of the Heat Exchanger in a Flat Plate Indirect Heating Integrated Collector Storage Solar Water Heating System. Renew. Energy 2013, 57, 413–421. [Google Scholar] [CrossRef]
- Han, L.; Yang, K.; Yang, J.; Li, R.; Li, Y.; Deng, L.; Che, D. A Thermal Calculation Model for Tubular Condensing Heat Exchanger. Appl. Therm. Eng. 2024, 244, 122701. [Google Scholar] [CrossRef]
- Chen, L.-Y.; Adi, V.S.K.; Laxmidewi, R. Shell and Tube Heat Exchanger Flexible Design Strategy for Process Operability. Case Stud. Therm. Eng. 2022, 37, 102163. [Google Scholar] [CrossRef]
- Feng, T.-H.; Chen, C.-K. Numerical Investigation on Thermal-Hydraulic Performance of a Spiral Plate Heat Exchanger. Int. Commun. Heat Mass Transf. 2022, 134, 106057. [Google Scholar] [CrossRef]
- Kapustenko, P.O.; Klemeš, J.J.; Matsegora, O.I.; Arsenyev, P.Y.; Arsenyeva, O.P. Accounting for Local Thermal and Hydraulic Parameters of Water Fouling Development in Plate Heat Exchanger. Energy 2019, 174, 1049–1059. [Google Scholar] [CrossRef]
- Kumar, M.; Pal, S.; Patil, D. Parametric Design Optimization and Thermodynamic Analysis of Plate Fin Heat Exchanger for Helium Liquefaction System. Cryogenics 2024, 139, 103833. [Google Scholar] [CrossRef]
- Shen, S.; Cai, W.; Wang, X.; Wu, Q.; Yon, H. Investigation of Liquid Desiccant Regenerator with Fixed-Plate Heat Recovery System. Energy 2017, 137, 172–182. [Google Scholar] [CrossRef]
- Abdelmoety, A.M.; Muhieldeen, M.W.; Yen Tey, W.; Yin, X.; Beit, N.E. Numerical Investigations on Optimised Shell Designs of a U-Tube Heat Exchanger. Therm. Sci. Eng. Prog. 2024, 47, 102327. [Google Scholar] [CrossRef]
- Zhu, G.-D.; Qian, C.-F.; Fang, Z. An Analytical Theory for the Strength Solution of Tubesheets in Floating-Head Heat Exchangers with Back Devices. Int. J. Press. Vessel. Pip. 2019, 175, 103936. [Google Scholar] [CrossRef]
- Yixiong, S.; Liqing, Q.; Jin, L.; Liang, Z.; Sheng, S.; Shuai, J. Thermal Design and Analysis of Intermediate Heat Exchanger with Alternative Coolants. Ann. Nucl. Energy 2024, 203, 110516. [Google Scholar] [CrossRef]
- Mickoleit, E.; Breitkopf, C.; Jäger, A. Influence of Equations of State and Mixture Models on the Design of a Refrigeration Process. Int. J. Refrig. 2021, 121, 193–205. [Google Scholar] [CrossRef]
- Nitsche, M.; Gbadamosi, R.O. Heat Exchanger Design Guide: A Practical Guide for Planning, Selecting and Designing of Shell and Tube Exchangers; Butterworth-Heinemann: Amsterdam, The Netherlands; Boston, MA, USA, 2015. [Google Scholar]
- Hong, B.; Li, Y.; Li, Y.; Gong, J.; Yu, Y.; Huang, A.; Li, X. Numerical Simulation of Solid Particle Erosion in the Gas-Liquid Flow of Key Pipe Fittings in Shale Gas Fields. Case Stud. Therm. Eng. 2023, 42, 102742. [Google Scholar] [CrossRef]
- Hong, B.; Li, Y.; Li, X.; Ji, S.; Yu, Y.; Fan, D.; Qian, Y.; Guo, J.; Gong, J. Numerical Simulation of Gas-Solid Two-Phase Erosion for Elbow and Tee Pipe in Gas Field. Energies 2021, 14, 6609. [Google Scholar] [CrossRef]
- Hao, B.; Gao, J.; Guo, B.; Ai, B.; Hong, B.; Jiang, X. Numerical Simulation of Premixed Methane–Air Explosion in a Closed Tube with U-Type Obstacles. Energies 2022, 15, 4909. [Google Scholar] [CrossRef]
- Hong, B.; Li, X.; Li, Y.; Li, Y.; Yu, Y.; Wang, Y.; Gong, J.; Ai, D. Numerical Simulation of Elbow Erosion in Shale Gas Fields under Gas-Solid Two-Phase Flow. Energies 2021, 14, 3804. [Google Scholar] [CrossRef]

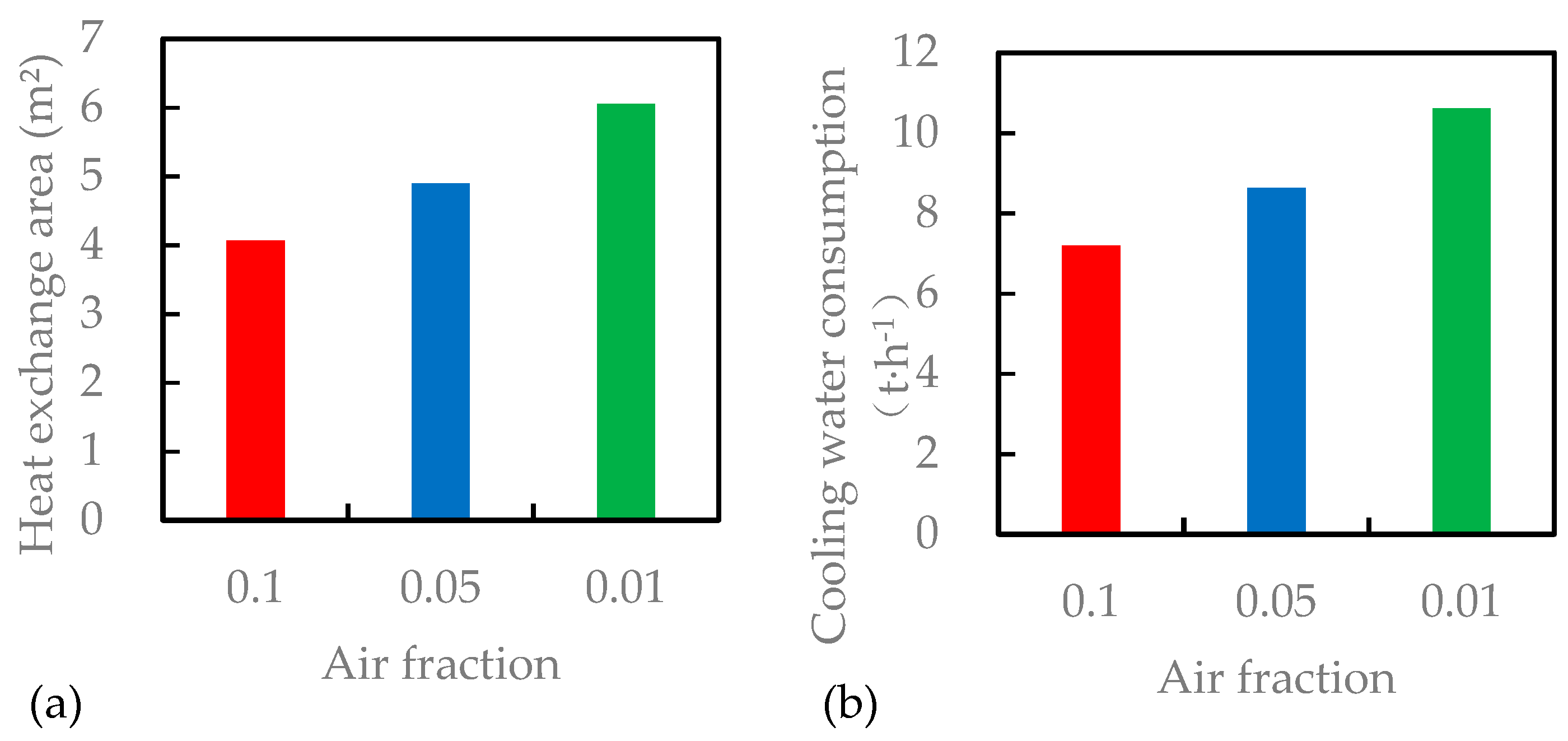
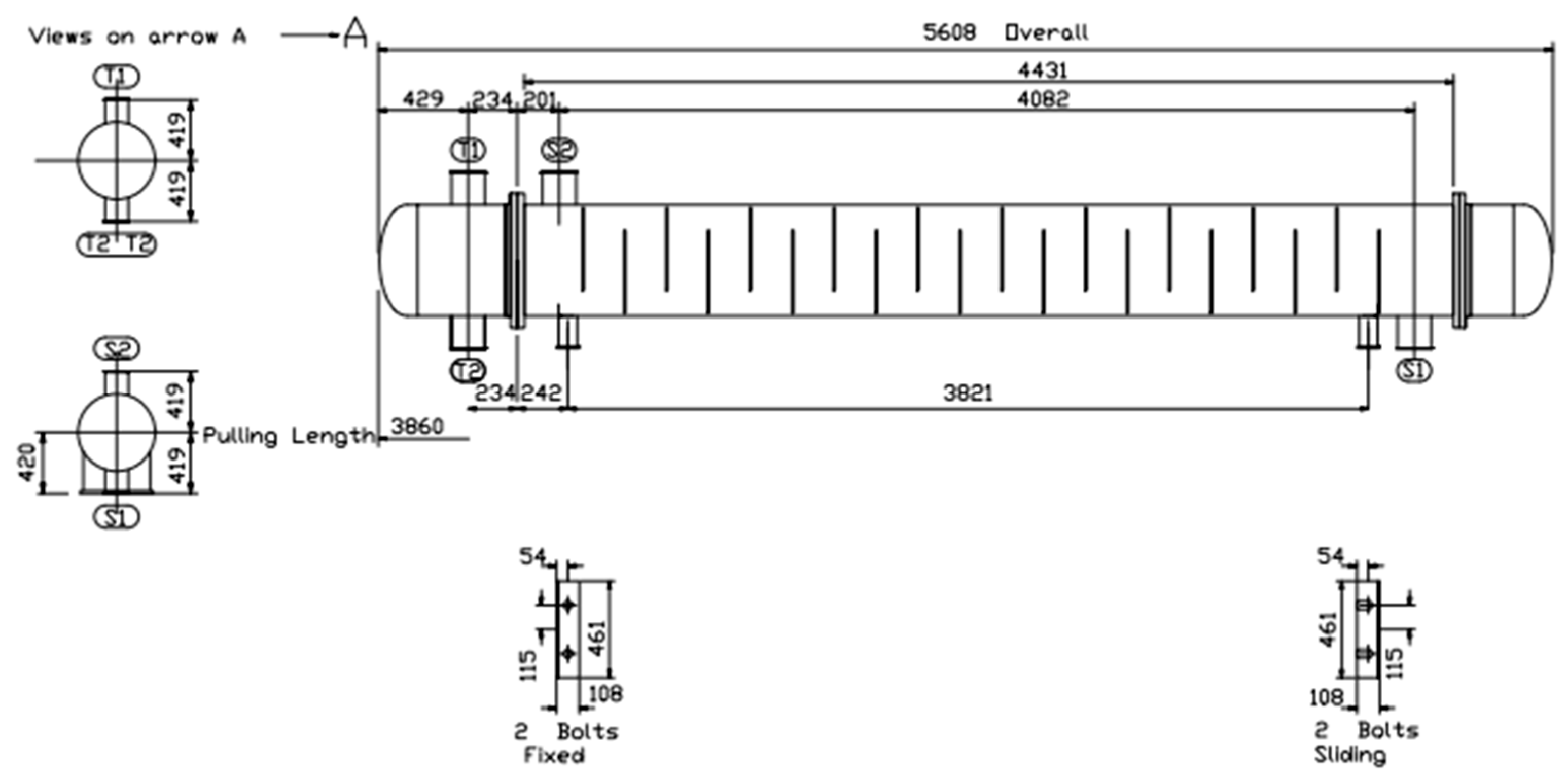
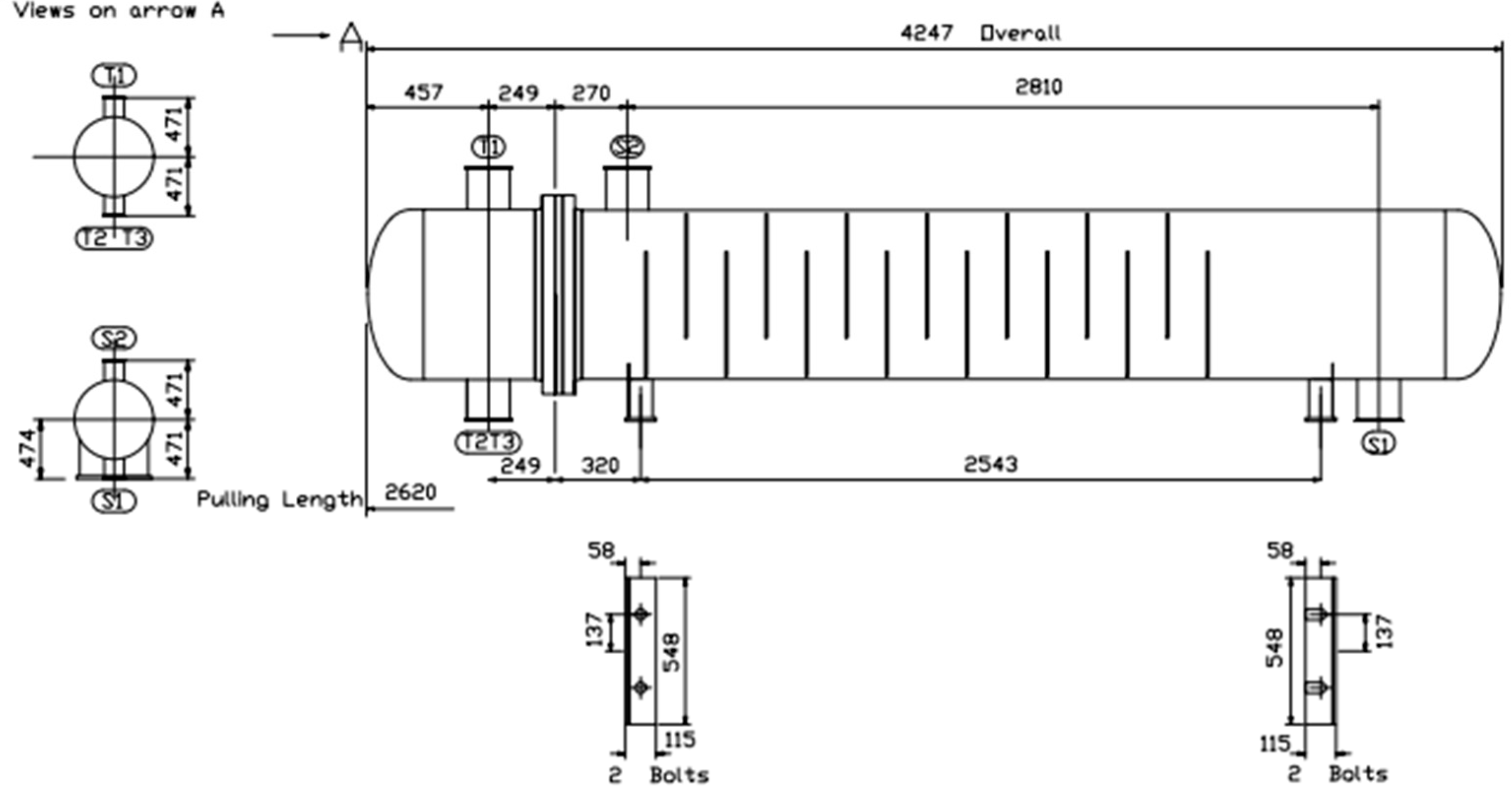
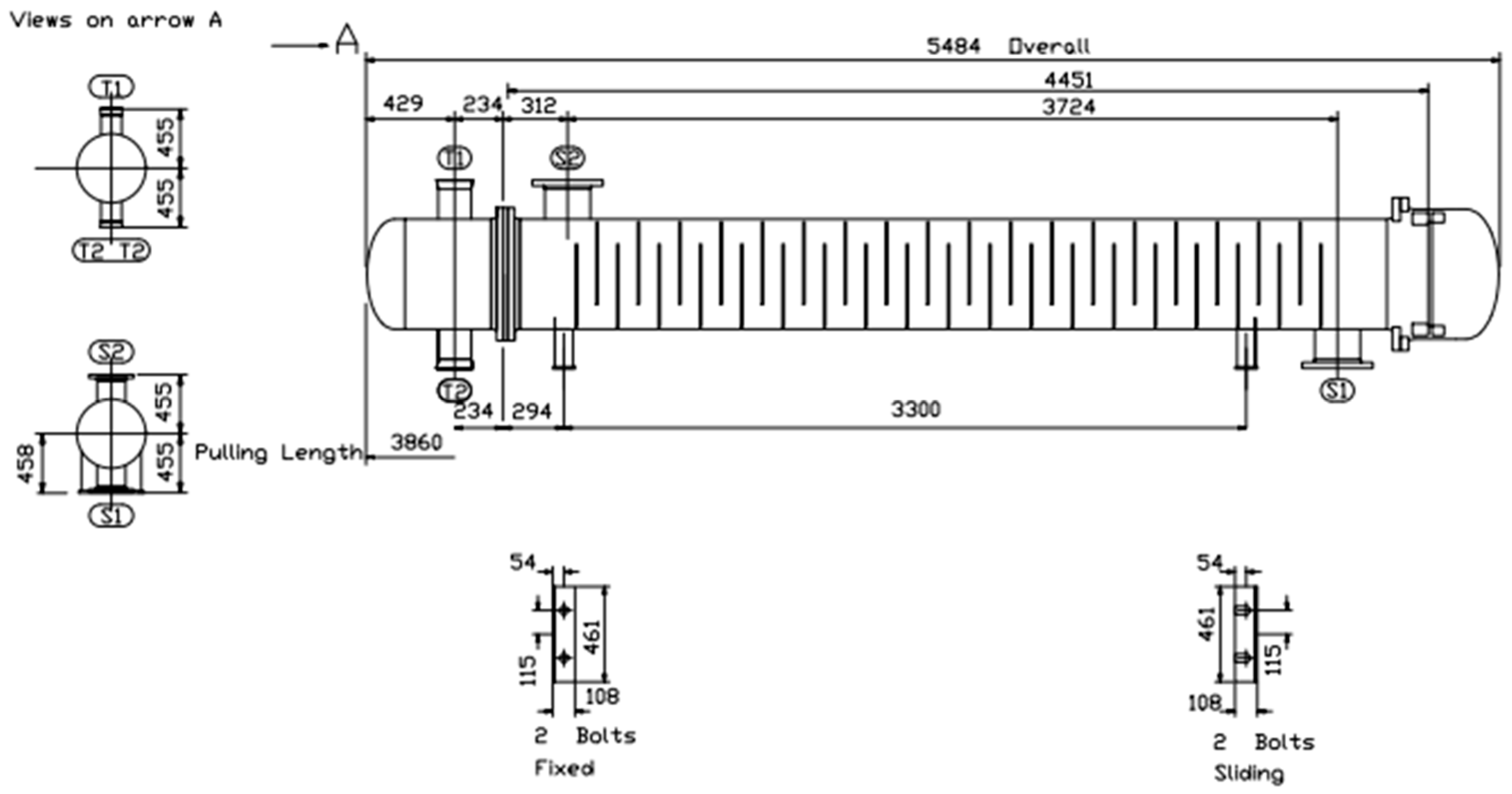




| Type | Advantages | Disadvantages |
|---|---|---|
| Spiral plate heat exchanger [21] | Compact structure design, small footprint; suitable for a variety of fluid media and temperatures, and a wide range of applications; the operation is relatively simple, and the maintenance and cleaning are convenient. | The ability to withstand pressure is relatively low, generally suitable for low or medium pressures; heat transfer efficiency is affected by fluid physical properties. Compared with other types of heat exchangers, the manufacturing cost is higher. |
| Plate heat exchanger [22] | High efficiency, corrugated sheet can increase the surface area of the heat exchange, improve heat exchange efficiency, and save energy; small capacity, convenient integration and layout; removable plate, easy to clean, maintain and replace, and extend service life. | The manufacturing cost is relatively high, the maintenance cost is also relatively high; generally suitable for lower pressure ranges, not suitable for high-pressure fluid handling. |
| Plate-fin heat exchanger [23] | The numerous small flow channels present between the fins significantly enhance the heat transfer area and improve the efficiency of heat transfer for the fluid. The compact structure design is suitable for a location with limited space; the finned structure allows for a higher utilization of metal materials and consumes less metal than other types of heat exchangers. | Because the flow path of plate-fin heat exchanger is small, it is easy to clog. Because the flow path is small, the fluid is subjected to greater resistance when passing through the plate fin. Because of the compact structure of plate-fin heat exchangers, cleaning and maintenance is more difficult. |
| Shell and tube heat exchanger [24] | A significant heat transfer area allows for the accommodation of larger heat transfer requirements. Simple structure, convenient manufacture and installation, easy to clean. Adaptable to different fluid media and temperatures. Suitable for high-pressure and high-temperature environments. | The heat transfer efficiency is limited; the unit metal consumption is large; the volume is relatively large and occupies a large space. |
| Cooling Water Fouling Coefficient (m2·K/W) | Process Material Fouling Coefficient (m2·K/W) | ||
|---|---|---|---|
| Thermal flow temperature | Below 115 °C | Gasoline | 0.000174 |
| Water temperature | Below 52 °C | Volatile oil | 0.000174 |
| Seawater | 0.000086 | Kerosene | 0.000174 |
| Tap water, well water, softened water | 0.000172 | Light diesel oil | 0.000344 |
| River water | 0.000516 | Heavy diesel oil | 0.000516 |
| Item | Oil and Gas | Underground Water |
|---|---|---|
| Volumetric flow (m3/h) | 870 | - |
| Inlet and outlet pressure (kPa) | Atmospheric pressure | Atmospheric pressure |
| Inlet temperature (°C) | 40 | 25 |
| Outlet temperature (°C) | 30 | 27 |
| Component | Volume Fraction (%) |
|---|---|
| C5H12-2 | 12.22 |
| C5H10-5 | 1.87 |
| C5H12-1 | 5.39 |
| C5H10-4 | 1.64 |
| C5H10-6 | 3.76 |
| C6H14-4 | 1.53 |
| C5H8-1 | 1.45 |
| C6H14-5 | 1.62 |
| C5H12O-D2 | 10.88 |
| C6H14-2 | 6.86 |
| C6H14-3 | 5.06 |
| C6H14-1 | 5.43 |
| C7H16-2 | 2.20 |
| C7H16-3 | 2.76 |
| C7H16-1 | 1.82 |
| C7H8 | 7.80 |
| C8H10-4 | 1.21 |
| C8H10-2 | 10.74 |
| C8H10-3 | 4.48 |
| C8H10-1 | 4.34 |
| C9H12-4 | 1.96 |
| C9H12-7 | 3.77 |
| Parameter (Unit) | Fixed Tube Sheet Heat Exchanger | U-Tube Heat Exchanger | Floating-Head Heat Exchanger |
|---|---|---|---|
| Shell diameter (mm) | 500 | 600 | 500 |
| Heat exchange tube specifications (mm × mm) | Φ25 × 2 | Φ25 × 2 | Φ25 × 2 |
| Length (mm) | 4500 | 3000 | 4500 |
| Heat transfer area (mm) | 56.8 | 47 | 41.6 |
| Number of heat exchange tubes (root) | 164 | 188 | 124 |
| Mean flow velocity of shell flow (m/s) | 0.07 | 0.07 | 0.09 |
| Mean flow velocity of pipe flow (m/s) | 9.89 | 7.43 | 12.75 |
| Total heat transfer coefficient (W/(m2·K)) | 187.7 | 148.9 | 221.5 |
| Fixed Tube Sheet Heat Exchanger | Detailed Design | CFD |
|---|---|---|
| Cold flow inlet temperature (°C) | 25 | 25 |
| Cold flow outlet temperature (°C) | 26.98 | 26.39 |
| Hot fluid inlet temperature (°C) | 40 | 40 |
| Hot fluid outlet temperature (°C) | 29.52 | 27.54 |
| Cold flow inlet flow (kg/s) | 2.95 | 2.95 |
| Hot fluid inlet flow (kg/s) | 0.53 | 0.53 |
| Cold flow outlet velocity (m/s) | 0.060 | 0.061 |
| Hot fluid Outlet Velocity (m/s) | 9.89 | 9.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Luo, Y.; Wang, Z.; Liu, Y.; Gai, L.; Wang, Q.; Hong, B. Optimization Design and Performance Study of a Heat Exchanger for an Oil and Gas Recovery System in an Oil Depot. Energies 2024, 17, 2631. https://doi.org/10.3390/en17112631
Chen Z, Luo Y, Wang Z, Liu Y, Gai L, Wang Q, Hong B. Optimization Design and Performance Study of a Heat Exchanger for an Oil and Gas Recovery System in an Oil Depot. Energies. 2024; 17(11):2631. https://doi.org/10.3390/en17112631
Chicago/Turabian StyleChen, Zengliang, Ye Luo, Zhihui Wang, Yulin Liu, Limei Gai, Qichao Wang, and Bingyuan Hong. 2024. "Optimization Design and Performance Study of a Heat Exchanger for an Oil and Gas Recovery System in an Oil Depot" Energies 17, no. 11: 2631. https://doi.org/10.3390/en17112631
APA StyleChen, Z., Luo, Y., Wang, Z., Liu, Y., Gai, L., Wang, Q., & Hong, B. (2024). Optimization Design and Performance Study of a Heat Exchanger for an Oil and Gas Recovery System in an Oil Depot. Energies, 17(11), 2631. https://doi.org/10.3390/en17112631








