Abstract
With the increasing number of electric vehicles (EVs), their uncoordinated charging poses a great challenge to the safe operation of the power grid. In addition, traditional individual-EV scheduling models may be difficult to solve due to the increasing number of constraints. Therefore, this paper proposes a cluster-based EV scheduling model. Firstly, electric vehicle clusters (EVCs) are formed based on the charging and discharging preferences of EV users and the expected time for EVs to leave. Secondly, the EVC energy and power boundary aggregation method based on the Minkowski addition algorithm is proposed. Finally, for the sake of reducing user charging cost and distribution network energy loss, and smoothing the daily load curve, an EVC scheduling model for EV participation in grid auxiliary services is proposed. The optimization model includes the reactive-power compensation of EV charging piles. The simulation results show that the proposed EVC scheduling model can greatly reduce the solution time compared to traditional individual-EV scheduling model. The model has high potential to be applied to large-scale EV scheduling. The reactive-power compensation provided by EV charging piles improves the voltage quality of the grid and enables more EVs to be connected to the grid.
1. Introduction
Global warming caused by greenhouse gas emissions has become a widespread challenge to the sustainability of the Earth. Replacing fossil fuel vehicles with electric vehicles (EVs) offers a promising way to reduce greenhouse gas emissions and dependence on traditional fossil energy sources [1]. The number of EVs is expected to reach 245 million globally by 2030 [2]. However, despite the environmental benefits of EVs, the uncoordinated charging of large numbers of EVs can jeopardize the reliability and economics of the power system. This can lead to increased energy losses, voltage reduction, peak-to-valley differentials, and transformer overloads. Studies have shown that when the penetration of uncoordinated charging EVs in the grid reaches 50%, the maximum voltage deviation in the distribution network may increase by more than 30% and the power losses in the transmission lines increase by 25% [3]. Therefore, it is crucial to explore how to minimize the negative impacts of EVs on the distribution system and how to further utilize EV flexibility to provide ancillary services to the grid.
To address the problem of the negative impact of the uncoordinated charging of large-scale EVs on the power distribution system, researchers have conducted in-depth studies. For example, study [4] proposed an optimal EV charging strategy for reducing network transmission loss while taking seasonal factors into consideration. Study [5] proposed an optimal-power flow-based EV charging and discharging strategy to improve the economic and technical performance of power grid operation by considering the constraints of power grid operation and battery function. Study [6] proposed a multi-objective EV charging and discharging scheduling strategy based on a local search and competitive learning particle swarm optimization algorithm. In the context of electricity market trading, study [7] proposed a stochastic-based optimal charging strategy for plug-in EV aggregators under a distribution system operator (DSO) incentive and regulatory policies. Study [8] proposed a large-scale EV grid scheduling model and solution algorithm based on improved second-order cone programming. Study [9] proposed two smart charging strategies whose objective functions consider the minimization of total daily cost and the minimization of the peak-to-average ratio, and investigated the impact of the two smart strategies on the charging of plug-in EVs from both economic and technological perspectives. While the aforementioned studies mainly focus on mitigating the impact of large-scale charging on the grid through active-power management, reactive-power management is equally crucial for the safe and economic operation of the distribution network [10].
Traditional distribution network reactive-power compensation devices mainly include capacitors and static reactive-power compensation devices, but the investment cost is high. With the development of charging devices, these devices are able to achieve active- and reactive-power management according to the demand of EVs and do not affect battery life when generating or consuming reactive power [11,12,13]. EV reactive-power compensation based on V2G technology not only reduces the investment cost of reactive-power compensation equipment, but also improves the safety and economy of distribution network operation [14]. Therefore, in order to further reduce the impact of large-scale charging on the grid, some researchers have begun to study active–reactive-power coupling management strategies for EVs. Study [15] proposed a model for conjugate active- and reactive-power management through EVs in distribution networks. Study [16] developed a hierarchical coordination framework for optimizing active- and reactive-power scheduling for EVs. The coordination framework consists of two optimization models; the first model is a comprehensive optimal power flow model at the distribution grid level, and the second model is an EV scheduling model that provides reactive-power support to the grid. The simulation results show the benefits of EV reactive-power scheduling for grid operation and EV owners, e.g., it helps to address under-voltage due to active-power consumption during EV charging. Study [17] proposes a double-layered smart energy management approach for EVs to manage active- and reactive-power flows to/from PEVs at the node and system levels of the distribution system. Study [18] proposed a two-stage optimization method for energy loss minimization in microgrids based on a smart power management scheme for EVs. Study [19] presented a two-stage optimization approach for the active- and reactive-power control of EVs to meet both the grid and EV users’ requirements. Although [15,16,17,18,19] have conducted in-depth studies on the modeling of EV participation in grid reactive-power optimization, this method does not take into account the charging preferences of the users, nor does it provide financial compensation to the EV users who participate in reactive-power compensation. In fact, EV users, as highly free individuals, can choose charging modes suitable for them according to their needs, such as fast charging, participation in charging optimization only, and participation in charging and discharging optimization. Furthermore, the approaches mentioned in studies [4,5,6,7,8,9] and study [15] are based on centralized control. Although centralized control is suitable for considering power flow constraints in the distribution network, as the number of EVs increases, the optimization model will face “dimensionality catastrophe”, and solving the optimization problem will be very time-consuming [20]. At the same time, direct control of the charging and discharging strategy of each EV by the distribution system operator will put a huge burden on the communication network. To overcome these problems, distributed optimization models have been developed in studies [16,17,18,19]. Although distributed optimization models can handle large-scale EV optimization problems, the power balance constraints of the load buses and the power flow constraints of the distribution network lines are usually ignored when actively managing EVs, which may reduce the possibility of safe and economic grid operation.
In order to solve the problem of the dramatic increase in variables and constraints brought by the large-scale EV issue to the optimal scheduling of power grids, the ideas of hierarchical optimization and cluster optimization can be adopted. The electric vehicle cluster (EVC) scheduling model is an equivalent aggregation of individual EVs within the cluster, i.e., any charging strategy that satisfies the cluster model can always find a distribution strategy that satisfies the individual constraints of EVs. Using the EVC scheduling model instead of the individual-EV scheduling model to carry out grid optimization scheduling can ignore individual device characteristics and focus on the EVC characteristics, thus reducing the computational difficulty. Moreover, the impact of individual-EV charging and discharging power on the grid is extremely weak, aggregating a certain number of EVs to form clusters can have a good effect, and cluster charging demand will show regularity, which can reduce the spatial and temporal uncertainty of individual EVs. Study [21] proposed a collaborative optimization model of generators, EVCs, and wind power, but the energy constraints of EVCs are ignored. Studies [22,23] developed an electricity pricing method to indirectly schedule the charging and discharging decision process of EVs, in which the EVC was modeled using the concept of a virtual battery. Study [24] designed a hierarchical multiagent system to schedule the active and reactive power of EVCs. Although EVC models are used in the EV scheduling models proposed in the above references to reduce the computational and communication problems in large-scale EV scheduling, they do not solve the EV charging and discharging power aggregation and allocation problems. They do not consider the charging preferences of users when dividing clusters either. In addition, these EVC scheduling models do not consider the reactive-power compensation of charging piles.
Based on the above analysis, this paper concentrates on the issue of EVC scheduling models for distribution systems while considering reactive-power compensation at charging piles. The main contributions of this paper are summarized as follows:
- (1)
- This paper proposes a double-layer scheduling framework for DSO and electric vehicle aggregators (EVAs) to systematically manage the charging and discharging power of EVs.
- (2)
- A method for classifying EVCs, a model for calculating energy and power boundaries, and a model for allocating EVC charging and discharging power are presented. Specifically, the EVC division method takes into account the charging preferences of EV users. The energy and power boundary aggregation method utilizes the Minkowski addition algorithm, while the allocation method is based on a consensus algorithm.
- (3)
- An EVC scheduling model is proposed for the participation of EVs in the auxiliary services of the grid, to reduce the user charging cost and distribution network energy loss, and to smooth the daily load profile. This optimization model takes into account the power flow constraints of the distribution network and the reactive-power compensation of EV charging piles.
The organization of the remainder of this paper is as follows: Section 2 provides the proposed double-layer scheduling framework for a DSO and EVAs. Section 3 introduces the proposed energy and power aggregation and distribution methods for EVCs. Section 4 presents the formulation of the proposed EVC scheduling model. Section 5 gives the simulation results and discussion. The conclusions and future studies are discussed in Section 6.
2. Double-Layer Scheduling Framework for DSO and EVAs
Figure 1 shows the proposed double-layer scheduling framework for a DSO and EVAs to manage the charging and discharging EVs. The first layer is controlled by the DSO, which optimizes the charging and discharging of the EVCs. The second layer is controlled by EVAs, which schedule individual EVs. First, the EVAs obtain the necessary information from the EV users. Then, they divide the EVs into different EVCs. The EVAs calculate the energy and power boundaries of each EVC, i.e., the operation constraints of each EVC, using the energy and power aggregation model provided by the paper. They report these boundaries to the DSO. Next, the EVAs receive the charging and discharging power signals of the EVCs from the DSO. They allocate the power of the each EVC to its EVs using the power allocation method. Finally, the EVAs send the charging and discharging schedules to the EV users. The EVs then execute the charging and discharging plans as instructed by the EVAs. The proposed scheduling framework requires robust communication infrastructure. This is crucial because continuous interaction is needed between the DSO, EVA, and EV users.
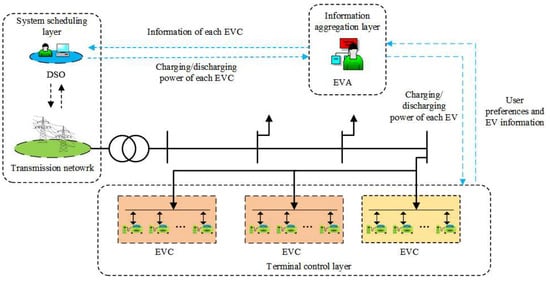
Figure 1.
Double-layer scheduling framework for DSO and EVAs for orderly scheduling of EVs.
The effectiveness of this scheduling framework relies on robust methods for energy and power aggregation and distribution for EVCs. With the double-layer scheduling framework established, the subsequent sections delve into the specific methodologies employed for the effective management of EV charging and discharging.
3. Energy and Power Aggregation and Distribution Methods for EVCs
This section introduces the proposed method for classifying EVCs. It also presents the model for calculating energy and power boundaries, as well as the model for allocating the charging and discharging power of EVCs. EVAs can use these methods and models to manage EVs.
3.1. EVC Division Method
Not all EV users are willing to participate in grid dispatch. Some only want to join in with charging power regulation, while others will participate in V2G. Therefore, the proposed EVC division method considers the charging preferences of EV users. Based on their willingness to participate, EVs can be classified into three categories.
Type I EVs (Non-participatory in Grid Dispatch): These EVs do not participate in dispatch. They start charging immediately upon connecting to the charging piles at their maximum rated power until either they disconnect from the station or the vehicle’s battery reaches the set target value.
Type II EVs (Participatory in Grid Dispatch but No Discharge): These EVs participate in dispatch for charging but are not allowed to discharge power back to the grid.
Type III EVs (Participatory in Grid Dispatch and Permitted Discharge): These EVs participate in dispatch for both charging and discharging power back to the grid.
Based on the above charging preference classification criteria, EVA firstly classifies EVs under its jurisdiction into three major clusters. Beyond charging preferences, the timing of EV usage also plays a crucial role in EVC scheduling. For example, commuter EVs tend to have a more concentrated off-grid time, typically occurring between 6:00 a.m. and 10:00 a.m. Therefore, this paper utilizes the off-grid time of EVs as a secondary criterion to group them into clusters. For instance, in the case of Type II EVs, if their off-grid time falls predominantly between 6:00 a.m. and 10:00 a.m., the EVs can be further categorized into five EVCs based on their off-grid time. Essentially, EVs with similar charging preferences and off-grid time are consolidated into the same EVC. This clustering approach reduces the number of variables in the scheduling optimization model, as it depends solely on the number of EVCs, independent of the number of EVs. As a result, this streamlining significantly reduces computation time.
3.2. EVC Energy and Power Boundary Aggregation Method
As stated in Section 2, once the EVs are divided into clusters, the EVA has to calculate the energy and power boundaries for each EVC, i.e., the operating limits for each EVC. This subsection describes the model for calculating the energy and power boundaries. First, the EVA needs to collect the charging and discharging power limit and capacity as well as trip information for each EV in the cluster. Therefore, for any EV, the following information is assumed to be reported to its EVA:
where and are the moments when EV arrives at and leaves the charging station; is the initial SOC of the battery for EV ; is the expected SOC when the EV disconnects the charging piles; and are the minimum and maximum SOC allowed for the battery; is the battery capacity; is the maximum apparent power of the charger; and and are the maximum charging and discharging power of the charger.
Using the aforementioned information and the traditional individual-EV charging and discharging power scheduling model, we can derive the charging and discharging power boundaries as well as energy boundaries of the EVC at any given moment. We first introduce a 0–1 variable that indicates whether or not EV is in the charging station at time . An value equal to 1 means that EV is in the charging station and can be scheduled. Therefore, the value of can be determined based on the arrival and departure times of the EVs.
is combined with the charging and discharging power limit of a single EV given in Equation (1), along with the energy boundaries for Type II EVs and Type III EVs, as shown in Figure 2 and Figure 3. In these two figures, the blue curve shows the highest possible EV battery energy change. This happens when the battery starts charging at full power as soon as it connects to the grid, reaching the maximum allowed energy level at a certain point. The yellow curve shows how the EV battery energy changes during the scheduled period. In Figure 2, the green curve represents the scenario where the EV does not charge immediately upon connecting to the grid. Instead, it charges at full power just before disconnection to meet the user’s expected energy level. In Figure 3, the green curve shows the lowest possible EV battery energy change. This happens when the battery starts discharging at full power immediately after connecting to the grid. We use the Minkowski addition algorithm to determine the charging and discharging power and energy boundaries for the EVC, as depicted in Equation (3).
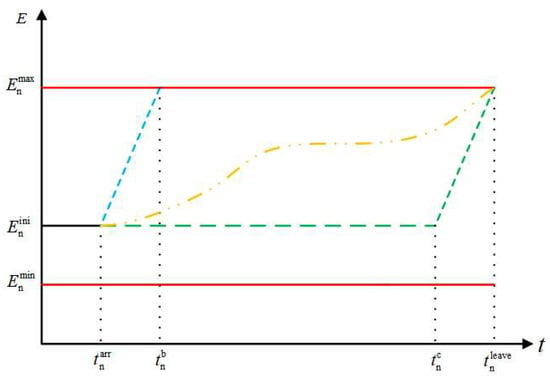
Figure 2.
Energy boundaries of a single Type II EV.
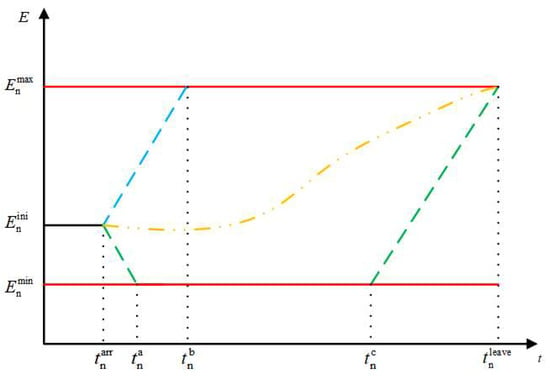
Figure 3.
Energy boundaries of a single Type III EV.
In the above equation, is the index of the EVC. Since there are two classification criteria for ECVs, we use two subscripts for an EVC. EVC is the EVC consisting of Type II EVs (k = 2) or Type III EVs (k = 3). is the set of EVCs. is the set of EVs inside EVC . and are the maximum charging and discharging power of EVC at moment . and are the maximum and minimum energy of the virtual batteries of EVC at moment . Since the arrival time of each EV in an EVC is different, the charging and discharging power and energy boundaries at each moment of the EVC are different. denotes the maximum energy available to EVC at time . When the EVs arrive, they start charging at maximum power up to moment . represents the minimum energy value that EVC needs to maintain in time , so that when the EVs leave the charging station, the battery has the amount of energy that the user expects. denotes the minimum energy of EVC consisting of Type III EVs at moment . When the EVs arrive, they start discharging at maximum power up to moment . is the apparent power capacity of the virtual charger for EVC at moment .
Since the arrival time of each EV in the EVC is not the same, it is possible for an EV to arrive the charging pile at every moment, which will result in a change in the energy of the virtual battery of the EVC; we need to compute this change in energy in order to use it for the energy calculation formulae in the EVC scheduling model.
By calculating the power and energy boundary parameters as well as the energy change parameters of EVCs based on the above formulas, we can establish the EVC operation constraints applicable to the EVC scheduling model, as shown in Equations (5)–(7).
The maximum charging and discharging power constraint of the EVCs is shown in Equation (5). EVCs composed of different types of EVs have different maximum charging and discharging power constraints.
where is the charging power of EVC at moment ; is the discharging power of EVC at time moment ; and and are binary variables used to ensure that only one state (i.e., charging or discharging) is true at each moment for each EVC consisting of Type III EVs.
Equation (6) shows the energy constraints of the EVCs.
where is the energy of the virtual batteries of EVC at time .
Equation (7) is the reactive-power constraint for the EVCs.
where is the charging/discharging power of EVC at time ; denotes the reactive power absorbed or released by the charger charging the virtual battery of EVC at time ; and is the apparent power capacity of the charger.
To summarize, Equations (5)–(7) are the EVC operating constraints. Therefore, the optimization variables for the EVC scheduling model are as follows.
Using the above constraints and variables, the DSO can optimize the charging and discharging power of EVCs without having to directly optimize the charging and discharging power of a large number of individual EVs, which can greatly reduce the time it takes to solve the optimization problem.
The above power and energy boundary calculation model is used for EVCs consisting of Type II EVs and Type III EVs, because Type I EVs do not participate in power system operation optimization. So, we do not need to calculate their cluster boundaries, but need to calculate their charging power at each moment, as shown in Equation (9).
where is the charging power of EV at moment . The first three equations in Equation (9) are used to calculate the amount of energy and charging time required to charge an EV when it was charged at its maximum charging power. is the time interval after the scheduling cycle is discretized, e.g., 15 min, 1 h. is the number of time intervals that EV needs to be charged. From moment to moment , the EV is no longer charged at maximum power; otherwise, the battery energy may exceed its capacity or exceed the user’s expectations. Using Equation (9), the charging power of a Type I EV can be calculated and then input as a known parameter into the EVC scheduling model.
3.3. EVC Charging and Discharging Power Allocation Method
As stated in Section 3.2, the DSO optimizes the charging and discharging of the Type II and Type III EVCs by using Equations (5)–(7). However, after obtaining the charging and discharging power of the EVC, it is still necessary to allocate the power to each EV inside the EVC to make it execute. There is also the question of how to allocate the power so that the power of all the EVs adds up to equal the cluster power while satisfying the individual constraints of each EV. Existing power allocation methods typically only distribute the total power equally among EVs without considering the differences in battery capacity and charging/discharging power constraints of each EV. Other optimization-model-based methods are able to take into account the operational constraints of individual EVs, but are unable to accurately track the cluster power scheduling commands sent by the DSO. In this paper, we propose a power allocation method based on a consistency algorithm that aims to accurately execute the scheduling instructions and takes into account EV energy differences.
The consensus algorithm [25,26] is an iterative algorithm in which the state variables of all individuals in the system tend to converge to an identical value as the iterations proceed. Therefore, when applying this algorithm, a state variable is first defined. The state variable used in the proposed EVC charging and discharging power allocation method is shown in Equation (10). Its updating law is shown in Equation (11).
In Equation (10), and are the initial charging power and discharging power of EV (belonging to EVC ) before starting the iteration at time , which can be calculated by Equation (12). In Equation (12), is the total number of EVs that belong to EVC and are connected to the grid at time . In Equation (11), constant is the weight between EV and at time , which is given by Equation (13). In Equation (13), the values of and are equal to minus one.
After updating the value of , the charging power or discharging power assigned to each EV can be calculated by Equation (15).
Note that if obtained from Equation (15) exceeds the charging power limit , it should be adjusted to , as shown in Equation (16). So should .
According to the above formula, a flowchart for the proposed charging and discharging power allocation method is shown in Figure 4.
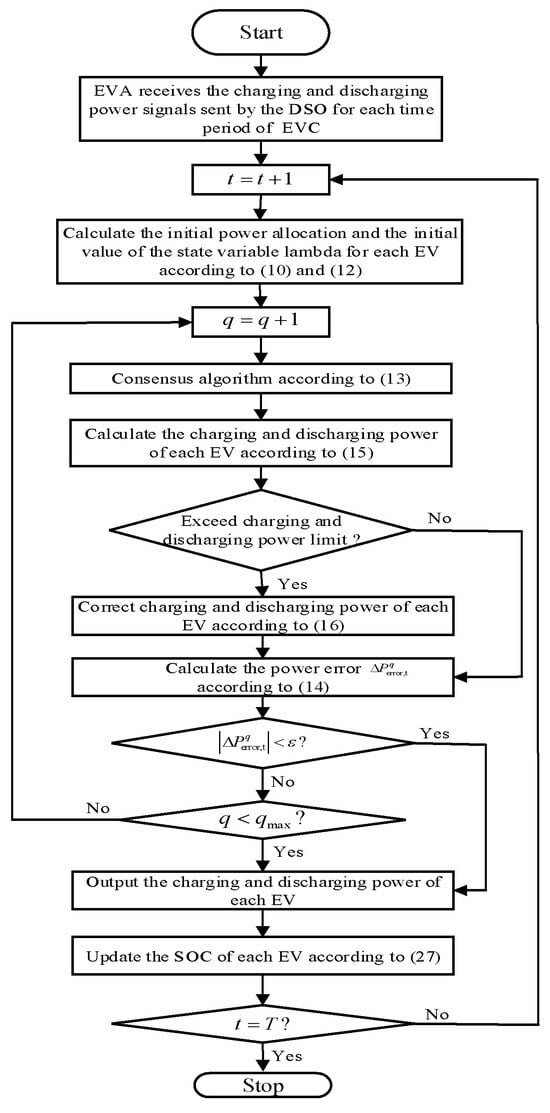
Figure 4.
Flowchart for the proposed charging and discharging power allocation method.
The specific steps are shown below.
- (1)
- The EVA receives the charging and discharging power signals sent by the DSO for each time period of each EVC.
- (2)
- For each EVC, the EVA calculates the initial power allocation for each EV in each time period based on the number of EVs connected to the grid in each time period using Equation (12).
- (3)
- For each period in the scheduling cycle, firstly, the initial value of the state variable lambda is calculated using Equation (10); then, the charging and discharging power of each EV is updated according to Equations (15) and (16), and the error between the sum of the charging or discharging power of all EVs and the cluster power is calculated according to Equation (14). If the error meets the requirements, the iteration is stopped; otherwise, the lambda is updated according to Equation (11), and then, the charging and discharging power of each EV is updated until the error meets the requirements or the number of iterations exceeds the set number.
- (4)
- After obtaining the power allocation result that meets the requirements, the energy of each EV for the current period is calculated according to Equation (17).
The above allocation algorithm only allocates the active charging and discharging power of the EVC and does not deal with the reactive power. For the allocation of reactive power, after obtaining the active-power allocation scheme that meets the requirements, the maximum reactive power that can be provided by individual EVs can be calculated according to Equation (18).
If the sum of the maximum reactive power that can be provided by individual EVs is less than the cluster reactive power , the real reactive charging and discharging power per EV charger is the maximum value. If it is greater, constraint Equation (19) is added to the scheduling model and re-optimization is performed to find another solution until the requirement is satisfied.
4. Formulation of the Proposed EVC Scheduling Model
Based on the operating constraints and variables for EVCs described in Section 3, this section proposes an optimal scheduling model for EVCs considering the network constraints of the distribution system. The proposed optimization model aims to reduce charging costs for EV users, minimize network energy losses, and decrease the peak-to-valley difference in the system’s daily load profile. Additionally, the model considers the absorption and release of reactive power by EV chargers to enhance grid voltage quality.
The objective function of the EVC scheduling model is as follows.
where is the total charging cost of the EVCs. If the EVC consists of Type III EVs, equals the cost of charging minus the revenue from discharging. is the objective function to reduce the peak-to-valley difference in the daily load curve, which is expressed by the daily load variance, as shown in Equation (22). The smaller the daily load variance, the smaller the fluctuation in the daily load curve and the smaller the peak-to-valley difference, and vice versa. is the total energy loss of the distribution network. denotes the charging power minus the discharging power of all EVCs at bus . is the active-power demand of other loads at bus . is the square of the current magnitude in the line, i.e., . is the total number of time periods during a scheduling cycle. Since the units and magnitudes of the two objective functions in Equation (20) are different, the coefficients , , and are introduced to turn the three objective functions into a unified measure.
The constraints of the EVC scheduling model include the operational constraints of the EVC (Equations (5)–(7) shown in Section 3.2), the bus power balance equation constraints (Equations (25)–(28)), the bus voltage magnitude constraints (Equations (29)–(31)), and the line current magnitude constraints (Equation (32)) as follows.
The DistFlow model [27] is used in the power flow constraints. In addition, for the nonlinear constraints between voltage, current, and power, the second-order cone relaxation method is used to transform them into second-order cone constraints. Therefore, is the square of the voltage magnitude on bus , i.e., , is the square of the current magnitude in the line, i.e., . When the charging time of multiple EVs is relatively concentrated, it may lead to overloading of the distribution network, a voltage drop, or even an over-limit, so the upper and lower limit constraints of the voltage amplitude at each bus and current magnitude in each line are considered.
With the above optimization model, the DSO can optimize the charging and discharging power of EVCs, and the absorption and release of reactive power by EV chargers. Then, the DSO passed the optimal results to the EVAs. The EVAs allocate the charging/discharging power of each EVC to its EVs according to the power allocation method, and, finally, send the information to the users. Finally, the EVs execute the charging and discharging power scheduling plan sent by the EVAs.
The proposed EVC scheduling model represents a second-order conic programming problem (SOCP). Common commercial solvers (e.g., Gurobi and CPLEX) can be used to find the global optimal solution quickly.
5. Simulation Results and Discussion
5.1. Description of Data Used for Simulation
An IEEE-33 bus test system rated at 12.66 kV was used as the simulation system. Its topology and parameters were taken from reference [28]. The daily load curve for basic loads and the time-of-use electricity prices are depicted in Figure 5. In parking clusters, coordinated pricing mechanisms have been proven to be an effective way to improve the satisfaction of users and the economy of the system [29]. This is another worthy research topic, but it is not covered in this paper. This paper mainly focuses on optimizing the charging and discharging schedule of electric vehicles participating in the ancillary services market based on time-of-use pricing mechanisms. Table 1 lists the basic parameters of the EVs, where is a normal distribution with a mathematical expectation of and a standard deviation of , and is a uniform distribution over the interval . The arrival and departure times as well as the initial state of charge (SOC) of all EVs are sampled from their respective probability distributions by Monte Carlo methods. According to the EVC division method presented in Section 3, all EVs are divided into different EVCs according to their charging preferences and leaving times. Table 2 shows the details of the EVC division rule used in the simulation. The proposed EVC scheduling model can be applied in both day-ahead and intra-day manners. In this paper, day-ahead scheduling is taken as an example, assuming that the scheduling period is from 12:00 to 12:00 the next day, with an interval of 1 h.
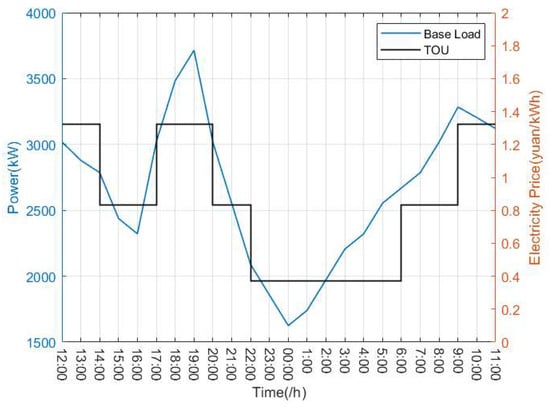
Figure 5.
The daily load curve for basic loads and the time-of-use electricity prices.

Table 1.
Basic parameters of EVs.

Table 2.
Division rule of the EVCs.
5.2. Case Study Settings
Four cases are studied in this paper.
Case 1: A study of the difference in solution efficiency between the EVC scheduling model and the traditional individual-EV scheduling model.
Case 2: A study of the effectiveness of the proposed EVC charging/discharging power allocation method.
Case 3: A study of the effects of different objective functions and reactive-power compensation provided by electric vehicle charging piles on the optimization results of the EVC scheduling model.
Case 4: A study of the impacts of different EV charging preferences on the economics and safety of distribution network operation.
All simulations were programmed in the MATLAB 2018a environment and the optimization problems were solved by YALMIP with Gurobi 10.0.1 solver.
5.3. Case 1: EVC Scheduling Model vs. Individual-EV Scheduling Model
In this case, we investigate the differences between the EVC scheduling model and the individual-EV scheduling model in terms of solution results and solution time. We conducted two simulations, the first assuming that all EVs involved in the scheduling are type II EVs, i.e., they only participate in the charging power scheduling process and do not participate in V2G. The second experiment assumes that all EVs are type III EVs, which not only participate in the charging power scheduling process but also participate in V2G. For the first experiment, the optimization objective is to minimize the charging cost of the EVs. For the second experiment, the optimization objective is to minimize charging cost minus discharging revenue. Note that in this case, both optimization models only consider the active-power dispatch of EVs and do not consider the reactive-power dispatch of charging piles. In each simulation, we tested three scenarios when the numbers of EVs involved in the scheduling were 1000, 2000, and 3000. The optimization results for each model in both experiments are shown in Table 3 and Table 4.

Table 3.
Optimization results of the EVC and the individual-EV scheduling models when EVs are Type II EVs.

Table 4.
Optimization results of the EVC and the individual-EV scheduling models when EVs are Type III EV.
As can be seen from Table 3, the solving time of the individual-EV scheduling model (IEV model) increases exponentially with an increase in the number of EVs. It can be imagined that if power flow constraints of the distribution network are introduced into the model, the solving time may sharply increase, or the problem may even fail to be solved successfully. However, the solving time of the EVC scheduling model (EVC model) does not increase significantly with an increase in the number of electric vehicles. This is because an increase in the number of EVs does not increase the number of EVCs. As for the optimization results, in simulation 1, both models gave the same results. This indicates that the proposed EVC scheduling model is correct and effective. It can effectively solve the large-scale EV scheduling problem.
As can be seen from Table 4, considering the V2G scenario does not increase the solution time of the EVC scheduling model, but there is a small difference in the optimization results between the EVC scheduling model and the individual-EV scheduling model. The optimization results of the EVC scheduling model will be better than those of the individual-EV scheduling model. Because the EV charging and discharging scheduling model is a multi-temporal coupling model, it is difficult to achieve full equivalence between the EVC scheduling model and the individual-EV scheduling model. Especially after considering V2G, the energy changes in EVC in adjacent time periods become larger, which is more likely to produce errors. Therefore, after obtaining the EVC optimization results, the results should be assigned according to the individual constraints of EVs to make them more reasonable.
5.4. Case 2: Investigate the Effectiveness of the Proposed EVC Charging/Discharging Power Allocation Method
In this case, we use the proposed allocation method to allocate the charging and discharging power of the EVCs of 1000 EVs obtained in the simulation in Case 1, i.e., the charging and discharging power of each EVC in each time slot is allocated to the EVs that are connected to the grid and belong to it, so that each EV receives a scheduling instruction to arrange its own charging and discharging power plan. The allocation results are shown in Figure 6 and Figure 7, and Table 5.
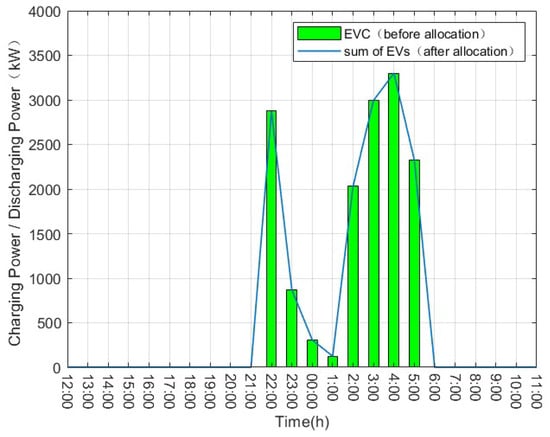
Figure 6.
Total power of all EVC before allocation vs. total power of all EVs after allocation for 1000 Type II EVs.
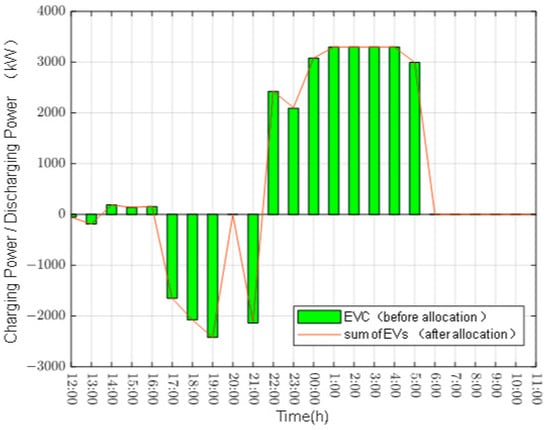
Figure 7.
Total power of all EVC before allocation vs. total power of all EVs after allocation for 1000 Type III EVs.

Table 5.
The charging/discharging power allocation results of the EVCs for Type II and Type III EVs.
Figure 6 shows the total power of all EVCs before allocation vs. the total power of all EVs after allocation for 1000 Type II EVs. Figure 7 shows the total power of all EVCs before allocation vs. the total power of all EVs after allocation for 1000 Type III EVs. As can be seen from the figure, overall, there is almost no difference between their pre-allocated and post-allocated power in each time slot. The results of the quantitative analyses are presented in Table 5.
In Table 5, denotes the total number of time slots in which the allocation error (calculated by Equation (14)) meets the requirement (<0.01 kW) out of the 24 time slots, and denotes the total number of time slots where the allocation error does not meet the requirement. (kW) represents the maximum allocation error of all EVCs and all time slots, and (%) represents the percentage of the maximum allocation error relative to the power of the EVC for that time slot. (%) represents the percentage of the maximum allocation error relative to the total power of all EVCs for that time slot. denotes the total time required for the successful allocation of the five EVCs.
As can be seen from Table 5, the solution time required by the allocation method is very short, so that the solution time for the EVC scheduling model given in case1, together with its allocation time, is also still much shorter than the solution time for an individual-EV scheduling model. As for the allocation error, the allocation error of the Type II EVs, which only participates in charging power scheduling, is very small. The allocation errors of each EVC in each time period are in line with the requirements. This result is consistent with Case 1. The EVC scheduling model for Type II EVs is more equivalent to the individual-EV scheduling model, so the differences in the optimization and allocation results are minimal. As for Type III EVs, it can be seen that the results of most of the time slots satisfy the allocation error requirement, and only one slot does not. The allocation error values are small. As analyzed in case 1, the EVC scheduling model of Type III EVs cannot easily be made equivalent to the individual-EV scheduling model because of the V2G, so there will be an error in the optimization results of both. The constraints of the individual models are taken into account to correct the optimization results when performing EVC power allocation, so that the difference between the allocation results and the EVC optimization results can be explained. The above analyses demonstrate the effectiveness of the allocation method proposed in this paper.
5.5. Case 3: Study the Effects of Different Objective Functions and Reactive-Power Compensation Provided by Electric Vehicle Charging Piles on the Optimization Results of the EVC Scheduling Model
In this case, we investigated the impact of EVC scheduling models with different objective functions on the grid and discuss the changes in the grid operation state after considering the reactive-power compensation provided by charging piles. The IEEE 33-bus system was used as the test system. Assume that buses 13, 18, and 32 are each equipped with one charging station and that each charging station can accommodate up to 200 EVs; the ratios of the number of EVs in the three types are 0.2, 0.3, and 0.5, respectively. Three optimization models with different objectives, listed below, were studied.
Case 3.A: In this model, EV users prioritize their own interests and take the minimum charging and discharging cost as the optimization objective without considering the network constraints.
Case 3.B: In this model, the optimization objective includes the reduction in distribution network loss and daily load variance in addition to the charging and discharging costs of EV users. It is assumed that the value of the coefficient w2 before the optimization objective of network loss is 0.1, and the value of the coefficient w3 before the optimization objective of daily load variation is 0.01.
Case 3.C: This optimization objective is the same as that of Case 3.B, but the reactive-power constraints of EV charging piles are added to the constraints.
By solving the above optimization model, we can determine the charging and discharging active power for each charging station. Figure 8 shows the active power for charging and discharging at the three charging stations for all cases. Figure 9 shows the reactive power supplied by the three charging stations for Case 3.C. In Figure 9, the “before allocation” curve represents the total reactive power based on the optimization model results; the “after allocation” curve represents the total reactive power for all EVs calculated using Equation (18); and the “correction” curve shows the results based on the reactive-power allocation method presented in Section 3.3.
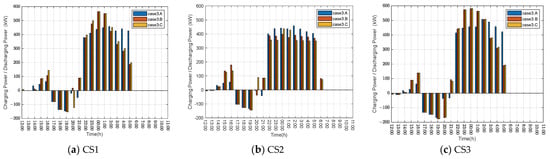
Figure 8.
Charging and discharging active power of the three charging stations in case 3.

Figure 9.
Reactive power supplied by the three charging stations in case 3.C.
After determining the charging and discharging power of all stations, Matpower was used to calculate the distribution network power flow. The simulation results are shown in Table 6 and Figure 10 and Figure 11. Figure 10 shows the daily load profile of the system obtained from the power flow distribution for all cases. Figure 11 shows the voltage at bus 18 for all cases.

Table 6.
Optimization results of different models in Case 3.
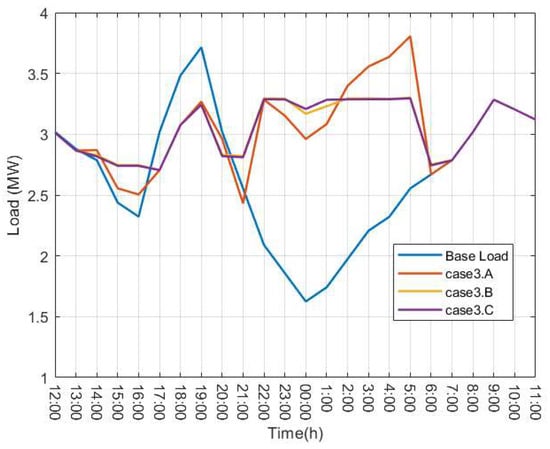
Figure 10.
Daily load profile of the system obtained from the power flow distribution in case 3.
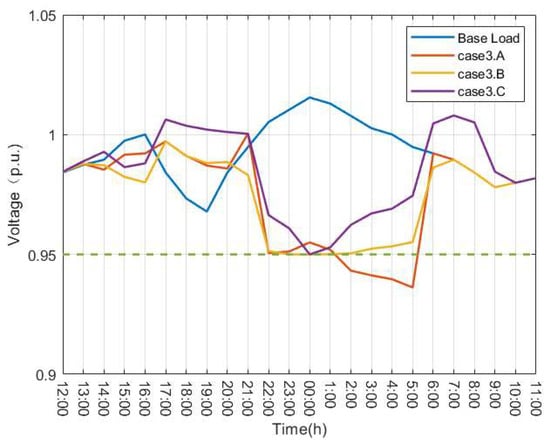
Figure 11.
Voltage of bus 18 obtained from the power flow distribution in case 3.
From Table 6, we can see that the charging and discharging costs of the user in case 3.MA are the lowest, but the load variance and the power loss are higher than those of the other two EVC scheduling models, which lead to the highest comprehensive cost of system operation. Higher load variance and power loss means a lower utilization rate of equipment in the distribution network, which is not conducive to the economic operation of the distribution network. Therefore, in Case 3.MB and Case 3.C, not only are the power loss and load variance of the distribution network included in the optimization objective, but the power flow constraints are also considered in the model. Compared to Case 3.A, although the charging and discharging costs of Csae3.B and case3.C increased by 12.8% and 11.8%, respectively, their load variance decreased by 58.5% and 57.1%, and the comprehensive cost of system operation decreased by 9.1% and 10.1%. From the perspective of the economic operation of the distribution network, the EVC scheduling models in Case 3.B and Case3.C perform better than that in Case 3.A.
Figure 10 and Figure 11 show the system load and the voltage value of bus 18 of the base load and the three studied models. From these two figures, it can be seen that Case 3.A, which does not take into account the peak shaving optimization objective and the distribution network power flow constraints, shows new load peaks and bus voltage violations during the night time compared to the other two models. For Case 3.B and Case 3.C, since the optimization objective of reducing the peak-to-valley difference in system load is taken into account, the solutions derived from these two models result in a smoother load profile. This outcome avoids high concentrations of users charging their electric vehicles during the low-tariff hours of 22:00 p.m. to 6:00 a.m. In Figure 11, the green line represents a voltage value of 0.95, which is the minimum node voltage generally allowed by the grid. As illustrated in Figure 11, the solutions derived from these two models also ensure that the distribution network’s bus voltage limits are not violated. This is achieved by considering the power flow constraints of the distribution network.
In summary, therefore, for the safe operation of the grid, EV scheduling should be carried out with the goal of not only minimizing the cost of EV charging, but also incentivizing the participation of EVs in the grid ancillary services market. In addition, the bus voltage magnitude of Case 3.C is improved compared to that of Case 3.B, as shown in Figure 11. This is due to the fact that Case 3.C takes into account the reactive-power compensation provided by the EV charging piles, as shown in Figure 9. This also results in a reduction of 9.8% in the distribution network energy losses, as shown in Table 6.
5.6. Case 4: Study the Impact of Different EV Charging Preferences on the Economics and Safety of Distribution Network Operation
This case investigates the impact of EV charging preferences on the operating state of the distribution network. Based on the parameter settings in Case 3, three simulation experiments are conducted in this case. The first experiment does not uniformly schedule the EVs and allows them to charge in an unorganized manner according to their respective travel plans. The second and third experiments use the Case 3.C scheduling model and assume that all EVs are Type II EVs and Type III EVs, respectively. These three experiments are named Case 4.A, Case 4.B, and Case 4.C. The simulation results are shown in Table 7 and Figure 12 and Figure 13.

Table 7.
Simulation results of different models in Case 4.
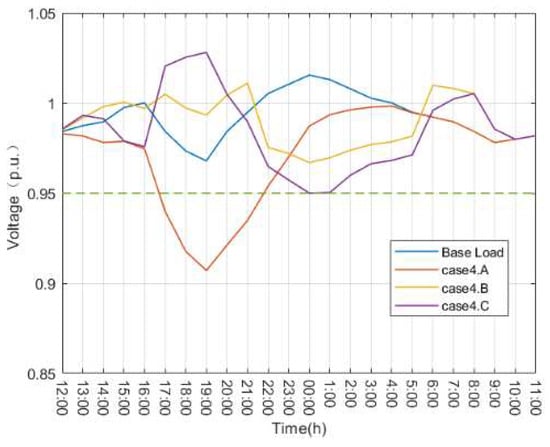
Figure 12.
Voltage of bus 18 under different models.
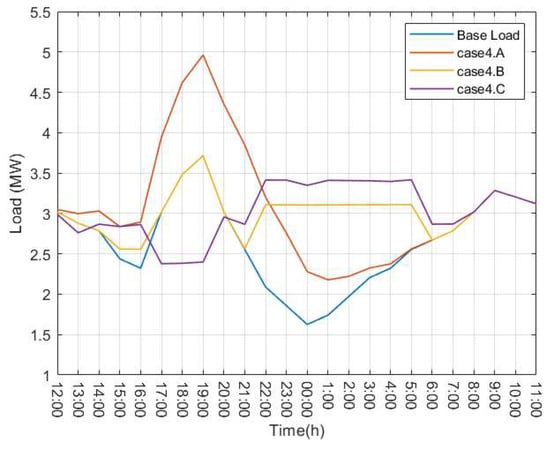
Figure 13.
Daily load profile of the system obtained from different optimization models.
From Table 7 it can be seen that disordered charging not only maximizes the charging cost for EV users, but also increases the network losses of the system and increases the peak-to-valley difference in the daily load profile of the system. In addition, from Figure 12, it can be seen that disordered charging leads to a significant drop in the voltage at bus 18, which is below the permissible lower limit. Therefore, disordered charging can pose a significant challenge to the safe operation of the grid.
Comparing the results of Case 4.B and Case 4.C, it is evident that EV participation in V2G can significantly reduce charging costs for users. However, excessive discharging during high-tariff hours and concentrated charging at night when tariffs are low can create new valleys and peaks in the system’s daily load profile, as shown in Figure 13. Therefore, more EVs participating in V2G is not always better for the grid. DSO and EV aggregators should strategically manage the number of EVs with different charging preferences connected to the grid at different times to benefit both users and the grid.
6. Conclusions
This paper proposes an electric vehicle cluster scheduling model that takes into account distribution network power flow constraints and reactive-power compensation provided by EV charging piles, for DSOs or EVAs to optimize the charging and discharging power of large-scale EVs. The proposed model includes an EVC division method, an energy and power boundary aggregation method, and a charging/discharging power allocation method. The proposed methods were applied to an IEEE-33 test system with large scale EVs. The simulation results show that the proposed EVC scheduling model can greatly reduce the solution time compared to the traditional individual-EV scheduling model. For the safe operation of the grid, EVC scheduling should be carried out with the goal of not only minimizing the cost of EV charging, but also incentivizing the participation of EVs in the grid ancillary services market, for example, reducing the energy losses and peak-to-valley difference. This not only reduces their adverse impact on the grid because of their uncoordinated charging behavior, but also improves the operational economics and security of the grid. However, it is not the case that more EVs participating in V2G is better for the grid. DSO and EV aggregators should strategically manage the number of EVs with different charging preferences that are connected to the grid, so that both users and the grid can benefit. Finally, the simulation results show that the reactive-power compensation provided by EV charging piles improves the voltage quality of the grid and enables more EVs to be connected to the grid. For future work, we will explore how renewable energy sources, such as solar and wind power, can be integrated into the proposed scheduling model. For example, we will investigate how EVC scheduling can reduce the output stochasticity of renewable energy and enhance the stability and safety of grid operation.
Author Contributions
Conceptualization and methodology, L.H., H.L. and C.S.L.; software, validation, and investigation, H.L.; data curation, B.Z. and Z.Z.; writing—original draft preparation, L.H. and H.L.; writing—review and editing, L.L.L., C.S.L. and A.F.Z.; funding acquisition, L.H., L.L.L., A.F.Z. and C.S.L.; Supervision, C.S.L. and L.L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Key Fields Special Project of Guangdong Provincial Colleges and Universities (New-Generation Information Technology; grant number 2021ZDZX1082); the Key Disciplines in Zhaoqing University—Electronic Science and Technology; and the seventh key discipline of Zhaoqing University—Electrical Engineering; National Natural Science Foundation of China (grant number 62206062).
Data Availability Statement
The data presented in this study are available on request from the author Liping Huang (e-mail address: huangliping@zqu.edu.cn). The data are not publicly available due to privacy restrictions.
Conflicts of Interest
Author Bang Zhong was employed by the company Zhaoqing Power Supply Bureau, Guangdong Power Grid Company, China Southern Power Grid. Author Loi Lei Lai was employed by the company DRPT International Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yao, M.; Liu, H.; Feng, X. The development of low-carbon vehicles in China. Energy Policy 2011, 39, 5457–5464. [Google Scholar] [CrossRef]
- Yang, X.; Niu, D.; Sun, L.; Ji, Z.; Zhou, J.; Wang, K.; Siqin, Z. A bi-level optimization model for electric vehicle charging strategy based on regional grid load following. J. Clean. Prod. 2021, 325, 129313. [Google Scholar] [CrossRef]
- Shafiee, S.; Fotuhi-Firuzabad, M.; Rastegar, M. Investigating the Impacts of Plug-in Hybrid Electric Vehicles on Power Distribution Systems. IEEE Trans. Smart Grid 2013, 4, 1351–1360. [Google Scholar] [CrossRef]
- Zhao, Y.; Che, Y.; Wang, D.; Liu, H.; Shi, K.; Yu, D. An Optimal Domestic Electric Vehicle Charging Strategy for Reducing Network Transmission Loss While Taking Seasonal Factors into Consideration. Appl. Sci. 2018, 8, 191. [Google Scholar] [CrossRef]
- Yang, J.; He, L.; Fu, S. An improved PSO-based charging strategy of electric vehicles in electrical distribution grid. Appl. Energy 2014, 128, 82–92. [Google Scholar] [CrossRef]
- Yin, W.J.; Ming, Z.F. Electric vehicle charging and discharging scheduling strategy based on local search and competitive learning particle swarm optimization algorithm. J. Energy Storage 2021, 42, 102966. [Google Scholar] [CrossRef]
- Hashemi, B.; Shahabi, M.; Teimourzadeh-Baboli, P. Stochastic-Based Optimal Charging Strategy for Plug-In Electric Vehicles Aggregator Under Incentive and Regulatory Policies of DSO. IEEE Trans. Veh. Technol. 2019, 68, 3234–3245. [Google Scholar] [CrossRef]
- Yin, W.; Qin, X.; Huang, Z. Optimal dispatching of large-scale electric vehicles into grid based on improved second-order cone. Energy 2022, 254, 124346. [Google Scholar] [CrossRef]
- Mehta, R.; Srinivasan, D.; Khambadkone, A.M.; Yang, J.; Trivedi, A. Smart Charging Strategies for Optimal Integration of Plug-In Electric Vehicles Within Existing Distribution System Infrastructure. IEEE Trans. Smart Grid 2018, 9, 299–312. [Google Scholar] [CrossRef]
- Manbachi, M.; Farhangi, H.; Palizban, A.; Arzanpour, S. A novel Volt-VAR Optimization engine for smart distribution networks utilizing Vehicle to Grid dispatch. Int. J. Electr. Power Amp Energy Syst. 2016, 74, 238–251. [Google Scholar] [CrossRef]
- Pirouzi, S.; Aghaei, J.; Niknam, T.; Khooban, M.H.; Dragicevic, T.; Farahmand, H.; Korpås, M.; Blaabjerg, F. Power Conditioning of Distribution Networks via Single-Phase Electric Vehicles Equipped. IEEE Syst. J. 2019, 13, 3433–3442. [Google Scholar] [CrossRef]
- Kisacikoglu, M.C.; Ozpineci, B.; Tolbert, L.M. EV/PHEV Bidirectional Charger Assessment for V2G Reactive Power Operation. IEEE Trans. Power Electron. 2013, 28, 5717–5727. [Google Scholar] [CrossRef]
- Kisacikoglu, M.C.; Kesler, M.; Tolbert, L.M. Single-Phase On-Board Bidirectional PEV Charger for V2G Reactive Power Operation. IEEE Trans. Smart Grid 2015, 6, 767–775. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Peng, C.; Zou, J. An MPC based optimized control approach for EV-based voltage regulation in distribution grid. Electr. Power Syst. Res. 2019, 172, 152–160. [Google Scholar] [CrossRef]
- Pirouzi, S.; Latify, M.A.; Yousefi, G.R. Conjugate active and reactive power management in a smart distribution network through electric vehicles: A mixed integer-linear programming model. Sustain. Energy Grids Netw. 2020, 22, 100344. [Google Scholar] [CrossRef]
- Wang, J.; Bharati, G.R.; Paudyal, S.; Ceylan, O.; Bhattarai, B.P.; Myers, K.S. Coordinated Electric Vehicle Charging with Reactive Power Support to Distribution Grids. IEEE Trans. Ind. Inform. 2019, 15, 54–63. [Google Scholar] [CrossRef]
- Mehta, R.; Verma, P.; Srinivasan, D.; Yang, J. Double-layered intelligent energy management for optimal integration of plug-in electric vehicles into distribution systems. Appl. Energy 2019, 233–234, 146–155. [Google Scholar] [CrossRef]
- Nafisi, H.; Agah, S.M.M.; Askarian Abyaneh, H.; Abedi, M. Two-Stage Optimization Method for Energy Loss Minimization in Microgrid Based on Smart Power Management Scheme of PHEVs. IEEE Trans. Smart Grid 2016, 7, 1268–1276. [Google Scholar] [CrossRef]
- Boonseng, T.; Sangswang, A.; Naetiladdanon, S.; Gurung, S. A New Two-Stage Approach to Coordinate Electrical Vehicles for Satisfaction of Grid and Customer Requirements. Appl. Sci. 2021, 11, 3904. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. Optimal Planning of PEV Charging Station with Single Output Multiple Cables Charging Spots. IEEE Trans. Smart Grid 2017, 8, 2119–2128. [Google Scholar] [CrossRef]
- He, L.; Yang, J.; Yan, J.; Tang, Y.; He, H. A bi-layer optimization based temporal and spatial scheduling for large-scale electric vehicles. Appl. Energy 2016, 168, 179–192. [Google Scholar] [CrossRef]
- Patnam, B.S.K.; Pindoriya, N.M. DLMP Calculation and Congestion Minimization with EV Aggregator Loading in a Distribution Network Using Bilevel Program. IEEE Syst. J. 2021, 15, 1835–1846. [Google Scholar] [CrossRef]
- Vuelvas, J.; Ruiz, F.; Gruosso, G. A time-of-use pricing strategy for managing electric vehicle clusters. Sustain. Energy Grids Netw. 2021, 25, 100411. [Google Scholar] [CrossRef]
- Kanellos, F.D. Optimal Scheduling and Real-Time Operation of Distribution Networks with High Penetration of Plug-In Electric Vehicles. IEEE Syst. J. 2021, 15, 3938–3947. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Yang, B.; Li, L. Virtual generation tribe based robust collaborative consensus algorithm for dynamic generation command dispatch optimization of smart grid. Energy 2016, 101, 34–51. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Hug, G.; Kar, S.; Li, Z. Cooperative Control of Distributed Energy Storage Systems in a Microgrid. IEEE Trans. Smart Grid 2015, 6, 238–248. [Google Scholar] [CrossRef]
- Rawat, T.; Niazi, K.R.; Gupta, N.; Sharma, S. Multi-objective techno-economic operation of smart distribution network integrated with reactive power support of battery storage systems. Sustain. Cities Soc. 2021, 75, 103359. [Google Scholar] [CrossRef]
- Singh, D.; Misra, R.K.; Singh, D. Effect of Load Models in Distributed Generation Planning. IEEE Trans. Power Syst. 2007, 22, 2204–2212. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Jin, X.; Bhakar, R.; Jurado, F. Coordinated pricing mechanism for parking clusters considering interval-guided uncertainty-aware strategies. Appl. Energy 2024, 355, 122373. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).