Numerical Study on Effect of Flow Field Configuration on Air-Breathing Proton Exchange Membrane Fuel Stacks
Abstract
1. Introduction
2. Numerical Method
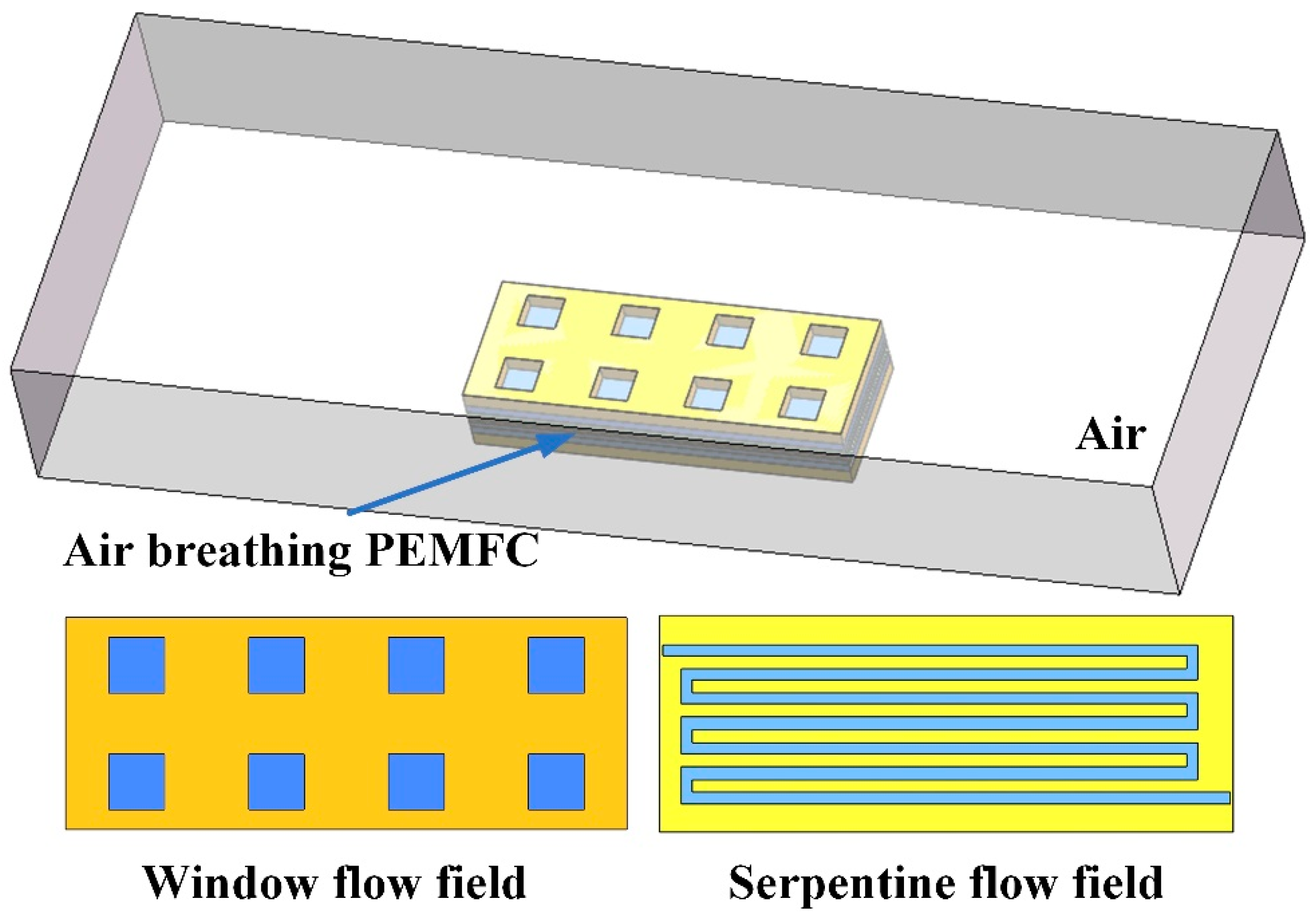
2.1. Description of the Computation Domain
2.2. Governing Equations
2.3. The Compression of GDL
2.4. Boundary Conditions
3. Results and Discussion
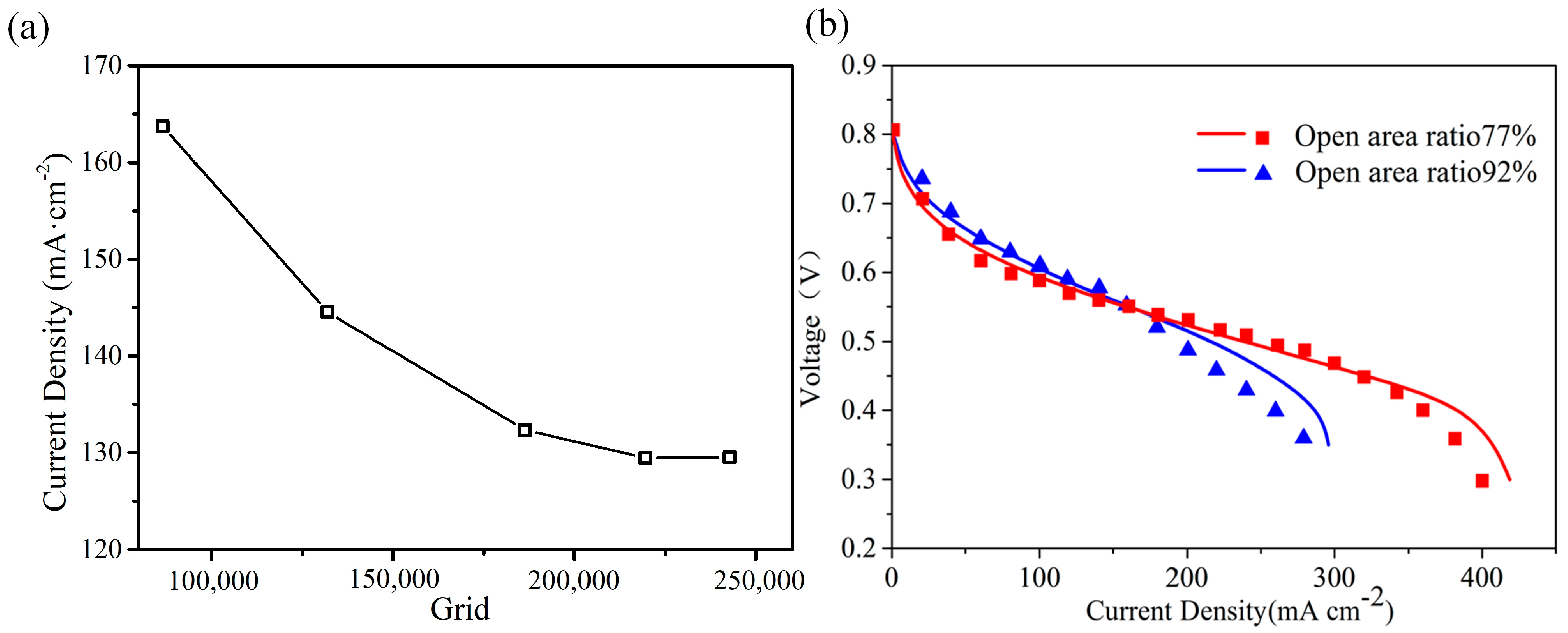
3.1. Validation of Grid Independence and Simulation Model
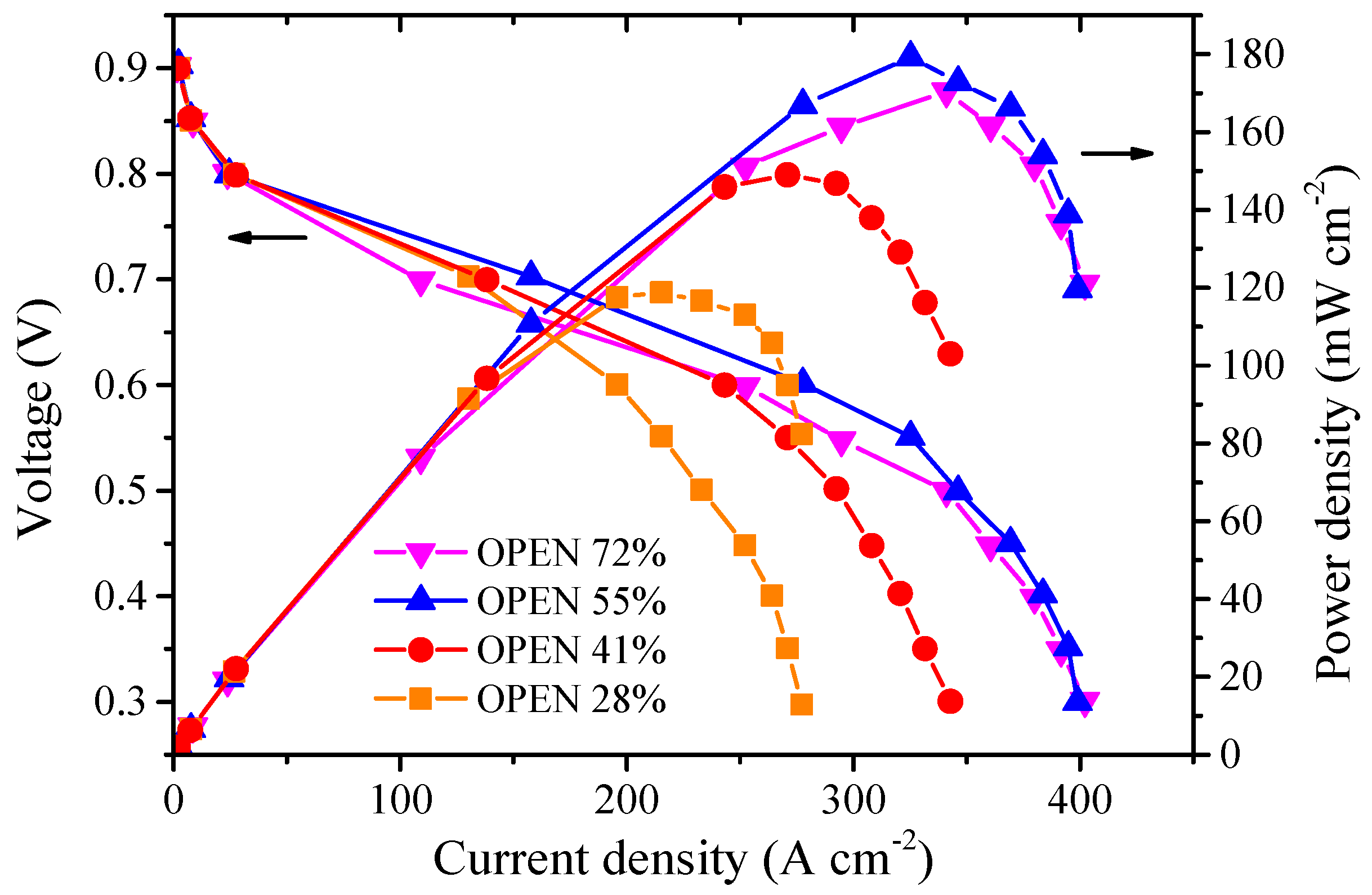
3.2. Effect of Cathode Open Area Ratio on the Performance of a Single Fuel Cell
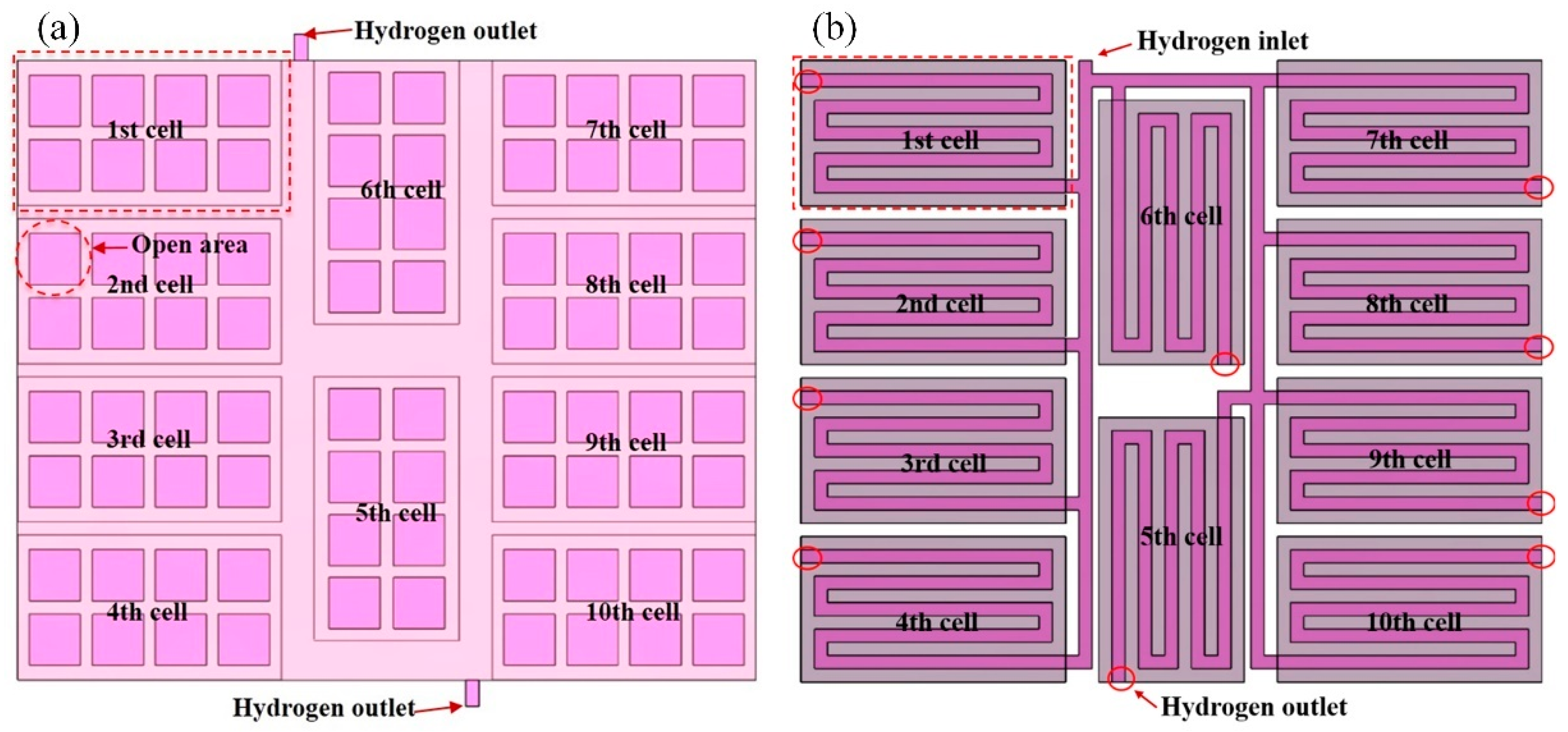
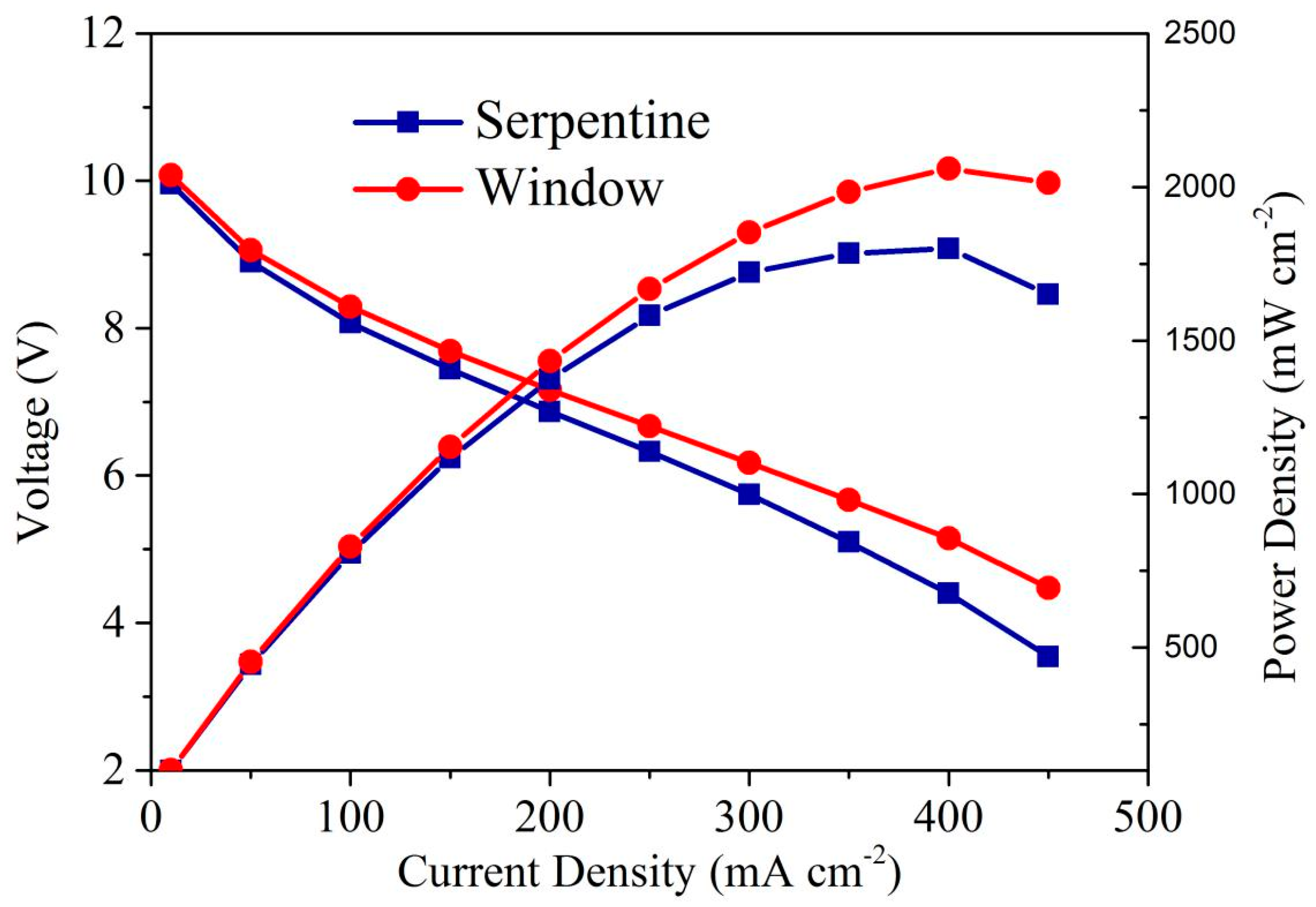
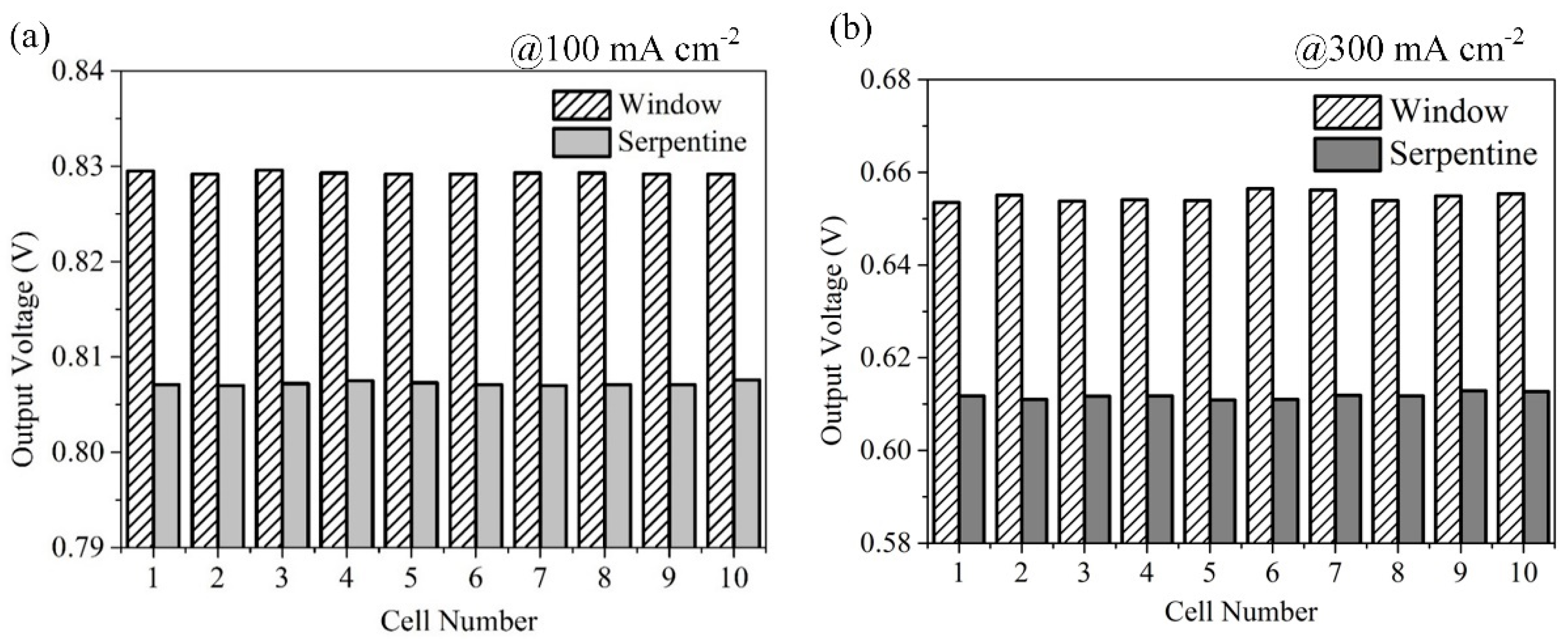
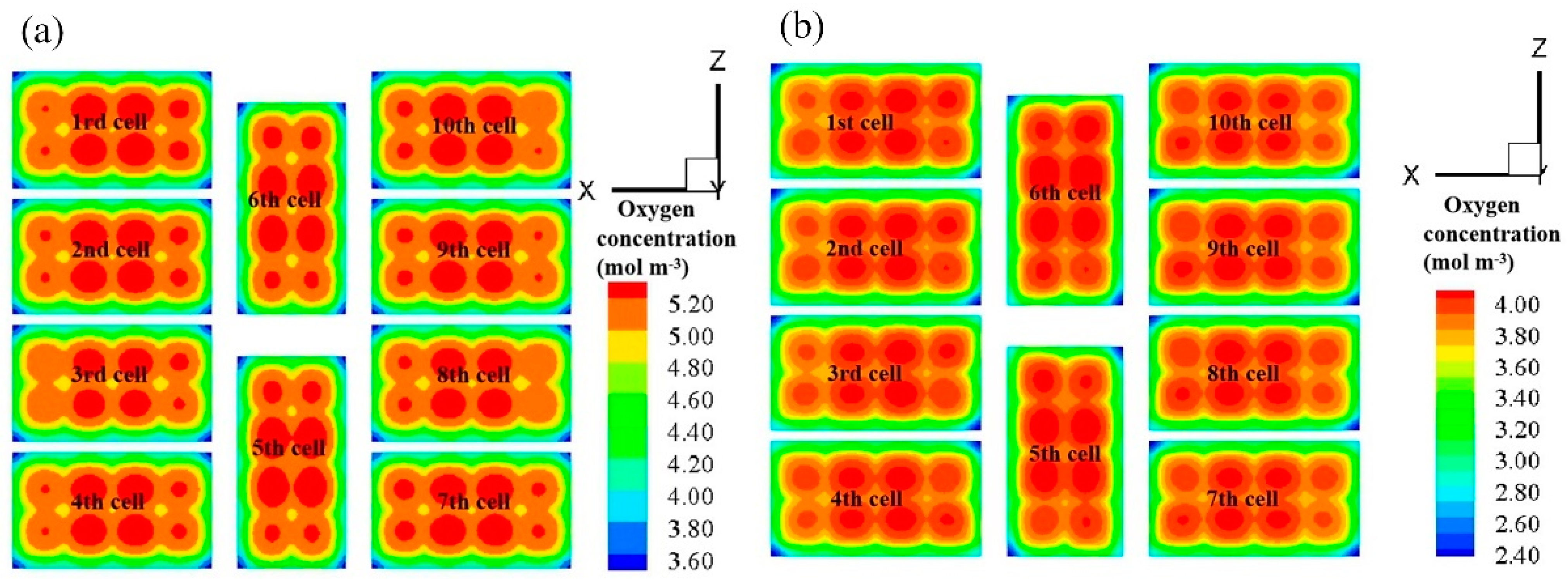
3.3. Effect of Anode Flow Field Configuration on Fuel Cell Stack Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmad, S.; Nawaz, T.; Ali, A.; Orhan, M.F.; Samreen, A.; Kannan, A.M. An overview of proton exchange membranes for fuel cells: Materials and manufacturing. Int. J. Hydrogen Energ. 2022, 47, 19086–19131. [Google Scholar] [CrossRef]
- Wang, H.; Qu, Z.; Yin, Y.; Zhang, J.; Ming, P. Thermal Management for Hydrogen Charging and Discharging in a Screened Metal–Organic Framework Particle Tank. ACS Appl. Mater. Inter. 2021, 13, 61838–61848. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, Z.; Fan, L.; Du, Q.; Jiao, K. Application progress of small-scale proton exchange membrane fuel cell. Energy Reviews 2023, 2, 100017. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Qu, Z.; Zhang, J. Deep-learning accelerating topology optimization of three-dimensional coolant channels for flow and heat transfer in a proton exchange membrane fuel cell. Appl. Energ. 2023, 352, 121889. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, C.; Xi, F.; Chen, W.; Jiao, K.; Du, Q.; Bai, F.; Liu, Z. Experimental study on the influence of environment conditions on the performance of paper-based microfluidic fuel cell. Appl. Therm. Eng. 2023, 219, 119487. [Google Scholar] [CrossRef]
- Zhe, W.; Wang, K.; Jiao, K.; Du, Q.; Peng, Z.; Bai, F.; Liu, Z. Application of template method in fabricating ordered gas diffusion layer of PEMFC. Int. J. Green Energy 2024, 1–10. [Google Scholar]
- Nunes, H.X.; Ferreira, M.J.F.; Rangel, C.M.; Pinto, A.M.F.R. Hydrogen generation and storage by aqueous sodium borohydride (NaBH4) hydrolysis for small portable fuel cells (H2–PEMFC). Int. J. Hydrogen Energ. 2016, 41, 15426–15432. [Google Scholar] [CrossRef]
- Wang, Y.; Seo, B.; Wang, B.; Zamel, N.; Jiao, K.; Adroher, X.C. Fundamentals, materials, and machine learning of polymer electrolyte membrane fuel cell technology. Energy AI 2020, 1, 100014. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Shum, C.; McPhee, J. A Review of Physics-based and Data-driven Models for Real-time Control of Polymer Electrolyte Membrane Fuel Cells. Energy AI 2021, 6, 100114. [Google Scholar] [CrossRef]
- Lin, T.; Hu, L.; Wisely, W.; Gu, X.; Cai, J.; Litster, S.; Kara, L.B. Prediction of high frequency resistance in polymer electrolyte membrane fuel cells using long short term memory based model. Energy AI 2021, 3, 100045. [Google Scholar] [CrossRef]
- Choi, H.; Choi, H.J.; Kang, S.Y.; Kim, J.; Choi, H.; Ahn, C.-Y.; Kang, H.J.; La, I.; Kim, O.-H.; Cho, Y.-H.; et al. Optimization of hydrophobic additives content in microporous layer for air breathing PEMFC. J. Electroanal. Chem. 2024, 952, 117963. [Google Scholar] [CrossRef]
- Ferreira-Aparicio, P.; Chaparro, A.M. Influence of the gas diffusion cathode structure on the performance of an air-breathing proton exchange membrane fuel cell. Int. J. Hydrogen Energ. 2014, 39, 3997–4004. [Google Scholar] [CrossRef]
- Xu, X.; Yang, W.; Zhuang, X.; Xu, B. Experimental and numerical investigation on effects of cathode flow field configurations in an air-breathing high-temperature PEMFC. Int. J. Hydrogen Energ. 2019, 44, 25010–25020. [Google Scholar] [CrossRef]
- Jin, H.; Zou, S.; Wen, Q.; Li, Y.; Ning, F.; Xu, P.; Pan, S.; Zhou, X. Performance improvement of air-breathing proton exchange membrane fuel cell (PEMFC) with a condensing-tower-like curved flow field. Chinese Chem. Lett. 2023, 34, 107441. [Google Scholar] [CrossRef]
- Bussayajarn, N.; Ming, H.; Hoong, K.K.; Ming Stephen, W.Y.; Hwa, C.S. Planar air breathing PEMFC with self-humidifying MEA and open cathode geometry design for portable applications. Int. J. Hydrogen Energ. 2009, 34, 7761–7767. [Google Scholar] [CrossRef]
- Folgado, M.A.; Duque, L.; Chaparro, A.M. Air-breathing fuel cell with a columnar cathodic plate for the passive removal of water. Int. J. Hydrogen Energ. 2024, 52, 1315–1324. [Google Scholar] [CrossRef]
- Omrani, R.; Shabani, B. Review of gas diffusion layer for proton exchange membrane-based technologies with a focus on unitised regenerative fuel cells. Int. J. Hydrogen Energ. 2019, 44, 3834–3860. [Google Scholar] [CrossRef]
- Sapkota, P.; Brockbank, P.; Aguey-Zinsou, K.-F. Development of self-breathing polymer electrolyte membrane fuel cell stack with cylindrical cells. Int. J. Hydrogen Energ. 2022, 47, 23833–23844. [Google Scholar] [CrossRef]
- Chen, J.; Sun, L.; Zhu, W.; Pei, H.; Xing, L.; Tu, Z. Influence of cathode air supply mode on the performance of an open cathode air-cooled proton exchange membrane fuel cell stack. Appl. Therm. Eng. 2024, 243, 122709. [Google Scholar] [CrossRef]
- Lee, J.; Gundu, M.H.; Lee, N.; Lim, K.; Lee, S.W.; Jang, S.S.; Kim, J.Y.; Ju, H. Innovative cathode flow-field design for passive air-cooled polymer electrolyte membrane (PEM) fuel cell stacks. Int. J. Hydrogen Energ. 2020, 45, 11704–11713. [Google Scholar] [CrossRef]
- Sapkota, P.; Boyer, C.; Dutta, R.; Cazorla, C.; Aguey-Zinsou, K.-F. Planar polymer electrolyte membrane fuel cells: Powering portable devices from hydrogen. Sustain. Energ. Fuels 2020, 4, 439–468. [Google Scholar] [CrossRef]
- Min, X.; Xie, Y.; Chai, D.; Zhang, X. Preliminary experimental study of the performances for a print circuit board based planar PEMFC stack. Int. J. Hydrogen Energ. 2022, 47, 5599–5608. [Google Scholar] [CrossRef]
- Kim, M.; Lee, D.G. Development of the anode bipolar plate/membrane assembly unit for air breathing PEMFC stack using silicone adhesive bonding. J. Power Sources 2016, 315, 86–95. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Lai, W.-H.; Weng, B.-J.; Chuang, H.-J.; Hsieh, C.-Y.; Kung, C.-C. Planar array stack design aided by rapid prototyping in development of air-breathing PEMFC. J. Power Sources 2008, 179, 147–154. [Google Scholar] [CrossRef]
- Bunyan, S.T.; Dhahad, H.A.; Khudhur, D.S.; Yusaf, T. The Effect of Flow Field Design Parameters on the Performance of PEMFC: A Review. Sustainability 2023, 15, 10389. [Google Scholar] [CrossRef]
- Ying, W.; Sohn, Y.-J.; Lee, W.-Y.; Ke, J.; Kim, C.-S. Three-dimensional modeling and experimental investigation for an air-breathing polymer electrolyte membrane fuel cell (PEMFC). J. Power Sources 2005, 145, 563–571. [Google Scholar] [CrossRef]
- Song, J.; Huang, Y.; Liu, Y.; Ma, Z.; Chen, L.; Li, T.; Zhang, X. Numerical Investigation and Optimization of Cooling Flow Field Design for Proton Exchange Membrane Fuel Cell. Energies 2022, 15, 2609. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, X.; Xie, B.; Du, Q.; Jiao, K. Large-scale multi-phase simulation of proton exchange membrane fuel cell. Int. J. Heat Mass Tran. 2019, 130, 555–563. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, G.; Jiang, Y.; Wang, R.; Sheng, X.; Xi, F.; Zhao, Z.; Chen, W.; Zhu, Y.; Wang, Y.; et al. “3D+1D” modeling approach toward large-scale PEM fuel cell simulation and partitioned optimization study on flow field. eTransportation 2020, 6, 100090. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, L.; Jiao, K.; Tian, P.; Wang, B.; Wang, Y.; Liu, Z. Optimization of porous media flow field for proton exchange membrane fuel cell using a data-driven surrogate model. Energ. Convers. Manag. 2020, 226, 113513. [Google Scholar] [CrossRef]
- Jiao, D.; Jiao, K.; Du, Q. Two-Phase Flow in Porous Electrodes of Proton Exchange Membrane Fuel Cell. Trans. Tianjin Univ. 2020, 26, 197–207. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, L.; Niu, Z.; Bao, Z.; Sun, X.; Liu, Z.; Li, Y.; Jiao, K.; Liu, Z.; Du, Q. Effects of surface wettability on two-phase flow in the compressed gas diffusion layer microstructures. Int. J. Heat Mass Tran. 2020, 151, 119370. [Google Scholar] [CrossRef]
- Sadeghi, E.; Djilali, N.; Bahrami, M. Effective thermal conductivity and thermal contact resistance of gas diffusion layers in proton exchange membrane fuel cells. Part 2: Hysteresis effect under cyclic compressive load. J. Power Sources 2010, 195, 8104–8109. [Google Scholar] [CrossRef]
- Sadeghi, E.; Djilali, N.; Bahrami, M. Effective thermal conductivity and thermal contact resistance of gas diffusion layers in proton exchange membrane fuel cells. Part 1: Effect of compressive load. J. Power Sources 2011, 196, 246–254. [Google Scholar] [CrossRef]
- Tamayol, A.; McGregor, F.; Bahrami, M. Single phase through-plane permeability of carbon paper gas diffusion layers. J. Power Sources 2012, 204, 94–99. [Google Scholar] [CrossRef]
- Movahedi, M.; Ramiar, A.; Ranjber, A.A. 3D numerical investigation of clamping pressure effect on the performance of proton exchange membrane fuel cell with interdigitated flow field. Energy 2018, 142, 617–632. [Google Scholar] [CrossRef]
- Fabian, T.; Posner, J.D.; O’Hayre, R.; Cha, S.-W.; Eaton, J.K.; Prinz, F.B.; Santiago, J.G. The role of ambient conditions on the performance of a planar, air-breathing hydrogen PEM fuel cell. J. Power Sources 2006, 161, 168–182. [Google Scholar] [CrossRef]
- Sun, T.; Xie, B.; Zhang, F.; Wu, L.; Jiao, K. Numerical investigation of GDL compression rate on air-breathing proton exchange membrane fuel cell. In Proceedings of the International Conference on Applied Energy (ICAE2020), Bangkok, Thailand, 1–10 December 2020. [Google Scholar]

| Source Terms | Equations |
|---|---|
| O2 (kg m−3 s−1) | |
| H2 (kg m−3 s−1) | |
| Liquid water (kg m−3 s−1) | |
| Gas water (kg m−3 s−1) | |
| Gas mixture (kg m−3 s−1) | |
| Water evaporates and condenses (kg m−3 s−1) | |
| Electron and ion potential (A m−3) | |
| Membrane water content (mol m−3 s−1) | |
| Membrane water by pressure difference (mol m−3 s−1) | |
| Absorption and desorption of membrane water (kg m−3 s−1) | |
| Energy (W m−3) |
| Parameters | Values |
|---|---|
| Thichnesses of GDL, MPL, ACL, CCL, PEM (μm) | 200, 20, 5, 10, 50.8 |
| Relative humidity | 0.1 @ anode; 0.2 @ cathode |
| Temperature (K) | 308.15 |
| Stoichiometric ratio | 1.5 @ anode |
| Outlet pressure (atm) | 1.0 |
| Intrinsic permeabilities of MPL, GDL, and CL (m2) | 1.0 × 10−12, 1.0 × 10−11, 1.0 × 10−13 |
| Porosities of MPL and GDL | 0.6, 0.78 |
| Contact angles of MPL, GDL, and CL (°) | 120, 120, 100 |
| Specific heat capacities of BP, GDL, MPL, CL, and PEM (J kg−1 K−1) | 1580, 568, 3300, 3300, 833 |
| Ionic conductivities of BP, GDL, MPL, and CL (S m−1) | 20,000, 8000, 5000, 5000 |
| Thermal conductivities of BP, MPL, CL, and PEM (W m−1 K−1) | 20, 1, 1, 0.95 |
| Condensation rate in MEA (s−1) | 100 |
| Condensation rate in flow channel (s−1) | 5000 |
| Phase change rate of membrane water and vapour (s−1) | 1.3, 1.3 |
| Evaporation rate (s−1) | 100 |
| Latent heat of water condensation (J mol−1) | 40,650 |
| Entropy change (J mol−1 K−1) | 3255 |
| Working current density (A m−2) | 16,000 |
| Reference concentration (mol m−3) | H2: 56.4, O2: 3.39 |
| Heat transfer coefficient | 9.0 |
| Density of dry membrane (kg m−3) | 1980 |
| Liquid water density (kg m−3) | 970 |
| Volume fraction of ionomer in CL | 0.3 |
| Equivalent weight of PEM (kg mol−1) | 1.1 |
| Surface tension coefficient (N m −1) | 0.0625 |
| Contact angle of interface between GDL and flow channel, flow channel and bipolar plate (°) | 120, 90 |
| Air composition | 21% O2, 79% N2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Sun, T.; Bai, F. Numerical Study on Effect of Flow Field Configuration on Air-Breathing Proton Exchange Membrane Fuel Stacks. Energies 2024, 17, 2501. https://doi.org/10.3390/en17112501
Liu Z, Sun T, Bai F. Numerical Study on Effect of Flow Field Configuration on Air-Breathing Proton Exchange Membrane Fuel Stacks. Energies. 2024; 17(11):2501. https://doi.org/10.3390/en17112501
Chicago/Turabian StyleLiu, Zhi, Tingting Sun, and Fuqiang Bai. 2024. "Numerical Study on Effect of Flow Field Configuration on Air-Breathing Proton Exchange Membrane Fuel Stacks" Energies 17, no. 11: 2501. https://doi.org/10.3390/en17112501
APA StyleLiu, Z., Sun, T., & Bai, F. (2024). Numerical Study on Effect of Flow Field Configuration on Air-Breathing Proton Exchange Membrane Fuel Stacks. Energies, 17(11), 2501. https://doi.org/10.3390/en17112501







