Multi-Regional Integrated Energy Economic Dispatch Considering Renewable Energy Uncertainty and Electric Vehicle Charging Demand Based on Dynamic Robust Optimization
Abstract
1. Introduction
- Aimed at the randomness of EV charging behavior, a charging demand model of an EV based on trip chain theory is proposed;
- Aimed at the RES uncertainty problem, an improved robust optimization over time algorithm based on the scenario method is proposed;
- Based on the existing comprehensive demand response, a cold–heat–electric alternative integrated demand response (IDR) model is proposed.
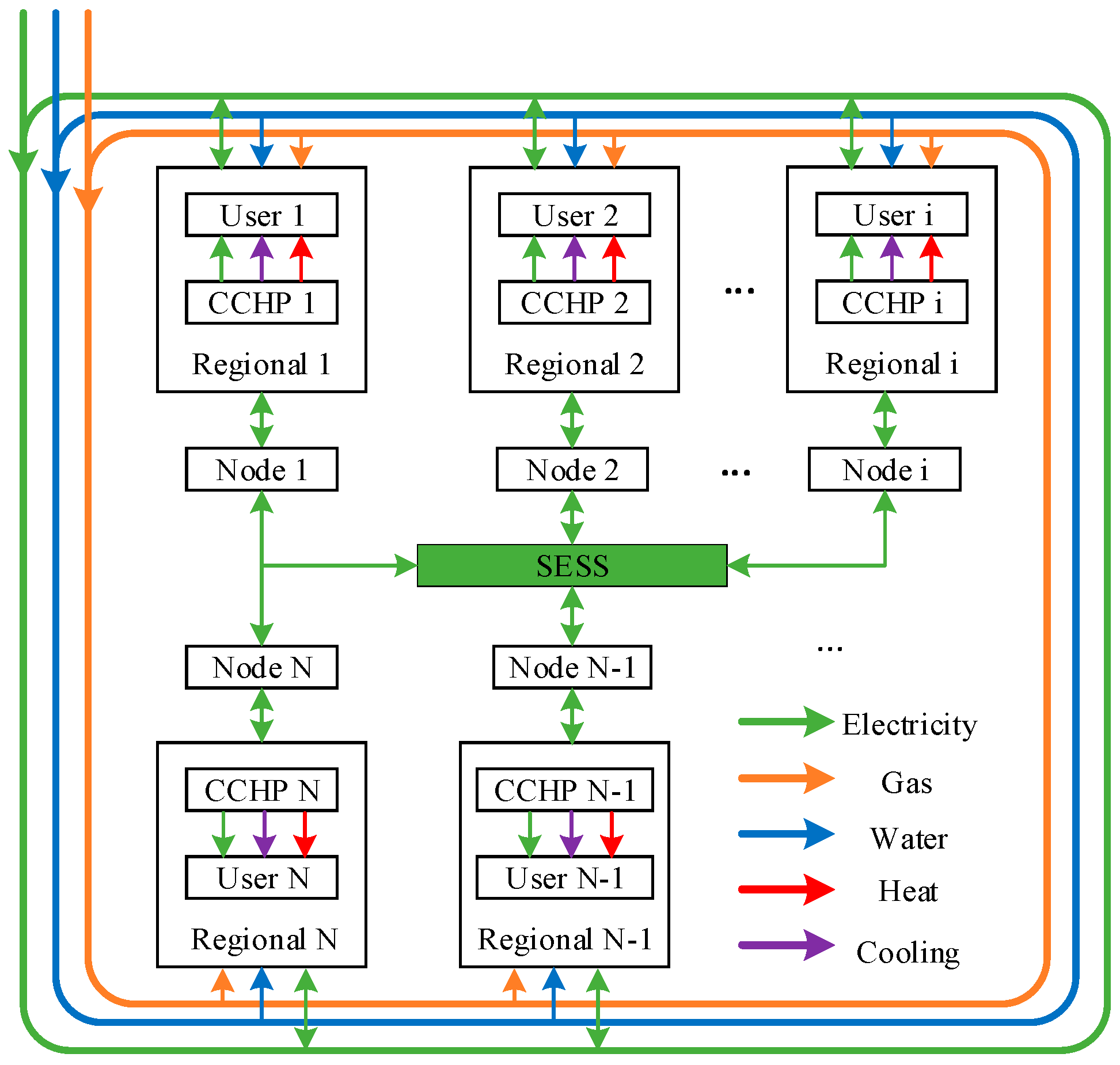
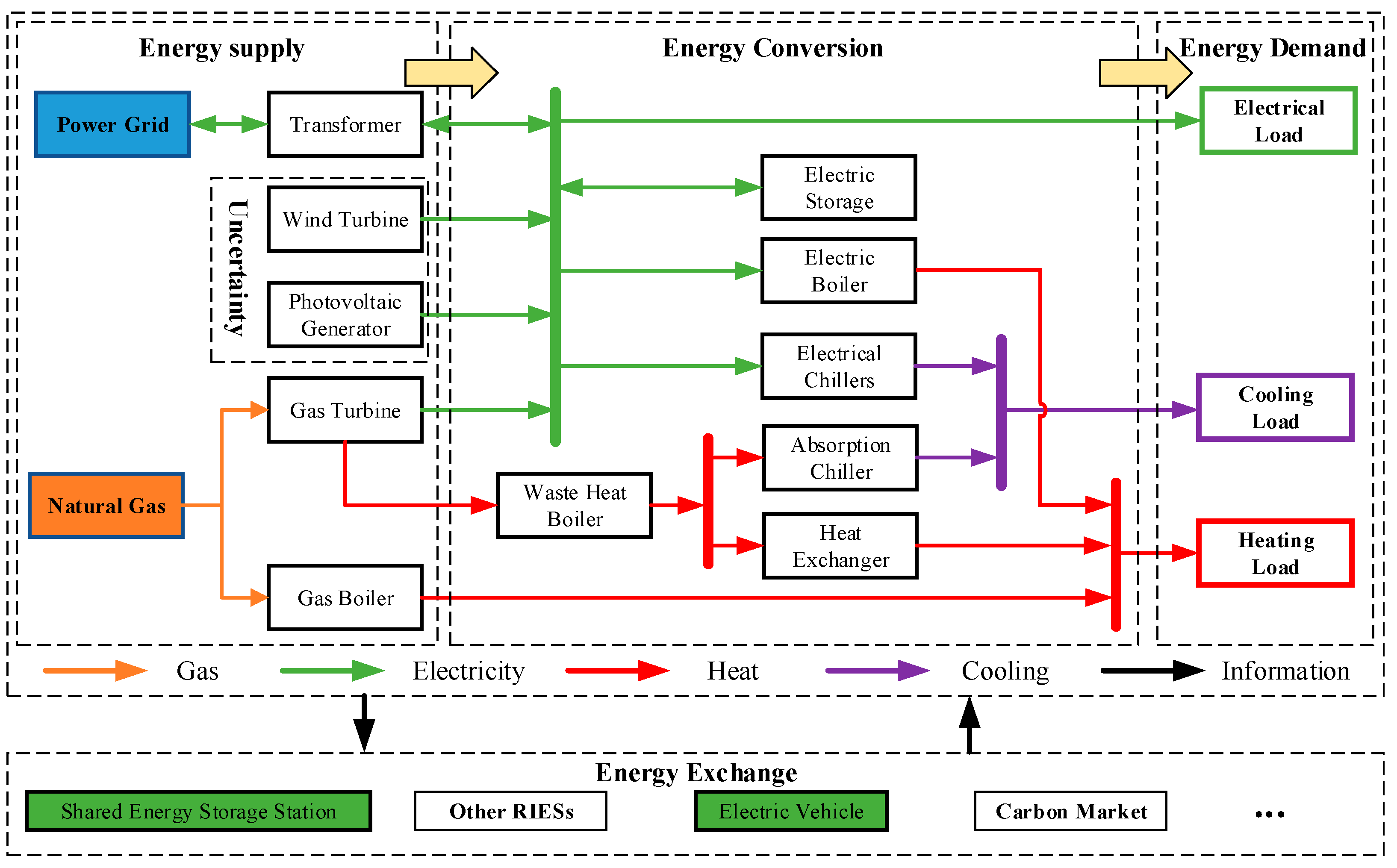
2. Structure Modeling of RIES Based on SESS and IDR
2.1. Overall Framework of RIES
2.2. Modeling of SESS
2.2.1. Power Continuity Constraint
2.2.2. SOC Constraints
2.2.3. Charge and Discharge Constraints
2.3. Modeling of IDR
2.3.1. Modeling of RL
2.3.2. Modeling of TL
2.3.3. Modeling of SL
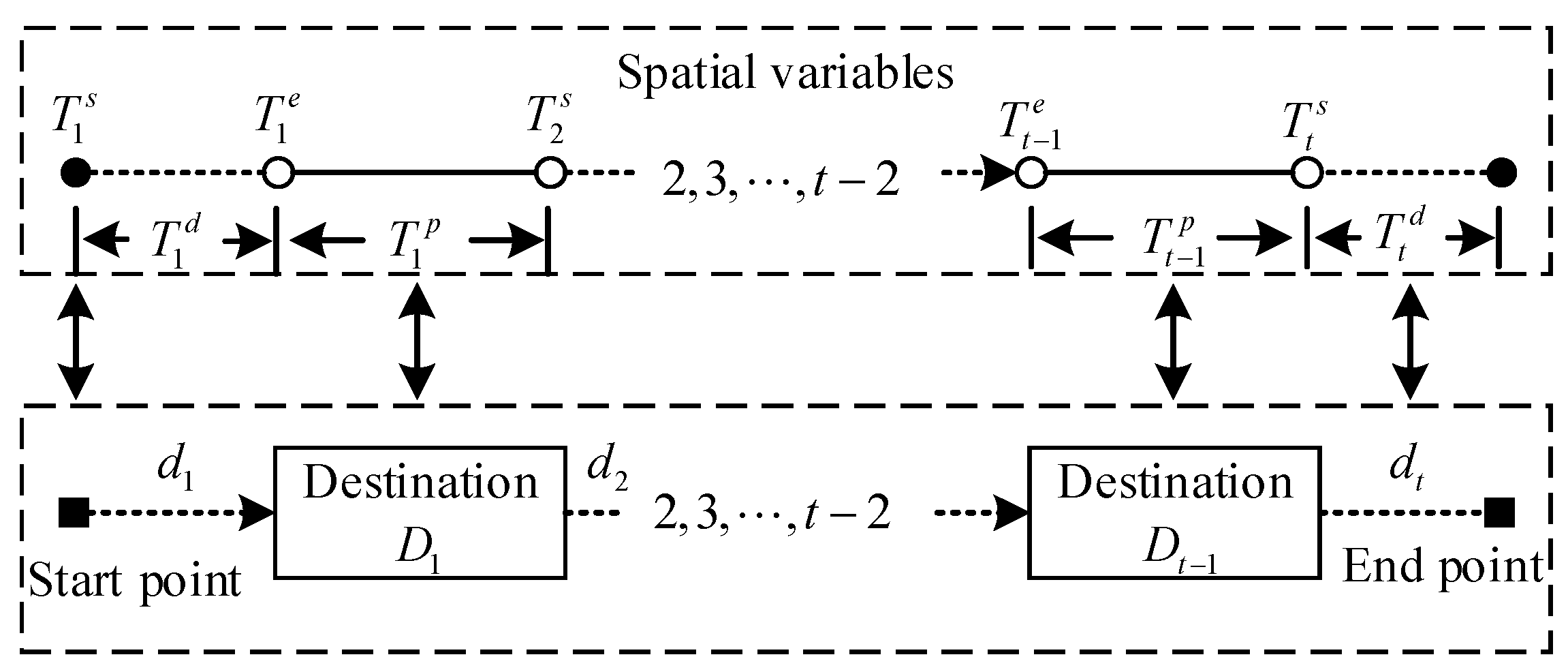
3. EV Modeling Based on Trip Chain Theory
3.1. Basic Theory of EV Trip Chain
3.2. Modeling of EV Trip Chain
- The PDF of the home area parking time:
- The PDF of the working area parking time:
- The PDF of the other area parking time:
4. Uncertainty Analysis of Renewable Energy Based on Scenario Method and Improved Robust Optimization over Time
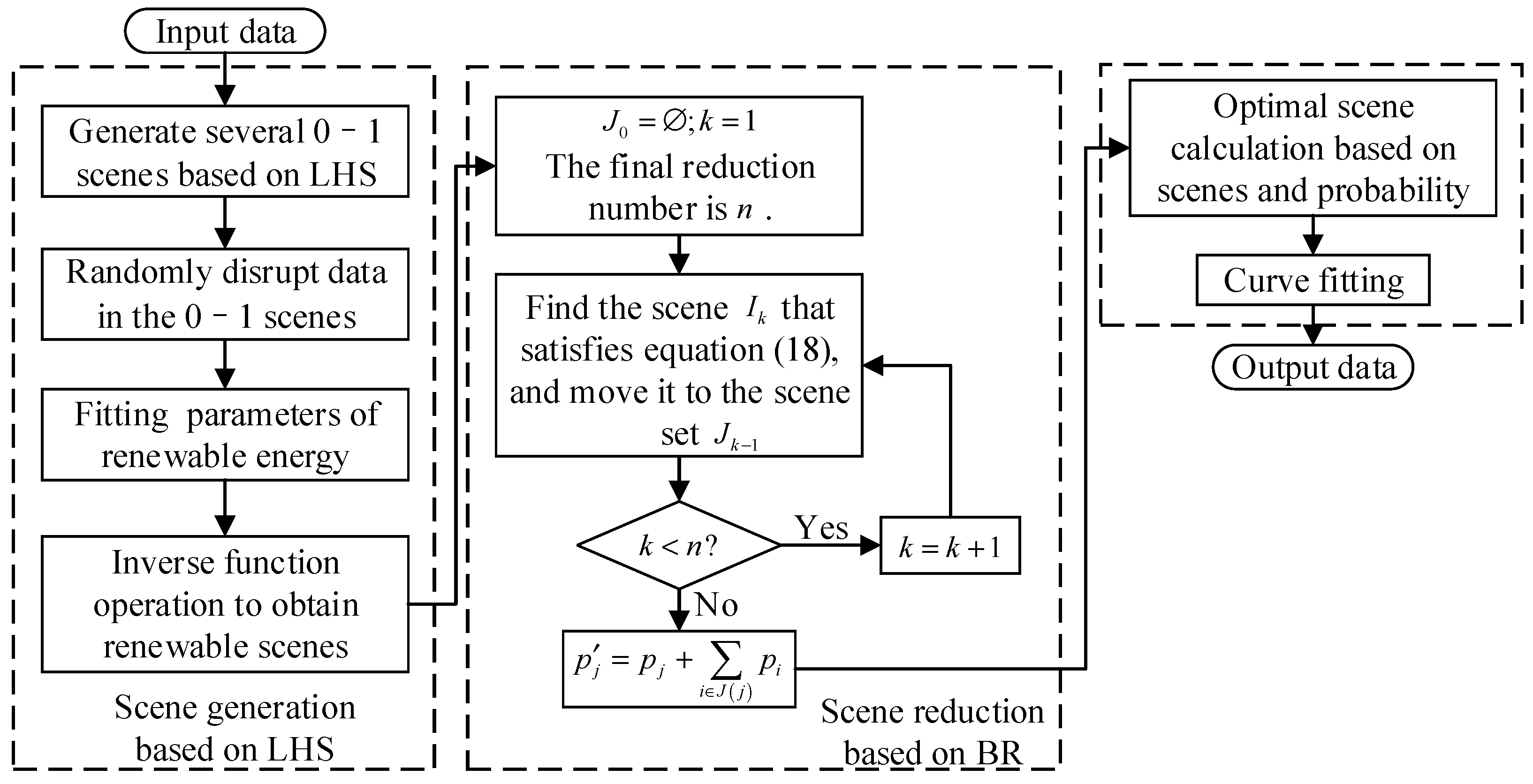
4.1. Scene Analysis Method
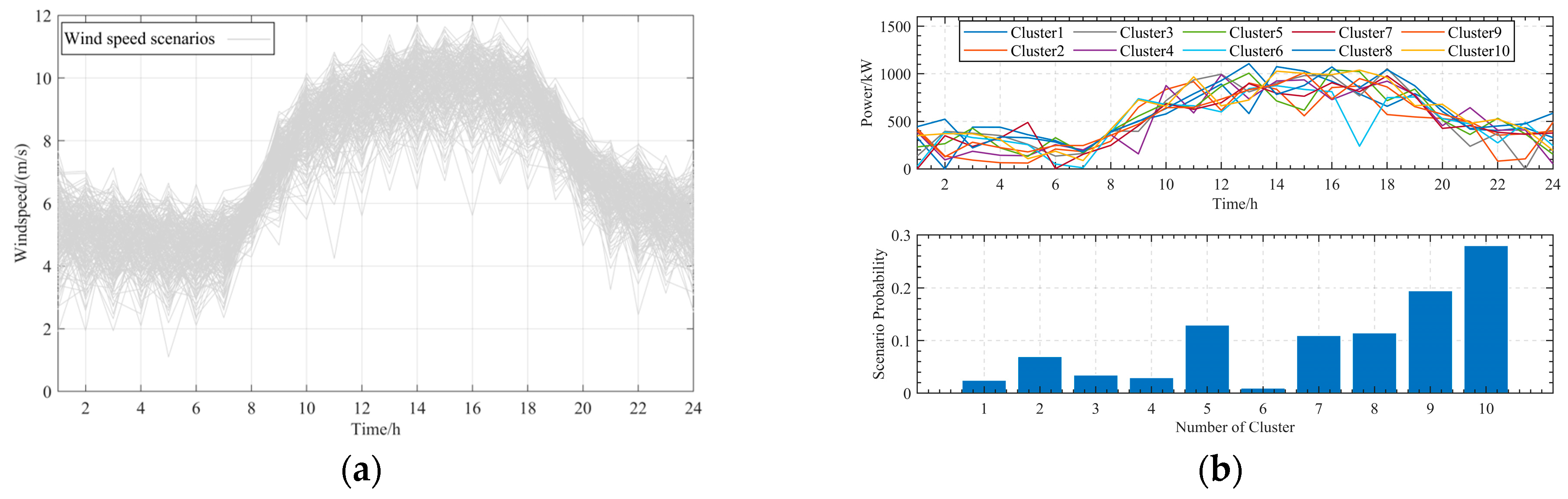
4.1.1. Scene Generation Based on LHS
4.1.2. Scene Reduction Based on BR
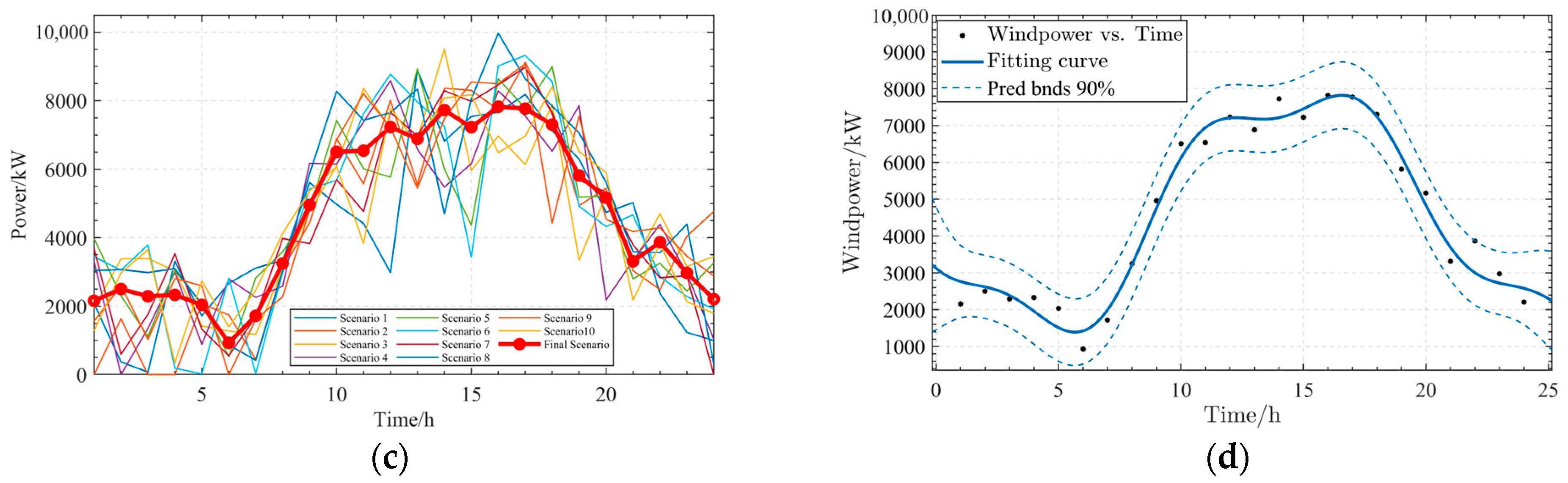
4.1.3. Curving Fitting
4.2. Uncertainty Analysis of Renewable Energy Based on the Scenario Method and Improved Robust Optimization over Time
4.2.1. Description of Renewable Uncertainty Problem
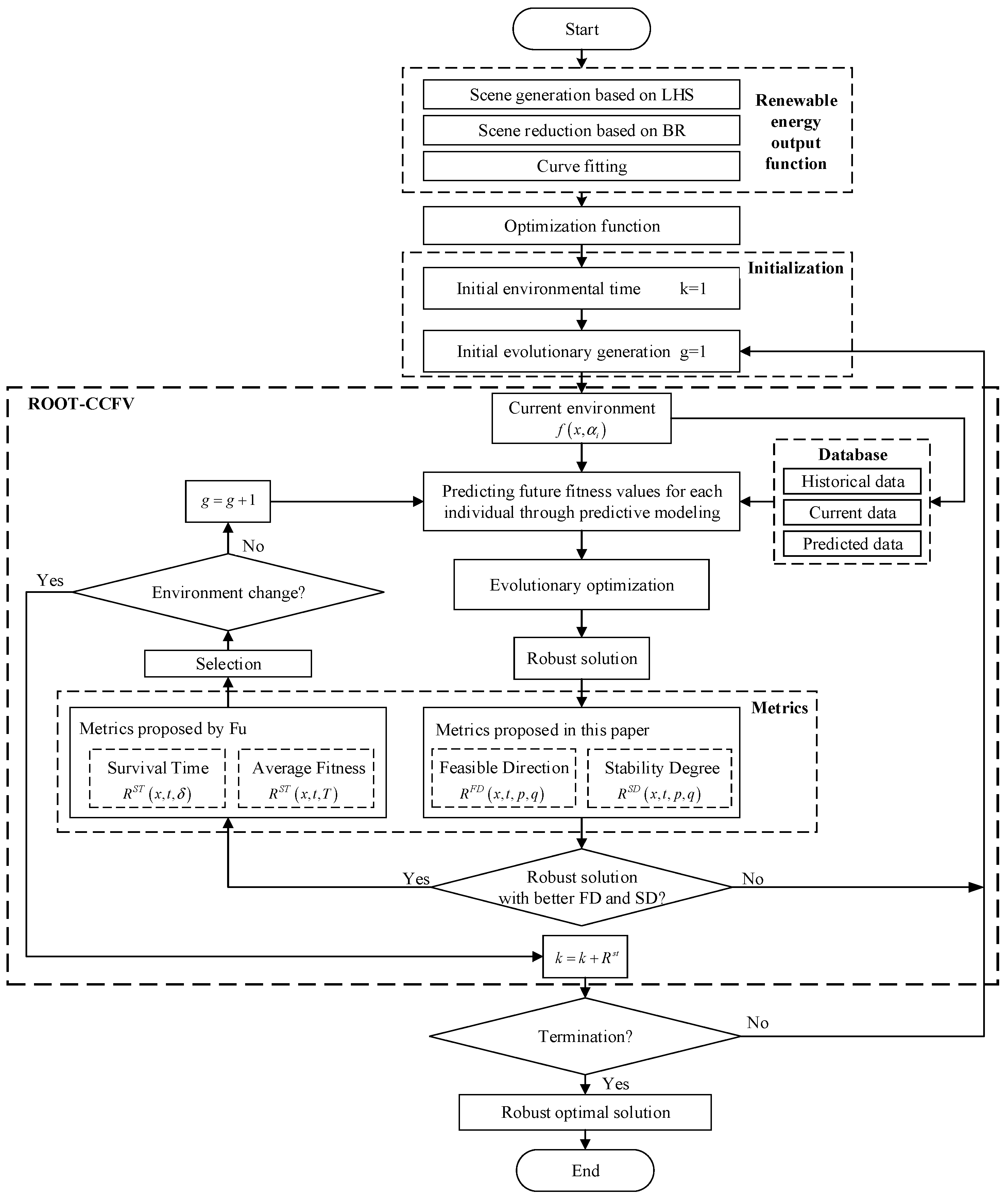
4.2.2. Improved ROOT
- Feasible direction
- Stability degree
- ROOT-CCFV
5. Optimal Scheduling Model Considering EV and Renewable Energy Uncertainty
5.1. Optimization Objective
5.2. Operational Constraints
5.3. Optimization Method
6. Case Study
6.1. Simulation System
6.2. Simulation Results and Analysis
6.2.1. Analysis of Charging Demand of EV
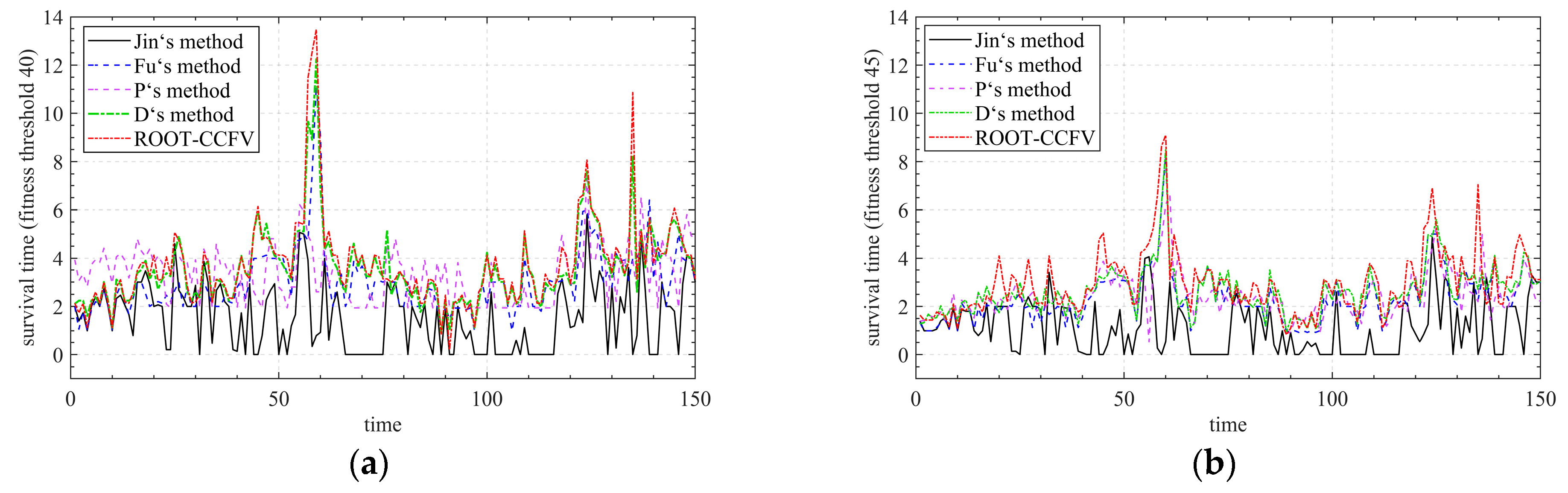
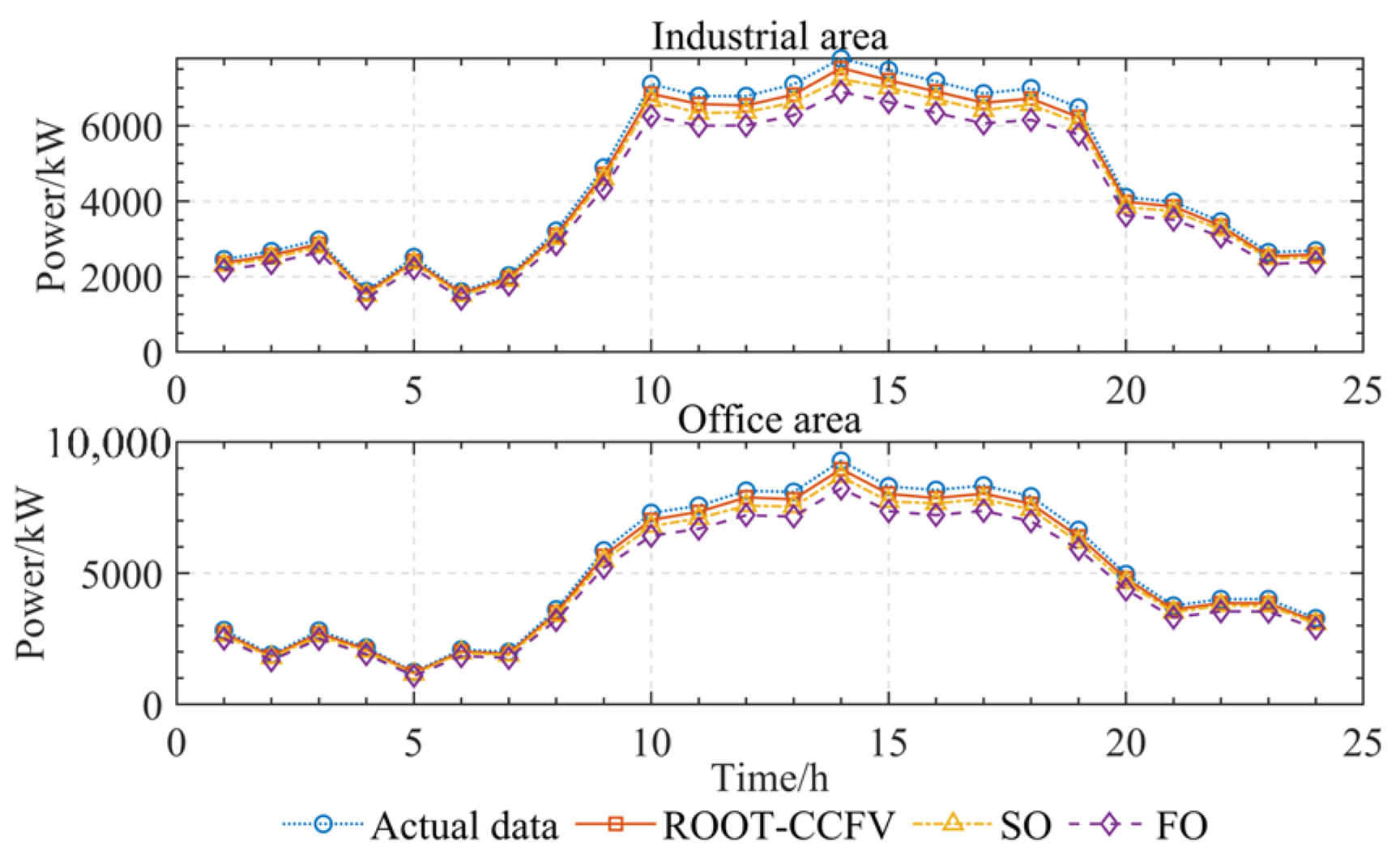
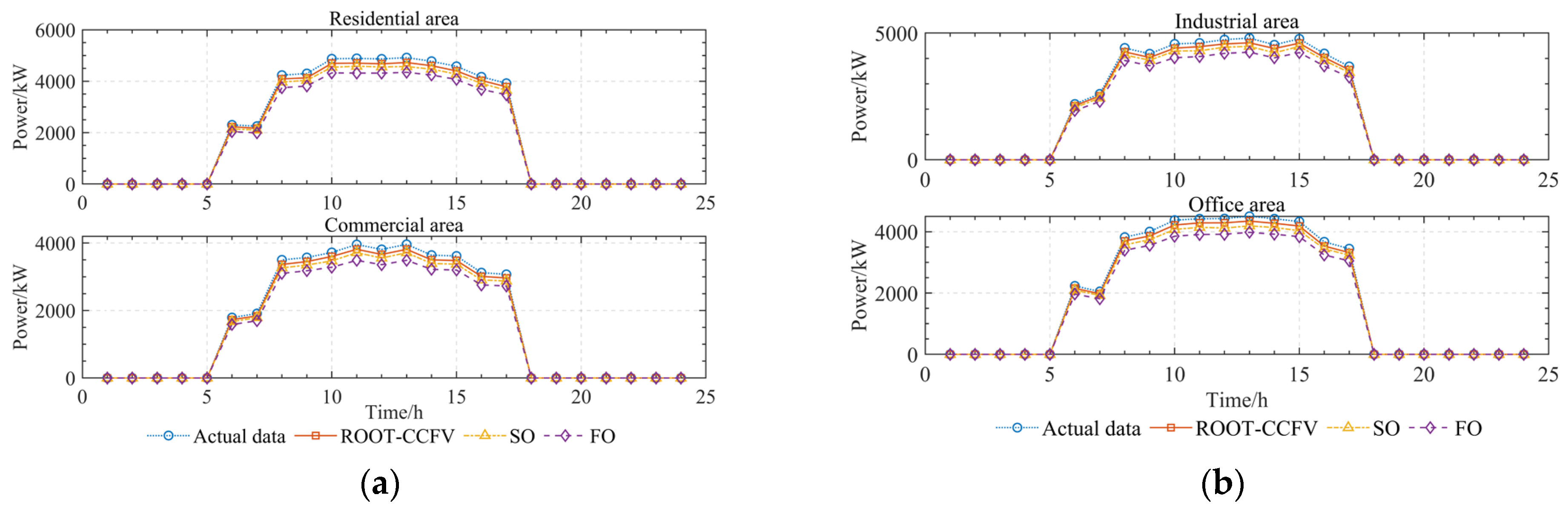
6.2.2. Analysis of the Effectiveness of ROOT-CCFV
6.2.3. Analysis of RES Uncertainty under ROOT-CCFV Based on Scene Method
6.2.4. Analysis of SESS Capacity Configuration Considering EV Charging Demand
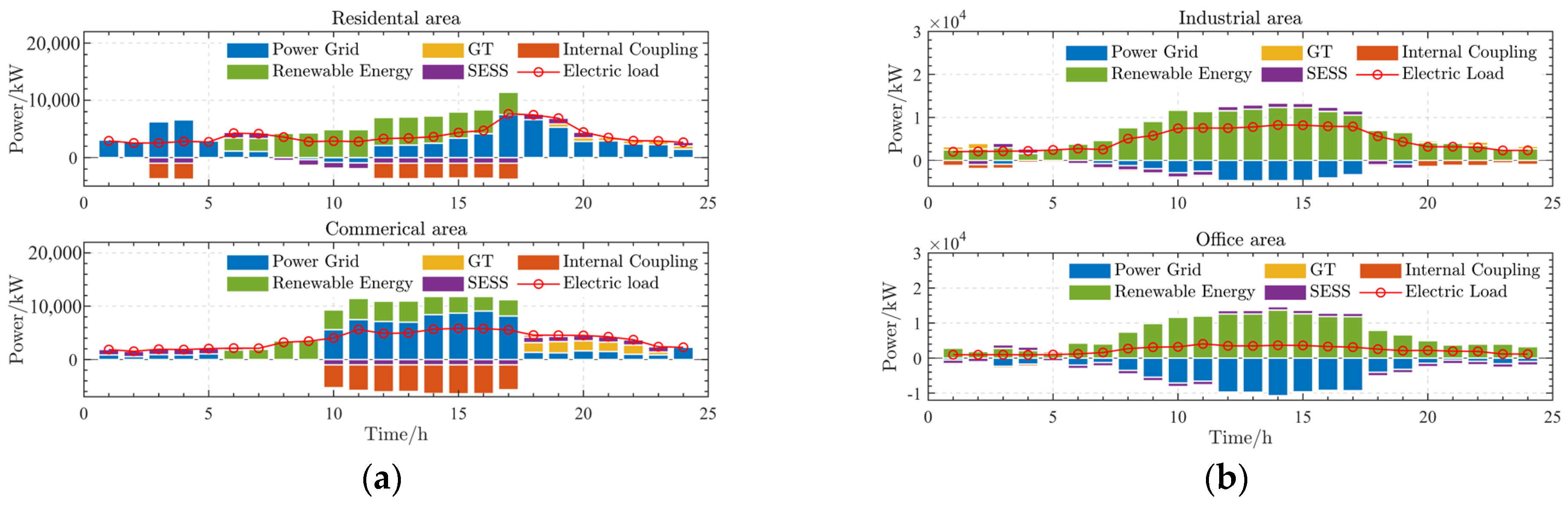
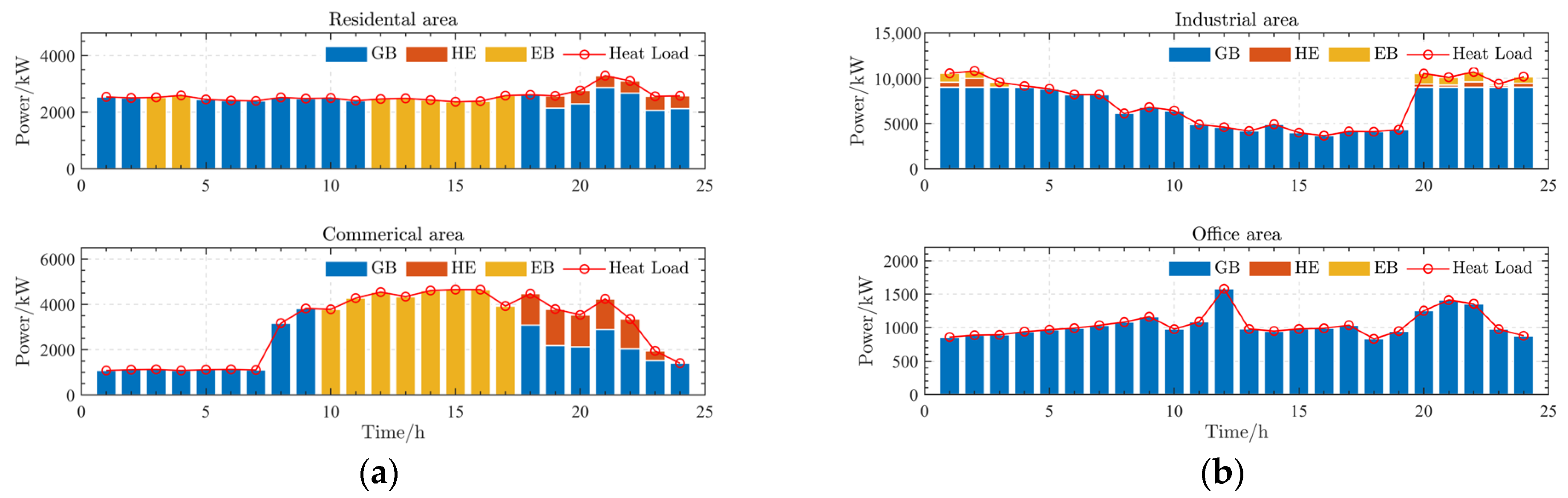
6.2.5. Analysis of Optimal Scheduling Results of the RIES Considering the EV Charging Demand
6.2.6. Analysis of IDR
7. Conclusions
- The ROOT-CCFV algorithm can better solve the dynamic optimization problem with time-varying parameters and obtain a more robust solution. Compared with the existing algorithms, in the mMPB test environment, the average survival time of the robust solution obtained by the ROOT-CCFV algorithm was increased by 46.1% on average. The proposed ROOT-CCFV algorithm provides a solution for solving dynamic optimization problems in the future.
- The reasonable modeling of an EV charging demand model can effectively reduce the capacity configuration cost of an SESS and the optimal operation cost of an RIES in this region. And the larger the EV load in the region, the less the SESS capacity required in the region. Under the same RES uncertainty solving algorithm, compared with the traditional EV charging model, the EV charging model based on the trip chain proposed in this paper can reduce the cost of its own charging expenditure by 3.5%, and at the same time reduce the operating cost of an RIES by 11.7%.
- The alternative IDR model proposed in this paper can realize the coupling of electric heating and cold energy, and effectively reduce the operation cost of an RIES. When the IDR model proposed in this paper is considered in RIES optimal scheduling, the operating cost can be reduced by 4.8%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Equipment | RA | CA | IA | OA |
|---|---|---|---|---|
| PV | 2000 | 4000 | 8000 | 2000 |
| WT | / | / | 6000 | 3000 |
| ES | / | 1000 | 2000 | / |
| GT | 2000 | 5000 | 8000 | 3000 |
| WHB | 5000 | 5000 | 8000 | 5000 |
| GB | 5000 | 5000 | 8000 | 5000 |
| EH | 5000 | 5000 | 8000 | 5000 |
| EC | 5000 | 5000 | 8000 | 5000 |
| AC | 5000 | 5000 | 8000 | 5000 |
| HE | 4000 | 4000 | 4000 | 4000 |
| Equipment | RA | CA | IA | OA |
|---|---|---|---|---|
| Efficiency of GT | 0.35 | 0.35 | 0.35 | 0.35 |
| Heat-to-electric ratio of GT | 2.3 | 2.3 | 2.3 | 2.3 |
| Efficiency of WHB | 0.73 | 0.73 | 0.73 | 0.73 |
| Efficiency of GB | 0.85 | 0.85 | 0.85 | 0.85 |
| Efficiency of EH | 0.98 | 0.98 | 0.98 | 0.98 |
| Efficiency of EC | 4 | 4 | 4 | 4 |
| Efficiency of AC | 1.2 | 1.2 | 1.2 | 1.2 |
| Efficiency of HE | 0.9 | 0.9 | 0.9 | 0.9 |
| Maximum charging of ES | / | 200 kW | 400 kW | / |
| Maximum discharging of ES | / | 200 kW | 400 kW | / |
| Charging efficiency of ES | / | 0.95 | 0.95 | / |
| Discharging efficiency of ES | / | 0.95 | 0.95 | / |
| Self-discharging efficiency of ES | / | 0.04 | 0.04 | / |
| Initial energy storage of ES | / | 200 kWh | 400 kWh | / |
| Maximum energy storage of ES | / | 900 kWh | 1800 kWh | / |
| Minimum energy storage of ES | / | 200 kWh | 400 kWh | / |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Charging efficiency | 0.95 | Initial state of SOC | 0.50 |
| Discharging efficiency | 0.95 | Maximum state of SOC | 0.90 |
| Self-discharging efficiency | 0.04 | Minimum state of SCO | 0.20 |
| Maximum charge/discharge power to each region | 1000 kW |
| RA | CA/IA/OA | ||||||
|---|---|---|---|---|---|---|---|
| Price Types | Time Interval | Purchase Price | Sale Price | Price Types | Time Interval | Purchase Price | Sale Price |
| Peak time | 07:00–09:00 18:00–24:00 | 0.759 | 0.415 | Peak time | 07:00–09:00 17:00–23:00 | 0.8650 | 0.415 |
| Usual time | 00:00–02:00 04:00–07:00 09:00–11:00 17:00–18:00 | 0.510 | 0.415 | Usual time | 23:00–00:00 00:00–07:00 | 0.5843 | 0.415 |
| Valley time | 02:00–04:00 11:00–17:00 | 0.261 | 0.415 | Valley time | 09:00–17:00 | 0.3036 | 0.415 |
| Price Types | Time Interval | Purchase Price | Sale Price |
|---|---|---|---|
| Peak time | 08:00–09:00, 19:00–24:00 | 0.725 | 0.435 |
| Usual time | 00:00–02:00, 05:00–07:00 10:00–11:00, 18:00–18:00 | 0.475 | 0.435 |
| Valley time | 03:00–04:00, 12:00–17:00 | 0.271 | 0.435 |
References
- European Commission. Horizon 2020 Work Programme 2018–2020: 10. Secure, Clean and Efficient Energy; Official Publications of the European Communities: Luxembourg, 2018. [Google Scholar]
- Zhou, S.; Han, Y.; Mahmoud, K.; Darwish, M.M.; Lehtonen, M.; Yang, P.; Zalhaf, A.S. A novel unified planning model for distributed generation and electric vehicle charging station considering multi-uncertainties and battery degradation. Appl. Energy 2023, 348, 121566. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-Triggered Distributed Hybrid Control Scheme for the Integrated Energy System. IEEE Trans. Ind. Inform. 2021, 18, 835–846. [Google Scholar] [CrossRef]
- Liu, L.; Yao, X.; Qi, X.; Han, Y. Low-carbon economy configuration strategy of electro-thermal hybrid shared energy storage in multiple multi-energy microgrids considering power to gas and carbon capture system. J. Clean. Prod. 2023, 428, 139366. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Yang, Z.; Li, G. Coordinating Flexible demand response and renewable uncertainties for scheduling of community integrated energy systems with an electric vehicle charging station: A bi-level approach. IEEE Trans. Sustain. Energy 2021, 12, 2321–2331. [Google Scholar] [CrossRef]
- Gan, L.; Chen, X.; Yu, K.; Zheng, J.; Du, W. A probabilistic evaluation method of household EVs dispatching potential considering users’ multiple travel needs. IEEE Trans. Ind. Appl. 2020, 56, 5858–5867. [Google Scholar] [CrossRef]
- Lan, T.; Jermsittiparsert, K.; Alrashood, S.T.; Rezaei, M.; Al-Ghussain, L.; Mohamed, M.A. An Advanced Machine Learning Based Energy Management of Renewable Microgrids Considering Hybrid Electric Vehicles’ Charging Demand. Energies 2021, 14, 569. [Google Scholar] [CrossRef]
- Taibi, E.; del Valle, C.F.; Howells, M. Strategies for solar and wind integration by leveraging flexibility from electric vehicles: The Barbados case study. Energy 2018, 164, 65–78. [Google Scholar] [CrossRef]
- Mwasilu, F.; Justo, J.J.; Kim, E.-K.; Do, T.D.; Jung, J.-W. Electric vehicles and smart grid interaction: A review on vehicle to grid and renewable energy sources integration. Renew. Sustain. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Rassaei, F.; Soh, W.S.; Chua, K.C. Demand response for residential electric vehicles with random usage patterns in smart grids. IEEE Trans. Sustain. Energy 2015, 6, 1367–1376. [Google Scholar] [CrossRef]
- Tan, J.; Wang, L. Real-Time charging navigation of electric vehicles to fast charging stations: A hierarchical game approach. IEEE Trans. Smart Grid 2015, 8, 846–856. [Google Scholar] [CrossRef]
- Li, G.; Wu, D.; Hu, J.; Li, Y.; Hossain, M.S.; Ghoneim, A. HELOS: Heterogeneous load scheduling for electric vehicle-integrated microgrids. IEEE Trans. Veh. Technol. 2016, 66, 5785–5796. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. A real-time demand-response algorithm for smart grids: A stackelberg game approach. IEEE Trans. Smart Grid 2015, 7, 879–888. [Google Scholar] [CrossRef]
- Wang, D.; Guan, X.; Wu, J.; Li, P.; Zan, P.; Xu, H. Integrated energy exchange scheduling for multimicrogrid system with electric vehicles. IEEE Trans. Smart Grid 2015, 7, 1762–1774. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.-Y. Day-Ahead Solar Irradiance Forecasting for Microgrids Using a Long Short-Term Memory Recurrent Neural Network: A Deep Learning Approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, L.; Guo, W.; Kang, Q.; Wu, Q. Chance constrained optimization in a home energy management system. IEEE Trans. Smart Grid 2016, 9, 252–260. [Google Scholar] [CrossRef]
- Baker, K.; Bernstein, A. Joint chance constraints in AC optimal power flow: Improving bounds through learning. IEEE Trans. Smart Grid 2019, 10, 6376–6385. [Google Scholar] [CrossRef]
- Zhang, Y.; Ai, Q.; Xiao, F.; Hao, R.; Lu, T. Typical wind power scenario generation for multiple wind farms using conditional improved Wasserstein generative adversarial network. Int. J. Electr. Power Energy Syst. 2020, 114, 105388. [Google Scholar] [CrossRef]
- Li, Y.; Wang, B.; Yang, Z.; Li, J.; Chen, C. Hierarchical stochastic scheduling of multi-community integrated energy systems in uncertain environments via Stackelberg game. Appl. Energy 2021, 308, 118392. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Shahidehpour, M.; Li, J.; Long, C. Data-driven distributionally robust scheduling of community integrated energy systems with uncertain renewable generations considering integrated demand response. Appl. Energy 2023, 335, 120749. [Google Scholar] [CrossRef]
- Yang, J.; Su, C. Robust optimization of microgrid based on renewable distributed power generation and load demand uncertainty. Energy 2021, 223, 120043. [Google Scholar] [CrossRef]
- Huang, S.; Lu, H.; Chen, M.; Zhao, W. Integrated energy system scheduling considering the correlation of uncertainties. Energy 2023, 283, 129011. [Google Scholar] [CrossRef]
- Kalathil, D.; Wu, C.; Poolla, K.; Varaiya, P. The sharing economy for the electricity storage. IEEE Trans. Smart Grid 2017, 10, 556–567. [Google Scholar] [CrossRef]
- Dai, R.; Esmaeilbeigi, R.; Charkhgard, H. The utilization of shared energy storage in energy systems: A comprehensive review. IEEE Trans. Smart Grid 2021, 12, 3163–3174. [Google Scholar] [CrossRef]
- Kang, C.; Liu, J.; Zhang, N. A new form of energy storage in future power system: Cloud energy storage. Autom. Electr. Power Syst. 2017, 41, 2–8. [Google Scholar]
- Walker, A.; Kwon, S. Analysis on impact of shared energy storage in residential community: Individual versus shared energy storage. Appl. Energy 2020, 282, 116172. [Google Scholar] [CrossRef]
- Liu, N.; Tan, L.; Sun, H.; Zhou, Z.; Guo, B. Bilevel Heat–Electricity Energy Sharing for Integrated Energy Systems with Energy Hubs and Prosumers. IEEE Trans. Ind. Inform. 2021, 18, 3754–3765. [Google Scholar] [CrossRef]
- Jabir, H.J.; Teh, J.; Ishak, D.; Abunima, H. Impacts of Demand-Side Management on Electrical Power Systems: A Review. Energies 2018, 11, 1050. [Google Scholar] [CrossRef]
- Tang, D.; Wang, P. Probabilistic modeling of nodal charging demand based on spatial-temporal dynamics of moving electric vehicles. IEEE Trans. Smart Grid 2015, 7, 627–636. [Google Scholar] [CrossRef]
- Yu, X.; Jin, Y.; Tang, K.; Yao, X. Robust optimization over time—A new perspective on dynamic optimization problems. In Proceedings of the 2010 IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 3998–4003. [Google Scholar]
- Jin, Y.; Tang, K.; Yu, X.; Sendhoff, B.; Yao, X. A framework for finding robust optimal solutions over time. Memetic Comput. 2013, 5, 3–18. [Google Scholar] [CrossRef]
- Fu, H.; Sendhoff, B.; Tang, K.; Yao, X. Finding Robust Solutions to Dynamic Optimization Problems. In Proceedings of the 16th European Conference on Applications of Evolutionary Computation, Vienna, Austria, 3–5 April 2013; pp. 616–625. [Google Scholar]
- Cao, M.; Shao, C.; Hu, B.; Xie, K.; Li, W.; Peng, L.; Zhang, W. Reliability Assessment of Integrated Energy Systems Considering Emergency Dispatch Based on Dynamic Optimal Energy Flow. IEEE Trans. Sustain. Energy 2021, 13, 290–301. [Google Scholar] [CrossRef]
- Lee, T.-K.; Bareket, Z.; Gordon, T.; Filipi, Z.S. Stochastic modeling for studies of real-world PHEV usage: Driving schedule and daily temporal distributions. IEEE Trans. Veh. Technol. 2012, 61, 1493–1502. [Google Scholar] [CrossRef]
- Novoa-Hernandez, P.; Pelta, D.A.; Corona, C.C. Approximation Models in Robust Optimization Over Time—An Experimental Study. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yazdani, D.; Nguyen, T.T.; Branke, J. Robust Optimization over Time by Learning Problem Space Characteristics. IEEE Trans. Evol. Comput. 2018, 23, 143–155. [Google Scholar] [CrossRef]





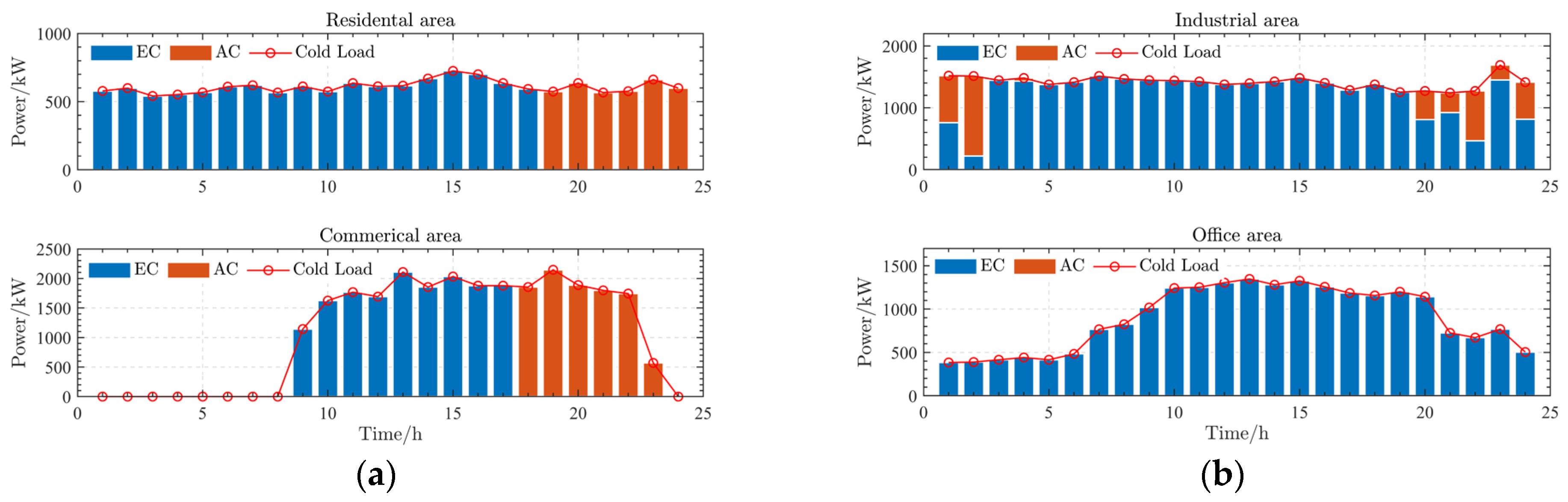
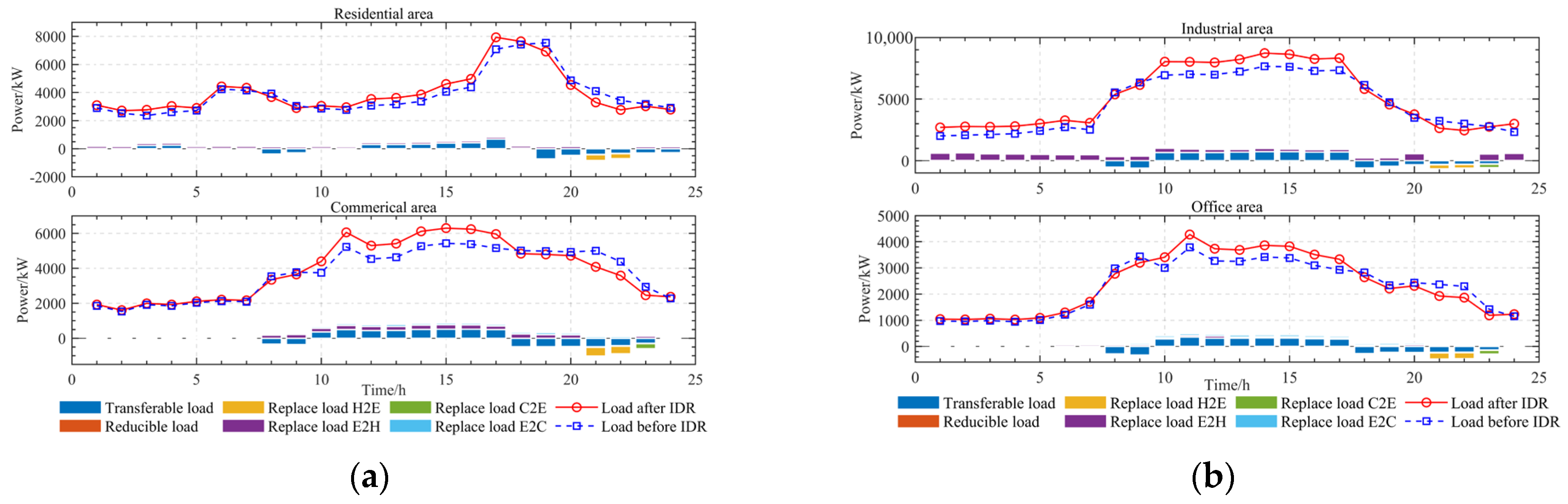
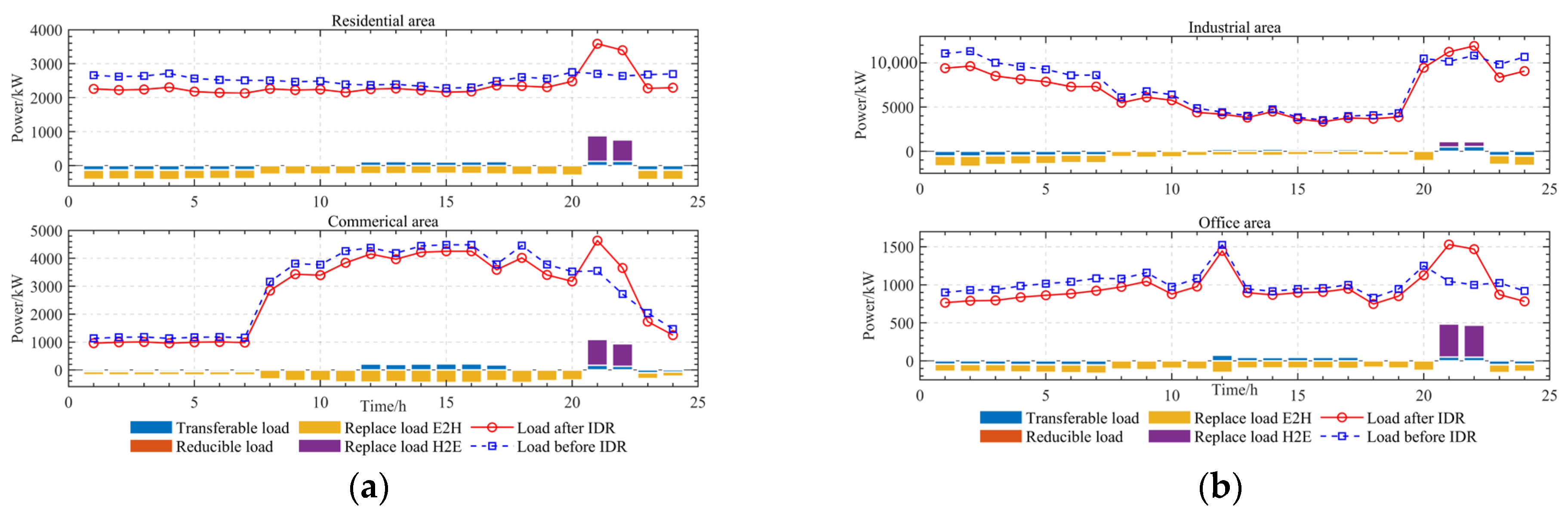
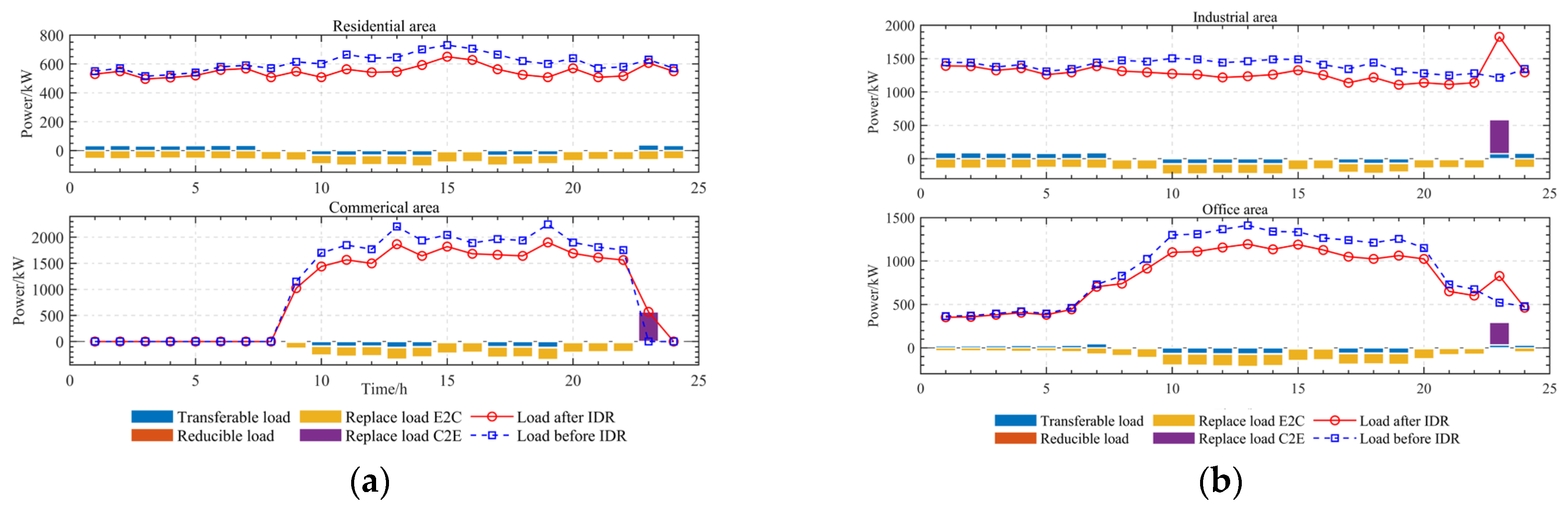
| Home | Work | Other | |
|---|---|---|---|
| Probability p | 0.9810 | 0.0027 | 0.0163 |
| Constraint Type | CCHP | SESS | Coupling Relationship |
|---|---|---|---|
| Equality constraints | 1. Power bus energy balance constraints | Energy continuity constraint | CCHP-SESS energy coupling constraint |
| 2. Electric storage energy relationship constraints | |||
| Inequality constraints | 1. Equipment operating power constraints | 1. Charging/discharging power constraints | / |
| 2. Electric storage charging/discharging power constraints | 2. Capacity constraints |
| Algorithm | Fitness Threshold | ||
|---|---|---|---|
| 40 | 45 | 50 | |
| Jin’s ROOT [31] | 1.53 | 1.11 | 0.69 |
| Fu’s ROOT [32] | 3.03 | 2.39 | 1.69 |
| P’s ROOT [35] | 3.35 | 2.46 | 1.82 |
| D’s ROOT [36] | 3.62 | 2.65 | 1.95 |
| ROOT-CCFV | 3.75 | 2.94 | 2.17 |
| Mode | Capacity Configuration | Charging Expenditure |
|---|---|---|
| Mode 1 | 18,180.31 kWh | 21,916.43 ¥ |
| Mode 2 | 17,511.84 kWh | 21,120.63 ¥ |
| Mode 3 | 19,433.79 kWh | 20,895.32 ¥ |
| Mode 4 | 18,919.55 kWh | 20,262.24 ¥ |
| EV Load Scale | Mode 2 | Mode 4 | ||
|---|---|---|---|---|
| Capacity Configuration | Operation Cost | Capacity Configuration | Operation Cost | |
| 15% of Total load | 17,232.17 kWh | CNY 110,462.33 | 18,746.26 kWh | CNY 103,908.74 |
| 20% of Total load | 16,634.31 kWh | CNY 119,153.54 | 18,296.35 kWh | CNY 110,280.87 |
| 25% of Total load | 16,278.97 kWh | CNY 127,855.19 | 17,767.79 kWh | CNY 116,781.45 |
| 30% of Total load | 15,728.46 kWh | CNY 136,542.37 | 17,373.30 kWh | CNY 122,976.14 |
| 35% of Total load | 15,395.42 kWh | CNY 145,246.72 | 16,899.01 kWh | CNY 129,187.59 |
| Details of Operating Cost | Mode 1 | Mode 2 | Mode 3 | Mode 4 |
|---|---|---|---|---|
| Electrical energy transaction expenditure | CNY 37,380.93 | CNY 31,740.59 | CNY 35,694.37 | CNY 30,477.46 |
| Gas energy transaction expenditure | CNY 60,872.21 | CNY 57,072.09 | CNY 55,624.14 | CNY 51,773.44 |
| Operation and maintenance expenditure | CNY 24,931.91 | CNY 20,431.22 | CNY 23,788.59 | CNY 19,118.81 |
| Energy transaction expenditure with the SESS | CNY 3143.58 | CNY 3021.33 | CNY 3332.67 | CNY 3219.21 |
| Total cost | CNY 126,319.63 | CNY 112,265.17 | CNY 118,439.77 | CNY 104,548.92 |
| Details of Operating Cost | Mode 5 | Mode 6 |
|---|---|---|
| Electrical energy transaction expenditure | CNY 30,477.46 | CNY 29,569.46 |
| Gas energy transaction expenditure | CNY 51,773.44 | CNY 48,846.58 |
| Operation and maintenance expenditure | CNY 19,118.81 | CNY 17,910.47 |
| Energy transaction expenditure with SESS | CNY 3219.21 | CNY 3176.10 |
| Total cost | CNY 104,548.92 | CNY 99,502,61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Li, E. Multi-Regional Integrated Energy Economic Dispatch Considering Renewable Energy Uncertainty and Electric Vehicle Charging Demand Based on Dynamic Robust Optimization. Energies 2024, 17, 2453. https://doi.org/10.3390/en17112453
Zhou B, Li E. Multi-Regional Integrated Energy Economic Dispatch Considering Renewable Energy Uncertainty and Electric Vehicle Charging Demand Based on Dynamic Robust Optimization. Energies. 2024; 17(11):2453. https://doi.org/10.3390/en17112453
Chicago/Turabian StyleZhou, Bo, and Erchao Li. 2024. "Multi-Regional Integrated Energy Economic Dispatch Considering Renewable Energy Uncertainty and Electric Vehicle Charging Demand Based on Dynamic Robust Optimization" Energies 17, no. 11: 2453. https://doi.org/10.3390/en17112453
APA StyleZhou, B., & Li, E. (2024). Multi-Regional Integrated Energy Economic Dispatch Considering Renewable Energy Uncertainty and Electric Vehicle Charging Demand Based on Dynamic Robust Optimization. Energies, 17(11), 2453. https://doi.org/10.3390/en17112453





