Using Quality Function Deployment to Assess the Efficiency of Mini-Channel Heat Exchangers
Highlights
- Identification of fundamental (material and geometric) and operating parameters of the compact heat exchanger;
- Application of the Quality Function Deployment (QFD) method analysis for the identification of the essential Critical-to-Quality features that most influence the efficiency of a model compact heat exchanger.
- This study provides an assessment of the main features of a compact heat exchanger in order to greatly improve its thermal efficiency;
- It also highlights a procedure for selecting the most important features of a high thermal efficiency heat exchanger, reducing the time and money needed for its design and material solutions, that is ready for use in designing heat exchangers.
Abstract
1. Introduction
2. Experimental Base
2.1. Test Stand
- Acquiring thermograms of the outer surface of the heated wall of the mini-channel using an infrared camera;
- Recording of fluid temperature (via K-type thermocouples), fluid pressure (using overpressure meters and an absolute pressure meter), mass flow rate (due to a Coriolis mass flow meter), current intensity (via ammeter), and voltage drop (via voltmeter) across the heated wall of the mini-channels;
- Capturing flow patterns using a high-speed camera.
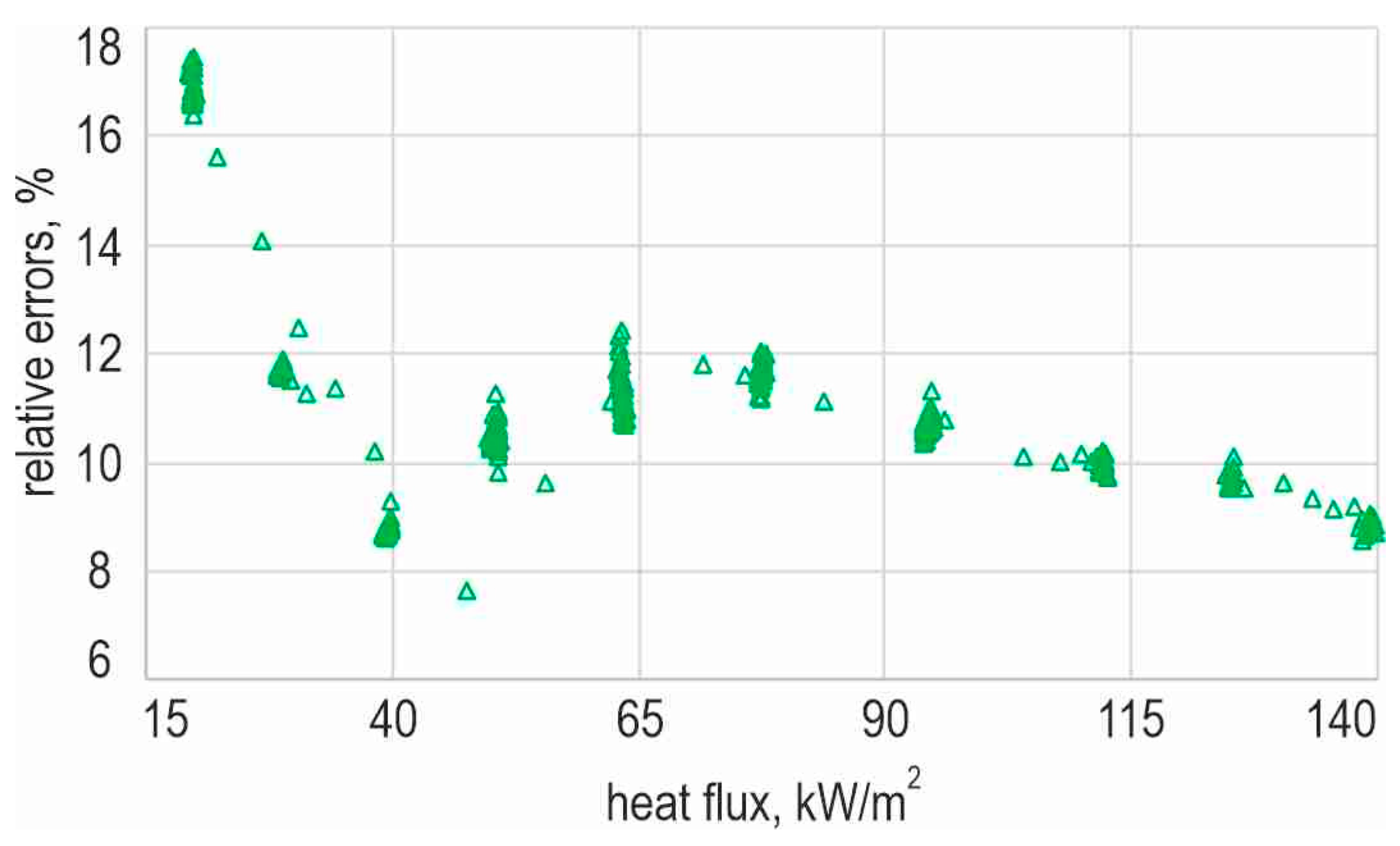
2.2. Experimental Uncertainties
2.3. Research Methodology
2.4. The Reference Experiment
3. Mathematical Model, Heat Transfer Calculations, and Example Results
3.1. Main Aim
3.2. Assumptions for Calculations
3.3. Analytical–Numerical Method with the Use of T-Functions
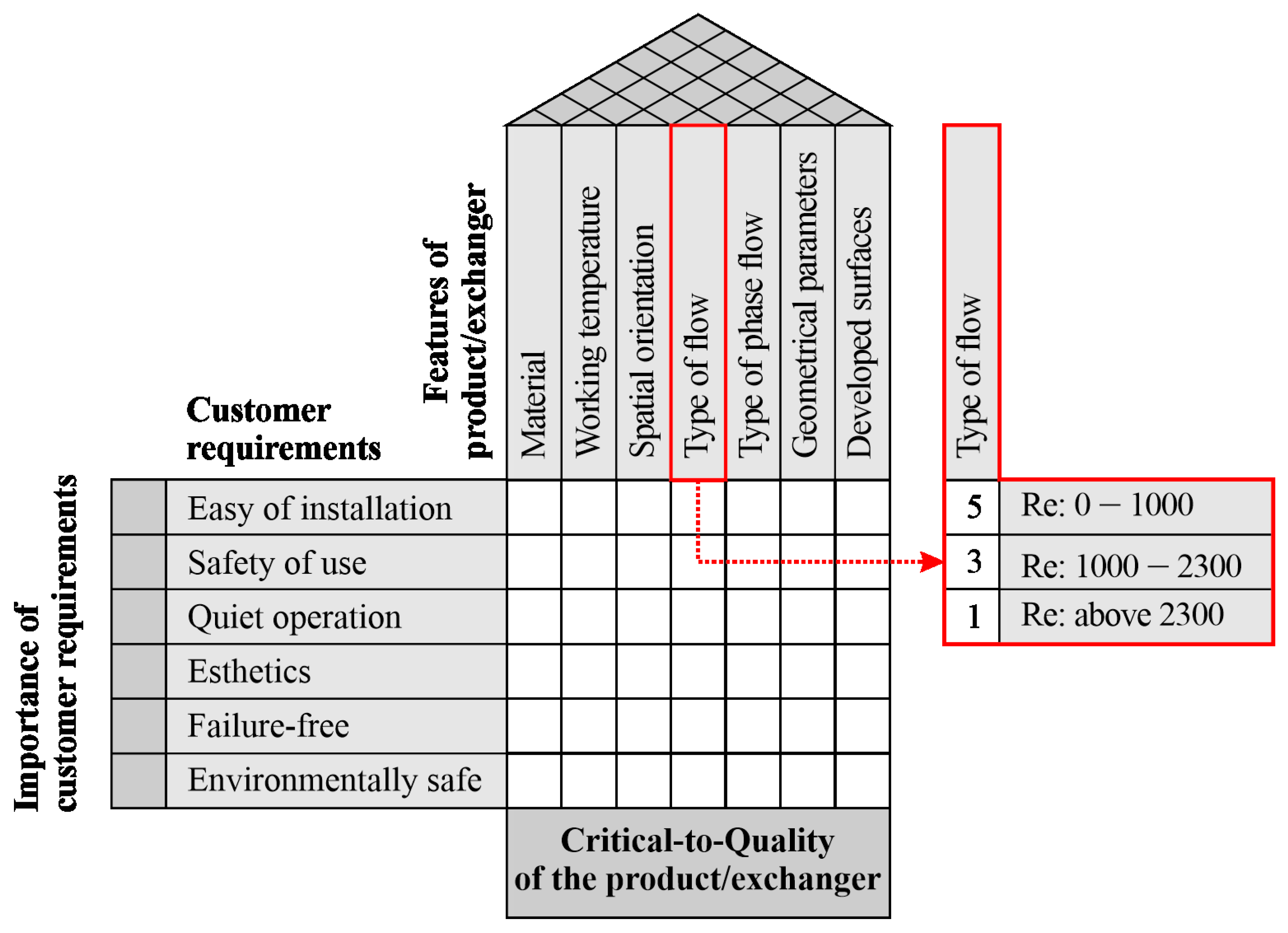
- The fluid flow in the mini-channel is steady and laminar (Reynolds number < 2300) with a constant mass flow rate;
- The temperature and pressure of the fluid at the inlet and outlet to/from the mini-channel are known from experimental measurements;
- The velocity of the fluid has only one non-zero parabolic component, v(y), parallel to the heating plate;
- the heating plate and the cooling fluid are in perfect thermal contact, meaning the temperature and heat flux are equal on the contact wall between the plate and the fluid;
- For saturated boiling, the emerging vapor bubbles absorb part of the energy supplied to the fluid and are treated as a negative heat source, [30].
3.4. Heat Transfer Coefficient Uncertainty
- the accuracy of the calculated heat flux density was estimated in parallel to [28], considering errors of: current intensity (supplied to the heated plate), voltage drop (across the heated plate), and area of the heated plate;
- —the accuracy of the heated plate temperature;
- —the accuracy of the fluid temperature;
- with the following assumptions:
- —uncertainty of the heated plate temperature, measured by the FLIR A655SC infrared camera (FLIR Systems Inc., Wilsonville, OR, USA), while the accuracy of this camera is ±2 °C or ±2% in the temperature range of −20 ÷ 120 °C (see Table 5);
- —uncertainty of fluid temperature data obtained with additionally calibrated K-type thermocouples, analogous to [30];
- Δx = 0.0001 m—uncertainty of infrared thermography temperature measurement location, as in [35].
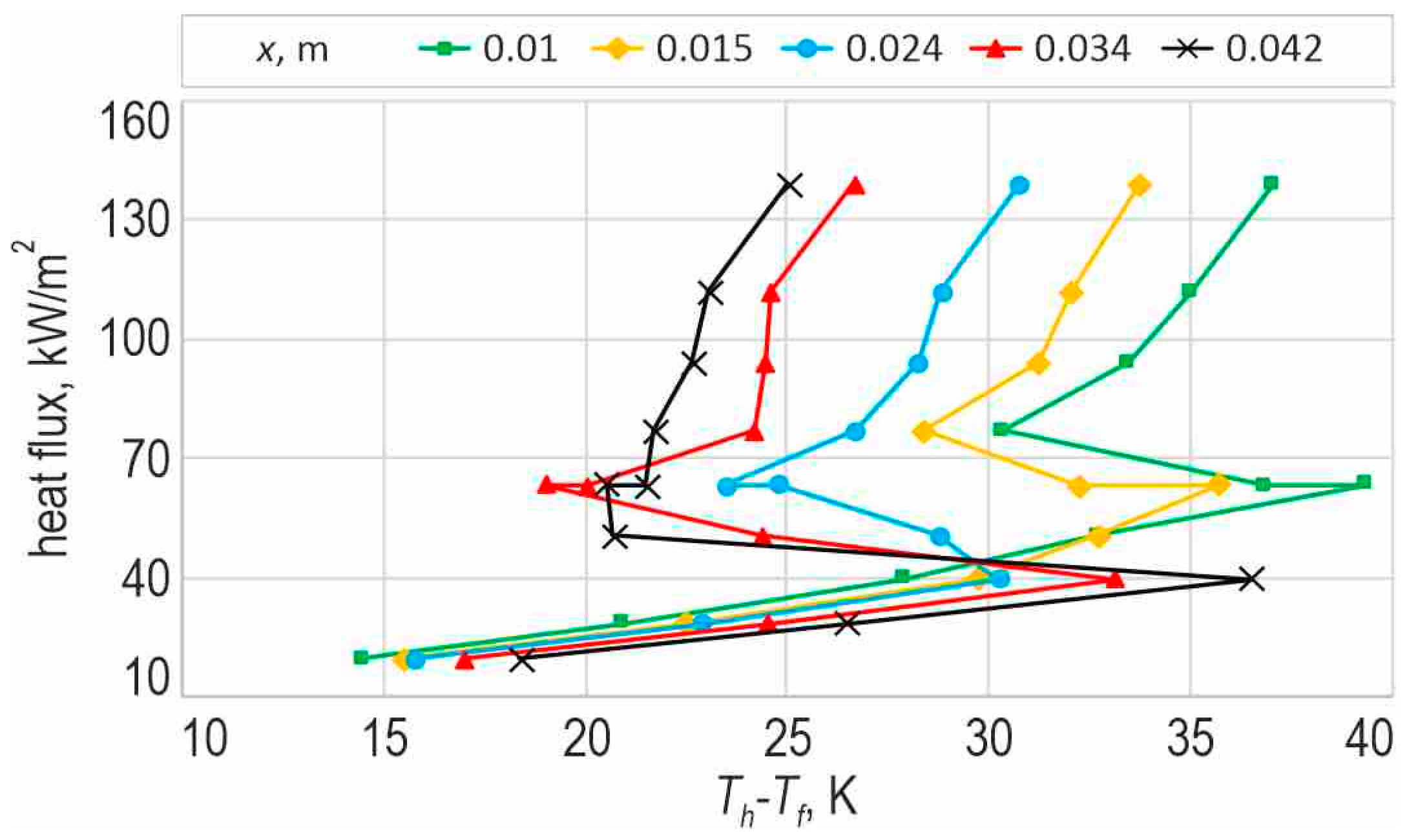
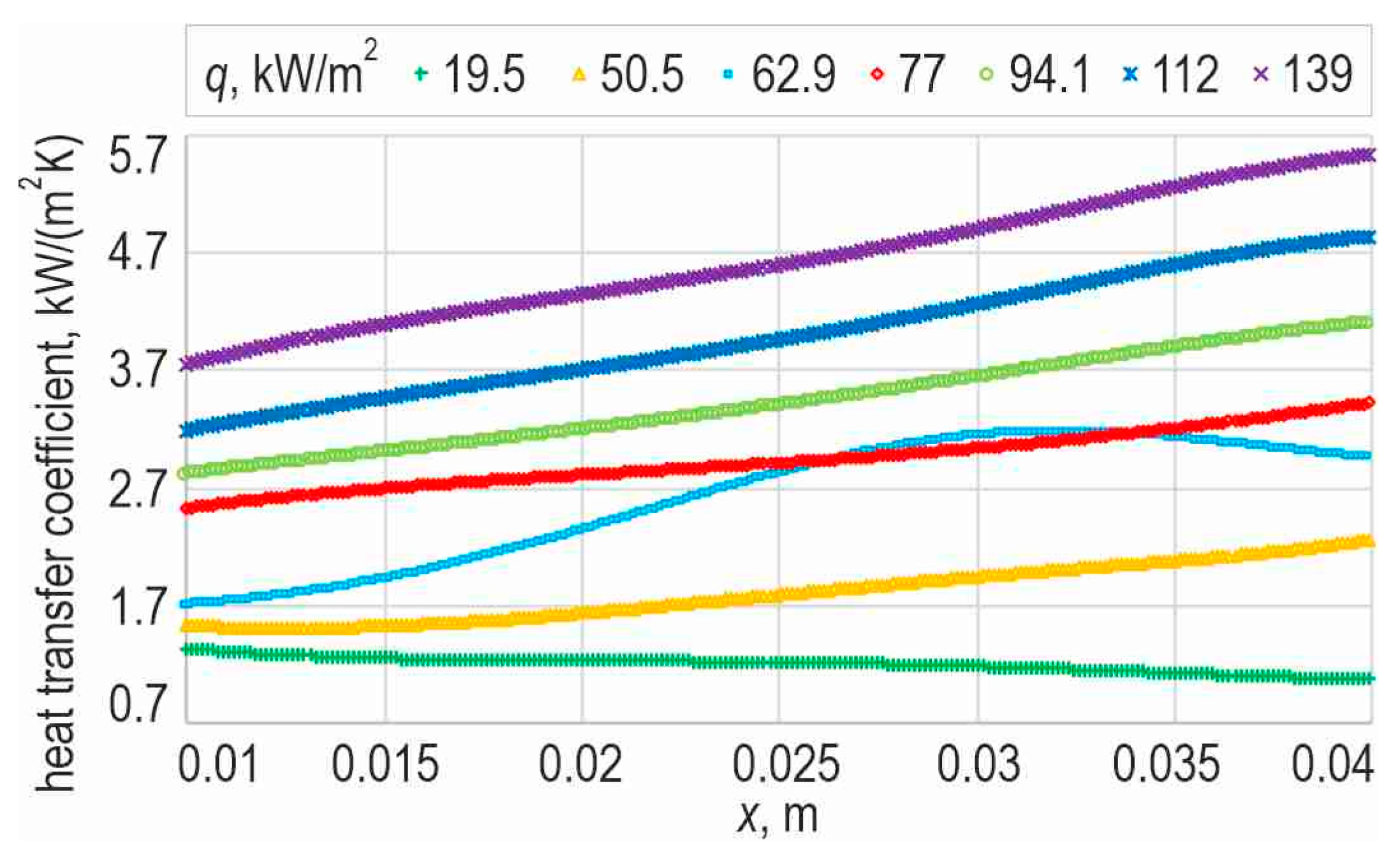
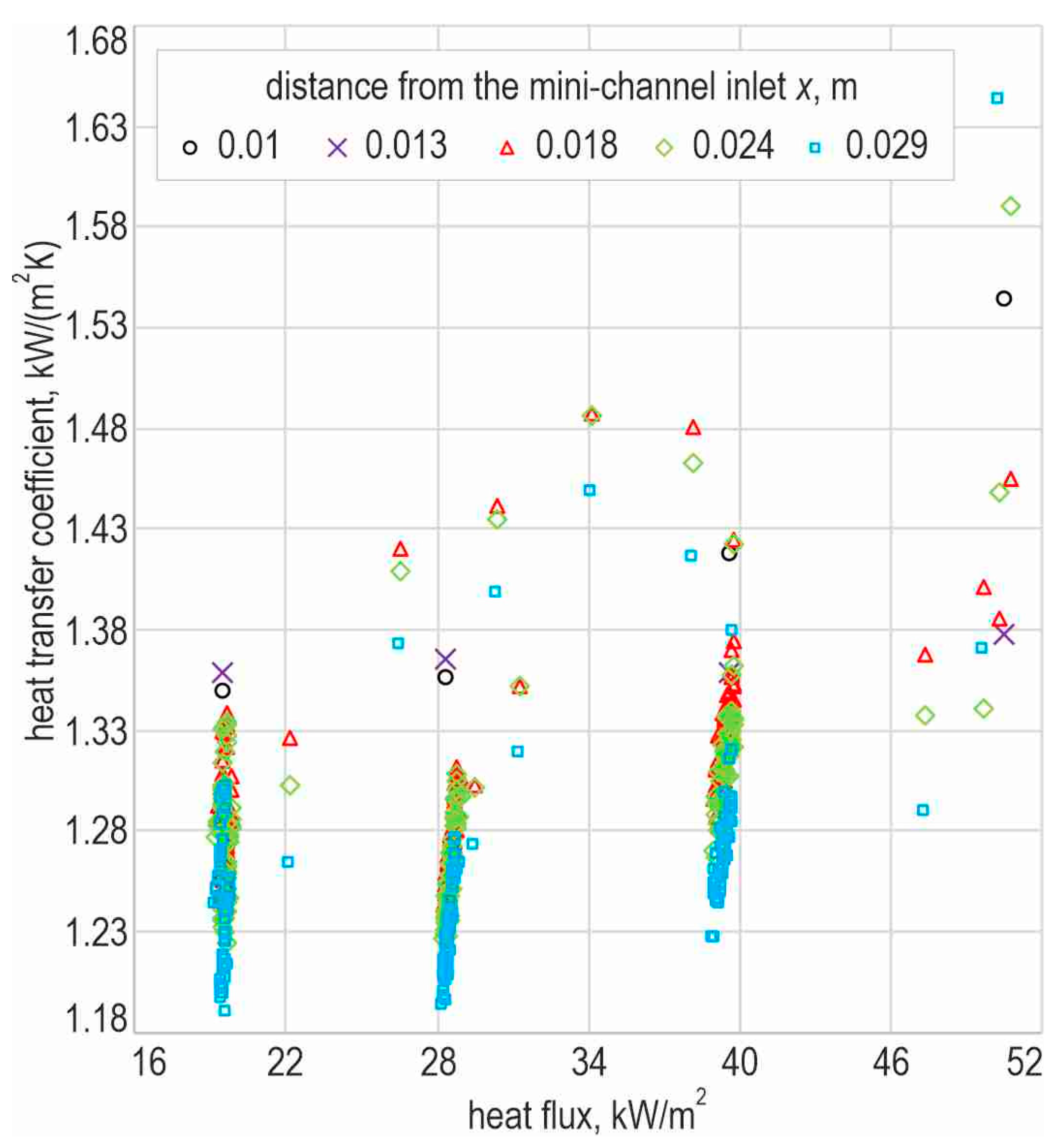
3.5. Example Heat Transfer Results
3.5.1. Data from Experiments
3.5.2. Heat Transfer Results According to Analytical–Numerical Method with the Use of T-Functions
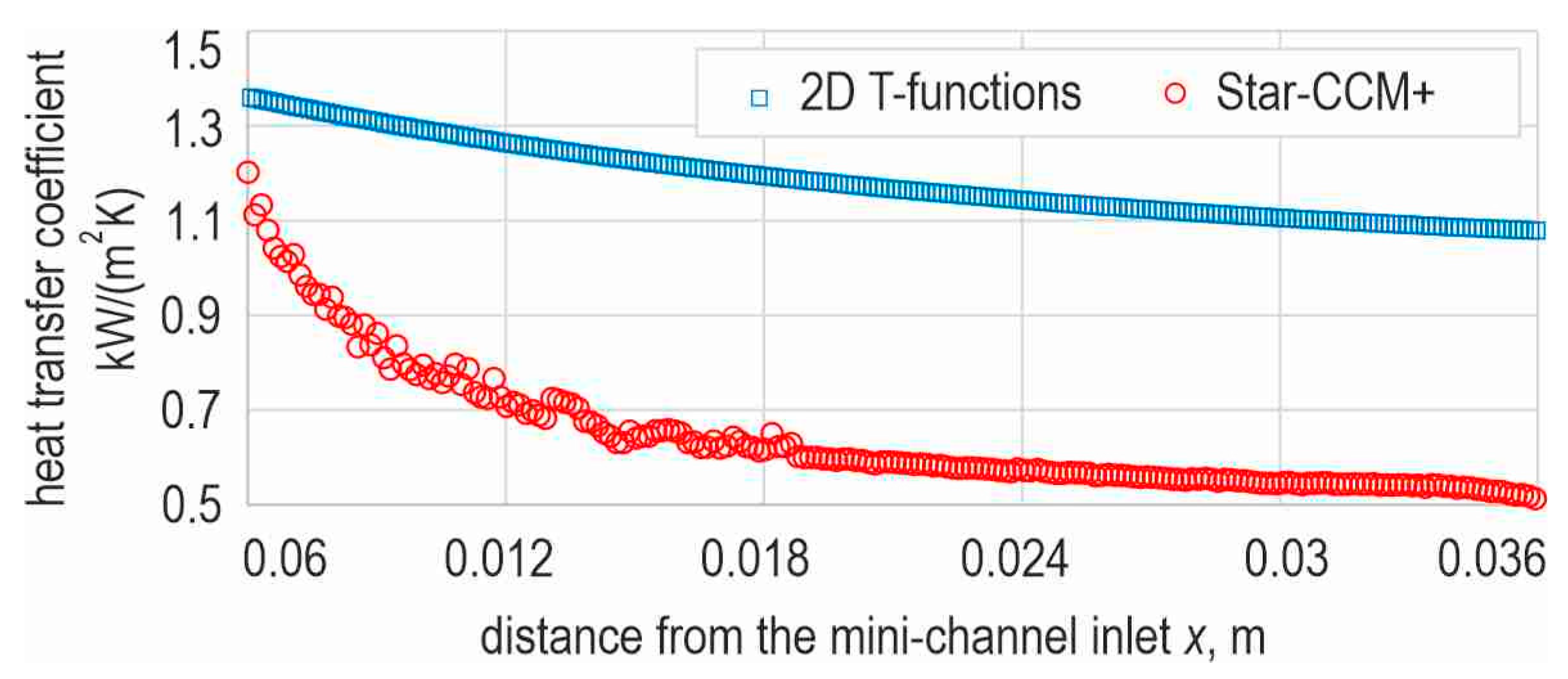
4. CFD Simulations in the Simcenter STAR-CCM+ Programme
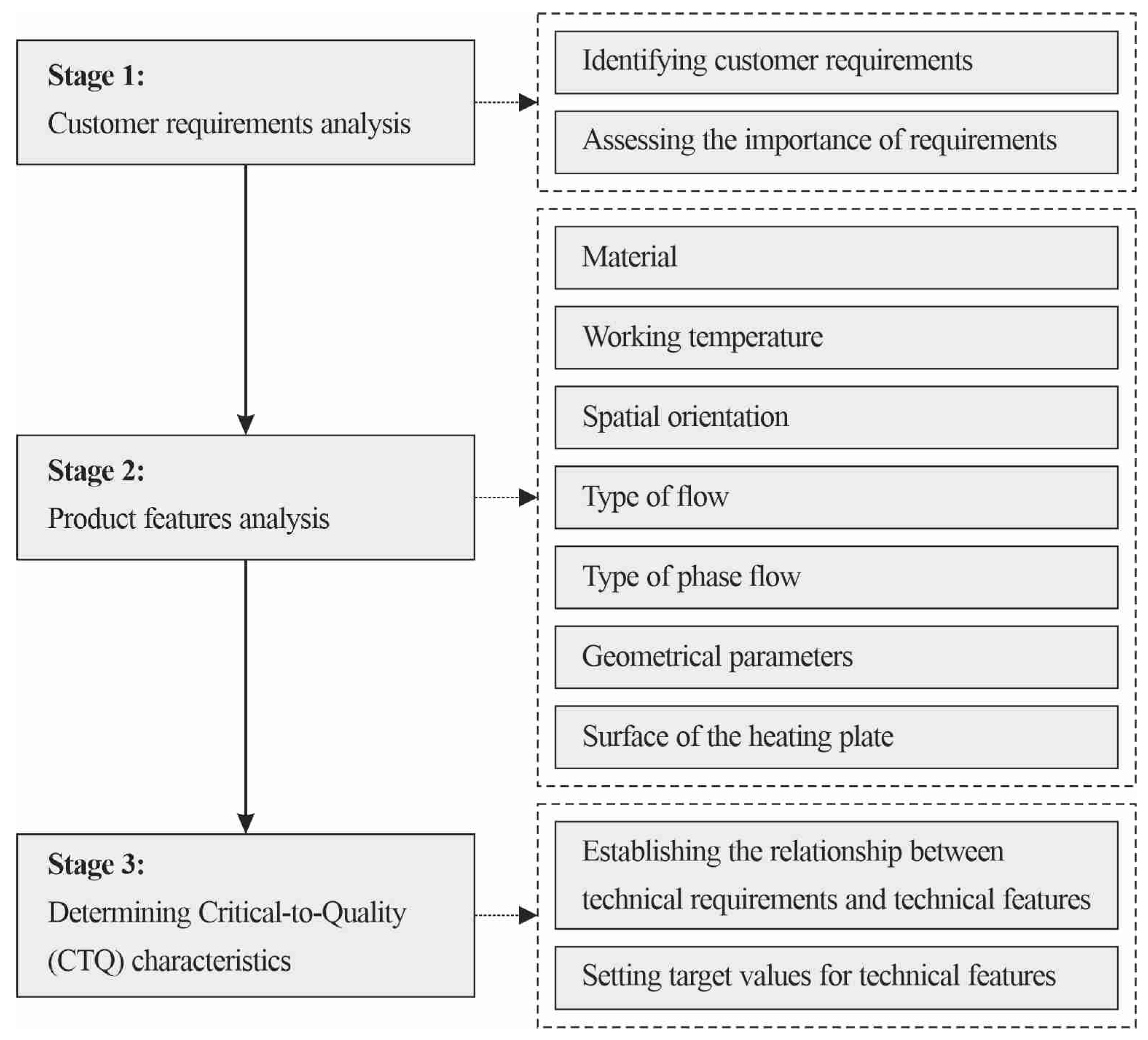
5. QFD Method
5.1. Characteristics of the QFD Method
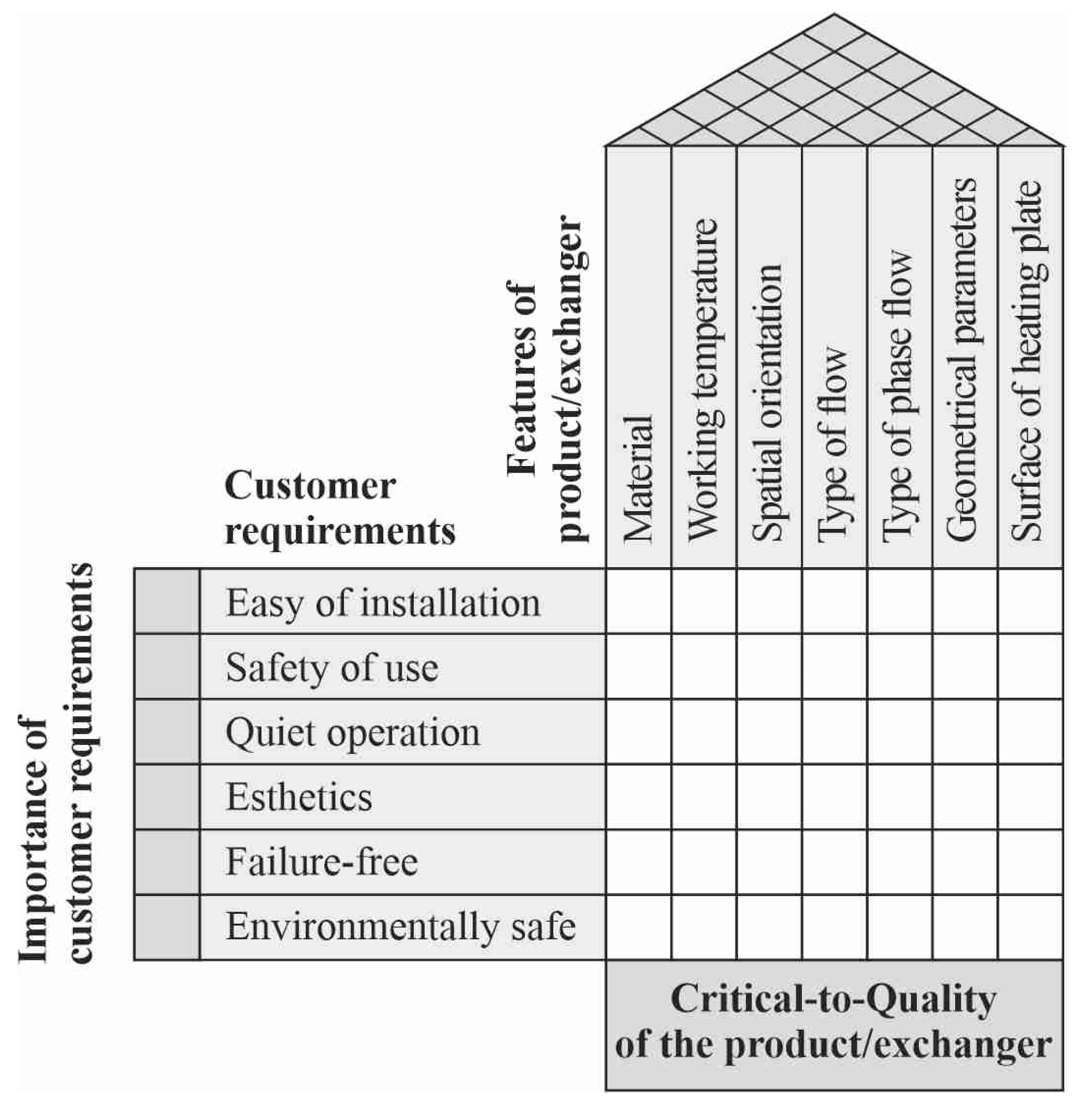
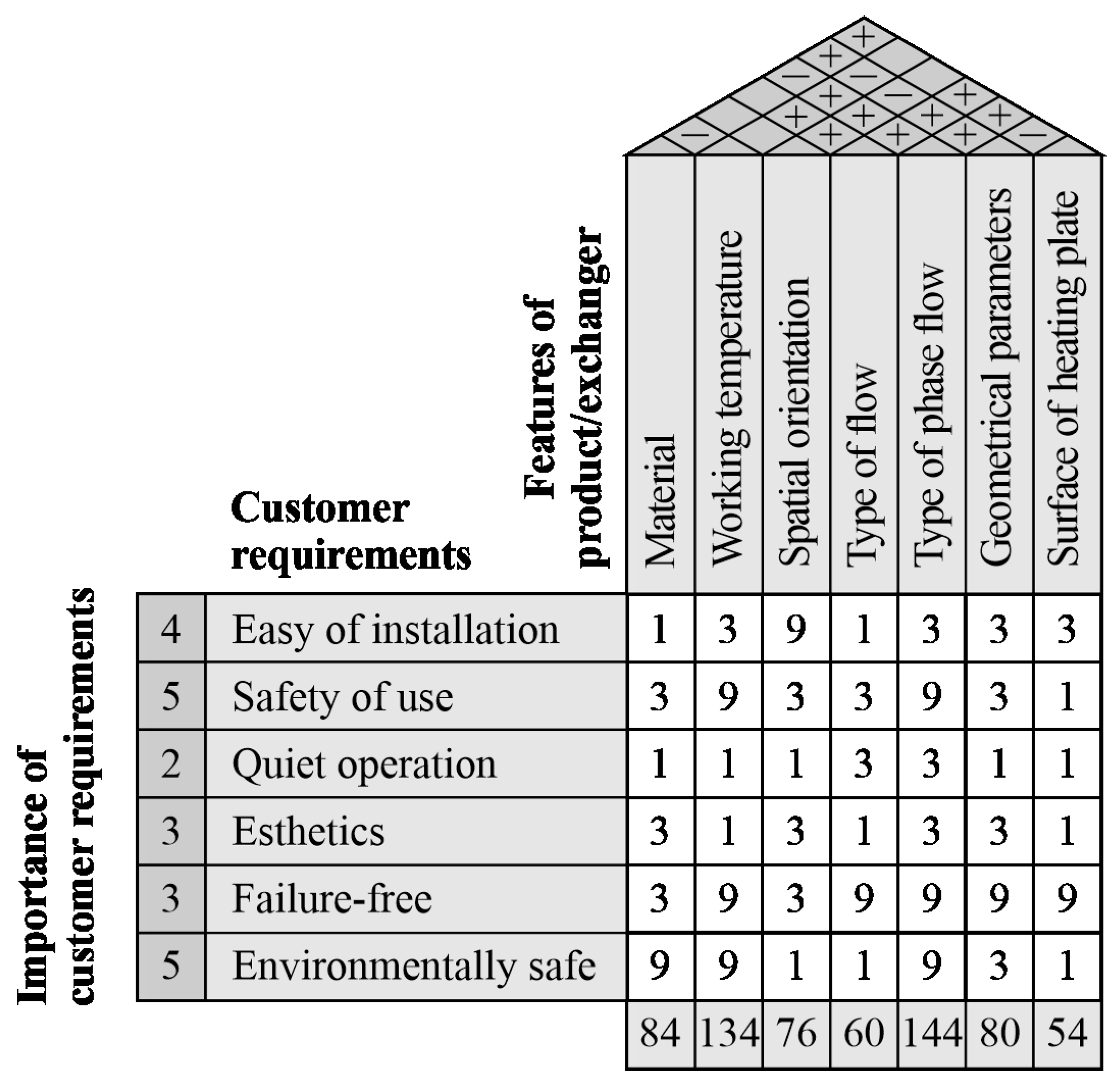
5.2. Main HOQ Matrix
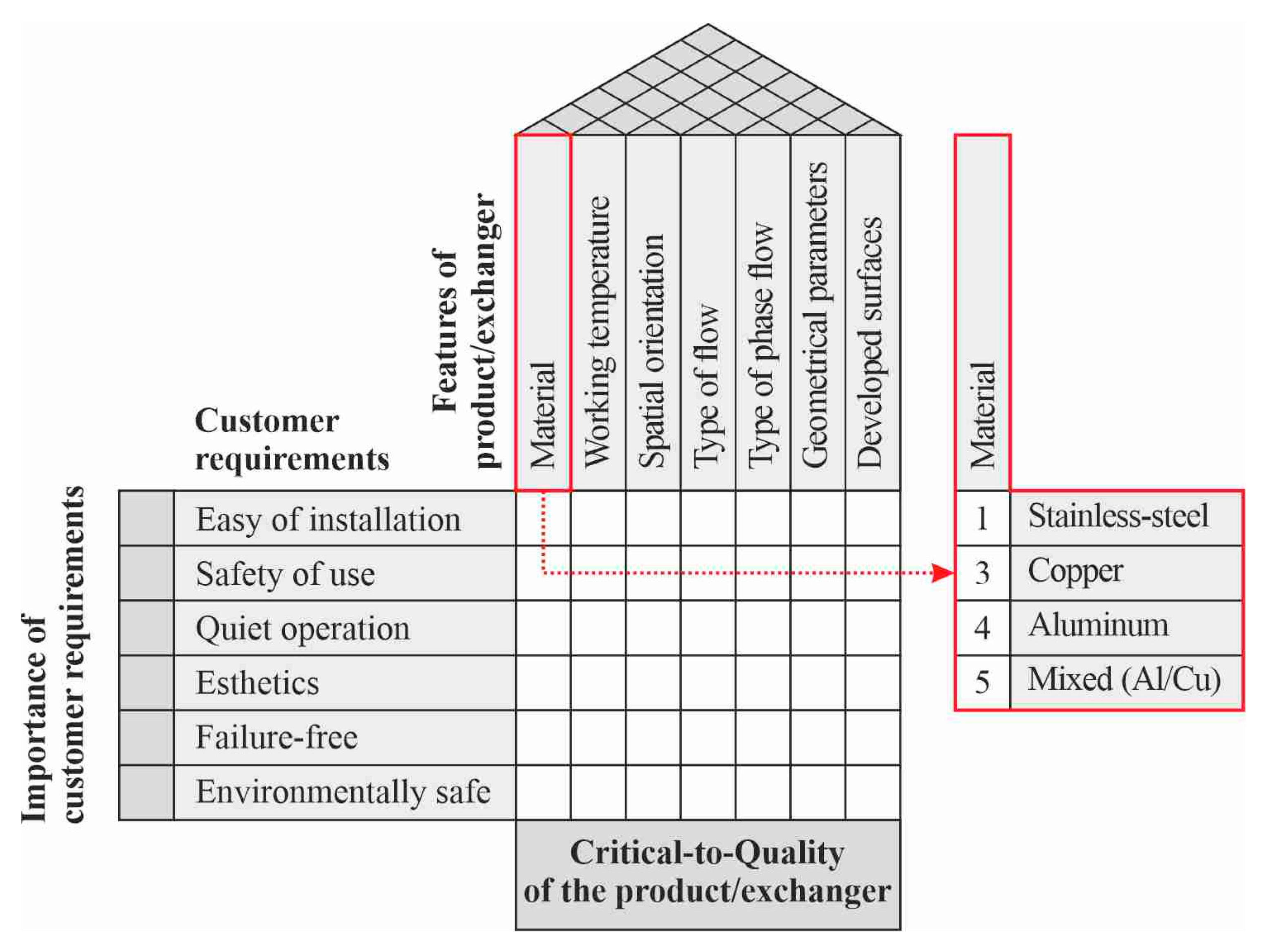
5.3. Feature of a Compact Heat Exchanger: Material
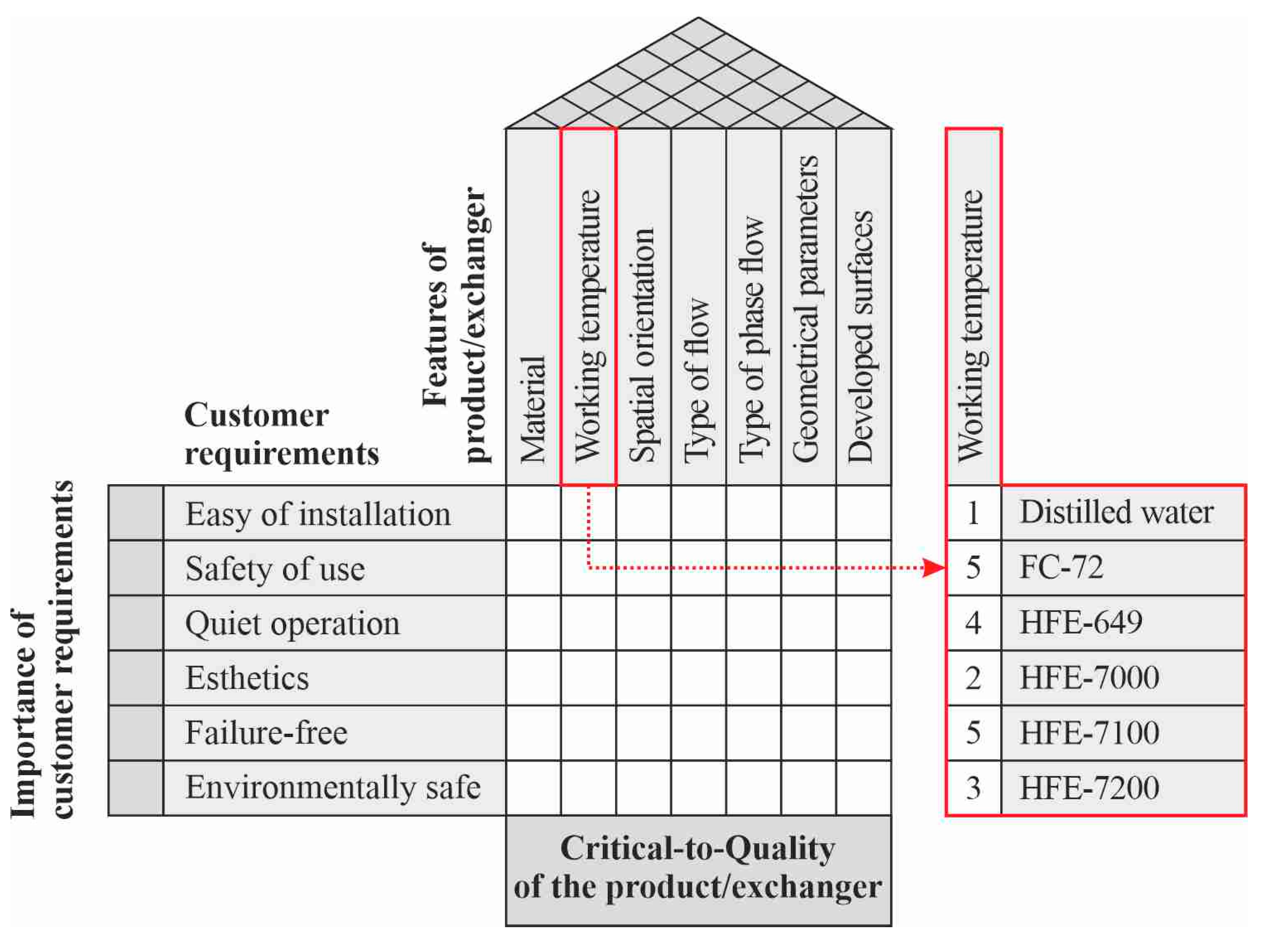
5.4. Feature of a Compact Heat Exchanger: Working Temperature
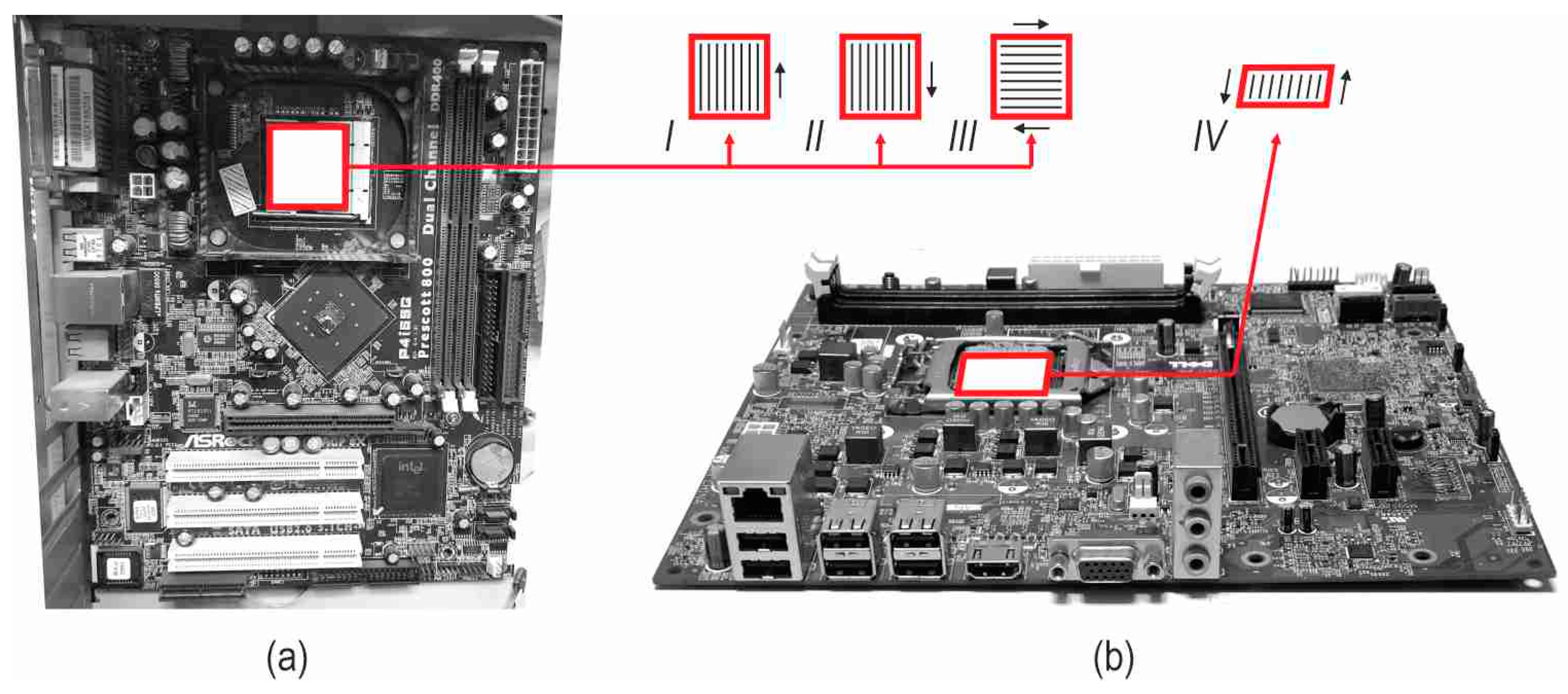
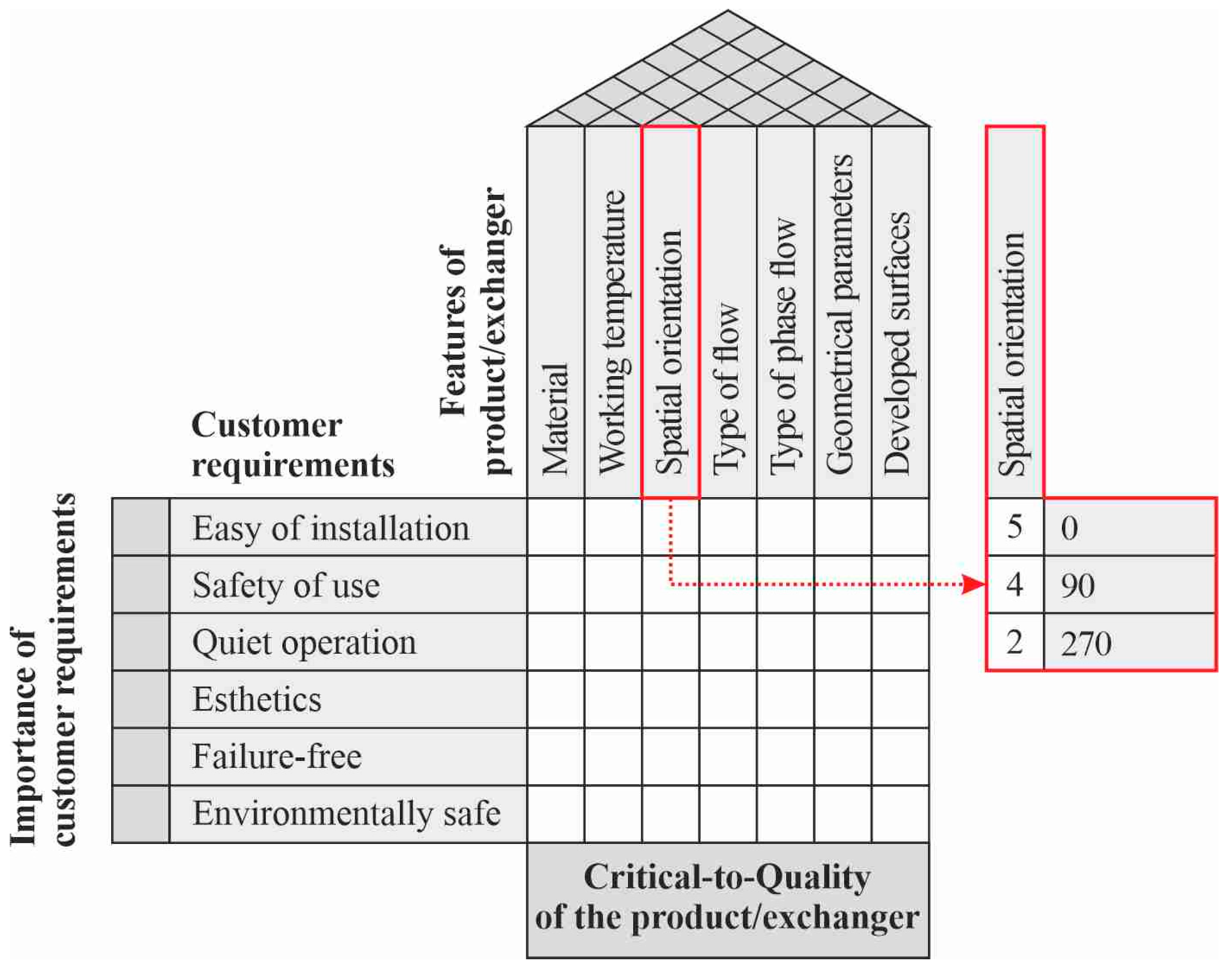
5.5. Feature of a Compact Heat Exchanger: Spatial Orientation
5.6. Feature of a Compact Heat Exchanger: Type of Flow
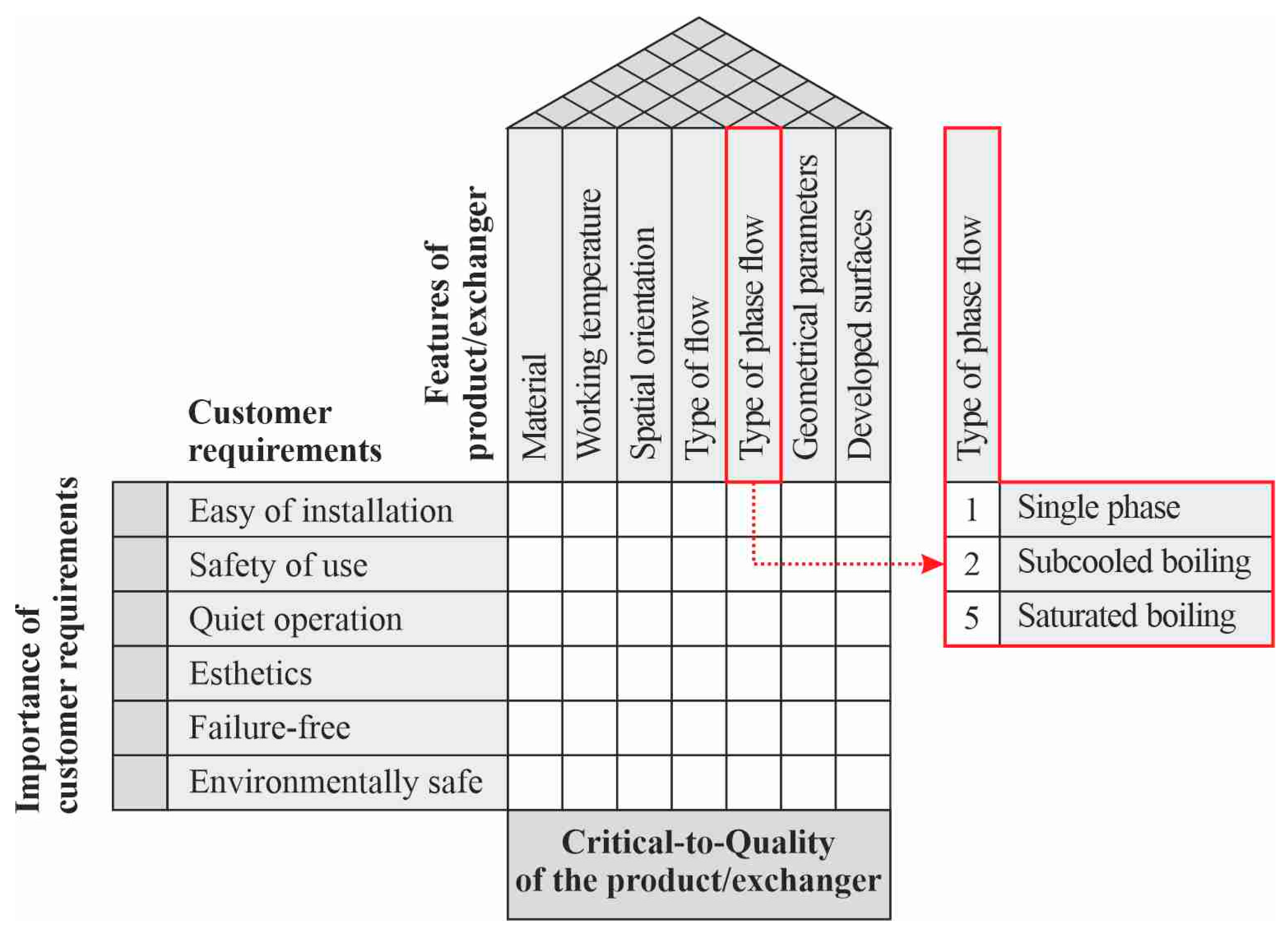
5.7. Feature of a Compact Heat Exchanger: Type of Phase Flow
- If superheating of the heating surface (the difference in temperature of the heated surface and the saturation temperature of the fluid) does not occur (the value of the difference is less than 0), subcooled boiling occurs;
- When surface superheat is positive, saturated boiling takes place.
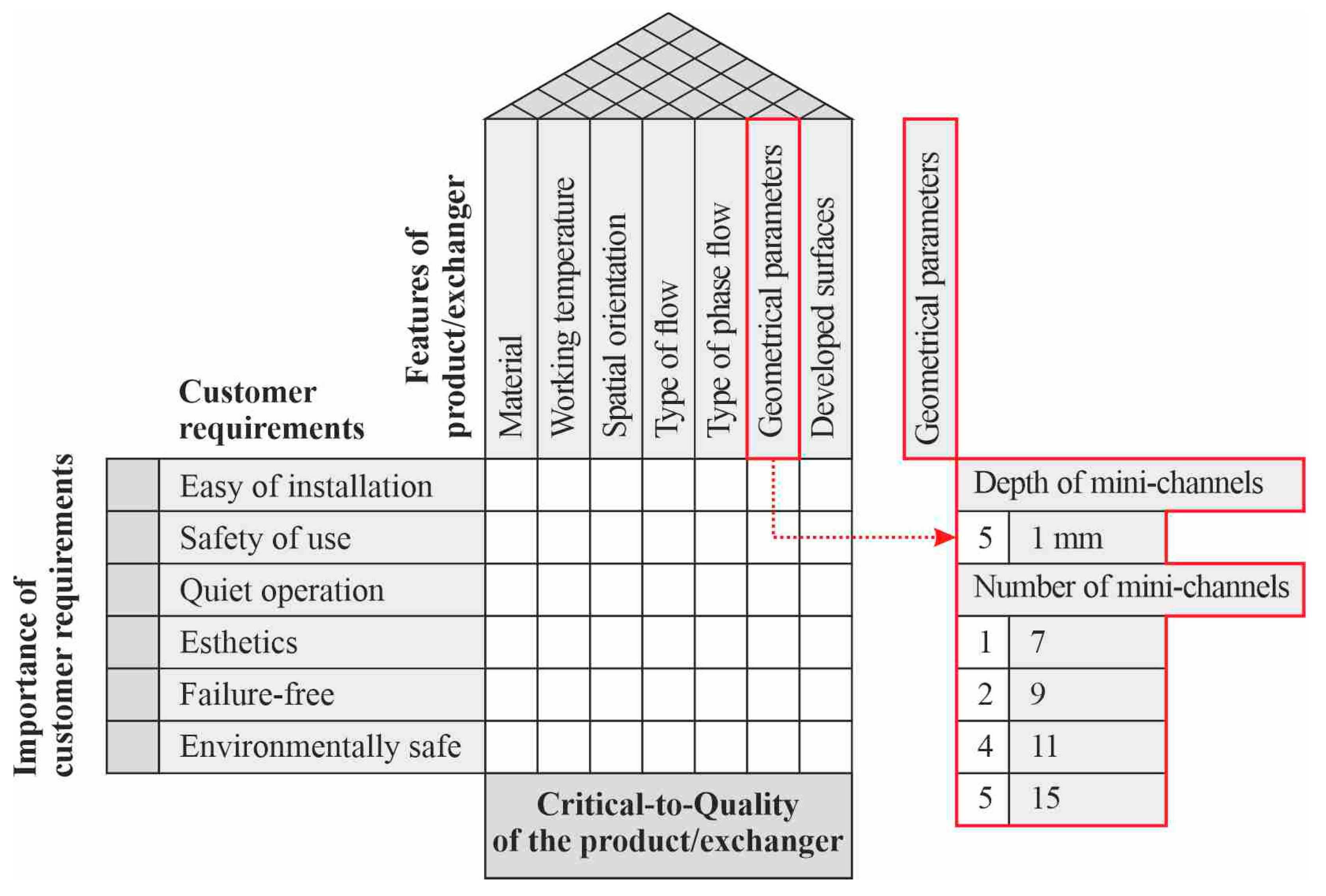
5.8. Feature of a Compact Heat Exchanger: Geometrical Parameters
5.9. Feature of a Compact Heat Exchanger: Surface of the Heating Plate
5.10. The Results of the QFD Analysis
- Material: ‘mixed’, i.e., the main construction elements of a compact heat exchanger made of aluminium and a heating plate made of copper;
- Working temperature: HFE-7100 fluid;
- Spatial orientation: horizontal position—‘0’ position;
- Type of flow: Reynolds number: 0–1000;
- Type of phase flow: saturated boiling;
- Geometrical parameters: 15 mini-channels (1 mm depth);
- Surface of heating plate: laser-textured.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| C | constant |
| cp | specific heat capacity, J kg−1 K−1 |
| CTQ | Critical-To-Quality |
| HOQ | House of Quality |
| L | mini-channel length, m |
| q | heat flux density, W m−2 |
| QFD | Quality Function Deployment |
| qV | volumetric heat flux, W m−3 |
| Ra | arithmetic mean deviation of the roughness profile, μm |
| Sa | arithmetic mean height of surface roughness, μm |
| Sp | maximum height of surface roughness, μm |
| T | temperature, K |
| v | velocity, m s−1 |
| x, y | Cartesian coordinates, m |
| Greek symbols | |
| ∇2 | Laplacian |
| α | heat transfer coefficient, W m−2 K−1 |
| accuracy | |
| δ | depth, thickness, m |
| mean relative error | |
| λ | thermal conductivity, W m−1 K−1 |
| ρ | density, kg m−3 |
| Ω | negative heat source, W m−3 |
| Subscripts | |
| ave | average |
| f | fluid |
| h | heating plate |
| pol | polynomial |
References
- Abeykoon, C. Compact Heat Exchangers—Design and Optimization with CFD. Int. J. Heat Mass Transf. 2020, 146, 118766. [Google Scholar] [CrossRef]
- Benallou, A. Heat Exchangers for Electronic Equipment Cooling. In Heat Exchangers; Castro Gómez, L., Velázquez Flores, V.M., Navarrete Procopio, M., Eds.; IntechOpen: London, UK, 2022; pp. 1–30. [Google Scholar]
- Mohamed, M.M.; Abd El-Baky, M.A. Air Cooling of Mini-Channel Heat Sink in Electronic Devices. J. Electron. Cool. Therm. Control 2013, 3, 49–57. [Google Scholar] [CrossRef]
- Sanjeev, K.; Singh, P.K. Effects of flow inlet angle on flow maldistribution and thermal performance of water cooled mini-channel heat sink. Int. J. Therm. Sci. 2019, 138, 504–511. [Google Scholar]
- Van de Poel, I. Methodological problems in QFD and directions for future development. Res. Eng. Des. 2007, 18, 21–36. [Google Scholar] [CrossRef]
- Mierzwa, M. Proposal of the implementation of the QFD method to improve the welding process in the chosen, really existing company X. Manag. Sys Prod. Eng. 2012, 4, 3–7. [Google Scholar]
- Andronikidis, A.; Georgiou, A.C.; Gotzamani, K.; Kamvysi, K. The application of quality function deployment in service quality management. TQM J. 2009, 21, 319–333. [Google Scholar] [CrossRef]
- Bernal, L.; Dornberger, U.; Suvelza, A.; Byrnes, T. Quality Function Deployment (QFD) for Services; International SEPT Program: Leipzig, Germany, 2009. [Google Scholar]
- Bahia, T.H.A.; Idan, A.R.; Athab, K.R. The Effect of Quality Function Deployment (QFD) in Enhancing Customer Satisfaction. Int. J. Profess Bus. Rev. 2023, 8, 18. [Google Scholar] [CrossRef]
- Verma, R.; Maher, T.; Pullman, M. Effective Product and Process Development Using Quality Function Deployment; Cornell University, School of Hotel Administration: Ithaca, NY, USA, 1998. [Google Scholar]
- Dursun, M.; Karsak, E.E.A. QFD-based fuzzy MCDM approach for supplier selection. Appl. Math. Model. 2013, 37, 5864–5875. [Google Scholar] [CrossRef]
- Zhang, X. User selection for collaboration in product development based on QFD and DEA approach. J. Intell. Manuf. 2019, 30, 2231–2243. [Google Scholar] [CrossRef]
- Cordeiro, E.C.; Barbosa, G.F.; Trabasso, L.G. A customized QFD (quality function deployment) applied to management of automation projects. Int. J. Adv. Manuf. Tech. 2016, 87, 2427–2436. [Google Scholar] [CrossRef]
- Darmawan, H.; Purba, H.H.; Rezeki, R.; Hidayat, N.; Siregar, A.R.; Retna, F.; Aisyah, S. Product development strategy with quality function deployment approach: A case study in automotive battery. Manag. Sci. Lett. 2017, 7, 601–610. [Google Scholar] [CrossRef]
- Hamidullah, R.; Akbar, S.; Noor, W. Shah & Inayatullah. QFD As a Tool for Improvement of Car Dashboard. J. Qual. Technol. Manag. 2010, 6, 1–22. [Google Scholar]
- Abu Bakari, M.S.; Hassan, M.Z.; Bakhori, S.; Daud, M.Y.M.; Sarip, S.; Ismail, Z. Improvement of universal parts for pick and place machine in semiconductor industry using QFD approach, ARPN. J. Eng. Appl. Sci. 2016, 11, 7735–7740. [Google Scholar]
- Hadi, H.A.; Purba, H.H.; Indarto, K.S.; Simarmata, R.G.P.; Putra, G.P.; Ghazali, D.; Aisyah, S. The implementation of Quality Function Deployment (QFD) in tire industry. ComTech 2017, 8, 223–228. [Google Scholar] [CrossRef]
- Jagusiak-Kocik, M. Advantages and limitations of using the QFD method in the production of copper products—Case study. In Proceedings of the 29th International Conference on Metallurgy and Materials, Brno, Czech Republic, 20–22 May 2020. [Google Scholar]
- Koleini Mamaghani, N.; Barzin, E. Application of Quality Function Deployment (QFD) to improve product design quality in school furniture. Int. J. Archit. Eng. Urban. Plan. 2019, 29, 277–287. [Google Scholar]
- Frizziero, L. A coffee machine design project through innovative methods: QFD, Value Analysis and Design for Assembly. ARPN J. Eng. Appl. Sci. 2014, 9, 1134–1139. [Google Scholar]
- Gunnam, S.C.; Eneyo, E.S. Quality Function Deployment and Value Engineering Applications in Smartphone Cost Management. Int. J. Emerg. Eng. Res. Technol. 2016, 4, 1–8. [Google Scholar]
- Rianmora, S.; Werawatganon, S. Applying Quality Function Deployment in Open Innovation Engineering. J. Open Innov. Technol. Mark. Complex. 2021, 7, 26. [Google Scholar] [CrossRef]
- Kowalska, M.; Paździor, M.; Krztoń-Maziopa, A. Implementation of QFD method in quality analysis of confectionery products. J. Intell. Manuf. 2018, 29, 439–447. [Google Scholar] [CrossRef]
- Lamers, T.L.; Milnes, D.; Goodson, K.; Ishii, K.; Pruitt, B.L. Application of a Modified Quality Function Deployment Method for MEMS. In Proceedings of the ASME 2007 International Mechanical Engineering Congress and Exposition, Seattle, WA, USA, 11–15 November 2007; pp. 159–168. [Google Scholar]
- Lamers, K.L. Components of an Improved Design Process for Micro-Electro-Mechanical System. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2008. [Google Scholar]
- Piasecka, M.; Piasecki, A.; Dadas, N. Experimental Study and CFD Modeling of Fluid Flow and Heat Transfer Characteristics in a Mini-channel Heat Sink Using Simcenter STAR-CCM+ Software. Energies 2022, 15, 536. [Google Scholar] [CrossRef]
- Haynes-230 Alloy. Available online: https://haynesintl.com/wp-content/uploads/2024/04/230-brochure.pdf (accessed on 13 May 2024).
- 3M Heat Transfer Fluids. Available online: https://www.3m.com/3M/en_US/p/c/electronics-components/specialty-fluids/heat-transfer-fluids/ (accessed on 6 November 2023).
- Piasecka, M.; Strąk, K. Boiling heat transfer during flow in vertical mini-channels with a modified heated surface. Energies 2022, 15, 7050. [Google Scholar] [CrossRef]
- Piasecka, M.; Strąk, K.; Maciejewska, B. Heat transfer characteristics during flow along horizontal and vertical minichannels. Int. J. Multiph. Flow 2021, 137, 103559. [Google Scholar] [CrossRef]
- Piasecka, M.; Hożejowska, S.; Maciejewska, B.; Pawińska, A. Time-Dependent Heat Transfer Calculations with Trefftz and Picard Methods for Flow Boiling in a Mini-Channel Heat Sink. Energies 2021, 14, 1832. [Google Scholar] [CrossRef]
- Hożejowski, L.; Hożejowska, S. Trefftz method in an in-verse problem of two-phase flow boiling in a minichannel. Eng. Anal. Bound. Elem. 2019, 98, 27–34. [Google Scholar] [CrossRef]
- Ciałkowski, M.; Olejnik, A.; Joachimiak, M.; Grysa, K.; Frąckowiak, A. Cauchy type nonlinear inverse problem in a two-layer area. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 313–331. [Google Scholar] [CrossRef]
- Maciąg, A.; Pawińska, A. The solution of nonlinear direct and inverse problems for beam by means of the Trefftz functions. Eur. J. Mech-A/Solids 2022, 92, 104476. [Google Scholar] [CrossRef]
- Piasecka, M.; Maciejewska, B.; Piasecki, A. Heat Transfer Calculations during Flow in Mini-Channels with Estimation of Temperature Uncertainty Measurements. Energies 2023, 16, 1222. [Google Scholar] [CrossRef]
- Chen, C.-C. Application of quality function deployment in the semiconductor industry: A case study. Comput. Ind. Eng. 2010, 58, 672–679. [Google Scholar] [CrossRef]
- Ishak, A.; Cinting, R.; Malik, A.F. Integration of quality function deployment (QFD) and value engineering in improving the quality of product: A literature review. In AIP Conference Proceedings; AIP Publishing: Surakatra, Indonesia, 2020. [Google Scholar]
- Piasecki, A. Design of Compact Heat Exchangers with the Use of Quality Management Methods. Ph.D. Thesis, Kielce University of Technology, Kielce, Poland, 2023. (In Polish). [Google Scholar]
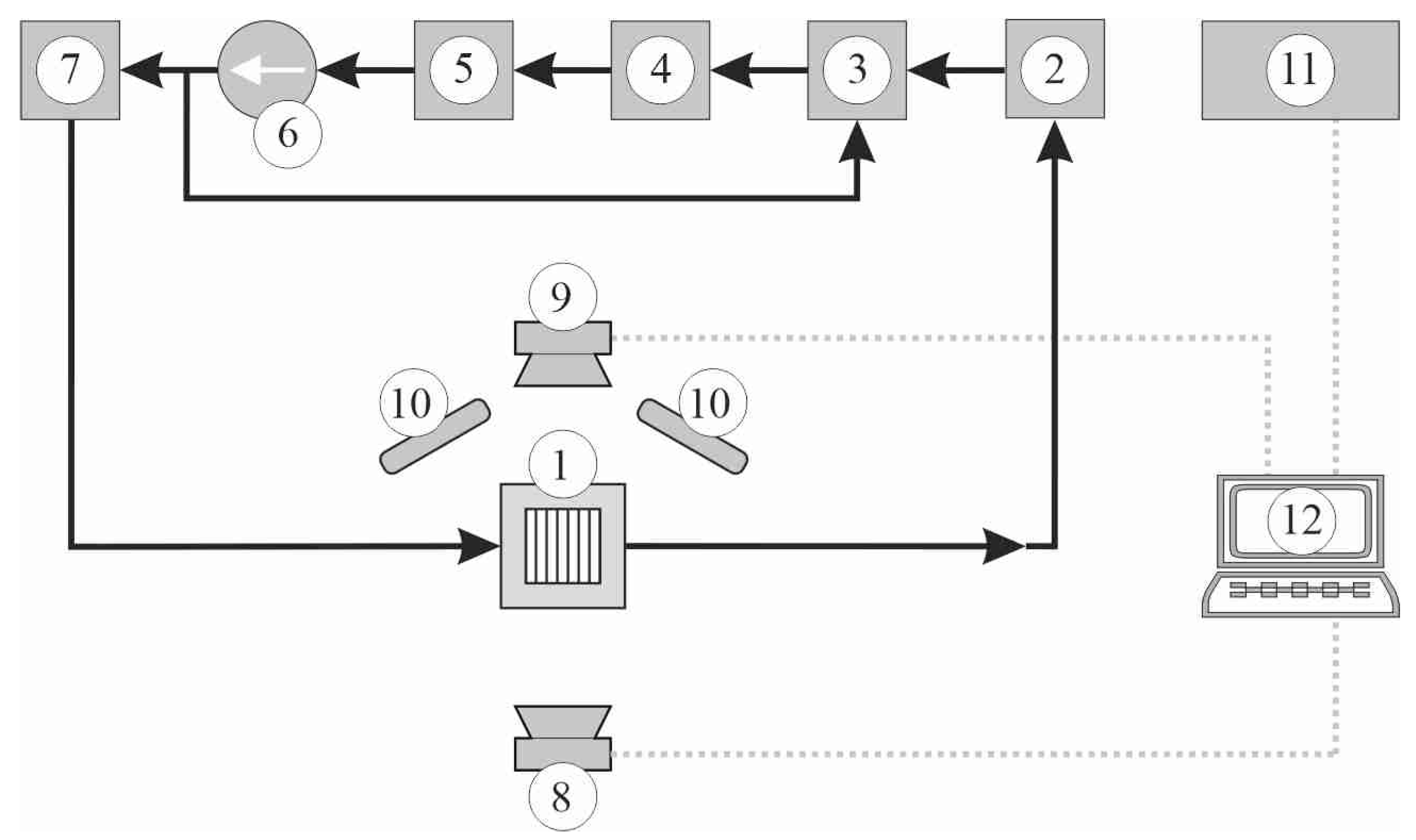




| Loop or system/device | Model of the device (manufacturer, city, country) |
| Flow loop | |
| Circulating pump | Tuthill DGS.99EEET2MM00000 (Tuthill Pump Group, Alsip, IL, USA) |
| Coriolis mass flow meter | Endress+Hauser Proline Promass A 100 (Endress+Hauser Polska, Wroclaw, Poland) |
| Pressure meters | Endress+Hauser Cerabar S PMP71, (Endress+Hauser Polska, Wroclaw, Poland) |
| Data acquisition system | |
| Data acquisition station | IOTech DaqLab 2005 (Measurement Computing, Norton, MA, USA) |
| Data acquisition station | MCC USB SC-1608G (Measurement Computing, Norton, MA, USA) |
| Temperature acquisition subsystem | |
| Infrared camera | FLIR A655SC (FLIR Systems Inc., Wilsonville, OR, USA) |
| Thermocouple | K-type thermocouple with a sensor diameter of 0.5 mm (Czaki Thermo-Product, Raszyn-Rybie, Poland) |
| Image acquisition subsystem | |
| High-speed camera | JAI SP-5000M-CXP2 (JAI Ltd., Yokohama, Kanagawa, Japan) |
| Electrical subsystem | |
| Inverter welder | Spartus ARC ZX7-400B (Spartus, Miszewko, Poland) |
| Shunt | Lumel B2-060400AB0100MA (Lumel, Zielona Gora, Poland) |
| Ammeter | Dataforth 8B32-01 (Dataforth Corp., Tucson, AZ, USA) + USB SC-1608G (Measurement Computing, Norton, MA, USA) |
| Voltmeter | Dataforth 8B40-01 (Dataforth Corp., Tucson, AZ, USA) + USB SC-1608G (Measurement Computing, Norton, MA, USA) |
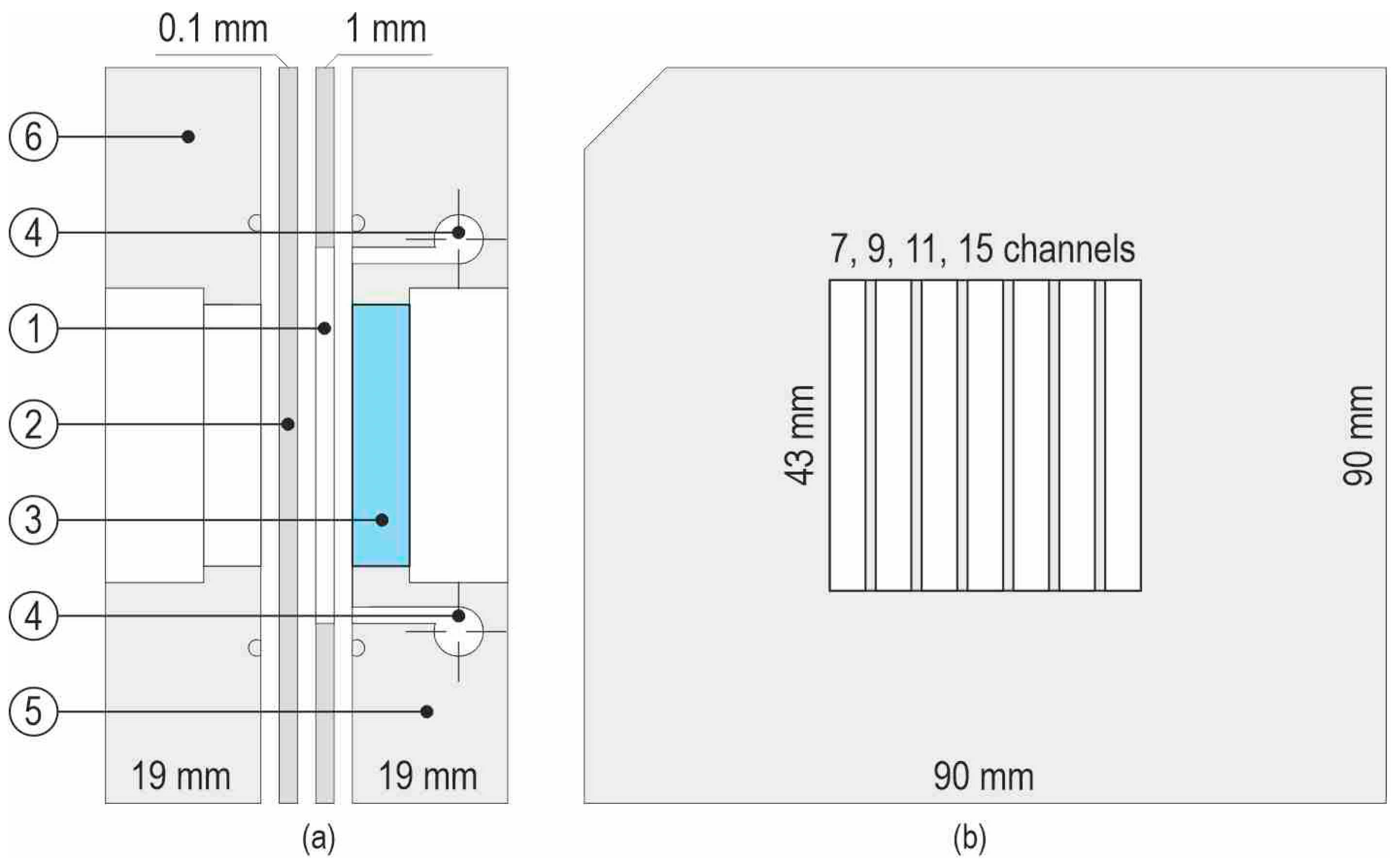
| Number of mini-channels in a group | 7 | 9 | 11 | 15 |
| Dimensions of each mini-channel in a group (mm) | ||||
| Length | 43 | 43 | 43 | 43 |
| Depth | 1 | 1 | 1 | 1 |
| Width | 4 | 3.3 | 2 | 1.6 |
| Fluid, Manufacturer | Boiling Point, K | Thermal Conductivity, W/(m·K) | Density, kg/m3 | Specific Heat, J/(kg K) | Expansion Coefficient (1/K) | Dynamic Viscosity, kg/(m s) | Surface Tension, N/m |
|---|---|---|---|---|---|---|---|
| FC-72 3M Center, St. Paul, MN, USA | 329 | 0.057 | 1680 | 1100 | 0.0016 | 0.00064 | 0.012 |
| HFE-649, 3M Center, St. Paul, MN, USA | 322 | 0.059 | 1600 | 1103 | 0.0018 | 0.00064 | 0.0108 |
| HFE-7000, 3M Center, St. Paul, MN, USA | 307 | 0.075 | 1400 | 1300 | 0.0022 | 0.00045 | 0.0124 |
| HFE-7100. 3M Center, St. Paul, MN, USA | 334 | 0.069 | 1510 | 1183 | 0.0018 | 0.00058 | 0.0136 |
| HFE-7200, 3M Center, St. Paul, MN, USA | 349 | 0.068 | 1430 | 1214 | 0.0016 | 0.00061 | 0.0136 |
| Distilled water | 373 | 0.591 | 998.2 | 4187 | 0.0021 | 0.001002 | 0.0728 |
| Surfaces/ Parameters | Smooth | Laser-Textured | Laser-Vibrating Textured | Electro-Erosion Textured | Fibrous | Powder |
|---|---|---|---|---|---|---|
| Arithmetic mean deviation of the roughness profile, Ra | 0.175 | 1.027 | 1.364 | 0.615 | 22.613 | 11.283 |
| Arithmetic mean height of surface roughness, Sa | 0.346 | 0.558 | 1.906 | 0.983 | 31.758 | 13.919 |
| Maximum height of surface roughness, Sp | 3.643 | 9.429 | 9.200 | 10.115 | 155.28 | 59.922 |
| Experimental Parameter (Device, Type; Manufacturer) | Error |
|---|---|
| Temperature of the heated plate (infrared camera, A655sc, FLIR; FLIR Systems Inc., Wilsonville, OR, USA) | ±2 °C or ±2% of the reading, −20 ÷ 120 °C |
| Pressure of the fluid at the inlet to the test section (gauge pressure meter, Cerabar S PMP71, Endress+Hauser; Endress+Hauser Polska, Wroclaw, Poland) | ±0.05% of the reading in the range, 0 ÷ 10 bar |
| Atmospheric pressure (absolute pressure meter, A-10, WIKA; WIKA Polska, Wloclawek, Poland) | 0.5% of the full scale, 0 ÷ 2.5 bar |
| Mass flow rate (Coriolis mass flow meter, Proline Promass A100, Endress+Hauser; Endress+Hauser Polska, Wroclaw, Poland) | ±0.1% of the reading, 0 ÷ 0.125 kg/s |
| Temperature of the working fluid (thermocouple, K-type; Czaki Thermo-Product, Raszyn Rybie, Poland) | ±1.5 °C in the range of −40 ÷ 375 °C, according to the applicable standard |
| Parameters, Unit | Value |
|---|---|
| Temperature of FC-72 at the inlet, K | 287.55 |
| Temperature of ambient air, K | 293.15 |
| Atmospheric pressure, kPa | 101.32 |
| Inlet overpressure, kPa | 101.38 |
| Outlet overpressure, kPa | 101.28 |
| Mass flow rate, kg/h | 20.76 |
| Heat flux supplied to the heating plate, W | 64.00 |
| Parameters, Unit | Range of the Parameter |
|---|---|
| Temperature of FC-72 at the inlet, K | 287–292 |
| Temperature of FC-72 at the outlet, K | 289–323 |
| Temperature of ambient air, K | 293.15 |
| Inlet overpressure, kPa | 6–57 |
| Heat flux, kW/m2 | 19.5–139 |
| Mass flow rate, kg/h | 20.6–21.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piasecki, A.; Hożejowska, S.; Masternak-Janus, A.; Piasecka, M. Using Quality Function Deployment to Assess the Efficiency of Mini-Channel Heat Exchangers. Energies 2024, 17, 2436. https://doi.org/10.3390/en17102436
Piasecki A, Hożejowska S, Masternak-Janus A, Piasecka M. Using Quality Function Deployment to Assess the Efficiency of Mini-Channel Heat Exchangers. Energies. 2024; 17(10):2436. https://doi.org/10.3390/en17102436
Chicago/Turabian StylePiasecki, Artur, Sylwia Hożejowska, Aneta Masternak-Janus, and Magdalena Piasecka. 2024. "Using Quality Function Deployment to Assess the Efficiency of Mini-Channel Heat Exchangers" Energies 17, no. 10: 2436. https://doi.org/10.3390/en17102436
APA StylePiasecki, A., Hożejowska, S., Masternak-Janus, A., & Piasecka, M. (2024). Using Quality Function Deployment to Assess the Efficiency of Mini-Channel Heat Exchangers. Energies, 17(10), 2436. https://doi.org/10.3390/en17102436







