AC Direct Charging for Electric Vehicles via a Reconfigurable Cascaded Multilevel Converter
Abstract
1. Introduction
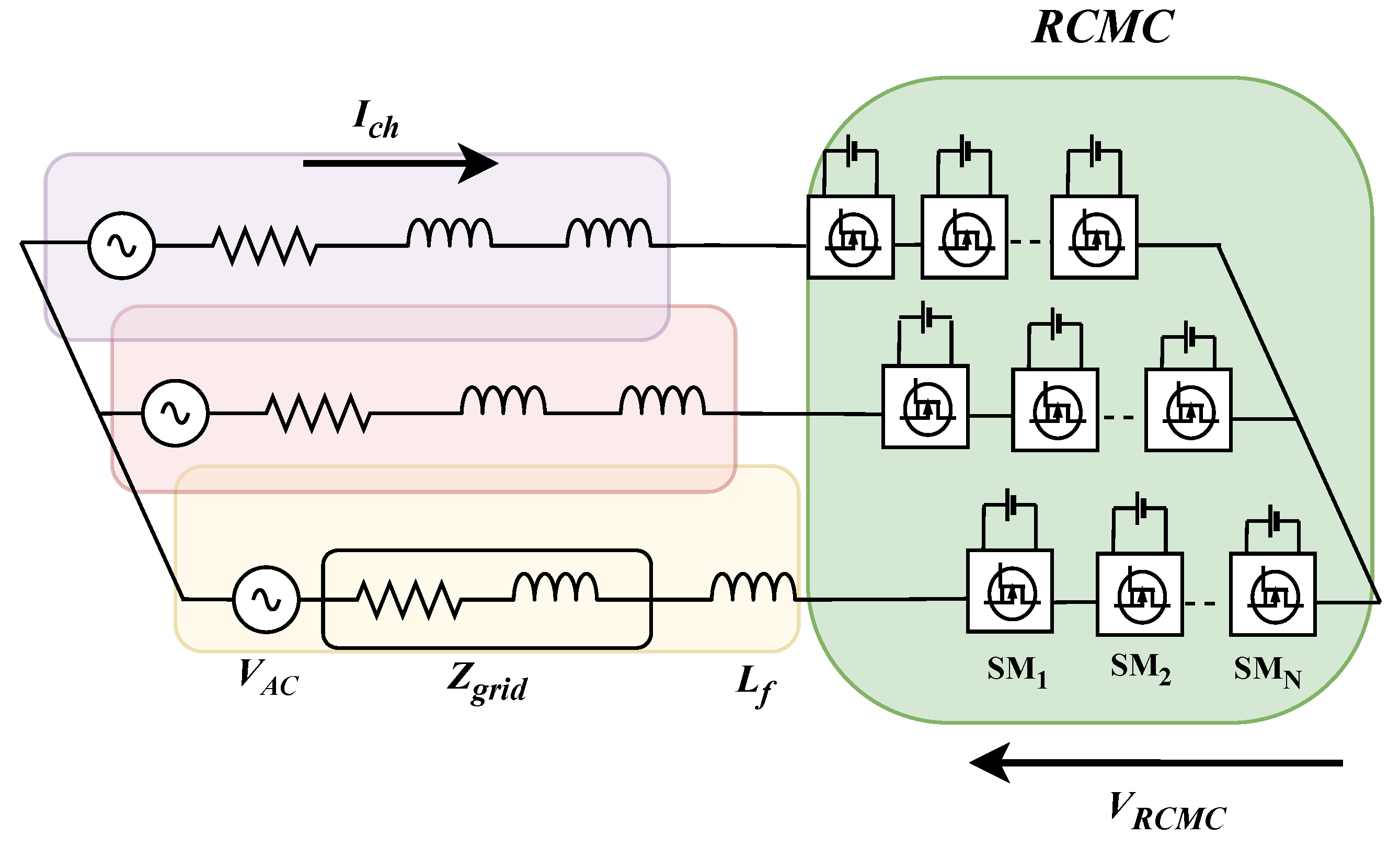
2. Overview of Reconfigurable Cascaded Multilevel Converter
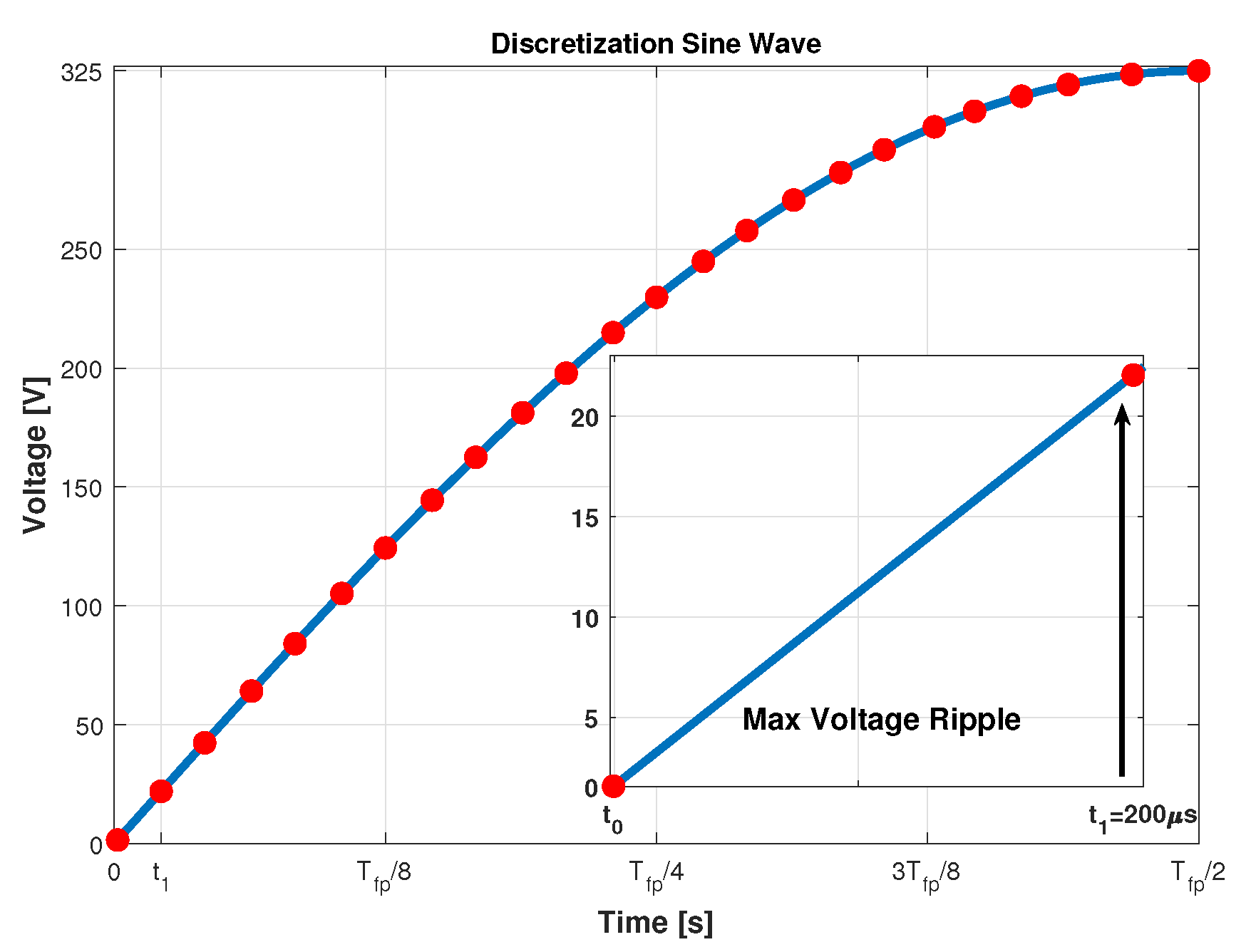
3. AC System Requirement and Filter Design
- Galvanic isolation between the power grid and the battery;
- Minimal additional hardware;
- Adherence to specified harmonic limits for grid current quality with a power factor larger than 0.9;
- Absence of stress or rotor movement on the motor;
- Bidirectional functionalities to enable Vehicle-to-Grid (V2G) capability;
- The capability to execute either Constant Current (CC) or Constant Voltage (CV) protocols.
Filter Design
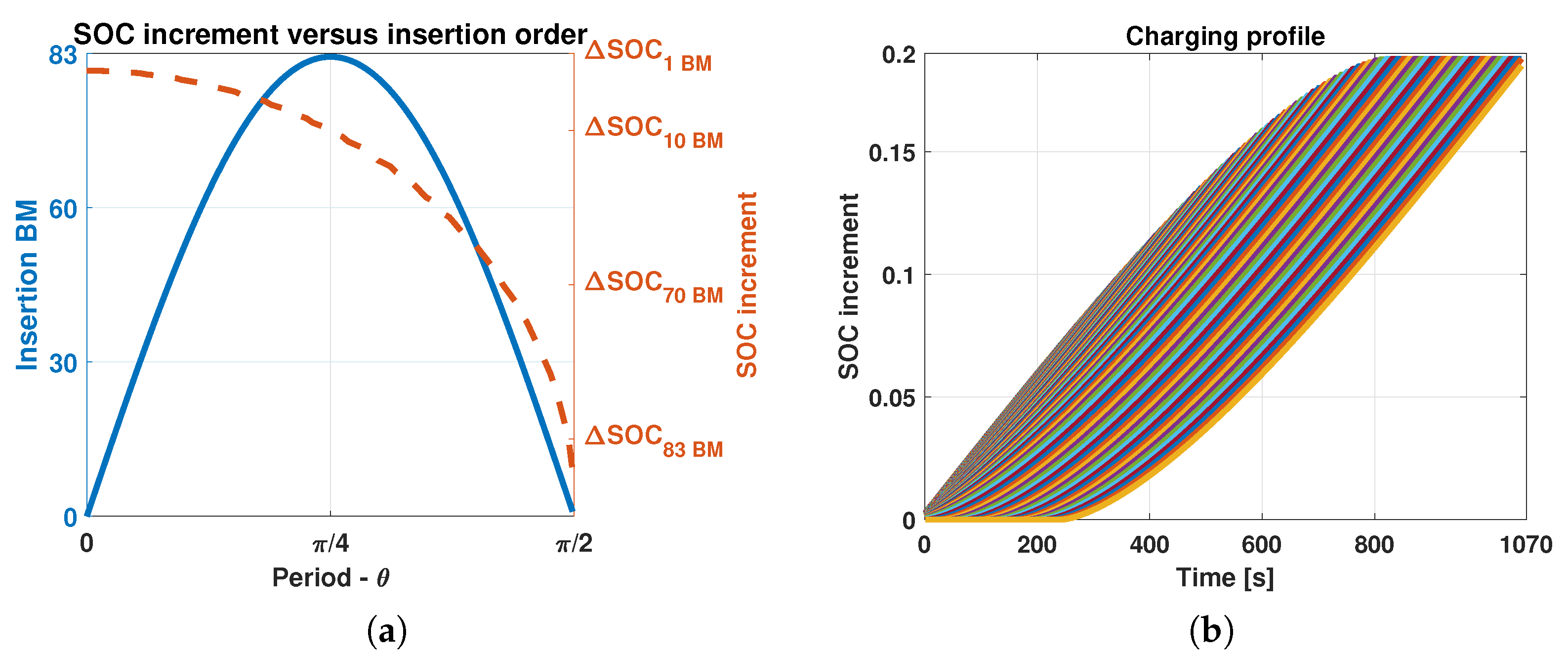
4. Charging Control and Algorithm
4.1. Charging Algorithms
- SOC balancing prioritization: Battery cells are inserted in ascending order based on their SOC, disregarding their position within the converter.
- Loss reduction prioritization: The average SOC of battery cells within each submodule is calculated. A progressive insertion is carried out by selecting battery cells installed within the less charged submodules.
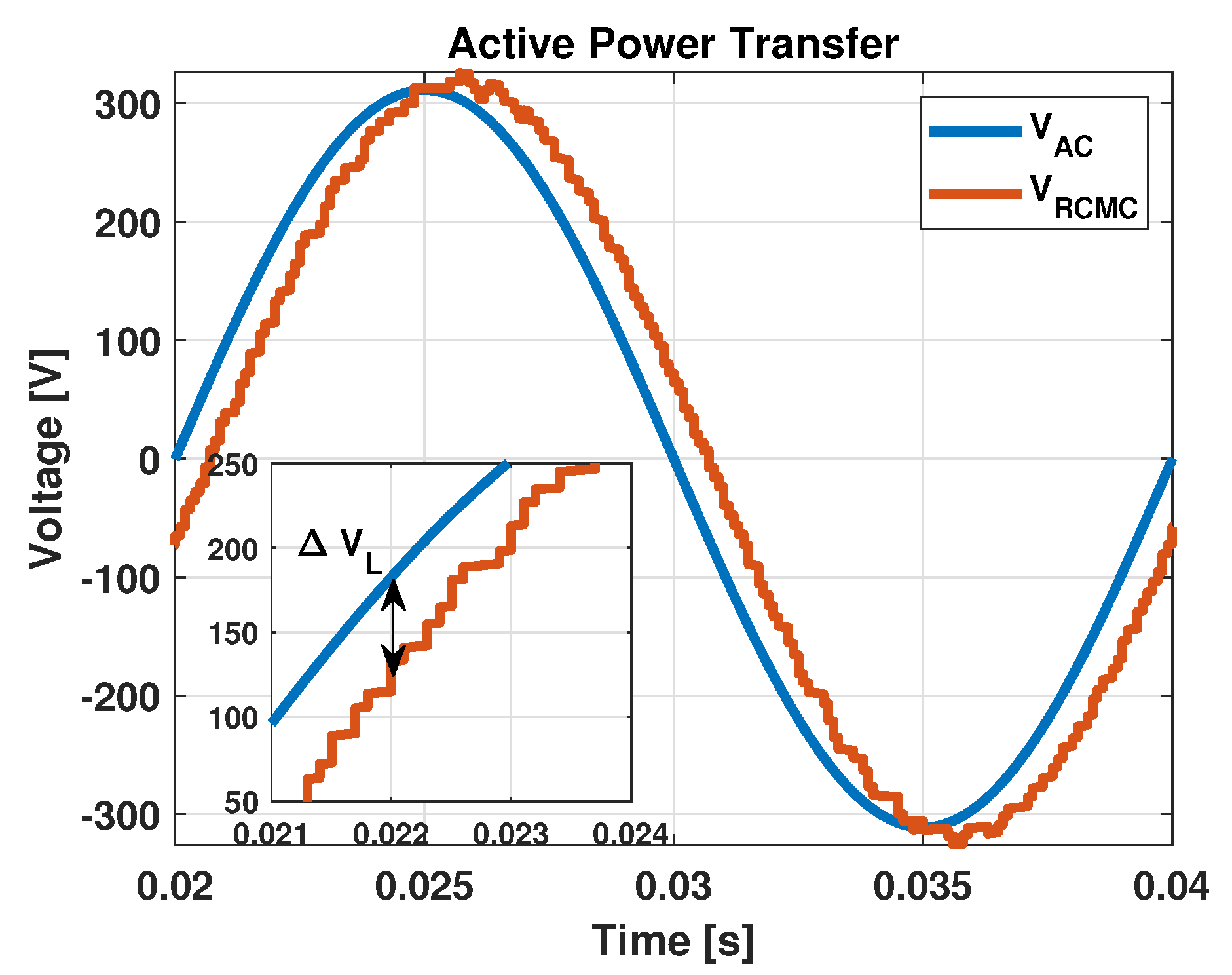
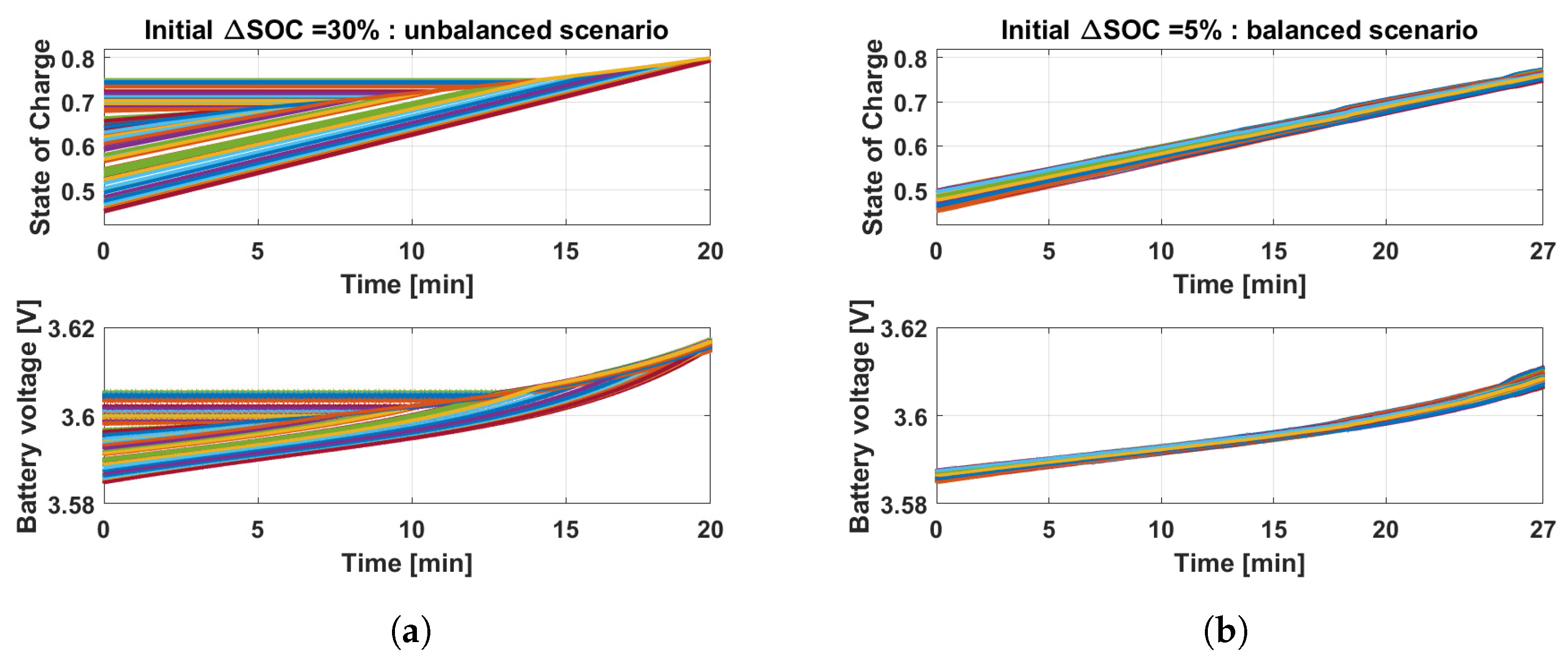
4.2. Simulation Results
5. Charging Time Comparison between the RCMC and Conventional Battery Pack
5.1. Conventional Battery Pack
5.2. RCMC
- The considered battery pack aligns with the contemporary trend of elevating the DC link voltage. If a conventional 400 V battery pack had been the focus, the charging time would have been 1.5 times longer, elevating the RCMC in terms of market competition.
- The battery pack assumes the integration of an additional stage to elevate the DC voltage to 627 V, assuming that the voltage grid is rectified. Conversely, the RCMC facilitates a direct connection to the AC system, featuring prior galvanic isolation.
- Typically, battery cells are not charged from a balanced starting point. In the case of RCMC, the charging process can start directly from unbalanced scenarios. Conversely, the Battery Management System (BMS) usually needs to passively enforce the balancing scenario in the battery pack, increasing power losses.
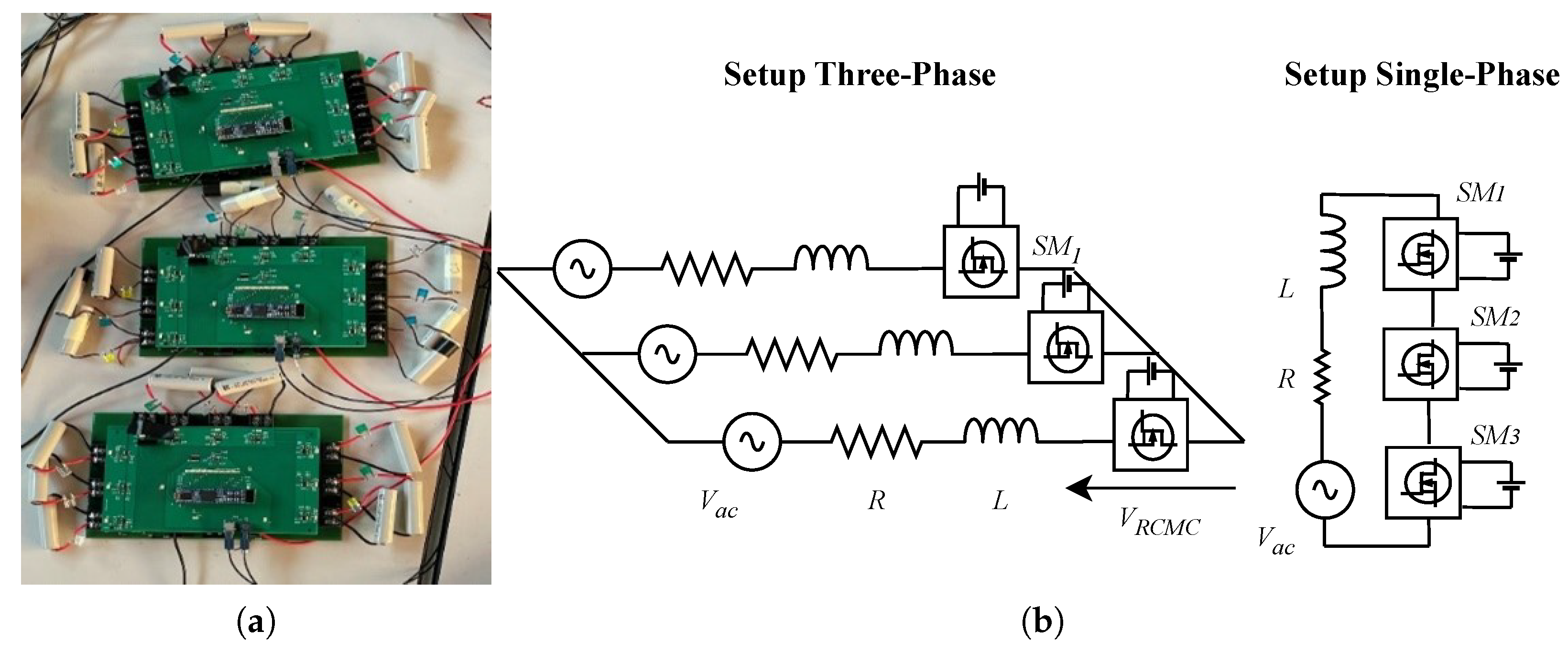
6. Experimental Activities
6.1. Control Architecture
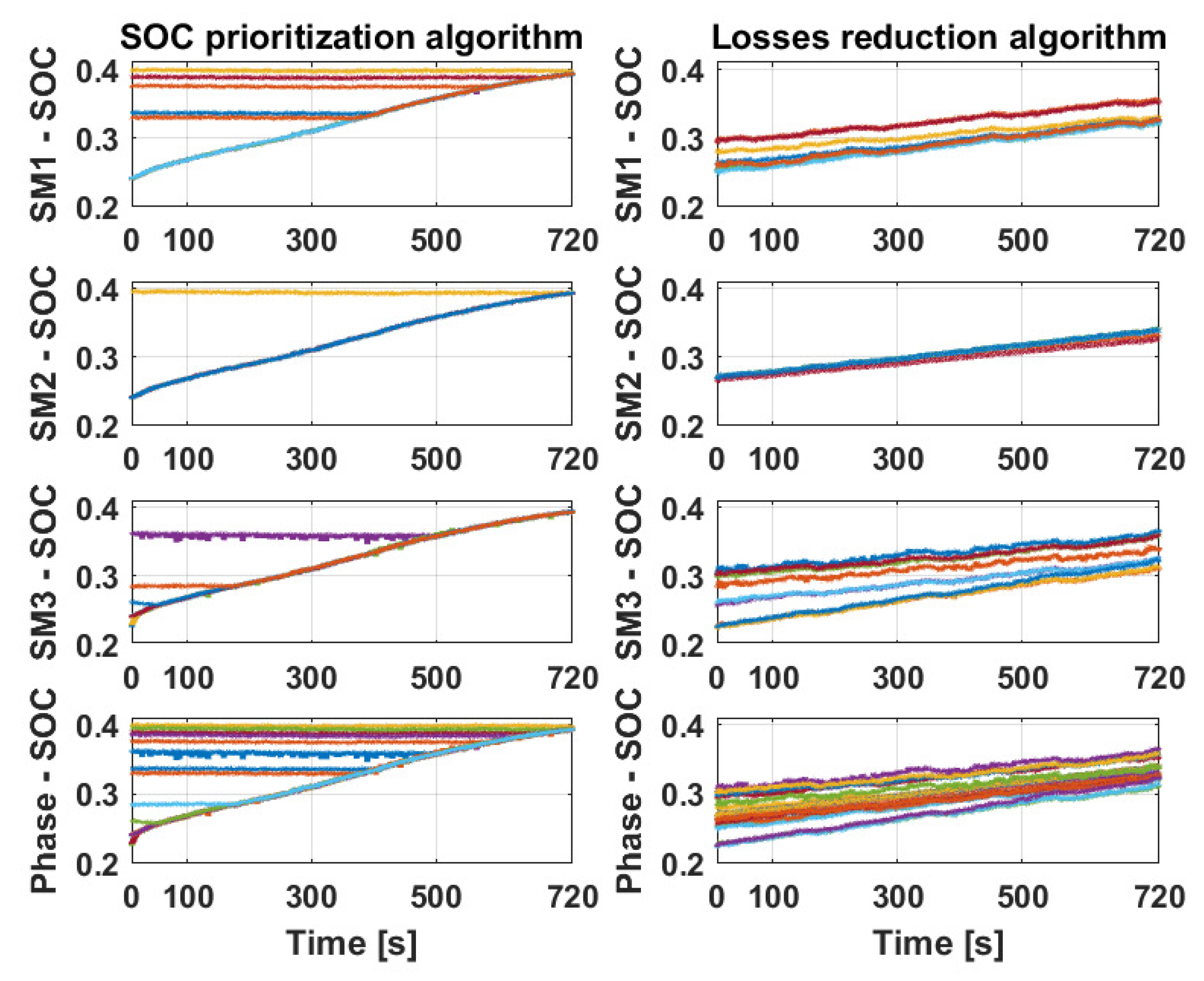
6.2. Experimental Results
- Firstly, the three submodules are connected in a three-phase configuration to validate the feasibility of the charging process performed directly from the AC system. In this case, the SOC prioritization algorithm can be only adopted, because the number of submodules is limited to one per phase.
- Secondly, the three submodules are connected in series to replicate a single-phase converter. This setup is used to test and validate the SOC and loss reduction prioritization algorithms.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOAJ | directory of open access journals |
| TLA | three-letter acronym |
| LD | linear dichroism |
References
- International Energy Agency. CO2 Emissions in 2023: A New Record High, but Is There Light at the End of the Tunnel? 2024. Available online: https://www.iea.org/reports/co2-emissions-in-2023 (accessed on 10 May 2024).
- Krishna, G. Understanding and identifying barriers to electric vehicle adoption through thematic analysis. Transp. Res. Interdiscip. Perspect. 2021, 10, 100364. [Google Scholar] [CrossRef]
- InsideClimate News. Electric Vehicles: Global Investment in the Energy Transition Soars. 2024. Available online: https://insideclimatenews.org/news/30012024/electric-vehicles-global-investment/#:~:text=Global%20investment%20in%20the%20energy,an%20increase%20of%2036%20percent (accessed on 10 May 2024).
- Srdic, S.; Lukic, S. Toward Extreme Fast Charging: Challenges and Opportunities in Directly Connecting to Medium-Voltage Line. IEEE Electrif. Mag. 2019, 7, 22–31. [Google Scholar] [CrossRef]
- IEEE Std 2030.1.1-2015; IEEE Standard Technical Specifications of a DC Quick Charger for Use with Electric Vehicles. IEEE: Piscataway, NJ, USA, 2016; pp. 1–97. [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Wang, L.; Qin, Z.; Slangen, T.; Bauer, P.; van Wijk, T. Grid Impact of Electric Vehicle Fast Charging Stations: Trends, Standards, Issues and Mitigation Measures—An Overview. IEEE Open J. Power Electron. 2021, 2, 56–74. [Google Scholar] [CrossRef]
- Hariri, R.; Sebaaly, F.; Ibrahim, C.; Williamson, S.; Kanaan, H.Y. A Survey on Charging Station Architectures for Electric Transportation. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Metwly, M.Y.; Maximos, F.A.; Ahmed, A.T.; Hawam, A.S.; Zaki, A.A.-M.; Helal, A.A.-M.; Mokhtar, A.-R.M.; Abdelghaffar, S.M.; Taha, R.A.; Hamdy, R.A.; et al. Design Case Study of A Nine-Phase Integrated On-Board Battery Charger. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 815–821. [Google Scholar] [CrossRef]
- Shi, C.; Tang, Y.; Khaligh, A. A Single-Phase Integrated Onboard Battery Charger Using Propulsion System for Plug-in Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 10899–10910. [Google Scholar] [CrossRef]
- Loudot, S.; Briane, B.; Ploix, O.; Villeneuve, A. Fast Charging Device for an Electric Vehicle. U.S. Patent 20120286740A1, 15 December 2012. [Google Scholar]
- Metwly, M.Y.; Abdel-Majeed, M.S.; Abdel-Khalik, A.S.; Hamdy, R.A.; Hamad, M.S.; Ahmed, S. A Review of Integrated On-Board EV Battery Chargers: Advanced Topologies, Recent Developments and Optimal Selection of FSCW Slot/Pole Combination. IEEE Access 2020, 8, 85216–85242. [Google Scholar] [CrossRef]
- Poorfakhraei, A.; Narimani, M.; Emadi, A. A Review of Multilevel Inverter Topologies in Electric Vehicles: Current Status and Future Trends. IEEE Open J. Power Electron. 2021, 2, 155–170. [Google Scholar] [CrossRef]
- Quraan, M.; Yeo, T.; Tricoli, P. Design and Control of Modular Multilevel Converters for Battery Electric Vehicles. IEEE Trans. Power Electron. 2016, 31, 507–517. [Google Scholar] [CrossRef]
- Tresca, G.; Formentini, A.; Riccio, J.; Anglani, N.; Zanchetta, P. A Reconfigurable Cascaded Multilevel Converter for EV Powertrain. IEEE Trans. Ind. Appl. 2023, 60, 3332–3344. [Google Scholar] [CrossRef]
- Han, W.; Wik, T.; Kersten, A.; Dong, G.; Zou, C. Next-Generation Battery Management Systems: Dynamic Reconfiguration. IEEE Ind. Electron. Mag. 2020, 14, 20–31. [Google Scholar] [CrossRef]
- Ronanki, D.; Williamson, S.S. Modular Multilevel Converters for Transportation Electrification: Challenges and Opportunities. IEEE Trans. Transp. Electrif. 2018, 2, 399–407. [Google Scholar] [CrossRef]
- Policy Department for Structural and Cohesion Policies, Directorate-General for Internal Policies. Environmental Challenges through the Life Cycle of Battery Electric Vehicles; European Parliament: Strasbourg, France, 2023; PE 733.112, STUDY.
- Chang, F.; Ilina, O.; Lienkamp, M.; Voss, L. Improving the Overall Efficiency of Automotive Inverters Using a Multilevel Converter Composed of Low Voltage Si mosfets. IEEE Trans. Power Electron. 2019, 34, 3586–3602. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, K.; Xu, L.; Li, Y. A Hybrid Cascaded Multilevel Converter for Battery Energy Management Applied in Electric Vehicles. IEEE Trans. Power Electron. 2014, 29, 3537–3546. [Google Scholar] [CrossRef]
- Gemma, F.; Tresca, G.; Formentini, A.; Zanchetta, P. Balanced Charging Algorithm for CHB in an EV Powertrain. Energies 2023, 16, 5565. [Google Scholar] [CrossRef]
- Tresca, G.; Formentini, A.; Granata, S.; Leuzzi, R.; Zanchetta, P. Direct AC charging of EV Reconfigurable Cascaded Multilevel Converter. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Tu, Q.; Xu, Z. Impact of Sampling Frequency on Harmonic Distortion for Modular Multilevel Converter. IEEE Trans. Power Deliv. 2011, 26, 298–306. [Google Scholar] [CrossRef]
- Deng, Y.; Harley, R.G. Space-Vector Versus Nearest-Level Pulse Width Modulation for Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 2962–2974. [Google Scholar] [CrossRef]
- Kouro, S.; Bernal, R.; Miranda, H.; Silva, C.A.; Rodriguez, J. High-Performance Torque and Flux Control for Multilevel Inverter Fed Induction Motors. IEEE Trans. Power Electron. 2007, 22, 2116–2123. [Google Scholar] [CrossRef]
- IEC 61851-1:2017-02; Electric Vehicle Conductive Charging System. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- Tresca, G.; Leuzzi, R.; Formentini, A.; Rovere, L.; Anglani, N.; Zanchetta, P. Reconfigurable Cascaded Multilevel Converter: A New Topology For EV Powertrain. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 1454–1460. [Google Scholar] [CrossRef]
- What Is an EV Battery State of Charge (SOC)? 2023. Available online: https://www.evengineeringonline.com/what-is-an-ev-battery-state-of-charge-soc/ (accessed on 10 May 2024).
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Lahlou, T.; Abdelrahem, M.; Valdes, S.; Herzog, H.-G. Filter design for grid-connected multilevel CHB inverter for battery energy storage systems. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 831–836. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.-A. Experimental Validation of a Battery Dynamic Model for EV Applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef]
- Nassary, M.; Orabi, M.; Ghoneima, M. Discussion of Single-Stage Isolated Unidirectional AC-DC On-Board Battery Charger for Electric Vehicle. In Proceedings of the 2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 10–13 December 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Chang, W.-Y. The state of charge estimating methods for battery: A review. Int. Sch. Res. Not. 2013, 2013, 953792. [Google Scholar] [CrossRef]
- Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. A new single-phase PLL structure based on second order generalized integrator. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Galassini, A.; Lo Calzo, G.; Formentini, A.; Gerada, C.; Zanchetta, P.; Costabeber, A. uCube: Control platform for power electronics. In Proceedings of the 2017 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Nottingham, UK, 20–21 April 2017; pp. 216–221. [Google Scholar] [CrossRef]
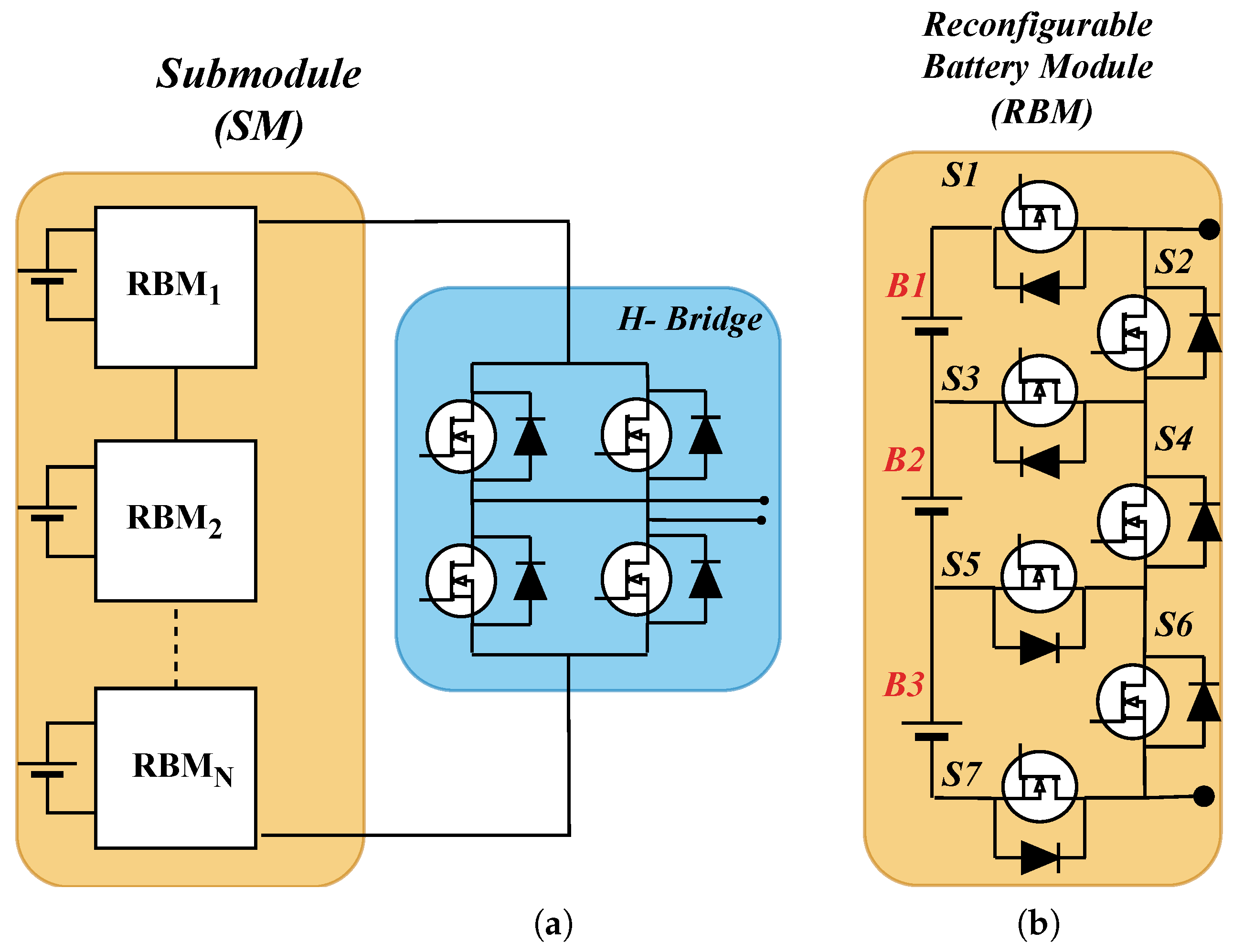


| Connected Batteries | Devices Turned On | Output Voltage |
|---|---|---|
| B1 | S1, S3, S4, S6 | |
| B2 | S2, S3, S5, S6 | |
| B3 | S2, S4, S5, S7 | |
| B1 & B2 | S1, S5, S6 | 2 |
| B2 & B3 | S2, S3, S7 | |
| B1 & B3 | Prohibited | - |
| B1 & B2 & B3 | S1, S7 | |
| None | S2, S4, S6 | 0 |
| AC system | |
| Nominal peak voltage | 325 V |
| Nominal current rms | 80 A |
| Frequency | 50 Hz |
| RCMC architecture | |
| RBM per SM | 3 |
| SM per phase | 12 |
| Battery cells per phase | 108 |
| DSP frequency | 5 kHz |
| Modulation | Nearest Level Modulation |
| Nominal voltage battery module | 3.6 V |
| Nominal peak voltage per phase | 388.8 V |
| I Algorithm | II Algorithm | |
|---|---|---|
| Initial Delta SOC 30% | 665 W | 396 W |
| Initial Delta SOC 5% | 668 W | 337 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tresca, G.; Zanchetta, P. AC Direct Charging for Electric Vehicles via a Reconfigurable Cascaded Multilevel Converter. Energies 2024, 17, 2428. https://doi.org/10.3390/en17102428
Tresca G, Zanchetta P. AC Direct Charging for Electric Vehicles via a Reconfigurable Cascaded Multilevel Converter. Energies. 2024; 17(10):2428. https://doi.org/10.3390/en17102428
Chicago/Turabian StyleTresca, Giulia, and Pericle Zanchetta. 2024. "AC Direct Charging for Electric Vehicles via a Reconfigurable Cascaded Multilevel Converter" Energies 17, no. 10: 2428. https://doi.org/10.3390/en17102428
APA StyleTresca, G., & Zanchetta, P. (2024). AC Direct Charging for Electric Vehicles via a Reconfigurable Cascaded Multilevel Converter. Energies, 17(10), 2428. https://doi.org/10.3390/en17102428






