Thermodynamic Analysis and Optimization of Binary CO₂-Organic Rankine Power Cycles for Small Modular Reactors

Abstract

Small nuclear power plants are a promising direction of research for the development of carbon-free energy in isolated power systems and in remote regions with undeveloped infrastructure. Improving the efficiency of power units integrated with small modular reactors will improve the prospects for the commercialization of such projects. Power cycles based on supercritical carbon dioxide are an effective solution for nuclear power plants that use reactor facilities with an initial coolant temperature above 550 °C. However, the presence of low temperature rejected heat sources in closed Bryton cycles indicates a potential for energy saving. This paper presents a comprehensive thermodynamic analysis of the integration of an additional low-temperature organic Rankine cycle for heat recovery to supercritical carbon dioxide cycles. A scheme for sequential heat recovery from several sources in S-CO₂ cycles is proposed. It was found that the use of R134a improved the power of the low-temperature circuit. It was revealed that in the S-CO₂ Brayton cycle with a recuperator, the ORC add-on increased the net efficiency by an average of 2.98%, and in the recompression cycle by 1.7–2.2%. With sequential heat recovery in the recuperative cycle from the intercooling of the compressor and the main cooler, the increase in efficiency from the ORC superstructure will be 1.8%.

1. Introduction

1.1. Current Status of Small Modular Reactors Projects

Today, the global energy industry faces a great challenge in reducing toxic and greenhouse gas emissions into the atmosphere. Special attention is paid to the problem of the increasing atmospheric concentration of carbon dioxide, which contributes to accelerating global climate change. Many countries are taking initiatives at the legislative level to reduce their carbon footprint, including through the development of carbon-free electricity generation. In regions isolated from integrated energy systems, including African and Arctic regions, the demand for environmentally friendly power plants is increasing.

A key component of isolated power systems is low-power energy sources with minimal harmful emissions. The high cost of fossil fuels in remote regions, combined with stricter environmental regulations, contributes to the growing relevance of the introduction of carbon free power generation technologies. Nuclear power plants with small modular reactors (SMR) are promising power plants whose performance is not largely dependent on weather conditions and whose operation is not associated with emissions of toxic substances and greenhouse gases [1].

Small nuclear power plants (SNPPs) are a promising way to provide energy to remote regions [2]. Due to stable energy production in areas where there is no access to fossil fuels, it becomes possible to implement new industrial projects. At the same time, the operation of SNPPs is not accompanied by emissions of carbon dioxide into the atmosphere, and unlike renewable sources, the released power of the power unit is stable and does not depend on weather conditions. In addition to power generation, such power units can be used as centralized heat supply for cities, enterprises, sea water desalination and hydrogen production, which makes it possible to meet a wide range of industrial requirements of remote locations.

SNPP operation is based on the use of a small modular reactor (SMR) characterized by a relatively small capacity (up to 300 MWe) and whose design is based on modular solutions with the possibility of capacity expansion and deployment in a remote region with undeveloped infrastructure. Small modular reactors can be manufactured and assembled directly at the factory and delivered to the site in an assembled state, which will reduce capital investments in the construction of new power plants in remote regions.

Many IAEA member countries are currently conducting research on reactor facilities with a capacity of less than 300 MW, and there are over 80 different small modular reactor projects [3]. Several of them have already been implemented. The Akademik Lomonosov nuclear power plant has an electric capacity of up to 70 MW and is the only floating nuclear power plant in the world. It is located in the city of Pevek in Siberia. This power plant includes two small KLT-40S reactors. The construction of a ground SNPP with RITM-200N reactor facilities has begun in Yakutia (Russia). A power unit with a small modular reactor ACR 100 has been under construction in China since 2021. A power unit with a small modular CAREM reactor is under construction in Argentina. The VAYGR SMR project has passed the licensing stage in the USA, but the project was canceled at the end of 2023. Developments are also underway in the UK (Rolls-Royce, London), Minato, Japan (MHI, Tokyo), and a number of other countries.

However, a number of issues need to be addressed before this technology can be actively disseminated. First of all, the commercialization prospects of NPP projects with small modular reactors remain unclear: the transition to a non-traditional scale will require the use of non-traditional technical solutions, and the cost of electricity should be maintained at a competitive level. The example of the VOYAGER project shows that today it is the final cost of electricity for the consumer that will largely determine the prospects of the small nuclear power industry.

1.2. Supercritical Carbon Dioxide Power Cycles

One way to improve the commercialization prospects for NPP projects may be to improve the energy efficiency of generation: a more rational use of heat released in the reactor core may increase the power unit capacity without complicating the design of the reactor itself. Electric power generation at power units with small modular reactors will require the use of new, non-traditional circuit solutions for high-power nuclear power plants. A large number of studies completed over the past 30 years were dedicated to the use of unconventional heat carriers at nuclear power plants. Today, the most frequently used generation solution is a steam–water cycle. However, as shown by many authors, a closed Bryton cycle on carbon dioxide in the range of supercritical parameters (S-CO₂) can be an alternative to such a power cycle.

Studies [4,5,6] present the results of thermodynamic analysis of various power cycle arrangements for nuclear power plants. The authors conclude that the Bryton cycle with recompression is one of the most efficient carbon dioxide cycles, in particular for liquid metal coolant reactors. Study [7] features a structural and parametric optimization of nuclear power plants with supercritical carbon dioxide cycles. Study [8] analyzed the Bryton cycle for small reactors in terms of efficiency and major equipment size. The authors found that for small modular reactors with sodium cooling, a carbon dioxide cycle will allow for creating a compact power unit with small-sized equipment. Previously, studies have been conducted on the possibility of using S-CO₂ cycles for SMART water-cooled small modular reactors [9,10] and SM-HTGR small modular high-temperature gas-cooled reactors [11]. In studies [12,13], a concept of a new small modular fast neutron reactor with a carbon dioxide coolant KAIST MMR is proposed, which will generate electricity for isolated regions based on the Bryton regenerative cycle. Study [14] is also dedicated to S-CO₂ cycles for small modular reactors. The authors found that for a sodium-cooled fast reactor, the use of the recompression cycle provides an efficiency of up to 45.7% at a turbine inlet temperature of 515 °C. In [15], the authors present a conceptual design of a power unit with a small modular reactor AFR-100 with a recompression cycle. In study [16], power cycles for a lead–bismuth molten nuclear micro-reactor are addressed: the efficiency of different variations of Rankine cycles with an organic coolant, as well as the Bryton recompression cycle on carbon dioxide was analyzed. It was concluded that the recompression cycle becomes more efficient at an initial temperature above 460 °C. In [17], it is concluded that the use of the S-CO₂ recompression cycle for small modular reactors may be feasible at initial temperatures above 550 °C; however, pressure losses in heat exchangers have a significant impact on energy efficiency.

Conventional steam power units in NPPs operate on the Rankine cycle, where the heat generated in the reactor plant is used to generate steam, which generates work by expanding in a turbine. In this case, the turbomachines have significant weight and dimensions, since the expansion degree of the working medium in the cycle is relatively high. In order to maximize efficiency, a sufficiently low pressure is maintained at the exhaust, which causes a large specific volume of steam at the last stage, and as a result, the height of the blades exceeds 1.2 m. To heat condensate and feed water, such schemes use a regenerative heating system consisting of a large number of heat exchangers (traditionally at least six). In supercritical carbon dioxide cycles, unlike the Rankine steam turbine cycle, the expansion degree usually does not exceed two–three and the working fluid density magnitude is higher than that of water vapor. Therefore, the turbomachines have significantly smaller dimensions, and the major equipment composition is usually limited to a small number. Reducing the metal consumption and amount of major equipment in the power cycle becomes essential for small nuclear power plants: this will reduce the capital cost of power unit construction and, as a result, reduce the cost of electricity supplied to consumers. This fact, combined with an increased efficiency level, makes the transition to carbon dioxide power cycles for small modular reactors promising.

1.3. Use of Organic Rankine Cycles in Small Modular Reactor Designs

Despite a relatively high energy efficiency level, carbon dioxide coolant power cycles have sources of dissipated low-potential heat. The temperature of such sources usually does not exceed 150–200 °C, which complicates the recovery process, but their beneficial use could provide an additional increase in supplied power. This could be achieved by using additional power units operating on coolants with low critical parameters (for instance, hydrocarbons, fluorocarbons, and hydrochlorofluorocarbons). The combination of organic Rankine cycles (ORC) with a S-CO₂ cycle may become relevant in resolving the issue of maximizing the energy generation efficiency of nuclear power plants with small modular reactors.

Several studies have addressed the efficiency of combined (binary) S-CO₂ ORC cycles over the past 10 years. In [18], an analysis and optimization of a combined cycle consisting of a supercritical S-CO₂ recompression cycle and a trans-critical CO₂ cycle recovering heat upstream of the cooler is presented. It was found that the efficiency of such a cycle can exceed the results of a conventional S-CO₂ cycle by more than 5.5%. Study [19] presents a thermo-economic analysis and optimization of the compression cycle in which an additional organic Rankine cycle is arranged upstream of the cooler. The energy efficiency of this cycle was improved by more than 11.7%, and the total production cost was reduced by 5.7% when using isobutane and RC318 in the ORC. In [20], it was found that an additional trans-critical carbon dioxide cycle upstream of a cold source of the recompression and recuperative cycle could improve the thermal efficiency by 19.34% and 10.12%, respectively. The topic of using an additional trans-critical CO₂ cycle is also discussed in [21,22].

In addition to carbon dioxide, azeotropic mixtures in cycles [23,24,25] can be used for heat recovery. Study [26] presents an advanced exergy analysis of the combined S-CO₂/ORC system. The combination of a S-CO₂ recompression cycle and an organic Rankine cycle is also the subject of the following works [27,28,29,30]. The authors highlight the prospects of this study direction and the opportunity to improve the efficiency of the cycle. In [31], a thermo-economic optimization and comparative analysis of different organic flash cycles for the supercritical CO₂ recompression Brayton cycle waste heat recovery is presented. Integrated cycles are expected to become promising technologies for high-efficiency power generation.

Despite the availability of studies addressing cycle combinations, today most studies are dedicated to additional low-temperature cycles upstream of a cold source of the S-CO₂ cycle; however, such cycles also contain other heat sources. There are also no generalized thermodynamic studies of combined cycles for small modular reactors with liquid–metal coolant for a wide range of initial parameters and the efficiency of sequential heat recovery from several low-temperature heat sources simultaneously has not been determined. This study presents the results of a comprehensive thermodynamic analysis of various binary S-CO₂/ORC cycles for small modular reactors. The net efficiency of binary recuperative, recompression, and cycles with supercooling has been determined. A scheme with sequential heat recovery from several sources of low-potential heat is considered. A comprehensive comparison of configurations and an analysis of the prospects for using various binary power cycles for small modular reactors were carried out.

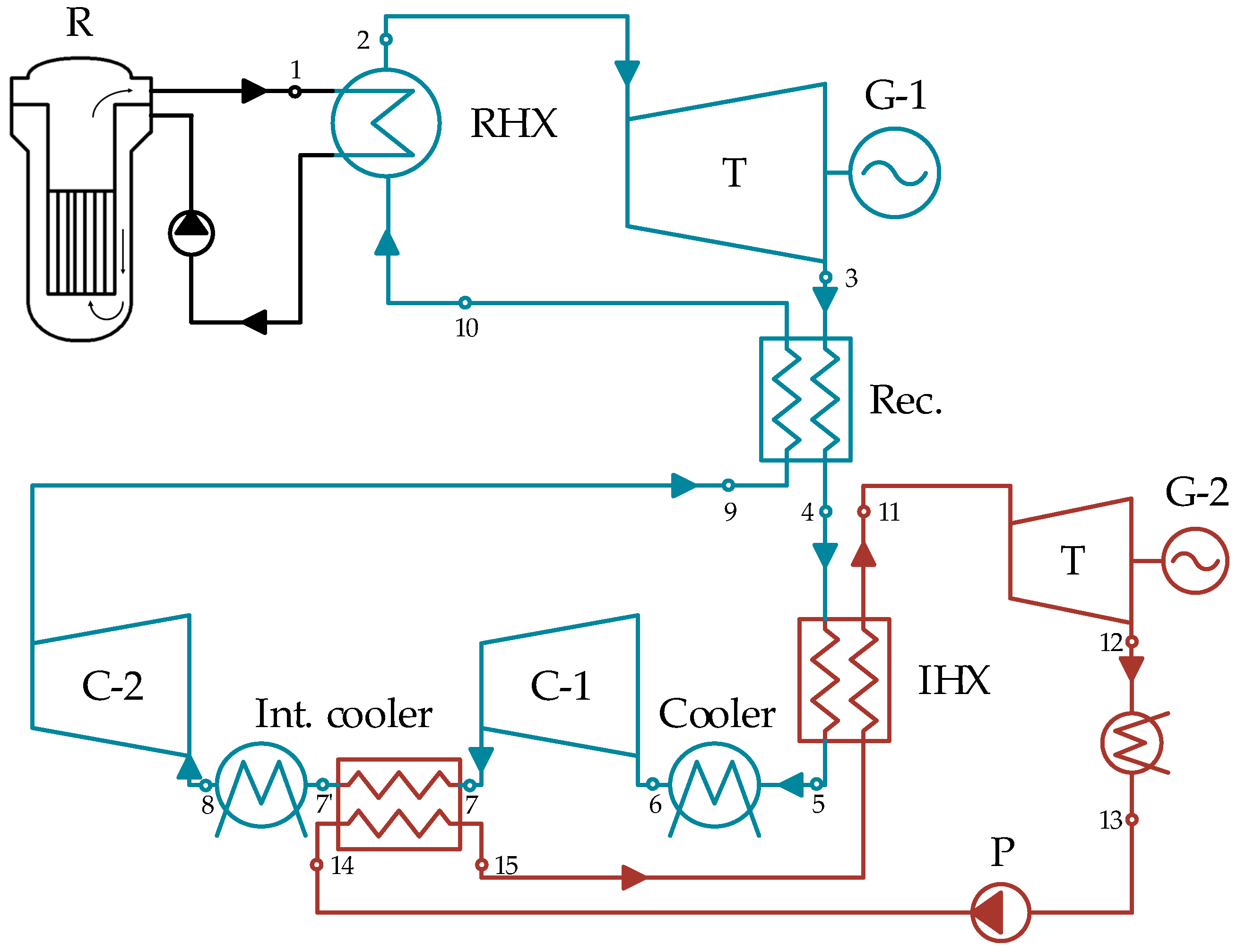
2. Research Object

This study concerns binary power cycles consisting of a high-temperature supercritical carbon dioxide cycle and a low-temperature organic Rankine cycle for nuclear power plants with small modular reactors. Reactor units are considered in the study as a heat source, and the heat is transferred from the reactor circuit to the carbon dioxide circuit. In the reactor circuit, the coolant (e.g., liquid metals or molten salts) receives heat from the core and transfers it through the reactor heat exchanger to the power cycle. Studies have been conducted in a wide range of initial temperatures: from 500 °C (the minimum temperature at which the efficiency of the S-CO₂ cycle can be higher than the steam–water reheat cycle) to 800 °C (the highest temperature for small modular reactor projects with liquid salt coolant).

The simplest solution in terms of the scope of S-CO₂ cycle equipment is the closed Bryton cycle. In this case, carbon dioxide is heated in a reactor heat exchanger without phase transformation, expanded in a turbine from an initial pressure P₀ to a final pressure Pc, and then cooled in a cooler to near critical temperature. Then, the medium is compressed in the compressor and supplied to the reactor heat exchanger, and the cycle closes. The expansion work in the turbine is used to drive the compressor and rotor of the electric generator.

In such a cycle, a large amount of heat is dissipated in a cold source, and to reduce the level of heat loss, a regenerative heat exchanger is used in which the coolant expanded in the turbine transfers heat to the working fluid compressed in the compressor. This improves the final efficiency of the power cycle by adding new heat exchange equipment; however, the hot medium temperature downstream of the recuperator is still rather high and is determined by the medium temperature downstream of the compressor and the minimum temperature drop in the heat exchanger. In general, low-temperature heat, which cannot be directly used in the S-CO₂ cycle, is dissipated in the cooler. In order to solve this problem, an additional heat exchanger can be used between a cold source and a recuperator, in which the rejected heat will be transferred to a low-temperature freon cycle, partially or completely replacing the heat absorption in the cooler (Figure 1).

One of the most promising solutions is the Bryton cycle with recompression: its efficiency may exceed the values of the regenerative cycle and even the values of the cycles with intermediate cooling in the compressor and intermediate reheating in the turbine. In this case, carbon dioxide, after turbine expansion, gives off heat in a high-temperature recuperator and a low-temperature recuperator before being separated into a main flow and a recompression flow. The temperature of the main flow is reduced in the cooler, after which the flow is compressed in the main compressor and enters the LTR. The recompression flow is compressed without pre-cooling in an additional compressor and mixed with the main flow. In such cycles, partial or complete rejected heat recovery upstream of the cooler is possible using the organic Rankine cycle (Figure 2).

In addition to the cooler, heat recovery is possible in S-CO₂ cycles if an intermediate compressor cooling is used (Figure 3). An intercooler is installed to reduce the work spent on compressing the medium, but the heat taken in this process, although of low temperature, can be usefully utilized in a low-temperature cycle. With the utilization of heat from several sources simultaneously, the organizing of an effective carbon dioxide cooling process with simultaneous complete evaporation of the organic coolant becomes important, and therefore thermodynamic analysis of such cycles becomes necessary.

3. Methods

For the earlier described cycles, this study provides a thermodynamic analysis of the effectiveness of the combination of S-CO₂ and ORC cycles. The study was carried out in several stages. First, material and thermal balances were compiled for simple carbon dioxide cycles, and their key parameters were optimized (taking into account technical feasibility limitations) for a wide range of initial temperatures. The results obtained were further used for comparisons with binary cycles, and an analysis of low-temperature heat sources, their power, and temperatures was carried out based on the calculation results. On the basis of the analysis, the ways of integration of low-temperature freon circuits were considered from the conditions of observance of the restrictions accepted in the study (primarily in terms of temperature differences). Since the final efficiency of the power cycle will now be determined by both the parameters of the high-temperature and low-temperature cycles, it becomes necessary to solve the problem of multiparametric cycle optimization (based on the parameters of the S-CO₂ cycle, which will determine the parameters in the intermediate heat exchanger, and based on the ORC parameters, which will determine the efficiency of heat recovery). A comparative analysis of the efficiency of power cycles performed based on the optimization results was conducted.

The parameters (temperature, pressure, and enthalpy) in the power cycle nodes were calculated based on the equations of thermal and material balances for each cycle element using the NIST REFPROP thermophysical properties database. The calculation and optimization tasks were solved using python 3.9 and the scipy.optimize 1.13 package.

The thermal energy from the SMR is transferred to the S-CO₂ cycle using liquid sodium through the reactor heat exchanger (RHX).

The enthalpy of fluid after expansion in the turbine was calculated as:

$$h_{T.out}=h_{T.in}-\left(h_{T.in}-{h_{T.out}}^{\prime }\right)·{\eta }_{oi.T},$$

(1)

where $h_{T.in}$ and $h_{T.out}$ are the enthalpies at the turbine inlet and outlet, kJ/kg;

${h_{T.out}}^{\prime }$ is the theoretical enthalpy at the outlet of the turbine, kJ/kg;

${\eta }_{oi.T}$ is the internal relative efficiency of the turbine.

The enthalpy resulting from compression in a compressor or a pump was calculated using the following formula:

$$h_{C.out}=h_{C.in}+\left({h_{C.out}}^{\prime }-h_{C.in}\right)/{\eta }_{oi.C},$$

(2)

where ${\eta }_{oi.C}$ is the isentropic efficiency of the compressor/pump;

$h_{C.in}$ and $h_{C.out}$ are the enthalpies at the compressor inlet and outlet, kJ/kg;

${h_{C.out}}^{\prime }$ is theoretical enthalpy at the outlet of the compressor, kJ/kg;

Heat balance of heat exchangers:

$$G_h·\left(h_{h.in}-h_{h.out}\right)=G_c·\left(h_{c.out}-h_{c.in}\right)=Q,$$

(3)

where $h_{h.in}$ and $h_{c.in}$ are the enthalpies of hot and cold fluids at the heat exchanger inlet, kJ/kg;

$h_{c.out}$ and $h_{h.out}$ are the enthalpies of cold and hot fluids at the heat exchanger outlet, kJ/kg;

$G_h$ and $G_c$ are flow rates of hot and cold fluid, kg/s;

$Q$ is the heat exchanger heat capacity, kW;

The net electrical efficiency of the power cycle was calculated as follows:

$${\eta }_{net}=\frac{\sum \left(N_T·{\eta }_m·{\eta }_g\right)-\frac{\sum N_C}{{\eta }_m·{\eta }_d}}{Q},$$

(4)

where $Q$ is reactor thermal power, kW;

$N_T$ and $N_C$ are the electric power of turbines and compressors/pumps, kW;

${\eta }_m$, ${\eta }_g$, and ${\eta }_d$ are the mechanical, electric generator, and electric drive efficiencies.

A combination of the two cycles is provided using heat exchangers where carbon dioxide transfers thermal energy to freon. Liquid freon heats up to the saturation line, evaporates, and the vapors are superheated. Such a process creates a point of minimum temperature drop that will limit the heat output of the heat exchanger. The value of the minimum temperature drop in this study was taken as 10 °C, and to support this value, it was necessary to carry out a series of calculations by varying both the freon pressure (determining the boiling point) and fluid flow rate (determining the heat output).

A limitation is accepted in the calculations: after heating in the heat exchanger, the freon must completely evaporate (humidity γ = 0), and as a result of its expansion, the humidity should not exceed 10%.

Table 1. The system of equations and limitations for calculating the cycle in Figure 3.

Component	Equations	Limitations
S-CO2
T	$h_3=h_2-\left(h_2-h_3^{\prime }\right)·{\eta }_{oi.T}$ $h_3^{\prime }=f(P_3,s_2)$
Rec.	$Q_{rec}=G_3\left(h_3-h_4\right)=G_9\left(h_{10}-h_9\right)$	$\min \left(\mathsf{\Delta }T\right)>10 °\mathrm{C}$
IHX	$Q_{IHX}=G_4\left(h_4-h_5\right)=G_{15}\left(h_{11}-h_{15}\right)$	$\min \left(\mathsf{\Delta }T\right)>10 °\mathrm{C}$ $\gamma =0$
Cooler	$T_6=32 °\mathrm{C}$
C-1	$h_7=h_6+\left(h_7^{\prime }-h_6\right)/{\eta }_{oi.C}$ $h_7^{\prime }=f(P_7,s_6)$$, P_7=\sqrt{P_9{P}_6}$
Int. cooler	$T_8=32 °\mathrm{C}$ $Q_{Int.}=G_7\left(h_{7\prime }-h_7\right)=G_{14}\left(h_{15}-h_{14}\right)$	$\min \left(\mathsf{\Delta }T\right)>10 °\mathrm{C}$
C-2	$h_9=h_8+\left(h_9^{\prime }-h_8\right)/{\eta }_{oi.C}$ $h_9^{\prime }=f(P_9,s_8)$$, P_9=\pi P_6$
ORC
T	$h_{12}=h_{11}-\left(h_{11}-h_{12}^{\prime }\right)·{\eta }_{oi.T.ORC}$ $h_{12}^{\prime }=f(P_{12},s_{11})$	$\gamma \le 0.1$
Condenser	$T_{13}=30 °\mathrm{C}$
Pump	$h_{14}=h_{13}+\left(h_{14}^{\prime }-h_{13}\right)/{\eta }_{oi.C.ORC}$ $h_{14}^{\prime }=f(P_{14},s_{13})$$, P_{14}={\pi }_{ORC}{P}_{13}$

shows an example of a system of equations and constraints for calculating the binary S-CO₂/ORC cycle.

The assumptions given in

Table 2. Assumptions that were used in the calculations.

Parameter	Value
Maximum temperature of the heat source	500–800 °C
Minimum temperature of the cooling source	30 °C
Minimum temperature difference in heat exchangers	10 °C
Pressure loss in S-CO2 heat exchangers	50 kPa
Isentropic efficiency of S-CO2 turbomachines	90%
Isentropic efficiency of ORC turbomachines	85%

were used in the thermodynamic calculation. The calculations were carried out in a reactor coolant temperature range from 500 °C to 800 °C with a minimum temperature in the cycle of 30 °C—a typical value for condensers of steam turbines at nuclear power plants. The minimum temperature difference in the heat exchangers was taken to be 10 °C, and the pressure loss during the carbon dioxide flow in the channels of the heat exchangers was assumed to be 50 kPa. As noted above, the calculation of the expansion and compression processes was performed with an isentropic efficiency assumed to be a constant value.

The main types of cycles presented in the literature were calculated to validate the model. The thermal efficiency (η_th) of the S-CO₂ recompression Brayton cycle, the organic Rankine cycle (ORC) using R236ea refrigerant, and the binary S-CO₂-ORC cycle with isobutane were calculated (

Table 3. Model validation.

Cycle	ηth (This Study)	ηth (Reference)	Error
S-CO2 recompression [32] (T0 = 550 °C, P0 = 20 MPa, Pmin = 7.69 MPa, x = 0.59)	0.457	0.453	0.84%
S-CO2 recompression [33] (T0 = 550 °C, P0 = 20 MPa, Pmin = 7.69 MPa, x = 0.59)	0.457	0.472	3.22%
ORC (R236ea) [34] (T0 = 104 °C, P0 = 1.72 MPa)	0.093	0.0822	8.3%
S-CO2-ORC (Isobutane) [27] (T0 = 550 °C, π = 3.61, TIHX = 103.15)	0.464	0.442	4.88%

). To ensure the correctness of the results, the calculations were performed under comparable boundary conditions (initial temperature, pressure), with thermal efficiency chosen as the comparison criteria. The validation results showed that the relative deviation in calculations compared to the existing works does not exceed 8.3% (the maximum deviation is observed in the ORC calculations).

4. Results and Discussion

4.1. Thermodynamic Analysis of the Efficiency of S-CO₂ Cycles

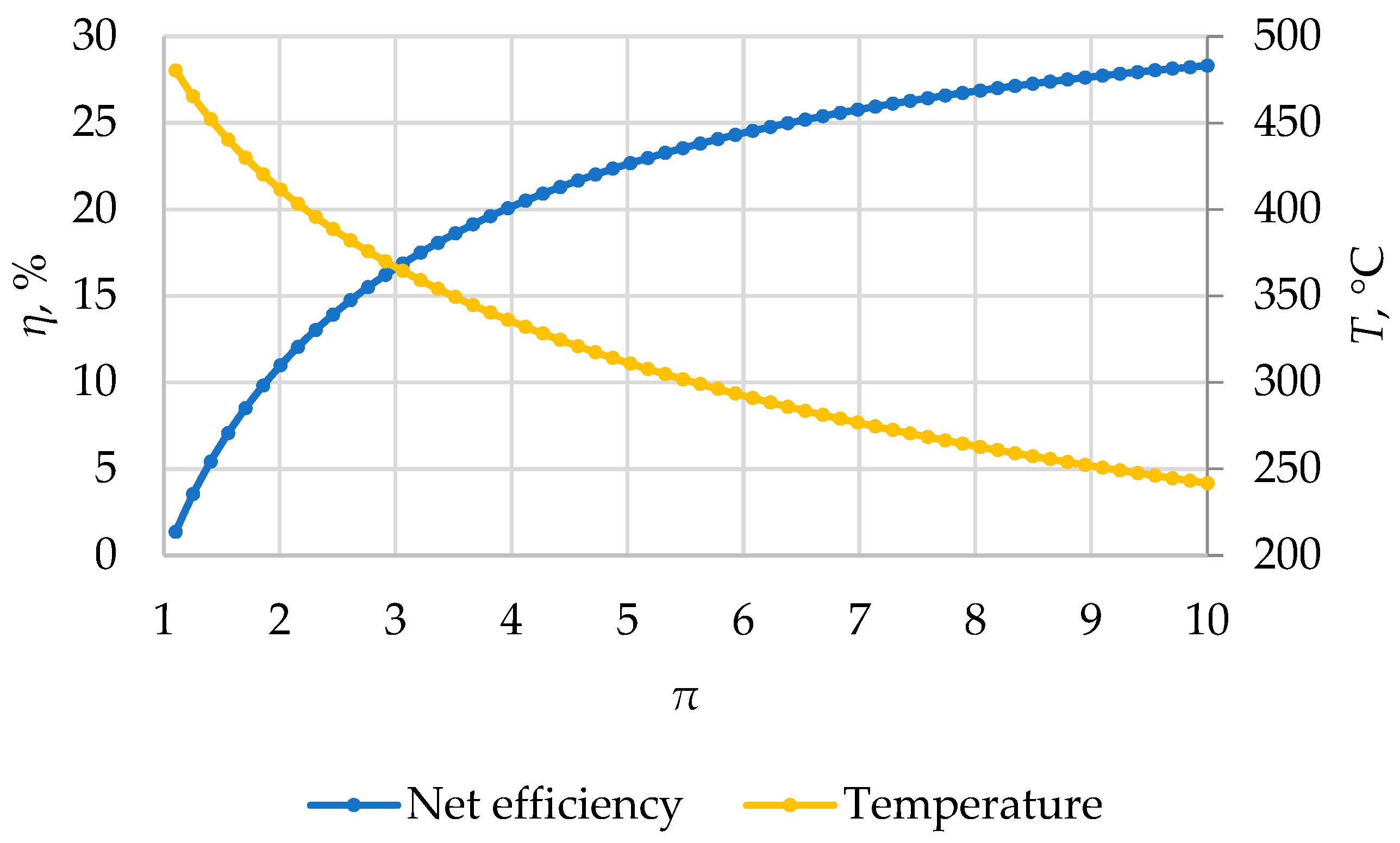
In a closed S-CO₂ Brayton cycle, thermal efficiency is largely determined by the inlet temperature, as inferred from the Carnot postulates, and is also dependent on the inlet and outlet pressures in the cycle. Figure 4 shows the dependencies of the net efficiency η of the Brayton cycle and the temperature of carbon dioxide after expansion in the turbine as a function of the pressure ratio in the compressor, π = P₀/P_c. In a simple Brayton cycle, maximum efficiency can be achieved when a very high-pressure ratio is maintained, which is technically unattainable due to the fact that the minimum pressure in a supercritical cycle must not fall below ~7.4 MPa. Increasing the pressure ratio from two to four increases the efficiency by 9.5%, and from four to six by 4.5%; further increases result in diminishing returns. Therefore, for a simple cycle, choosing the pressure becomes primarily a task of techno-economic analysis, considering the current level of development in the power engineering industry. In this study, a maximum pressure of 35 MPa was chosen (corresponding to the pressure in prospective power units with ultra-supercritical steam parameters). The increase in efficiency with π is due to the increase in the specific work of the CO₂ turbine (which increases faster than the energy consumption for compression in the compressor). Simultaneously, the temperature of the working fluid decreases before that of the cooler, but its sufficiently high heat capacity makes heat recovery feasible.

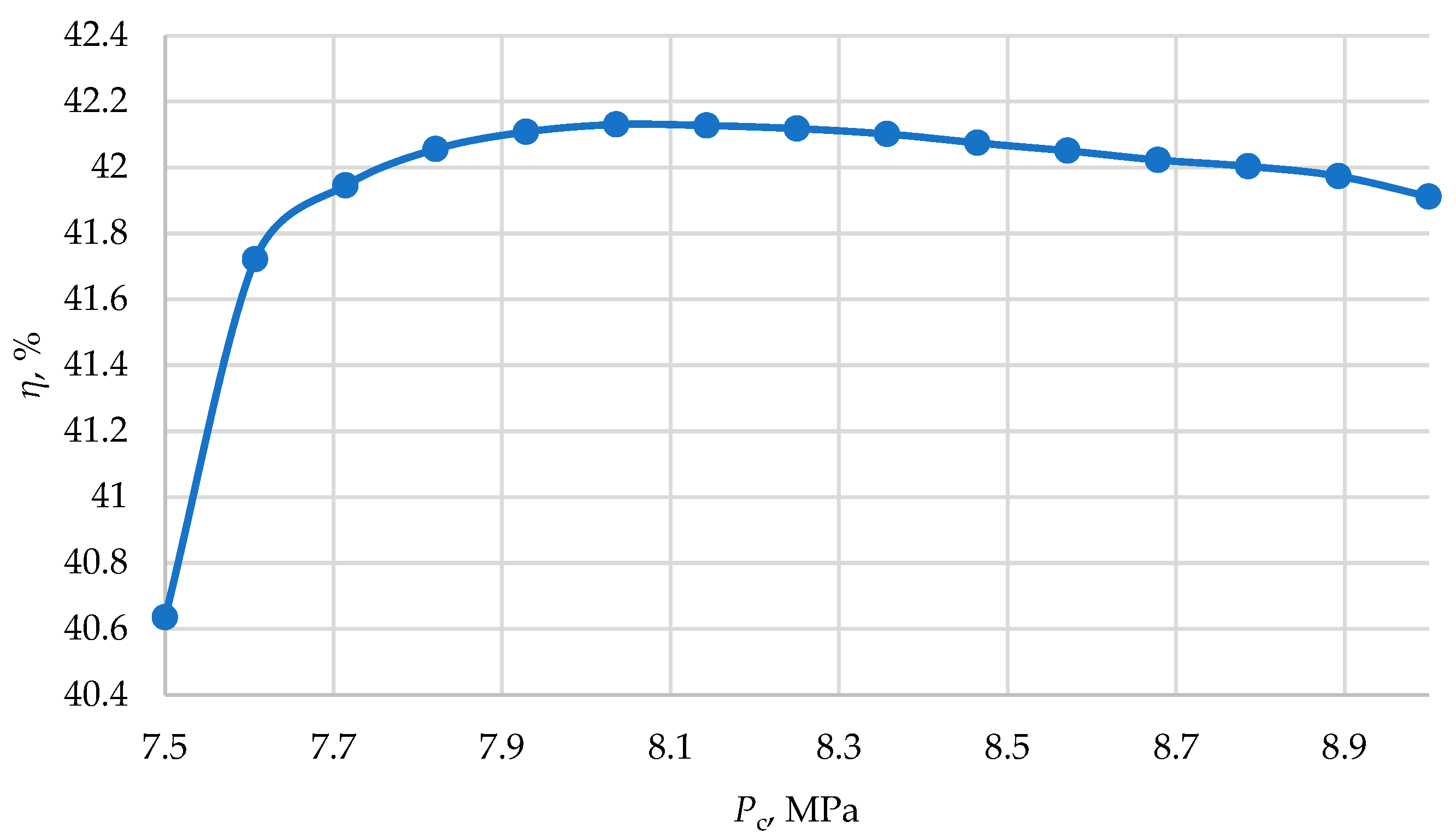
Heat recovery allows for an increase in the thermal efficiency of the cycle. Figure 5 shows the graphs of efficiency dependence on pressure ratios and final pressures. For a S-CO₂ cycle in the temperature range of 500–800 °C, there exists a set of optimal parameters that achieve maximum efficiency. For instance, at 500 °C, the maximum efficiency of 38.46% is achieved at a pressure ratio of 5.625 and a final pressure of 7.9 MPa. This indicates that in such power cycles, it may be more efficient to compress carbon dioxide parameters not close to critical but at higher pressures. A similar trend is observed with increasing temperature, although the optimal pressure ratio increases: at 600 °C, the net efficiency of 43.467% is achieved at π = 6.53, at 700 °C—47.69% at 7.285, and at 800 °C—51.3% at 8.04. Therefore, in a recuperative cycle, a higher level of efficiency can be achieved at lower working pressures.

One of the most efficient S-CO₂ cycles is the recompression Brayton cycle. In such a cycle, efficiency will be determined not only by the pressure ratio but also by the fraction of the flow entering the second compressor (Figure 6). Based on the calculation results, the optimal ratios of these parameters were determined, ensuring maximum efficiency. At 500 °C, an efficiency of 42.1% is achieved at π = 3.34 and x = 0.67, at 600 °C the maximum value is 47.3%, at 700 °C—51.6%, and at 800 °C—55.2%.

It should be noted that in the recompression cycle, similar to the recuperative cycle, the highest efficiency is achieved at pressures above the critical point in the cooler: at 500 °C, a final pressure of around 8 MPa is optimal (see Figure 7).

Figure 8 shows the efficiency curves of S-CO₂ cycles as a function of pressure ratios at different initial temperatures. In the recuperative cycle, higher efficiency can be achieved at lower working pressures compared to a simple closed Brayton cycle, and in the recompression cycle, this difference becomes even greater, highlighting the advantages of this cycle. On average, increasing the temperature by 100 °C leads to a 3.5–5% increase in efficiency for both the recompression and recuperative cycles, while the efficiency of the simple closed Brayton cycle remains almost unchanged in the pressure ratio range up to π = 10 with changes in temperature.

The conclusion can be drawn that the use of the recompression cycle is the most promising compared to other power cycle variants. However, the potential for further increasing the efficiency has not yet been exhausted: low-grade heat dissipated in the S-CO₂ cycles can be effectively utilized.

4.2. Waste Heat Recovery Analysis

In binary cycles, the overall efficiency of electricity production is determined by both the high-temperature and low-temperature efficiency, which are often conflicting factors. Improving the efficiency of the high-temperature loop is achieved by increasing thermal efficiency, leading to a reduction in the potential heat dissipated in the cold source. On the other hand, the efficiency of the low-temperature loop will largely depend on the temperature of the heat source.

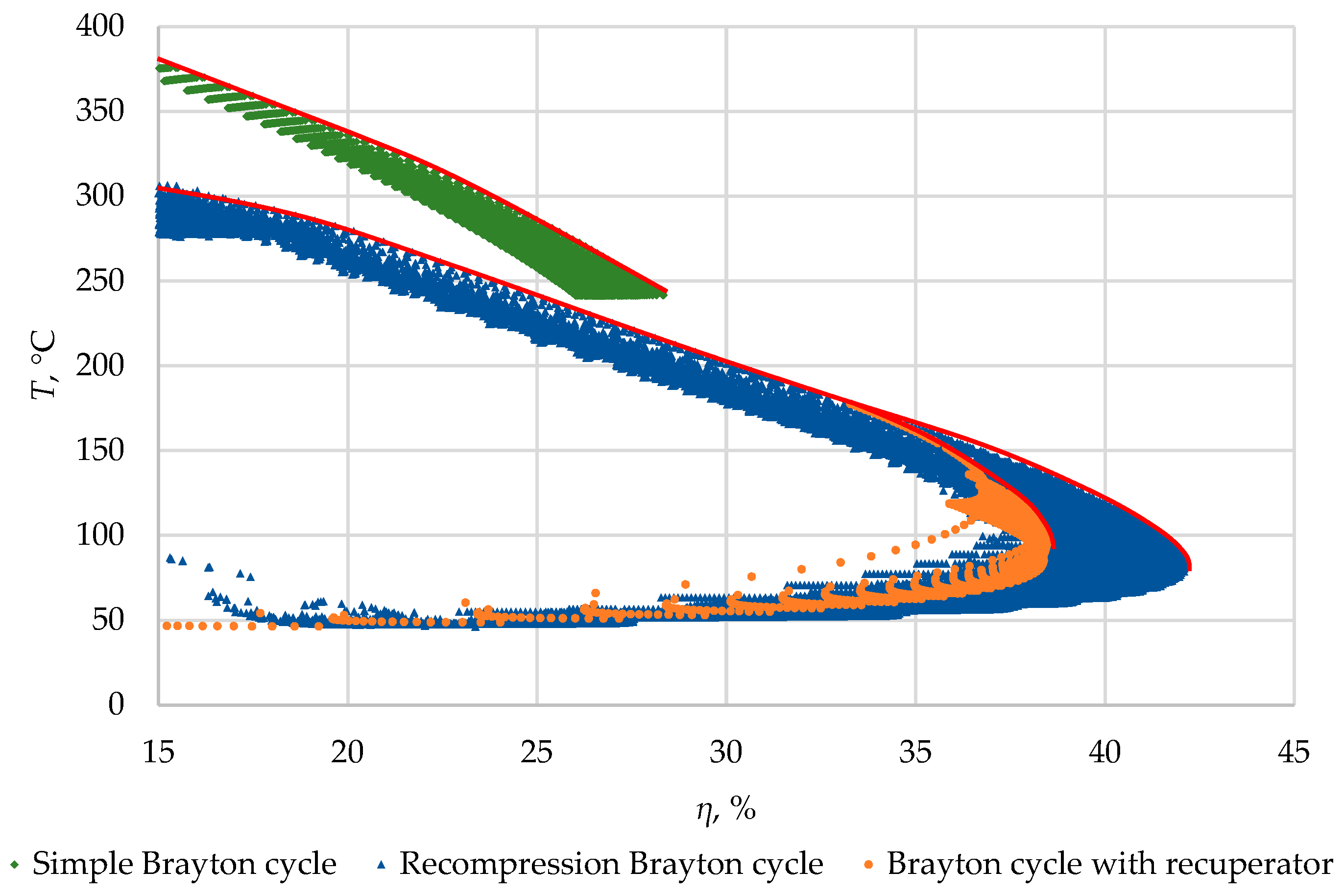
Figure 9 presents a graph of working fluid temperature before the cold source in S-CO₂ cycles as a function of efficiency (for the previously discussed range of calculation points). The efficiency of a simple closed Brayton cycle at 500 °C, as noted earlier, is comparatively low primarily because the cooler receives high-temperature heat: the temperature of carbon dioxide exceeds 250 °C. In recuperative and recompression cycles, the temperature of the rejected heat is usually lower, reaching 100 °C for recuperative and 80 °C for recompression at peak efficiency. For each cycle, the same level of efficiency can be achieved with a different set of parameters (pressure ratios, etc.), and for binary cycles, the most promising option is when the maximum efficiency corresponds to the highest temperature before the cooler (indicated by the lines).

The final optimal set of parameters in a binary cycle will also be determined by the power generation in the low-temperature loop, making it necessary to study heat utilization processes in the organic Rankine cycle.

The sources of waste heat in the considered cycles are the cooler and the intermediate compressor cooler. The useful heat recovery from these sources is complicated by the cooling curve of carbon dioxide at near-critical parameters: the specific heat capacity of S-CO₂ significantly increases in the low-temperature range. Heat transfer from carbon dioxide to the low-temperature cycle working fluid occurs through heat exchange surfaces in the intermediate heat exchanger, where the condition for operation is maintaining a nonzero temperature difference. In the organic Rankine cycle, the low-boiling-point working fluid needs to be heated to its boiling temperature, vaporized, and superheated with a sufficient amount of high-temperature heat.

Figure 10 shows the T-Q diagram of carbon dioxide cooling at a pressure of 7.8 MPa. Part of the heat from the S-CO₂ cycle is transferred to the organic working fluid through the intermediate heat exchanger, while the remaining heat, which cannot be effectively utilized, is dissipated with cooling water. The share of heat effectively utilized and the efficiency of utilization are determined by several factors: the working fluid pressure, mass flow rate, total heat transfer in the heat exchanger, and the working fluid itself. The working fluid pressure determines the available heat drop in the ORC turbine and the boiling temperature of the fluid, consequently affecting the minimum temperature difference in the heat exchanger. The mass flow rate and total heat transfer in the heat exchanger determine the amount of heat supplied to the low-temperature cycle and the temperature of the refrigerant before the turbine, while the type of working fluid affects the internal efficiency of the cycle. Therefore, for efficient utilization of low-temperature heat in a binary cycle, an optimization problem needs to be solved based on these parameters.

This work considered the freons R134a, R236ea and isobutane as the working medium for organic Rankine cycles. The considered freons can work stably in the considered temperature range and have found wide application in ORC.

Figure 11 shows the dependencies of the specific power output of the ORC (per unit CO₂ flow rate) on the fraction of heat transferred to the cooler (1—all heat goes to the cooler, 0—all heat is transferred to the ORC) at T = 250 °C. Based on the calculation results, it was found that there are optimal values for the ratio of flows in the high-temperature and low-temperature loops, as well as for the fraction of heat transferred to the low-temperature loop when utilizing the heat of carbon dioxide at parameters close to critical. The presence of these optima is due to the fact that at a low ratio of Q/Q_max, a small amount of thermal energy is transferred to the ORC, resulting in a low electrical power output. Conversely, when utilizing a large amount of heat (Q/Q_max < 0.36), including low-temperature S-CO₂ heat due to increasing heat capacity near the critical point, it is necessary to lower the refrigerant’s evaporation temperature. This, in turn, reduces the thermal efficiency of the ORC.

When effectively utilizing the rejected heat from the high-temperature loop in the organic Rankine cycle, the choice of working fluid will determine the degree of approximation of the low-temperature loop to the Carnot cycle and, consequently, its thermal efficiency. Through extensive calculations, efficiency curves of heat utilization in the ORC were obtained based on parameters of the carbon dioxide flow entering the intermediate heat exchanger (Figure 12) at optimal values of G_orc/G_CO2, P_orc, and Q/Q_max. It was found that using R134a as the working fluid in the temperature range of 75–250 °C for the utilization of residual heat from carbon dioxide at near-critical pressure allows for maximum power generation compared to the working fluids R236ea and Isobutane. The power output of the low-temperature loop will be determined by the temperature of the carbon dioxide entering the intermediate heat exchanger.

4.3. Comparison of Energy Parameters of Binary Power Cycles for SMR

In a Brayton S-CO₂ cycle with a recuperator, as noted earlier, the temperature of the carbon dioxide before the cooler depends on the pressure ratio and the pressure in the cooler. In a binary cycle, this leads to changes in the efficiency of the high-temperature and low-temperature loops. Figure 13a shows the dependence of the specific power (per unit of supplied heat) of the S-CO₂ cycle and the ORC on the pressure ratio. The power of the high-temperature loop has an optimum corresponding to the point of maximum efficiency of the Brayton cycle with a recuperator, while the power of the low-temperature loop increases proportionally to the temperature before the cooler (depending on π). The overall efficiency of the binary cycle, determined by the sum of the powers of both loops, reaches its maximum value, with the optimal value of π being higher than that of a standard S-CO₂ cycle with a recuperator. The maximum efficiency of the binary cycle exceeds that of a single cycle, indicating the potential of using an ORC in such setups. Figure 13b shows the dependence of the net efficiency of the binary cycle on π and P_c, indicating that in such a cycle, maximum efficiency can be achieved with a cooler pressure of about 7.5 MPa, which does not correspond to the optimal value of an S-CO₂ cycle. At these parameters, the temperature of the rejected heat is high, leading to a high-power output of the low-temperature cycle.

A similar effect is observed in the compression cycle. The presence of an optimal efficiency value of a binary cycle exceeding the efficiency value of a single compression cycle indicates the prospects of using organic Rankine cycles in such cycles.

Table 4. Parameters at the main points of optimized S-CO₂/ORC cycles at T₀ = 500 °C.

Point	Fluid	T	P	H	S	G/G0
Recompression
1	Na	500.000	0.100	-	-	-
2	S-CO2	490.000	28.312	954.193	2.571	1.000
3	S-CO2	343.978	7.750	803.322	2.598	1.000
4	S-CO2	212.823	7.700	655.236	2.330	1.000
5	S-CO2	87.225	7.650	506.222	1.977	0.683
6	S-CO2	87.225	7.650	506.222	1.977	0.683
7	S-CO2	50.400	7.625	444.319	1.793	0.683
8	S-CO2	32.000	7.600	315.085	1.376	0.683
9	S-CO2	78.162	28.275	349.289	1.386	1.000
10	S-CO2	202.823	28.412	578.216	1.948	0.317
11	S-CO2	87.225	7.650	506.222	1.977	0.317
12	S-CO2	218.569	28.412	601.418	1.996	1.000
13	S-CO2	310.369	28.362	726.302	2.230	0.215
14	R134a	30.271	1.155	242.104	1.144	0.215
15	R134a	58.896	1.098	438.556	1.765	0.215
16	R134a	46.436	0.770	431.794	1.769	0.215
17	R134a	30.000	0.770	241.722	1.144	0.215
With recuperator
1	Na	500.000	0.100	-	-	-
2	CO2	490.000	40.959	946.294	2.486	1.000
3	CO2	303.239	7.650	757.225	2.523	1.000
4	CO2	137.604	7.600	569.354	2.140	1.000
5	CO2	67.211	7.550	476.576	1.892	1.000
6	CO2	32.000	7.500	362.206	1.531	1.000
7	CO2	127.604	41.059	428.143	1.548	1.000
8	CO2	243.488	41.009	616.014	1.961	1.000
9	R134a	96.818	2.944	449.348	1.736	0.451
10	R134a	39.038	0.770	424.255	1.745	0.451
11	R134a	30.000	0.770	241.722	1.144	0.451
12	R134a	31.417	2.944	243.748	1.144	0.451

shows the parameters at the main points of the power cycle at T₀ = 500 °C.

The final efficiency of the binary S-CO₂/ORC Brayton cycle with a recuperator in the temperature range from 500 to 800 °C is higher than that of the basic cycle with a recuperator by an average of 2.98%: net efficiency is 41.43% at 500 °C, 46.66% at 600 °C, 50.68% at 700 °C and 54.28% at 800 °C (Figure 14). In the recompression cycle, the increase in net efficiency from the ORC superstructure averages 1.7–2.2% in the initial temperature range of 500–800 °C: at 500 °C the efficiency is 44.37%, at 600 °C—49.31%, at 700 °C—53.32%, and at 800 °C—56.85%. Heat recovery in a recuperative cycle with intermediate cooling in the compressor leads to an increase in efficiency by an average of 1.8%.

Therefore, the use of organic Rankine cycles for waste heat recovery allows for an increase in the net efficiency of S-CO₂ power cycles for small modular reactors. Among the considered working fluids, R134a provides the maximum efficiency gain.

The use of small modular reactors will enable the generation of electricity for remote regions without emitting greenhouse gases into the atmosphere, making this direction promising. Implementing binary S-CO₂/ORC cycles in small nuclear power plants will increase their energy efficiency and reduce the specific consumption of nuclear fuel. The use of organic Rankine cycles will reduce fuel consumption by 1.7–2.2% in the recompression cycle, which can have a positive impact on the technical and economic indicators, as well as on the amount of generated nuclear waste.

It should be noted that despite the increase in the energy efficiency of power cycles due to the utilization of waste heat, the use of additional equipment increases the capital cost of a nuclear power unit. Thus, the issue of choosing a specific scheme for generating electricity at small modular reactors will be determined primarily by economic indicators. There may also be technical limitations when creating binary power cycles. Heat recovery in heat exchangers at low temperature differences leads to the need to increase the heat transfer area.

5. Conclusions

This paper presents a thermodynamic analysis and parametric optimization of binary cycles consisting of a high-temperature S-CO₂ cycle and a low-temperature ORC for nuclear power plants with small modular reactors. Various schemes of cycles were considered, and their effectiveness was analyzed. It was found that S-CO₂ power cycles contain sources of low-grade heat that can be used in organic Rankine cycles. In recompression and recuperator cycles, waste heat temperatures can reach 150 °C or higher at moderate efficiency levels. To effectively utilize this heat, it is necessary to conduct optimization studies.

• The coolants isobutane, R236ea and R134a were considered in the organic Rankine cycle for recycling the heat of the carbon dioxide flow. Based on the results of thermodynamic analysis, it was found that the use of R134a makes it possible to provide the highest power of the low-temperature circuit: the specific energy production in the ORC can reach 48 kJ/kg_CO2 at a maximum heat recovery temperature of 250 °C.
• It has been established that in order to achieve maximum heat recovery power in the ORC, there is a set of optimal values for the ratio of coolant flow rates in the intermediate heat exchanger and the ratio of heat between it and the cooler. Thus, at a carbon dioxide temperature in front of the heat exchanger equal to 250 °C, the optimal flow ratio is G_orc/G_CO2 = 0.76 and the thermal power ratio Q_cooler/Q_max = 0.36%.
• It was revealed that in the S-CO₂ Brayton cycle, a recuperator and ORC integration makes it possible to increase the net efficiency by an average of 2.98%. In the recompression cycle, the increase in efficiency is 1.7–2.2%.
• A scheme is proposed for sequential heat recovery from the compressor intercooling and the main cooler in the Brayton recuperative cycle. In such a cycle, sequential heat recovery increases the efficiency by an average of 1.8%, and the net efficiency at 800 °C reaches 54.5%.