Characteristics of Permeability Evolution and Pore Structure of Coal with High Gas

Abstract

To study the influence of gas pressure on coal permeability evolution, we conducted experiments on coal samples from the No. 9 coal seam in Tangshan Coal Mine, Hebei Province, China. Different gas pressures (helium and nitrogen) were applied, and nitrogen-induced deformations were measured. We also analyzed the coal samples’ pore structure using mercury injection porosimetry, obtaining pore surface fractal dimensions. The increase in nitrogen pressure from 0.3 MPa to 3 MPa resulted in an elevation of adsorption strain from 0.168 × 10⁻³ to 1.076 × 10⁻³, with a gradual decrease observed in the extent of this increase. However, the permeability of coal samples initially decreased from 16.05 × 10⁻¹⁸ m² to 4.91 × 10⁻¹⁸ m² and subsequently rose to 5.69 × 10⁻¹⁸ m². Helium showed similar trends to nitrogen, with average permeability 1.42–1.88 times higher under the same pressure. The lowest permeability occurred at 1.5 MPa for helium and 2.5 MPa for nitrogen. Gas absorptivity plays a crucial role in coal permeability evolution. Additionally, we observed coal’s compressibility to be 7.2 × 10⁻¹¹ m²/N and corrected porosity to be 53.8%, considering matrix compression. Seepage pores larger than 100 nm accounted for 80.4% of the total pore volume, facilitating gas seepage. Surface fractal dimension D_s1 correlated positively with micropore volume, while D_s2 and D_s3 correlated negatively with pore volume and gas permeability.

1. Introduction

Natural gas is currently regarded as an efficient and clean energy source. As a kind of unconventional natural gas, coalbed methane (CBM) has received more and more attention, and it has gradually become an important emerging energy source.

Previous research and practice have shown that during CBM mining, permeability is the main factor affecting CBM production [1,2]. It is of great significance to study the evolution of permeability to improve CBM production. The main factors affecting permeability include the physical properties of coal, pore structure, reservoir depth, in situ stress, reservoir pressure, temperature, gas adsorption and desorption capacity, among others. During the production of coalbed methane, permeability varies over time and conditions during the mining process. In the early stages of coalbed methane production, the effective stress increased due to the decrease in fluid pressure, which resulted in a decrease in gas reservoir pressure [3]. When the reservoir pressure dropped below the critical desorption pressure, the desorption of methane in the adsorbed state caused the shrinkage of the coal matrix, the pore fissure opening increased, and the permeability increased [4,5]. When the fluid pressure dropped below 1 MPa, gas slippage increased permeability. Therefore, the main factors for permeability evolution include effective stress, desorption-induced shrinkage of the coal matrix, and gas slippage. In addition to the fact that reservoir pressure affects changes in permeability, the physical properties of coal will also affect permeability during coalbed methane production. Coal permeability is influenced by in situ factors like pore structure (cleavage distance, pore size, heterogeneity) and stress conditions [6]. Experimental studies have shown that as gas pressure decreases, permeability also decreases due to the increase in effective stress, and the effective stress and permeability have an exponential relationship [7,8]. McKee et al. [9] found that as the depth of a coal seam increases, porosity is negatively correlated with the effective stress, and permeability decreases following a negative exponential curve. Seidle et al. [10] established a model that explained the exponential relationship between permeability and effective stress. Previous studies indicate that not only effective stress but also adsorption and desorption affect permeability [11]. In the experimental study, comparing permeability in coal with adsorbed and non-adsorbed gas revealed how gas properties affect coal adsorption/desorption strain [12,13]. Shi and Durucan [3] proposed a series of permeability models to describe the dynamic changes in permeability. Connell [14] established a linear relationship between adsorption amount and strain in his model.

Accurate identification of coal structure is of great significance to CBM exploration and development [15,16,17]. As a porous material, coal rock contains abundant pores and fractures. Pore and fracture structure affect the permeability and deformation of coal. The methods used to measure the pore structure of coal mainly include the mercury injection method, low-temperature liquid nitrogen adsorption method, low-temperature carbon dioxide adsorption method, small angle X-ray scattering method, atomic force microscope, scanning electron microscope, and other physical and photoelectromagnetic methods. The pore structure is studied by the high-pressure mercury injection method in this paper [18,19,20,21,22,23,24,25,26,27]. The pores measured, by pore diameter d, are divided into the micropore (d < 10 nm), transition pore (10 nm < d < 100 nm), mesopore (100 nm < d < 1 μm), macropore (1 μm < d < 10 μm) and micro fracture (d > 10 μm) [28]. The fractal dimension is used to quantificationally measure the features of pore surface and structure space, revealing the characteristics of space or structures. The volume fractal dimension is used to characterize the spatial heterogeneity of pore structure, and the surface fractal dimension is used to characterize the roughness of pore surface [20,29,30,31,32,33,34,35,36].

The relationship between pore properties and permeability has been extensively investigated by numerous researchers. Zhang et al. [37] combined the mercury injection experiment, computed tomography (CT) experiment, gas adsorption and desorption experiment, and the seepage experiment, and concluded that the degree of pore accumulation is the dominant factor affecting permeability change. Cheng [38] and Qin [39] obtained pore throat parameters at the scale of porous media with the mercury injection porosity (MIP) digital core reconstruction model and micro-computed tomography (micro-CT) images, respectively. The permeability contribution was evaluated according to pore connectivity, connectivity parameters, fractal dimension, and pore throat parameters. In addition, Hu et al. [40] established a multiple regression model of the influence of pore structure on the porosity and permeability of low-permeability sandstone reservoirs using multiple stepwise regression analysis; the multiple regression equation has high reliability and practicability.

This paper used the developed coal rock seepage–adsorption–deformation synchronous test device to test coal permeability evolution. Using nitrogen and helium as experimental gases, the coal permeability at different pressures was measured. The relationship between adsorption strain and permeability was analyzed, and the mechanism of adsorption on permeability was described in detail. In addition, the pore structure characteristics of coal samples were tested, and the roughness of the pore surface was measured by surface fractal dimension.

2. Experimental Tests

2.1. Coal Sample Preparation

Some coal blocks were collected from No. 9 coal seam of Tangshan Mine, situated in the northwestern region of the Kaiping coalfield in Hebei Province, China. The samples were taken at a depth of 900 m and exhibited an initial coalbed methane content of approximately 8 m³/t, classifying the mine as high gas. The measured average maximum vitrinite reflectance (R_0,max%) of coal is 0.97%; considering this, No. 9 coal in Tangshan Mine belongs to the middle rank of coal. Coal samples were processed as cylinders with a diameter of approximately 2.5 cm and a height of approximately 5.0 cm, oriented along the parallel bedding direction. Following a 30 h dehumidification and drying process, the samples were stored in a dry environment. Cylindrical coal samples were used for simultaneous adsorption–permeation–deformation testing. Additionally, coal fragments were gathered for pore structure analysis using MIP tests.

2.2. Adsorption-Permeability Experiment

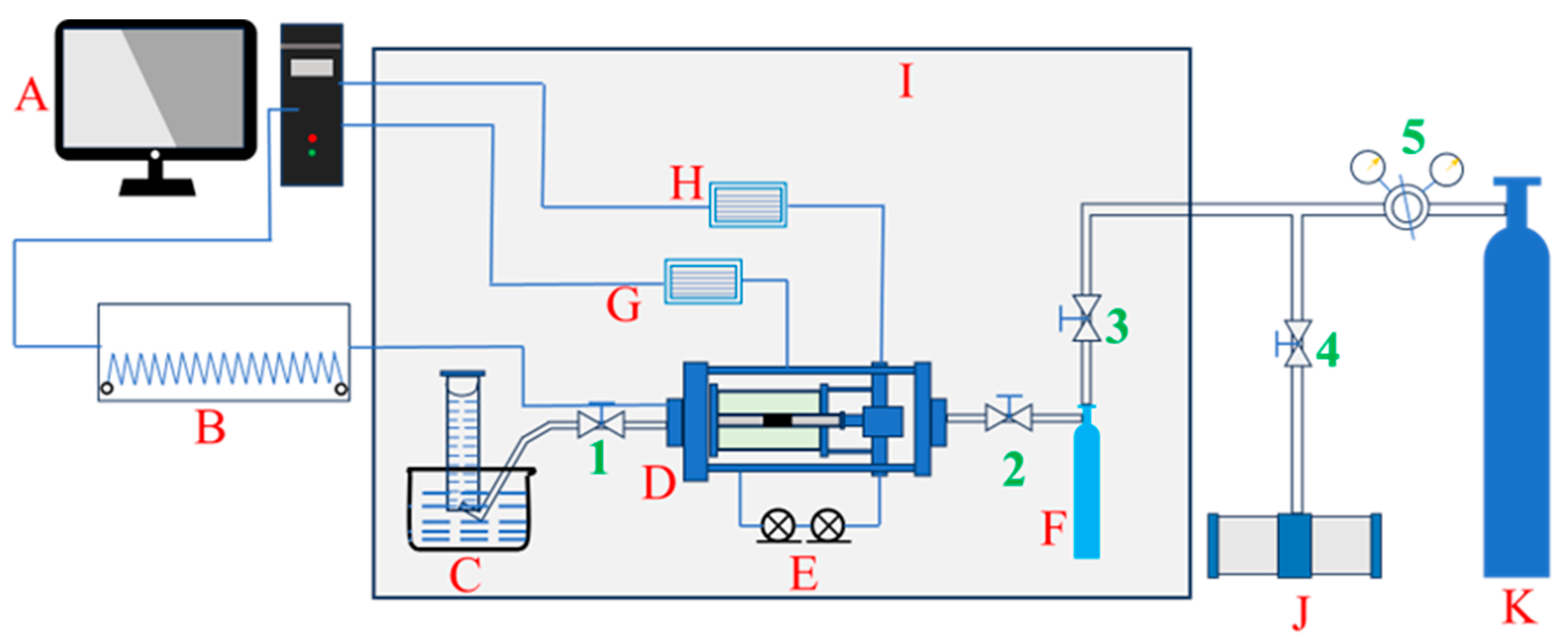
2.2.1. Experimental Equipment

The adsorption–permeability experiment was conducted using a “Permeation and Adsorption Simultaneous Test System”, which primarily consists of four integral components: a gas flowrate quantification module, a coal deformation measurement system, a gas pressure regulation mechanism, and an autonomous stress control unit, as depicted in Figure 1. This system is capable of simultaneously measuring the permeability, coal deformation, and gas adsorption capacity of samples. The permeability assessment was conducted in compliance with the Chinese National Standard SY/T 5336-2006 [41], pertaining to Core Analysis Methods. Given the low permeability of the Tangshan coal samples, the gas flow at the device’s outlet was minimal during the permeability test. Therefore, a gas collection device, indicated as element C in Figure 1, was employed to measure the outlet gas flow using the drainage method. The reference cylinder was connected to the stress sensor to monitor the inlet pressure and the gas pressure in the reference cylinder in real time.

2.2.2. Experimental Method

With the injection of gas into the coal samples, the gas adsorbs or fills the pores and cracks of the sample, thus causing deformation of the sample. This deformation is attributable to pore pressure in cases where the coal does not adsorb gas. Conversely, when the coal adsorbs gas, the deformation arises from both pore pressure and adsorption phenomena. To isolate the impact of gas adsorption on coal deformation, it is imperative to negate the deformation instigated solely by pore pressure. To this end, helium (He), a non-adsorptive gas [42], was initially injected into the coal sample, inducing strain solely through pore pressure influence. Subsequently, the sample was subjected to vacuum conditions before the introduction of an adsorbable gas. Given nitrogen’s (N₂) adsorptive properties and its weaker adsorption capacity relative to methane (CH₄), it serves as an effective proxy for CH₄ in adsorption–permeability experiments on coal samples, in accordance with the principle of inclusivity. Moreover, the inert nature of N₂ enhances the safety parameters of such experimental procedures. Therefore, N₂ was injected into the coal as the adsorbable gas [43]. The experimental procedures are as follows:

(1)

The dried coal samples were set in the core holder along with two sets of axial–radial resistance strain gauges. With a flex flat cable (FFC), the strain gauges were joined to the axial–radial strain transducer.

(2)

To simulate the real stress of coal seam, the axial pressure and confining pressure were kept at 7 MPa, and a vacuum pump was used to vacuum the coal sample, and then the air tightness of the pipeline was checked.

(3)

Helium gas (He) was injected into the reference cylinder at a predetermined pressure from the gas source. Helium injection was performed with incremental pressure levels, including 0.3 MPa, 0.5 MPa, 1 MPa, 1.5 MPa, 2 MPa, 2.5 MPa, and 3 MPa. At each injection pressure, the pressure was kept constant while the outlet was sealed before injection. The valve connecting the gas source to the reference cylinder was then closed, while the outlet of the reference cylinder was opened to inject He into the core gripper. This process was maintained for 72 h to calibrate the pore volume of the coal sample.

(4)

The outlet valve of the core gripper was kept open to the atmosphere until all specified injection pressures were completed, while measuring the radial strain of the sample under different injection pressures. The flow rate of helium (He) was measured using a gas collection device to calculate the permeability of the coal sample. The gas flow volume was measured by a gas collecting device for a certain period of time, thereby calculating the flow rate, and calculating the coal sample permeability based on Darcy’s law, as demonstrated as Equation (1).

$$k=\frac{2Q{p}_0\mu L}{\mathrm{A}\left(p_1^2-p_2^2\right)}$$

(1)

where k is coal permeability (10⁻³ μm²); Q is the flow rate (mL/s) through coal sample; p₀ is atmospheric pressure (take 0.1 MPa); μ is the hydrodynamic viscosity (Pa·s); L is the length of coal sample (cm); A is the cross-sectional area of coal sample (cm²) of the cylinder; and p₁ and p₂ are the gas pressures (MPa) at both ends of the inlet and outlet of coal sample.

(5)

We removed the gas pressure and closed the outlet, and then pumped the vacuum for more than 12 h.

(6)

Following the same procedure as the helium injection, nitrogen (N₂) was introduced for a duration of 72 h to obtain the volume of gas adsorbed by the coal sample. The flow rate was then measured to determine the sample’s permeability.

(7)

For each experimental set, the gas pressure was varied, starting from 0.3 MPa and incrementally increasing to 3 MPa, with the entire experimental procedure repeated seven times. The effective stress of the coal samples varied with the increase in pore pressure, calculated by Equation (2).

$${\sigma }_e=(2{\sigma }_r+{\sigma }_z)/3-\frac{p_1+p_2}{2}$$

(2)

Here, σ_e represents effective stress, MPa; σ_r represents radial stress, MPa; σ_z represents axial stress, MPa. The inlet gas pressure and effective stress changes are listed in

Table 1. Permeability experiments for different stress conditions.

Stress Condition	Value
Gas inlet pressure (MPa)	0.3	0.5	1	1.5	2	2.5	3
Effective stress (MPa)	6.8	6.7	6.45	6.2	5.95	5.7	5.45

.

2.3. Mercury Injection Porosimetry Experiment

2.3.1. Experimental Method

The MIP experiment was conducted at Tsinghua University in China with the Auto Pore IV 9520 device, according to the standard GB/T 21650.1-2008 [44] of China. The coal specimens were cube-shaped with 1 cm long sides. The surface tension was 0.485 N/cm and the contact angle between the mercury and coal was 130°, respectively. Washburn’s equation [45] can describe the relationship between mercury intrusion pressure and the pore size of the coal sample, as shown as Equation (3).

$$d=-\frac{4\sigma \cos \theta }{P}$$

(3)

where d represents pore diameter injected, nm; σ represents the surface tension of mercury, MPa; θ represents the angle of coal surface and mercury, °; P represents mercury injection pressure, MPa.

The pore size decreased as the injection pressure increased. The highest intrusion pressure reached 413 MPa, and the corresponding pore diameter was 3 nm. The largest pore diameter injected was about 370 μm at a low mercury injection pressure. Furthermore, we can obtain the pore volume at different pore sizes according to the mercury quantity injected.

2.3.2. Surface Fractal Dimension Calculation Method

It is universally acknowledged that the surface of coal is highly uneven [46]. Surface fractal dimension D_s can quantitatively estimate the roughness and complex characteristics of coal surface. The value of D_s, generally speaking, is between 2 and 3. Coal surface tends to be smoothy when D_s is close to 2. Coal surface is more complex and rougher when D_s approaches 3. Based on mercury intrusion volume modified data, Zhang’s model was adopted in this work [35,36], calculated by Equation (4).

$$D_s=\frac{d\ln \left(\raisebox{1ex}{$W_n$}\!\left/ \!\raisebox{-1ex}{$r_n^2$}\right.\right)}{d\ln \left(\raisebox{1ex}{$V_n^{1/3}$}\!\left/ \!\raisebox{-1ex}{$r_n$}\right.\right)}$$

(4)

where W_n represents the accumulative surface energy, J; r_n represents the smallest pore radius injected by mercury pressure P_i, nm; V_n represents cumulative mercury injecting volume, mL/g.

Where

$$W_n={\displaystyle \sum _{i=1}^{i=n}{P}_i}∆V_i$$

(5)

The surface fractal dimension D_s is equal to the slope of the $\ln \left(\raisebox{1ex}{$V_n^{1/3}$}\!\left/ \!\raisebox{-1ex}{$r_n$}\right.\right)$ vs. $\ln \left(\raisebox{1ex}{$W_n$}\!\left/ \!\raisebox{-1ex}{$r_n^2$}\right.\right)$ as the ordinate.

3. Experimental Results and Analysis

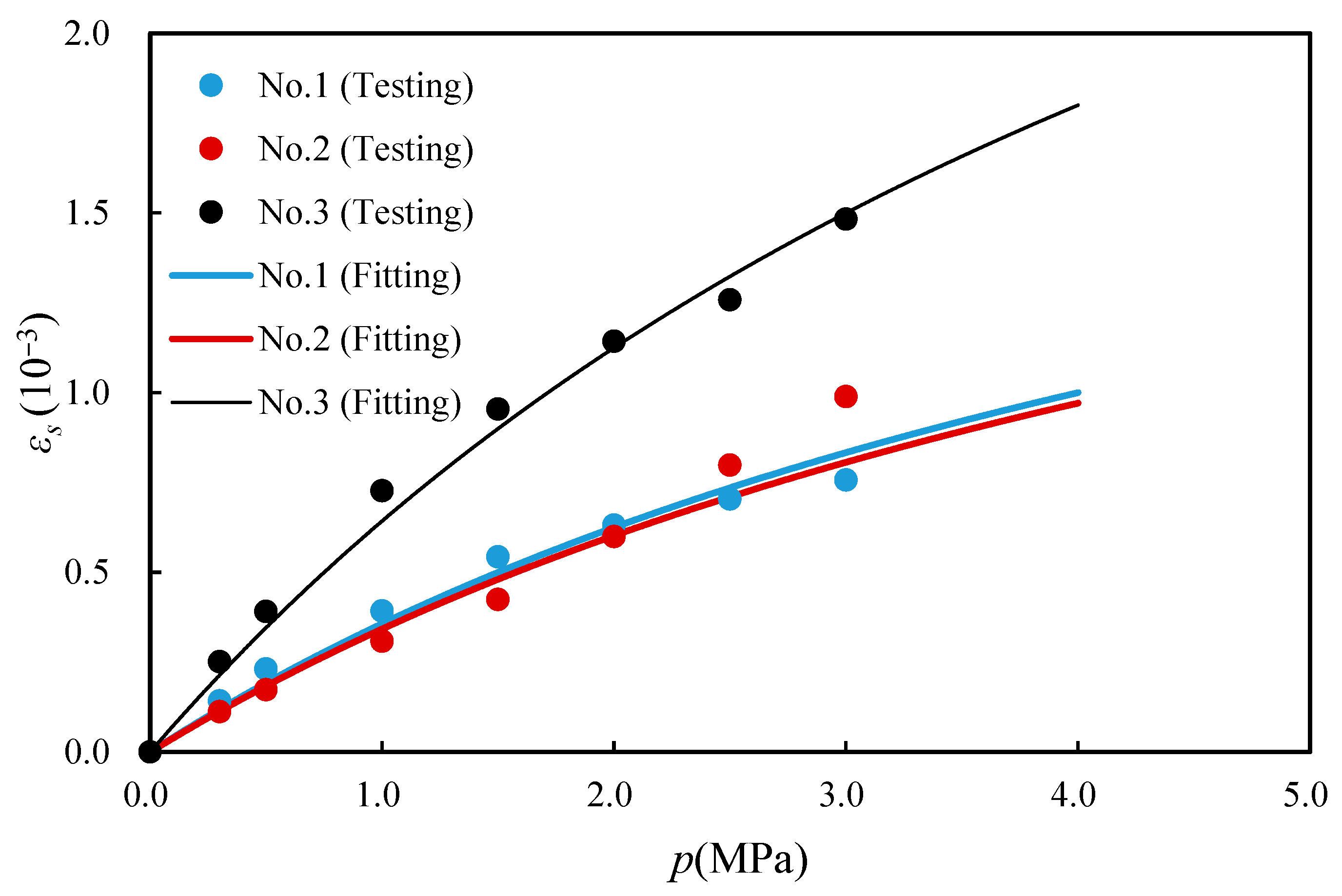
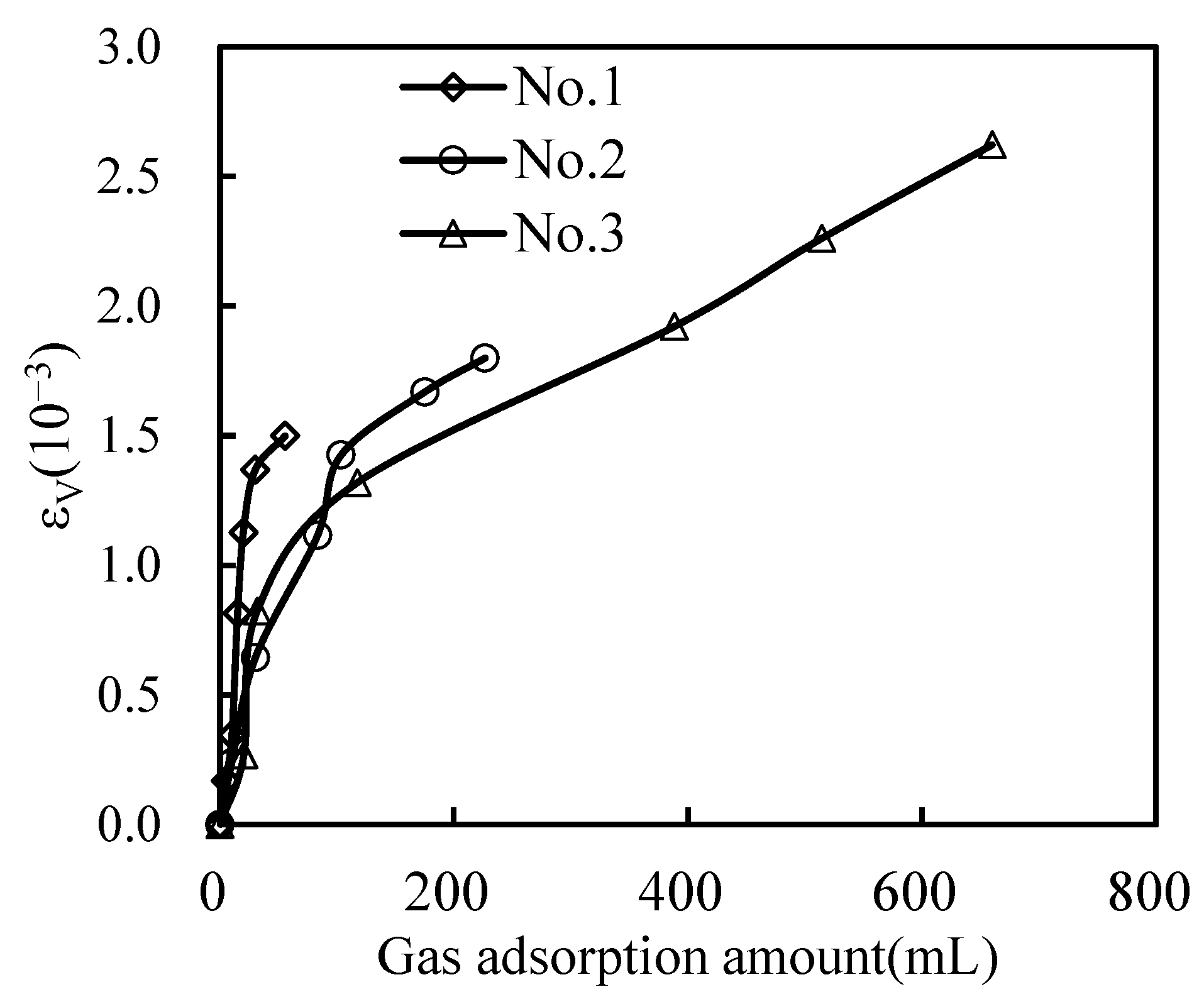
3.1. Nitrogen Adsorption Strain of Coal Samples

Nitrogen is an adsorbent gas. The deformation of three coal samples at various gas pressure points is influenced not only by effective stress changes, but also by gas adsorption. The adsorption of nitrogen in coal causes the coal matrix to expand, resulting in a negative volumetric strain on the nitrogen-containing coal sample under identical experimental circumstances, indicating that each sample creates a considerable expansion strain. Helium has no absorbability, and its strain value reflects other stress conditions except adsorption effect. Therefore, the adsorption strain is equal to the difference between the strain values of nitrogen and helium, which is obtained from Equation (6). The adsorption strain results are listed in

Table 2. Testing adsorption strain data at different pressure points.

Pressure/MPa	No. 1 (10−3)	No. 2 (10−3)	No. 3 (10−3)
0.3	0.142	0.112	0.251
0.5	0.231	0.173	0.391
1.0	0.392	0.308	0.727
1.5	0.543	0.424	0.954
2.0	0.631	0.599	1.143
2.5	0.704	0.798	1.258
3.0	0.757	0.989	1.483

.

$${\epsilon }_s=\left|{\epsilon }_{\left({\mathrm{N}}_2\right)}-{\epsilon }_{\left(\mathrm{He}\right)}\right|$$

(6)

The adsorption strain of three coal samples rises as the gas pressure increases, as seen in Figure 2. The results demonstrate that when the gas pressure increases, the change rate of the coal sample strain slows, indicating that the adsorption strain is suppressed by effective stress [47,48]. To evaluate the law of coal adsorption gas, a Langmuir-type strain model was employed to fit the relationship between sorption-induced deformation and injection pressure. The strain induced by adsorption in coal is intrinsically linked to its gas adsorption capacity. Consequently, an equation analogous to the Langmuir equation was utilized in this study to characterize the adsorption deformation across varying coal ranks.

$${\epsilon }_s=\frac{{\epsilon }_{L}p}{p+p_L}$$

(7)

where ε_L denotes the Langmuir strain, defined as the theoretical maximum axial, radial, or volumetric strain of coal, also in percentages; p_L is the gas pressure at which the strain attains half of its theoretical maximum value, analogous to the Langmuir pressure, measured in MPa; p signifies the gas pressure, in MPa.

To fit the experimental data, Equation (7) is employed, and the fitting parameters are provided in

Table 3. Langmuir fitting parameters.

Sample Number	No.1	No.2	No.3
εL (10−3)	2.516	2.524	4.513
pL (MPa)	6.0	6.3	6.0

. The solid points in Figure 2 represent experimental data, while the solid lines are fitting curves. The fitting correlative parameters are more than 0.99.

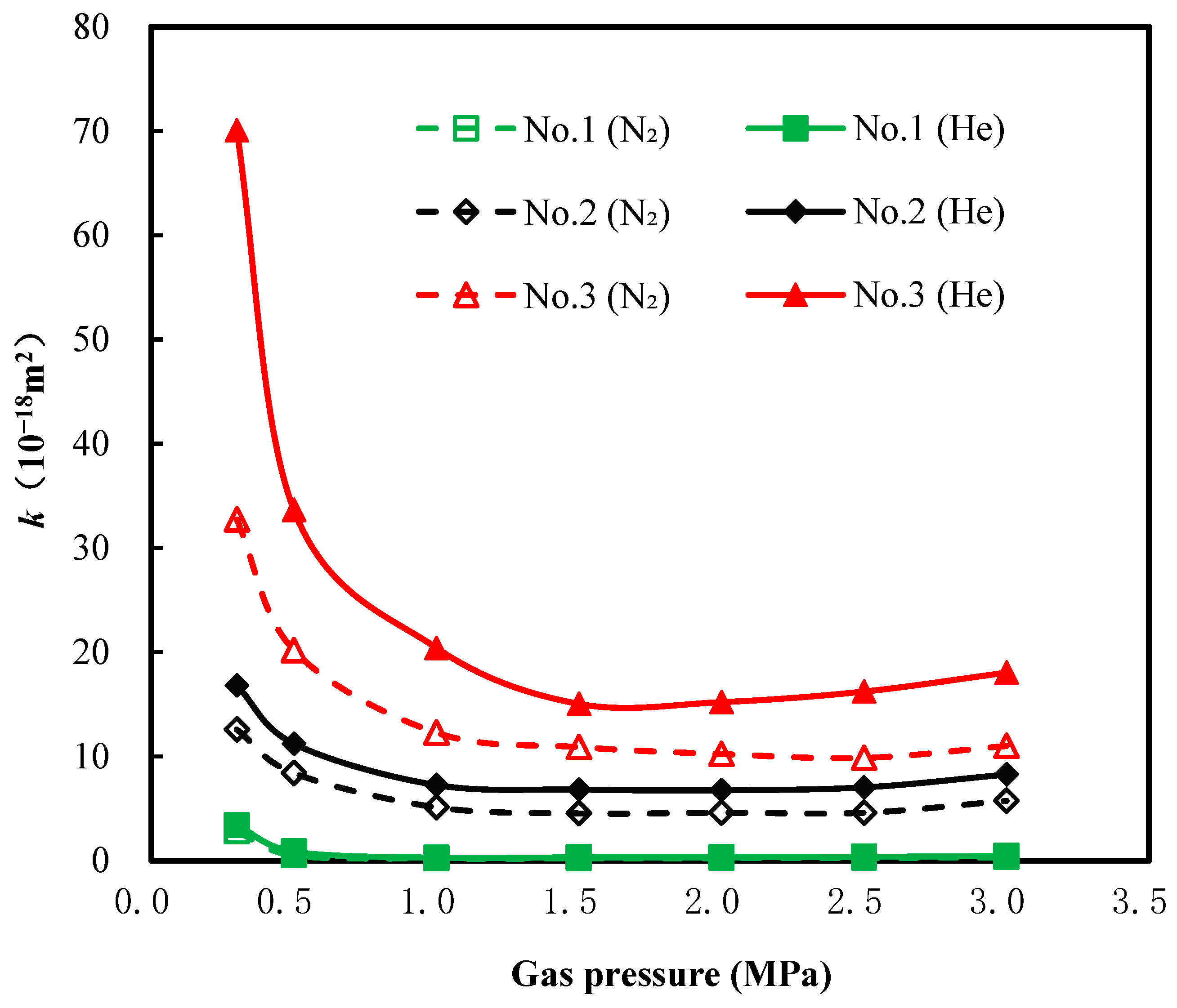
3.2. Coal Permeability under Different Gas Pressure

Based on the outlet flow rate measured at each specified gas pressure point, the permeability curves of three coal samples were calculated by Equation (1), as shown in Figure 3. The maximum permeability of the coal samples was determined to be 70 × 10⁻¹⁸ m². Tangshan Coal Mine is clearly associated with a poor-permeability coal seam.

The confining pressure and axial pressure remain constant, and the effective stress decreases with the increase in gas pressure. Coal permeability changes with the increase in gas pressure, as described in Figure 3. As the gas pressure increases, the permeability decreases first and then increases. The turning point corresponding to lowest permeability is called the permeability rebound point [49]. The permeability rebound point of Tangshan coal samples is approximately equal to 1.0 MPa. The lowest permeabilities of the three samples are found to be 0.98 × 10⁻¹⁸ m², 6.76 × 10⁻¹⁸ m², and 15.0 × 10⁻¹⁸ m², suggesting that, despite the fact that the coal samples are from the same mining location, the internal pore structure is different, resulting in considerable variances in permeability.

Previous studies held that effective stress was the primary factor influencing coal permeability variations. The relationship between permeability k and effective stress increments ∆σ_e is commonly expressed using Equation (8) [3].

$$k=k_0\exp \left(-3C_f∆{\sigma }_{\mathrm{e}}\right)$$

(8)

where k₀ is the initial permeability, (10⁻³ μm²); C_f is the pore compression factor.

We can observe from Equation (8) that permeability decreases as the effective stress increases. However, the permeability–effective stress curve recorded in our experiment is V-shaped, which contradicts Equation (8), suggesting that the effective stress is not the only factor affecting the permeability change. The permeability variation of helium is V-shaped too, indicating that the Klinkenberg effect exists.

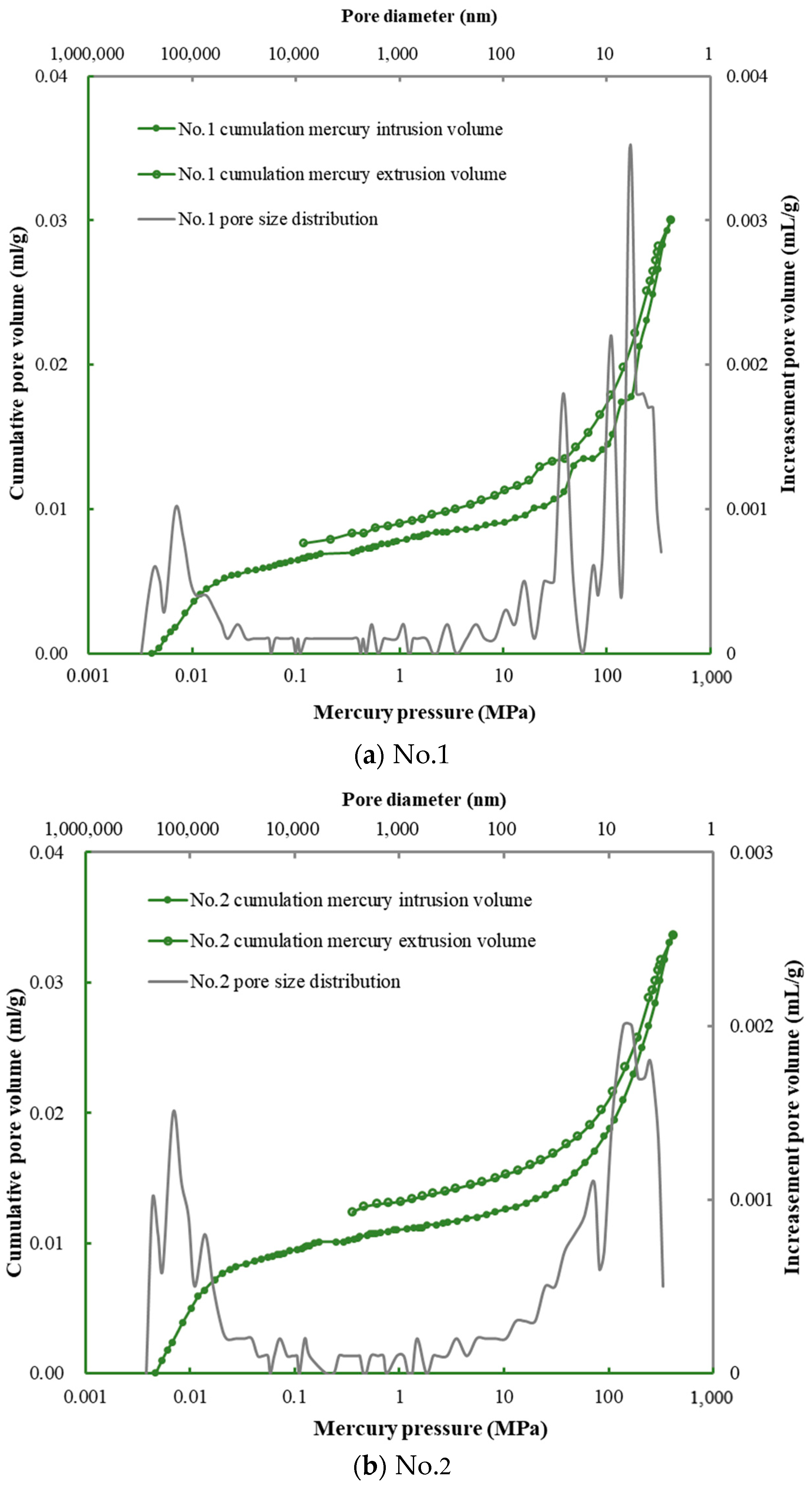
3.3. Pore Structure Characteristics Detected by MIP

Mercury intrusion and extrusion curves of Tangshan coal samples are deployed in Figure 4. Mercury intrusion curves are in a reverse “S” shape. Mercury filled the interspaces of pores rapidly when the injecting pressure is less than 0.01 MPa, and the corresponding pore diameter is 12 μm. The mercury injection volume increases slowly as the mercury increases. The slopes of the cumulative mercury intrusion curves rise faster when the mercury injection pressure is greater than 100 MPa. The mercury injection curves also reveal that the pores with a diameter greater than 10 μm, and less than 100 nm, are more developed. There is a narrow hysteresis loop formed between the mercury intrusion and extrusion curves of each sample, indicating that seepage pores mainly consist of semi-closed pores. Meanwhile, a certain amount of open pores also exist [50]. Overall, Tangshan coal samples mainly consist of micropores, transport pores, and micro fractures. Some pore feature parameters of the coal samples are listed in

Table 4. Pore parameters from MIP test.

Sample No.	Porosity/%	Median Pore Diameter in Volume/nm	Average Pore Size/nm	Total Pore Volume/cm3/g	The Efficiency of Mercury Withdrawal/%
No. 1	3.963	11.4	9.7	0.03	74.7
No. 2	5.586	127.5	13.8	0.0336	63.1
No. 3	5.451	52.6	12.9	0.042	54.8

. What is noteworthy is that the coal matrix produces elastic compression when the mercury injection pressure is greater than 20 MPa, resulting in the pore volume measured the pore in this range being larger than the actual volume [24,51]. An intrusion pressure of 20 MPa corresponds to a pore diameter of 60 nm in this work. So, the pore volume measured should be modified when the size less than 60 nm.

4. Discussion

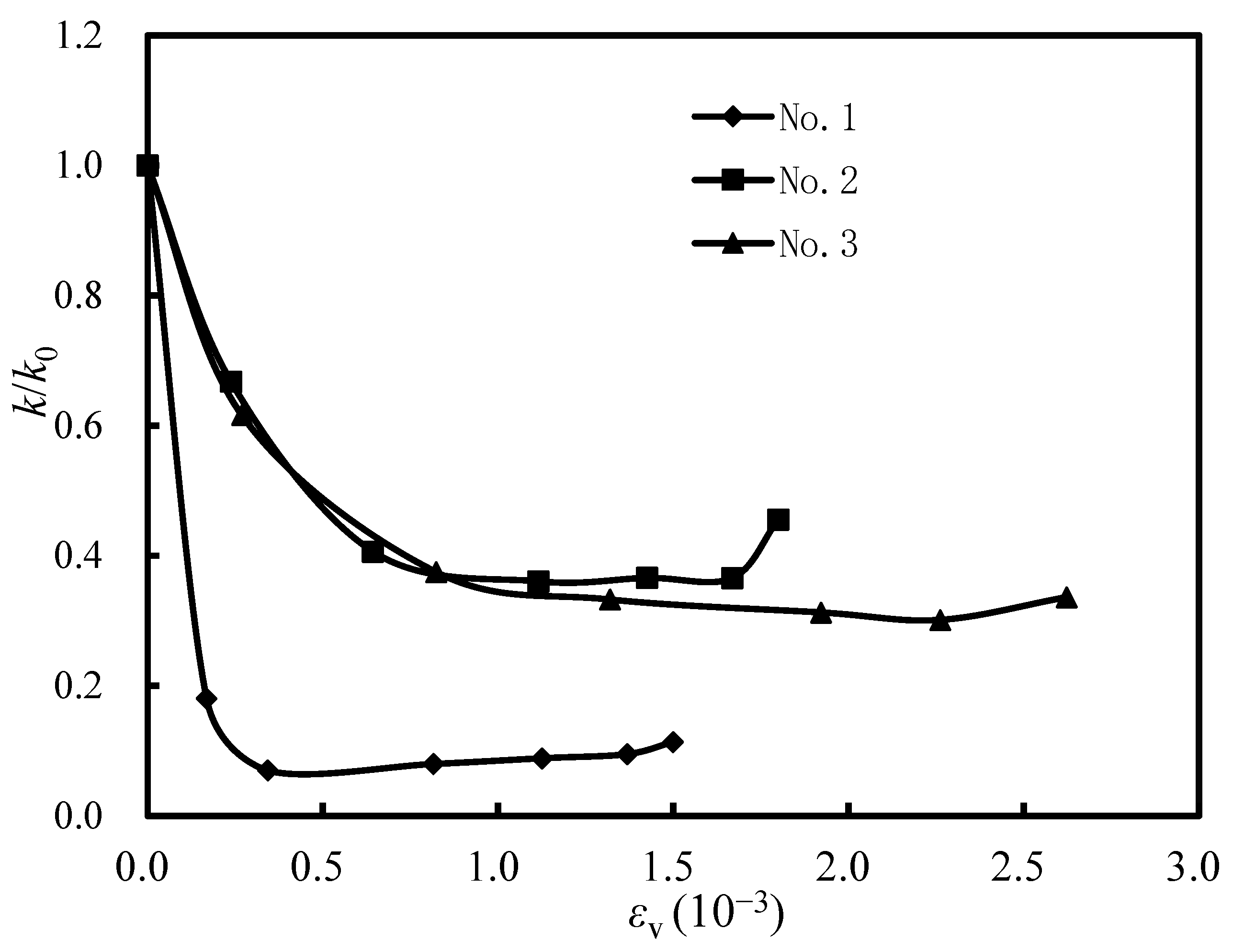
4.1. The Relationship between Permeability and Adsorption Strain

For convenience, a dimensionless permeability ratio k/k₀ was used to show the trend of permeability. As shown in Figure 5, the three coal samples all show a trend of k/k₀ decreasing sharply at first and then rising slowly with the increase in gas pressure, and the volumetric strain increases gradually with the increase in gas pressure, and the permeability is basically negatively correlated with the volumetric strain. The permeability of the coal samples is affected by a variety of factors. The external confining pressure and axial pressure compress the coal sample, and the internal pores of the coal body are squeezed inward, resulting in a decrease in coal permeability [7]. After gas fills the coal, the gas pressure makes the pores expand, resulting in an increase in coal penetration and permeability. At the same time, the adsorption effect also makes the coal matrix swell [28,29,30]. There are competition mechanisms with several functions, which makes gives permeability change complex rules. When the external confining pressure and axial pressure remain unchanged, gas pressure keeps increasing, and the pores under the action of gas pressure will expand, and the permeability will increase with the increase in coal permeability. However, the experimental data show that the permeability basically shows a downward trend with the increase in gas pressure, indicating that the adsorption effect has a negative effect on permeability.

The volumetric strain of the coal sample increasing with the increase in adsorption capacity is shown in Figure 6. The more gas is adsorbed by the coal matrix, the greater the expansion deformation. The volumetric strain has a linear relationship with the adsorption capacity when the gas pressure is in low-pressure conditions (less than 2 MPa). The increase in volumetric strain slows down when the gas pressure is greater than 2 MPa.

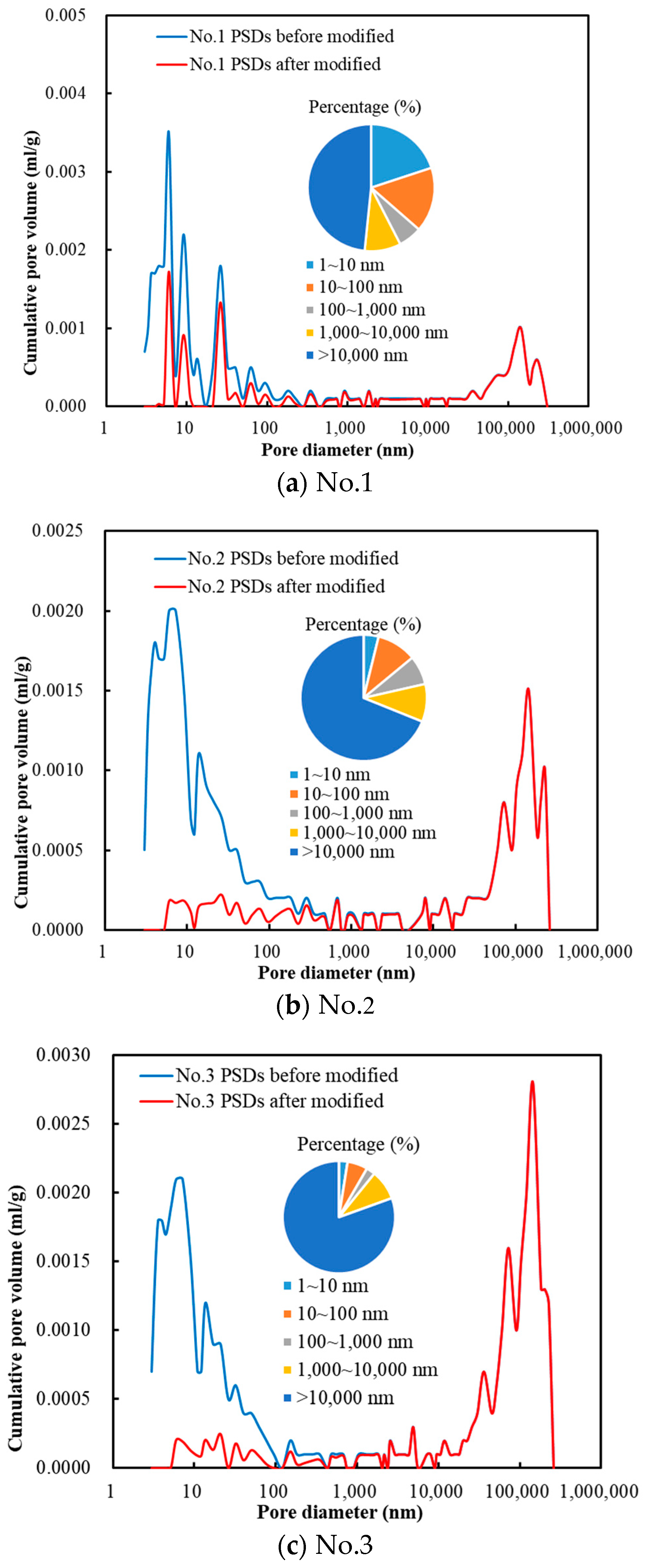
4.2. Pore Size Distributions

The MIP test results for mesopores and macropores should have relatively high reliability. However, coal’s skeleton structure will be damaged under very high injection pressure. So, the results of mercury injection experiment are not suitable to be directly used as the results of nano-aperture, so it is necessary to revise the results of mercury injection experiment. In this paper, only mercury injection data were used for correction, which is the same as Li [26]. The matrix compressibility k_c can be expressed as Equation (9) [52].

$$k_c=\frac{d{V}_m}{V_{m}dP}$$

(9)

Here, V_m represents the volume of the matrix skeleton, m³.

For a more practical approach to MIP data correction, it is assumed that the same effective compressibility can be applied as a component-independent parameter. In other words, the organic matrix, inorganic minerals, pores, and fissures without mercury filling have the same effective compressibility, which represents a bulk behavior. Once the pores and fractures are filled with mercury, they are not compressed. The compressed coal matrix volume exhibits the following relationship with the observed mercury volume (see Equation (10) [26].

$$V_{mc}\left(P_i\right)=V_{bulk}-V_{obs}\left(P_{i-1}\right)$$

(10)

Here, $V_{mc}\left(P_i\right)$ represents the coal matrix compressive volume at pressure P_i, V_bulk represents the bulk volume of the coal sample, and V_obs (P_i−1) represents the observed mercury volume at pressure P_i−1.

According to coal matrix compressibility, the pore volume modified at P_i can be expressed by Equation (11).

$$V_{pore}\left(P_i\right)=V_{pore}\left(P_{i-1}\right)+\left[\left(V_{obs}\left(P_i\right)-V_{obs}\left(P_{i-1}\right)\right)-\left(V_{bulk}-V_{obs}\left(P_{i-1}\right)\right)\times k_c\times \left(P_i-P_{i-1}\right)\right]$$

(11)

Here, $V_{pore}\left(P_i\right)$ and $V_{pore}\left(P_{i-1}\right)$ represent the pore volume at P_i and P_i−1, respectively.

The compressibility of the coal matrix and other related parameters are listed in

Table 5. The parameters of compressibility of coal samples.

Sample No.	Volume of Coal Matrix Skeleton (cm3/g)	Bulk Volume of Coal Sample (cm3/g)	km (×10−11 m2/N)	Pore Volume before Modified (cm3/g)	Pore Volume after Modified (cm3/g)	Volume Correction Rate (%)
No.1	0.7269	0.7569	6.9616	0.0300	0.0136	54.557
No.2	0.7135	0.7557	7.1995	0.0336	0.0141	58.124
No.3	0.7283	0.7702	7.4372	0.0420	0.0215	48.868

. The average compressibility of coal samples is 7.199 × 10⁻¹¹ m²/N, and the mean volume correction rate is 53.85%. The larger the micropores’ volume, the smaller the matrix compressibility k_m.

The pore size distributions of the coal samples before being modified and after being modified are displayed by Figure 7. The dominant pores of Tangshan coal samples are micro fractures (pore diameter > 10,000 nm), accounting for 65.93%, which were convenient for coalbed gas seepage. The content of the other types of pores is low, which is not conducive to the storage and diffusion migration of coalbed methane. As shown in Figure 7, pore content fluctuates significantly at different pore size stages, indicating that pore size and pore volume are independent of each other.

4.3. Fractal Analysis on Pore Structure

As shown in Figure 8, the surface fractal dimension curves consist of three obvious regions. Namely, D_s1, micropore, and transport pore region (r < 50 nm); D_s2, mesopore, and macropore region (50 nm < r < 5000 nm); D_s3 and micro fracture region (r > 5000 nm). Compared to cement-based porous materials, Tangshan coal samples have distinct fractal characteristics in the mesopore and macropore regions [30,31]. The pore fractal features of the Tangshan coal samples in all regions are obvious (R² > 0.99). The fractal dimensions of different regions are listed in

Table 6. The results of pore fractal dimensions and other parameters.

Sample No.	Ds1	Ds2	Ds3	Va (mL/g)	Vs (mL/g)	Permeability N2 * (10−18 m2)
No. 1	2.99	2.76	2.56	0.0050	0.0087	0.32
No. 2	2.89	2.53	2.55	0.0020	0.0121	5.73
No. 3	2.89	2.53	2.55	0.0018	0.0197	13.76

Note: V_a represents adsorption pore volume of r < 50 nm; V_s represents seepage pore volume of r > 50 nm; * the permeability measured in 3.0 MPa gas pressure.

. For the surface fractal dimensions of sample No. 1, D_s1 > D_s2 > D_s3, indicating that the pore surface with a smaller pore size is coarser and more complex. At the same time, the pore surface roughness of each pore size segment of sample No. 1 is greater than that of sample No. 2 and sample No. 3.

In Table 6, the adsorption pores make contributions to the corresponding pore surface fractal dimension D_s1, and the larger the adsorption pore volume is, the rougher the pore surface is and the larger the fractal dimension D_s1 is. Therefore, the surface fractal dimension D_s1 is positively correlated with the adsorption pore content. The more pore seepage content, the smoother the porous channel, the smaller pore surface dimensions D_s2 and D_s3, and the more conducive the sample is to gas seepage. Numerically, pore surface fractal dimensions D_s2 and D_s3 are negatively correlated to seepage pore content and permeability.

5. Conclusions

(1)

Under the condition that the axial and confining stresses are both 7 MPa, with the increase in gas pressure, the nitrogen adsorption strain aggrandizes and follows the laws of the Langmuir trend. The trend of permeability for helium is similar to a “V” shape, revealing that the permeability of helium is affected by effective stress and the slippage effect. The evolution of nitrogen permeability is similar to that of nitrogen. The permeability difference between them shows the influence of nitrogen adsorption effect on gas permeability, and adsorption effect reduces the permeability of coal samples.

(2)

The pore structure characteristics of coal samples with pore sizes ranging from 3 nm to 370 μm was investigated with a high-pressure mercury injection experiment. The coal matrix produces compressibility when the mercury injection pressure is greater than 20 MPa, and the mercury injection data are used merely for compressibility correction in this work. The dominant pores of Tangshan coal samples are micro-cracks, accounting for 66% of the total pore volume. The pores are mainly composed of semi-open pores with one end closed, which is convenient for gas seepage.

(3)

Surface fractal dimension D_s can reveal the roughness and complexion of the pore surface, and its value is between two and three. The larger D_s is, the rougher and more complex the pore surface is. The surface fractal dimension D_s1 is larger than D_s2 and D_s3, indicating that the surface roughness of adsorbed pores is higher than that of seepage pores. D_s1 is positively correlated with micropore volume content, while D_s2 and D_s3 are negatively correlated with pore volume content and gas permeability.