Hybrid (Optimal) Selection Model for Phase Change Materials Used in the Cold Energy Storage of Air Conditioning Systems
Abstract
:1. Introduction
1.1. Phase Change Material (PCM)
1.2. Basic Principle of Phase Change Material
1.3. Desired Properties of PCMs for Cold Storage
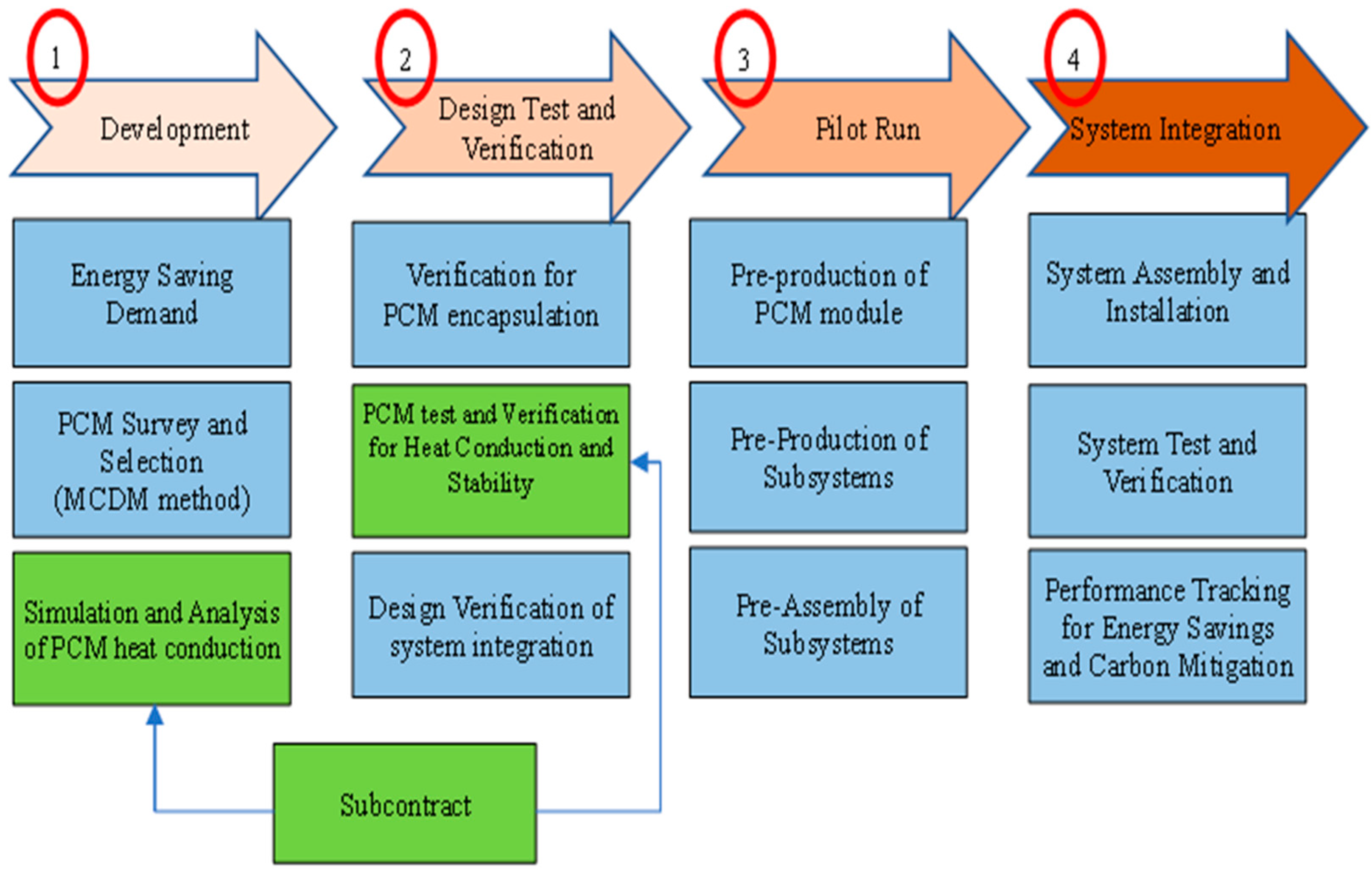
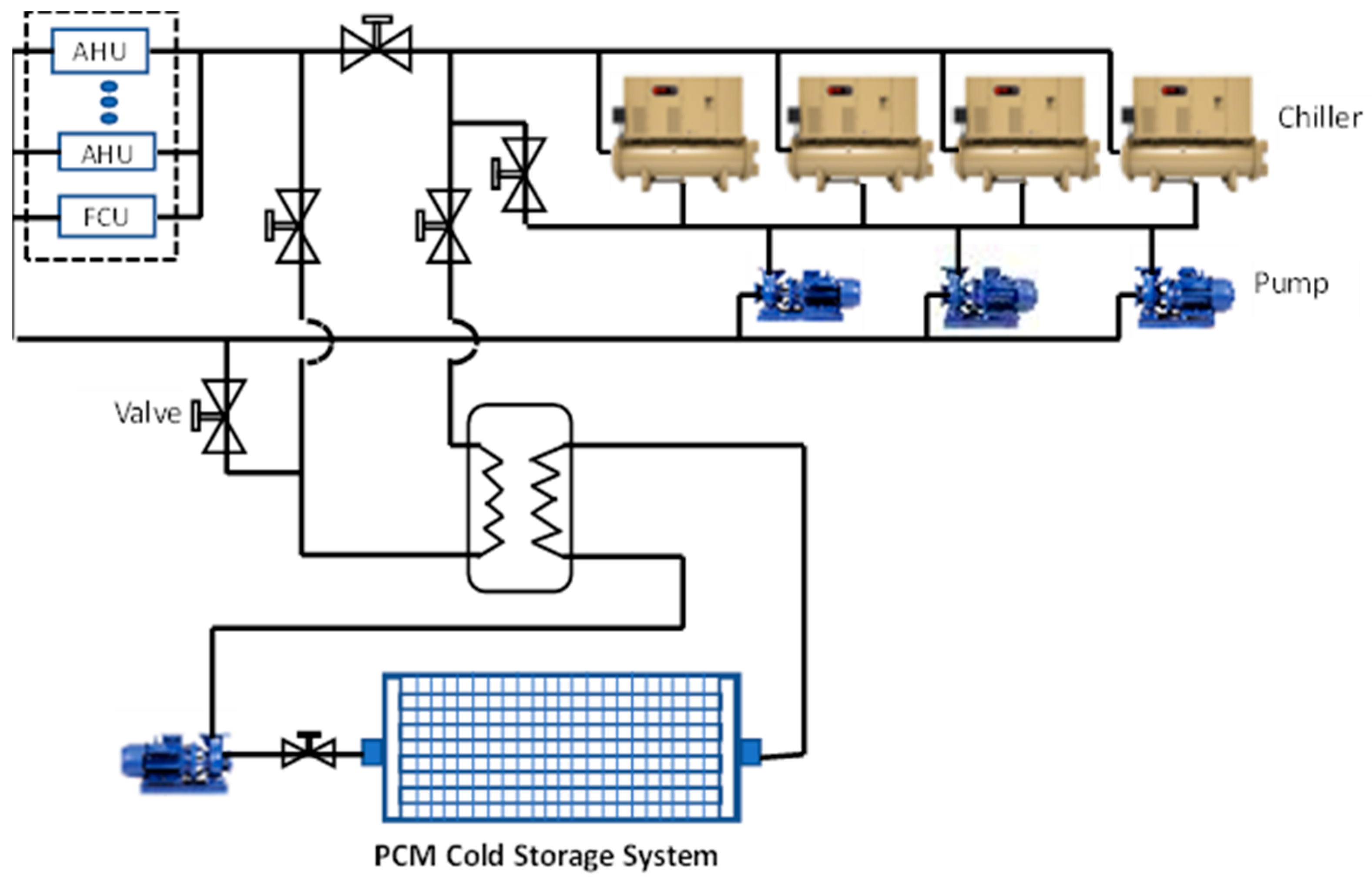
1.4. PCM Application for the Cold Storage of Air Conditioning
2. Material and Methods
2.1. PCMs for the Cold Storage of Air Conditioning Systems
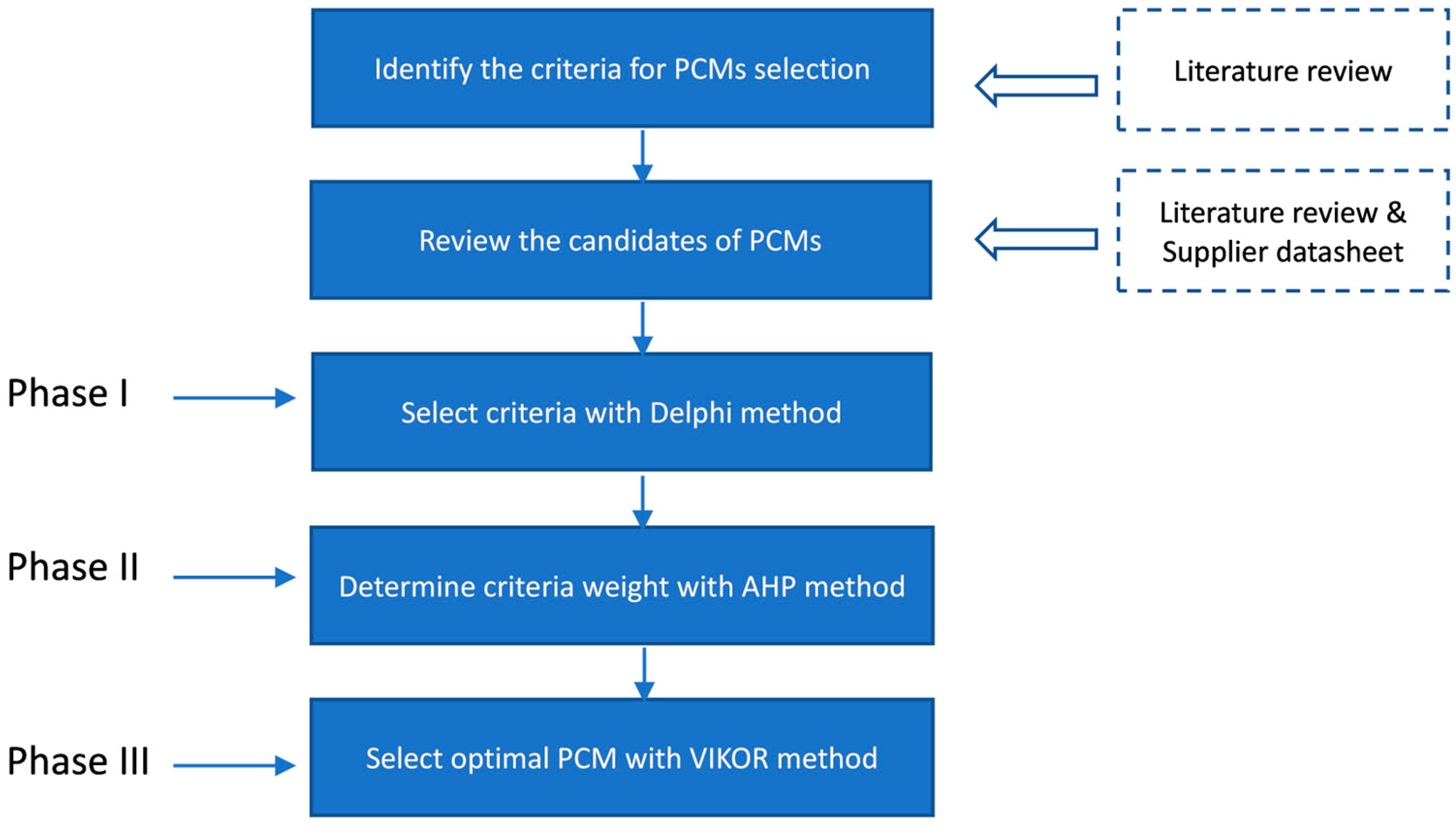
2.2. PCM Selection Model for Cold Storage
2.3. Methods and Model Calculation Steps
2.3.1. Delphi Method
2.3.2. AHP Method
2.3.3. VIKOR Method
3. Model Calculation
3.1. Criteria Selection Using Delphi Method
3.2. Criteria Weighting from Using AHP Method
3.3. VIKOR Calculation and Ranking
4. Results and Discussion
4.1. Delphi Results
4.2. AHP Results
4.3. VIKOR Results
4.4. Discussion
4.4.1. Limitations
4.4.2. Future Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chua, K.J.; Chou, S.K.; Yang, W.; Yan, J. Achieving better energy-efficient air conditioning—A review of technologies and strategies. Appl. Energy 2013, 104, 87–104. [Google Scholar] [CrossRef]
- Nie, B.; Du, Z.; Chen, J.; Zou, B.; Ding, Y. Performance enhancement of cold energy storage using phase change materials with fumed silica for air-conditioning applications. Int. J. Energy Res. 2021, 45, 16565–16575. [Google Scholar] [CrossRef]
- Omara, A.A.; Abuelnour, A.A. Improving the performance of air conditioning systems by using phase change materials: A review. Int. J. Energy Res. 2019, 43, 5175–5198. [Google Scholar] [CrossRef]
- Hlanze, P.; Elhefny, A.; Jiang, Z.; Cai, J.; Shabgard, H. In-duct phase change material-based energy storage to enhance building demand flexibility. Appl. Energy 2022, 310, 118520. [Google Scholar] [CrossRef]
- Emovon, I.; Oghenenyerovwho, O.S. Application of MCDM method in material selection for optimal design: A review. Results Mater. 2020, 7, 100115. [Google Scholar] [CrossRef]
- Imghoure, O.; Belouaggadia, N.; Ezzine, M.; Lbibb, R.; Younsi, Z. Performance evaluation of phase change materials for thermal comfort in a hot climate region. Appl. Therm. Eng. 2021, 186, 116509. [Google Scholar] [CrossRef]
- Socaciu, L.; Giurgiu, O.; Banyai, D.; Simion, M. PCM selection using AHP method to maintain thermal comfort of the vehicle occupants. Energy Proc. 2016, 85, 489–497. [Google Scholar] [CrossRef]
- Oluah, C.; Akinlabi, E.T.; Njoku, H.O. Selection of phase change material for improved performance of Trombe wall systems using the entropy weight and TOPSIS methodology. Energy Build. 2020, 217, 109967. [Google Scholar] [CrossRef]
- Xu, H.; Sze, J.Y.; Romagnoli, A.; Py, X. Selection of phase change material for thermal energy storage in solar air conditioning systems. Energy Proc. 2017, 105, 4281–4288. [Google Scholar] [CrossRef]
- Nicolalde, J.F.; Cabrera, M.; Martínez-Gómez, J.; Salazar, R.B.; Reyes, E. Selection of a PCM for a vehicle’s rooftop by multicriteria decision methods and simulation. Appl. Sci. 2021, 11, 6359. [Google Scholar] [CrossRef]
- Wong-Pinto, L.S.; Milian, Y.; Ushak, S. Progress on use of nanoparticles in salt hydrates as phase change materials. Renew. Sustain. Energy Rev. 2020, 122, 109727. [Google Scholar] [CrossRef]
- Kenfack, F.; Bauer, M. Innovative Phase Change Material (PCM) for heat storage for industrial applications. Energy Proc. 2014, 46, 310–316. [Google Scholar] [CrossRef]
- Podara, C.V.; Kartsonakis, I.A.; Charitidis, C.A. Towards phase change materials for thermal energy storage: Classification, improvements and applications in the building sector. Appl. Sci. 2021, 11, 1490. [Google Scholar] [CrossRef]
- Mofijur, M.; Mahlia, T.M.I.; Silitonga, A.S.; Ong, H.C.; Silakhori, M.; Hasan, M.H.; Putra, N.; Ashrafur Rahman, S.M. Phase Change Materials (PCM) for solar energy usages and storage: An overview. Energies 2019, 12, 3167. [Google Scholar] [CrossRef]
- Selvnes, H.; Allouche, Y.; Manescu, R.I.; Hafner, A. Review on cold thermal energy storage applied to refrigeration systems using phase change materials. Therm. Sci. Eng. Prog. 2021, 22, 100807. [Google Scholar] [CrossRef]
- Akeiber, H.; Nejat, P.; Majid, M.Z.A.; Wahid, M.A.; Jomehzadeh, F.; Zeynali Famileh, I.; Calautit, J.K.; Hughes, B.R.; Zaki, S.A. A review on phase change material (PCM) for sustainable passive cooling in building envelopes. Renew. Sustain. Energy Rev. 2016, 60, 1470–1497. [Google Scholar] [CrossRef]
- Tatsidjodoung, P.; Le Pierrès, N.; Luo, L. A review of potential materials for thermal energy storage in building applications. Renew. Sustain. Energy Rev. 2013, 18, 327–349. [Google Scholar] [CrossRef]
- Faraj, K.; Khaled, M.; Faraj, J.; Hachem, F.; Castelain, C. Phase change material thermal energy storage systems for cooling applications in buildings: A review. Renew. Sustain. Energy Rev. 2020, 119, 109579. [Google Scholar] [CrossRef]
- Farid, M.M.; Khudhair, A.M.; Razack, S.A.K.; Al-Hallaj, S. A review on phase change energy storage: Materials and applications. Energy Convers. Manag. 2004, 45, 1597–1615. [Google Scholar] [CrossRef]
- Iten, M.; Liu, S. A work procedure of utilising PCMs as thermal storage systems based on air-TES systems. Energy Convers. Manag. 2014, 77, 608–627. [Google Scholar] [CrossRef]
- Kalnaes, S.E.; Jelle, B.P. Phase change materials and products for building applications: A state-of-the-art review and future research opportunities. Energy Build. 2015, 94, 150–176. [Google Scholar] [CrossRef]
- Li, S.F.; Liu, Z.H.; Wang, X.J. A comprehensive review on positive cold energy storage technologies and applications in air conditioning with phase change materials. Appl. Energy 2019, 255, 113667. [Google Scholar] [CrossRef]
- Gujarathi, H. Use of Nanoparticle Enhanced Phase Change Material (NEPCM) for Data Center Cooling Application. Master’s Thesis, The University of Texas at Arlington, Arlington, TX, USA, 2014. [Google Scholar]
- Ushak, S.; Galazutdinova, Y.; Grágeda, M.; Gutierrez, A.; Cabeza, L.F.; Farid, M.M. Thermal Management System of Li-Ion Batteries Using Inorganic Phase-Change Materials. In Proceedings of the EuroSun 2014 Conference, Aix-les-Bains, France, 16–19 September 2014; pp. 1–7. [Google Scholar]
- Frigione, M.; Lettieri, M.; Sarcinella, A. Phase change materials for energy efficiency in buildings and their use in mortars. Materials 2019, 12, 1260. [Google Scholar] [CrossRef] [PubMed]
- Oro, E.; de Gracia, A.; Castell, A.; Farid, M.M.; Cabeza, L.F. Review on phase change materials (PCMs) for cold thermal energy storage applications. Appl. Energy 2012, 99, 513–533. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Wang, X.L.; Wang, T.; Wang, R.Z. A review on phase change cold storage in air-conditioning system: Materials and applications. Renew. Sustain. Energy Rev. 2013, 22, 108–120. [Google Scholar] [CrossRef]
- Anilkumar, B.; Maniyeri, R.; Anish, S. Optimum selection of phase change material for solar box cooker integrated with thermal energy storage unit using multi-criteria decision-making technique. J. Energy Storage 2021, 40, 102807. [Google Scholar] [CrossRef]
- Sharma, A.; Chauhan, R.; Ali Kallioğlu, M.; Chinnasamy, V.; Singh, T. A review of phase change materials (PCMs) for thermal storage in solar air heating systems. Mater. Today Proc. 2021, 44, 4357–4363. [Google Scholar] [CrossRef]
- Said, M.A.; Hassan, H. Parametric study on the effect of using cold thermal storage energy of phase change material on the performance of air-conditioning unit. Appl. Energy 2018, 230, 1380–1402. [Google Scholar] [CrossRef]
- Li, G.; Hwang, Y.; Radermacher, R. Review of cold storage materials for air conditioning application. Int. J. Refrig. 2012, 35, 2053–2077. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Turoff, M.; Linstone, H.A. The Delphi Method-Techniques and Applications. 2002. Available online: https://www.foresight.pl/assets/downloads/publications/Turoff_Linstone.pdf (accessed on 22 November 2023).
- Shariff, N. Utilizing the Delphi survey approach: A review. J. Nurs. Care 2015, 4, 246. [Google Scholar] [CrossRef]
- Keeney, S.; Hasson, F.; McKenna, H.P. A critical review of the Delphi technique as a research methodology for nursing. Int. J. Nurs. Stud. 2001, 38, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Rathod, M.K.; Kanzaria, H.V. A methodological concept for phase change material selection based on multiple criteria decision analysis with and without fuzzy environment. Mater. Des. 2011, 32, 3578–3585. [Google Scholar] [CrossRef]
- Saaty, T.L. Fundamentals of the Analytic Hierarchy Process. In The Analytic Hierarchy Process in Natural Resource and Environmental Decision Making; Springer: Berlin/Heidelberg, Germany, 2001; pp. 15–35. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Extended VIKOR method in comparison with outranking methods. Eur. J. Oper. Res. 2007, 178, 514–529. [Google Scholar] [CrossRef]
- ISO 5001; Energy Management Systems—Requirements with Guidance for Use. International Organization for Standardization: Geneva, Switzerland, 2018.
- ISO 14001; Environmental Management Systems—Requirements with Guidance for Use. International Organization for Standardization: Geneva, Switzerland, 2015.

| Category | Requirements | Literatures |
|---|---|---|
| Thermal–Physical Properties | Suitable phase change temperature | [7,10,20,25,26,27] |
| High value of the latent heat of fusion | [7,10,20,25,26,27,28,29] | |
| High thermal conductivity | [7,10,20,25,26,27,28,29] | |
| High value of specific heat capacity | [7,25,26,28,29] | |
| Thermally reliable | [25] | |
| Cycling stability | [20] | |
| Little subcooling | [20,27] | |
| Large density | [7,27,28,29] | |
| Chemical Properties | Chemically stable | [20,25,27,29] |
| Non-toxic | [25,26,27,29] | |
| Non-flammable | [25,26,29] | |
| Non-explosive | [25,26,27] | |
| Corrosion-resistant | [25,26,27,29] | |
| Kinetic Properties | High rate of nucleation | [25,26,29] |
| High rate of crystal growth | [25,26,29] | |
| High melting rate | [27] | |
| Environmental Properties | Low environmental impact | [25] |
| Non-polluting during service life | [25,26] | |
| Easy recycling and treatment | [25,26] | |
| Economic Properties | Cost-effective | [20,25,26,27,28,29] |
| Commercially available | [25,26,29] | |
| Technical Properties | Low vapor pressure | [20] |
| Small volume change | [20,26,27,29] | |
| Compatibility with other materials | [25] |
| PCM Component or Type | Phase Change Temperature (°C) | Heat of Fusion (KJ/kg) | Thermal Conductivity (W/m K) | Density (kg/m3) | Specific Heat Capacity (KJ/kg K) | Literature |
|---|---|---|---|---|---|---|
| Na2SO4, H2O, NaCl, NH4Cl | 7.5 | 121 | 0.55 (liquid), 0.70 (solid) | 1490 | – | [31] |
| Na2SO4·10H2O, NaCl, NH4Cl, Na2B4O7·10H2O, NH4Br | 9.5–10 (melting point) 8.0 (freezing point) | 179, 122 (after 100 recycles) | 0.75 (liquid), 0.93 (solid) | 1470 | – | [31] |
| S7 | 7 | 150 | 0.4 | 1700 | 1.85 | PCM products |
| S8 | 8 | 150 | 0.44 | 1475 | 1.9 | PCM products |
| S10 | 10 | 155 | 0.43 | 1470 | 1.9 | PCM products |
| SP | 8 | 182 | 0.8 | 1503 | 1.8 | MGEC |
| A6 | 6 | 185 | 80 | 768 | 2.17 | PCM products |
| A6.5 | 6.5 | 190 | 82 | 770 | 2.18 | PCM products |
| A7 | 7 | 190 | 82 | 770 | 2.18 | PCM products |
| A8 | 7 | 180 | 77 | 770 | 2.16 | PCM products |
| A9 | 9.5 | 190 | 82 | 770 | 2.16 | PCM products |
| E8 | 8 | 140 | 1469 | 0.67 | PCM Products | |
| E7 | 7 | 120 | 1542 | 0.62 | PCM Products | |
| C7 | 8 | 135 | 0.78 | 1400 | 1.4 | ClimSel |
| C10 | 6–11 | 32–116 | 0.83 | 1400 | 1.6 | ClimSel |
| OM08 | 7 | 175 | 0.235 | 1190 | 1.71 | Pluss Tech. |
| PureTemp 8 | 8 | 178 | 0.22 | 0.86 | 1.85 | PureTemp |
| Item | Criteria | Average (1~5) | Coefficient of Variation (0~1) | Result |
|---|---|---|---|---|
| 1 | Phase change temp. | 4.6000 | 0.1979 | Selected |
| 2 | Material density | 4.5333 | 0.1412 | Selected |
| 3 | Heat of fusion | 4.7333 | 0.0967 | Selected |
| 4 | Specific heat capacity | 4.6667 | 0.1323 | Selected |
| 5 | Thermal conductivity | 4.7333 | 0.0967 | Selected |
| 6 | Material cost | 4.6000 | 0.1102 | Selected |
| 7 | Environmental impact | 4.8000 | 0.0863 | Selected |
| PCM Criteria | Phase Change Temp. (°C) | Material Density (kg/m3) | Heat of Fusion (KJ/kg) | Specific Heat Capacity (KJ/kg K) | Thermal Conductivity (W/m K) | Material Cost (USD/Kg) | Environmental Impact (1~9) |
|---|---|---|---|---|---|---|---|
| Phase Change Temp. (°C) | 1.000 | 3.117 | 3.431 | 3.431 | 3.550 | 3.416 | 3.117 |
| Material Density (kg/m3) | 0.321 | 1.000 | 0.250 | 0.250 | 0.333 | 0.374 | 0.333 |
| Heat of Fusion (KJ/kg) | 0.291 | 4.000 | 1.000 | 2.111 | 3.000 | 2.111 | 2.111 |
| Specific Heat Capacity (KJ/kg K) | 0.291 | 4.000 | 0.474 | 1.000 | 3.117 | 3.178 | 3.178 |
| Thermal Conductivity (W/m K) | 0.282 | 3.000 | 0.333 | 0.321 | 1.000 | 1.320 | 3.000 |
| Material Cost (USD/Kg) | 0.293 | 2.671 | 0.474 | 0.315 | 0.758 | 1.000 | 1.000 |
| Environmental Impact (1~9) | 0.321 | 3.000 | 0.474 | 0.315 | 0.333 | 1.000 | 1.000 |
| Criteria | Geometric Mean | Priority Weight | Matrix Calculation Result |
|---|---|---|---|
| Phase Change Temp. (°C) | 2.811 | 0.32904 | 7.91633 |
| Material Density (kg/m3) | 0.363 | 0.04251 | 7.76713 |
| Heat of Fusion (KJ/kg) | 1.647 | 0.19281 | 7.61527 |
| Specific Heat Capacity (KJ/kg K) | 1.504 | 0.17601 | 7.68281 |
| Thermal Conductivity (W/m K) | 0.863 | 0.10106 | 7.70480 |
| Material Cost (USD) | 0.707 | 0.08276 | 7.15044 |
| Environmental Impact (1~9) | 0.648 | 0.07581 | 7.54589 |
| λmax | CI | RI | CR | Consistence Check |
|---|---|---|---|---|
| 7.62610 | 0.10435 | 1.32000 | 0.07905 | PASS |
| PCM Type | Phase Change Temp. (°C) | Material Density (kg/m3) | Heat of Fusion (KJ/kg) | Specific Heat Capacity (KJ/kg K) | Thermal Conductivity (W/m K) | Material Cost (USD/Kg) | Environmental Impact (1~9) |
|---|---|---|---|---|---|---|---|
| S7 | 7 | 1700 | 150 | 1.85 | 0.4 | 6 | 1 |
| S8 | 8 | 1475 | 150 | 1.9 | 0.44 | 6 | 2 |
| SP | 9 | 1503 | 182 | 1.8 | 0.8 | 5 | 0 |
| A6 | 6 | 768 | 185 | 2.17 | 80 | 7 | 2 |
| A6.5 | 6.5 | 770 | 190 | 2.18 | 82 | 7 | 2 |
| A7 | 7 | 770 | 190 | 2.18 | 82 | 7.5 | 1 |
| A8 | 7 | 770 | 180 | 2.16 | 77 | 9 | 2 |
| A9 | 9.5 | 770 | 190 | 2.16 | 82 | 7.2 | 1 |
| C7 | 8 | 1400 | 135 | 1.4 | 0.78 | 8.2 | 2 |
| OM08 | 7 | 1190 | 175 | 1.71 | 0.235 | 9.3 | 3 |
| 0.329 | 0.043 | 0.193 | 0.176 | 0.101 | 0.083 | 0.076 |
| Criteria | Phase Change Temp. (°C) | Material Density (kg/m3) | Heat off Fusion (KJ/kg) | Specific Heat Capacity (KJ/kg K) | Thermal Conductivity (W/m K) | Material Cost (USD/Kg) | Environmental Impact (1~9) |
|---|---|---|---|---|---|---|---|
| Ideal Solution | Higher is Better | Higher is Better | Higher is Better | Higher is Better | Higher is Better | Lower is Better | Lower is Better |
| f*j (PIS) | 9.50 | 190.00 | 82.00 | 1700.00 | 2.18 | 5.00 | 0.00 |
| f−j (NIS) | 6.00 | 135.00 | 0.24 | 768.00 | 1.40 | 9.30 | 3.00 |
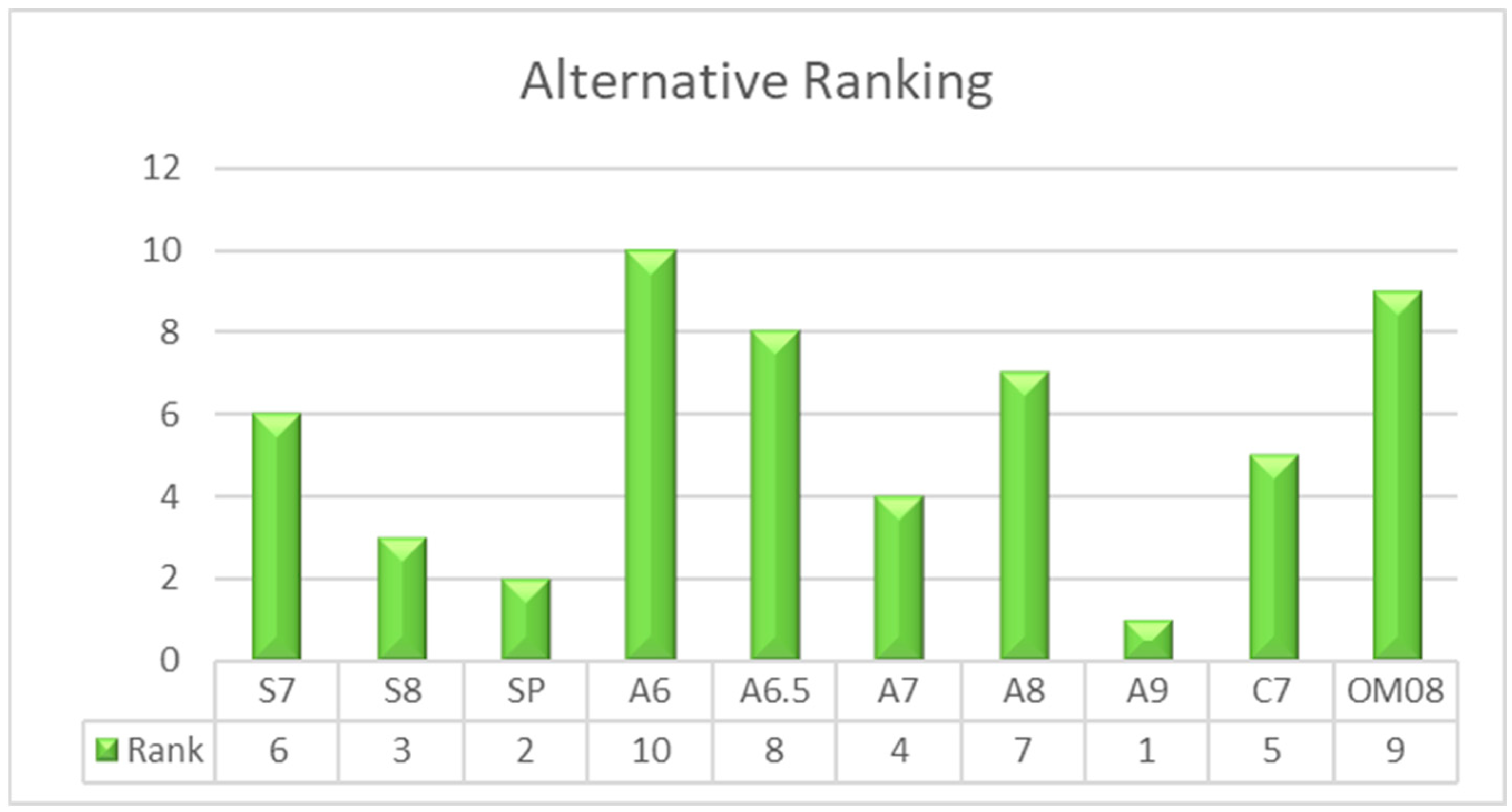
| Material | Sj | Rj | Qj (v = 0.5) | Ranking |
|---|---|---|---|---|
| S7 | 0.54564 | 0.23503 | 0.48147 | 6 |
| S8 | 0.51282 | 0.19232 | 0.30906 | 3 |
| SP | 0.35035 | 0.19147 | 0.14185 | 2 |
| A6 | 0.60396 | 0.32904 | 0.84690 | 10 |
| A6.5 | 0.54670 | 0.28204 | 0.63575 | 8 |
| A7 | 0.48404 | 0.23503 | 0.41913 | 4 |
| A8 | 0.56030 | 0.23503 | 0.49631 | 7 |
| A9 | 0.26123 | 0.17563 | 0.00000 | 1 |
| C7 | 0.64490 | 0.19152 | 0.44014 | 5 |
| OM08 | 0.75521 | 0.23503 | 0.69360 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, S.-H.; Lo, S.-L. Hybrid (Optimal) Selection Model for Phase Change Materials Used in the Cold Energy Storage of Air Conditioning Systems. Energies 2024, 17, 63. https://doi.org/10.3390/en17010063
Peng S-H, Lo S-L. Hybrid (Optimal) Selection Model for Phase Change Materials Used in the Cold Energy Storage of Air Conditioning Systems. Energies. 2024; 17(1):63. https://doi.org/10.3390/en17010063
Chicago/Turabian StylePeng, Shun-Hsiung, and Shang-Lien Lo. 2024. "Hybrid (Optimal) Selection Model for Phase Change Materials Used in the Cold Energy Storage of Air Conditioning Systems" Energies 17, no. 1: 63. https://doi.org/10.3390/en17010063
APA StylePeng, S.-H., & Lo, S.-L. (2024). Hybrid (Optimal) Selection Model for Phase Change Materials Used in the Cold Energy Storage of Air Conditioning Systems. Energies, 17(1), 63. https://doi.org/10.3390/en17010063






