Sensitivity Analysis and Multi-Objective Optimization of Skylight Design in the Early Design Stage

Abstract

Building geometry design decisions are important for energy efficiency and daylight performance. Sensitivity analysis, coupled with optimization, is an important approach to investigate and optimize building geometry in the early design stage. Incorporating skylights is an important daylighting strategy in commercial buildings; however, skylight-to-floor ratio (SFR) is often the only design variable evaluated in precedent studies. More design variables related to skylight geometry, clerestory geometry, skylight material, and building geometry need to be evaluated. This study investigates the skylight design of a 2000-square-meter commercial building. Eighteen design variables are evaluated according to their influence on building energy and daylight performance. One-at-a-time (OAT), linear regression, and Morris sensitivity analysis approaches are utilized to identify the most influential variables. Seven of the twelve building geometry variables and two of the six building material variables are considered as important. Then, a multi-objective optimization with genetic algorithms is processed to find out the optimal design solution. The three objectives are energy use intensity (EUI), daylight autonomy (DA), and daylight uniformity (DU). After the optimization, five candidate design options are picked from the Pareto front. Discussions are made on the features of these designs, and one design is selected as the optimal solution.

1. Introduction

Building geometry has a great impact on a building’s energy demand and daylight availability. Daylight is important for a building’s energy efficiency, occupant comfort, health, mood, and productivity. The early design stage is when the most building geometry design decisions are made; thus, it has the most potential for designers to make energy-efficient design decisions. However, currently, most energy modeling work happens in a later design stage, where no significant changes can be made to the building geometry design. Also, building geometry is usually significantly simplified in building energy models, which makes the influence of building geometry design unknown. Sensitivity analysis in the early design stage is an important tool to identify the key variables in building energy models, and it enables architects to receive timely feedback on how the building geometry design is correlated with the energy performance. Understanding the importance of building geometry variables could also stimulate the appropriate simplification of building geometry in building energy models, which leads to a more accurate building energy model and more chances for energy efficiency.

Sensitivity analysis has been widely applied in building performance analysis throughout the design process. Input variables evaluated in sensitivity analysis include urban-level design parameters, building-level design parameters, building envelope, ventilation and infiltration, HVAC and other mechanical systems, occupant behavior, economic factors, etc. [1]. Building-level design is also called building geometry design or building shape design. Researchers have found that building geometry design variables are usually highly sensitive and have a great influence on the energy performance compared to other variables. For example, Li et al. [2] found that building orientation, window-to-wall ratio (WWR), and skylight-to-roof ratio are all highly sensitive in the 29 variables. Bre et al. [3] found that the azimuth of the building ranks 3rd and the window area fraction ranks 8th among the 21 variables. Hemsath and Alagheband Bandhosseini [4] found that building geometric variations are as sensitive as certain material aspects related to building energy; WWR ranks 1st among 11 variables in four cities and stacking ranks 1st in two cities. However, building geometry design variables were not extensively evaluated in previous studies. Recent studies on sensitivity analysis and optimization of building performance with a consideration of building geometry variables are listed in Table 1. Very few studies are specifically dedicated to the analysis of building geometry variables.

Only limited building geometry variables are considered in building energy analysis, such as the number of floors, orientation, aspect ratio, window size, the position of the window, window orientation, and WWR [1,5,6,7]. However, it is usually unrealistic for some variables to be changed, or the room for adjustment is limited. For example, the building orientation variable is problematic, because it is usually impossible to rotate a whole building after the building design is finished, considering the site restrictions, the traffic flow, and the design aesthetics. It is necessary to explore the mass and the shape of the building from the very beginning of the design stage. While the mass of the building is determined, design variations need to be made on top of that. The WWR design variable is also not reasonable. First, a higher WWR is preferred by the occupants because of the view and the daylight factors. Sometimes, designers would like to sacrifice building energy performance for more view. The WWR is usually fixed, or possible variation is limited after the design decisions are made by the architects. Second, with the WWR fixed, the shape and the location of the window could significantly influence the building performance considering the different lighting energy savings from different daylight distributions. Therefore, it is not ideal to treat the WWR as a variable in the energy simulation process. Similarly, a simple skylight-to-floor ratio (SFR) would not be enough, since a single SFR could not be enough for providing guidelines about the layout, the size, and the material of the skylight. Therefore, it is reasonable to propose that more detailed and specific building geometry design variables be discussed.

Table 1. Building geometry variables studied in previous studies.

Reference	Number of Design Variables	Building Geometry Design Variables	Objectives	Study Type	Sensitivity Analysis Methods
Ioannou and Itard, 2015 [5]	10	Orientation	Annual heating energy consumption, predicted mean vote comfort index	Sensitivity analysis	Regression method
Hemsath and Alagheband Bandhosseini, 2015 [4]	11	Window-to-wall ratio (WWR), stacking, orientation, eave, roof aspect ratio	Annual energy use	Sensitivity analysis	One-at-a-time (OAT) method, Morris method
Bre et al., 2016 [3]	21	Windows area fraction, window area fraction for natural ventilation, window shading size, azimuth of the building	Thermal discomfort degree hours, energy consumption of air conditioners	Sensitivity analysis, optimization	Morris method
Mangkuto et al., 2016 [6]	3	Window size, orientation, wall reflectance	Average daylight factor, average uniformity, daylight autonomy (DA), useful daylight illuminance (UDI), simplified daylight glare probability, total annual lighting energy demand	Sensitivity analysis, optimization	Regression method
Chen and Yang, 2018 [8]	10	Building orientation, external obstruction angle, overhang projection fraction, window-to-ground ratio	Lighting energy demand, cooling energy demand, heating energy demand	Sensitivity analysis, optimization	Fourier amplitude sensitivity test (FAST) method
Delgarm et al., 2018 [7]	11	Building orientation, window size, overhang tilt angle, overhang depth	Annual cooling energy, annual heating energy, annual lighting energy, total building energy consumption	Sensitivity analysis	OAT method, variance-based sensitivity analysis
Li et al., 2018 [2]	29	Building orientation, WWR, skylight-to-roof ratio	Annual energy consumption, winter thermal discomfort	Sensitivity analysis, optimization	Regression method, Morris method, FAST method, OAT method
Gagnon et al., 2018 [9]	30	WWR for each façade orientation, length of the building orientation of the building	Annual energy consumption, peak power demand, number of discomfort hour	Sensitivity analysis	Regression method, Sobol method
Salimzadeh et al., 2020 [10]	2	Photovoltaic (PV) tilt angle, PV pan	Annual cumulative radiation	Sensitivity analysis	OAT method
Ebrahimi-Moghadam et al., 2020 [11]	3	Angle of light shelves, depth of light shelves, number of light shelves	Thermal comfort, building energy consumption	Sensitivity analysis, optimization	OAT method
Yip et al., 2021 [12]	9	Orientation, plan shape, building integrated photovoltaics/thermal (BIPV/T) tilt angle, east/west/south/north WWR	Annual net energy use intensity	Sensitivity analysis	Analysis of variance (ANOVA) method, Sobol method
Huo et al., 2021 [13]	16	Shape factor, east/west/south/north WWR, shading orientation, slat angle, space-to-length ratio, slat arrangement	Building cooling demand	Sensitivity analysis, prediction	Sensitivity index (SI)
Zhu et al., 2022 [14]	11	Building aspect ratio, number of floors, east/west/south/north WWR	Peak cooling load, peak heating load, annual cooling demand annual heating demand	Uncertainty analysis, sensitivity analysis	Meta-modeling method, regression method

Table 1. Building geometry variables studied in previous studies.

Reference	Number of Design Variables	Building Geometry Design Variables	Objectives	Study Type	Sensitivity Analysis Methods
Ioannou and Itard, 2015 [5]	10	Orientation	Annual heating energy consumption, predicted mean vote comfort index	Sensitivity analysis	Regression method
Hemsath and Alagheband Bandhosseini, 2015 [4]	11	Window-to-wall ratio (WWR), stacking, orientation, eave, roof aspect ratio	Annual energy use	Sensitivity analysis	One-at-a-time (OAT) method, Morris method
Bre et al., 2016 [3]	21	Windows area fraction, window area fraction for natural ventilation, window shading size, azimuth of the building	Thermal discomfort degree hours, energy consumption of air conditioners	Sensitivity analysis, optimization	Morris method
Mangkuto et al., 2016 [6]	3	Window size, orientation, wall reflectance	Average daylight factor, average uniformity, daylight autonomy (DA), useful daylight illuminance (UDI), simplified daylight glare probability, total annual lighting energy demand	Sensitivity analysis, optimization	Regression method
Chen and Yang, 2018 [8]	10	Building orientation, external obstruction angle, overhang projection fraction, window-to-ground ratio	Lighting energy demand, cooling energy demand, heating energy demand	Sensitivity analysis, optimization	Fourier amplitude sensitivity test (FAST) method
Delgarm et al., 2018 [7]	11	Building orientation, window size, overhang tilt angle, overhang depth	Annual cooling energy, annual heating energy, annual lighting energy, total building energy consumption	Sensitivity analysis	OAT method, variance-based sensitivity analysis
Li et al., 2018 [2]	29	Building orientation, WWR, skylight-to-roof ratio	Annual energy consumption, winter thermal discomfort	Sensitivity analysis, optimization	Regression method, Morris method, FAST method, OAT method
Gagnon et al., 2018 [9]	30	WWR for each façade orientation, length of the building orientation of the building	Annual energy consumption, peak power demand, number of discomfort hour	Sensitivity analysis	Regression method, Sobol method
Salimzadeh et al., 2020 [10]	2	Photovoltaic (PV) tilt angle, PV pan	Annual cumulative radiation	Sensitivity analysis	OAT method
Ebrahimi-Moghadam et al., 2020 [11]	3	Angle of light shelves, depth of light shelves, number of light shelves	Thermal comfort, building energy consumption	Sensitivity analysis, optimization	OAT method
Yip et al., 2021 [12]	9	Orientation, plan shape, building integrated photovoltaics/thermal (BIPV/T) tilt angle, east/west/south/north WWR	Annual net energy use intensity	Sensitivity analysis	Analysis of variance (ANOVA) method, Sobol method
Huo et al., 2021 [13]	16	Shape factor, east/west/south/north WWR, shading orientation, slat angle, space-to-length ratio, slat arrangement	Building cooling demand	Sensitivity analysis, prediction	Sensitivity index (SI)
Zhu et al., 2022 [14]	11	Building aspect ratio, number of floors, east/west/south/north WWR	Peak cooling load, peak heating load, annual cooling demand annual heating demand	Uncertainty analysis, sensitivity analysis	Meta-modeling method, regression method

The optimization of building form and geometry has been investigated by many researchers [15,16,17,18,19], but they mostly focused on the optimization result. Without a sensitivity analysis, the relationship between variables and simulation results is not discussed, and the importance of variables is not compared.

The studies that coupled sensitivity analysis and optimization include [2,8,20,21,22]. Sensitivity analysis is before the optimization process to identify the key design variables so that the optimization problem can be simplified and the time can be significantly reduced, and then an optimization process is performed to locate the best combination of design variables for the best energy performance.

This study aims to fully explore the potential and importance of building geometry variables, specifically skylight design variables, through sensitivity analysis and optimization. A skylight is a common daylighting strategy; however, SFR is often the only design variable evaluated in precedent building performance optimization studies. This study investigates variables including the dimension of the skylights and the clerestory windows, the shape, number, and layout of skylights, and the building geometry. Properties of skylight materials are also evaluated to be compared to the influence of building geometry variables. Three different sensitivity analysis methods are applied to prioritize the design variables considering both daylight and energy performance. Then, important design variables will be evaluated in the consequent optimization study.

2. Methodology

2.1. Research Framework

The main platform of this research is the 3D modeling software Rhino (Version 7) and its parametric design plug-in Grasshopper. The energy modeling tools are Ladybug (Version 0.0.65) and Honeybee (Version 0.0.62), which are plug-ins for Grasshopper. The simulation engines are EnergyPlus (Version 8.5) and Radiance (Version 5.0). In grasshopper, the input of 18 design variables can vary independently, and the change in the design variable will result in a corresponding change in the energy model and daylighting and energy simulation result. The data of the simulation input and output are recorded in an Excel file for analysis. A detailed explanation of the simulation tools and simulation process can be found in the authors’ previous study [23].

The research framework is illustrated in Figure 1. After this simulation setup is prepared, three sensitivity analysis methods are used to prioritize the design variables. The three methods are the local method, linear regression method, and Morris method. The sensitivity analysis used will determine how the input of the design variables is sampled. Nine variables, i.e., half of the total variables, will be selected for the optimization phase through the evaluation of the results of the three methods for both daylighting and energy performance.

In the optimization phase, multi-objective optimization is performed. The three objectives are energy use intensity (EUI), daylight autonomy (DA), and daylight uniformity (DU), which represent the building energy efficiency, daylight availability, and the distribution of daylight. The optimization engine will automatically generate an initial population for simulation, and it will evaluate how the input of design variables are related to the performance of the three objectives and then generate another population for better performance. This process will continue until a threshold is met, or the simulation is manually terminated. After the optimization is terminated, the Pareto front method is used to determine the optimal design solutions. One optimal design solution is selected, and features of the optimal design solutions are discussed.

2.2. Building Description

The case study’s building is a single-story commercial building located in Atlanta, Georgia (Figure 2). Daylight is provided by both skylights and clerestory windows. The skylights are raised from the roof plane, and the footprint of each skylight is a square shape. There are 10 clerestory windows on the four facades. There are 12 building geometry design variables. Figure 2a shows the southeast isometric view of the building, and Figure 2b shows the enlargement of its southeast corner. Design variables include the building depth (v1), the distance between skylights and roof perimeter (v2), the side length of skylights (v3), number of skylights (v4), monitor height (v5), monitor tilt angle (v6), the height of south (v7), north (v8), and east/west windows (v9), and the width of the south (v10), north (v11), and east/west windows (v12). All the design variables that are visible in the two figures are marked. The top borders of the clerestory windows are fixed; the height of the clerestory windows depends on the location of the bottom border. Fixed parameters include the ceiling height, which is 6 m, and the size of the building, which is 2000 square meters. The skylight dimension varies between 0.25 and 2.25 square meters. The number of skylights varies from 16 to 90. Considering the skylight number and the skylight dimension, the SFR varies from 0.02% to 10.125%.

There are 6 building material variables, i.e., skylight transmittance (v13), window transmittance (v14), skylight translucence (v15), window translucence (v16), skylight U value (v17), and window U value (v18). The visible transmittance and solar heat gain coefficient (SHGC) are usually two independent variables. However, they usually have very close values, except for windows with low-e coatings. To simplify the research question, in this study, these two variables are consolidated as one variable—transmittance, to depict the percentage of solar radiation, including the visible light, passing through a window. Translucence measures how the light passes through glass. When the translucence is 0, it means the glass is clear, and all the light passes through the glass specularly. When the translucence is 1, it means the glass is frosted, and all the light passes through the glass diffusely. Translucent glass (or frosted glass, diffused glass) is becoming popular in the industry as a skylight material. The purpose of the inclusion of this variable is to test if translucent glass performs better than clear glass and if it is important compared to other variables.

The description and the range of the variables are explained in

Table 2. Design variables.

	Variable	Short Name	Range		Unit
			Min	Max
Building geometry and fenestration	Building depth	v1	30	66.7	m
	Distance between skylights and roof perimeter	v2	0.5	8	m
	Side length of the skylights	v3	0.5	1.5	m
	Number of skylights	v4	16	90
	Monitor height	v5	0.1	1	m
	Monitor tilt angle	v6	30° south	30° north	Degree
	Height of south windows	v7	0.1	2	m
	Height of north windows	v8	0.1	2	m
	Height of east and west windows	v9	0.1	2	m
	Width of south windows	v10	0	(2000/Building depth)/10	m
	Width of north windows	v11	0	(2000/Building depth)/10	m
	Width of east and west windows	v12	0	Building depth/10	m
Building material	Skylight transmittance	v13	0.1	0.8
	Window transmittance	v14	0.1	0.8
	Skylight translucence	v15	0 *	1 *
	Window translucence	v16	0 *	1 *
	Skylight U value	v17	0.2	6	W/(m2·K)
	Window U value	v18	0.2	6	W/(m2·K)

* 0 indicates clear glass; 1 indicates 100% diffused glass.

. The range of each variable is normalized to the range of 0 to 1, and it changes by 0.1. Each variable can vary independently, but it needs to be noticed that the value of one variable could influence the range of the other variables. For example, the building depth could influence the maximum number of skylights and the width of clerestory windows.

2.3. Daylight and Energy Modeling

As discussed in the research framework session, the platform for the whole sensitivity analysis and optimization process is Rhino and Grasshopper with Ladybug and Honeybee plug-ins. The energy model created with Ladybug and Honeybee is exported to Radiance for daylighting simulation and to EnergyPlus for energy simulation. The simulation result is imported into Grasshopper for analysis. The energy model is built with U.S. Department of Energy’s commercial reference buildings template. The building type is a supermarket, and the climate zone is 3A.

Thirty daylight sensors are spaced on a grid at a height of 0.76 m above the floor. The daylighting and energy model information is the same as the authors’ previous study [23]; therefore, it will not be discussed in full detail. The main settings such as the loads, schedules, building envelope materials, HVAC system, and construction quality are not changed from the template, except for those chosen as design variables. The EnergyPlus and Radiance building envelope materials are listed in

Table 3. Building material thermal properties.

Representative City and Climate Zone	Construction	Construction Name in OpenStudio Library	U-Value W/(m2∙K)
Atlanta (Climate zone 3A)	Roof	ASHRAE 90.1-2004 ExtRoof IEAD ClimateZone 1–4	0.40
	Exterior Wall	ASHRAE 90.1-2004 ExtWall Mass ClimateZone 3–4	0.97
	Exterior Floor	ExtSlabCarpet 4 in ClimateZone 1–8	5.62

and

Table 4. Building material optical properties.

Construction	Material Type	Values
Shading	Radiance opaque material	Reflectance: 0.8
Interior Wall	Radiance opaque material	Reflectance: 0.5
Interior Ceiling	Radiance opaque material	Reflectance: 0.8
Interior Floor	Radiance opaque material	Reflectance: 0.2

.

2.4. Simulation Output

Both daylighting and energy performance are evaluated in the optimization processes. Annual heating, cooling, and lighting loads are included in the energy simulation output. Equipment load is not included as it is fixed. The energy efficiency indicator used is EUI, which expresses the energy demand of a building relative to its size. It is calculated by taking the quotient of a building’s yearly energy demand by its total floor area. The unit for EUI is kWh/m²/yr.

Differences between daylighting performance metrics have been discussed by many researchers [6,24,25]. One of the most commonly used dynamic daylight metrics is DA. DA is calculated as the percentage of time during a year that the illuminance at the sensor location is above the threshold, which is usually defined as 300 lux. For useful daylight illuminance (UDI), both a lower threshold and an upper threshold are defined. The purpose of an upper threshold is to minimize the glaring possibility. However, the daylighting method of this study is skylight and clerestory windows, which are above the field of view of occupants. Therefore, there is no need to consider the glare issues and upper threshold.

SDA is also a frequently used daylighting metric. SDA evaluates the percentage of sensors throughout the space that meets a specific lighting threshold, such as DA 300 for at least 50% of the time. SDA is not appropriate for this study because the daylight distribution in the space is relatively even because of the skylight. Usually, the daylight availability at each sensor is similar. For the common threshold DA 300, 50%, there are lots of design options that can achieve SDA 100%. If the threshold is raised, the majority of the design options will have SDA 0%. So, SDA is not sensitive enough to tell the difference between designs.

Based on the above discussion, the daylighting metric is decided to be DA. The illuminance threshold in this study is 500 lux since the illuminance requirement for retail buildings is higher. So, the DA at each sensor point is the percentage of annual daytime hours when the daylight illumination level exceeds 500 lux. The final DA is calculated as the average for all sensor points. Even though there is no upper threshold for daylight performance, design options with too much sunlight exposure will be eliminated through the energy performance metric.

DU is another metric to be evaluated, which is used to determine if the daylight distribution is uniform. In this study, the DA value is the average DA value at all sensor points, but a lot of information is lost when an average calculation is performed. For example, design with uniform daylight distribution and design with a mix of extremely high and low daylight distribution could result in the same average DA value. Therefore, it is necessary to further utilize the data and analyze the uniformity of the daylight. DU is calculated in many other previous studies [26,27,28]. DU is traditionally calculated as the ratio of the minimum illuminance to the average illuminance over the specified task areas [29]. Another similar metric is daylight diversity [29], which is the ratio of the minimum to the maximum illuminance over the core area. However, there are problems with these traditional methods. First, they are point-in-time methods, like daylight factor, which means it only evaluates the daylight performance of one moment throughout the year. Second, taking only the maximum, minimum, and average values could not evaluate how the illuminance values vary in the middle. Therefore, in this study, the DU is defined as the standard deviation of DA at each sensor point.

In brief, the three performance objectives are EUI, DA, and DU. For an optimal design with balanced performance, it should have a low EUI, a high DA, and a low DU, as it indicates lower energy demand, high daylight availability, and even daylight distribution.

3. Sensitivity Analysis

Sensitivity analysis methods can be generally divided into local [2,4,7,10,11,30] and global approaches. Local sensitivity analysis aims to analyze the effects of local changes in a parameter. It focuses on a single variable’s behavior while other variables remain the same. The typical methodology for local sensitivity analysis is one-at-a-time (OAT) or one-factor-at-a-time (OFAT). It is easy to establish the relationship between the variables and the results, and it does not require much computational power. However, it only explores the variation in results around a single point or a base case, and the interactions of other design parameters are not considered [31].

Global sensitivity analysis aims to evaluate the entire parameter space. It varies all model inputs simultaneously, and the sensitivities are calculated over the entire range of each model input. Global sensitivity analysis is often preferred, but it could be computationally expensive. Typical global sensitivity analysis includes regression method [2,5,6,9], screening-based approach [2,3,4], and variance-based approach [2,7,9,32].

Choosing the appropriate sensitivity analysis methods is important to obtain results accurately and efficiently. The results of different sensitivity analysis methods can be different. Yang et al. [33] suggested that in building energy assessment, at least two fundamentally different sensitivity analysis methods should be performed to achieve robust results. Three sensitivity analysis methods are selected in this study, i.e., the OAT method, linear regression method, and Morris method (screening-based approach). The variance-based approach is suitable for complex non-linear problems [31], but it is very computationally expensive and hence not included in this study.

3.1. OAT Method

The OAT method analyzes the effect of one parameter at a time while keeping all the other parameters fixed. The effect of each design variable on the building performance is evaluated in turn. In building energy analysis, the term ‘influence coefficient’ (IC) is commonly used [30,34]. IC is essentially the ratio of percentage change in output to the percentage change in input. The IC is calculated as:

$$\mathrm{I}\mathrm{C}=\frac{\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e} \mathrm{i}\mathrm{n} \mathrm{o}\mathrm{u}\mathrm{t}\mathrm{p}\mathrm{u}\mathrm{t}}{\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e} \mathrm{i}\mathrm{n} \mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}}=\frac{\mathsf{\partial }\mathrm{O}\mathrm{P}}{\mathsf{\partial }\mathrm{I}\mathrm{P}}\approx \frac{∆\mathrm{O}\mathrm{P}}{∆\mathrm{I}\mathrm{P}}$$

(1)

where OP represents the simulation output, and IP represents the input. Since the partial derivative is difficult to obtain, the ratio of output and input difference is usually used instead. The IC can be expressed in various forms, and one of the variations, ‘sensitivity index’ (SI), is utilized to calculate how much each design variable contributes to the output variation over its entire range [4,35]. A standard value for all design variables is selected as a control, which in this study is the medium value in the range. Then, two extreme values are selected on both sides of the standard value. For the evaluation of each design variable, the simulation will run twice with the variable set to the minimum and the maximum values, while all the other variables are fixed at the standard value. The SI is calculated as:

$$\mathrm{S}\mathrm{I}=\frac{{\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{E}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mathrm{E}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}100\%$$

(2)

where E_max and E_min represent the simulation output when the variable is changed to the minimum or the maximum value. The percentage change in output is used instead of absolute change, and the percentage change in input is removed from the SI since it is the same for all variables.

A larger SI means this design variable has more influence on the building performance and is considered to be more important. However, it should be noted that if the relationship between the input and the output is non-linear, the sensitivity will vary from point to point [34]. Both the SI values for daylighting (DA) and energy performance (EUI) are calculated and shown in Figure 3. From Figure 3, we can see that overall daylight (DA) fluctuates more than energy (EUI) as the variables change from the minimum to maximum values. Design variables usually have opposite effects on the daylight and energy performance, which is expected as more daylight would reduce the lighting energy required. For daylight performance, the most influential variables for daylight performance are v14 window transmittance, v3 side length of the skylight, v12 width of east and west windows, and v9 height of east and west windows. The most influential variables for energy performance are v3 side length of the skylight and v4 number of skylights.

3.2. Linear Regression

Linear regression is an approach for modeling the relationship between two variables by fitting a linear equation to the data. In building energy performance analysis, the regression method is one of the most widely used methods, because this method is relatively straightforward and easy to perform [31]. In this study, multiple linear regression is used to evaluate the effect of the design variables on the building performance indicators. The output variable is denoted by y_i, and the input variables are demoted by x_i. This relationship between the input and output variables is modeled as below:

$${\mathrm{y}}_{\mathrm{i}}={{\mathsf{\beta }}_0+\mathsf{\beta }}_1{\mathrm{x}}_{\mathrm{i}1}+{\mathsf{\beta }}_2{\mathrm{x}}_{\mathrm{i}2}+\dots +{\mathsf{\beta }}_{18}{\mathrm{x}}_{\mathrm{i}18}+{\mathsf{\epsilon }}_{\mathrm{i}}\mathrm{i}=1,2,3,\dots ,\mathrm{n}$$

(3)

where ${\mathsf{\epsilon }}_{\mathrm{i}}$ is the error variable, and ${\mathsf{\beta }}_1$, ${\mathsf{\beta }}_2$, …, ${\mathsf{\beta }}_{18}$ are regression coefficients. The regression coefficients are then standardized using the variance of the model output ${\mathrm{V}(\mathrm{y}}_{\mathrm{i}})$ and the variance of the input ${\mathrm{V}(\mathrm{x}}_{\mathrm{i}})$ to make the regression coefficients comparable. The results are called the standard regression coefficients (SRCs):

$${\mathsf{\beta }}_{\mathrm{i}}^{\prime }=\frac{{{\mathsf{\beta }}_{\mathrm{i}}\mathrm{V}(\mathrm{x}}_{\mathrm{i}})}{{\mathrm{V}(\mathrm{y}}_{\mathrm{i}})}$$

(4)

The standardized rank regression coefficient (SRRC) is the rank transformation of SRC. The calculation of SRC requires the assumption of a linear relationship between input and output, while SRRC can be used for non-linear but monotonic relationships. As SRRC has fewer restrictions on the data, it is selected as the sensitivity analysis metric for the linear regression method. Same as SRC, the absolute value of the SRRC represents the importance of a variable. The larger the value is, the more influence the variable has on the output. A positive value corresponds to a high, positive influence of the input, while a negative value corresponds to a negative influence of the input.

The SRRC values for DA and EUI are shown in Figure 4. Figure 3 and Figure 4 show very similar patterns, only the fluctuation in daylight is not as significant as that in Figure 3.

3.3. Morris Method

The Morris method [36] is a type of OAT design experiment, but it is still a global sensitivity analysis method because the input variables vary over the entire domain. The Morris method is an efficient screening method. Due to its low computing cost, it is ideally suited for situations with a large number of input variables, and it is valuable to identify the non-influential parameters of a model.

The Morris method is based on repetitions of OAT design with a sequential variation in the inputs. In each OAT design, the variation in the model output due to the change in input parameter is called elementary effect (EE) [36]. The EE of a model y = y(x₁,…,x_k) with input parameters x_i is defined as below:

$${\mathrm{E}\mathrm{E}}_{\mathrm{i}}=\frac{\mathrm{y}\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{i}-1},{\mathrm{x}}_{\mathrm{i}}+∆,{\mathrm{x}}_{\mathrm{i}+1},\dots ,{\mathrm{x}}_{\mathrm{k}}\right)-\mathrm{y}({\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{k}})}{∆}$$

(5)

In this study, we adopted r = 6 repetitions considering the computation cost, so that there are 6 EEs calculated for each input variable (k = 18). The total number of simulations is r(k + 1) = 114.

For each parameter, two sensitivity indices are obtained. The first index μ is the mean value of the absolute values of the EEs, which is used to determine if the design parameter is important. The second index σ is the standard deviation of the EEs, which is used to detect the interactions of x_i with other parameters and its non-linear effects. μ and σ are calculated as below:

$$\mathsf{\mu }=\sum _{\mathrm{i}=1}^{\mathrm{r}}\left|{\mathrm{E}\mathrm{E}}_{\mathrm{i}}\right|/\mathrm{r}$$

(6)

$$\mathsf{\sigma }=\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{r}}\left|{\mathrm{E}\mathrm{E}}_{\mathrm{i}}-\mathsf{\mu }\right|/\mathrm{r}}$$

(7)

The Morris method sensitivity analysis results for DA and EUI are shown in Figure 5a,b. Each graph is a plot of μ against σ, where μ is on the x-axis and σ is on the y-axis. A larger μ value represents that the parameter is more important. A larger σ value shows that the parameter has more non-linear effects and/or it has more correlations with other parameters. A small σ value means that the parameter mainly has a linear impact on the objective.

From the plot, we can find that for daylight performance, the most important variables are v14 window transmittance, v1 building depth, and v12 width of east and west windows. For energy performance, the most important variables are v1 building depth, v3 side length of the skylight, v13 skylight transmittance, and v10 width of south windows. Most of the points are on the line between the top right and the bottom left corners, which means that those variables have both linear and non-linear/correlated impacts. The location of the two points in Figure 5b is quite interesting. V18 window U value has a medium μ value but a very large σ value, which means that most of the parameters’ impact is non-linear/correlated. It makes sense as the impact of the U value must be correlated with the dimension of the window. The v3 side length of the skylight has a large μ but has a medium σ value, which means most of its impact is linear.

3.4. Summary of the Sensitivity Analysis Results

Since daylight and energy performance need to be evaluated simultaneously in the optimization process, the influence of the variables on both performance metrics should be considered. The rank of the variables for daylight and energy performance for the three sensitivity analysis methods are listed in

Table 5. Ranking of design variables based on three methods and the final ranking.

Ranking	OAT		Linear Regression		Morris Method		Final Ranking
	Daylight	Energy	Daylight	Energy	Daylight	Energy
1	v14	v3	v14	v3	v14	v1	v3
2	v3	v4	v3	v4	v1	v3	v12
3	v12	v13	v9	v5	v12	v13	v14
4	v9	v12	v4	v13	v7	v10	v9
5	v4	v5	v12	v14	v9	v12	v13
6	v13	v14	v10	v9	v10	v9	v4
7	v7	v9	v7	v12	v3	v18	v10
8	v10	v1	v13	v7	v16	v6	v1
9	v5	v18	v5	v6	v2	v5	v5
10	v16	v2	v6	v1	v8	v2	v7
11	v11	v8	v16	v17	v13	v15	v6
12	v8	v6	v15	v10	v4	v7	v2
13	v6	v10	v11	v18	v11	v8	v16
14	v2	v11	v1	v16	v6	v14	v8
15	v15	v17	v17	v2	v15	v11	v18
16	v1	v16	v18	v11	v5	v4	v11
17	v17	v15	v8	v15	v17	v16	v15
18	v18	v7	v2	v8	v18	v17	v17

.

It can be found that the local and linear regression methods generate similar results, especially since the top two ranked variables are the same. The Morris method generates some different results. For example, variable 1 ranks second for daylight and ranks first for energy. However, it has relatively low rankings in the other two methods.

To select the variables for the optimization study, a weight is applied to each variable according to its rank. The variable that ranks first receives the weight of 18; the variable that ranks second receives the weight of 17, etc. After adding up all the weight of each variable, the final rank of the variables is shown in the last column of Table 5. The top nine variables are going to be selected. The monitor height (v5) ranks ninth according to this ranking method. However, it is easy to predict that a higher monitor would contribute to higher EUI since it increases the volume of the building. A higher monitor would also be likely to reduce the DA since it is likely to prevent direct sunlight into the space.

The authors decided that v7 the height of the south windows would be more appropriate in the optimization study. Some design variables are in pairs, such as the side length of light and the number of the skylight, the height of the windows, and the width of windows. A balance between the pair of variables usually can be found. Therefore, it is reasonable to include v7, since v10 width of the south windows is already included. It is interesting to investigate how the height and width of the south clerestory windows would work together, and which combination would contribute to the best design option. Therefore, the final variables selected are v3, v12, v14, v9, v13, v4, v10, v1, and v7.

From the ranking of the importance of design variables, there are the following findings:

• The dimensions of the skylights and the dimensions of the east and west windows show the most importance.
• The dimensions of the north windows rank in the middle, while the dimensions of the north windows rank relatively low.
• The number of skylights ranks sixth, while all the other variables about the details of the skylights show less importance. The distance between the skylight and roof perimeter does not significantly affect the daylight performance.
• Building depth ranks in the middle. It has more influence on energy than daylight.
• Out of all the building material variables, the transmittance of windows and skylights shows the most importance. U values and translucence values both rank at the bottom. Window transmittance has more influence on daylight than energy. It ranks first for daylight in all three methods.

4. Optimization

After the sensitivity analysis, the nine most important variables are selected for the optimization process, and the other variables are fixed at the median value of its range. Three optimization objectives are investigated, i.e., DA, EUI, and DU. The optimization process uses the Grasshopper platform. Ladybug and Honeybee [37] are used for daylight and energy modeling. The optimization engine is Octopus (Version 0.4) [38], and the optimization algorithm used is the genetic algorithm. A detailed explanation of the optimization process can be found in a previous study [23]. The total number of simulations is 500, and the total simulation time is about 48 h.

To test if the inclusion of DU as an optimization objective is effective, a second optimization study with only DA and EUI as objectives is also performed, with other settings remaining the same. Results show that the addition of DU as an objective can effectively eliminate the situation of uneven daylight distribution, such as too much daylight around the perimeter or too much daylight in the south. The daylight variation in the designs in the optimization with two objectives is overall much larger than the optimization with three objectives. Also, the DA and EUI performance of the optimized designs with three objectives is slightly better than the optimization with two objectives. Therefore, it can be concluded that DU is an important building performance metric, and it is beneficial to be included in optimization studies.

5. Results

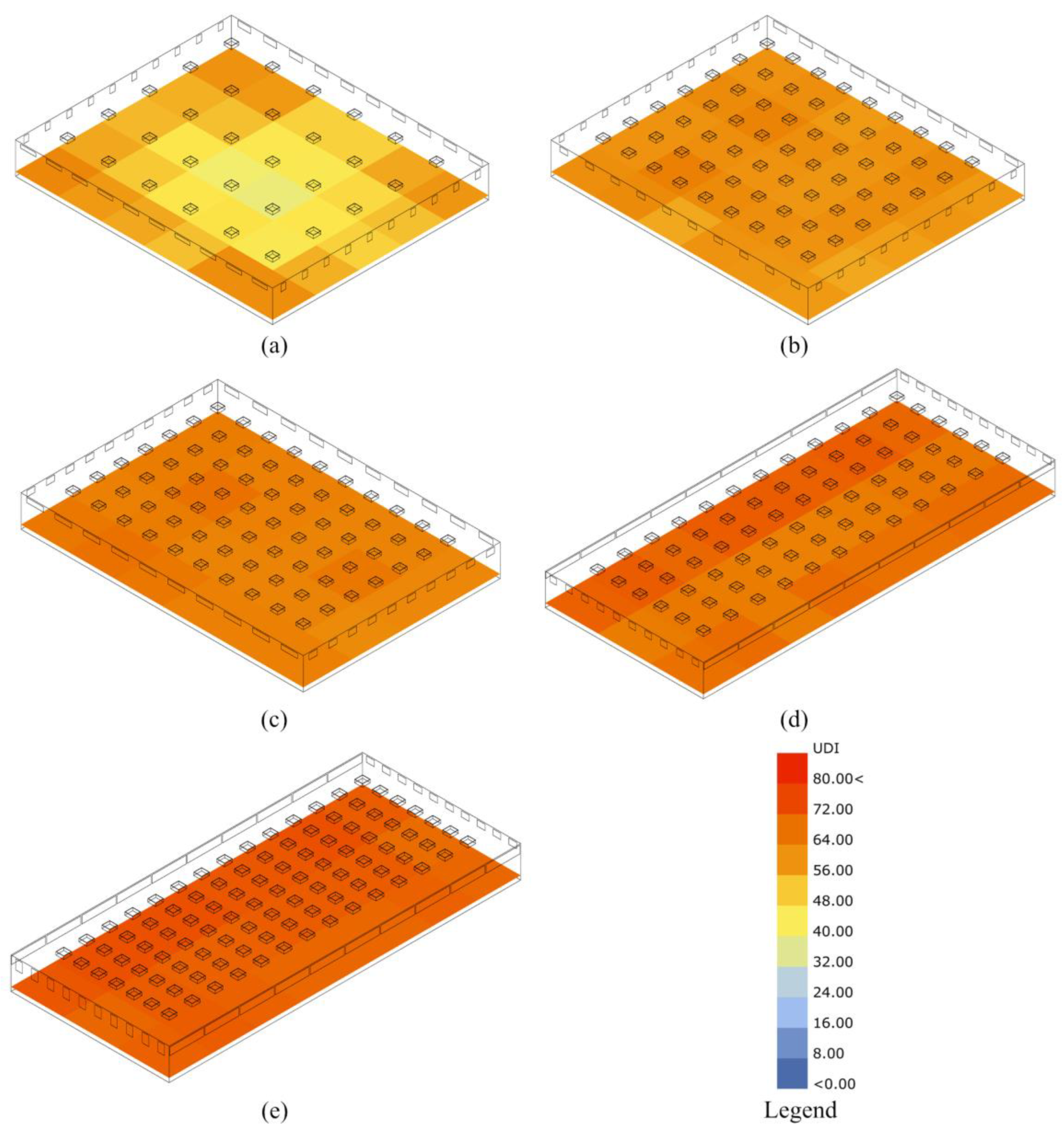
The plot of all the data points is shown in a 3D graph in Figure 6d. Figure 6a–c shows the 2D plot of data points. The Pareto front is a set of solutions, which cannot be improved without sacrificing at least one other objective. As identifying the Pareto front in a 3D graph is not straightforward, a 2D plot is used instead. DA and EUI are the most important objectives; therefore, Figure 6a, the plot of DA against EUI, is used to determine the optimal designs on the Pareto front. The Pareto front is the curve near the bottom left corner of the graph. Five design options on the curve are selected for further investigation, which are marked in yellow circles. These five options are candidates for the optimal solution. The geometry of the five solutions is shown in Figure 7. The values of their variables and the performance results can be found in

Table 6. Design variable values of the 5 options.

	Option 1	Option 2	Option 3	Option 4	Option 5
v1: Building depth (m)	41.0	41.0	37.3	66.7	66.7
v3: Side length of the skylights (m)	1.4	1.4	1.4	1.4	1.5
v4: Number of skylights	30	63	70	72	98
v7: Height of south windows (m)	0.7	0.9	0.9	1.1	1.8
v9: Height of east and west windows (m)	1.2	1.1	1.1	1.1	1.4
v10: Width of south windows (m)	2.9	1.5	3.2	1.2	1.2
v12: Width of east and west windows (m)	0.9	0.9	1.5	6.5	6.5
v13: Skylight transmittance	0.7	0.7	0.7	0.5	0.5
v14: Window transmittance	0.7	0.7	0.7	0.7	0.5
DA (%)	48.5	56.1	61.1	64.5	67.7
EUI (kWh/m2/yr)	106.0	110.6	113.1	117.6	126.3
DU	5.9	2.0	1.5	2.3	1.5

. Out of the five solutions, option 1 has the best energy performance, option 5 has the best daylight performance, and the other options are in between.

Out of the five design options, as the daylight performance becomes better, the building geometry becomes slimmer, and the number of skylights increases. Options 4 and 5 both have very good DA values and have very slim building footprints. They are very wide in the east and west direction and narrow in the north and south direction. They also have very big clerestory windows in the east and west. In the other optimization with only DA and EUI as objectives, the same shape is found in the designs with the best DA. A possible reason is that the daylight availability in the north is the weakest no matter how large the windows are, so in order to maximize the daylight availability throughout the building, it tends to find designs with short north façades, thus long east and west facades. However, energy performance is sacrificed with this building shape, so options 4 and 5 are not ideal.

Option 1 has the best energy performance, but the daylight distribution is not as even as options 2 and 3. Options 2 and 3 are quite similar in geometry and performance. Option 2 has slightly less daylight availability, less energy loads, and less daylight uniformity. The authors decided that energy performance is the most important objective; thus, option 2 is selected as the optimal solution.

The optimal design option has a building width-to-depth ratio of 1.19. There are 63 skylights, and the skylight dimensions are 1.4 m by 1.4 m. The SFR is 6.2%. The south clerestory window dimensions are 1.54 m by 0.86 m, and the WWR is 4.5%. The east/west clerestory window dimensions are 0.94 m by 1.05 m, and the WWR is 4.0%. The north clerestory window dimensions are 2.44 m by 1.05 m, and the WWR is 8.8%. Both the skylight transmittance and window transmittance are 0.66.

6. Conclusions

This study proposes an approach to finding the optimal design solution for daylight and energy performance in the early design stage. The case study’s building is a commercial building with skylights and clerestory windows. There are 18 design variables investigated including the building shape, dimensions, layout, and materials of the skylights and clerestory windows. Sensitivity analysis is used to identify the key design variables before the optimization to simplify the optimization problem. Since different sensitivity analyses tend to obtain different results, to make the results more reliable, three sensitivity analysis methods—the OAT method, linear regression method, and Morris method—are used. Combining the results of the three methods, nine design variables are considered important. In order of importance, the selected variables are sorted as follows: side length of the skylights, width of east and west windows, window transmittance, height of east and west windows, skylight transmittance, number of skylights, width of south windows, building depth, and height of south windows.

After the selection of design variables, a multi-objective optimization is performed using the genetic algorithm. The three optimization objectives are DA, EUI, and DU. After the simulation of 500 design options, five design solutions are selected from the Pareto front. Then, through a thorough comparison of the five solutions, one design is selected as the final solution. The optimal design has a SFR of 6.2%. Its south WWR is 4.5%, its east/west WWR is 4.0%, and its north WWR is 8.8%.

The research also found that the inclusion of DU as an optimization objective can effectively eliminate the situation of uneven daylight distribution and can find overall better design options. UD in this study is calculated as the standard deviation of the DA values at each sensor. Future research could explore and compare different metrics to accurately assess the uniformity of daylight distribution.

The research findings are applicable to commercial buildings with similar design constraints and objectives. Moreover, the research methodology, combining sensitivity analysis with multi-objective optimization, offers a versatile framework that can be applied to a wide variety of buildings in the early design stage aiming for improved daylight and energy efficiency.