Abstract
Magnetic fields in transformer cores are typically assumed to be one-dimensional fields, thus allowing magnetization processes to be regarded as axial magnetization. However, in the core corners or T-joint points of medium- and high-power rating transformers, the magnetic lines have different directions with respect to the rolling direction. This paper describes a method that allows changes in the flux density of transformer steel sheets to be calculated for any magnetization direction. These changes are assumed to depend only on certain limiting hysteresis loops assigned separately to the rolling and transverse directions of a tested transformer sheet, where these loops depend on the magnetization direction on the sheet plane. The selection of coefficients that define the limiting hysteresis loops for several magnetization directions is described, and the condition for the flux density saturation is considered. The resultant flux density in a specified magnetization direction is the geometric sum of the corresponding flux densities assigned to both the rolling and transverse directions. The limiting and partial hysteresis loops determined based on the proposed method for several magnetization directions are compared with analogous measured loops. Additionally, a comparison of the calculated hysteresis loops with loops showing changes in the resultant flux density for several magnetization direction is presented.
1. Introduction
The magnetization processes of soft magnetic materials are typically characterized by axial or rotational magnetization. In the first type of magnetization process, the magnetic field strength changes along a specified direction. This type of magnetization occurs primarily in the sheets of transformer cores and chokes; however, in the connection areas of yokes and the internal columns of the cores, the magnetization process cannot be regarded as axial magnetization. During rotational magnetization, both the field strength and flux density vectors change their directions. This typically occurs in the magnetic circuits of electric machines.
In the magnetization processes of transformer steel sheets, two phenomena occur: the domain wall displacements and the rotation of the flux density vectors toward the direction of the magnetic field strength vector [1,2,3,4]. Both phenomena occur simultaneously; however, in the range of low to medium field strength values, irreversible displacements of the domain walls are dominant; for high field strength values, this process ends, and rotations of the flux density vectors toward the direction of the field strength vector dominate the magnetization process. If the field strength increases, then domains whose flux density vectors are closest to the direction of the field strength increase in volume at the expense of the other domains. At high field strengths, the domain walls disappear and individual crystals become single domains, and then changes in the resultant flux density in the transformer sheets are mainly caused by the rotations of the flux density vectors of individual crystals toward the direction of the field strength. The characteristics of the magnetization process depend not only on the nature of the changes in the magnetic field strength, but also on the parameters of the ferromagnetic material. This process in isotropic materials (non-oriented sheets) does not depend on the field strength direction. In practice, ideal isotropic materials do not exist. Generator sheets, which are referred to as sheets with non-oriented grains, typically exhibit significantly different magnetic properties for field strength changes in different directions [5].
The next section contains a brief description of the magnetization of the transformer sheets for two directions differing from the rolling direction and the transverse direction. This section also describes the method of preparing strips of the tested transformer sheet to measure hysteresis loops for several magnetization directions. Section 3 presents various proposals for modeling the magnetization process in electrical sheets, paying attention to the shortcomings of these proposals. Section 4 contains the determination of the limiting hysteresis loops depending on the magnetization direction on the transformer sheet plane. Section 5 concerns the comparison of changes in the measured and calculated flux density for four magnetization directions using the proposed method of determining the limiting hysteresis loops. This section shows the changes in the resultant flux densities relative to the flux densities measured along the magnetization directions.
2. Description of Magnetization Process in Transformer Steel Sheets
The magnetization process in anisotropic materials, which mainly includes transformer steel sheets (grain-oriented sheets), differs significantly from that in isotropic materials. Owing to various technological treatments, the grains in these sheets are arranged such that the axes of easy magnetization of most grains are parallel to the selected direction, which is typically the rolling direction (RD). The most typical type of grain arrangement is the Goss texture (Figure 1) [6].
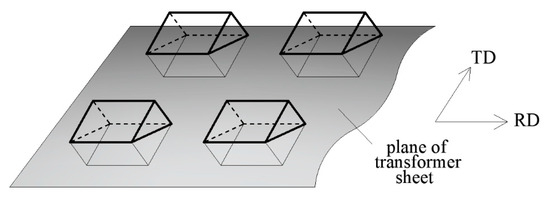
Figure 1.
Arrangement of grains in a transformer sheet with Goss texture; RD and TD—the rolling and transverse directions, respectively.
In these materials, magnetization depends significantly on the field strength. If the magnetization direction is the same as or perpendicular to the RD, then the flux density vector is in the same direction as the magnetic field strength. Otherwise, the field strength and flux density vectors are not collinear. Figure 2 shows examples of changes in the resultant flux density vector for two directions where changes occur in the magnetic field strength. If the field strength direction is close to the RD, then the direction of the resultant flux density vector is close to the RD (Figure 2a). Notably, the flux density measured along the field strength direction is the projection of the resultant flux density vector in this direction, which is crucial because in calculations of the magnetic field distribution, the resultant flux density at a specified point on the transformer sheet should be considered instead of its projection in the magnetization direction. The magnetization process is more complex when the field strength direction is close to the transverse direction (TD). In the initial phase where the field strength increases, the flux density component increases along the RD, whereas the flux density component increases slightly along the TD. When the field strength is further increased, the flux density component along the RD reaches a certain maximum value and then begins to decrease. Simultaneously, the flux density component increases along the TD (Figure 2b). In fact, such tendencies of the flux density have been described by H. Pfützner [7], who reported that such a magnetization process was due to the “disintegration” of domains whose flux density vectors were close to the RD and the growth of domains whose flux density vectors were parallel to the TD. In iron crystals, the most difficult magnetization occurs when the magnetization direction creates an angle of 54.7° with respect to the RD. If magnetization occurs at an angle smaller than 54.7°, then 180° domain walls are reconstructed. Otherwise, the 180° walls are rebuilt as 90° walls. Similar conclusions were presented by Mao and Atherton [8]. In this magnetization process, the flux density vector can be located on one side or on the other in the field strength direction.
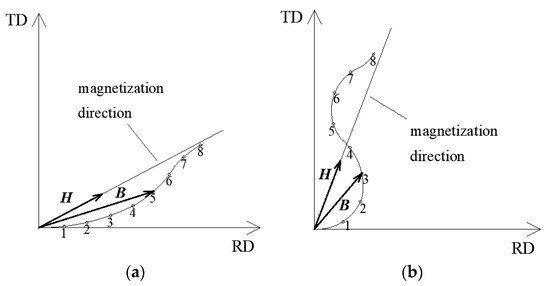
Figure 2.
Changes in position of resultant flux density vector during magnetization in transformer sheet: (a) field strength direction is close to rolling direction (RD); (b) field strength direction is close to transverse direction (TD); digits indicate successive positions of resultant flux density vector.
The dependence of the magnetization process on the field strength direction causes the hysteresis loops to differ significantly. Figure 3 shows the limiting hysteresis loops of a M120-27S (This transformer sheet is produced in Stalprodukt SA in Bochnia (Poland))-type transformer steel sheet in the four magnetization directions.
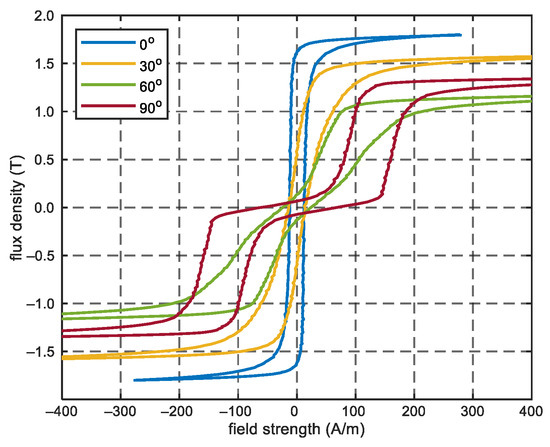
Figure 3.
Limiting hysteresis loops of M120-27S-type transformer sheet measured along four directions with respect to RD.
Changes in the flux density in individual points of the transformer steel sheet depend also on the field strength value. Both the limiting loop for a given magnetization direction and minor loops, which are located inside the limiting hysteresis loop, should be taken into account [2,3]. For example, Figure 4 shows the family of minor hysteresis loops for two magnetization direction.
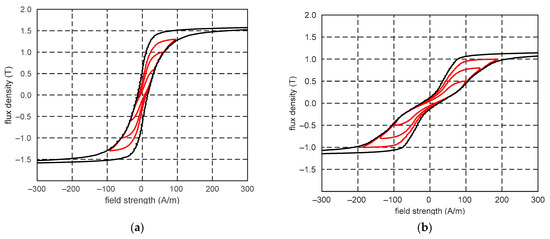
Figure 4.
Family of minor hysteresis loops (red lines) inside the limiting hysteresis loop (black line) for magnetization angles 30° (a) and 60° (b).
The hysteresis loops were determined using the Epstein frame, which is described in detail in [9]. Despite some shortcomings, the Epstein frame is widely used for commercial magnetic measurements. The measurements of the hysteresis loops were performed at a frequency of 3 Hz (the influence of eddy currents on the measurement results can be omitted). Strips 330 mm long and 30 mm wide were cut at an assumed angle α relative to the rolling direction (RD) from a given transformer sheet (Figure 5). Then, 16 such strips were placed in the Epstein frame and appropriate measurements were made for various currents in the winding forcing the magnetic field. As a result, a family of the minor hysteresis loops was obtained for the assumed magnetization direction.
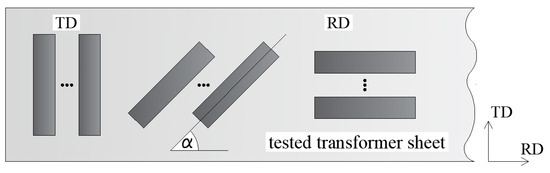
Figure 5.
Preparation of strips of transformer sheet for the Epstein frame; α is the angle between an assumed magnetization direction and RD.
Determining the changes in the flux density at the corners of the transformer cores, particularly in the areas of column connections with yokes (T-joint points) in three-phase transformers, is difficult. In this case, the magnetic field cannot be regarded as one-dimensional field, unlike the magnetic field in the columns (Figure 6). In certain cases, the magnetic field in certain areas of the core at the ends of the transformer windings cannot be regarded as a one-dimensional field when the winding currents are significantly higher than the rated values. Consequently, the leakage flux near air indicates high values, thus altering the direction of the field strength and flux density in the aforementioned fragments of the core [10].
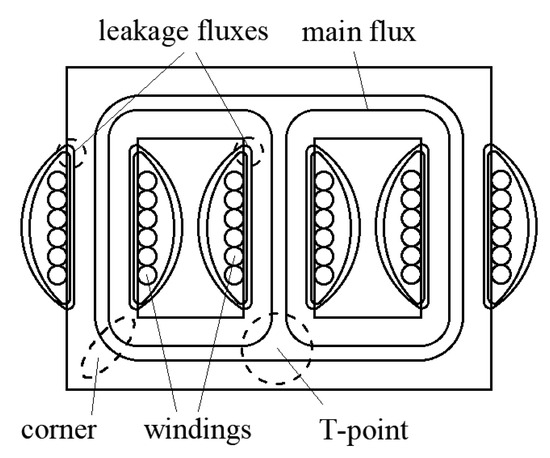
Figure 6.
Section of transformer core with field strength directions.
In these areas, the core temperature is typically higher than that in other sections of the transformer core. Therefore, the different characteristics of the magnetization process should be considered when calculating the flux density distribution and power losses.
3. Proposals for Modeling Magnetization Process
As it is emphasized in [11], so far there are no satisfactory methods that make it possible to calculate changes in the flux density for any magnetization direction in grain-oriented transformer sheets. Note that the total losses should be estimated according to the general formula [5,12]:
where Bx, By—components of the flux density in a rectangular coordinate system in a considered point of a transformer steel sheet, Hx, Hy—components of the magnetic strength.
Therefore, it is advisable to determine changes in the flux density in the coordinate system whose axes are the same as the rolling and transverse directions. Losses in transformer cores have been determined in recent studies [13,14]. The nonlinear and anisotropic properties of transformer sheets, particularly the phenomenon of magnetic hysteresis, significantly hinder the analysis of the flux density distribution in the transformer sheets, thus affecting the accuracy of power loss determination. Nonetheless, advanced software makes it possible for one to consider the nonlinear and anisotropic properties of electrical sheets, as discussed in [15]. The method that makes it possible to take the magnetic hysteresis into account is described in [16], but that method concerns non-oriented grain sheets. Magnetic hysteresis can be directly included in the equations of magnetic field distribution when these equations are based on the integral form of Maxwell’s equations. A proposal to introduce a hysteresis model into magnetic field distribution equations is described in [17]. In some approaches for modeling the magnetization process, the domain structure is used to represent changes in the magnetic flux density [18,19,20,21,22,23]. However, a method to determine the changes in the flux density for any magnetization direction has not been devised. This proposal is discussed in [24], which presents a comparison between the measured and calculated loops for different magnetization directions; however, a method to determine minor hysteresis loops was not presented. Some researchers proposed the use of tensor relationships to determine the flux density of the transformer sheets [25,26].
The changes in the flux density at the individual corner points or T-joint point areas differ from each other. This indicates the necessity to consider the magnetization characteristics, and more precisely, the hysteresis loops in many directions of the magnetization process. This applies not only to the limiting hysteresis loops, but also to the minor hysteresis loops within the limiting loops. In this regard, infinitely many minor loops may be involved. To simplify the problem of modeling the magnetization process for any alternating excitation, the changes in the resultant flux density were determined based on the flux density along the RD and TD. The proposed method is based on a static hysteresis loop.
Each cubic iron crystal comprises three easy magnetization axes (Figure 7) [1,4,27]. The sheets investigated in this study were most easily magnetized along the RD. When the field strength direction was not parallel to the RD, magnetization processes occurred to varying degrees along each easy magnetization axis. Notably, magnetization first occurred along the easy magnetization axes; subsequently, the domain structure was rebuilt. Figure 7 shows a certain magnetization direction with the vector Hα of the magnetic field strength and the components HRD and HTD along the RD and TD, respectively, whereas the components H2 and H3 indicate the field strength values along two directions of easy magnetization, which formed a 45° angle with the sheet plane; the magnetization processes along these two axes are the same. Consequently, the changes in the flux density along these two axes are the same, and the projection of the sum of these flux densities onto the sheet plane can be regarded as the flux density in the TD.
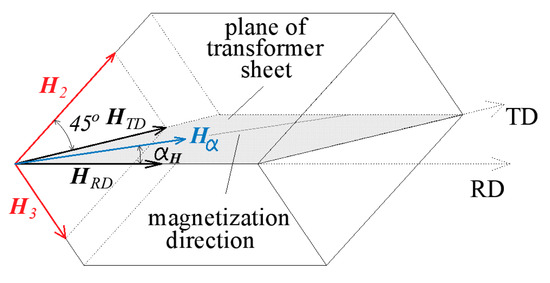
Figure 7.
Iron crystal in transformer sheet exhibiting magnetic field strength along particular directions.
The resultant flux density, which cannot be measured directly, can be regarded as the geometric sum of the flux densities along the RD and TD (Figure 8).
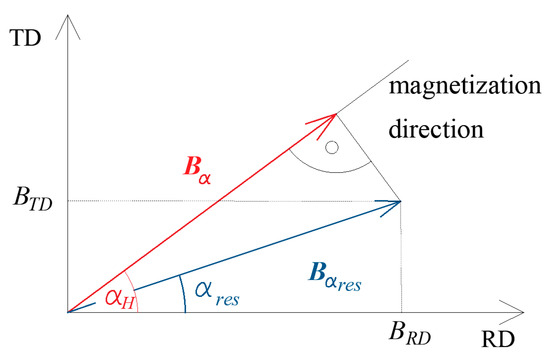
Figure 8.
Components of flux density.
This approach makes it possible for one to consider the hysteresis if the equations of the magnetic field are based on the integral form of Maxwell’s equations; subsequently, the flux densities along the RD and TD can be introduced into the orthogonal coordinate system of the field strength and flux density.
The main issue in the calculation of hysteresis changes for any magnetization direction is determining the limiting hysteresis loops for both the RD and TD. These loops are not the same as the limiting hysteresis loops measured along the RD or TD because they depend significantly on the magnetization direction. After reaching saturation, the flux density along the TD may decrease and continue to increase in the RD or vice versa, depending on the magnetization direction, as described in Section 2. If the limiting hysteresis loops are defined, then the changes in the flux density for minor hysteresis loops can be estimated, as described in detail in [28].
4. Determination of Limiting Hysteresis Loops
The hysteresis loops measured along directions close to the RD exhibit a “classic” shape. If the magnetization direction is closer to the TD, then the hysteresis loops are significantly deformed and thus cannot be described using simple analytical functions. Owing to the “atypical” shape of the hysteresis loops measured for large magnetization angles, the bottom curve BRDb(HRD) and upper curve BRDu(HRD) of the limiting hysteresis loop along the RD can be approximated as follows:
where aRD is the saturation flux density divided by 1.57, bRD(αH) is the coefficient determining the rate of increase in the flux density along the RD, and HRDc(αH) is the coercive force along the RD for particular magnetization angles.
Based on the hysteresis loops measured for individual magnetization directions, the coercive force Hc is determined and then the coercive force along the directions RD and TD is calculated as cosαHc and sinαHc, respectively. The dependence of the coercive force Hc on the magnetization angle αH for transformer sheet M120-27S is shown in Figure 9. Similarly, the curves along the TD can be expressed as follows:
where aTD = cos45°aRD, bTDb(αH, HTD), and bTdu(αH, HTD) are coefficients that determine the rate of increase in the flux densities along the TD; and HTDc(αH) denotes the coercive force for particular magnetization angles determined similarly.
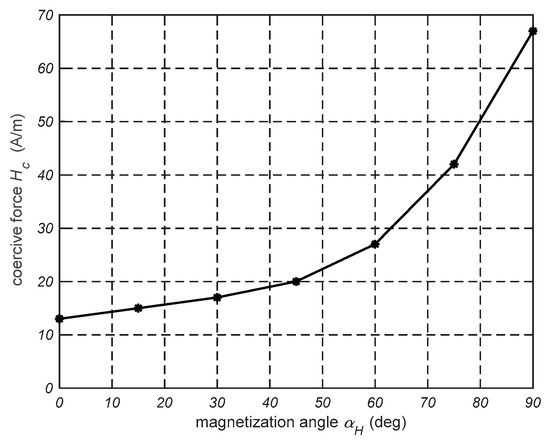
Figure 9.
Dependence of coercive force Hc on magnetization angle αH.
The coefficient bRD depends only on the magnetization angle αH. However, the coefficients bTDb and bTdu depend on two parameters, i.e., αH and HTD, respectively; therefore, their determination is more difficult compared with that of bRD. These coefficients are expressed as follows:
where wTD and dTD depend on the magnetization angle αH, and Hk = Hk1 for HTD < HTDc or Hk = Hk2 for HTD > HTDc. Additionally,
where Hk = Hk1 for HTD > −HTDc or Hk = Hk2 for HTD < −HTDc. Here, Hk denotes the field strength when the irreversible displacements of domain walls end. Figure 10 shows an example of a certain “atypical” hysteresis loop with parameters HTDc, Hk1, and Hk2.
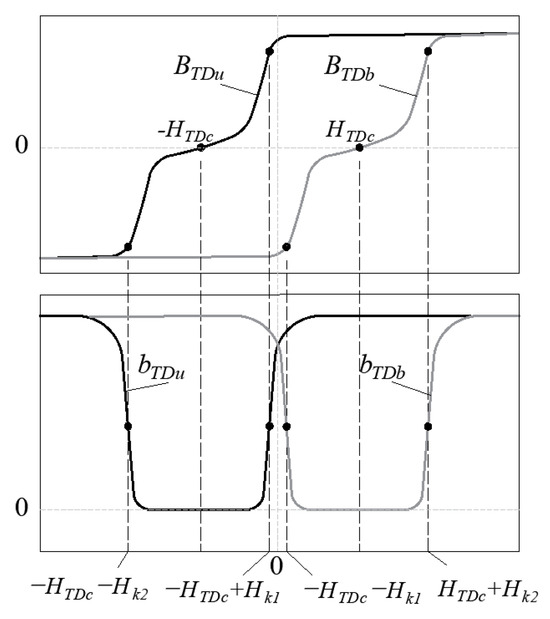
Figure 10.
Example of “atypical” hysteresis loop with parameters HTDc, Hk1, and Hk2.
The coefficients wTD and dTD in Equation (4a,b) significantly affect the changes in the values of bTDb and bTdu. The parameter Hk1 is the distance between the HTDc and the inflection point on the curve BTDb. Meanwhile, Hk2 is a distance between HTDc and the inflection point on the curve BTDb. The coefficients bRD, wTD, dTD, and Hk were determined using the least-squares method to minimize differences between the measured and calculated hysteresis loop. Their dependence on the magnetization angle is shown in Figure 11, Figure 12, Figure 13 and Figure 14.
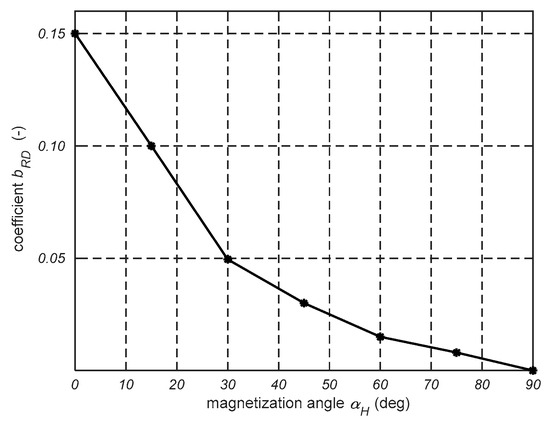
Figure 11.
Dependence of coefficient bRD on magnetization angle αH.
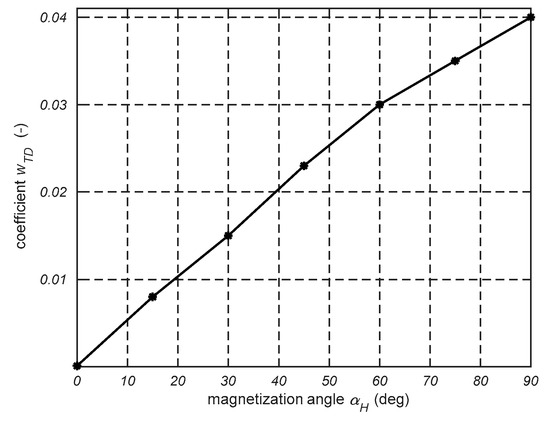
Figure 12.
Dependence of coefficient wTD on magnetization angle αH.
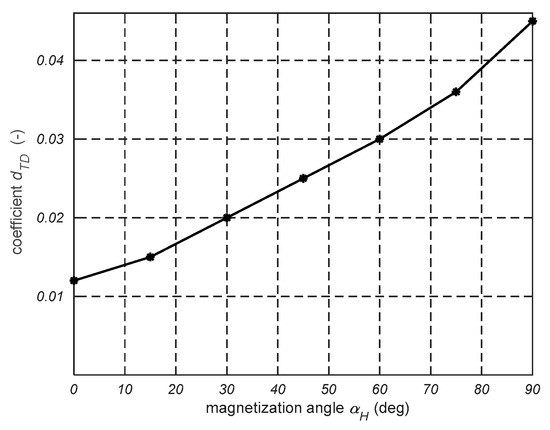
Figure 13.
Dependence of coefficient dTD on magnetization angle αH.
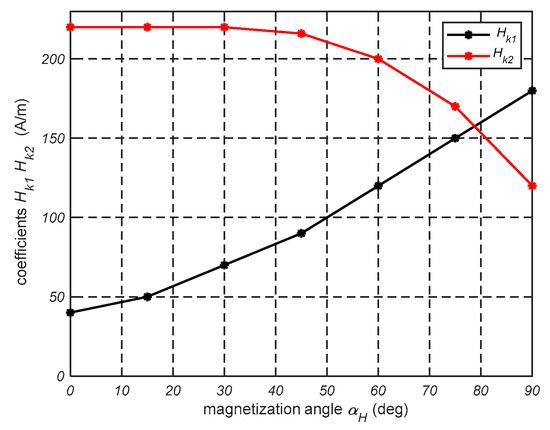
Figure 14.
Dependence of parameters Hk1 and Hk2 on magnetization angle αH.
Determining the dependence of the aforementioned coefficients on the magnetization angle makes it possible for one to calculate the hysteresis loops along the RD and TD for any magnetization angle and magnetic field strength. If the hysteresis loops are not measured for a specified magnetization direction, then the values of these parameters are determined by approximating the values determined based on measurements. Figure 15 and Figure 16 show the hysteresis loops for four magnetization angles.
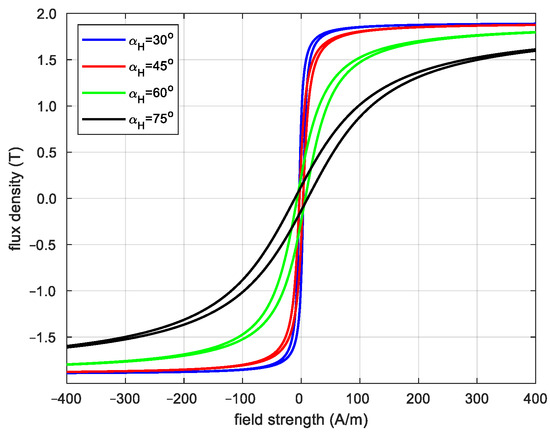
Figure 15.
Hysteresis loops along rolling direction.
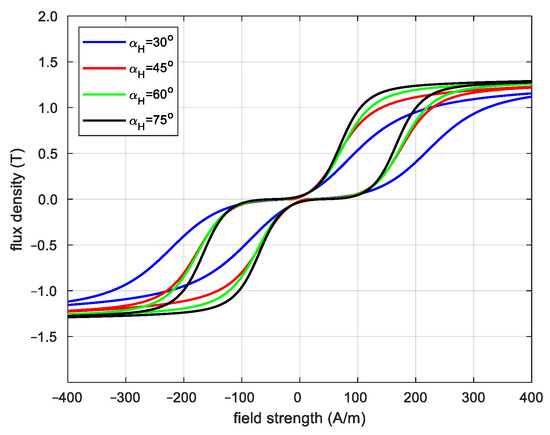
Figure 16.
Hysteresis loops along transverse direction.
These considerations pertain to the determination of the limiting hysteresis loops, which should be determined to calculate the minor hysteresis loops.
The resultant flux density for a specified field strength value is the vector sum of the flux densities along the RD and TD because the value of the resultant flux density should be considered when calculating the changes in the magnetic field.
5. Comparison between Measured and Calculated Hysteresis Loops
For a specified field strength and magnetization direction, the flux density values are determined along the RD and TD. As mentioned previously, the resultant flux density is the vector sum of the flux densities along both directions. However, the magnetic flux density must not exceed the saturation flux density Bsat. This implies that the algebraic sum (not the vector sum) of BRDb and BTDb cannot exceed Bsat if the field strength Hα increases:
Here, BTDb is the perpendicular projection of the resultant flux density (for increasing field strength Hα) along the easy magnetization axes inclined to the sheet plane at an angle of 45° (Figure 7).
A similar condition applies to the flux densities BRdu and BTdu if the field strength Hα decreases:
The flux density BTdu for decreasing field strength Hα is defined similarly to BTDb.
As previously mentioned, magnetization occurs mainly along the three easy magnetization axes but to different degrees depending on the field strength direction. Magnetic saturation occurs when all the flux density vectors of the elementary particles of the transformer sheet are parallel to the field strength direction. Assuming that the flux density vectors do not rotate at a certain value of field strength in the considered range of field strength changes, the flux density vectors of all particles are parallel to the easy magnetization axes. Subsequently, the sum of the resultant flux densities along the individual easy magnetization axes is equal to Bsat.
If the algebraic sum of BRDb and BTDb exceeds Bsat, then for increasing Hα, the flux density BTDb decreases when the magnetization angle is less than 54.7°:
Otherwise, the flux density BRDb decreases and is equal to:
Similar dependences refer to the flux densities BTdu and BRdu:
The angle αres (Figure 8) between the RD and the direction of the resultant flux density is not constant; for increasing Hα, it can be expressed as:
and for decreasing Hα:
Figure 17 shows the flowchart for determining the flux density of the limiting hysteresis loop for any magnetization direction if the field strength increases. The similar form has the flowchart for decreasing field strength values.
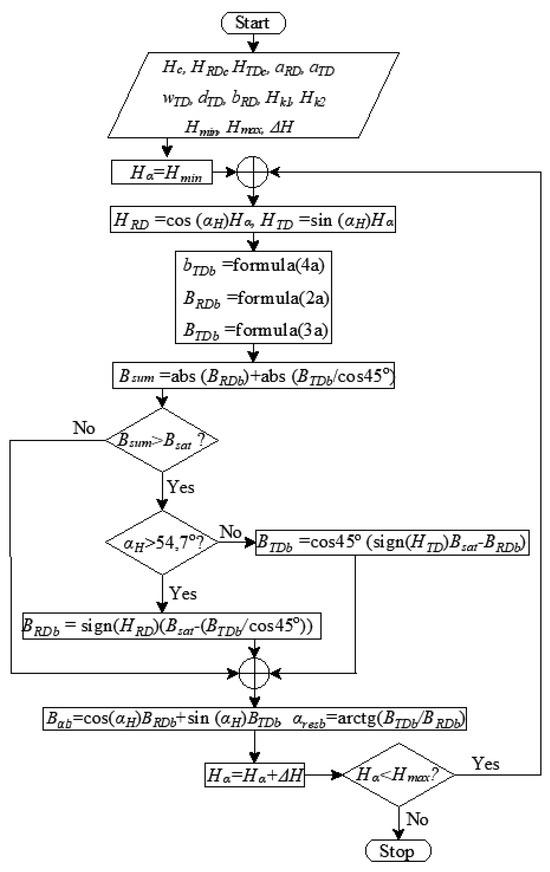
Figure 17.
Determination of the flux density of limiting hysteresis loop for increasing field strength values.
To determine the flux density of the limiting hysteresis loop, the measured coercive force Hc and the saturation flux density Bsat are introduced into the algorithm. The values of the parameters occurring in Equations (2a,b) and (3a,b) are also determined. For subsequent values of the field strength Hα, the field strength values along the RD and TD are determined, and then the flux densities BRDb and BTDb (or BRdu and BTdu if Hα decreases) are calculated. In the next step, the saturation condition (5a) or (5b) is checked. If the sum of BRDb and BTDb (or BrDu and BtDu) is greater than Bsat, the value of either the flux density along TD or RD is modified depending on the magnetization direction. At the final step, it is possible to determine the flux density Bα along the magnetization direction, the position of the resultant flux density vector, and its value, which is the geometric sum of the flux densities along the RD and TD.
Determining the limiting hysteresis loops for a given magnetization direction makes it possible to calculate minor hysteresis loops (which are located inside limiting loop) for any changes in the field strength. As it was widely described in [28], the changes in the flux density Br(H) of any point P(H0, B0) (Figure 18) can be described as follows if the field strength H increases:
where kBr(H) is an attenuation coefficient when H increases.
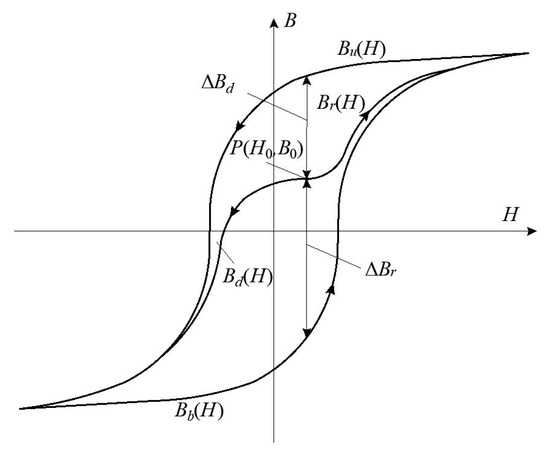
Figure 18.
Possible trajectories of any point P(H0, B0) inside the limiting hysteresis loop.
If H decreases, the changes in the flux density Bd(H) can be written as:
where kBd(H) is an attenuation coefficient when H decreases.
Figure 19 and Figure 20 show the limiting and minor hysteresis loops for the four magnetization angles. In these figures, (a, b) show the measured and calculated hysteresis loops for individual magnetization angles, (c, d) show the appropriate changes in the flux density along the RD and TD, and (e, f) show the calculated hysteresis loops and the loops showing changes in the resultant flux density for a specified magnetization direction. Under a magnetization angle of 30° and a field strength of approximately 200 A/m (HRD = 173 A/m, HTD = 100 A/m), the sum of flux densities BRD and BTD/cos45° was equal to Bsat. Changes in the flux density BRD were predominant, and the flux density BRD increased to Bsat, and BTD decreased to zero. The magnetization process has a similar character at an angle of 45°. For the field strength of approximately 212 A/m (HRD = 150 A/m, HTD = 150 A/m), the sum of BRD and BTD/cos45° was equal to Bsat, and BRD also increases to Bsat. Unlike the previous angles, at a magnetization angle of 60°, BRD decreased to zero and BTD increased to Bsat when the field strength exceeded 101 A/m (HRD = 51 A/m, HTD = 88 A/m). In this case, changes in BTD significantly affected the magnetization process. The flux densities BRD and BTD change similarly at a magnetization angle of 75°. When the field strength exceeded 204 A/m (HRD = 53 A/m, HT D = 198 A/m), BRD starts to decrease to zero.
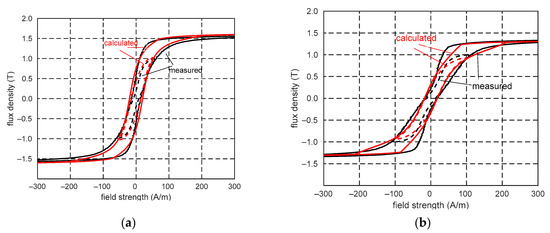
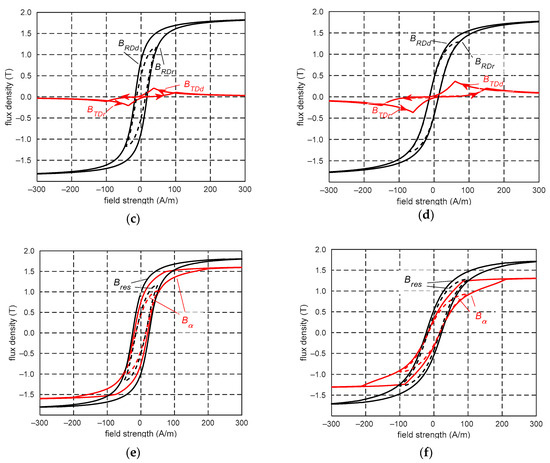
Figure 19.
Limiting loops (continuous lines) and minor loops (dashed lines) for magnetization angles 30° (a,c,e) and 45° (b,d,f): (a,b) measured loops (black lines) and calculated loops (red lines) along magnetization direction, (c,d) estimated loops along rolling direction (black lines) and transverse direction (red lines), (e,f) loops of resultant flux density (black lines) and calculated loops (red lines); BRDr, BRDd—flux densities along RD for increasing and decreasing field strengths, respectively; BTDr, BTDd—flux densities along TD for increasing and decreasing field strengths, respectively; Bres—resultant flux density; Bα—flux density along magnetization direction.
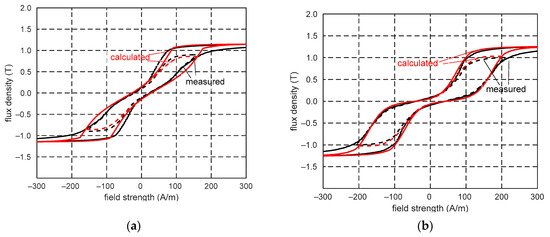
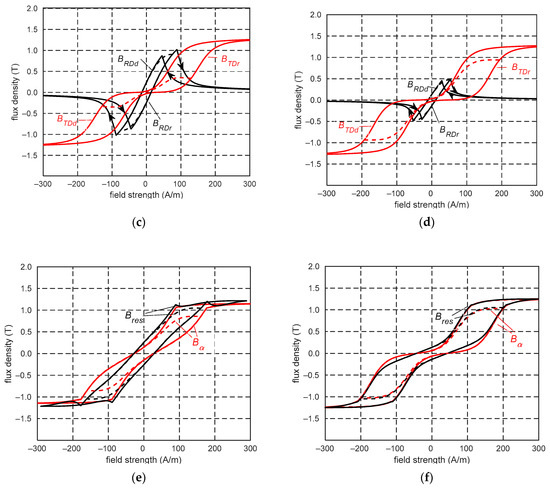
Figure 20.
Limiting loops (continuous lines) and minor loops (dashed lines) for magnetization angles 60° (a,c,e) and 75° (b,d,f): (a,b) measured loops (black lines) and calculated loops (red lines), (c,d) estimated loops along rolling direction (black lines) and transverse direction (red lines), and (e,f) loops of resultant flux density (black lines) and calculated loops (red lines); curve markings as in Figure 19.
The hysteresis loops of the resultant flux densities differed from those calculated and measured along the magnetization angles (Figure 19e,f and Figure 20e,f). This implies that the magnetization process in the transformer steel sheets cannot be regarded as axial magnetization.
Note that the resultant flux density for a given field strength cannot be determined as the geometric sum of the flux densities determined using hysteresis loops (without their modification in relation to the magnetization direction) determined separately for both the rolling and transverse directions. Figure 21 shows an example of the comparison of the limiting and minor hysteresis loops determined incorrectly with the measured hysteresis loops.
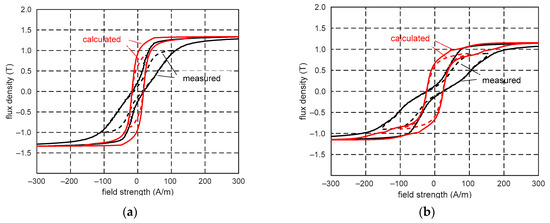
Figure 21.
Limiting loops (continuous lines) and minor loops (dashed lines) for magnetization angles 45° (a) and 60° (b); measured loops (black lines) and calculated incorrectly loops (red lines) along magnetization direction.
The described proposal for determining changes in the flux density in transformer steel sheets is intended to facilitate the introduction of the hysteresis model to the equations of the magnetic field distribution. This applies to the method of equivalent reluctance network method and especially to the significant modification of this method presented in [17]. In the mentioned method, the field strength components and the corresponding flux density components are assigned to the edges of the grid dividing the magnetic field area, which are parallel to the rolling direction (RD) or transverse direction (TD).
6. Conclusions
Determining the changes in the flux density in the corners and T-joint areas of transformer cores is challenging because, at individual points of the transformer sheet plane, the directions of the magnetic strength and flux density are different. To eliminate the necessity to store the limiting and partial hysteresis loops for each magnetization direction, a method for determining changes in the flux density was proposed. Changes in the flux density for any value of the magnetic field strength were assumed to depend only on certain limiting hysteresis loops assigned separately to the RD and TD; these limiting hysteresis loops depended on the magnetization direction on the sheet plane. This approach makes it possible for one to determine the resultant flux density vector for any magnetization direction, as the geometric sum of the flux density along RD and TD.
The coefficients defining the limiting hysteresis loops for the individual magnetization directions were selected using the least-squares method such that the differences between the limiting hysteresis loops determined using the proposed approximation method and the measured hysteresis loops were minimal. The partial hysteresis loops, which were within the limiting hysteresis loop for a specified magnetization direction, were determined as described in [28]; this was performed separately for the loops assigned to the RD and TD, where the resultant flux density value is the geometric sum of the flux densities in both directions. In each calculation step, the saturation condition should be verified because the algebraic sum of the flux densities in both directions cannot be greater than the saturated flux density.
The proposed method is not recommended for determining changes in the flux density in the transformer sheets when the field strength is relatively high because the resultant flux density vectors of the individual domains rotate toward the direction of the magnetic field. The method of determining the flux density for any magnetization direction based on changes in the RD and TD, which are mutually perpendicular, renders it relatively easy to incorporate magnetization in the equations of magnetic field distributions, particularly those based on the integral form of Maxwell’s equations. Then, the power losses in transformer steel sheets, especially in corners and T-joint points, can be directly determined using the general formula presented at the beginning of Section 3.
Author Contributions
Conceptualization, W.M. and M.S.; methodology, W.M.; formal analysis, M.S. and M.T.; investigation, W.M. and M.S.; validation, W.M. and M.S.; writing—original draft preparation, W.M. and M.T.; writing—review and editing, W.M. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Polish Ministry of Education and Science and performed by the Department of Electrical Engineering of Cracow University of Technology.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bozorth, R.M. Ferromagnetism; IEEE Press: New York, NY, USA, 1978. [Google Scholar]
- Iványi, A. Hysteresis Models in Electromagnetic Computation; Akadémiai Kiadó: Budapest, Hungary, 1997. [Google Scholar]
- Bertotti, G. Hysteresis in Magnetism; Academic Press: London, UK, 1998. [Google Scholar]
- Jiles, D.C. Introduction to Magnetism and Magnetic Materials; Chapman & Hall: London, UK, 1998. [Google Scholar]
- Tumański, S. Investigations of the anisotropic behaviour of SiFe Steel. J. Magn. Magn. Mater. 2003, 254–255, 50–53. [Google Scholar] [CrossRef]
- Beckley, P. Electrical Steels for Rotating Machines; Bell & Bain Ltd.: Glasgow, UK, 2002. [Google Scholar]
- Pfützner, H. Rotational Magnetization and Rotational Losses of Grain Oriented Silicon Steel Sheets—Fundamental Aspects and Theory. IEEE Trans. Magn. 1994, 30, 2802–2807. [Google Scholar] [CrossRef]
- Mao, W.; Atherton, D.L. Magnetization Vector Directions in a Steel Cube. IEEE Trans. Magn. 2000, 36, 3084–3086. [Google Scholar]
- IEC 60404-2; Magnetic Materials, Part 2: Methods of Measurement of the Magnetic Properties of Electrical Steel Sheet and Strip by Means of an Epstein Frame. International Electrotechnical Comission Std: Geneva, Switzerland, 1996.
- Wang, W.; Nysveen, A.; Magnusson, N. The influence of multidirectional leakage flux on transformer core losses. J. Magn. Magn. Mater. 2021, 539, 168370. [Google Scholar] [CrossRef]
- Quondam Antonio, S.; Ghanim, A.M.; Faba, A.; Laudani, A. Numerical simulations of vector hysteresis processes via the Preisach model and the Energy Based Model: An application to Fe-Si laminated alloys. J. Magn. Magn. Mater. 2021, 539, 168372. [Google Scholar] [CrossRef]
- Tumański, S. Handbook of Magnetic Measurements; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Mousavi, S.; Shamei, M.; Siadatan, A.; Nabizadeh, F.; Mirimani, S.H. Calculation of Power Transformer Losses by Finite Element Method. In Proceedings of the IEEE Electrical Power and Energy Conference, Toronto, ON, Canada, 10–11 October 2018. [Google Scholar]
- Sarac, V. FEM 2D and 3D design of transformer for core losses computation. Int. Sci. J. Mach. Technol. Mater. 2017, 2, 119–122. [Google Scholar]
- Mikula, L.; Ramdane, B.; Blatter Martinho, L.; Kedous-Lebouc, A.; Meunier, G. Numerical modelling of static hysteresis phenomena using a vector extension of the Loss Surface model. In Proceedings of the IEEE Conference on Electromagnetic Field Computation, Denver, CO, USA, 24–26 October 2022. [Google Scholar]
- Tousignant, T.; Sirois, F.; Meunier, G.; Guerin, C. Incorporation of a Vector Preisach–Mayergoyz Hysteresis Model in 3-D Finite Element Analysis. IEEE Trans. Magn. 2019, 55, 7300504. [Google Scholar] [CrossRef]
- Mazgaj, W.; Szular, Z.; Sierżęga, M.; Szczurek, P. Equation of the magnetic field distribution of dynamo sheets taking into account crystallographic structure. Arch. Electr. Eng. 2019, 68, 185–194. [Google Scholar]
- Shin, S.; Schaefer, R.; DeCooman, B.C. Anisotropic magnetic properties and domain structure in Fe-3%Si(110) steel sheet. J. Appl. Phys. 2011, 109, 07A307. [Google Scholar] [CrossRef]
- Sudo, M.; Matsuo, T. Magnetization modeling of silicon steel using a simplified domain structure model. J. Appl. Phys. 2012, 111, 07D107. [Google Scholar] [CrossRef]
- Furuya, A.; Fujisaki, J.; Uehara, Y.; Shimizu, K.; Oshima, H.; Matsuo, T. Micromagnetic Hysteresis Model Dealing with Magnetization Flip Motion for Grain-Oriented Silicon Steel. IEEE Trans. Magn. 2014, 50, 7300604. [Google Scholar] [CrossRef]
- Bernard, L.; Mailhe, B.J.; Avila, S.L.; Daniel, L.; Batistela, N.J.; Sadowski, N. Magnetic Hysteresis Under Compressive Stress: A Multiscale-Jiles–Atherton Approach. IEEE Trans. Magn. 2020, 56, 7506304. [Google Scholar] [CrossRef]
- Zhang, Z.; Hamzehbahmani, H.; Gaskell, P.H. A Novel Dynamic Hysteresis Model for Grain-Oriented Electrical Steels Based on Magnetic Domain Theory. IEEE Trans. Magn. 2022, 58, 7300109. [Google Scholar] [CrossRef]
- Ducharne, B.; Zurek, S.; Daniel, L.; Sebald, G. An anisotropic vector hysteresis model of ferromagnetic behavior under alternating and rotational magnetic field. J. Magn. Magn. Mater. 2022, 549, 169045. [Google Scholar] [CrossRef]
- Fiorillo, L.; Dupré, R.; Appino, C.; Rietto, A.M. Comprehensive model of magnetization curve, hysteresis loops, and losses in any direction in grain-oriented Fe–Si. IEEE Trans. Magn. 2002, 38, 1467–1475. [Google Scholar] [CrossRef]
- Ferreira da Luz, M.V.; Leite, J.V.; Benabou, A.; Sadowski, N. Three-Phase Transformer Modeling Using a Vector Hysteresis Model and Including the Eddy Current and the Anomalous Losses. IEEE Trans. Magn. 2010, 46, 3237–3240. [Google Scholar] [CrossRef]
- Sande, H.V.; Boonen, T.; Podoleanu, I.; Henrotte, F.; Hameyer, K. Simulation of a Three-Phase Transformer Using an Improved Anisotropy Model. IEEE Trans. Magn. 2004, 40, 850–855. [Google Scholar]
- Soiński, M.; Moses, A.J. Handbook of Magnetic Materials; Elsevier Science B.V.: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Mazgaj, W.; Sierzega, M.; Szular, Z. Approximation of Hysteresis Changes in Electrical Steel Sheets. Energies 2021, 14, 4110. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).