Long-Term Self-Discharge Measurements and Modelling for Various Cell Types and Cell Potentials
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
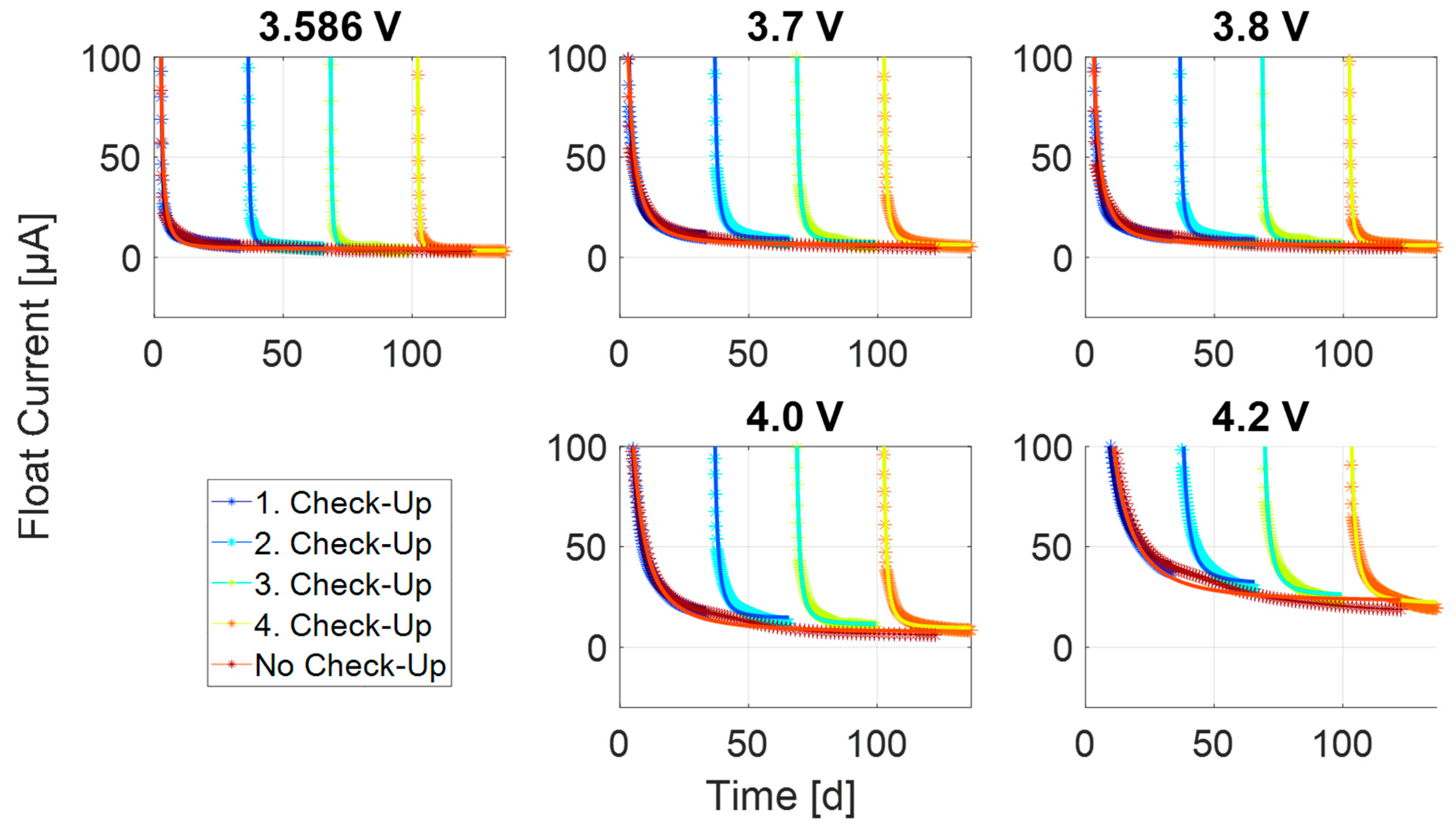
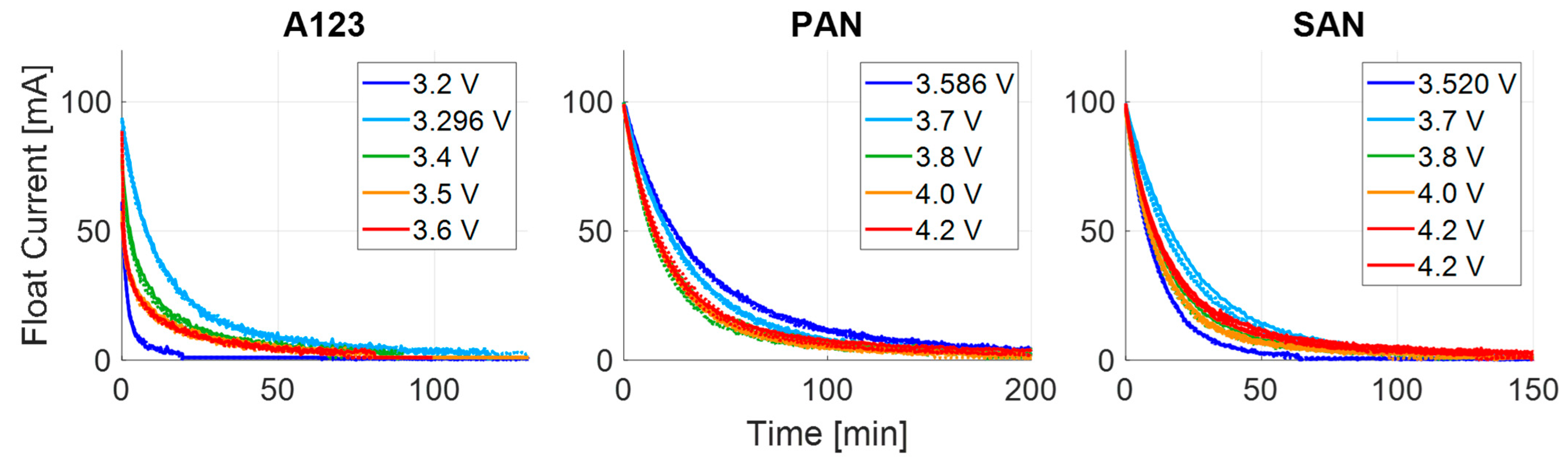
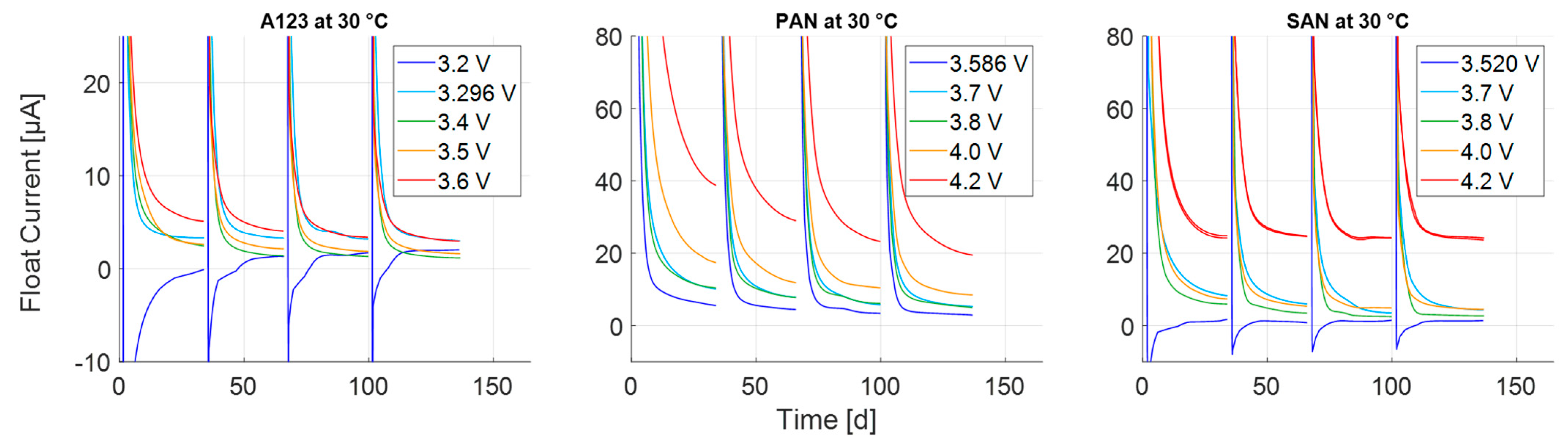
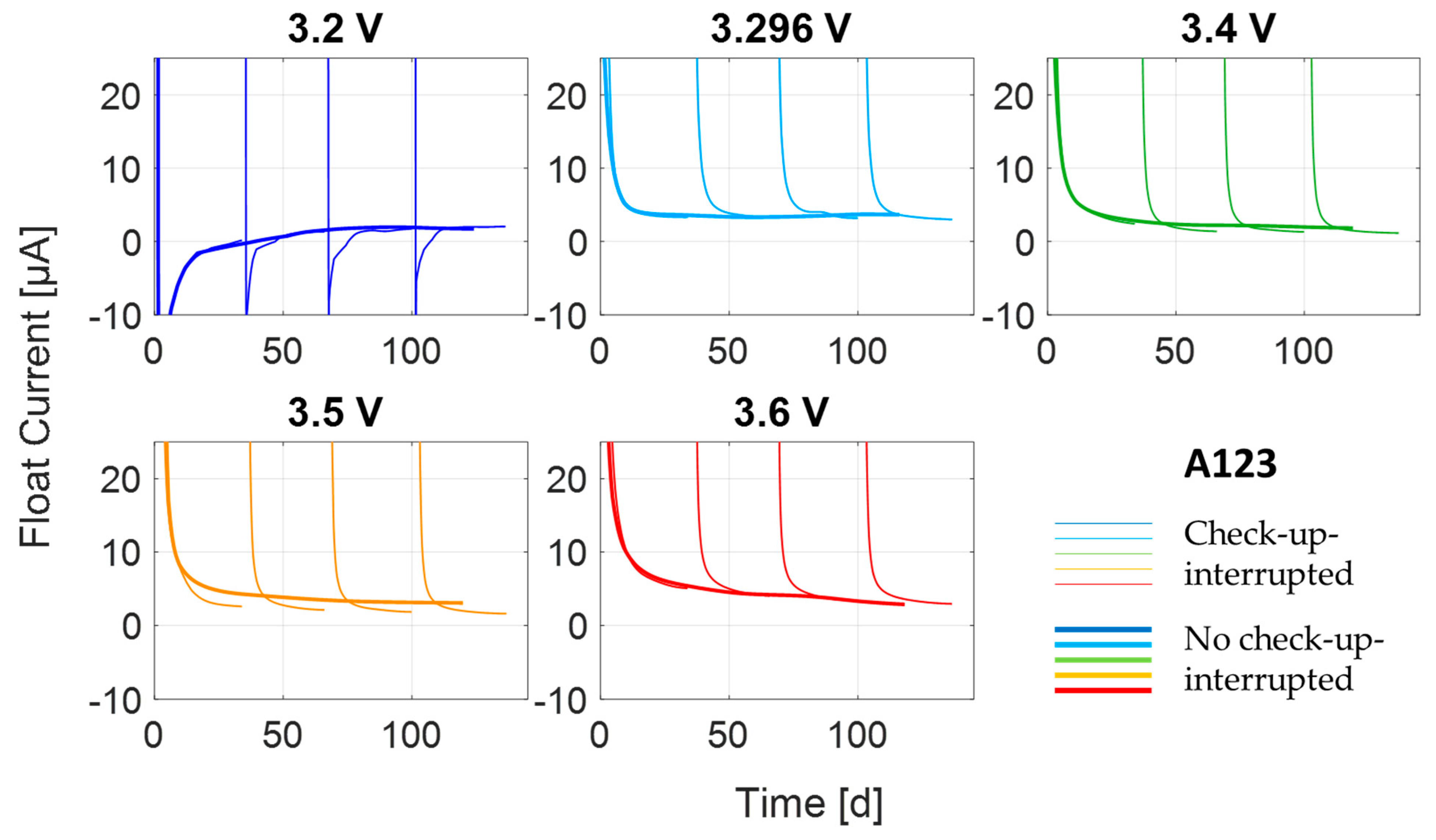
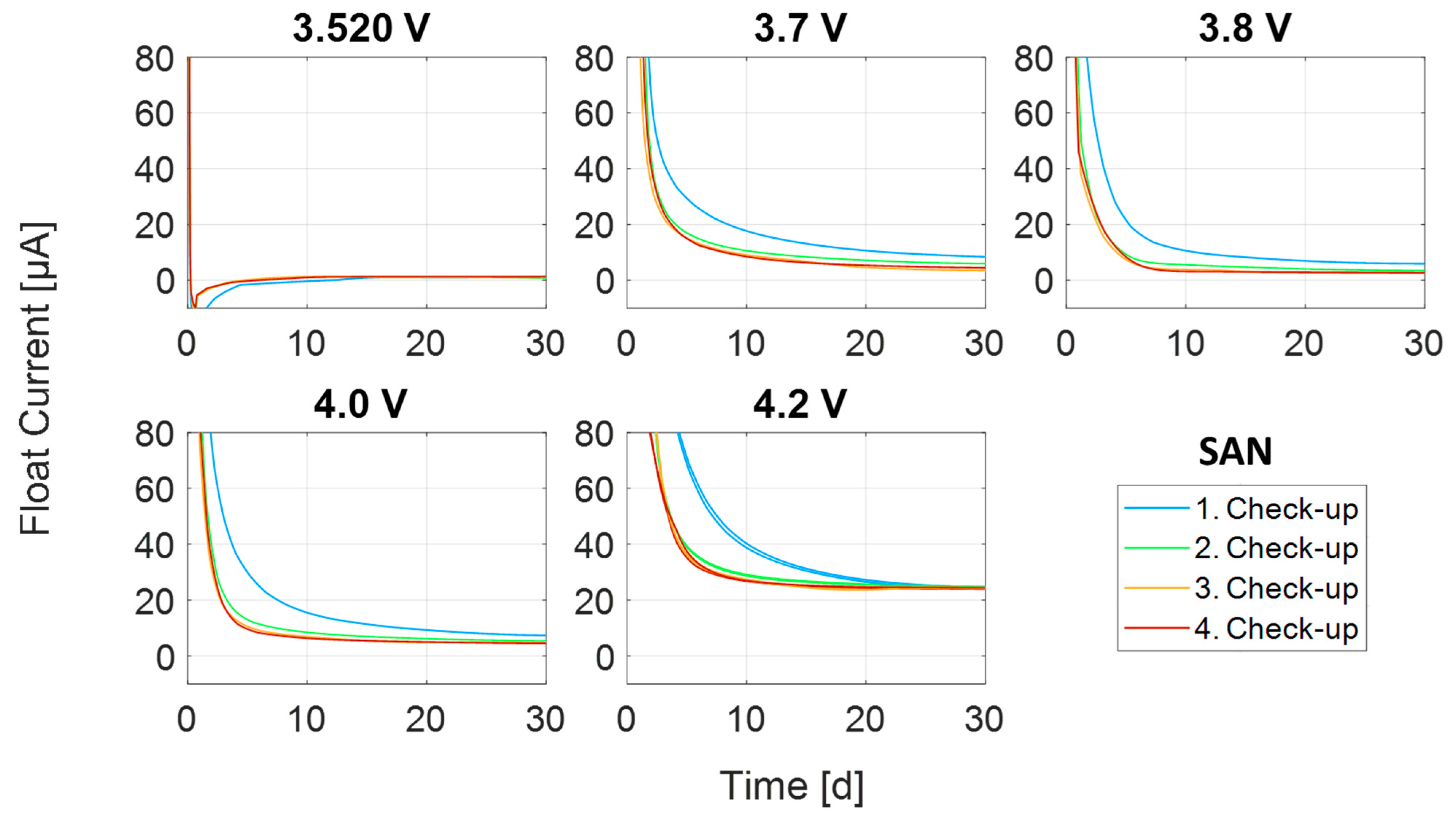
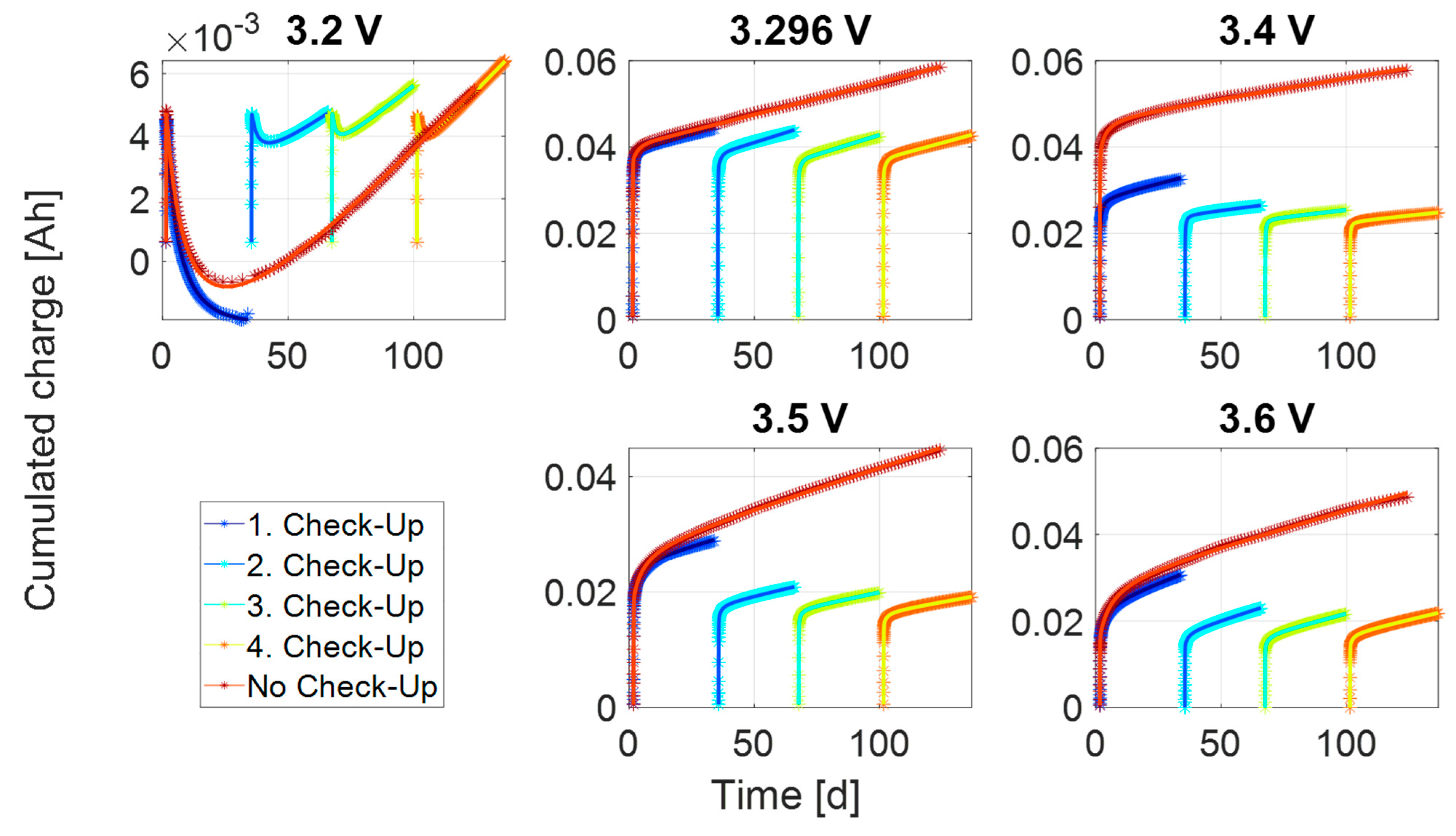
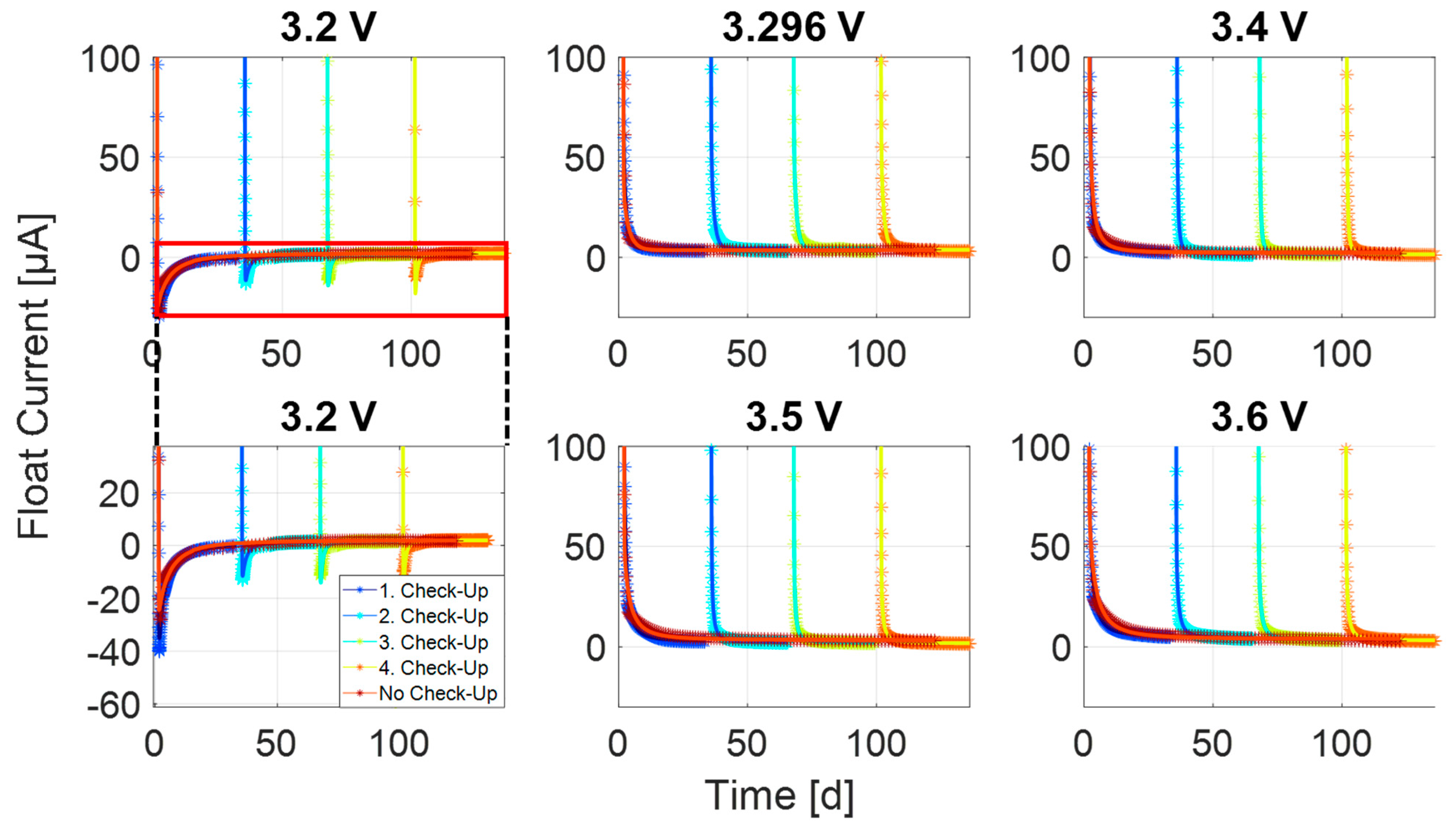
3.1. Transient Process at High Currents
3.2. Transient Process at Low Currents
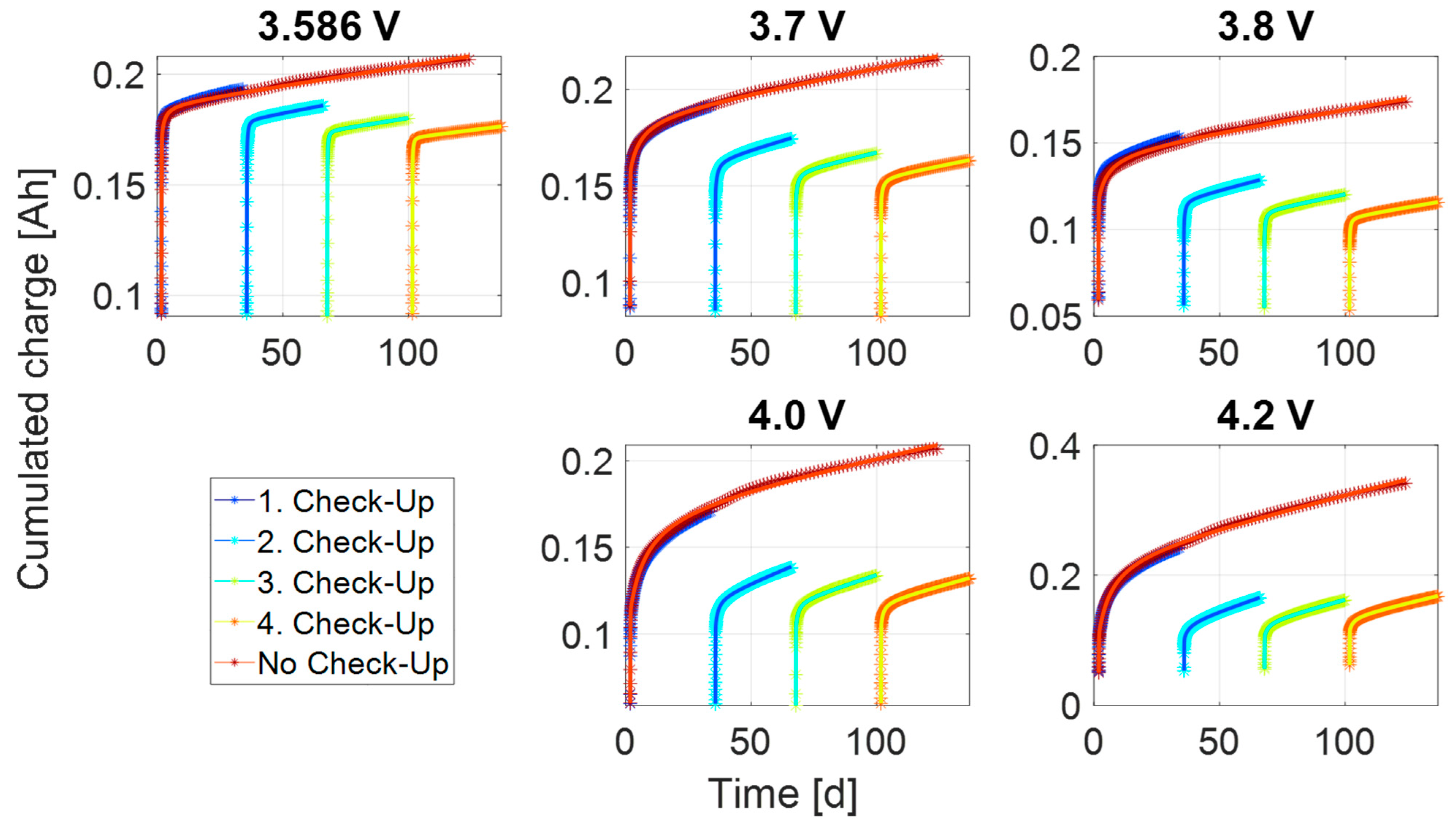
3.3. Steady-State Process
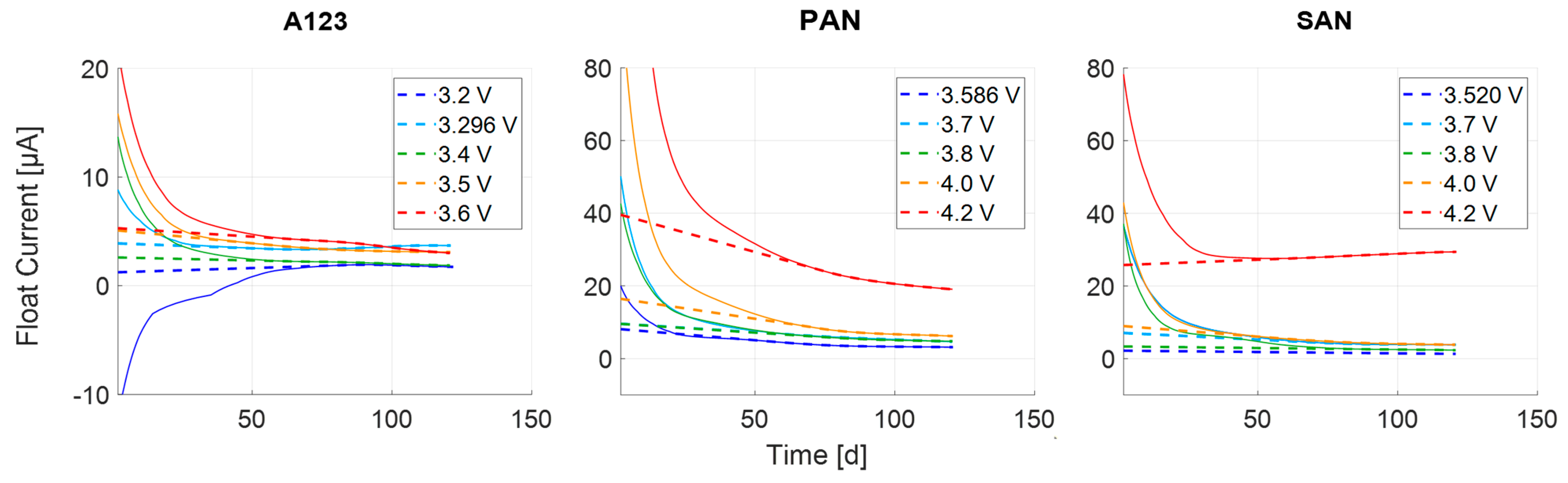
3.4. Modelling
3.4.1. Mathematical Physical Model
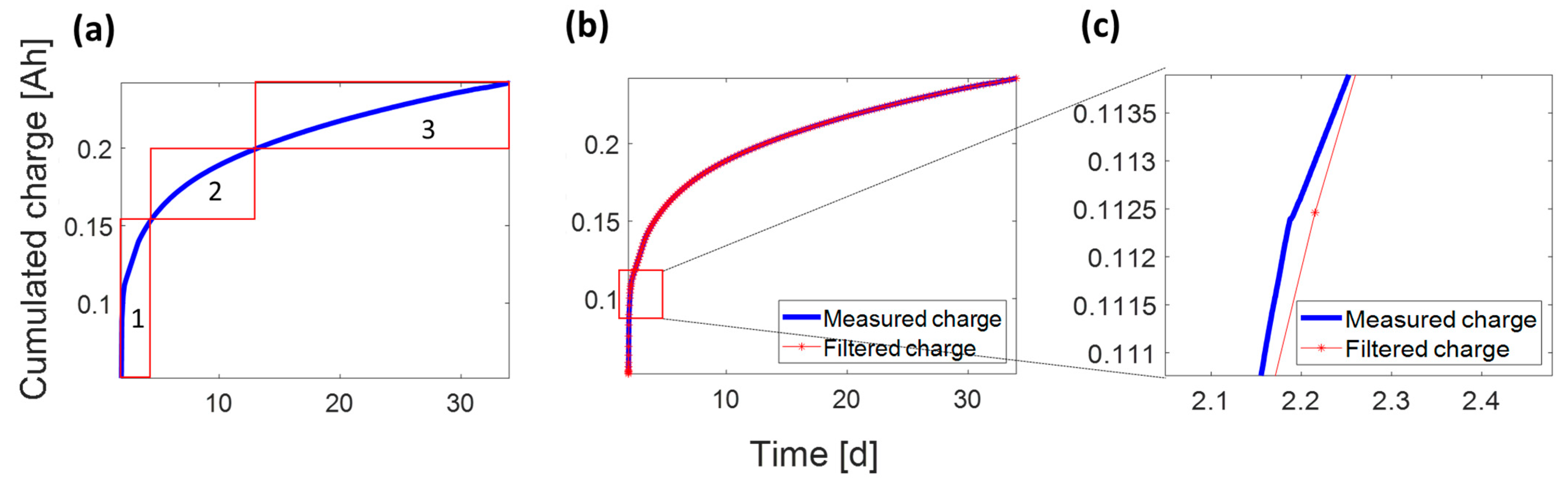
3.4.2. Optimization and Fitting
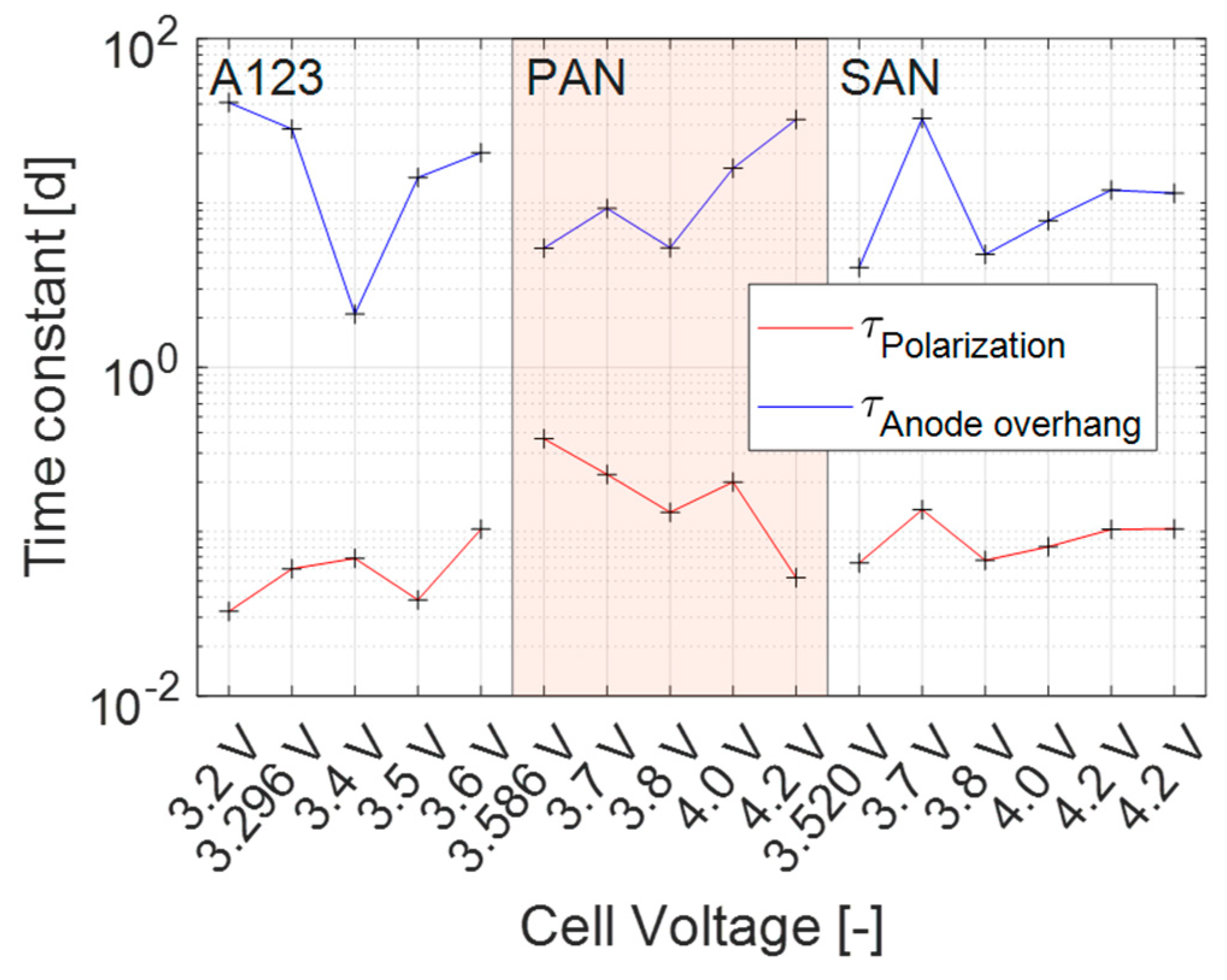
3.4.3. Transient Process
3.4.4. Steady-State Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1
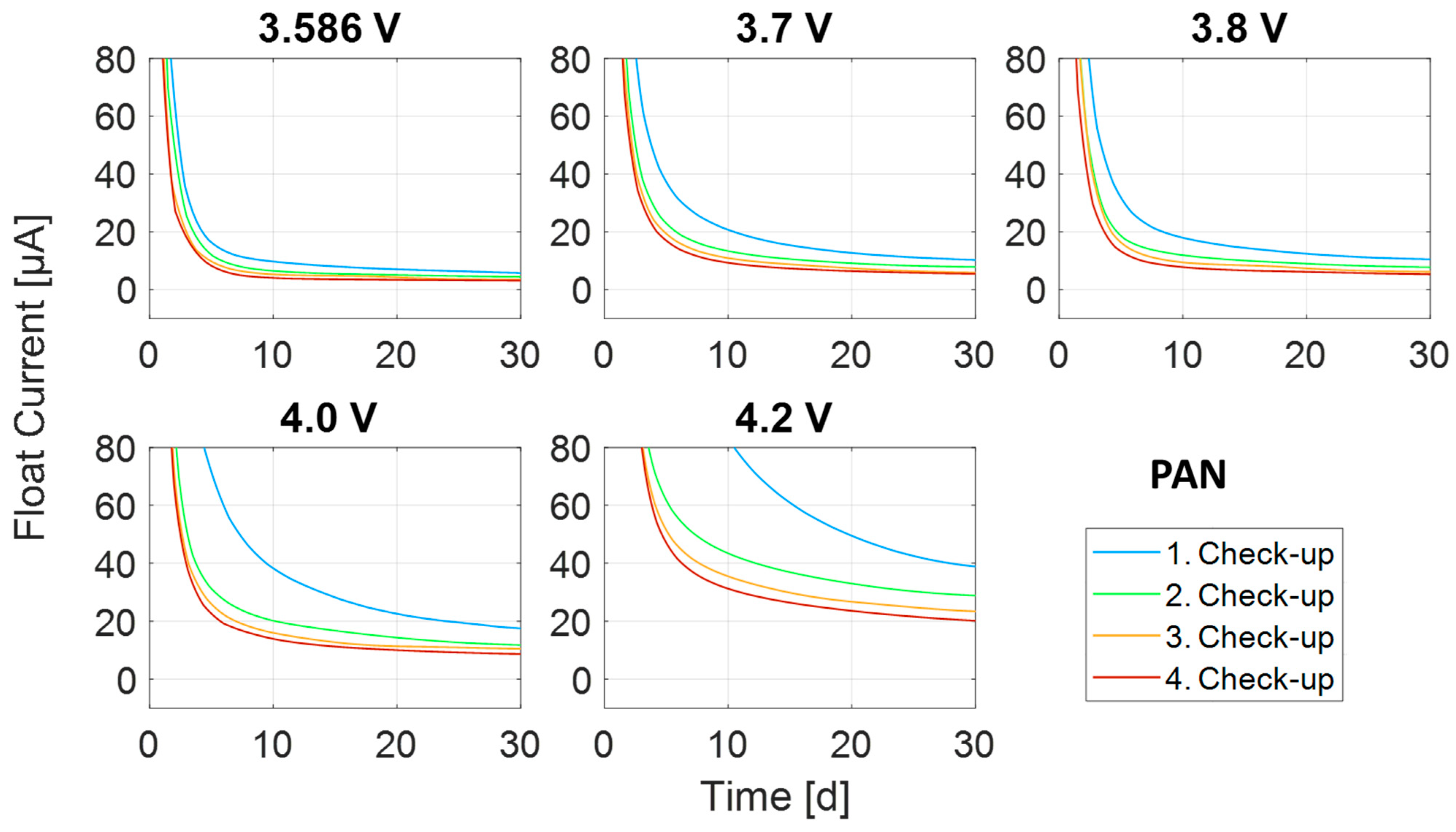
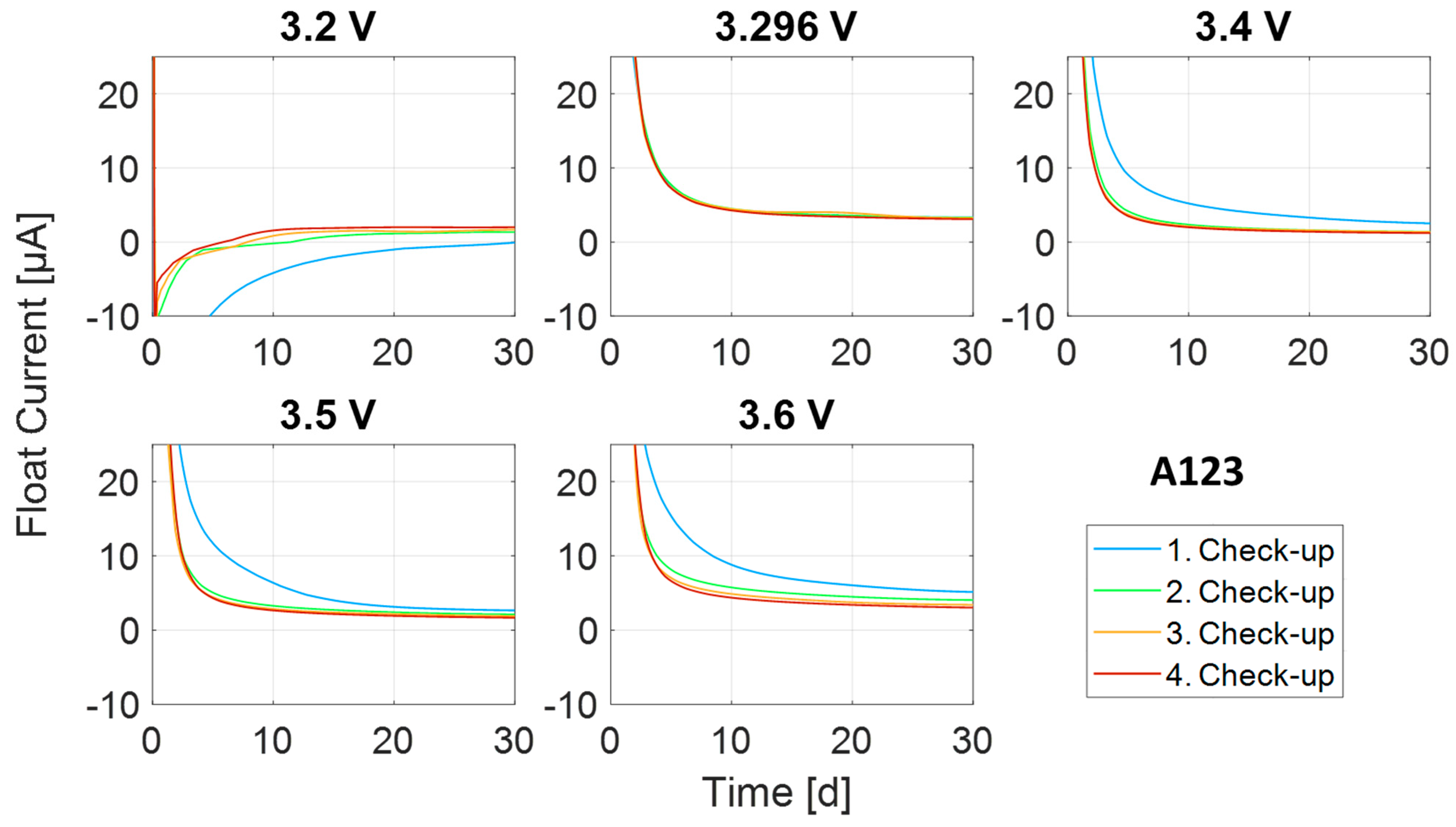
Appendix A.2
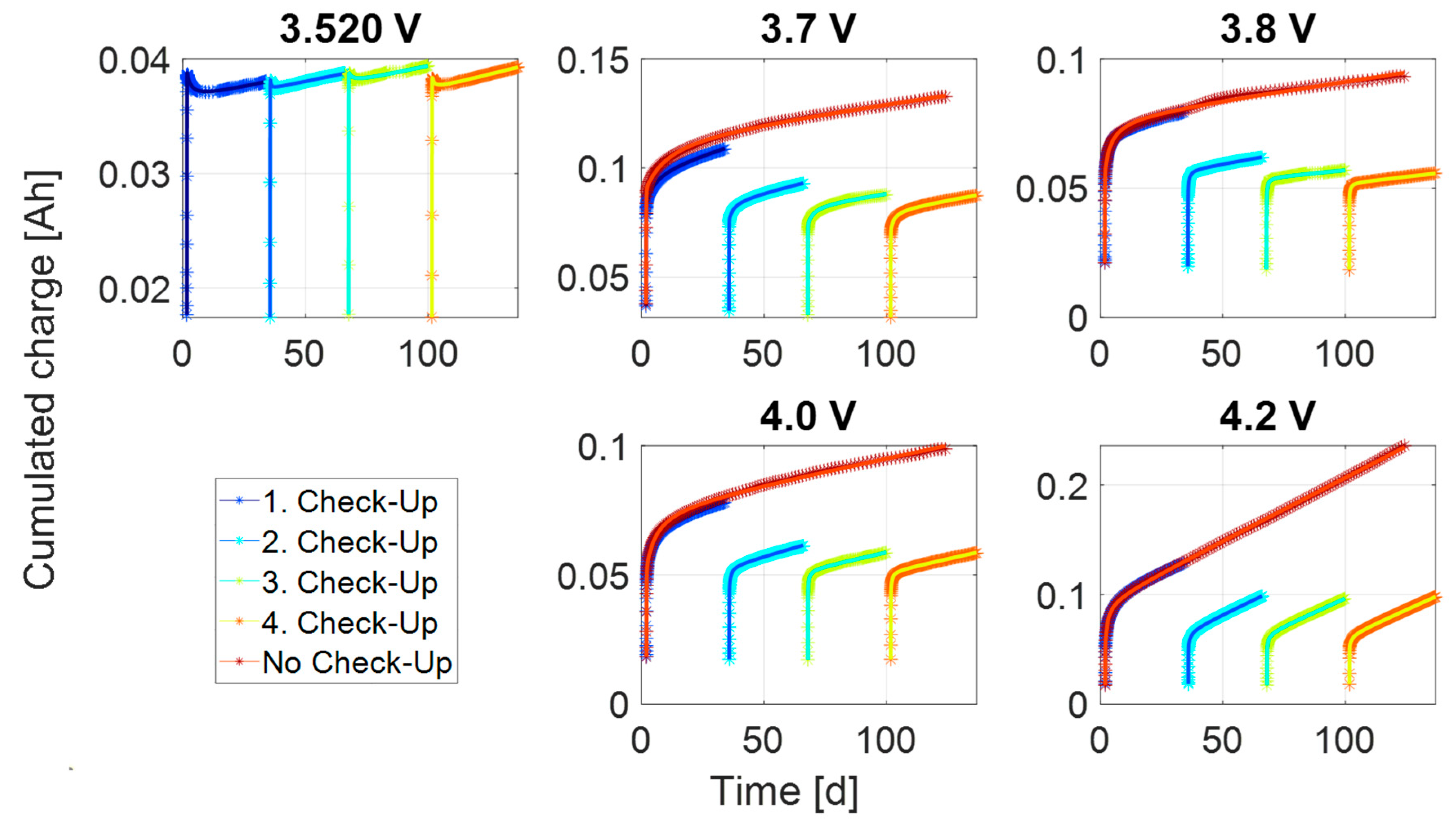
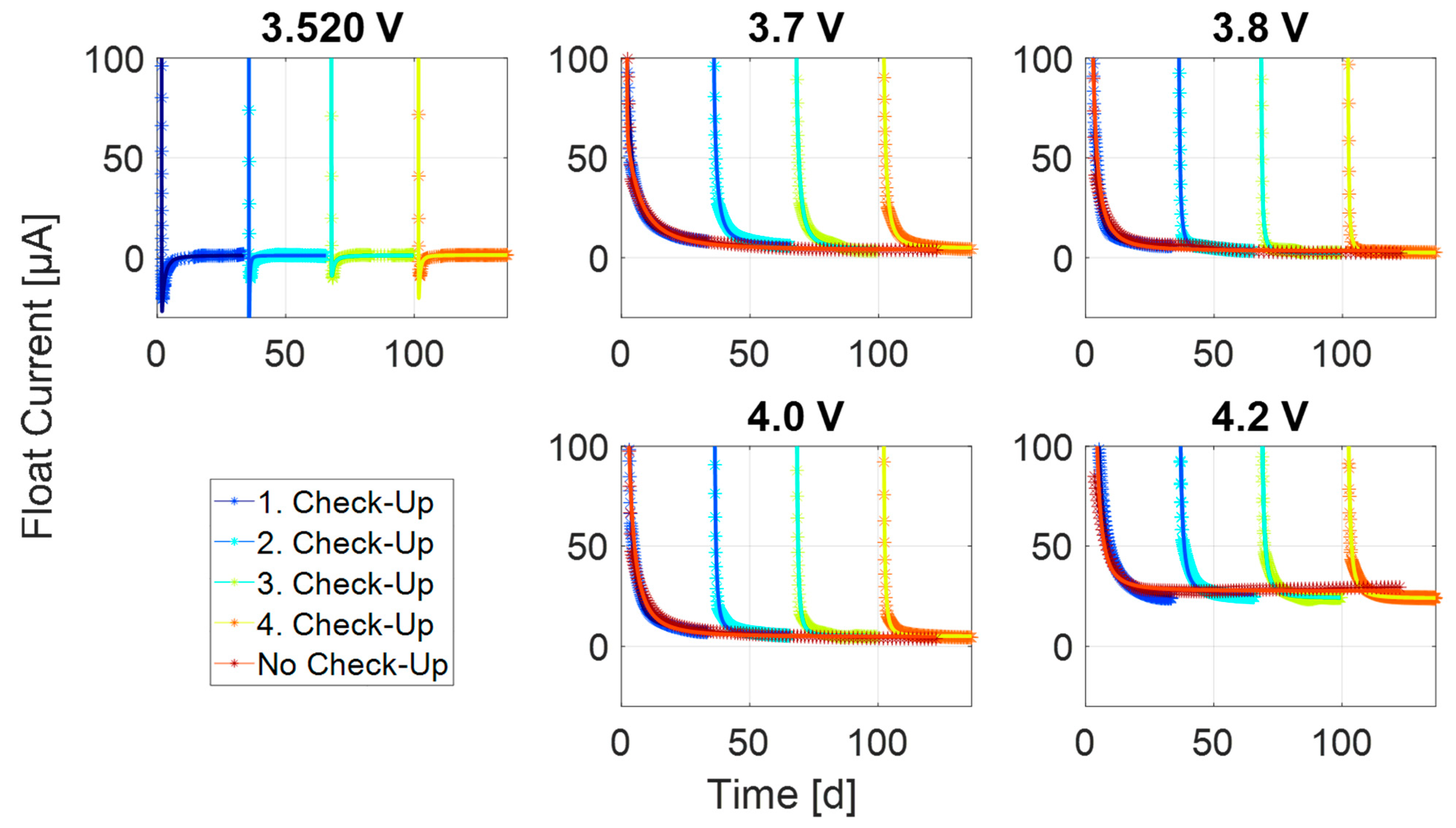
References
- Diouf, B.; Pode, R. Potential of lithium-ion batteries in renewable energy. Renew. Energy 2015, 76, 375–380. [Google Scholar] [CrossRef]
- Dai, Q.; Kelly, J.C.; Gaines, L.; Wang, M. Life Cycle Analysis of Lithium-Ion Batteries for Automotive Applications. Batteries 2019, 5, 48. [Google Scholar] [CrossRef]
- Saw, L.H.; Ye, Y.; Tay, A. Electro-thermal analysis and integration issues of lithium ion battery for electric vehicles. Appl. Energy 2014, 131, 97–107. [Google Scholar] [CrossRef]
- Abdul-Jabbar, T.A.; Obed, A.A.; Abid, A.J. Design of an Uninterrupted Power Supply with Li-Ion Battery Pack: A Proposal for a Cost-Efficient Design with High Protection Features. J. Tech. 2021, 3, 1–10. [Google Scholar] [CrossRef]
- Käbitz, S.; Gerschler, J.B.; Ecker, M.; Yurdagel, Y.; Emmermacher, B.; André, D.; Mitsch, T.; Sauer, D.U. Cycle and calendar life study of a graphite|LiNi1/3Mn1/3Co1/3O2 Li-ion high energy system. Part A: Full cell characterization. J. Power Sources 2013, 239, 572–583. [Google Scholar] [CrossRef]
- Deutschen, T.; Gasser, S.; Schaller, M.; Siehr, J. Modeling the self-discharge by voltage decay of a NMC/graphite lithium-ion cell. J. Energy Storage 2018, 19, 113–119. [Google Scholar] [CrossRef]
- Lewerenz, M.; Münnix, J.; Schmalstieg, J.; Käbitz, S.; Knips, M.; Sauer, D.U. Systematic aging of commercial LiFePO4|Graphite cylindrical cells including a theory explaining rise of capacity during aging. J. Power Sources 2017, 345, 254–263. [Google Scholar] [CrossRef]
- Theiler, M.; Endisch, C.; Lewerenz, M. Float Current Analysis for Fast Calendar Aging Assessment of 18650 Li(NiCoAl)O2/Graphite Cells. Batteries 2021, 7, 22. [Google Scholar] [CrossRef]
- Zilberman, I.; Sturm, J.; Jossen, A. Reversible self-discharge and calendar aging of 18650 nickel-rich, silicon-graphite lithium-ion cells. J. Power Sources 2019, 425, 217–226. [Google Scholar] [CrossRef]
- Lewerenz, M.; Dechent, P.; Sauer, D.U. Investigation of capacity recovery during rest period at different states-of-charge after cycle life test for prismatic Li(Ni1/3Mn1/3Co1/3)O2-graphite cells. J. Energy Storage 2019, 21, 680–690. [Google Scholar] [CrossRef]
- Gyenes, B.; Stevens, D.A.; Chevrier, V.L.; Dahn, J.R. Understanding Anomalous Behavior in Coulombic Efficiency Measurements on Li-Ion Batteries. J. Electrochem. Soc. 2015, 162, A278–A283. [Google Scholar] [CrossRef]
- Lewerenz, M.; Fuchs, G.; Becker, L.; Sauer, D.U. Irreversible calendar aging and quantification of the reversible capacity loss caused by anode overhang. J. Energy Storage 2018, 18, 149–159. [Google Scholar] [CrossRef]
- Fath, J.P.; Alsheimer, L.; Storch, M.; Stadler, J.; Bandlow, J.; Hahn, S.; Riedel, R.; Wetzel, T. The influence of the anode overhang effect on the capacity of lithium-ion cells—A 0D-modeling approach. J. Energy Storage 2020, 29, 101344. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Hildenbrand, F.; Ditscheid, D.; Barbers, E.; Sauer, D.U. Influence of the anode overhang on the open-circuit voltage and the ageing of lithium-ion batteries—A model based study. Appl. Energy 2023, 332, 120395. [Google Scholar] [CrossRef]
- Hüfner, T.; Oldenburger, M.; Bedürftig, B.; Gruhle, A. Lithium flow between active area and overhang of graphite anodes as a function of temperature and overhang geometry. J. Energy Storage 2019, 24, 100790. [Google Scholar] [CrossRef]
- Friedrich, F.; Pieper, S.; Gasteiger, H.A. Entropy Measurements of Li-Ion Battery Cells with Li- and Mn-Rich Layered Transition Metal Oxides via Linear Temperature Variation. J. Electrochem. Soc. 2021, 168, 120502. [Google Scholar] [CrossRef]
- Shi, W.; Zheng, J.; Xiao, J.; Chen, X.; Polzin, B.J.; Zhang, J.-G. The Effect of Entropy and Enthalpy Changes on the Thermal Behavior of Li-Mn-Rich Layered Composite Cathode Materials. J. Electrochem. Soc. 2016, 163, A571–A577. [Google Scholar] [CrossRef]
- D’Errico, J. SLM—Shape Language Modeling. Available online: https://www.mathworks.com/matlabcentral/fileexchange/24443-slm-shape-language-modeling (accessed on 10 October 2022).
- The MathWorks, Inc. Global Optimization Toolbox User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 2011. [Google Scholar]
- Ugray, Z.; Lasdon, L.; Plummer, J.; Glover, F.; Kelly, J.; Martí, R. Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization. INFORMS J. Comput. 2007, 19, 313–484. [Google Scholar] [CrossRef]
- Persson, K.; Sethuraman, V.A.; Hardwick, L.J.; Hinuma, Y.; Meng, Y.S.; van der Ven, A.; Srinivasan, V.; Kostecki, R.; Ceder, G. Lithium Diffusion in Graphitic Carbon. J. Phys. Chem. Lett. 2010, 1, 1176–1180. [Google Scholar] [CrossRef]
- Kizilyalli, M.; Corish, J.; Metselaar, R. Definitions of Terms for Diffusion in the Solid State. Pure Appl. Chem. 1999, 71, 1307–1325. [Google Scholar] [CrossRef]
- Katopodes, N.D. Diffusive Mass Transfer. In Free-Surface Flow; Elsevier: Amsterdam, The Netherlands, 2019; pp. 184–270. ISBN 9780128154892. [Google Scholar]
- Yang, J.; Du, C.; Wang, T.; Gao, Y.; Cheng, X.; Zuo, P.; Ma, Y.; Wang, J.; Yin, G.; Xie, J.; et al. Rapid Prediction of the Open-Circuit-Voltage of Lithium Ion Batteries Based on an Effective Voltage Relaxation Model. Energies 2018, 11, 3444. [Google Scholar] [CrossRef]
- Wilhelm, J.; Seidlmayer, S.; Keil, P.; Schuster, J.; Kriele, A.; Gilles, R.; Jossen, A. Cycling capacity recovery effect: A coulombic efficiency and post-mortem study. J. Power Sources 2017, 365, 327–338. [Google Scholar] [CrossRef]
- Pei, L.; Wang, T.; Lu, R.; Zhu, C. Development of a voltage relaxation model for rapid open-circuit voltage prediction in lithium-ion batteries. J. Power Sources 2014, 253, 412–418. [Google Scholar] [CrossRef]




| Short Name | A123 | PAN | SAN |
|---|---|---|---|
| Producer | A123 | Panasonic | Sanyo |
| Cell type | APR18650M-A1 | NCR18650B | UR18650AAN |
| Cathode | LFP: LiFePO4 | NCA:Li(Ni0.81Co0.16Al0.03)O2 | NMC: Li(NixMnyCoz)O2 |
| Anode | Graphite | Graphite | Graphite |
| Nom. Capacity | 1.1 Ah | 3.2 Ah | 2.15 Ah |
| Nom. Voltage | 3.3 V | 3.6 V | 3.6 V |
| Max charge current | 3.6 C | 0.5 C | 0.7 C |
| Max. discharge voltage | 2.0 V | 3.0 V | 3.0 V |
| Max. charge voltage | 3.6 V | 4.2 V | 4.2 V |
| Energy density | 93 Wh/kg | 248 Wh/kg | 180 Wh/kg |
| Storage voltage (SOC) before test | 3.296 V (26%) | 3.586 V (28%) | 3.520 V (14%) |
| Cell Type | Float Voltage | # Checkup- Interrupted | # Not Interrupted |
|---|---|---|---|
| A123 | 3.2 V | 1 | 1 |
| 3.296 V | 1 | 1 | |
| 3.4 V | 1 | 1 | |
| 3.5 V | 1 | 1 | |
| 3.6 V | 1 | 1 | |
| PAN | 3.586 V | 1 | 1 |
| 3.7 V | 1 | 1 | |
| 3.8 V | 1 | 1 | |
| 4.0 V | 1 | 1 | |
| 4.2 V | 1 | 1 | |
| SAN | 3.520 V | 1 | 0 |
| 3.7 V | 1 | 1 | |
| 3.8 V | 1 | 1 | |
| 4.0 V | 1 | 1 | |
| 4.2 V | 2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azzam, M.; Ehrensberger, M.; Scheuer, R.; Endisch, C.; Lewerenz, M. Long-Term Self-Discharge Measurements and Modelling for Various Cell Types and Cell Potentials. Energies 2023, 16, 3889. https://doi.org/10.3390/en16093889
Azzam M, Ehrensberger M, Scheuer R, Endisch C, Lewerenz M. Long-Term Self-Discharge Measurements and Modelling for Various Cell Types and Cell Potentials. Energies. 2023; 16(9):3889. https://doi.org/10.3390/en16093889
Chicago/Turabian StyleAzzam, Mohamed, Moritz Ehrensberger, Reinhard Scheuer, Christian Endisch, and Meinert Lewerenz. 2023. "Long-Term Self-Discharge Measurements and Modelling for Various Cell Types and Cell Potentials" Energies 16, no. 9: 3889. https://doi.org/10.3390/en16093889
APA StyleAzzam, M., Ehrensberger, M., Scheuer, R., Endisch, C., & Lewerenz, M. (2023). Long-Term Self-Discharge Measurements and Modelling for Various Cell Types and Cell Potentials. Energies, 16(9), 3889. https://doi.org/10.3390/en16093889







