Algorithm for Energy Resource Selection Using Priority Degree-Based Aggregation Operators with Generalized Orthopair Fuzzy Information and Aczel–Alsina Aggregation Operators

Abstract

Many aggregation operators are studied to deal with multi-criteria group decision-making problems. Whenever information has two aspects, intuitionistic fuzzy sets and Pythagorean fuzzy sets are employed to handle the information. However, q-rung orthopair fuzzy sets are more flexible and suitable because they cover information widely. The current paper primarily focuses on the multi-criteria group decision-making technique based on prioritization and two robust aggregation operators based on Aczel–Alsina t-norm and t-conorm. This paper suggests two new aggregation operators based on q-rung orthopair fuzzy information and Aczel–Alsina t-norm and t-conorm, respectively. Firstly, novel q-rung orthopair fuzzy prioritized Aczel–Alsina averaging and q-rung orthopair fuzzy prioritized Aczel–Alsina geometric operators are proposed, involving priority weights of the information. Several related results of the proposed aggregation operators are investigated to see their diversity. A multi-criteria group decision-making algorithm based on newly established aggregation operators is developed, and a comprehensive numerical example for the selection of the most suitable energy resource is carried out. The proposed aggregation operators are compared with other operators to see some advantages of the proposed work. The proposed aggregation operators have a wider range for handling information, with priority degrees, and are based on novel Aczel–Alsina t-norm and t-conorm.

1. Introduction

Multi-criteria group decision making (MCGDM) is a sophisticated approach in practical situations to deal with difficult and complex data. The MCGDM technique can provide scoring values for limited alternatives using the distinct characteristics of various possibilities. Uncertainty and imperfection are constant issues in real-world decision-making situations when one is examining data, especially large data. According to the notion of crisp sets, an object either belongs to a class or it does not. However, several phenomena in the real world cannot be presented on this scale. Zadeh [1] introduced the fuzzy set (FS) theory, where the membership grade (MG) is introduced to describe the belongingness of an element to a set.

The concept of FS is sometimes shown to be limited regarding its applicability. For example, whenever we have information about having two or more aspects, both of them are independent. To deal with such type of information, Atanassov [2] proposed the intuitionistic FS (IFS), a modified form of the FS that can accept complex and imprecise data with the help of an MG and a non-membership grade (NMG). The IFS theory has received lots of attention and has been used in various problems [3,4,5]. However, the IFS data set is constrained and depends on the irrational condition that the sum of MG and NMG must be contained within the unit interval, i.e., $\left[0, 1\right]$. To deal with complex and inaccurate information, Yager [6] proposed the concept of Pythagorean fuzzy sets (PyFS), a modified version of IFS. Similar to IFS, PyFS has a limited range and follows the condition that the sum of the squares of MG and NMG should lie within the interval$\left[0, 1\right]$. If the sum of the squares of the MG and NMG for a given Pythagorean fuzzy value (PyFV) becomes greater than the unit interval, for example, if MG is set at $0.5$ and NMG is set as$0.9$, then $\left(0.5, 0.9\right)$ cannot be considered as a PyFV. Yager [7] developed the q-rung orthopair fuzzy set (q-ROFS) to handle complex and uncertain conditions, including the abovementioned difficulty, to overcome this problem. A pair of MG and NMG requiring that the sum of the $q$ powers of both of them should be within the unit interval is known as a q-ROF value (q-ROFV). The parameter $q$ enables us to choose any MG and NMG from $\left[0, 1\right]$ as for every duplet $\left(MG,NMG\right)$. we have a $q$, such that $0\le M{G}^q+NM{G}^q\le 1$.

There are many applications of FSs and their generalizations, and one of the most widely discussed applications is MCGDM. To solve an MCGDM problem, we need some aggregation tools to give us collective preference value of information in decision making. A variety of aggregation operators (AOs) are very helpful in MCGDM approaches as mentioned in Table 1 below.

Table 1. Literature review concerning MCGDM problems.

Source	Results	Applications
Darko & Liang [8]	Hamacher Aggregation Operators	Mobile payment platform selection using EDAS method
Garg & Chen [9]	Neutrality-based Aggregation Operators	Selection of companies using neutrality AOs
Wei et al. [10]	Heronian mean Operators	MCGDM for enterprise resource planning system
Liu et al. [11]	Normalized bidirectional projection	Decision making with normalized bidirectional knowledge-based entropy measure
Garg & Rani [12]	Exponential AOs	Factors affecting the Indian stock exchange
Garg [13]	Trigonometric AOs	Decision maker preference toward the evaluation of the objects
Xia et al. [14]	Intuitionistic fuzzy AOs using Archimedean TN and TCN	Selection of manager by using Archimedean AOs
Wei & Zhao [15]	Induced interval-valued hesitant fuzzy AOs based on Einstein TN and TCN	MCGDM for technology commercialization
Seikh & Mandal [16]	q-ROF Frank Aggregation operators	Selection of government projects using MCGDM
Ali et al. [17]	Weighted interval-valued dual hesitant fuzzy AOs	Assessment of teaching quality using MCGDM
Liu et al. [18]	Complex q-ROF Muirhead mean operators	Analysis of investment policies using MCGDM
Aczél & Alsina [19]	AATN and AATCN	In this paper, novel Aczel–Alsina triangular norms are introduced
Senapati et al. [20]	Aczel–Alsina (A-A) AOs based on interval-valued intuitionistic fuzzy	Selection of research scientist using MCGDM
Hussain et al. [21]	PyF Aczel–Alsina AOs	Human resource management in multinational companies
Khan et al. [22]	q-ROF Aczel–Alsina AOs	Green supplier selection using MCGDM
Senapati [23]	Aczel–Alsina AOs with picture fuzzy information	Policy management using MCGDM
Hussain et al. [24]	T-spherical fuzzy AOs based on AATN and AATCN	Assessments of project based on AOs of TSF information
Ahmmad et al. [25]	Intuitionistic Fuzzy Rough Aczel–Alsina Average Aggregation Operators	Medical diagnosis based on AATN and AATCN
Ali & Naeem [26]	Complex Q-Rung Orthopair Fuzzy Aczel–Alsina Aggregation Operators	Analysis of factors effecting Pakistan stock exchange

Various circumstances that frequently happen in daily life require the application of a mathematical function that may reduce a collection of numbers into a single number. The examination of AOs has a big impact on MCGDM issues. In recent years, many researchers have concentrated on how to aggregate data because of their extensive application in various sectors. However, there are many situations where the data that need to be aggregated have a strict relationship in prioritizing. Assume a scenario where we are choosing a motorcycle for our child based on price and security considerations. In this case, we cannot permit an expense to fix a safety-related loss. Therefore, the criteria are the types that are prioritized. The priority is more for security. Choosing between different priority orders to determine priority degrees expands the scope of the prioritized operators. To deal with MCGDM problems, several prioritized AOs have been investigated in various real-life fields. The concept of prioritized AOs was first proposed by Yager [27,28]. Later, this concept was further extended to many fuzzy frameworks, and Yan et al. [29] discussed prioritized weighted AOs for MCGDM. Chen [30] developed the conception of prioritized AOs in the Atanassov intuitionistic fuzzy environment. Arora and Garg [31] discussed the significance of prioritized AOs using intuitionistic fuzzy soft sets. Some other recent work on prioritization-based AOs in several fuzzy settings can be seen in [32,33,34,35,36].

As discussed earlier, MCGDM algorithms and techniques have been used to deal with several real-life and energy-related problems. Akram et al. [37] investigated the applications of interval-valued T-spherical fuzzy Bonferroni means for selecting solar cells based on the MCGDM algorithm. Baumann et al. [38] presented a systematic review of energy storage systems for grid applications using the techniques and algorithms of MCGDM. The problem of offshore wind farm site selection was analyzed by Deveci et al. [39] based on the CoCoSo method and q-ROF information. Haiyun et al. [40] analyzed some strategies in the energy industry for Green Supply Chain Management using intuitionistic fuzzy details based on the QFD-based hybrid decision approach. Naseem et al. [41] studied some power Maclaurin symmetric mean operators to study their application in the assessment of smart grids for electricity. Some more recent work on the theory and application of MCGDM approaches on energy systems can be found in [42,43,44,45].

Previously, Senapati et al. [20] proposed Aczel–Alsina AOs for IFSs, and Hussain et al. [21] proposed Aczel–Alsina AOs for PyFSs. These AOs deal with uncertain information, but there are certain restrictions on them. Khan et al. [22] proposed improved AOs with a larger range using q-rung orthopair fuzzy details. However, these discussed AOs do not consider prioritization to be a critical factor in decision-making problems. Farahbod and Eftekhari [46] have shown the significance of using Aczel–Alsina t-norm and t-conorm with the help of a classification problem. Due to the significance of Aczel–Alsina AOs, prioritization, and the diverse nature of q-ROF information, this paper aims to develop the theory of prioritized AOs based on q-ROF information and Aczel–Alsina t-norm (AATN) and Aczel–Alsina t-Conorm (AATCN). The novelty of the proposed approach is based on the following facts:

• AATN and AATCN generalize other triangular norms and provide more accuracy, as suggested by [46].
• The framework of q-ROFS provides a wide range for describing uncertain information with no limitations.
• To solve the energy-related problems, prioritization phenomena are associated with the proposed AOs.

The structure of this article is as follows: The core concepts of AATN and AATCN and q-ROFPSs are presented in Section 1. Aczel–Alsina operational laws for q-ROFPVs are described in Section 2. In Section 3, q-ROFPAAA and q-ROFPAAG operators are proposed, and some of their desirable characteristics and exceptional cases are demonstrated. Section 4 constructs an MCGDM framework for handling the problem of energy resource selection using q-ROFP information, where attributes experts are prioritized. An application of the proposed approach is demonstrated in a practical example in Section 5. Section 6 compares a variety of proven methods to show the effectiveness of the suggested method. The article is concluded in Section 7.

2. Preliminaries

To help readers understand the work, we recall the novel Aczel–Alsina t-norm, Aczel–Alsina t-norms, and some fundamentals of q-ROFSs in this section.

Definition 1.

Let $X$ be any non-empty set. Then a q-ROFS ${\rm T}$ is dined as:

$${\rm T}=\left\{\left(m_{{\rm T}}\left(x\right),n_{{\rm T}}\left(x\right)\right)|x\in X\right\}$$

(1)

where$m_{{\rm T}}: X\to \left[0,1\right]$ and $n_{{\rm T}}: X\to \left[0,1\right]$ denote the MG and NMG of $x\in X,$respectively, provided that$0\le m_{{\rm T}}^q\left(x\right)+n_{{\rm T}}^q\left(x\right)\le 1$. Moreover, the term ${ȓ}_{{\rm T}}\left(x\right)=\left(\sqrt[q]{1-\left(m_{{\rm T}}^q\left(x\right)+n_{{\rm T}}^q\left(x\right)\right)}\right),$${ȓ}_{{\rm T}}\left(x\right)\in \left[0,1\right]$ is considered to be a hesitancy degree, and $\left(m_{{\rm T}}\left(x\right), n_{{\rm T}}\left(x\right)\right)$ is known as q-ROFV.

Definition 2.

For any q-ROFV  ${\rm T}=\left(m_{{\rm T}}\left(x\right),n_{{\rm T}}\left(x\right)\right)$, the scoreunction is defined as:

$$Śc\left({\rm T}\right)=m_{{\rm T}}^q\left(x\right)-n_{{\rm T}}^q\left(x\right),Śc\left({\rm T}\right)\in \left[-1,1\right]$$

(2)

Definition 3.

The A-A TN and TCN are defined respectively as folls: $\forall , 0\le Պ\le +\infty$:

$$T_A^{Պ}=\left\{\begin{array}{c}{T}_D\left(a,b\right) if Պ=0\\ min\left(a,b\right) if Պ=\infty \\ e^{{\left({\left(-loga\right)}^{Պ}+{\left(-logb\right)}^{Պ}\right)}^{1/Պ}} otherwise\end{array}\right. \mathit{\text{and}} S_A^{Պ}=\left\{\begin{array}{c}{S}_D\left(a,b\right) if Պ=0\\ max\left(a,b\right) if Պ=\infty \\ 1-e^{{\left({\left(-loga\right)}^{Պ}+{\left(-logb\right)}^{Պ}\right)}^{1/Պ}} otherwise\end{array}\right.$$

In the next section, we aim to consider Aczel–Alsina AOs with prioritization degrees, which helps in modeling the opinion of experts.

3. q-Rung Orthopair Fuzzy Prioritized Aczel–Alsina Operators

This section contains some core concepts of q-ROFPAA operators based on A-A TN and A-A TCN. These AOs include averaging and geometric operators and involve the prioritization degree experts and attributes for decision-making problems. We also studied the fundamental features of proposed AOs.

Definition 4.

If we suppose ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ is the collection of q-ROFVs, where $j=1,2,3,\dots ,k$, then, the q-ROFPAAA operator is defined as:

$$q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)={\oplus }_{j=1}^k\left(\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}\left({{\rm T}}_j\right)\right)$$

(3)

Here,  $\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}$ is the priority degree, which works as a weight of q-ROFV ${{\rm T}}_j$. Based on the operational laws of the q-ROFVs, we obtain the succeeding theorem.

Theorem 1.

If we suppose  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$is the collection of q-ROFVs, then, the q-ROFPAAA operator is given by:

$$q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)=\left(\begin{array}{c}\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{j=1}^k\left(\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}\right){\left(-ln \left(1-m_{{{\rm T}}_j}^q\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}}},\\ e^{-{\left({\displaystyle \sum }_{j=1}^k\left(\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}\right){\left(-ln\left(n_{{{\rm T}}_j}\right)\right)}^{Պ}\right)}^{1/Պ}}\end{array}\right)$$

(4)

The proof is given in Appendix B.

In the following few theorems, we aim to discuss how q-ROFPAAA operators satisfy the basic characteristics of aggregation. These features include idempotency, monotonicity, and boundedness. Further, in the next sections, $j=1,2,3,\dots ,k$ shall be used for indexing purposes.

Theorem 2.

Consider any number of q-ROFVs ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$. If we let${{\rm T}}_j={\rm T}=\left(m_{{\rm T}},n_{{\rm T}}\right)$, then

$$q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)={\rm T}$$

(5)

Proof. 

Since

$$\begin{gathered} q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)=\left(\begin{array}{c}\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{j=1}^k\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}{\left(-ln \left(1-m_{{{\rm T}}_j}^q\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}}}\\ e^{-{\left({\displaystyle \sum }_{j=1}^k\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}{\left(-ln\left(n_{{{\rm T}}_j}\right)\right)}^{Պ}\right)}^{1/Պ}}\end{array}\right) \\ =\left(m_{{\rm T}},n_{{\rm T}}\right)={\rm T} \end{gathered}$$

□

Theorem 3.

Consider any number of q-ROFVs  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$. If ${{\rm T}}^{-}=min\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)$ and ${{\rm T}}^{+}=max\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)$, then,

$${{\rm T}}^{-}\le q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)\le {{\rm T}}^{+}$$

(6)

For proof see Appendix C.

Theorem 4.

It we consider  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ and${{\rm T}}_j^{’}=\left(m_{{{\rm T}}_j}^{’}\left(x\right),n_{{{\rm T}}_j}^{’}\left(x\right)\right)$  as the two collections of q-ROFVs. If  ${{\rm T}}_j\le {{\rm T}}_j^{’}$, then

$$q-ROFPAAA\left({{\rm T}}_{1 }, {{\rm T}}_2,{{\rm T}}_3,\dots ,{{\rm T}}_j\right)\le q-ROFPAAA\left({{\rm T}}_1^{’},{{\rm T}}_2^{’},{{\rm T}}_3^{’},\dots ,{{\rm T}}_j^{’}\right)$$

(7)

Proof. 

The proof is straightforward. □

Theorem 5.

Let  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ be a collection of q-ROFVs, $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_1=1$ and $S\left({{\rm T}}_k\right)$ are the scores of q-ROFVs ${{\rm T}}_k$. If $\beta =\left(a,b\right)$ is a q-ROFV, then

$$q-ROFPAAA\left({{\rm T}}_1\oplus \beta ,{{\rm T}}_2\oplus \beta ,\dots ,{{\rm T}}_j\oplus \beta \right)=q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_j\right)\oplus \beta$$

(8)

For proof see Appendix D.

Theorem 6.

Let  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ be a collection of q-ROFVs, $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_j=1$ and $S\left({{\rm T}}_k\right)$ are the scores of q-ROFV ${{\rm T}}_k$. If $\phi >0$, then:

$$q-ROFPAAA\left(\phi {{\rm T}}_1,\phi {{\rm T}}_2,\dots ,\phi {{\rm T}}_j\right)=\phi q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_j\right)$$

(9)

For proof see Appendix E.

Theorem 7.

Let  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ $\left(j=1,2,3,\dots ,k\right)$ be a collection of q-ROFVs, $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_j=1$ and $S\left({{\rm T}}_k\right)$ are the scores of q-ROFV ${{\rm T}}_k$ if $\phi >0$, $\beta =\left(a,b\right)$ is a q-ROFV, then

$$q-ROFPAAA\left(\phi {{\rm T}}_1\oplus \beta ,\phi {{\rm T}}_2\oplus \beta ,\dots ,\phi {{\rm T}}_j\oplus \beta \right)=\phi q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_j\right)\oplus \beta$$

(10)

Proof. 

Straightforward. □

Theorem 8.

Let  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ and ${\beta }_j=\left(a_{{{\rm T}}_j}\left(x\right),b_{{{\rm T}}_j}\left(x\right)\right)$ $\left(j=1,2,3,\dots ,k\right)$ be two collection of q-ROFVs, $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_1=1$ and $S\left({{\rm T}}_k\right)$ are the scores of q-ROFV ${{\rm T}}_k$, then:

$$\begin{gathered} q-ROFPAAA\left({{\rm T}}_1\oplus {\beta }_1,{{\rm T}}_2\oplus {\beta }_2,\dots ,{{\rm T}}_k\oplus {\beta }_k\right) \\ =q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)\oplus q-ROFPAAA\left({\beta }_1,{\beta }_2,\dots ,{\beta }_k\right) \end{gathered}$$

(11)

Proof. 

Similar. □

Definition 5.

If we suppose ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ is the collection of q-ROFVs where$j=1,2,3,\dots ,k$, then, the q-ROFPAAG operator is defined as:

$$q-ROFPAAA\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_P\right)={\otimes }_{j=1}^k\left({\left({{\rm T}}_j\right)}^{\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}}\right)$$

(12)

Here,  $\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}$  is the priority degree, which works as a weight of q-ROFV${{\rm T}}_j$. We obtain the succeeding theorem based on the operational laws of the q-ROFVs.

Theorem 9.

If we suppose  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$is the collection of q-ROFVs, then, the q-ROFPAAG operator is given by:

$$\begin{gathered} q-ROFPAAG\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)= \\ \left(\begin{array}{c}{e}^{-{\left({\displaystyle \sum }_{j=1}^k\left(\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}\right){\left(-ln\left(m_{{{\rm T}}_j}\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}},\\ \sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{j=1}^k\left(\frac{T_j}{{{\displaystyle \sum }}_{j=1}^k{T}_j}\right){\left(-ln \left(1-n_{{{\rm T}}_j}^q\right)\right)}^{Պ}\right)}^{1/Պ}}}\end{array}\right) \end{gathered}$$

(13)

Proof. 

Similar to Theorem 1. □

Remark 1:

The q-ROFPAAG AOs satisfy the aggregation properties as stated in Theorems 2–4.

Theorem 10.

Let ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ be a collection of q-ROFVs,  $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_1=1$  and  $S\left({{\rm T}}_k\right)$  are the scores of q-ROFVs  ${{\rm T}}_k$. If  $\beta =\left(a,b\right)$  is a q-ROFV, then

$$q-ROFPAAG\left({{\rm T}}_1\otimes \beta ,{{\rm T}}_2\otimes \beta ,\dots ,{{\rm T}}_k\otimes \beta \right)=q-ROFPAAG\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)\otimes \beta$$

(14)

Proof. 

Straightforward. □

Theorem 11.

Let  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ be a collection of q-ROFVs, $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_j=1$ and $S\left({{\rm T}}_k\right)$ are the scores of q-ROFV ${{\rm T}}_k$. If $\phi >0$, then:

$$q-ROFPAAG\left({\left({{\rm T}}_1\right)}^{\phi },{\left({{\rm T}}_2\right)}^{\phi },\dots ,{\left({{\rm T}}_k\right)}^{\phi }\right)={\left(q-ROFPAAG\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)\right)}^{\phi }$$

(15)

Proof. 

Straightforward. □

Theorem 12.

Let  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ be a collection of q-ROFVs, $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_j=1$ and $S\left({{\rm T}}_k\right)$ are the scores of q-ROFV ${{\rm T}}_k$, if $\phi >0$, $\beta =\left(a,b\right)$ is a q-ROFV, then:

$$q-ROFPAAG\left({\left({{\rm T}}_1\right)}^{\phi }\otimes \beta ,{\left({{\rm T}}_2\right)}^{\phi }\otimes \beta ,\dots ,{\left({{\rm T}}_k\right)}^{\phi }\otimes \beta \right)={\left(q-ROFPAAG\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)\right)}^{\phi }\otimes \beta$$

(16)

Proof. 

Straightforward. □

Theorem 13.

Let  ${{\rm T}}_j=\left(m_{{{\rm T}}_j}\left(x\right),n_{{{\rm T}}_j}\left(x\right)\right)$ and ${\beta }_j=\left(a_{{{\rm T}}_j}\left(x\right),b_{{{\rm T}}_j}\left(x\right)\right)$ be two collections of q-ROFVs, $T_j={\prod }_{k=1}^{j-1}S\left({{\rm T}}_k\right)$. $T_1=1$ and $S\left({{\rm T}}_k\right)$ are the scores of q-ROFV ${{\rm T}}_k$, then:

$$q-ROFPAAG\left({{\rm T}}_1\otimes {\beta }_1,{{\rm T}}_2\otimes {\beta }_2,\dots ,{{\rm T}}_k\otimes {\beta }_k\right)=q-ROFPAAG\left({{\rm T}}_1,{{\rm T}}_2,\dots ,{{\rm T}}_k\right)\otimes q-ROFPAAG\left({\beta }_1,{\beta }_2,\dots ,{\beta }_k\right)$$

(17)

Proof. 

Straightforward. □

4. Algorithm for Multi-Criteria Group Decision Making

This section utilizes the proposed AOs in an MCGDM in a q-ROF environment. In a group decision-making problem, suppose $\alpha =\left({\alpha }_1,{\alpha }_2,{\alpha }_3,\dots ,{\alpha }_m\right)$ is the set of alternatives. Let $\mathsf{\beta }=\left({\mathsf{\beta }}_1,{\mathsf{\beta }}_2,{\mathsf{\beta }}_3,\dots ,{\mathsf{\beta }}_n\right)$ be a collection of criteria/attributes, and there is a prioritization between the criteria expressed by the linear ordering ${\mathsf{\beta }}_1>{\mathsf{\beta }}_2>{\mathsf{\beta }}_3,\dots >{\mathsf{\beta }}_n$, which indicate criteria ${\mathsf{\beta }}_j$ has a higher priority, then ${\beta }_i$ if $j<i$, and $\mathsf{\epsilon }=\left({\mathsf{\epsilon }}_1,{\mathsf{\epsilon }}_2,{\mathsf{\epsilon }}_3,\dots ,{\mathsf{\epsilon }}_k\right)$ is the set of decision makers, and there is a prioritization between the decision makers expressed by the linear ordering ${\mathsf{\epsilon }}_1>{\mathsf{\epsilon }}_2>{\mathsf{\epsilon }}_3,\dots >{\mathsf{\epsilon }}_k$, which indicates that expert ${\mathsf{\epsilon }}_{\sigma }$ has a higher priority than expert ${\mathrm{e}}_{\tau }$ if $\sigma <\tau$ does. Let $K^{\left(q\right)}={\left(k_{ij}^q\right)}_{m\times n}$ be a q-ROF decision matrix and q-ROFV $k_{ij}^{\left(q\right)}=\left(m_{{{\rm T}}_j}^{\left(q\right)},n_{{{\rm T}}_j}^{\left(q\right)}\right)$ is the information of the experts about the alternatives under given attributes, where $\left[m_{{{\rm T}}_j}^{\left(q\right)}\right]$ indicates the degree range, and the alternative ${\alpha }_i$ satisfies the attribute ${\mathsf{\beta }}_j$, and ${\mathsf{\epsilon }}_q$, $\left[n_{{{\rm T}}_j}^{\left(q\right)}\right]$ indicates the degree range, and the alternative ${\alpha }_i$ does not satisfy the attribute ${\mathsf{\beta }}_j$ expressed by the decision maker ${\mathsf{\epsilon }}_q$, such that: $m_{{{\rm T}}_j}\in \left[0,1\right], n_{{{\rm T}}_j}\in \left[0,1\right],0\le m_{{{\rm T}}_j}^{\left(q\right)}+n_{{{\rm T}}_j}^{\left(q\right)}\le 1, i=1,2,\dots ,m$.

If the criteria ${\mathsf{\beta }}_j’s$ have same nature, the information is not necessarily normalized; otherwise $K^{\left(q\right)}={\left(k_{ij}^{\left(q\right)}\right)}_{m\times n}$ into $R^{\left(q\right)}={\left(x_{ij}^{\left(q\right)}\right)}_{m\times n}$ where:

$$x_{ij}^{\left(q\right)}=\left\{\begin{array}{c}{k}_{ij}^{\left(q\right)} for benefit attribute{\mathsf{\beta }}_j \\ {ḱ}_{ij}^{\left(q\right)} for cost attribute{\mathsf{\beta }}_j\end{array}\right.$$

where ${ḱ}_{ij}^{\left(q\right)}$ is the complement of $k_{ij}^{\left(q\right)}$, such that ${ḱ}_{ij}^{\left(q\right)}=\left(n_{{{\rm T}}_j}^{\left(q\right)}, m_{{{\rm T}}_j}^{\left(q\right)}\right)$. The complete steps of the MCGDM algorithm are as follows:

Step 1:

Formation of decision matrices using the information of experts in the form of q-ROFVs.

Step 2:

Normalization of decision matrices (if needed).

Step 3:

Calculate the value of $T_{ij}^{\left(q\right)}$, based on the following equations:

$$T_{ij}^{\left(q\right)}={⨅}_{k=1}^{q-1}S\left(x_{ij}^q\right)\left(q=2,\dots ,k\right), T_{ij}^1=1$$

Step 4:

Utilize the q-ROFPAAA or q-ROFPAAG operator, given below, to aggregate the individual preferences of the decision-makers and form a collective decision matrix.

$$\begin{gathered} x_{ij}=q-ROFPAAA\left(x_{ij}^{\left(1\right)},x_{ij}^{\left(2\right)},x_{ij}^{\left(3\right)},\dots ,x_{ij}^{\left(k\right)}\right) \\ =\left(\left[\begin{array}{c}\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln \left(1-m_{{{\rm T}}_j}^q\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}}}\\ e^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln\left(n_{{{\rm T}}_j}\right)\right)}^{Պ}\right)}^{1/Պ}}\end{array}\right]\right) \end{gathered}$$

Or the q-ROFPAAG operator:

$$\begin{gathered} x_{ij}=q-ROFPAAG\left(x_{ij}^{\left(1\right)},x_{ij}^{\left(2\right)},x_{ij}^{\left(3\right)},\dots ,x_{ij}^{\left(k\right)}\right) \\ =\left(\left[\begin{array}{c}{e}^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln\left(n_{{{\rm T}}_j}\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}},\\ \sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln \left(1-m_{{{\rm T}}_j}^q\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}}}\end{array}\right]\right) \end{gathered}$$

Step 5:

Calculate the values of $T_{ij}$ based on the following equations:

$$T_{ij}={\prod }_{k=1}^{j-1}S\left(x_{ik}\right)\mathrm{where} i=1,2,\dots ,m,T_{1j}=1.$$

Step 6:

Aggregating the collective information against each $x_{ij}$ for each alternative ${{\rm T}}_i$ by using q-ROFAAA (or q-ROFAAG) operator:

$$q-ROFPAAA\left(x_{i1},x_{i2},\dots ,x_{in}\right)=\left(\left[\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln \left(1-m_{{{\rm T}}_j}^q\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}},}{e}^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln\left(n_{{{\rm T}}_j}\right)\right)}^{Պ}\right)}^{1/Պ}}\right]\right)$$

Or

$$q-ROFPAAG\left(x_{i1},x_{i2},\dots ,x_{in}\right)=\left(\left[e^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln\left(n_{{{\rm T}}_j}\right)\right)}^{Պ}\right)}^{1/Պ}},\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{j=1}^{k+1}\frac{T_j}{{{\displaystyle \sum }}_{j=1}^n{T}_j}{\left(-ln \left(1-m_{{{\rm T}}_j}^q\right)\right)}^{Պ}\right)}^{\frac{1}{Պ}}}}\right]\right)$$

Step 7:

Rank all the alternatives by using the score function.

$$S\left(x\right)={\left(m_{{{\rm T}}_j}\right)}^q-{\left(n_{{{\rm T}}_j}\right)}^q$$

5. Application

Energy is one of the most critical factors for achieving advancement and comfort in everyday life. Due to the improvement in living standards, population increase, and global economic growth, the energy demand has been steadily increasing over the years. But on the other hand, natural gas supplies are rapidly growing, raising the price of these resources. Water energy and thermal energy are also facing deficiencies. Managing energy resources in efficient power systems presents significant hurdles for today’s decision makers. Determining the efficiency and reliability of energy systems is important. These systems are affected by several parameters, and due to the uncertainty in real-life situations, determining the efficiency of energy resource systems is challenging. As a result, it is essential to develop efficient and practical techniques for managing successful energy systems at various social and biological levels. Well-known and widely utilized techniques address various energy management and efficiency issues. When one is dealing with complicated, ambiguous, imprecise, and multi-objective challenges such as the management control of efficient energy, decision support systems are typically designed under fuzzy logic.

In the below example, we aim to analyze an energy resource selection problem, where we consider some energy resources and try to evaluate the most efficient resource among a finite list of energy sources. The main feature of this algorithm is that it involves the priority preference of the experts and attributes during decision-making problems. The prioritization allows us to take the expert’s opinion about any energy resource, considering all the parameters that affect the energy resource’s efficiency.

Example 1.

We define several criteria to include technical, economic, environmental, and social issues in the management of energy resources when one is comparing different energy resources selection. Four criteria are selected from the research for this purpose to evaluate energy sources using the MCGDM approach. The cost ($C_1$) criteria include all the expenses and costs associated with establishing the generation of energy, including those related to land, machinery, labor, installation, and infrastructure. The energy information management agency offered capital prices, as well as operations and maintenance expenses, for renewable energy technology alternatives. Energy cost ($C_2$) denotes the expected cost of the energy (electricity) a plant will obtain from renewable energy technology alternatives during its lifespan. Capacity ($C_3$) denotes how quickly a renewable energy system transforms its fundamental energy source into electricity. Resources that can be used to create power utilizing renewable energy technologies are represented by ($C_4$). The team of decision makers evaluates the four energy resources, where ${\mathit{X}}_{\mathbf{1}}:$coal; ${\mathit{X}}_{\mathbf{2}}:$ petroleum; ${\mathit{X}}_{\mathbf{3}}:$ natural gas; ${\mathit{X}}_{\mathbf{4}}:$ wind energy; ${\mathit{X}}_{\mathbf{5}}:$solar energy, as given in Figure 1.

Figure 1. Different energy resources.

Three experts evaluate these five energy resources under four attributes; the information is expressed as q-ROFVs in Step 1. The expert’s evaluation of the energy resources is given in Table 2, Table 3 and Table 4, respectively.

Table 2. Expert e₁ about energy resources under the given criteria.

	C1		C2		C3		C4
X1	0.7	0.6	0.9	0.5	0.7	0.6	0.9	0.5
X2	0.8	0.7	0.8	0.6	0.8	0.7	0.8	0.6
X3	0.9	0.6	0.7	0.6	0.9	0.5	0.8	0.7
X4	0.9	0.3	0.8	0.4	0.8	0.6	0.9	0.4
X5	0.8	0.7	0.9	0.5	0.6	0.5	0.8	0.6

Table 3. Expert e₂ about energy resources under the given criteria.

	C1		C2		C3		C4
X1	0.9	0.6	0.8	0.4	0.9	0.5	0.9	0.4
X2	0.8	0.4	0.9	0.6	0.8	0.7	0.8	0.5
X3	0.8	0.7	0.7	0.5	0.7	0.6	0.7	0.6
X4	0.8	0.6	0.9	0.6	0.8	0.6	0.8	0.6
X5	0.9	0.5	0.7	0.5	0.9	0.3	0.9	0.5

Table 4. Expert e₃ about energy resources under the given criteria.

	C1		C2		C3		C4
X1	0.8	0.5	0.9	0.6	0.9	0.5	0.9	0.6
X2	0.9	0.4	0.8	0.5	0.8	0.6	0.8	0.7
X3	0.8	0.3	0.9	0.7	0.7	0.6	0.7	0.6
X4	0.7	0.6	0.8	0.6	0.8	0.6	0.8	0.5
X5	0.8	0.7	0.9	0.5	0.9	0.5	0.9	0.4

Step 1: 

Formation of decision matrix.

Step 2: 

In the current example, we have two attributes as cost attributes. To unify all the attributes, we normalize the decision matrices as follows in Table 5, Table 6 and Table 7, respectively.

Table 5. Expert e₁ about energy resources under given criteria (after normalization).

	C1		C2		C3		C4
X1	0.6	0.7	0.5	0.9	0.7	0.6	0.9	0.5
X2	0.7	0.8	0.6	0.8	0.8	0.7	0.8	0.6
X3	0.6	0.9	0.6	0.7	0.9	0.5	0.8	0.7
X4	0.3	0.9	0.4	0.8	0.8	0.6	0.9	0.4
X5	0.7	0.8	0.5	0.9	0.6	0.5	0.8	0.6

Table 6. Expert e₂ about energy resources under given criteria (after normalization).

	C1		C2		C3		C4
X1	0.6	0.9	0.4	0.8	0.9	0.5	0.9	0.4
X2	0.4	0.8	0.6	0.9	0.8	0.7	0.8	0.5
X3	0.7	0.8	0.5	0.7	0.7	0.6	0.7	0.6
X4	0.6	0.8	0.6	0.9	0.8	0.6	0.8	0.6
X5	0.5	0.9	0.5	0.7	0.9	0.3	0.9	0.5

Table 7. Expert e₃ about energy resources under given criteria (after normalization).

	C1		C2		C3		C4
X1	0.5	0.8	0.6	0.9	0.9	0.5	0.9	0.6
X2	0.4	0.9	0.5	0.8	0.8	0.6	0.8	0.7
X3	0.3	0.8	0.7	0.9	0.7	0.6	0.7	0.6
X4	0.6	0.7	0.6	0.8	0.8	0.6	0.8	0.5
X5	0.7	0.8	0.5	0.9	0.9	0.5	0.9	0.4

Step 3: 

Calculate the values of$T_{ij}^1$, $T_{ij}^2$, and $T_{ij}^3$ using Step 3 of the algorithm as follows.

$$T_{ij}^1=\left(\begin{array}{cccc}\begin{array}{c}\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}\end{array}& \begin{array}{c}\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}\end{array}& \begin{array}{c}\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}\end{array}& \begin{array}{c}\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}\end{array}\end{array}\right)$$

$$T_{ij}^2=\left(\begin{array}{ccc}\begin{array}{c}0.127\\ 0.169\\ 0.513\\ 0.702\\ 0.169\end{array}& \begin{array}{c}0.604\\ 0.296\\ 0.127\\ 0.448\\ 0.604\end{array}& \begin{array}{c}0.127\\ 0.169\\ 0.604\\ 0.296\\ 0.091\end{array}\end{array}\begin{array}{c}0.604\\ 0.296\\ 0.169\\ 0.665\\ 0.296\end{array}\right)$$

$$T_{ij}^3=\left(\begin{array}{cccc}\begin{array}{c}0.0651551\\ 0.075712\\ 0.086697\\ 0.207792\\ 0.102076\end{array}& \begin{array}{c}0.270592\\ 0.151848\\ 0.027686\\ 0.229824\\ 0.131672\end{array}& \begin{array}{c}0.076708\\ 0.028561\\ 0.076708\\ 0.087616\\ 0.063882\end{array}& \begin{array}{c}0.40166\\ 0.114552\\ 0.021463\\ 0.19684\\ 0.178784\end{array}\end{array}\right)$$

Step 4: 

Utilize the q-ROFPAAA operator to aggregate the q-ROF decision matrix $R^q={\left(x_{ij}^q\right)}_{4x5}\left(q=1,2,3\right)$ into the collective q-ROF decision matrix $R={\left(x_{ij}\right)}_{5x4}$, as given in Table 8.

Table 8. Collective preferences using q-ROFAAA of expert’s information given in Table 5, Table 6 and Table 7.

	C1		C2		C3		C4
X1	0.6417	0.5941	0.8200	0.4777	0.6591	0.5818	0.8538	0.4849
X2	0.7274	0.6271	0.7532	0.5886	0.7155	0.6974	0.7155	0.5848
X3	0.8137	0.6072	0.5973	0.5903	0.7824	0.5383	0.6987	0.6829
X4	0.7935	0.4174	0.7635	0.4712	0.7155	0.6000	0.8026	0.4734
X5	0.7407	0.6694	0.7945	0.5000	0.5658	0.4803	0.7721	0.5507

Step 5: 

Calculate the values of $T_{ij},\left(i=1,2,\dots m, j=1,2,\dots n\right)$ based on the equation given in Step 3 of the algorithm.

$$T_{ij}=\left(\begin{array}{cccc}\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}& \begin{array}{c}0.0546\\ 0.1383\\ 0.3150\\ 0.4268\\ 0.1065\end{array}& \begin{array}{c}0.0242\\ 0.0309\\ 0.0024\\ 0.1453\\ 0.0401\end{array}& \begin{array}{c}0.002\\ 0.001\\ 0.001\\ 0.022\\ 0.003\end{array}\end{array}\right)$$

Step 6: 

Utilize the q-ROFPAAA operator to aggregate all the preference values $x_i\left(i=1,2,\dots 5\right)$ given in Table 8. The overall aggregated values are given in Table 9 below.

Table 9. Collective preference information.

	Aggregated Information
X1	0.6417	0.5941
X2	0.7274	0.6271
X3	0.8137	0.6072
X4	0.7935	0.4174
X5	0.7407	0.6694

Step 7: 

Calculate the scores of $x_i\left(1,2,\dots ,5\right),$ respectively, in Table 10 as given below.

Table 10. The score values of the aggregated information.

Alternatives	Scores	Ranking
X1	−0.0511	S4 > S3 > S2 > S5 > S1
X2	0.0001
X3	0.1089
X4	0.2379
X5	−0.0047

Thus, the best alternative is $X_4$ and $X_3$ are the most suitable energy resources, respectively, according to the q-ROFPAAA operator. Now, we apply the same algorithm to classify the energy resources using the q-ROFPAAG operator, and the main steps are given below. (The first three steps have already been completed.)

Step 4: 

Utilize the q-ROFPAAG operator to aggregate the q-ROF decision matrix $R^q={\left(x_{ij}^q\right)}_{4x5}\left(q=1,2,3\right)$ into the collective q-ROF decision matrix $R={\left(x_{ij}\right)}_{5x4}$ as given in Table 11.

Table 11. Collective preferences using q-ROFAAG of expert’s information given in Table 5, Table 6 and Table 7.

	C1		C2		C3		C4
X1	0.7243	0.4597	0.866485	0.346201	0.730414	0.448658	0.9	0.355645
X2	0.8058	0.5437	0.819498	0.454883	0.80000	0.583288	0.80000	0.457335
X3	0.8611	0.5005	0.704231	0.458071	0.812901	0.403812	0.78309	0.569349
X4	0.8386	0.3495	0.825559	0.3587	0.8000	0.464758	0.852244	0.357274
X5	0.8126	0.5635	0.824634	0.353553	0.63353	0.343001	0.830917	0.425587

Step 5: 

Calculate the values of $T_{ij},\left(i=1,2,\dots m, j=1,2,\dots n\right)$ based on the equation given in Step 3 of the algorithm.

$$T_{ij}=\left(\begin{array}{cccc}\begin{array}{c}1\\ 1\\ 1\\ 1\\ 1\end{array}& \begin{array}{c}0.2828\\ 0.3624\\ 0.5132\\ 0.5471\\ 0.3577\end{array}& \begin{array}{c}0.17224\\ 0.165322\\ 0.129912\\ 0.2825683\\ 0.184798\end{array}& \begin{array}{c}0.051563\\ 0.051837\\ 0.061231\\ 0.116314\\ 0.039532\end{array}\end{array}\right)$$

Step 6: 

Utilize the q-ROFPAAA operator to aggregate all the preference values $x_i\left(i=1,2,\dots 5\right)$ given in Table 8. The overall aggregated values are given in Table 12 below.

Table 12. Collective preference information.

	Aggregated Information
X1	0.7554	0.2905
X2	0.8081	0.3846
X3	0.8042	0.3383
X4	0.8300	0.2290
X5	0.7924	0.3634

Step 7: 

Calculate the score of $x_i\left(1,2,\dots ,5\right),$ respectively, in Table 13, as given below.

Table 13. The score values of the aggregated information.

Alternatives	Scores	Ranking
X1	0.486197	S4 > S3 > S2 > S5 > S1
X2	0.505076
X3	0.532325
X4	0.636522
X5	0.495845

Thus, the best alternatives $X_4$ and $X_3$ are the most appropriate energy resources, respectively, using the q-ROFPAAG operator. Table 10 and Table 13 shows that the outcomes using q-ROFPAAA and q-ROFPAAG operators are the same. However, the results may vary and may not always be the same. The choice of the AOs is up to the decision makers. The ranking results obtained using q-ROFAAA and q-ROFAAG operators, as given in Table 10 and Table 13, are geometrically expressed, as shown in Figure 2 below.

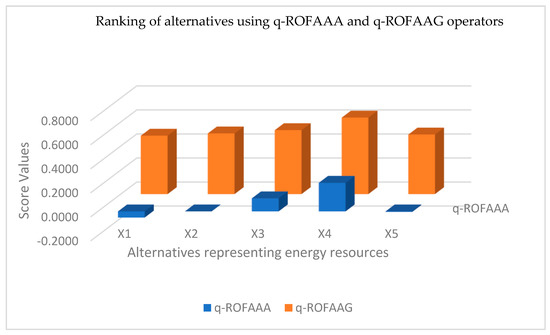
Figure 2. Representation of ranking results using q-ROFAA operators.

The above-discussed results are reliable and significant because of the prioritization of experts and attributes. If we keep all the experts and characteristics at the same level, then the proposed operators reduce to previous traditional AOs. As prioritization is a more realistic approach, using q-ROFPAAA and q-ROFPAAG operators is essential.

6. Comparative Study

This section will compare the aggregated results achieved using q-ROFPAAA and q-ROFPAAG operators with various other AOs based on q-ROF information. For this purpose, we applied averaging and geometric AOs of the q-ROFSs [22], q-ROF Hamacher operators [8], and q-ROF Dombi operators [47]. We also show the comparison with the AOs in some other frameworks [21,48], which shows the superiority of the proposed work. The aggregated results are portrayed in Table 14 below.

Table 14. The comparison of current and previous approaches.

Aggregation Operator	Operator	Ranking Result
Proposed Work	Averaging	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
	Geometric	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
Khan et al. [22]	Averaging	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
	Geometric	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
Jana et al. [47]	Averaging	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
	Geometric	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
Darko and Liang [8]	Averaging	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
	Geometric	Τ4 > Τ3 > Τ2 > Τ5 > Τ1
Hussain et al. [21]	Averaging	Not Applicable
	Geometric	Not Applicable
Senapati et al. [48]	Averaging	Not Applicable
	Geometric	Not Applicable

From the data in Table 14, we noticed that the theory of Hussain et al. [21] was proposed based on Pythagorean fuzzy sets. The theory of Senapati et al. [48] is based on intuitionistic fuzzy sets, which failed to evaluate the considered data because these concepts are the special cases of the proposed work. The comparison results of proposed q-ROFPAAA and q-ROFPAAG operators with other AOs shown in Table 14 are geometrically described in Figure 3 below.

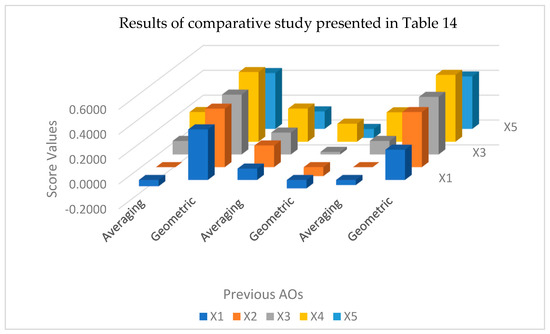
Figure 3. Score values using Khan et al. [23], Jana et al. [49] and Darko and Liang [8].

The analysis of Table 14 shows the result of the MCGDM problems considered in Example 1 and using some previous approaches. From the study, we conclude that the results were obtained using previous AOs. However, they solved the current example, but did not utilize prioritization, proving the proposed approach’s worth. Further, some AOs established in the framework of PyFSs and IFSs cannot solve the given problem showing the diverse nature of q-ROFSs and the proposed q-ROFPAAA and q-ROFPAAG operators.

7. Conclusions

In this paper, we introduced the conception of the prioritization of AATN and AATCN-based AOs using q-ROF information. Prioritization is eminent in decision-making problems for prioritizing the attributes and experts and is similar to real-life phenomena. We introduced two types of AOs, q-ROFPAAA, and q-ROFPAAG operators, and noticed their basic features. We provided some interesting additional results for aggregation operators. Based on the proposed AOs, we developed an MCGDM algorithm, which was further applied to examine a real-life problem of energy resource selection. Comparing the proposed work with existing work shows its feasibility and applicability. Some key findings and advantages of the proposed work are given:

• q-ROFPAA operators consider the relation of prioritization while they are aggregating information, while existing AOs do not have such a feature.
• q-ROFPAA operators can be applied to a more extensive range of information, whereas other information is not used.
• The proposed AOs generalize the previous AOs.

We aim to study the present concept in some well-known methods [49,50,51] involving unknown weights of the attributes, where weights are obtained using the information of experts. We also aim to develop power AOs [52] associated with q-ROFPAA operators to see their impact on real-life problems.