Numerical Study of the Erosion Distribution of Sulfur-Containing Particulate Gas in 90-Degree Gathering Elbow
Abstract
:1. Introduction
2. Numerical Model
2.1. Continuous Phase Control Equation
2.2. Discrete Phase Model
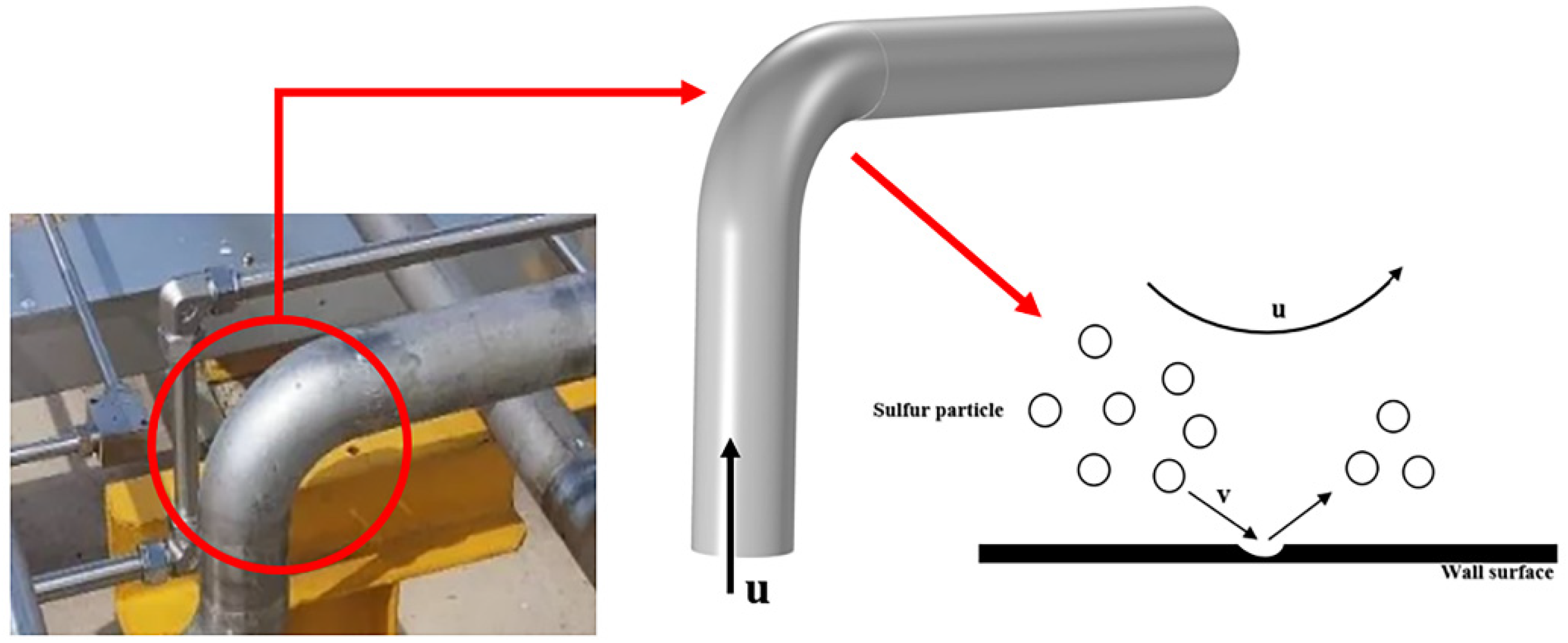
2.3. Particle-Wall Interaction
2.4. E/CRC Erosion Model
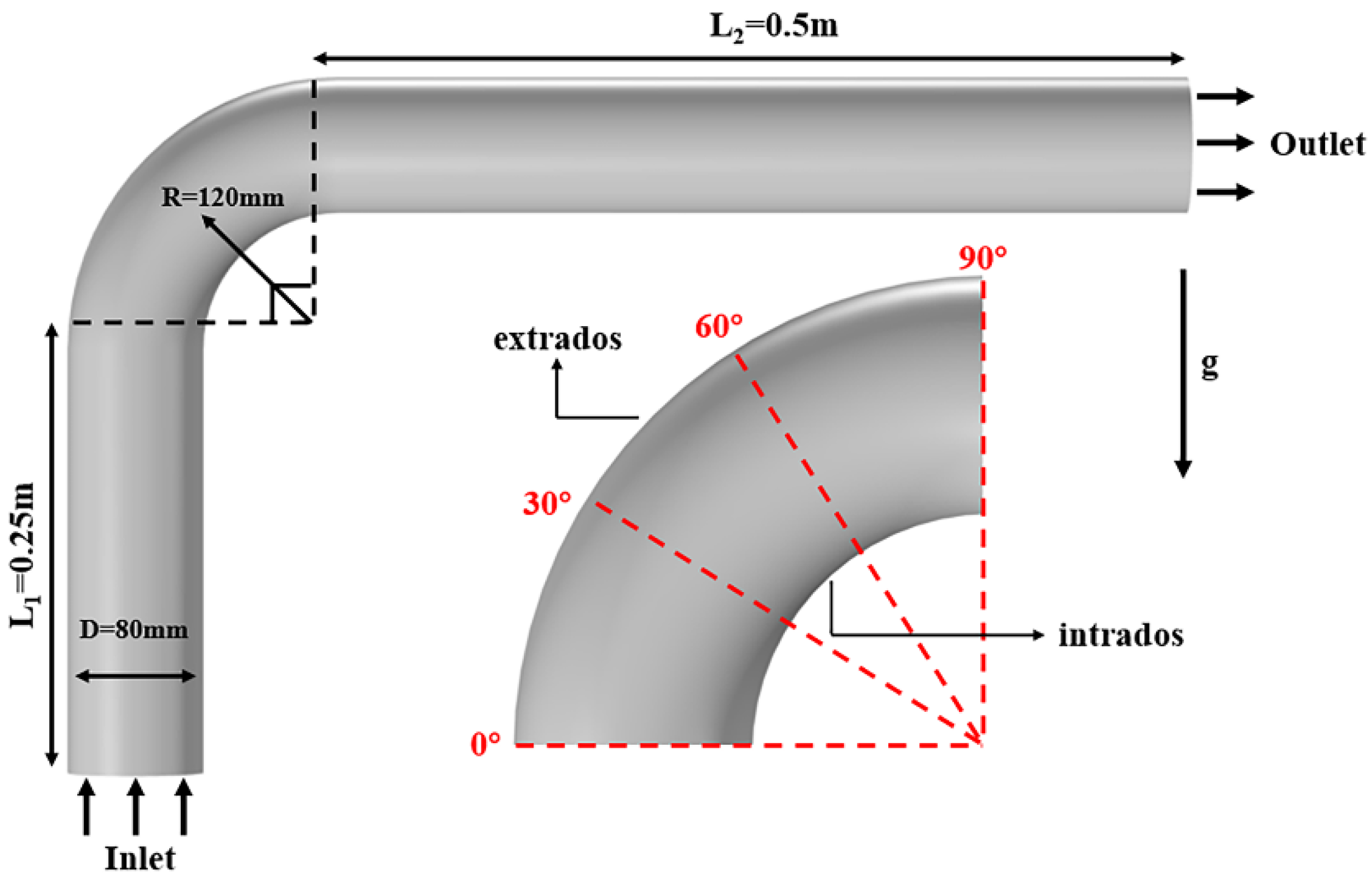
3. Physical Model
3.1. Basic Settings
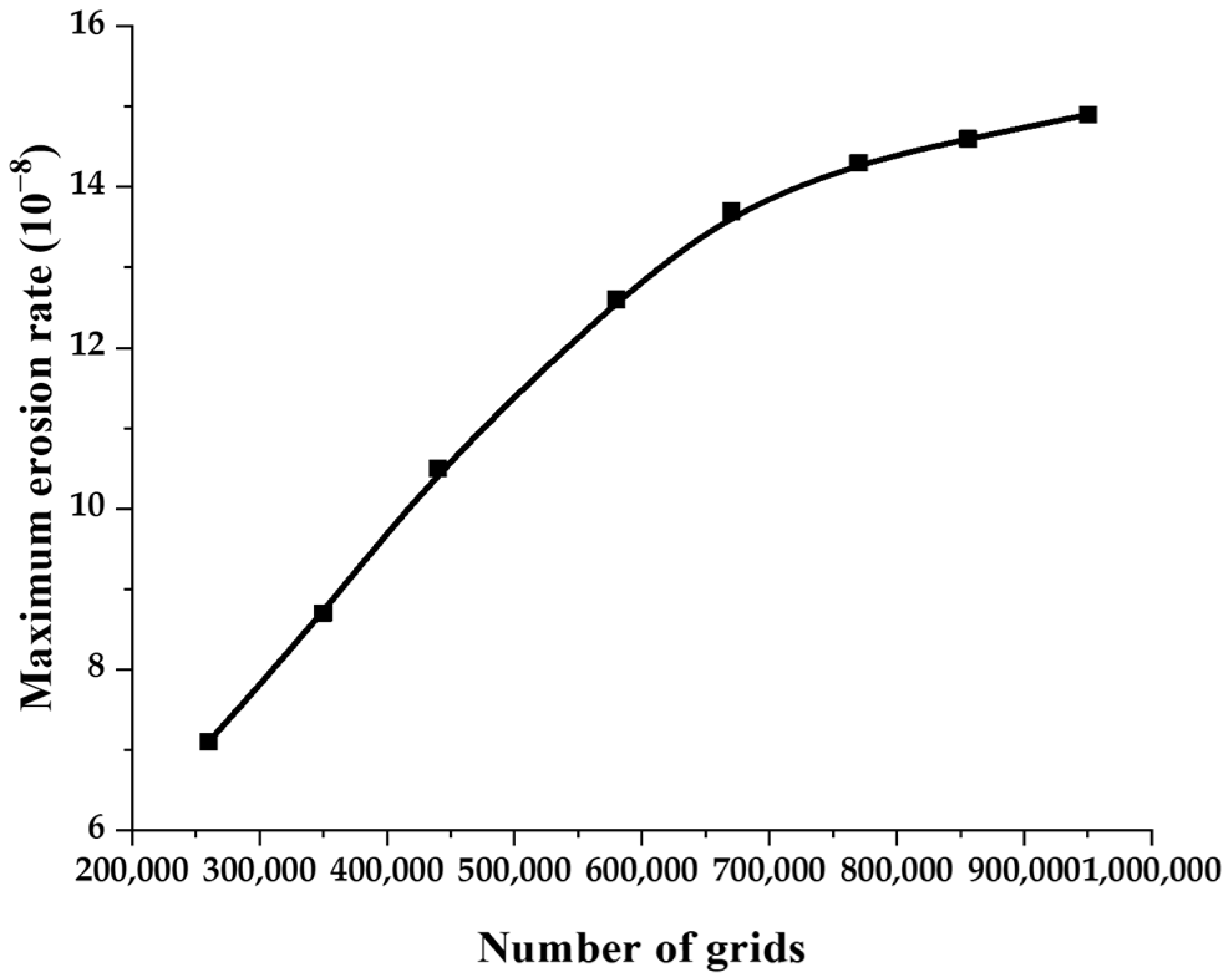
3.2. Wall Treatment and Mesh Setting
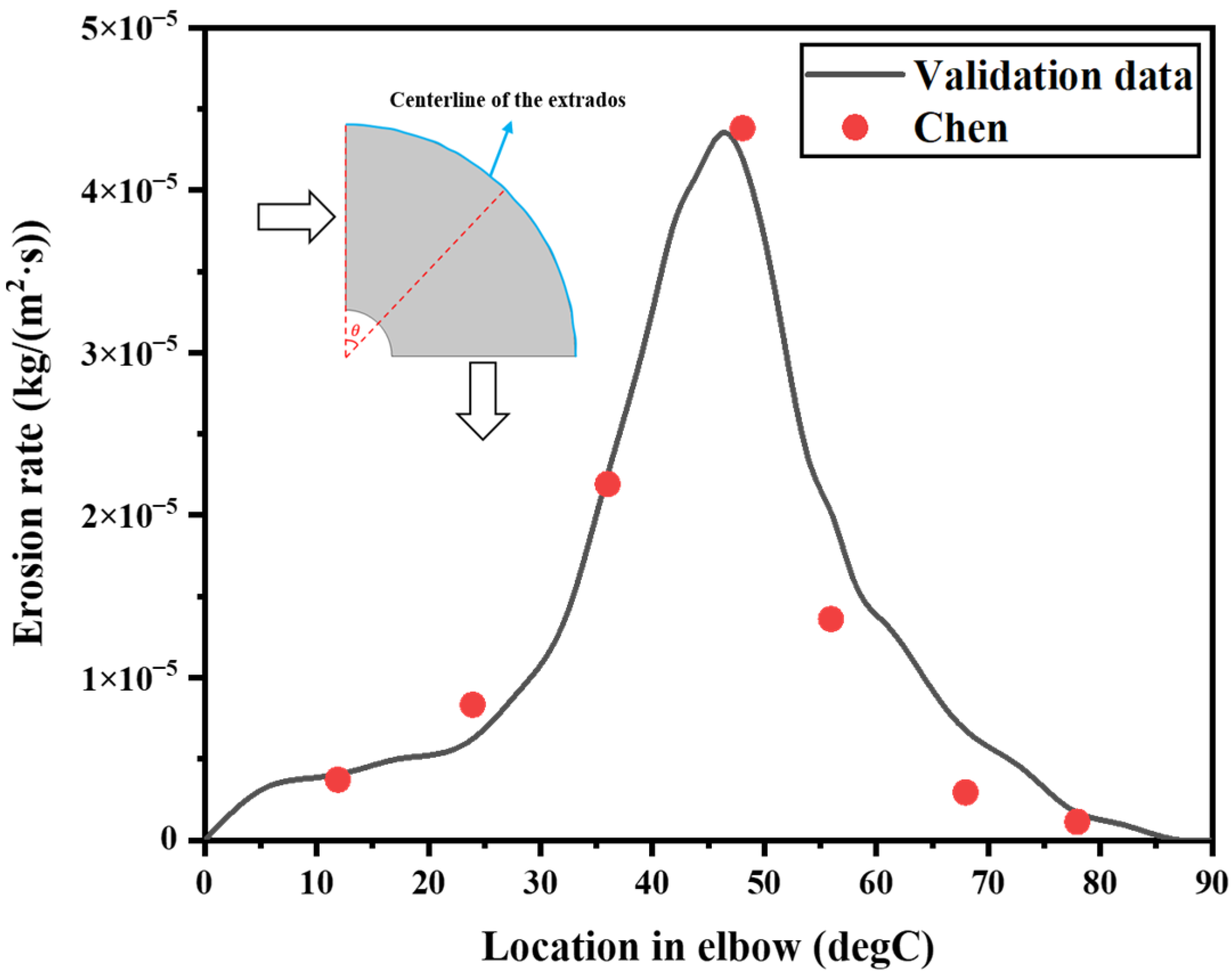
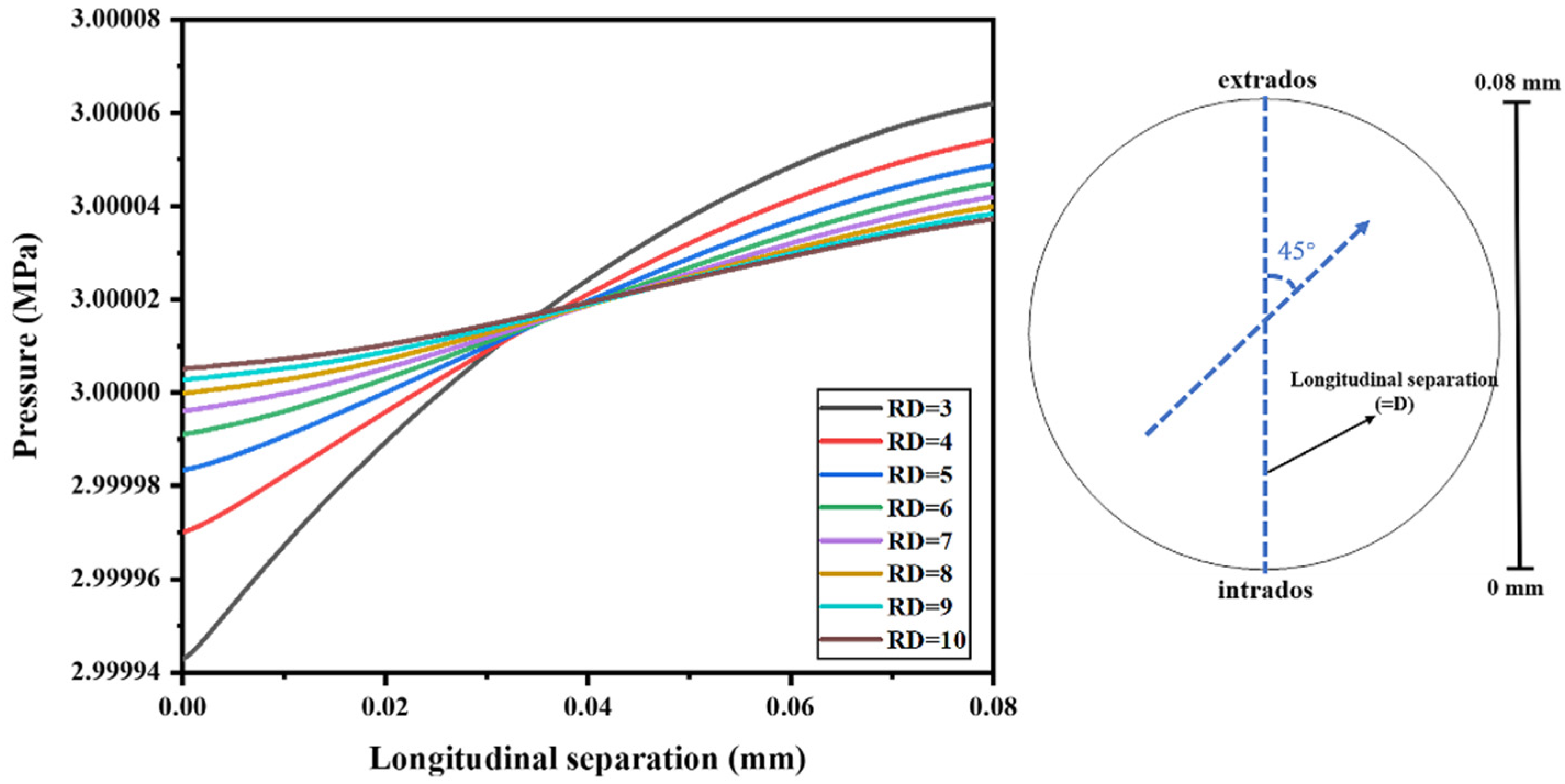
4. Model Validation
5. Results and Discussions
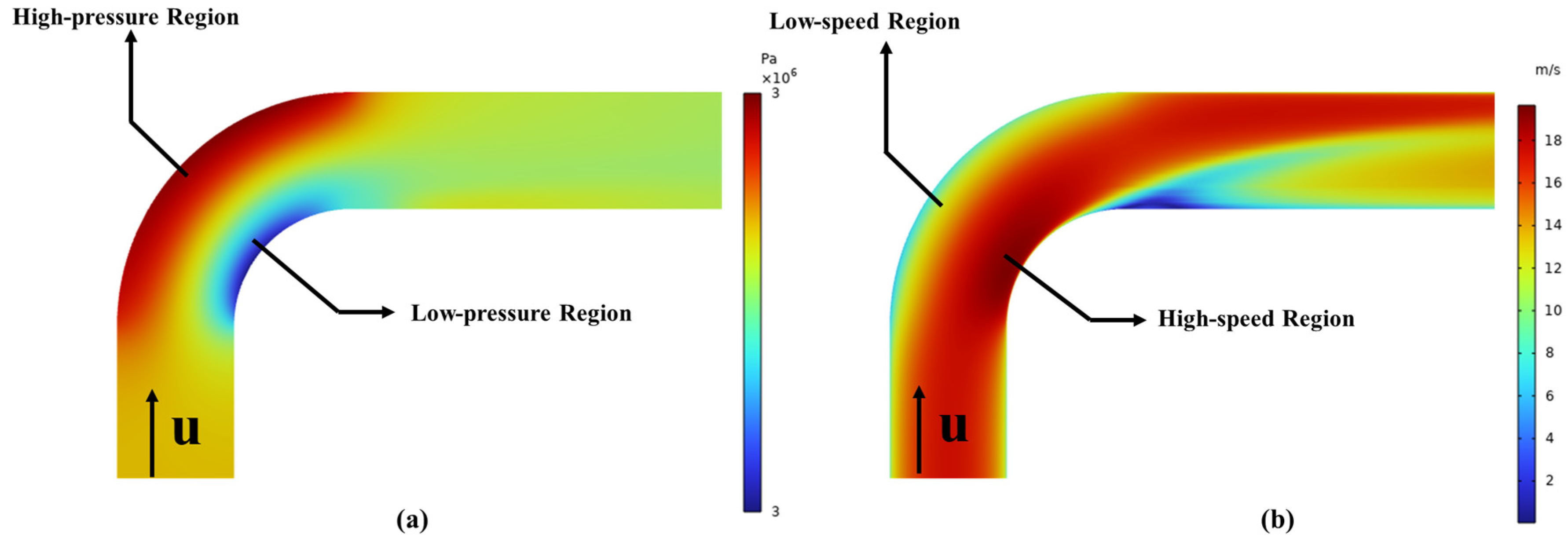
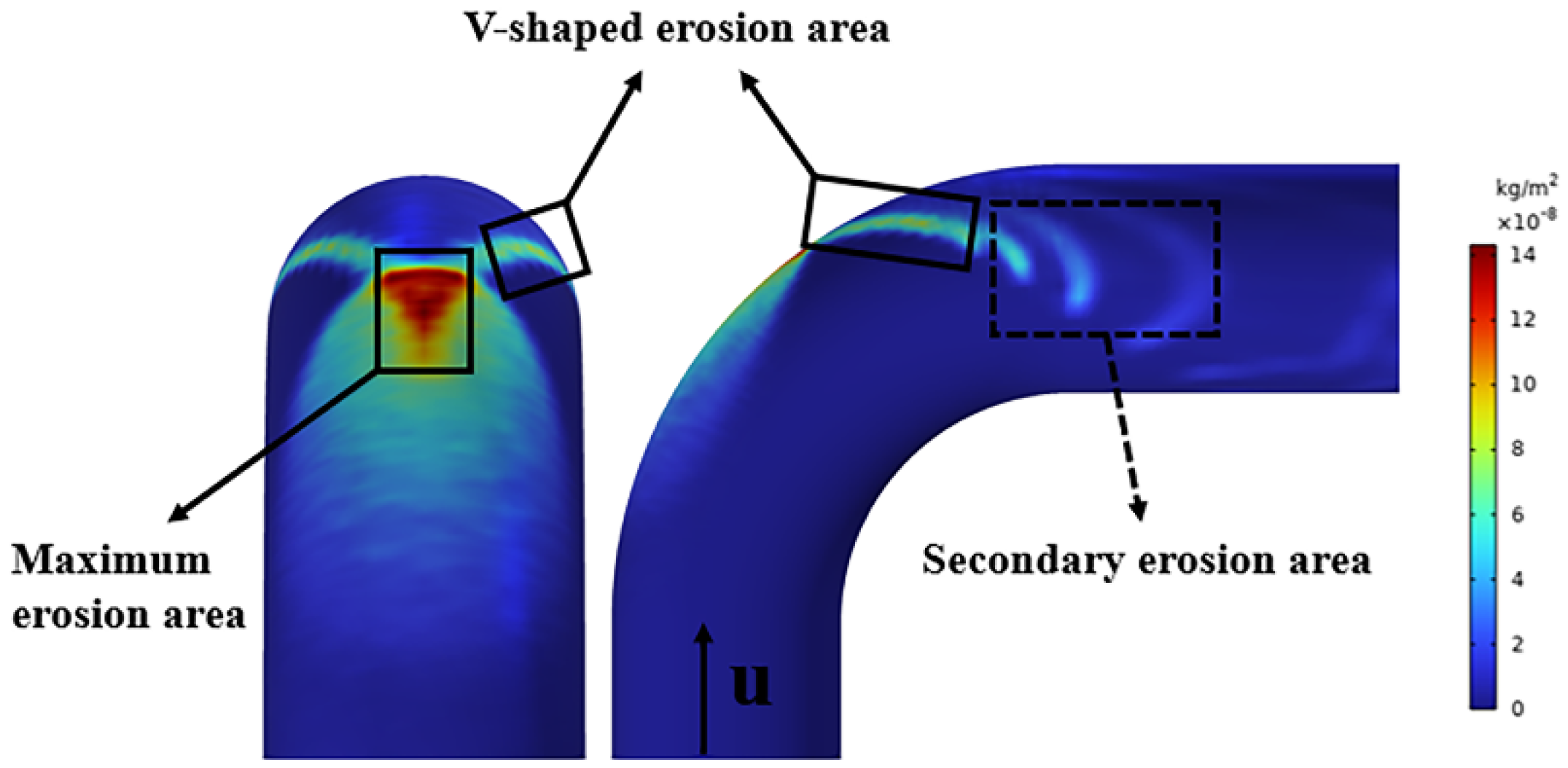
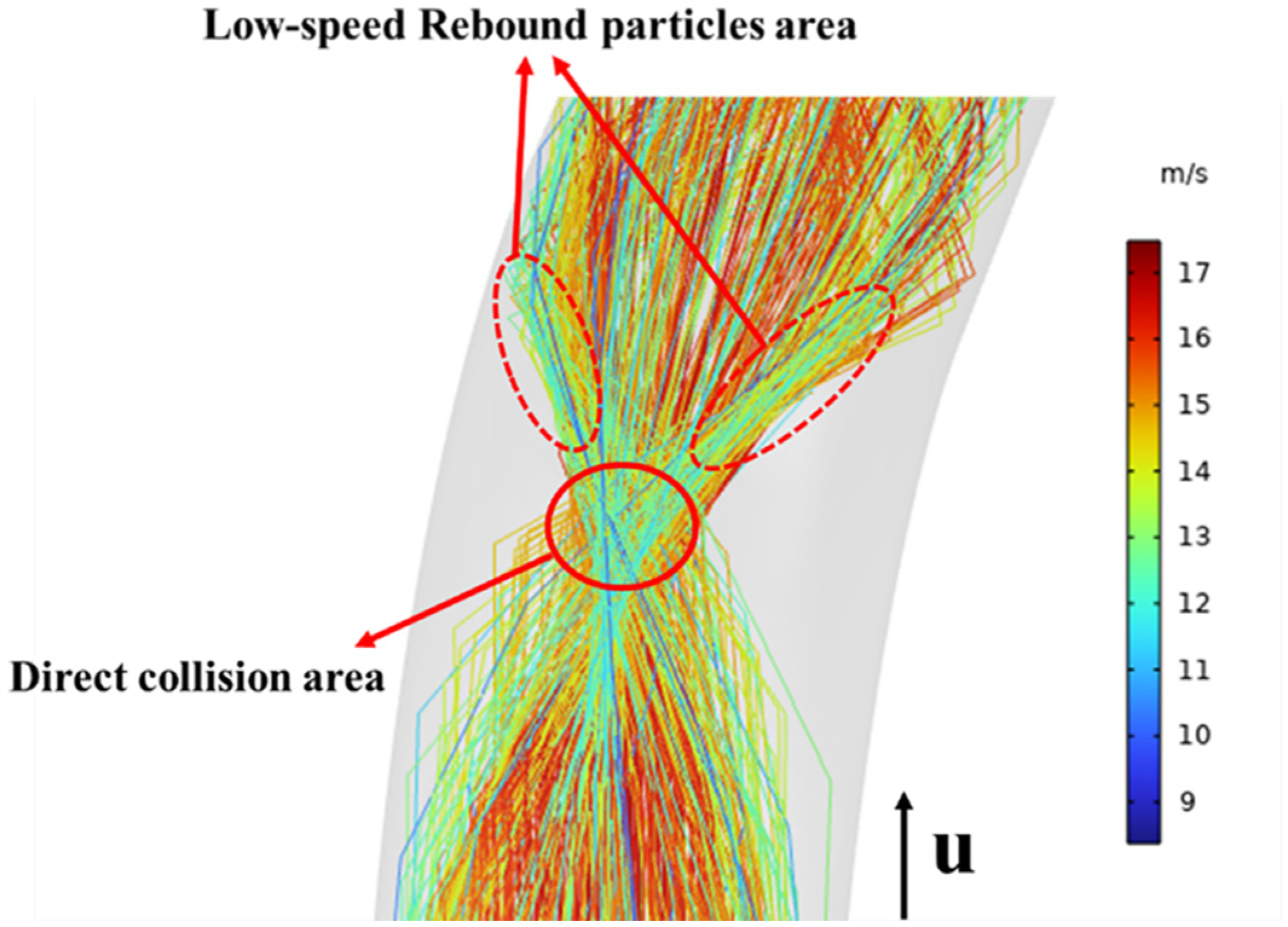
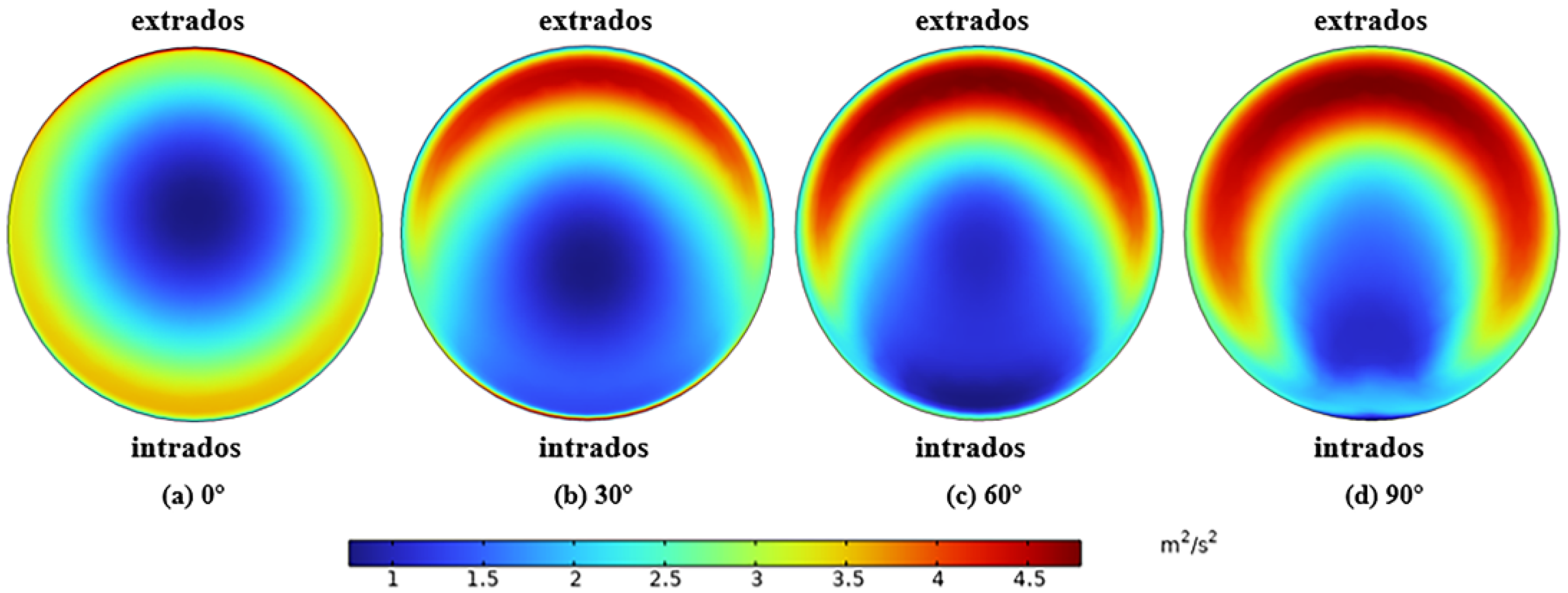
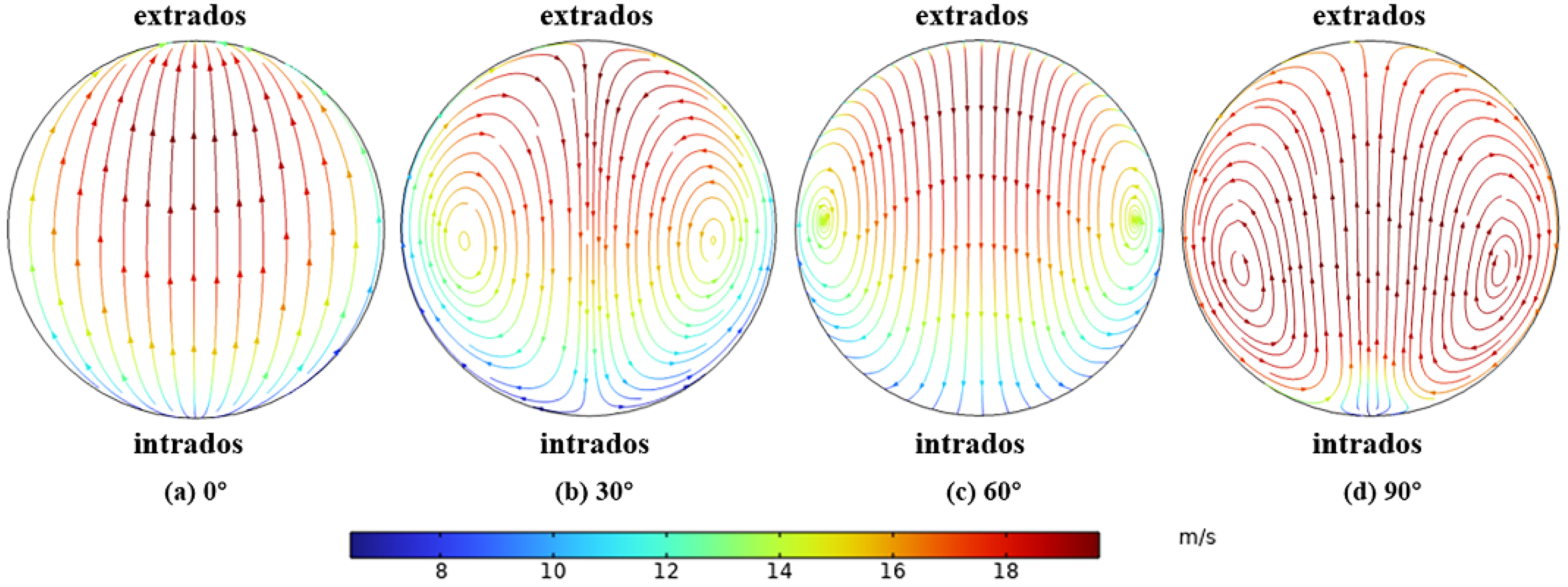
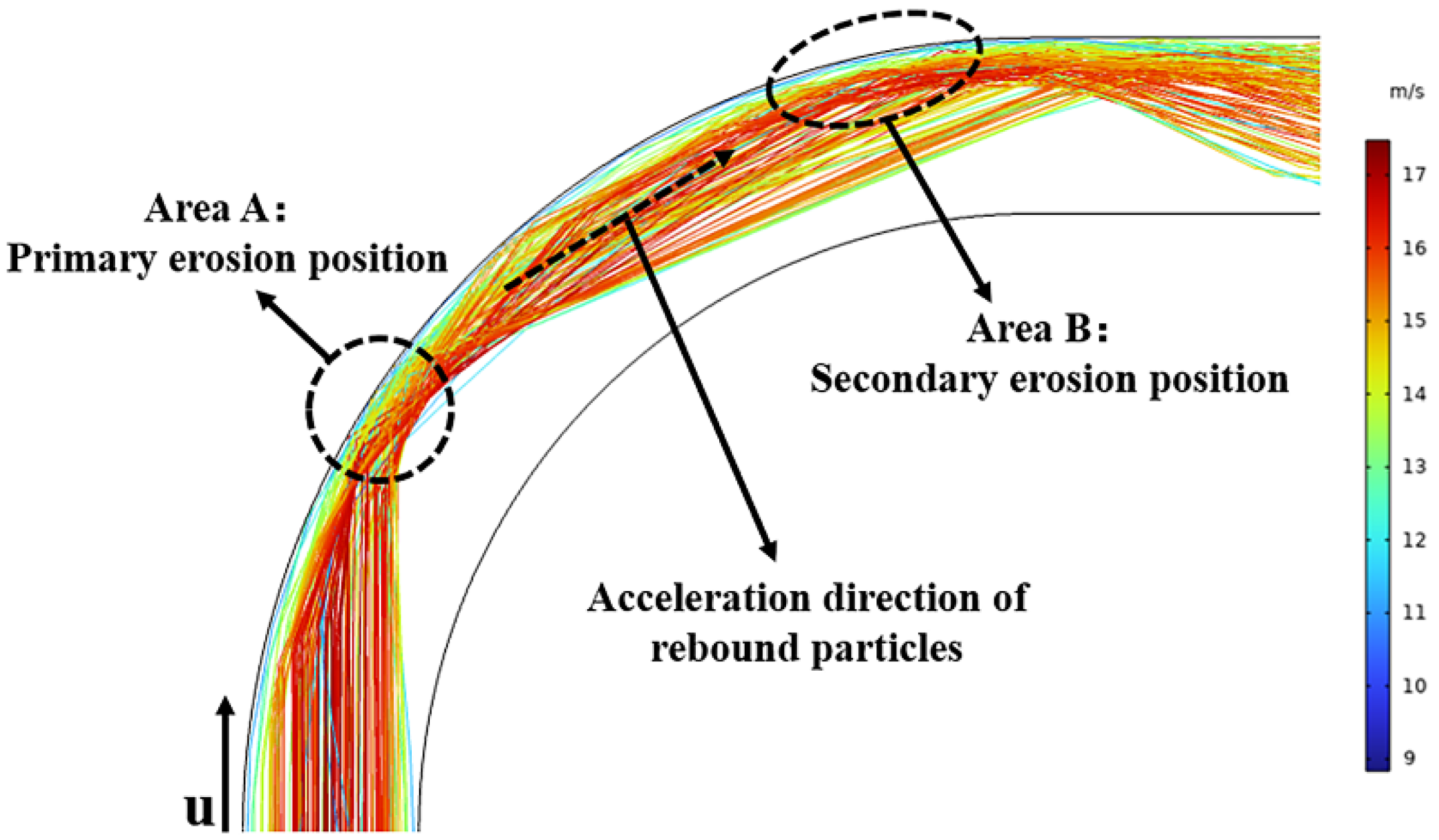
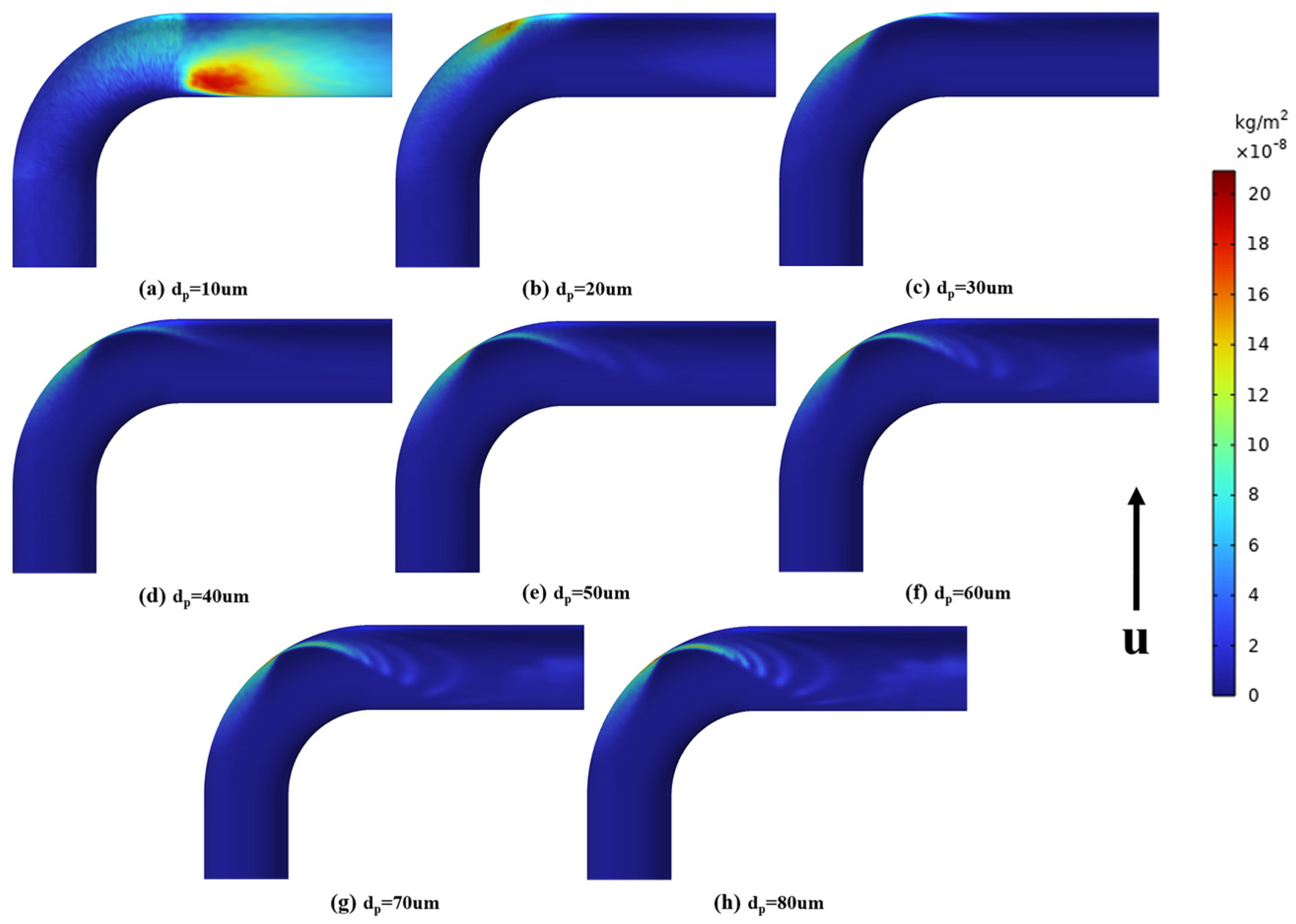
5.1. Main Erosion Distribution
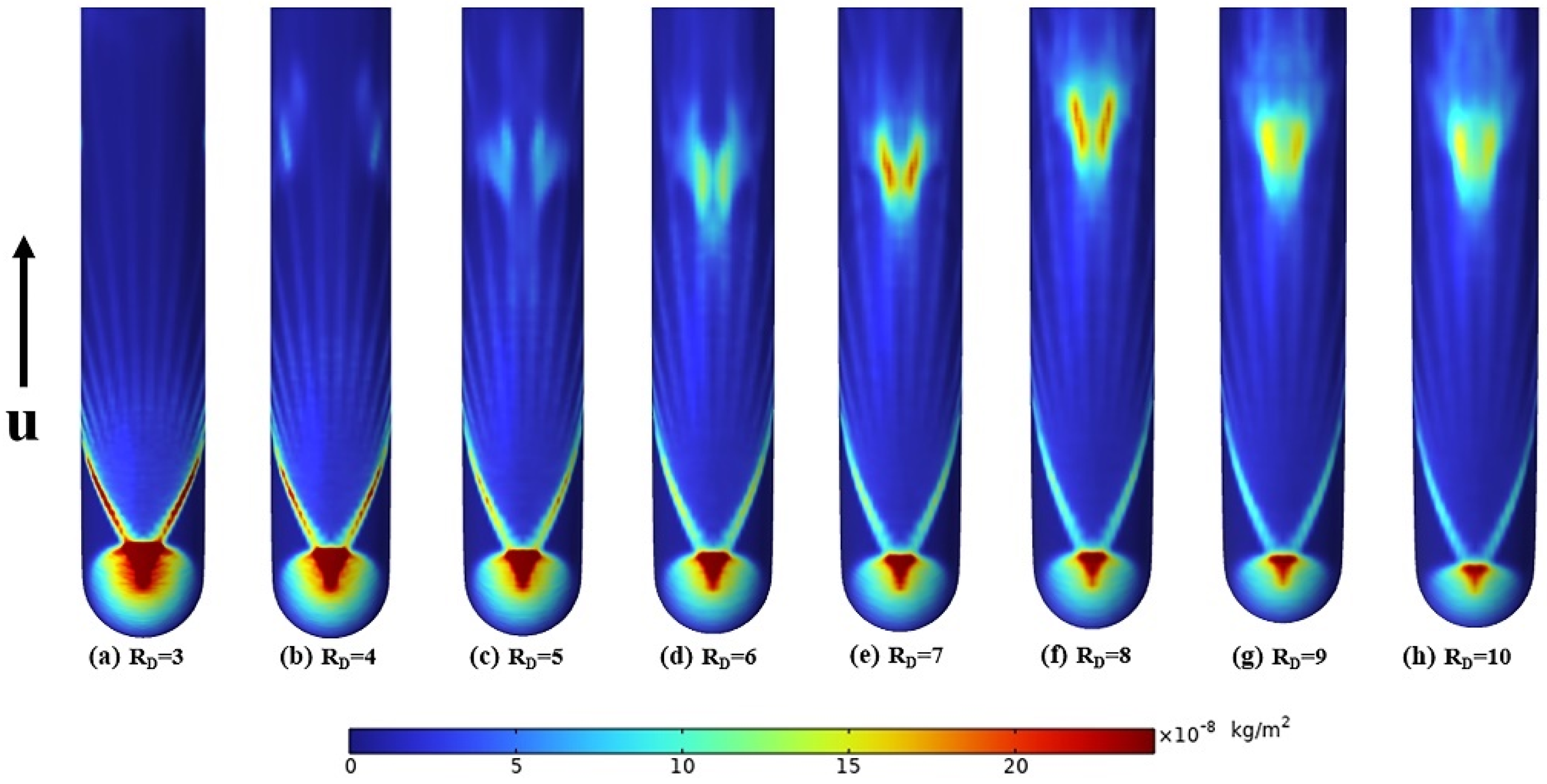
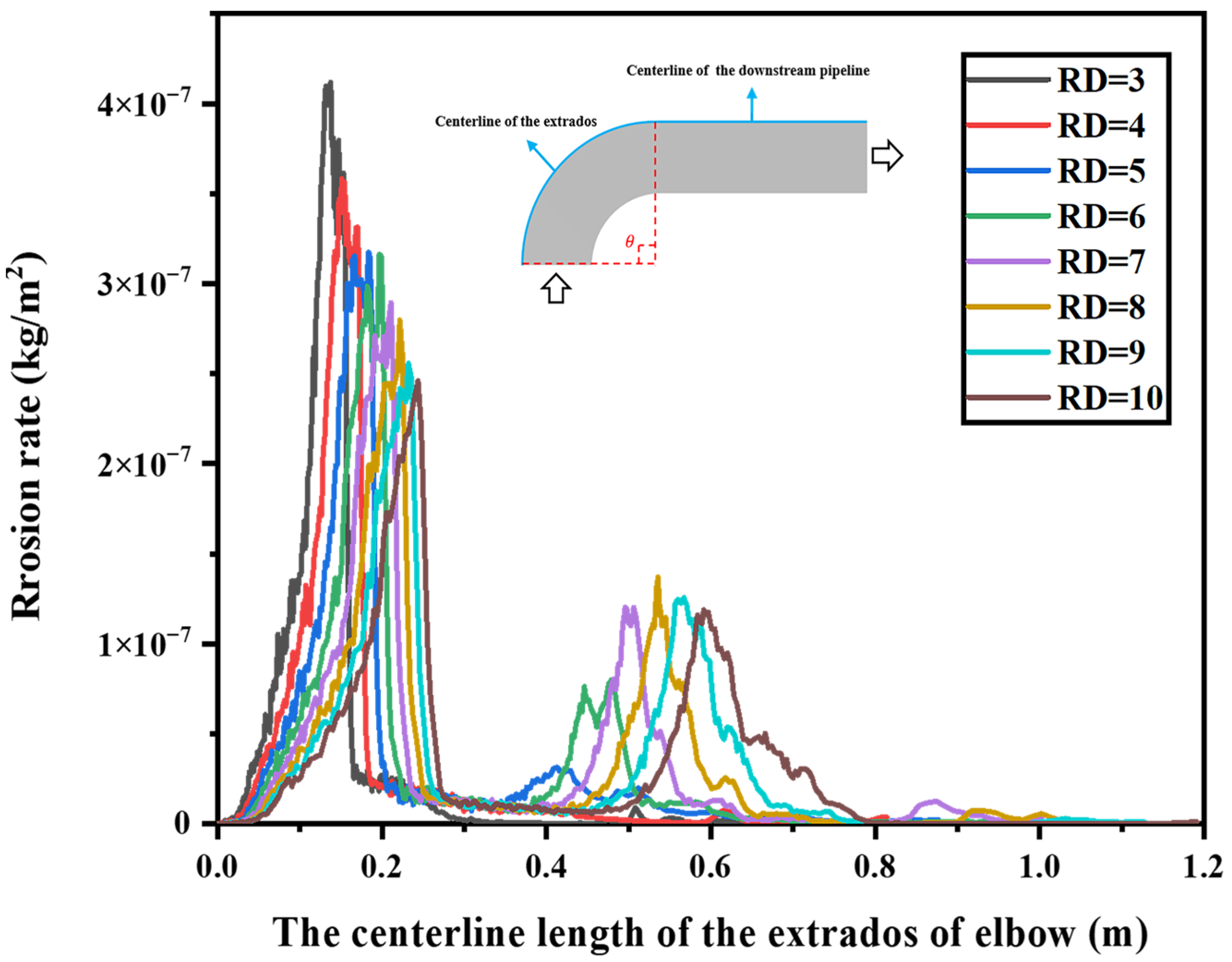
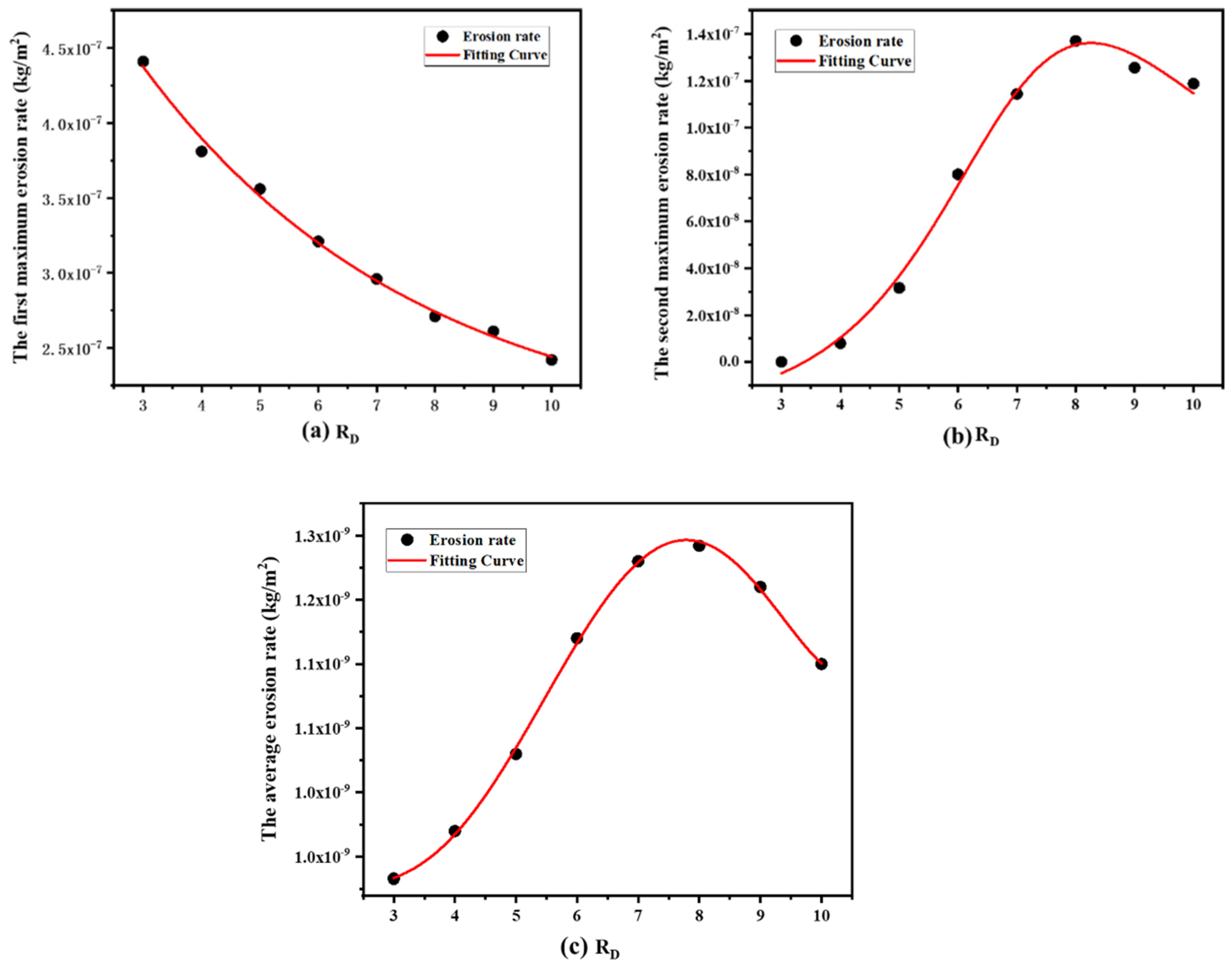
5.2. Effect of Curvature Ratio RD on Erosion
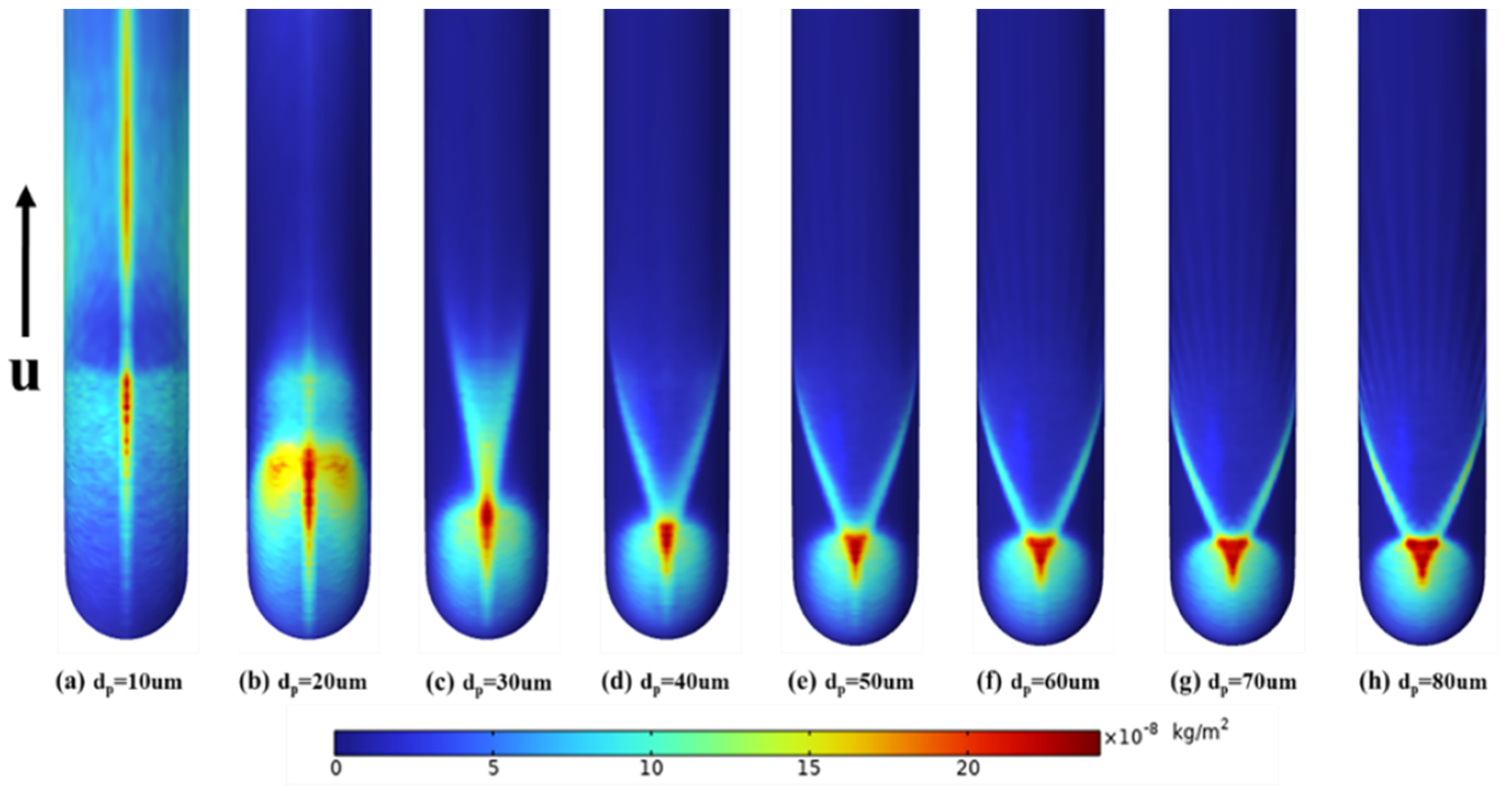
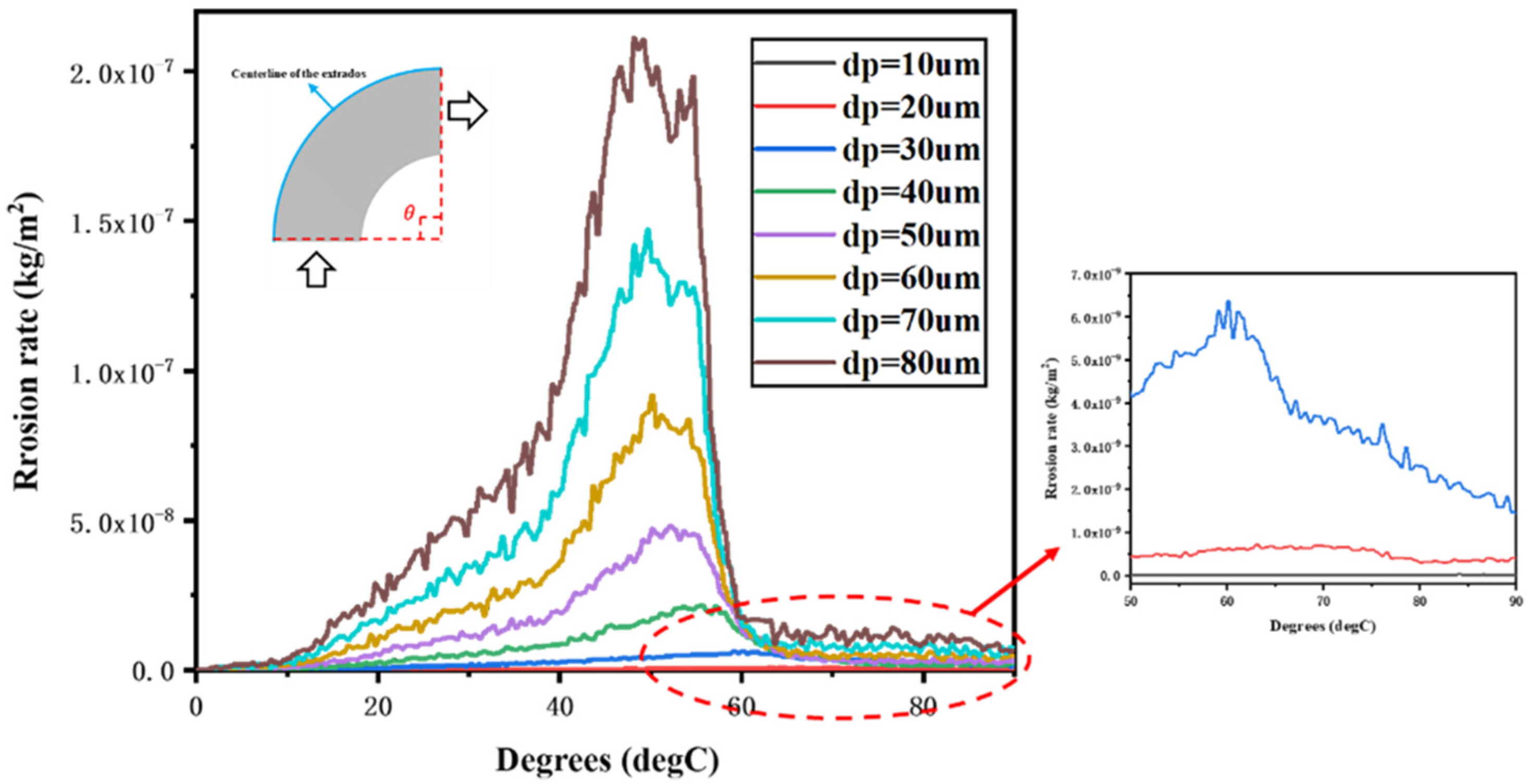
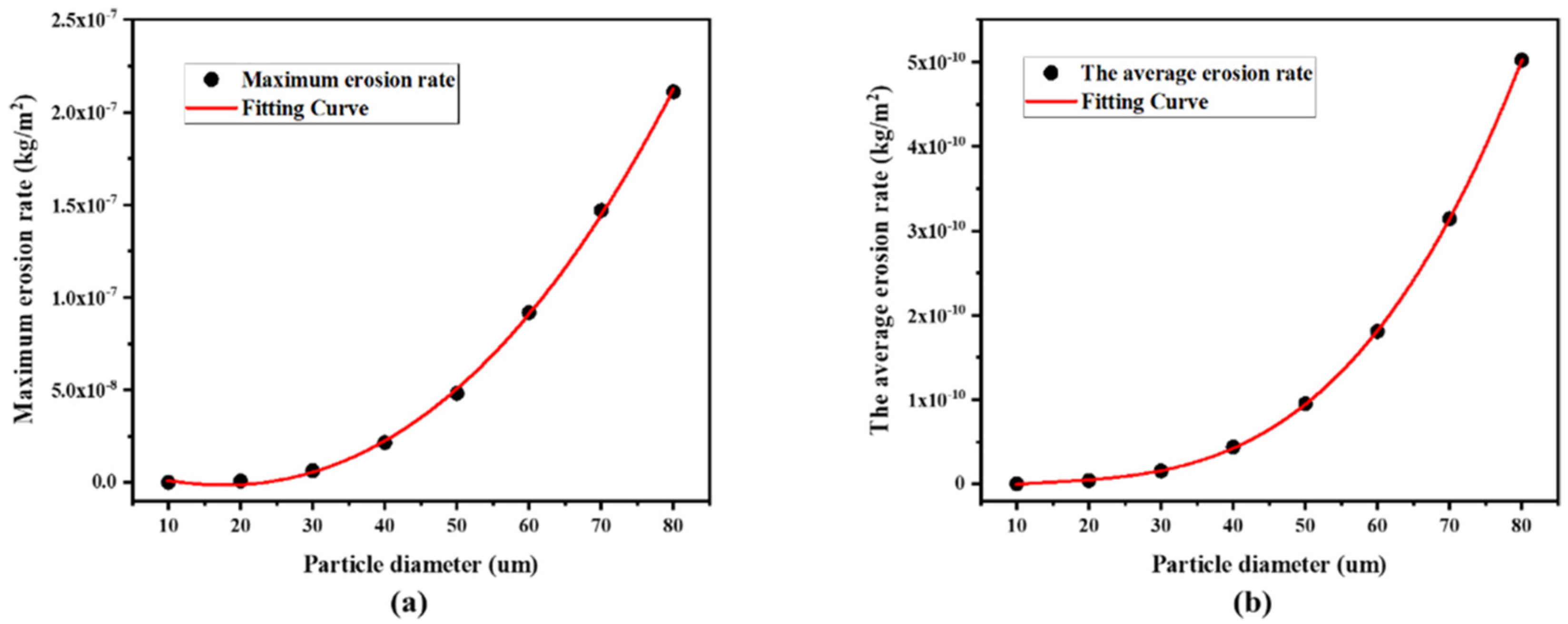
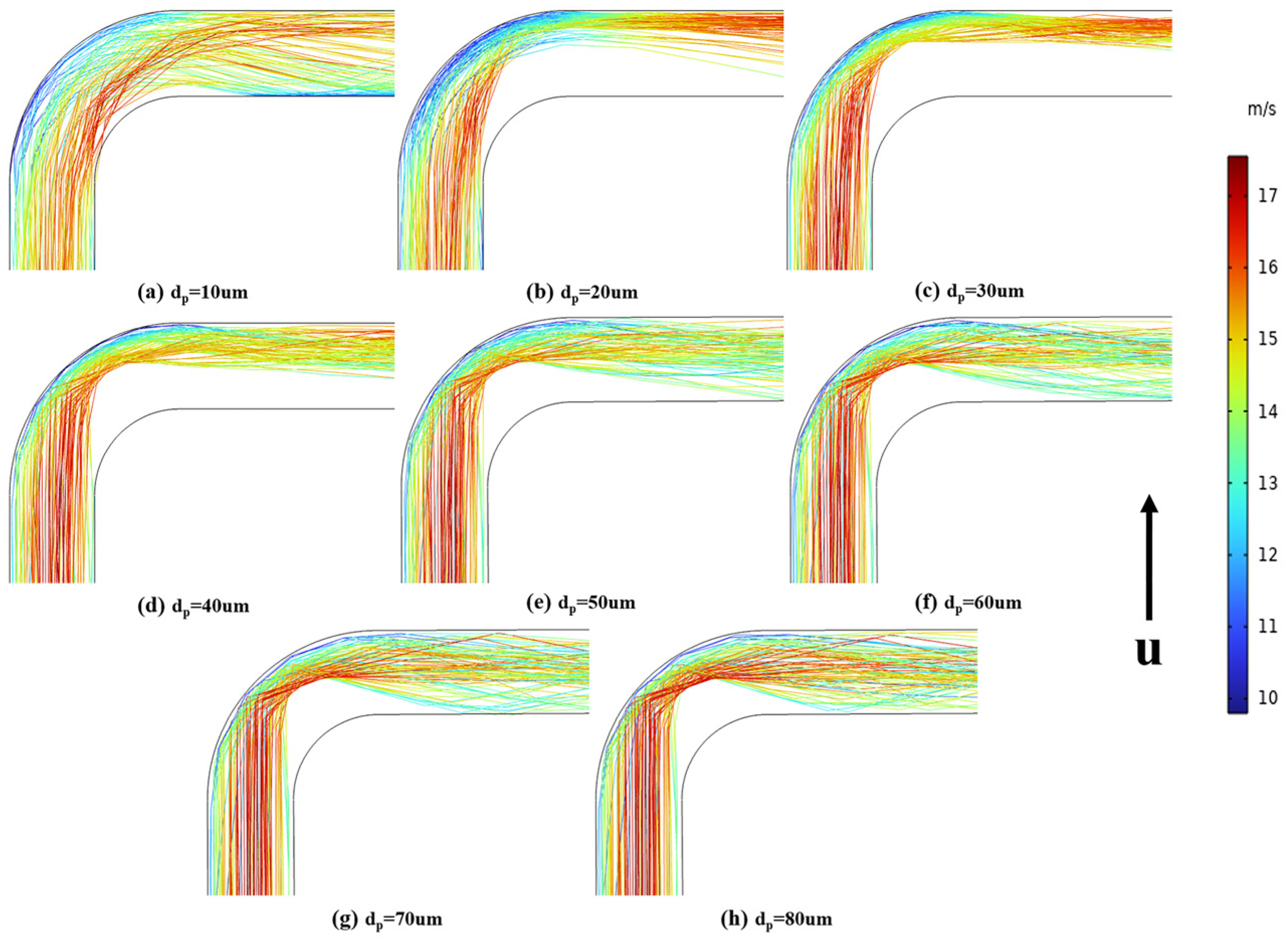
5.3. Effect of Particle Factors on Erosion
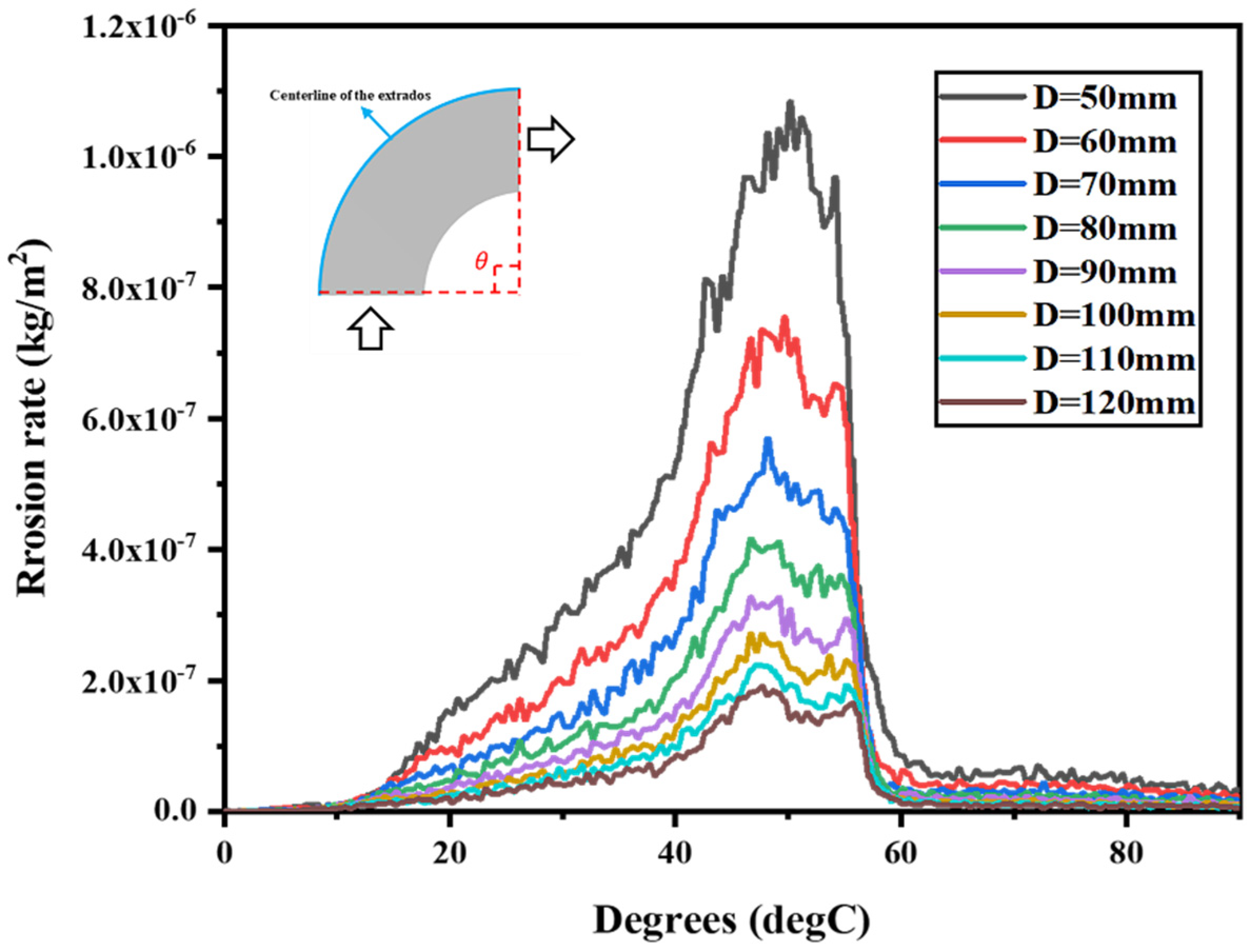
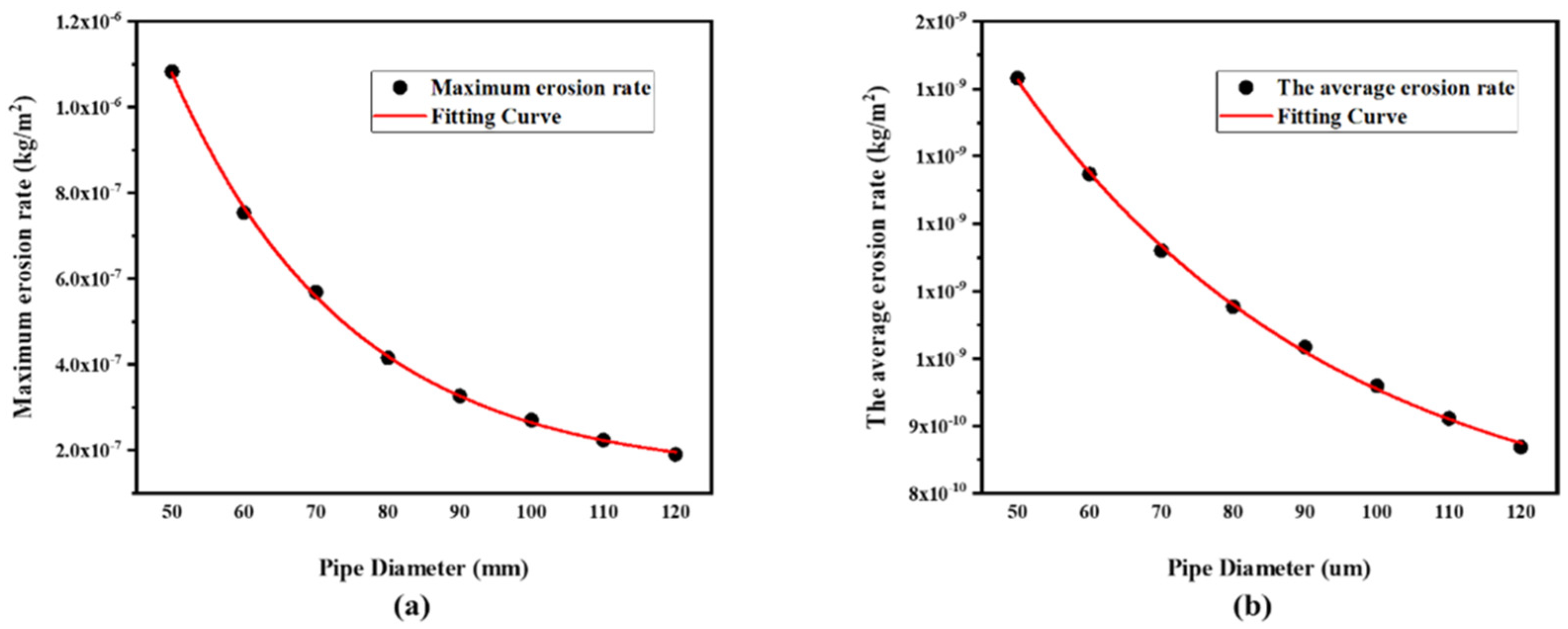
5.4. Effect of Pipe Diameter on Erosion
6. Conclusions
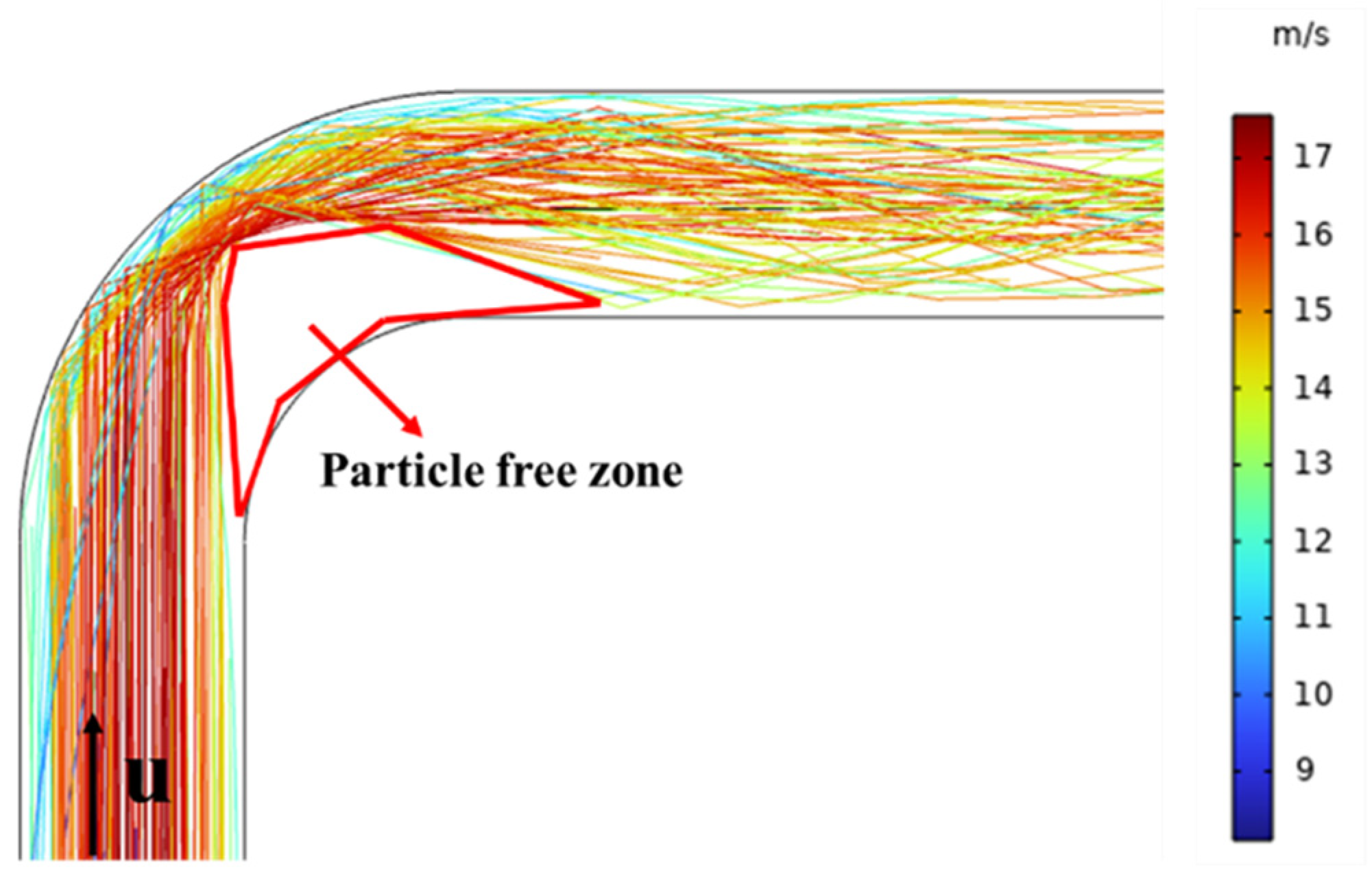
- The Stoke number considered in this case is 19.61 and the Dean number is 4.6 × 104, and the motion of the sulfur particles will be significantly influenced by the secondary eddy currents. The secondary erosion trace developed from the tip of the V-shaped erosion trace to the outlet on the side wall of the pipeline may be caused by the secondary vortex effect.
- Increasing the curvature ratio RD can reduce the severity of the maximum erosion area, but it will cause a new secondary erosion distribution near the pipe downstream of the elbow and reach the maximum when RD = 8. For the transportation of sulfur-containing gas pipelines, bends with RD of 8 or so should be avoided as far as possible to prevent the secondary erosion from becoming serious.
- The maximum erosion areas at the elbow are mainly distributed between 48.2° and 84.2° for sulfur particle sizes from 10 μm to 80 μm, and the inertial movement is more pronounced when the particle size exceeds 30 μm; the maximum erosion areas at the elbow are mainly distributed between 46.6° and 50.2° for the pipe diameter range from 50 mm to 120 mm. The change of Stoke number can reflect the movement state of particles in the fluid. If the value is greater, the more obvious it is that particles will remain their original initial movement state when passing through the elbow, and the more serious the erosion degree in the elbow will be. Therefore, the erosion rate can be reduced by appropriately increasing the pipe diameter and reducing the polymerization phenomenon of sulfur by using a separator.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Liu, S.; Wang, Y.; Xiang, Y.; Qing, C.; Zhang, H.; Ren, H.; Li, C. Estimation method of heterogeneous sulfur saturation distribution in high sulfur content gas reservoirs based on well test data. Environ. Earth Sci. 2023, 82, 115. [Google Scholar] [CrossRef]
- Habib, M.A.; Badr, H.M.; Ben-Mansour, R.; Kabir, M.E. Erosion rate correlations of a pipe protruded in an abrupt pipe contraction. Int. J. Impact Eng. 2007, 34, 1350–1369. [Google Scholar] [CrossRef]
- Ferng, Y.M.; Lin, B.H. Predicting the wall thinning engendered by erosion-corrosion using CFD methodology. Nucl. Eng. Des. 2010, 240, 2836–2841. [Google Scholar] [CrossRef]
- Finnie, I. The Mechanism of Erosion of Ductile Metals. Proc. 3rd Natl. Cong. Appl. Mech. 1958, 527–532. [Google Scholar] [CrossRef]
- Bitter, J. A Study of Erosion Phenomena. Wear 1963, 6, 5–21. [Google Scholar] [CrossRef]
- Levy, A.V. The erosion of structural alloys, cermets and in situ oxide scales on steels. Wear 1988, 127, 31–52. [Google Scholar] [CrossRef]
- Evans, A.G.; Biswas, D.R.; Fulrath, R.M. Accept/Reject Criteria for Structural Ceramics: Some Effects of Cavities on the Fracture of Ceramics Cylindrical Holes. J. Am. Ceram. Soc. 1979, 62, 95–100. [Google Scholar] [CrossRef]
- Berger, S.A.; Talbot, L.; Yao, L.S. Flow in Curved Pipes. Annu. Rev. Fluid Mech. 1983, 15, 461–512. [Google Scholar] [CrossRef]
- Smith, F.T. Fluid Flow into a Curved Pipe. Proc. R. Soc. A Math. Phys. Eng. Sci. 1976, 351, 71–87. [Google Scholar]
- Ahlert, K.R. Effects of Particle Impingement Angle and Surface Wetting on Solid Particle Erosion of AISI 1018 Steel. Ph.D. Thesis, University of Tulsa, Tulsa, OK, USA, 1994. [Google Scholar]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 1: Effects of impact parameters on a predictive equation. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Zhang, Y.; Reuterfors, E.P.; Mclaury, B.S.; Shirazi, S.A.; Rybicki, E.F. Comparison of computed and measured particle velocities and erosion in water and air flows. Wear 2007, 263, 330–338. [Google Scholar] [CrossRef]
- Veritas, N. Recommended Practice, RP O501: Erosive Wear in Piping Systems. DNV Recomm. Pract. 2007, 4, 1–34. [Google Scholar]
- Khan, R.; Ya, H.H.; Shah, I.; Niazi, U.M.; Ahmed, B.A.; Irfan, M.; Glowacz, A.; Pilch, Z.; Brumercik, F.; Azeem, M.; et al. Influence of Elbow Angle on Erosion-Corrosion of 1018 Steel for Gas–Liquid–Solid Three Phase Flow. Materials 2022, 15, 3721. [Google Scholar] [CrossRef]
- Wang, J.; Shirazi, S.A. A CFD Based Correlation for Erosion Factor for Long-Radius Elbows and Bends. J. Energy Resour. Technol. 2003, 125, 26–34. [Google Scholar] [CrossRef]
- McLaury, B.S.; Shirazi, S.A.; Burden, T.L. Effect of entrance shape on erosion in the throat of chokes. J. Energy Resour. Technol.-Trans. ASME 2000, 122, 198–204. [Google Scholar] [CrossRef]
- Edwards, J.K.; Mclaury, B.S.; Shirazi, S.A. Evaluation of alternative pipe bend fittings in erosive service. ASME 2000, 253. Available online: https://www.researchgate.net/publication/285907230 (accessed on 18 January 2023).
- Haugen, K.; Kvernvold, O.; Ronold, A.; Sandberg, R. Sand erosion of wear-resistant materials: Erosion in choke valves. Wear 1995, 186, 179–188. [Google Scholar] [CrossRef]
- Bozzini, B.; Ricotti, M.E.; Boniardi, M.; Mele, C. Evaluation of erosion–corrosion in multiphase flow via CFD and experimental analysis. Wear 2003, 255, 237–245. [Google Scholar] [CrossRef]
- Zeng, D.Z.; Zhang, E.B.; Ding, Y.Y.; Yi, Y.G.; Xian, Q.B.; Yao, G.J.; Zhu, H.J.; Shi, T.H. Investigation of erosion behaviors of sulfur-particle-laden gas flow in an elbow via a CFD-DEM coupling method. Powder Technol. 2018, 329, 115–128. [Google Scholar] [CrossRef]
- Zhang, E.; Zeng, D.; Zhu, H.; Li, S.; Chen, D.; Li, J.; Ding, Y.; Tian, G. Numerical simulation for erosion effects of three-phase flow containing sulfur particles on elbows in high sour gas fields. Petroleum 2018, 4, 158–167. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Li, X.; He, R.; Chen, Y. Reprint of: Erosion prediction of liquid-particle two-phase flow in pipeline elbows via CFD-DEM coupling method. Powder Technol. 2015, 282, 25–31. [Google Scholar] [CrossRef]
- Pei, J.; Lui, A.; Zhang, Q.; Xiong, T.; Jiang, P.; Wei, W. Numerical investigation of the maximum erosion zone in elbows for liquid-particle flow. Powder Technol. 2018, 333, 47–59. [Google Scholar] [CrossRef]
- Peng, W.; Cao, X. Numerical simulation of solid particle erosion in pipe bends for liquid–solid flow. Powder Technol. 2016, 294, 266–279. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Lain, S. From elementary processes to the numerical prediction of industrial particle-laden flows. Multiph. Sci. Technol. 2008, 21, 123–140. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Lain, S. Parameters influencing dilute-phase pneumatic conveying through pipe systems: A computational study by the Euler/Lagrange approach. Can. J. Chem. Eng. 2015, 93, 1–17. [Google Scholar] [CrossRef]
- Lain, S.; Sommerfeld, M. Numerical prediction of particle erosion of pipe bends. Adv. Powder Technol. 2019, 30, 366–383. [Google Scholar] [CrossRef]
- Laín, S.; Sommerfeld, M. Numerical calculation of pneumatic conveying in horizontal channels and pipes: Detailed analysis of conveying behaviour. Int. J. Multiph. Flow 2012, 39, 105–120. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-(Eddy Viscosity Model for High Reynolds Number Turbulent Flows: Model Development and Validation. Comput. Fluids 1994, 24. Available online: https://www.researchgate.net/publication/24292638 (accessed on 18 January 2023).
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 2006. [Google Scholar]
- Forder, A.; Thew, M.; Harrison, D. A numerical investigation of solid particle erosion experienced within oilfield control valves. Wear 1998, 216, 184–193. [Google Scholar] [CrossRef]
- Zhang, P.; Zheng, S.; Jing, J.; Zhou, Y.; Li, Q.; Wang, K.; Lv, N.; Sun, N. Surface erosion behavior of an intrusive probe in pipe flow. J. Nat. Gas Sci. Eng. 2015, 26, 480–493. [Google Scholar] [CrossRef]
- Souza, F.; Martins], D. Numerical prediction of the erosion due to particles in elbows. Powder Technol. 2014, 261, 105–117. [Google Scholar]
- Wang, H.; Yu, Y.; Yu, J.; Wang, Z.; Li, H. Development of erosion equation and numerical simulation methods with the consideration of applied stress. Tribol. Int. 2019, 137, 387–404. [Google Scholar] [CrossRef]
- Shirazi, S.A.; McLaury, B.S.; Karimi, S.; Mansouri, A.; Arabnejad, H. Improved CFD modeling and validation of erosion damage due to fine sand particles. Wear 2015, 338, 339–350. [Google Scholar]
- Chen, X.; Mclaury, B.S.; Shirazi, S.A. Application and experimental validation of a computational fluid dynamics (CFD)-based erosion prediction model in elbows and plugged tees. Comput. Fluids 2004, 33, 1251–1272. [Google Scholar] [CrossRef]
- Zolfagharnasab, M.H.; Salimi, M.; Zolfagharnasab, H.; Alimoradi, H.; Aghanajafi, C. A novel numerical investigation of erosion wear over various 90-degree elbow duct sections. Powder Technol. 2020, 380, 1–17. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Huber, N. Experimental analysis and modelling of particle-wall collisions. Int. J. Multiph. Flow 1999, 25, 1457–1489. [Google Scholar] [CrossRef]
- Bahmani, S.; Nazif, H.R. Erosion of rectangular channel bend in two-phase natural gas particles turbulent flow. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–17. [Google Scholar] [CrossRef]


| 5.3983 | −10.1068 | 10.9327 | −6.3283 | 1.4234 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Fluid | Methane | Mass flow rate (kg/s) | 0.05 |
| Particle | Sulfur particle | Tube wall material | Steel |
| Flow rate (m/s) | 15 | Tube wall density (kg/m3) | 7860 |
| Fluid density (kg/m3) | 0.7174 | Brinell hardness (BH) | 120 |
| Hydrodynamic viscosity (Pa/s) | 1.087 × 10−5 | Pipe diameter (mm) | 80 |
| Particle density (kg/m3) | 2046 | Curvature ratio (RD) | 3 |
| Particle diameter (μm) | 40 | Angle of bend (°) | 90 |
| Particle shape coefficient | 0.2 | / | / |
| Mesh numbers | 260,600 | 356,610 | 448,200 | 581,000 | 672,400 | 770,000 | 856,440 | 950,000 |
| Time (h) | 8.2 | 10.5 | 13.2 | 14.2 | 16.6 | 25.1 | 48.5 | 91.7 |
| Maximum erosion rate (10−8) | 7.1 | 9.4 | 11.7 | 13 | 13.9 | 14.3 | 14.5 | 14.7 |
| Differential value | / | 2.3 | 1.9 | 1.3 | 0.9 | 0.4 | 0.2 | 0.2 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Fluid | Air | Mass flow rate (kg/s) | 0.000208 |
| Particle | Sand | Tube wall material | Aluminum |
| Flow rate (m/s) | 45.72 | Tube wall density (kg/m3) | 2700 |
| Fluid density (kg/m3) | 1.225 | Brinell hardness (BH) | 95 |
| Hydrodynamic viscosity (Pa/s) | 1.7894 × 10−5 | Pipe diameter (mm) | 25.4 |
| Particle density (kg/m3) | 2320 | Curvature ratio (RD) | 1.5 |
| Particle diameter (μm) | 150 | Angle of bend (°) | 90 |
| Particle shape coefficient | 0.2 | / | / |
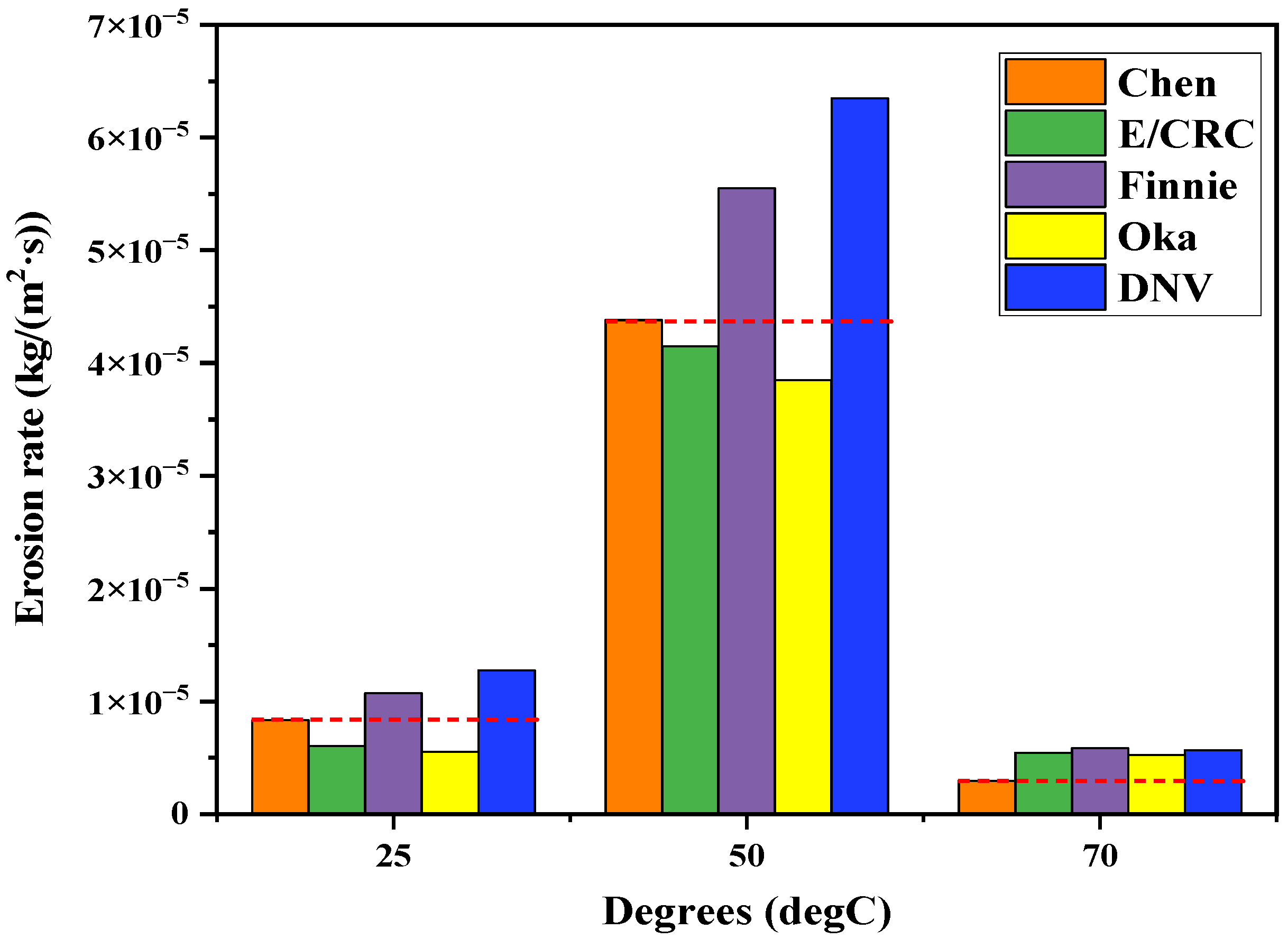
| E/CRC | Finnie | Oka | DNV | |
|---|---|---|---|---|
| 25° | 2.30 × 10−6 | 2.48 × 10−6 | 2.80 × 10−6 | 4.40 × 10−6 |
| 50° | 2.33 × 10−6 | 1.17 × 10−5 | 5.33 × 10−6 | 1.97 × 10−5 |
| 70° | 2.49 × 10−6 | 2.89 × 10−6 | 2.29 × 10−6 | 2.69 × 10−6 |
| Gas Flow Rate (m/s) | Particle Density (kg/m3) | Pipe Diameter (mm) | Hydrodynamic Viscosity (Pa/s) | Particle Diameter (μm) | Stoke Number |
|---|---|---|---|---|---|
| 15 | 2046 | 80 | 1.087 × 10−5 | 10 | 0.196 |
| 20 | 0.784 | ||||
| 30 | 1.765 | ||||
| 40 | 3.137 | ||||
| 50 | 4.902 | ||||
| 60 | 7.058 | ||||
| 70 | 9.607 | ||||
| 80 | 12.548 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Ren, H.; Fang, Q.; Ren, Y.; Jiang, D.; Liu, Y.; Liu, S.; Li, C.; Tang, D. Numerical Study of the Erosion Distribution of Sulfur-Containing Particulate Gas in 90-Degree Gathering Elbow. Energies 2023, 16, 2707. https://doi.org/10.3390/en16062707
Zhu R, Ren H, Fang Q, Ren Y, Jiang D, Liu Y, Liu S, Li C, Tang D. Numerical Study of the Erosion Distribution of Sulfur-Containing Particulate Gas in 90-Degree Gathering Elbow. Energies. 2023; 16(6):2707. https://doi.org/10.3390/en16062707
Chicago/Turabian StyleZhu, Runhua, Hongming Ren, Qiang Fang, Yang Ren, Dong Jiang, Yongliang Liu, Shudong Liu, Chengyong Li, and Danni Tang. 2023. "Numerical Study of the Erosion Distribution of Sulfur-Containing Particulate Gas in 90-Degree Gathering Elbow" Energies 16, no. 6: 2707. https://doi.org/10.3390/en16062707
APA StyleZhu, R., Ren, H., Fang, Q., Ren, Y., Jiang, D., Liu, Y., Liu, S., Li, C., & Tang, D. (2023). Numerical Study of the Erosion Distribution of Sulfur-Containing Particulate Gas in 90-Degree Gathering Elbow. Energies, 16(6), 2707. https://doi.org/10.3390/en16062707






