A Review of Physics-Informed Machine Learning in Fluid Mechanics
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Fundamentals and History
1.3. Applications of ML in Fluid Mechanics
1.4. Outline
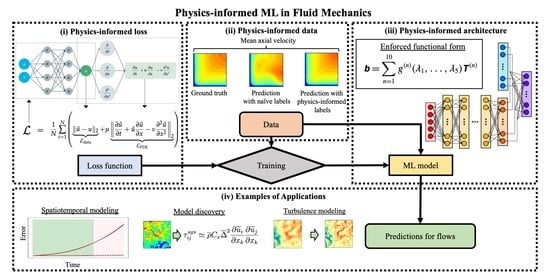
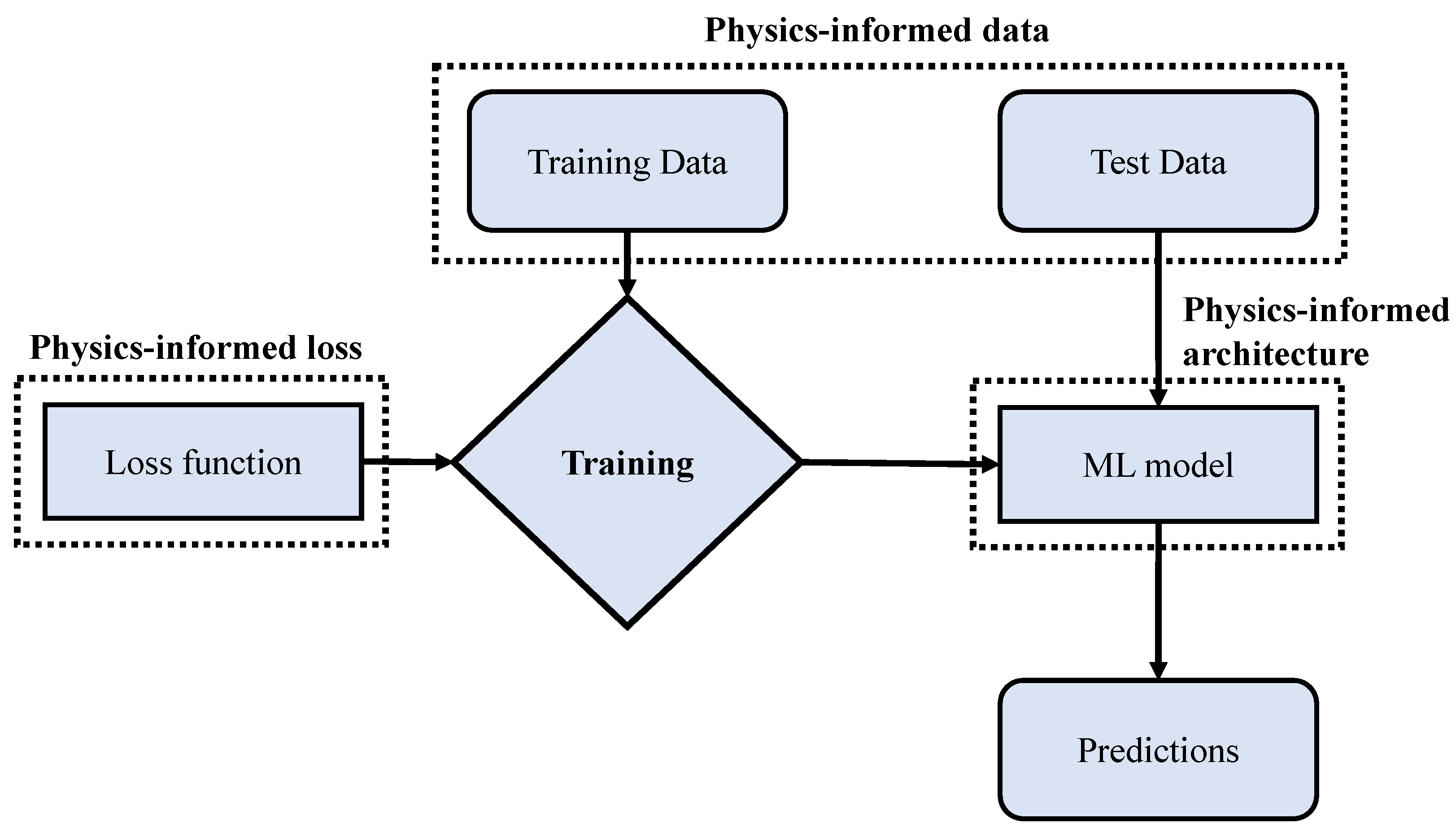
2. Physics-Informed Machine Learning
2.1. Physics-Informed Features and Labels
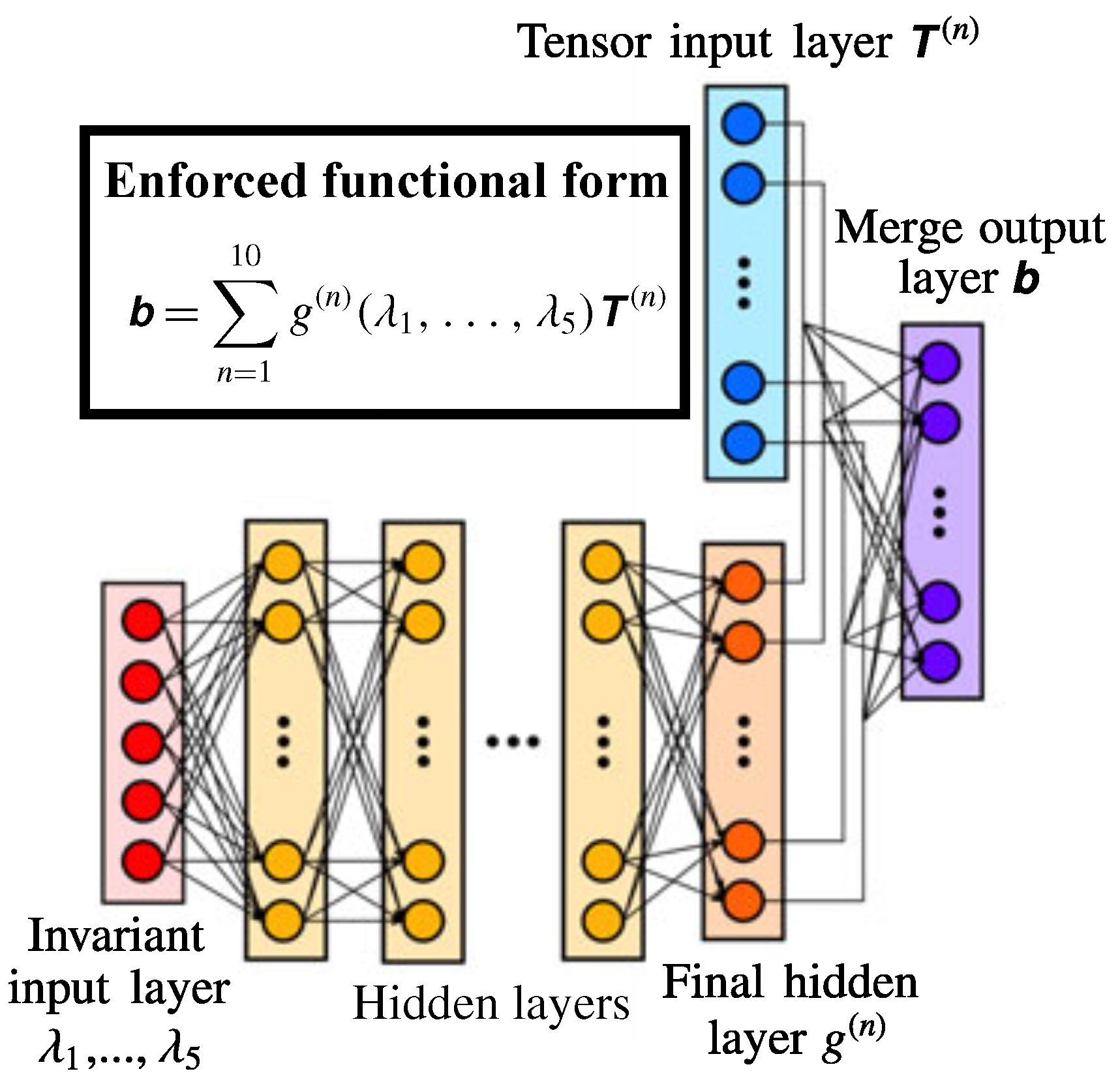
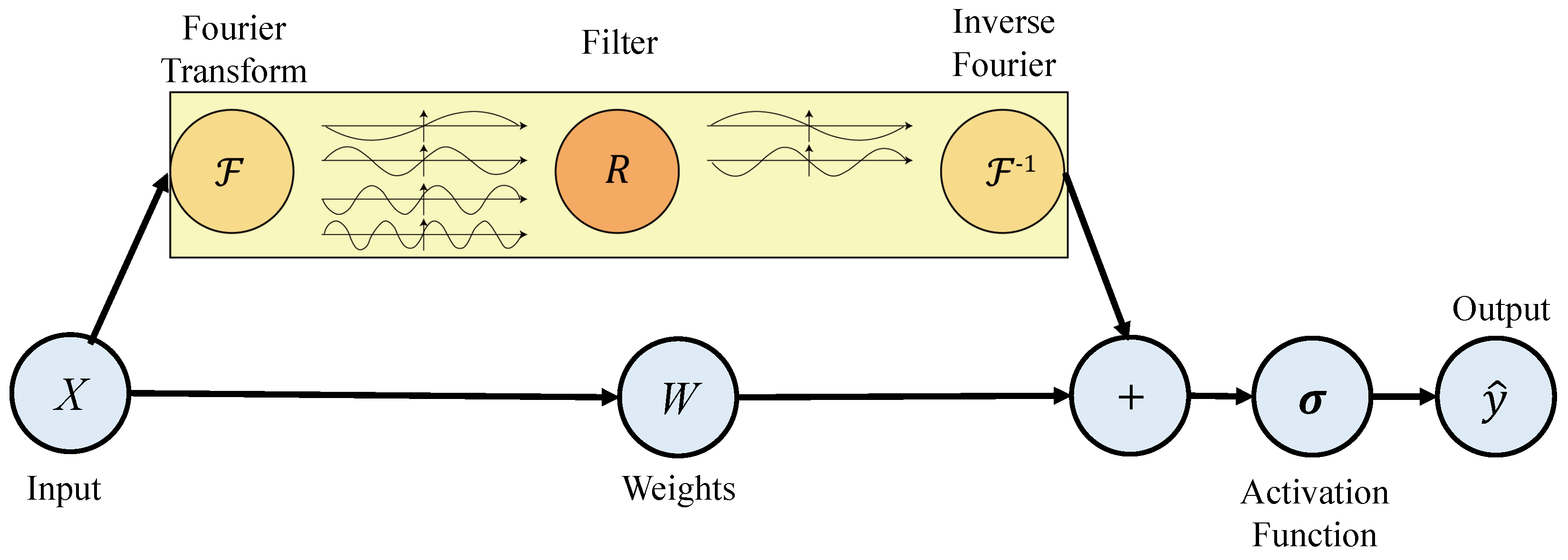
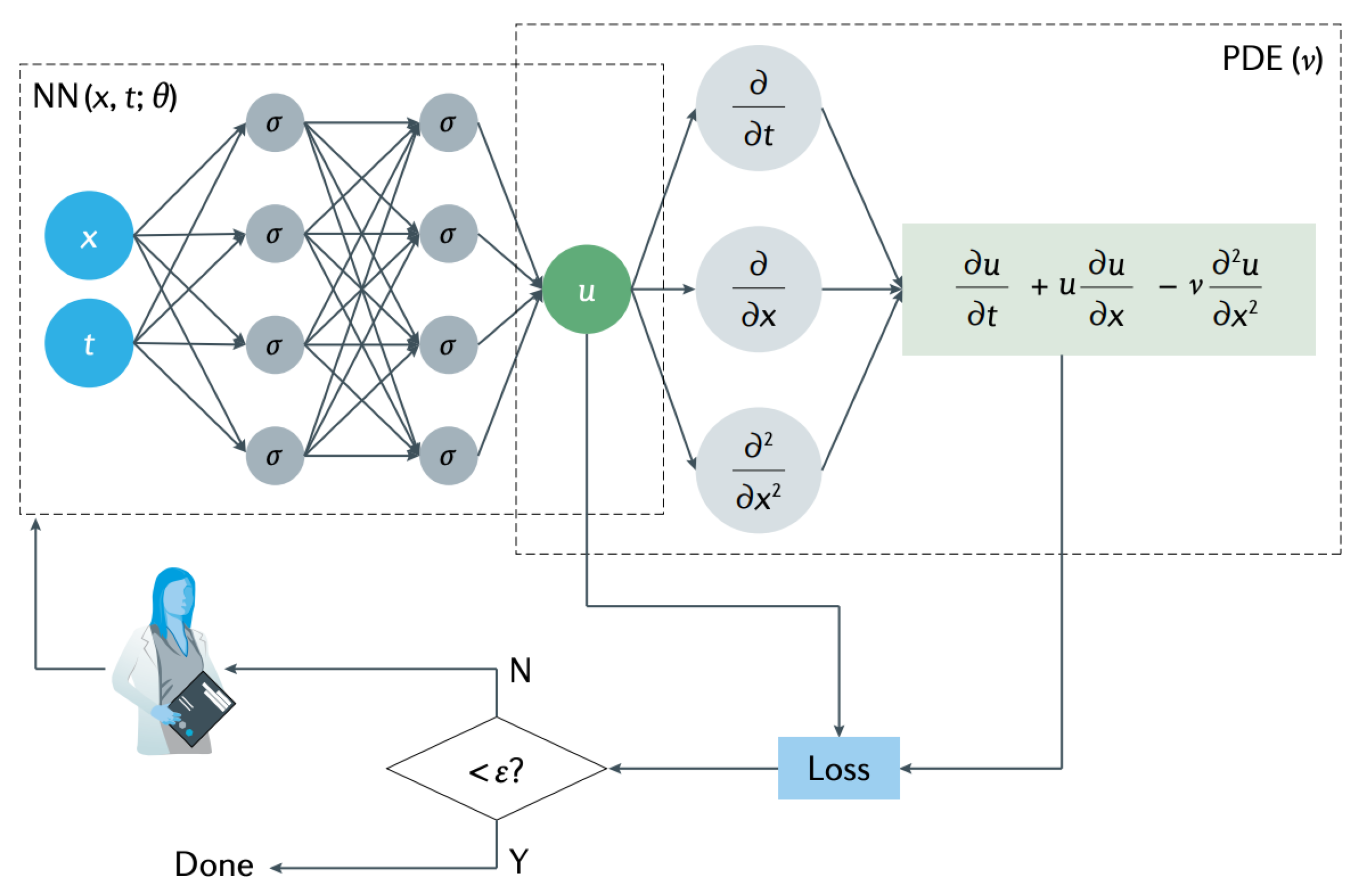
2.2. Physics-Informed Architecture
2.3. Physics-Informed Loss Functions
2.4. Open-Source PIML Resources
3. Case Study: Lid-Driven Cavity
3.1. Problem Setup
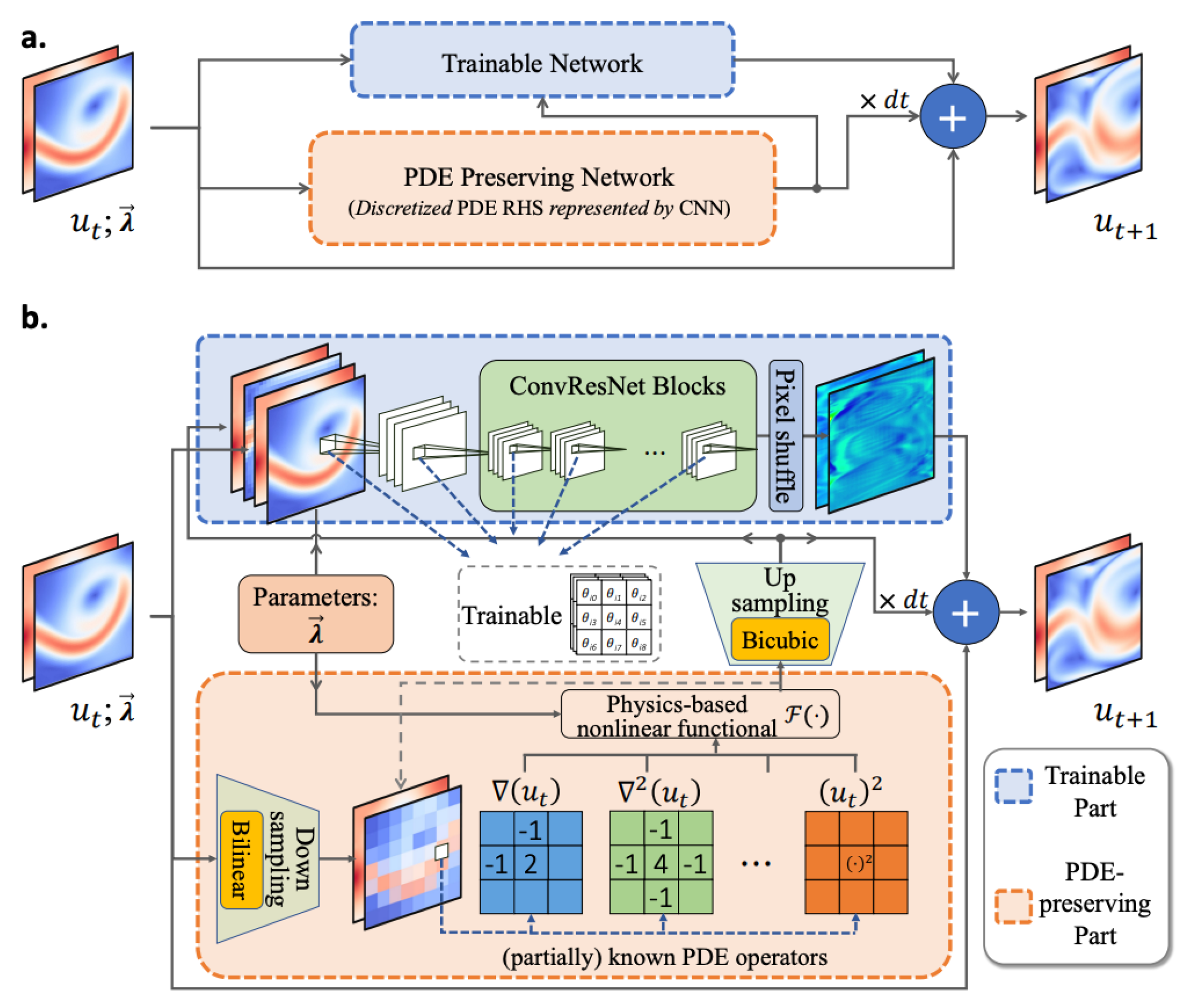
3.2. Implementation of PPNN
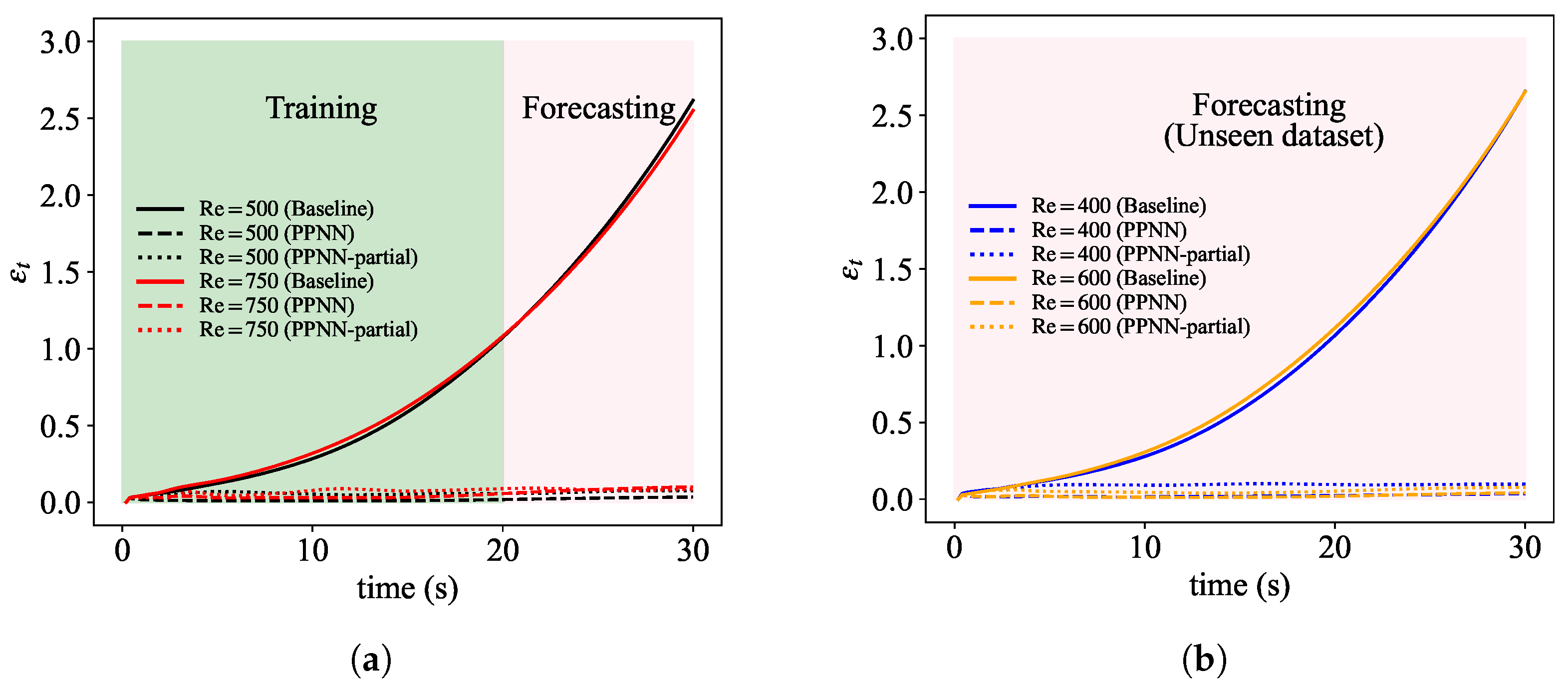
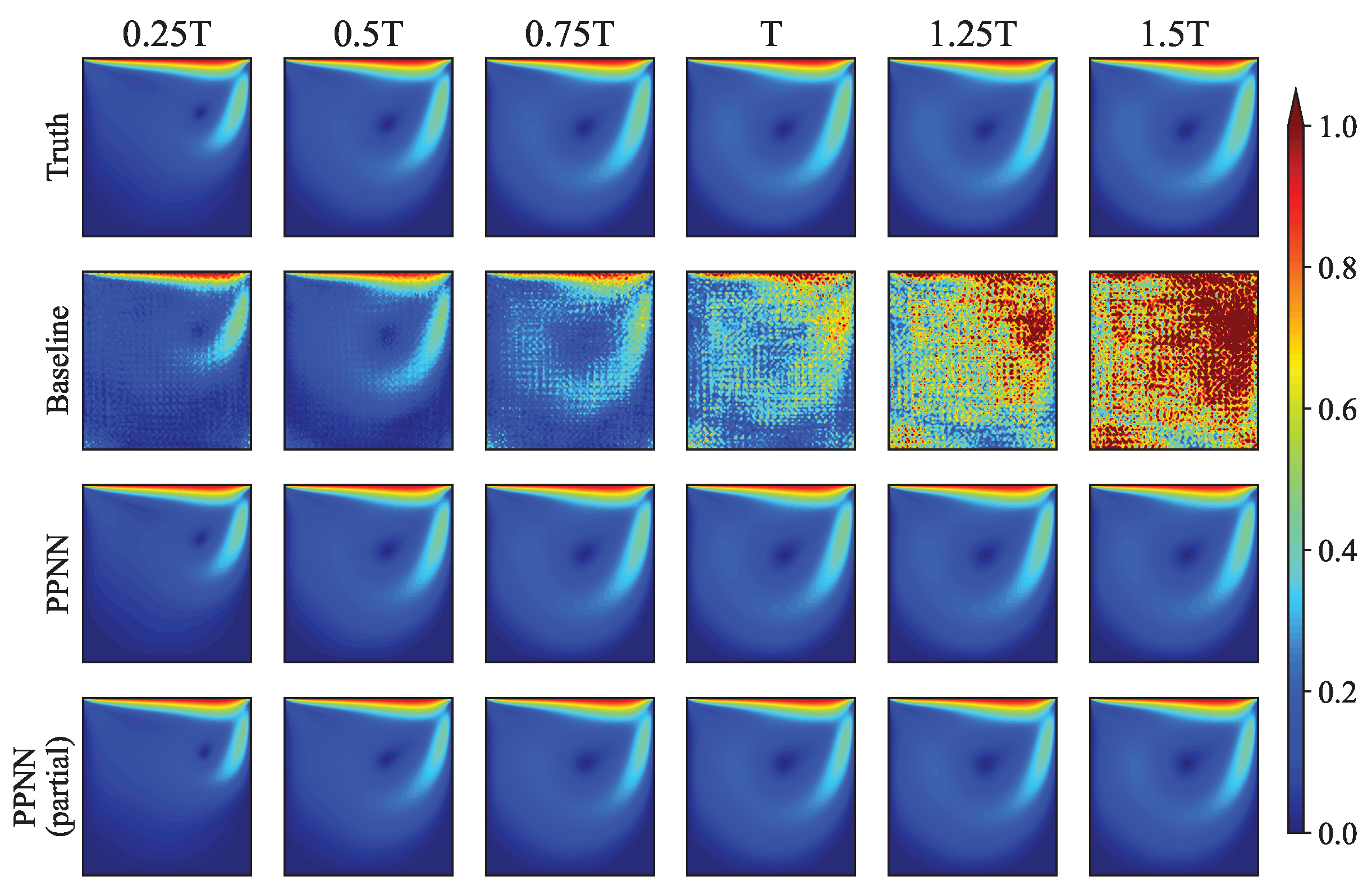
3.3. Results and Discussion
4. Challenges and Opportunities
4.1. Benchmarking Existing PIML Methods
4.2. Optimization and Loss
4.3. Embedding Physics to New Algorithms and Applications
4.4. Limitations in Predicting Complex Configurations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine learning |
| PIML | Physics-informed machine learning |
| NN | Neural network |
| CFD | Computational fluid dynamics |
| DNS | Direct numerical simulation |
| GPU | Graphics processing unit |
| TPU | Tensor processing unit |
| MLP | Multi-layer perceptron |
| CNN | Convolutional neural network |
| RL | Reinforcement learning |
| Re | Reynolds number |
| PINN | Physics-informed neural network |
| PPNN | PDE-preserved neural network |
| LES | Large-eddy simulation |
| RANS | Reynolds average Navier-Stokes |
| ODE | Ordinary differential equation |
| PDE | Partial differential equation |
| POD | Proper orthogonal decomposition |
| TBNN | Tensor basis neural network |
| VBNN | Vector basis neural network |
| RHS | Right-hand side |
| TFNet | TurbulentFlowNet |
| FNO | Fourier neural operator |
| MSE | Mean-squared error |
| VP | Velocity–pressure |
| VV | Velocity–vorticity |
| GAN | Generative adversarial network |
| PIESR-GAN | Physics-informed enhanced super-resolution GAN |
| FD | Finite difference |
| NLP | Natural language processing |
| QSS | Quasi-steady species |
| GNN | Graph neural network |
References
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. Proc. Int. Conf. Mach. Learn. 2010, 27, 807–814. [Google Scholar]
- Amari, S.i. Backpropagation and stochastic gradient descent method. Neurocomputing 1993, 5, 185–196. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar]
- Tracey, B.D.; Duraisamy, K.; Alonso, J.J. A machine learning strategy to assist turbulence model development. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1287. [Google Scholar]
- Duraisamy, K.; Zhang, Z.J.; Singh, A.P. New approaches in turbulence and transition modeling using data-driven techniques. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1284. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. Royal Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Reddy, G.; Celani, A.; Sejnowski, T.J.; Vergassola, M. Learning to soar in turbulent environments. Proc. Natl. Acad. Sci. USA 2016, 113, E4877–E4884. [Google Scholar] [CrossRef]
- Novati, G.; de Laroussilhe, H.L.; Koumoutsakos, P. Automating turbulence modelling by multi-agent reinforcement learning. Nat. Mach. Intell. 2021, 3, 87–96. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3365–3387. [Google Scholar] [CrossRef] [PubMed]
- Maulik, R.; San, O.; Jacob, J.D.; Crick, C. Sub-grid scale model classification and blending through deep learning. J. Fluid Mech. 2019, 870, 784–812. [Google Scholar] [CrossRef]
- Chung, W.T.; Mishra, A.A.; Perakis, N.; Ihme, M. Data-assisted combustion simulations with dynamic submodel assignment using random forests. Combust. Flame 2021, 227, 172–185. [Google Scholar] [CrossRef]
- Li, B.; Yang, Z.; Zhang, X.; He, G.; Deng, B.Q.; Shen, L. Using machine learning to detect the turbulent region in flow past a circular cylinder. J. Fluid Mech. 2020, 905, A10. [Google Scholar] [CrossRef]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Callaham, J.L.; Rigas, G.; Loiseau, J.C.; Brunton, S.L. An empirical mean-field model of symmetry-breaking in a turbulent wake. Sci. Adv. 2022, 8, eabm4786. [Google Scholar] [CrossRef]
- Chung, W.T.; Mishra, A.A.; Ihme, M. Interpretable data-driven methods for subgrid-scale closure in LES for transcritical LOX/GCH4 combustion. Combust. Flame 2022, 239, 111758. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comp. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comp. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Fuest, F.; Jeon, Y.J.; Gray, C.; Karniadakis, G.E. Flow over an espresso cup: Inferring 3-D velocity and pressure fields from tomographic background oriented Schlieren via physics-informed neural networks. J. Fluid Mech. 2021, 915, A102. [Google Scholar] [CrossRef]
- Eivazi, H.; Tahani, M.; Schlatter, P.; Vinuesa, R. Physics-informed neural networks for solving Reynolds-averaged Navier–Stokes equations. Phys. Fluids 2022, 34, 075117. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Wang, S. Dense velocity reconstruction from particle image velocimetry/particle tracking velocimetry using a physics-informed neural network. Phys. Fluids 2022, 34, 017116. [Google Scholar] [CrossRef]
- Qiu, R.; Huang, R.; Xiao, Y.; Wang, J.; Zhang, Z.; Yue, J.; Zeng, Z.; Wang, Y. Physics-informed neural networks for phase-field method in two-phase flow. Phys. Fluids 2022, 34, 052109. [Google Scholar] [CrossRef]
- Aliakbari, M.; Mahmoudi, M.; Vadasz, P.; Arzani, A. Predicting high-fidelity multiphysics data from low-fidelity fluid flow and transport solvers using physics-informed neural networks. Int. J. Heat Fluid Flow 2022, 96, 109002. [Google Scholar] [CrossRef]
- Ji, W.; Qiu, W.; Shi, Z.; Pan, S.; Deng, S. Stiff-PINN: Physics-informed neural network for stiff chemical kinetics. J. Phys. Chem. A 2021, 125, 8098–8106. [Google Scholar] [CrossRef] [PubMed]
- Weng, Y.; Zhou, D. Multiscale physics-informed neural networks for stiff chemical kinetics. J. Phys. Chem. A 2022, 126, 8534–8543. [Google Scholar] [CrossRef]
- Laubscher, R. Simulation of multi-species flow and heat transfer using physics-informed neural networks. Phys. Fluids 2021, 33, 087101. [Google Scholar] [CrossRef]
- Liu, X.Y.; Sun, H.; Zhu, M.; Lu, L.; Wang, J.X. Predicting parametric spatiotemporal dynamics by multi-resolution PDE structure-preserved deep learning. arXiv 2022, arXiv:2205.03990. [Google Scholar]
- Ren, P.; Rao, C.; Liu, Y.; Wang, J.X.; Sun, H. PhyCRNet: Physics-informed convolutional-recurrent network for solving spatiotemporal PDEs. Comput. Methods Appl. Mech. Eng. 2022, 389, 114399. [Google Scholar] [CrossRef]
- Kochkov, D.; Smith, J.A.; Alieva, A.; Wang, Q.; Brenner, M.P.; Hoyer, S. Machine learning-accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. USA 2021, 118, e2101784118. [Google Scholar] [CrossRef] [PubMed]
- De Avila Belbute-Peres, F.; Economon, T.; Kolter, Z. Combining differentiable PDE solvers and graph neural networks for fluid flow prediction. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 2402–2411. [Google Scholar]
- Um, K.; Brand, R.; Fei, Y.R.; Holl, P.; Thuerey, N. Solver-in-the-loop: Learning from differentiable physics to interact with iterative PDE-solvers. Adv. Neural Inf. Process. Syst. 2020, 33, 6111–6122. [Google Scholar]
- Gao, H.; Sun, L.; Wang, J.X. PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. J. Comp. Phys. 2021, 428, 110079. [Google Scholar] [CrossRef]
- Geneva, N.; Zabaras, N. Modeling the dynamics of PDE systems with physics-constrained deep auto-regressive networks. J. Comp. Phys. 2020, 403, 109056. [Google Scholar] [CrossRef]
- Ranade, R.; Hill, C.; Pathak, J. DiscretizationNet: A machine-learning based solver for Navier–Stokes equations using finite volume discretization. Comput. Methods Appl. Mech. Eng. 2021, 378, 113722. [Google Scholar] [CrossRef]
- Rao, C.; Sun, H.; Liu, Y. Embedding physics to learn spatiotemporal dynamics from sparse data. arXiv 2021, arXiv:2106.04781. [Google Scholar]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Ling, J.; Templeton, J. Evaluation of machine learning algorithms for prediction of regions of high Reynolds averaged Navier-Stokes uncertainty. Phys. Fluids 2015, 27, 085103. [Google Scholar] [CrossRef]
- Ling, J.; Jones, R.; Templeton, J. Machine learning strategies for systems with invariance properties. J. Comp. Phys. 2016, 318, 22–35. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Parish, E.J.; Duraisamy, K. A paradigm for data-driven predictive modeling using field inversion and machine learning. J. Comp. Phys. 2016, 305, 758–774. [Google Scholar] [CrossRef]
- Xiao, H.; Wu, J.L.; Wang, J.X.; Sun, R.; Roy, C. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier-Stokes simulations: A data-driven, physics-informed Bayesian approach. J. Comp. Phys. 2016, 324, 115–136. [Google Scholar] [CrossRef]
- Singh, A.P.; Medida, S.; Duraisamy, K. Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils. AIAA J. 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
- Wang, J.X.; Wu, J.L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Lapeyre, C.J.; Misdariis, A.; Cazard, N.; Veynante, D.; Poinsot, T. Training convolutional neural networks to estimate turbulent sub-grid scale reaction rates. Combust. Flame 2019, 203, 255–264. [Google Scholar] [CrossRef]
- Beck, A.; Flad, D.; Munz, C.D. Deep neural networks for data-driven LES closure models. J. Comp. Phys. 2019, 398, 108910. [Google Scholar] [CrossRef]
- Maulik, R.; San, O. A neural network approach for the blind deconvolution of turbulent flows. J. Fluid Mech. 2017, 831, 151–181. [Google Scholar] [CrossRef]
- Bode, M.; Gauding, M.; Lian, Z.; Denker, D.; Davidovic, M.; Kleinheinz, K.; Jitsev, J.; Pitsch, H. Using physics-informed enhanced super-resolution generative adversarial networks for subfilter modeling in turbulent reactive flows. Proc. Combust. Inst. 2021, 38, 2617–2625. [Google Scholar] [CrossRef]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Brunton, S.L. Applying machine learning to study fluid mechanics. Acta Mech. Sin. 2022, 37, 1–9. [Google Scholar] [CrossRef]
- Zhu, L.T.; Chen, X.Z.; Ouyang, B.; Yan, W.C.; Lei, H.; Chen, Z.; Luo, Z.H. Review of machine learning for hydrodynamics, transport, and reactions in multiphase flows and reactors. Ind. Eng. Chem. Res. 2022, 61, 9901–9949. [Google Scholar] [CrossRef]
- Ihme, M.; Chung, W.T.; Mishra, A.A. Combustion machine learning: Principles, progress and prospects. Prog. Energy Combust. Sci. 2022, 91, 101010. [Google Scholar] [CrossRef]
- Zhou, L.; Song, Y.; Ji, W.; Wei, H. Machine learning for combustion. Energy AI 2022, 7, 100128. [Google Scholar] [CrossRef]
- Echekki, T.; Farooq, A.; Ihme, M.; Sarathy, S.M. Machine Learning for Combustion Chemistry. In Machine Learning and Its Application to Reacting Flows: ML and Combustion; Springer International Publishing: Cham, Switzerland, 2023; pp. 117–147. [Google Scholar]
- Zhong, S.; Zhang, K.; Bagheri, M.; Burken, J.G.; Gu, A.; Li, B.; Ma, X.; Marrone, B.L.; Ren, Z.J.; Schrier, J.; et al. Machine learning: New ideas and tools in environmental science and engineering. Environ. Sci. Technol. 2021, 55, 12741–12754. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating scientific knowledge with machine learning for engineering and environmental systems. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Hao, Z.; Liu, S.; Zhang, Y.; Ying, C.; Feng, Y.; Su, H.; Zhu, J. Physics-informed machine learning: A survey on problems, methods and applications. arXiv 2022, arXiv:2211.08064. [Google Scholar]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2022, 37, 1–12. [Google Scholar] [CrossRef]
- Wu, J.L.; Wang, J.X.; Xiao, H.; Ling, J. A priori assessment of prediction confidence for data-driven turbulence modeling. Flow Turbul. Combust. 2017, 99, 25–46. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Ding, S.; Zhu, H.; Jia, W.; Su, C. A survey on feature extraction for pattern recognition. Artif. Intell. Rev. 2012, 37, 169–180. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Beck, A.; Kurz, M. A perspective on machine learning methods in turbulence modeling. GAMM-Mitteilungen 2021, 44, e202100002. [Google Scholar] [CrossRef]
- Duraisamy, K. Perspectives on machine learning-augmented Reynolds-averaged and large eddy simulation models of turbulence. Phys. Rev. Fluids 2021, 6, 050504. [Google Scholar] [CrossRef]
- Arridge, S.; Maass, P.; Öktem, O.; Schönlieb, C.B. Solving inverse problems using data-driven models. Acta Numer. 2019, 28, 1–174. [Google Scholar] [CrossRef]
- Cruz, M.A.; Thompson, R.L.; Sampaio, L.E.; Bacchi, R.D. The use of the Reynolds force vector in a physics informed machine learning approach for predictive turbulence modeling. Comput. Fluids 2019, 192, 104258. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Davis, L. Bit-climbing, representational bias, and test suit design. Proc. Int. Conf. Genetic Algorithm 1991, 18–23. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Meyer, K.E.; Pedersen, J.M.; Özcan, O. A turbulent jet in crossflow analysed with proper orthogonal decomposition. J. Fluid Mech. 2007, 583, 199–227. [Google Scholar] [CrossRef]
- Lui, H.F.S.; Wolf, W.R. Construction of reduced-order models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 2019, 872, 963–994. [Google Scholar] [CrossRef]
- Xie, C.; Xiong, X.; Wang, J. Artificial neural network approach for turbulence models: A local framework. Phys. Rev. Fluids 2021, 6, 084612. [Google Scholar] [CrossRef]
- Milani, P.M.; Ling, J.; Eaton, J.K. On the generality of tensor basis neural networks for turbulent scalar flux modeling. Int. Commun. Heat Mass Transf. 2021, 128, 105626. [Google Scholar] [CrossRef]
- Fang, R.; Sondak, D.; Protopapas, P.; Succi, S. Neural network models for the anisotropic Reynolds stress tensor in turbulent channel flow. J. Turbul. 2020, 21, 525–543. [Google Scholar] [CrossRef]
- Berrone, S.; Oberto, D. An invariances-preserving vector basis neural network for the closure of Reynolds-averaged Navier–Stokes equations by the divergence of the Reynolds stress tensor. Phys. Fluids 2022, 34, 095136. [Google Scholar] [CrossRef]
- Frezat, H.; Balarac, G.; Le Sommer, J.; Fablet, R.; Lguensat, R. Physical invariance in neural networks for subgrid-scale scalar flux modeling. Phys. Rev. Fluids 2021, 6, 024607. [Google Scholar] [CrossRef]
- Wang, R.; Walters, R.; Yu, R. Incorporating symmetry into deep dynamics models for improved generalization. arXiv 2020, arXiv:2002.03061. [Google Scholar]
- Wang, R.; Kashinath, K.; Mustafa, M.; Albert, A.; Yu, R. Towards physics-informed deep learning for turbulent flow prediction. Proc. ACM Int. Conf. Knowl Discov Data Min. 2020, 26, 1457–1466. [Google Scholar]
- Li, Z.; Kovachki, N.B.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. Proc. Int. Conf. Learn. Represent. 2021, 9. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Li, Z.; Peng, W.; Yuan, Z.; Wang, J. Fourier neural operator approach to large eddy simulation of three-dimensional turbulence. Theor. App. Mech. Lett. 2022, 12, 100389. [Google Scholar] [CrossRef]
- Li, Y.; Perlman, E.; Wan, M.; Yang, Y.; Meneveau, C.; Burns, R.; Chen, S.; Szalay, A.; Eyink, G. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 2008, 9, N31. [Google Scholar] [CrossRef]
- Eivazi, H.; Vinuesa, R. Physics-informed deep-learning applications to experimental fluid mechanics. arXiv 2022, arXiv:2203.15402. [Google Scholar]
- Jiang, C.M.; Esmaeilzadeh, S.; Azizzadenesheli, K.; Kashinath, K.; Mustafa, M.; Tchelepi, H.A.; Marcus, P.; Prabhat, M.; Anandkumar, A. MESHFREEFLOWNET: A physics-constrained deep continuous space-time super-resolution framework. In Proceedings of the SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, Virtual, 9–19 November 2020; pp. 1–15. [Google Scholar]
- Sun, X.; Cao, W.; Liu, Y.; Zhu, L.; Zhang, W. High Reynolds number airfoil turbulence modeling method based on machine learning technique. Comput. Fluids 2022, 236, 105298. [Google Scholar] [CrossRef]
- Guan, Y.; Subel, A.; Chattopadhyay, A.; Hassanzadeh, P. Learning physics-constrained subgrid-scale closures in the small-data regime for stable and accurate LES. Physica D 2023, 443, 133568. [Google Scholar] [CrossRef]
- Xiao, H.; Wu, J.L.; Laizet, S.; Duan, L. Flows over periodic hills of parameterized geometries: A dataset for data-driven turbulence modeling from direct simulations. Comput. Fluids 2020, 200, 104431. [Google Scholar] [CrossRef]
- Rumsey, C.; Smith, B.; Huang, G. Description of a website resource for turbulence modeling verification and validation. Proc. Fluid Dyn. Conf. Exhib. 2010, 40, 4742. [Google Scholar]
- Eckert, M.L.; Um, K.; Thuerey, N. ScalarFlow: A large-scale volumetric data set of real-world scalar transport flows for computer animation and machine learning. ACM Trans. Graph. 2019, 38, 239. [Google Scholar] [CrossRef]
- Bonnet, F.; Mazari, J.A.; Cinnella, P.; Gallinari, P. AirfRANS: High fidelity computational fluid dynamics dataset for approximating Reynolds-Averaged Navier–Stokes solutions. arXiv 2022, arXiv:2212.07564. [Google Scholar]
- Goldbloom, A.; Hamner, B. Kaggle: Your Machine Learning and Data Science Community. 2010. Available online: https://www.kaggle.com (accessed on 6 February 2023).
- Chung, W.T.; Jung, K.S.; Chen, J.H.; Ihme, M. BLASTNet: A call for community-involved big data in combustion machine learning. Appl. Energy Combust. Sci. 2022, 12, 100087. [Google Scholar] [CrossRef]
- Hennigh, O.; Narasimhan, S.; Nabian, M.A.; Subramaniam, A.; Tangsali, K.; Fang, Z.; Rietmann, M.; Byeon, W.; Choudhry, S. NVIDIA SimNet™: An AI-accelerated multi-physics simulation framework. In Proceedings of the Computational Science–ICCS 2021: 21st International Conference, Krakow, Poland, 16–18 June 2021; pp. 447–461. [Google Scholar]
- Wang, Q.; Ihme, M.; Chen, Y.F.; Anderson, J. A tensorflow simulation framework for scientific computing of fluid flows on tensor processing units. Comput. Phys. Commun. 2022, 274, 108292. [Google Scholar] [CrossRef]
- Bezgin, D.A.; Buhendwa, A.B.; Adams, N.A. JAX-Fluids: A fully-differentiable high-order computational fluid dynamics solver for compressible two-phase flows. Comput. Phys. Commun. 2023, 282, 108527. [Google Scholar] [CrossRef]
- Takamoto, M.; Praditia, T.; Leiteritz, R.; MacKinlay, D.; Alesiani, F.; Pflüger, D.; Niepert, M. PDEBench: An extensive benchmark for scientific machine learning. arXiv 2022, arXiv:2210.07182. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Krishnapriyan, A.; Gholami, A.; Zhe, S.; Kirby, R.; Mahoney, M.W. Characterizing possible failure modes in physics-informed neural networks. Adv. Neural Inf. Process. Syst. 2021, 35, 26548–26560. [Google Scholar]
- Hu, W.; Fey, M.; Zitnik, M.; Dong, Y.; Ren, H.; Liu, B.; Catasta, M.; Leskovec, J. Open graph benchmark: Datasets for machine learning on graphs. Adv. Neural Inf. Process. Syst. 2020, 33, 22118–22133. [Google Scholar]
- Psichogios, D.C.; Ungar, L.H. A hybrid neural network-first principles approach to process modeling. AIChE J. 1992, 38, 1499–1511. [Google Scholar] [CrossRef]
- Moradi, R.; Berangi, R.; Minaei, B. A survey of regularization strategies for deep models. Artif. Intell. Rev. 2020, 53, 3947–3986. [Google Scholar] [CrossRef]
- Standley, T.; Zamir, A.; Chen, D.; Guibas, L.; Malik, J.; Savarese, S. Which tasks should be learned together in multi-task learning? In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020.
- Sener, O.; Koltun, V. Multi-task learning as multi-objective optimization. Adv. Neural Inf. Process. Syst. 2018, 31, 525–536. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neur. Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 10684–10695. [Google Scholar]
- Baddoo, P.J.; Herrmann, B.; McKeon, B.J.; Kutz, J.N.; Brunton, S.L. Physics-informed dynamic mode decomposition (piDMD). arXiv 2021, arXiv:2112.04307. [Google Scholar]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wang, J.X. Physics-informed Dyna-style model-based deep reinforcement learning for dynamic control. Proc. Math. Phys. Eng. Sci. 2021, 477, 20210618. [Google Scholar] [CrossRef]
- Stachenfeld, K.; Fielding, D.B.; Kochkov, D.; Cranmer, M.; Pfaff, T.; Godwin, J.; Cui, C.; Ho, S.; Battaglia, P.; Sanchez-Gonzalez, A. Learned Simulators for Turbulence. Proc. Int. Conf. Learn. Represent. 2022. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Peng, J.Z.; Wang, Y.Z.; Chen, S.; Chen, Z.H.; Wu, W.T.; Aubry, N. Grid adaptive reduced-order model of fluid flow based on graph convolutional neural network. Phys. Fluids 2022, 34, 087121. [Google Scholar] [CrossRef]
- He, X.; Wang, Y.; Li, J. Flow completion network: Inferring the fluid dynamics from incomplete flow information using graph neural networks. Phys. Fluids 2022, 34, 087114. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Proceedings of the Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Hinton, G.E.; van Camp, D. Keeping the neural networks simple by minimizing the description length of the weights. Proc. Annu. Conf. Comput. Learn. Theory 1993, 6, 5–13. [Google Scholar]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comp. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Champion, K.; Lusch, B.; Kutz, J.N.; Brunton, S.L. Data-driven discovery of coordinates and governing equations. Proc. Natl. Acad. Sci. USA 2019, 116, 22445–22451. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, P.; Chung, W.T.; Akoush, B.; Ihme, M. A Review of Physics-Informed Machine Learning in Fluid Mechanics. Energies 2023, 16, 2343. https://doi.org/10.3390/en16052343
Sharma P, Chung WT, Akoush B, Ihme M. A Review of Physics-Informed Machine Learning in Fluid Mechanics. Energies. 2023; 16(5):2343. https://doi.org/10.3390/en16052343
Chicago/Turabian StyleSharma, Pushan, Wai Tong Chung, Bassem Akoush, and Matthias Ihme. 2023. "A Review of Physics-Informed Machine Learning in Fluid Mechanics" Energies 16, no. 5: 2343. https://doi.org/10.3390/en16052343
APA StyleSharma, P., Chung, W. T., Akoush, B., & Ihme, M. (2023). A Review of Physics-Informed Machine Learning in Fluid Mechanics. Energies, 16(5), 2343. https://doi.org/10.3390/en16052343