A Bayesian Optimization-Based LSTM Model for Wind Power Forecasting in the Adama District, Ethiopia
Abstract
1. Introduction
- Bayesian optimization (BO) was employed to identify optimal hyperparameters, such as the number of neurons and activation function, for the purpose of enhancing wind power forecasting.
- The BO-LSTM model proposed in this paper was evaluated using real wind power data and found to outperform baseline methods in terms of statistical error metrics.
- The paper presents a robust BO-LSTM model for day-ahead wind power forecasting, utilizing actual wind power data.
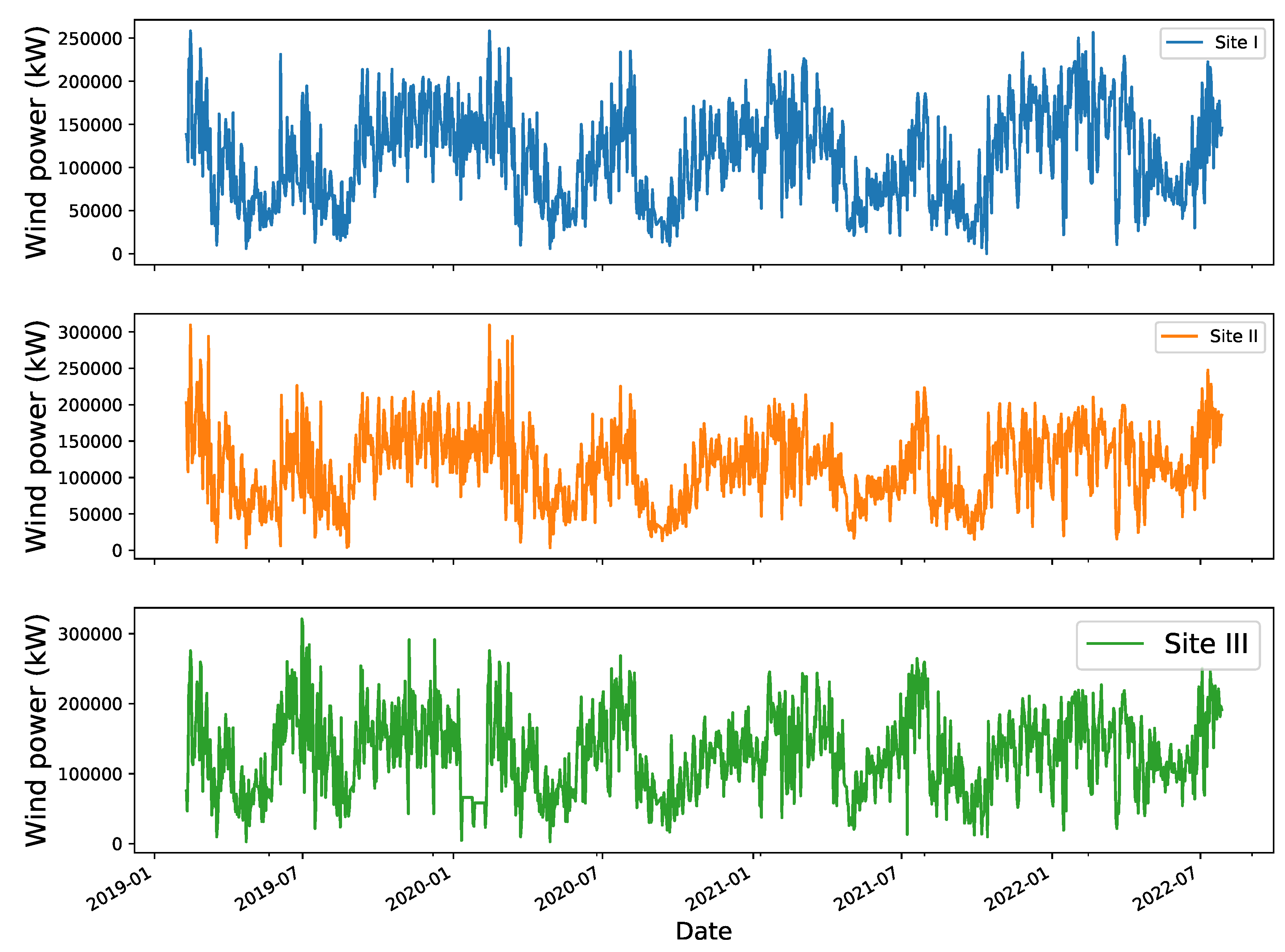
- A wind power dataset was created for the first time in the Adama district of Ethiopia, following a comprehensive and arduous data collection process.
2. Related Works
- Physics-based methods: This approach predicts desired variables using real-time atmospheric variables, such as temperature, pressure, surface roughness, and obstacles. However, it is computationally intensive and may not be suitable for short-term forecasting tasks due to the high computation time and computing resources required [29,30].
- Traditional statistical methods: Autoregressive (AR), autoregressive moving average (ARMA), and autoregressive integrated moving average (ARIMA) models are conventional statistical methods for time series forecasting, and they are effective in capturing linear mathematical relationships in time series data. However, their prediction accuracy decreases for longer forecast horizons, and they struggle to model complex seasonal patterns and exogenous variables [31,32,33]. Nevertheless, the combination of ARIMA and LSTM techniques has resulted in successful approaches in recent years [34].
- Machine learning methods: Machine learning is a data-driven approach that maps between dependent and independent variables and is widely used for classification and prediction tasks [29]. This category includes feed-forward neural networks, support vector regression (SVR), k-nearest neighbor, fuzzy neural networks, extreme learning machines, and others. For example, Ahmed et al. [35] proposed using gradient boosting machines (GBMs) and support vector machines (SVMs) to predict wind power over medium to long-term time frames and found that the SVM model performed better with some computational run-time concerns. Another study proposed a wind turbine power generation prediction model using linear regression, k-nearest neighbor regression, and decision tree regression algorithms to predict one-minute time resolution data [36]. Shabbir et al. [37] used an SVM-based algorithm to predict wind energy production one day ahead, and they found that the proposed algorithms had better forecasting results with the lowest root mean square error (RMSE) values. However, conventional machine learning algorithms may struggle to capture temporal information effectively and produce more accurate forecasts for complex and nonlinear wind power data [38]. In [39], a method was proposed to predict power generation by exploiting wind speed data from different heights in the same area and achieved a 3.1% improvement in accuracy compared to the traditional support vector machine method. Gao proposed an approach based on grey models and machine learning for monthly wind power forecasting using data from China [40]. A hybrid model based on Laguerre polynomials and the multi-objective Runge-Kutta algorithm was proposed in [41] for wind power forecasting, and the effectiveness of the method was demonstrated using wind power data from a Chinese wind farm.
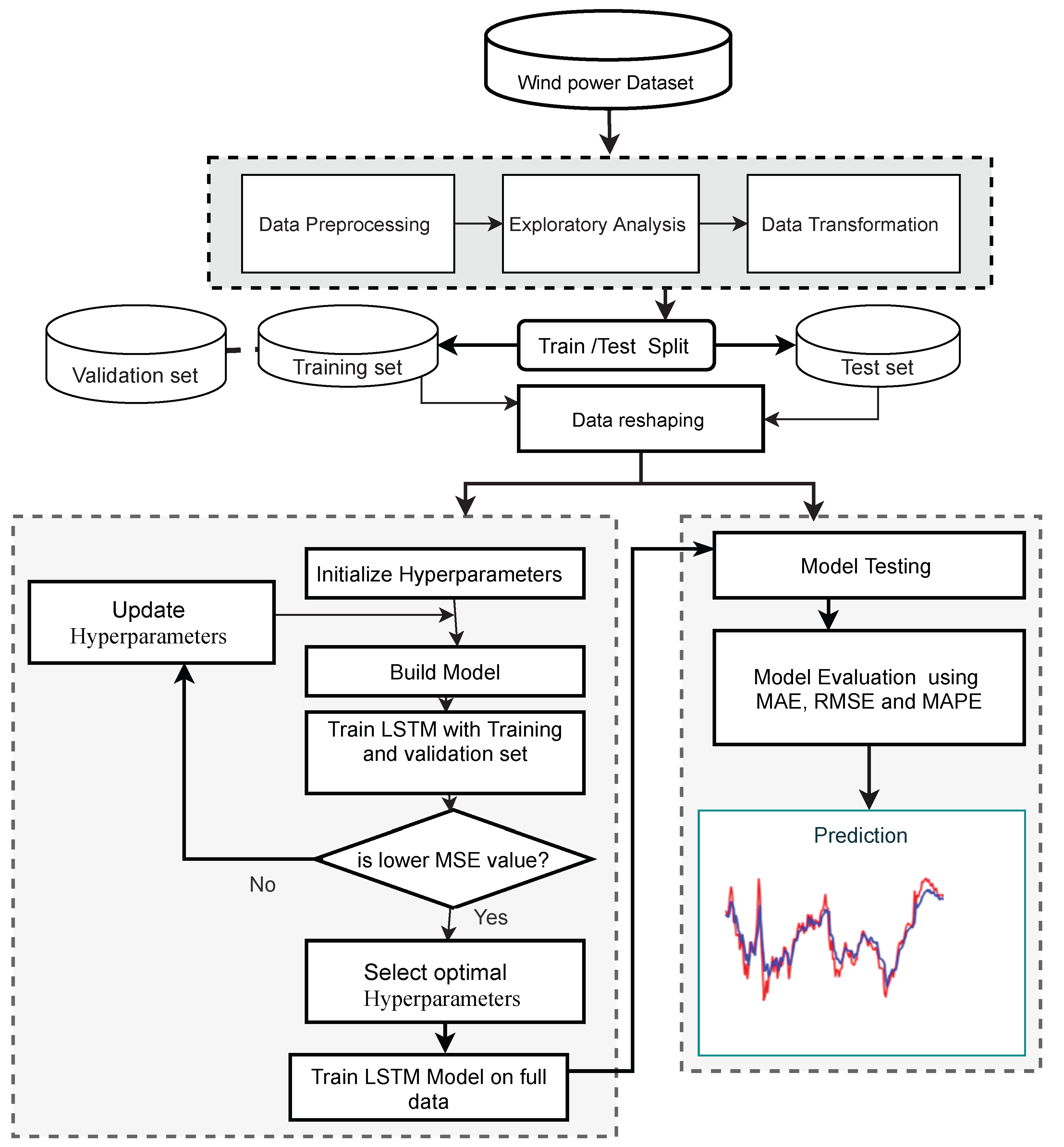
3. Materials and Methods
3.1. Deep Learning Architectures
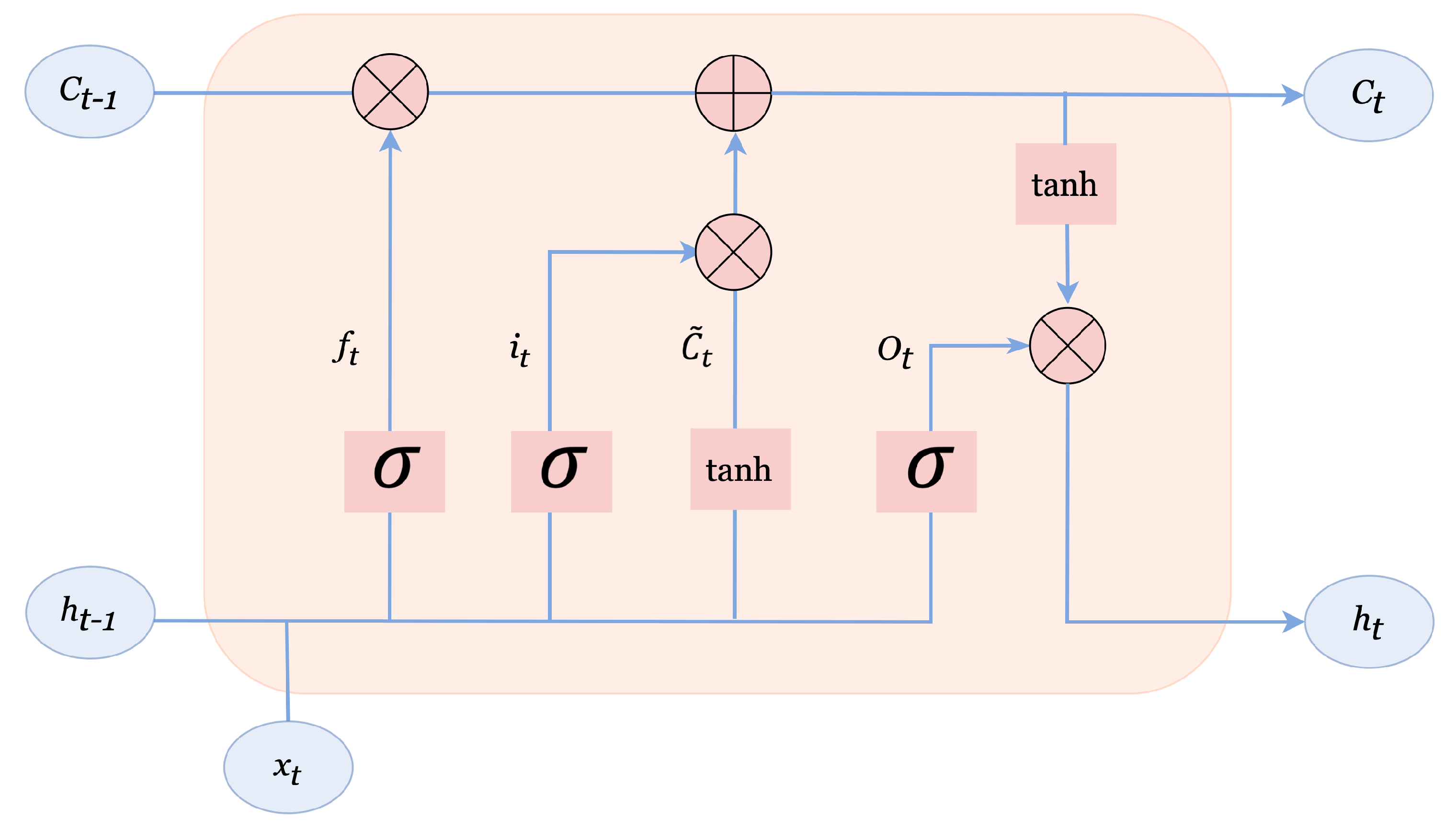
3.1.1. Long-Short Term Memory Network
- Handling long-term dependencies: One of the main challenges in wind energy forecasting is capturing long-term dependencies in the data. LSTMs are particularly well suited for this task because they are designed to handle long-term dependencies by selectively forgetting or retaining information from previous time steps.
- Handling non-linear relationships: Wind energy is affected by many non-linear factors, such as temperature, humidity, and pressure. LSTMs are capable of capturing non-linear relationships in the data, making them a good choice for wind energy forecasting.
- Handling multivariate time series: LSTMs can handle multiple inputs, making them well suited for multivariate time series data, such as wind energy data, which often includes multiple sources of information.
- Good performance: LSTMs have shown good performance in wind energy forecasting tasks, outperforming traditional time series forecasting methods, such as ARIMA and SARIMA.
- Robustness to noise: LSTMs are less sensitive to noise in the data compared to traditional time series methods, making them a good choice for wind energy forecasting where data quality can be a challenge.
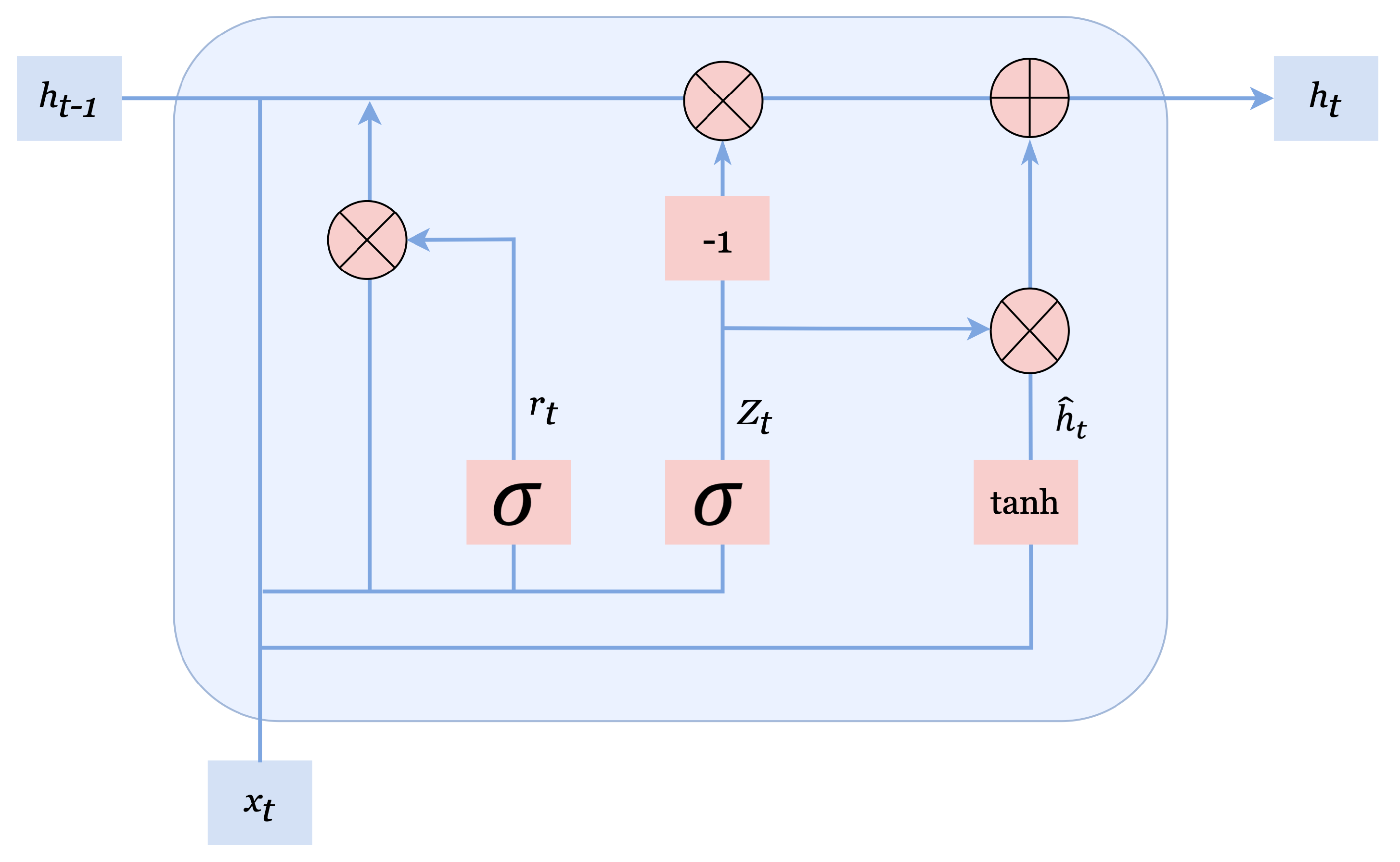
3.1.2. Gated Recurrent Unit Neural Network
3.2. Bayesian Optimization
- Surrogate (probabilistic) model: BO is guided by Bayes’ theorem, and in each iteration, it uses a surrogate model to approximate the objective function, which can be sampled efficiently. A Gaussian process is the most effective surrogate model for selecting the promising set of hyperparameters to be evaluated in the true objective function [74]. The surrogate model estimates the objective function, which is used to guide future sampling.
- Acquisition function: BO uses an acquisition function [75] to determine which points in the search space should be evaluated and to provide information on the optimal value of f. The purpose of the acquisition function is to use posterior information to find the best sample point in each iteration and to propose a new sampling point to identify the most promising set of hyperparameters to be evaluated next. The acquisition function balances exploitation and exploration. Exploitation involves focusing on the search space with a higher likelihood of improving the current solution based on the current surrogate model, while exploration is the strategy of moving towards less explored regions of the search space.
- Efficient hyperparameter tuning: BO provides a more efficient and effective way of tuning the hyperparameters of an LSTM model than traditional grid search or random search methods. It does this by intelligently selecting the next set of hyperparameters to evaluate based on the results of previous evaluations, leading to faster convergence and better results.
- Improved model performance: By tuning the hyperparameters of an LSTM model using BO, the model can be improved to better fit the wind energy data and achieve higher accuracy in its predictions.
- Better understanding of the model: BO can provide insights into the impact of different hyperparameters on the performance of the LSTM model, allowing for better understanding of the model and its behavior.
- Robustness to hyperparameter selection: By using BO to select the hyperparameters, the model can be made more robust to the choice of hyperparameters, reducing the risk of poor performance due to poor hyperparameter selection.
3.3. Data Description
3.4. Data Pre-Processing
3.5. Problem Formulation
3.6. Performance Evaluation
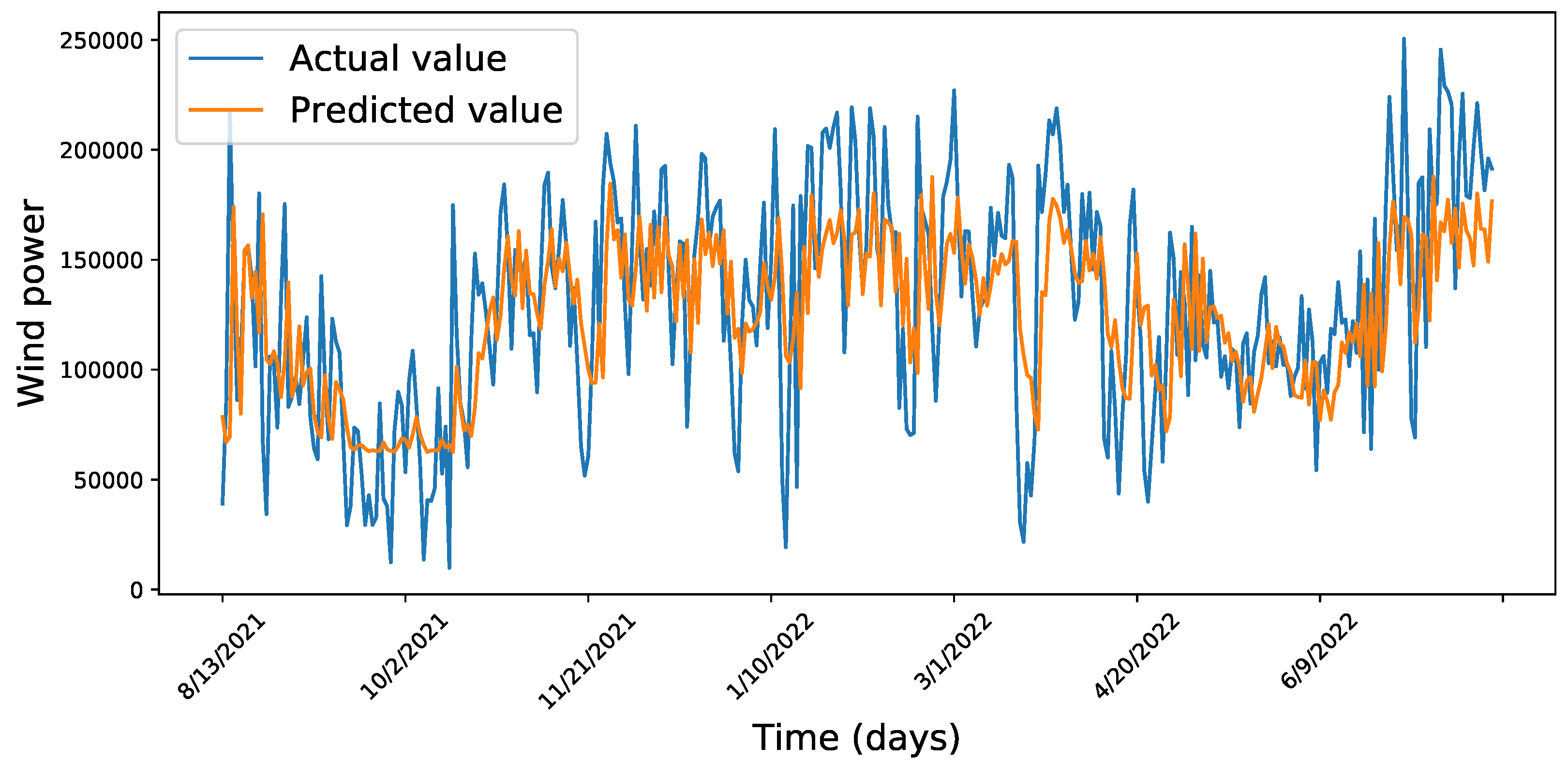
4. Results Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Acronym
| ANN | artificial neural network |
| ARIMA | autoregressive integrative moving average |
| BO-LSTM | Bayesian optimized long short-term memory |
| GRU | gated recurrent unit |
| KNN | K-nearest neighbor |
| LSTM | Long-short term memory |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| RNN | recurrent neural network |
| RMSE | root mean square error |
| SCADA | supervisory control and data acquisition |
| SVM | support vector machine |
References
- Yürek, Ö.; Birant, D.; Yürek, İ. Wind Power Generation Prediction Using Machine Learning Algorithms. Dokuz Eylül Üniversitesi Mühendislik Fakültesi Fen Mühendislik Derg. 2021, 23, 107–119. [Google Scholar]
- Khan, N.; Ullah, F.U.M.; Haq, I.U.; Khan, S.U.; Lee, M.Y.; Baik, S.W. AB-net: A novel deep learning assisted framework for renewable energy generation forecasting. Mathematics 2021, 9, 2456. [Google Scholar] [CrossRef]
- Shahiduzzaman, K.M.; Jamal, M.N.; Nawab, M.R.I. Renewable Energy Production Forecasting: A Comparative Machine Learning Analysis. Int. J. Eng. Adv. Technol. 2021, 10, 11–18. [Google Scholar] [CrossRef]
- Mishra, S.; Bordin, C.; Taharaguchi, K.; Palu, I. Comparison of deep learning models for multivariate prediction of time series wind power generation and temperature. Energy Rep. 2020, 6, 273–286. [Google Scholar] [CrossRef]
- Delgado, I.; Fahim, M. Wind turbine data analysis and LSTM-based prediction in SCADA system. Energies 2020, 14, 125. [Google Scholar] [CrossRef]
- Tiruye, G.A.; Besha, A.T.; Mekonnen, Y.S.; Benti, N.E.; Gebreslase, G.A.; Tufa, R.A. Opportunities and Challenges of Renewable Energy Production in Ethiopia. Sustainability 2021, 13, 10381. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Y.; Liang, L.; Li, X.; Duan, Q. Short-term wind power prediction using GA-BP neural network based on DBSCAN algorithm outlier identification. Processes 2020, 8, 157. [Google Scholar] [CrossRef]
- Prema, V.; Bhaskar, M.S.; Almakhles, D.; Gowtham, N.; Rao, K.U. Critical Review of Data, Models and Performance Metrics for Wind and Solar Power Forecast. IEEE Access 2021, 10, 667–688. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. A novel genetic LSTM model for wind power forecast. Energy 2021, 223, 120069. [Google Scholar] [CrossRef]
- Alkhayat, G.; Mehmood, R. A review and taxonomy of wind and solar energy forecasting methods based on deep learning. Energy AI 2021, 4, 100060. [Google Scholar] [CrossRef]
- Torres, J.F.; Hadjout, D.; Sebaa, A.; Martínez-Álvarez, F.; Troncoso, A. Deep learning for time series forecasting: A survey. Big Data 2021, 9, 3–21. [Google Scholar] [CrossRef]
- Victoria, A.H.; Maragatham, G. Automatic tuning of hyperparameters using Bayesian optimization. Evol. Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Paramasivan, S.K. Deep Learning Based Recurrent Neural Networks to Enhance the Performance of Wind Energy Forecasting: A Review. Rev. d’Intelligence Artif. 2021, 35, 1–10. [Google Scholar] [CrossRef]
- Hossain, M.A.; Chakrabortty, R.K.; Elsawah, S.; Gray, E.M.; Ryan, M.J. Predicting wind power generation using hybrid deep learning with optimization. IEEE Trans. Appl. Supercond. 2021, 31, 0601305. [Google Scholar] [CrossRef]
- Shamshirband, S.; Rabczuk, T.; Chau, K.W. A survey of deep learning techniques: Application in wind and solar energy resources. IEEE Access 2019, 7, 164650–164666. [Google Scholar] [CrossRef]
- Peng, L.; Wang, L.; Xia, D.; Gao, Q. Effective energy consumption forecasting using empirical Wavelet transform and Long Short-Term Memory. Energy 2022, 238, 121756. [Google Scholar] [CrossRef]
- Khalid, R.; Javaid, N. A survey on hyperparameters optimization algorithms of forecasting models in smart grid. Sustain. Cities Soc. 2020, 61, 102275. [Google Scholar] [CrossRef]
- Perrone, V.; Shen, H.; Seeger, M.W.; Archambeau, C.; Jenatton, R. Learning search spaces for bayesian optimization: Another view of hyperparameter transfer learning. Adv. Neural Inf. Process. Syst. 2019, 32, 1–11. [Google Scholar]
- Yue, W.; Liu, Q.; Ruan, Y.; Qian, F.; Meng, H. A prediction approach with mode decomposition-recombination technique for short-term load forecasting. Sustain. Cities Soc. 2022, 85, 104034. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Shekhar, S.; Bansode, A.; Salim, A. A Comparative study of Hyper-Parameter Optimization Tools. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Brisbane, Australia, 8–10 December 2021; pp. 1–6. [Google Scholar]
- Blanchard, A.; Sapsis, T. Bayesian optimization with output-weighted optimal sampling. J. Comput. Phys. 2021, 425, 109901. [Google Scholar] [CrossRef]
- Yang, Y.; Haq, E.U.; Jia, Y. A Novel Deep Learning Approach for Short and Medium-Term Electrical Load Forecasting Based on Pooling LSTM-CNN Model. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–15 July 2020; pp. 26–34. [Google Scholar]
- Li, C.; Tang, G.; Xue, X.; Saeed, A.; Hu, X. Short-term wind speed interval prediction based on ensemble GRU model. IEEE Trans. Sustain. Energy 2019, 11, 1370–1380. [Google Scholar] [CrossRef]
- Kedia, A.; Sanyal, A.; Gogoi, A.; Kumar, A.; Goswani, A.K.; Tiwari, P.K.; Choudhury, N.B.D. Wind Power Uncertainties Forecasting based on Long Short Term Memory Model for Short-Term Power Market. In Proceedings of the 2020 IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bilaspur, India, 19–22 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Abdeltawab, H.; Mohamed, Y.A.R.I. Hybrid deep learning-based model for wind speed forecasting based on DWPT and bidirectional LSTM network. IEEE Access 2020, 8, 229219–229232. [Google Scholar] [CrossRef]
- Hossain, M.A.; Chakrabortty, R.K.; Elsawah, S.; Ryan, M.J. Very short-term forecasting of wind power generation using hybrid deep learning model. J. Clean. Prod. 2021, 296, 126564. [Google Scholar] [CrossRef]
- Chen, H.; Birkelund, Y.; Zhang, Q. Data-augmented sequential deep learning for wind power forecasting. Energy Convers. Manag. 2021, 248, 114790. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Fang, S.; Hou, Z. A novel hybrid model based on nonlinear weighted combination for short-term wind power forecasting. Int. J. Electr. Power Energy Syst. 2022, 134, 107452. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Zhang, Y.; Huang, C.; Wang, L. Short-term wind speed forecasting based on information of neighboring wind farms. IEEE Access 2020, 8, 16760–16770. [Google Scholar] [CrossRef]
- Khodayar, M.; Wang, J. Spatio-Temporal Graph Deep Neural Network for Short-Term Wind Speed Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 670–681. [Google Scholar] [CrossRef]
- Optis, M.; Perr-Sauer, J. The importance of atmospheric turbulence and stability in machine-learning models of wind farm power production. Renew. Sustain. Energy Rev. 2019, 112, 27–41. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 2021, 304, 117766. [Google Scholar] [CrossRef]
- Ju, J.; Liu, K.; Liu, F. Prediction of SO2 Concentration Based on AR-LSTM Neural Network. Neural Process. Lett. 2022. [Google Scholar] [CrossRef]
- Ahmed, S.I.; Ranganathan, P.; Salehfar, H. Forecasting of Mid-and Long-Term Wind Power Using Machine Learning and Regression Models. In Proceedings of the 2021 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 19–20 April 2021; pp. 1–6. [Google Scholar]
- Eyecioglu, O.; Hangun, B.; Kayisli, K.; Yesilbudak, M. Performance comparison of different machine learning algorithms on the prediction of wind turbine power generation. In Proceedings of the 2019 8th IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 922–926. [Google Scholar]
- Shabbir, N.; AhmadiAhangar, R.; Kütt, L.; Iqbal, M.N.; Rosin, A. Forecasting short term wind energy generation using machine learning. In Proceedings of the 2019 IEEE 60th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 7–9 October 2019; pp. 1–4. [Google Scholar]
- Wei, D.; Wang, J.; Niu, X.; Li, Z. Wind speed forecasting system based on gated recurrent units and convolutional spiking neural networks. Appl. Energy 2021, 292, 116842. [Google Scholar] [CrossRef]
- Qiao, L.; Chen, S.; Bo, J.; Liu, S.; Ma, G.; Wang, H.; Yang, J. Wind power generation forecasting and data quality improvement based on big data with multiple temporal-spatial scale. In Proceedings of the IEEE International Conference on Energy Internet, Nanjing, China, 27–31 May 2019; pp. 554–559. [Google Scholar]
- Gao, X. Monthly Wind Power Forecasting: Integrated Model Based on Grey Model and Machine Learning. Sustainability 2022, 14, 15403. [Google Scholar] [CrossRef]
- Ye, J.; Xie, L.; Ma, L.; Bian, Y.; Xu, X. A novel hybrid model based on Laguerre polynomial and multi-objective Runge–Kutta algorithm for wind power forecasting. Int. J. Electr. Power Energy Syst. 2023, 146, 108726. [Google Scholar] [CrossRef]
- Peng, X.; Wang, H.; Lang, J.; Li, W.; Xu, Q.; Zhang, Z.; Cai, T.; Duan, S.; Liu, F.; Li, C. EALSTM-QR: Interval wind-power prediction model based on numerical weather prediction and deep learning. Energy 2021, 220, 119692. [Google Scholar] [CrossRef]
- Wang, R.; Li, C.; Fu, W.; Tang, G. Deep learning method based on gated recurrent unit and variational mode decomposition for short-term wind power interval prediction. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3814–3827. [Google Scholar] [CrossRef]
- Afrasiabi, M.; Mohammadi, M.; Rastegar, M.; Afrasiabi, S. Advanced deep learning approach for probabilistic wind speed forecasting. IEEE Trans. Ind. Inform. 2020, 17, 720–727. [Google Scholar] [CrossRef]
- Yu, R.; Gao, J.; Yu, M.; Lu, W.; Xu, T.; Zhao, M.; Zhang, J.; Zhang, R.; Zhang, Z. LSTM-EFG for wind power forecasting based on sequential correlation features. Future Gener. Comput. Syst. 2019, 93, 33–42. [Google Scholar] [CrossRef]
- Basu, S.; Watson, S.J.; Arends, E.L.; Cheneka, B. Day-ahead Wind Power Predictions at Regional Scales: Post-processing Operational Weather Forecasts with a Hybrid Neural Network. In Proceedings of the 2020 17th IEEE International Conference on the European Energy Market (EEM), Stockholm, Sweden, 16–18 September 2020; pp. 1–6. [Google Scholar]
- Meng, X.; Wang, R.; Zhang, X.; Wang, M.; Ma, H.; Wang, Z. Hybrid Neural Network Based on GRU with Uncertain Factors for Forecasting Ultra-short-term Wind Power. In Proceedings of the 2020 IEEE 2nd International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 23–25 October 2020; pp. 1–6. [Google Scholar]
- Wang, H.K.; Song, K.; Cheng, Y. A Hybrid Forecasting Model Based on CNN and Informer for Short-Term Wind Power. Front. Energy Res. 2022, 9, 1041. [Google Scholar] [CrossRef]
- Lv, J.; Zheng, X.; Pawlak, M.; Mo, W.; Miśkowicz, M. Very short-term probabilistic wind power prediction using sparse machine learning and nonparametric density estimation algorithms. Renew. Energy 2021, 177, 181–192. [Google Scholar] [CrossRef]
- Akbal, Y.; Ünlü, K.D. A univariate time series methodology based on sequence-to-sequence learning for short to midterm wind power production. Renew. Energy 2022, 200, 832–844. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Yao, J.; Cai, Z.; Han, G.; Xie, X. Ultra-short-term Forecasting Method of Wind Power Based on W-BiLSTM. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Xia, M.; Shao, H.; Ma, X.; de Silva, C.W. A Stacked GRU-RNN-Based Approach for Predicting Renewable Energy and Electricity Load for Smart Grid Operation. IEEE Trans. Ind. Inform. 2021, 17, 7050–7059. [Google Scholar] [CrossRef]
- Putz, D.; Gumhalter, M.; Auer, H. A novel approach to multi-horizon wind power forecasting based on deep neural architecture. Renew. Energy 2021, 178, 494–505. [Google Scholar] [CrossRef]
- Lin, W.H.; Wang, P.; Chao, K.M.; Lin, H.C.; Yang, Z.Y.; Lai, Y.H. Wind power forecasting with deep learning networks: Time-series forecasting. Appl. Sci. 2021, 11, 10335. [Google Scholar] [CrossRef]
- Prema, V.; Sarkar, S.; Rao, K.U.; Umesh, A. LSTM based Deep Learning model for accurate wind speed prediction. Data Sci. Mach. Learn 2019, 1, 6–11. [Google Scholar]
- Yi, L.; Sun, H.; Qiu, D.; Chen, Z.; Chang, F.; Zhao, J. Short-term Wind Power Forecasting with Evolutionary Deep Learning. In Proceedings of the 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2019; pp. 1508–1513. [Google Scholar]
- Dehnavi, S.D.; Shirani, A.; Mehrjerdi, H.; Baziar, M.; Chen, L. New Deep Learning-Based Approach for Wind Turbine Output Power Modeling and Forecasting. IEEE Trans. Ind. Appl. 2020. [Google Scholar] [CrossRef]
- Akash, R.; Rangaraj, A.; Meenal, R.; Lydia, M. Machine learning based univariate models for long term wind speed forecasting. In Proceedings of the 2020 IEEE International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–28 February 2020; pp. 779–784. [Google Scholar]
- Rahaman, H.; Bashar, T.R.; Munem, M.; Hasib, M.H.H.; Mahmud, H.; Alif, A.N. Bayesian Optimization Based ANN Model for Short Term Wind Speed Forecasting in Newfoundland, Canada. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Virtual, 22–31 October 2020; pp. 1–5. [Google Scholar]
- Saini, V.K.; Bhardwaj, B.; Gupta, V.; Kumar, R.; Mathur, A. Gated Recurrent Unit (GRU) Based Short Term Forecasting for Wind Energy Estimation. In Proceedings of the 2020 IEEE International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 10–11 December 2020; pp. 1–6. [Google Scholar]
- Wu, L.; Kong, C.; Hao, X.; Chen, W. A short-term load forecasting method based on GRU-CNN hybrid neural network model. Math. Probl. Eng. 2020, 2020, 1428104. [Google Scholar] [CrossRef]
- Yang, J.; Tan, K.K.; Santamouris, M.; Lee, S.E. Building energy consumption raw data forecasting using data cleaning and deep recurrent neural networks. Buildings 2019, 9, 204. [Google Scholar] [CrossRef]
- Hadjout, D.; Torres, J.F.; Troncoso, A.; Sebaa, A.; Martínez-Álvarez, F. Electricity consumption forecasting based on ensemble deep learning with application to the Algerian market. Energy 2022, 243, 123060. [Google Scholar] [CrossRef]
- Saini, V.K.; Kumar, R.; Mathur, A.; Saxena, A. Short term forecasting based on hourly wind speed data using deep learning algorithms. In Proceedings of the 2020 3rd IEEE International Conference on Emerging Technologies in Computer Engineering: Machine Learning and Internet of Things (ICETCE), Jaipur, India, 7–8 February 2020; pp. 1–6. [Google Scholar]
- Rafi, S.H.; Deeba, S.R.; Hossain, E. A short-term load forecasting method using integrated CNN and LSTM network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Rafi, S.H. Highly Efficient Short Term Load Forecasting Scheme Using Long Short Term Memory Network. In Proceedings of the 2020 8th IEEE International Electrical Engineering Congress (iEECON), Chiang Mai, Thailand, 4–6 March 2020; pp. 1–4. [Google Scholar]
- Bui, K.T.T.; Torres, J.F.; Gutiérrez-Avilés, D.; Nhu, V.H.; Martínez-Álvarez, F.; Bui, D.T. Deformation forecasting of a hydropower dam by hybridizing a Long Short-Term Memory deep learning network with the Coronavirus Optimization Algorithm. Comput.-Aided Civ. Infrastruct. Eng. 2021, 37, 1368–1386. [Google Scholar] [CrossRef]
- Torres, J.F.; Martínez-Álvarez, F.; Troncoso, A. A deep LSTM network for the Spanish electricity consumption forecasting. Neural Comput. Appl. 2022, 34, 10533–10545. [Google Scholar] [CrossRef]
- Rahman, M.O.; Hossain, M.S.; Junaid, T.S.; Forhad, M.S.A.; Hossen, M.K. Predicting prices of stock market using gated recurrent units (GRUs) neural networks. Int. J. Comput. Sci. Netw. Secur 2019, 19, 213–222. [Google Scholar]
- Zhou, X.; Xu, J.; Zeng, P.; Meng, X. Air pollutant concentration prediction based on GRU method. J. Phys. Conf. Ser. 2019, 1168, 032058. [Google Scholar]
- Liu, H.; Shen, L. Forecasting carbon price using empirical wavelet transform and gated recurrent unit neural network. Carbon Manag. 2020, 11, 25–37. [Google Scholar] [CrossRef]
- Yang, T.; Li, B.; Xun, Q. LSTM-attention-embedding model-based day-ahead prediction of photovoltaic power output using Bayesian optimization. IEEE Access 2019, 7, 171471–171484. [Google Scholar] [CrossRef]
- Jiménez-Navarro, M.J.; Martínez-Álvarez, F.; Troncoso, A.; Asencio-Cortés, G. HLNet: A Novel Hierarchical Deep Neural Network for Time Series Forecasting. Adv. Intell. Syst. Comput. 2021, 1401, 717–727. [Google Scholar]
- Abdalla, E.M.H.; Pons, V.; Stovin, V.; De-Ville, S.; Fassman-Beck, E.; Alfredsen, K.; Muthanna, T.M. Evaluating different machine learning methods to simulate runoff from extensive green roofs. Hydrol. Earth Syst. Sci. 2021, 25, 5917–5935. [Google Scholar] [CrossRef]
- Sultana, N.; Hossain, S.; Almuhaini, S.H.; Düştegör, D. Bayesian Optimization Algorithm-Based Statistical and Machine Learning Approaches for Forecasting Short-Term Electricity Demand. Energies 2022, 15, 3425. [Google Scholar] [CrossRef]

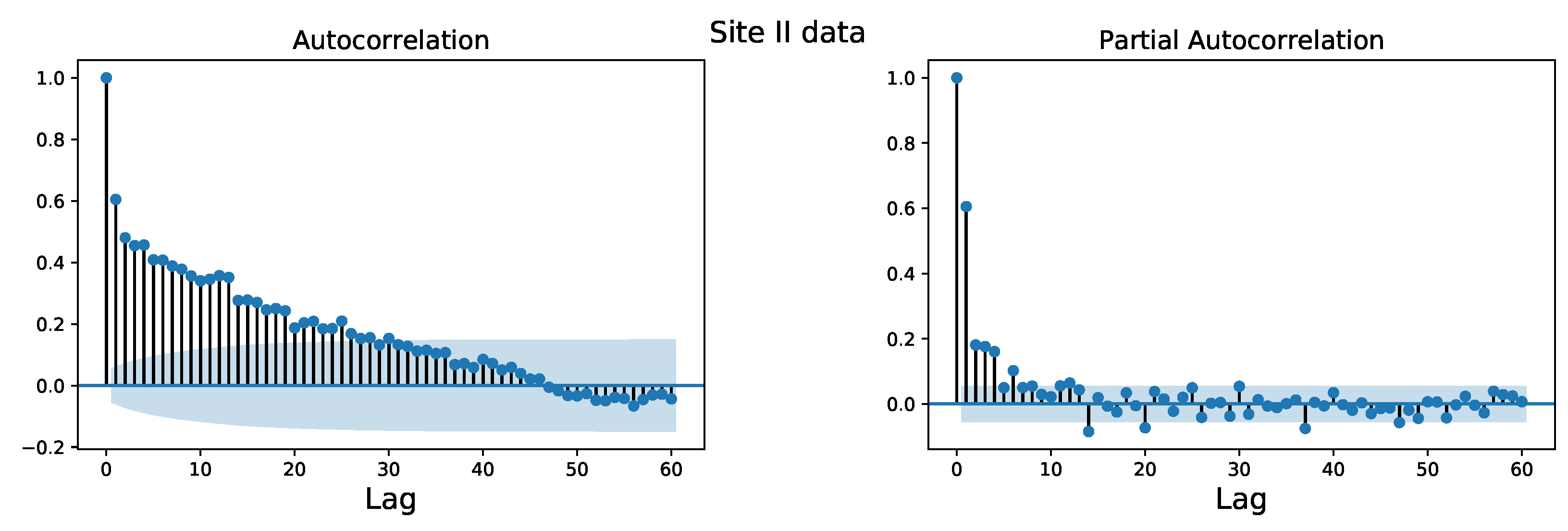

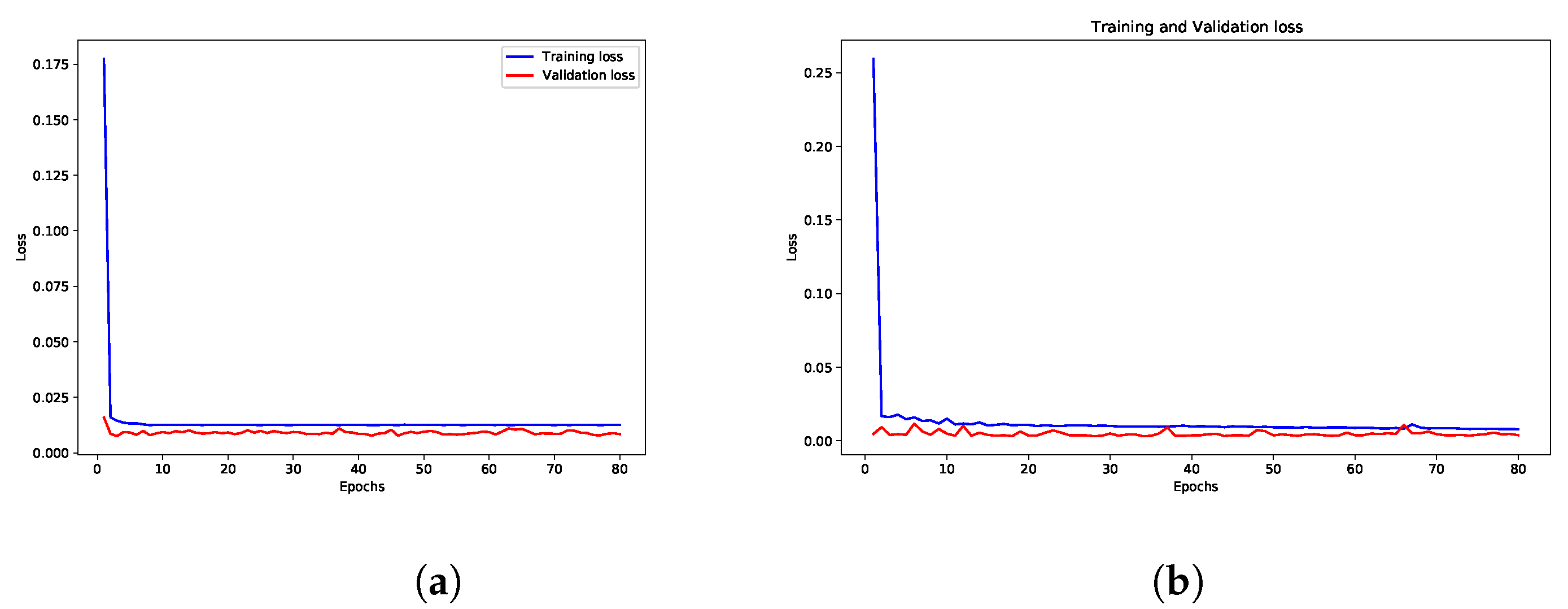
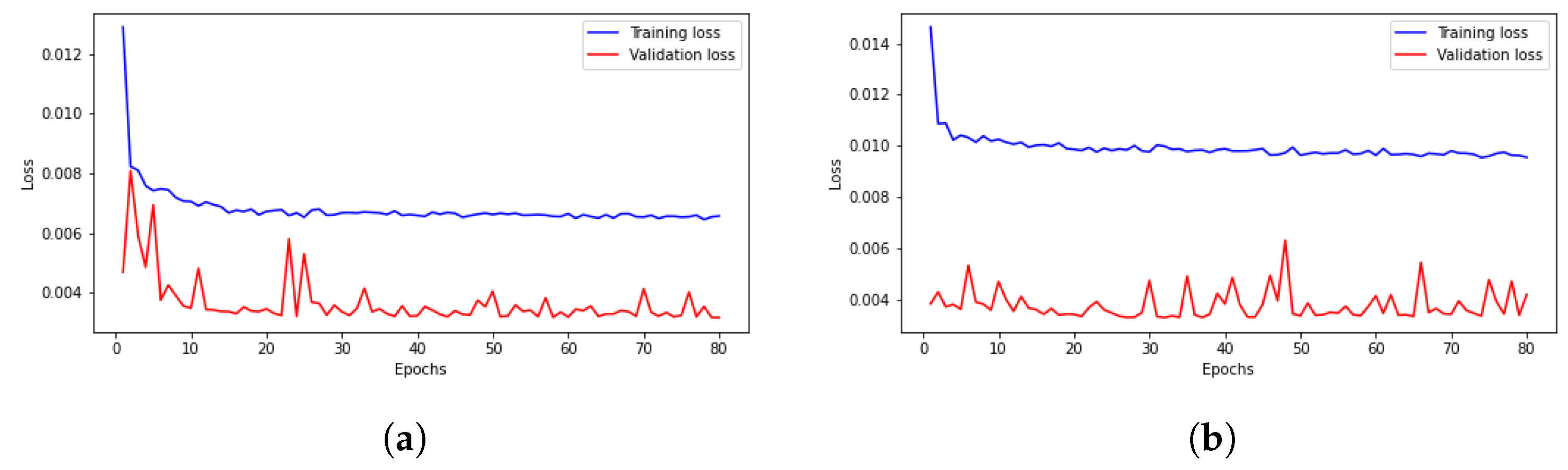

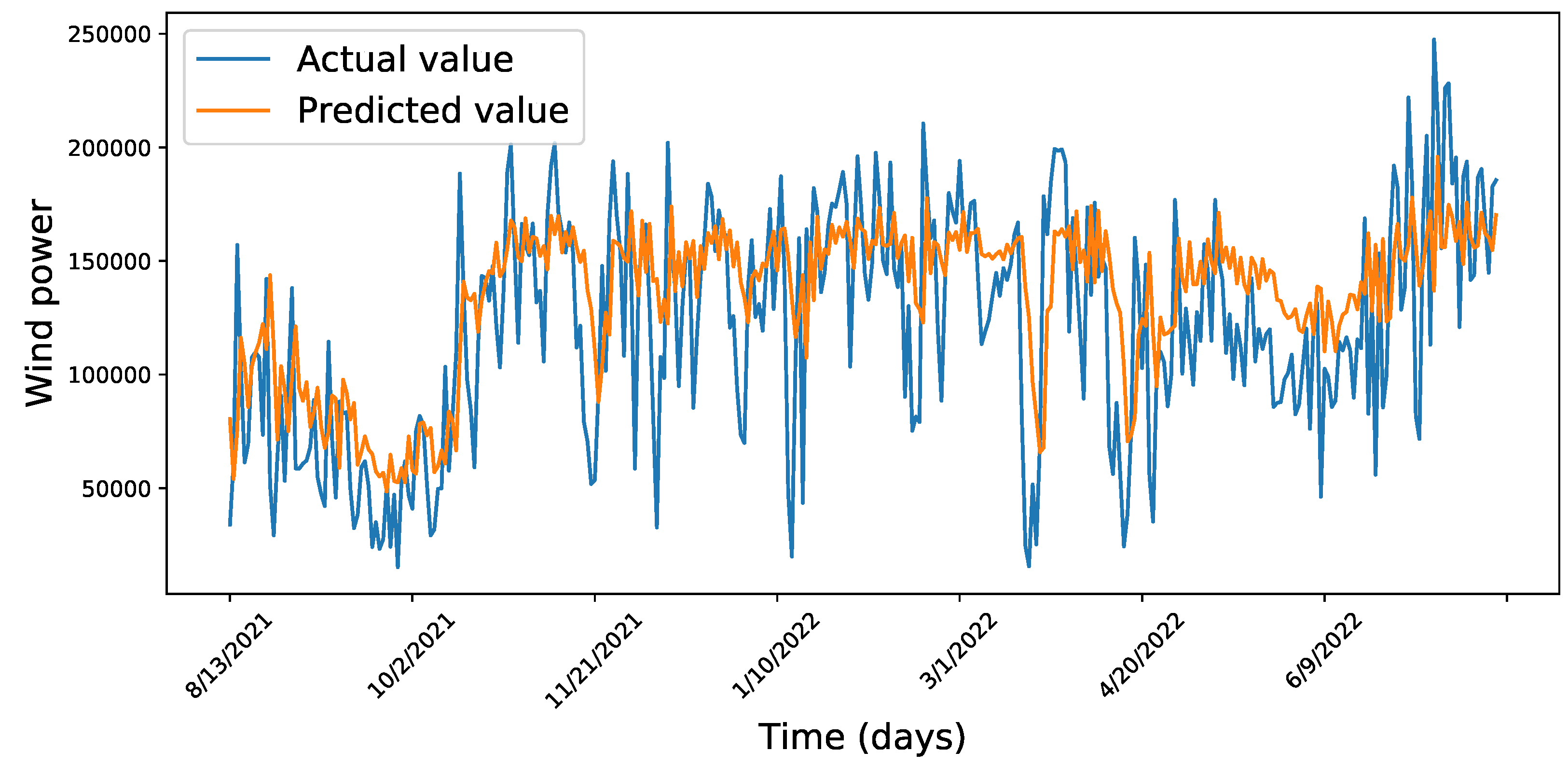
| Hyperparameters | Range Values | Optimal Parameters Selected by Bayesian Optimization |
|---|---|---|
| Learning rate | 0.01 | |
| Epochs | 80 | |
| Batch size | 32 | |
| Dropout | 0.2 | |
| Activation function | tanh | |
| Optimizer | RMSprop | |
| Neurons |
| Models | Parameters | Values/Type |
|---|---|---|
| ANN | Epoch | 4 |
| Learning rate | 0.001 | |
| Batch size | 32 | |
| Neuron at hidden layer | 20 | |
| Optimizer | Adam | |
| Activation function | ReLu | |
| XGBoost | n_estimators | 116 |
| Learning rate | 0.3 | |
| max_depth | 3 | |
| gamma | 5 | |
| min_child_weight | 6 | |
| colsample_bytree | 0.6 | |
| ARIMA | P | 4 |
| d | 0 | |
| q | 1 | |
| GRU | Learning _rate | 0.0001 |
| Batch size | 32 | |
| Epoch | 80 | |
| Neuron at hidden layers | 100, 20 | |
| Dropout_rate | 0.1 | |
| Activation function | ReLu | |
| Optimizer | Adam | |
| LSTM | Learning_rate | 0.001 |
| Batch size | 32 | |
| Neuron at hidden layer | 20 | |
| Activation function | ReLu | |
| Optimizer | Adam |
| Data | Models | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| Site I | ANN | 0.1009 | 0.1310 | 0.916 |
| XGBoost | 0.1312 | 0.1664 | 1.3737 | |
| ARIMA | 0.1939 | 0.2277 | 1.8680 | |
| LSTM | 0.1070 | 0.1264 | 2.0642 | |
| BO-GRU | 0.0651 | 0.0826 | 1.1470 | |
| BO-LSTM | 0.0621 | 0.0793 | 1.1353 | |
| Site II | ANN | 0.1024 | 0.1307 | 2.4062 |
| XGBoost | 0.1489 | 0.1926 | 1.7796 | |
| ARIMA | 0.1844 | 0.2214 | 2.2057 | |
| LSTM | 0.1137 | 0.1399 | 1.1725 | |
| BO-GRU | 0.0707 | 0.0910 | 1.1621 | |
| BO-LSTM | 0.0708 | 0.0893 | 1.2275 | |
| Site III | ANN | 0.1440 | 0.1791 | 1.9741 |
| XGBoost | 0.1452 | 0.1878 | 1.6768 | |
| ARIMA | 0.1748 | 0.2106 | 2.1963 | |
| LSTM | 0.1137 | 0.1401 | 1.1903 | |
| BO-GRU | 0.0972 | 0.1247 | 1.0896 | |
| BO-LSTM | 0.0948 | 0.1220 | 1.0674 |
| Dataset | Models | Training | Testing | ||
|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | ||
| Site I | LSTM | 0.0909 | 0.1167 | 0.1118 | 0.1371 |
| GRU | 0.0825 | 0.1046 | 0.1004 | 0.1205 | |
| BO-GRU | 0.0611 | 0.0807 | 0.0693 | 0.0881 | |
| BO-LSTM | 0.0590 | 0.0782 | 0.0627 | 0.0800 | |
| Site II | LSTM | 0.0848 | 0.1104 | 0.0950 | 0.1146 |
| GRU | 0.0875 | 0.1142 | 0.0970 | 0.1163 | |
| BO-GRU | 0.0714 | 0.0967 | 0.0775 | 0.0989 | |
| BO-LSTM | 0.0689 | 0.0956 | 0.0741 | 0.0930 | |
| Site III | LSTM | 0.1167 | 0.1461 | 0.1095 | 0.1386 |
| GRU | 0.1219 | 0.1505 | 0.1088 | 0.1363 | |
| BO-GRU | 0.1063 | 0.1377 | 0.0993 | 0.1274 | |
| BO-LSTM | 0.1032 | 0.1352 | 0.0986 | 0.1258 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habtemariam, E.T.; Kekeba, K.; Martínez-Ballesteros, M.; Martínez-Álvarez, F. A Bayesian Optimization-Based LSTM Model for Wind Power Forecasting in the Adama District, Ethiopia. Energies 2023, 16, 2317. https://doi.org/10.3390/en16052317
Habtemariam ET, Kekeba K, Martínez-Ballesteros M, Martínez-Álvarez F. A Bayesian Optimization-Based LSTM Model for Wind Power Forecasting in the Adama District, Ethiopia. Energies. 2023; 16(5):2317. https://doi.org/10.3390/en16052317
Chicago/Turabian StyleHabtemariam, Ejigu Tefera, Kula Kekeba, María Martínez-Ballesteros, and Francisco Martínez-Álvarez. 2023. "A Bayesian Optimization-Based LSTM Model for Wind Power Forecasting in the Adama District, Ethiopia" Energies 16, no. 5: 2317. https://doi.org/10.3390/en16052317
APA StyleHabtemariam, E. T., Kekeba, K., Martínez-Ballesteros, M., & Martínez-Álvarez, F. (2023). A Bayesian Optimization-Based LSTM Model for Wind Power Forecasting in the Adama District, Ethiopia. Energies, 16(5), 2317. https://doi.org/10.3390/en16052317







