New Method of Modeling Daily Energy Consumption
Abstract
1. Introduction
1.1. Forecasting Techniques
1.1.1. Linear Regression
1.1.2. Artificial Neural Networks
1.1.3. Time-Series Forecasting
1.2. Methodologies
1.2.1. Similar Day Methods
1.2.2. Variable Selection
1.2.3. Hierarchical Forecasting
2. The Data
3. Model Construction and Evaluation
3.1. The Model
3.2. Model Construction
3.3. Statistical Evaluation of the Model
4. Testing the Model
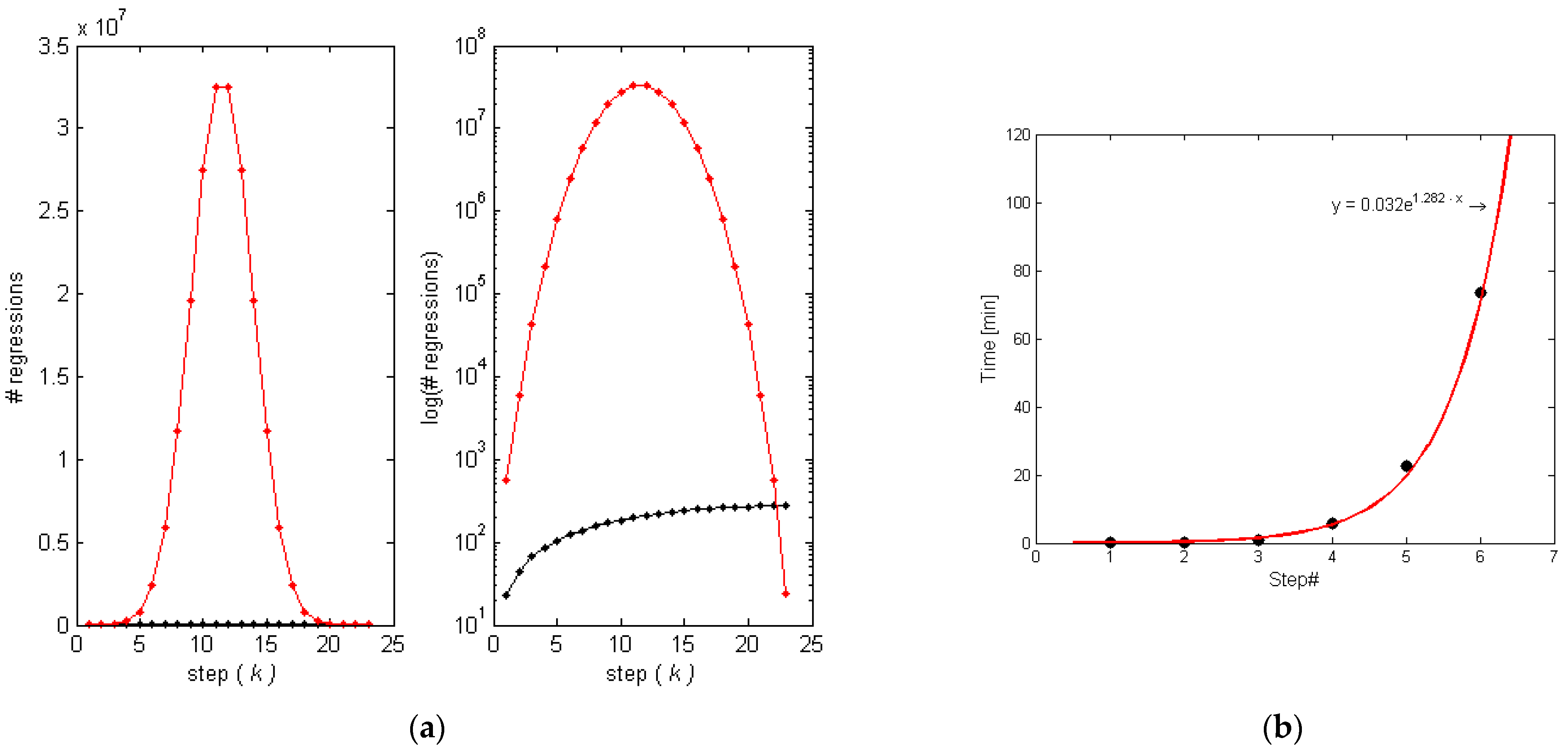
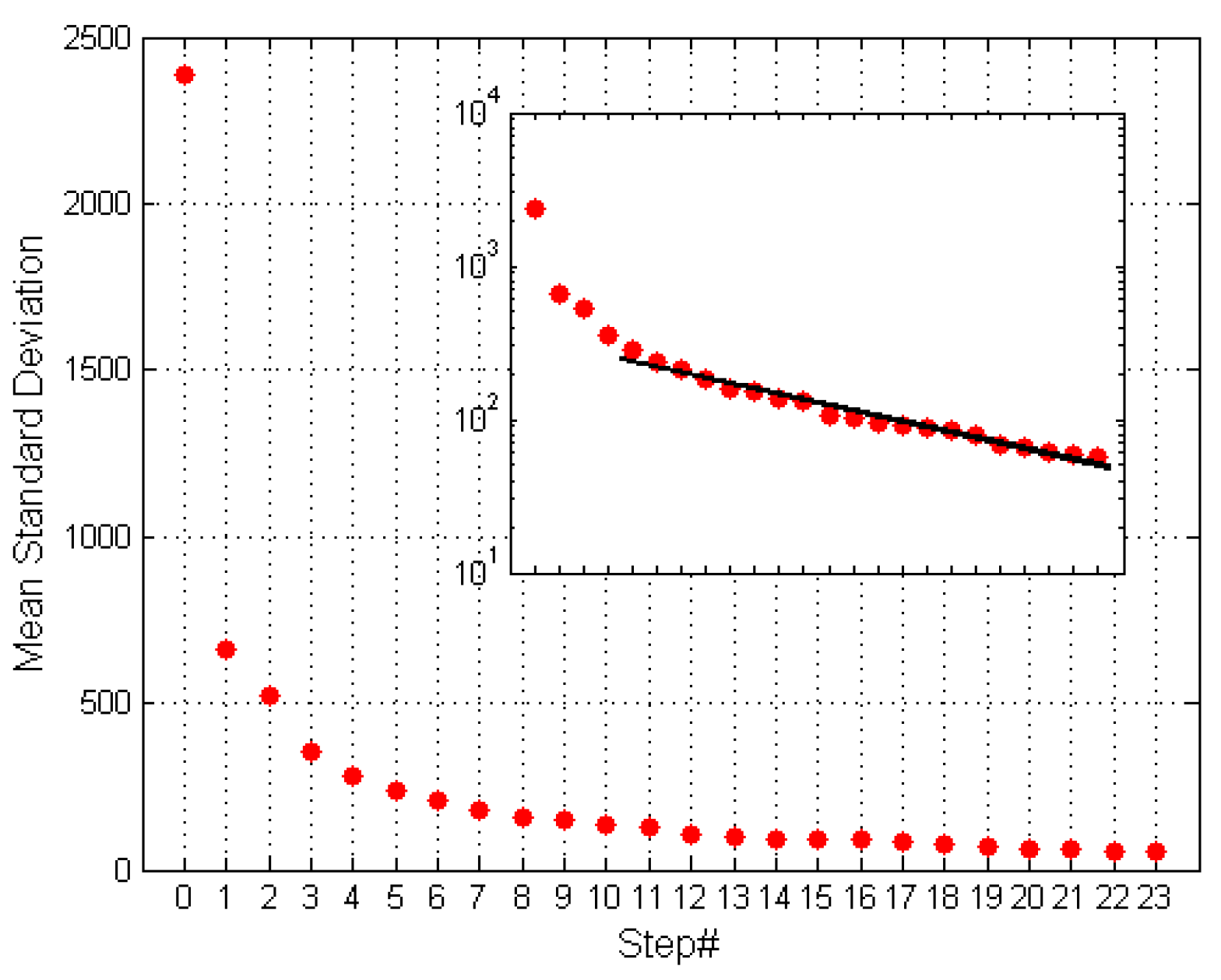
4.1. Choosing the Optimal Model
4.2. Testing the Optimal Model
4.3. Typical Days and Outliners
- First Thursday of March;
- First day of school holidays;
- Last Monday of school holidays;
- Tuesday in the middle of October;
- Friday in the middle of January;
- Christmas;
- First Wednesday of December.
5. Discussion
5.1. Novelty of the Presented Approach
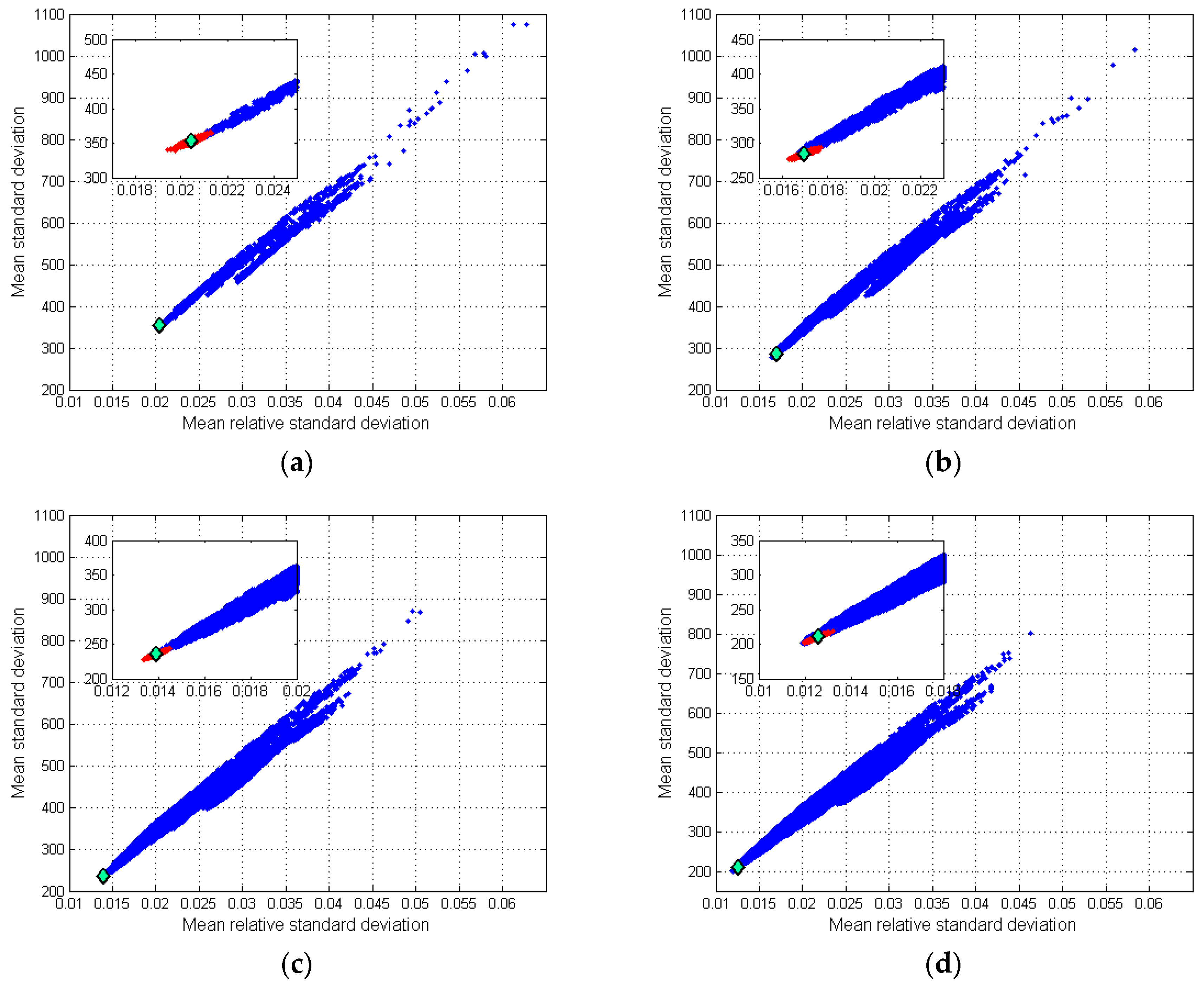
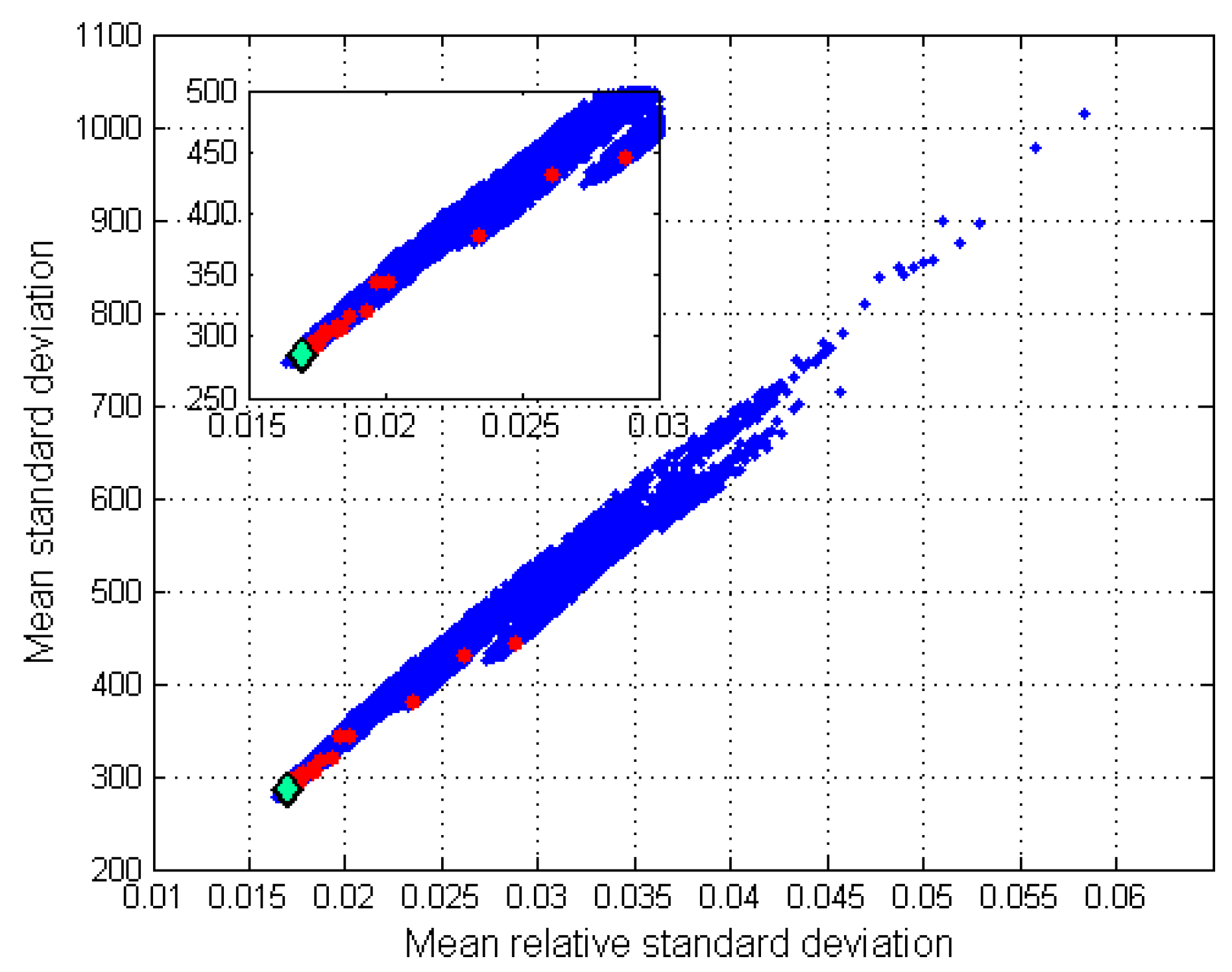
5.2. Selection of the Best Variable Set
5.3. The Issue of Overfitting
6. Summary
- All the model equations are statistically significant and the agreement with empirical data is very high. In the first step, the relative error of the model does not exceed 7% and decreases to below 3% in step 4.
- For approximately 71% of equations, the residual distribution is fully compatible with a Gaussian distribution. The observed differences in the remaining cases are very small.
- When compared to the standard approach based on the analysis of all possible combinations of describing hours, the model yields the best result.
- The algorithm is very fast. With limited computation power it detects the optimal describing variables, and calculates the parameters of the model.
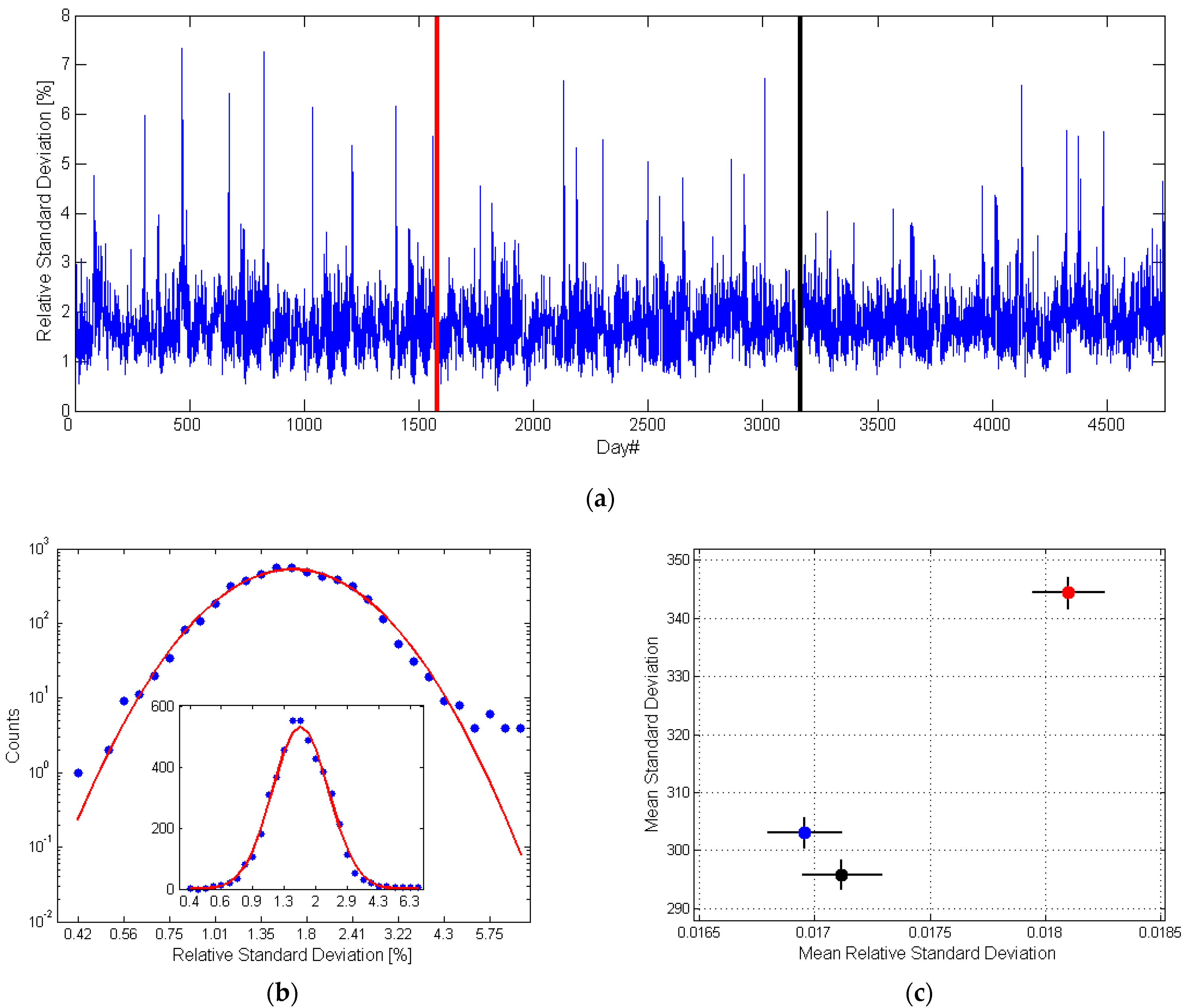
- Only four hours are sufficient to describe the energy consumption for the remaining hours with high precision. We obtained a mean relative uncertainty of 1.72% in the learning data set, and 1.69% and 1.82% in the two testing data sets.
- The highest daily errors of the model do not exceed 7.5%, but the majority of days are described with an uncertainty better than 2.5%.
- Days for which the model has the highest uncertainty, greater than 5%, are public holidays in Poland. They exhibit nontypical energy consumption.
- The detection of days with nontypical energy consumption. The values of the model quality measures are high for such days. Detecting these days is critical, not only for forecasting purposes, but also for optimizing the energy supplier system.
- The classification of days based on the energy consumption profile is another issue that is of great interest. On the other hand, the classification and clustering of the daily energy consumption require the consideration of 24 variables. The proposed method allows for a significant reduction of the space dimension.
- The standard methods of long-term forecasting deal with the forecasting of energy consumption, which exhibits strong daily periodicity. At the same time, forecasting energy consumption at separate hours allows for the elimination of problems arising from such periodicity. The model will allow for the reconstruction of the energy consumption for the entire day based on the forecasted energy demand for only a few hours.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alfares, H.K.; Nazeeruddin, M. Electric load forecasting: Literature survey and classification of methods. Int. J. Syst. Sci. 2002, 33, 23–34. [Google Scholar] [CrossRef]
- Feinberg, E.A.; Genethliou, D. Load forecasting. In Applied Mathematics for Restructured Electric Power Systems. Power Electronics and Power Systems; Chow, J.H., Wu, F.F., Momoh, J., Eds.; Springer: Boston, MA, USA, 2005; pp. 269–285. [Google Scholar] [CrossRef]
- Hong, T. Energy forecasting: Past, present, and future. Int. J. Appl. Forecast. 2014, 32, 43–48. [Google Scholar]
- Hong, T.; Gui, M.; Baran, M.E.; Willis, H.L. Modeling and forecasting hourly electric load by multiple linear regression with interactions. In Proceedings of the 2010 Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Karpio, K.; Łukasiewicz, P.; Nafkha, R. Regression Technique for Electricity Load Modeling and Outlined Data Points Explanation. In Advances in Soft and Hard Computing; Advances in Intelligent Systems and, Computing; Pejaś, J., El Fray, I., Hyla, T., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2019; Volume 889, pp. 56–67. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Seljom, P.; Madsen, H.; Fischer, D.; Korpas, M. Long-term electricity load forecasting: Current and future trends. Util. Policy 2019, 58, 102–119. [Google Scholar] [CrossRef]
- Rajakovic, N.L.; Shiljkut, V.M. Long-term forecasting of annual peak load considering effects of demand-side programs. J. Mod. Power Syst. Clean Energy 2018, 6, 145–157. [Google Scholar] [CrossRef]
- Mojica, J.L.; Petersen, D.; Hansen, B.; Powell, K.M.; Hedengren, J.D. Optimal combined long-term facility design and short-term operational strategy for CHP capacity investments. Energy 2017, 118, 97–115. [Google Scholar] [CrossRef]
- Torkzadeh, R.; Mirzaei, A.; Mirjalili, M.M.; Anaraki, A.S.; Sehhati, M.R.; Behdad, F. Medium term load forecasting in distribution systems based on multi linear regression & principal component analysis: A novel approach. In Proceedings of the 19th Electrical Power Distribution Networks (EPDC), Tehran, Iran, 6–7 May 2014; pp. 66–70. [Google Scholar]
- Taleb, I.; Guerard, G.; Fauberteau, F.; Nguyen, N. A Flexible Deep Learning Method for Energy Forecasting. Energies 2022, 15, 3926. [Google Scholar] [CrossRef]
- Elkamel, M.; Schleider, L.; Pasiliao, E.; Diabat, A.; Zheng, Q.P. Long-Term Electricity Demand Prediction via Socioeconomic Factors—A Machine Learning Approach with Florida as a Case Study. Energies 2020, 13, 3996. [Google Scholar] [CrossRef]
- Angelopoulos, D.; Siskos, Y.; Psarras, J. Disaggregating time series on multiple criteria for robust forecasting: The case of long-term electricity demand in Greece. Eur. J. Oper. Res. 2019, 275, 252–265. [Google Scholar] [CrossRef]
- Abu-Shikhah, N.; Elkarmi, F.; Aloquili, O. Medium-Term Electric Load Forecasting Using Multivariable Linear and Non-Linear Regression. Smart Grid Renew. Energy 2011, 2, 126–135. [Google Scholar] [CrossRef]
- Eneje, I.S.; Fadare, D.A.; Simolowo, O.E.; Falana, A. Modelling and Forecasting Periodic Electric Load for a Metropolitan City in Nigeria. Afr. Res. Rev. 2012, 6, 101–115. [Google Scholar] [CrossRef]
- Bruhns, A.; Deurveilher, G.; Roy, J.S. A non-linear regression model for midterm load forecasting and improvements in seasonality. In Proceedings of the 15th Power Systems Computation Conference, Liege, Belgium, 22–26 August 2005; pp. 22–26. [Google Scholar]
- Charytoniuk, W.; Chen, M.S.; Van Olinda, P. Nonparametric regression based short-term load forecasting. IEEE Trans. Power Syst. 1998, 13, 725–730. [Google Scholar] [CrossRef]
- Dudek, G. Pattern-based local linear regression models for short-term load forecasting. Electr. Power Syst. Res. 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Sood, R.; Koprinska, I.; Agelidis, V.G. Electricity load forecasting based on autocorrelation analysis. In Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Fan, S.; Hyndman, R.J. Short-term load forecasting based on a semi-parametric additive model. IEEE Trans. Power Syst. 2012, 27, 134–141. [Google Scholar] [CrossRef]
- Sharma, P.; Said, Z.; Kumar, A.; Nižetić, S.; Pandey, A.; Hoang, A.T.; Huang, Z.; Afzal, A.; Li, C.; Le, A.T.; et al. Recent Advances in Machine Learning Research for Nanofluid-Based Heat Transfer in Renewable Energy System. Energy Fuels 2022, 36, 6626–6658. [Google Scholar] [CrossRef]
- Said, Z.; Nguyen, T.H.; Sharma, P.; Li, C.; Ali, H.M.; Nguyen, V.N.; Pham, V.V.; Ahmed, S.F.; Van, D.N.; Truong, T.H. Multi-attribute optimization of sustainable aviation fuel production-process from microalgae source. Fuel 2022, 324, 124759. [Google Scholar] [CrossRef]
- Jihoon, M.; Yongsung, K.; Minjae, S.; Eenjun, H. Hybrid Short-Term Load Forecasting Scheme Using Random Forest and Multilayer Perceptron. Energies 2018, 11, 3283. [Google Scholar] [CrossRef]
- Dahl, M.; Brun, A.; Kirsebom, O.S.; Gorm, B.; Andresen, G.B. Improving Short-Term Heat Load Forecasts with Calendar and Holiday Data. Energies 2018, 11, 1678. [Google Scholar] [CrossRef]
- Ping-Huan, K.; Chiou-Jye, H. A High Precision Artificial Neural Networks Model for Short-Term Energy Load Forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Campo, R.; Ruiz, P. Adaptive weather-sensitive short term load forecast. IEEE Trans. Power Syst. 1987, 2, 592–598. [Google Scholar] [CrossRef]
- Ghosh, S. Univariate time-series forecasting of monthly peak demand of electricity in northern India. Int. J. Indian Cult. Bus. Manag. 2008, 1, 466–474. [Google Scholar] [CrossRef]
- Mirasgedis, S.; Sarafidis, Y.; Georgopoulou, E.; Lalas, D.P.; Moschovits, M.; Karagiannis, F.; Papakonstantinou, D. Models for Mid-Term Electricity Demand Forecasting Incorporating Weather Influences. Energy 2006, 31, 208–227. [Google Scholar] [CrossRef]
- Hong, T.; Wilson, J.; Xie, J. Long Term Probabilistic Load Forecasting and Normalization with Hourly Information. IEEE Trans. Smart Grid 2014, 5, 456–462. [Google Scholar] [CrossRef]
- Chen, Y.; Luh, P.B.; Guan, C.; Zhao, Y.; Michel, L.D.; Coolbeth, M.A.; Friedland, P.B.; Rourke, S.J. Short-term load forecasting: Similar day-based wavelet neural networks. IEEE Trans. Power Syst. 2010, 25, 322–330. [Google Scholar] [CrossRef]
- Ailing, Y.; Weide, L.; Xuan, Y. Short-term electricity load forecasting based on feature selection and Least Squares Support Vector Machines. Knowl.-Based Syst. 2019, 163, 159–173. [Google Scholar] [CrossRef]
- Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-Term Electricity Load Forecasting Model Based on EMD-GRU with Feature Selection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
- Hong, T. Short Term Electric Load Forecasting. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 20 November 2010. [Google Scholar]
- Hyndman, R.J.; Ahmed, R.A.; Shang, H.L. Optimal combination forecasts for hierarchical time-series. Comput. Stat. Data Anal. 2011, 55, 2579–2589. [Google Scholar] [CrossRef]
- Pang, Y.; Jin, C.; Zhou, X.; Guo, N.; Zhang, Y. Hierarchical Electricity Demand Forecasting by Exploring the Electricity Consumption Patterns. In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), Madeira, Portugal, 16–18 January 2018; pp. 576–581. [Google Scholar]
- Karpio, K.; Łukasiewicz, P.; Nafkha, R.; Orłowski, A. Description of Electricity Consumption by Using Leading Hours Intra-day Model. In Computational Science—ICCS 2021. Lecture Notes in Computer Science; Paszynski, M., Kranzlmüller, D., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M., Eds.; Springer: Cham, Switzerland, 2021; Volume 12745, pp. 392–404. [Google Scholar] [CrossRef]
- Polskie Sieci Elektroenergetyczne. Available online: http://www.pse.pl (accessed on 15 January 2023).
- Marsaglia, G.; Tsang, W.W.; Wang, J. Evaluating Kolmogorov’s Distribution. J. Stat. Softw. 2003, 8, 1–4. [Google Scholar] [CrossRef]
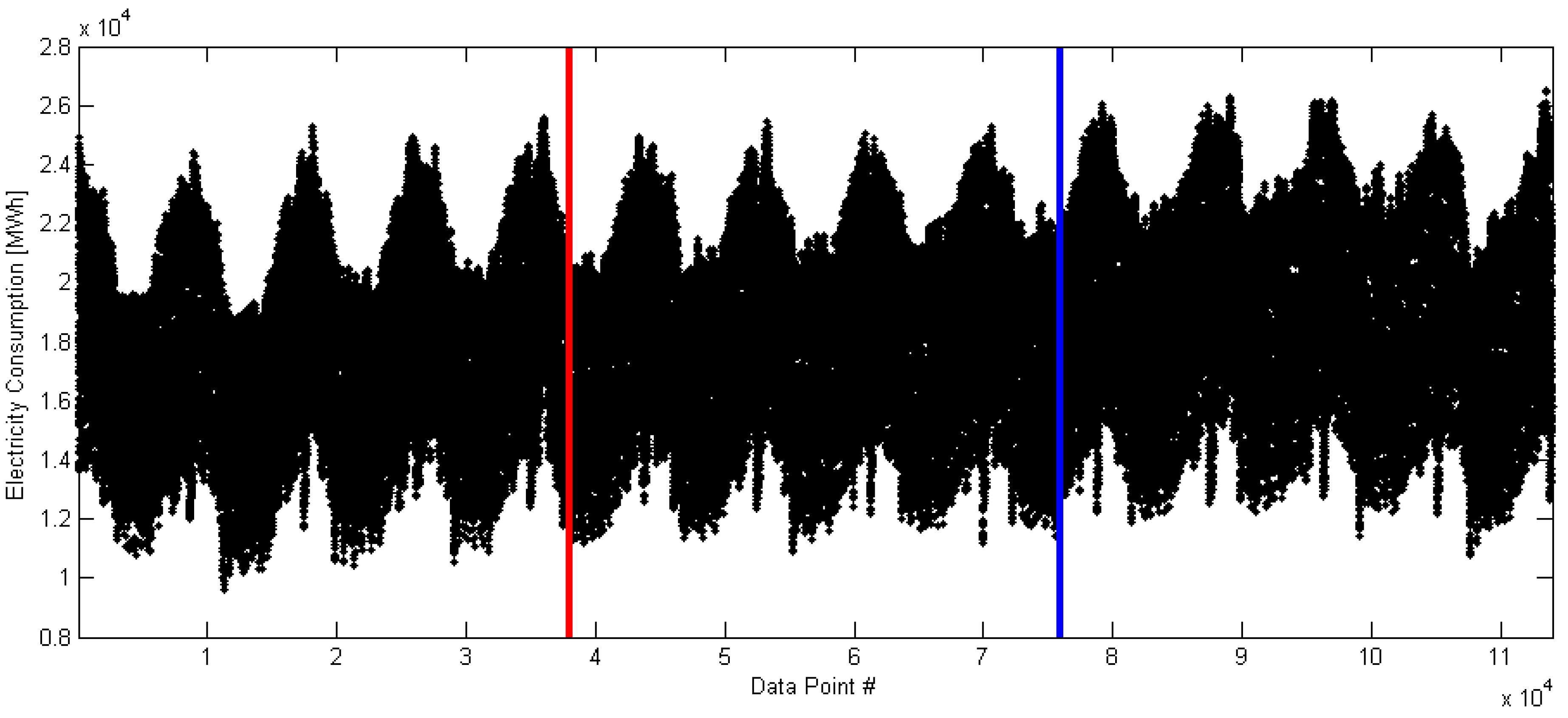


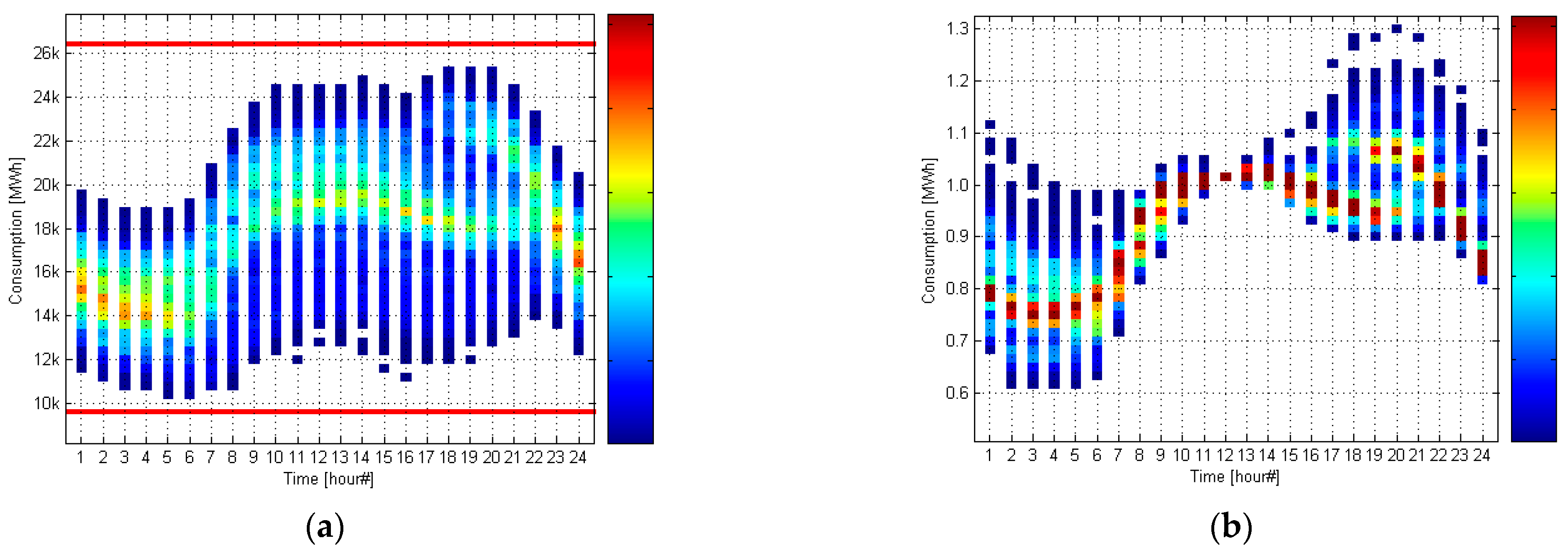

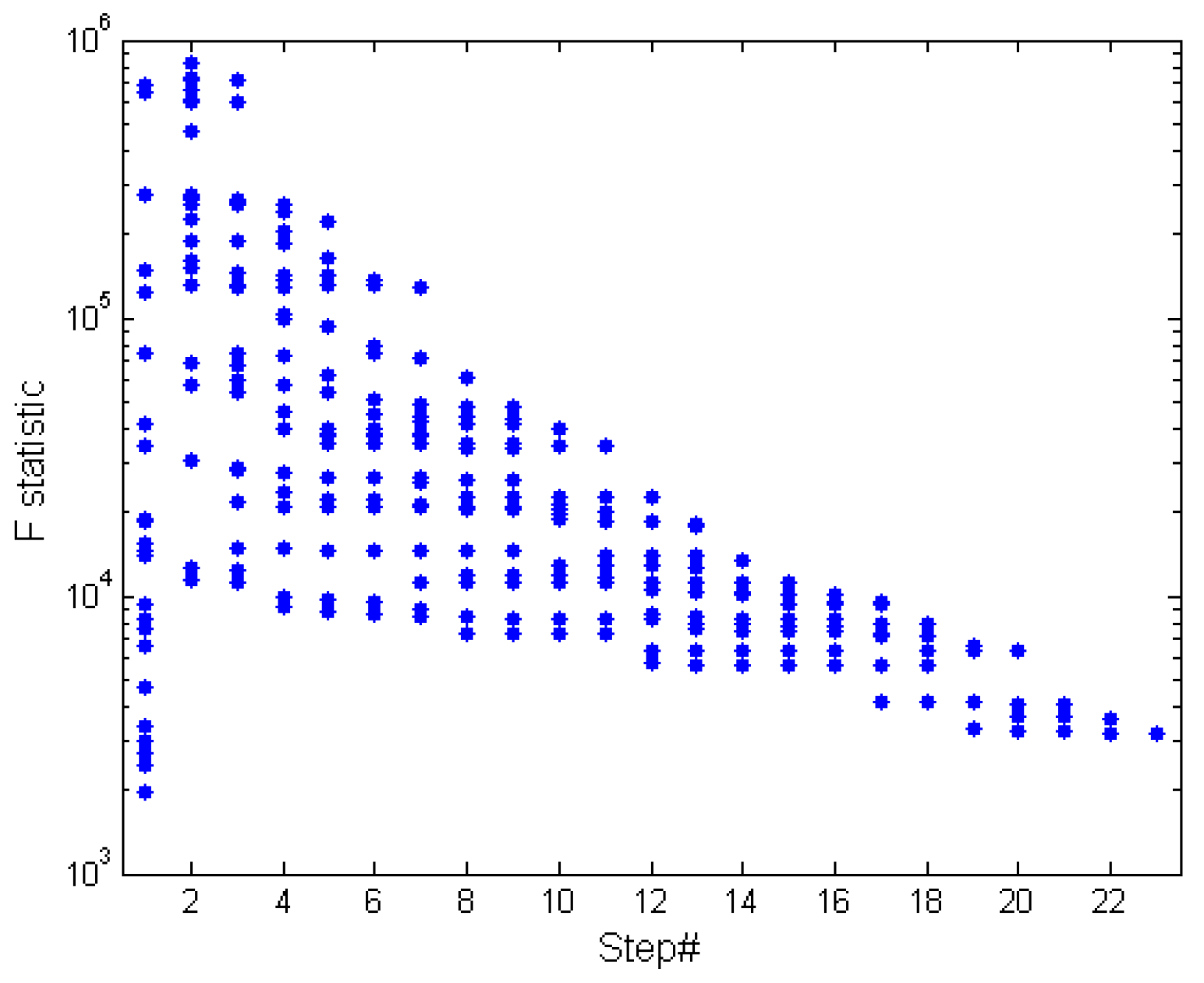


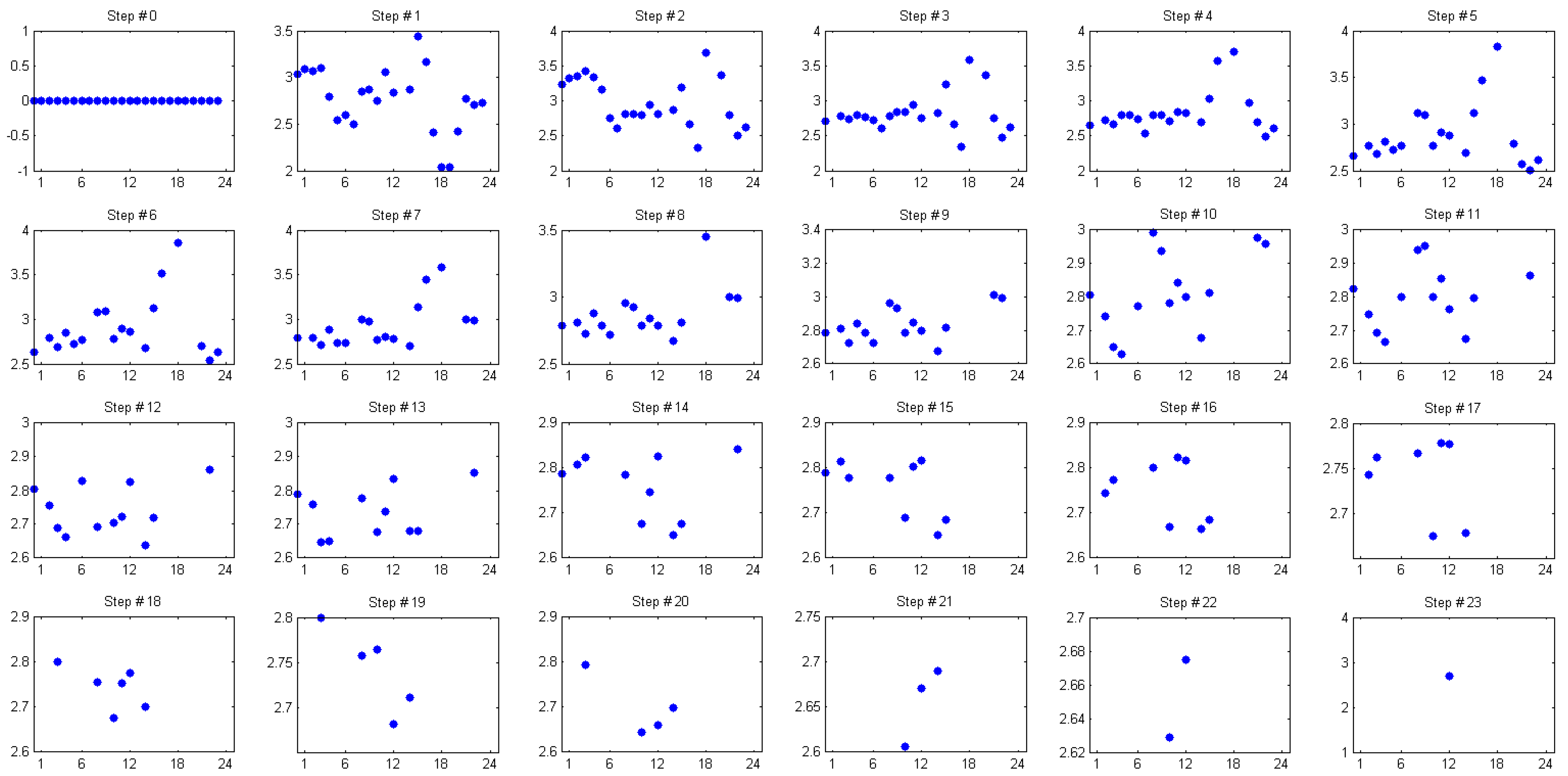
| Subset | Date | Number of Days | Number of Hours |
|---|---|---|---|
| learning set | 1 January 2008–1 May 2012 | 1583 | 37,992 |
| testing set I | 2 May 2012–31 August 2016 | 1583 | 37,992 |
| testing set II | 1 September 2016–31 December 2020 | 1583 | 37,992 |
| Symbol | h1 | h2 | h3 | h4 | h5 | h6 | h7 | h8 | h9 | h10 | h11 | h12 |
| Hour | 14 | 20 | 2 | 18 | 8 | 21 | 24 | 17 | 19 | 6 | 22 | 10 |
| Symbol | h13 | h14 | h15 | h16 | h17 | h18 | h19 | h20 | h21 | h22 | h23 | |
| Hour | 7 | 5 | 23 | 1 | 16 | 3 | 12 | 9 | 4 | 15 | 11 |
| Step (k) | 3 | 4 | 5 | 6 |
|---|---|---|---|---|
| MRSD | 353.08 ± 9.38 | 284.80 ± 9.00 | 236.08 ± 8.08 | 210.66 ± 6.96 |
| MRRSD | 0.0205 ± 0.0008 | 0.0170 ± 0.0007 | 0.0140 ± 0.0006 | 0.0126 ± 0.0006 |
| Measure | Learning Set | Testing Set I | Testing Set II |
|---|---|---|---|
| MRSD | 0.0172 ± 0.0018 | 0.0169 ± 0.0017 | 0.0182 ± 0.0017 |
| RSD [MWh] | 296.5 ± 2.8 | 302.8 ± 2.7 | 344.2 ± 2.7 |
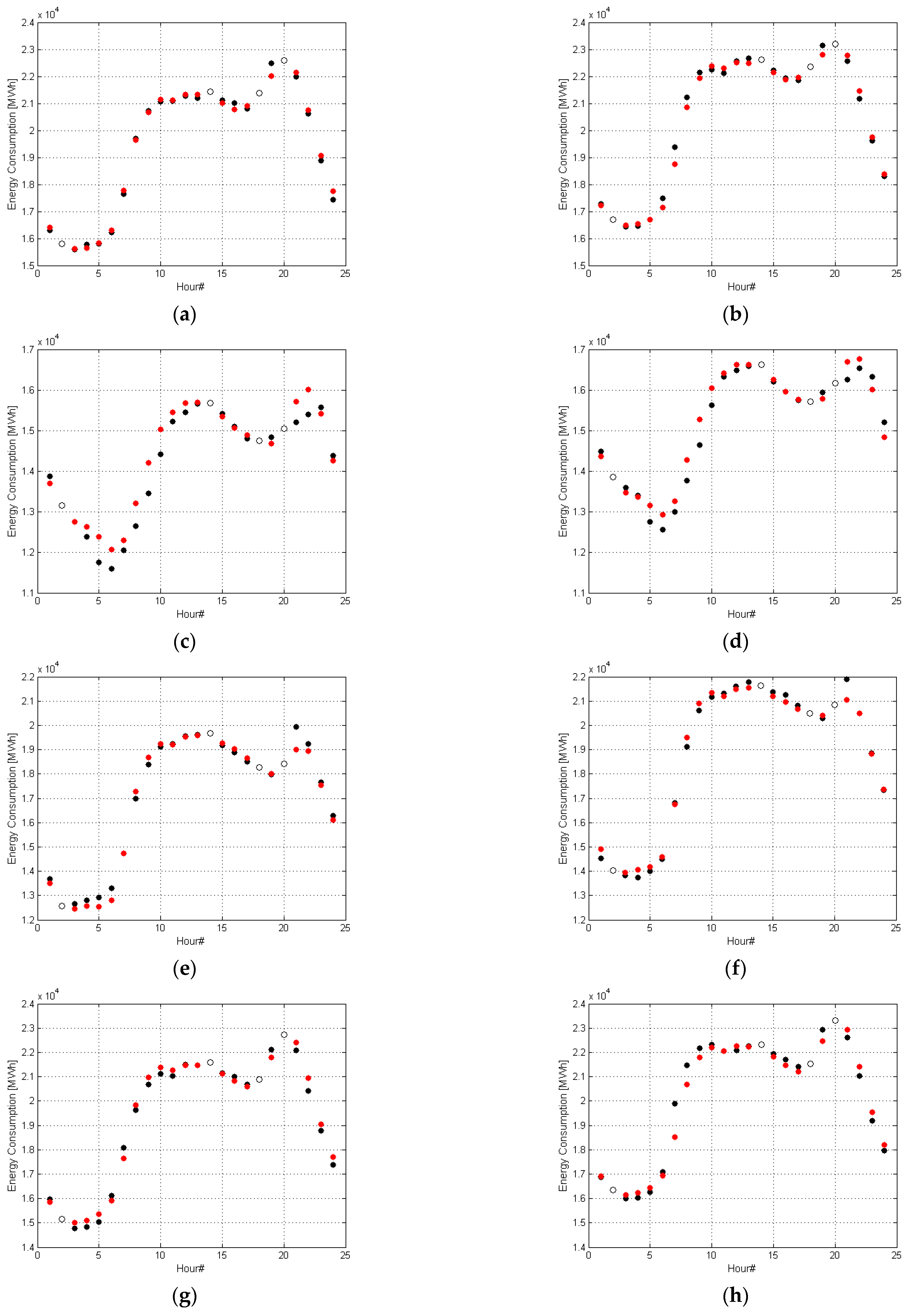
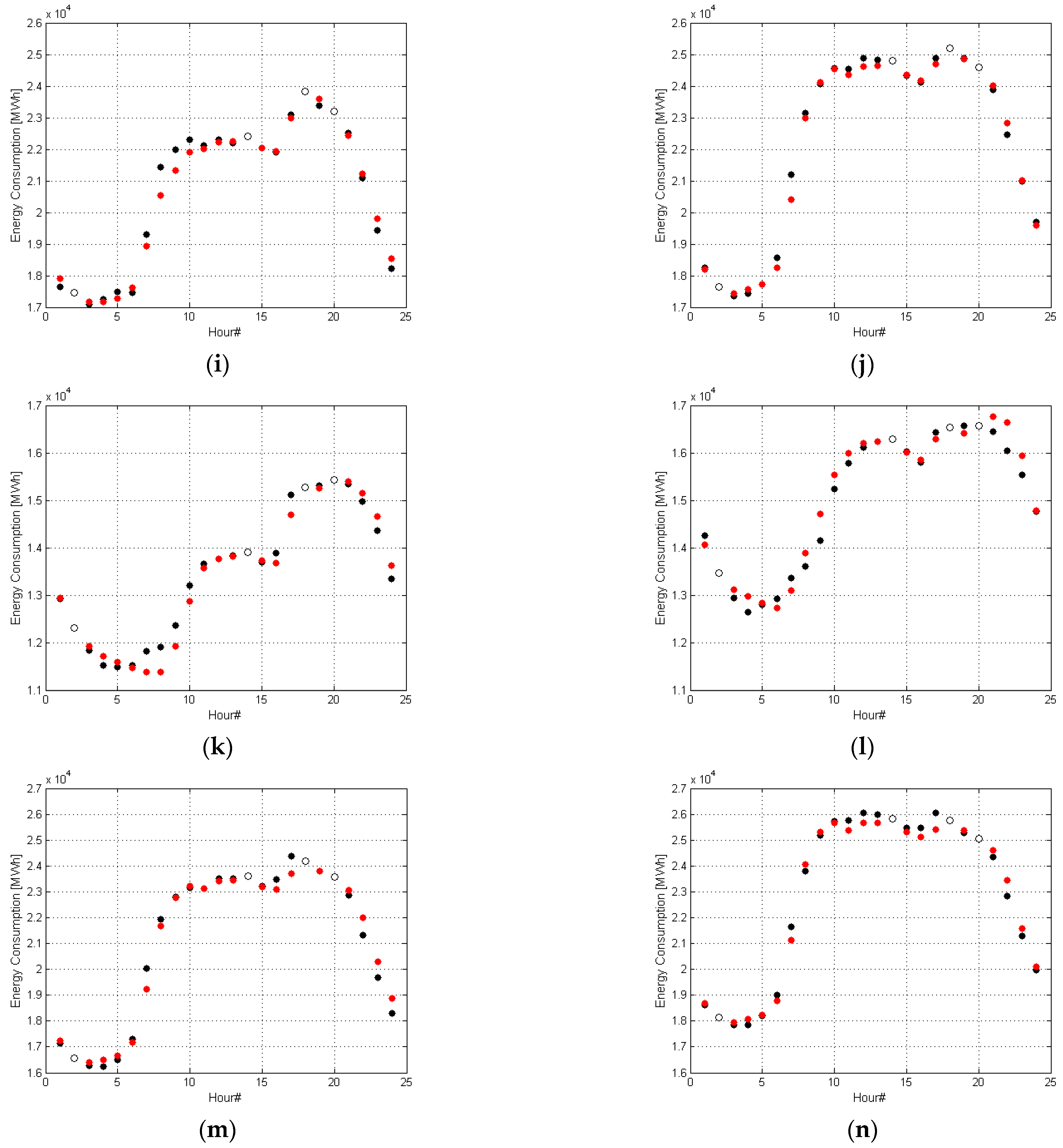
| No | Date Testing Set I | RSD (%) | Date Testing Set II | RSD (%) | Weekday | Figure 14 |
|---|---|---|---|---|---|---|
| 1 | 7 March 2013 | 0.882 | 2 March 2017 | 1.139 | Thursday | (a), (b) |
| 2 | 1 July 2012 | 2.671 | 2 July 2017 | 1.958 | Sunday | (c), (d) |
| 3 | 27 August 2012 | 1.736 | 28 August 2017 | 1.440 | Monday | (e), (f) |
| 4 | 14 October 2014 | 1.366 | 16 October 2018 | 2.069 | Tuesday | (g), (h) |
| 5 | 16 January 2015 | 1.553 | 18 January 2019 | 1.052 | Friday | (i), (j) |
| 6 | 25 December 2015 | 1.858 | 25 December 2020 | 1.830 | Friday | (k), (l) |
| 7 | 2 December 2015 | 1.725 | 2 December 2020 | 1.386 | Wednesday | (m), (n) |
| Day# | Date | RSD (%) | Description |
|---|---|---|---|
| 306 | 1 November 2008 | 5.972 | All Saints’ Day |
| 468 | 12 April 2009 | 7.330 | Easter |
| 671 | 1 November 2009 | 6.420 | All Saints’ Day |
| 825 | 4 April 2010 | 7.254 | Easter |
| 1036 | 1 November 2010 | 6.149 | All Saints’ Day |
| 1210 | 24 April 2011 | 5.379 | Easter |
| 1401 | 1 November 2011 | 6.170 | All Saints’ Day |
| 1560 | 8 April 2012 | 5.553 | Easter |
| 2132 | 1 November 2013 | 6.673 | All Saints’ Day |
| 2185 | 24 December 2013 | 5.333 | Christmas Eve |
| 2302 | 20 April 2014 | 5.484 | Easter |
| 2497 | 1 November 2014 | 5.036 | All Saints’ Day |
| 2862 | 1 November 2015 | 5.091 | All Saints’ Day |
| 3009 | 27 March 2016 | 6.717 | Easter |
| 4129 | 21 April 2019 | 6.578 | Easter |
| 4323 | 1 November 2019 | 5.672 | All Saints’ Day |
| 4376 | 24 December 2019 | 5.546 | Christmas Eve |
| 4486 | 12 April 2020 | 5.660 | Easter |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karpio, K.; Łukasiewicz, P.; Nafkha, R. New Method of Modeling Daily Energy Consumption. Energies 2023, 16, 2095. https://doi.org/10.3390/en16052095
Karpio K, Łukasiewicz P, Nafkha R. New Method of Modeling Daily Energy Consumption. Energies. 2023; 16(5):2095. https://doi.org/10.3390/en16052095
Chicago/Turabian StyleKarpio, Krzysztof, Piotr Łukasiewicz, and Rafik Nafkha. 2023. "New Method of Modeling Daily Energy Consumption" Energies 16, no. 5: 2095. https://doi.org/10.3390/en16052095
APA StyleKarpio, K., Łukasiewicz, P., & Nafkha, R. (2023). New Method of Modeling Daily Energy Consumption. Energies, 16(5), 2095. https://doi.org/10.3390/en16052095






