Techno-Economic Assessment of PV Power Systems to Power a Drinking Water Treatment Plant for an On-Grid Small Rural Community
Abstract
1. Introduction
2. State of the Art
3. Methodology
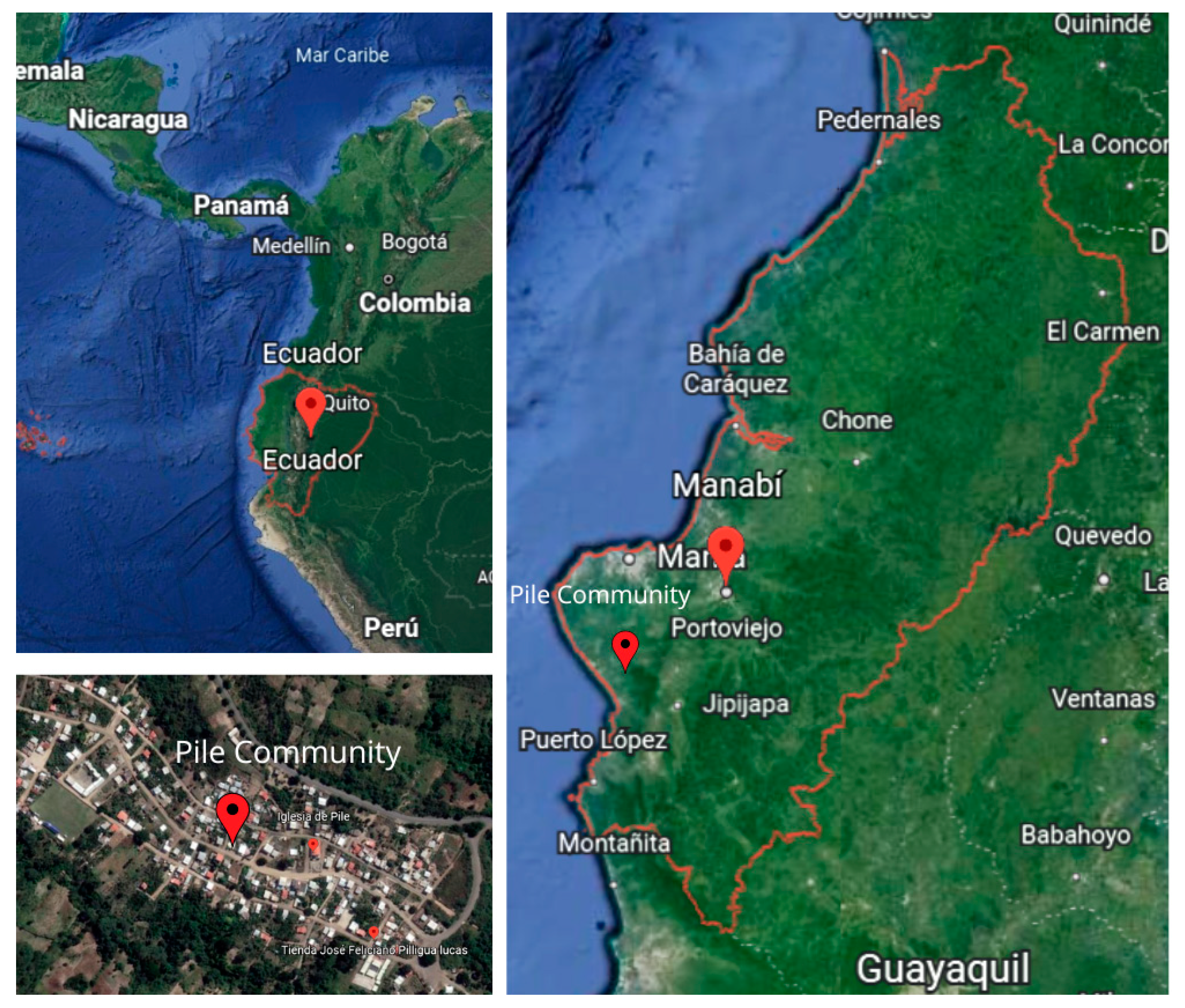
3.1. Location
3.2. Weather Conditions
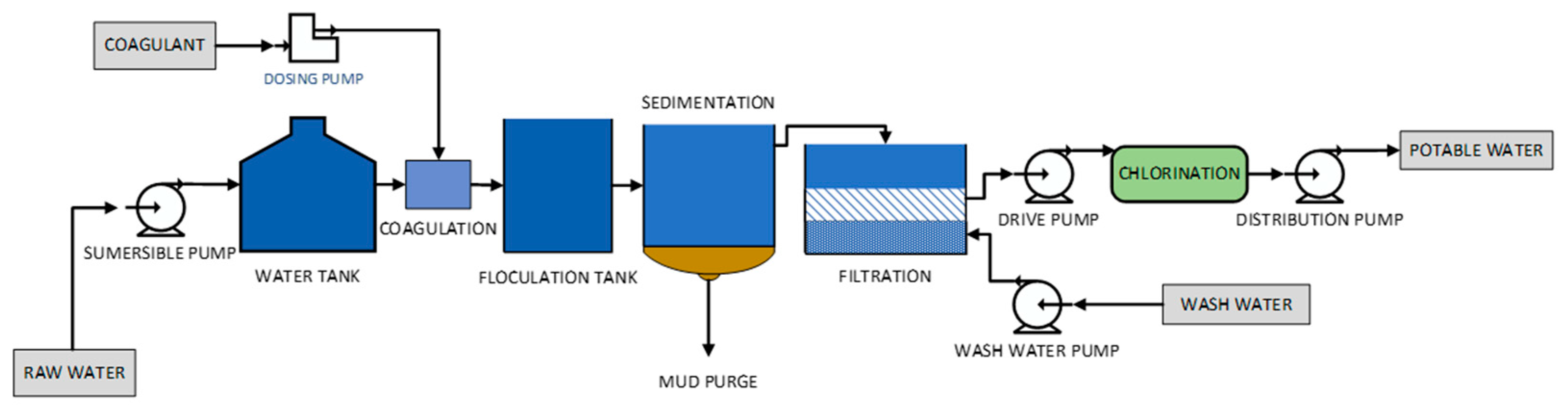
3.3. Description of the DWTP Modeling
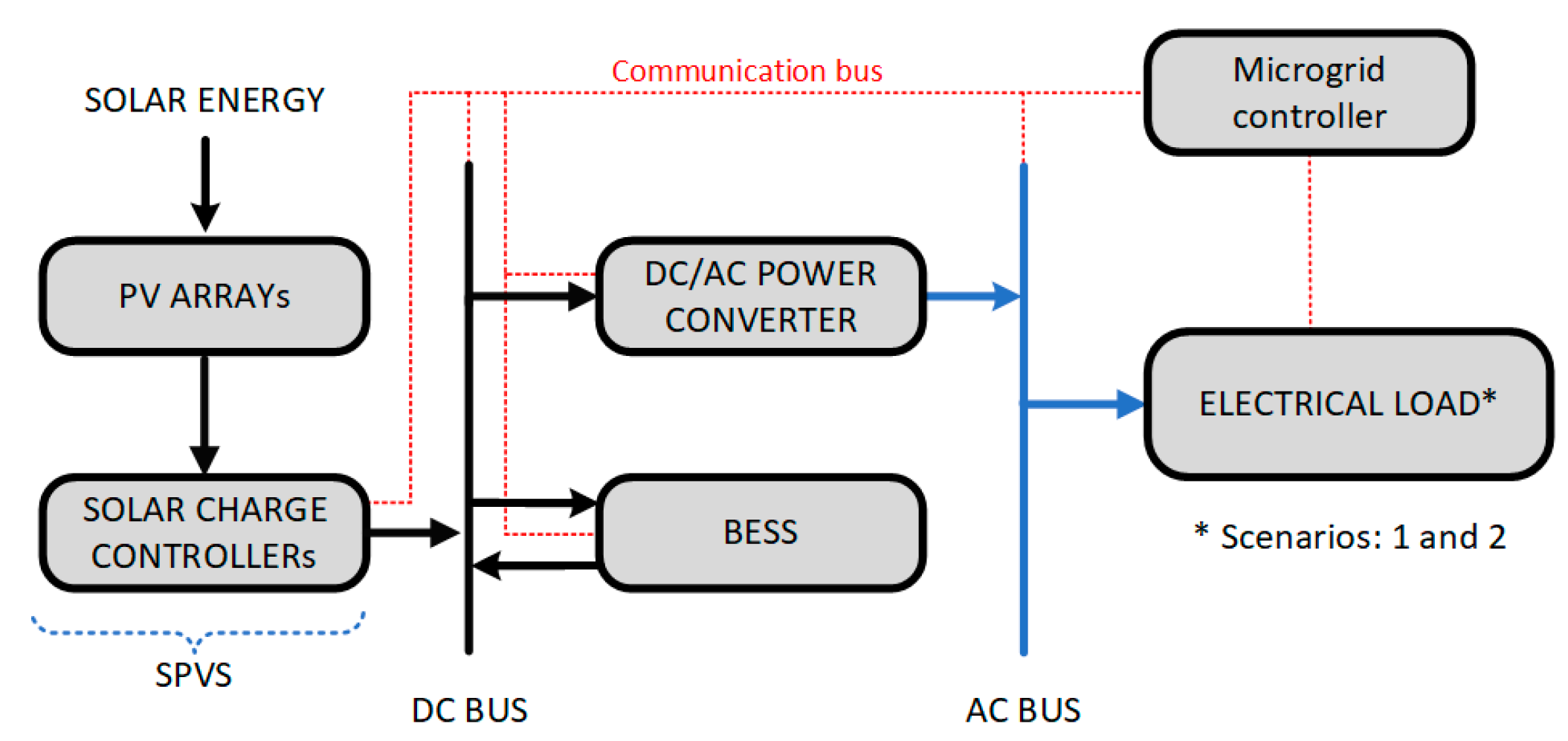
3.4. Topology and Design Principle of the Proposed PV Power Systems (Grid-Connected and Stand-Alone Systems)
- Stand-alone solar PV system supplies power to plant in 12H-DWTP (SPVS12);
- Stand-alone solar PV system supplies power to plant in 24H-DWTP (SPVS24);
- Grid-connected solar PV system supplies power to plant in 12H-DWTP (G-SPVS12);
- Grid-connected solar PV system supplies power to plant in 24H-DWTP (G-SPVS24).
3.5. Modeling Approach
3.5.1. Power Output from Solar PV System
3.5.2. Discharge/Charge Process of the BESS
3.5.3. Net Present Cost (NPC)
3.5.4. Levelized Cost of Energy (LCOE)
3.5.5. Renewable Fraction (RF)
3.6. Components of PV Power Systems
4. Results
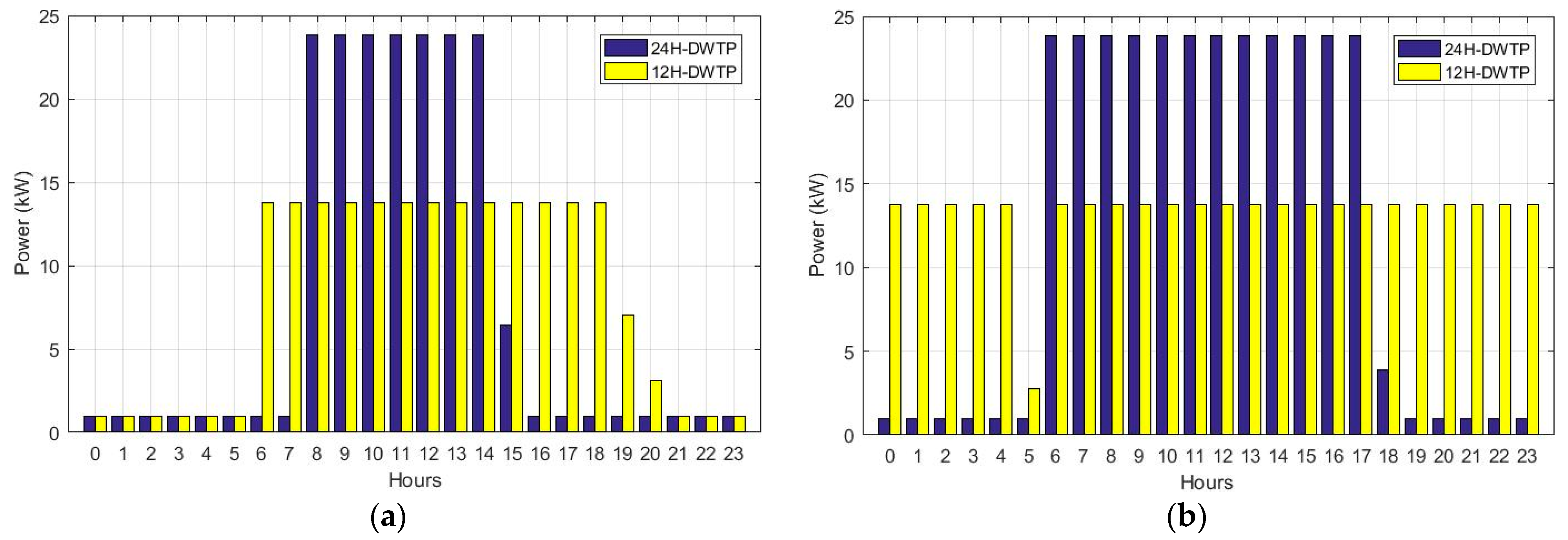
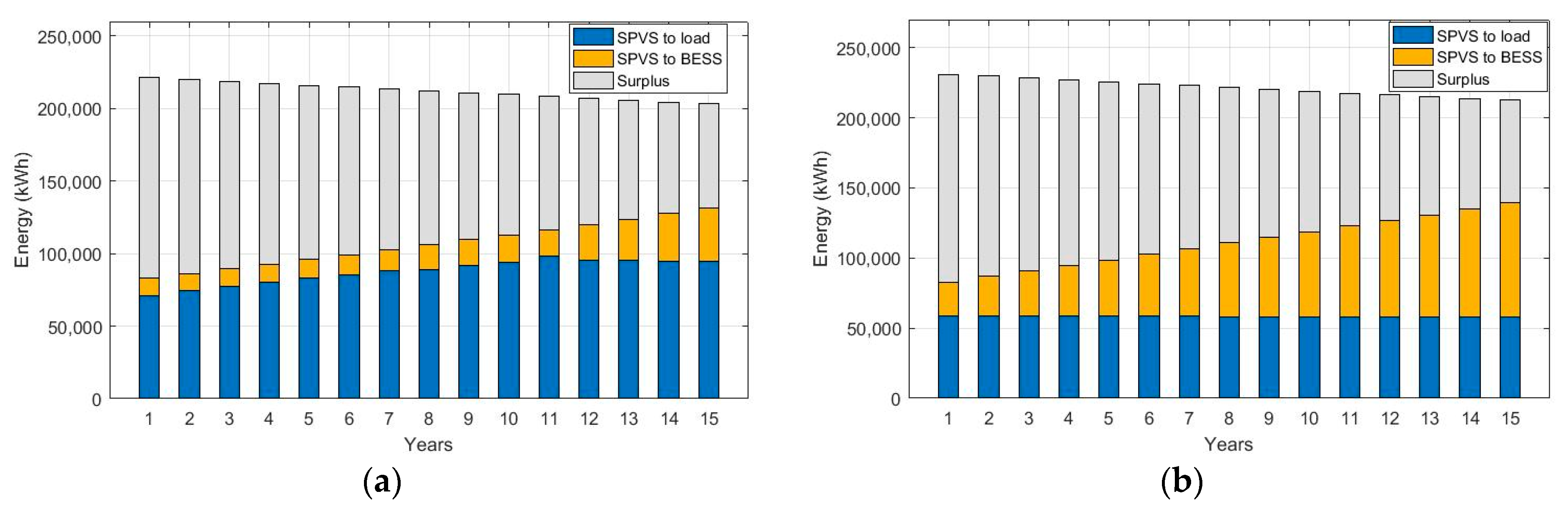
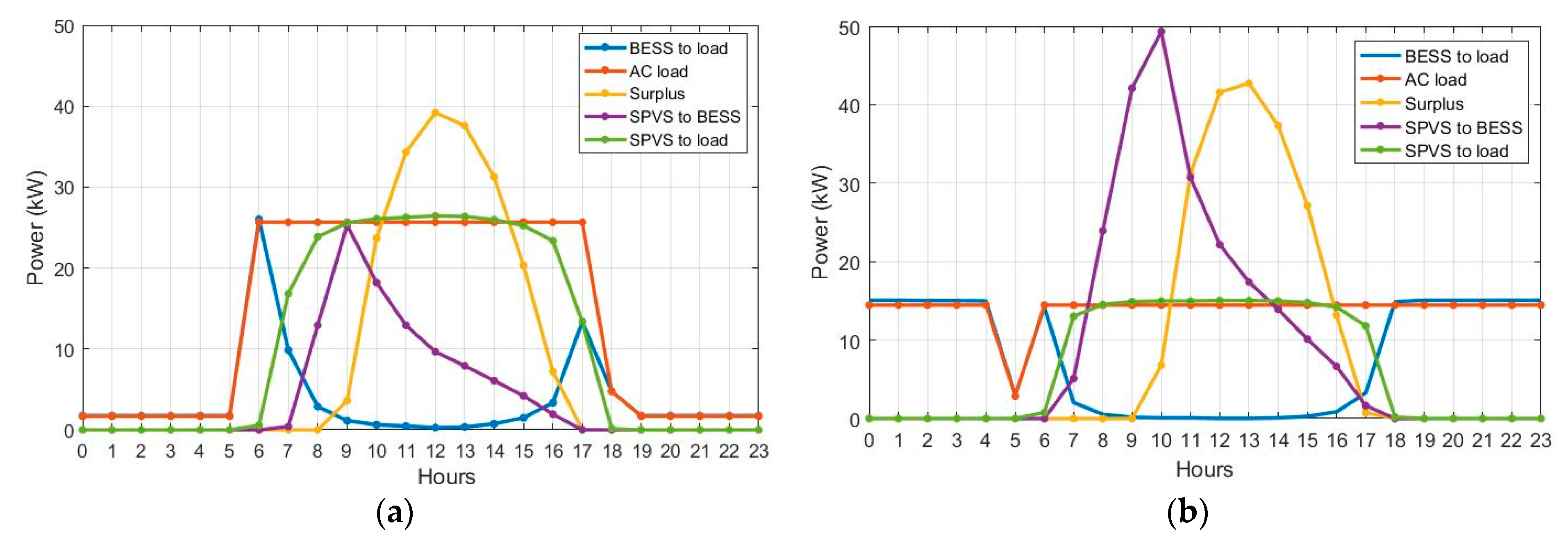
4.1. Stand-Alone Solar PV Systems: SPVS12 and SPVS24 Scenarios
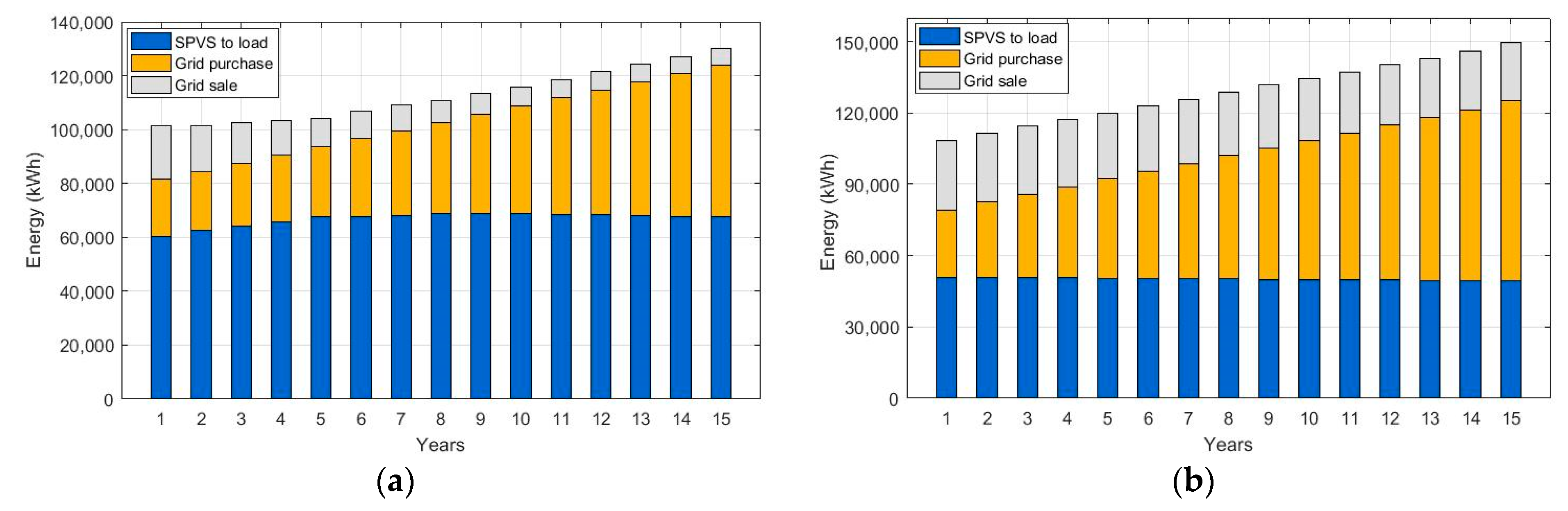
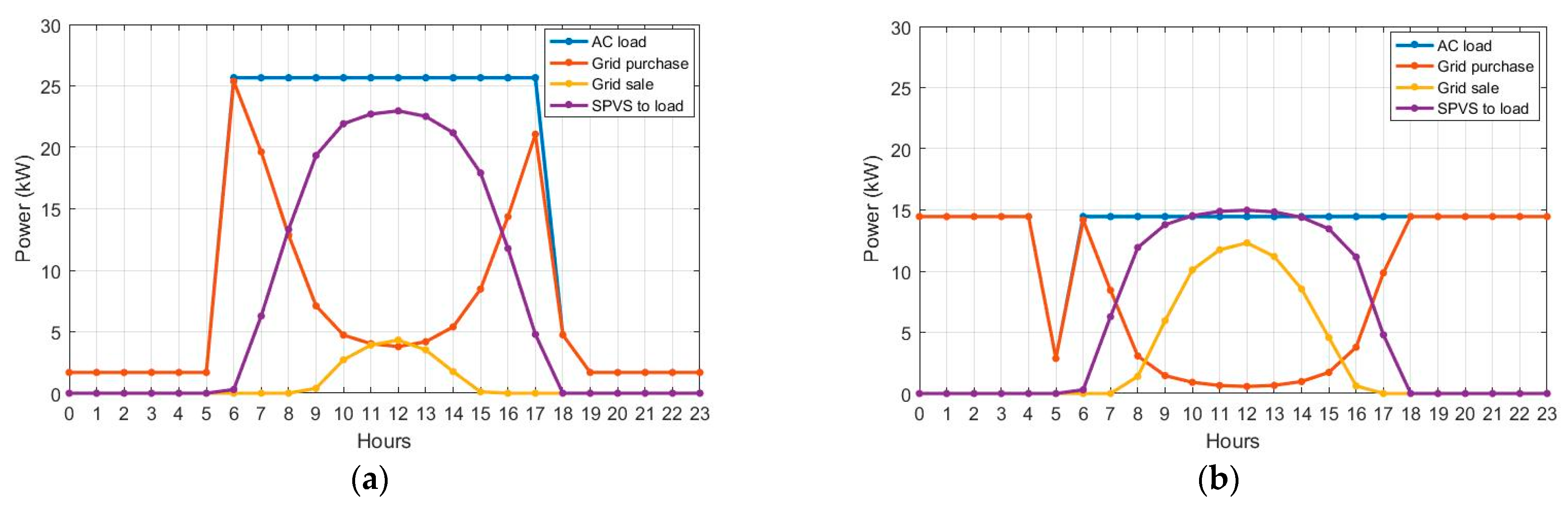
4.2. Grid-Connected Solar PV System: G-SPVS12 and G-SPVS24 Scenarios
5. Discussion
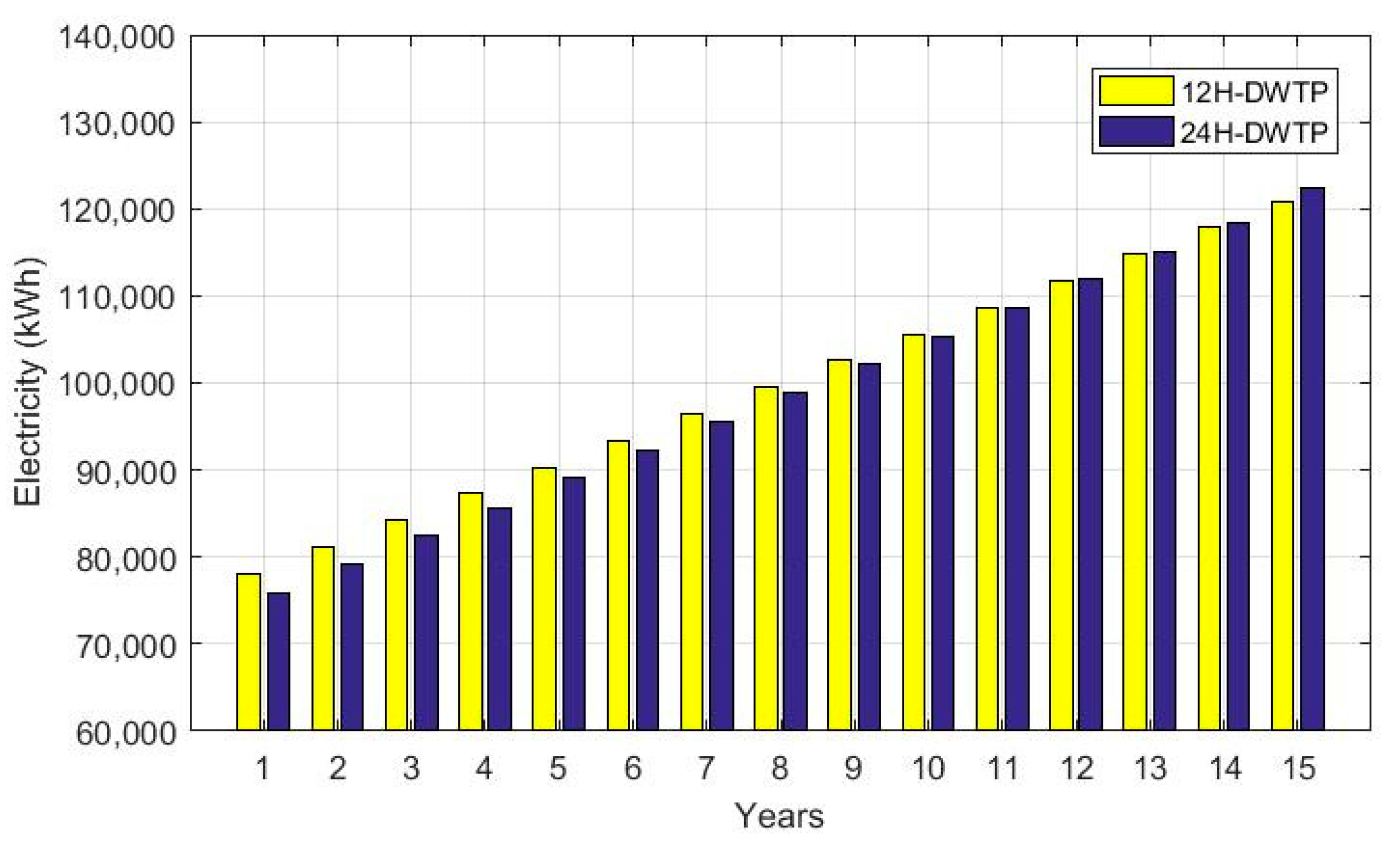
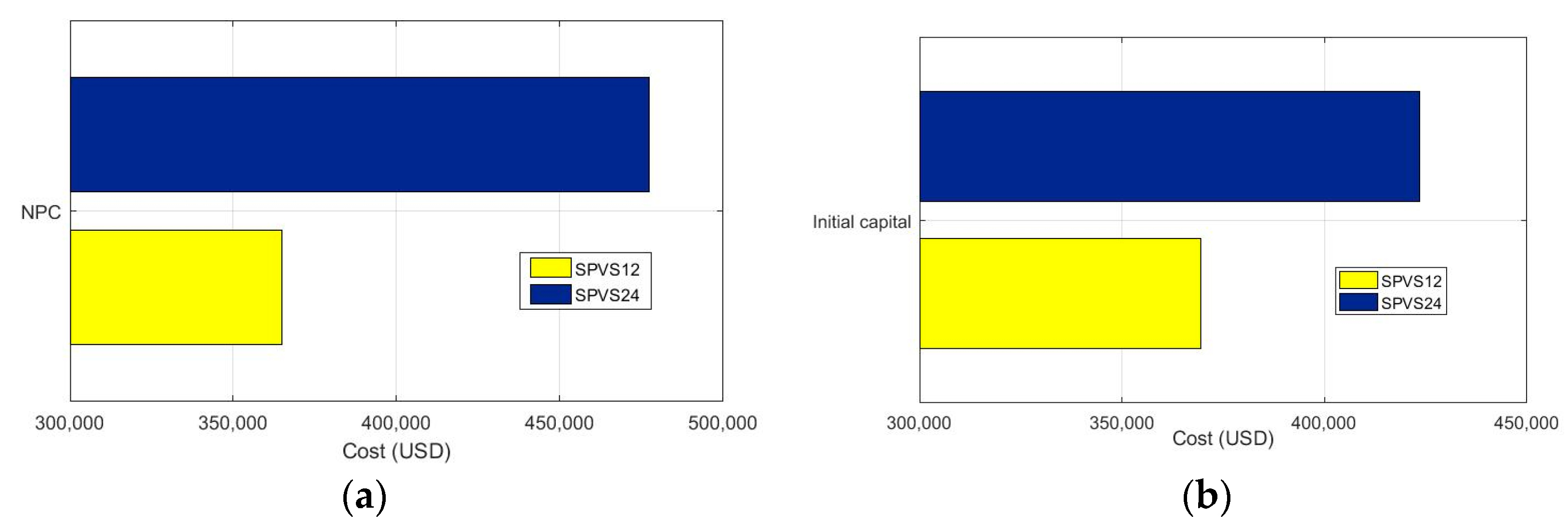
5.1. Comparative Analysis by PV Power System
5.2. Comparative Analysis among All Scenarios
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| BESS | Battery energy storage system |
| DC | Direct current |
| DG | Distributed generation |
| G-SPVS12 | Grid-connected solar PV system supplies power to plant in 12H-DWTP |
| G-SPVS24 | Grid-connected solar PV system supplies power to plant in 24H-DWTP |
| LCOE | Levelized Cost of Energy |
| MPPT | Maximum power point tracker |
| masl | Meters above sea level |
| NPC | Net present cost |
| PV | Photovoltaic |
| RF | Renewable fraction |
| SPVS | Solar photovoltaic system |
| SPVS12 | Stand-alone solar PV system supplies power to plant in 12H-DWTP |
| SPVS24 | Stand-alone solar PV system supplies power to plant in 24H-DWTP |
| UNICEF | United Nations International Children’s Emergency Fund |
References
- The World Bank. Population, Total. 2022. Available online: https://data.worldbank.org/indicator/SP.POP.TOTL (accessed on 14 March 2022).
- United Nations. GLOBAL ISSUES: Population. 2022. Available online: https://www.un.org/en/global-issues/population (accessed on 14 March 2022).
- United Nations. 68% of the World Population Projected to Live in Urban Areas by 2050, Says UN. 2018. Available online: https://www.un.org/development/desa/en/news/population/2018-revision-of-world-urbanization-prospects.html (accessed on 14 March 2022).
- Ebeke, C.H.; Etoundi, S. The effects of natural resources on urbanization, concentration, and living standards in Africa. World Dev. 2017, 96, 408–417. [Google Scholar] [CrossRef]
- United Nations. Las Zonas Rurales Son Clave Para El Crecimiento Económico de los Países en Desarrollo, Dice la FAO. 2017. Available online: https://www.un.org/sustainabledevelopment/es/2017/10/las-zonas-rurales-son-clave-para-el-crecimiento-economico-de-los-paises-en-desarrollo-dice-la-fao/ (accessed on 14 March 2022).
- United Nations. Goal 3: Ensure Healthy Lives and Promote Well-Being for All At All Ages. 2022. Available online: https://www.un.org/sustainabledevelopment/health/ (accessed on 8 October 2022).
- United Nations. Goal 6: Ensure Access to Water and Sanitation for All. 2022. Available online: https://www.un.org/sustainabledevelopment/water-and-sanitation/ (accessed on 8 October 2022).
- United Nations. Goal 7: Ensure Access to Affordable, Reliable, Sustainable and Modern Energy. 2022. Available online: https://www.un.org/sustainabledevelopment/energy/ (accessed on 8 October 2022).
- Yousefi, M.; Ghalehaskar, S.; Asghari, F.B.; Ghaderpoury, A.; Dehghani, M.H.; Ghaderpoori, M.; Mohammadi, A.A. Distribution of fluoride contamination in drinking water resources and health risk assessment using geographic information system, northwest Iran. Regul. Toxicol. Pharmacol. 2019, 107, 104408. [Google Scholar] [CrossRef]
- World Health Organization. Drinking-Water. Available online: https://www.who.int/news-room/fact-sheets/detail/drinking-water (accessed on 14 February 2023).
- Ribas, A.; Jollivet, C.; Morand, S.; Thongmalayvong, B.; Somphavong, S.; Siew, C.-C.; Ting, P.-J.; Suputtamongkol, S.; Saensombath, V.; Sanguankiat, S. Intestinal parasitic infections and environmental water contamination in a rural village of northern Lao PDR. Korean J. Parasitol. 2017, 55, 523. [Google Scholar] [CrossRef]
- Unicef Ecuador. Combatir la Desnutrición a Través del acceso a Agua Segura. 2020. Available online: https://www.unicef.org/ecuador/historias/combatir-la-desnutrición-través-del-acceso-agua-segura#:~:text=Además del agua potable y,para su edad y estar (accessed on 10 December 2022).
- Kumar, R.; Patel, M.; Singh, P.; Bundschuh, J.; Pittman Jr, C.U.; Trakal, L.; Mohan, D. Emerging technologies for arsenic removal from drinking water in rural and peri-urban areas: Methods, experience from, and options for Latin America. Sci. Total Environ. 2019, 694, 133427. [Google Scholar] [CrossRef]
- Unicef Ecuador. UNICEF Ecuador Desarrolla Intervenciones Para Que Cada Niño, Niña y Adolescente Acceda a Servicios de Agua, Saneamiento e Higiene de Calidad. 2017. Available online: https://www.unicef.org/ecuador/acceso-agua-saneamiento-e-higiene (accessed on 10 December 2022).
- Banco de Desarrollo del Ecuador. Cierre de Brechas en la Cobertura de Agua Potable y Alcantarillado Sanitario Período 2007–2015, Quito, Ecuador. 2017. Available online: https://sni.gob.ec/documents/10180/4534845/Brechas+Saneamiento+Ambiental.pdf/b2ed65ef-520b-4847-bb44-9e610da4c048 (accessed on 10 December 2022).
- The World Bank. Access to Electricity, Rural (% of Rural Population). 2019. Available online: https://data.worldbank.org/indicator/EG.ELC.ACCS.RU.ZS (accessed on 16 March 2022).
- Ministerio de Energía y Recursos Naturales No Renovables. Plan Maestro de Electricidad: Transformación y Situación Actual del Sector Eléctrico. 2020. Available online: https://www.cnelep.gob.ec/wp-content/uploads/2020/01/Plan-Maestro-de-Electricidad-2018-2027.pdf (accessed on 10 December 2022).
- Lin, W.; Xia, R.; He, D.; Harley, R.G.; Habetler, T.G. The impact of demand response on rural island power system operation. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Zhai, M.; Liu, Y.; Zhang, T.; Zhang, Y. Robust model predictive control for energy management of isolated microgrids. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2049–2053. [Google Scholar]
- Muñoz, K.; Amoroso, F. Diseño de una Planta Potabilizadora de Agua Abastecida Por Energía Solar. Bachelor’s Thesis, Undergraduate Dissertation, ESPOL, Guayaquil, Ecuador, 2021. [Google Scholar]
- Soshinskaya, M.; Crijns-Graus, W.H.J.; van der Meer, J.; Guerrero, J.M. Application of a microgrid with renewables for a water treatment plant. Appl. Energy 2014, 134, 20–34. [Google Scholar] [CrossRef]
- Wang, F.; Xu, J.; Liu, L.; Yin, G.; Wang, J.; Yan, J. Optimal design and operation of hybrid renewable energy system for drinking water treatment. Energy 2021, 219, 119673. [Google Scholar] [CrossRef]
- Ravindiran, G.; Saravanan, P.; Jeyaraju, R.M.; Josephraj, J. Water—Conventional and novel treatment methods. In Solar-Driven Water Treatment; Elsevier: Amsterdam, The Netherlands, 2022; pp. 37–66. [Google Scholar]
- Chen, L.; Deng, Y.; Dong, S.; Wang, H.; Li, P.; Zhang, H.; Chu, W. The occurrence and control of waterborne viruses in drinking water treatment: A review. Chemosphere 2021, 281, 130728. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Ouyang, W.; Qian, Y.; Su, C.; Su, J.; Chen, H. High-throughput profiling of antibiotic resistance genes in drinking water treatment plants and distribution systems. Environ. Pollut. 2016, 213, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Zhao, W.; Wang, Z.; Ma, R.; Luo, Y.; Wang, Z.; Sun, Q.; Liang, H. Rural drinking water treatment system combining solar-powered electrocoagulation and a gravity-driven ceramic membrane bioreactor. Sep. Purif. Technol. 2021, 276, 119383. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency. Distributed Generation of Electricity and Its Environmental Impacts. 2022. Available online: https://www.epa.gov/energy/distributed-generation-electricity-and-its-environmental-impacts#:~:text=Distributed generation can benefit the,environmental impacts of centralized generation (accessed on 10 December 2022).
- Bukhary, S.; Batista, J.; Ahmad, S. Water-energy-carbon nexus approach for sustainable large-scale drinking water treatment operation. J. Hydrol. 2020, 587, 124953. [Google Scholar] [CrossRef]
- Bukhary, S.; Batista, J.; Ahmad, S. An analysis of energy consumption and the use of renewables for a small drinking water treatment plant. Water 2019, 12, 28. [Google Scholar] [CrossRef]
- Rodriguez, M.; Espin, V.; Arcos-Aviles, D.; Martinez, W. Energy management system for an isolated microgrid based on Fuzzy logic control and meta-heuristic algorithms. In Proceedings of the 2022 IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 462–467. [Google Scholar]
- Hidalgo-Leon, R.; Amoroso, F.; Urquizo, J.; Villavicencio, V.; Torres, M.; Singh, P.; Soriano, G. Feasibility Study for Off-Grid Hybrid Power Systems Considering an Energy Efficiency Initiative for an Island in Ecuador. Energies 2022, 15, 1776. [Google Scholar] [CrossRef]
- Hidalgo-Leon, R.; Amoroso, F.; Litardo, J.; Urquizo, J.; Torres, M.; Singh, P.; Soriano, G. Impact of the Reduction of Diesel Fuel Subsidy in the Design of an Off-Grid Hybrid Power System: A Case Study of the Bellavista Community in Ecuador. Energies 2021, 14, 1730. [Google Scholar] [CrossRef]
- Macias, L. Memoria técnica de los estudios y diseños para el mejoramiento del sistema de agua potable para la localidad de Pile, Cantón Montecriti; Pile, Manabi; 2010. [Google Scholar]
- Rodríguez-Gámez, M.; Vázquez-Pérez, A.; Vélez-Quiroz, A.M.; Saltos-Arauz, W.M. Mejora de la calidad de la energía con sistemas fotovoltaicos en las zonas rurales. Rev. Científica 2018, 265–274. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef]
- CERA-ESPOL. Weather Parameters of Pile Community; Pile Community. 2022. Available online: https://meteonorm.com/en/ (accessed on 10 December 2022).
- CPE INEN 5, N.T.E. Normas Para Estudio Y Diseño De Sistemas De Agua Potable Y Disposición De Aguas Residuales Para 1992, 291. Available online: https://www.normalizacion.gob.ec/buzon/normas/cpe_inen_5%20Parte_9-1.pdf (accessed on 15 November 2022).
- Nwaigwe, K.N.; Mutabilwa, P.; Dintwa, E. An overview of solar power (PV systems) integration into electricity grids. Mater. Sci. Energy Technol. 2019, 2, 629–633. [Google Scholar] [CrossRef]
- Mohanty, P.; Sharma, K.R.; Gujar, M.; Kolhe, M.; Azmi, A.N. PV System Design for Off-Grid Applications; Springer: Cham, Switzerland, 2016; Volume 196, ISBN 9783319146638. [Google Scholar]
- Homer Energy. Net Present Cost. Available online: https://www.homerenergy.com/products/pro/docs/latest/net_present_cost.html (accessed on 9 October 2022).
- Petrillo, A.; De Felice, F.; Jannelli, E.; Autorino, C.; Minutillo, M.; Lavadera, A.L. Life cycle assessment (LCA) and life cycle cost (LCC) analysis model for a stand-alone hybrid renewable energy system. Renew. Energy 2016, 95, 337–355. [Google Scholar] [CrossRef]
- Oulis Rousis, A.; Tzelepis, D.; Konstantelos, I.; Booth, C.; Strbac, G. Design of a hybrid AC/DC microgrid using Homer Pro: Case study on an islanded residential application. Inventions 2018, 3, 55. [Google Scholar] [CrossRef]
- HOMER Energy. Net Present Cost—Main Economic Output. 2022. Available online: https://www.homerenergy.com/products/pro/docs/3.11/total_net_present_cost.html (accessed on 9 October 2022).
- jasolar. 470 MBB Half-Cell Module. 2022. Available online: https://www.jasolar.com/uploadfile/2021/0602/20210602105327260.pdf (accessed on 22 August 2022).
- Hoppecke. OPzV Solar Power: Valve Regulated Lead-Acid Batteries for Cyclic Applications. 2022. Available online: https://www.europe-solarstore.com/download/hoppecke/opzv/OPzV_solar.power_en.pdf (accessed on 22 August 2022).
- SMA. Sunny Island 6.0H/8.0H for Off-Grid And On-Grid Applications. Available online: http://www.go-pure.eu/download/SMA-6.0-8.0.pdf (accessed on 22 August 2022).
- Systellar. Systellar Innovations: Products and Services. 2022. Available online: https://systellar.co.in/mppt-high-voltage-solar-charge-controller/ (accessed on 22 August 2022).
- ARCONEL-035/19. Pliego Tarifario Para Las Empresas Eléctricas de Distribución—Servicio Público de Energía Eléctrica. Resolución Nro. ARCONEL–035/19 2020, 19, 35. Available online: https://www.regulacionelectrica.gob.ec/wp-content/uploads/downloads/2019/07/P-Tarifario-SPEE-2019_Codif.pdf (accessed on 15 November 2022).
- ARCONEL. Resolución No. ARCONEL -042/18 Regulacion No. ARCONEL-003/18 Codificación. Arconel 2018, 43. Available online: https://www.regulacionelectrica.gob.ec/wp-content/uploads/downloads/2019/03/042-18.pdf (accessed on 15 November 2022).
- Rodríguez, M.; Salazar, A.; Arcos-Aviles, D.; Llanos, J.; Martínez, W.; Motoasca, E. A brief approach of Microgrids implementation in Ecuador: A review. In Recent Advances in Electrical Engineering, Electronics and Energy: Proceedings of the CIT 2020 Volume 1, 149–163; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Bhayo, B.A.; Al-Kayiem, H.H.; Gilani, S.I. Assessment of standalone solar PV-Battery system for electricity generation and utilization of excess power for water pumping. Sol. Energy 2019, 194, 766–776. [Google Scholar] [CrossRef]
- Dahbi, S.; Aziz, A.; Messaoudi, A.; Mazozi, I.; Kassmi, K.; Benazzi, N. Management of excess energy in a photovoltaic/grid system by production of clean hydrogen. Int. J. Hydrogen Energy 2018, 43, 5283–5299. [Google Scholar] [CrossRef]




| Month | Air Temperature (°C) | Global Horizontal Radiation (kWh/m2/Day) | Wind Speed (m/s) |
|---|---|---|---|
| January | 25.6 | 5.10 | 3.0 |
| February | 25.7 | 5.83 | 2.3 |
| March | 25.9 | 6.29 | 2.3 |
| April | 25.7 | 5.88 | 2.5 |
| May | 25.1 | 5.17 | 3.1 |
| June | 23.9 | 4.33 | 3.6 |
| July | 23.7 | 3.89 | 3.8 |
| August | 23.5 | 4.16 | 3.9 |
| September | 23.3 | 4.74 | 4.0 |
| October | 23.6 | 4.29 | 4.1 |
| November | 24.0 | 4.22 | 4.0 |
| December | 24.8 | 5.15 | 3.8 |
| Year | 24.6 | 4.92 | 3.4 |
| Components | Power Consumption (kW) | |
|---|---|---|
| 12H-DWTP | 24H-DWTP | |
| Submersible pump | 5.74 | 3.00 |
| Drive pump | 1.00 | 0.70 |
| Distribution pump | 16.00 | 9.00 |
| Wash water pump | 2.21 | 1.21 |
| Dosing pump | 0.09 | 0.09 |
| Others | 0.98 | 0.98 |
| Total | 26.02 | 14.98 |
| Component | Description | Source |
|---|---|---|
| PV modules | Capacity, 0.45 kWp; efficiency, 20.3%; type, monocrystalline; annual degradation, 0.55%; temperature coefficient, −0.35%/°C; operating temperature, 45 °C; lifetime, 25 years; capital cost, USD 340. | [45] |
| BESS | Nominal capacity, 2900 Ah; nominal voltage, 2 V; type, stationary lead acid served OPzS rechargeable batteries; minimum SoC, 20%. Capital cost, USD 1950. | [46] |
| Power Converter | Efficiency, 96%; lifetime, 10 years; capital cost, USD 5670 each 6 kW. | [47] |
| Solar charge controller | 1. Type, MPPT; efficiency, 98%; lifetime, 10 years; maximum voltage of PV array, 750 V; maximum capacity of PV array, 16.5 kW; capital cost, USD 1820. 2. Type, MPPT; efficiency, 98%; lifetime, 10 years; maximum voltage of PV array, 750 V; maximum capacity of PV array, 13 kW; capital cost, USD 1490. | [48] |
| Days | Daily Schedule | Price (USD/kWh) |
|---|---|---|
| Monday to Sunday | 08:00–18:00 | 0.056 |
| 22:00–08:00 | 0.045 | |
| Monday to Friday | 18:00–22:00 | 0.095 |
| Saturday and Sunday | 18:00–22:00 | 0.056 |
| G-SPVS12 | G-SPVS24 | |||||
|---|---|---|---|---|---|---|
| Year | Purchase (USD) | Sale (USD) | Grid Cost (USD) | Purchase (USD) | Sale (USD) | Grid Cost (USD) |
| 1 | 2043.72 | 1182.81 | 860.91 | 2319.01 | 1755.27 | 563.74 |
| 2 | 2074.70 | 1004.61 | 1070.09 | 2622.87 | 1734.28 | 888.59 |
| 3 | 2156.02 | 876.55 | 1279.47 | 2915.17 | 1713.15 | 1202.02 |
| 4 | 2247.73 | 758.78 | 1488.95 | 3168.50 | 1691.96 | 1476.54 |
| 5 | 2321.29 | 627.98 | 1693.31 | 3439.50 | 1670.65 | 1768.85 |
| 6 | 2494.87 | 586.61 | 1908.26 | 3608.91 | 1649.29 | 1959.62 |
| 7 | 2675.31 | 550.73 | 2124.58 | 3771.63 | 1627.85 | 2143.78 |
| 8 | 2748.82 | 490.43 | 2258.39 | 3942.58 | 1606.37 | 2336.21 |
| 9 | 2932.79 | 461.87 | 2470.92 | 4112.17 | 1584.80 | 2527.37 |
| 10 | 3108.75 | 428.01 | 2680.74 | 4275.04 | 1563.18 | 2711.86 |
| 11 | 3338.51 | 415.63 | 2922.88 | 4446.18 | 1541.55 | 2904.63 |
| 12 | 3537.47 | 403.32 | 3134.15 | 4615.95 | 1519.90 | 3096.05 |
| 13 | 3819.82 | 391.12 | 3428.70 | 4778.99 | 1498.20 | 3280.79 |
| 14 | 3875.37 | 378.98 | 3496.39 | 4950.33 | 1476.54 | 3473.79 |
| 15 | 4073.50 | 366.95 | 3706.55 | 5156.04 | 1454.91 | 3701.13 |
| Total | 43,448.67 | 8924.38 | 34,524.29 | 58,122.87 | 24,087.90 | 34,034.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amoroso, F.; Hidalgo-León, R.; Muñoz, K.; Urquizo, J.; Singh, P.; Soriano, G. Techno-Economic Assessment of PV Power Systems to Power a Drinking Water Treatment Plant for an On-Grid Small Rural Community. Energies 2023, 16, 2027. https://doi.org/10.3390/en16042027
Amoroso F, Hidalgo-León R, Muñoz K, Urquizo J, Singh P, Soriano G. Techno-Economic Assessment of PV Power Systems to Power a Drinking Water Treatment Plant for an On-Grid Small Rural Community. Energies. 2023; 16(4):2027. https://doi.org/10.3390/en16042027
Chicago/Turabian StyleAmoroso, Fernando, Rubén Hidalgo-León, Kevin Muñoz, Javier Urquizo, Pritpal Singh, and Guillermo Soriano. 2023. "Techno-Economic Assessment of PV Power Systems to Power a Drinking Water Treatment Plant for an On-Grid Small Rural Community" Energies 16, no. 4: 2027. https://doi.org/10.3390/en16042027
APA StyleAmoroso, F., Hidalgo-León, R., Muñoz, K., Urquizo, J., Singh, P., & Soriano, G. (2023). Techno-Economic Assessment of PV Power Systems to Power a Drinking Water Treatment Plant for an On-Grid Small Rural Community. Energies, 16(4), 2027. https://doi.org/10.3390/en16042027











