Abstract
A natural laminar flow (NLF) airfoil is designed to reduce drag by expanding laminar flow areas. In-depth knowledge of transition performance is essential for its aerodynamic design. The k-ω-γ-Reθ framework, which consists of the SST k-ω turbulence model and γ-Reθ transition model, is employed to simulate transitional flows around an NLF wing RAE5243 airfoil. The transition performances of the RAE5243 airfoil under various values of turbulent intensity, temperature, angle of attack, and Mach number are simulated and compared. The results show that the rise of inflow turbulent intensity will promote an earlier transition on both the suction and pressure sides. The influence of wall temperature on transition is limited. The rise of angle of attack will lead to an earlier transition on the pressure side but a later transition on the suction side. With the rise of Mach number, the transition happens earlier under a zero and positive angle of attack but later under a negative angle of attack. In addition, the correlation of transition onset locations with respect to turbulent intensity, surface temperature, angle of attack, and Mach number is established based on numerical results.
1. Introduction
The laminar-turbulent transition is a typical flow phenomenon inside boundary layers, and it is related to flow instability, friction resistance, and heat transfer [1,2]. Because of the significant influence of transition on flow characteristics, it has become a hotspot and difficulty in aerodynamic design [3,4,5]. The natural laminar flow (NLF) and hybrid laminar flow (HFL) aerodynamic designs have attracted many scholars’ attention, since the flow friction, aerodynamic heat, and aerodynamic noise can be greatly reduced under a laminar state. These types of aerodynamic designs rely on knowledge of the transition, especially its onset, and therefore various studies have been carried out to predict the transition process.
The Reynolds averaged Navier–Stokes (RANS) method is the most commonly used computational fluid dynamics (CFD) approach in engineering practice [6,7], since it can seek a balance between simulation accuracy and calculation cost [8,9]. Therefore, most transition models are coupled with the RANS framework, and the transition model based on intermittency mode is the most popular type. The intermittency γ is defined by the occurrence probability of turbulent fluctuation, which is equal to 0 in a laminar boundary layer, and equal to 1 in fully turbulent flow. Dhawan established a prediction model of intermittency along the streamwise direction according to experimental data [10], which was an early attempt to estimate the transition process using intermittency. To improve the accuracy and generality of intermittency mode, the transport equations of intermittency have been constructed by different scholars [11,12]. The intermittency mode is effective in estimating the transition process from laminar to turbulent flow, but it cannot be employed as the criterion to predict transition onset directly. Other parameters are applied to serve as onset criteria, including laminar kinetic energy kL and momentum thickness Reynolds number Reθ. The concept of laminar kinetic energy kL was first proposed by Bradshaw [13]. According to experimental data, it is considered that the energy in the transition region can be split into laminar kinetic energy and turbulent energy, and the laminar kinetic energy plays a vital role in amplifying perturbations and bursting transitions before the transition. The transport equation of laminar kinetic energy has also been constructed in different forms by various scholars [14,15]. The momentum thickness Reynolds number is another commonly used parameter as transition criterion. The relation between Reθ and turbulent intensity is established empirically according to experiments with a flat plate under a varying pressure gradient [16,17]. However, nonlocal variables are required in the established empirical relation, and the transport equation of momentum thickness Reynolds number has also been constructed to solve its local distribution accurately [18]. So far, based on the combination of RANS framework, intermittency mode, laminar kinetic energy, and momentum thickness Reynolds number, different types of transition models have been developed and implemented into CFD codes, such as k-ω-γ mode [19,20], k-ε-γ-kL mode [21], and k-ω-γ-Reθ mode [7,18].
With the development of a transition model with sufficient accuracy and efficiency, the aerodynamic design of an NLF airfoil has been greatly improved using numerical techniques. The transition modes based on linear stability theory [22,23,24] and eN [25,26] method are widely employed in the numerical simulations of transitional flow around an NLF airfoil. Since these methods always require non-local boundary-layer parameters, and these are difficult to implement in RANS codes, the k-ω-γ mode [27,28] and k-ω-γ-Reθ [30,31,32] mode have become more widely used in RANS solvers to investigate the flow structure around an NLF airfoil. By means of these numerical techniques, various optimization algorithms are employed to improve the aerodynamic performance of an NLF airfoil, including the adjoint method [27,28], particles swarm optimization [29], and genetic algorithm [30,31]. However, despite the various studies on aerodynamic design, comprehensive investigations on the aerodynamic characteristics of NLF airfoils are relatively rare.
According to the best knowledge of the authors, the k-ω-γ-Reθ transition model, as a typical representative of the transition model, has proven its effectiveness in a large number of numerical simulations, making it an important and efficient tool for investigating the transition characteristics of airfoils. However, systematic analysis of the influence of different operation conditions on the transition characteristics is relatively limited. It is of great significance to clarify the correlation between the transition position and operation conditions. To this end, in the present paper, the k-ω-γ-Reθ transition model is employed to investigate the transitional flow around an NLF wing RAE5243 airfoil [32] under various conditions. The influences of turbulent intensity, temperature, angle of attack, and Mach number on transition location and aerodynamic characteristics are discussed and analyzed, which can provide a guide for the aerodynamic design of an NLF airfoil under wide operating conditions.
2. Numerical Method
2.1. Transition Model
The k-ω-γ-Reθ transition model [7], which is coupled with the SST k-ω turbulence model [6], is applied in the present study. The governing equations of turbulent kinetic energy k, turbulent frequency ω, intermittency γ, and momentum thickness Reynolds number Reθ are listed as follows:
The details of each source term in the above governing equations can be checked in the previous literature [6,7], and the default values of model constants are employed in the present study. In the k-ω-γ-Reθ transition model, the governing equation of intermittency γ is solved to predict the development from laminar flow to turbulent flow, and the governing equation of momentum thickness Reynolds number Reθ is employed to evaluate the transition onset. The main advantage of the γ-Reθ transition model lies in the fact that only local flow variables, rather than the integral of the boundary layer flow, are required during simulation, and therefore it can be easily coupled with other turbulence models.
2.2. Physical Model and Computational Domain
The NLF wing RAE5243 airfoil [32,33] with chord length C = 0.24 m is investigated in the present study. A three-dimensional computational domain with a size of 10C × 2C × C is established, as shown in Figure 1. The inlet of the computational domain is set at the location 3C away from the leading edge of the airfoil, and the outlet is set at the location 7C downstream the leading edge. The height of the computational domain is two times the chord length, and the spanwise length of the computational domain is set the same as the chord length. In the present numerical simulation, a three-dimensional compressible transitional flow around the airfoil under steady state is considered. The density of the fluid is subject to the ideal gas equation of state, and the Sutherland model is employed to determine fluid viscosity.
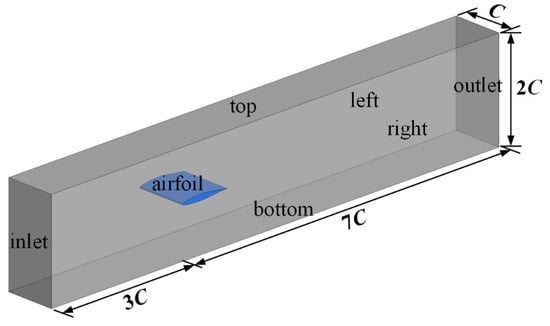
Figure 1.
Computational domain.
The commercial software ANSYS ICEM 19.0 is employed to generate the hexahedral structured mesh in the computational domain. To account for the mesh requirement for simulating the transitional flow, mesh refinement is employed around the airfoil surface. The maximum value of y+ on the airfoil surface is within 2, and most values of y+ are at the level of 1. The gird growth ratio near the surface is equal to 1.05. The mesh distribution around the airfoil surface is illustrated in Figure 2.

Figure 2.
Mesh distribution.
2.3. Numerical Settings
The commercial CFD software ANSYS Fluent 19.0 is employed to solve the steady transitional flow around the RAE5243 airfoil. The k-ω-γ-Reθ turbulence and transition coupled model described in Section 2.1 is applied in the present simulation. The pressure-based solver is used to simulate these subsonic and transonic flows, and the SIMPLEC algorithm is used for pressure-velocity coupling. For the boundary conditions, a pressure far-field condition is given at the inlet, with total temperature of 303 K and total pressure of 1 atm, and a pressure outlet condition is given at the outlet. The free slip and adiabatic conditions are imposed on the top and bottom walls of the domain, and the periodic condition is applied on the left and right boundaries. The airfoil surface is treated as a no-slip and isothermal wall in the present simulation. Since steady states are considered in the present study, the simulations start from freestream values in the entire domain.
2.4. Independence Test of Mesh
Mesh quantity can significantly influence the simulation results. In order to validate the independence of the employed mesh, four sets of mesh are employed in the present study, and the simulation results of the lift coefficient cL and drag coefficient cD are compared. The mesh quantity and corresponding simulation results are listed in Table 1.

Table 1.
Independence test of mesh.
During the independence test of the mesh, the mesh distribution along the spanwise direction and normal direction remains the same, while the grids along the streamwise direction gradually increase. Therefore, the mesh quantity rises from 2.39 × 106 to 4.43 × 106, with streamwise grids rising from 282 to 564. From Table 1, it can be seen that the lift coefficient and drag coefficient hardly vary when the mesh reaches 3.75 × 106. To find a tradeoff between computation cost and simulation accuracy, Mesh 3, with 3.75 × 106 elements, is employed for the following simulations.
2.5. Verification of Numerical Methods
The experimental results of an NLF(1)-0416 airfoil [34,35] are referred to in the present study to verify the accuracy of the numerical methods. The same size of computational domain and the same topology of mesh as the RAE5243 airfoil are established. The numerical methods mentioned in Section 2.3 are also applied for the NLF(1)-0416 airfoil. The freestream incoming flow condition for the NLF(1)-0416 airfoil includes the Mach number Ma = 0.1, the Reynolds number Re = 2.0 × 106, the static temperature T∞ = 215.91 K, and turbulent intensity of 0.03%. The experimental and numerical results of the pressure coefficient cp = (p − p∞)/(0.5ρu∞2) under these conditions are illustrated in Figure 3, where p, ρ, and u denote pressure, density, and velocity, respectively, and subscript ∞ represent freestream.
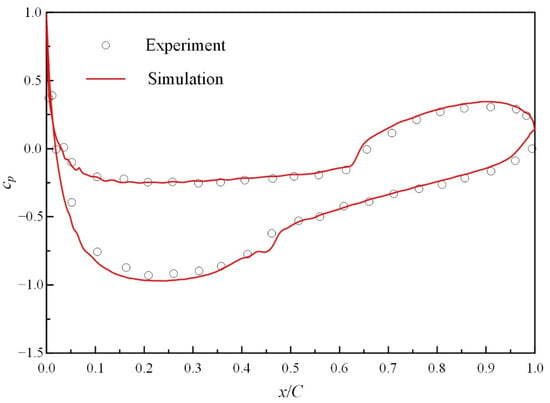
Figure 3.
Pressure coefficient around NLF(1)-0416 airfoil.
From Figure 3, it can be seen that the experimental and numerical pressure coefficients along the streamwise direction agree well, and the sudden rise of pressure coefficient due to transition onset can be captured. Therefore, the accuracy of the numerical methods can be validated.
In addition, experimental measurement for the RAE5243 airfoil is also carried out by means of the technique of temperature-sensitive paint (TSP) [33], and the only difference lies in the surface of the airfoil being treated as an adiabatic wall rather than a constant-temperature wall. The airfoil is tested in a wind tunnel with channel walls. Therefore, it is reasonable to assume free-slip boundary conditions on the side walls to avoid the interaction between boundary layer and shock wave under no-slip boundary conditions. In addition, the experimental measurement is conducted within a time in the order of minutes, so the wall of the airfoil can be treated as adiabatic. Following these experimental settings, the boundary condition for the surface of the airfoil is revised into an adiabatic wall, and the other numerical methods remain the same as those mentioned in Section 2.3. The RAE5243 airfoil with three angles of attack (α = −3°, 0°, 3°) under a Mach number of 0.4 is tested in the present research. Figure 4 illustrates the distribution of temperature along the streamwise direction on the suction surface. According to Figure 4, the sudden variation of temperature due to transition onset can be predicted accurately, which verifies the accuracy of the employed numerical methods again. It can be seen from Figure 4 that the main difference between the experimental and numerical results appears at the leading and trailing edge of the airfoil. In the present experiment, the TSP technique is employed to measure the distribution of temperature on the airfoil surface. Although the insulation paint is coated on the airfoil surface to achieve adiabatic conditions, a certain heat flux still appears at the leading edge and trailing edge of the airfoil due to the large temperature gradient and thin thickness. Therefore, the distribution of temperature at both ends is more significantly affected by heat conduction effects and no longer meets the conditions of adiabatic walls, which is still the main shortcoming of the TSP technique. Despite this, the agreement on the transition onset location between the experimental and numerical results validates the reliability of the present numerical method.
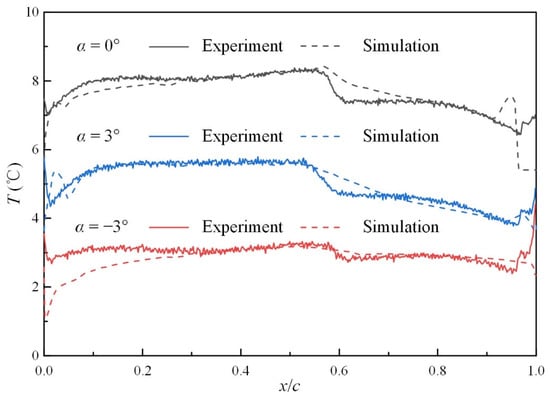
Figure 4.
Temperature around RAE5243 airfoil.
3. Result and Discussion
Using the verified numerical methods, the aerodynamic performance of an RAE5243 airfoil, with a special emphasis on the transition onset location under various conditions, is investigated in the present research, including turbulent intensity, temperature, angle of attack, and Mach number. The angle of attack is defined by the angle between the chord line of the airfoil and the inflow direction. In the present study, we built models of airfoils under various angles of attack and generated the corresponding meshes. The operating conditions for the present study are listed in Table 2. These conditions are determined according to the range of conditions of interest and the range of parameters in which our experiments can be carried out. For turbulent intensity and angle of attack, the conditions are set almost uniformly within the range. For surface temperature, the conditions are chosen at equal intervals on both sides of the freestream temperature. For Mach number, the conditions are set with decreasing intervals within the range due to more complex flow under high Mach number. Detailed results of the simulated transition onset location are listed in Appendix A.

Table 2.
Operating conditions.
3.1. Influence of Turbulent Intensity
To investigate the influence of turbulent intensity on transitional flow around an RAE5243 airfoil, the other conditions are fixed as Ma = 0.4 and α = 0°. The transition onset locations under different operating conditions are depicted in Figure 5. According to Figure 5, it can be seen that a rise of inflow turbulent intensity will promote earlier transition on both the suction and pressure sides, and the influence on the suction side is larger than that on the pressure side.
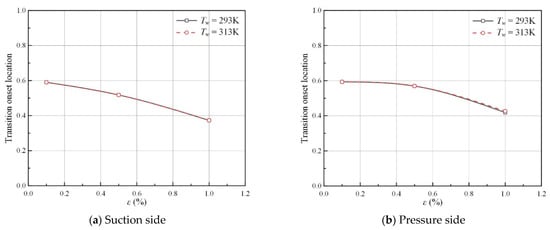
Figure 5.
Transition onset locations under various turbulent intensities (α = 0°, Ma = 0.4).
The distribution of intermittency on the midplane of the RAE5243 airfoil under different levels of inflow turbulent intensity is depicted in Figure 6. It can be clearly seen that, with the rise of turbulent intensity, the non-zero region of intermittency gradually expands, and the thickness of the high-intermittency region around the airfoil also increases. This distribution is related the earlier transition onset under higher inflow turbulent intensity.
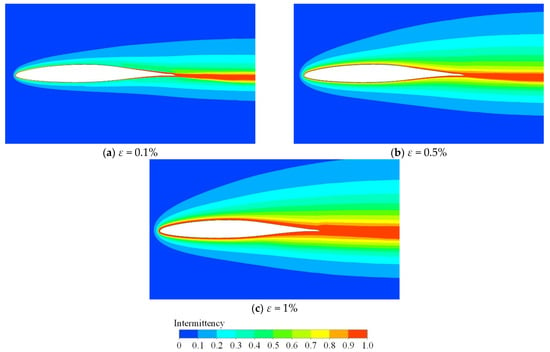
Figure 6.
Influence of turbulent intensity on distribution of intermittency (Tw = 293 K, α = 0°, Ma = 0.4).
Figure 7 shows the distribution of intermittency along the streamwise direction under various turbulent intensities. An obvious sharp rise of the intermittency appears on both the suction and pressure sides, which indicates the onset of the transition. After the sharp rise, the intermittency gradually decreases on the suction side, while it remains at a relatively stable level on the pressure side. Finally, the intermittency rises rapidly near the trailing edge of the airfoil.
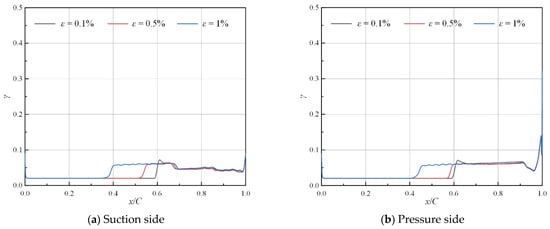
Figure 7.
Distribution of intermittency along streamwise direction under various levels of turbulent intensity (Tw = 293 K, α = 0°, Ma = 0.4).
3.2. Influence of Surface Temperature
The influence of the RAE5243 airfoil’s wall temperature on the transition is discussed in this section under various angles of attack and Mach numbers, while the turbulent intensity is fixed at a value of 0.5%. The simulation results of the transition onset location are depicted in Figure 8, Figure 9, Figure 10 and Figure 11, with respect to different Mach numbers.
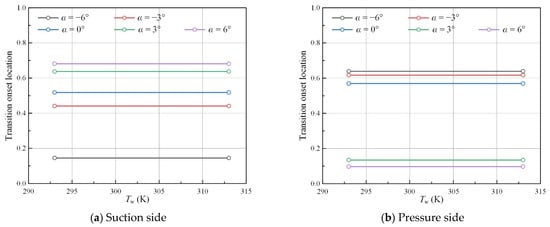
Figure 8.
Transition onset locations under various surface temperatures (ε = 0.5%, Ma = 0.4).
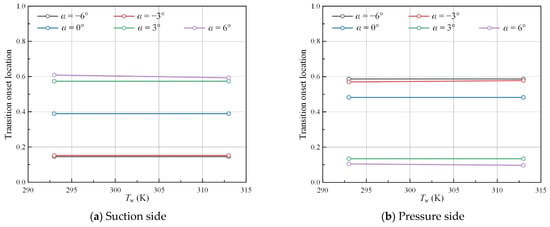
Figure 9.
Transition onset locations under various surface temperatures (ε = 0.5%, Ma = 0.6).
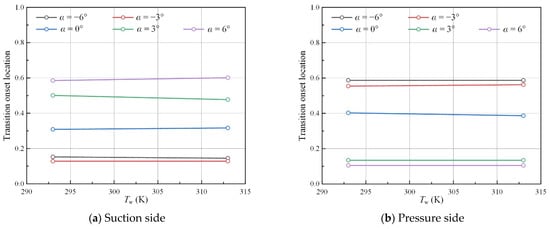
Figure 10.
Transition onset locations under various surface temperatures (ε = 0.5%, Ma = 0.7).
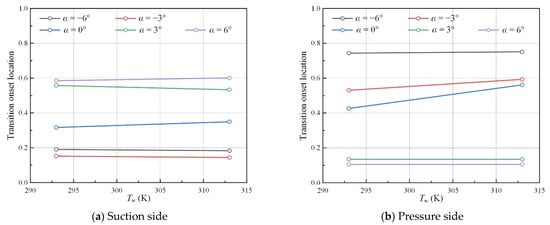
Figure 11.
Transition onset locations under various surface temperatures (ε = 0.5%, Ma = 0.75).
The influence of surface temperature on transition onset locations is relatively weak on both the suction and pressure sides. Under low-Mach-number conditions (Ma = 0.4, 0.6), the simulated transition onset location hardly varies under different temperatures. When it comes to higher Mach numbers (Ma = 0.7, 0.75), some discrepancies can be observed at different surface temperatures, especially on the suction side.
Figure 12 depicts the distribution of intermittency under two wall temperatures. The distributions under Tw = 293 K and Tw = 313 K are almost the same, and therefore the transition onset locations under these two temperatures are quite similar.
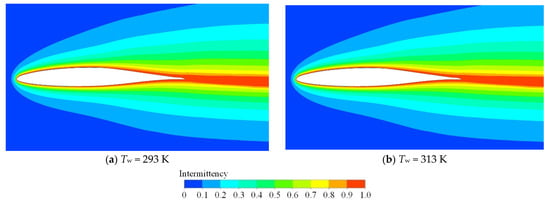
Figure 12.
Influence of surface temperature on distribution of intermittency (ε = 0.5%, α = 0°, Ma = 0.7).
The distribution of intermittency along the streamwise direction under two surface temperatures is shown in Figure 13. The distribution patterns of the intermittency on both the suction and pressure sides are basically the same as those we discussed in the previous section. Moreover, it can be seen that larger oscillations appear under higher surface temperature.
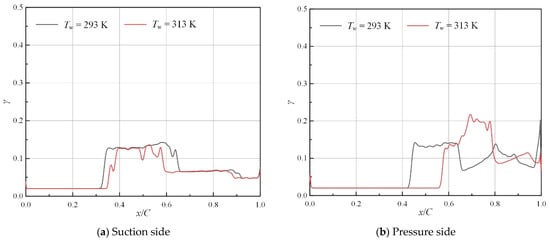
Figure 13.
Distribution of intermittency along streamwise direction under various surface temperatures (ε = 0.5%, α = 0°, Ma = 0.75).
3.3. Influence of Angle of Attack
The transition performances of the RAE5243 airfoil under different angle of attacks are compared in this section. The angles of attack vary from −6° to 6°, and the inflow turbulent intensity and surface temperature are fixed at 0.5% and 293 K, respectively. The simulated results are depicted in Figure 14.
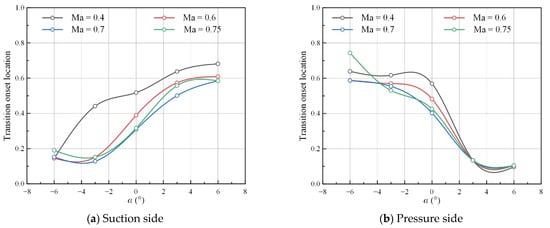
Figure 14.
Transition onset locations under various angles of attack (ε = 0.5%, Tw = 293 K).
Under all four values of Mach number, with the rise in the angle of attack from negative values to positive values, the transition on the suction side appears later, while the transition on the pressure side appears earlier. The variation of the transition onset location with respect to the angle of attack decreases as the Mach number rises. In addition, the transition onset location on the suction side is earlier than that on the pressure side under negative angles of attack, and the transition onset location on the pressure side is earlier than that on the suction side under positive angles of attacks. By comparison, under a zero angle of attack, the transition onset locations on the suction and pressure sides are relatively close.
The distribution of intermittency under various angles of attack is plotted, as shown in Figure 15. It can be found that the thickness of the non-zero region at the leeward side is always larger than that at the windward side. As the angle of attack rises from negative values to positive values, the suction side of the RAE5243 airfoil converts from windward side to leeward side, while the pressure surface is the opposite. Since the transition onset happens earlier on the suction side under a negative angle of attack and on the pressure side under a positive angle of attack, it can be concluded that the transition onset always happens earlier on the windward side.
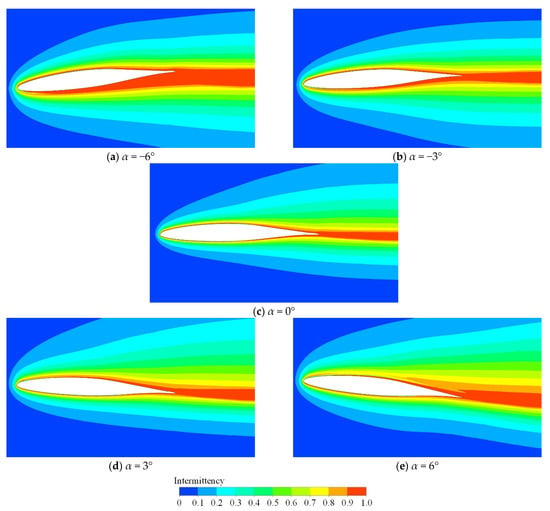
Figure 15.
Influence of angle of attack on distribution of intermittency (ε = 0.5%, Tw = 293 K, Ma = 0.6).
Figure 16 illustrates the distribution of intermittency on the suction and pressure sides under various angles of attack. Under negative angles of attack, the rapid rise of the intermittency appears near the leading edge on the suction side. Similarly, under positive angles of attack, the rapid rise of the intermittency exists near the leading edge but on the pressure side. Such a rapid rise near the leading edge can also lead to a more oscillating distribution afterwards, especially under large angles of attack (α = ±6°).
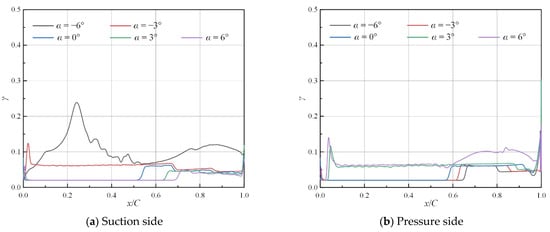
Figure 16.
Distribution of intermittency along streamwise direction under various angles of attack (ε = 0.5%, Ma = 0.4, Tw = 293 K).
3.4. Influence of Mach Number
In this section, the influence of Mach number on transition onset location is depicted in Figure 17. The values of inflow turbulent intensity and surface temperature are also fixed at 0.5% and 293 K, respectively.
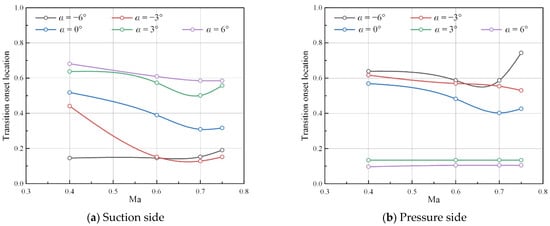
Figure 17.
Transition onset locations under various Mach numbers (ε = 0.5%, Tw = 293 K).
From Figure 17, it can be seen that the variation law of the transition onset location with respect to Mach number is related to the angles of attack. Under a negative angle of attack, the transition happens later with the rise of the Mach number. By comparison, under a zero or positive angle of attack, the transition happens earlier with the rise of the Mach number.
To illustrate the influence of the Mach number on intermittency, Figure 18 and Figure 19 show the distribution of intermittency with various Mach numbers under negative and positive angles of attack, respectively. Under both negative and positive angles of attack, the non-zero regions of intermittency gradually expand as the Mach number rises. Under the relatively high Mach number (Ma = 0.75), there exists a sharp rise of intermittency on the suction side near the trailing edge. This is due to the appearance of a shock wave under a high Mach number.
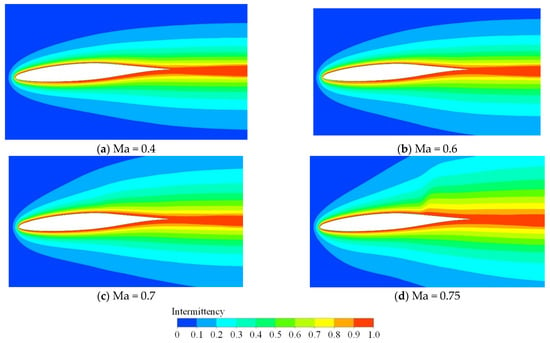
Figure 18.
Influence of Mach number on distribution of intermittency (ε = 0.5%, Tw = 293 K, α = −3°).
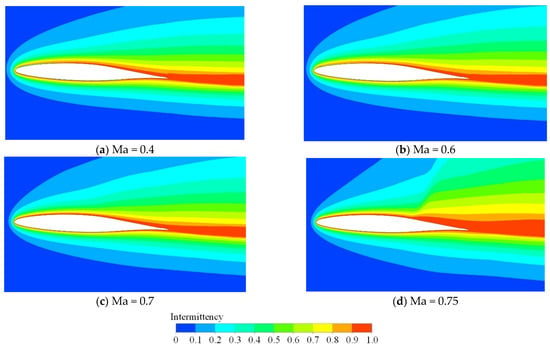
Figure 19.
Influence of Mach number on distribution of intermittency (ε = 0.5%, Tw = 293 K, α = 3°).
The influence of Mach number on the streamline distribution of the intermittency under negative and positive angles of attack is illustrated in Figure 20 and Figure 21, respectively. As the Mach number increases, the intermittency can rise to a higher level, associated with a more complicated distribution of larger oscillations. This complicated distribution is even more significant on the suction side under negative angles of attack, and on the pressure side under positive angles of attack.
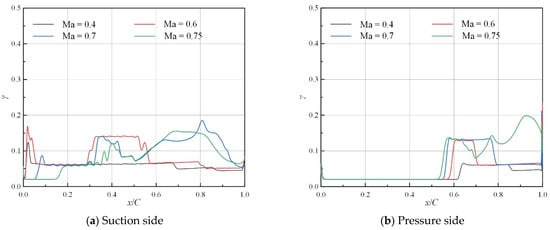
Figure 20.
Distribution of intermittency along streamwise direction under various Mach numbers (ε = 0.5%, α = −3°, Tw = 293 K).
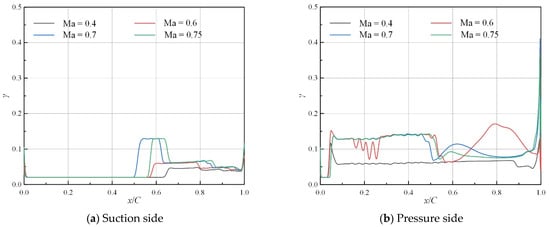
Figure 21.
Distribution of intermittency along streamwise direction under various Mach numbers (ε = 0.5%, α = 3°, Tw = 293 K).
3.5. Correlation
On the basis of the above numerical results, the following correlation of transition onset locations with respect to turbulent intensity, surface temperature, angle of attack, and Mach number is established.
where xtol,s and xtol,p denote the transition onset location on the suction side and the pressure side, respectively. θ is non-dimensional angle of attack normalized within the range of [−π/2, π/2], as follows:
and τ is the non-dimensional surface temperature normalized by freestream total temperature T∞, as follows:
The above relations are determined by multiple linear regression based on the least squares method in logarithmic form. The R-square values for transition onset locations on the suction and pressure sides are 0.8621 and 0.8097, respectively. By means of the above correlations, the average errors of predicted transition onset locations on suction and pressure sides are 15.44% and 25.72%, respectively. Figure 22 shows the distribution of simulation–prediction pairs. It can be found that most prediction results are located within the error range of ±20%.
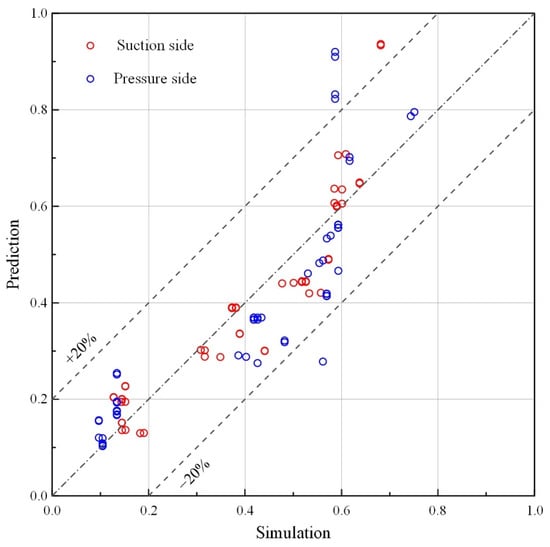
Figure 22.
Distribution of simulation–prediction pairs.
4. Conclusions
In the present study, a numerical investigation based on the k-ω-γ-Reθ framework is carried out on transitional flows around an RAE5243 airfoil. The numerical methods are validated by NLF airfoil results and experimental measurement. The influences of inflow turbulent intensity, wall temperature, angle of attack, and Mach number on transition performance are analyzed.
The numerical results show that the rise of inflow turbulent intensity will promote an earlier transition on both the suction and pressure sides. The influence of wall temperature on transition is limited. The rise of angle of attack will lead to an earlier transition on the pressure side but a later transition on the suction side. With the rise of Mach number, the transition happens earlier under a zero or positive angle of attack but later under a negative angle of attack.
Based on the numerical results, the correlation of transition onset locations with respect to turbulent intensity, surface temperature, angle of attack, and Mach number is established. The average prediction errors on the suction and pressure sides are 15.44% and 25.72%, respectively.
Author Contributions
Conceptualization, H.W., M.L. and L.T.; methodology, H.W. and M.L.; software, H.W. and M.L; validation, H.W. and M.L.; formal analysis, H.W. and M.L; investigation, H.W. and M.L; resources, H.W., M.L. and L.T.; data curation, H.W., M.L. and L.T.; writing—original draft preparation, H.W. and M.L.; writing—review and editing, M.L. and L.T.; visualization, H.W. and M.L.; supervision, L.T., X.L. and B.Z.; project administration, L.T. and B.Z.; funding acquisition, H.W. and L.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2020YFB1901401), the State Key Laboratory of Hydroscience and Engineering (2021-KY-04).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| γ | intermittency |
| k | turbulent kinetic energy |
| ω | turbulent frequency |
| kL | laminar kinetic energy |
| Reθ | momentum thickness Reynolds number |
| ρ | density |
| ui | velocity |
| μ | dynamic viscosity |
| μt | turbulent eddy viscosity |
| σk | constant in governing equation of k |
| γeff | effective intermittency |
| S | strain rate |
| β | model coefficient |
| σω | constant in governing equation of ω |
| αω | model coefficient in governing equation of ω |
| F1 | function in k-ω turbulence model |
| σω,2 | constant in governing equation of ω |
| Ce1 | constant in governing equation of γ |
| Ca1 | constant in governing equation of γ |
| Flength | empirical correlation that controls the length of the transition region |
| Fonset | empirical correlation that controls the transition onset location |
| Ce2 | constant in governing equation of γ |
| Ca2 | constant in governing equation of γ |
| Ω | vorticity magnitude |
| Fturb | model coefficient in governing equation of γ |
| cθ | constant in governing equation of Reθ |
| Reθt | transition Reynolds number |
| Fθ | blending function to turn off the source term in the boundary layer |
| σθ | constant in governing equation of Reθ |
| C | chord length |
| ε | turbulent intensity |
| α | angle of attack |
| Tw | surface temperature |
| xtol,s | transition onset location on suction side |
| xtol,p | transition onset location on pressure side |
| θ | normalized angle of attack |
| τ | normalized surface temperature |
Appendix A

Table A1.
Influence of turbulent intensity on transition onset location (α = 0°, Ma = 0.4).
Table A1.
Influence of turbulent intensity on transition onset location (α = 0°, Ma = 0.4).
| ε/% | Tw/K | Transition Onset Location | |
|---|---|---|---|
| Suction Side | Pressure Side | ||
| 0.1 | 293 | 0.5903 | 0.5931 |
| 0.5 | 293 | 0.5180 | 0.5694 |
| 1 | 293 | 0.3731 | 0.4182 |
| 0.1 | 313 | 0.5903 | 0.5931 |
| 0.5 | 313 | 0.5180 | 0.5694 |
| 1 | 313 | 0.3731 | 0.4262 |

Table A2.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.4).
Table A2.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.4).
| Tw/K | α/° | Transition Onset Location | |
|---|---|---|---|
| Suction Side | Pressure Side | ||
| 293 | −6 | 0.1447 | 0.6391 |
| 313 | −6 | 0.1447 | 0.6391 |
| 293 | −3 | 0.4409 | 0.6169 |
| 313 | −3 | 0.4409 | 0.6169 |
| 293 | 0 | 0.5180 | 0.5694 |
| 313 | 0 | 0.5180 | 0.5694 |
| 293 | 3 | 0.6374 | 0.1344 |
| 313 | 3 | 0.6374 | 0.1344 |
| 293 | 6 | 0.6815 | 0.0969 |
| 313 | 6 | 0.6815 | 0.0969 |

Table A3.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.6).
Table A3.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.6).
| Tw/K | α/° | Transition Onset Location | |
|---|---|---|---|
| Suction Side | Pressure Side | ||
| 293 | −6 | 0.1447 | 0.5869 |
| 313 | −6 | 0.1447 | 0.5869 |
| 293 | −3 | 0.1519 | 0.5697 |
| 313 | −3 | 0.1519 | 0.5776 |
| 293 | 0 | 0.3892 | 0.4819 |
| 313 | 0 | 0.3892 | 0.4819 |
| 293 | 3 | 0.5732 | 0.1344 |
| 313 | 3 | 0.5732 | 0.1344 |
| 293 | 6 | 0.6092 | 0.1048 |
| 313 | 6 | 0.5931 | 0.0969 |

Table A4.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.7).
Table A4.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.7).
| Tw/K | α/° | Transition Onset Location | |
|---|---|---|---|
| Suction Side | Pressure Side | ||
| 293 | −6 | 0.1523 | 0.5869 |
| 313 | −6 | 0.1447 | 0.5869 |
| 293 | −3 | 0.1278 | 0.5539 |
| 313 | −3 | 0.1278 | 0.5618 |
| 293 | 0 | 0.3086 | 0.4023 |
| 313 | 0 | 0.3166 | 0.3863 |
| 293 | 3 | 0.5009 | 0.1344 |
| 313 | 3 | 0.4768 | 0.1344 |
| 293 | 6 | 0.5851 | 0.1048 |
| 313 | 6 | 0.6012 | 0.1048 |

Table A5.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.75).
Table A5.
Influence of surface temperature on transition onset location (ε = 0.5%, Ma = 0.75).
| Tw/K | α/° | Transition Onset Location | |
|---|---|---|---|
| Suction Side | Pressure Side | ||
| 293 | −6 | 0.1904 | 0.7436 |
| 313 | −6 | 0.1827 | 0.7511 |
| 293 | −3 | 0.1519 | 0.5303 |
| 313 | −3 | 0.1439 | 0.5933 |
| 293 | 0 | 0.3166 | 0.4262 |
| 313 | 0 | 0.3489 | 0.5614 |
| 293 | 3 | 0.5572 | 0.1344 |
| 313 | 3 | 0.5331 | 0.1344 |
| 293 | 6 | 0.5851 | 0.1048 |
| 313 | 6 | 0.6012 | 0.1048 |

Table A6.
Influence of angle of attack on transition onset location (ε = 0.5%, Tw = 293 K).
Table A6.
Influence of angle of attack on transition onset location (ε = 0.5%, Tw = 293 K).
| α/° | Ma | Transition Onset Location | |
|---|---|---|---|
| Suction Side | Pressure Side | ||
| −6 | 0.4 | 0.1447 | 0.6391 |
| −3 | 0.4 | 0.4409 | 0.6169 |
| 0 | 0.4 | 0.5180 | 0.5694 |
| 3 | 0.4 | 0.6374 | 0.1344 |
| 6 | 0.4 | 0.6815 | 0.0969 |
| −6 | 0.6 | 0.1447 | 0.5869 |
| −3 | 0.6 | 0.1519 | 0.5697 |
| 0 | 0.6 | 0.3892 | 0.4819 |
| 3 | 0.6 | 0.5732 | 0.1344 |
| 6 | 0.6 | 0.6092 | 0.1048 |
| −6 | 0.7 | 0.1523 | 0.5869 |
| −3 | 0.7 | 0.1278 | 0.5539 |
| 0 | 0.7 | 0.3086 | 0.4023 |
| 3 | 0.7 | 0.5009 | 0.1344 |
| 6 | 0.7 | 0.5851 | 0.1048 |
| −6 | 0.75 | 0.1904 | 0.7436 |
| −3 | 0.75 | 0.1519 | 0.5303 |
| 0 | 0.75 | 0.3166 | 0.4262 |
| 3 | 0.75 | 0.5572 | 0.1344 |
| 6 | 0.75 | 0.5851 | 0.1048 |

Table A7.
Influence of Mach number on transition onset location (ε = 0.5%, Tw = 293 K).
Table A7.
Influence of Mach number on transition onset location (ε = 0.5%, Tw = 293 K).
| α/° | Ma | Transition Onset Location | |
|---|---|---|---|
| Suction Side | Pressure Side | ||
| −6 | 0.4 | 0.1447 | 0.6391 |
| −6 | 0.6 | 0.1447 | 0.5869 |
| −6 | 0.7 | 0.1523 | 0.5869 |
| −6 | 0.75 | 0.1904 | 0.7436 |
| −3 | 0.4 | 0.4409 | 0.6169 |
| −3 | 0.6 | 0.1519 | 0.5697 |
| −3 | 0.7 | 0.1278 | 0.5539 |
| −3 | 0.75 | 0.1519 | 0.5303 |
| 0 | 0.4 | 0.5180 | 0.5694 |
| 0 | 0.6 | 0.3892 | 0.4819 |
| 0 | 0.7 | 0.3086 | 0.4023 |
| 0 | 0.75 | 0.3166 | 0.4262 |
| 3 | 0.4 | 0.6374 | 0.1344 |
| 3 | 0.6 | 0.5732 | 0.1344 |
| 3 | 0.7 | 0.5009 | 0.1344 |
| 3 | 0.75 | 0.5572 | 0.1344 |
| 6 | 0.4 | 0.6815 | 0.0969 |
| 6 | 0.6 | 0.6092 | 0.1048 |
| 6 | 0.7 | 0.5851 | 0.1048 |
| 6 | 0.75 | 0.5851 | 0.1048 |
References
- Fedorov, A. Transition and Stability of High-Speed Boundary Layers. Annu. Rev. Fluid Mech. 2011, 43, 79–95. [Google Scholar] [CrossRef]
- Jovanovic, M.R. From Bypass Transition to Flow Control and Data-Driven Turbulence Modeling: An Input–Output Viewpoint. Annu. Rev. Fluid Mech. 2021, 53, 311–345. [Google Scholar] [CrossRef]
- Chen, X.; Dong, S.; Tu, G.; Yuan, X.; Chen, J. Boundary layer transition and linear modal instabilities of hypersonic flow over a lifting body. J. Fluid Mech. 2022, 938, A8. [Google Scholar] [CrossRef]
- Halila, G.L.O.; Martins, J.R.A.; Fidkowski, K.J. Adjoint-based aerodynamic shape optimization including transition to turbulence effects. Aerosp. Sci. Technol. 2020, 107, 106243. [Google Scholar] [CrossRef]
- Halila, G.L.O.; Antunes, A.P.; da Silva, R.G.; Azevedo, J.L.F. Effects of boundary layer transition on the aerodynamic analysis of high-lift systems. Aerosp. Sci. Technol. 2019, 90, 233–245. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Xiao, H.; Cinnella, P. Quantification of model uncertainty in RANS simulations: A review. Prog. Aerosp. Sci. 2019, 108, 1–31. [Google Scholar] [CrossRef]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Dhawan, S.; Narasimha, R. Some properties of boundary layer during the transition from laminar to turbulent motion. J. Fluid Mech. 1958, 3, 418–435. [Google Scholar] [CrossRef]
- Cho, J.R.; Chung, M.K. A k-ε-γ equation turbulence model. J. Fluid Mech. 1992, 237, 301–322. [Google Scholar] [CrossRef]
- Steelant, J.; Dick, E. Modeling of laminar-turbulent transition for high freestream turbulence. ASME J. Fluids Eng. 2001, 123, 22–30. [Google Scholar] [CrossRef]
- Bradshaw, P. Turbulence: The chief outstanding difficulty of our subjects. Exp. Fluids 1994, 16, 203–216. [Google Scholar] [CrossRef]
- Mayle, R.E.; Schula, A. The path to predicting bypass transition. ASME J. Turbomach. 1997, 119, 405–411. [Google Scholar] [CrossRef]
- Walters, D.K.; Cokljat, D. A three equation eddy viscosity model for Reynolds Averaged Navier Stokes simulations of transitional flow. ASME J. Fluids Eng. 2008, 130, 121401. [Google Scholar] [CrossRef]
- Mayle, R.E. The role of laminar-turbulent transition in gas turbine engines. ASME J. Turbomach. 1991, 113, 509–537. [Google Scholar] [CrossRef]
- Abu-Ghannam, B.J.; Shaw, R. Natural transition pf boundary layers—The effects of turbulence, pressure gradient, and flow history. J. Mech. Eng. Sci. 1980, 22, 213–228. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.B.; Volker, S. Transition modelling for general purpose CFD codes. Flow Turbul. Combust. 2006, 77, 277–303. [Google Scholar] [CrossRef]
- Wang, L.; Fu, S. Modeling flow transition in a hypersonic boundary layer with Reynolds-averaged Navier-Stokes approach. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 768–774. [Google Scholar] [CrossRef]
- Fu, S.; Wang, L. RANS modeling of high-speed aerodynamic flow transition with consideration of stability theory. Prog. Aerosp. Sci. 2013, 58, 36–59. [Google Scholar] [CrossRef]
- Papp, J.L.; Dash, S.M. Rapid engineering approach to modeling hypersonic laminar to turbulent transitional flows. J. Spacecr. Rocket. 2005, 42, 467–475. [Google Scholar] [CrossRef]
- Robitaille, M.; Mosahebi, A.; Laurendeau, E. Design of adaptive transonic laminar airfoils using the γ-Reθt transition model. Aerosp. Sci. Technol. 2015, 46, 60–71. [Google Scholar] [CrossRef]
- Reeh, A.D.; Tropea, C. Behaviour of a natural laminar flow aerofoil in fight through atmospheric turbulence. J. Fluid Mech. 2015, 767, 394–429. [Google Scholar] [CrossRef]
- Malik, M.; Liao, W.; Li, F.; Choudhari, M. Discrete-Roughness-Element-Enhanced Swept-Wing Natural Laminar Flow at High Reynolds Numbers. AIAA J. 2015, 53, 2321–2334. [Google Scholar] [CrossRef]
- Rashad, R.; Zingg, D.W. Aerodynamic Shape Optimization for Natural Laminar Flow Using a Discrete-Adjoint Approach. AIAA J. 2016, 54, 3321–3337. [Google Scholar] [CrossRef]
- Shi, Y.; Mader, C.A.; He, S.; Haila, G.L.O.; Martins, J.R.R.A. Natural Laminar-Flow Airfoil Optimization Design Using a Discrete Adjoint Approach. AIAA J. 2020, 58, 4702–4722. [Google Scholar] [CrossRef]
- Xu, J.; Bai, J.; Qiao, L.; Zhang, Y.; Fu, Z. Fully Local Formulation of a Transition Closure Model for Transitional Flow Simulations. AIAA J. 2016, 54, 3015–3023. [Google Scholar] [CrossRef]
- Xu, J.; Fu, Z.; Bai, J.; Zhang, Y.; Duan, Z.; Zhang, Y. Study of boundary layer transition on supercritical natural laminar flow wing at high Reynolds number through wind tunnel experiment. Aerosp. Sci. Technol. 2018, 80, 221–231. [Google Scholar] [CrossRef]
- Li, J.; Gao, Z.; Huang, J.; Zhao, K. Robust design of NLF airfoils. Chin. J. Aeronaut. 2013, 26, 309–318. [Google Scholar] [CrossRef]
- Zhao, K.; Gao, Z.H.; Huang, J. Robust design of natural laminar flow supercritical airfoil by multi-objective evolution method. Appl. Math. Mech. 2014, 35, 191–202. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, X.; Chen, H.; Fu, S.; Duan, Z.; Zhang, Y. Supercritical natural laminar flow airfoil optimization for regional aircraft wing design. Aerosp. Sci. Technol. 2015, 43, 152–164. [Google Scholar] [CrossRef]
- Qin, N.; Wong, W.S.; Moigne, A.L. Three-dimensional contour bumps for transonic wing drag reduction. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2008, 222, 619–629. [Google Scholar] [CrossRef]
- Huang, H.; Xiong, J.; Liu, X.; Zhu, M.; Li, Y. Study of the boundary layer transition detection technique based on TSP. J. Exp. Fluid Mech. 2019, 33, 79–84. [Google Scholar]
- Somers, D.M. Design and Experimental Results for a Natural-Laminar-Flow Airfoil for General Aviation Applications; NASA Technical Paper 1861; NASA: Washington, DC, USA, 1981. [Google Scholar]
- Sammak, S.; Mojgani, R.; Boroomand, M. RANS Investigation of the Transitional Flow Over Stepped NLF(1)-0416. In Proceedings of the ASME 2012 International Mechanical Engineering Congress & Exposition, Houston, TX, USA, 9–15 November 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).