Abstract
The continuous increase in the demand for electricity makes it necessary to modernize or build new transmission lines. This, in turn, results in research that is still being carried out on the optimal use of power cables. In the paper, an improved analytical method for the determination of the current rating of power cables was proposed. The method for determining the ampacity of the power cable presented in the IEC standard assumes that power losses in the phase conductors and screens are determined by taking into account skin and the proximity effects on the basis of tabulated coefficients. The methodology proposed in the paper is based on the method presented in the IEC standard, but the power losses in the conductive elements of the cable are determined analytically, which offers higher accuracy. In order to validate the analytical method proposed in this paper, numerical calculations based on the finite element method with very fine mesh were also performed. Exemplary calculations carried out for three types of cables with use of the proposed method, IEC standard and finite elements showed very good agreement in the results. The proposed method requires more computational effort, but it offers more accurate results than the IEC standard and can be used when higher accuracy is required. It can also serve as a reference point for simplified calculations.
1. Introduction
The progressing electro-mobility and the formation of new wind farms and photovoltaic farms entail the need to build new transmission lines. The increase in the power of transmission lines and high requirements for the reliability of their operation, as well as difficulties in obtaining land for overhead lines and environmental protection requirements, especially in large urban agglomerations, force engineers to search for optimal solutions for electricity transmission devices. Due to the increased load on power grids, the existing low-power overhead lines and cable networks will have to be replaced with higher-power cable lines, and thus with a larger cross-section. It is therefore necessary to conduct scientific research on the optimal use of power cables [1,2,3,4,5].
The XLPE (cross-linked polyethylene) insulated cable is currently the main type of cable used in power networks. The service life of power cables depends on the condition of the cable insulation. The temperature of the working conductor has a fundamental influence on the condition of the cable insulation. There are many factors that determine the temperature value reached by a cable. These factors include, first of all, the value of the conducted current, the value of the rated voltage, the ambient temperature and the environmental conditions in which the cable is placed [6]. The current flowing through the working conductor generates heat and an electromagnetic field in the insulating layers of the cable. Thus, there are losses in the cable insulation layers and the generation of eddy currents in the metal sheath. The greater the value of the current flowing through the cable core, the greater the amount of heat generated. If a current exceeding the permissible value flows for a long time, the heated core melts the insulation and cable sheath, which damages the cable structure. Damage to any insulation layer of the cable significantly shortens the life of the cable [7,8,9,10].
The calculation, estimation and modeling of cable life (cable aging) are some of the basic aspects in designing cable lines. The service life of the cable does not change when the temperature of the cable is lower than the maximum permissible temperature, but it decreases exponentially when the temperature of the cable is higher [11,12,13].
In recent years, the use of power cables has been gradually increasing. Due to high initial costs, as well as the costs of installing and maintaining underground or marine cables, it seems necessary to use cable systems with the maximum current carrying capacity. In addition, it is necessary to find a possible fault location and the overall maintenance or repair time is longer than for overhead lines. Therefore, optimal design, condition monitoring and proactive maintenance are important to extending the service life of this type of device [14,15,16,17,18].
The literature on the subject includes many works on the research of cable service life, ampacity, aging, temperature field, etc. The calculation of power cables’ ampacity is also the subject of several standards [19]. In general, the methods used to determine current carrying capacity can be divided into two groups: analytical and numerical. The analytical method is based on the IEC 60287 standard and uses the equivalent thermal resistance method. The analytical method has high efficiency and accuracy in determining the ampacity of the direct buried cables, but it is not suitable for forced cooling. Numerical methods are used for more complex issues. So far, several professional computer programs used to calculate current carrying capacity have been developed for various cable configurations, taking into account different soil layers and installation conditions, such as CYMCAP and CAAS [4,20]. Numerical methods allow one to simulate real working conditions and perform calculations of coupling of many physical fields. Therefore, in recent years, numerical methods have become the main approach used to analyze the temperature and current rating of cables [20,21].
Despite the presence of more and more advanced and sophisticated computational programs, many researchers dealing with the subject of power cables still use more or less complex analytical methods that can then be implemented in any standard software to aid engineers. The determination of cable impedance and the assessment of the proximity effect impact on power losses in individual elements of power cables, as shown in publications [22,23,24,25,26], are conducted using analytical methods. In the case of power losses in the cable, research is still being carried out to improve the method contained in the IEC 60287 standard [24,27,28,29]. There are also ongoing studies on eddy current losses and hysteresis losses occurring in individual layers of the cable [30]. In addition, a number of studies on the thermal behavior of cables have been conducted [31].
Determining how much heat is generated in a cable during power transmission is critical to ensuring the long-term, reliable operation of these devices. The literature in which the thermal behavior of cables has been presented, both from an analytical perspective and with the use of various types of numerical techniques, is particularly rich [32,33,34,35]. The literature that deals with the work of HV cables buried under the seabed is somewhat more modest. Accurate calculations of the current carrying capacity and temperature field around the submarine cable are of key importance to the optimization of construction costs and the efficiency of the use of a submarine transmission line [4,36,37].
The determination of the continuous allowable cable current depends on various factors, which can generally be classified as internal or external. Internal factors include, among others, the maximum allowable temperature of the individual cable components, whereas external ones take into account the thermal characteristics of the environment in which the cable is laid [38,39].
In this paper, an improved analytical method for the determination of the current rating of the power cable is proposed. The analytical method to determine the ampacity of the power cable presented in the IEC standard and used by many scientists and engineers assumes that the power losses in the phase conductors and screens are determined by taking into account the skin and proximity effects on the basis of tabulated coefficients. The method proposed by the authors of this paper is based on the method presented in the IEC standard, but the power losses in the phase conductors of the cable and the screens are determined analytically, taking into account the skin and proximity effects. It was assumed that the phase wires are cylindrical conductors, and the screens are tubular conductors. In addition to conduction losses, analytical formulas that enable the determination of power losses in the insulation layers of a power cable are used.
2. Current Rating of the Power Cable
2.1. General Methodology
The amount of energy carried by the cable can vary with time. The frequency of the voltage or current can be constant or it also change with time. All these factors influence the current rating of the cable. Common methods used to determine the current rating assume that the cable temperature reaches a steady state after a long period of continuous operation. Therefore, a steady state is assumed, to which a substitute scheme is assigned and calculations are performed for such a scheme. For this load pattern, only the heat generated, the thermal resistance of the system and the temperature limits need to be considered. The current rating is usually calculated using an equivalent thermal model (Figure 1) [2].
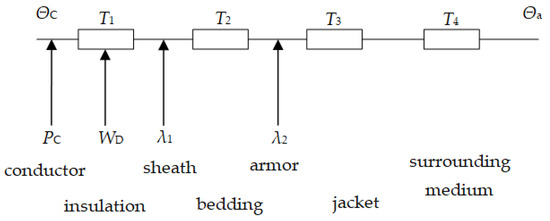
Figure 1.
Thermal model of the power cable. PC: power losses in the phase conductors; WD: dielectric losses; ΘC: conductor temperature; Θa: ambient temperature; λ1, λ2: loss factors; T1, T2, T3, T4: thermal resistances.
The current rating of a power cable is determined from the commonly known formula [1,2,14]:
where
- ΔΘ is the temperature rise of the conductor above the ambient temperature [K],
- R is the conductor resistance determined for the maximum operating temperature [Ω/m],
- WD refers to the dielectric losses per length unit [W/m],
- T1 is the thermal resistance between the conductor and the screen [Km/W],
- T2 is the thermal resistance of the bedding between the screen and the armor [Km/W],
- T3 is the thermal resistance of the external jacket [Km/W],
- T4 is the thermal resistance of the surrounding medium [Km/W],
- λ1 is the screen losses factor (ratio of the total losses in the screens to the total conductor losses or ratio of losses in one sheath to the losses in one conductor),
- λ2 is the armor losses factor (ratio of the total losses in the armor to the total conductor losses, or ratio of losses in one armor to the losses in one conductor),
- n is the number of conductors in a cable.
Based on Equation (1), the following methodology for the determination of the rated current in the cable can be used:
- Establishing of the cable type and its geometrical and physical parameters.
- Determining the physical conditions in which the cable is laid.
- Assuming the acceptable increase in temperature (ΔΘ).
- Evaluating the thermal resistances of the individual insulation layers of the cable.
- Computing the resistance of the phase conductors.
- Determining the power ratios λ1 and λ2 using tables for specific placement of conductors, their material and excitation parameters.
- Evaluating the dielectric losses in a similar manner.
- Calculating the rated current of the cable.
More precise results can be obtained if the resistances, power losses in conductors and dielectric losses are calculated directly for the specific cable using analytical formulas. We deal with this problem by considering a three-phase cable.
2.2. Three-Phase Cable with Round Conductors
The parameters in Equation (1) are defined individually depending on the type of cable and the environment in which the cable is located. To be more specific, let us consider a three-core cable, the general layout of which is shown in Figure 2. For the cable shown in Figure 2, the thermal resistance T1 is determined by the following formula [2,16,19]:
where ρins and ρf are the thermal resistances of the insulation and the filling material, respectively; t1 is the material thickness between the conductor and the screen; dc is the diameter of the conductor; and G is a geometrical coefficient, which also depends on the t1/dc ratio and can be obtained from the geometrical coefficient curve in [19].
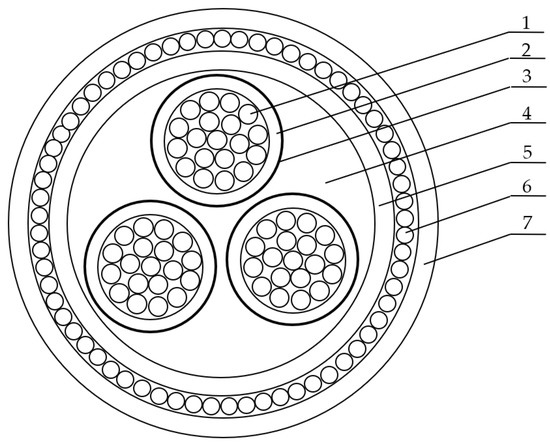
Figure 2.
Layout of the three-core power cable. 1: braided conductor; 2: insulation; 3: copper tape screen; 4: filler; 4: armor bedding; 5: armor; 6: jacket.
In turn, thermal resistances T2 and T3 are given by the following relationships [16,19]:
and
where t2 is the thickness of the armor bedding, Ds refers to the internal diameter of the armor bedding, t3 is thickness of the outer jacket and Da is the external diameter of the armor.
Moreover, if a single cable is buried in the ground, then the resistance T4 is given by formula [19]:
in which ρsoil is the thermal resistivity of the soil and parameter u equals:
where L is the distance from the surface of the ground to the cable axis and De is the external diameter of the cable.
As can be seen from Equation (1), the parameters determining the amperage of the cable, apart from the thermal parameters, represent the resistance of the cable core and dielectric losses in the insulation. Thus, the resistance is the main parameter determining the power losses in the cable core. The structure of the cable core has a decisive influence on the method of determining its resistance. The resistance of the cable core is usually determined using simple analytical relationships. In more complex designs, it is usually determined using numerical methods or measurements. The accurate analytical determination of resistance is fully possible only for solid cylindrical conductors. The complexity of the structure of the cable core implies the necessity of the experimental verification of the results of calculations of its resistance [1,40]. The frequency of the current flowing through the cable also determines the resistance of the cable core. In the case of a sinusoidal alternating current, it is necessary to take into account the skin and proximity effects [41]. The analytical determination of the core resistance of the cable shown in Figure 2 is possible if we assume that the phase conductors are cylindrical wires (Figure 3).
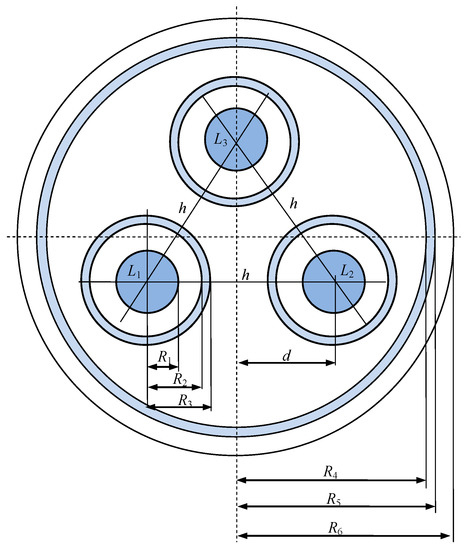
Figure 3.
Simplified model of power cable.
Using Maxwell’s equations under standard assumptions (sinusoidal currents, linear media, neglecting the displacement currents, infinitely long straight wires), one obtains the Helmholtz equation for the vector magnetic potential in conductive regions and the Laplace equation for non-conductive regions. The solutions yield the determination of the current density in each phase conductor of the cable shown in Figure 3. In the cylindrical coordinates system related to conductor 1, the total current density (its complex phasor) in the conductor can be expressed as follows:
where is the versor of the z-axis, and are discussed below, and the underbars indicate complex notation. The current density takes into account the skin effect and has the following form:
where I1 refers to the complex rms value of the phase current; , are the modified Bessel functions of the first kind, order 0 or order 1 [42]; is a complex propagation constant; j is the imaginary unit; is the angular frequency; stands for the electrical conductivity of the conductor; and is the magnetic permeability of the vacuum.
The current density takes into account the proximity effect and can be expressed as follows:
where
If the phase currents form a symmetrical three-phase system of the positive sequence, i.e., and , then the current density in the second conductor has the following form:
where
In turn, the total current density in the third-phase conductor can be expressed by the formula:
where
The resistance of the individual phase conductors can be determined based on the following formula:
Moreover, if we take into account that:
then, it can be proved that the resistance of each phase conductor is equal to:
where resistance R11, taking into account the skin effect, has a form:
and resistance R123, due to the proximity effect, can be written as follows:
In addition to the resistance determined above, the quantity that determines the permissible value of the current flowing through the cable is the losses in the insulation layers. These dielectric losses are described by the following equation:
where f is the frequency, U is the operating voltage, C is the capacitance of the insulation layer, and tanδ is the loss tangent. If ω is the angular frequency, γ is the electrical conductivity of the insulation and ε is its electrical permittivity, then the loss tangent can be expressed as follows:
In the case of the three-phase cable, there are several partial capacitances between individual conductors (Figure 4) as follows: the capacitance between the phase conductor and the screen; mutual capacitances between the screens, capacitances between screens and armor; and the capacitance between the armor and the outer surface of the cable. Using the method of specular reflections, it can be proved that the capacitance between the phase conductor and the screen is equal to [43]:
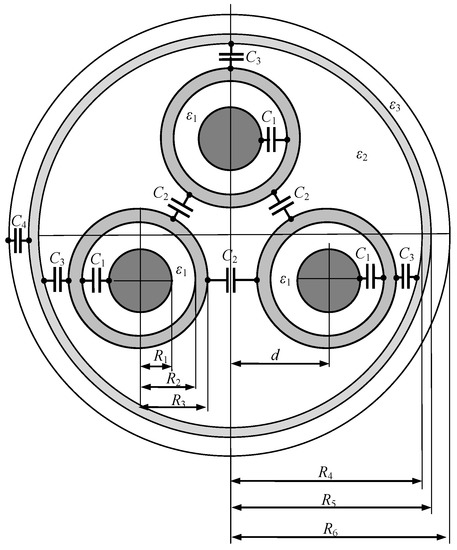
Figure 4.
Partial capacitances in the considered power cable.
In turn, the mutual capacitance between screens can be written as follows:
The capacitance between the screens and the armor has the following form:
In addition, the capacitance between the armor and the outer surface of the cable can be expressed by the formula:
In order to determine the allowable current carrying capacity of the power cable based on Equation (1), the coefficients λ1 and λ2 must first be calculated. It is therefore necessary to determine the power losses in the phase conductors and the losses in the sheaths and armor. Power losses in the phase conductors can be calculated from the following formula:
where the resistance R is given by Formula (17). If we assume that the screens are made of non-magnetic material, then the power losses in the screens will be given by:
in which:
and
In the above formulas, , , and are the modified Bessel functions of order 0, 1, calculated for and . The symbol * denotes the complex conjugate value, whereas is the complex propagation constant in the screen, is electrical conductivity of the screen, and l is the length of the cable.
In turn, the power Ps123 can be expressed by the following equation:
where
and
If we also assume that the armor consists of infinitely many filaments, then the power losses in the armor will be equal to:
where
and
In Formulas (38)–(42), refers to the complex propagation constant in the armor, and is the electrical conductivity of the armor.
The knowledge of power losses in the phase conductors, screens and armor allows factors λ1 and λ2 to be determined as follows:
and
where PC is given by Formula (26), Ps by Formula (27) and Pa by Formula (38).
When determining the permissible current of the cable, it should be remembered that the physical properties of the individual layers of the cable also change with temperature. The thermal conductivity of the individual layers of the cable can be determined using physical tables. In turn, the electrical conductivity of the conductors, screens and armor should be calculated from the commonly known equation:
where is the electrical conductivity at 20 °C, α is the temperature coefficient and Θ is the temperature.
3. Exemplary Computations
Using the analytical formulas presented in the previous sections, exemplary calculations of the rated current of cables laid in the soil with different thermal resistivities and at different depths were made. The calculations were carried out for three different cable types, i.e., for 11 kV 400 mm2, 22 kV 240 mm2 and 22 kV 500 mm2 [44]. In each case, it was assumed that the cables operate in a three-phase balanced mode with a frequency of f = 50 Hz. The geometric dimensions and thermal parameters of the individual layers of these cables are included in Table 1 and Table 2.

Table 1.
Power cable parameters.

Table 2.
Thermal properties of power cables.
The results presented in this section were obtained, taking into account the dielectric losses and assuming the dielectric constants of the insulation layers ε1 = ε2 = ε3 = 2.25 and conductivity γ = 10−12 S/m. The screens and armor of the cable were assumed to begrounded. The ambient temperature was assumed to be +20 °C.
Figure 5 shows the temperature rise of the cables as a function of the rated current. The calculations were made for cables buried at a depth of 1 m in the ground (thermal resistivity of ρsoil = 1.25 Km/W). The calculations presented in Figure 5 were performed assuming that the temperature rise of the conductor above the ambient temperature ΔΘ was in the range of 10 to 50 degrees. This resulted in the rated current of 372 A to 795 A for a 11 kV 400 mm2 cable. In the case of a 22 kV 240 mm2 cable, the rated current for this temperature range was from 295 A to 622 A. As for a 22 kV 500 mm2 cable, the rated current for this temperature range was from 398 A to 853 A.
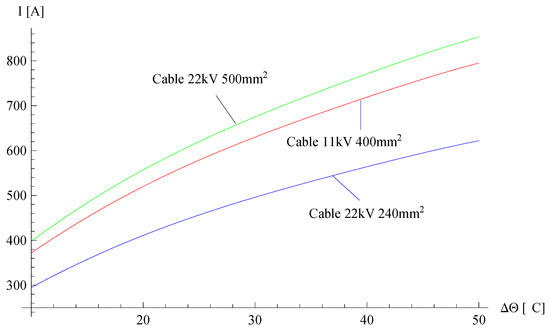
Figure 5.
Cable temperature rise as a function of rated current.
The traces included in Figure 6 show the dependence of the rated current of the cables on the thermal resistivity of the ground. The curves shown in Figure 6 were made for cables buried at a depth of 1 m. It follows that the transmission capability of the cables decreases with an increase in soil resistivity. This is related to the fact that the higher thermal resistivity of soil lowers the dissipation of heat generated in the cable.
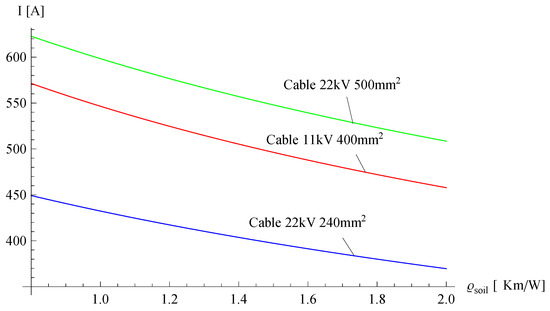
Figure 6.
The dependence of the current rating of the cable on the thermal resistivity of the soil.
Figure 7 shows the dependence of the rated current of the cable on the depth of burial. The calculations were made for cables buried in the soil of thermal resistivity ρsoil = 1.25 Km/W. The thicker the soil layer around the cable, the lower the transmission capability of the cable. The soil plays the role of thermal insulation around cable. Thus, the thicker the layer of insulation around the cable, the lower the rated current.
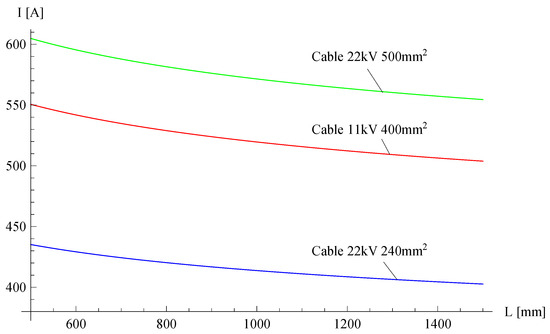
Figure 7.
The dependence of the current rating of the cable on the depth of burial.
The curves presented in Figure 5, Figure 6 and Figure 7 were determined for cables with a rated voltage of 11 kV and 22 kV, respectively. From a practical point of view, it is extremely interesting to present calculations for cables with a higher rated voltage. For this purpose, further calculations were made for the cases of 38 kV 400 mm2 and 87 kV 800 mm2 cables (Table 3) [29]. The temperature rise of these cables as a function of the rated current is presented in Figure 8. The thermal parameters of the individual layers of these cables are included in Table 2. As shown in Figure 5, calculations were made for cables buried at a depth of 1 m in the ground. An increase in the rated voltage of the cables caused an increase in dielectric losses in the insulation layers. As a consequence, these losses caused an additional increase in temperature in relation to cables with the same cross-section but with a lower rated voltage. The curves presented in Figure 8 were drawn assuming that the temperature rise of the conductor above the ambient temperature ΔΘ was in the range of 10 to 50 degrees. This resulted in the rated current of 365 A to 775 A for a 37 kV 400 mm2 cable. In the case of an 87 kV 800 mm2 cable, the rated current for this temperature range was from 486 A to 1030 A.

Table 3.
Power cable parameters.
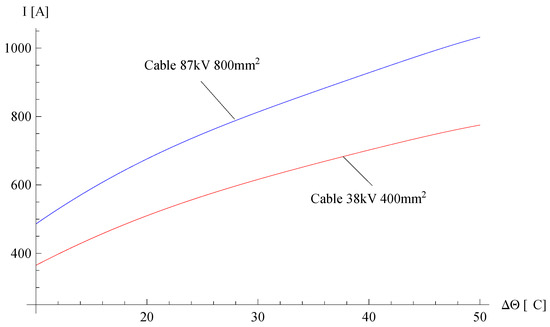
Figure 8.
Cable temperature rise as a function of rated current.
4. Validation
In order to validate the analytical method presented in this paper, numerical calculations based on the finite element method were performed. For this purpose, calculations of the temperature reached by the core conductors of the cables were carried out using Comsol software. As part of the Comsol computations, the Heat Transfer in Solid module with two interfaces, namely Heat Transfer in Solid and Heat Transfer in Fluid, were used. The computational model for the cable buried in the soil is presented in Figure 9. During the computations, a finite element mesh called “Physics-controlled mesh” was used with the size of the elements set as “Extra fine”. The same cable models as in the previous section and the same parameter values were used in the calculations. The calculations were repeated for various currents. The results obtained using the analytical method and the finite element method are presented in Table 4.
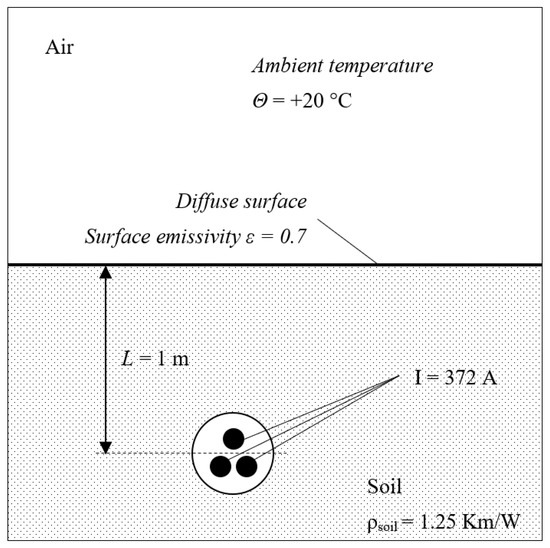
Figure 9.
Computational model for cable buried in the soil.

Table 4.
Temperature rises in the cable core above the ambient temperature.
The results shown in Table 4 indicate that the values of the temperature rises of the cable cores above the ambient temperature determined by means of the proposed analytical method are slightly lower than those calculated by the finite element method. The differences between the values of the temperature rises, however, do not exceed 10%. These differences may be caused by the accuracy of mapping individual cable layers in both methods.
In addition to numerical calculations, a comparison of the analytical method proposed in this paper with the method contained in the IEC 60287 standard was also performed. For this purpose, calculations of the temperature rise of the cables as a function of the rated current were performed, the same as is shown in Figure 4. The same cable models as in the previous section and the same parameter values were also used in the calculations. The results obtained by the analytical method and the method based on the coefficients given in the IEC standard are shown in Figure 10. The results obtained with the analytical method proposed in this paper are represented as solid lines, whereas the results based on the IEC standard are plotted with dashed lines. It follows that the differences between the two methods are relatively small. For a better assessment, Table 5 shows more precise values.
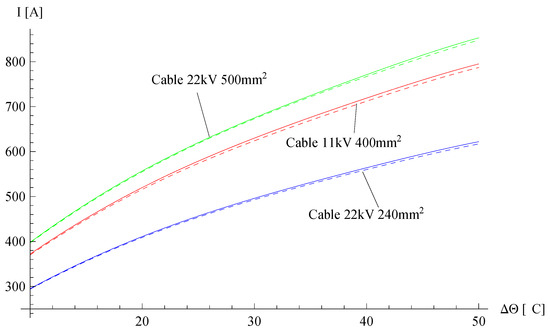
Figure 10.
Cable temperature rise as a function of rated current.

Table 5.
Cable temperature rises as a function of rated current.
The results presented in Figure 10 and Table 5 indicate that the values of temperature increases in the cable cores above the ambient temperature determined by the method based on the coefficients contained in the IEC 60287 standard are achieved for rated currents are slightly lower than in the case of the analytical method proposed in this paper. However, the differences between the current values do not exceed a few percent. Therefore, both of these methods can be successfully used by designers of cable networks. Nevertheless, the analytical method presented in the paper uses more accurate formulas for the resistances of the conductors, which can give larger differences in certain cases.
5. Conclusions
This paper presents an improved analytical method to determine the permissible rated current of a power cable operating in a three-phase system. The method is based on analytical formulas contained in the IEC 60287 standard; however, the resistance of phase conductors and power losses in screens and armor are determined analytically, taking into account the skin and proximity effects more accurately. The analytical determination of resistance and power losses was possible under the assumption that the phase conductors are cylinders, while the screens and armor are tubes. The results obtained via the proposed method were also compared with those by the finite element method using Comsol software. In addition to numerical calculations, the analytical method proposed in this paper was also compared with the method based on the coefficients contained in the IEC 60287 standard. Three models of power cables, i.e., 11 kV 400 mm2, 22 kV 240 mm2 and 22 kV 500 mm2, were used in the exemplary calculations.
The analytical method of cable amperage determination presented in the paper can be used to validate calculations made with other methods. Many engineers and designers of cable systems use commercial software such as Ansys, Comsol or Flux. When designing cable lines, it is also important to confront the results obtained numerically with measurements or another computational method. Measurements are often impossible to carry out, especially at the design stage; therefore, the presented method can be a reference point. The results of the cable temperature rise calculations presented in Table 3 show that the values obtained for the analytical and numerical methods are close. This means that the analytical method of determining the cable ampacity presented in this paper can be successfully used by engineers and designers of cable lines.
The specific formulas presented in this paper are for single cables operating in three-phase balanced mode. However, the method may be developed for more complex configurations. It is possible to develop an analytical method to determine the amperage for a system of cables laid in the ground in the following arrangements: vertical; horizontal; or triangular. In addition, under certain assumptions, the proposed method can be further extended with formulas yielding a determination of the power losses in the armor if it is made of ferromagnetic material.
Author Contributions
Conceptualization, T.S.; methodology and validation, T.S., P.J. and D.K.; writing—original draft preparation, T.S.; writing—review and editing, D.K. and P.J.; formal analysis, P.J. and D.K.; supervision, P.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by Czestochowa University of Technology.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| C | capacitance of the insulation layer |
| Da | external diameter of the cable armor |
| De | external diameter of the cable |
| Ds | internal diameter of the armor bedding |
| d | distance between the conductor axes |
| dc | diameter of the conductor |
| f | frequency |
| G | geometrical coefficient |
| complex rms current | |
| modified Bessel function of the first kind and of n order | |
| complex rms current density vector | |
| j | imaginary unit |
| modified Bessel function of the second kind and of n order | |
| L | distance from the surface of the ground to the cable axis |
| l | length of the cable |
| n | number of conductors in the cable |
| PC | power losses in the phase conductors |
| r, θ, z | cylindrical coordinates |
| Wd | dielectric losses |
| Θa | ambient temperature |
| ΘC | conductor temperature |
| ΔΘ | temperature rise of the conductor above the ambient temperature |
| R | conductor resistance |
| R1 | radius of the phase conductor |
| R2 | internal radius of the screen |
| R3 | external radius of the screen |
| R4 | internal radius of the armor |
| R5 | external radius of the armor |
| R6 | radius of the cable |
| T1 | thermal resistance between conductor and screen |
| T2 | thermal resistance of bedding between screen and armor |
| T3 | thermal resistance of external jacket |
| T4 | thermal resistance of surrounding medium |
| t1 | material thickness between the conductor and the screen |
| t2 | thickness of the armor bedding |
| t3 | thickness of outer jacket |
| U | operating voltage |
| α | temperature coefficient for resistivity |
| ε | electrical permittivity |
| electrical conductivity of the conductor | |
| electrical conductivity of the armor | |
| electrical conductivity of the screen | |
| complex propagation constant | |
| λ1 | screen losses factor |
| λ2 | armor losses factor |
| ρins | thermal resistance of the insulation |
| ρf | thermal resistance of the filling material |
| ρsoil | thermal resistivity of the soil |
| μo | magnetic permeability of the vacuum |
| ω | angular frequency of current and voltage |
References
- Benato, R.; Colla, L.; Dambone Sessa, S.; Marelli, M. Review of high current rating insulated cable solutions. Electr. Power Syst. Res. 2016, 133, 36–41. [Google Scholar] [CrossRef]
- Cigre 640. A Guide for Rating Calculations of Insulated Cables. In Proceedings of the 9th International Conference on Insulated Power Cables, Versailles, France, 21–25 June 2015. [Google Scholar]
- Chengke, Z.; Huajie, Y.; Xiang, D. Review of recent research towards power cable life cycle management. High Volt. 2017, 2, 179–187. [Google Scholar]
- Holyk, C.; Anders, G.J. Power cable rating calculations—A historical perspective. IEEE Ind. Appl. Mag. 2015, 21, 6–64. [Google Scholar] [CrossRef]
- Worzyk, T. Submarine Power Cables; Springer: Berlin, Germany, 2009. [Google Scholar]
- Park, K.; Kwon, I.; Lee, B. Calculation Method of Allowable Continuous Current for Direct Burial Laying HVDC Underground Cable. Energies 2021, 14, 6431. [Google Scholar] [CrossRef]
- Rachek, M.; Larbi, S.N. Magnetic eddy-current and thermal coupled models for the finite-element behavior analysis of underground power cables. IEEE Trans. Magn. 2008, 44, 4739–4746. [Google Scholar] [CrossRef]
- Del Pino, J.C.; Cruz, P. Magnetic field shielding of underground cable duct banks. Prog. Electromagn. Res. 2013, 138, 1–19. [Google Scholar] [CrossRef]
- Mazzanti, G. Life estimation of HVDC cables under the time-varying electrothermal stress associated with load cycles. IEEE Trans. Power Deliv. 2015, 30, 931–939. [Google Scholar] [CrossRef]
- Sedaghat, A.; De Leon, F. Thermal Analysis of Power Cables in Free Air: Evaluation and Improvement of the IEC Standard Ampacity Calculations. IEEE Trans. Power Deliv. 2014, 29, 2306–2314. [Google Scholar] [CrossRef]
- Bicen, Y. Trend adjusted lifetime monitoring of underground power cable. Electr. Power Syst. Res. 2017, 143, 189–196. [Google Scholar] [CrossRef]
- Shabani, H.; Vahidi, B. A probabilistic approach for optimal power cable ampacity computation by considering uncertainty of parameters and economic constraints. Electr. Power Energy Syst. 2019, 106, 432–443. [Google Scholar] [CrossRef]
- Zarchi, D.A.; Vahidi, B. Multi objective self adaptive optimization method to maximize ampacity and minimize cost of underground cables. J. Comput. Des. Eng. 2018, 5, 401–408. [Google Scholar] [CrossRef]
- Gouda, O.E.; Dein, A.Z.E.; Amer, G.M. Effect of the Formation of the Dry Zone around Underground Power Cables on Their Ratings. IEEE Trans. Power Deliv. 2011, 26, 972–978. [Google Scholar] [CrossRef]
- Zarchi, D.A.; Vahidi, B. Optimal placement of underground cables to maximise total ampacity considering cable lifetime. IET Gener. Transm. Distrib. 2016, 10, 263–269. [Google Scholar] [CrossRef]
- Jiang, X.; Corr, E.; Stephen, B.; Stewart, B.G. Impact of increased penetration of low carbon technologies on cable lifetime estimations. Electricity 2022, 3, 13. [Google Scholar] [CrossRef]
- De Leon, F. Major Factors Affecting Cable Ampacity. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Brakelmann, H.; Anders, G.J. Current rating considerations in designing HVDC cable installations. IEEE Trans. Power Deliv. 2018, 33, 2315–2323. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Calculation of the Current Rating, Parts 1 and 2, IEC Standard 60287-1 and IEC Standard 60287-2; International Electrotechnical Commission: Geneva, Switzerland, 2006. [Google Scholar]
- De Leon, F.; Anders, G.J. Effects of Backfilling on Cable Ampacity Analyzed With the Finite Element Method. IEEE Trans. Power Deliv. 2008, 23, 537–543. [Google Scholar] [CrossRef]
- Kocar, I.; Ertas, A. Thermal analysis for determination of current carrying capacity of PE and XLPE insulated power cables using finite element method. In Proceedings of the 12th IEEE Mediterranean Electrotechnical Conference, Dubrovnik, Croatia, 12–15 May 2004. [Google Scholar]
- Benato, R.; Dambone Sessa, S. A New Multiconductor Cell Three-Dimension Matrix based Analysis Applied to a Three-Core Armored Cable. IEEE Trans. Power Deliv. 2017, 33, 1636–1646. [Google Scholar] [CrossRef]
- Chien, C.H.; Bucknall, R.W.G. Harmonic Calculations of Proximity Effect on Impedance Characteristics in Subsea Power Transmission Cables. IEEE Trans. Power Deliv. 2009, 24, 2150–2158. [Google Scholar] [CrossRef]
- Chatzipetros, D.; Pilgrim, J.A. Impact of Proximity Effects on Sheath Losses in Trefoil Cable Arrangements. IEEE Trans. Power Deliv. 2019, 35, 455–463. [Google Scholar] [CrossRef]
- Gudmundsdottir, U.S. Proximity effect in fast transient simulations of an underground transmission cable. Electr. Power Syst. Res. 2014, 111, 50–56. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, Z. Cable Sheath Loss Reduction Strategy Research Based on Coupled Line Model. Trans. Power Deliv. 2015, 30, 2303–2311. [Google Scholar] [CrossRef]
- Del-Pino-Lopez, J.C.; Cruz-Romero, P. Use of 3D-FEM Tools to Improve Loss Allocation in Three-Core Armored Cables. Energies 2021, 14, 2434. [Google Scholar] [CrossRef]
- Del-Pino-López, J.C.; Cruz-Romero, P.; Sanchez-Díaz, L.C. Loss Allocation in Submarine Armored Three-core HVAC Power Cables. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I and CPS Europe), Madrid, Spain, 9–12 June 2020. [Google Scholar]
- Kossyvakis, D.N.; Chrysochos, A.I.; Pavlou, K. Calculation of Losses in Three-Core Submarine Cables for Fractional Frequency Transmission Operation. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athens, Greece, 10–13 September 2018. [Google Scholar]
- Moutassem, W.; Anders, G.J. Calculation of the Eddy Current and Hysteresis Losses in Sheathed Cables Inside a Steel Pipe. Trans. Power Deliv. 2010, 35, 2054–2063. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, W.; Li, Z.; Li, S. Thermoelectric Coupling Study of Three-core XLPE Submarine Cable by Finite Element Simulation. In Proceedings of the 2019 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Richland, WA, USA, 20–23 October 2019. [Google Scholar]
- Garrido, C.; Otero, A.F.; Cidras, J. Theoretical model to calculate steady-state and transient ampacity and temperature in buried cables. IEEE Trans. Power Deliv. 2003, 18, 667–678. [Google Scholar] [CrossRef]
- Xu, X.B.; Liu, G. Investigation of the magnetic field produced by unbalanced phase current in an underground three-phase pipe type cable. Electr. Power Syst. Res. 2002, 62, 153–160. [Google Scholar] [CrossRef]
- Millar, R.J.; Lehtonen, M. A robust framework for cable rating and temperature monitoring. IEEE Trans. Power Deliv. 2006, 21, 313–321. [Google Scholar] [CrossRef]
- Demoulias, C.; Labridis, D.P.; Dokopoulos, P.S.; Gouramanis, K. Ampacity of Low Voltage Power Cables Under Non-sinusoidal Currents. IEEE Trans. Power Deliv. 2007, 22, 584–594. [Google Scholar] [CrossRef]
- Hughes, T.; Henstock, T.J.; Pilgrim, J.A.; Dix, J.K.; Gernon, T.M.; Thompson, C.E.L. Effect of Sediment Properties on the Thermal Performance of Submarine HV Cables. IEEE Trans. Power Deliv. 2015, 30, 2443–2450. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Zhang, H.; Liu, J.; Zhang, C.; Jiao, J. Analysis on the Temperature Field and the Ampacity of XLPE Submarine HV Cable Based on Electro-Thermal-Flow Multiphysics Coupling Simulation. Polymers 2020, 12, 952. [Google Scholar] [CrossRef]
- Yang, L.; Qiu, W.; Huang, J.; Hao, Y.; Fu, M.; Hou, S.; Li, L. Comparison of Conductor-Temperature Calculations Based on Different Radial-Position-Temperature 531 Detection for High-Voltage Power Cable. Energies 2018, 11, 117. [Google Scholar] [CrossRef]
- Terracciano, M.; Purushothaman, S.; Leon, F.D.; Farahani, A.V. Thermal analysis of cables in unfilled troughs: Investigation of the IEC standard and a methodical approach for cable rating. IEEE Trans. Power Deliv. 2012, 27, 1423–1431. [Google Scholar] [CrossRef]
- Benato, R.; Paolucci, A. Multiconductor cell analysis of skin effect in Milliken type cables. Electr. Power Syst. Res. 2012, 90, 99–106. [Google Scholar] [CrossRef]
- Pagnetti, A.; Xemard, A.; Paladian, F.; Nucci, C.A. An improved method for the calculation of the internal impedances of solid and hollow conductors with the inclusion of proximity effect. IEEE Trans. Power Deliv. 2012, 27, 2063–2072. [Google Scholar] [CrossRef]
- McLachlan, N.W. Bessel Functions for Engineering; PWN: Warsaw, Poland, 1964. [Google Scholar]
- Piątek, Z. Modeling of Lines, Cables and High Current Busducts; Wydawnictwo Politechniki Częstochowskiej: Czestochowa, Poland, 2007. (In Polish) [Google Scholar]
- Fernandez, E.; Patrick, J. Emergency and Cyclic Ratings of HV Cables. 2019. Available online: https://elek.com.au/wp-content/uploads/2019/02/Emergency-and-cyclic-ratings-of-HV-cables.pdf (accessed on 20 September 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).