A Preliminary Analysis of In-Situ Stress at Mount Meager by Displacement Discontinuity Method with Topography and Tectonics Considered
Abstract
1. Introduction
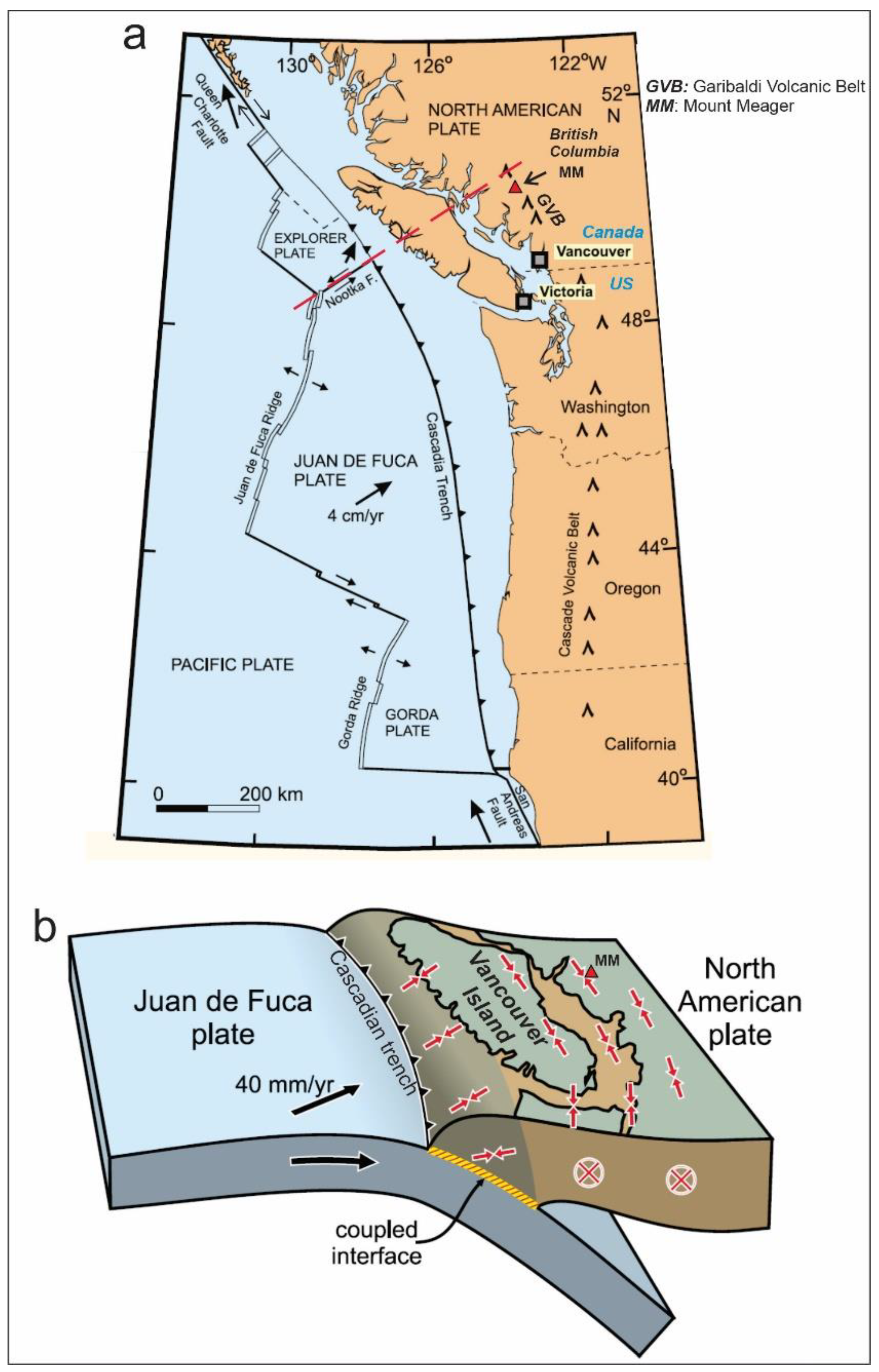
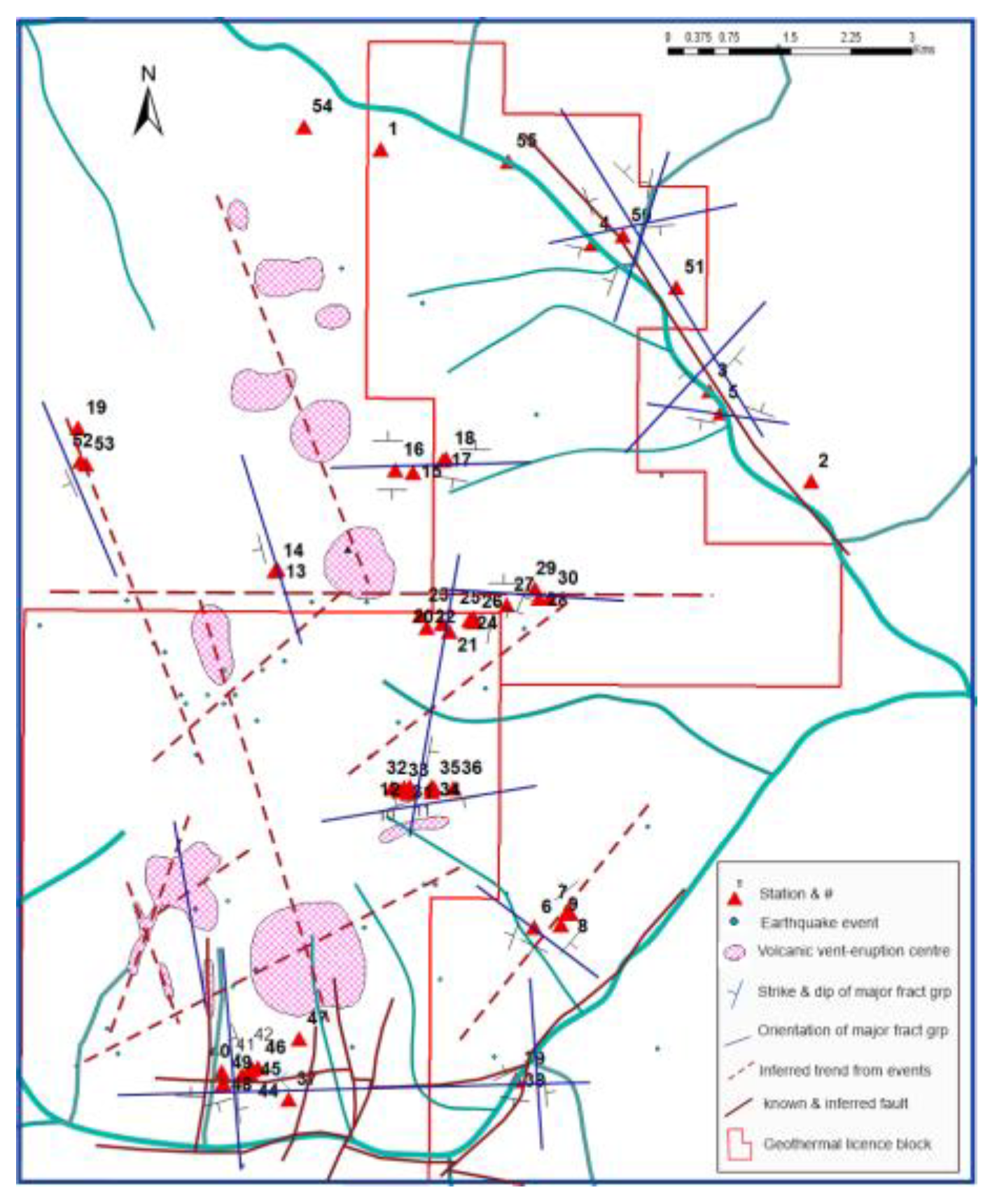
2. Regional Tectonics
3. Methods
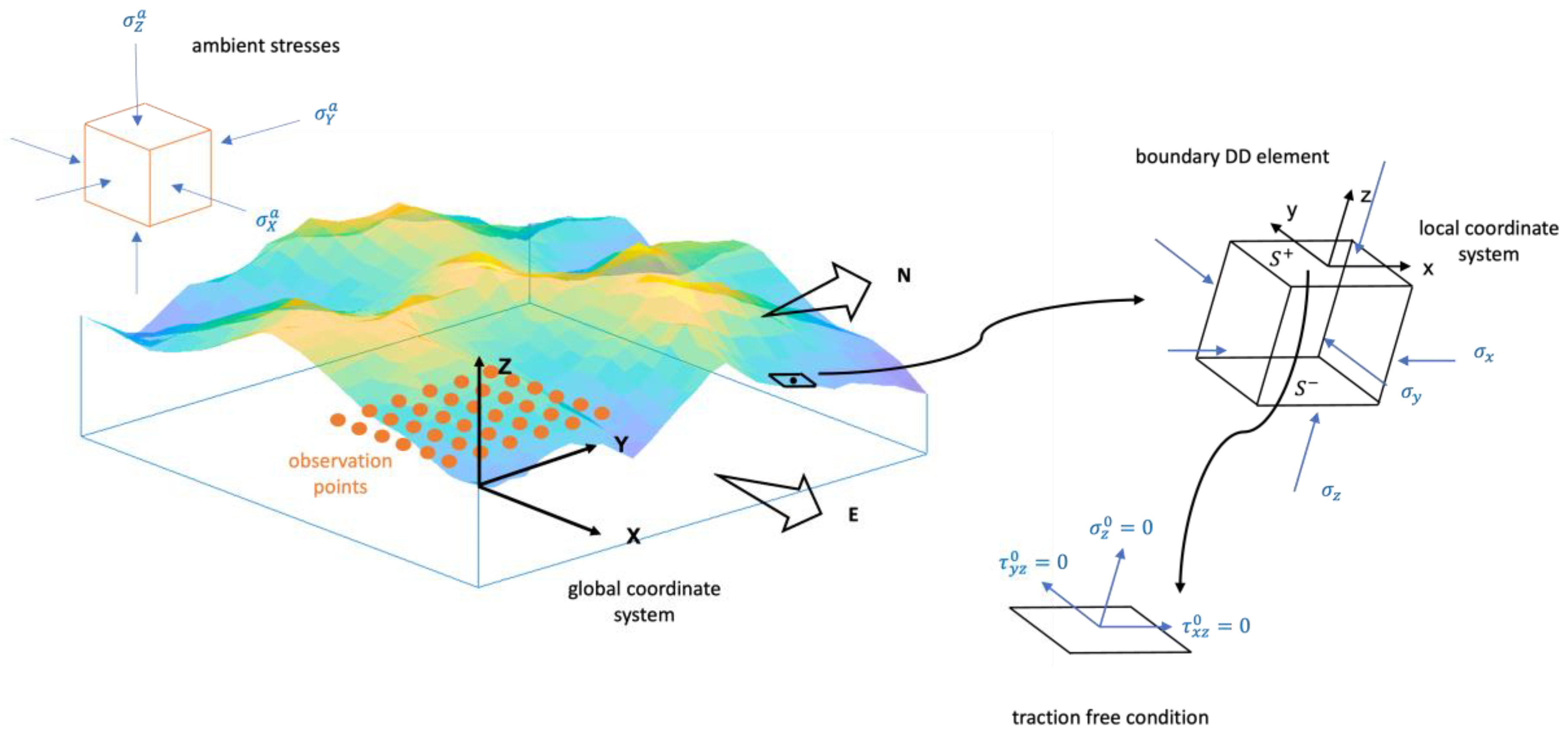
3.1. Stresses Induced by the Gravitational Load in an Elastic Body
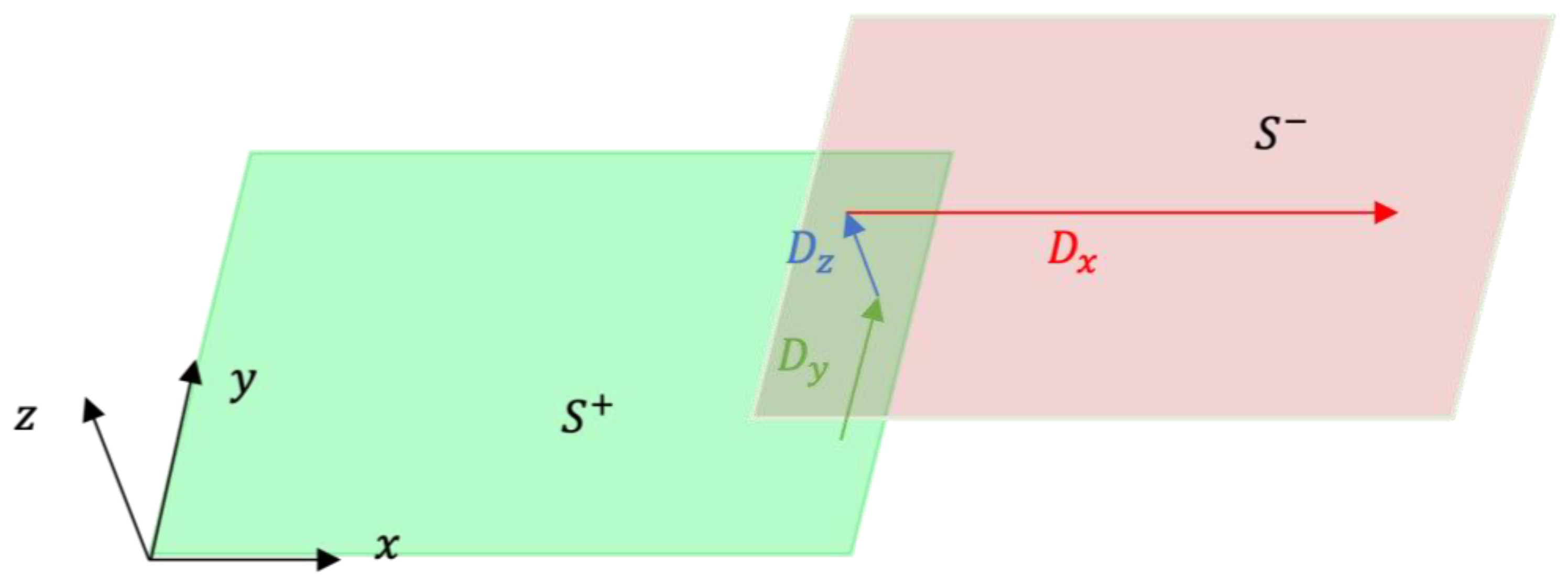
3.2. Formulations of the 3D Displacement Discontinuity Method
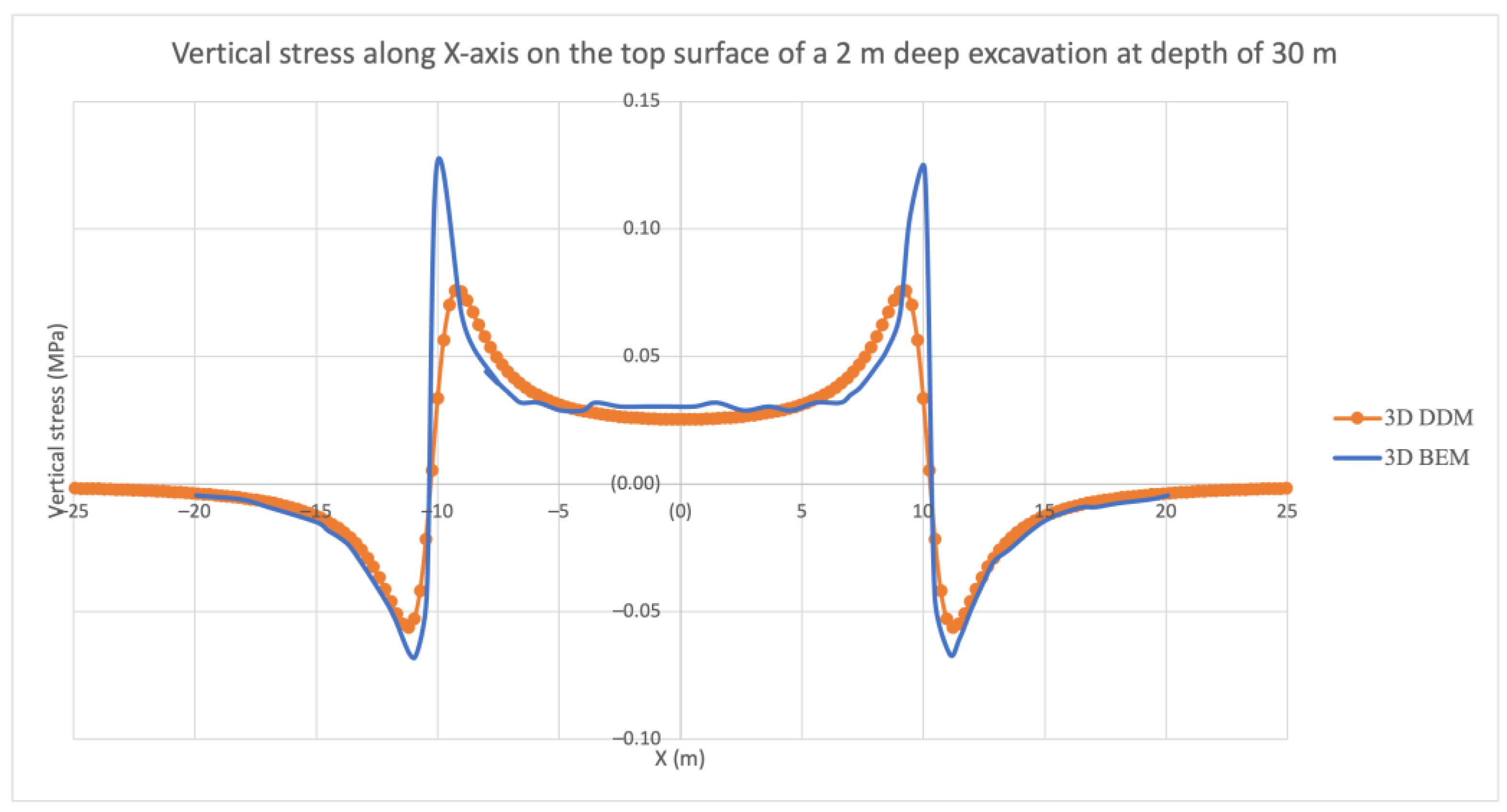
4. Verification
- Domain: semi-infinite;
- 20 m × 20 m area of excavation at 30 m deep below the topographic surface. The excavation volume is 2 m in height, which occupies from 29 m to 31 m underground;
- The boundary area that contains rectangular DD elements includes the horizontal ground surface and a horizontal plane with top and bottom surfaces that represent the underground excavation;
- A constant 1 m displacement discontinuity in the surface-normal direction is prescribed on each side of the DD plane;
- The displacement discontinuities in the horizontal directions are negligible;
- Poisson’s ratio is 0.333, Elastic modulus is 1 GPa;
- The observation points are placed along the X-axis at 28.5 m deep (0.5 m above the top surface of the excavation).
- Domain: semi-infinite;
- The boundary element plane covers the same area as DDM;
- 20 m × 20 m × 2 m excavation volume at 30 m deep;
- Uz = −0.5427 m, Uz = 0.4573 m are prescribed on top and bottom surface, respectively;
- Traction-free surface is applied;
- Poisson’s ratio is 0.333, elastic modulus is 1 GPa;
- Discretized with 4-node rectangular elements.
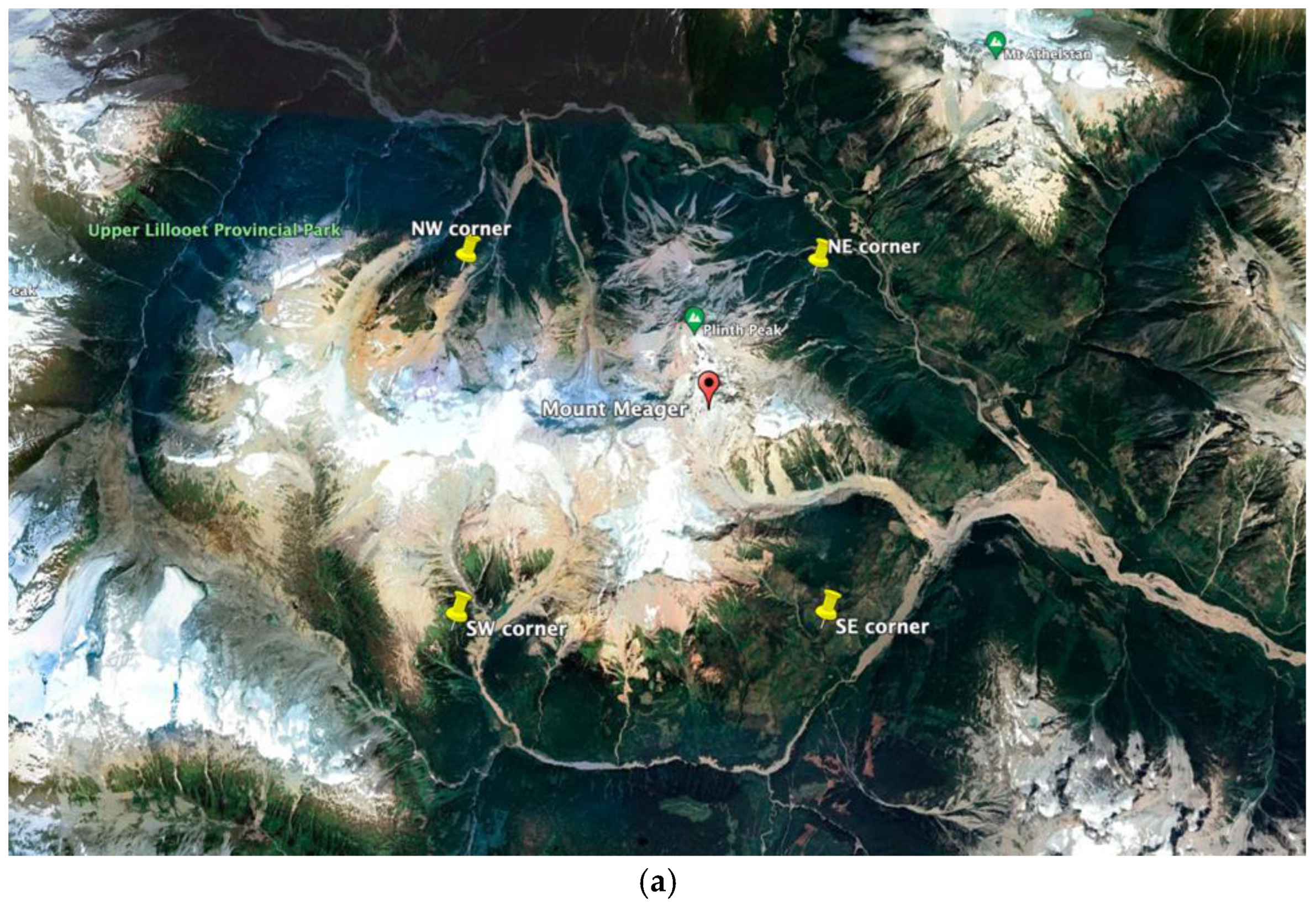
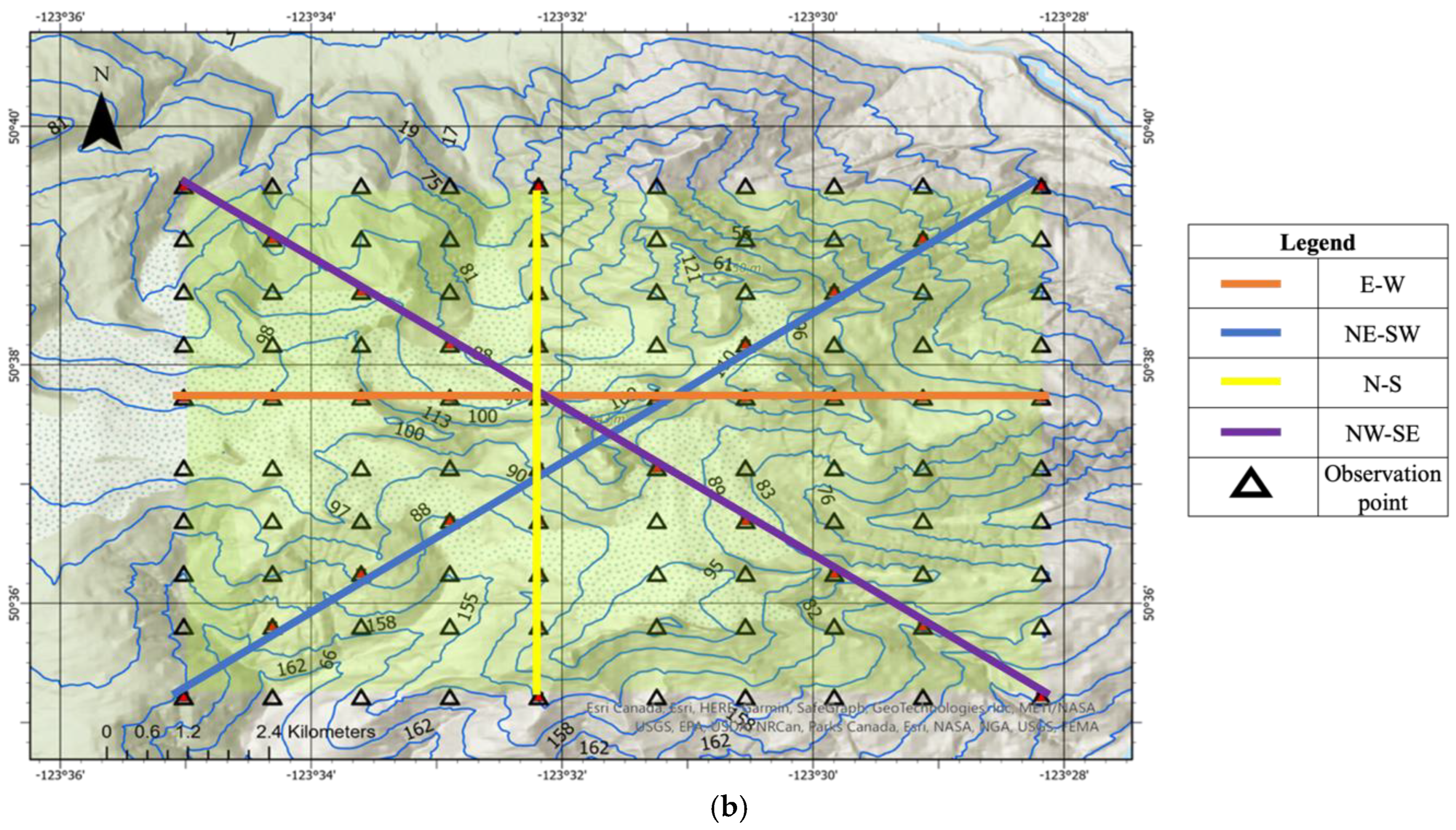
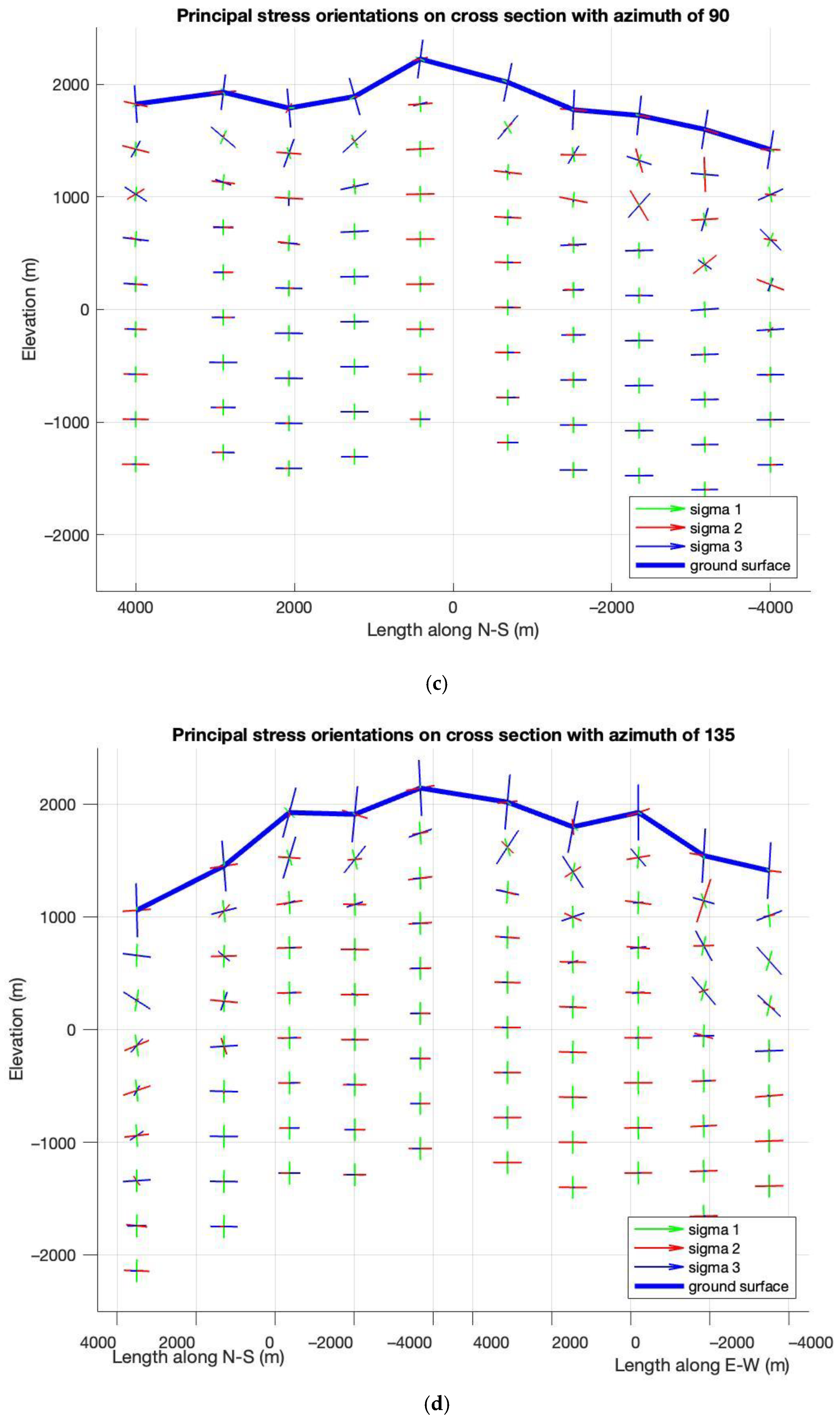
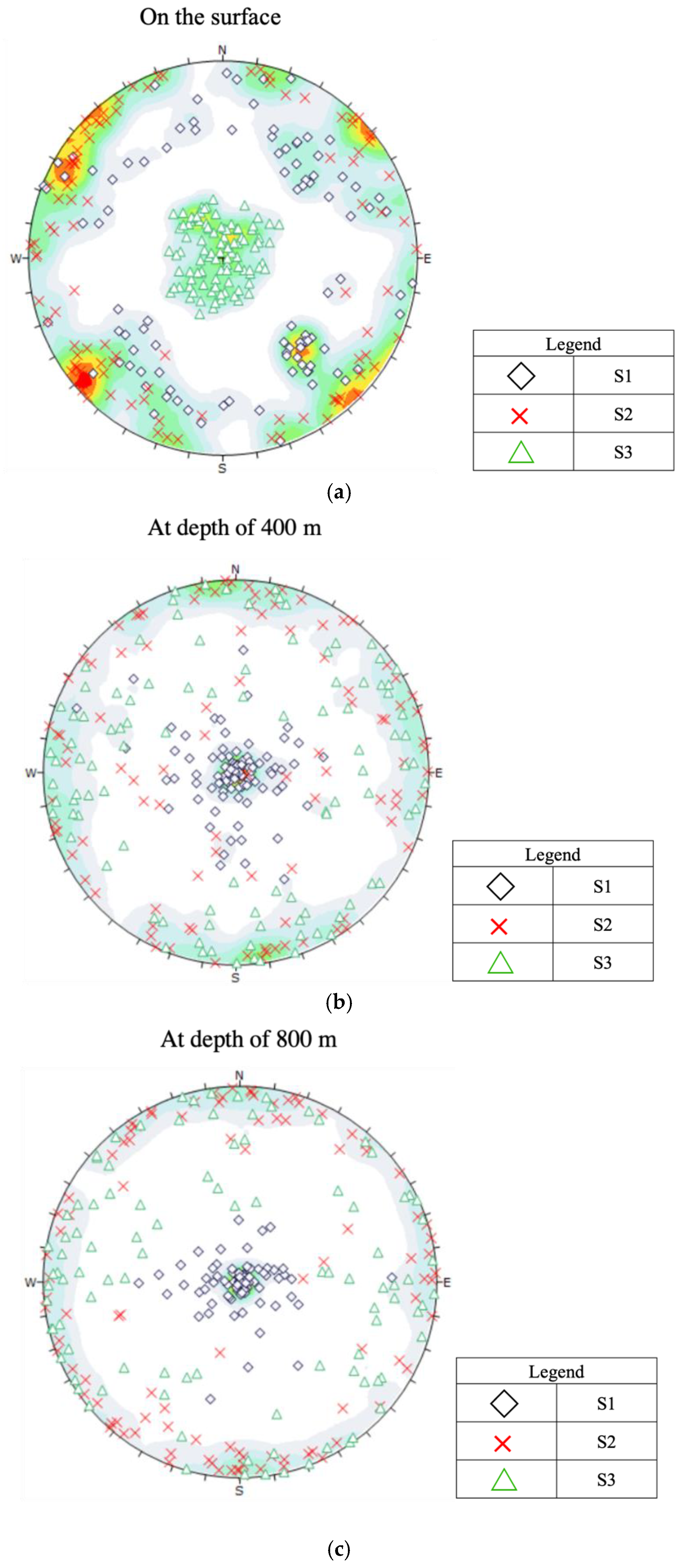
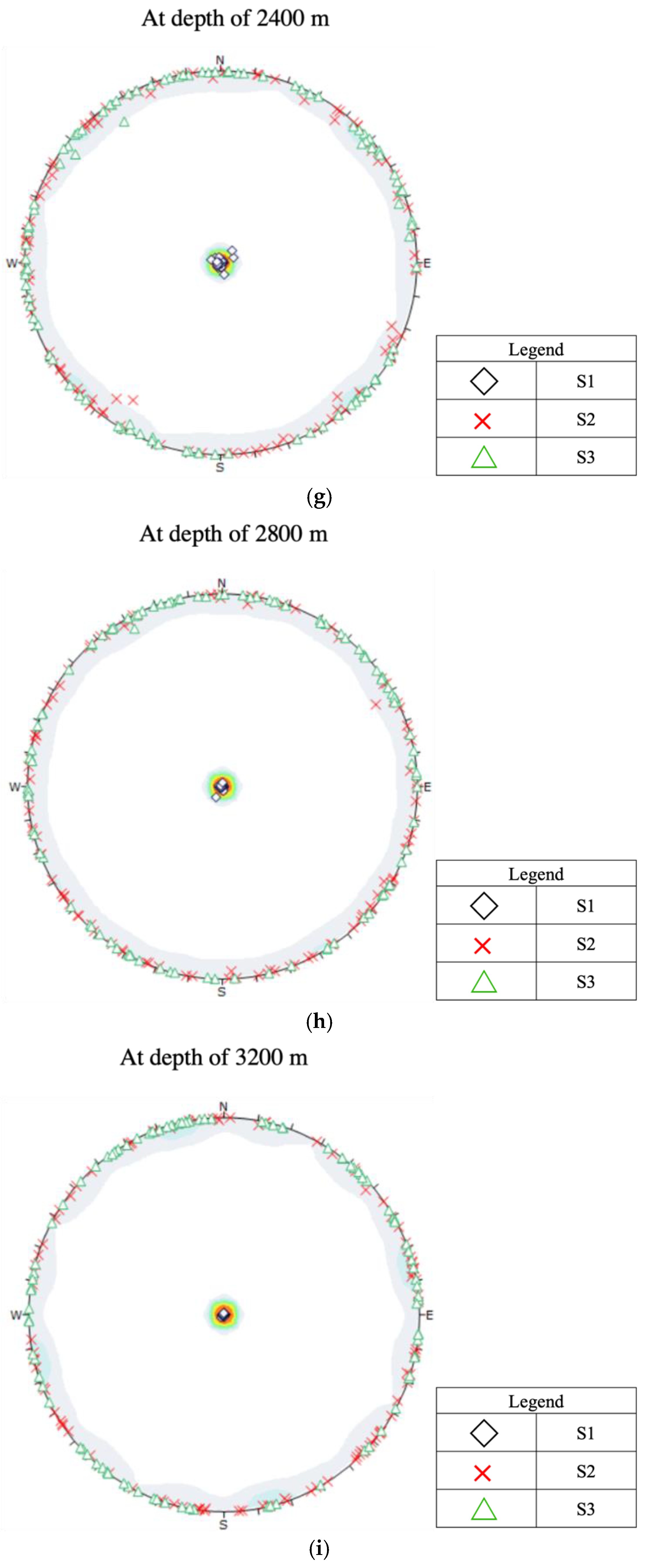
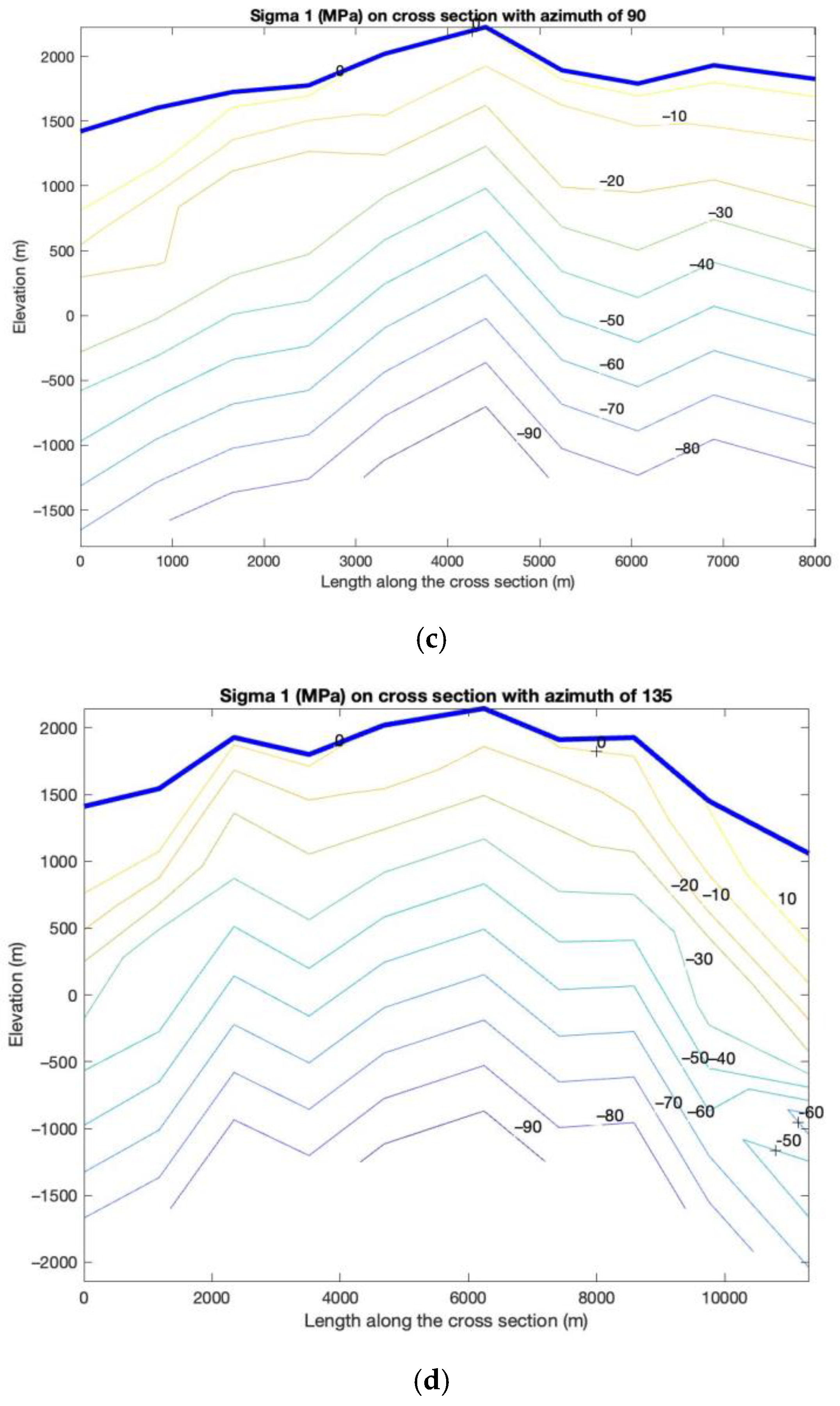
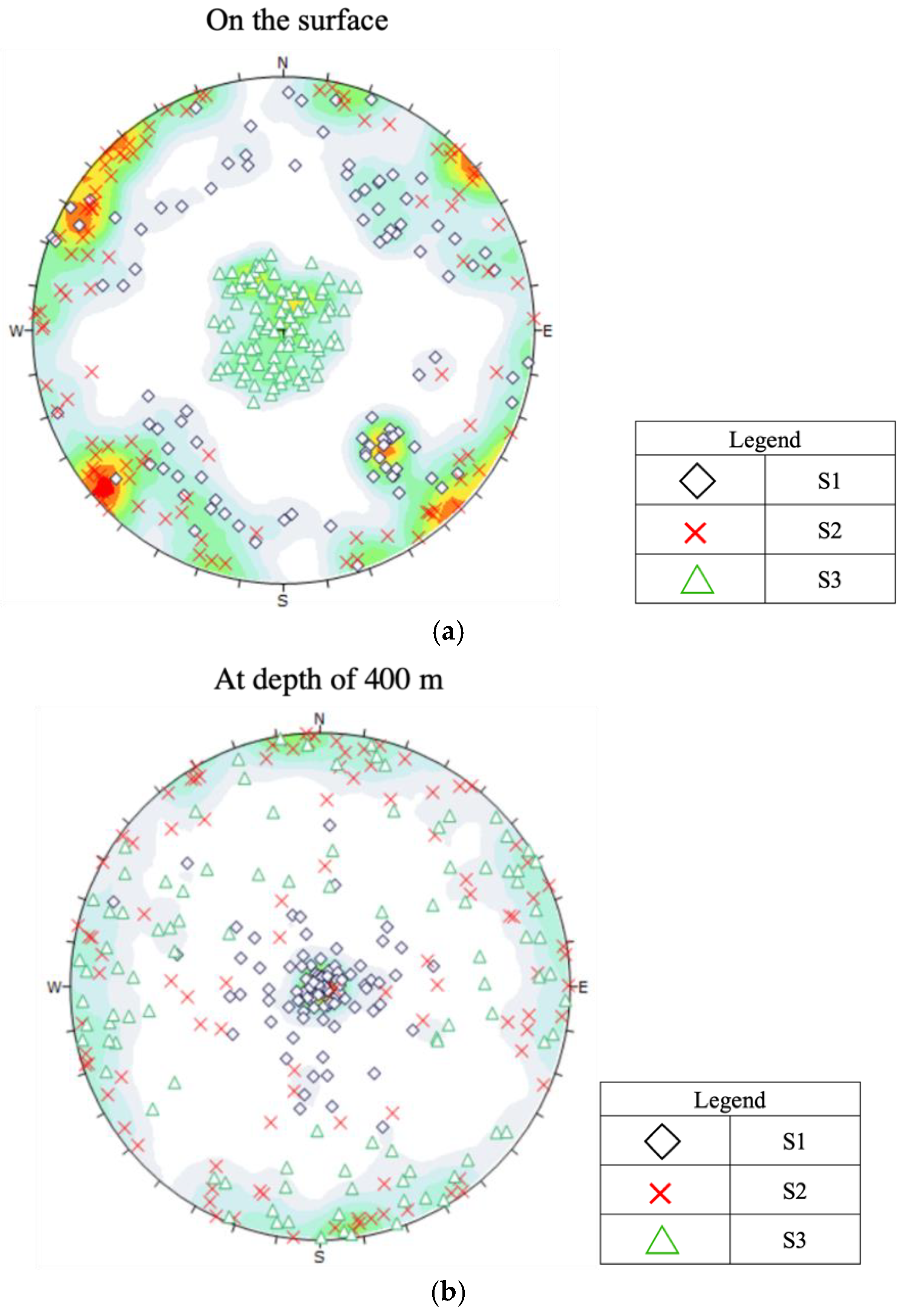
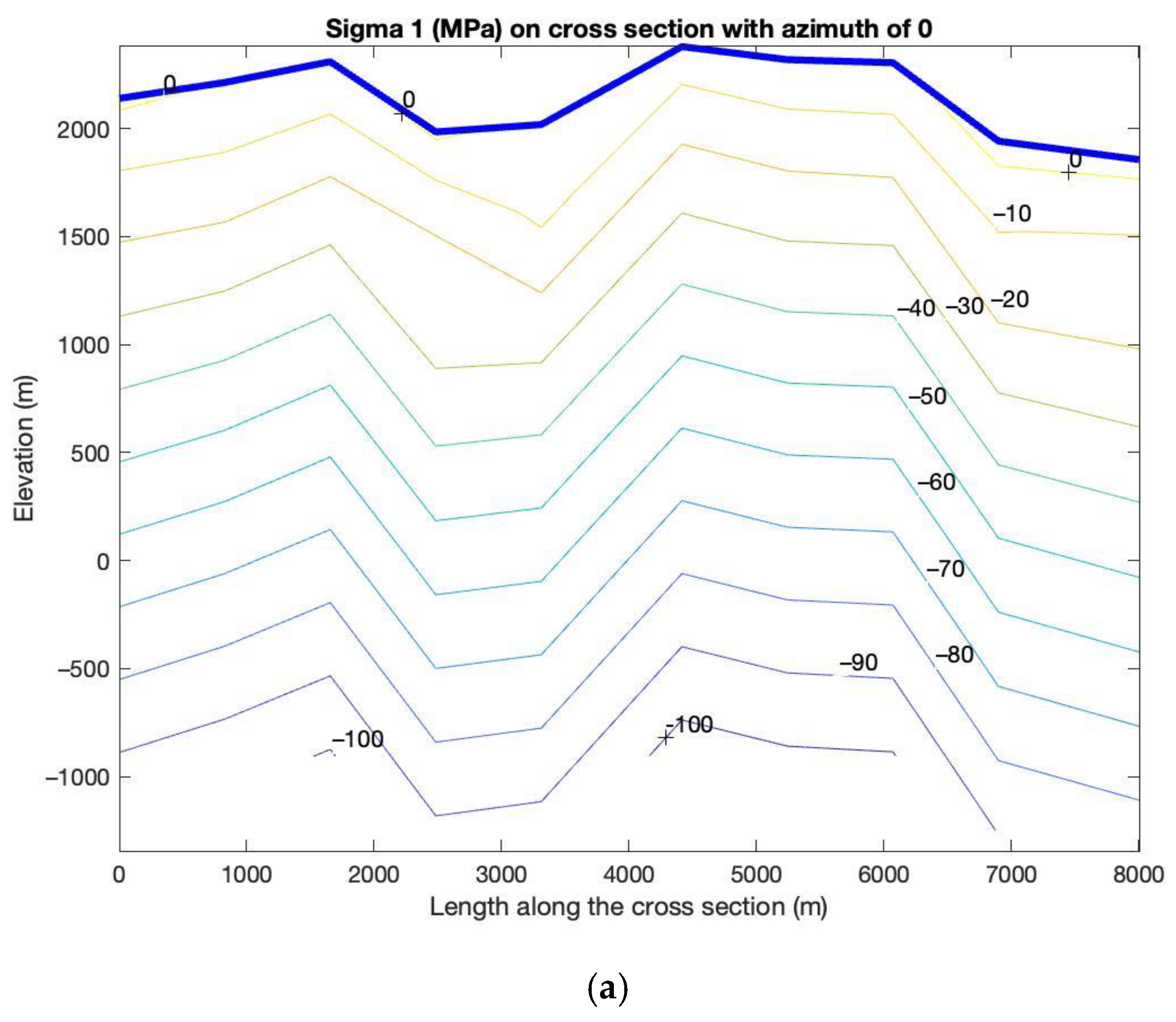
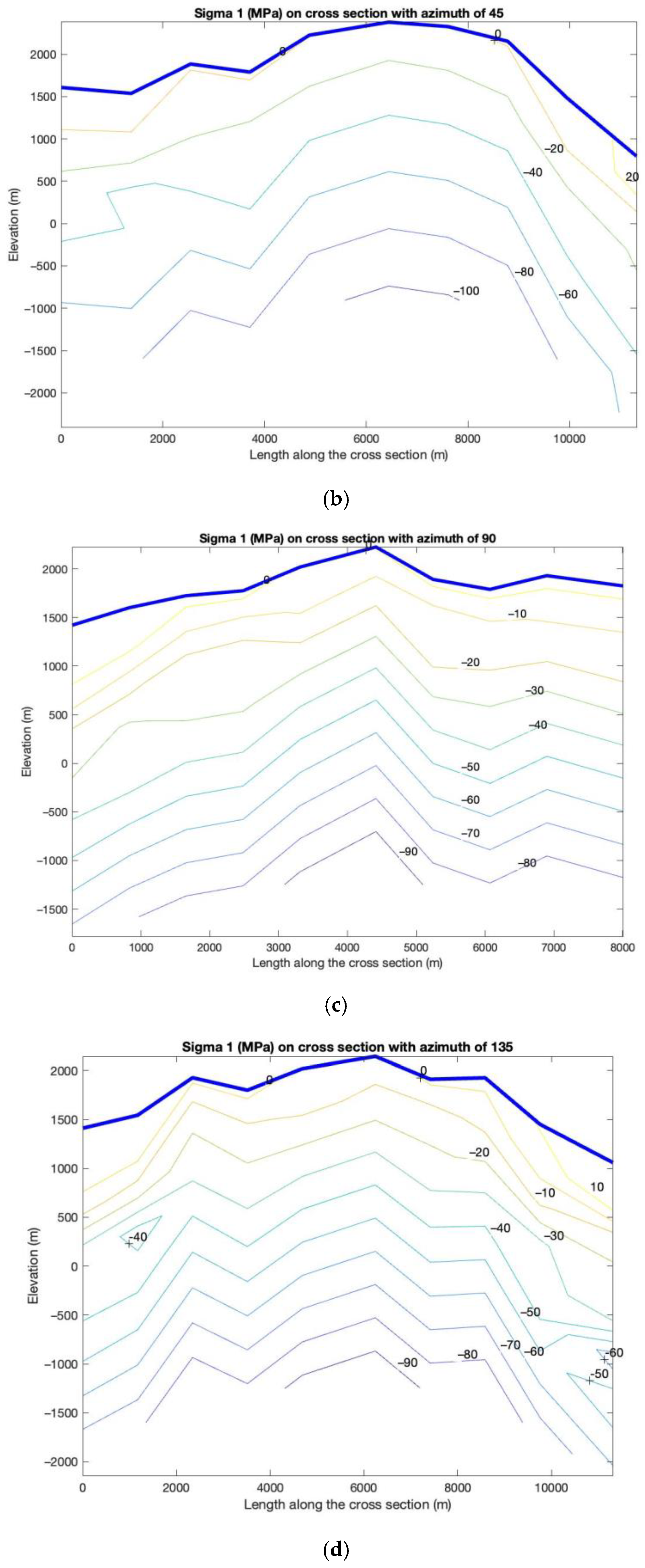
5. Results
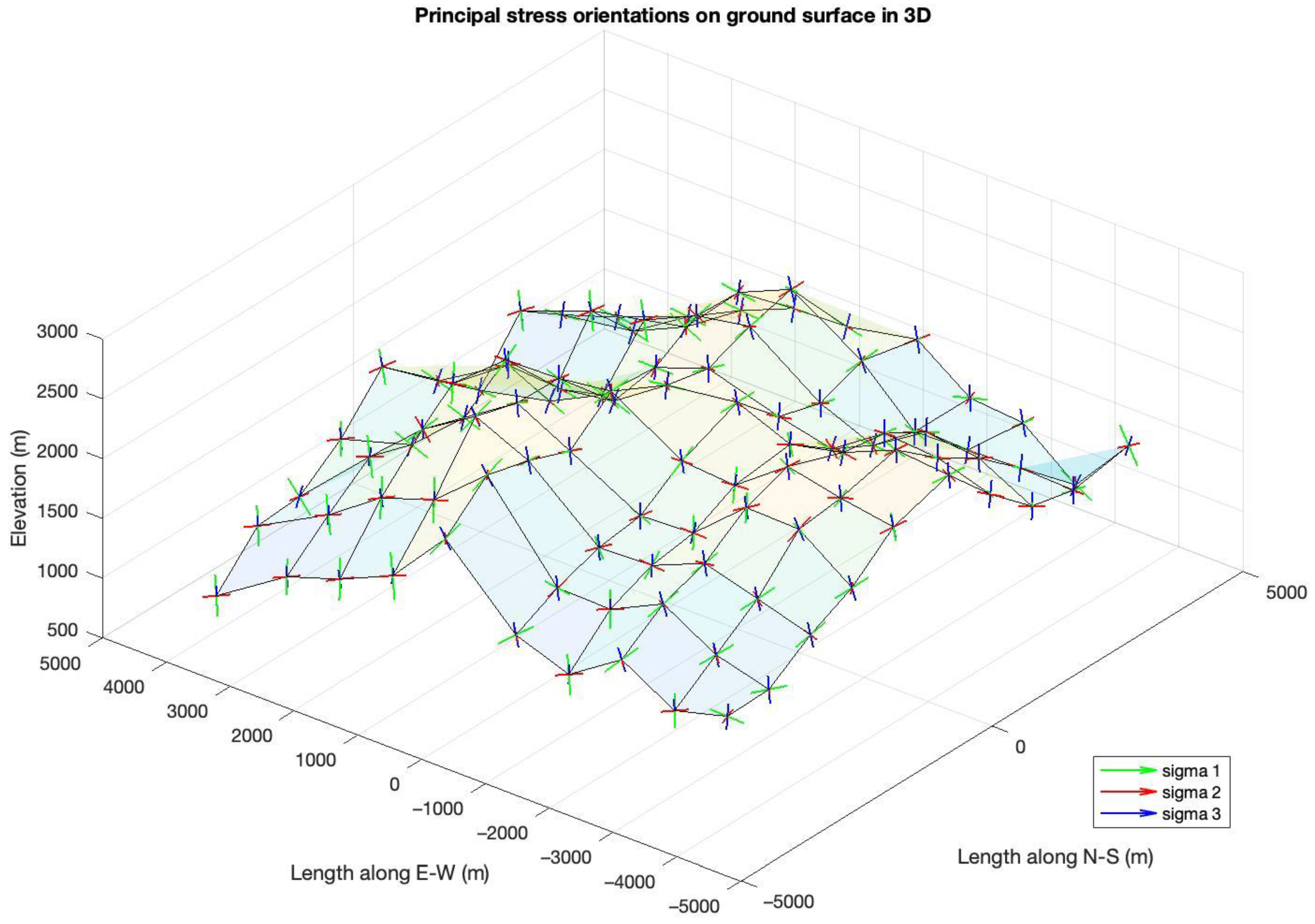
5.1. Base Case with Zero Tectonic Stress
5.2. Induced Stress State with Tectonic Stress
6. Discussion
7. Conclusions
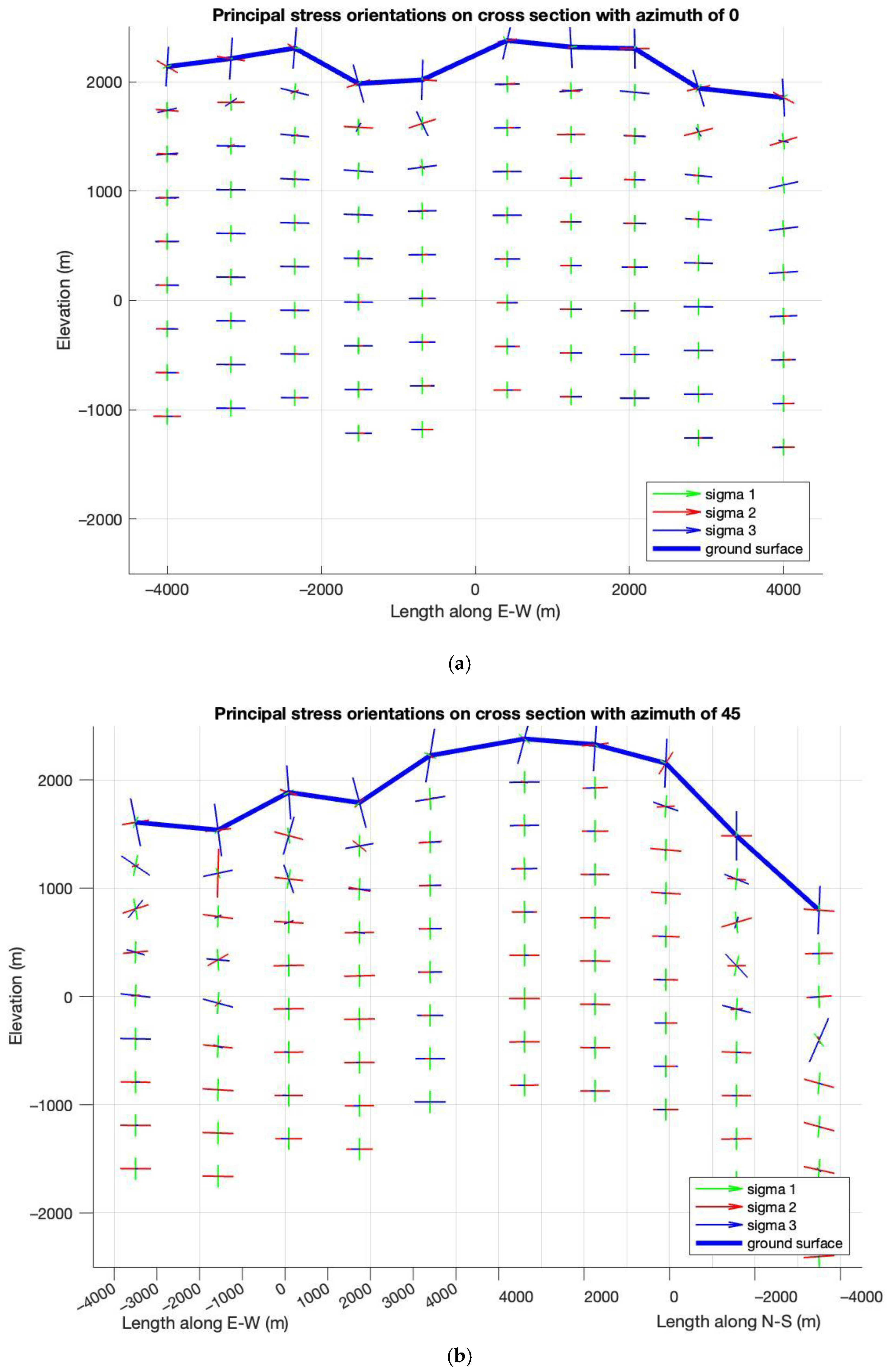
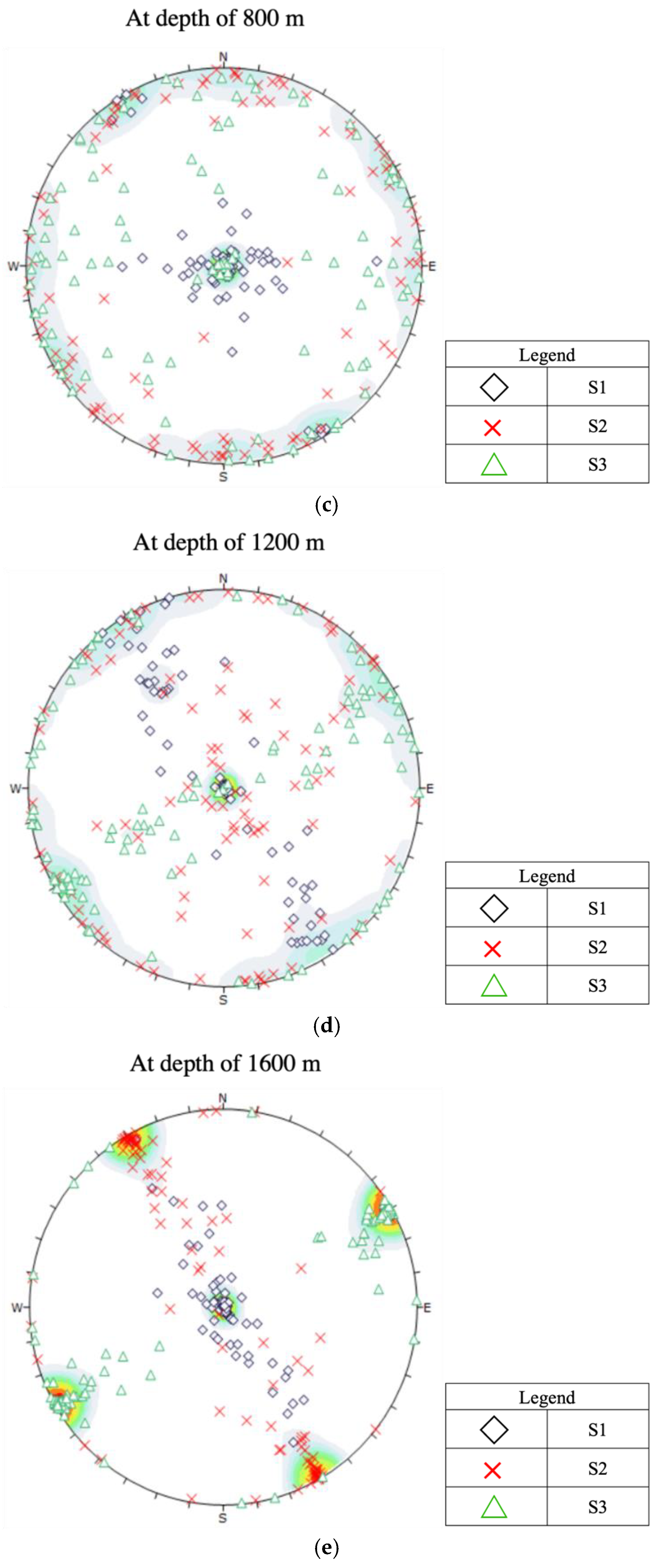
- In shallow depths, (<800 m), where the in-situ stress is similar to the tectonic-stress free case, a normal faulting regime ( > ) prevails. The orientations of and depend on local topographic variation.
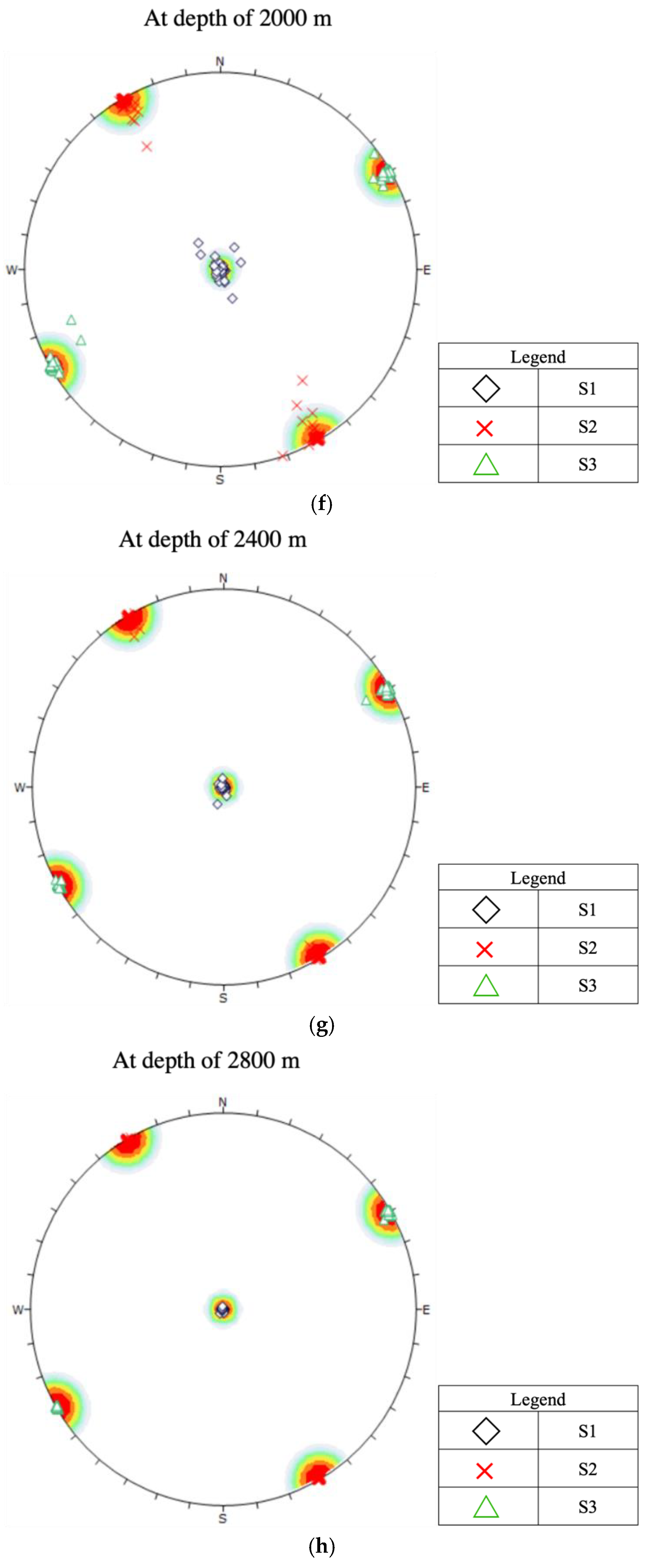
- In a depth interval of approximately between 800 m to 1600 m, we see a transition from a normal faulting regime through a strike-slip faulting regime ( > > ) to a thrust faulting regime ( > > ) taking place, due to the interplays between tectonic stresses and topography induced stresses.
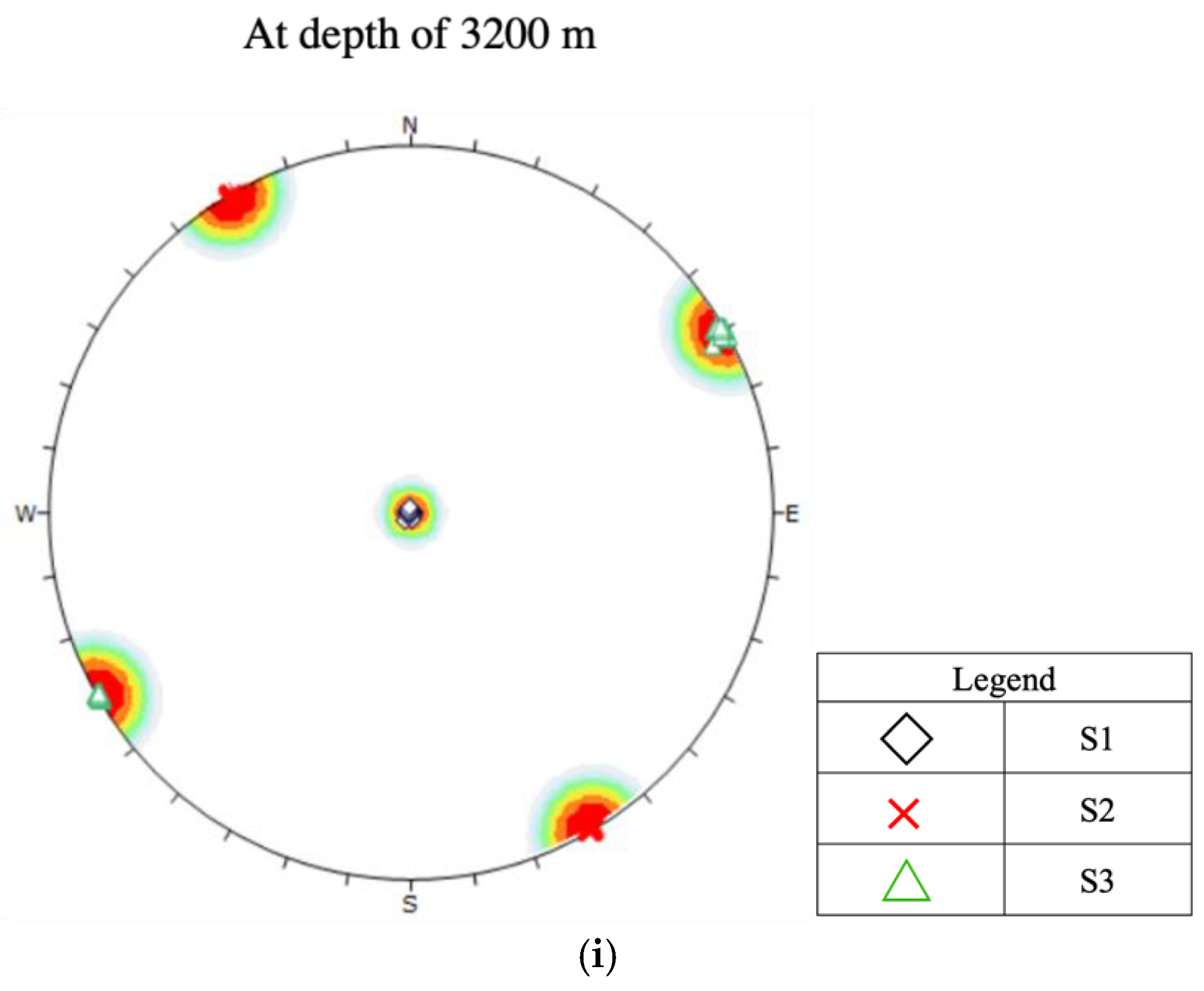
- As the gravity load of the rock mass (vertical stress) increases linearly with depth, the vertical stress surpasses the magnitude of tectonic exerted principal stress at depth > 1800 m and the fault type once again becomes normal faulting ( > > ). The orientations of and are converged toward to the orientations of major and minor horizontal stresses at NWN-SES 330° and NEE-SWW 60°, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Witter, J. South Meager Geothermal Project: New Perspectives from Recently Unearthed Data; Innovate Geothermal Ltd.: Vancouver, BC, Canada, 2019. [Google Scholar]
- Grasby, S.E.; Ansari, S.M.; Barendregt, R.W.; Borch, A.; Calahorrano-DiPatre, A.; Chen, Z.; Craven, J.A.; Dettmer, J.; Gilbert, H. Garibaldi Geothermal Energy Project—Phase 1; Geoscience BC: Vancouver, BC, Canada, 2021. [Google Scholar]
- Lewis, T.J.; Souther, J.G. Meager Mountain, B.C.: A Possible Geothermal Energy Resource; Geothermal Series; Energy, Mines and Resources Canada, Earth Physics Branch: Ottawa, ON, Canada, 1978. [Google Scholar]
- Chen, Z.; Grasby, S.E.; Yuan, W.; Liu, X. Ground Surface Temperature Monitoring Data Analysis and Applications to Geothermal Exploration in Volcanic Areas, Mount Meager, Western Canada. Geothermics 2023, 108, 102610. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Z.; Grasby, S.E. Using Shallow Temperature Measurements to Evaluate Thermal Flux Anomalies in the Southern Mount Meager Volcanic Area, British Columbia, Canada; Geological Survey of Canada: Ottawa, ON, Canada, 2022; p. 8890. [Google Scholar]
- Meixner, J.; Schill, E.; Gaucher, E.; Kohl, T. Inferring the in Situ Stress Regime in Deep Sediments: An Example from the Bruchsal Geothermal Site. Geotherm. Energy 2014, 2, 7. [Google Scholar] [CrossRef]
- Sun, Z.; Jiang, C.; Wang, X.; Zhou, W.; Lei, Q. Combined Effects of Thermal Perturbation and In-Situ Stress on Heat Transfer in Fractured Geothermal Reservoirs. Rock Mech. Rock Eng. 2021, 54, 2165–2181. [Google Scholar] [CrossRef]
- Griffith, W.A.; Becker, J.; Cione, K.; Miller, T.; Pan, E. 3D Topographic Stress Perturbations and Implications for Ground Control in Underground Coal Mines. Int. J. Rock Mech. Min. Sci. 2014, 70, 59–68. [Google Scholar] [CrossRef]
- Haimson, B.C. A Simple Method for Estimating Stresses at Great Depths. In Proceedings of the Field Testing and Instrumentation of Rock; ASTM International: West Conshohoncken, PA, USA, 1974; pp. 156–182. [Google Scholar]
- Haimson, B.; Fairhurst, C. Initiation and Extension of Hydraulic Fractures in Rocks. Soc. Pet. Eng. J. 1967, 7, 310–318. [Google Scholar] [CrossRef]
- Aadnoy, B.S. Inversion Technique to Determine the In-Situ Stress Field from Fracturing Data. J. Pet. Sci. Eng. 1990, 4, 127–141. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, S. Determination of in Situ Stresses and Elastic Parameters from Hydraulic Fracturing Tests by Geomechanics Modeling and Soft Computing. J. Pet. Sci. Eng. 2014, 124, 484–492. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, S. Determination of Horizontal In-Situ Stresses and Natural Fracture Properties from Wellbore Deformation. Int. J. Oil 2014, 7, 1–28. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, S. Determination of Earth Stresses Using Inverse Analysis Based on Coupled Numerical Modelling and Soft Computing. Int. J. Comput. Appl. Technol. 2015, 52, 18–28. [Google Scholar] [CrossRef]
- Han, H.; Yin, S. Determination of In-Situ Stress and Geomechanical Properties from Borehole Deformation. Energies 2018, 11, 131. [Google Scholar] [CrossRef]
- Han, H.; Yin, S. In-Situ Stress Inversion in Liard Basin, Canada, from Caliper Logs. Petroleum 2020, 6, 392–403. [Google Scholar] [CrossRef]
- Martel, S.J.; Muller, J.R. A Two-Dimensional Boundary Element Method for Calculating Elastic Gravitational Stresses in Slopes. Pure Appl. Geophys. 2000, 157, 989–1007. [Google Scholar] [CrossRef]
- Slim, M.; Perron, J.T.; Martel, S.J.; Singha, K. Topographic Stress and Rock Fracture: A Two-Dimensional Numerical Model for Arbitrary Topography and Preliminary Comparison with Borehole Observations: Topographic Stress and Rock Fracture. Earth Surf. Process. Landf. 2015, 40, 512–529. [Google Scholar] [CrossRef]
- Pan, E.; Amadei, B.; Savage, W.Z. Gravitational and Tectonic Stresses in Anisotropic Rock with Irregular Topography. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 201–214. [Google Scholar] [CrossRef]
- Moon, S.; Perron, J.T.; Martel, S.J.; Holbrook, W.S.; St. Clair, J. A Model of Three-Dimensional Topographic Stresses with Implications for Bedrock Fractures, Surface Processes, and Landscape Evolution. J. Geophys. Res. Earth Surf. 2017, 122, 823–846. [Google Scholar] [CrossRef]
- Yin, S. Geomechanics-Reservoir Modeling by Displacement Discontinuity-Finite Element Method; University of Waterloo: Waterloo, ON, Canada, 2008. [Google Scholar]
- Venugopal, S.; Moune, S.; Williams-Jones, G.; Druitt, T.; Vigouroux, N.; Wilson, A.; Russell, J.K. Two Distinct Mantle Sources beneath the Garibaldi Volcanic Belt: Insight from Olivine-Hosted Melt Inclusions. Chem. Geol. 2020, 532, 119346. [Google Scholar] [CrossRef]
- Balfour, N.J.; Cassidy, J.F.; Dosso, S.E.; Mazzotti, S. Mapping Crustal Stress and Strain in Southwest British Columbia. J. Geophys. Res. 2011, 116, 00B03314. [Google Scholar] [CrossRef]
- Natural Resources Canada Plate Tectonics Shape (and Shake) British Columbia. Available online: https://earthquakescanada.nrcan.gc.ca/pprs-pprp/pubs/GF-GI/GEOFACT_plate-tectonics_e.pdf (accessed on 18 January 2023).
- Dusseault, M.B.; Bruno, M.S.; Barrera, J. Casing Shear: Causes, Cases, Cures; OnePetro: Richardson, TX, USA, 1998. [Google Scholar]
- Yong, R.; Wu, J.; Huang, H.; Xu, E.; Xu, B. Complex in Situ Stress States in a Deep Shale Gas Reservoir in the Southern Sichuan Basin, China: From Field Stress Measurements to in Situ Stress Modeling. Mar. Pet. Geol. 2022, 141, 105702. [Google Scholar] [CrossRef]
- Teraghi, K.; Richart, F.E. Stresses in Rock about Cavities. Géotechnique 1952, 3, 57–90. [Google Scholar] [CrossRef]
- Amadei, B.; Pan, E. Gravitational Stresses in Anisotropic Rock Masses with Inclined Strata. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1992, 29, 225–236. [Google Scholar] [CrossRef]
- Perloff, W.; Baladi, G.; Harr, M. Stress Distribution within and under Long Elastic Embankments: Research Paper; Joint Highway Research Project; Indiana Department of Transportation and Purdue University: West Lafayette, IN, USA, 1967. [Google Scholar]
- Savage, W.Z.; Swolfs, H.S.; Powers, P.S. Gravitational Stresses in Long Symmetric Ridges and Valleys. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 291–302. [Google Scholar] [CrossRef]
- McTigue, D.F.; Mei, C.C. Gravity-Induced Stresses near Topography of Small Slope. J. Geophys. Res. Solid Earth 1981, 86, 9268–9278. [Google Scholar] [CrossRef]
- Zhang, H.; Yin, S.; Aadnoy, B.S. Poroelastic Modeling of Borehole Breakouts for In-Situ Stress Determination by Finite Element Method. J. Pet. Sci. Eng. 2018, 162, 674–684. [Google Scholar] [CrossRef]
- Lobatskaya, R.M.; Strelchenko, I.P.; Dolgikh, E.S. Finite-Element 3D Modeling of Stress Patterns around a Dipping Fault. Geosci. Front. 2018, 9, 1555–1563. [Google Scholar] [CrossRef]
- Homberg, C.; Hu, J.C.; Angelier, J.; Bergerat, F.; Lacombe, O. Characterization of Stress Perturbations near Major Fault Zones: Insights from 2-D Distinct-Element Numerical Modelling and Field Studies (Jura Mountains). J. Struct. Geol. 1997, 19, 703–718. [Google Scholar] [CrossRef]
- Hazeghian, M.; Soroush, A. Numerical Modeling of Dip-Slip Faulting through Granular Soils Using DEM. Soil Dyn. Earthq. Eng. 2017, 97, 155–171. [Google Scholar] [CrossRef]
- Brady, B.H. Boundary Element Method for Mine Design; University of London: London, UK, 1979. [Google Scholar]
- Ritz, E.; Mutlu, O.; Pollard, D.D. Integrating Complementarity into the 2D Displacement Discontinuity Boundary Element Method to Model Faults and Fractures with Frictional Contact Properties. Comput. Geosci. 2012, 45, 304–312. [Google Scholar] [CrossRef]
- Li, K. Numerical Analysis of Undersea Geostress Field around Fault. Electron. J. Geotech. Eng. 2015, 20, 1887. [Google Scholar]
- Chai, Y.; Yin, S. 3D Displacement Discontinuity Analysis of In-Situ Stress Perturbation near a Weak Fault. Adv. Geo-Energy Res. 2021, 5, 286–296. [Google Scholar] [CrossRef]
- Cheng, A.H.-D.; Cheng, D.T. Heritage and Early History of the Boundary Element Method. Eng. Anal. Bound. Elem. 2005, 29, 268–302. [Google Scholar] [CrossRef]
- Rizzo, F.J. An Integral Equation Approach to Boundary Value Problems of Classical Elastostatics. Q. Appl. Math. 1967, 25, 83–95. [Google Scholar] [CrossRef]
- Crouch, S.L.; Starfield, A.M. Boundary Element Methods in Solid Mechanics: With Applications in Rock Mechanics and Geological Engineering; Allen & Unwin: Crows Nest, Australia, 1983; ISBN 978-0-04-620010-7. [Google Scholar]
- Liu, Y. On the Displacement Discontinuity Method and the Boundary Element Method for Solving 3-D Crack Problems. Eng. Fract. Mech. 2016, 164, 35–45. [Google Scholar] [CrossRef]
- Brady, B.H.G.; Bray, J.W. The Boundary Element Method for Elastic Analysis of Tabular Orebody Extraction, Assuming Complete Plane Strain. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 29–37. [Google Scholar] [CrossRef]
- Pan, E.; Amadei, B. Three-Dimensional in Situ Stress Analysis of Rock Masses Perturbed by Irregular Topographies and Underground Openings; Colorado University at Boulder Department of Mechanical Engineering: Boulder, CO, USA, 1998. [Google Scholar]
- Hetherington, R.M. Slope Stability Analysis of Mount Meager, Southwestern British Columbia, Canada. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2014. [Google Scholar]
- Sibson, R.H. Fault Rocks and Fault Mechanisms. J. Geol. Soc. 1977, 133, 191–213. [Google Scholar] [CrossRef]
- Mendoza, W. Dips: Plotting, Analysis and Presentation of Structural Data Using Spherical Projection Techniques; Rocscience Inc.: Toronto, ON, Canada, 2002. [Google Scholar]
- Ristau, J.; Rogers, G.C.; Cassidy, J.F. Stress in Western Canada from Regional Moment Tensor Analysis. Can. J. Earth Sci. 2007, 44, 127–148. [Google Scholar] [CrossRef]
- Chen, Z.; Grasby, S.E.; Liu, X. Fracture System Analyses of the Mount Meager Area; Natural Resources Canada: Ottawa, ON, Canada, 2021. [Google Scholar]
- Chen, Z.; Grasby, S.; Deblonde, C.; Liu, X. AI-Enabled Remote Sensing Data Interpretation for Geothermal Resource Evaluation as Applied to the Mount Meager Geothermal Prospective Area; Natural Resources Canada: Ottawa, ON, Canada, 2022. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Y.; Chen, Z.; Yin, S. A Preliminary Analysis of In-Situ Stress at Mount Meager by Displacement Discontinuity Method with Topography and Tectonics Considered. Energies 2023, 16, 1397. https://doi.org/10.3390/en16031397
Chai Y, Chen Z, Yin S. A Preliminary Analysis of In-Situ Stress at Mount Meager by Displacement Discontinuity Method with Topography and Tectonics Considered. Energies. 2023; 16(3):1397. https://doi.org/10.3390/en16031397
Chicago/Turabian StyleChai, Yutong, Zhuoheng Chen, and Shunde Yin. 2023. "A Preliminary Analysis of In-Situ Stress at Mount Meager by Displacement Discontinuity Method with Topography and Tectonics Considered" Energies 16, no. 3: 1397. https://doi.org/10.3390/en16031397
APA StyleChai, Y., Chen, Z., & Yin, S. (2023). A Preliminary Analysis of In-Situ Stress at Mount Meager by Displacement Discontinuity Method with Topography and Tectonics Considered. Energies, 16(3), 1397. https://doi.org/10.3390/en16031397







