Numerical Simulation of Geothermal Energy Development at Mount Meager and Its Impact on In Situ Thermal Stress
Abstract
1. Introduction
2. Methodology
- Components such as casing, cement, and rock exhibit homogeneity and isotropy.
- The rocks are fully saturated with water. Little groundwater movement is simulated due to the rock matrix’s low permeability and porosity [28]. In fact, given that a BHE operates as a closed-loop system, the impact of seepage is not deemed critical. The heat transfer effectiveness of the BHE is not significantly enhanced by the groundwater flow unless there is a simultaneous improvement in the thermal conductivity of the borehole and the velocity of groundwater. For this study, the heat transfer within the reservoir follows the theory of local thermal equilibrium.
- The non-isothermal pipe flow model characterizes fluid movement and heat transfer within the injection and production pipe, and the radial flow of the circulating fluid is neglected.
- The occurrence of phase change in the circulating fluid is neglected, as the pressures are maintained at a sufficiently high level to prevent any phase change within the well.
- Since the wellbore is circular, a circular rock matrix is simulated; so, the 3D model can be simplified into a 2D axisymmetric model.
2.1. Geometric Configuration of the Coaxial BHE
2.2. Fluid Heat Transfer Formulations
2.3. Thermally Induced Stress Formulations
2.4. Initial Values and Boundary Conditions
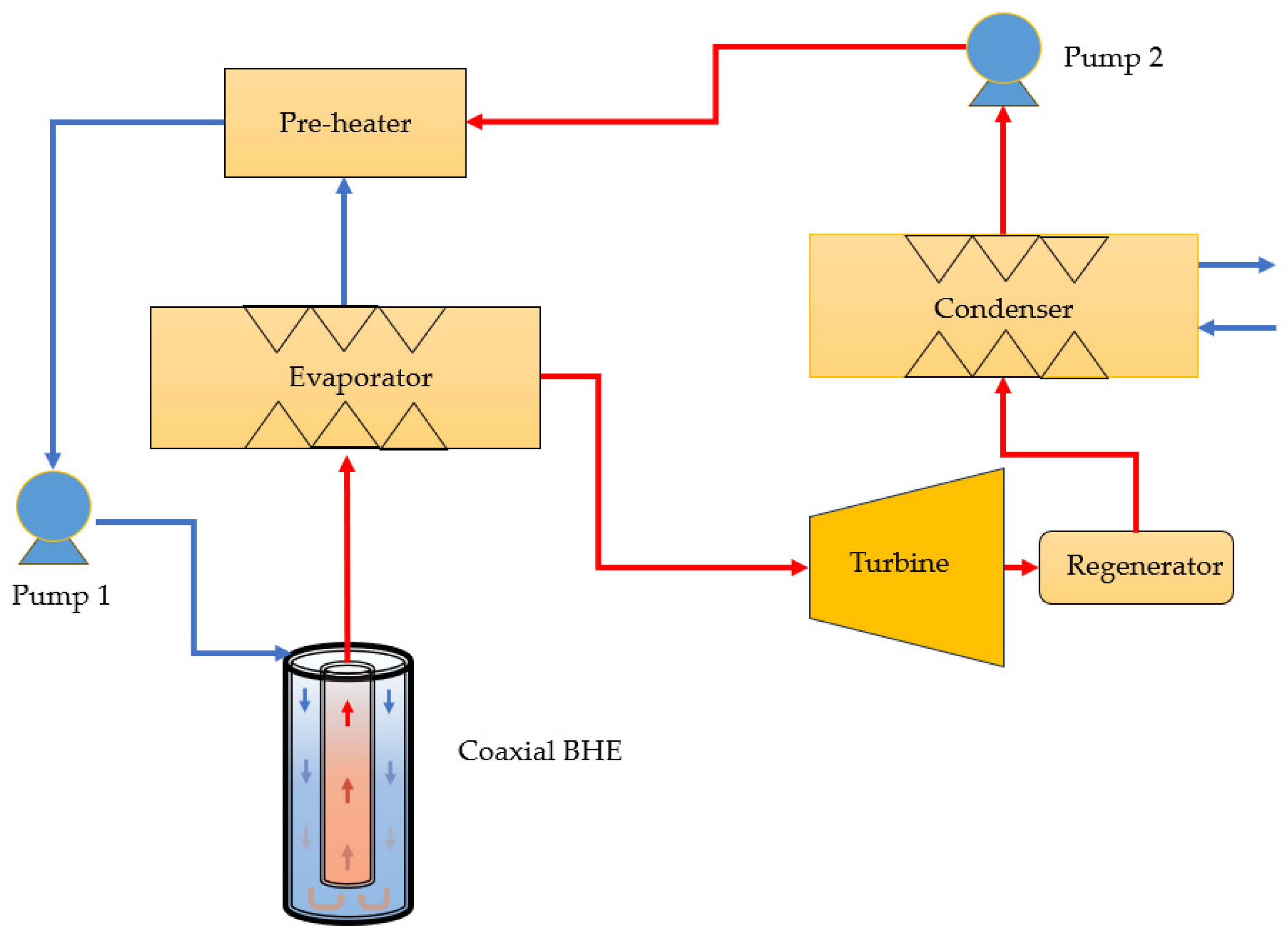
2.5. Organic Rankine Cycle
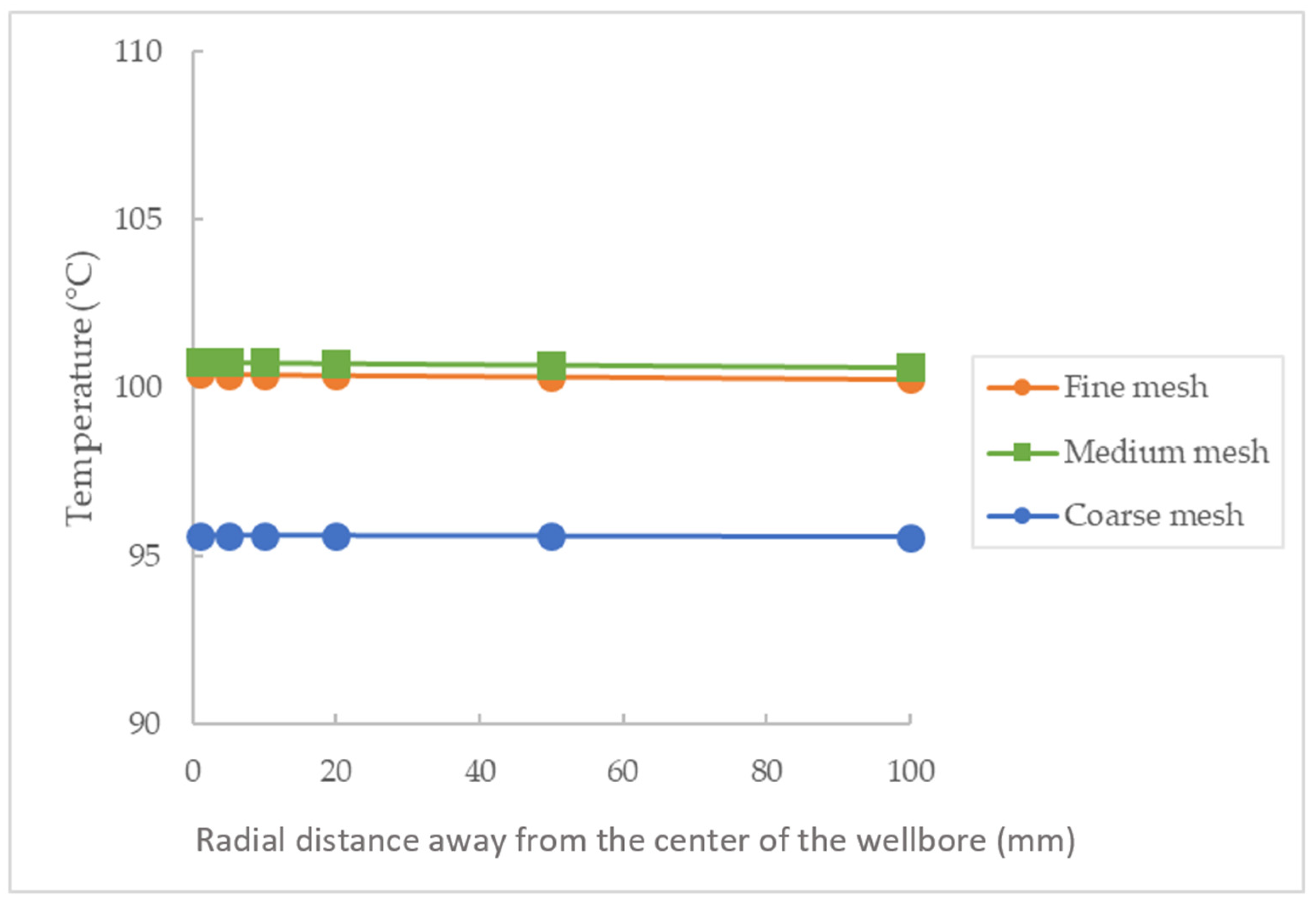
3. Model Sensitivity and Study Limitations
4. Results and Discussion
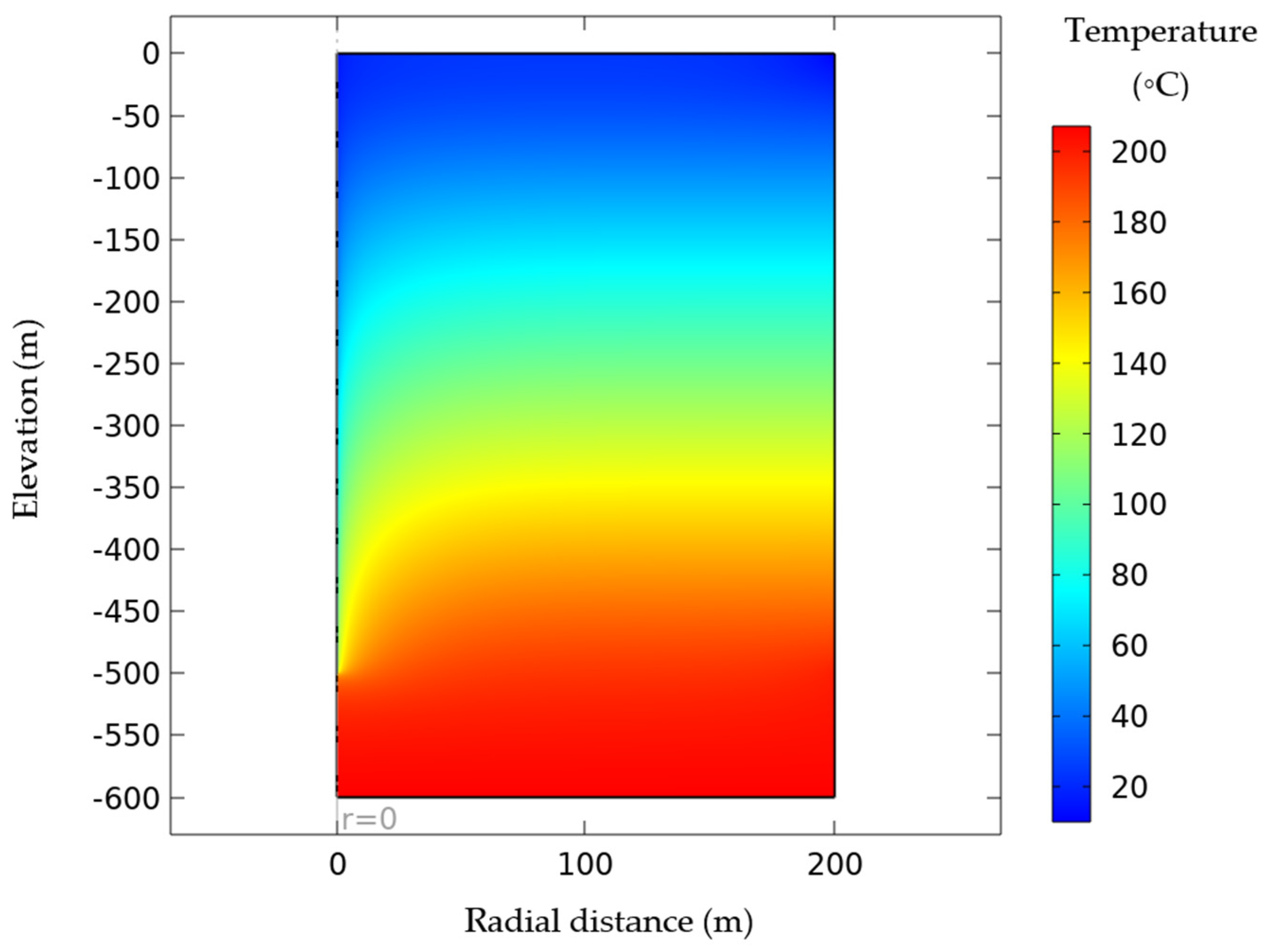
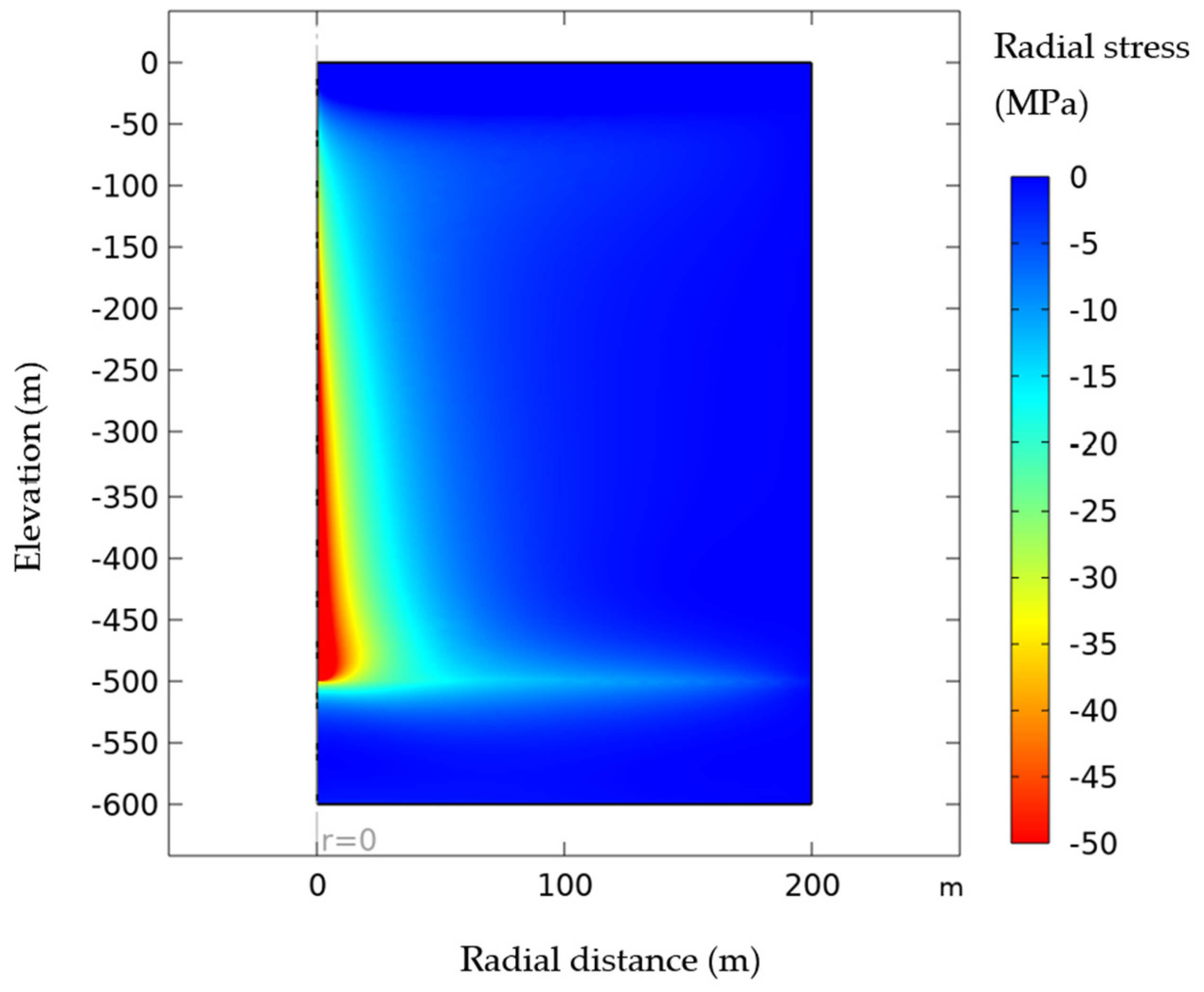
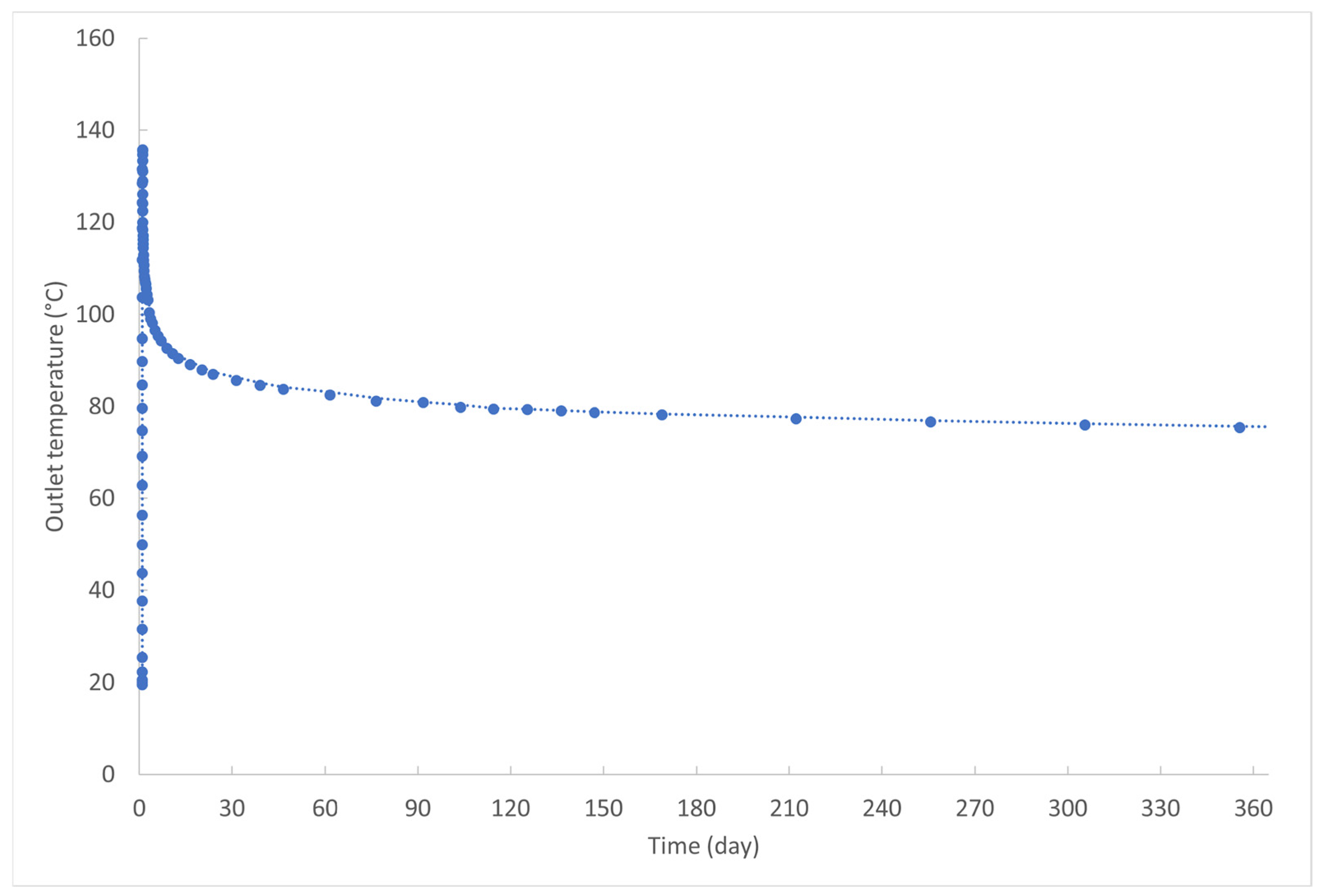
4.1. Base Case
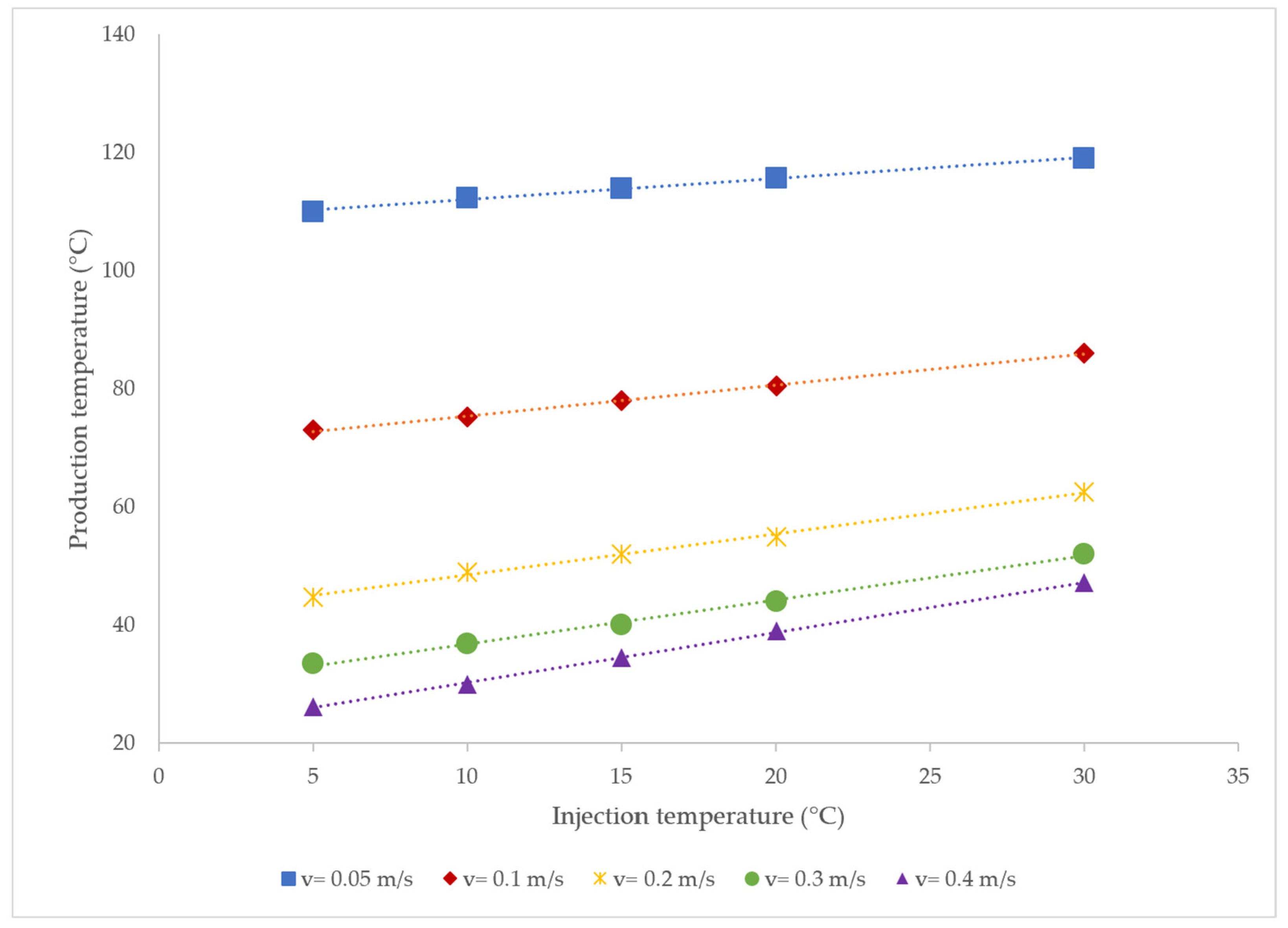
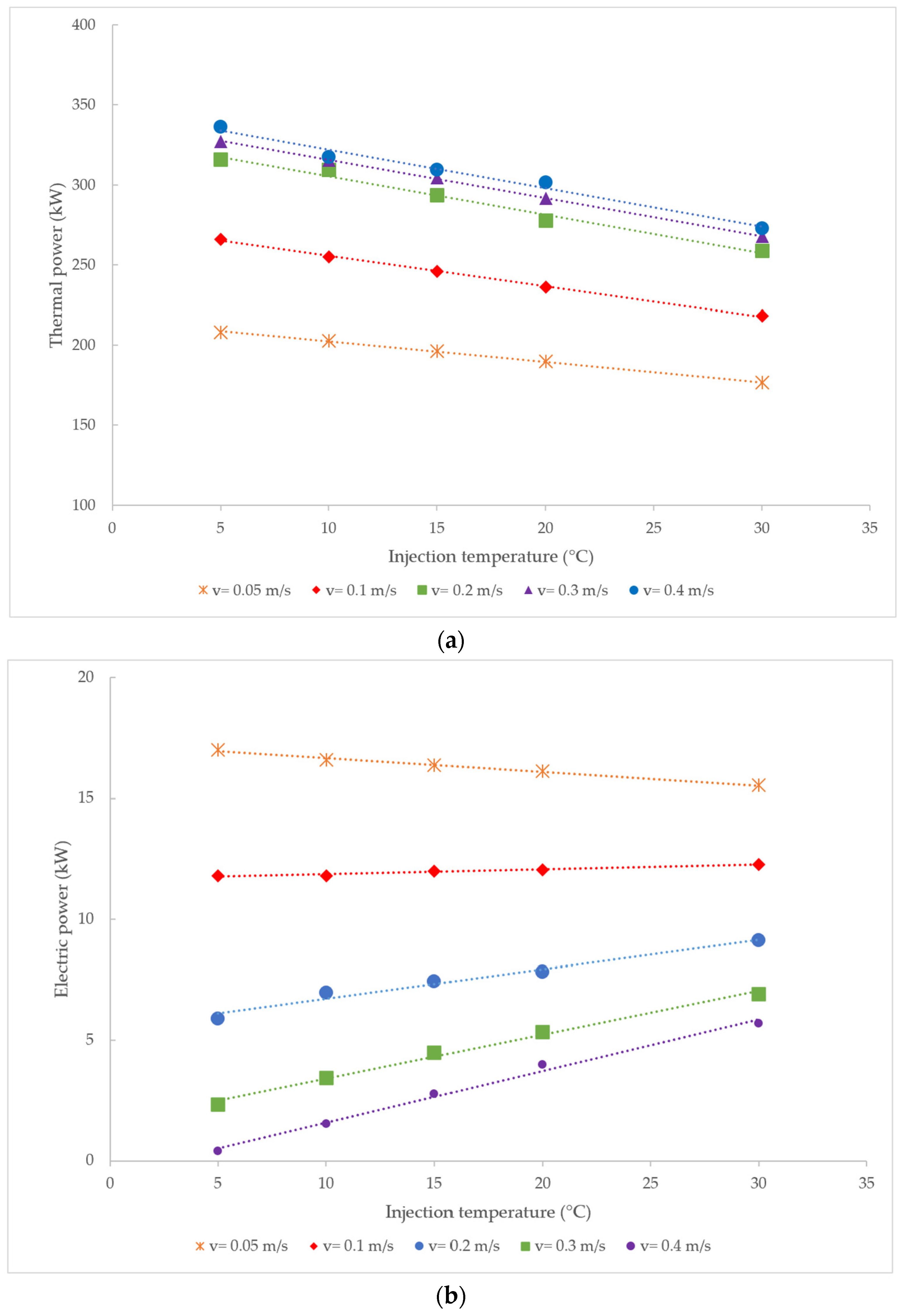
4.2. Sensitivity Analyses
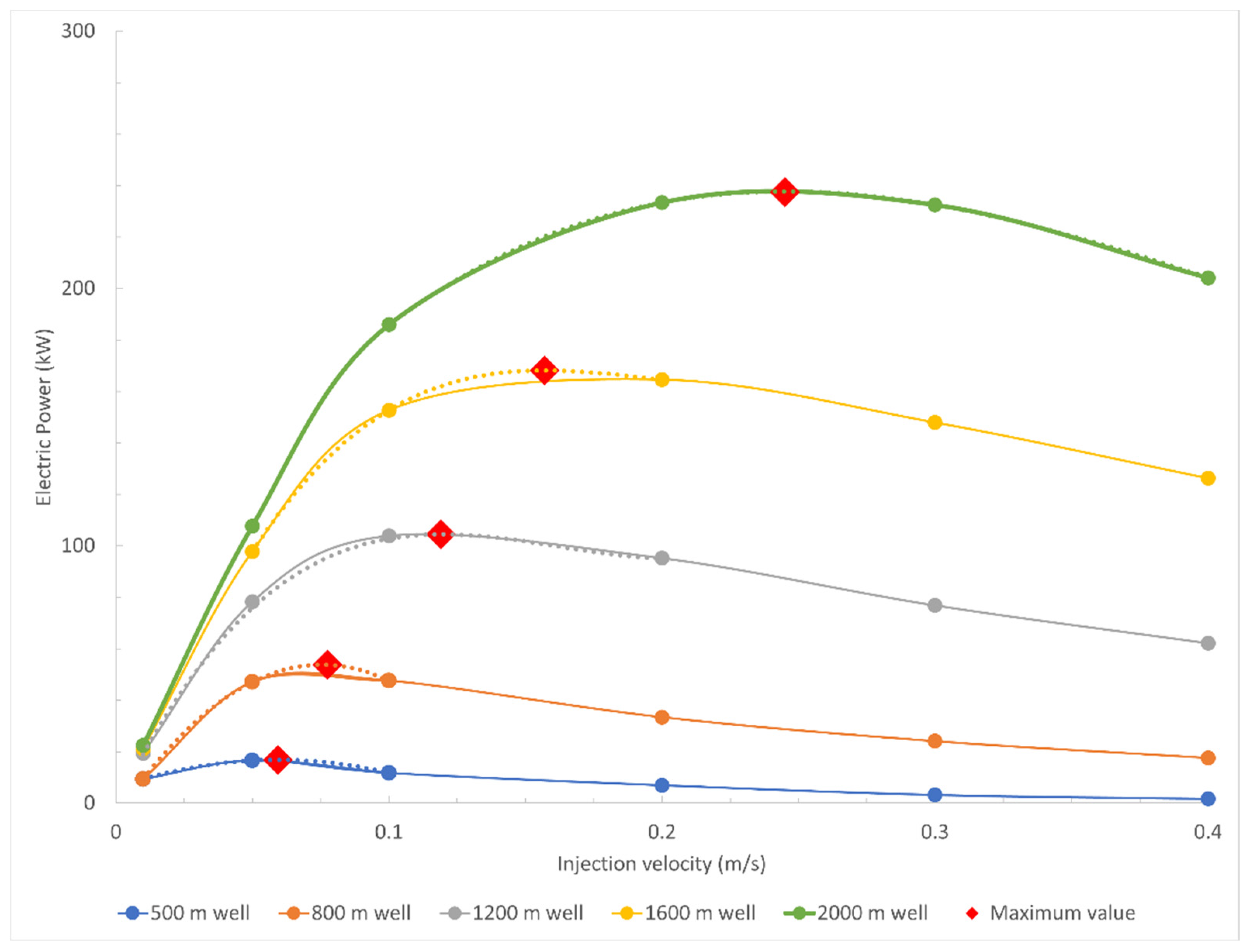
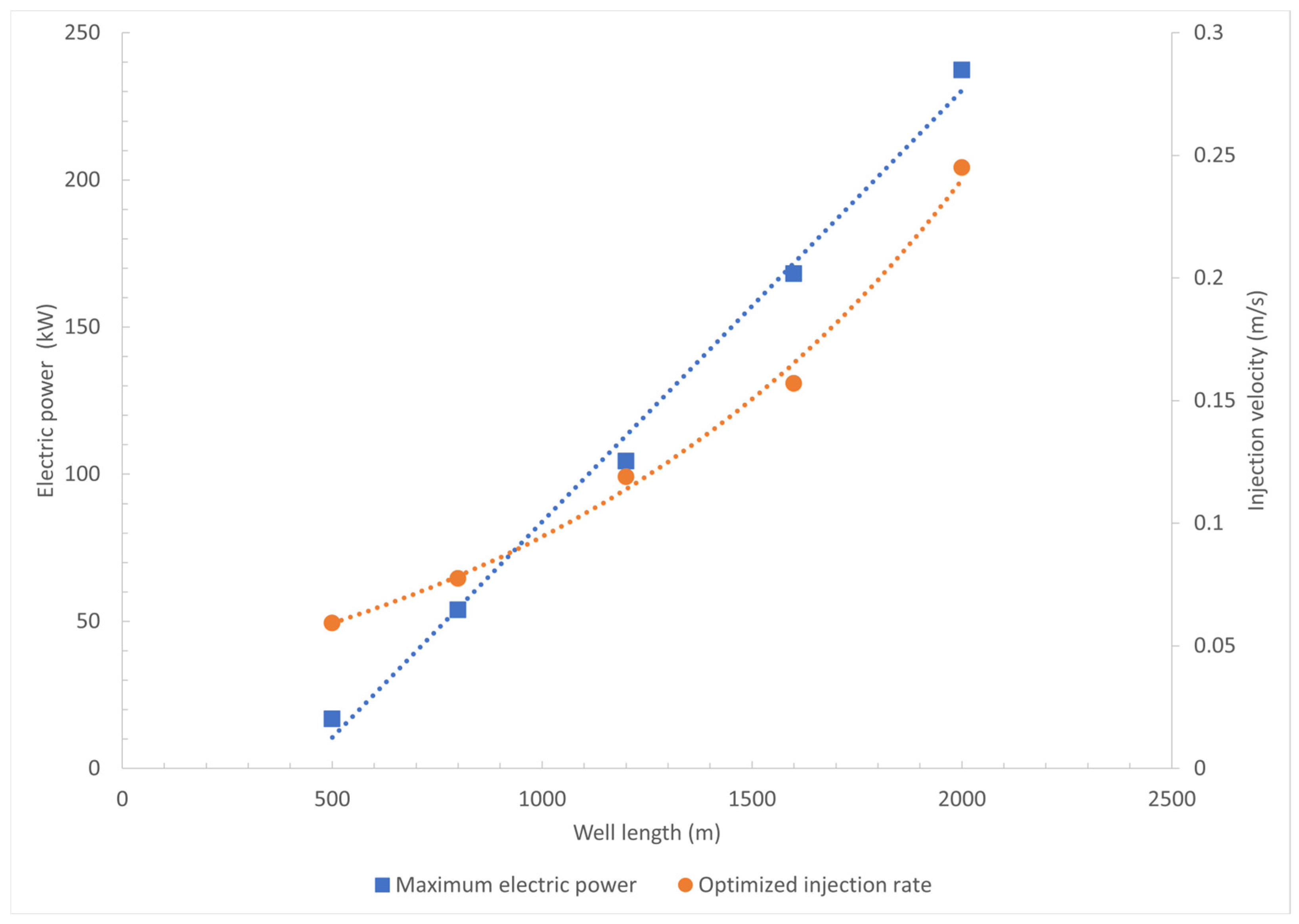
Power Generation
4.3. Non-Linear Thermal Gradient
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Han, Y.; Liu, X.; Ansari, U.; Cheng, Y.; Yan, C. Hydrate as a By-Product in CO2 Leakage during the Long-Term Sub-Seabed Sequestration and Its Role in Preventing Further Leakage. Environ. Sci. Pollut. Res. 2022, 29, 77737–77754. [Google Scholar] [CrossRef] [PubMed]
- Cano, N.; Cespedes, S.; Redondo, J.; Foo, G.; Jaramillo, D.; Martinez, D.; Gutiérrez, M.; Pataquiba, J.; Rojas, J.; Cortés, F.; et al. Power from Geothermal Resources as a Co-Product of the Oil and Gas Industry: A Review. ACS Omega 2022, 7, 40603–40624. [Google Scholar] [CrossRef] [PubMed]
- Witter, J. South Meager Geothermal Project: New Perspectives from Recently Unearthed Data. Innovate Geothermal Ltd., 2019. Available online: https://cdn.geosciencebc.com/pdf/Report-2019-07-Innovate-Geothermal.pdf (accessed on 30 June 2024).
- Lewis, T.J.; Souther, J.G. Meager Mountain, B.C.: A Possible Geothermal Energy Resource; Geothermal Series; Energy, Mines and Resources Canada, Earth Physics Branch: Ottawa, ON, Canada, 1978.
- Chen, Z.; Grasby, S.E.; Yuan, W.; Liu, X. Ground Surface Temperature Monitoring Data Analysis and Applications to Geothermal Exploration in Volcanic Areas, Mount Meager, Western Canada. Geothermics 2023, 108, 102610. [Google Scholar] [CrossRef]
- Geoscience BC Mount Meager Geothermal Data Compilation Project. Available online: https://www.geosciencebc.com/projects/2017-006/ (accessed on 28 November 2023).
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. Impact of Enhanced Geothermal Systems on US Energy Supply in the Twenty-First Century. Philos. Trans. A Math. Phys. Eng. Sci. 2007, 365, 1057–1094. [Google Scholar] [CrossRef]
- Walch, A.; Mohajeri, N.; Gudmundsson, A.; Scartezzini, J.-L. Quantifying the Technical Geothermal Potential from Shallow Borehole Heat Exchangers at Regional Scale. Renew. Energy 2021, 165, 369–380. [Google Scholar] [CrossRef]
- Bu, X.; Jiang, K.; Li, H.; Ma, F.; Wang, L. Experimental Study on Convective Heat Transfer of an Open-Loop Borehole Heat Exchanger. Geotherm. Energy 2023, 11, 8. [Google Scholar] [CrossRef]
- Ma, H.; Mao, R.; Zhou, J.; Pei, P.; Tian, X.; Zhang, Z. Study on Influence of Geotechnical Characteristics on Heat Transfer Performance of Borehole Heat Exchanger. Energy Sources Part A-Recovery Util. Environ. Eff. 2023, 45, 1822–1841. [Google Scholar] [CrossRef]
- Amanzholov, T.; Belyayev, E.; Mohanraj, M.; Toleukhanov, A. Study of borehole heat exchanger heat transfer enhancement parameters. J. Math. Mech. Comput. Sci. 2022, 115, 65–77. [Google Scholar] [CrossRef]
- Sun, L.; Fu, B.; Wei, M.; Zhang, S. Analysis of Enhanced Heat Transfer Characteristics of Coaxial Borehole Heat Exchanger. Processes 2022, 10, 2057. [Google Scholar] [CrossRef]
- Renaud, T.; Pan, L.; Doran, H.; Falcone, G.; Verdin, P.G. Numerical analysis of enhanced conductive deep borehole heat exchangers. Sustainability 2021, 13, 6918. [Google Scholar] [CrossRef]
- Bräunig, L.; Jusri, T.; Seupel, C.; Bertani, R.; Buske, S. A Comprehensive Seismic Data Analysis for Geothermal Reservoir Characterization within Project DESCRAMBLE. 2018. Available online: https://www.researchgate.net/publication/323218989_A_comprehensive_seismic_data_analysis_for_geothermal_reservoir_characterization_within_project_DESCRAMBLE (accessed on 30 June 2024).
- Alimonti, C.; Soldo, E.; Bocchetti, D.; Berardi, D. The wellbore heat exchangers: A technical review. Renew. Energy 2018, 123, 353–381. [Google Scholar] [CrossRef]
- Tarrad, A.H. 3D numerical modeling to evaluate the thermal performance of single and double U-tube ground-coupled heat pump. HighTech Innov. J. 2022, 3, 115–129. [Google Scholar] [CrossRef]
- Li, C.; Guan, Y.; Wang, X.; Li, G.; Zhou, C.; Xun, Y. Experimental and numerical studies on heat transfer characteristics of vertical deep-buried U-bend pipe to supply heat in buildings with geothermal energy. Energy 2018, 142, 689–701. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xie, Y.; Zhang, Y.; Gao, X.; Ma, J. Field Test and Numerical Investigation on Deep Coaxial Borehole Heat Exchanger Based on Distributed Optical Fiber Temperature Sensor. Energy 2020, 210, 118643. [Google Scholar] [CrossRef]
- Song, X.; Zheng, R.; Li, G.; Shi, Y.; Wang, G.; Li, J. Heat Extraction Performance of a Downhole Coaxial Heat Exchanger Geothermal System by Considering Fluid Flow in the Reservoir. Geothermics 2018, 76, 190–200. [Google Scholar] [CrossRef]
- Hu, X.; Banks, J.; Wu, L.; Liu, W.V. Numerical Modeling of a Coaxial Borehole Heat Exchanger to Exploit Geothermal Energy from Abandoned Petroleum Wells in Hinton, Alberta. Renew. Energy 2020, 148, 1110–1123. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Pourarshad, M.; Jalilinasrabady, S.; Yousefi, H. Numerical Simulation of Power Production from Abandoned Oil Wells in Ahwaz Oil Field in Southern Iran. Geothermics 2015, 55, 16–23. [Google Scholar] [CrossRef]
- Kolo, I.; Sousa, R.; Zhang, T. Heat Transmission in a Geothermal Wellbore: Modelling and Application. In Proceedings of the 19th Australasian Fluid Mechanics Conference, AFMC 2014, Melbourne, Australia, 8–11 December 2014. [Google Scholar]
- Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Simulations and Global Sensitivity Analysis of the Thermo-Hydraulic-Mechanical Processes in a Fractured Geothermal Reservoir. Energy 2022, 247, 123511. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Bär, K.; Sass, I. Thermo-Hydro-Mechanical Modeling of an Enhanced Geothermal System in a Fractured Reservoir Using Carbon Dioxide as Heat Transmission Fluid- A Sensitivity Investigation. Energy 2022, 254, 124266. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Mahyapour, R.; Tangirala, S.K.; Bar, K.; Sass, I. Numerical Simulation of Thermo-Hydro-Mechanical Processes at Soultz-Sous-Forêts. Energies 2022, 15, 9285. [Google Scholar] [CrossRef]
- Abe, H.; Sekine, H.; Shibuya, Y. Thermoelastic Analysis of a Cracklike Reservoir in a Hot Dry Rock During Extraction of Geothermal Energy. J. Energy Resour. Technol. Trans. Asme 1983, 105, 503–508. [Google Scholar] [CrossRef]
- Nakagawa, M.; Jahanbakhsh, K.; Arshad, M. Beyond Hydrocarbon Extraction: Enhanced Geothermal Systems. In New Frontiers in Oil and Gas Exploration; Springer: Cham, Switzerland, 2016; pp. 487–506. ISBN 978-3-319-40122-5. [Google Scholar]
- Guo, L.; Zhang, J.; Li, Y.; McLennan, J.; Zhang, Y.; Jiang, H. Experimental and Numerical Investigation of the Influence of Groundwater Flow on the Borehole Heat Exchanger Performance: A Case Study from Tangshan, China. Energy Build. 2021, 248, 111199. [Google Scholar] [CrossRef]
- Paul Day, J. Substrate Contributions to Automotive Catalytic Converter Performance: The Role of Channel Shape on Catalyst Efficiency. In Studies in Surface Science and Catalysis; Kruse, N., Frennet, A., Bastin, J.-M., Eds.; Catalysis and Automotive Pollution Control IV; Elsevier: Amsterdam, The Netherlands, 1998; Volume 116, pp. 453–463. [Google Scholar]
- Saeid, S.; Al-Khoury, R.; Barends, F. An Efficient Computational Model for Deep Low-Enthalpy Geothermal Systems. Comput. Geosci. 2013, 51, 400–409. [Google Scholar] [CrossRef]
- Chai, Y.; Chen, Z.; Yin, S. A Preliminary Analysis of In-Situ Stress at Mount Meager by Displacement Discontinuity Method with Topography and Tectonics Considered. Energies 2023, 16, 1397. [Google Scholar] [CrossRef]
- Fairbank Engineering Ltd. 2001–2002 Drilling Program South Meager Geothermal Project British Coloumbia; Fairbank Engineering Ltd.: Worcester, MA, USA, 2002. [Google Scholar]
- Water—Density, Specific Weight and Thermal Expansion Coefficients. Available online: https://www.engineeringtoolbox.com/water-density-specific-weight-d_595.html (accessed on 1 May 2024).
- Zeb, A.; Abid, M.; Zeb, M.A.; Qureshi, M.O.; Younas, U.; Batool, I. Measurement and Prediction of Thermal Conductivity of Volcanic Basalt Rocks from Warsak Area. Adv. Mater. Sci. Eng. 2020, 2020, e4756806. [Google Scholar] [CrossRef]
- Yuan, W.; Chen, Z.; Grasby, S.E.; Little, E. Closed-Loop Geothermal Energy Recovery from Deep High Enthalpy Systems. Renew. Energy 2021, 177, 976–991. [Google Scholar] [CrossRef]
- Alimonti, C.; Soldo, E. Study of Geothermal Power Generation from a Very Deep Oil Well with a Wellbore Heat Exchanger. Renew. Energy 2016, 86, 292–301. [Google Scholar] [CrossRef]
- Massachusetts Institute of Technology (Ed.) The Future of Geothermal Energy: Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century: An Assessment; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; ISBN 978-0-615-13438-3. [Google Scholar]
- COMSOL Multiphysics Reference Manual. Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 1 May 2024).

| Parameters | Value |
|---|---|
| Radius of the injection well (mm) | 108 |
| Radius of the production well (mm) | 55 |
| Thickness of the insulated tube (mm) | 8.1 |
| Thickness of the cement (mm) | 38.1 |
| Well depth (m) | 500 |
| Length of the production pipe (m) | 499 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Y.; Chen, Z.; Yin, S. Numerical Simulation of Geothermal Energy Development at Mount Meager and Its Impact on In Situ Thermal Stress. Energies 2024, 17, 3466. https://doi.org/10.3390/en17143466
Chai Y, Chen Z, Yin S. Numerical Simulation of Geothermal Energy Development at Mount Meager and Its Impact on In Situ Thermal Stress. Energies. 2024; 17(14):3466. https://doi.org/10.3390/en17143466
Chicago/Turabian StyleChai, Yutong, Zhuoheng Chen, and Shunde Yin. 2024. "Numerical Simulation of Geothermal Energy Development at Mount Meager and Its Impact on In Situ Thermal Stress" Energies 17, no. 14: 3466. https://doi.org/10.3390/en17143466
APA StyleChai, Y., Chen, Z., & Yin, S. (2024). Numerical Simulation of Geothermal Energy Development at Mount Meager and Its Impact on In Situ Thermal Stress. Energies, 17(14), 3466. https://doi.org/10.3390/en17143466






