A New Methodology for Early Detection of Failures in Lithium-Ion Batteries
Abstract
1. Introduction
2. Data and Spectral Analysis
3. Battery Test Methodology
4. Results and Discussion
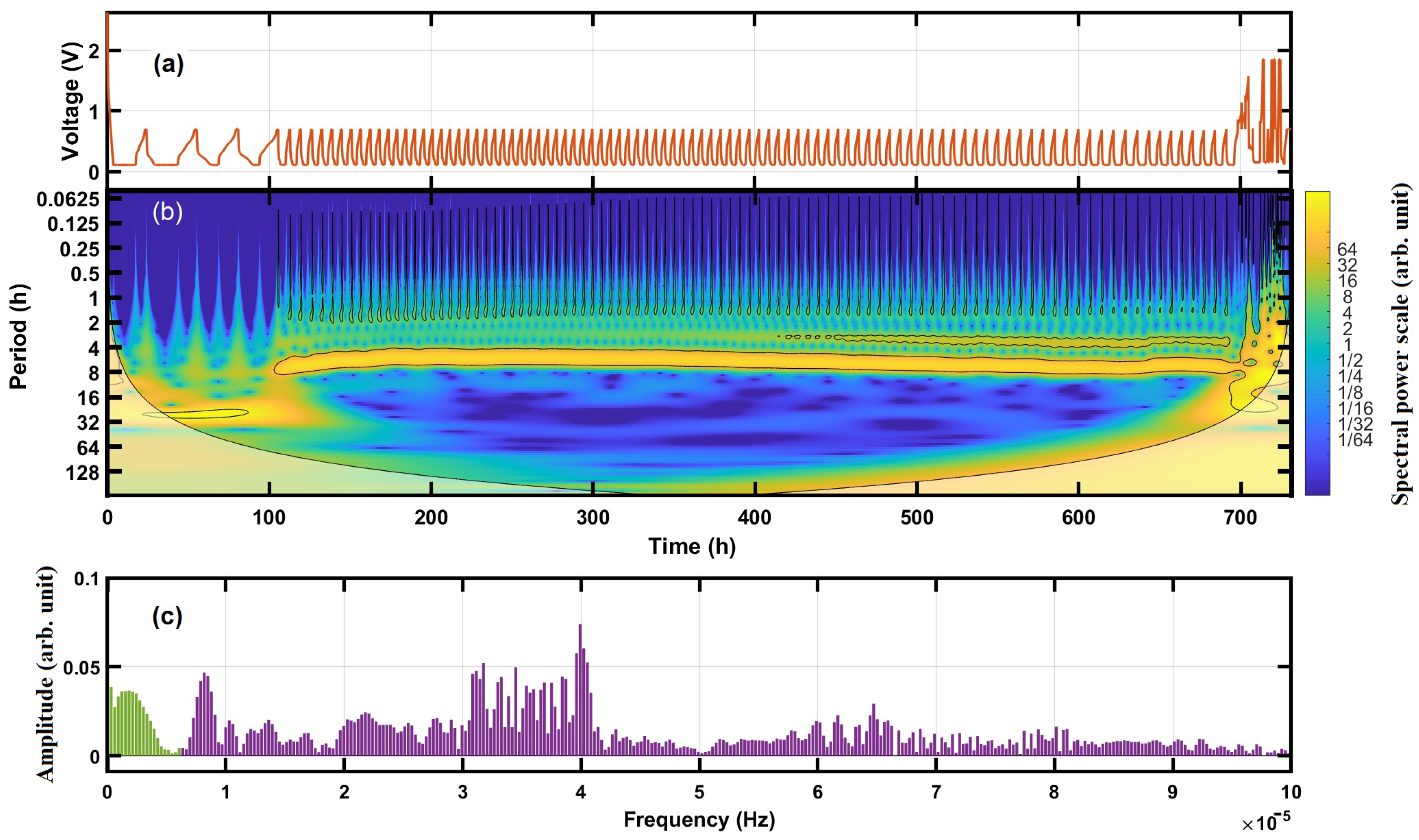
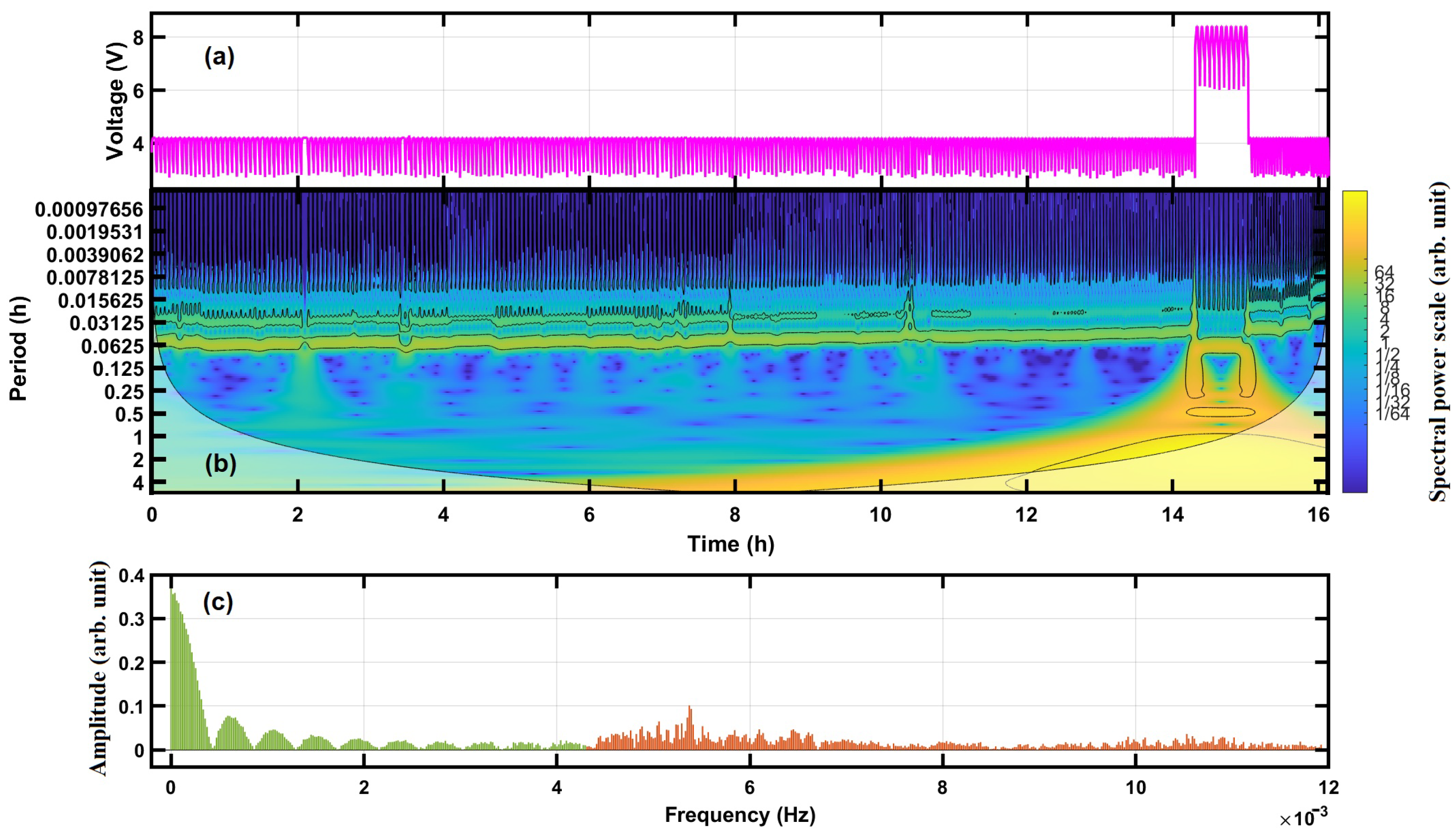
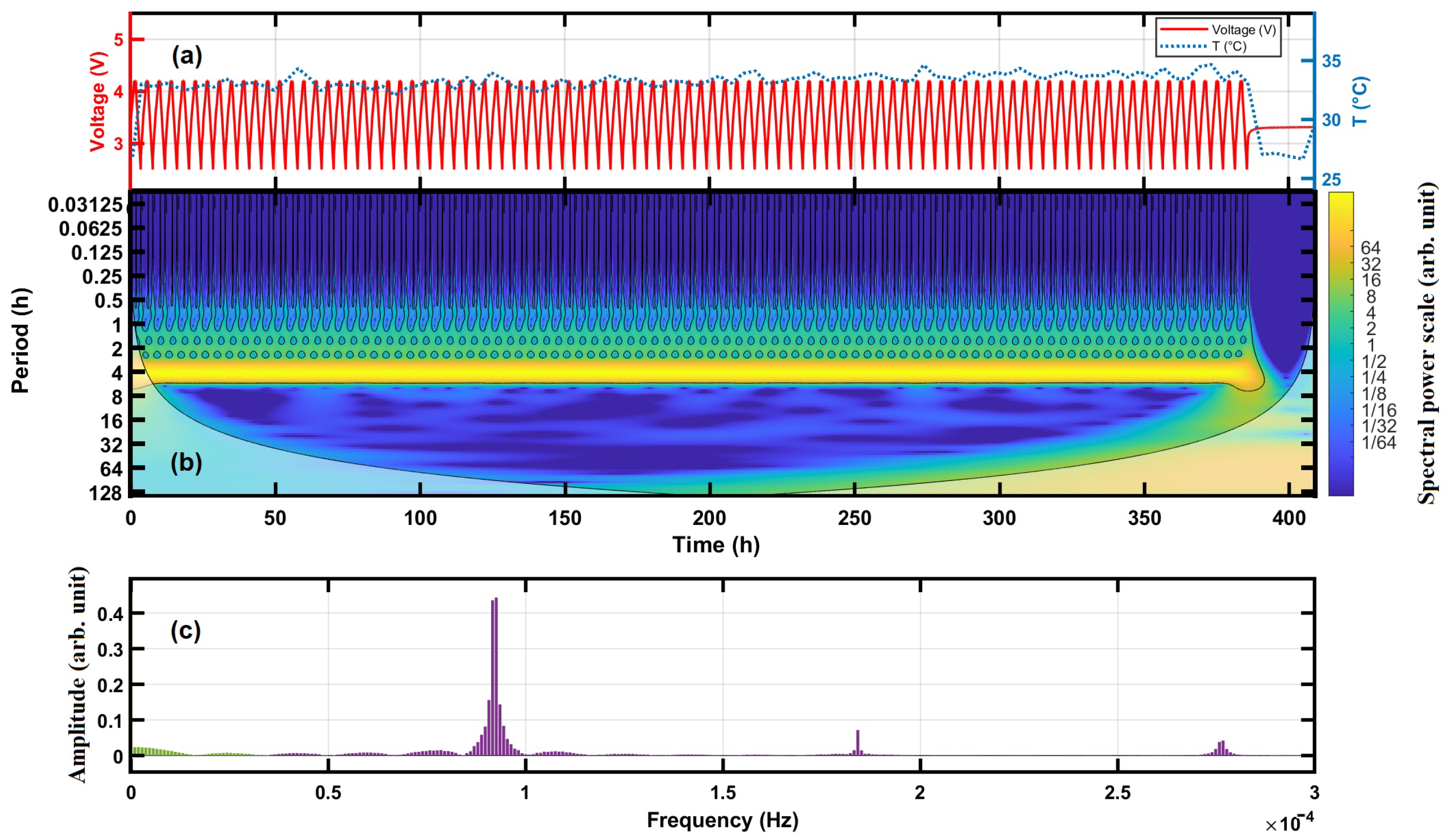
4.1. Frequency Spectra of Cycling Voltage
4.2. Time-Frequency Analysis by the Continuous Wavelet Transform
5. A Model for Early Battery Failure Detection
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MCMA | Mexico City Metropolitan Area |
| SEDEMA | Secretariat of Environment |
| VOCs | Volatile Organic Compounds |
| EVs | Electric Vehicles |
| Li-ion | lithium-ion |
| IF-BUAP | Institute of Physics of the University of Puebla |
| CALCE | Center for Advanced Life Cycle Engineering of University of Maryland |
| NASA-PCE | NASA’s Prognostics Center of Excellence |
| UCL | University College London |
| FT | Fourier Transform |
| FFT | Fast Fourier Transform |
| DFT | Discrete Fourier Transform |
| CWT | Continuous Wavelet Transform |
| CC | Constant Current |
| CV | Constant Voltage |
| HC | Half Cells |
| PC | Prismatic Cell |
| C-LIC | Commercial Lithium-ion Cells |
References
- Pan, Y.; Feng, X.; Zhang, M.; Han, X.; Lu, L.; Ouyang, M. Internal short circuit detection for lithium-ion battery pack with parallel-series hybrid connections. J. Clean. Prod. 2020, 255, 120277. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Hendricks, C.; Pecht, M. Lessons learned from the 787 dreamliner issue on lithium-ion battery reliability. Energies 2013, 6, 4682–4695. [Google Scholar] [CrossRef]
- Xue, Q.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Fault diagnosis and abnormality detection of lithium-ion battery packs based on statistical distribution. J. Power Sources 2021, 482, 228964. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium-ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Xu, J.; Lan, C.; Qiao, Y.; Ma, Y. Prevent thermal runaway of lithium-ion batteries with minichannel cooling. Appl. Therm. Eng. 2017, 110, 883–890. [Google Scholar] [CrossRef]
- Ma, G.; Xu, S.; Cheng, C. Fault detection of lithium-ion battery packs with a graph-based method. J. Energy Storage 2021, 43, 103209. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive nonlinear model-based fault diagnosis of li-ion batteries. IEEE Trans. Ind. Electron. 2015, 62, 1002–1011. [Google Scholar] [CrossRef]
- Liu, Z.; He, H. Sensor fault detection and isolation for a lithium-ion battery pack in electric vehicles using adaptive extended Kalman filter. Appl. Energy 2017, 185, 2033–2044. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; He, H.; Chen, Z. A fractional-order model-based battery external short circuit fault diagnosis approach for all-climate electric vehicles application. J. Clean. Prod. 2018, 187, 950–959. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Ma, M.; Wang, Y.; Duan, Q.; Wu, T.; Sun, J.; Wang, Q. Fault detection of the connection of lithium-ion power batteries in series for electric vehicles based on statistical analysis. Energy 2018, 164, 745–756. [Google Scholar] [CrossRef]
- Kang, Y.; Yang, X.; Zhou, Z.; Duan, B.; Liu, Q.; Shang, Y.; Zhang, C. A comparative study of fault diagnostic methods for lithium-ion batteries based on a standardized fault feature comparison method. J. Clean. Prod. 2021, 278, 123424. [Google Scholar] [CrossRef]
- Spitthoff, L.; Shearing, P. Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies 2021, 14, 1248. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques–Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Bosire Omariba, Z.; Zhang, L.; Kang, H.; Sun, D. Parameter Identification and State Estimation of Lithium-Ion Batteries for Electric Vehicles with Vibration and Temperature Dynamics. World Electr. Veh. J. 2020, 11, 50. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Modelling Lithium-Ion Battery Ageing in Electric Vehicle Applications–Calendar and Cycling Ageing Combination Effects. Batteries 2020, 6, 14. [Google Scholar] [CrossRef]
- Cong, X.; Zhang, C.; Jiang, J.; Zhang, W.; Jiang, Y.; Zhang, L. A Comprehensive Signal-Based Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles. Energies 2021, 14, 1221. [Google Scholar] [CrossRef]
- Karagulian, F.; Belis, C.A.; Dora, C.F.; PrÃŒss-UstÃŒn, A.M.; Bonjour, S.; Adair-Rohani, H.; Amann, M. Contributions to cities’ ambient particulate matter (PM): A systematic review of local source contributions at global level. Atmos. Environ. 2015, 120, 475–483. [Google Scholar] [CrossRef]
- Knibbs, L.D.; Cole-Hunter, T.; Morawska, L. A review of commuter exposure to ultrafine particles and its health effects. Atmos. Environ. 2011, 45, 2611–2622. [Google Scholar] [CrossRef]
- DOF (Diario Oficial de la Federación). Criterio para Evaluar la Calidad del aire Ambiente con Respecto al Bióxido de Nitrógeno (NO2). Valor Normado para la Concentración de bióxido de Nitrógeno (NO2) en el aire Ambiente como Medida de Protección a la Salud de la Población. Norma Oficial Mexicana NOM-023-SSA1-1993. 1994. Available online: http://www.aire.cdmx.gob.mx/descargas/monitoreo/normatividad/NOM-023-SSA1-1993.pdf (accessed on 13 September 2022).
- Inventario de Emisiones de la CDMX, 2016; SEDEMA (Secretarà a del Medio Ambiente del Gobierno de la Ciudad de México): Ciudad de México, Mexico, 2018. Available online: http://www.aire.cdmx.gob.mx/default.php?opc=Z6BhnmI=&dc=Zg== (accessed on 20 October 2022).
- Molina, L.T.; Velasco, E.; Retama, A.; Zavala, M. Experience from Integrated Air Quality Management in the Mexico City Metropolitan Area and Singapore. Atmosphere 2019, 10, 512. [Google Scholar] [CrossRef]
- Koupal, J.; Palacios, C. Impact of new fuel specifications on vehicle emissions in Mexico. Atmos. Environ. 2019, 201, 41–49. [Google Scholar] [CrossRef]
- Schmidt, M.; Staudt, P.; Weinhardt, C. Evaluating the importance and impact of user behavior on public destination charging of electric vehicles. Appl. Energy 2020, 258, 114061. [Google Scholar] [CrossRef]
- Ferrero, E.; Alessandrini, E.; Balanzino, A. Impact of the electric vehicles on the air pollution from a highway. Appl. Energy 2016, 169, 450–459. [Google Scholar] [CrossRef]
- Franke, T.; Neumann, I.; BÃŒhler, F.; Cocron, P.; Krems, J.F. Experiencing range in an electric vehicle: Understanding psychological barriers. Appl. Psychol 2012, 61, 368–391. [Google Scholar] [CrossRef]
- Flores, R.J.; Shaffer, B.P.; Brouwer, J. Electricity costs for an electric vehicle fueling station with Level 3 charging. Appl. Energy 2016, 169, 813–830. [Google Scholar] [CrossRef]
- Aaldering, L.J.; Song, C.H. Tracing the technological development trajectory in post-lithium-ion battery technologies: A patent-based approach. J. Clean. Prod. 2019, 241, 118343. [Google Scholar] [CrossRef]
- Loganathan, M.K.; Mishra, B.; Tan, C.M.; Kongsvik, T.; Rai, R.N. Multi-criteria decision making (MCDM) for the selection of Li-ion batteries used in electric vehicles (EVs). Mater. Today Proc. 2021, 41, 1073–1077. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Yang, X.; Zuo, F.; Liu, S.; Lin, C. A smart Li-ion battery with self-sensing capabilities for enhanced life and safety. J. Power Sources 2022, 546, 231705. [Google Scholar] [CrossRef]
- Hu, Z.; Prado, R. Fast bayesian inference on spectral analysis of multivariate stationary time series. Comput. Stat. Data Anal. 2023, 178, 107596. [Google Scholar] [CrossRef]
- Bracewell, R.N. The Fourier Transform and Its Applications, 3rd ed.; McGraw-hill Inc.: New York, NY, USA, 2000; pp. 5–18. ISBN 0-07-303938-1. [Google Scholar]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Cochran, W.T.; Cooley, J.W.; Favin, D.L.; Helms, H.D.; Kaenel, R.A.; Lang, W.W.; Maling, G.C.; Nelson, D.E.; Rader, C.M.; Welch, P.D. What is the fast Fourier transform? Proc. IEEE 1967, 55, 1664–1674. [Google Scholar] [CrossRef]
- Mahafza, B.R. Radar Systems Analysis and Processing Using Matlab, 3rd ed.; CRC Press/Taylor & Francis Group: Huntsville, AL, USA, 2013; pp. 93–101. ISBN 978-1-4398-8496-6. [Google Scholar]
- Farge, M. Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 1992, 24, 395–458. [Google Scholar] [CrossRef]
- Fouladi, R.F.; Ermiş, O.; Anarim, E. A novel approach for distributed denial of service defense using continuous wavelet transform and convolutional neural network for software-Defined network. Comput. Secur. 2022, 112, 102524. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Yang, W.R. Discrete wavelet transform and radial basis neural network for semiconductor wet-etching fabrication flow-rate analysis. IEEE Trans. Instrum. Meas. 2012, 61, 865–875. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, S.N. Low-order dominant harmonic estimation using adaptive wavelet neural network. IEEE Trans. Ind. Electron. 2014, 61, 428–435. [Google Scholar] [CrossRef]
- Slavič, J.; Simonovski, I.; Boltežar, M. Damping identification using a continuous wavelet transform: Application to real data. J. Sound Vib. 2003, 262, 291–307. [Google Scholar] [CrossRef]
- Costa, F.B. Fault-induced transient detection based on real-time analysis of the wavelet coefficient energy. IEEE Trans. Power Deliv. 2014, 29, 140–153. [Google Scholar] [CrossRef]
- Ghaffari, A.; Golbayani, H.; Ghasemi, M. A new mathematical based qrs detector using continuous wavelet transform. Comput. Electr. Eng. 2008, 34, 81–91. [Google Scholar] [CrossRef]
- Rucka, M.; Wilde, K. Application of continuous wavelet transform in vibration based damage detection method for beams and plates. J. Sound Vib. 2006, 297, 536–550. [Google Scholar] [CrossRef]
- Park, C.K.; Zhang, Z.; Xu, Z.; Kakirde, A.; Kang, K.; Chai, C.; Au, G.; Cristo, L. Variables study for the fast charging lithium ion batteries. J. Power Sources 2017, 165, 892–896. [Google Scholar] [CrossRef]
- Quiroga, E.; Carstensen, J.; Föll, H. Good cycling performance of high-density arrays of si microwires as anodes for li ion batteries. Electrochim. Acta 2013, 101, 93–98. [Google Scholar] [CrossRef]
- Center for Advanced Life Cycle Engineering, Data and Test Description CX2. Available online: https://web.calce.umd.edu/batteries/data.htm (accessed on 2 November 2021).
- Xing, Y.; Ma, E.W.; Tsui, K.L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- NASA Ames Prognostics Data Repository, Battery Dataset. Available online: http://ti.arc.nasa.gov/project/prognostic-data-repository (accessed on 3 November 2021).
- Heenan, T.M.; Jnawali, A.; Kok, M.; Tranter, T.G.; Tan, C.; Dimitrijevic, A.; Jervis, R.; Brett, D.J.; Shearing, P.R. Data for an advanced microstructural and electrochemical datasheet on 18650 Li-ion batteries with nickel-rich NMC811 cathodes and graphite-silicon anodes. Data Brief 2020, 32, 106033. [Google Scholar] [CrossRef] [PubMed]
- Heenan, T.M.; Jnawali, A.; Kok, M.; Tranter, T.G.; Tan, C.; Dimitrijevic, A.; Jervis, R.; Brett, D.J.; Shearing, P.R. Lithium-Ion Battery INR18650 MJ1 Data: 400 Electrochemical Cycles (EIL-015); University College London UCL: London, UK, 2020. [Google Scholar] [CrossRef]
- Lathi, B.P.; Green, R.A. Essentials of Digital Signal Processing, 1st ed.; Cambridge University Press: New York, NY, USA, 2014; pp. 155–200. ISBN 978-110-705-932-0. [Google Scholar]
- Grinsted, A.; Moore, J.C.; Jevrejera, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Soon, W.; Dutta, K.; Legates, D.R.; Velasco, V.; Zhang, W. Variation in surface air temperature of China during the 20th century. J. Atmos. Sol.-Terr. Phys. 2011, 73, 2331–2344. [Google Scholar] [CrossRef]
- Mendoza, E.; Velasco, M.; Velasco, G.; Martell, R.; Silva, R.; Escudero, M.; Ocampo, F.J.; Mariño-Tapiaf, I. Spectral analysis of sea surface elevations produced by big storms: The case of hurricane wilma. Reg. Stud. Mar. Sci. 2022, 39, 101390. [Google Scholar] [CrossRef]
- López, F.; Velasco, V.M.; Álvarez, R.; Gómez, S.; Gazzola, J. Analysis of ground penetrating radar data from the tunnel beneath the temple of the feathered serpent in teotihuacan, Mexico, using new multi-cross algorithms. Adv. Space Res. 2016, 58, 2164–2179. [Google Scholar] [CrossRef]
- Cheng, V.Y.; Saber, A.; Arnillas, C.A.; Javed, A.; Richards, A.; Arhonditsis, G.B. Effects of hydrological forcing on short- and long-term water level fluctuations in lake huron-michigan: A continuous wavelet analysis. J. Hydrol. 2021, 603, 127164. [Google Scholar] [CrossRef]
- Velasco, V.M.; Perez-Peraza, J.; Soon, W.; Marquez-Adame, J.C. The quasi-biennial oscillation of 1.7 years in ground level enhancement events. New Astron. 2018, 60, 7–13. [Google Scholar] [CrossRef]
- Velasco, V.M.; Mendoza, B.; Velasco, G. Reconstruction and prediction of the total solar irradiance: From the medieval warm period to the 21st century. New Astron. 2015, 34, 221–233. [Google Scholar] [CrossRef]


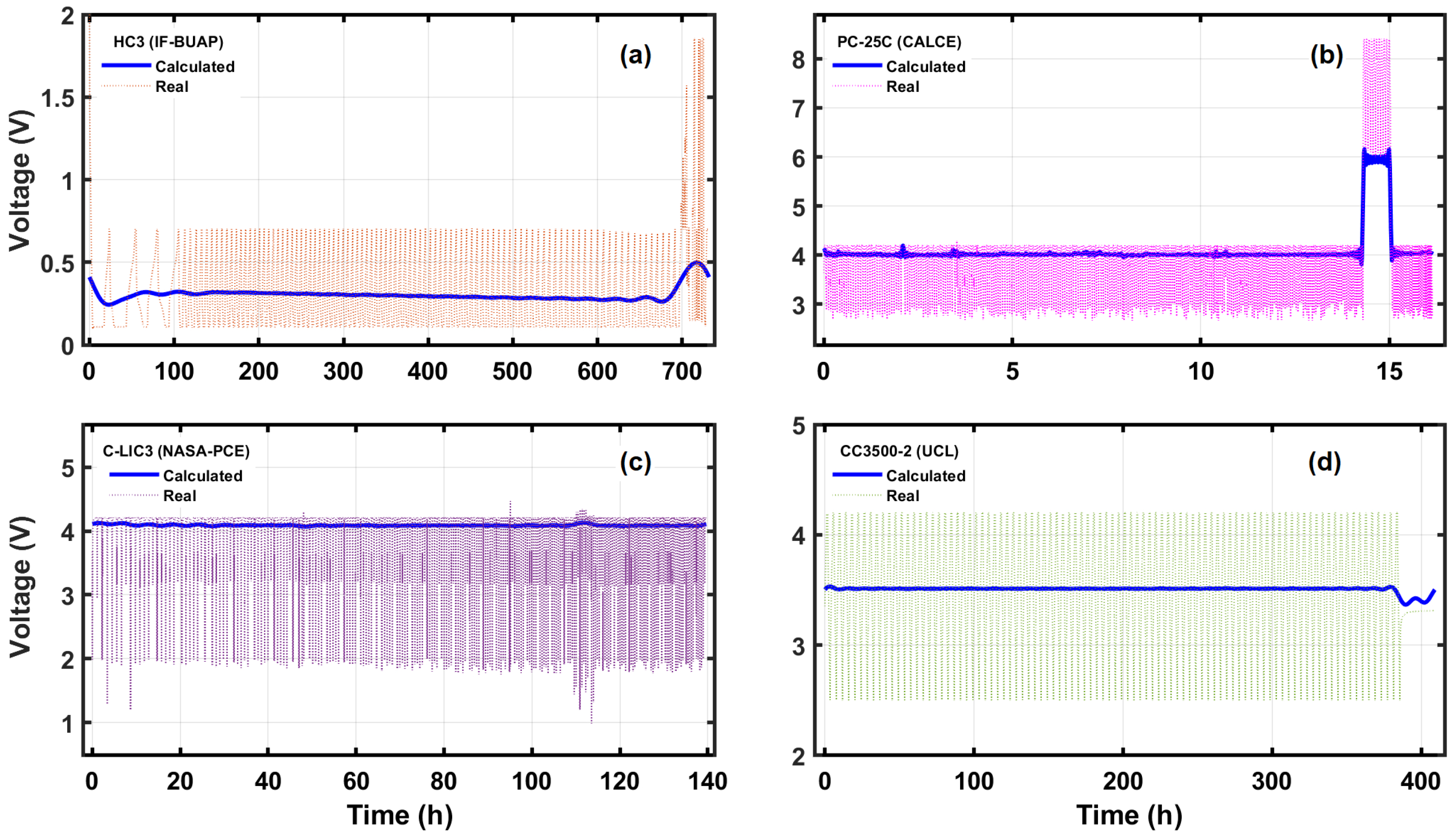
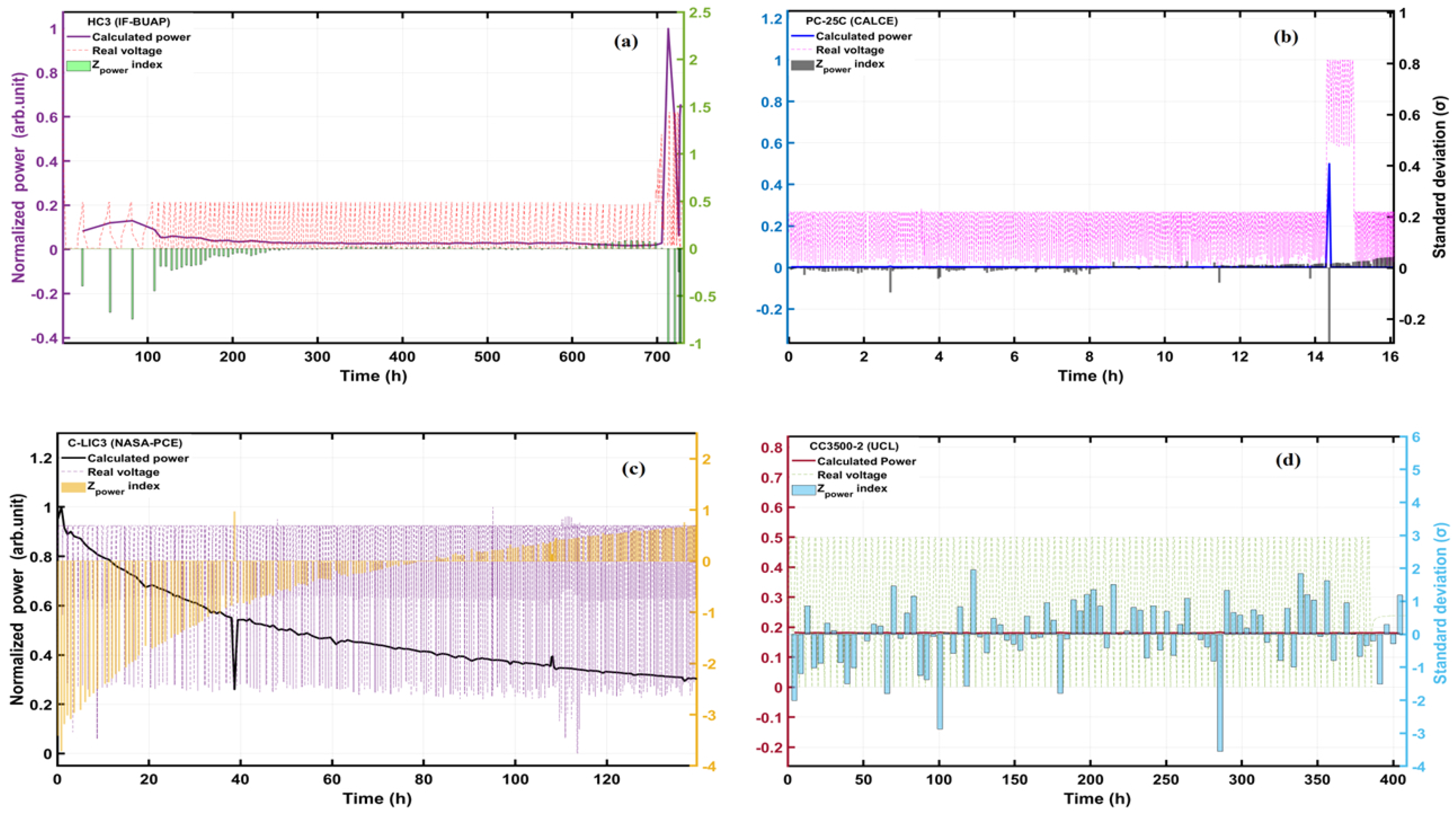
| Research Group | Cell Type | Cathode | Anode | Capacity (mAh) |
|---|---|---|---|---|
| IF-BUAP | Half Swagelok | Si | Li | 4200/g |
| CALCE | Prismatic | LiCoO | Graphite | 1350 |
| NASA-PCE | 18,650 | LiCoO | Li-C | 2000 |
| UCL | 18,650 | LiNiCoAlO (NCA) | Graphite- Si | 3500 |
| Cell | Charge | Discharge | Cycles | T (C) | |||
|---|---|---|---|---|---|---|---|
| CC (mA) | Cut-Off Voltage (V) | Cut-Off Current (mA) | CC (mA) | Cut-Off Voltage (V) | |||
| IF-BUAP | |||||||
| HC1 | 0.86 | 0.7 | 0.18 | 0.86 | 0.11 | 104 | 25 |
| HC2 | 0.86 | 0.7 | 0.18 | 0.86 | 0.11 | 72 | 25 |
| HC3 | 0.86 | 0.7 | 0.18 | 0.86 | 0.11 | 109 | 25 |
| HC4 | 1.33 | 0.7 | 0.13 | 1.33 | 0.11 | 28 | 25 |
| CALCE | |||||||
| PC-25C | 675 | 4.2 | 50 | 1350 | 2.7 | 256 | 25 |
| PC-35C | 675 | 4.2 | 50 | 1350 | 2.7 | 315 | 35 |
| PC-45C | 675 | 4.2 | 50 | 1350 | 2.7 | 304 | 45 |
| PC-55C | 675 | 4.2 | 50 | 1350 | 2.7 | 303 | 55 |
| NASA-PCE | |||||||
| C-LIC1 | 1500 | 4.2 | 20 | 2000 | 2.5 | 162 | 24 |
| C-LIC2 | 1500 | 4.2 | 20 | 4000 | 2.0 | 41 | 24 |
| C-LIC3 | 1500 | 4.2 | 20 | 4000 | 2.0 | 244 | 24 |
| C-LIC4 | 1500 | 4.2 | 20 | (2000, 4000, | 2.2 | 134 | 4 |
| 1000) | |||||||
| UCL | |||||||
| CC3500-1 | 1500 | 4.2 | 100 | 4000 | 2.5 | 1–84 | 24 |
| CC3500-2 | 1500 | 4.2 | 100 | 4000 | 2.5 | 110–202 | 24 |
| CC3500-3 | 1500 | 4.2 | 100 | 4000 | 2.5 | 203–285 | 24 |
| CC3500-4 | 1500 | 4.2 | 100 | 4000 | 2.5 | 286–400 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbonó dela Rosa, M.E.; Velasco Herrera, G.; Nava, R.; Quiroga González, E.; Sosa Echeverría, R.; Sánchez Álvarez, P.; Gandarilla Ibarra, J.; Velasco Herrera, V.M. A New Methodology for Early Detection of Failures in Lithium-Ion Batteries. Energies 2023, 16, 1073. https://doi.org/10.3390/en16031073
Carbonó dela Rosa ME, Velasco Herrera G, Nava R, Quiroga González E, Sosa Echeverría R, Sánchez Álvarez P, Gandarilla Ibarra J, Velasco Herrera VM. A New Methodology for Early Detection of Failures in Lithium-Ion Batteries. Energies. 2023; 16(3):1073. https://doi.org/10.3390/en16031073
Chicago/Turabian StyleCarbonó dela Rosa, Mario Eduardo, Graciela Velasco Herrera, Rocío Nava, Enrique Quiroga González, Rodolfo Sosa Echeverría, Pablo Sánchez Álvarez, Jaime Gandarilla Ibarra, and Víctor Manuel Velasco Herrera. 2023. "A New Methodology for Early Detection of Failures in Lithium-Ion Batteries" Energies 16, no. 3: 1073. https://doi.org/10.3390/en16031073
APA StyleCarbonó dela Rosa, M. E., Velasco Herrera, G., Nava, R., Quiroga González, E., Sosa Echeverría, R., Sánchez Álvarez, P., Gandarilla Ibarra, J., & Velasco Herrera, V. M. (2023). A New Methodology for Early Detection of Failures in Lithium-Ion Batteries. Energies, 16(3), 1073. https://doi.org/10.3390/en16031073







