Abstract
The role of prosumers is changing as they become active and empowered members of the grid by exchanging energy. This introduces bidirectional power flow and other challenges into the existing power systems, which require new approaches capable of dealing with the increased decentralization and complexity. Such approaches rely on game-theoretic models and mechanisms to analyze strategic decisions in competitive settings. More specifically, a coalitional game can encourage participants to trade energy with one another and obtain fair and sustainable outcomes. Therefore, the contents of this work address the coalitional game for sustainable energy trading, as well as the challenges associated with its application in power systems. This is achieved by identifying literature works that successfully implemented coalitional games in energy trading and management applications while providing an overview of solution concepts and discussing their properties and contributions to sustainability. Moreover, this work also proposes conditions that peer-to-peer energy trading should satisfy to be considered sustainable. Finally, a case study is presented to demonstrate how a coalitional game and various solution concepts can be successfully implemented to ensure the benefits and stability of cooperation in power systems. The weighted Shapley value is proposed to allocate profits among communities according to their level of sustainability.
1. Introduction
The electrification of societies and increased penetration of distributed energy resources (DERs) such as renewable energy sources (RES), energy storage systems (ESSs), and plug-in electric vehicles (PEVs) have been changing the way energy is produced, transferred, and used in electrical power systems [1,2]. The consideration of stability, security, and reliability requirements in power systems is a fundamental concern of their design, planning, and operation. These requirements are necessary to allow power systems to fulfill the needs of consumers while providing an acceptable level of power quality [3]. The increased penetration of RESs can jeopardize the quality of the power supplied to consumers [2,3]. In particular, the uncertainty of power generated from photovoltaic (PV) systems and wind turbines can cause an imbalance between power generation and consumption, leading to frequency fluctuations. Frequency is one of the most important factors for assessing the level of power quality and ensuring a secure and stable system operation [3]. Moreover, there is a need for sustainable electricity markets and communities due to the ever-increasing energy demand and carbon emission intensity of cities, which currently account for around 75% of global energy consumption and generate around 70% of global carbon emissions [4]. This calls for auxiliary services and grid reinforcements at the local level provided by small producers, prosumers, and consumers through peer-to-peer (P2P) energy trading in local energy markets (LEMs) [2,5].
Based on the concept of a sharing economy, P2P energy trading enables peers (i.e., producers, or prosumers, and consumers) to directly sell and buy energy with each other within the same distribution system and without the intervention of conventional energy suppliers or utility companies [6,7,8]. It is usually implemented in local energy communities and facilitated by various information and communication technologies (ICTs) to allow prosumers to trade their surplus electricity generated from PV systems and wind turbines as these RESs are considered non-dispatchable sources [6,7]. Because of this, the role of prosumers and consumers changes as they become active and empowered members of the grid by participating in energy trading activities to sell and buy energy in LEMs, potentially lowering the need for increased generation, transmission, and distribution capacity [5,8]. This change introduces bidirectional power flow and a variety of challenges into the existing power systems that cannot be addressed using centralized methods, requiring new approaches capable of analyzing decision-making behaviors and interactions between peers to deal with the increased decentralization and complexity [9]. In general, such approaches rely on models and mechanisms based on the concept of game theory to analyze strategic decisions in competitive settings [10]. Ultimately, an effective scheme for P2P energy trading is one that encourages participants to trade energy with one another through attractive energy prices and creates incentives to form goal-oriented communities [11,12,13].
When considering strategic decisions within the concept of sustainable development, the design of game-theoretic approaches also needs to take into consideration various aspects of economic, social, and environmental sustainability [14,15,16]. Hence, these game-theoretic approaches need to be capable of obtaining an outcome that is in line with sustainable development, meaning that it can optimize transaction costs for participants, improve social welfare, and mitigate environmental impacts. In this scenario, the aspects of sustainability can range from socio-economic fairness to carbon emission and resource depletion [8].
This results in two possible strategies. One strategy relies on a cooperative/coalitional game to promote collaboration with a fair agreed-upon strategy, and another one relies on a non-cooperative game to stimulate competition without a shared strategy [17,18,19]. Cooperative/coalitional game theory is used to encourage peers to form coalitions through mutual agreements for more informed decisions and cooperation in P2P energy trading [17,18]. This agreement between players can be a result of negotiations, and the agreed-upon strategy is reinforced through a binding contract usually overseen by an external or central entity, determining the distribution of generated value among the players [19]. Without this binding contract to reinforce the agreed-upon strategy, certain players can move independently from others and differently from what is stipulated or promised in the agreement, resulting in a non-cooperative game. Non-cooperative game theory is often used for P2P energy trading without coordination and agreements among peers due to the conflicting interests and strategies of players [17,18]. However, when considering the integration of sustainability into the game, one might feel reluctant to adopt a non-cooperative game theoretic approach. In [20], Crowther and Seifi address environmental sustainability regarding the depletion of natural resources by using the prisoner’s dilemma version of game theory, arguing that the only way to obtain the best sustainable outcome in a non-zero-sum game is through collaboration. The prisoner’s dilemma shows, in a simplified manner, that competition between two players may not achieve sustainability because the success of one player occurs at the expense of the other player while a fair and relatively good outcome can only be achieved if both players cooperate [20,21]. Even though the non-cooperative game has been widely adopted to deal with energy transactions to obtain the best possible result and develop pricing mechanisms, it contradicts the goal of sustainability in the sense that only one player succeeds while the others lose, resulting in a loss of potential profits or cost savings for some players [20].
With the absence of a proper payoff distribution or compensation mechanism for economic benefits, non-cooperative game approaches can lead to decreased social welfare when compared to solutions involving cooperation among players [22]. Because of this, a cooperative game may be the suitable strategy to achieve a more sustainable outcome, being able to increase the total benefits and share them among all the participating players [19]. In the literature, the coalitional game is widely used for the analysis and design of various energy systems involving P2P energy trading markets, smart grids (SGs) and microgrid (MG) systems, transmission line expansion projects, and PEV charging stations [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. In particular, game theory can be important for modeling the optimal and coordinated operation of interconnected MGs or multi-microgrids (MMGs) [45], in which two or more MGs can share their energy resources and transact energy through an LEM to ensure continuous power supply and improve the reliability and stability of individual MGs [8,46]. The design of LEMs for P2P energy trading using game-theoretic approaches has the potential to mitigate some of the challenges associated with uncertain renewable energy generation, energy market prices, and load demand [8,45]. Regarding MMG systems, the formulation of cooperative/coalitional games is often focused on the optimization and coordination of energy transactions among MGs [34,35]. Generally, the main goals of the coalitional game models available in the literature include, among others, the fair allocation of profits or costs, maximization of profits, and minimization of costs, power losses, and carbon emissions by means of cooperation [11,12].
Given the panoply of applications relying on cooperation, the contents of this work provide an overview of the coalitional game and the properties of its solution concepts with consideration for economic, social, and environmental sustainability. Essentially, it addresses how the use of the coalitional game can contribute to a sustainable outcome while ensuring and distributing the benefits of cooperation in P2P energy trading applications. A lack of literature works focusing on the sustainability of energy transactions has been identified, which calls for a common understanding or definition that integrates sustainability into the concept of transactive energy. Therefore, this work aims to help analyze and determine in which way or under which conditions a state of sustainability can be attained in P2P energy trading through coalitional game approaches. Sustainable energy trading is tackled by proposing conditions that P2P energy trading should satisfy to be considered sustainable while highlighting the need for a central entity or community manager to coordinate the transactions and reinforce cooperative behaviors.
This paper is organized as follows: Section 2 presents a simple bibliometric analysis to help visualize the general direction of the literature regarding cooperative and non-cooperative game theory, energy trading, and sustainability. Section 3 introduces the concept of the coalitional game and its three distinct categories or classes along with commonly used solution concepts for fair payoff allocation. Section 4 addresses and discusses the sustainability of P2P energy trading based on contributions to sustainability associated with various applications of coalitional games in power systems. Section 5 demonstrates how coalitional games can be implemented in power systems by providing an illustrative case study to analyze the stability of cooperative energy trading among three and four communities. Section 6 discusses the main challenges and limitations associated with the implementation of coalitional games in practical applications. Finally, Section 7 presents the main conclusions based on the various aspects addressed and discussed throughout the paper.
2. Bibliometric Analysis
In order to provide a brief overview and visualization of the direction and recent research trends of the literature, a simple bibliometric analysis is performed in this section. The most relevant keywords associated with key aspects of game theory, energy trading, and sustainability were selected through an article title, abstract, and keyword search using the Scopus database. This search contained a high degree of restriction in the selection of documents, meaning that it only included works related to energy trading and management in power systems containing the terms “coalitional/cooperative game” or “non-cooperative game” in their title, abstract, and keywords. Because of the need to achieve more sustainable electricity markets and communities, literature works containing terms related to the concept of sustainability were also included in the analysis. The number and percentage of peer-reviewed documents published between the years 2000 and 2023 is presented in Figure 1 and Figure 2, respectively.
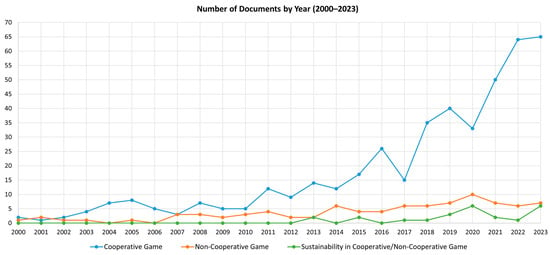
Figure 1.
Number of documents by year related to cooperative and non-cooperative game theory and sustainability in the field of energy trading and management using article title, abstract, and keyword search.
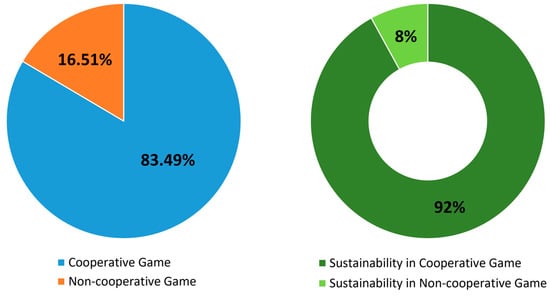
Figure 2.
Percentage of documents related to cooperative and non-cooperative game theory and sustainability in the field of energy trading and management using article title, abstract, and keyword search.
The results of the search within article titles, abstracts, and keywords revealed that the concepts of cooperative and non-cooperative game theory are mentioned and used in at least 545 peer-reviewed documents related to energy trading and management applications in power systems. Furthermore, the concept of sustainability appears to only be considered in 25 peer-reviewed documents regarding cooperative and non-cooperative game theory. For a short bibliometric analysis using VOSviewer version 1.6.16, only the keywords with a minimum of 10 occurrences were used to filter out most of the less relevant keywords and facilitate the analysis and interpretation of the keyword map. In addition, some of the keywords were then merged with their shorter counterparts or entirely replaced by synonyms to obtain a simpler and clearer visualization of the keyword map. This generated the network of co-occurring keywords shown in Figure 3, revealing the current research hotspots related to game theory, energy trading, and sustainability. Each node depicted in Figure 3 represents a keyword, and its size relative to other nodes is determined by the frequency of occurrence for the corresponding keyword, denoting its relative importance in the scope of the search. The relationship between two keywords can be visualized through the distance between nodes. This is denoted by the total link strength, which indicates the frequency of keywords appearing together in the documents gathered. As expected, the keyword with the most occurrences is “game theory”, with 442 occurrences and a total link strength of 2731, and is closely followed by “cooperative game”, with 322 occurrences and a total link strength of 1932. Other relevant keywords include “power markets”, “electric power transmission networks”, “renewable energy sources”, and “Shapley value” with more than 75 occurrences and total link strengths of more than 468. This shows that the current research related to P2P energy trading market applications is mostly focused on coalitional or cooperative game approaches.
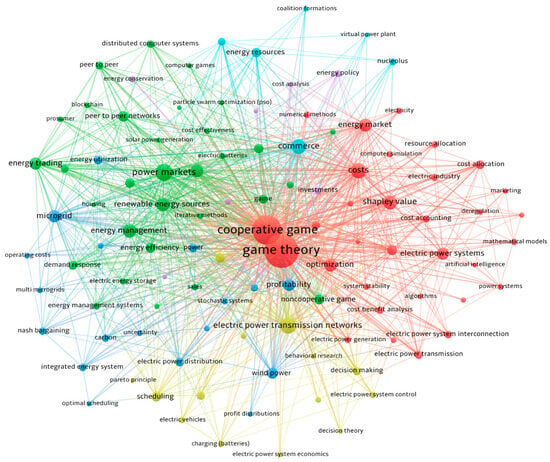
Figure 3.
Map of the most relevant keywords related to game theory, energy trading, and sustainability using VOSviewer with association strength normalization method.
From the bibliometric analysis, it can be concluded that non-cooperative game approaches considering sustainability goals in P2P energy trading and management applications are relatively scarce in the literature. The article title, abstract, and keyword search using the Scopus database only managed to return two peer-reviewed documents, corresponding to 8% of the total documents gathered for this analysis, as shown in Figure 2. These were the work performed by Cui and Xiao in [47] to obtain a non-cooperative-game-based P2P energy sharing management for a community consisting of self-interested buildings and the work developed by Li et al. in [48] to introduce a two-stage non-cooperative electric vehicle management scheme with the goal of promoting sustainable transport and overcoming the challenges of increased charging demand. This lack of consideration for sustainability goals seems to reinforce the reluctance to adopt non-cooperative game approaches, which may stimulate competition in a scenario where the success of one player occurs at the expense of others.
Non-cooperative games in the field of P2P energy trading and management applications have been widely used to develop effective pricing mechanisms in energy trading markets, often with the goal of maximizing profits for self-interested customers [49,50]. Most of these non-cooperative game approaches generally rely on the use of the Stackelberg game, which denotes a game model based on the set of actions selected by a leader being followed by another set of actions selected by the followers [8]. For instance, in [51], Zheng et al. proposed a Stackelberg game approach for energy trading management in an MG system to allow DERs to play more active energy trading roles, in which the energy management trading system (EMTS) acted as leader and the DERs acted as followers. This approach resulted in a positive effect on the total net energy of the MG and allowed a reduction in the dependency of the MG on the upper distribution grid, an increase in the utility of each DER when compared to direct grid trading, and a significant improvement in the profit of the EMTS. In [52], Hua et al. formulated the interactions between a distribution system operator (DSO) and multiple MGs as a Stackelberg game to manage energy transactions in LEMs and facilitate the provision of flexibility services. In this approach, the goal of the DSO is to achieve local energy balance, determine imbalance prices, and schedule the operation of the MGs, while each MG aims to maximize the profits for its prosumers through local energy trading and flexibility services. Similarly, Erol and Filik in [53] also relied on the Stackelberg game for the energy sharing management of an MG integrated with a variety of DERs such as RESs, ESSs, and PEV charging stations acting as followers, changing the role of prosumers to more active members and resulting in a significant increase in total profit for the leader (i.e., MG operator) as well as a reduction in the dependency of the MG on the distribution grid.
Other non-cooperative approaches may involve the formulation of an evolutionary game to model the dynamics of changes in strategic interactions and select potential sellers in energy trading markets [49]. An evolutionary game has been proposed by Paudel et al. in [49] for the selection of sellers in conjunction with the Stackelberg game to model the interaction between buyers and sellers.
On the contrary, the article title, abstract, and keyword search managed to return 23 peer-reviewed documents considering sustainability goals in cooperative or coalitional game approaches, corresponding to 92% of the total documents gathered for this analysis, as shown in Figure 2. In the next sections, coalitional game theory is explored in the context of P2P energy trading markets along with its contributions to sustainability and potential challenges in practical power system applications.
3. Coalitional Game
Game theory, namely cooperative and non-cooperative games, is a well-established mathematical tool used in highly competitive settings to analyze the decision-making behaviors of individual players, allowing the proper justification of all the potential strategic interactions between them and helping predict the outcome of their interactions [54,55]. Non-cooperative game theory is mainly used to assist with strategic decision making when players have conflicting interests and it becomes impossible to establish agreements between them or difficult to combine their strategies [8]. On the other hand, cooperative or coalitional game theory allows players to form coalitions through mutual agreements with the goal of making more informed decisions and maximizing their benefits [23,54]. This type of game, in contrast to the non-cooperative game, requires coordination among players and encourages them to cooperate with each other and join coalitions by improving their utility or value in the game and distributing the benefits/gains (e.g., profits and savings) or the costs fairly among them [17,18]. It has also been widely applied in various energy management applications and used to develop market models and incentive designs for P2P energy trading, mainly to encourage cooperation and guarantee a fair profit or cost share among peers and coalition stability [56,57,58]. In a coalitional game, it is important to properly analyze player strategies at different instances and determine the conditions in which the scenarios favor cooperation.
To understand the use and application of coalitional games in P2P energy trading, it is important to briefly explain some definitions and solution concepts. A coalitional game with transferable utility (TU) is given by a pair that specifies a cost for every coalition, where is a finite set of players and a subset of is a coalition [9,10]. In practical applications, it can be impossible or difficult to properly quantify the value of cooperation as a transferable unit such as profits or costs. In many cases, the outcome of cooperation can also be multivalued, being simultaneously represented through profits or cost savings, carbon emission reduction, and power loss mitigation [9]. The coalitional function of the game that associates every coalition with a real number or value is given by with the number of possible player coalitions or scenarios being , which excludes the scenario corresponding to a coalition without players [59]. The largest possible coalition that contains all players is known as the grand coalition, while the remaining coalitions can be called minor coalitions. In general, coalitional games can be formulated as profit games or cost games [10]. In a profit game, the value associated with a coalition represents the profit that players can obtain by cooperating with one another, allocating a mutual gain or payoff among them. On the other hand, in a cost game, the same value represents the cost players may have to pay collectively through cooperation, resulting in a mutual cost reduction and allocation of the total cost associated with their coalition [9,10].
3.1. Categories of Coalitional Games
Depending on the main purpose of the study, coalitional games are often classified or grouped into three distinct categories: canonical coalition games [23,24,25,26,27,28,29,30,31,32], coalition formation games [33,34,35,36,37,38,39,40,41], and coalition graph games [42,43,44]. These categories or classes of coalitional games are briefly represented in Figure 4.
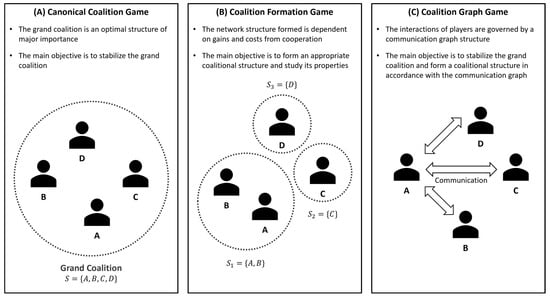
Figure 4.
Representation of the three distinct categories of coalitional games: (A) canonical coalition games; (B) coalition formation games; (C) coalition graph games (based on [10]).
3.1.1. Canonical Coalition Game
Canonical coalition games aim to study the stability of the grand coalition and formulate a scheme for the distribution of benefits/gains or costs among all participating players in a fair manner [23,60]. In a canonical coalition game with TU, the formation of the grand coalition should not be detrimental to players, implying the mathematical property of superadditivity [11]. The Core is the solution concept commonly used to analyze the stability of the grand coalition [23,60], while the Shapley value, the Nucleolus, and the Kernel are the solution concepts selected for the distribution of benefits/gains or costs among players [60].
A canonical coalition game can be used to design a P2P energy trading scheme in which the peers are motivated to rely on each other to achieve common goals (e.g., reduction in energy costs or carbon emissions). By studying the stability of the grand coalition and the fair distribution of benefits/gains or costs resulting from the cooperation, this type of coalitional game allows the determination of whether participants can form a stable coalition with each other and whether it is beneficial for them to remain in a coalition for cooperative energy trading [23,61].
Most works available in the literature are focused on showing the economic benefits obtained from stable cooperation in LEMs and on providing an effective model for profit allocation among prosumers [23,27]. As presented in Table 1, the Shapley value or the Core appears to be the most common solution concept adopted for a fair allocation of profits in P2P energy trading applications based on a canonical coalition game [23,24,25,26,27,28,29,30,31,32]. With the goal of endorsing user participation, Tushar et al. [23] proposed a consumer-centric scheme to motivate prosumers to participate in P2P energy trading using a canonical coalition game, which enabled them to trade within the coalition they formed as well as with other coalitions. Similarly, in [61], Yap et al. proposed an auction-based two-stage market clearing scheme for P2P energy trading in Malaysia studied under multi-city and intra-city test cases. This relied on a motivational game-theory-based price scheme to maximize cost savings and payoffs for prosumers and to guarantee unbiased market operation while benefiting the utility company. In [25], Du et al. developed a coalitional model for cooperation in an MMG system to achieve the economic stability of the grand coalition. The fair allocation of costs among the individual MGs is ensured by the Shapley value and the Core solution concepts. In addition, the authors also implemented the Benders decomposition method to deal with scalability issues, enabling the large-scale cost allocation problem to be solved with efficiency and the approach to become feasible in potential real-world MMG applications.

Table 1.
Comparison of literature works on P2P energy trading and energy management using coalitional game theory (✓—considered and ✗—not considered in the reference study).
While most works rely on the Shapley value for a fair allocation of profits or cost savings, some authors choose to develop more efficient and simplified allocation methods to overcome the computational burden and scalability issues associated with the Shapley value. For instance, in [24], Tushar et al. proposed a canonical game approach for surplus energy trading and management in an SG community with household nanogrid systems. In this work, a proportional fair payoff division method was adopted for the distribution of benefits among the nanogrids in the coalition based on the amount of surplus energy each nanogrid contributes to the aggregated energy supply. In [28], Chakraborty et al. used a coalitional game in two distinct scenarios, one to explore cooperation among households with individual energy storage devices with the goal of minimizing their energy consumption cost and the other to allow a group of consumers to invest in and cooperatively operate joint energy storage capacity. To avoid costly computations, the authors developed an efficient method based on analytical expressions to allocate the expected cost of daily energy storage. In [31], Ma et al. presented a cooperative energy trading scheme for a community energy system consisting of an energy hub and prosumers to promote the local consumption of renewable energy from PV systems, increase profits for the hub manager, and decrease costs for prosumers. In this study, a simplified method for profit allocation in accordance with the contribution of each player was developed to overcome the complex and time-consuming computation of the Shapley value.
3.1.2. Coalition Formation Game
Coalition formation games aim to study the formation of a coalitional structure using the interactions between players and analyze its properties and adaptability to external factors, environmental variations, and changes in the number of players and network topology [23,60]. Unlike canonical coalition games, this type of coalitional game does not implicitly assume that the formation of a coalition is always beneficial. Thus, in a coalition formation game with TU, the grand coalition may not be formed and the property of superadditivity may not be verified, because the potential benefits/gains of players obtained from coalitions are limited by the costs of forming the coalitions [10,11].
A coalition formation game can be effective in attaining a prosumer-centric scheme for P2P energy trading by helping each peer make a decision. Players participating in P2P energy trading may be prone to leave a coalition and join a new coalition if their utility is improved in the new coalition. This can be performed through merge and split operations to dynamically change coalition structures [10], which enables the new coalition to yield better benefits/gains and become ultimately more beneficial for all its players [35,36].
As presented in Table 1, the works available in the literature rely on merge and split operations for the formation and division of coalitions [33,34,35,36,37,38,39,40,41]. In [36], Tushar et al. presented a coalition formation game to assist prosumers with the decision of how to intelligently use their battery energy storage systems (BESSs) to participate in P2P energy trading. This is achieved by comparing the net benefits each prosumer can potentially receive and by forming coalitions among similar prosumers. In [35], Saad et al. relied on a coalition formation game to develop an algorithm for forming coalitions of MGs while minimizing their utility function based on power loss costs. This enabled them to cooperatively adjust their decision to form or break into disjoint coalitions through merge and split operations and meet their power surplus or demand requirements. Due to space limitations, the authors adopted a proportional fair payoff division based on non-cooperative utility, enabling the benefits obtained from the cooperation to be divided in weights in accordance with the non-cooperative utilities of the cooperating MGs. In [37], a fractional hedonic coalition formation game is used to formulate an algorithm for coalition formation in P2P energy trading, allowing the selection of the most stable and optimal coalition while increasing social welfare and the payoff of users in the network. In [38], Karimi and Jadid proposed a coalition formation game model using a probabilistic analytic strategy-based algorithm to determine and select the best coalition of MGs in MMG systems, which showed significant reductions in total operating costs for small-scale and large-scale MMG systems. This is performed by determining and evaluating the utility of all player strategies and then ranking them from the perspective of the MGs. The cost of the stable coalition is fairly allocated among the cooperative MGs in accordance with their contributions through the Shapley value. In [39], Marzband et al. used a coalition formation game to propose a bi-level methodology structure for profit maximization in a competitive energy market containing multiple energy districts and then allocate profits fairly among them. In this study, the merge and split operation and solution concepts such as the Shapley value and the Nucleolus are analyzed and compared with the amount of profit each energy district can obtain individually.
3.1.3. Coalition Graph Game
Coalition graph games aim to investigate the communication between players by building directed or undirected network graphs and studying their stability and efficiency through low-complexity distributed algorithms [10,23,60]. Unlike canonical coalition and coalition formation games, the communication structures and interactions between players within a coalition play a major impact on the utility of the coalition and the outcome of the coalitional game [11,43]. In a coalition graph game with TU, the internal interactions and negotiation patterns of players are taken into consideration, and cooperation can be described or carried out in both complete and incomplete networks using graph theory [42,43]. An incomplete network denotes a lack of connection between two or more nodes, whereas a complete network denotes a fully connected network with complete connection between all nodes [44]. The Myerson value is a solution concept that can be used for cooperation under incomplete networks to help distribute profits among players in a fair manner. This means that the use of coalition graph games is encouraged to design schemes for P2P energy trading when cooperation between peers is carried out in an incomplete network, being suitable to describe energy and carbon interactions [42].
As presented in Table 1, studies using coalition graph games in P2P energy trading applications are relatively scarce in the literature [42,43,44]. In [42], Zhong et al. used a coalition graph game to analyze the communication and interactions between energy hubs under a complete network for local carbon trading and an incomplete network for local energy trading. Due to this hybrid network topology, a two-stage optimization framework is developed to achieve a fair distribution of profits using both the Shapley value and the Myerson value while reducing communication costs and total carbon emissions for the coalitions. In [43], Azim et al. developed a framework based on a coalition graph game for P2P energy trading to allow prosumers to form a coalition and negotiate the parameters of energy trading in terms of quantity and price. The allocation of total payoff among the peers is achieved in a fair manner through the Myerson value. In [44], Suh and Yoon investigate the fair distribution of profit among interconnected MGs in accordance with the contributions resulting from their connection. To achieve this, the authors relied on the Myerson value for an incomplete network, as well as on the Shapley value and Nash bargaining solution based on the feasible cooperative payoff set and disagreement point (i.e., player payoff during non-cooperation) in a complete network [44].
3.2. Coalition Stability
A canonical coalition game is considered stable if the stability of the grand coalition is guaranteed, meaning that no player has an incentive to leave the grand coalition to further increase its gains or benefits. In order words, players are encouraged to cooperate with each other and form the grand coalition. This grand coalition is stable if its Core is non-empty and if the gain of each player lies within the Core [23]. It is worth noting that the stability of a coalition is not always guaranteed in a coalitional game, especially in real-world applications. In order to ensure the stability of the grand coalition and encourage players to cooperate, the property of convexity needs to be verified. Convex games are a class of coalitional games that always possess a non-empty Core, and their value function is supermodular [24].
Superadditivity and convexity are important properties for the characterization of cooperative games and denote the stability of the cooperation between players [9,62]. A coalitional game is considered superadditive if the value of a union of separate coalitions and satisfying is equal to or larger than the sum of the separate values of the coalitions [62], as follows:
A coalitional game is considered convex if the value of a union of separate coalitions and plus the value of their intersection is equal to or larger than the sum of the separate values of the coalitions [62], as follows:
When a convex game is played cooperatively, it leads to an increase in the incentives for joining a coalition as the size of the coalition increases, having a “snowballing” effect [62].
The Core
The Core was introduced by Gillies in 1953 and can be defined as an intersection or region formed by a set of payoff vectors (i.e., imputations) [63], in which no coalition has a value greater than the sum of individual player payoffs [9,62]. This set of imputations denotes the feasible allocation of payoff or profit which cannot be improved further, and players have no incentive to reject the proposed payoff allocation and deviate from the grand coalition [10,31]. In the context of P2P energy trading, the payoff of players can correspond to profits or cost savings for choosing to cooperate. The Core of a TU game is given by
where is the set of feasible payoff allocations or imputations for every player .
3.3. Coalition Payoff
The value of a coalition usually corresponds to the monetary benefit that players may obtain by cooperating with each other as a coalition. In the context of P2P energy trading, this monetary benefit is generally identified as profits or cost savings obtained from the cooperation, being the difference between potential revenue and the cost of forming the coalition [23]. Ultimately, the goal of coalitional games is to offer a rational solution for the distribution of profits or cost savings from the grand coalition among the players [24]. From an economic perspective, it is important for producers to invest in a profitable generation portfolio and obtain a fair return on their investment. At the community level, prosumers also seek a fair distribution of profits or cost savings among them in accordance with their respective contributions to the generation portfolio [64]. While the benefits can be distributed equally in a straightforward way through equal sharing, there are solution concepts such as the Shapley value, the Myerson value, the Nucleolus, and the Kernel that can be used to provide a fair allocation of profits or cost savings and reduce the level of dissatisfaction of coalitions [9,42]. This can ensure the desired level of social welfare and equity required to attain a state of social and economic sustainability.
3.3.1. The Shapley Value
The Shapley value was introduced by Shapley in 1953, and it defines the solution of cooperative games that distributes the total benefits/gains and costs among all the players cooperatively participating in the coalition according to the contribution of each individual player [65]. This means that each player has an incentive to collaborate in the coalition and players can gain at least as much as they would have if they acted non-cooperatively or individually [9,66]. It is a fair allocation solution used to determine the bargaining power of players [9,42]. The Shapley value of a TU game is given by
where is the number of players in a coalition , which is a subset of the total number of players . The component denotes the marginal contribution of player to the coalition .
The Shapley value needs to satisfy the axioms of efficiency, symmetry, linearity, and null player [65,67]. These axioms can be seen as requirements to compute the allocation solution and determine the bargaining power of players and the fair amount of profit each player receives based on their contribution to the coalition [9,68]. It is assumed that players join the coalitions randomly and that all possible coalitions formed are equally probable [68].
- Axiom 1—Efficiency denotes that the sum of the payoffs of players is equal to the value of the grand coalition and this exact value is distributed among the players [9,68]. The allocation of the total utility or payoff is considered efficient if
- Axiom 2—Symmetry denotes that the players with the same amount of marginal contribution to any coalition receive the same equal share independent of the name and order of the players [9,68]. Players and are considered symmetric if for every coalition the following condition holds:
- Axiom 3—Linearity or additivity denotes that the combination of two coalitional games results in each player receiving a sum of payoff in each independent coalition [9,68]. The property of linearity is achieved if the combination of two coalitional games described by their respective utility functions and verifies the following condition:
- Axiom 4—Dummy or null player denotes that there is no payoff allocated for players not adding value or contributing to any coalition they join [9,68]. This does not change the Shapley value obtained for the other players in the game [68]. A player is considered a null player if for every coalition the following condition holds:
In many applications of coalitional games, it may be appropriate to attribute each player an “a priori” measure of importance using weighted Shapley values [69]. For instance, in power systems, weights attributed to players could be related to the distance between the power plant and the loads of each player. It is also possible to add potential costs of distribution grid usage and maintenance depending on the number and location of players. Given the uncertainty of power generated from RESs and its effect on the level of power quality due to frequency fluctuations, weighted Shapley values can also be used to allow a weighted allocation of costs in accordance with player resources that support power quality. Another possibility could be attributing weights in order to characterize players in P2P energy trading based on their relative level of economic, social, and environmental sustainability by using sustainability scores for different energy resources, as performed in Section 5.3. The weighted Shapley value is a weighted generalization of the Shapley value and allows the allocation of benefits/gains and costs in accordance with the different bargaining abilities or weights of each player [69,70]. Weighted Shapley values of a TU game with a set of non-negative weights are given by the following equation [70,71,72]:
where is the Harsanyi dividend and are the weighted Shapley values [70,71,72]. For any TU game , the Harsanyi dividend can be determined by the following equation [71,72]:
The weighted Shapley values need to satisfy the axioms of efficiency, symmetry, linearity, and null/dummy player [69,70,71,72].
3.3.2. The Aumann–Shapley Value
The Aumann–Shapley value is an extension of the discrete Shapley value concept to fractional or non-atomic games with an infinite number of players. Essentially, it splits players into infinitesimal segments and performs permutations of player joining order as the size of each sub-player reaches zero, allowing the Aumann–Shapley value to have an analytical expression [73]. This is achieved by first dividing the players into infinitesimal segments and then applying the Shapley value to each segment as if it were an individual player [74,75]. The Aumann–Shapley value can be solved iteratively and provide an analytical solution based on a cost function as follows [73,75]:
where is the vector of the resources of each player and is an infinitesimal value (i.e., fraction) of player resources, with belonging to the interval [0, 1].
In the context of P2P energy trading, the division of players simply means that their size or, in this case, generation capacity is divided into infinitesimal segments and that each segment is represented as a sub-player [73,74,75,76]. Even though the number of permutations increases significantly, the allocation procedure of the Aumann–Shapley value can become a parametric linear optimization problem when the cost function is obtained from an optimization problem, thus allowing it to have an analytical expression or solution and decreasing computational burden, as concluded by Junqueira et al. in [74].
3.3.3. The Myerson Value
The Myerson value is applied in incomplete networks to distribute the total benefits/gains and costs among all the players in a fair manner [42,43]. In incomplete networks, the contribution of players to a coalition is dependent on the heterogeneity of their positions [42]. The Myerson value of a graph game is given by
where is the number of players in a coalition , which is a subset of the total number of players . Like the Shapley value, the component denotes the marginal contribution of player to the coalition .
3.3.4. The Nucleolus
The Nucleolus solution concept was introduced by Schmeidler in 1969 [77], being defined as the excess of a coalition for every payoff vector and every coalition [9,10]. It is the lexicographically minimal imputation of a TU game (i.e., lexicographic order of vectors) and measures the dissatisfaction or satisfaction of players in a coalition towards the payoff vector of each player [39,41]. When the characteristic function is based on benefit, the excess of a coalition is a measure of dissatisfaction. On the other hand, when the characteristic function is based on cost, the excess is a measure of satisfaction. Both benefit and cost approaches are solved in an equivalent way. Let be a balanced TU game; the Nucleolus is given by the following [59]:
The Nucleolus can be used to guarantee that all excess allocated, i.e., dissatisfaction or satisfaction, is minimized or maximized among all coalitions [10,59]. More specifically, in an approach involving benefits, an imputation vector belongs to the Core of a game only if all the excesses obtained are negative or zero [10]. This makes the Nucleolus capable of finding a solution within the Core whenever it is proven to be non-empty [9,10,59]. Although the Nucleolus is a more complex solution concept to compute, it can provide the best allocation solution under min–max criteria [10]. It possesses properties that may constitute an advantage over the Shapley value given that it is not empty even if the Core of the game is an empty set. Moreover, the Nucleolus not only satisfies the properties of efficiency, symmetry, additivity, and null player, but also decreases the overall level of dissatisfaction of the least satisfied coalitions while ensuring coalition stability [9,10]. While this solution concept may be preferred over the Shapley value in certain cases, some authors may consider it to be relatively unfair when compared to the former as it allocates larger profits to the most dissatisfied coalitions without considering the individual contributions of players [9]. In [59], the authors discuss the most common mistakes in computing the Nucleolus and illustrate them using five examples, including an example of an allocation problem in electricity markets. This can be useful to avoid such mistakes when computing the Nucleolus solution concept in coalitional games involving more practical applications.
3.3.5. The Kernel
The Kernel solution concept is also defined by a metric of excess, being used to effectively measure the bargaining power of players [78]. Essentially, it represents the maximum surplus of a player over another player with respect to an imputation [9,10]. This maximum surplus is determined by
The Kernel denotes that player has more bargaining power than player with respect to an imputation if is lower than . It is defined as the set of all imputations that satisfy for each distinct pair of players [9,10]. Thus, the Kernel of a TU game is given by
A particularly important property is that the Kernel always contains the Nucleolus, and these solution concepts coincide when the game is convex [9,10].
3.4. Coalition Formation and Division
Due to the nature of P2P energy trading, coalitions should contain both buyers and sellers. For a coalition to form and be valuable, it needs to contain at least one buyer and one seller [35,36]. Furthermore, any coalition can be divided into a group of buyers denoted by and a group of sellers with surplus energy denoted by while satisfying . Then, a seller and a buyer can be matched together based on their needs and preferences [35,40]. Such a division of coalitions into groups of buyers and sellers was successfully performed for several coalitions of MGs by Saad et al. in [35]. Under a coalition formation game framework, this can be achieved by following fundamental rules for merge and split operations to allow the division or formation of coalitions with the goal of increasing their utility or payoff [36,41].
In addition, this division or formation of coalitions needs to improve the payoff of at least one player without decreasing the payoffs of others, which can be ensured by the Pareto order [35]. Consider two distinct sets of disjoint coalitions, and , formed by the same players. For a set , the utility or payoff of a player in a coalition is , which can be determined by the Shapley value. The basic definition of the Pareto order denotes that set is preferred over set only if with at least one strict “greater than” inequality for the utility or payoff of a player [33,35]. Because many of the possible combinations of coalitions are unstable, the Pareto order can be applied iteratively to find a stable coalition partition among all possible combinations of coalitions [33]. It takes into consideration the individual player payoffs [36], being implemented to study the decision-making process of each player to choose a coalition with the purpose of maximizing its expected individual utility or payoff. Hence, players may decide to leave a certain coalition if it is unstable and decide to join another if it is more beneficial for them [33,36].
For a coalition formation game, the merge and split rules based on the Pareto order can be defined as follows [36,40,41]:
- The merging operation enables one to merge any set of disjoint coalitions into a single coalition where . Hence, .
- The splitting operation enables one to split any coalition into smaller coalitions where . Hence, .
Essentially, the merge rule enables two or more coalitions to merge into a single larger coalition if the formation leads to an increase in payoff for at least one of the players without decreasing the payoffs of others. On the other hand, the split rule allows a coalition to be divided into smaller coalitions if the division leads to an increase in payoffs for players in the smaller coalitions [36,41]. The merge and split operations occur over multiple iterations until the final stable partition is reached [35,36].
In mechanisms for coalition formation and profit allocation, the profits for each player in a coalition can be determined by the following [39,41]:
4. Sustainable Energy Trading
The long-term sustainability of P2P energy trading can be improved and secured by performing a profitable and effective management of peers at the community level [79,80,81]. Hence, it is important for these local energy communities to group prosumers, producers, and consumers in accordance with a common goal or based on their energy trading patterns and interests. This can lead to fewer disagreements and stronger ties among peers, improving the bargaining power of community members and motivating them to cooperate with each other to fulfill their shared goal [79,80]. Ultimately, a cooperative and goal-oriented community helps promote the active participation and involvement of prosumers towards the sustainability of the energy supply chain [79]. Relationships between providers and consumers can impact the overall reliability and costs of balancing power generation and consumption [79,80]. This also has an effect on the prices in the P2P energy market, highlighting the need to maximize social welfare through cooperation among market participants and optimization of prices for both sellers and buyers [82,83].
However, it can be difficult to establish harmonious bilateral relationships between participants and form cohesive groups due to competitive behaviors when conflicting strategies and interests are involved. This is especially due to potential negative interactions among competitors and rival organizations, which can deteriorate social welfare and decrease overall market efficiency [8]. Unwanted competition can also arise from energy providers focusing on the maximization of revenue among themselves while consumers look forward to lower energy prices [79]. There is a fundamental challenge of forming stable goal-oriented groups of prosumers working cooperatively towards the long-term sustainability of LEMs and efficient management of communities. To alleviate this challenge, it is essential to build mechanisms and frameworks capable of aligning energy trading behaviors and similar preferences of prosumers to form stable coalitions while providing incentives for cooperation using a fair distribution of profits [79,80,84].
The concept of sustainable development should not be overlooked when formulating approaches based on coalitional games. More specifically, these approaches should take into consideration various aspects of economic, social, and environmental sustainability when modeling player behaviors [8]. Techniques based on coalitional game theory can help analyze the stability and formation of prosumer groups to ensure the economic, social, and environmental benefits provided by P2P energy trading. Moreover, communities involving SGs and MG systems can be considered relatively heterogeneous and dynamic with various competitive players with distinct goals or preferences [58], further encouraging the use of approaches based on game theory. Such game-theoretic approaches can provide robust and analytic frameworks to analyze the strategies of individual market participants and obtain the desired fair and optimal outcome in a highly competitive market environment [11,58]. This also has the potential to establish a sense of social trust among players and motivate them to combine their strategies, contributing to the social sustainability of the P2P energy trading market [11,85].
When integrated into optimization problems, coalitional game theory has the potential to successfully design an LEM for sustainable energy trading. This can be made evident when examining the panoply of coalitional game models for power systems being proposed in the literature [11,12,13].
Table 2 presents some of the economic, social, environmental, and technical contributions for sustainability associated with various applications of coalitional games in power systems available in the literature.

Table 2.
Economic, social, environmental, and technical sustainability contributions associated with the application of coalitional game theory in power systems.
The potential contributions of a game-theoretic energy trading market to economic sustainability may include goals such as the allocation and maximization of profits and minimization of energy costs for all participants trading surplus energy [86,87]. This can be achieved by using coalitional game approaches to develop energy pricing schemes [23,86], coordinate PEV charging and discharging operations [35,90], optimize the sizing and placement of PEV fast charging stations and DERs [93,94], and establish cost and benefit models [85]. Essentially, the outcome of sustainable energy trading in a state of sustainability needs to be profitable for the participants, further incentivizing participation [33]. Contributions to environmental sustainability may include goals involving the allocation and minimization of energy waste and carbon emissions from non-renewable energy sources (NRESs) [98], as well as a reduction in network power losses [40,97]. Coalitional game approaches have been employed in power system applications for the implementation of load shedding [40], cooperative energy management [97], and optimal planning of integrated energy systems with ancillary services [98]. Contributions to the social sustainability of the energy trading market can be provided by relying on a coalitional game to maximize social welfare and fairness in the market through consumer-centric schemes [23,61] and based on player preferences [32,37,54], in which no player is better off at the expense of others. The fair allocation of benefits/gains based on the contributions of players to the coalition constitutes the main reason for the use of a coalitional game over other tools to address socially sustainable energy transactions.
The implementation of P2P energy trading in a complex and large-scale system with dozens of market participants such as a large SG or a smart city can quickly become unsustainable without proper coordination and decision-making schemes. Because of this, the use of a coalitional game and its solution concepts can help deal with complex decision making in energy transactions and ensure economic, social, and environmental sustainability in the P2P energy trading market. With this in mind, P2P energy trading could be considered sustainable if the following conditions are met:
- The transactions occur without one of the parties (i.e., buyer or seller) becoming better off at the expense of the other;
- The transactions lead to an increase in profits or cost savings, as well as a reduction in natural resource consumption or emissions.
Moreover, energy transactions in a state of sustainability should be able to provide unquantifiable benefits associated with improved power system flexibility and reliability, increased access to renewable energy, and empowered prosumers and consumers [106]. For these conditions of sustainability to be satisfied, a central entity or community manager may be required to reinforce cooperative behavior, ensure coordination, and avoid irrational interactions among participants [9,107]. This is increasingly important when the P2P energy trading scheme involves a payoff allocation process or mechanism [107]. The central entity, as a rational agent, should be able to anticipate potential player decisions and coordinate each energy transaction by performing the management of players with similar preferences, dictating the formation of like-minded coalitions, and evaluating the coalitional values for the grand coalition [107,108].
5. Problem Formulation
In this section, a simple application of a coalitional game (i.e., a canonical coalition game) is demonstrated for power systems based on the game-theoretic aspects and solution concepts addressed in Section 3. Essentially, this illustrative case study aims to show, in a simplified manner, how a coalitional game with TU can be implemented in power system applications to study decision making and analyze the stability of cooperative energy trading. Three-player and four-player examples are provided to properly analyze and illustrate the benefits of cooperation in energy trading between communities with the goal of minimizing the total fuel costs and emissions while providing a fair allocation of profits. Therefore, the case study becomes a linearly constrained quadratic optimization problem with two minimization objectives, and the local energy trading can be modeled as a combined economic and emission dispatch (CEED) problem [109,110]. This allows the optimal economic and emission dispatch of thermal generators for each player to be performed [60,111]. Furthermore, the estimation of power losses in the network can be performed by relying on the B-coefficient loss formula method to express and compute incremental power losses as a function of the power output of each generator [3]. A simple method based on Kron’s B-coefficients is relatively efficient and avoids the use of power flow equations to compute incremental power losses [3,112], which may help reduce the computational burden associated with the application of a coalitional game. While this method can be easily integrated into the decision-making process of power system operation, the increased penetration of RESs can jeopardize the accuracy of the B-coefficient loss formula due to highly variable nodal power injections [112].
5.1. Generator Costs and Emissions
The formulation of a multi-objective problem is necessary to achieve a desirable level of sustainability in P2P energy trading and obtain an optimal portfolio for the community that is attractive to both market participants and investors. This often results in the minimization of generator fuel costs and emissions to help strategize an economically feasible system operation while taking into consideration environmental impacts. A quadratic programming approach is commonly used to solve the cost and emission minimization problem given the quadratic nature of the objective function [113]. To this end, cost functions can be derived from the input/output characteristics, design parameters, efficiency, and fuel costs of the different types of generator units [111,114]. Besides the cost of fuel consumption, the operating cost of a thermal generator also includes the costs associated with maintenance, labor, and fuel transportation. These costs are included as a fixed portion of the overall operating cost. In practice, the input–output characteristic of typical thermal generators that consist of boiler, steam turbine, and generator units is usually nonlinear and a convex curve, being obtained by directly combining the input/output characteristic of the boiler unit and the input/output characteristic of the turbine generator unit [3]. The emission functions correspond to all types of emissions (e.g., NOx, SOx, and CO2) emitted from thermal generators that rely on fossil fuels for power generation [115].
Quadratic cost and emission functions allow an economically and environmentally optimal allocation of power generation among the available generators to be found and a less discriminatory sell price for the energy traded in the cooperative market environment to be obtained. The effect of valve-point loading (VPL) can also be considered for a more practical and accurate projection of fuel costs associated with multi-valve turbines in thermal generators [116,117,118,119,120]. This effect is mainly a result of wire drawing effects when the steam admission valves open, leading to nonlinear rippled input–output curves and increasing losses [120].
Therefore, the minimization of generators costs and emissions can be formulated as follows [116,117,118,119,120]:
where is the number of generators, represents the total fuel cost of each generator , and represents the total emissions of each generator [117,118,119,120,121,122].
5.1.1. Fuel Cost Function
Generally, the fuel cost of operating a thermal generator with and without the VPL effect can be represented by the following quadratic function [116,117,118,119,120,121,122]:
where is the number of generators, is the active power generation of each generator , is the cost coefficient of generator in USD/MWh2, is the cost coefficient of generator in USD/MWh, and is the cost coefficient of generator in USD/h [117,118,119,120,121,122]. The constant cost component is equivalent to the fuel consumption associated with the operation of the thermal generator without power output [3]. The parameters and are additional fuel cost coefficients of each generator when the VPL effect is considered, and is the minimum active power generation capacity of the generator [118,119,120].
5.1.2. Emission Function
Similarly, the overall level of emissions emitted by a thermal generator with and without the VPL effect can also be represented by the following quadratic function [116,117,118,119,120,121,122]:
where is the number of generators, is the active power generation of each generator , is the emission coefficient of generator in kg/MWh2, is the emission coefficient of generator in kg/MWh, and is the emission coefficient of generator in kg/h [105,106,107,108,109,110]. The parameters and are additional emission coefficients of each generator when the VPL effect is considered [118,119,120].
5.1.3. Power Constraints and Limits
The minimization of fuel costs and emissions needs to satisfy certain equality and inequality constraints. Therefore, the objective function is constrained by the power balance of the system, where the total power generation must be equal to load demand plus transmission losses [116,117,118,119,120]:
where is the total load demand and corresponds to the total power transmission losses which can be determined from Kron’s loss formula by using the matrix of power loss coefficients [118,119,120].
The objective function is also limited by the operational range of generators, where total power generation is bounded by the minimum and maximum power output of each generator [118,119,120]:
where is the minimum power output and is maximum power output of generator [117,118,119,120,121,122].
5.2. Energy Trading Price
In general, prosumers receive less monetary compensation for any surplus renewable generation injected into the grid and sold to retailers as this type of power generation is considered non-dispatchable. Taking this into consideration, an LEM for P2P energy trading can motivate prosumers to cooperate and trade surplus renewable generation with each other [23]. This allows prosumers to obtain a fair and higher price for the electricity traded with other market participants. A mid-market rate (MMR) can be used as a pricing mechanism to set the price of P2P energy trade between prosumers, which can benefit each pair of participants trading surplus electricity in the LEM [23,54]. Such an approach can be economically attractive as it enables prosumers to buy surplus electricity from other market participants at a lower rate than the retail price of the grid or sell surplus electricity to other participants at a higher rate than the price of selling to the grid or retailers [23,61]. In [123], Zhang et al. assessed and compared the MMR method with other pricing mechanisms such as double auction (DA) and supply and demand ratio (SDR). Based on their results, they concluded that the MMR shows the best performance in terms of power flatness. In [124], the MMR method obtained a reduction in costs when compared to the bill-sharing (BS) method.
Using the MMR, the P2P energy trading price is equal to both P2P selling price and P2P buying price when the total available surplus energy is equal to the total energy demand (), which can be determined by the following [23,61]:
where and are the selling and buying energy prices imposed by the grid, respectively.
Interaction with the grid is required to allow players to sell their surplus renewable energy or buy energy from the grid. According to [23], in cases where the total available surplus energy is greater than the total energy demand (), the P2P buying price is given by (24), and the P2P selling price for any surplus energy sold to the grid can then be determined by the following [23,61]:
where and are the energy surplus and energy deficit of a prosumer part of a set of sellers or buyers , respectively.
In cases where the total energy demand is greater than the total available surplus energy (), the P2P selling price is given by (24), and the P2P buying price for energy purchased from the grid can then be determined by the following [23,61]:
where and are the energy surplus and energy deficit of a prosumer part of a set of sellers or buyers , respectively.
In [54], a ratio between energy demand and surplus energy is integrated into the MMR approach to determine a different price of P2P energy trade that is dependent on the total energy demand and surplus energy in the LEM. Therefore, through this variation of the MMR, the energy trading price is then determined by the following [54]:
where and are the total amounts of energy surplus and energy demand, respectively.
Besides encouraging participation in P2P energy trading, this approach can also improve revenue for prosumers, induce electricity bill savings for consumers, and motivate all participants to reduce their energy consumption during times of low surplus energy [23,54].
5.3. Case Study for Three-Player and Four-Player Games
The case study assumes an LEM for P2P energy trading among large-scale communities coordinated by a central entity that provides complete information to all market participants. Essentially, in a complete information game, the payoff and strategy of each player are open and known to all participating players. This means that all network parameters and player preferences are known to both the central entity and participating communities/players. The communities depicted in Figure 5 are fully capable of operating individually, consisting of either thermal or solar generators as presented in Table 3 and Table 4. Each community can choose to supply their own members or cooperate with others to meet the aggregated demand. In the four-player example, community D contains solar generators and can sell its surplus renewable energy to the grid at a lower rate. In solutions to CEED problems, non-dispatchable power from RESs has transmission priority over conventional thermal generators and is often seen as a negative load used to decrease the total load demand of the power system [117,122]. Renewable generators based on solar and wind power have no fuel costs associated with their operation for power generation. In P2P energy trading applications, it may be suitable to determine the total cost of operating solar or wind power generators based on operation, maintenance, and equipment investment costs [117,121,122].
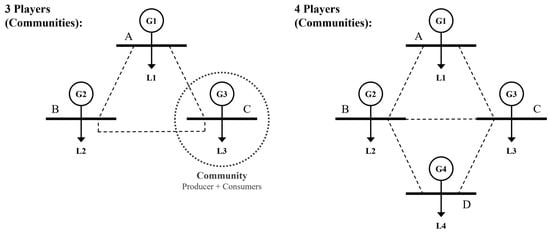
Figure 5.
Simplified model of the interconnected network for the 3-player and 4-player examples.

Table 3.
Generator power limits, costs, and emission coefficients.

Table 4.
Player data related to generator fuel, energy sell price, aggregated load, and sustainability score.
It is noteworthy that the combined costs of operating solar and wind power generators can also be considered for a more realistic approach by determining three distinct cost components [125]. This includes the weighted cost function based on solar irradiance and wind speed profile using probability density functions (PDFs), the penalty cost or underestimation cost function for not using all the available generated power, and the penalty reserve requirement cost or overestimation cost function related to the uncertainty of power generation [116,125]. The variability and uncertainty of load demand and renewable generation from solar or wind power generators can be modeled using probabilistic methods to obtain solar irradiance and wind speed profiles. This can be performed by considering the PDFs for solar and wind power generation and loads based on a Weibull, beta, and normal distribution [38]. For this illustrative case study, no cost of operation was considered for the community/player with solar power generators, relying only on the cost of purchasing energy from the grid or other communities/players.
For the sake of simplicity, the VPL effect is not considered for the three thermal generators in both examples. Table 3 presents some of the network data related to power limits, costs, and emission coefficients for each of the thermal generators (G1, G2, and G3) considered in this case study, which are based on the IEEE 6-unit test system found in [126]. Moreover, the model also takes into consideration transmission losses using a matrix of line loss coefficients (i.e., B-coefficients) as follows [127]:
Community D consists of solar power generators with ESSs and can buy energy from other communities or trade its surplus renewable energy with others when cooperating. In the case of separate operation, the operation cost of community D is dependent on whether it can rely on its own solar power generated from PV systems and grid imports to fulfill its energy requirements or on grid exports to sell surplus renewable energy. The buying and selling prices of the grid, and , are assumed to be around 97.25 USD/MWh and 272.7 USD/MWh, respectively. These values were determined based on average rates implemented in the European Union [128,129] and were used to obtain the MMR denoted in (24) for the renewable energy sold by community D to its own community members or to other communities, as addressed in Section 5.2. Sustainability scores of players can be integrated into the game by using the weighted version of the Shapley value, which enables an asymmetric allocation of profits based on the relative level of economic, social, and environmental sustainability of each individual player. The sustainability scores are dependent on the type of generation unit used by each community/player, and they were obtained from the sustainability assessment of different electricity generation technologies presented in [130]. These sustainability assessments rely on several indicators (e.g., investment costs, maintenance and operation costs, human health impacts, population displacement, job creation, GHG emissions and global warming potential, land occupation and rate of deforestation, acidification potential, water depletion, and lifetime) calculated using a life cycle perspective which integrates the complex relationships between all involved systems [130,131], constituting a transparent and effective way to communicate the sustainability performance of different energy resources to policymakers and the general population [131,132,133]. Table 4 presents the data related to generator fuel type, energy sell price, aggregated load (L1, L2, L3, and L4), and sustainability score for each player.
5.3.1. Bi-Objective Optimization Problem
The bi-objective optimization problem of simultaneously minimizing two independent functions (i.e., fuel costs and emissions) while satisfying equality and inequality constraints can be converted into a single-objective optimization problem [118,120]. This is usually achieved in a relatively straightforward way by determining the price penalty factor for the generators, which is formulated as follows [117,118,119,120]:
where is the price penalty factor of each generator in USD/kg, being denoted by the ratio between maximum fuel cost and maximum emissions of the thermal generators. This is determined as follows [117,118,119,120]:
The values obtained for the price penalty factors are arranged in ascending order and the maximum power output of each thermal generator is then added, starting from the generator with the smallest until the condition is verified [119,120]. The objective function is subjected to the power balance constraint (21) and limited by (23).
An algorithm was developed in Matlab to solve the CEED optimization problem, and the TUGlab and MatTuGames toolboxes were used to compute and plot the solution concepts of the coalitional game. Figure 6 presents the general structure of the algorithm developed to model the coalitional game and minimize generator fuel costs and emissions. The level of complexity of the optimization algorithm is mostly determined by the number of possible scenarios denoted by , which corresponds to 7 and 15 possible scenarios in these three-player and four-player examples, respectively. Therefore, 7 and 15 CEED optimization problems need to be solved for each possible player coalition or scenario of cooperation to formulate the vector of the profit-based characteristic function for the coalitional game, which denotes the potential profits each coalition can obtain.
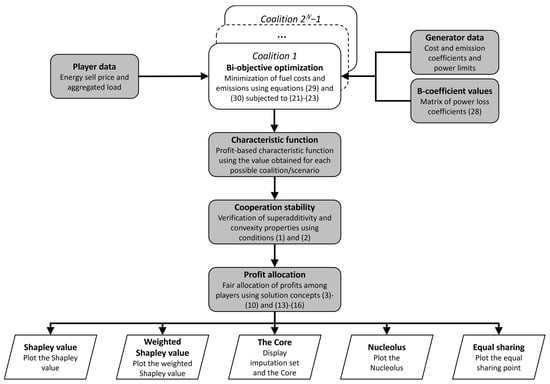
Figure 6.
Flowchart of the general structure of the algorithm developed for the 3-player and 4-player examples.
The optimized results in terms of costs, profits, and emissions obtained from all possible coalitions for the three-player and four-player examples are presented in Table 5 and Table 6, respectively. Figure 7 and Figure 8 show that the cooperation leads to the best possible outcome with the grand coalition granting the highest total profits and lowest total emissions in both three-player and four-player examples. In particular, the total profit obtained from the individual operation of the A, B, and C communities is around 212,210.03 USD/h in the three-player example or around 216,553.96 USD/h with the addition of community D in the four-player example. When all players decide to cooperate and participate in energy trading by forming a grand coalition, the total profit becomes around 213,276.03 USD/h in the three-player example or around 218,009.65 USD/h in the four-player example. This corresponds to a 1066 USD/h and 1455.69 USD/h increase in profits in the three-player example and four-player example, respectively. Total emissions are significantly reduced when all communities cooperate, resulting in a reduction of around 320.89 kg/h or 22.46% for the three-player example and 330.73 kg/h or 23.14% for the four-player example.

Table 5.
Profits and emissions for each possible player coalition/scenario of cooperation obtained in the 3-player example.

Table 6.
Profits and emissions for each possible player coalition/scenario of cooperation obtained in the 4-player example.
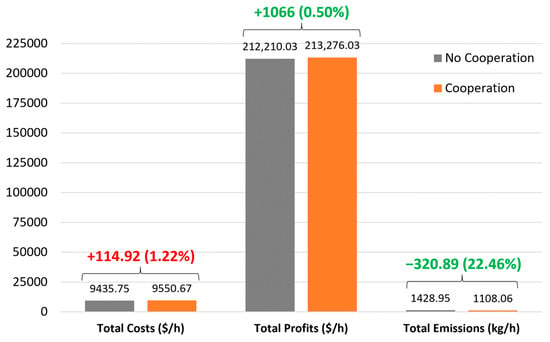
Figure 7.
Total costs, profits, and emissions for the 3-player example with and without cooperation.
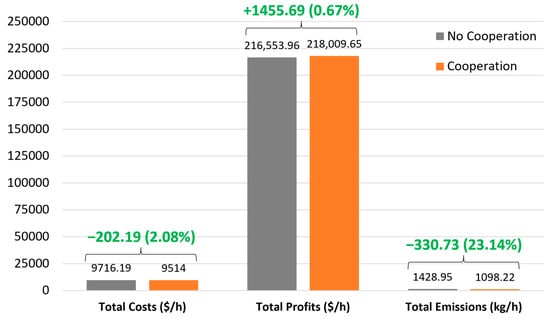
Figure 8.
Total costs, profits, and emissions for the 4-player example with and without cooperation.
5.3.2. Fair Allocation of Profits
After the formulation of the profit-based characteristic function, the fair allocation of profits among the communities is performed using the Shapley value, the weighted Shapley value, and the Nucleolus, as addressed in Section 3.3. The profits allocated by implementing these solution concepts are presented and compared with an equal sharing solution for both three-player and four-player examples in Table 7 and Table 8 (and Figure 9 and Figure 10), respectively. This equal sharing solution is a simple and straightforward approach to distribute the profits equally without consideration for the contributions of each player to the coalitions. It is used in this case study to provide a point of reference for an equal distribution of profits in which all players contribute the same value to the coalitions. Both the Shapley value and the Nucleolus denote that community C in the three-player example and community D in the four-player example are the least important or useful players, contributing less value to the respective coalitions and having reduced bargaining power. Therefore, fewer profits are allocated to these players while larger and significant profits are allocated to the most important players such as communities A and B. In both three-player and four-player examples, the weighted Shapley value effectively allocated the profits in accordance with the communities’ relative level of sustainability. Community A relies on coal-fired power generation, which has the lowest sustainability score of the four types of generators assumed in the case study, and thus, fewer profits are allocated to this player in both examples. On the other hand, community D in the four-player example relies on solar power generation, and it is allocated higher profits due to the high sustainability score attributed to solar power generators. This can provide an incentive for players to invest in more sustainable energy resources with the goal of increasing the allocated profits.

Table 7.
Solutions for the allocation of profits in the 3-player example.

Table 8.
Solutions for the allocation of profits in the 4-player example.
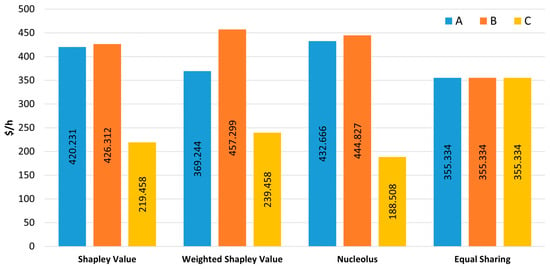
Figure 9.
Increase in profit (USD/h) for each player (communities A, B, and C) resulting from cooperation in the three-player example.
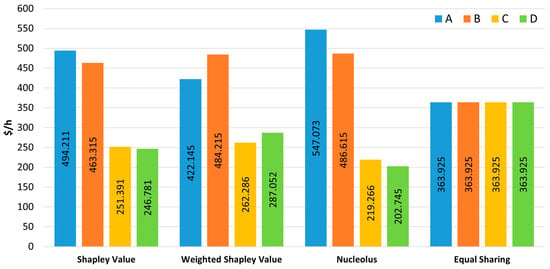
Figure 10.
Increase in profit (USD/h) for each player (communities A, B, C, and D) resulting from cooperation in the 4-player example.
While a solution concept such as the Shapley value offers a fair and unique solution for allocating profits, it does not guarantee the stability of cooperation. It is necessary to verify if the solution obtained by the Shapley value lies within the Core of the game [134]. Therefore, in order to effectively analyze the stability of cooperation, the Core is implemented for both three-player and four-player examples. As represented in Figure 11 and Figure 12, this solution concept obtains a region containing many feasible allocations and allows the visualization and examination of the set of imputations and the Core of the game, as well as the plotting of the Shapley value, the weighted Shapley value, the Nucleolus, and the equal sharing point. Essentially, each vertex of the triangle represents the point at which the corresponding player is allocated the maximum profit, with the equal sharing point lying in the center of mass of the triangle [9,134]. For instance, in a three-player game, the allocated profits for player A decrease the farther the solution is from its corresponding vertex, with the player being allocated zero profits and contributing nothing to the grand coalition if the solution lies on the opposite BC line between players B and C.
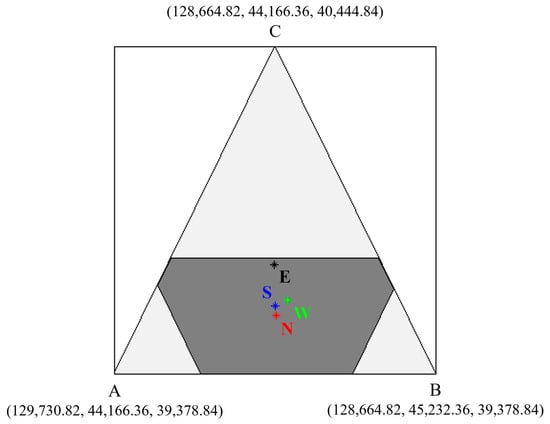
Figure 11.
Set of imputations (triangle) and the Core (grey polytope) of the coalitional game for the 3-player example (communities A, B, and C) with the respective solution concepts: S—Shapley value (blue); W—weighted Shapley value (green); N—Nucleolus (red); E—equal sharing (black).
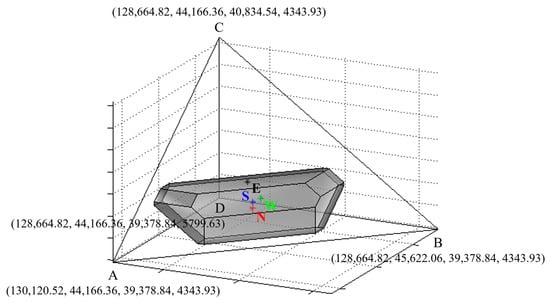
Figure 12.
Set of imputations (triangle) and the Core (grey polytope) of the coalitional game for the 4-player example (communities A, B, C, and D) with the respective solution concepts: S—Shapley value (blue); W—weighted Shapley value (green); N—Nucleolus (red); E—equal sharing (black).
The Core is defined as the set of coalitional and rational imputations represented by the convex polytope in grey color shown in both Figure 11 and Figure 12. It denotes the region of rational solutions considered feasible for this case study in which no player has an incentive to leave the grand coalition. In particular, the Core of the game is more distant from community C in the three-player example or more distant from communities C and D in the four-player example, meaning less bargaining space is available for these players.
The coalitional game modeled for both the three-player and four-player examples satisfies the condition of superadditivity denoted by (1). When verifying the property of convexity for all possible contributions of players to each coalition, the game also satisfies the convexity conditions denoted by (2) for these specific examples. This ensures that the Core exists and means that the Shapley value and the Nucleolus can provide rational solutions with the Shapley value being the center of the Core, as shown in Figure 11 and Figure 12. In practical terms, the convexity of the game enables each community to increase their allocated profits when joining larger coalitions and provides an incentive for them to cooperate [62]. Moreover, the Nucleolus and the Kernel solution concepts coincide given the convexity of the game [9,10].
6. Discussion of Challenges and Limitations
In Section 5, a coalitional game was implemented in a simple power system application for P2P energy trading among communities. The network data and parameters (i.e., load demand; energy sell prices; line loss coefficients; and generator power limits, costs, and emission coefficients) correspond to a particular instance of the case study, which happens to result in a convex game. The algorithm was able to successfully minimize both fuel costs and emissions in the CEED optimization stage, and solution concepts such as the Shapley value and the Nucleolus were able to obtain a rational solution for the profit allocation. For this instance, cooperation resulted in a reduction in total costs and emissions while profits were fairly allocated among the communities in the grand coalition, ensuring contributions to economic, social, and environmental sustainability. However, given the practical nature of the case study, there was also a panoply of instances where the problem constraints and technical limits associated with power systems did not allow for a convex game.
To illustrate this loss of convexity, Figure 13 presents some examples obtained upon changing the energy sell prices of players while keeping the other network parameters unchanged.
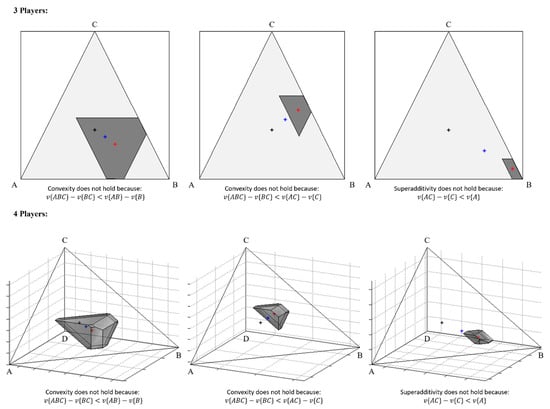
Figure 13.
The Core of different non-convex games for the 3-player and 4-player examples with the respective solution concepts: Shapley value (blue), Nucleolus (red), and equal sharing (black).
It can be observed in Figure 13 that the property of convexity does not always hold for the same network parameters. In fact, certain changes in player preferences such as energy sell prices can cause convexity to fail and the volume of the Core to decrease or become distant from some players, indicating a problem with the stability of cooperation or a lack of rational solutions for players to consider. This means that the incentives for adding more players to the coalitions do not increase or do not possess a “snowballing” effect. Moreover, larger variations in network parameters and player preferences can result in many instances where the Core becomes an empty set, indicating that cooperation is not rational for the players. As observed in the second/middle examples presented in Figure 13, the Shapley value does not belong to the Core, indicating that it was not able to provide a rational solution and that the contributions of players to the grand coalition are underestimated. More extreme examples may result in the loss of the superadditivity property, as seen in the third/last examples (from left to right) depicted in Figure 13.
It has been observed that the convexity of a game and the rationality and stability of cooperation among all players can easily be jeopardized under a slight change in certain parameters. Moreover, the risk of losing convexity appears to increase with the number of players and with the addition of stricter constraints. In particular, the integration of a community containing non-dispatchable RESs may further increase the risk of non-convexity and reduce player bargaining power due to the inflexibility of power generation associated with this type of energy source. In a state of sustainability, the energy transactions need to occur under stable cooperation, and the solution concepts should be able to obtain a rational solution for the fair allocation of payoffs, increasing the potential benefits and incentivizing players to cooperate.
A central entity can be used to anticipate potential player decisions and coordinate energy transactions by formulating a coalitional game with stable cooperation under complete information. However, the arrangement of cooperation over a non-convex game by a central entity can impose a major practical problem, and certain player contributions may be undervalued, leading to an unfair decrease in allocated profits for some players. This limitation and other challenges of coalitional games in practical applications are explained in the next subsections.
6.1. Game Convexity
The Shapley value is only able to ensure a rational solution when the game is convex. However, the convexity of the cooperative game in practical applications is not always guaranteed due to the nature of P2P energy trading and the various constraints of the network associated with generation, transmission, and consumption limits [9,23]. This may lead to a non-convex game, in which the marginal contributions of some players to minor coalitions can be higher than the contributions to the grand coalition. Consequently, a non-convex game results in non-rational scenarios where the Core becomes an empty set and other scenarios where the Core is small or distant from certain players, resulting in unstable cooperation and substantial bargaining power for some players [29,41].
Some cooperative games can also obtain a Shapley value completely outside of the Core, which indicates that the contribution of these players to the grand coalition is underestimated. Ensuring the stability of cooperation may constitute a challenge as the number of players increases. For instance, in [135], Lozano et al. found that while the property of convexity held for some instances involving four players, convexity did not hold for any instance involving eight players. This lack of rationality in non-convex games may lead to some players breaking agreements and rejecting cooperation.
Therefore, it is important and useful to verify the stability and convexity of a game and identify parameters that can cause the game to become a non-convex game [9]. The stability of coalitional games is dependent on superadditivity and given by a non-empty Core with the Shapley value inside the Core, meaning that no player has the incentive to reject cooperation and leave the grand coalition [23]. In contrast to the Shapley value, the Nucleous may provide a stabilizing allocation solution, being often preferred by many researchers due to this stabilizing capability [41]. In [30], Han et al. addressed this by comparing both the Shapley value and the Nucleous in reducing local load profile variability of a network with distributed ESSs, demonstrating that only the Nucleolus lies in the Core and provides a stabilizing solution to allocate the extra benefit/gain when the game is not convex. Moreover, the work in [29] presents a non-convex game example where the Shapley value cannot provide a stable value-sharing mechanism for the grand coalition. A stabilizing value-sharing mechanism that lies in the Core of the game is then found by applying the worst-case excess minimization concept. A fair and stabilizing value-sharing mechanism can be reached if the constraints in the worst-case excess minimization problem are satisfied. However, while relying on worst-case excess minimization can effectively allocate the extra benefit/gain among the coalition members, such an approach is associated with many constraints. The number of constraints grows exponentially with the number of coalition members, which may constitute a potential barrier and limit the application of this approach to smaller games [29].
It can also be important and useful to develop mechanisms capable of ensuring the convexity of coalitional games. This could be achieved by identifying the potential points or parameters in which cooperation might fail for a variety of player numbers and cause the game to become non-convex [9,23]. Then, optimization problems could be solved by imposing superadditivity and convexity constraints that facilitate or enable the rationality of solution concepts and stability of cooperation.
6.2. Coalition Formation
In practical applications for P2P energy trading, the grand coalition may not form because players can refuse to join the grand or minor coalitions due to a lack of compatibility with their fundamental goal or even lack of access to accurate, transparent, and complete information regarding various network parameters and player preferences [33,36]. Therefore, it may be necessary to implement protocols and establish a coordinating entity for effective cooperation [9].
The introduction of multiple objectives and a reduction in assumptions in terms of information accuracy, player participation, and coalition formation can be valuable for the study of player behavior in a more realistic P2P energy trading environment. Moreover, most works available in the literature only consider static problems of cooperation. It can be interesting to model the game-theoretic energy trading as a more dynamic problem where player strategies and environmental conditions change and evolve over time. Solving such dynamic cooperative problems can constitute a challenging and demanding task, requiring new mechanisms and further research work to properly establish them [134]. Some players may also possess certain requirements related to their contribution to the coalition and the minimal benefits they receive from it [9,23], increasing the challenge of forming stable coalitions.
6.3. Game Scalability
A major known challenge when it comes to the use and application of coalitional games is the scalability of the allocation solution concepts, which leads to a high computational burden in games with a large number of players, and its computation can be unfeasible in highly complex systems [29]. This is because with the Shapley value, the number of possible coalitions increases exponentially with the number of players, and the number of all possible orders of players joining coalitions increases factorially as seen in (4) [42,65]. For small games with a relatively low number of players (e.g., up to six players), the Shapley value can be an effective and reliable solution concept for analyzing the behavior of players based on all possible orders of players joining the coalitions. However, a highly complex system such as a smart city ecosystem consisting of many players participating in a P2P energy trading market, in which the size of each individual player is negligibly small compared to the large size of the market, can create major challenges. In such settings, the consideration of all possible orders of players becomes a substantial computational burden with long computation times. This may be infeasible for applications in P2P energy trading involving many players in intraday or day-ahead markets.
One solution to overcome this problem is the use of the Aumann–Shapley value as the allocation solution concept for cooperative games with many players. This allows the computational burden to be significantly decreased and grants scalability because it only considers infinitesimal segments of players, as briefly explained in Section 3.3.2. Essentially, it provides an allocation solution that is indifferent to player joining order and independent of the number and size of players participating in P2P energy trading [9,74]. In [75], Faria et al. recommended the use of the Aumann–Shapley value as the allocation method to provide computational efficiency and tested it for firm-energy rights in a power system with 100 hydro plants.
Another potential solution is to rely on the Benders decomposition method to overcome the complexity and combinatorial explosion. It has been successfully used to find the Nucleolus solution of cooperative games [136,137]. This method may provide the necessary computational efficiency to solve a game with various objectives and many possible scenarios. In [136], Du et al. relied on a Benders decomposition algorithm to find the Nucleolus solution for a coalitional game with 30 MGs simulated in an IEEE 123-bus distribution system. In certain cases, allocation solution concepts such as the Nucleolus may fail entirely in games with many players. For instance, in [137], Freire et al. failed to compute the Nucleolus solution for the share of quotas for an RES pool with 50 different companies. Nonetheless, the authors overcame this problem by implementing an MILP-based Benders decomposition method to efficiently find the Nucleolus quota allocation that maximizes the worst-case gain among all possible coalitions.
Other authors, such as Sharma and Abhyankar [138], suggested a sequential Shapley value method to allocate power losses among generators and loads in radial distribution systems with reduced computational burden while satisfying the axioms of fairness. Furthermore, in [139], Han et al. proposed an approach based on the K-means clustering method to reduce the computational time in a cooperative scheme for P2P energy sharing among 200 players. The K-means clustering algorithm is also applied to the profiles of prosumers in [29], being able to remove several redundant constraints and successfully make the problem computationally tractable.
In addition, increased computational burden can also be associated with the way coalitional games are formulated and modeled in practical applications. In power system applications, coalitional game models generally involve optimization problems with many technical limits and constraints that need to be solved several times for each possible player coalition or scenario. This significantly increases the overall complexity of the model and, thus, the computational power needed to solve it. There is a need for further research and work to develop techniques to formulate and solve larger-scale coalitional models with many players in a more efficient way. For instance, this may include decomposition methods [136,137] or the approximation of allocation rules and coalition structures [138,139].
6.4. Player Rationality and Complete Information
In cooperative games, or game theory in general, it is assumed that players are rational with the goal of maximizing their utility or payoff. This assumption of player rationality is not guaranteed in practical scenarios when the game involves human entities, in which the decision-making process is heavily affected by personal interests and emotions [140]. Moreover, it may be necessary to introduce appropriate penalties and jeopardize the interests and preferences of players to guarantee the overall rationality of the grand coalition and solution concepts [134].
Another assumption is the access to perfect and complete information by all players participating in the game, which may not occur in a practical scenario involving human entities. The loss of complete information can degrade the outcome of the game due to business confidentiality agreements, potential communication failures, or players not being willing to share private data, resulting in irrational solutions and players breaking cooperation. Moreover, complete information is crucial to maximize social welfare in markets for P2P energy trading [11]. Without perfect and complete information, players may have an incentive to cheat and manipulate data for their own benefit [78]. For instance, in highly competitive settings such as LEMs, certain players may be prone to provide false reports regarding their market preferences and data in terms of energy generation, load, or fuel costs in order to manipulate the allocation rules in their favor and obtain a larger payoff. In such practical applications, it can be difficult to gather accurate information from a large number of independent players without safeguards against data manipulation and misreporting [9,78]. In particular, the Kernel requires perfect information between players for the coalition creation because of the excess of the different coalitions. Without perfect information (i.e., information asymmetry), the allocation of the Kernel becomes biased or unfair for certain players [78].
Guaranteeing perfect and complete information in practical applications of coalitional games can constitute a major challenge and become detrimental to a sustainable outcome. This is because the uncertainty of load demand and renewable generation from solar or wind power generators is difficult to predict with a high level of accuracy or impossible to predict on an hourly basis without prediction errors [30,38]. However, studies in the literature have shown that the impact of uncertainties on the outcome of a coalitional game can be insignificant. In particular, in [30], Han et al. evaluated the impact of uncertainty on energy cost savings of players in a coalitional game model. The study showed that the addition of prediction errors led to a relatively small reduction in energy cost savings of 2% to 3% in the low-uncertainty case and 4% to 5% in the high-uncertainty case. This is because both coalitional energy cost and individual player energy cost are affected by the uncertainties in the same manner, remaining relatively unchanged with an increase in the number of players [30]. On the other hand, in [32], Feng et al. assessed the impact of uncertainties in power generated from PV systems, showing a loss of total realized payoff for the grand coalition when the uncertainties of output power are neglected. This is a result of the maximization of the expected payoff for the grand coalition performed by the proposed model, which minimizes the risk of loss when output power deviates from the forecasted values. The use of ESSs to store surplus renewable generation can also help mitigate potential uncertainties of renewable generation from solar or wind power generators, especially in SGs and MG systems [38].
There should be a transparent way to successfully collect and distribute accurate information regarding various network parameters and player preferences, as well as regulate and develop the processes involved in coalition creation [78]. This can mitigate inaccurate data reports and malicious manipulation from certain players intending to gain a competitive advantage of the cost and benefit allocation over other players, which helps establish social trust between players. Fortunately, these problems can be mitigated in SG and MG applications with the integration of various ICTs such as automated energy management systems, smart meters, and smart appliances. These systems enable access to data reporting and real-time information regarding energy consumption and provide the tools to optimize or reduce it, allowing human users to make more rational and informed decisions [8].
7. Conclusions
Game-theoretic models and mechanisms allow the analysis of strategic decisions in competitive settings. In particular, coalitional games can be effective in the design of schemes for P2P energy trading to encourage participants to trade energy with one another and obtain a fair and sustainable outcome. While the literature review in this work showed that both cooperative/coalitional and non-cooperative games are widely used in P2P energy trading applications, non-cooperative games may not achieve sustainability because the success of one player occurs at the expense of another player.
The contents of this work have addressed various aspects related to coalitional game approaches for sustainable P2P energy trading and the major challenges of implementing this type of approach in practical power system applications. Therefore, this work started by identifying relevant literature works that successfully implemented coalitional games to improve P2P energy trading and energy management in power system applications. This was accomplished through a literature review of the three main classes of coalitional games, namely canonical coalition games, coalition formation games, and coalition graph games. The literature review showed that canonical coalition games and coalition formation games are the most common classes, allowing the effective study of the stability of the grand coalition and the formation of appropriate coalitional structures and their properties. On the other hand, coalition graph games are still relatively scarce in P2P energy trading and energy management applications. In view of this, the stability, payoff, formation, and division of coalitions are addressed by providing a comprehensive overview of commonly used solution concepts for coalitional games and a discussion of their most important properties. This work has also addressed the potential of coalitional games to contribute towards sustainability in power system applications and proposed certain conditions that P2P energy trading should satisfy to be considered sustainable. Finally, a case study was presented to illustrate how the various aspects of coalitional games can be successfully implemented in power system applications for P2P energy trading. The benefits of cooperation among communities with the goal of minimizing the total fuel costs and emissions have been demonstrated through both three-player and four-player examples, being modeled as a CEED problem. The stability of the grand coalition was analyzed using the Core, and the fair allocation of profits among the communities was performed by relying on the Shapley value and the Nucleolus. In this case study, the weighted Shapley value was proposed to effectively allocate the profits among the communities in accordance with their relative level of sustainability, which was dependent on the type of generation unit used by each community. However, there are some challenges and limitations associated with the formulation and implementation of game-theoretic approaches and solution concepts in practical applications. In particular, the use and application of coalitional games in highly complex systems with many players can be problematic, resulting in non-convex games without rational solutions.
The case study carried out in this work allowed the demonstration of the fragility associated with the property of convexity, as this fragility led to potential issues with the stability of cooperation and rationality of the payoff allocation solutions under certain changes in network parameters and player preferences. Other challenges may include assumptions of player rationality and complete information, as well as major scalability issues that lead to a high computational burden. Nevertheless, potential solutions have been proposed in the literature (e.g., integration of ICTs, decomposition methods, or approximation of allocation rules and coalition structures) and can be used to mitigate these challenges. The sustainability of P2P energy trading should be facilitated by relying on a central entity or community manager to anticipate player decisions and coordinate the energy transactions if stable cooperation under complete information can be guaranteed. Despite the challenges in need of solving, the use of coalitional game theory in power system applications constitutes a valuable tool for assisting with decision making and evaluating the stability and rationality of cooperation. It is particularly important to achieve a fair allocation of profits or costs in scenarios involving a large amount of monetary value.
Future research should focus on the development of mechanisms to identify the potential points or parameters that might jeopardize the stability of cooperation and cause the game to become non-convex. This could allow optimization problems to be solved in a way that enables the rationality of solution concepts and the stability of cooperation.
Author Contributions
Conceptualization, F.B., Á.G., M.G. and P.C.; methodology, F.B.; validation, Á.G., M.G. and P.C; formal analysis, F.B.; investigation, F.B.; resources, M.G. and P.C.; writing—original draft preparation, F.B.; writing—review and editing, F.B., Á.G., M.G. and P.C.; visualization, Á.G.; supervision, Á.G., M.G. and P.C.; project administration, Á.G., M.G. and P.C.; funding acquisition, F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Portuguese Foundation for Science and Technology (FCT) under the Ph.D. research grant 2020.07048.BD.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Eid, C.; Codani, P.; Perez, Y.; Reneses, J.; Hakvoort, R. Managing electric flexibility from Distributed Energy Resources: A review of incentives for market design. Renew. Sustain. Energy Rev. 2016, 64, 237–247. [Google Scholar] [CrossRef]
- Vahl, F.P.; Rüther, R.; Filho, N.C. The influence of distributed generation penetration levels on energy markets. Energy Policy 2013, 62, 226–235. [Google Scholar] [CrossRef]
- Zhu, J. Optimization of Power System Operation, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- World Cities Report 2020: The Value of Sustainable Urbanization. United Nations Human Settlements Programme (UN-Habitat). 2020. Available online: https://unhabitat.org/sites/default/files/2020/10/wcr_2020_report.pdf (accessed on 20 October 2023).
- Kotilainen, K. Energy Prosumers’ Role in the Sustainable Energy System. In Affordable and Clean Energy. Encyclopedia of the UN Sustainable Development Goals; Leal Filho, W., Azul, A., Brandli, L., Özuyar, P., Wall, T., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Zheng, B.; Wei, W.; Chen, Y.; Wu, Q.; Mei, S. A peer-to-peer energy trading market embedded with residential shared energy storage units. Appl. Energy 2022, 308, 118400. [Google Scholar] [CrossRef]
- Bandeiras, F.; Gomes, Á.; Gomes, M.; Coelho, P. Exploring Energy Trading Markets in Smart Grid and Microgrid Systems and Their Implications for Sustainability in Smart Cities. Energies 2023, 16, 801. [Google Scholar] [CrossRef]
- Churkin, A.; Bialek, J.; Pozo, D.; Sauma, E.; Korgin, N. Review of Cooperative Game Theory applications in power system expansion planning. Renew. Sustain. Energy Rev. 2021, 145, 111056. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Debbah, M.; Hjorungnes, A.; Basar, T. Coalitional game theory for communication networks. IEEE Signal Process. Mag. 2009, 26, 77–97. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Mohsenian-Rad, H.; Saha, T.; Poor, H.V.; Wood, K.L. Transforming Energy Networks via Peer-to-Peer Energy Trading: The potential of game-theoretic approaches. IEEE Signal Process. Mag. 2018, 35, 90–111. [Google Scholar] [CrossRef]
- Gautam, M.; Ben-Idris, M. Coalitional Game Theory in Power Systems: Applications, Challenges, and Future Directions, Systems and Control. In Proceedings of the 2023 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 13–14 February 2023. [Google Scholar] [CrossRef]
- Navon, A.; Ben Yosef, G.; Machlev, R.; Shapira, S.; Roy Chowdhury, N.; Belikov, J.; Orda, A.; Levron, Y. Applications of Game Theory to Design and Operation of Modern Power Systems: A Comprehensive Review. Energies 2020, 13, 3982. [Google Scholar] [CrossRef]
- Orchestrating Infrastructure for Sustainable Smart Cities, International Electrotechnical Commission (IEC). 2014. Available online: https://www.iec.ch/basecamp/orchestrating-infrastructure-sustainable-smart-cities (accessed on 30 November 2023).
- Maria, T.A.; Niamh, M. The Concept of Sustainability in Smart City Definitions. Front. Built Environ. 2020, 6, 77. [Google Scholar] [CrossRef]
- Basiago, A.D. Economic, social, and environmental sustainability in development theory and urban planning practice. Environmentalist 1998, 19, 145–161. [Google Scholar] [CrossRef]
- Bandeiras, F.; Pinheiro, E.; Gomes, M.; Coelho, P.; Fernandes, J. Review of the cooperation and operation of microgrid clusters. Renew. Sustain. Energy Rev. 2020, 133, 110311. [Google Scholar] [CrossRef]
- Javed, H.; Irfan, M.; Shehzad, M.; Muqeet, H.A.; Akhter, J.; Dagar, V.; Guerrero, J.M. Recent Trends, Challenges, and Future Aspects of P2P Energy Trading Platforms in Electrical-Based Networks Considering Blockchain Technology: A Roadmap Toward Environmental Sustainability. Front. Energy Res. 2022, 10, 134. [Google Scholar] [CrossRef]
- Gilles, R.P. The Cooperative Game Theory of Networks and Hierarchies; Theory and Decision Library C, 44; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Seifi, S.; Crowther, D. Using Game Theory to Develop Sustainability Strategies in an Era of Resource Depletion. Ind. Eng. Manag. 2018, 7, 1000240. [Google Scholar] [CrossRef]
- Stewart, A.J.; Plotkin, J.B. Extortion and cooperation in the Prisoner’s Dilemma. Proc. Natl. Acad. Sci. USA 2012, 109, 10134–10135. [Google Scholar] [CrossRef] [PubMed]
- Tohidi, Y.; Hesamzadeh, M.R. Multi-Regional Transmission Planning as a Non-Cooperative Decision-Making. IEEE Trans. Power Syst. 2014, 29, 2662–2671. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Morstyn, T.; McCulloch, M.D.; Poor, H.V.; Wood, K.L. A motivational game-theoretic approach for peer-to-peer energy trading in the smart grid. Appl. Energy 2019, 243, 10–20. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Smith, D.B.; Hassan, N.U.; Poor, H.V. A canonical coalitional game theoretic approach for energy management for nanogrids. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Du, Y.; Li, F.; Kou, X.; Pei, W. Coordinating multi-microgrid operation within distribution system: A cooperative game approach. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar] [CrossRef]
- Chiş, A.; Koivunen, V. Coalitional Game-Based Cost Optimization of Energy Portfolio in Smart Grid Communities. IEEE Trans. Smart Grid 2019, 10, 1960–1970. [Google Scholar] [CrossRef]
- Acuña, L.G.; Ríos, D.R.; Arboleda, C.P.; Ponzón, E.G. Cooperation model in the electricity energy market using bi-level optimization and Shapley value. Oper. Res. Perspect. 2018, 5, 161–168. [Google Scholar] [CrossRef]
- Chakraborty, P.; Baeyens, E.; Poolla, K.; Khargonekar, P.P.; Varaiya, P. Sharing Storage in a Smart Grid: A Coalitional Game Approach. IEEE Trans. Smart Grid 2019, 10, 4379–4390. [Google Scholar] [CrossRef]
- Safdarian, A.; Astero, P.; Baranauskas, M.; Keski-Koukkari, A.; Kulmala, A. Coalitional Game Theory Based Value Sharing in Energy Communities. IEEE Access 2021, 9, 78266–78275. [Google Scholar] [CrossRef]
- Han, L.; Morstyn, T.; McCulloch, M. Incentivizing Prosumer Coalitions with Energy Management Using Cooperative Game Theory. IEEE Trans. Power Syst. 2019, 34, 303–313. [Google Scholar] [CrossRef]
- Ma, L.; Liu, N.; Zhang, J.; Wang, L. Real-Time Rolling Horizon Energy Management for the Energy-Hub-Coordinated Prosumer Community from a Cooperative Perspective. IEEE Trans. Power Syst. 2019, 34, 1227–1242. [Google Scholar] [CrossRef]
- Feng, C.; Wen, F.; You, S.; Li, Z.; Shahnia, F.; Shahidehpour, M. Coalitional Game-Based Transactive Energy Management in Local Energy Communities. IEEE Trans. Power Syst. 2020, 35, 1729–1740. [Google Scholar] [CrossRef]
- Mei, J.; Chen, C.; Wang, J.; Kirtley, J.L. Coalitional game theory based local power exchange algorithm for networked microgrids. Appl. Energy 2019, 239, 133–141. [Google Scholar] [CrossRef]
- Essayeh, C.; El Fenni, M.R.; Dahmouni, H. Optimization of energy exchange in microgrid networks: A coalition formation approach. Prot. Control. Mod. Power Syst. 2019, 4, 24. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V. Coalitional Game Theory for Cooperative Micro-Grid Distribution Networks. In Proceedings of the 2011 IEEE International Conference on Communications Workshops (ICC), Kyoto, Japan, 5–9 June 2011. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Azim, M.I.; Morstyn, T.; Poor, H.V.; Niyato, D.; Bean, R. A coalition formation game framework for peer-to-peer energy trading. Appl. Energy 2020, 261, 114436. [Google Scholar] [CrossRef]
- Malik, S.; Duffy, M.; Thakur, S.; Breslin, J.G. Fractional Hedonic Coalition Formation Game for Peer to Peer Energy Trading in a Microgrid. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Karimi, H.; Jadid, S. A strategy-based coalition formation model for hybrid wind/PV/FC/MT/DG/battery multi-microgrid systems considering demand response programs. Int. J. Electr. Power Energy Syst. 2022, 136, 107642. [Google Scholar] [CrossRef]
- Marzband, M.; Ardeshiri, R.R.; Moafi, M.; Uppal, H. Distributed generation for economic benefit maximization through coalition formation–based game theory concept. Int. Trans. Electr. Energy Syst. 2017, 27, e2313. [Google Scholar] [CrossRef]
- Ni, J.; Ai, Q. Economic power transaction using coalitional game strategy in micro-grids. IET Gener. Transm. Distrib. 2016, 10, 10–18. [Google Scholar] [CrossRef]
- Moafi, M.; Ardeshiri, R.R.; Mudiyanselage, M.W.; Marzband, M.; Abusorrah, A.; Rawa, M.; Guerrero, J.M. Optimal coalition formation and maximum profit allocation for distributed energy resources in smart grids based on cooperative game theory. Int. J. Electr. Power Energy Syst. 2023, 144, 108492. [Google Scholar] [CrossRef]
- Zhong, X.; Zhong, W.; Liu, Y.; Yang, C.; Xie, S. A communication-efficient coalition graph game-based framework for electricity and carbon trading in networked energy hubs. Appl. Energy 2023, 329, 120221. [Google Scholar] [CrossRef]
- Azim, M.I.; Tushar, W.; Saha, T.K. Coalition Graph Game-Based P2P Energy Trading with Local Voltage Management. IEEE Trans. Smart Grid 2021, 12, 4389–4402. [Google Scholar] [CrossRef]
- Suh, J.; Yoon, S.-G. Profit-Sharing Rule for Networked Microgrids Based on Myerson Value in Cooperative Game. IEEE Access 2021, 9, 5585–5597. [Google Scholar] [CrossRef]
- Moghateli, F.; Taher, S.A.; Karimi, A.; Shahidehpour, M. Multi-objective design method for construction of multi-microgrid systems in active distribution networks. IET Smart Grid 2020, 3, 331–341. [Google Scholar] [CrossRef]
- Chiu, W.-Y.; Sun, H.; Vincent Poor, H. A Multiobjective Approach to Multimicrogrid System Design. IEEE Trans. Smart Grid 2015, 6, 2263–2272. [Google Scholar] [CrossRef]
- Cui, S.; Xiao, J.-W. Game-based peer-to-peer energy sharing management for a community of energy buildings. Int. J. Electr. Power Energy Syst. 2020, 123, 106204. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Luo, F.; Chen, G.; Dong, Z.Y.; Huang, T. Electric Vehicles Charging Dispatch and Optimal Bidding for Frequency Regulation Based on Intuitionistic Fuzzy Decision Making. IEEE Trans. Fuzzy Syst. 2023, 31, 596–608. [Google Scholar] [CrossRef]
- Paudel, A.; Chaudhari, K.; Long, C.; Gooi, H.B. Peer-to-Peer Energy Trading in a Prosumer-Based Community Microgrid: A Game-Theoretic Model. IEEE Trans. Ind. Electron. 2019, 66, 6087–6097. [Google Scholar] [CrossRef]
- Kim, B.; Ren, S.; van der Schaar, M.; Lee, J. Bidirectional Energy Trading and Residential Load Scheduling with Electric Vehicles in the Smart Grid. IEEE J. Sel. Areas Commun. 2013, 31, 1219–1234. [Google Scholar] [CrossRef]
- Zheng, X.; Li, Q.; Bai, C.; Nie, Y.; Huang, C. Energy trading management based on Stackelberg game theory to increase independence of microgrids. Energy Rep. 2022, 8, 771–779. [Google Scholar] [CrossRef]
- Hua, W.; Xiao, H.; Pei, W.; Chiu, W.-Y.; Jiang, J.; Sun, H.; Matthews, P. Transactive Energy and Flexibility Provision in Multi-microgrids Using Stackelberg Game. CSEE J. Power Energy Syst. 2023, 9, 505–515. [Google Scholar] [CrossRef]
- Erol, Ö.; Filik, Ü.B. A Stackelberg game approach for energy sharing management of a microgrid providing flexibility to entities. Appl. Energy 2022, 316, 118944. [Google Scholar] [CrossRef]
- Malik, S.; Duffy, M.; Thakur, S.; Hayes, B.; Breslin, J. A priority-based approach for peer-to-peer energy trading using cooperative game theory in local energy community. Int. J. Electr. Power Energy Syst. 2022, 137, 107865. [Google Scholar] [CrossRef]
- Osborne, M.J. An Introduction to Game Theory; Department of Economics, University of Toronto: Toronto, ON, Canada, 2000. [Google Scholar]
- Huang, H.; Nie, S.; Lin, J.; Wang, Y.; Dong, J. Optimization of Peer-to-Peer Power Trading in a Microgrid with Distributed PV and Battery Energy Storage Systems. Sustainability 2020, 12, 923. [Google Scholar] [CrossRef]
- Modarresi, J. Coalitional game theory approach for multi-microgrid energy systems considering service charge and power losses. Sustain. Energy Grids Netw. 2022, 31, 100720. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V.; Basar, T. Game-Theoretic Methods for the Smart Grid: An Overview of Microgrid Systems, Demand-Side Management, and Smart Grid Communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]
- Guajardo, M.; Jörnsten, K. Common mistakes in computing the nucleolus. Eur. J. Oper. Res. 2015, 241, 931–935. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Smith, D.; Poor, H.V. Peer-to-Peer Trading in Electricity Networks: An Overview. IEEE Trans. Smart Grid 2020, 11, 3185–3200. [Google Scholar] [CrossRef]
- Yap, Y.-H.; Tan, W.-S.; Wong, J.; Ahmad, N.A.; Wooi, C.-L.; Wu, Y.-K.; Ariffin, A.E. A two-stage multi microgrids p2p energy trading with motivational game-theory: A case study in malaysia. IET Renew. Power Gener. 2021, 15, 2615–2628. [Google Scholar] [CrossRef]
- Shapley, L.S. Cores of Convex Games. Int. J. Game Theory 1971, 1, 11–26. [Google Scholar] [CrossRef]
- Gillies, D.B. Solutions to general non-zero-sum games. In Contributions to the Theory of Games IV; Tucker, A.W., Luce, R.D., Eds.; Annals of Mathematics Studies, 40; Princeton University Press: Princeton, NJ, USA, 1959; pp. 47–85. [Google Scholar] [CrossRef]
- Moncecchi, M.; Meneghello, S.; Merlo, M. A Game Theoretic Approach for Energy Sharing in the Italian Renewable Energy Communities. Appl. Sci. 2020, 10, 8166. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for n-person Games. In Contributions to the Theory of Games; Kuhn, H.W., Tucker, A.W., Eds.; Annals of Mathematical Studies, 28; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–317. [Google Scholar] [CrossRef]
- Hausken, K.; Mohr, M. The value of a player in n-person games. Soc. Choice Welf. 2001, 18, 465–483. [Google Scholar] [CrossRef]
- van den Brink, R. Null or nullifying players: The difference between the Shapley value and equal division solutions. J. Econ. Theory 2007, 136, 767–775. [Google Scholar] [CrossRef]
- Pinto de Moura, G.N.; Legey, L.F.L.; Howells, M. A Brazilian perspective of power systems integration using OSeMOSYS SAMBA—South America Model Base—And the bargaining power of neighbouring countries: A cooperative games approach. Energy Policy 2018, 115, 470–485. [Google Scholar] [CrossRef]
- Nowak, A.S.; Radzik, T. On axiomatizations of the weighted Shapley values. Games Econ. Behav. 1995, 8, 389–405. [Google Scholar] [CrossRef]
- Chun, Y. On the symmetric and weighted shapley values. Int. J. Game Theory 1991, 20, 183–190. [Google Scholar] [CrossRef]
- Pal, S.V.; Aijaz, A.; Manoharrao, J.K. Weighted shapley value: A cooperative game theory for loss allocation in distribution systems. Front. Energy Res. 2023, 11, 1129846. [Google Scholar] [CrossRef]
- Casajus, A. Weakly balanced contributions and the weighted Shapley values. J. Math. Econ. 2021, 94, 102459. [Google Scholar] [CrossRef]
- Molina, Y.P.; Saavedra, O.R.; Amarís, H. Transmission Network Cost Allocation Based on Circuit Theory and the Aumann-Shapley Method. IEEE Trans. Power Syst. 2013, 28, 4568–4577. [Google Scholar] [CrossRef]
- Junqueira, M.; da Costa, L.C.; Barroso, L.A.; Oliveira, G.C.; Thome, L.M.; Pereira, M.V. An Aumann-Shapley Approach to Allocate Transmission Service Cost Among Network Users in Electricity Markets. IEEE Trans. Power Syst. 2007, 22, 1532–1546. [Google Scholar] [CrossRef]
- Faria, E.; Barroso, L.A.; Kelman, R.; Granville, S.; Pereira, M.V. Allocation of Firm-Energy Rights among Hydro Plants: An Aumann–Shapley Approach. IEEE Trans. Power Syst. 2009, 24, 541–551. [Google Scholar] [CrossRef]
- Banez-Chicharro, F.; Olmos, L.; Ramos, A.; Latorre, J.M. Estimating the benefits of transmission expansion projects: An Aumann-Shapley approach. Energy 2017, 118, 1044–1054. [Google Scholar] [CrossRef]
- Schmeidler, D.D. The nucleolus of a characteristic function game. SIAM J. Appl. Math. 1969, 17, 1163–1170. [Google Scholar] [CrossRef]
- Evans, F.; Zolezzi, J.M.; Rudnick, H. Cost assignment model for electrical transmission system expansion: An approach through the Kernel theory. IEEE Trans. Power Syst. 2003, 18, 625–632. [Google Scholar] [CrossRef]
- Espe, E.; Potdar, V.; Chang, E. Prosumer Communities and Relationships in Smart Grids: A Literature Review, Evolution and Future Directions. Energies 2018, 11, 2528. [Google Scholar] [CrossRef]
- Taik, A.; Nour, B.; Cherkaoui, S. Empowering Prosumer Communities in Smart Grid with Wireless Communications and Federated Edge Learning. IEEE Wirel. Commun. 2021, 28, 26–33. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Smith, D.B.; Poor, H.V. Price Discrimination for Energy Trading in Smart Grid: A Game Theoretic Approach. IEEE Trans. Smart Grid 2017, 8, 1790–1801. [Google Scholar] [CrossRef]
- Lyu, C.; Jia, Y.; Xu, Z. Fully decentralized peer-to-peer energy sharing framework for smart buildings with local battery system and aggregated electric vehicles. Appl. Energy 2021, 299, 117243. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, X.; Qian, L.; Tsang, D.H.K.; Song, W.-Z.; Yu, L. Optimal Pricing and Energy Scheduling for Hybrid Energy Trading Market in Future Smart Grid. IEEE Trans. Ind. Inform. 2015, 11, 1585–1596. [Google Scholar] [CrossRef]
- Sumesh, S.; Krishna, A.; Potdar, V.; Nimmagadda, S. On framework development for the dynamic prosumer coalition in a smart grid and its evaluation by analytic tools. Procedia Comput. Sci. 2019, 159, 892–901. [Google Scholar] [CrossRef]
- Bayram, I.S.; Shakir, M.Z.; Abdallah, M.; Qaraqe, K. A Survey on Energy Trading in Smart Grid. In Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Atlanta, GA, USA, 3–5 December 2014; pp. 258–262. [Google Scholar] [CrossRef]
- Lee, W.; Xiang, L.; Schober, R.; Wong, V.W.S. Direct electricity trading in smart grid: A coalitional game analysis. IEEE J. Sel. Areas Commun. 2014, 32, 1398–1411. [Google Scholar] [CrossRef]
- Erli, G.; Takahasi, K.; Chen, L.; Kurihara, I. Transmission expansion cost allocation based on cooperative game theory for congestion relief. Int. J. Electr. Power Energy Syst. 2005, 27, 61–67. [Google Scholar] [CrossRef]
- Banez-Chicharro, F.; Olmos, L.; Ramos, A.; Latorre, J.M. Beneficiaries of transmission expansion projects of an expansion plan: An Aumann-Shapley approach. Appl. Energy 2017, 195, 382–401. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Cooperative Planning of Renewable Generations for Interconnected Microgrids. IEEE Trans. Smart Grid 2016, 7, 2486–2496. [Google Scholar] [CrossRef]
- Yu, R.; Ding, J.; Zhong, W.; Liu, Y.; Xie, S. PHEV Charging and Discharging Cooperation in V2G Networks: A Coalition Game Approach. IEEE Internet Things J. 2014, 1, 578–589. [Google Scholar] [CrossRef]
- Karimizadeh, K.; Soleymani, S.; Faghihi, F. Optimal placement of DG units for the enhancement of MG networks performance using coalition game theory. IET Gener. Transm. Distrib. 2020, 14, 853–862. [Google Scholar] [CrossRef]
- Gautam, M.; Bhusal, N.; Benidris, M. A cooperative game theory-based approach to sizing and siting of distributed energy resources. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ali, L.; Muyeen, S.; Bizhani, H.; Ghosh, A. Optimal planning of clustered microgrid using a technique of cooperative game theory. Electr. Power Syst. Res. 2020, 183, 106262. [Google Scholar] [CrossRef]
- Pahlavanhoseini, A.; Sepasian, M.S. Optimal planning of PEV fast charging stations using nash bargaining theory. J. Energy Storage 2019, 25, 100831. [Google Scholar] [CrossRef]
- Han, X.; Ji, T.; Zhao, Z.; Zhang, H. Economic evaluation of batteries planning in energy storage power stations for load shifting. Renew. Energy 2015, 78, 643–647. [Google Scholar] [CrossRef]
- Shaloudegi, K.; Madinehi, N.; Hosseinian, S.; Abyaneh, H.A. A novel policy for locational marginal price calculation in distribution systems based on loss reduction allocation using game theory. IEEE Trans. Power Syst. 2012, 27, 811–820. [Google Scholar] [CrossRef]
- Querini, P.L.; Chiotti, O.; Fernadez, E. Cooperative energy management system for networked microgrids. Sustain. Energy Grids Netw. 2020, 23, 100371. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, K.; Wang, H.; Hu, J.; Zhou, B.; Zhang, Y.; Qiu, J. Game-theoretic planning for integrated energy system with independent participants considering ancillary services of power-to-gas stations. Energy 2019, 176, 249–264. [Google Scholar] [CrossRef]
- Pourahmadi, F.; Fotuhi-Firuzabad, M.; Dehghanian, P. Identification of critical components in power systems: A game theory application. In Proceedings of the 2016 IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Gautam, M.; Bhusal, N.; Thapa, J.; Benidris, M. A cooperative game theory-based approach to formulation of distributed slack buses. Sustain. Energy Grids Netw. 2022, 32, 100890. [Google Scholar] [CrossRef]
- Gautam, M.; Bhusal, N.; Benidris, M. A cooperative game theory-based approach to under-frequency load shedding control. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Han, L.; Morstyn, T.; McCulloch, M.D. Scaling up cooperative game theory-based energy management using prosumer clustering. IEEE Trans. Smart Grid 2020, 12, 289–300. [Google Scholar] [CrossRef]
- Kumar, N.; Misra, S.; Chilamkurti, N.; Lee, J.H.; Rodrigues, J.J.P.C. Bayesian coalition negotiation game as a utility for secure energy management in a vehicles-to-grid environment. IEEE Trans. Dependable Secur. Comput. 2016, 13, 133–145. [Google Scholar] [CrossRef]
- Hasan, K.N.; Preece, R.; Milanovic, J.V. Application of game theoretic approaches for identification of critical parameters affecting power system small-disturbance stability. Int. J. Electr. Power Energy Syst. 2018, 97, 344–352. [Google Scholar] [CrossRef]
- Gautam, M.; Benidris, M. A graph theory and coalitional game theory-based pre-positioning of movable energy resources for enhanced distribution system resilience. Sustain. Energy Grids Netw. 2023, 35, 101095. [Google Scholar] [CrossRef]
- Peer-to-Peer Electricity Trading: Innovation Landscape Brief. International Renewable Energy Agency (IRENA). 2020. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2020/Jul/IRENA_Peer-to-peer_electricity_trading_2020.pdf (accessed on 20 October 2023).
- Raja, A.A.; Grammatico, S. Payoff Distribution in Robust Coalitional Games on Time-Varying Networks. IEEE Trans. Control Netw. Syst. 2022, 9, 511–520. [Google Scholar] [CrossRef]
- Pinto, T.; Wooldridge, M.; Vale, Z. Consumer Flexibility Aggregation Using Partition Function Games with Non-Transferable Utility. IEEE Access 2021, 9, 51519–51535. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Q.; Huang, Y.; Du, P. Peer-to-peer energy trading market considering renewable energy uncertainty and participants’ individual preferences. Int. J. Electr. Power Energy Syst. 2023, 148, 108931. [Google Scholar] [CrossRef]
- Belgioioso, G.; Ananduta, W.; Grammatico, S.; Ocampo-Martinez, C. Energy Management and Peer-to-peer Trading in Future Smart Grids: A Distributed Game-Theoretic Approach. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; pp. 1324–1329. [Google Scholar] [CrossRef]
- Durvasulu, V.; Hansen, T.M. Market-based generator cost functions for power system test cases. IET Cyber-Phys. Syst. Theory Appl. 2018, 3, 194–205. [Google Scholar] [CrossRef]
- Liu, B.; Liu, F.; Wei, W.; Wang, J. Estimating B-coefficients of power loss formula considering volatile power injections: An enhanced least square approach. IET Gener. Transm. Distrib. 2018, 12, 2854–2860. [Google Scholar] [CrossRef]
- Raj, V.M.; Chanana, S. Fuel Cost Optimization of an Islanded Microgrid Considering Environmental Impact. J. Clean Energy Technol. 2016, 4, 120–124. [Google Scholar] [CrossRef]
- McLarty, D.; Panossian, N.; Jabbari, F.; Traverso, A. Dynamic economic dispatch using complementary quadratic programming. Energy 2019, 166, 755–764. [Google Scholar] [CrossRef]
- Apostolopoulos, T.; Vlachos, A. Application of the Firefly Algorithm for Solving the Economic Emissions Load Dispatch Problem. Int. J. Comb. 2010, 2011, 523806. [Google Scholar] [CrossRef]
- Mohapatra, P. Combined economic emission dispatch in hybrid power systems using competitive swarm optimization. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 8955–8971. [Google Scholar] [CrossRef]
- Nagarajan, K.; Rajagopalan, A.; Angalaeswari, S.; Natrayan, L.; Mammo, W.D. Combined Economic Emission Dispatch of Microgrid with the Incorporation of Renewable Energy Sources Using Improved Mayfly Optimization Algorithm. Comput. Intell. Neurosci. 2022, 2022, 6461690. [Google Scholar] [CrossRef]
- Güvenç, U.; Sönmez, Y.; Duman, S.; Yörükeren, N. Combined economic and emission dispatch solution using gravitational search algorithm. Sci. Iran. 2012, 19, 1754–1762. [Google Scholar] [CrossRef]
- Rezaie, H.; Kazemi-Rahbar, M.H.; Vahidi, B.; Rastegar, H. Solution of combined economic and emission dispatch problem using a novel chaotic improved harmony search algorithm. J. Comput. Des. Eng. 2019, 6, 447–467. [Google Scholar] [CrossRef]
- Zaoui, S.; Belmadani, A. Solution of combined economic and emission dispatch problems of power systems without penalty. Appl. Artif. Intell. 2022, 36, 1976092. [Google Scholar] [CrossRef]
- Elattar, E.E. Modified harmony search algorithm for combined economic emission dispatch of microgrid incorporating renewable sources. Energy 2018, 159, 496–507. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Bhoye, M.; Jangir, N. An economic load dispatch and multiple environmental dispatch problem solution with microgrids using interior search algorithm. Neural Comput. Appl. 2018, 30, 2173–2189. [Google Scholar] [CrossRef]
- Zhang, B.; Du, Y.; Lim, E.G.; Jiang, L.; Yan, K. Design and Simulation of Peer-to-Peer Energy Trading Framework with Dynamic Electricity Price. In Proceedings of the 2019 29th Australasian Universities Power Engineering Conference (AUPEC), Nadi, Fiji, 26–29 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-peer energy trading in a community microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. Optimization of economic/emission load dispatch for hybrid generating systems using controlled Elitist NSGA-II. Electr. Power Syst. Res. 2013, 105, 142–151. [Google Scholar] [CrossRef]
- Al-Roomi, A.R. Economic Load Dispatch Test Systems Repository, Halifax, Nova Scotia, Canada: Dalhousie University, Electrical and Computer Engineering. 2016. Available online: https://al-roomi.org/economic-dispatch/6-units-system/system-i (accessed on 20 October 2023).
- Zaraki, A.; Othman, M.F.B. Implementing Particle Swarm Optimization to Solve Economic Load Dispatch Problem. In Proceedings of the 2009 International Conference of Soft Computing and Pattern Recognition, Malacca, Malaysia, 4–7 December 2009; pp. 60–65. [Google Scholar] [CrossRef]
- Eurostat, Databse. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_price_statistics (accessed on 20 October 2023).
- OECD.Stat, Database. Available online: https://stats.oecd.org/Index.aspx?DataSetCode=RE_FIT# (accessed on 20 October 2023).
- Bhandari, R.; Arce, B.E.; Sessa, V.; Adamou, R. Sustainability Assessment of Electricity Generation in Niger Using a Weighted Multi-Criteria Decision Approach. Sustainability 2021, 13, 385. [Google Scholar] [CrossRef]
- Mainali, B.; Silveira, S. Using a sustainability index to assess energy technologies for rural electrification. Renew. Sustain. Energy Rev. 2015, 41, 1351–1365. [Google Scholar] [CrossRef]
- Akber, M.Z.; Thaheem, M.J.; Arshad, H. Life cycle sustainability assessment of electricity generation in Pakistan: Policy regime for a sustainable energy mix. Energy Policy 2017, 111, 111–126. [Google Scholar] [CrossRef]
- Turkson, C.; Acquaye, A.; Liu, W.; Papadopoulos, T. Sustainability assessment of energy production: A critical review of methods, measures and issues. J. Environ. Manag. 2020, 264, 110464. [Google Scholar] [CrossRef]
- Luo, C.; Zhou, X.; Lev, B. Core, shapley value, nucleolus and nash bargaining solution: A Survey of recent developments and applications in operations management. Omega 2022, 110, 102638. [Google Scholar] [CrossRef]
- Lozano, S.; Moreno, P.; Adenso-Díaz, B.; Algaba, E. Cooperative game theory approach to allocating benefits of horizontal cooperation. Eur. J. Oper. Res. 2013, 229, 444–452. [Google Scholar] [CrossRef]
- Du, Y.; Wang, Z.; Liu, G.; Chen, X.; Yuan, H.; Wei, Y.; Li, F. A cooperative game approach for coordinating multi-microgrid operation within distribution systems. Appl. Energy 2018, 222, 383–395. [Google Scholar] [CrossRef]
- Freire, L.; Street, A.; Lima, D.A.; Barroso, L.A. A hybrid MILP and Benders decomposition approach to find the nucleolus quota allocation for a renewable energy portfolio. IEEE Trans. Power Syst. 2015, 30, 3265–3275. [Google Scholar] [CrossRef]
- Sharma, S.; Abhyankar, A.R. Loss allocation of radial distribution system using Shapley value: A sequential approach. Int. J. Electr. Power Energy Syst. 2017, 88, 33–41. [Google Scholar] [CrossRef]
- Han, L.; Morstyn, T.; Crozier, C.; McCulloch, M. Improving the Scalability of a Prosumer Cooperative Game with K-Means Clustering. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Cho, J.-H.; Wang, Y.; Chen, I.-R.; Chan, K.S.; Swami, A. A Survey on Modeling and Optimizing Multi-Objective Systems. IEEE Commun. Surv. Tutor. 2017, 19, 1867–1901. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).