Voltage Stability Assessment of a Campus DC Microgrid Implemented in Korea as a Blockchain-Based Power Transaction Testbed
Abstract
:1. Introduction
1.1. Motivation and Incitement
1.2. Literature Review
1.3. Contribution and Paper Organization
- The transaction schedule maximizes the sales revenue per time period according to the participant bids and maximizes the efficiency of power trading, reflecting the constraint of the DC microgrid and the flexibility of the supply and demand balance.
2. The Campus DC Microgrid Implemented in Korea
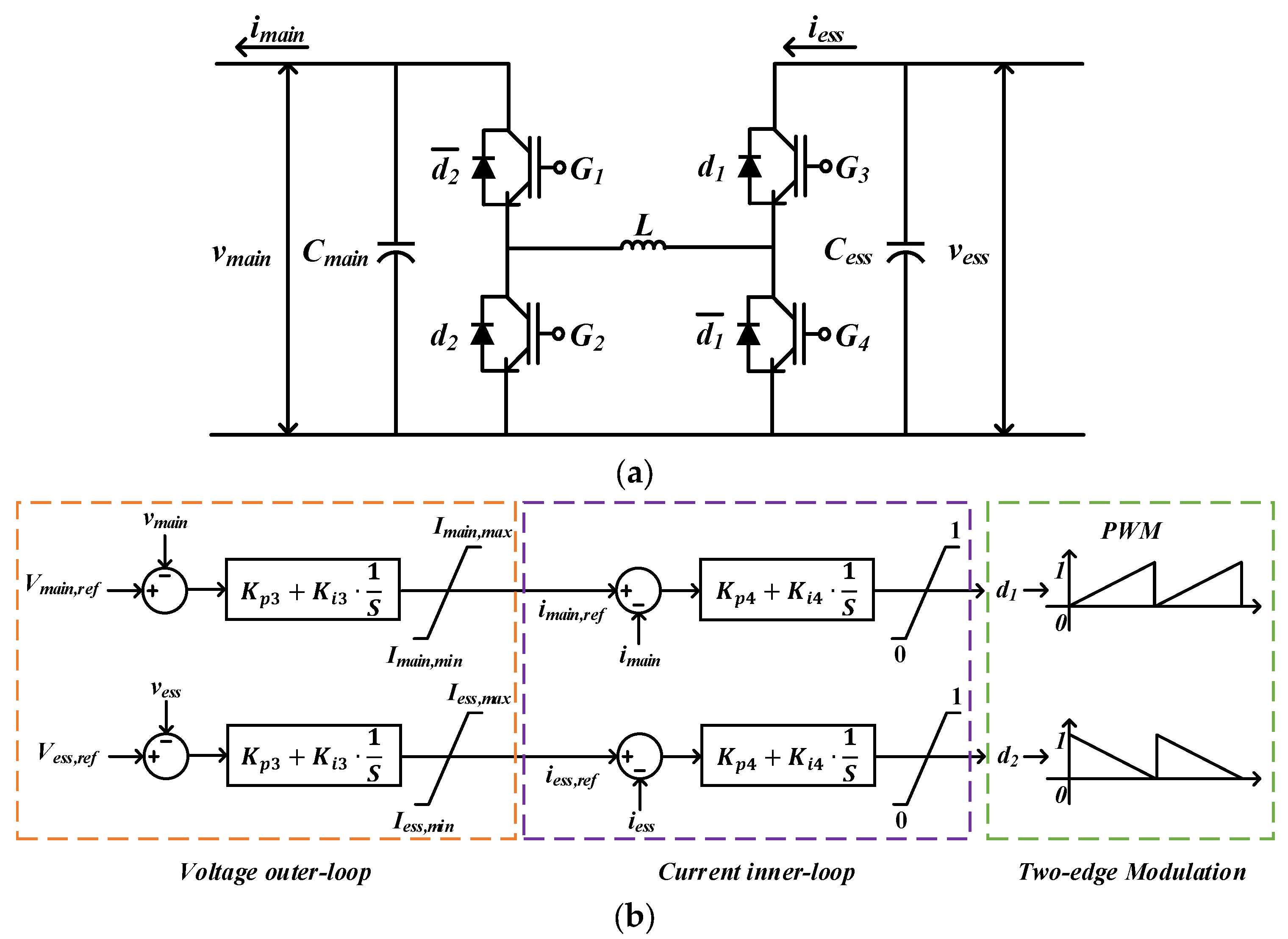
Unit Configuration and Control
3. Transaction Schedule
- The output metering of each DER is measured through the metering point Mn, as shown in Figure 4 (n: 1, ⋯, 15).
- The operating capacity of the ESSs is set to 70% (maximum charge 80% – minimum charge 10%) of the installed capacity (750 kWh + 273 kWh), and the capacity sharing of the ESSs is allocated as 73.3% for ESS #1 and 26.7% for ESS #2 after scheduling. Accordingly, the maximum output of ESS #1 is 91 kW.
- The hourly transaction price is based on the existing power provider’s tariff, which is reflected in the real-time power transaction price of the day.
- Bidding transactions are excluded during the nighttime hours (22:00~23:00), including the late-night hours (22:00~08:00). During the nighttime hours, the remaining power of the ESSs is analyzed to set the charging and transaction schedule of the ESSs for the next day.
- The transaction schedule here is the transaction schedule in independent operation, excluding uncertainty factors such as faults and DR.
- t: trading time in m minutes per day (total daily transaction data: 60/m × 24).
- b, c: bidding, transaction contract.
- : power of BLs, EVs, G2Vs, PVs, ESSs, V2Gs.
- : supply(sales) power of PVs, ESSs, V2Gs.
4. Voltage Stability Assessment of the Campus DC Microgrid Testbed
4.1. Grid Test Operation
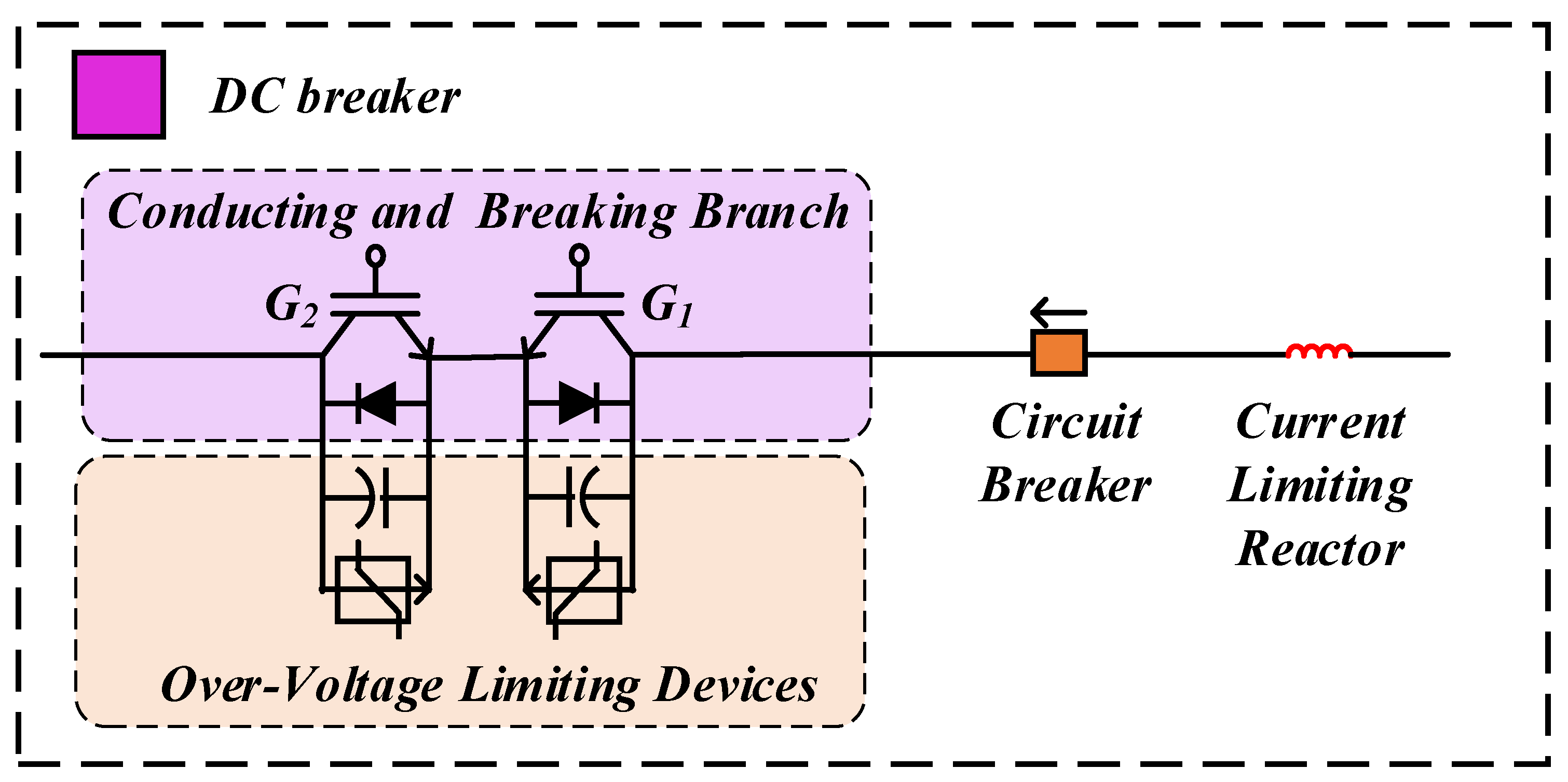
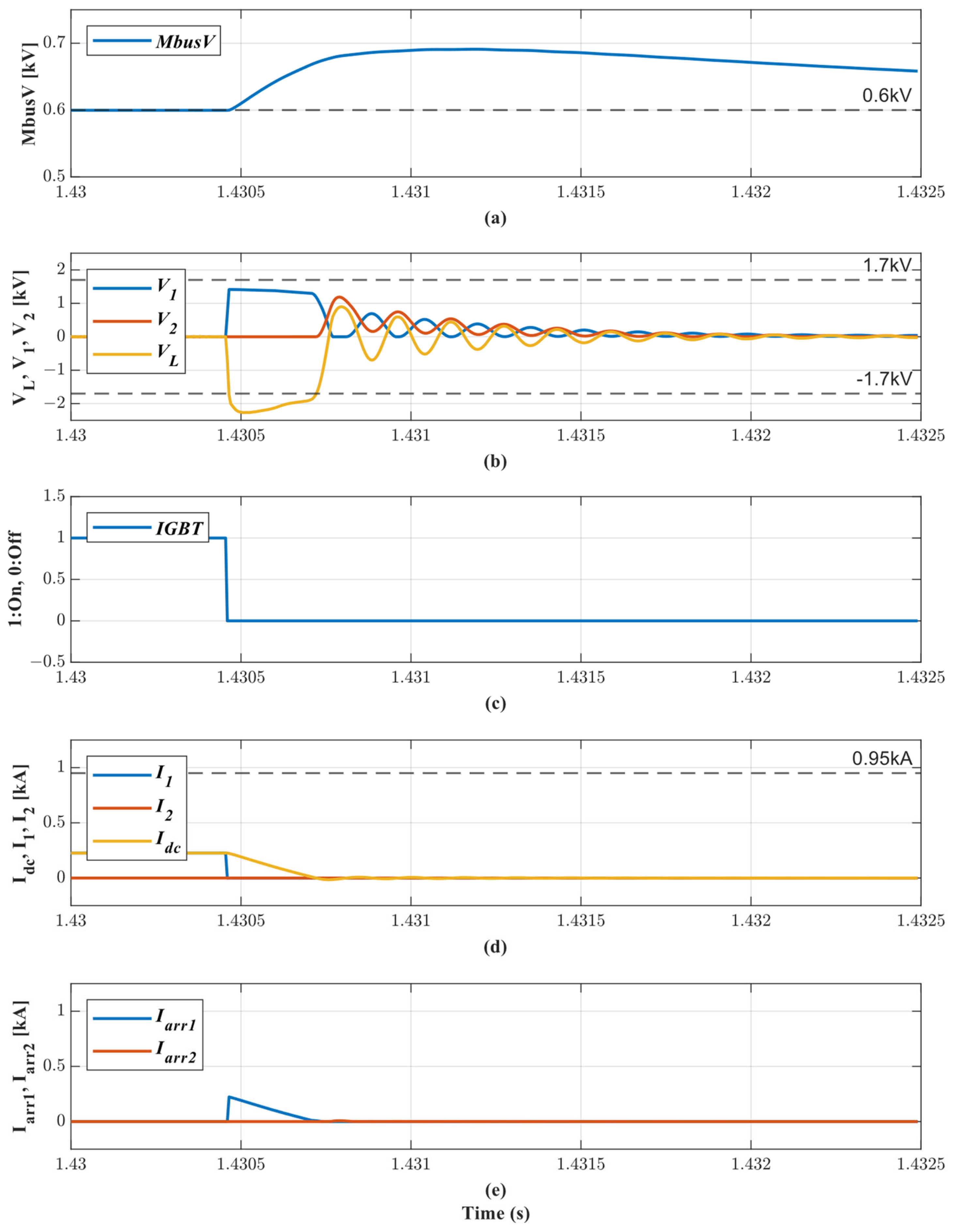
4.2. DC Breaker
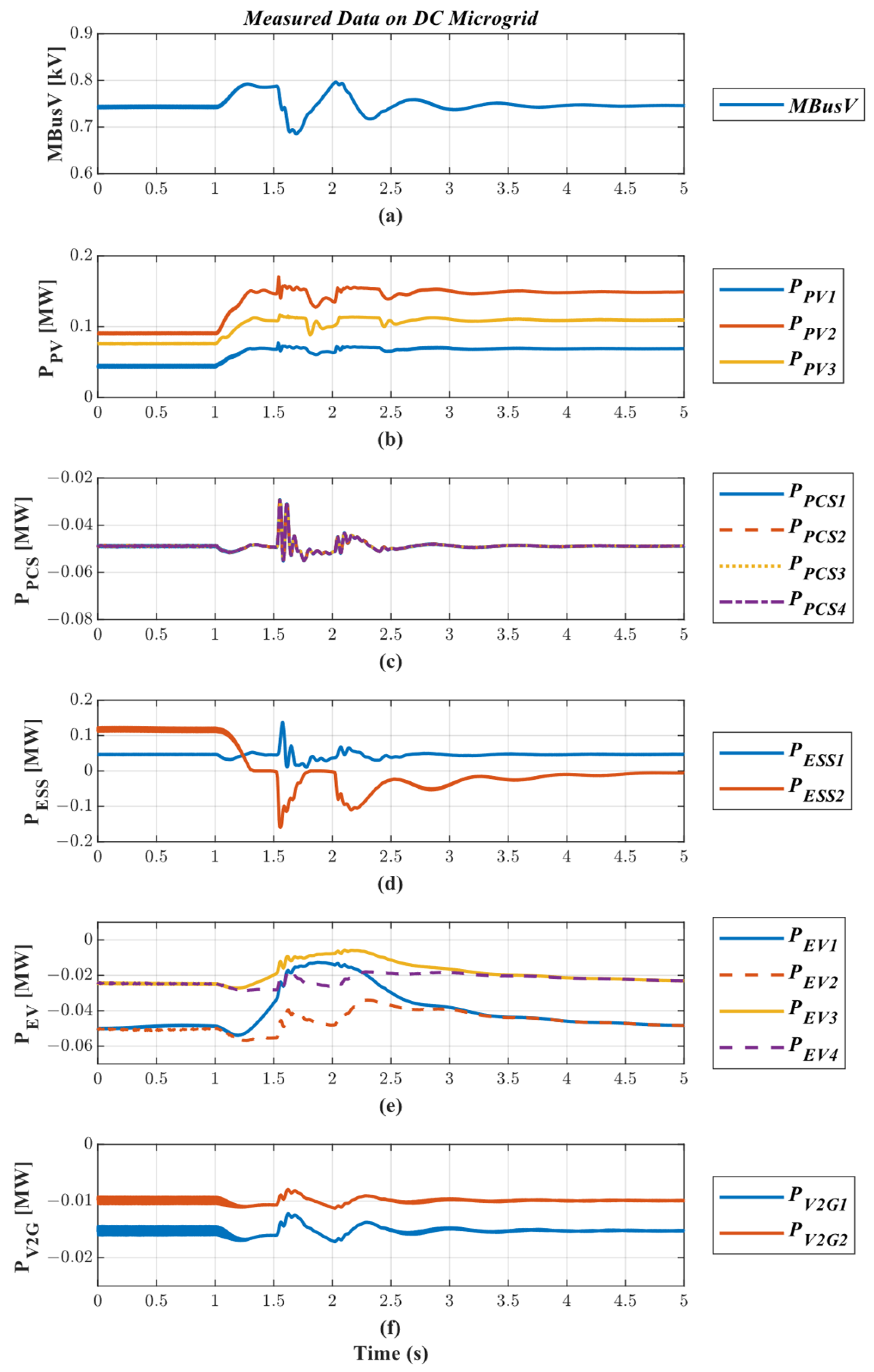
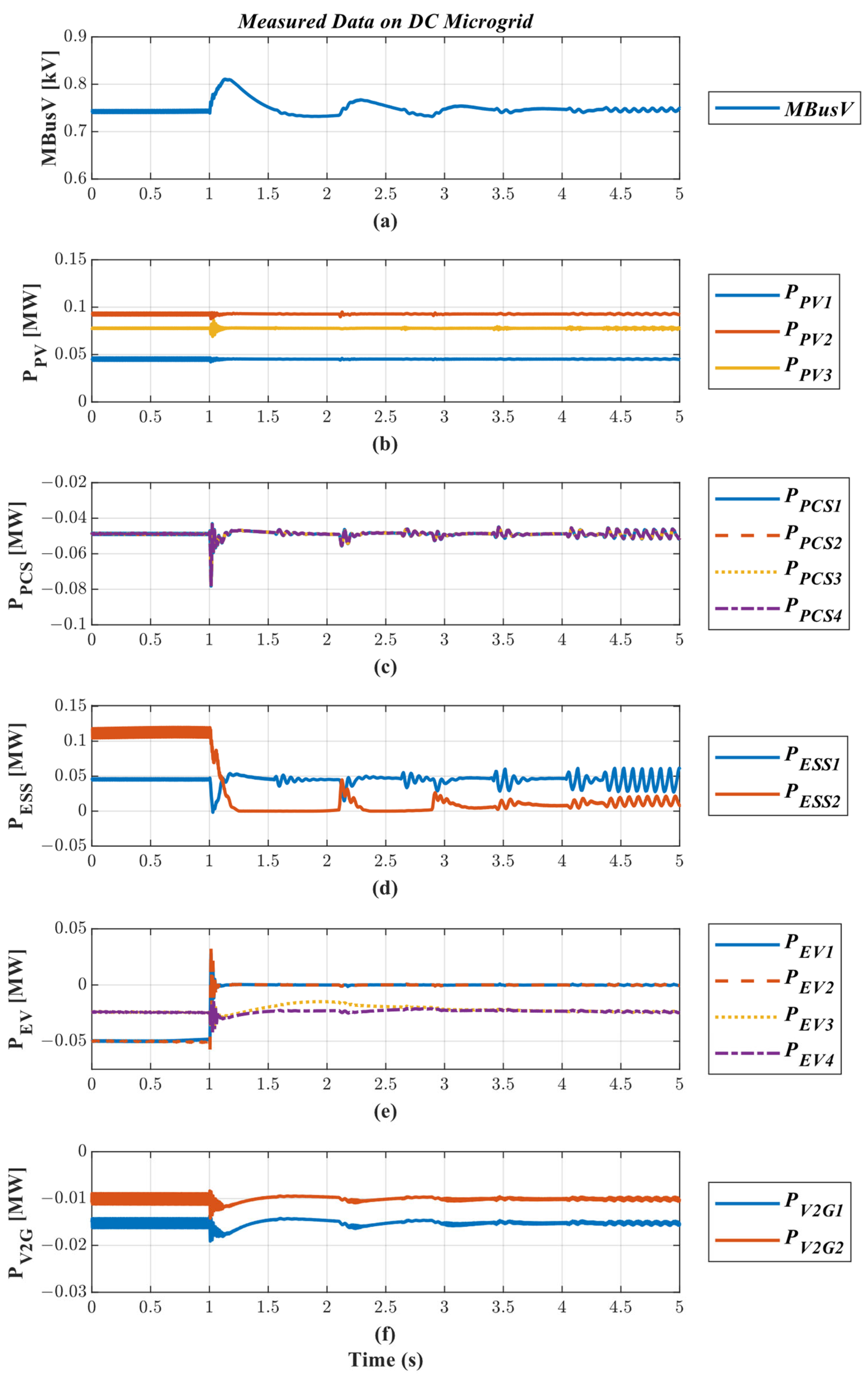
4.3. Case Studies
- [Load]
- (a)
- DC Charger #1 (PEV1 + PEV2): −0.1 MW
- (b)
- DC Charger #2 (PEV3 + PEV4): −0.05 MW
- (c)
- V2G #1: −0.015 MW
- (d)
- V2G #2: −0.01 MW
- [Source]
- (a)
- ESS #2(0.128275 MW): 73.3% of load
- (b)
- ESS #1(0.046725 MW): 26.7% of load
4.3.1. Case 1: Increase in PV Generations
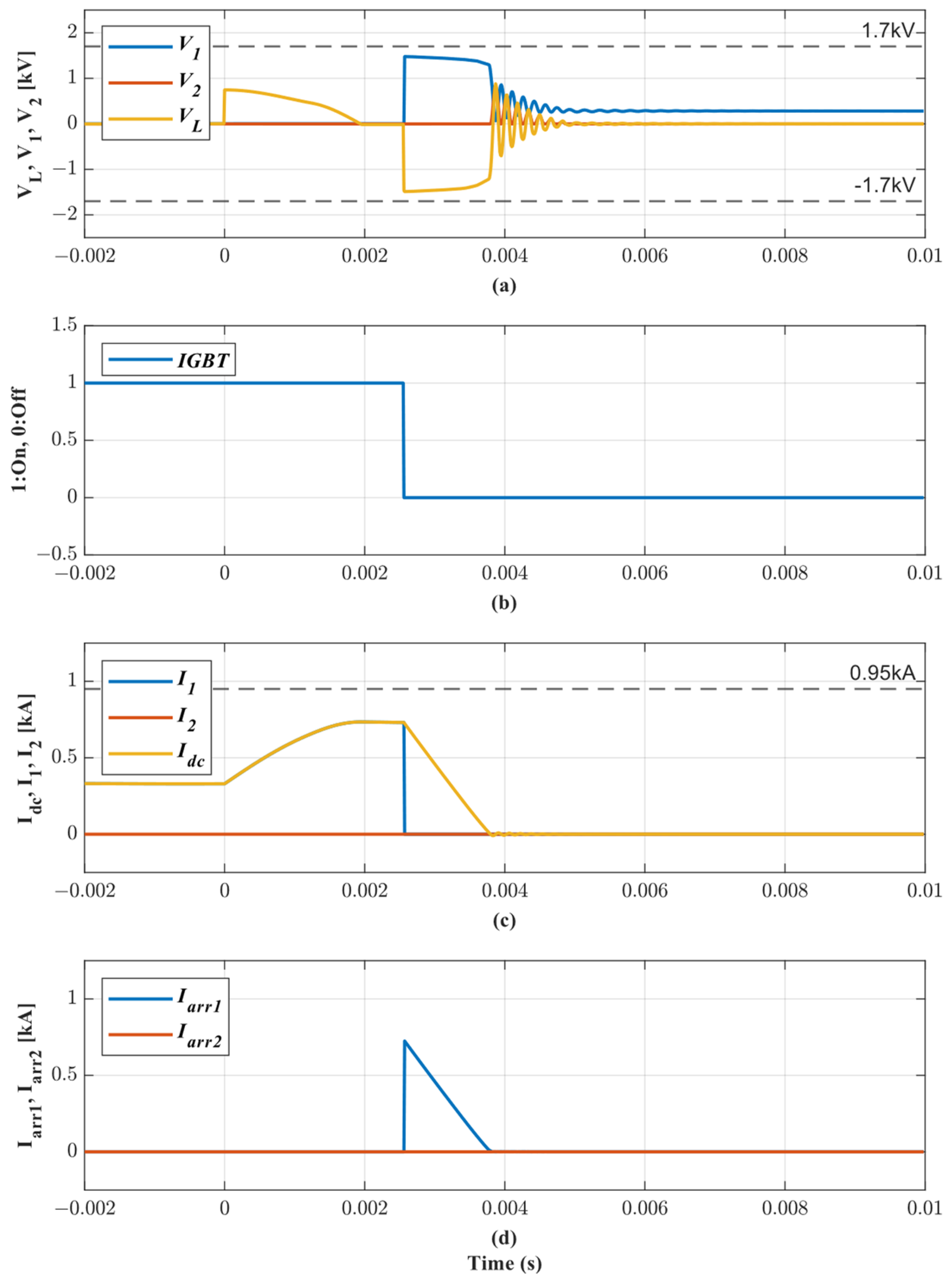
4.3.2. Case 2: Line-to-Ground Fault between DC Charger #1 and Converter #1
4.3.3. Case 3: ESS #2 Disconnection
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Topology Parameters | Values |
|---|---|
| Filter Inductance of PCS, Lf (mH) | 1 |
| DC-Link Capacitor of PCS, Cf (mF) | 10 |
| Switching Frequency of PCS, fs (kHz) | 10 |
| Inductance of FSBB, L (mH) | 1.5 |
| Input and Output side capacitance of FSBB, C (mF) | 0.28 |
| IGBT Turn-On Resistance of FSBB, Ri,on (mΩ) | 1.1 |
| IGBT Forward Breakover Voltage of FSBB, Vi,brk (kV) | 1.7 |
| IGBT Continuous DC collector current of FSBB, IC (kA) | 0.95 |
| IGBT Turn-off delay time of FSBB, td,off (us) | 0.73 |
| Antiparallel Diode Turn-On Resistance of FSBB, Rd,on (mΩ) | 1.1 |
| Antiparallel Diode Forward Breakover Voltage of FSBB, Vd,brk (kV) | 1.7 |
| Antiparallel Diode Continuous DC forward current FSBB, IF (kA) | 0.6 |
| Switching Frequency of FSBB, fs (kHz) | 4 |
| of Power Outer Loop | 10, 10 |
| in Current Inner Loop | 1, 100 |
| in Voltage Outer Loop | 1, 100 |
| in Power Outer Loop | 1, 10 |
| in Current Inner Loop | 0.1, 100 |
Appendix B
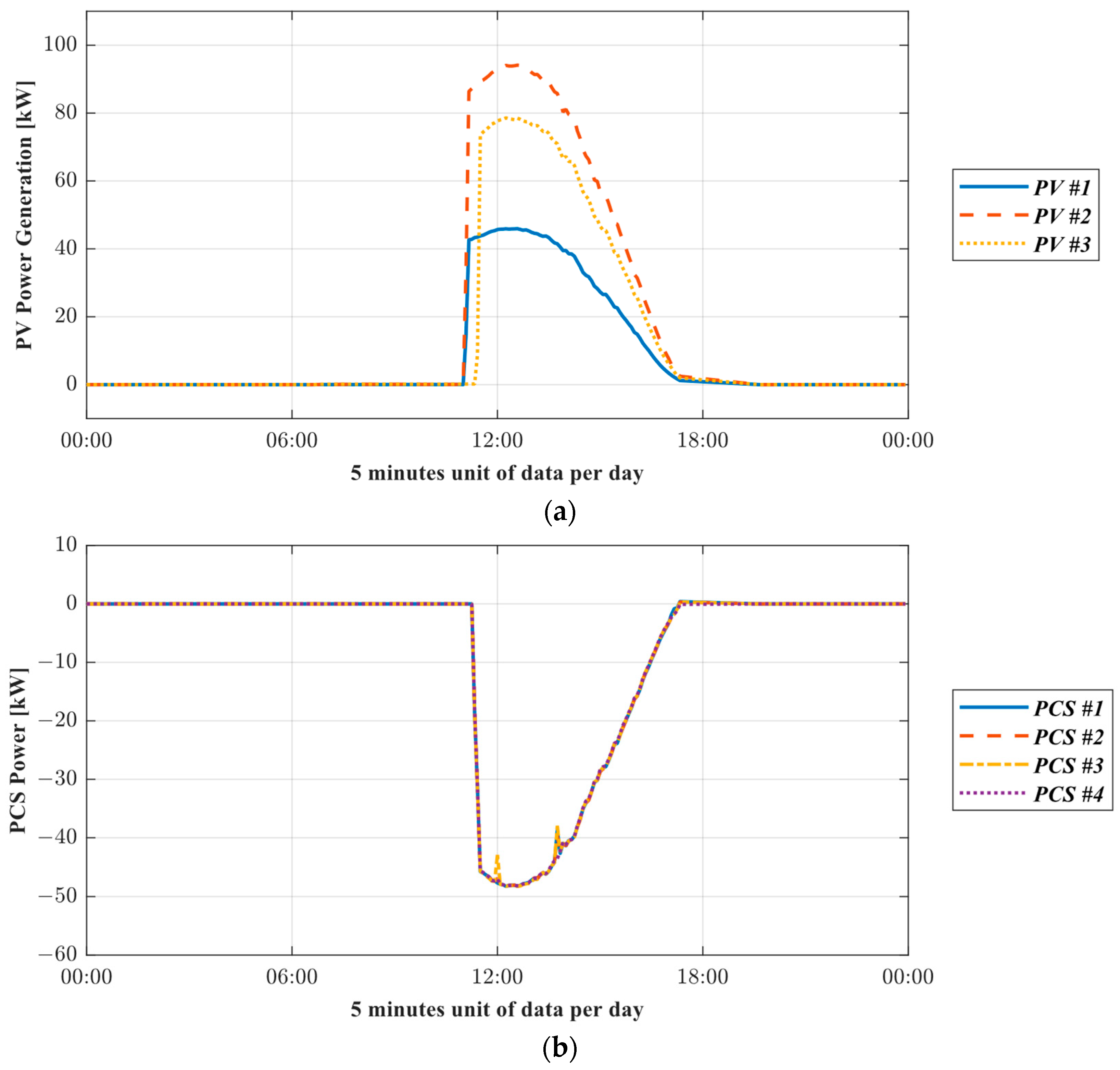
| Time (12:15, 8 November 2022) | Value |
|---|---|
| PV #1 (kW) | 45.91 |
| PV #2 (kW) | 94.05 |
| PV #3 (kW) | 78.59 |
| PCS #1 (kW) | −48.24 |
| PCS #2 (kW) | −48.23 |
| PCS #3 (kW) | −48.23 |
| PCS #4 (kW) | −48.21 |
Appendix C
| Topology Parameters | Values |
|---|---|
| L of DC breaker on PV #1 input and output side (mH) | 1.8, 1.9 |
| L of DC breaker on PV #2 input and output side (mH) | 2.2, 2.1 |
| L of DC breaker on PV #3 input and output side (mH) | 1.9, 1.9 |
| L of DC breaker between PV bus and ESS #2 (mH) | 2.4 |
| L of DC breaker on ESS #1 input and output side (mH) | 2.4, 2.4 |
| L of DC breaker on ESS #2 input and output side (mH) | 1.9, 1.9 |
| L of DC breaker on EV #1 input and output side (mH) | 2.5, 2.6 |
| L of DC breaker on EV #2 input and output side (mH) | 2.5, 2.6 |
| L of DC breaker on EV #3 input and output side (mH) | 2.5, 2.6 |
| L of DC breaker on EV #4 input and output side (mH) | 2.5, 2.6 |
| L of DC breaker on V2G #1 input and output side (mH) | 1.6, 1.6 |
| L of DC breaker on V2G #2 input and output side (mH) | 1.6, 1.6 |
| L of DC breaker on PCS #1 input side (mH) | 1.9 |
| L of DC breaker on PCS #2 input side (mH) | 1.9 |
| L of DC breaker on PCS #3 input side (mH) | 1.9 |
| L of DC breaker on PCS #4 input side (mH) | 1.9 |
| C in all DC breakers (uF) | 0.5 |
References
- United Nations General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development; A/RES/70/1; United Nations General Assembly: New York, NY, USA, 2015.
- Ramsebner, J.; Haas, R.; Auer, H.; Ajanovic, A.; Gawlik, W.; Maier, C.; Nemec-Begluk, S.; Nacht, T.; Puchegger, M. From single to multi-energy and hybrid grids: Historic growth and future vision. Renew. Sustain. Energy Rev. 2021, 151, 111520. [Google Scholar] [CrossRef]
- Microgrid Deployment Tracker 4Q18. Available online: https://www.navigantresearch.com/reports/microgrid-deployment-tracker-4q18 (accessed on 19 April 2019).
- Nejabatkhah, F.; Li, Y.W.; Tian, H. Power Quality Control of Smart Hybrid AC/DC Microgrids: An Overview. IEEE Access 2019, 7, 52295–52318. [Google Scholar] [CrossRef]
- Qu, Z.-W.; Chong, Z.-X.; Wang, Y.-J.; Shi, Z. Control Method for Grid-connected/Islanding Switching of Hybrid AC/DC Microgrid. JEET 2023, 18, 15–25. [Google Scholar] [CrossRef]
- Ahmed, M.; Meegahapola, L.; Vahidnia, A.; Datta, M. Stability and Control Aspects of Microgrid Architectures—A Comprehensive Review. IEEE Access 2020, 8, 144730–144766. [Google Scholar] [CrossRef]
- Yadav, M.; Pal, N.; Saini, D.K. Microgrid Control, Storage, and Communication Strategies to Enhance Resiliency for Survival of Critical Load. IEEE Access 2020, 8, 169047–169069. [Google Scholar] [CrossRef]
- Mohan, H.M.; Dash, S.K. Renewable Energy-Based DC Microgrid with Hybrid Energy Management System Supporting Electric Vehicle Charging System. Systems 2023, 11, 273. [Google Scholar] [CrossRef]
- Gelani, H.E.; Dastgeer, F.; Siraj, K.; Nasir, M.; Niazi, K.A.K.; Yang, Y. Efficiency Comparison of AC and DC Distribution Networks for Modern Residential Localities. Appl. Sci. 2019, 9, 582. [Google Scholar] [CrossRef]
- Shrestha, A.; Bishwokarma, R.; Chapagain, A.; Banjara, S.; Aryal, S.; Mali, B.; Thapa, R.; Bista, D.; Hayes, B.P.; Papadakis, A.; et al. Peer-to-Peer Energy Trading in Micro/Mini-Grids for Local Energy Communities: A Review and Case Study of Nepal. IEEE Access 2019, 7, 131911–131928. [Google Scholar] [CrossRef]
- Lasseter, R.H. Smart Distribution: Coupled Microgrids. Proc. IEEE 2021, 99, 1074–1082. [Google Scholar] [CrossRef]
- Hatziargyriou, N.D.; Dimeas, A.; Tsikalakis, A.G.; Lopes, J.A.P.; Karniotakis, G.; Oyarzabal, J. Management of microgrids in market environment. In Proceedings of the 2005 International Conference of Future Power Systems, Amsterdam, The Netherlands, 18 November 2005; p. 7. [Google Scholar]
- Gupta, P.K.; Duchon, M. Developing Self-Similar Hybrid Control Architecture Based on SGAM-Based Methodology for Distributed Microgrids. Designs 2018, 2, 41. [Google Scholar] [CrossRef]
- Li, X.; Zheng, T.; Huang, J.; Li, X.; Xiong, W. Decentralized Multiple Control for DC Microgrid with Hybrid Energy Storage. JEET 2023, 18, 1301–1311. [Google Scholar] [CrossRef]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar]
- EEE Std 1547.4-2011; IEEE Guide for Design, Operation, and Integration of Distributed Resource Island Systems with Electric Power Systems. IEEE: Piscataway, NJ, USA, 20 July 2011; pp. 1–54.
- Dou, C.X.; Liu, B. Multi-agent based hierarchical hybrid control for smart microgrid. IEEE Trans. Smart Grid 2013, 4, 771–778. [Google Scholar] [CrossRef]
- Bintoudi, A.D.; Zyglakis, L.; Apostolos, T.; Ioannidis, D.; Al-Agtash, S.; Martinez-Ramos, J.L.; Onen, A.; Azzopardi, B.; Hadjidemetriou, L.; Martensen, N.; et al. Novel hybrid design for microgrid control. In Proceedings of the IEEE PES Asia–Pacific Power and Energy Engineering Conference, APPEEC, Bangalore, India, 8–10 November 2017; pp. 1–6. [Google Scholar]
- Steinmetz, R.; Wehrle, K. 2. What Is This “Peer-to-Peer” About? In Peer-to-Peer Systems and Applications; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3485, pp. 9–16. [Google Scholar]
- Xia, Y.; Peng, Y.; Yang, P.; Yu, M.; Wei, W. Distributed Coordination Control for Multiple Bidirectional Power Converters in a Hybrid AC/DC Microgrid. IEEE Trans. Power Electron. 2017, 32, 4949–4959. [Google Scholar] [CrossRef]
- Andoni, M.; Robu, V.; Flynn, D.; Abram, S.; Geach, D.; Jenkins, D.; McCallum, P.; Peacock, A. Blockchain technology in the energy sector: A systematic review of challenges and opportunities. Renew. Sustain. Energy Revies 2019, 100, 143–174. [Google Scholar] [CrossRef]
- Barnes, M.; Vilchis-Rodriguez, D.S.; Pei, X.; Shuttleworth, R.; Cwikowski, O.; Smith, A.C. HVDC Circuit Breakers—A Review. IEEE Access 2020, 8, 211829–211848. [Google Scholar] [CrossRef]
- Lee, S.H. Scaled-Up Slack Generator Based on Parallel Inverters for a Reliable IFSA Microgrid. IEEE Access 2021, 9, 133204–133214. [Google Scholar] [CrossRef]
- Ekin, Ö.; Arena, G.; Waczowicz, S.; Hagenmeyer, V.; De Carne, G. Comparison of Four-Switch Buck-Boost and Dual Active Bridge Converter for DC Microgrid Applications. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; pp. 1–6. [Google Scholar]
- Orellana, M.; Petibon, S.; Estibals, B.; Alonso, C. Four Switch Buck-Boost Converter for Photovoltaic DC-DC power applications. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 469–474. [Google Scholar]
- Ren, X.; Ruan, X.; Qian, H.; Chen, Q. Three-Mode Dual Frequency Two-Edge Modulation Scheme for Four-Switch Buck-Boost Converter. IEEE Trans. Power Electron. 2009, 24, 499–509. [Google Scholar]
- Zen, S.; Inada, Y.; Ohnishi, W.; Fukai, Y.; Takayasu, N.; Maeyama, M.; Yamano, Y. Prototype Current-Limiting Hybrid DC Circuit Breaker Incorporating a Fuse and a Semiconductor Device. IEEE Trans. Power Deliv. 2021, 36, 2231–2233. [Google Scholar] [CrossRef]
- IEEE Std 1547-2018 (Revision of IEEE Std 1547-2003); IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 6 April 2018; pp. 1–138.






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, H.; Lee, S.H.; Choi, D.; Choi, S.; Sung, B. Voltage Stability Assessment of a Campus DC Microgrid Implemented in Korea as a Blockchain-Based Power Transaction Testbed. Energies 2023, 16, 7297. https://doi.org/10.3390/en16217297
Hwang H, Lee SH, Choi D, Choi S, Sung B. Voltage Stability Assessment of a Campus DC Microgrid Implemented in Korea as a Blockchain-Based Power Transaction Testbed. Energies. 2023; 16(21):7297. https://doi.org/10.3390/en16217297
Chicago/Turabian StyleHwang, Hyeonseok, Soo Hyoung Lee, Donghee Choi, Sangbong Choi, and Backsub Sung. 2023. "Voltage Stability Assessment of a Campus DC Microgrid Implemented in Korea as a Blockchain-Based Power Transaction Testbed" Energies 16, no. 21: 7297. https://doi.org/10.3390/en16217297
APA StyleHwang, H., Lee, S. H., Choi, D., Choi, S., & Sung, B. (2023). Voltage Stability Assessment of a Campus DC Microgrid Implemented in Korea as a Blockchain-Based Power Transaction Testbed. Energies, 16(21), 7297. https://doi.org/10.3390/en16217297







