Multi-Objective Capacity Optimization of Grid-Connected Wind–Pumped Hydro Storage Hybrid Systems Considering Variable-Speed Operation
Abstract
:1. Introduction
2. Coordination Scheme of Wind Power and Pumped Storage
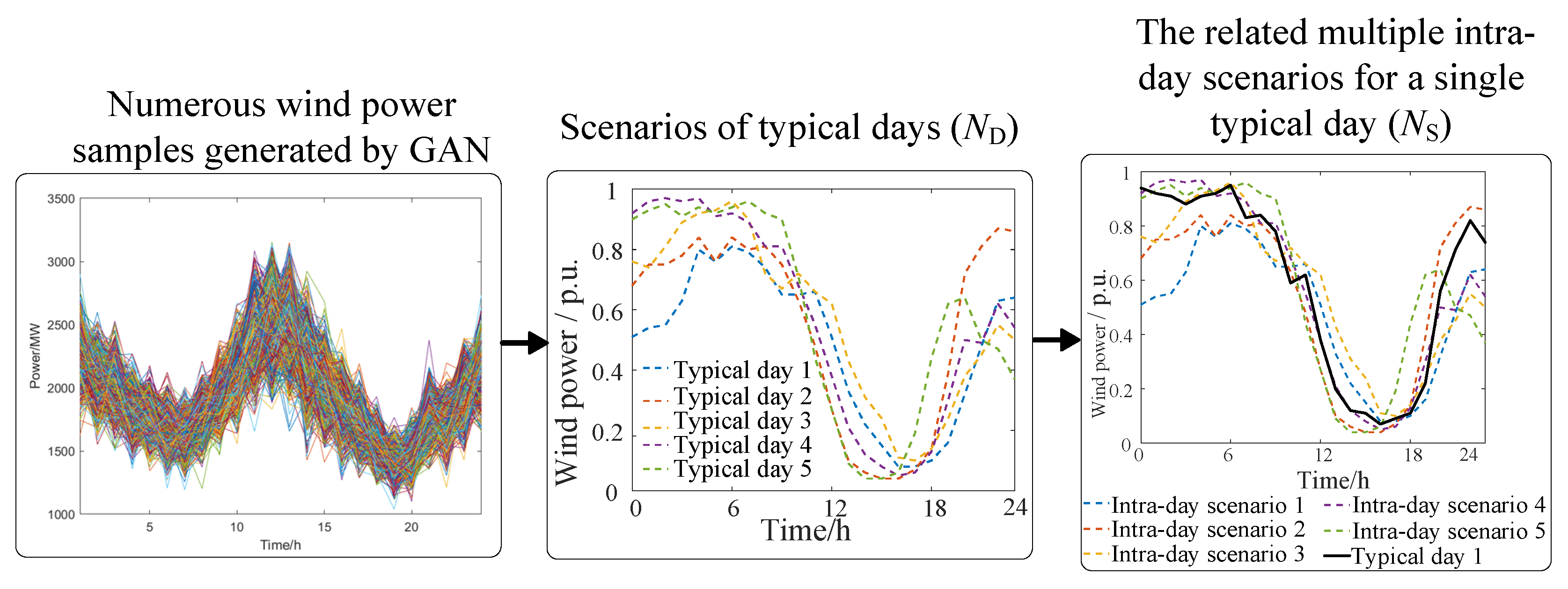
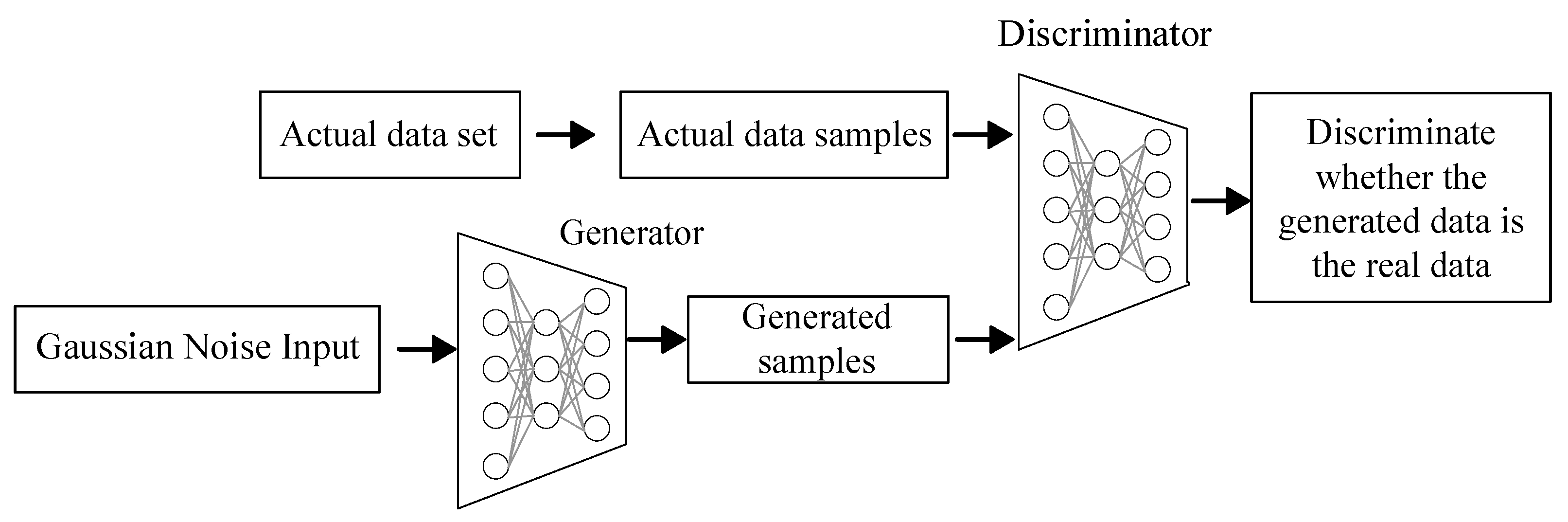
3. Scenario Generation for the Fluctuation and Uncertainty of Wind Power
- (1)
- Input historical data and alternately train GAN networks.
- (2)
- Generate a high number of data to establish a dataset of scenarios for wind power output.
- (3)
- Reduce scenarios based on the K-means clustering algorithm to generate representative scenarios of typical days with the number of .
- (4)
- For the representative scenario of one typical day, we choose the related scenarios based on Euclidean distance. In other words, scenarios that are closer to the representative scenario are chosen to formulate related intra-day scenarios based on the K-means clustering method.
- (5)
- Finally, representative scenarios of typical days and related intra-day scenarios are acquired, and the probability of scenarios can also be obtained.
4. Multi-Objective Capacity Optimization Model
4.1. Multiple Objective Functions
4.1.1. Objective 1: Minimizing the Levelized Cost of Energy (LCOE)
4.1.2. Objective 2: Minimizing Peak–Valley Difference (PVD)
4.1.3. Objective 3: Minimizing Power Output Deviation (POD)
4.2. Constraints
4.2.1. Installed Capacity Constraint
4.2.2. Operational Constraints
- Day-ahead stage operational constraints
- (1)
- Reservoir operational constraints
- (2)
- Power constraints
- (3)
- Unit commitment constraints
- (4)
- Wind power output constraints
- (5)
- Delivery constraints
- 2.
- Intra-day stage operational constraints
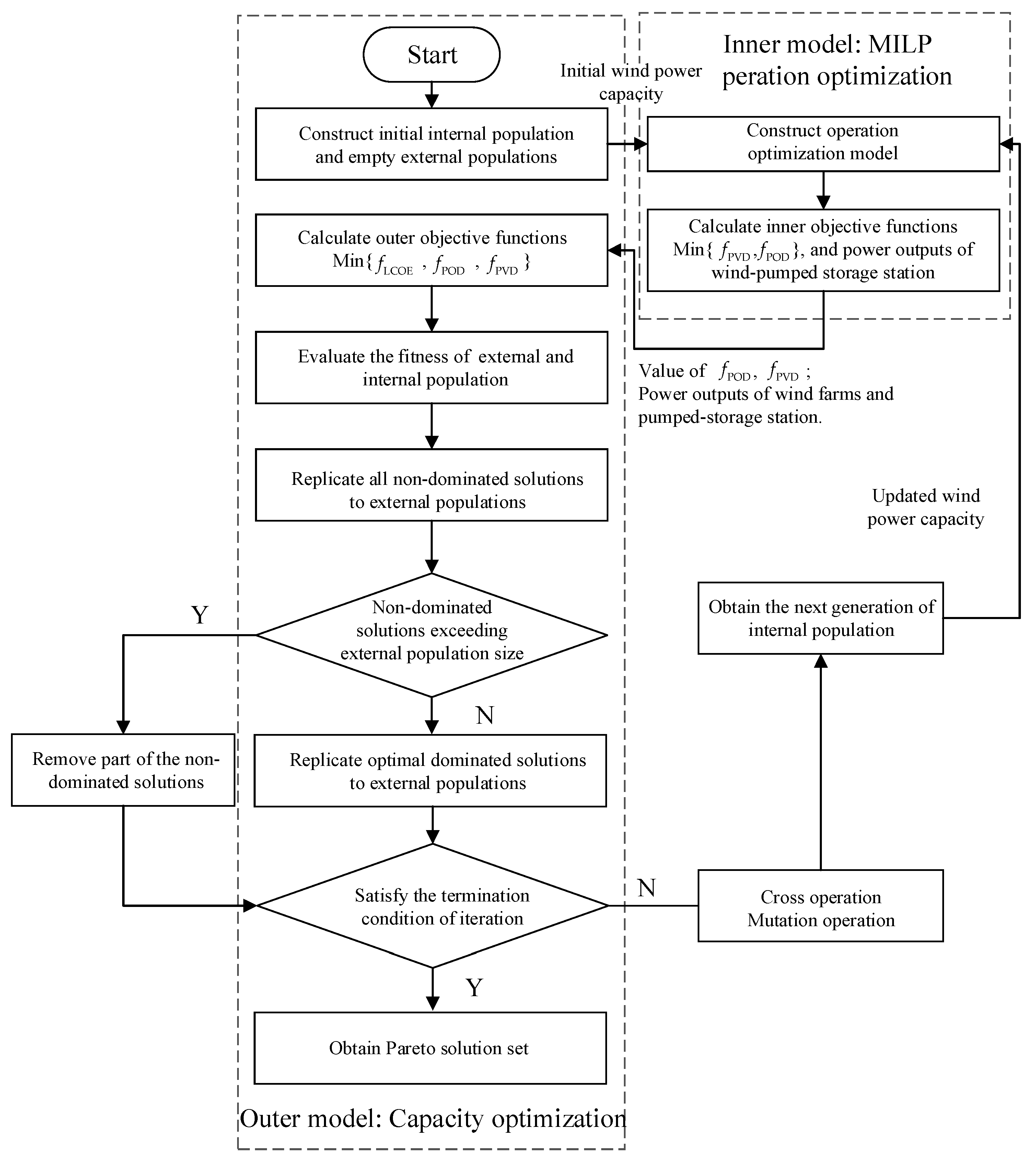
4.3. Optimization Algorithm
5. Case Study
5.1. Case Parameters
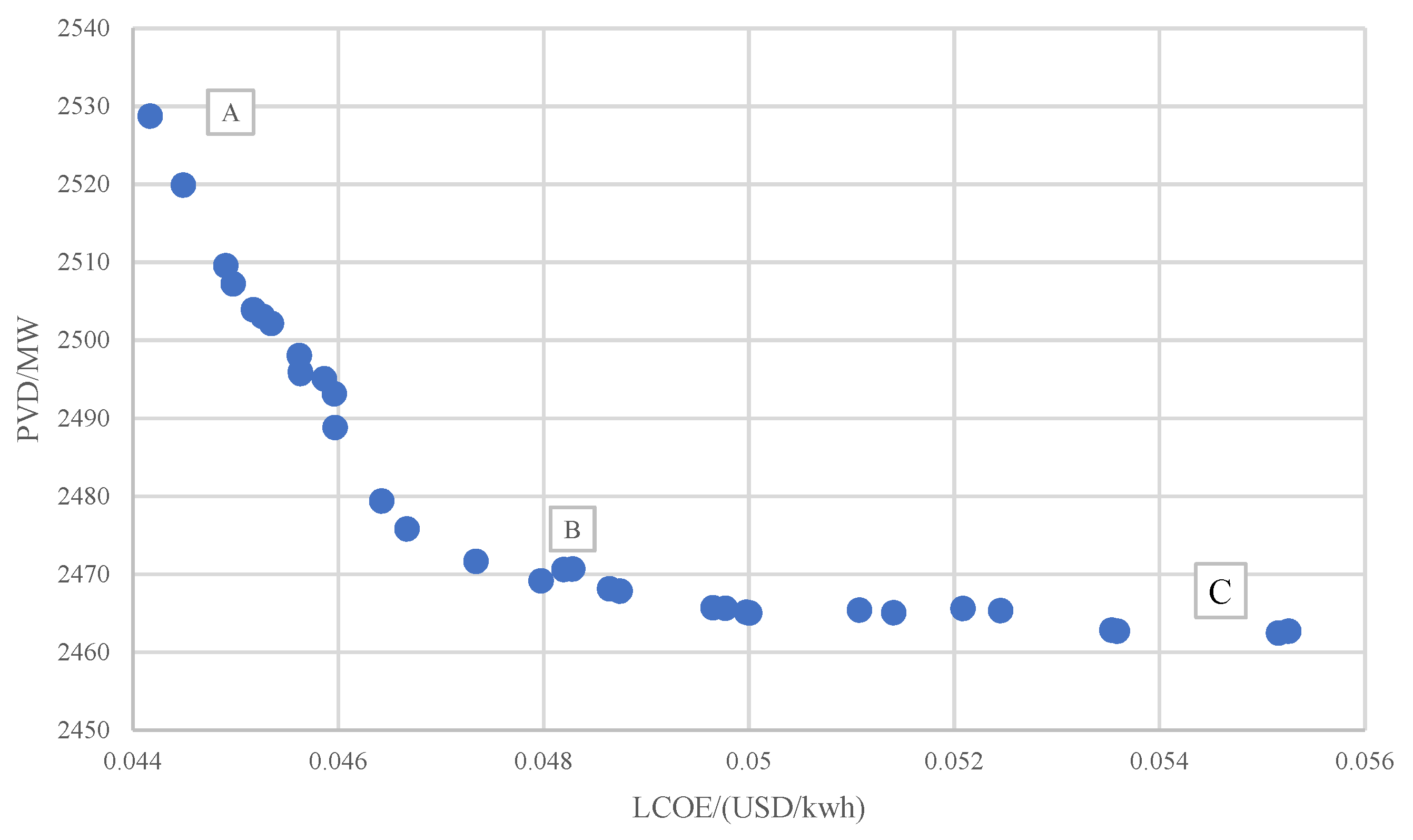
5.2. Optimization Results
5.3. Fixed-Speed and Variable-Speed Pumped Storage Operation Comparison Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.Z.; Wu, F.; Li, Y.; Li, J.Y.; Liu, Y.; Liu, W.E. Day-ahead dispatch approach for cascaded hydropower-photovoltaic complementary system based on two-stage robust optimization. Energy 2023, 265, 126145. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Zhang, Z.; Zheng, J.H.; Zheng, Y.; Zhang, J.S.; Liu, Z.Q.; Fernandez-Rodriguez, E. Research of the array spacing effect on wake interaction of tidal stream turbines. Ocean Eng. 2023, 276, 114227. [Google Scholar] [CrossRef]
- Guo, S.; He, Y.; Pei, H.J.; Wu, S.Y. The multi-objective capacity optimization of wind-photovoltaic-thermal energy storage hybrid power system with electric heater. Sol. Energy 2020, 195, 138–149. [Google Scholar] [CrossRef]
- Wang, C.; Ju, P.; Lei, S.; Wang, Z.; Wu, F.; Hou, Y. Markov decision process-based resilience enhancement for distribution systems: An approximate dynamic programming approach. IEEE Trans. Smart Grid 2020, 11, 2498–2510. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Wu, F.; Li, Y.; Shi, L.J.; Lee, K.Y.; Wu, J.W. Itô-theory-based multi-time scale dispatch approach for cascade hydropower-photovoltaic complementary system. Renew. Energy 2023, 202, 127–142. [Google Scholar] [CrossRef]
- Li, R.; Guo, S.; Yang, Y.; Liu, D.Y. Optimal sizing of wind/concentrated solar plant/ electric heater hybrid renewable energy system based on two-stage stochastic programming. Energy 2020, 209, 118472. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, M.; He, M.; Gao, Y.; Li, J.; Han, S.; Liu, Z.; Lei, L.; Díaz, J.I.P.; Cavazzini, G.; et al. Beyond fixed-speed pumped storage: A comprehensive evaluation of different flexible pumped storage technologies in energy systems. J. Clean. Prod. 2023, 139994. [Google Scholar] [CrossRef]
- Boroomandnia, A.; Rismanchi, B.; Wu, W.; Anderson, R. Optimal design of micro pumped-storage plants in the heart of a city. Sustain. Cities Soc. 2024, 101, 105054. [Google Scholar] [CrossRef]
- Canales, F.A.; Jurasz, J.K.; Guezgouz, M.; Beluco, A. Cost-reliability analysis of hybrid pumped-battery storage for solar and wind energy integration in an island community. Sustain. Energy Technol. Assess. 2021, 44, 101062. [Google Scholar] [CrossRef]
- Pradhan, A.; Marence, M.; Franca, M.J. The adoption of seawater pump storage hydropower systems increases the share of renewable energy production in small island developing states. Renew. Energy 2021, 177, 448–460. [Google Scholar] [CrossRef]
- Pali, B.S.; Vadhera, S. An Innovative Continuous Power Generation System Comprising of Wind Energy Along With Pumped-Hydro Storage and Open Well. IEEE Trans. Sustain. Energy 2018, 11, 145–153. [Google Scholar] [CrossRef]
- Perez-Diaz, J.I.; Jimenez, J. Contribution of a pumped-storage hydropower plant to reduce the scheduling costs of an isolated power system with high wind power penetration. Energy 2016, 109, 92–104. [Google Scholar] [CrossRef]
- Bhayo, B.A.; Al-Kayiem, H.H.; Gilani, S.I.U.; Ismail, F.B. Power management optimization of hybrid solar photovoltaic-battery integrated with pumped-hydro-storage system for standalone electricity generation. Energy Convers. Manag. 2020, 215, 112942. [Google Scholar] [CrossRef]
- Zohbi, G.A.; Hendrick, P.; Renier, C.; Bouillard, P. The contribution of wind-hydro pumped storage systems in meeting Lebanon’s electricity demand. Int. J. Hydrog. Energy 2016, 41, 6996–7004. [Google Scholar] [CrossRef]
- Yao, W.; Deng, C.; Li, D.; Chen, M.; Peng, P.; Zhang, H. Optimal Sizing of Seawater Pumped Storage Plant with Variable-Speed Units Considering Offshore Wind Power Accommodation. Sustainability 2019, 11, 1939. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.X.; Lu, L.; Peng, J.Q. Optimal design of an autonomous solar-wind-pumped storage power supply system. Appl. Energy 2015, 160, 728–736. [Google Scholar] [CrossRef]
- Gao, J.J.; Zheng, Y.; Li, J.M.; Zhu, X.M.; Kan, K. Optimal Model for Complementary Operation of a Photovoltaic-Wind-Pumped Storage System. Math. Probl. Eng. 2018, 2018, 5346253. [Google Scholar] [CrossRef]
- Segurado, R.; Madeira, J.F.A.; Costa, M.; Duic, N.; Carvalho, M.G. Optimization of a wind powered desalination and pumped hydro storage system. Appl. Energy 2016, 177, 487–499. [Google Scholar] [CrossRef]
- Xu, X.; Hu, W.H.; Cao, D.; Huang, Q.; Chen, C.; Chen, Z. Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system. Renew. Energy 2020, 147, 1418–1431. [Google Scholar] [CrossRef]
- Yuan, W.; Xin, W.; Su, C.; Cheng, C.; Yan, D.; Wu, Z. Cross-regional integrated transmission of wind power and pumped-storage hydropower considering the peak shaving demands of multiple power grids. Renew. Energy 2022, 190, 1112–1126. [Google Scholar] [CrossRef]
- Su, C.; Cheng, C.; Wang, P.; Shen, J.; Wu, X. Optimization model for long-distance integrated transmission of wind farms and pumped-storage hydropower plants. Appl. Energy 2019, 242, 285–293. [Google Scholar] [CrossRef]
- Wang, R.; Yang, W.J.; Li, X.D.; Zhao, Z.G.; Zhang, S.S. Day-ahead multi-objective optimal operation of Wind-PV-Pumped Storage hybrid system considering carbon emissions. Energy Rep. 2022, 8, 1270–1279. [Google Scholar] [CrossRef]
- Tang, Y.J.; Fang, G.H.; Tan, Q.F.; Wen, X.; Lei, X.H.; Ding, Z.Y. Optimizing the sizes of wind and photovoltaic power plants integrated into a hydropower station based on power output complementarity. Energy Conv. Manag. 2020, 206, 11. [Google Scholar] [CrossRef]
- Zhu, Z.A.; Wang, X.; Jiang, C.W.; Wang, L.L.; Gong, K. Multi-objective optimal operation of pumped-hydro-solar hybrid system considering effective load carrying capability using improved NBI method. Int. J. Electr. Power Energy Syst. 2021, 129, 106902. [Google Scholar] [CrossRef]
- Yang, W.J.; Yang, J.D. Advantage of variable-speed pumped storage plants for mitigating wind power variations: Integrated modelling and performance assessment. Appl. Energy 2019, 237, 720–732. [Google Scholar] [CrossRef]
- Feng, C.; Zheng, Y.; Li, C.S.; Mai, Z.J.; Wu, W.; Chen, H.X. Cost advantage of adjustable-speed pumped storage unit for daily operation in distributed hybrid system. Renew. Energy 2021, 176, 1–10. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A. Optimal scheduling of variable speed pumped storage, solar and wind energy system. Energy Sources Part A-Recovery Util. Environ. Eff. 2021. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Wang, Y.S.; Kirschen, D.; Zhang, B.S. Model-Free Renewable Scenario Generation Using Generative Adversarial Networks. IEEE Trans. Power Syst. 2018, 33, 3265–3275. [Google Scholar] [CrossRef]
- Zhou, B.; Duan, H.R.; Wu, Q.W.; Wang, H.Z.; Or, S.W.; Chan, K.W.; Meng, Y.F. Short-term prediction of wind power and its ramp events based on semi-supervised generative adversarial network. Int. J. Electr. Power Energy Syst. 2021, 125, 106411. [Google Scholar] [CrossRef]
- Li, S.; Ma, H.J.; Li, W.Y. Typical solar radiation year construction using k-means clustering and discrete-time Markov chain. Appl. Energy 2017, 205, 720–731. [Google Scholar] [CrossRef]
- Benmouiza, K.; Cheknane, A. Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models. Energy Conv. Manag. 2013, 75, 561–569. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, C.; Yu, S.; Su, H. Chance-constrained co-optimization for day-ahead generation and reserve scheduling of cascade hydropower–variable renewable energy hybrid systems. Appl. Energy 2022, 324, 119732. [Google Scholar] [CrossRef]
- Wang, P.L.; Yuan, W.L.; Su, C.G.; Wu, Y.; Lu, L.; Yan, D.H.; Wu, Z.N. Short-term optimal scheduling of cascade hydropower plants shaving peak load for multiple power grids. Renew. Energy 2022, 184, 68–79. [Google Scholar] [CrossRef]
- Liu, B.X.; Lund, J.R.; Liao, S.L.; Jin, X.Y.; Liu, L.J.; Cheng, C.T. Optimal power peak shaving using hydropower to complement wind and solar power uncertainty. Energy Convers. Manag. 2020, 209, 112628. [Google Scholar] [CrossRef]
- Khaleghi, A.; Eydi, A. Multi-period hub location problem considering polynomial time-dependent demand. Comput. Oper. Res. 2023, 159, 106357. [Google Scholar] [CrossRef]
- Pan, L.; Liu, X.; Jia, Z.; Xu, J.; Li, X. A multi-objective clustering evolutionary algorithm for multi-workflow computation offloading in mobile edge computing. IEEE Trans. Cloud Comput. 2023, 11, 1334–1351. [Google Scholar] [CrossRef]




| Component | Operational Parameters | Value | Unit |
|---|---|---|---|
| Pumped storage | Upper reservoir | 18,000,000 | m3 |
| Lower reservoir | 18,000,000 | m3 | |
| Water density | 1000 | kg/m3 | |
| Gravitational acceleration | 9.81 | m/s2 | |
| Pumped storage unit | 300 | MW | |
| Pipeline conveying efficiency | 95% | -- | |
| Pumping efficiency | 80% | -- | |
| Generating efficiency | 90% | -- | |
| wind | Maximum installed capacity | 2000 | MW |
| Discount rate | 0.08 | -- | |
| Electricity purchase | 0.075 | USD/kwh |
| Component | Economic Parameters | Value | Unit |
|---|---|---|---|
| Wind | Initial investment cost | 1695 | USD/kW |
| Operation cost | 51 | USD/kW | |
| Degradation rate | 0% | - | |
| Replacement cost | 1695 | USD/kW | |
| Expected lifetime | 20 | year | |
| Fixed-speed pumped storage | Initial investment cost | 453 | USD/kW |
| Operation cost | 9.06 | USD/kW | |
| Replacement cost | 453 | USD/kW | |
| Expected lifetime | 15 | year | |
| Variable-speed pumped storage | Initial investment cost | 985 | USD/kW |
| Operation cost | 19.7 | USD/kW | |
| Replacement cost | 985 | USD/kW | |
| Expected lifetime | 15 | year |
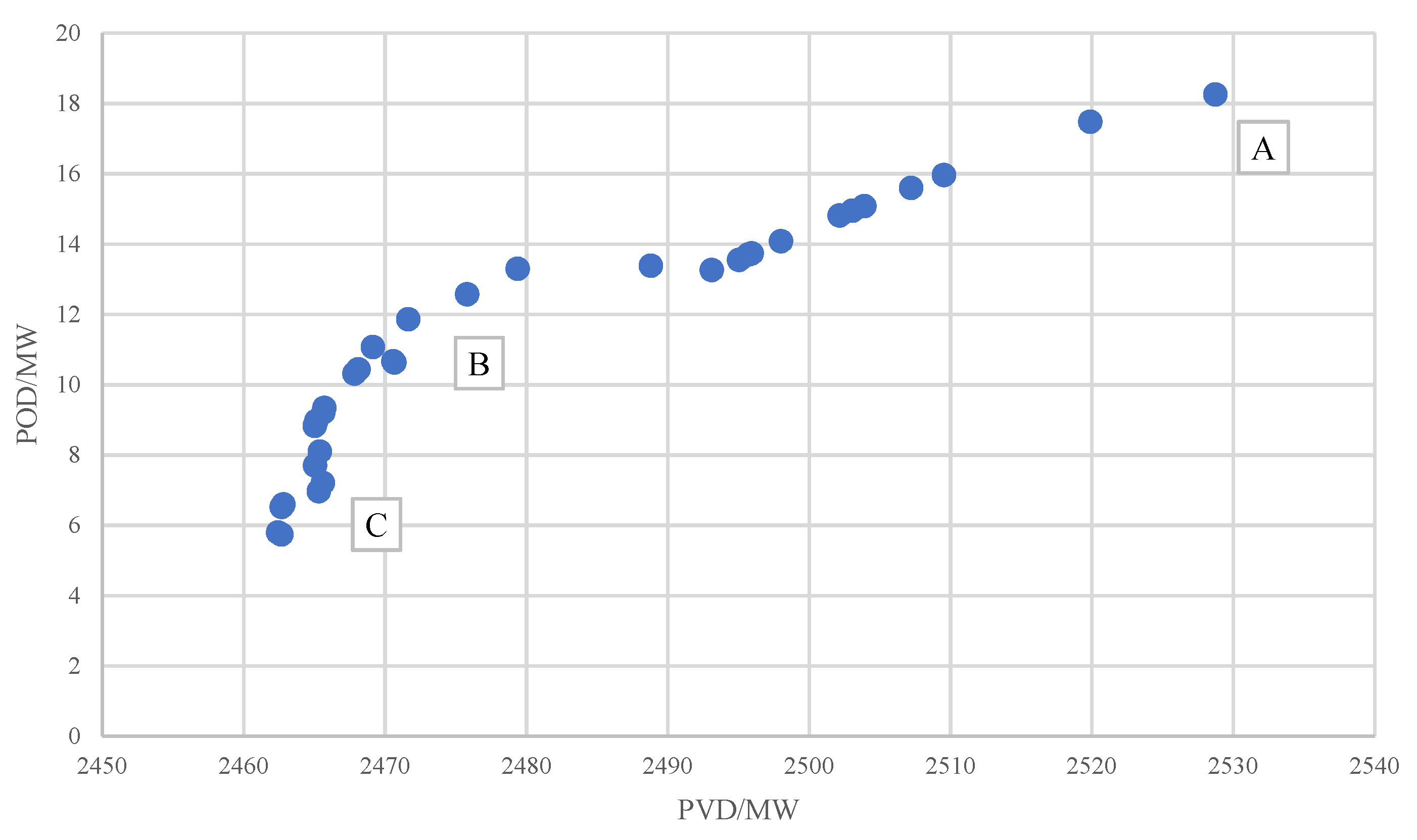
| A | B | C | |
|---|---|---|---|
| Installed capacity of wind turbine/MW | 1429 | 956 | 532 |
| LCOE/(USD/kwh) | 0.044 | 0.047 | 0.053 |
| PVD/MW | 2528 | 2472 | 2462 |
| POD/MW | 18.2 | 11.8 | 6.5 |
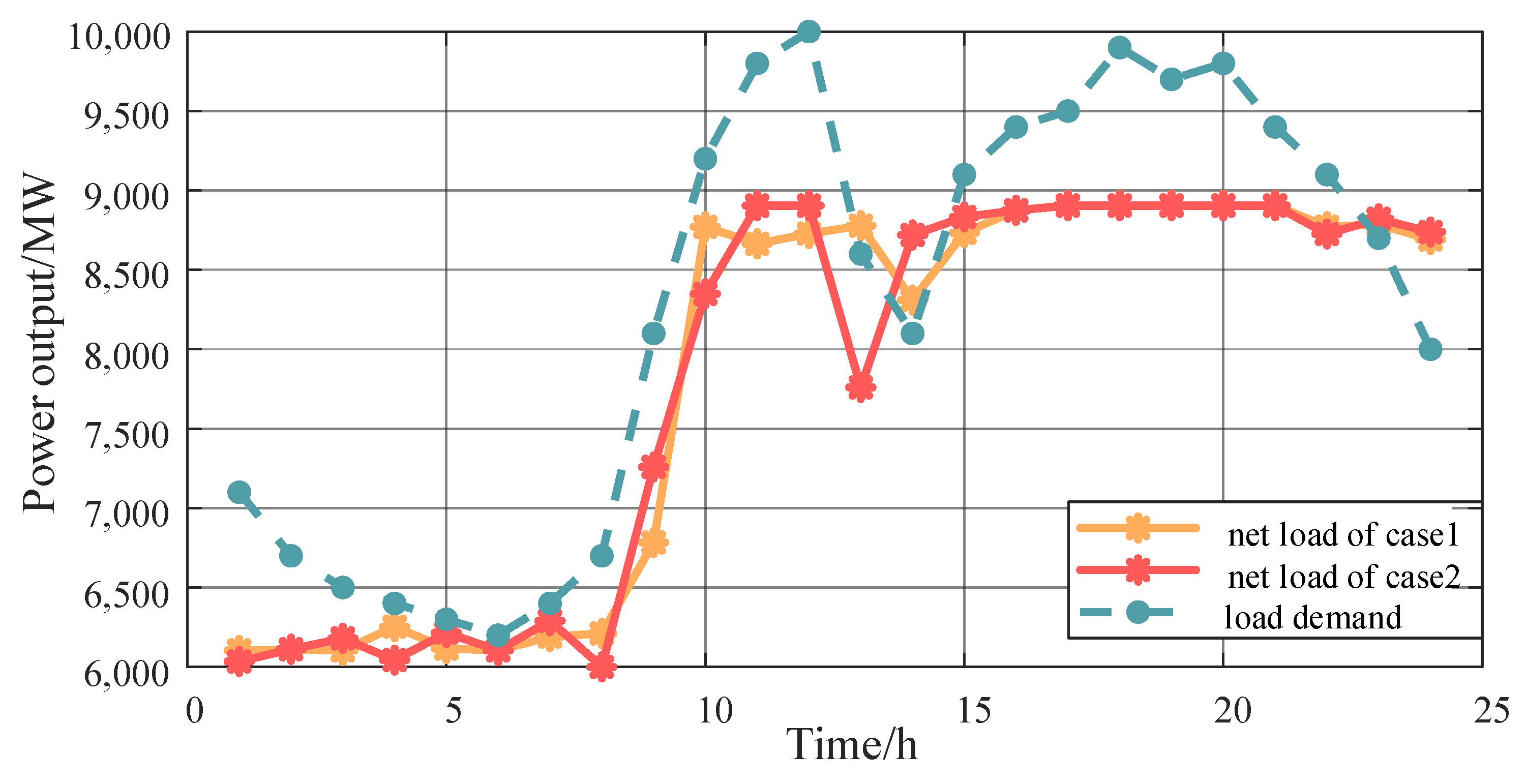
| Case 1 | Case 2 | |
|---|---|---|
| LCOE/(USD/kwh) | 0.047 | 0.042 |
| PVD/MW | 2472 | 2547 |
| POD/MW | 11.8 | 21.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, O.; Wu, F.; Ma, S.; Shi, L.; Hong, F. Multi-Objective Capacity Optimization of Grid-Connected Wind–Pumped Hydro Storage Hybrid Systems Considering Variable-Speed Operation. Energies 2023, 16, 8113. https://doi.org/10.3390/en16248113
Li Y, Li O, Wu F, Ma S, Shi L, Hong F. Multi-Objective Capacity Optimization of Grid-Connected Wind–Pumped Hydro Storage Hybrid Systems Considering Variable-Speed Operation. Energies. 2023; 16(24):8113. https://doi.org/10.3390/en16248113
Chicago/Turabian StyleLi, Yang, Outing Li, Feng Wu, Shiyi Ma, Linjun Shi, and Feilong Hong. 2023. "Multi-Objective Capacity Optimization of Grid-Connected Wind–Pumped Hydro Storage Hybrid Systems Considering Variable-Speed Operation" Energies 16, no. 24: 8113. https://doi.org/10.3390/en16248113
APA StyleLi, Y., Li, O., Wu, F., Ma, S., Shi, L., & Hong, F. (2023). Multi-Objective Capacity Optimization of Grid-Connected Wind–Pumped Hydro Storage Hybrid Systems Considering Variable-Speed Operation. Energies, 16(24), 8113. https://doi.org/10.3390/en16248113






