Increasing the Level of Autonomy of Control of the Electric Arc Furnace by Weakening Interphase Interactions
Abstract
:1. Introduction
2. Overview of the Proposed Approach
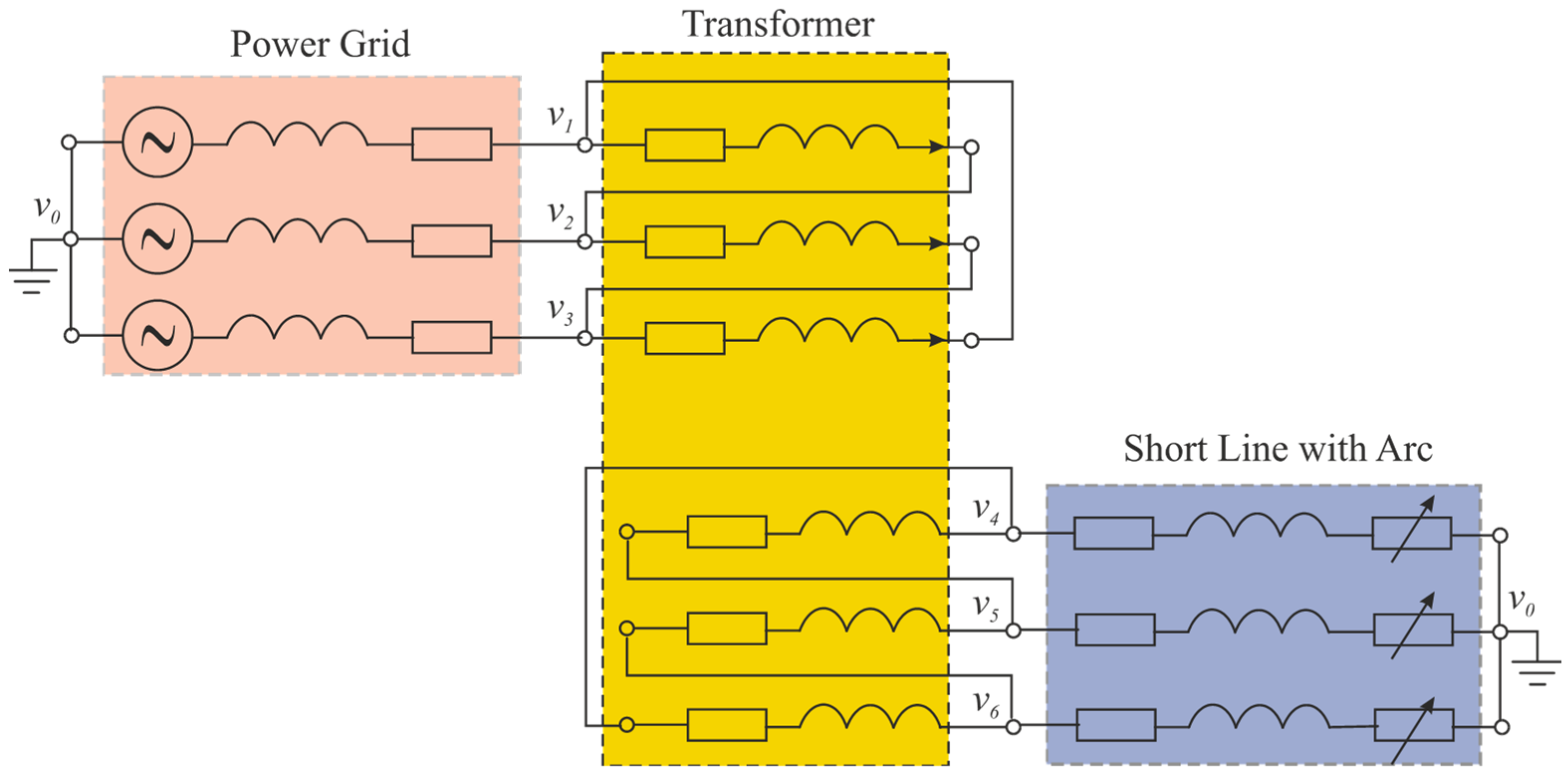
3. Mathematical Model for Conducting Research
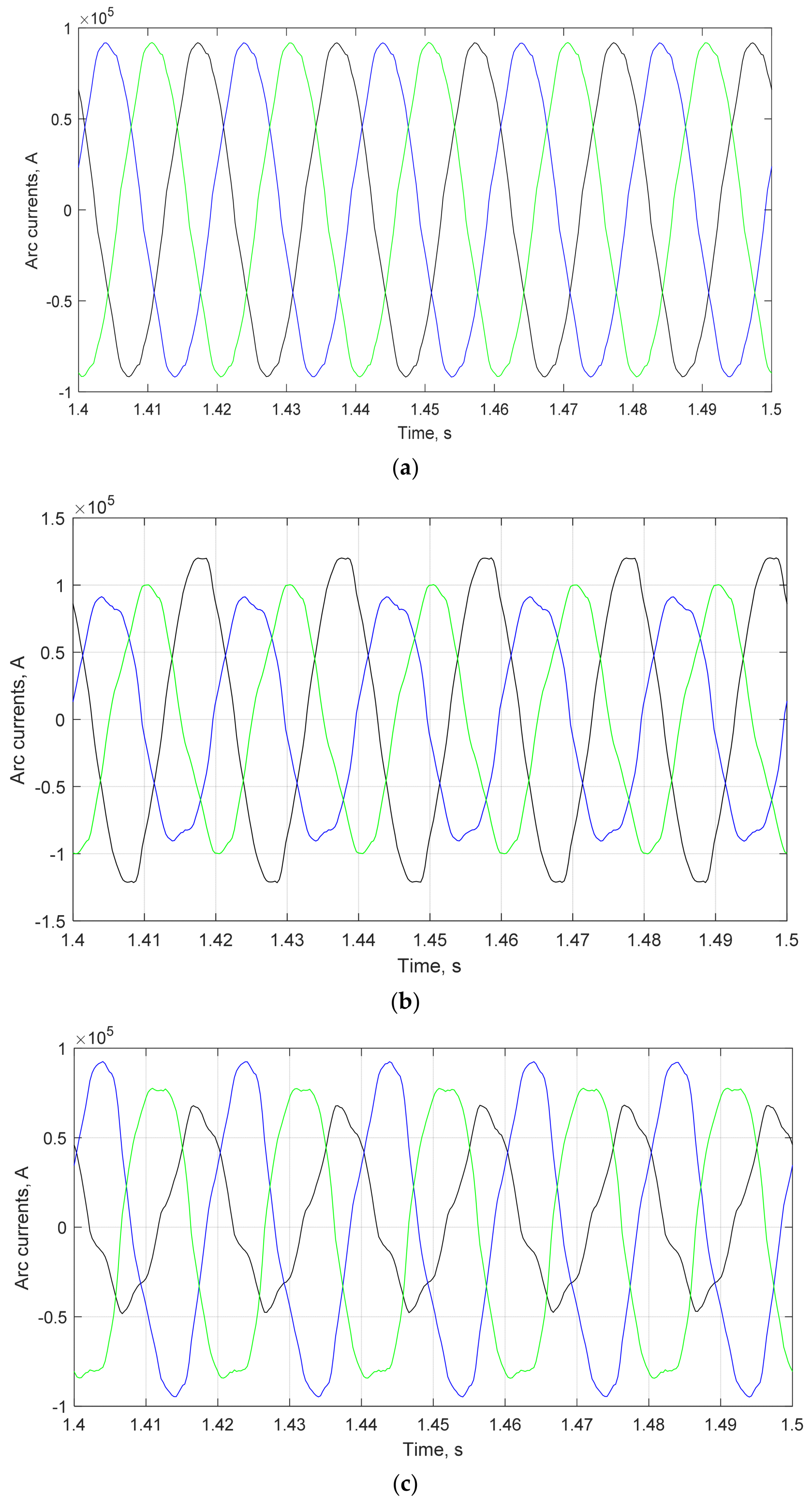
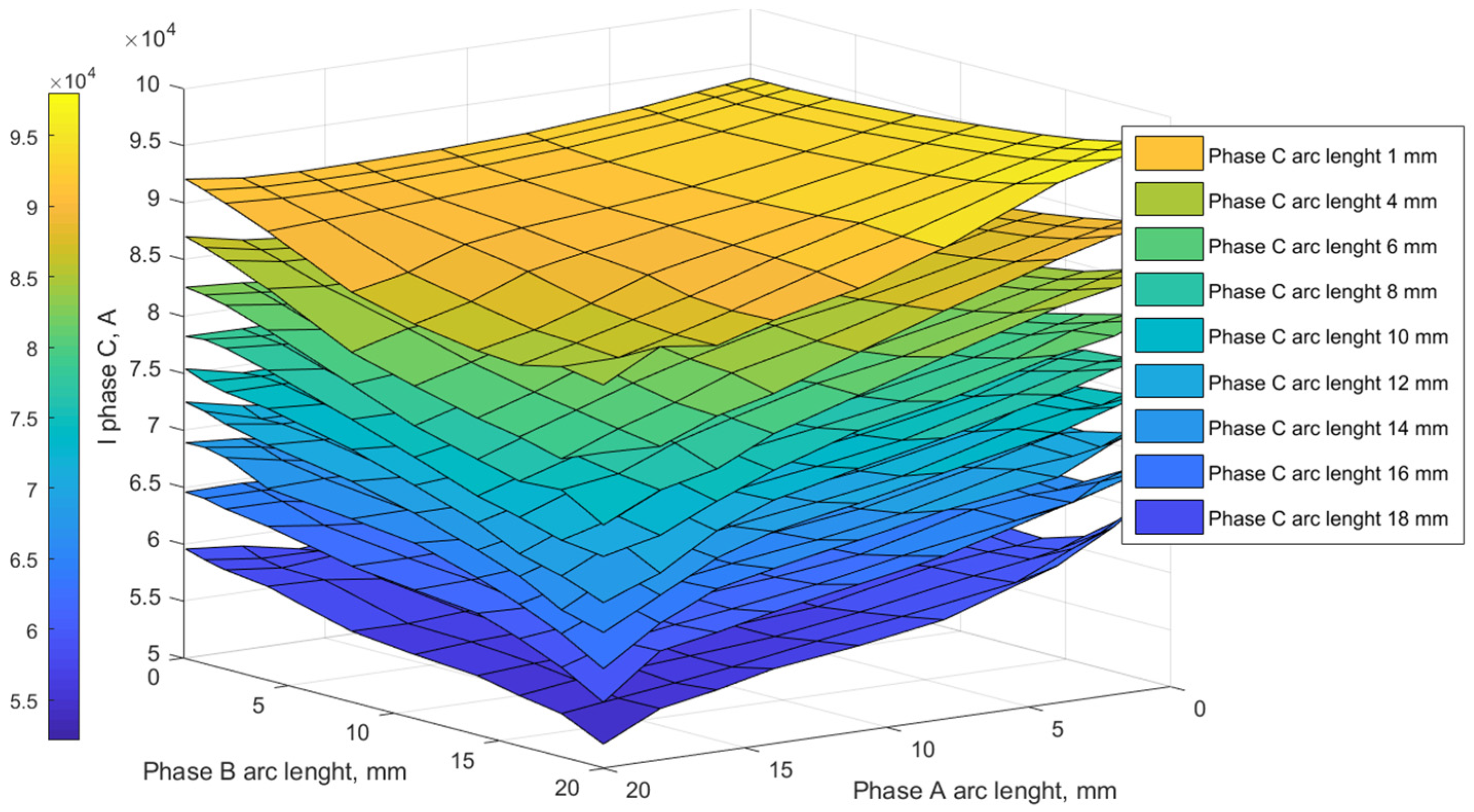
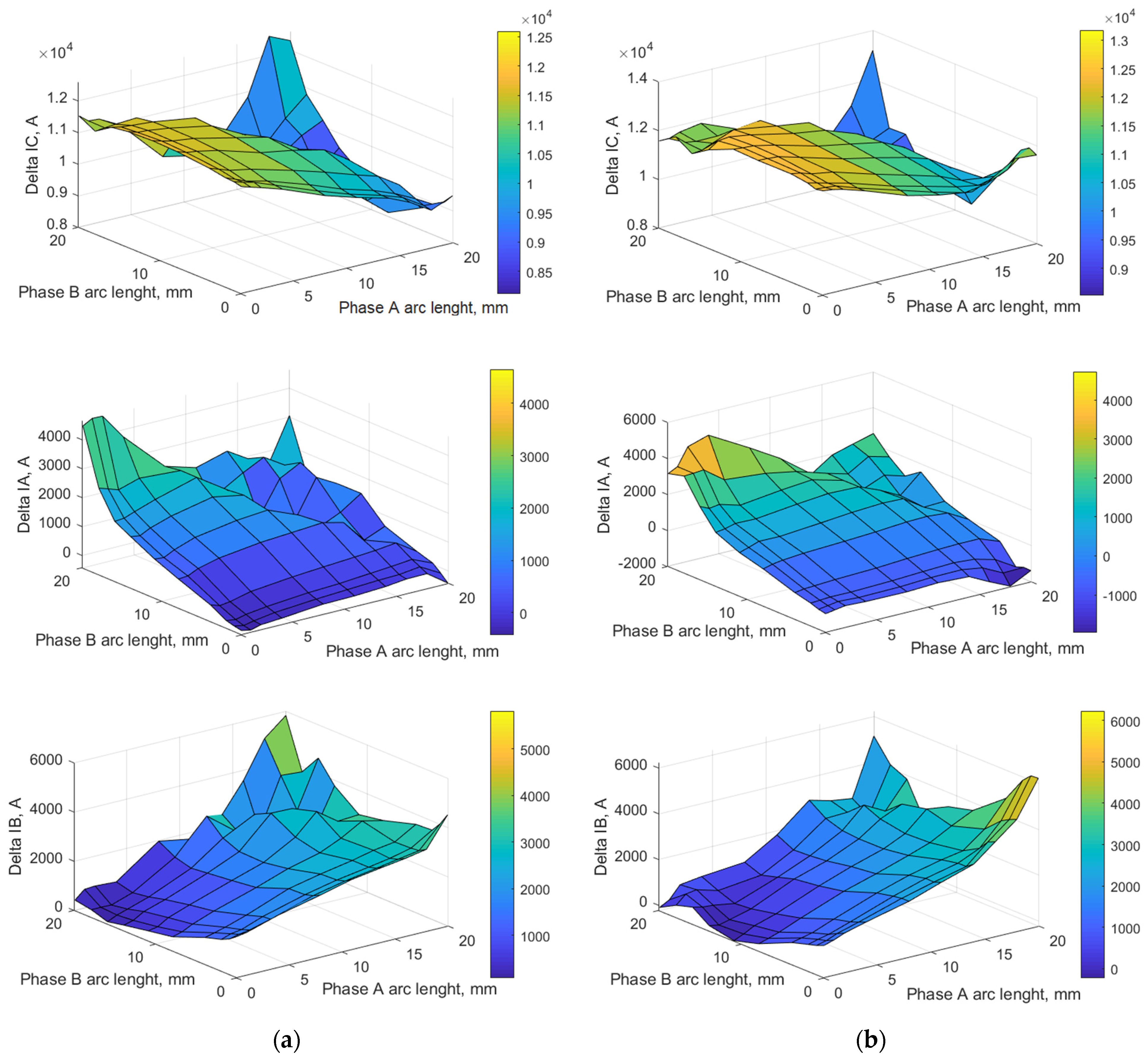
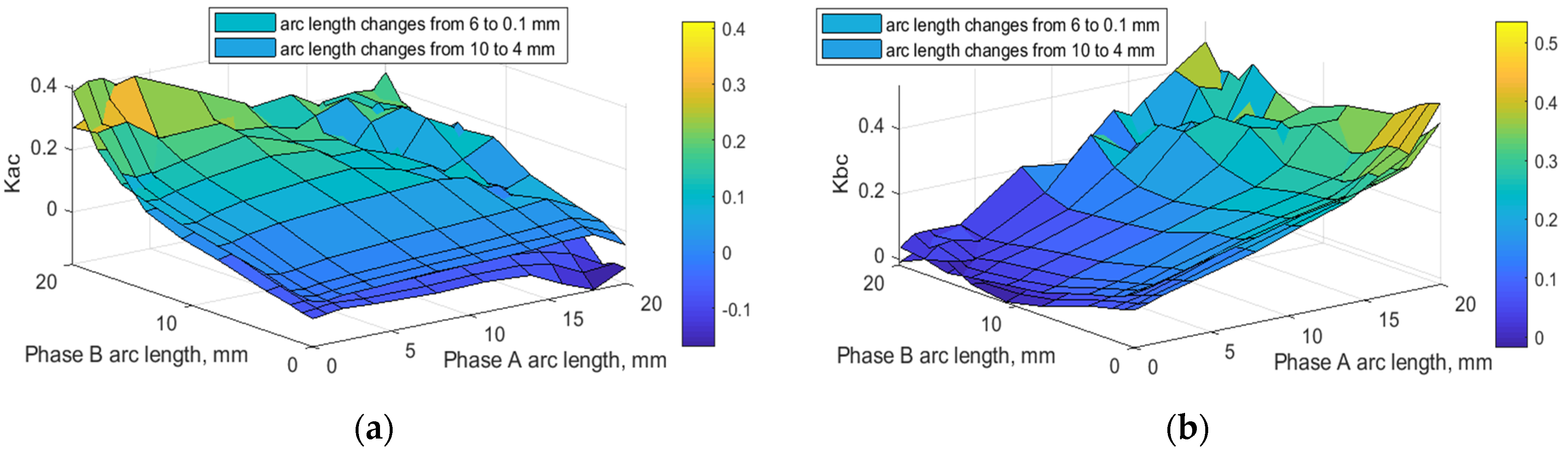
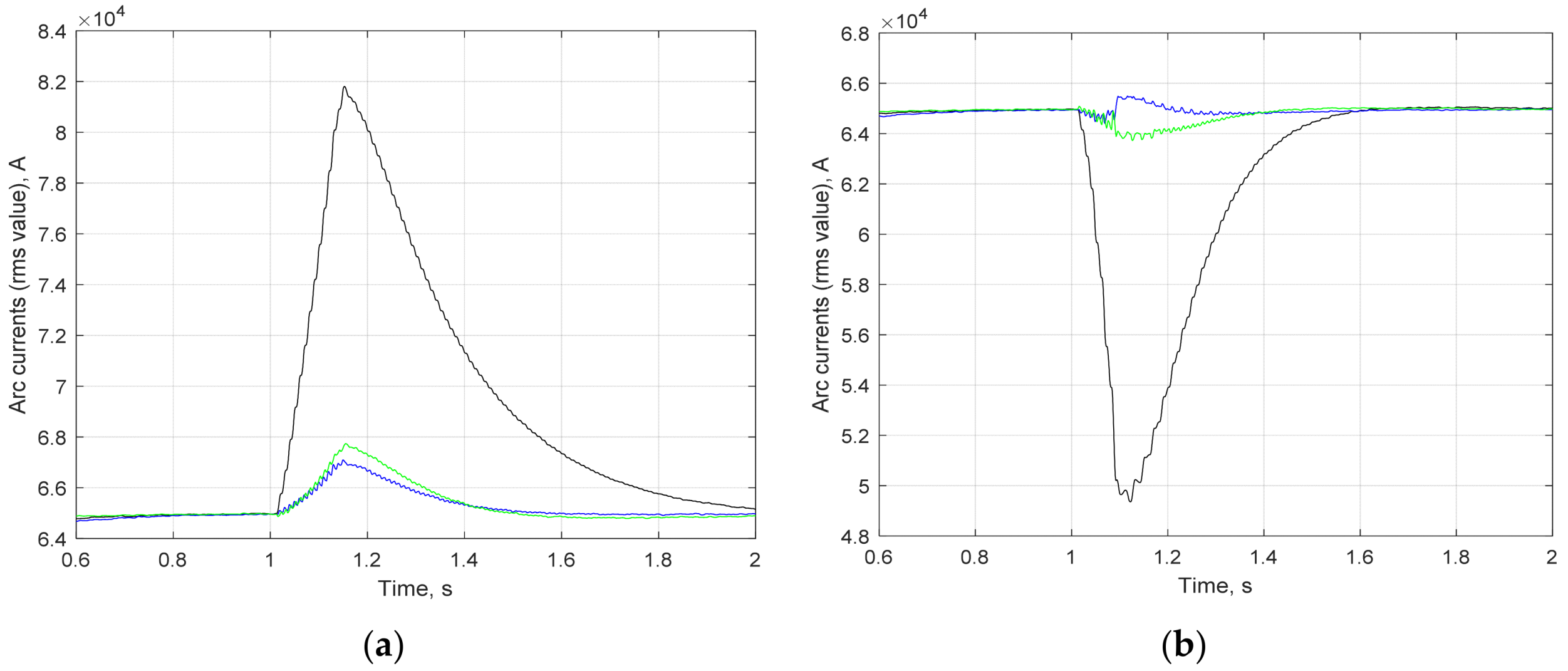
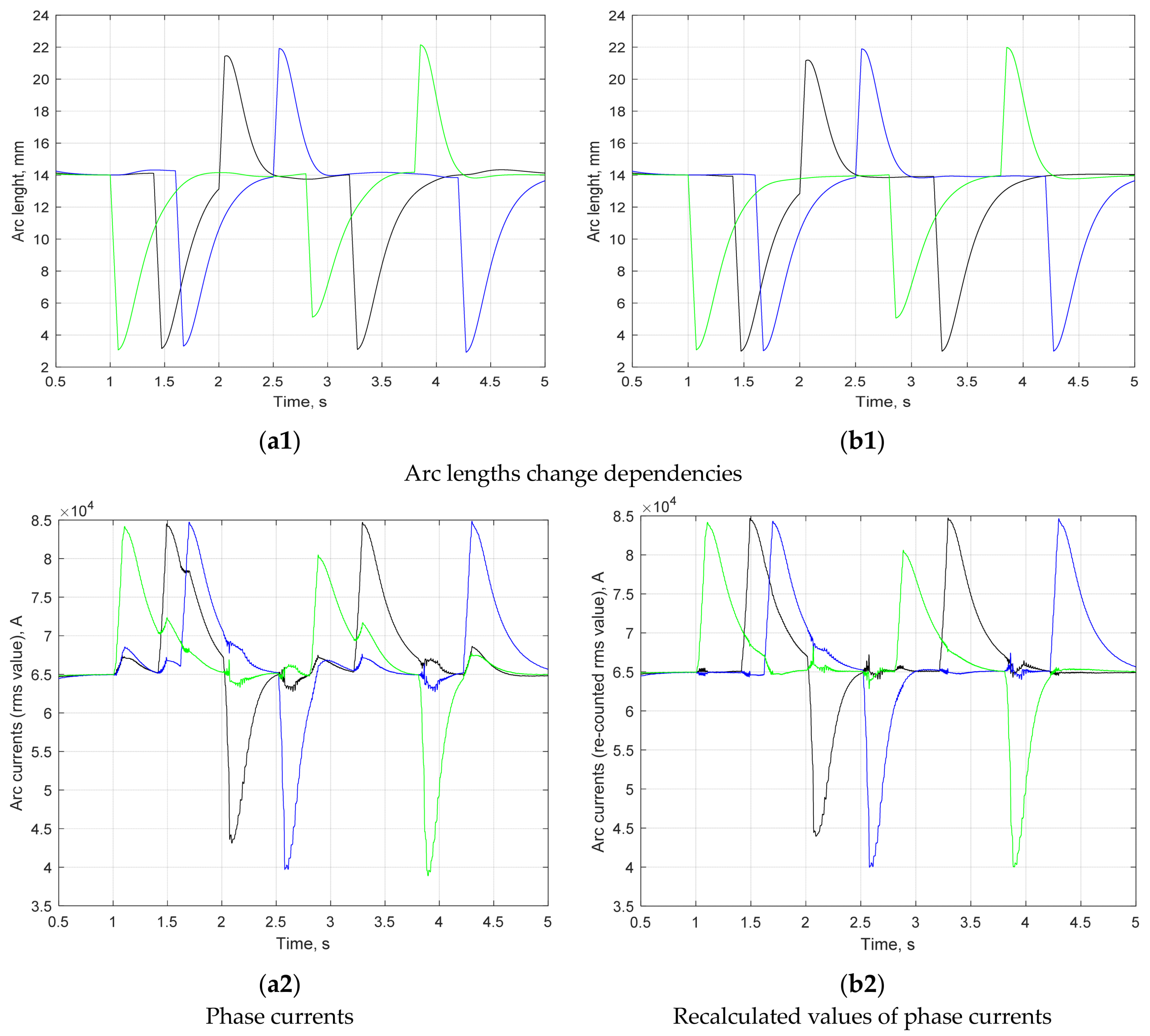
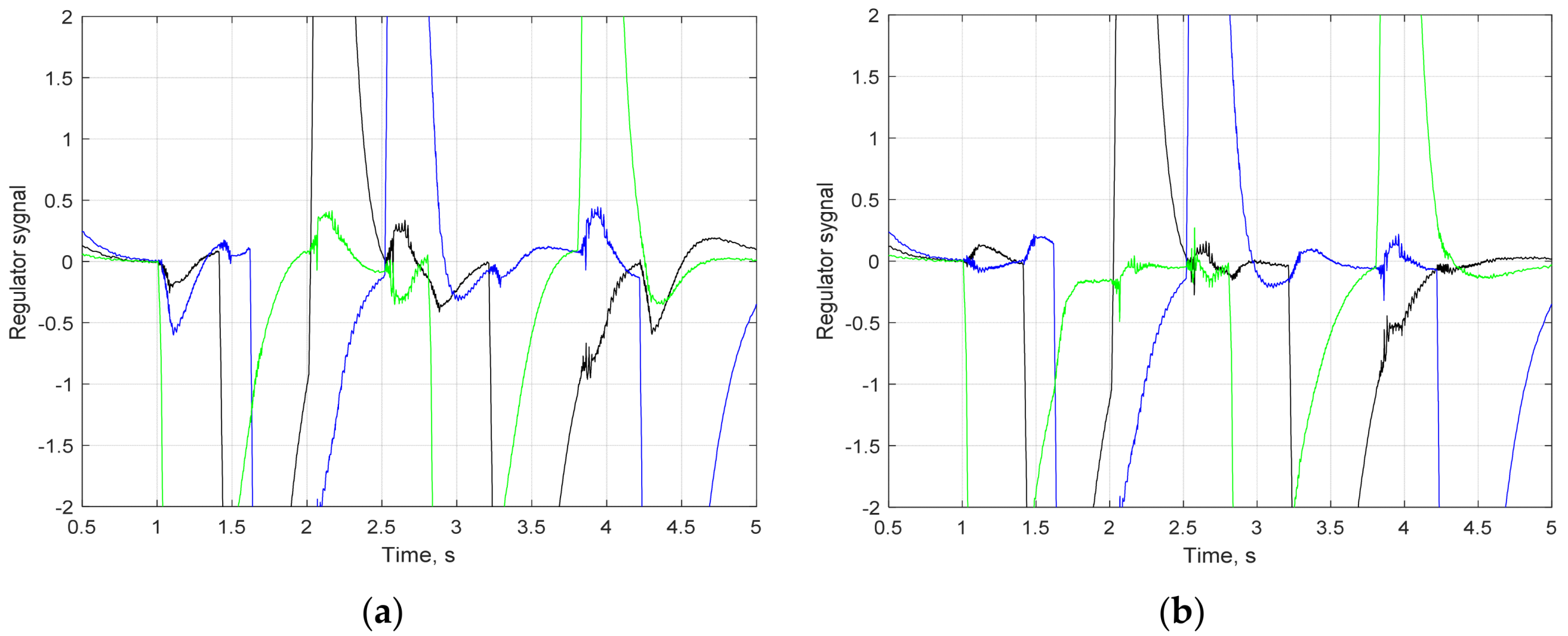
4. The Results of Research and Analysis of the Proposed Approach’s Effectiveness
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Framework of Measures for Strengthening Europe’s Net-Zero Technology Products Manufacturing Ecosystem (Net Zero Industry Act). Available online: https://www.europarl.europa.eu/doceo/document/TA-9-2023-0401_EN.pdf (accessed on 10 April 2023).
- Strengthening Sustainability|Decarbonizing Manufacturing Industries. Available online: https://www.ifc.org/content/dam/ifc/doc/2023-delta/ss-decarbonizing-manufacturing-industries-v8.pdf (accessed on 21 March 2023).
- Kim, J.; Sovacool, B.K.; Bazilian, M.; Griffiths, S.; Lee, J.; Yang, M.; Lee, J. Decarbonizing the iron and steel industry: A systematic review of sociotechnical systems, technological innovations, and policy options. Energy Res. Soc. Sci. 2022, 89, 102565. [Google Scholar] [CrossRef]
- Jia, L.; Cheng, P.; Yu, Y.; Chen, S.; Wang, C.; He, L.; Nie, H.; Wang, J.; Zhang, J.; Fan, B.; et al. Regeneration mechanism of a novel high-performance biochar mercury adsorbent directionally modified by multimetal multilayer loading. J. Environ. Manag. 2023, 326, 116790. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Sohn, I. Review of Innovative Energy Savings Technology for the Electric Arc Furnace. JOM 2014, 66, 1581–1594. [Google Scholar] [CrossRef]
- Li, L.; Mao, Z.Z. A novel robust adaptive controller for EAF electrode regulator system based on approximate model method. J. Cent. South Univ. 2012, 19, 2158–2166. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control Systems; Springer: London, UK, 2013; p. 549. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, X.; Wang, H. Feedback linearization control of the electric arc furnace electrode control system based on the dSPACE. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 1092–1095. [Google Scholar]
- Mintsa, H.A.; Venugopal, R.; Kenne, J.-P.; Belleau, C. Feedback Linearization-Based Position Control of an Electrohydraulic Servo System with Supply Pressure Uncertainty. IEEE Trans. Control Syst. Technol. 2012, 20, 1092–1099. [Google Scholar] [CrossRef]
- Smaoui, M.; Brun, X.; Thomasset, D. Systematic control of an electropneumatic system: Integrator backstepping and sliding mode control. IEEE Trans. Control Syst. Technol. 2006, 14, 905–913. [Google Scholar] [CrossRef]
- Liu, X.-H.; Gao, N. The robust adaptive control of arc furnace system based on backstepping method. In Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 6–8 July 2012; pp. 1987–1992. [Google Scholar] [CrossRef]
- Wen, Y.; Lou, X.; Wu, W.; Cui, B. Backstepping Boundary Control for a Class of Gantry Crane Systems. IEEE Trans. Cybern. 2022, 53, 5802–5814. [Google Scholar] [CrossRef]
- Patel, R.; Li, C.; Meegahapola, L.; McGrath, B.; Yu, X. Enhancing Optimal Automatic Generation Control in a Multi-Area Power System with Diverse Energy Resources. IEEE Trans. Power Syst. 2019, 34, 3465–3475. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, H. Coupling Control Strategy of Force and Displacement for Electric Differential Power Steering System of Electric Vehicle with Motorized Wheels. IEEE Trans. Veh. Technol. 2018, 67, 8118–8128. [Google Scholar] [CrossRef]
- Lu, K.; Liu, Z.; Yu, H.; Chen, C.L.P.; Zhang, Y. Decentralized Adaptive Neural Inverse Optimal Control of Nonlinear Interconnected Systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 8840–8851. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, Y.; Dong, N.; Wei, Q. Adaptive Critics for Decentralized Stabilization of Constrained-Input Nonlinear Interconnected Systems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4187–4199. [Google Scholar] [CrossRef]
- Ortega, R.; Loría, A.; Johan Nicklasson, P.; Sira-Ramírez, H. Passivity-based Control of Euler-Lagrange Systems. In Mechanical, Electrical and Electromechanical Applications; Springer: London, UK, 1998; p. 543. [Google Scholar] [CrossRef]
- Lee, W.; Yoo, S.; Nam, S.; Kim, K.; Chung, W.K. Passivity-Based Robust Compliance Control of Electro-Hydraulic Robot Manipulators with Joint Angle Limit. IEEE Robot. Autom. Lett. 2020, 5, 3190–3197. [Google Scholar] [CrossRef]
- Ortega, R.; Schaft, A.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Perzyński, T.; Kozyra, J.; Biletskyi, Y.; Kasha, L. The Interconnection and Damping Assignment Passivity-Based Control Synthesis via the Optimal Control Method for Electric Vehicle Subsystems. Energies 2021, 14, 3711. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Marushchak, Y.; Lozynskyy, O.; Kasha, L. Synthesis of Combine Feedback Control of Electromechanical System by Feedback Linearization Method. In Proceedings of the 2020 IEEE Problems of Automated Electrodrive. Theory and Practice (PAEP), Kremenchuk, Ukraine, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Sadeghian, A.R.; Lavers, J.D. Nonlinear black-box modeling of electric arc furnace: An application of fuzzy logic systems, FUZZ-IEEE’99. In Proceedings of the 1999 IEEE International Fuzzy Systems. Conference Proceedings (Cat. No.99CH36315), Seoul, Republic of Korea, 22–25 August 1999; Volume 1, pp. 234–239. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Vantsevitch, V.; Demkiv, L. Enhancement of dynamical characteristics of a fuzzy control system by using unstable subsystem. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Bu, F.; Zhuang, S.; Huang, W.; Su, N.; Hu, Y. Asymmetrical Operation Analysis for Dual Stator-Winding Induction Generator Variable Frequency AC Generating System with Unbalanced Loads. IEEE Trans. Ind. Electron. 2016, 64, 52–59. [Google Scholar] [CrossRef]
- Tanrioven, M.; Gulez, K. The determination and realization of compensation degrees in power control systems having load asymmetry by using fuzzy logic controller supported by artificial neural networks. In Proceedings of the MELECON ‘98. 9th Mediterranean Electrotechnical Conference, Proceedings (Cat. No. 98CH36056), Tel-Aviv, Israel, 18–20 May 1998; Volume 1, pp. 590–594. [Google Scholar] [CrossRef]
- Czarnecki, L.S.; Bhattarai, P.D. A Method of Calculating LC Parameters of Balancing Compensators for AC Arc Furnaces. IEEE Trans. Power Deliv. 2016, 32, 688–695. [Google Scholar] [CrossRef]
- Olczykowski, Z. Electric Arc Furnaces as a Cause of Current and Voltage Asymmetry. Energies 2021, 14, 5058. [Google Scholar] [CrossRef]
- Gała, M.; Sawicki, A.; Jagieła, K. Modeling of asymmetrical operating states of AC electric arc furnace in the power system. In Proceedings of the 2019 Applications of Electromagnetics in Modern Engineering and Medicine (PTZE), Janow Podlaski, Poland, 9–12 June 2019; pp. 42–46. [Google Scholar] [CrossRef]
- Comprehensive Industry Document on Electric Arc a Induction Furnaces. Available online: https://cpcb.nic.in/openpdffile.php?id=UHVibGljYXRpb25GaWxlLzIwXzE0NTY5ODUzMTZfUHVibGljYXRpb25fNTI0X0luZHVzdHJ5X2RvY3VtZW50LnBkZg== (accessed on 21 March 2023).
- Brusa, E.G.M.; Morsut, S. Design and Structural Optimization of the Electric Arc Furnace through a Mechatronic-Integrated Modeling Activity. IEEE/ASME Trans. Mechatron. 2014, 20, 1099–1107. [Google Scholar] [CrossRef]
- Kozyra, J.; Lozynskyy, A.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kutsyk, A.; Podskarbi, G.; Paranchuk, Y.; Kasha, L. Combined Control System for the Coordinates of the Electric Mode in the Electrotechnological Complex “Arc Steel Furnace-Power-Supply Network”. Energies 2022, 15, 5254. [Google Scholar] [CrossRef]
- Paranchuk, Y.; Lis, M. Double-Circuit Adaptive System of Fuzzy Phase-Autonomous and Energy-Efficient Control of Arc Furnace Electric Modes. Energies 2023, 16, 5350. [Google Scholar] [CrossRef]
- Köhle, S.; Madill, J.; Lichterbeck, R. Optimisation of High Voltage AC Electric Arc Furnace Control: Final Report; Directorate-General for Research and Innovation; Publications Office, European Commission: Brussels, Belgium, 2002. Available online: https://op.europa.eu/en/publication-detail/-/publication/bfd85b07-e9fe-4e69-8a75-1a87e6083a2c (accessed on 21 March 2023).
- Hoholyuk, O.; Stakhiv, P.; Paranchuk, Y.; Musykhina, N.; Rudyy, T.; Tsiapa, V. Study of the dynamics of arc length regulation of an arc furnace based on the fuzzy impedance-admittance law. In Proceedings of the 2023 24th International Conference on Computational Problems of Electrical Engineering (CPEE), Grybów, Poland, 10–13 September 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Electrode Regulation System. Available online: https://www.amiautomation.com/meltshops-solutions/electrode-regulation-systems/ (accessed on 21 March 2023).
- Q-REG+ Advanced Electrode Control System. Available online: https://www.dca.it/media/download/q-reg.pdf (accessed on 21 March 2023).
- Hubmer, R.; Döbbeler, A. Improved performance with modern automation solutions for electric steemaking. In Proceedings of the 17º Seminário de Automação, São Paulo, Brazil, 18 July 2013; pp. 318–328. [Google Scholar]
- Paranchuk, Y.; Jancarczyk, D.; Falat, P. Study and Analysis of Dynamics and Energy Efficiency of Arc Steelmaking Furnace Electrical Mode with a Fuzzy Control Algorithm. Energies 2023, 16, 3451. [Google Scholar] [CrossRef]
- Ghiormez, L.; Prostean, O. Electric arc current control for an electric arc furnace based on fuzzy logic. In Proceedings of the 2015 IEEE 10th Jubilee International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 21–23 May 2015; pp. 359–364. [Google Scholar] [CrossRef]
- Panoiu, M.; Panoiu, C.; Deaconu, S. Study about the possibility of electrodes motion control in the EAF based on adaptive impedance control. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 1409–1415. [Google Scholar] [CrossRef]
- Amado, S.; Crispín, H.; Martínez, P.; Haydee, R.O.; Malaquías, Q.P. Energy efficiency of an Electric Arc Furnace with SVM-RFE. In Proceedings of the 2015 International Conference on Electronics, Communications and Computers (CONIELECOMP), Cholula, Mexico, 25–27 February 2015; pp. 161–167. [Google Scholar] [CrossRef]
- Taslimian, M.; Shabaninia, F.; Vaziri, M.; Vadhva, S. Fuzzy type-2 electrode position controls for an Electric Arc Furnace. In Proceedings of the 2012 IEEE 13th International Conference on Information Reuse & Integration (IRI), Las Vegas, NV, USA, 8–10 August 2012; pp. 498–501. [Google Scholar] [CrossRef]
- Ghiormez, L.; Prostean, O.; Panoiu, M.; Panoiu, C. Fuzzy Logic and PD Control Strategies of a Three-Phase Electric Arc Furnace. In Computational Collective Intelligence, ICCCI 2016; Nguyen, N.T., Iliadis, L., Manolopoulos, Y., Trawiński, B., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9875. [Google Scholar] [CrossRef]
- Zhao, H.; Li, L. Research on Fuzzy-PID control strategy for AC arc furnace electrode regulator system. In Proceedings of the 2010 2nd International Conference on Industrial and Information Systems, Dalian, China, 10–11 July 2010; pp. 483–486. [Google Scholar] [CrossRef]
- Hong, H.; Mao, Z. Controller design for electrode regulating system of electric arc furnace. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 864–867. [Google Scholar] [CrossRef]
- Feliu-Batlle, V.; Rivas-Perez, R.; Castillo-Garcia, F.J.; Rodriguez-Martinez, C.A. A robust fractional order controller for an EAF electrode position system. IFAC Proc. Vol. 2014, 47, 10670–10675. [Google Scholar] [CrossRef]
- Jawahery, S.; Visuri, V.-V.; Wasbø, S.O.; Hammervold, A.; Hyttinen, N.; Schlautmann, M. Thermophysical Model for Online Optimization and Control of the Electric Arc Furnace. Metals 2021, 11, 1587. [Google Scholar] [CrossRef]
- Hay, T.; Visuri, V.-V.; Aula, M.; Echterhof, T. A Review of Mathematical Process Models for the Electric Arc Furnace Process. Steel Res. Int. 2020, 92, 2000395. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Kozyra, J.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kutsyk, A.; Paranchuk, Y.; Kasha, L. A Mathematical Model of Electrical Arc Furnaces for Analysis of Electrical Mode Parameters and Synthesis of Controlling Influences. Energies 2022, 15, 1623. [Google Scholar] [CrossRef]
- Klimas, M.; Grabowski, D. Application of long short-term memory neural networks for electric arc furnace modeling. Appl. Soft Comput. 2023, 145, 110574. [Google Scholar] [CrossRef]
- Lozynskyi, A.O.; Paranchuk, J.S.; Demkiv, L.I. Investigation of the electrodes movement system of arc furnace fuzzy controller. Tech. Electrodyn. 2014, 2, 73–77. (In Ukrainian) [Google Scholar]
- Zhang, S. Decoupling Control for Electrode System in Electric Arc Furnace based on Neural Network Inverse Identification. In Proceedings of the 6th International Conference on Intelligent Systems Design and Applications, Jian, China, 16–18 October 2006; pp. 112–116. [Google Scholar] [CrossRef]
- Kozyra, J.; Lozynskyy, A.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kutsyk, A.; Kasha, L. Electric Arc Furnace Electrode Movement Control System Based on a Fuzzy Arc Length Identifier. Energies 2023, 16, 7281. [Google Scholar] [CrossRef]
- Plakhtyna, O.; Kutsyk, A.; Lozynskyy, A. Method of average voltages in integration step: Theory and application. Electr. Eng. 2020, 102, 2413–2422. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozyra, J.; Lozynskyy, A.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kutsyk, A.; Kasha, L. Increasing the Level of Autonomy of Control of the Electric Arc Furnace by Weakening Interphase Interactions. Energies 2023, 16, 8114. https://doi.org/10.3390/en16248114
Kozyra J, Lozynskyy A, Łukasik Z, Kuśmińska-Fijałkowska A, Kutsyk A, Kasha L. Increasing the Level of Autonomy of Control of the Electric Arc Furnace by Weakening Interphase Interactions. Energies. 2023; 16(24):8114. https://doi.org/10.3390/en16248114
Chicago/Turabian StyleKozyra, Jacek, Andriy Lozynskyy, Zbigniew Łukasik, Aldona Kuśmińska-Fijałkowska, Andriy Kutsyk, and Lidiia Kasha. 2023. "Increasing the Level of Autonomy of Control of the Electric Arc Furnace by Weakening Interphase Interactions" Energies 16, no. 24: 8114. https://doi.org/10.3390/en16248114
APA StyleKozyra, J., Lozynskyy, A., Łukasik, Z., Kuśmińska-Fijałkowska, A., Kutsyk, A., & Kasha, L. (2023). Increasing the Level of Autonomy of Control of the Electric Arc Furnace by Weakening Interphase Interactions. Energies, 16(24), 8114. https://doi.org/10.3390/en16248114







