Lithium Battery State-of-Health Estimation Based on Sample Data Generation and Temporal Convolutional Neural Network
Abstract
:1. Introduction
| Methods | Authors, Year | Novelty | Result |
|---|---|---|---|
| WOA-Elman | Zhang et al. [20], 2023 | Health features are extracted based on surface temperature, incremental capacity, and differential voltage; SOH estimation using Elman neural network; optimization of Elman neural network parameters using the whale optimization algorithm (WOA). | Root mean square error less than 2% |
| CAE-BiLSTM | Zhu et al. [21], 2023 | Health features were extracted directly from the raw data with a convolutional auto-encoder (CAE); SOH estimation was performed using a bidirectional LSTM (BiLSTM) neural network. | Mean absolute error less than 2% |
| VMD-DBO-SVR | Wu et al. [22], 2023 | The SOH sequence is decomposed into a series of modal component subsequences by variational modal decomposition (VMD); the subsequences are predicted and reconstructed by support vector regression (SVR); the SVR model parameters are optimized using the dung beetle optimization algorithm (DBO). | Average absolute percentage error less than 2% |
| ECM-Transformer | Luo et al. [23], 2023 | Fitting electrochemical impedance spectra using equivalent circuits model (ECM); health features are extracted from the equivalent circuit parameters, and SOH estimation is performed using a transformer neural network. | Mean absolute percentage error less than 1.63% |
| ECM-ACO-EBM | Lin et al. [24], 2023 | Identify the internal resistance during constant-current charging using an equivalent circuit model; the SOH estimation model is built using the explanation boosting machine (EBM); optimization of EBM model parameters using ant colony optimization (ACO) algorithm. | Average absolute error less than 1% |
| EIS-GPR | Zhou et al. [25], 2022 | Geometrical properties of the electrochemical impedance spectrum (EIS) are found for the high and medium frequency cases; health features were extracted from the high-frequency and mid-frequency impedance spectra; the SOH estimation model was constructed using Gaussian process regression (GPR). | Root mean square error less than 1.12% |
| AR-RVM | Feng et al. [26], 2022 | A framework for battery SOH prediction was developed based on autoregressive (AR) model; an error compensation mechanism based on isobaric discharge time is constructed using a relevance vector machine (RVM). | Root mean square error less than 1% |
| EM-GWO-IRBFNN | Wu et al. [27], 2022 | An empirical model (EM) is proposed to describe the general trend of SOH decay; capacity regeneration of the battery is simulated using an improved radial basis function neural network (IRBFNN) as compensation for the empirical model; optimization of model parameters for IRBFNN using the gray wolf algorithm. | Root mean square error less than 1% |
- (1)
- Historical battery operating data were analyzed, from which features related to SOH decay were extracted;
- (2)
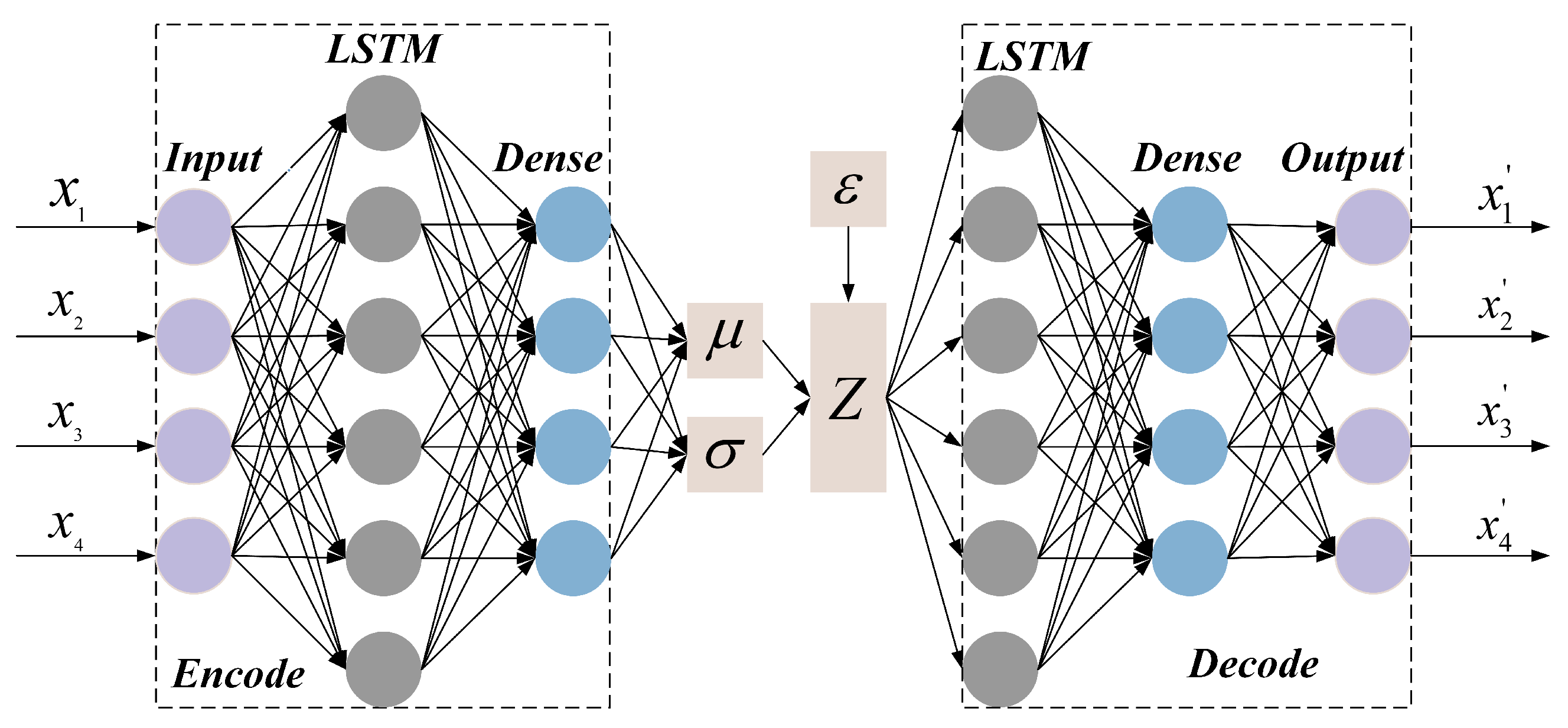
- A Variational Auto-Encoder (VAE) was built to generate data that are highly similar to the samples, which enriches the number of samples and solves the difficulty of model development in the case of a small number of samples;
- (3)
- A temporal convolutional neural network was built to capture the decaying trajectory of SOH accurately.
2. Introduction to the Dataset
2.1. SOH Definition
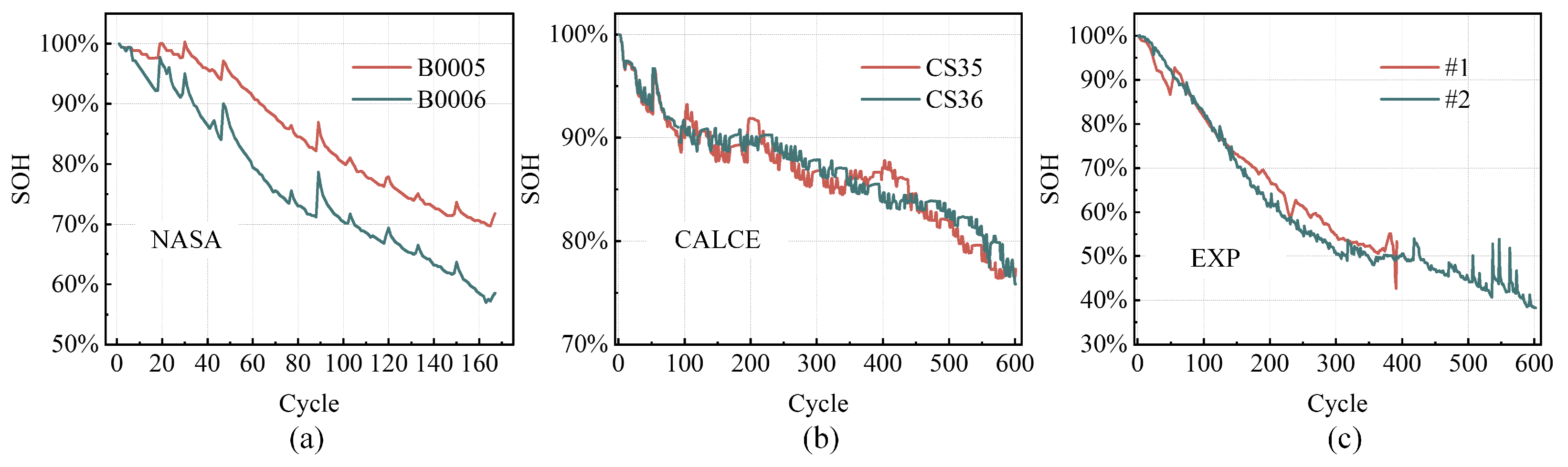
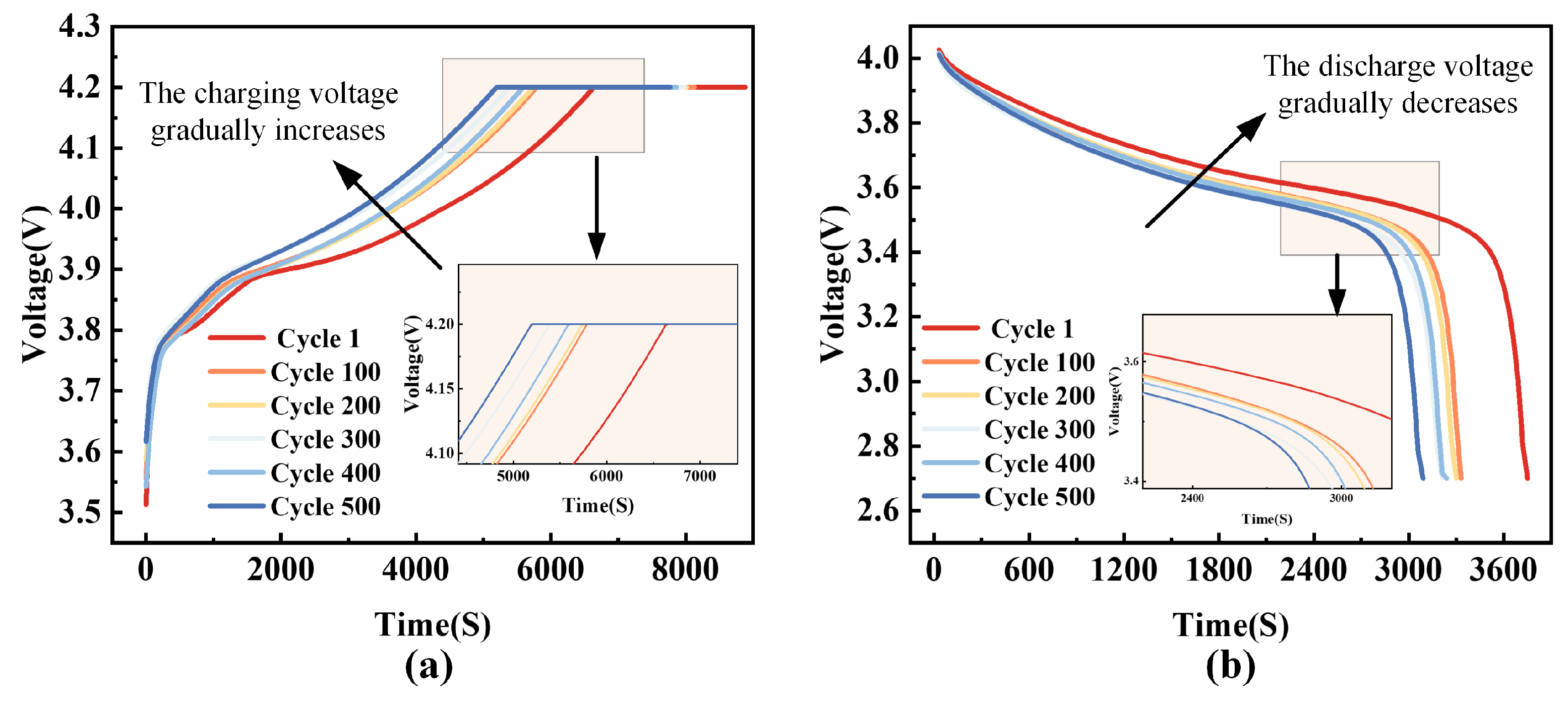
2.2. Battery Dataset
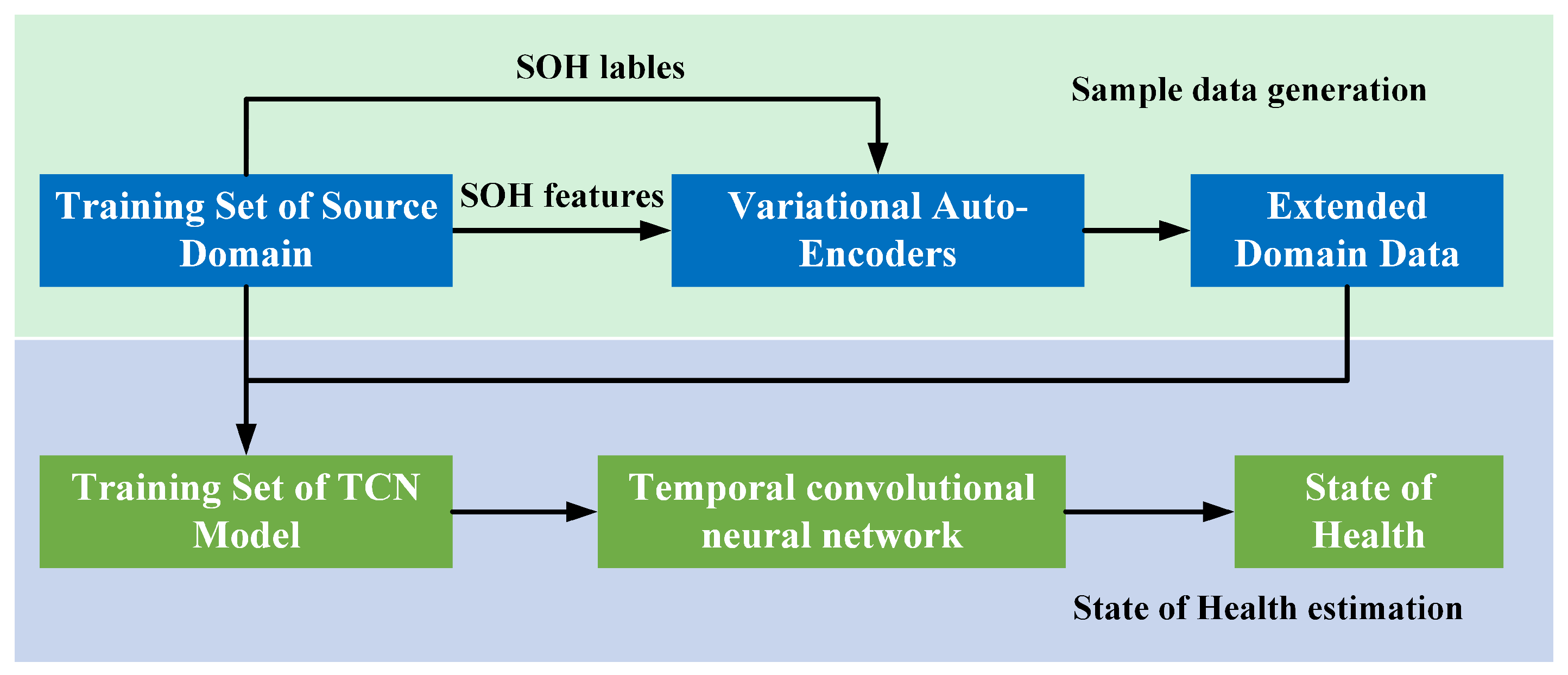
3. SOH Estimation Process
3.1. Feature Extraction
3.2. Variational Auto-Encoder
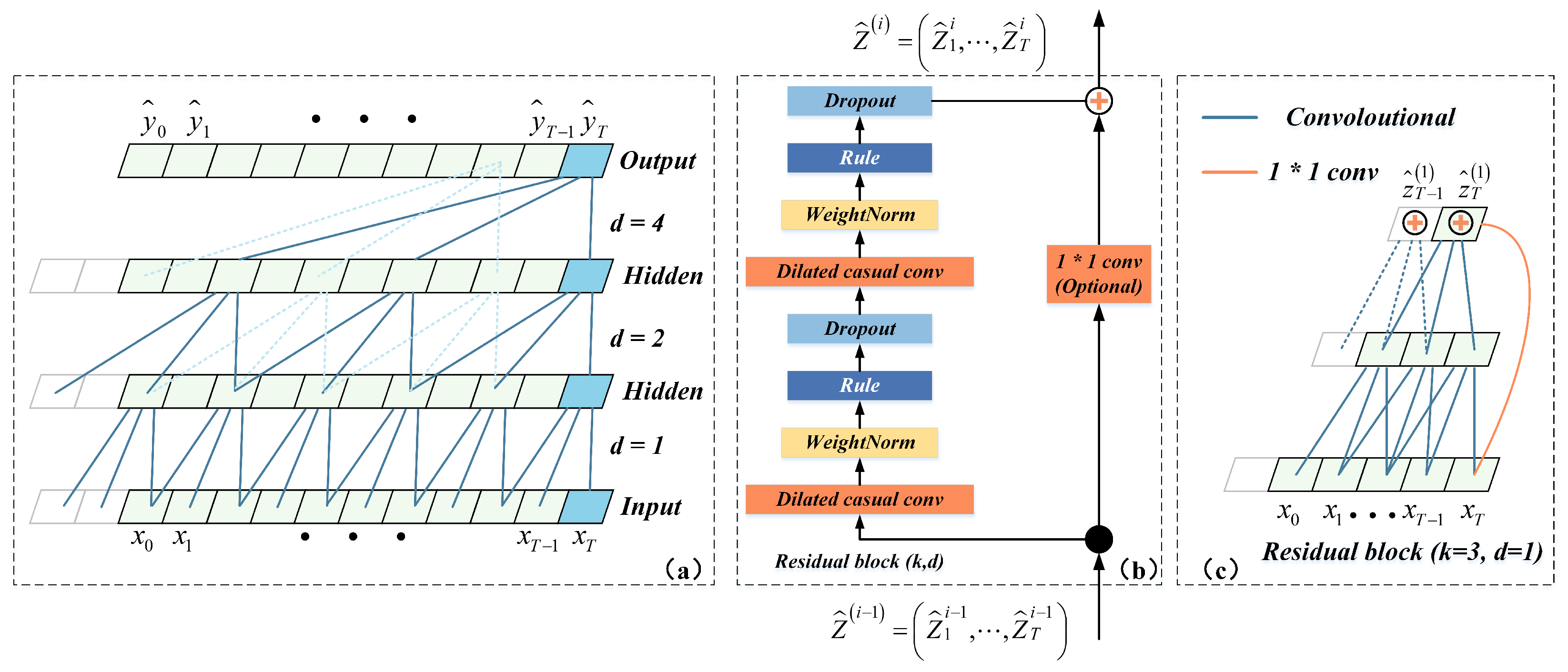
3.3. Temporal Convolutional Network
3.4. VAE-TCN Model
4. Results
4.1. Evaluation Indicators
4.2. Experimental Results
4.3. Model Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, T.; Huang, Y.; Xu, Y.; Jiang, J.; Liu, S.; Li, Z. SOH Prediction for Lithium-Ion Battery Based on Improved Support Vector Regression. Int. J. Green Energy 2022, 20, 227–236. [Google Scholar] [CrossRef]
- Zhang, W.; Qiu, J.; Yin, X.; Wang, D. A Novel Heat Pipe Assisted Separation Type Battery Thermal Management System Based on Phase Change Material. Appl. Therm. Eng. 2020, 165, 114571. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Wang, J.; Zhang, T. State-of-Health Estimation for Lithium-Ion Batteries by Combining Model-Based Incremental Capacity Analysis with Support Vector Regression. Energy 2022, 239, 121986. [Google Scholar] [CrossRef]
- Zhang, J.; Lee, J. A Review on Prognostics and Health Monitoring of Li-ion Battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Chen, Y.; Duan, W.; Ding, Z.; Li, Y. Battery Life Prediction Based on a Hybrid Support Vector Regression Model. Front. Energy Res. 2022, 10, 899804. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, C.; Jiang, J.; Zhang, W.; Zhang, L.; Wang, Y. Review on State-of-Health of Lithium-Ion Batteries: Characterizations, Estimations and Applications. J. Clean. Prod. 2021, 314, 128015. [Google Scholar] [CrossRef]
- Tang, X.; Liu, K.; Wang, X.; Gao, F.; Macro, J.; Widanage, W.D. Model Migration Neural Network for Predicting Battery Aging Trajectories. IEEE Trans. Transp. Electrif. 2020, 6, 363–374. [Google Scholar] [CrossRef]
- Ospina Agudelo, B.; Zamboni, W.; Monmasson, E. Application Domain Extension of Incremental Capacity-Based Battery SoH Indicators. Energy 2021, 234, 121224. [Google Scholar] [CrossRef]
- Gu, X.; See, K.; Li, P.; Shan, K.; Wang, Y.; Zhao, L.; Lim, K.C.; Zhang, N. A Novel State-of-Health Estimation for the Lithium-Ion Battery Using a Convolutional Neural Network and Transformer Model. Energy 2023, 262, 125501. [Google Scholar] [CrossRef]
- Sun, T.; Wu, R.; Cui, Y.; Zheng, Y. Sequent Extended Kalman Filter Capacity Estimation Method for Lithium-Ion Batteries Based on Discrete Battery Aging Model and Support Vector Machine. J. Energy Storage 2021, 39, 102594. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Zhao, X.; Wang, Y.; He, Z. Online State of Charge Estimation of Li-ion Battery Based on an Improved Unscented Kalman Filter Approach. Appl. Math. Model. 2019, 70, 532–544. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Gong, Q.; Cheng, Z. SOH Estimation of Lithium-Ion Batteries Based on Least Squares Support Vector Machine Error Compensation Model. J. Power Electron. 2021, 21, 1712–1723. [Google Scholar] [CrossRef]
- Song, L.; Zhang, K.; Liang, T.; Han, X.; Zhang, Y. Intelligent State of Health Estimation for Lithium-Ion Battery Pack Based on Big Data Analysis. J. Energy Storage 2020, 32, 101836. [Google Scholar] [CrossRef]
- Li, S.; He, H.; Zhao, P.; Cheng, S. Health-Conscious Vehicle Battery State Estimation Based on Deep Transfer Learning. Appl. Energy 2022, 316, 119120. [Google Scholar] [CrossRef]
- Chen, L.; Wang, H.; Liu, B.; Wang, Y.; Ding, Y.; Pan, H. Battery State-of-Health Estimation Based on a Metabolic Extreme Learning Machine Combining Degradation State Model and Error Compensation. Energy 2021, 215, 119078. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of Health Estimation of Lithium-Ion Battery Based on Improved Ant Lion Optimization and Support Vector Regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Chang, C.; Wang, Q.; Jiang, J.; Wu, T. Lithium-Ion Battery State of Health Estimation Using the Incremental Capacity and Wavelet Neural Networks with Genetic Algorithm. J. Energy Storage 2021, 38, 102570. [Google Scholar] [CrossRef]
- Deng, Z.; Lin, X.; Cai, J.; Hu, X. Battery Health Estimation with Degradation Pattern Recognition and Transfer Learning. J. Power Sources 2022, 525, 231027. [Google Scholar] [CrossRef]
- Wu, J.; Cui, X.; Meng, J.; Peng, J.; Lin, M. Data-Driven Transfer-Stacking-Based State of Health Estimation for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2024, 71, 604–614. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Ma, R.; Zhao, Y.; Shi, M.; Qu, W. Prediction of Lithium Battery Health State Based on Temperature Rate of Change and Incremental Capacity Change. Energies 2023, 16, 7581. [Google Scholar] [CrossRef]
- Zhu, C.; Gao, M.; He, Z.; Wu, H.; Sun, C.; Zhang, Z.; Bao, Z. State of Health Prediction for Li-Ion Batteries with End-to-End Deep Learning. J. Energy Storage 2023, 65, 107218. [Google Scholar] [CrossRef]
- Wu, C.; Fu, J.; Huang, X.; Xu, X.; Meng, J. Lithium-Ion Battery Health State Prediction Based on VMD and DBO-SVR. Energies 2023, 16, 3993. [Google Scholar] [CrossRef]
- Luo, K.; Zheng, H.; Shi, Z. A Simple Feature Extraction Method for Estimating the Whole Life Cycle State of Health of Lithium-Ion Batteries Using Transformer-Based Neural Network. J. Power Sources 2023, 576, 233139. [Google Scholar] [CrossRef]
- Lin, M.; Yan, C.; Wang, W.; Dong, G.; Meng, J.; Wu, J. A Data-Driven Approach for Estimating State-of-Health of Lithium-Ion Batteries Considering Internal Resistance. Energy 2023, 277, 127675. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, G.; Tan, Q.; Han, X.; Chen, C.; Wei, J. State of Health Estimation for Lithium-Ion Batteries Using Geometric Impedance Spectrum Features and Recurrent Gaussian Process Regression. Energy 2023, 262, 125514. [Google Scholar] [CrossRef]
- Feng, H.; Yan, H. State of Health Estimation of Large-Cycle Lithium-Ion Batteries Based on Error Compensation of Autoregressive Model. J. Energy Storage 2022, 52, 104869. [Google Scholar] [CrossRef]
- Wu, J.; Fang, L.; Dong, G.; Lin, M. State of Health Estimation of Lithium-Ion Battery with Improved Radial Basis Function Neural Network. Energy 2023, 262, 125380. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A Novel Gaussian Process Regression Model for State-of-Health Estimation of Lithium-Ion Battery Using Charging Curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Xu, W.; Wang, S.; Jiang, C.; Fernandez, C.; Yu, C.; Fan, Y.; Cao, W. A Novel Adaptive Dual Extended Kalman Filtering Algorithm for the Li-ion Battery State of Charge and State of Health Co-estimation. Int. J. Energy Res. 2021, 45, 14592–14602. [Google Scholar] [CrossRef]
- Tang, T.; Yuan, H. The Capacity Prediction of Li-ion Batteries Based on a New Feature Extraction Technique and an Improved Extreme Learning Machine Algorithm. J. Power Sources 2021, 514, 230572. [Google Scholar] [CrossRef]
- Tan, X.; Liu, X.; Wang, H.; Fan, Y.; Feng, G. Intelligent Online Health Estimation for Lithium-Ion Batteries Based on a Parallel Attention Network Combining Multivariate Time Series. Front. Energy Res. 2022, 10, 844985. [Google Scholar] [CrossRef]
- Deng, Y.; Ying, H.; E, J.; Zhu, H.; Wei, K.; Chen, J.; Zhang, F.; Liao, G. Feature Parameter Extraction and Intelligent Estimation of the State-of-Health of Lithium-Ion Batteries. Energy 2019, 176, 91–102. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2022, arXiv:1312.6114. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Guo, F.; Huang, G.; Zhang, W.; Liu, G.; Li, T.; Ouyang, N.; Zhu, S. State of Health Estimation Method for Lithium Batteries Based on Electrochemical Impedance Spectroscopy and Pseudo-Image Feature Extraction. Measurement 2023, 220, 113412. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L.; Lopes, A.M.; Li, X.; Xie, S.; Li, P.; Chen, Y. Hybrid Deep Neural Network with Dimension Attention for State-of-Health Estimation of Lithium-ion Batteries. Energy 2023, 278, 127734. [Google Scholar] [CrossRef]
- Pan, R.; Liu, T.; Huang, W.; Wang, Y.; Yang, D.; Chen, J. State of Health Estimation for Lithium-Ion Batteries Based on Two-Stage Features Extraction and Gradient Boosting Decision Tree. Energy 2023, 129460. [Google Scholar] [CrossRef]

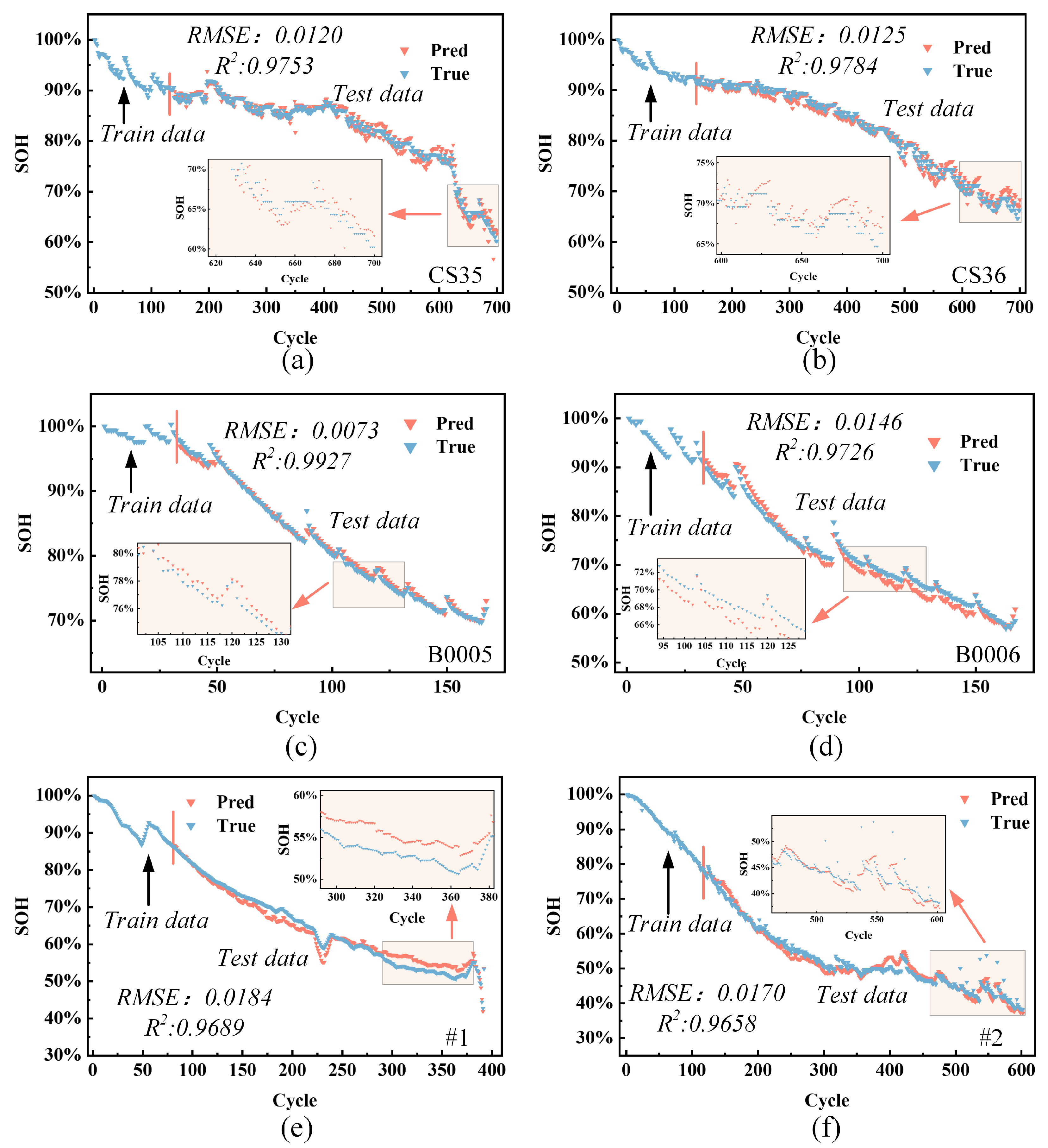

| Battery | Accuracy | |||
|---|---|---|---|---|
| RMSE | MAE | MAPE | R2 | |
| CS35 | 0.0120 | 0.0089 | 0.0115 | 0.9753 |
| CS36 | 0.0125 | 0.0093 | 0.0120 | 0.9784 |
| B0005 | 0.0073 | 0.0058 | 0.0072 | 0.9927 |
| B0006 | 0.0146 | 0.0129 | 0.0181 | 0.9726 |
| #1 | 0.0184 | 0.0156 | 0.0260 | 0.9689 |
| #2 | 0.0170 | 0.0134 | 0.0260 | 0.9658 |
| Battery | Model | Accuracy | |||
|---|---|---|---|---|---|
| RMSE | MAE | MAPE | R2 | ||
| CS35 | LSTM | 0.0255 | 0.0189 | 0.0251 | 0.8882 |
| TCN | 0.0192 | 0.0121 | 0.0165 | 0.9367 | |
| VAE-TCN | 0.0120 | 0.0089 | 0.0115 | 0.9753 | |
| CS36 | LSTM | 0.0237 | 0.0164 | 0.0223 | 0.9215 |
| TCN | 0.0168 | 0.0145 | 0.0178 | 0.9606 | |
| VAE-TCN | 0.0125 | 0.0093 | 0.0120 | 0.9784 | |
| B0005 | LSTM | 0.0394 | 0.0367 | 0.0471 | 0.7879 |
| TCN | 0.0208 | 0.0192 | 0.0232 | 0.9409 | |
| VAE-TCN | 0.0073 | 0.0058 | 0.0072 | 0.9927 | |
| B0006 | LSTM | 0.0352 | 0.0313 | 0.0466 | 0.8400 |
| TCN | 0.0203 | 0.0175 | 0.0251 | 0.9467 | |
| VAE-TCN | 0.0146 | 0.0129 | 0.0181 | 0.9726 | |
| #1 | LSTM | 0.0287 | 0.0243 | 0.0419 | 0.9246 |
| TCN | 0.0238 | 0.0161 | 0.0269 | 0.9484 | |
| VAE-TCN | 0.0184 | 0.0156 | 0.0260 | 0.9689 | |
| #2 | LSTM | 0.0396 | 0.0354 | 0.0740 | 0.8117 |
| TCN | 0.0260 | 0.0219 | 0.0415 | 0.9191 | |
| VAE-TCN | 0.0170 | 0.0134 | 0.0260 | 0.9658 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Huang, G.; Zhang, W.; Wen, A.; Li, T.; He, H.; Huang, H.; Zhu, S. Lithium Battery State-of-Health Estimation Based on Sample Data Generation and Temporal Convolutional Neural Network. Energies 2023, 16, 8010. https://doi.org/10.3390/en16248010
Guo F, Huang G, Zhang W, Wen A, Li T, He H, Huang H, Zhu S. Lithium Battery State-of-Health Estimation Based on Sample Data Generation and Temporal Convolutional Neural Network. Energies. 2023; 16(24):8010. https://doi.org/10.3390/en16248010
Chicago/Turabian StyleGuo, Fang, Guangshan Huang, Wencan Zhang, An Wen, Taotao Li, Hancheng He, Haolin Huang, and Shanshan Zhu. 2023. "Lithium Battery State-of-Health Estimation Based on Sample Data Generation and Temporal Convolutional Neural Network" Energies 16, no. 24: 8010. https://doi.org/10.3390/en16248010
APA StyleGuo, F., Huang, G., Zhang, W., Wen, A., Li, T., He, H., Huang, H., & Zhu, S. (2023). Lithium Battery State-of-Health Estimation Based on Sample Data Generation and Temporal Convolutional Neural Network. Energies, 16(24), 8010. https://doi.org/10.3390/en16248010






