Electromagnetic Vibration Analysis of Transverse Flux Permanent Magnet Linear Submersible Motor for Oil Production
Abstract
:1. Introduction
2. The Structure and Operating Principle of TFPMLSM
2.1. Structure of TFPMLSM
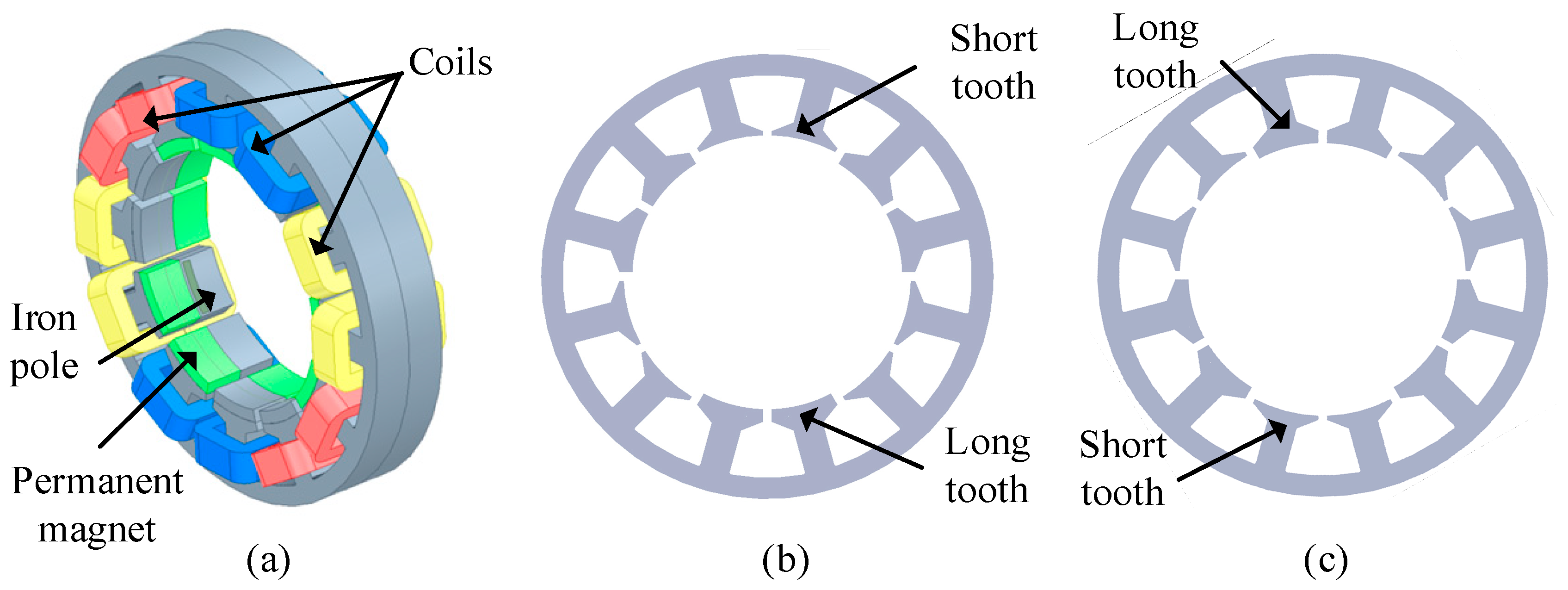
2.1.1. Primary Structure
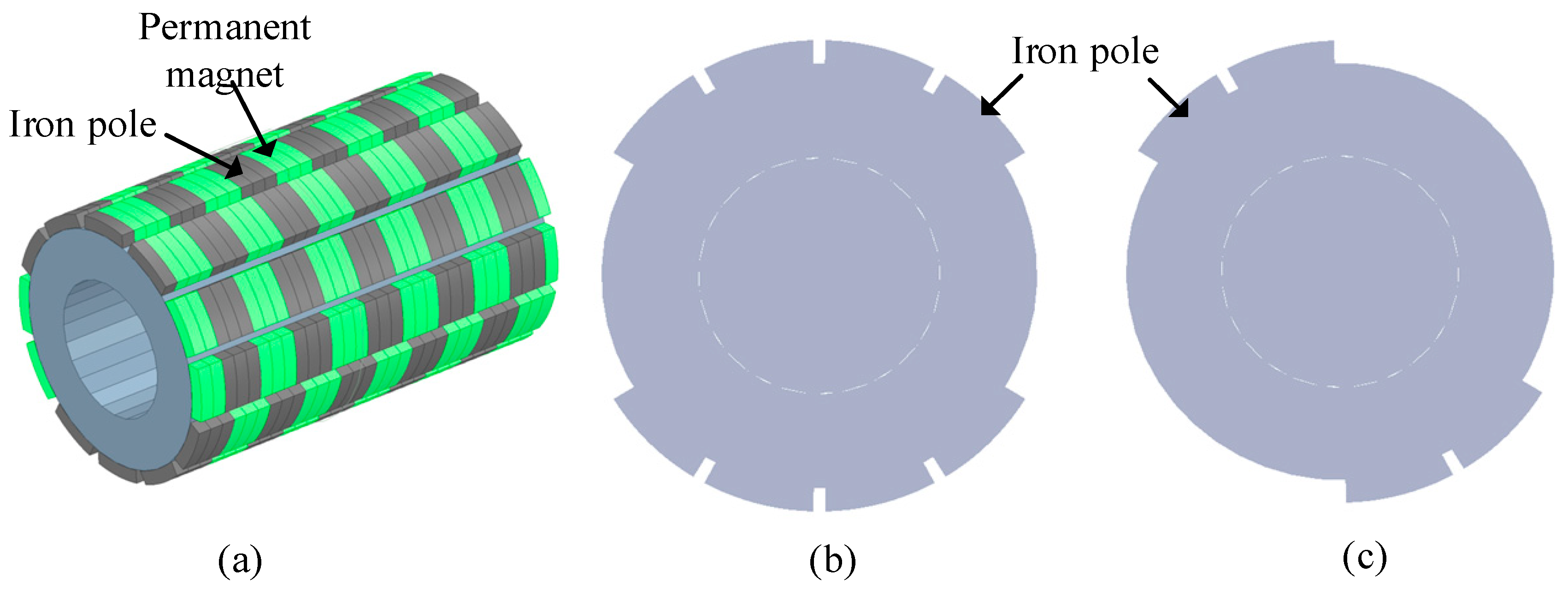
2.1.2. Secondary Structure
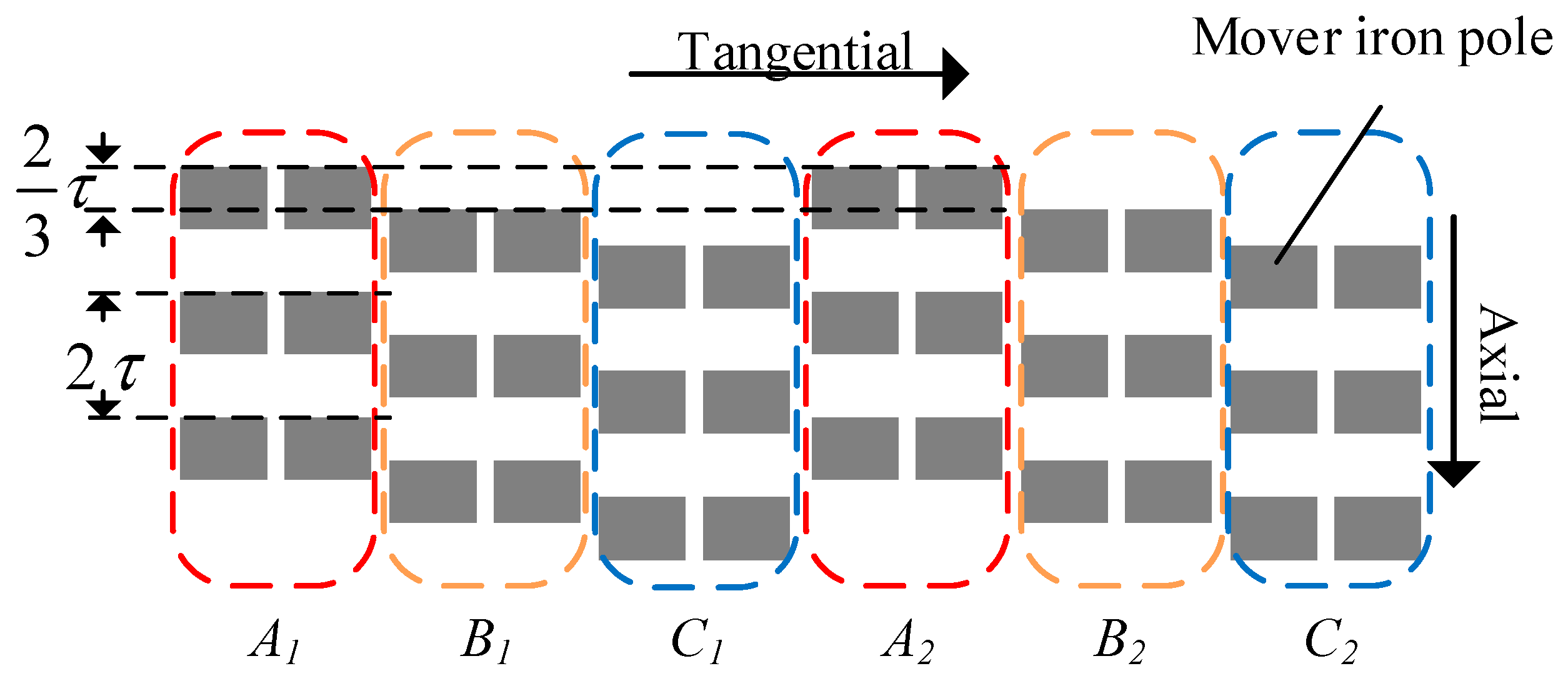
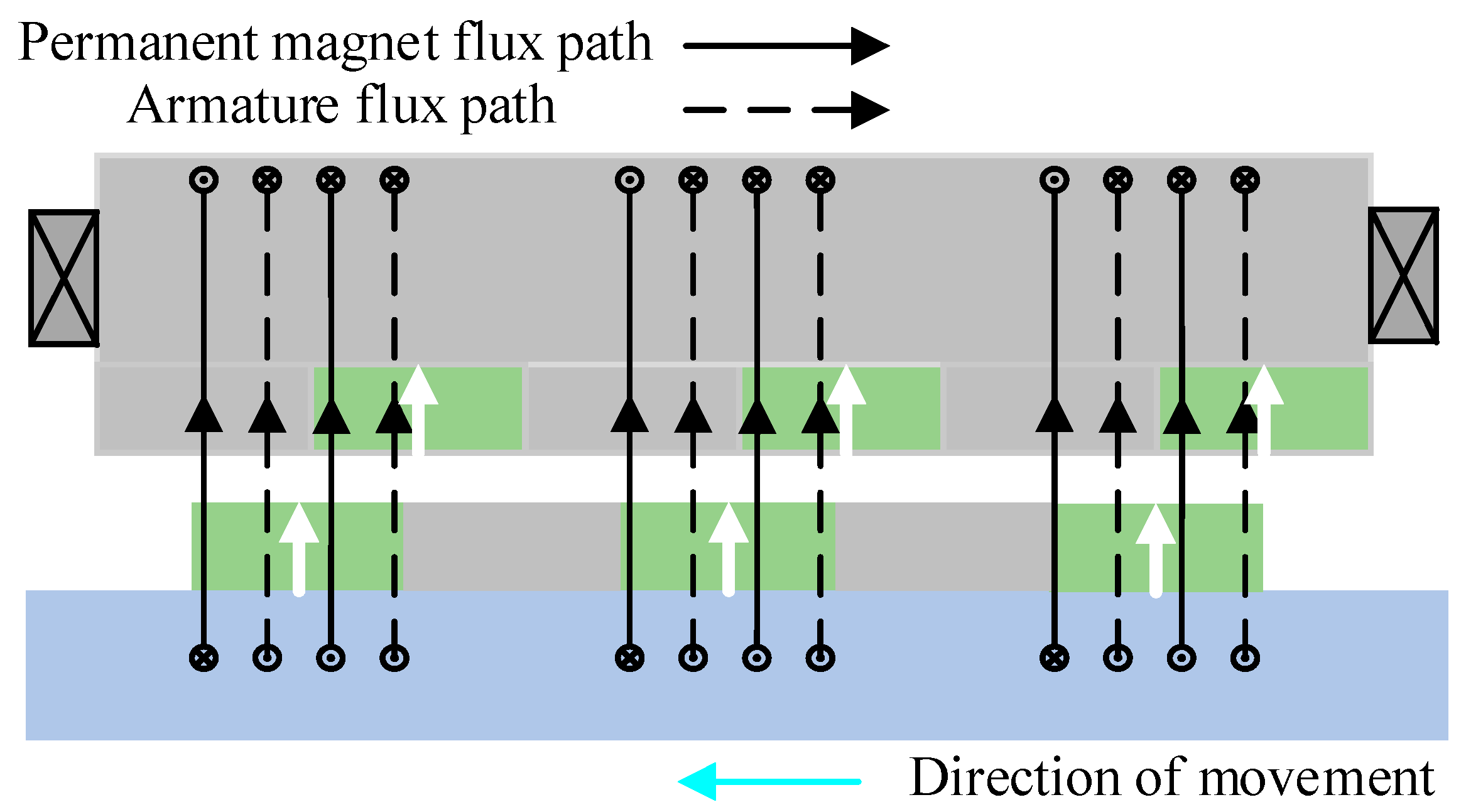
2.1.3. Structure of Unit Motor
2.2. Working Principle of TFPMLSM
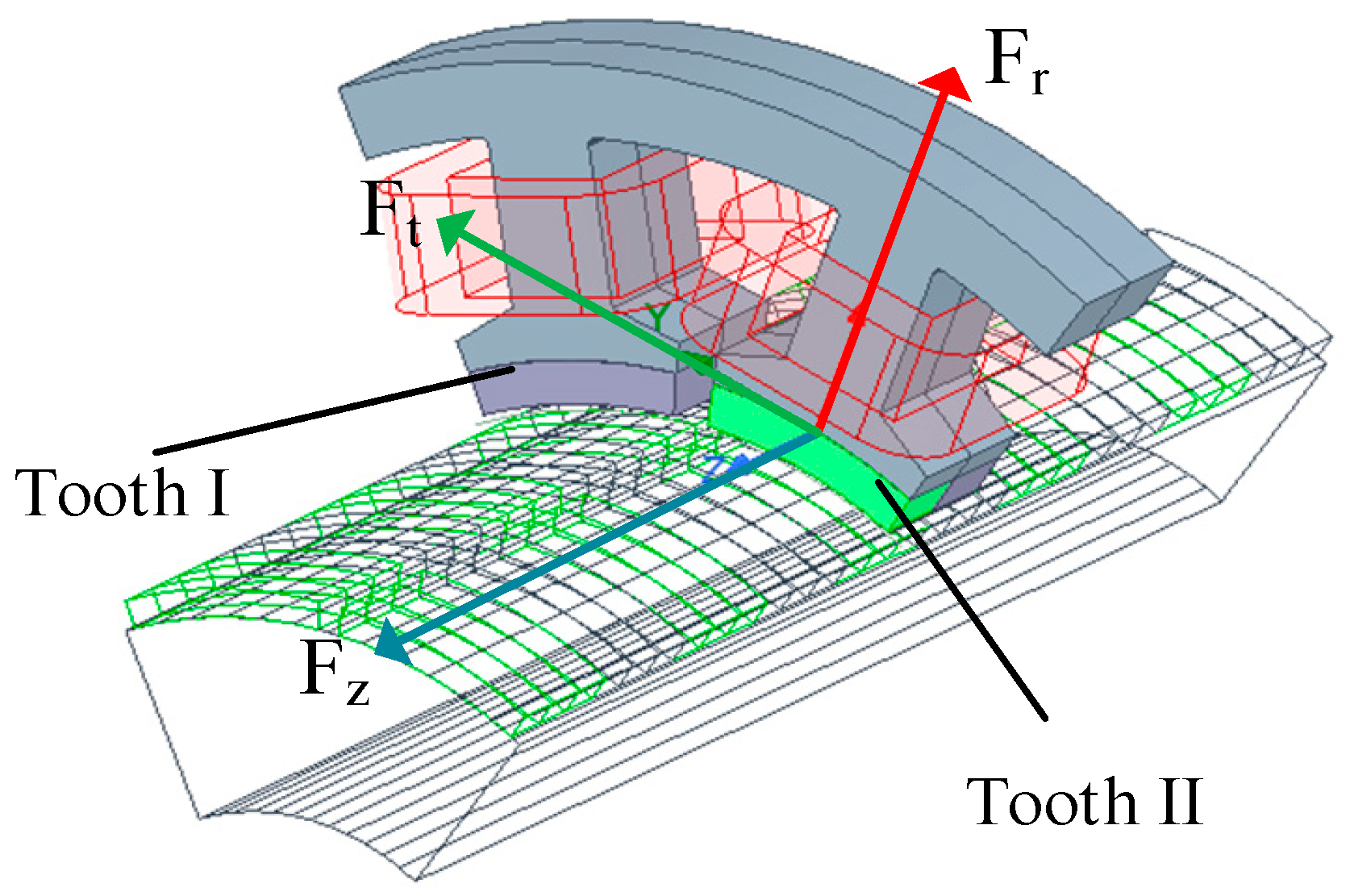
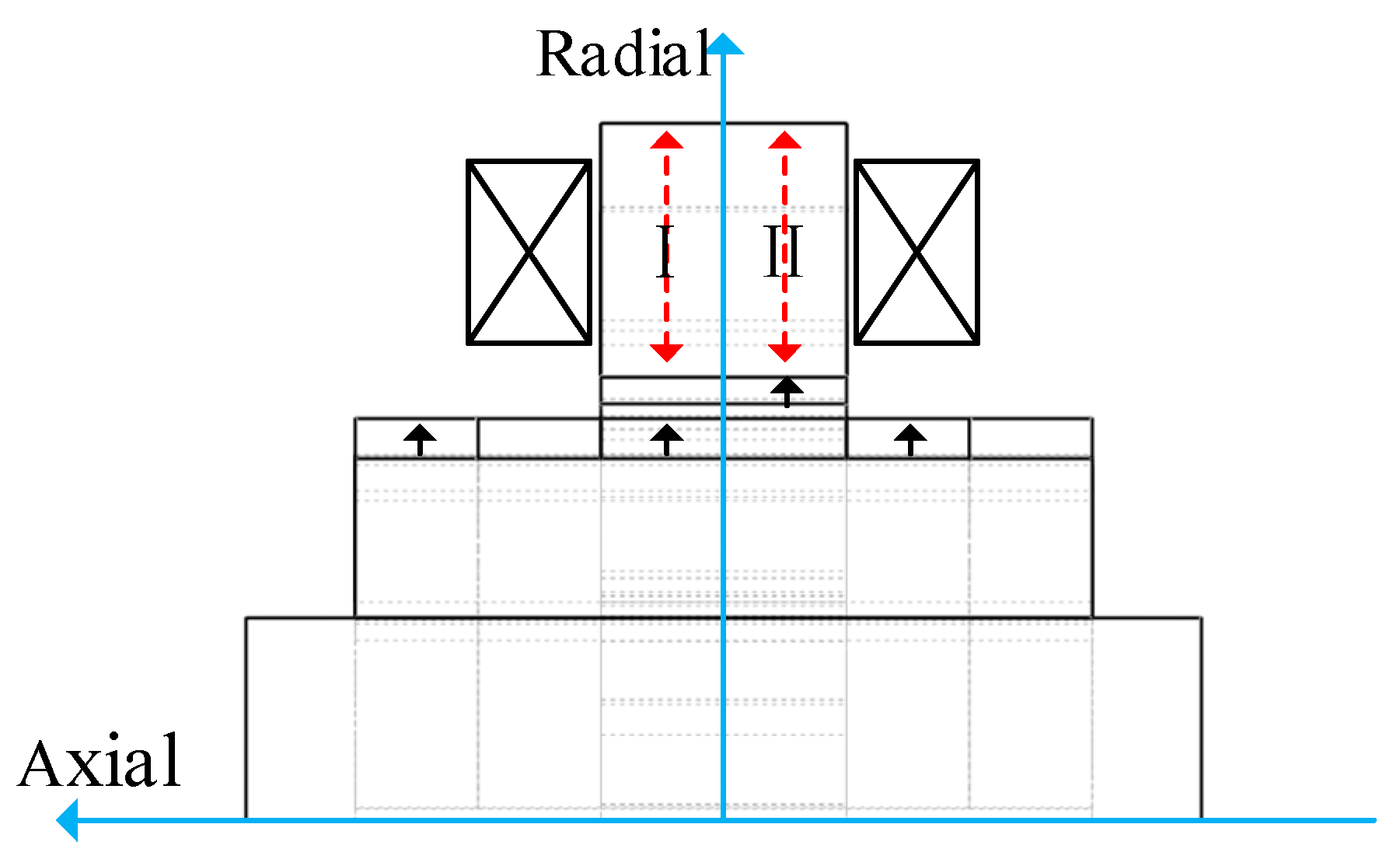
3. Analysis of Radial Electromagnetic Force
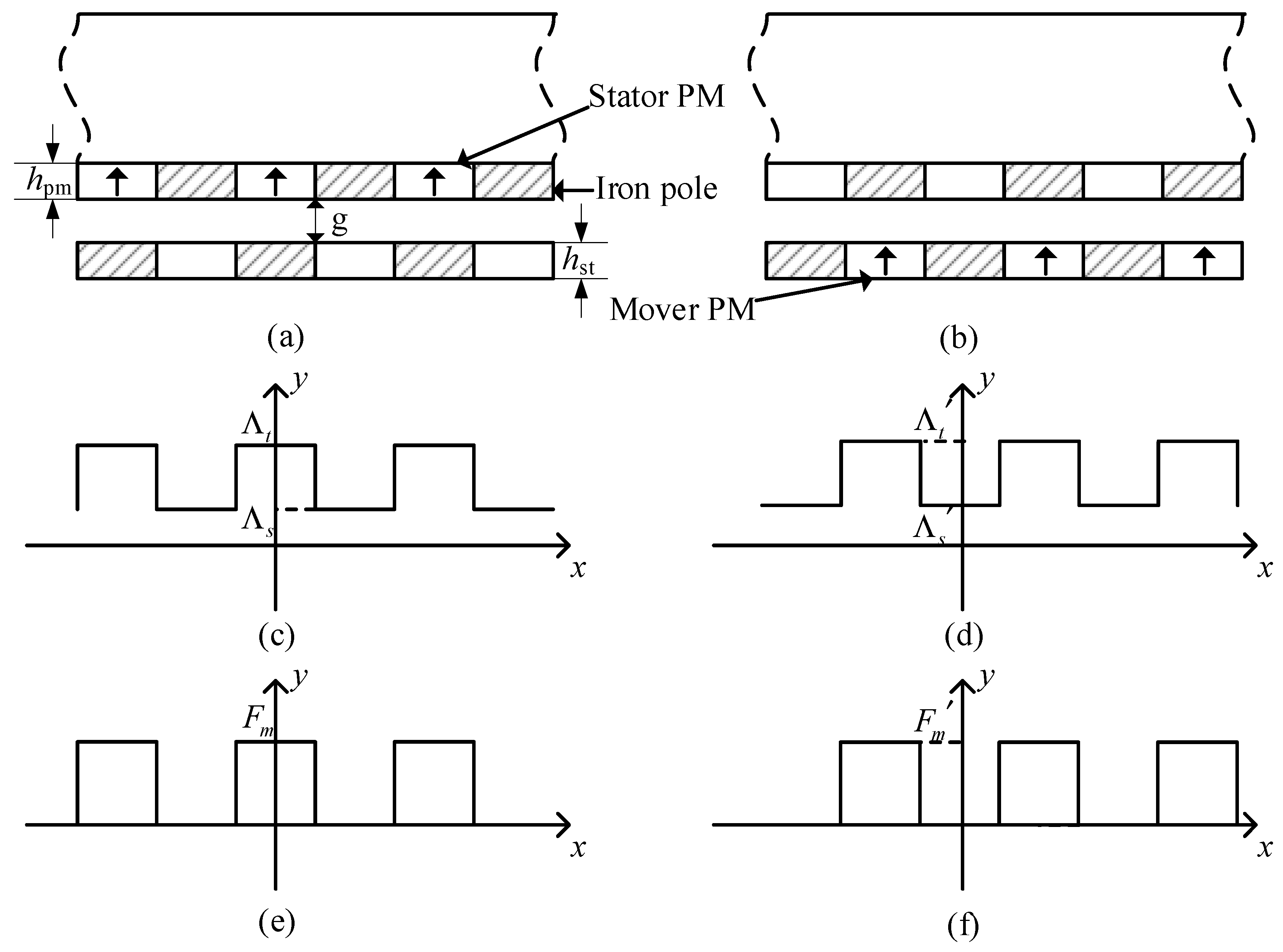
3.1. No-Load Air Gap Flux Density
- The core saturation is ignored;
- The eddy current losses and hysteresis losses are excluded;
- Magnetic field only changes in the radial direction.
3.2. Mathematical Analysis of Radial Electromagnetic Force
- The armature flux density generated by the armature winding. The radial and axial flux density of the armature can be expressed as:
- 2.
- The flux density generated by the interaction between the stator PMs and the mover iron poles. The radial and axial air gap flux density of stator PMs can be expressed as:
- 3.
- The flux density generated by the interaction between the mover PMs and the stator iron poles. The radial and axial air gap flux density of mover PMs can be expressed as:
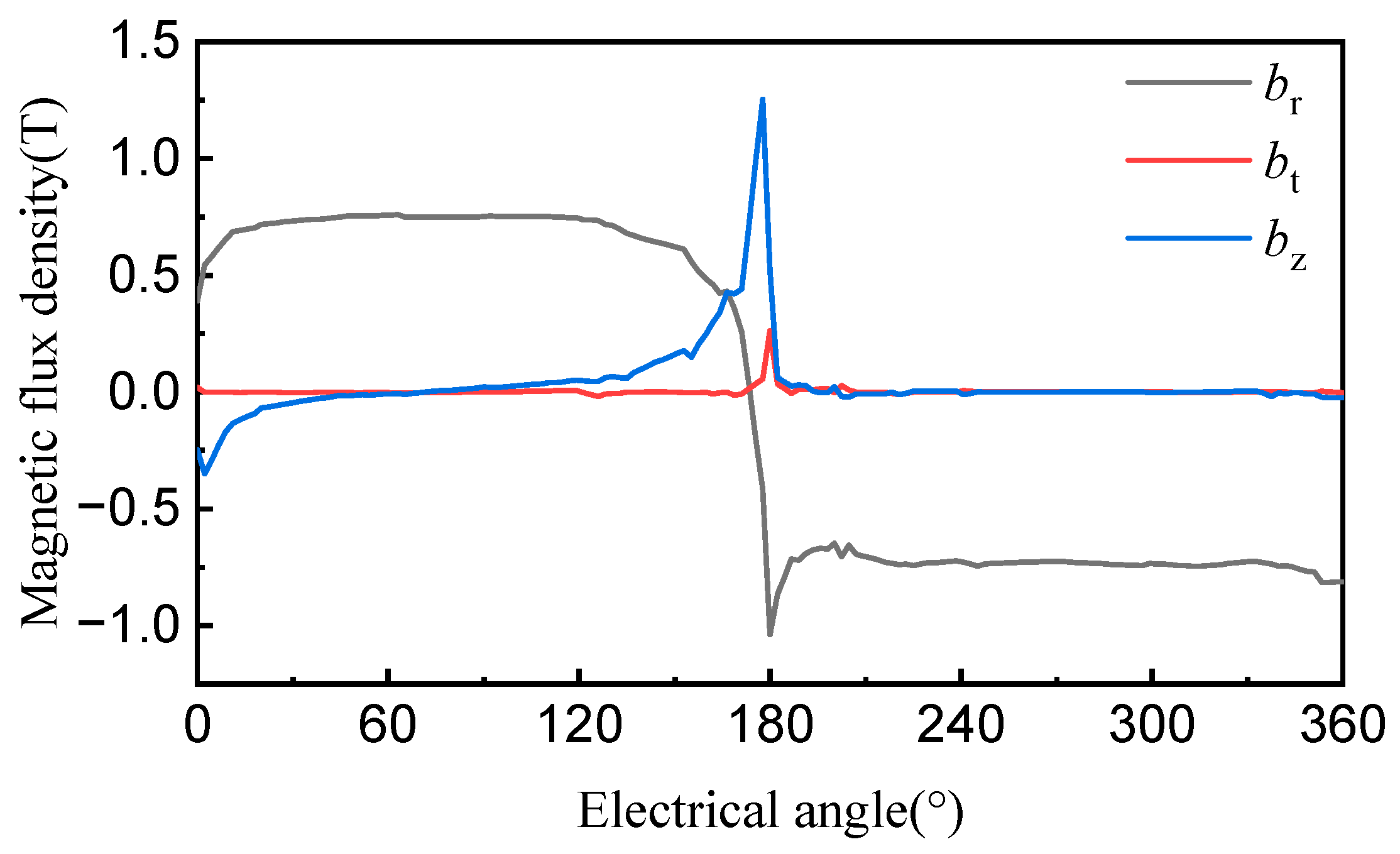
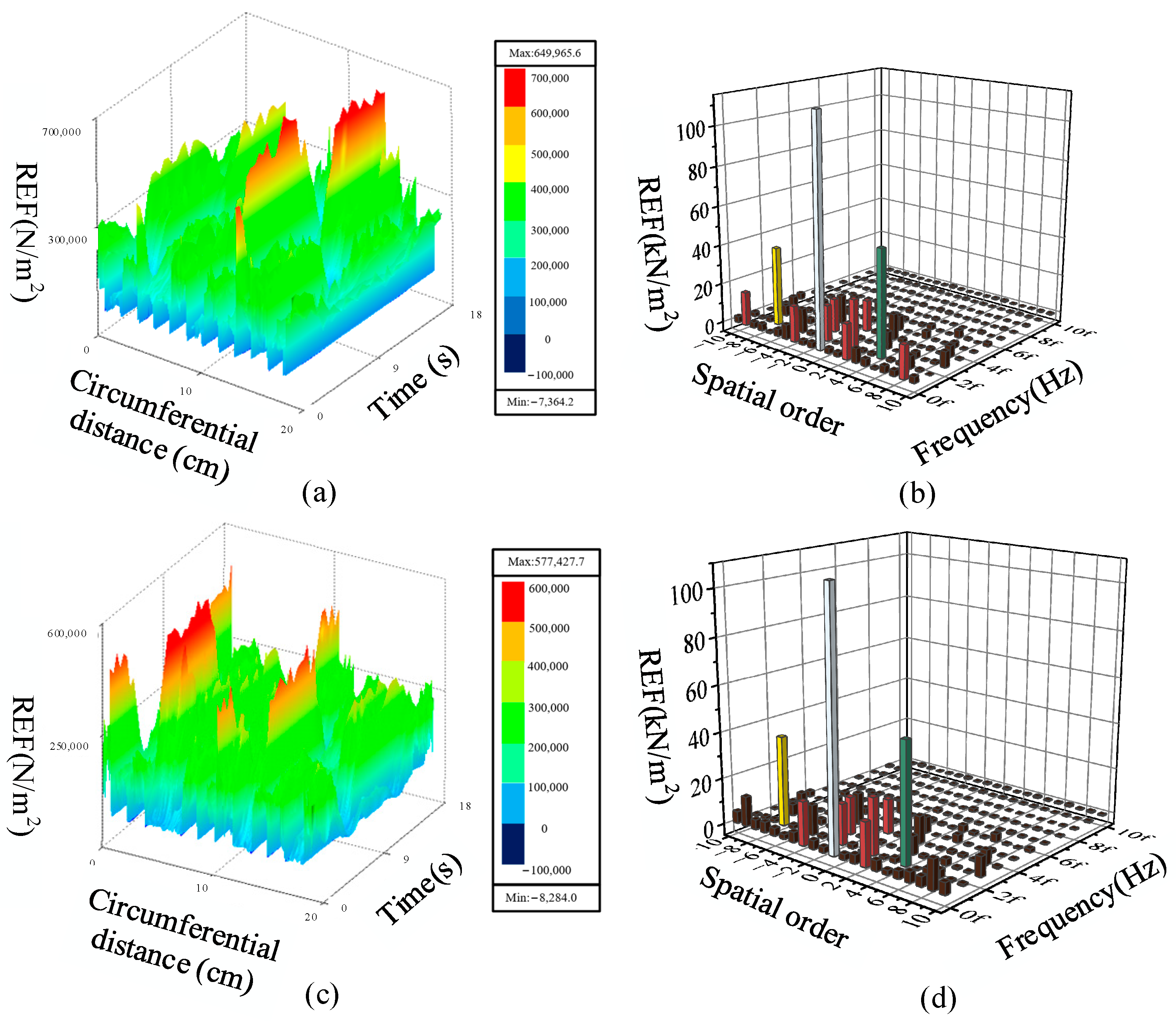
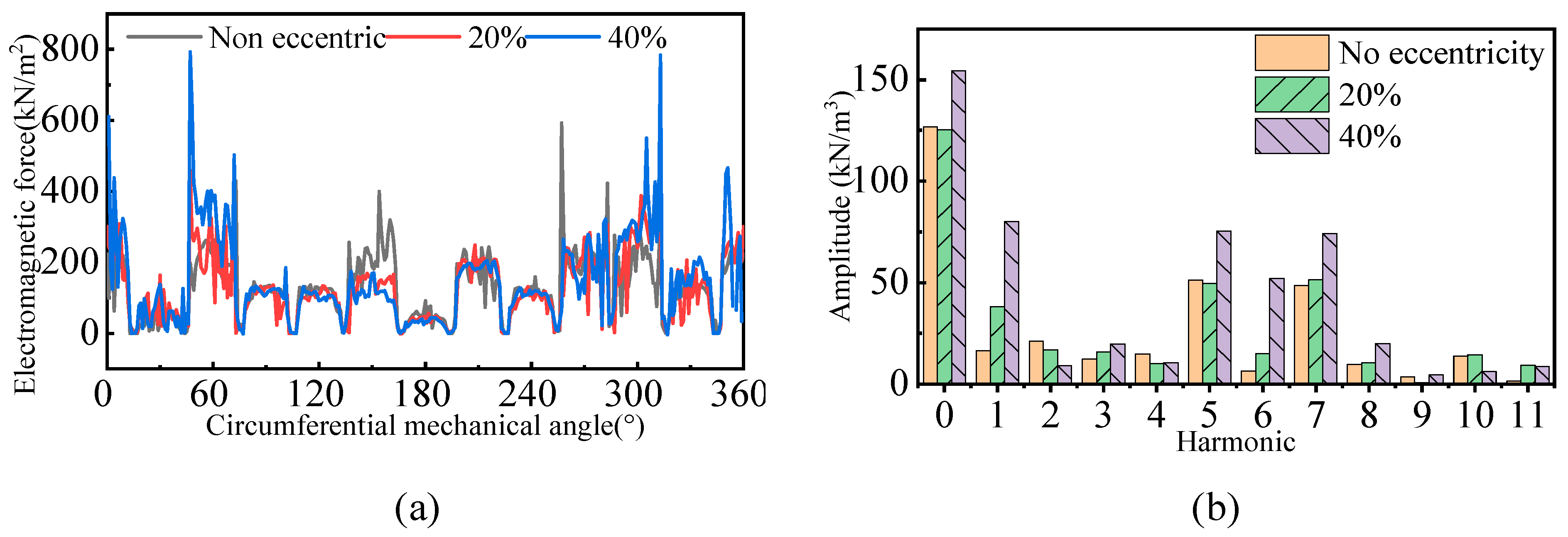
3.3. Analysis of Spatiotemporal and Spectral Characteristics of REF
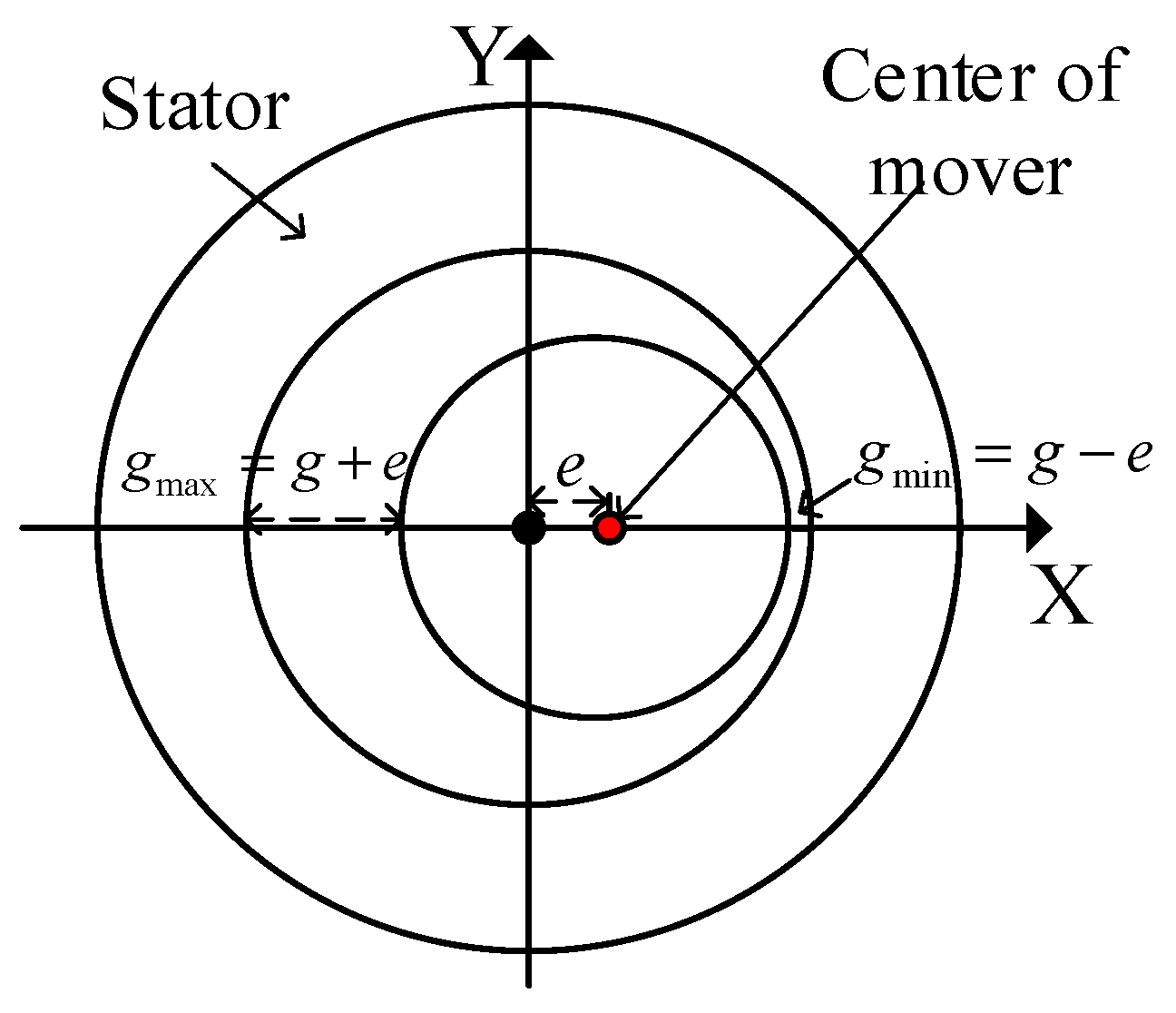
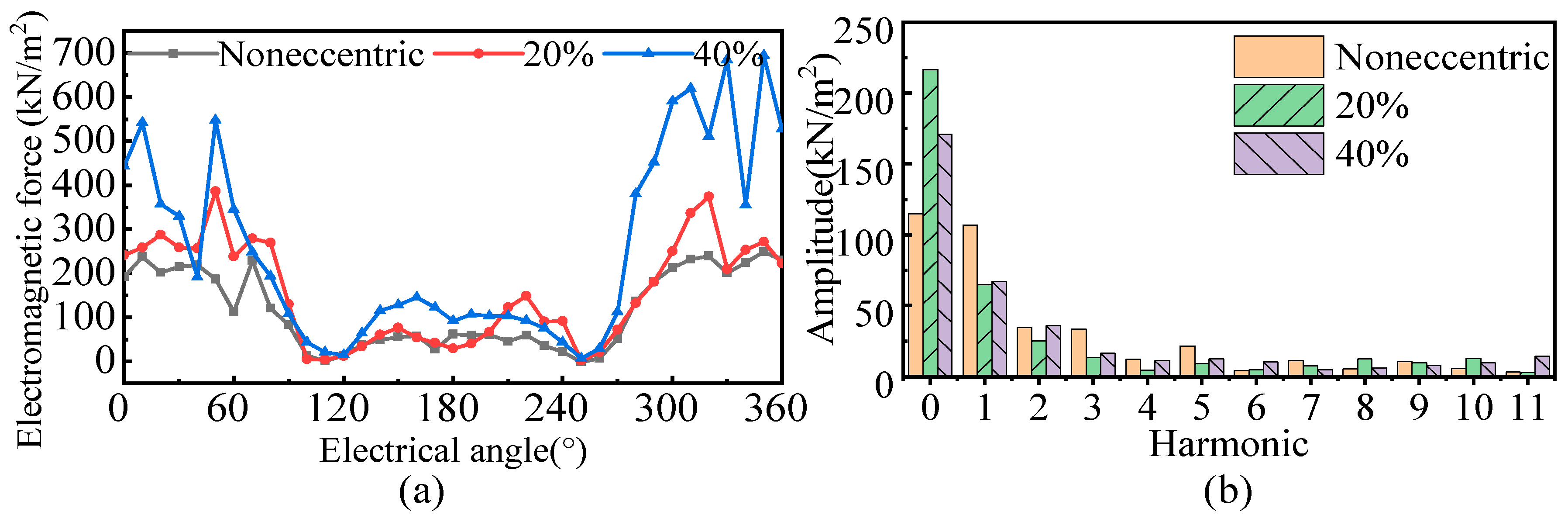
4. Influence of Mover Eccentricity on the Spectral Characteristics of REF
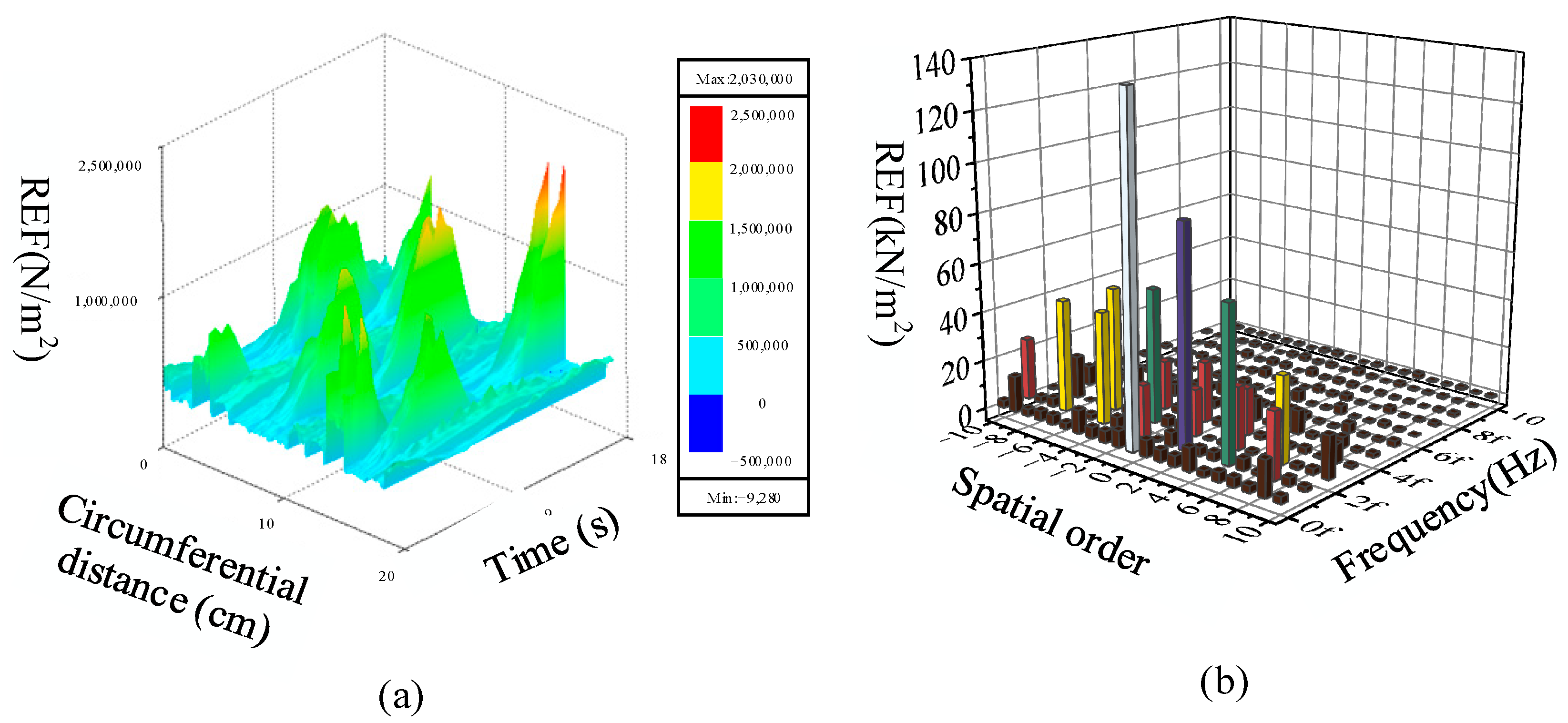
4.1. The Influence of Eccentricity on the Spectral Characteristics of Electromagnetic Forces
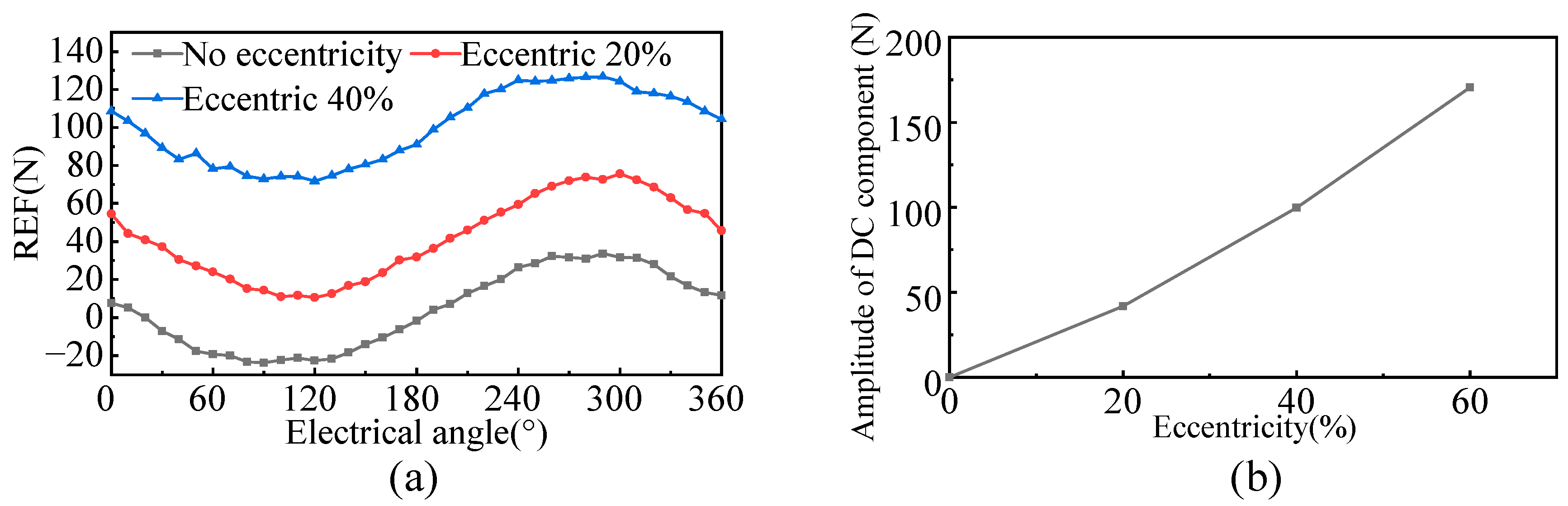
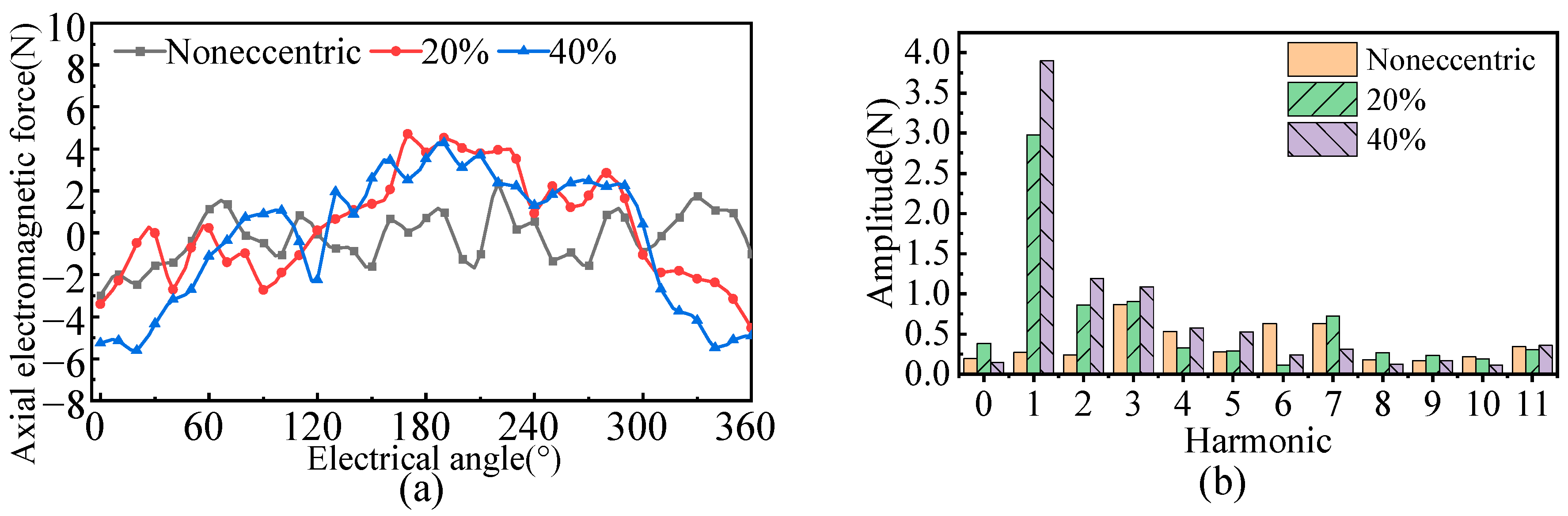
4.2. Analysis of Unbalanced Electromagnetic Force under Mover Eccentricity
5. Analysis of Stator Mode and Electromagnetic Vibration of TFPMLSM
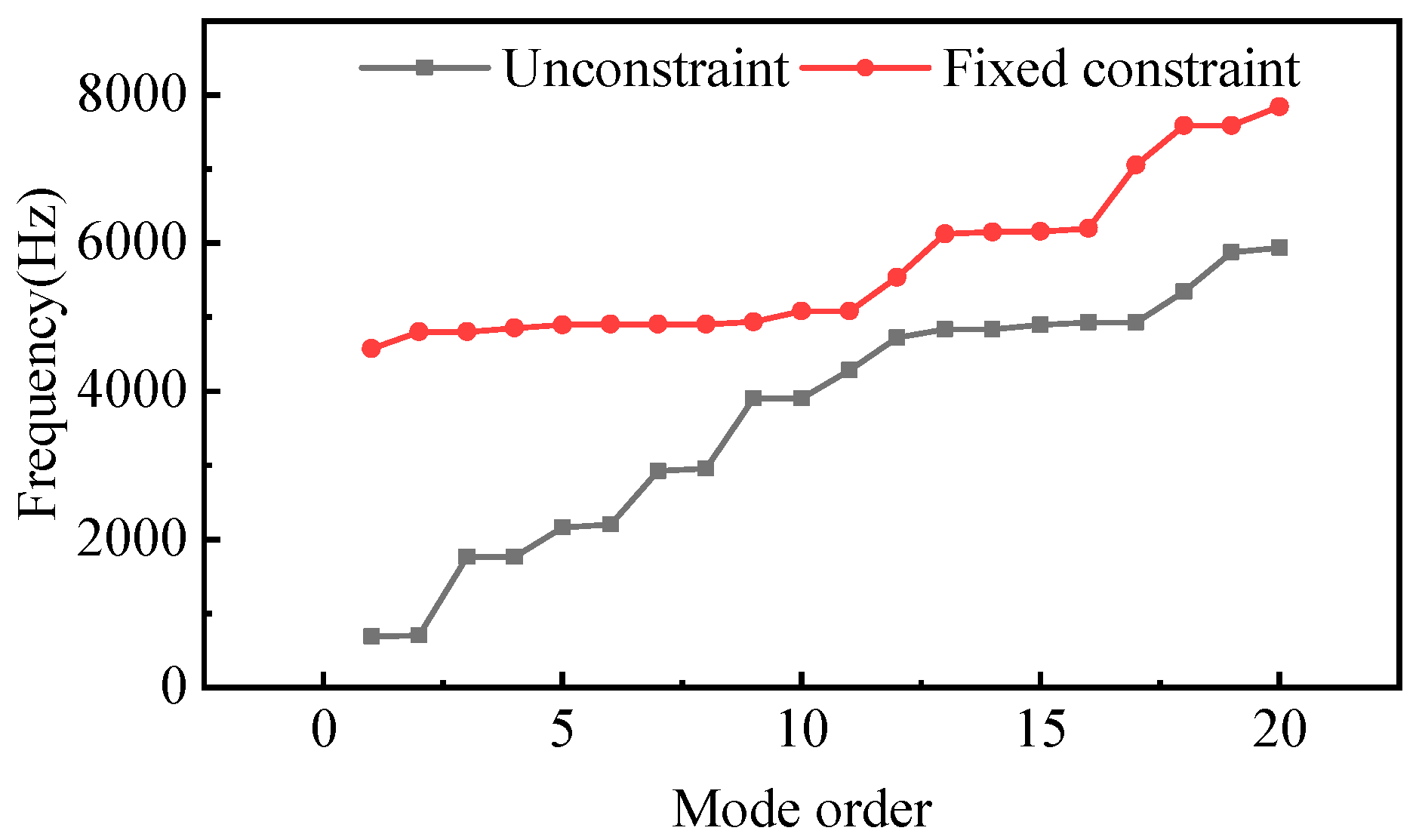
5.1. Characteristics of Stator Modal by Finite Element Analysis
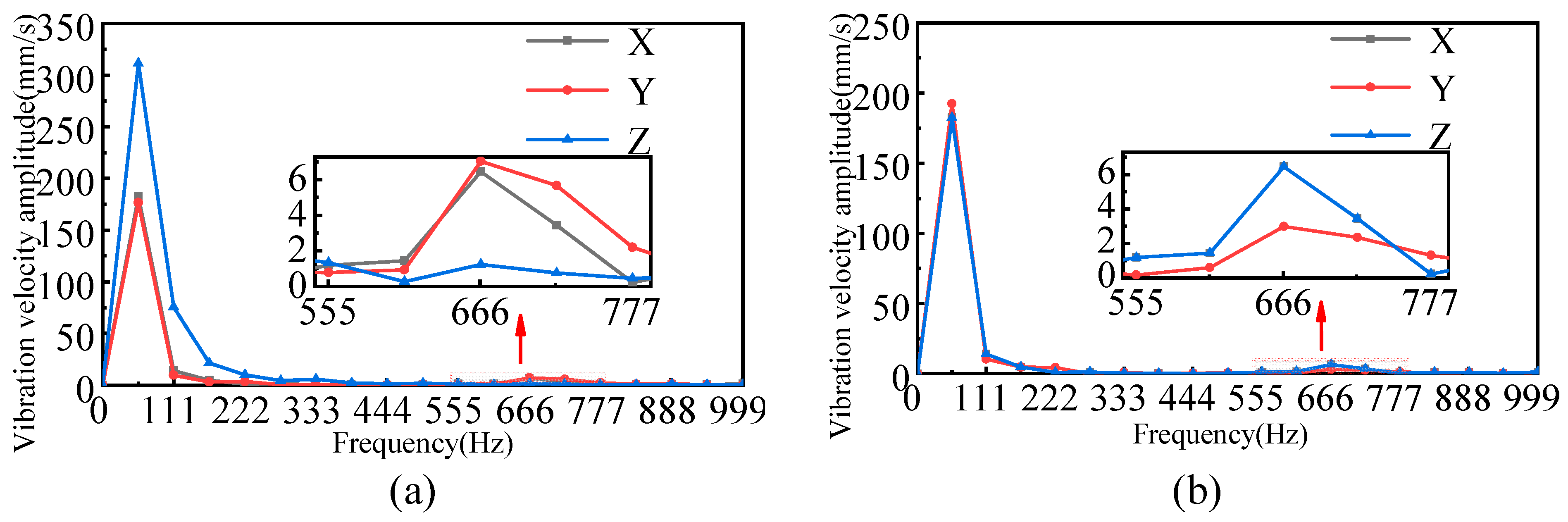
5.2. Harmonic Response Analysis
6. Conclusions
- Based on the Maxwell tensor method, it is obtained that the REF of the TFPMLSM is not only related to the radial flux density component, but also to the axial component, which is different from traditional longitudinal flux motors.
- A large magnetic pull in the radial direction will be produced as the mover eccentricity occurs, and the thrust fluctuation amplitude of the motor increases, which will affect the motor load-carrying capacity.
- The natural frequencies of the motor are obtained based on MSM. Compared to the fundamental working frequency, which is 55.56 Hz at maximum speed of 1 m/s, each natural frequency of the motor is much higher, therefore, resonance will not occur at a low speed.
- The fundamental frequency of the electromagnetic force has the greatest impact on the electromagnetic vibration of the TFPMLSM, which is different from the traditional rotating motor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smadi, I.A.; Omori, H.; Fujimoto, Y. Development, analysis, and experimental realization of a direct-drive helical motor. IEEE Trans. Ind. Electron. 2012, 59, 2208–2216. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Kominami, T.; Hamada, H. Development and analysis of a high thrust force direct-drive linear actuator. IEEE Trans. Ind. Electron. 2009, 56, 1383–1392. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Jewell, G.W.; Howe, D. A low-power, linear, permanent-magnet generator/energy storage system. IEEE Trans. Ind. Electron. 2002, 49, 640–648. [Google Scholar] [CrossRef]
- Colli, V.D.; Cancelliere, P.; Marignetti, F.; Stefano, R.D.; Scarano, M. A tubular-generator drive for wave energy conversion. IEEE Trans. Ind. Electron. 2006, 53, 1152–1159. [Google Scholar] [CrossRef]
- Zhao, M.; Zou, J.M.; Xu, Y.X.; Zou, J.B.; Wang, Q. The thrust characteristic investigation of transverse flux tubular linear machine for electromagnetic launcher. IEEE Trans. Plasma Sci. 2011, 39, 925–930. [Google Scholar] [CrossRef]
- Zou, J.; Zhao, M.; Wang, Q.; Zou, J.; Wu, G. Development and analysis of tubular transverse flux machine with permanent magnet excitation. IEEE Trans. Ind. Electron. 2012, 59, 2198–2207. [Google Scholar] [CrossRef]
- Zhao, J.; Mou, Q.; Guo, K.; Liu, X.; Li, J.; Guo, Y. Reduction of the detent force in a flux-switching permanent magnet linear motor. IEEE Trans. Energy Convers. 2019, 34, 1695–1705. [Google Scholar] [CrossRef]
- Suzuki, K.; Kim, Y.J.; Dohmeki, H. Driving method of permanent magnet linear synchronous motor with the stationary discontinuous armature for long-distance transportation system. IEEE Trans. Ind. Electron. 2012, 59, 2227–2235. [Google Scholar] [CrossRef]
- Lu, Q.; Li, Y.; Huang, X.; Ye, Y. Analysis of transverse-flux linear switched-flux permanent magnet machine. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Ueda, Y.; Takahashi, H.; Akiba, T.; Yoshida, M. Fundamental design of a consequent-pole transverse-flux motor for direct-drive systems. IEEE Trans. Magn. 2013, 49, 4096–4099. [Google Scholar] [CrossRef]
- Zhang, B.; Epskamp, T.; Doppelbauer, M.; Gregor, M. A comparison of the transverse, axial and radial flux PM synchronous motors for electric vehicle. In Proceedings of the IEEE International Electric Vehicle Conference, Florence, Italy, 17–19 December 2014. [Google Scholar]
- Jang, I.S.; Ham, S.H.; Kim, W.H.; Jin, C.S.; Cho, S.Y.; Lee, K.D.; Lee, J.J.; Kang, D.; Lee, J. Method for analyzing vibrations due to electromagnetic force in electric motors. IEEE Trans. Magn. 2014, 50, 297–300. [Google Scholar] [CrossRef]
- Islam, R.; Husain, I. Analytical model for predicting noise and vibration in permanent-magnet synchronous motors. IEEE Trans. Ind. Appl. 2010, 46, 2346–2354. [Google Scholar] [CrossRef]
- Islam, M.S.; Islam, R.; Sebastian, T. Noise and vibration characteristics of permanent-magnet synchronous motors using electromagnetic and structural analyses. IEEE Trans. Ind. Appl. 2014, 50, 3214–3222. [Google Scholar] [CrossRef]
- Cho, S.; Hwang, J.; Kim, C.-W. A study on vibration characteristics of brushless DC motor by electromagnetic-structural coupled analysis using entire finite element model. IEEE Trans. Energy Convers. 2018, 33, 1712–1718. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J.; Qu, R.; Ye, D.; Lu, H.; Sun, J.; Ge, M.; Xu, H. Electromagnetic force and vibration analysis of permanent-magnet-assisted synchronous reluctance machines. IEEE Trans. Ind. Appl. 2018, 54, 4246–4256. [Google Scholar] [CrossRef]
- Li, J.; Cho, Y. Investigation into reduction of vibration and acoustic noise in switched reluctance motors in radial force excitation and frame transfer function aspects. IEEE Trans. Magn. 2009, 45, 4664–4667. [Google Scholar]
- Wang, S.; Hong, J.; Sun, Y.; Cao, H. Analysis and reduction of electromagnetic vibration of PM brush DC motors. IEEE Trans. Ind. Appl. 2019, 55, 4605–4612. [Google Scholar] [CrossRef]
- He, G.; Huang, Z.; Chen, D. Two-dimensional field analysis on electro-magnetic vibration-and-noise sources in permanent-magnet direct current commutator motors. IEEE Trans. Magn. 2011, 47, 787–794. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, S.; Wu, X.; Lin, F.; Zhong, H.; Zhang, Y. Vibroacoustic prediction and mechanism analysis of claw pole alternators. IEEE Trans. Ind. Electron. 2016, 64, 4463–4473. [Google Scholar] [CrossRef]
- Sun, T.; Kim, J.M.; Lee, G.H.; Hong, J.P.; Choi, M.R. Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor. IEEE Trans. Magn. 2011, 47, 1038–1041. [Google Scholar] [CrossRef]
- Luo, J.; Kou, B.; Yang, X.; Zhang, H.; Zhang, L. Development, design, and analysis of a dual-consequent-pole transverse flux linear machine for direct-drive applications. IEEE Trans. Ind. Electron. 2020, 68, 6097–6108. [Google Scholar] [CrossRef]
- Zheng, P.; Zhu, S.; Yu, B.; Cheng, L.; Fan, Y. Analysis and optimization of a novel tubular staggered-tooth transverse-flux PM linear machine. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Sui, Y.; Yin, Z.; Wang, M.; Yu, B.; Zheng, P. A tubular staggered-teeth transverse-flux PMLM with circumferentially distributed three-phase windings. IEEE Trans. Ind. Electron. 2018, 66, 4837–4848. [Google Scholar] [CrossRef]
- Arshad, W.M.; Thelin, P.; Backstrom, T.; Sadarangani, C. Use of transverse-flux machines in a free-piston generator. IEEE Trans. Ind. Appl. 2004, 40, 1092–1100. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Yan, B.; Hua, W.; Wang, X. Electromagnetic performance analysis of a field-modulated permanent magnet motor using improved hybrid subdomain method. IEEE Trans. Energy Convers. 2023, 38, 1753–1766. [Google Scholar] [CrossRef]
- Li, X.; Wei, Z.; Zhao, Y.; Wang, X.; Hua, W. Design and Analysis of Surface-Mounted Permanent-Magnet Field-Modulation Machine for Achieving High Power Factor. IEEE Trans. Ind. Electron. 2023. early access. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Wang, Q.; Yan, B.; Huang, Z.; Wang, K. Performance investigation and experimental testing of a stator-PM-excitation axial-flux magnetic gear. IEEE Trans. Transp. Electrif. 2022, 9, 2593–2605. [Google Scholar] [CrossRef]

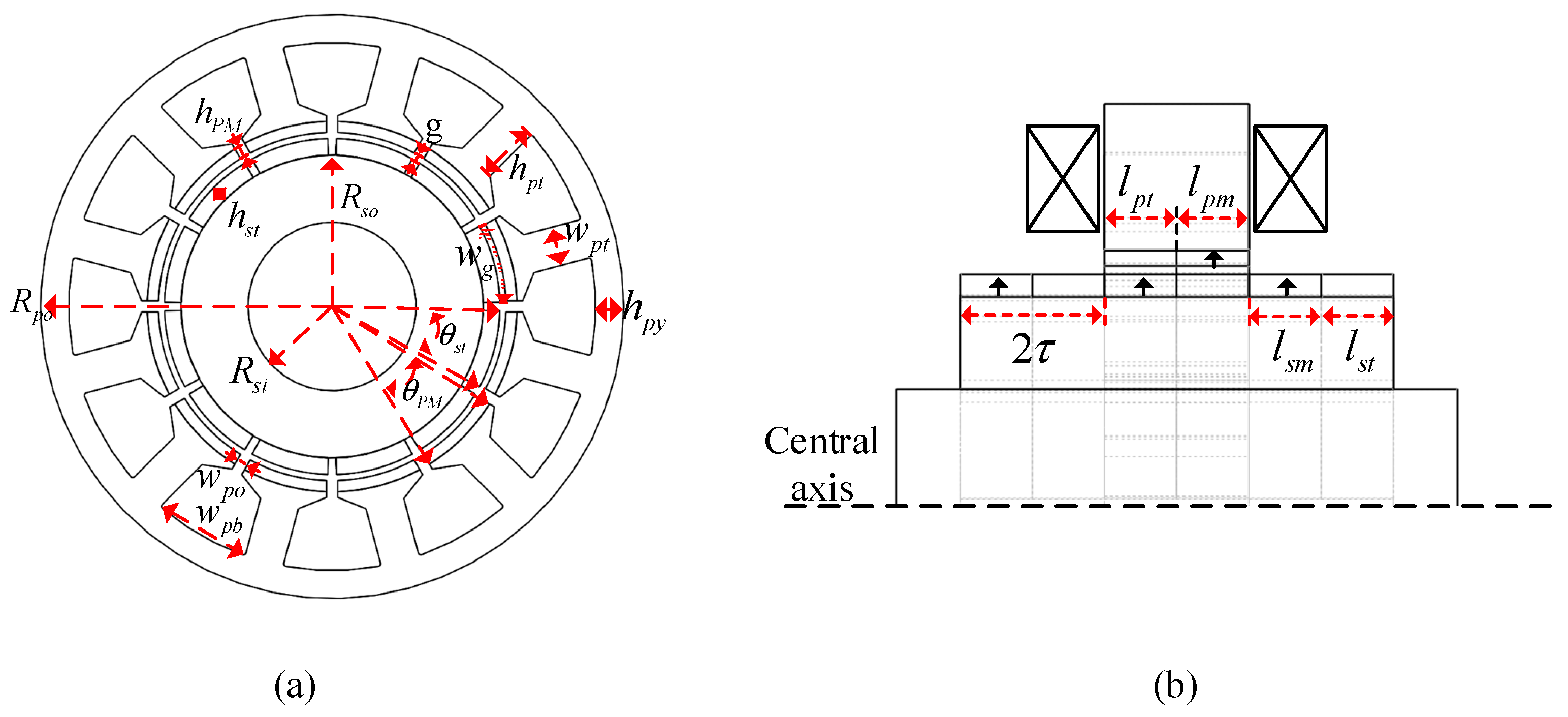

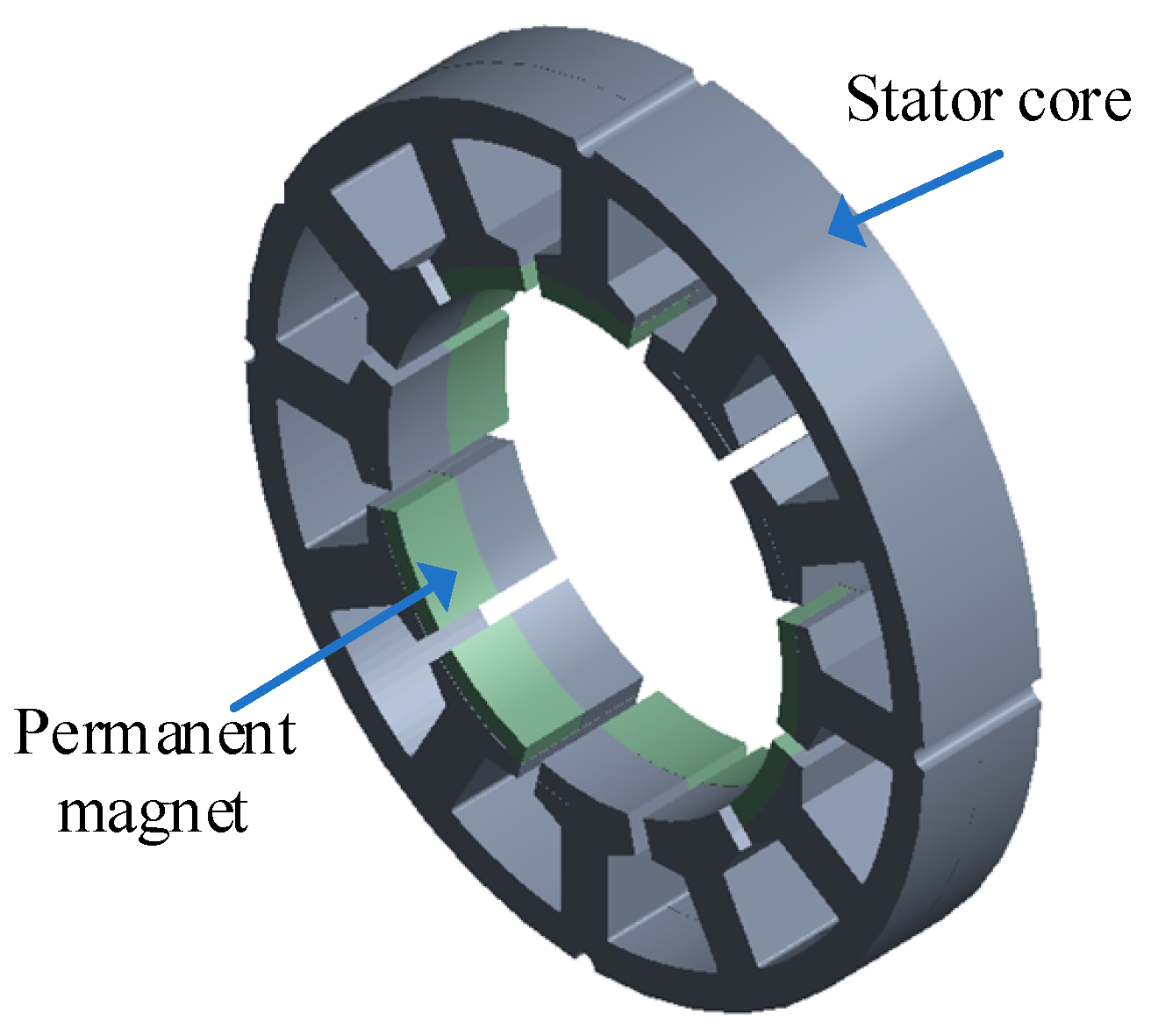


| Parameter | Symbol | Value | Parameter | Symbol | Value |
|---|---|---|---|---|---|
| Outer radius of stator iron core/mm | Rpo | 52 | Axial length of mover PM (Pole distance)/mm | τ | 9 |
| Stator slot height/mm | hpt | 10.8 | Inner radius of mover iron core/mm | Rsi | 15 |
| Axial length of stator PM/mm | lpm | 8 | Stator PM height/mm | hPM | 3 |
| Stator yoke height/mm | hpy | 5 | Mover PM height/mm | hst | 3 |
| Stator tooth width/mm | wpt | 7 | Mover pole arc coefficient | αst | 0.8 |
| Air gap/mm | g | 1 | Stator slot width/mm | wpo | 3.5 |
| Radius of mover cylinder/mm | Rso | 27.4 |
| Material Name | Model Number | Density (kg/m3) | Young’s Modulus (Gpa) | Young’s Modulus |
|---|---|---|---|---|
| Silicon steel sheet | DW465_50 | 7700 | 170 | 0.26 |
| Permanent magnet | NdFe30 | 7550 | 160 | 0.24 |
| Mode Number | Mode Shapes | Natural Frequency [Hz] |
|---|---|---|
| Radial 2nd mode |  | 683.75 |
| Radial 3nd mode |  | 699.55 |
| Axial 1st mode, radial 2nd mode | 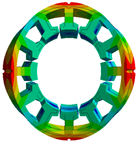 | 1758.9 |
| Radial 4nd mode | 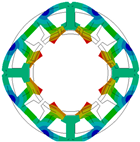 | 2159.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Li, Y.; Zuo, S.; Tang, P.; Yao, T.; Zhang, H.; Wu, S. Electromagnetic Vibration Analysis of Transverse Flux Permanent Magnet Linear Submersible Motor for Oil Production. Energies 2023, 16, 7911. https://doi.org/10.3390/en16237911
Zhao M, Li Y, Zuo S, Tang P, Yao T, Zhang H, Wu S. Electromagnetic Vibration Analysis of Transverse Flux Permanent Magnet Linear Submersible Motor for Oil Production. Energies. 2023; 16(23):7911. https://doi.org/10.3390/en16237911
Chicago/Turabian StyleZhao, Mei, Yihao Li, Sicheng Zuo, Pingpeng Tang, Tong Yao, Huaqiang Zhang, and Shunjie Wu. 2023. "Electromagnetic Vibration Analysis of Transverse Flux Permanent Magnet Linear Submersible Motor for Oil Production" Energies 16, no. 23: 7911. https://doi.org/10.3390/en16237911
APA StyleZhao, M., Li, Y., Zuo, S., Tang, P., Yao, T., Zhang, H., & Wu, S. (2023). Electromagnetic Vibration Analysis of Transverse Flux Permanent Magnet Linear Submersible Motor for Oil Production. Energies, 16(23), 7911. https://doi.org/10.3390/en16237911







