Stability Control Technology for Surrounding Rocks in Gob-Side Entry Driving with Small Coal Pillars under Dynamic Pressure

Abstract

To address the support difficulties caused by the dynamic pressure from the adjacent working face in gob-side entry driving, this study, taking the 8103 working face of the Jinhuagong Coal Mine in Shanxi Province as an example, adopted methods such as theoretical analysis, physical experiments, numerical simulations, and field practices to explore roof-cutting and pressure-relieving techniques to control the surrounding rocks in gob-side entry driving with small coal pillars under dynamic pressure. Fractures of the lateral roof, stresses on the surrounding rock, and deformations with different cutting-roof parameters were analyzed to determine the reasonable parameters for applications. The following results have been obtained. The longer the lateral cantilever length of the roof, the greater the load borne by the surrounding rock. Therefore, the key to reducing the confining pressure in a roadway is reducing the lateral cantilever length of the roof. After roof cutting, the roof of the gob area collapsed more completely. The stress on both sides of the coal pillar and that on the ribs of the solid coal dropped by 7.72 MPa and 4.16 MPa, respectively. The key roof-cutting parameters were analyzed by the UDEC numerical software, and the reasonable roof-cutting angle and height were determined to be 12° and 14 m. A support scheme combining “steel strip + bolt + anchor cable + roof cutting” was proposed. With the scheme applied, the displacement of both sides of the coal pillar was 61 mm shorter than that in the non-test section, and the duration in which the roadway was affected by mining was 11 days shorter. Therefore, the rationality of the selected roof-cutting and support parameters in this study is verified. The proposed scheme can effectively control the stability of surrounding rocks in gob-side entry driving with small coal pillars under dynamic pressure.

1. Introduction

Wide coal pillars were commonly used for roadway protection in China. The pillar width ranges from 20 to 30 m, and from 40 to 60 m for thick coal seams or deep mines, resulting in a significant loss of resources [1,2,3,4,5]. To improve resource recovery rates, the new technique of using small coal pillars in gob-side entry driving has been adopted for the layout and maintenance of mining roadways in mines in China and gained increasing popularity [6,7,8,9].

A significant number of successful cases of gob-side entry driving with small coal pillars can be found. However, excavation along a gob area cannot be performed before fractures and overlying strata movement in the gob area of the adjacent working face stabilize, which severely affects the normal continuity of the working face [10,11]. At the same time, with the increase in mining intensity, the incidence of gas outburst and fire accidents also increases [12,13,14], which seriously threatens the life safety of underground workers. In recent years, due to the tight succeeding problem between mining and excavation, the method of roadway driving toward the mining working face has been adopted in some mines. Extensive research has been conducted on the stability control of the surrounding rock of roadways under dynamic pressure at the edge of unstable gob areas. Zhang et al. [15] used pre-tensioned combination technology to effectively control the deformation of small coal pillars in roadway driving along next gob toward the mining working face. Kang [16] and Wang et al. [17] improved the stability and bearing capacity of coal pillars by determining a reasonable pillar width of the coal pillar, thus effectively controlling the amount of deformation of the surrounding rock of roadways. Chen [18] and Liu [19] met the spatiotemporal relationship between mining and roadway support by reinforcing and supporting different sections of roadways in different periods. Jian-biao Bai [20] studied stress superposition and spatial distribution of dynamic pressure disturbance during roadway driving toward the direction of mining to propose a segmented control and support technology based on the distance distribution between the heading and the working face, which has achieved good performance. Han Chang-liang [21] analyzed the key factors causing gob-side entry retaining disturbances under the effect of mining and obtained the superposed disturbance mechanism of side roof collapse characteristics for roadways. Several techniques, including “dual-layer” anchorage support, roadside filling with dynamic strength matching, and auxiliary support during disturbance, were proposed, which have performed well.

It can be argued that the waiting time for gob-side entry driving along the lower working face is reduced by roadway driving toward the direction of mining, which, to some extent, alleviates the tight succeeding problem between mining and excavation in mines. However, during this kind of roadway driving, the lateral abutment pressure of the coal pillars is superimposed with the advanced abutment pressure of the adjacent working face. The superimposition, under high stress and strong dynamic pressure, is likely to cause serious deformation and damage in gob-side roadways, and the difficulty in support significantly increases the costs [22,23,24]. Additionally, according to the Regulations for Safe Operation in Coal Mines, in mines with high rock burst risk, working faces need to be at least 350 m apart. When the distance is 350 m, the excavating face needs to stop and restarts after the mining face advances 700 m. The waiting time is long. At this point, the gob-side entry driving of the mining face can be delayed to solve this problem. This study aims to alleviate the tight succeeding problem between mining and excavation and improve the stress environment in roadways. Specifically, the geological conditions of the Jinhuagong Coal Mine were studied. In the roadway under dynamic pressure at the edge of an unstable gob area, the mining method of delaying the mining face layout using small coal pillars was adopted to investigate the surrounding rock control in the roof cutting and pressure relief gob-side entry driving in roadways under dynamic pressure with small coal pillars.

2. Mechanism of Roof Cutting and Pressure Relief with Small Coal Pillars

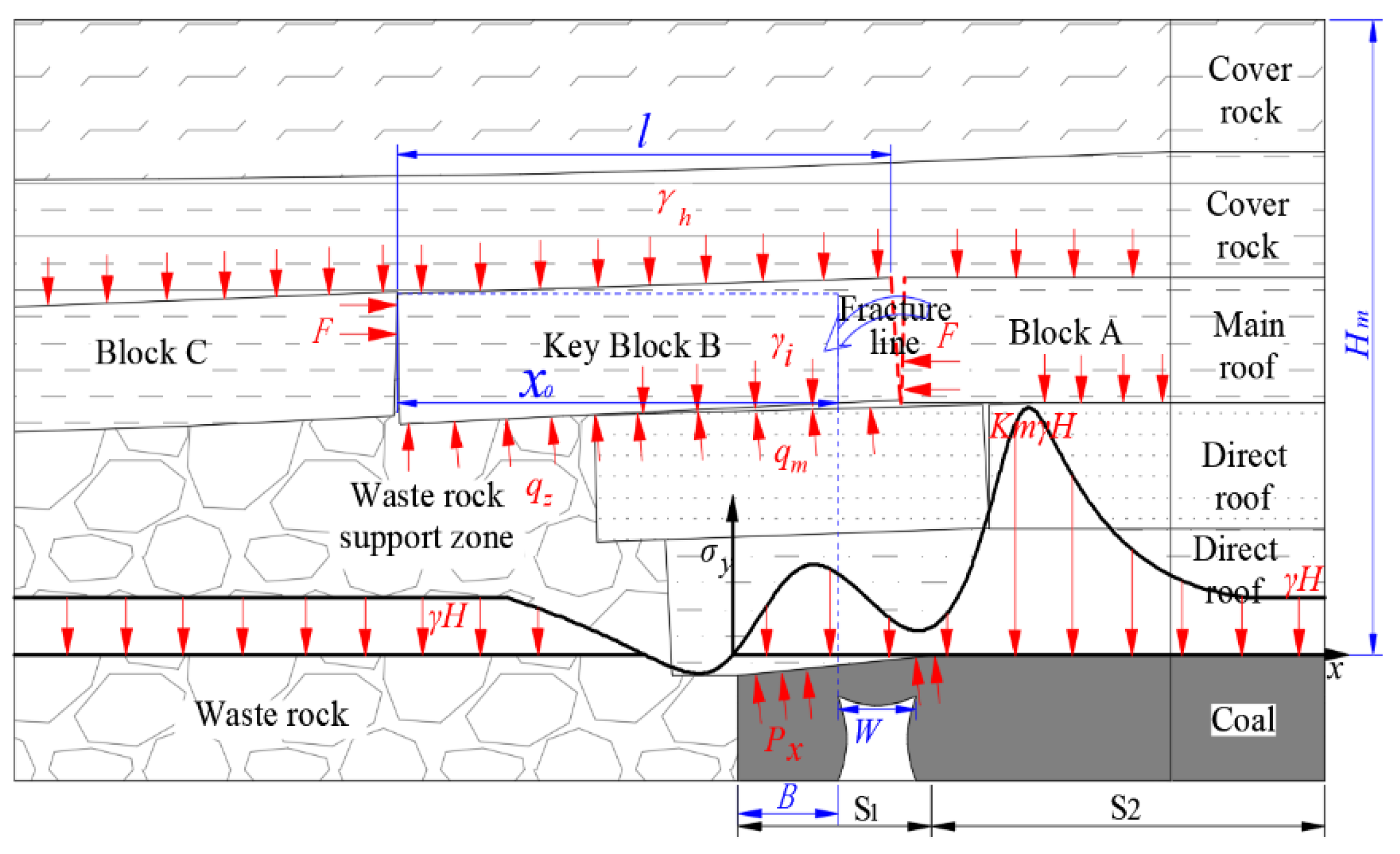
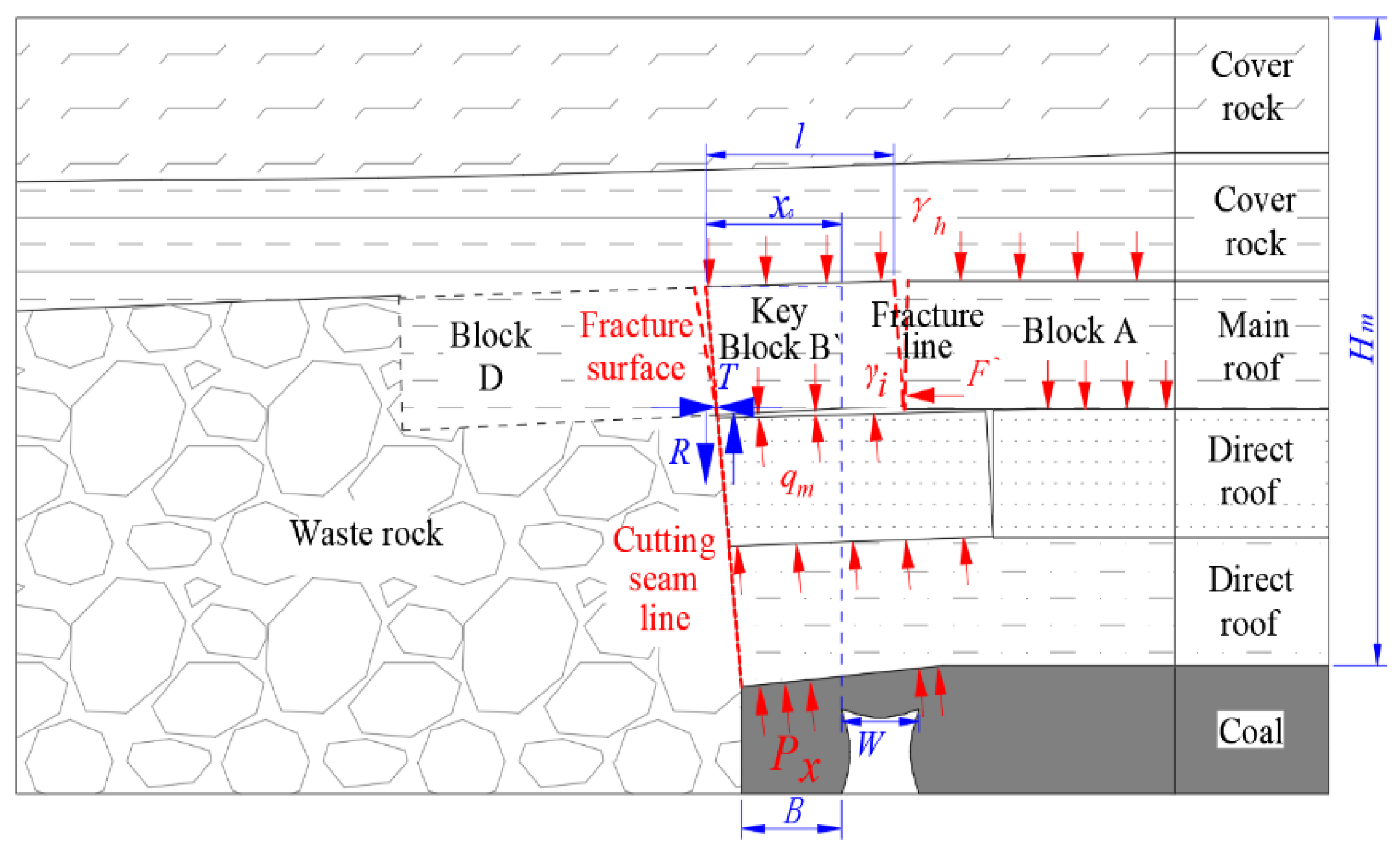
2.1. Fractures Characteristics of the Key Blocks above Coal Pillars

As a working face advances, its main roof undergoes fracture and subsidence under the effect of its own weight and the overlying strata [25,26,27]. The structural model of the roof above the gob drift, as shown in Figure 1, is established. The model of the overlying strata structure in a gob-side roadway is shown in Figure 1. At this stage, the main roof undergoes lateral fracture, forming a cantilever beam structure that bears the overlying strata. At the same time, at the elastic and plastic hinges inside the coal body at the gob edge, key blocks are formed due to the fracture [14,28,29]. One end of key block B rotates and is supported by the gangue (q_z), while the other end fractures within the rock mass at the gob edge, the bottom of which is effectively supported by the coal pillar and the immediate roof (q_m) and is interlocked with adjacent blocks to form a hinged structure. The hinged structure is relatively stable under the horizontal thrust (F) exerted by blocks A and C [3]. Key block B bears the gravity of the cantilever beam and the overlying strata. The longer the cantilever beam is, the greater the load transferred to the coal pillar through key block B. According to the equilibrium equation, the load borne by the coal pillar and the length of the cantilever beam can be calculated by Equation (1) [30]:

$$\sigma =\frac{\sum {\gamma }_i{h}_i{l}^3}{B\left(2x_0+2w+B\right)},$$

(1)

where γ_i is the body force of the main roof and overlying strata (KN/m³); h_i is the thickness of the main roof and overlying strata on it (m); l is the length of the cantilever beam (m); B is the width of a coal pillar (m); x₀ is the horizontal distance from the fracture line of the main roof to the gob-side roadway (m); and w is the width of the roadway (m).

$$x_0=\frac{\lambda m}{2\tan {\phi }_0}In\left(\frac{K\gamma H_m+\frac{C_0}{\tan {\phi }_0}}{\frac{C_0}{\tan {\phi }_0}+\frac{p_x}{\lambda }}\right),$$

(2)

where λ is the lateral pressure coefficient; φ₀ is the internal friction angle of the coal seam (°); C₀ is the cohesion of the coal seam (Mpa); K is the stress concentration factor; γ is the average bulk density of the overlying strata (kN/m³); H_m is the burial depth (m); and P_x is the load borne by the coal pillar [31,32].

When the main roof breaks, the abutment pressure transmitted from the overlying strata pressure to the solid coal can be divided into two parts. As shown in Figure 1, S₁ is the “internal stress field” (stress reduction zone), and S₂ is the “external stress field” (stress increase zone). The “internal stress field” abutment pressure comes from the moving main roof force, and its distribution and variation characteristics mainly depend on the weight and movement of the main roof.

It can be seen from the abutment pressure curve in Figure 1 that when gob-side entry driving is carried out, if the roadway is arranged in the range of S₂, the coal recovery rate will be reduced, so the roadway should be arranged in the range of S₁. The coal seam with larger mining height is affected by mining for a longer period. For the mine with tight mining replacement, it is difficult to realize the gob-side entry driving with small coal pillars under the condition of mining. At this time, roof cutting of gob-side entry can better solve this problem. In the diagram, γH is the original rock stress, and KmγH is the maximum stress above the coal seam.

2.2. Mechanism of Roof Cutting and Pressure Relief with Small Coal Pillars

(1)

Roof cutting to reduce the cantilever beam length for pressure relief

The gob formed in the extraction of thick coal seams is high, and the collapsed immediate roof cannot fill up the gob. A big space is created between the collapsed rock mass and the overlying hard strata, resulting in significant subsidence of the immediate roof [32]. With a great mining height, it takes a longer time for the overlying roof to stabilize, and the effect of mining is longer. Additionally, the rotation and subsidence of long cantilever beams caused by a great mining height impose a substantial load on the roadway, posing a severe threat to the stability of the gob-side roadway [28]. Therefore, the gob area can be filled up by cutting off the cantilever beam of the immediate roof to reduce the cantilever length, which can effectively reduce the load borne by the gob-side roadway and enable the stability control of the surrounding rock of the roadway. The fracture pattern of the overlying strata in a gob-side roadway after roof cutting to shorten the length of the cantilever beam is shown in Figure 2.

After the lateral roof fractures along the roof-cutting line, the interlocking between the rock beams changes, and the long cantilever beam transforms into a short cantilever structure. According to Equation (1), the load borne by the coal pillar (P_x) decreases after the length of the cantilever beam (l) shortens. As key block B‘ is cut off, the force exerted by it on block A decreases, reducing the additional load on block A and thus reducing the load borne by the solid coal on the right side.

(2)

Mechanism of pressure relief by reducing the fracture length of the roof after the first weighting through roof cutting

Before roof cutting, all four sides of the working face roof are clamped, as shown in Figure 3a. The roof is not prone to fracture, and the fracture length can be calculated by Equation (3) [33]. After roof cutting, during the initial loading, the structure of the working face roof can be regarded as a plate with two sides clamped and two sides simply supported during weighting, as shown in Figure 3b. The fracture length can be calculated via Equation (4) [31].

$$L=\frac{h}{1-{\mu }^2}\sqrt{\frac{2{\sigma }_s}{q}\cdot \frac{1+{\lambda }^4}{1+\mu {\lambda }^2}}$$

(3)

$$L_2=\frac{2h}{1-{\mu }^2}\sqrt{\frac{{\sigma }_s}{3q}\cdot \frac{1+{\lambda }^4}{4+\mu {\lambda }^2}}$$

(4)

where h is the thickness of the main roof; q is the weight of the main roof and the load borne by it; σ_z is the tensile strength of the strata; μ is the Poisson’s ratio of the strata; and λ is the geometric coefficient of the gob. $\lambda =a/b$. a and b are shown in Figure 3.

Equations (3) and (4) show that L > L₂ since $2+2{\lambda }^4>1+{\lambda }^4$ and $1+\mu {\lambda }^2<12+3\mu {\lambda }^2$. This suggests that without roof cutting, the fracture length of the main roof after the first weighting is large, and the mine pressure behavior is strong, and after roof cutting, the fracture length of the main roof along the cutting plane shortens, decreasing the mine pressure behavior. Therefore, roof-cutting and pressure-relief measures taken in roadways can not only reduce the fracture length of the roof strata but also effectively reduce the load borne by the surrounding rock in gob-side roadways.

3. Materials and Methods

The physical model test is a test method to simulate the field geological conditions according to the similarity theory in a certain proportion. After the model is excavated, the movement characteristics of the roof overburden can be observed intuitively. In order to intuitively understand the fracture morphology of the lateral roof after roof cutting, the experimental study on similar materials for roof cutting and pressure relief with respect to small coal pillars was carried out to reveal the influence of roof cutting and pressure relief on the stress characteristics of surrounding rock of gob-side entry. Due to the two-dimensional model test system, the analysis was carried out only on the model after excavation.

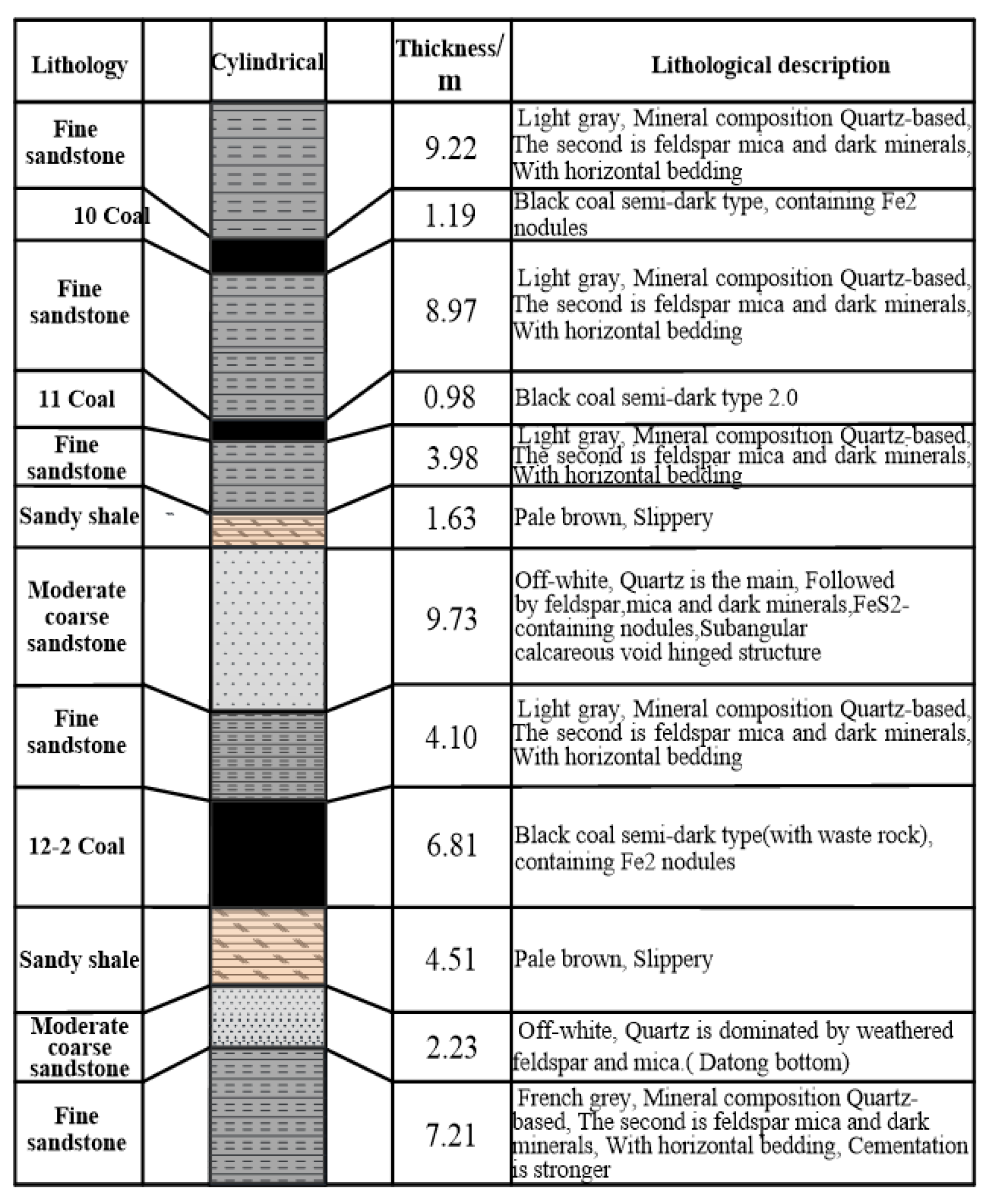
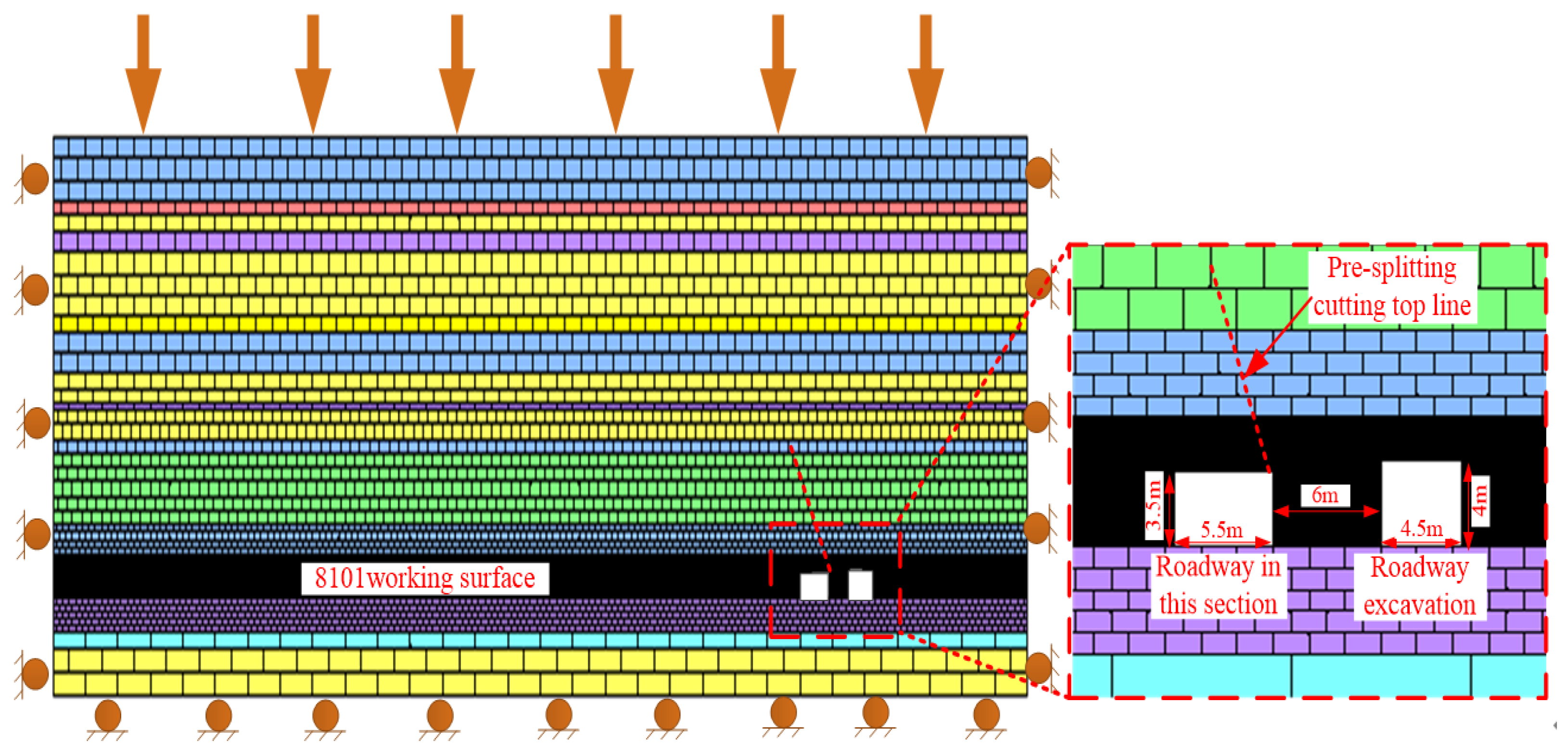
3.1. Selection of Similar Materials

In this test model, river sand, gypsum, calcium carbonate, and water were selected as the main raw materials, and the test model was laid according to the ratio of each material and the height of each rock layer. Among them, river sand is the main aggregate, gypsum and calcium carbonate are cementing materials, and mica powder is used as a layered material between rock strata.

The laying parameters of the model were determined based on the geological conditions of the 8101 working face in the Jinhuagong Coal Mine. The main coal seam in the mine is the 12-2# coal seam, with a thickness of 5.5 to 7.5 m, 6.81 m on average. The immediate roof of the working face is fine sandstone with a thickness of 4.10 m; the main roof is medium-coarse sandstone with a thickness of 9.73 m. The floor of the coal seam is sandy shale. The comprehensive column map of the working face is shown in Figure 4.

When the basic roof above the coal seam is a sandstone with large thickness and strength, with the mining of the working face, the direct roof will fall. Due to the large thickness and strength of the basic roof, the overlying strata of the goaf are not fully collapsed, and the hanging roof easily appears, which is not conducive to the maintenance of the roadway along the goaf. At this time, the thickness of hard rock should not be too large. If the lithology of the strata above the coal seam is mudstone with low strength, with the advancement of the working face, the overlying strata fall more fully, and the thickness of the strata can change within a certain range.

3.2. Test Scheme Design and Parameter Determination

(1)

Experimental design

The dimensions of the two-dimensional model test system used in the experiment are 190 cm in length × 22 cm in width × 136 cm in height. The left and right boundaries of the model were ones with horizontal displacement, and the bottom of the model was a fixed boundary. Due to the limited experimental conditions, only 144 m of overlying strata were simulated. The rest of the rock weight is loaded by the top cylinder pressure, and the loading stress is as follows:

$$q_m=q_p\times {\alpha }_{\sigma }={\gamma }_p\times (H-H_1)\times {\alpha }_{\sigma }=2.5\times {10}^4\times 187\times 1/180=0.025 \mathrm{MPa}.$$

In the formula, q_m is the load applied to the upper part of the model, N; q_n is the self-weight stress of the original overburden rock, N; γ_p is the prototype overburden bulk density, N/m; H is buried depth, m; H₁ is the thickness of overlying strata of coal seam, m; and α_σ is the stress ratio.

(2)

Determination of similar parameters

This experiment investigated the movement of the overlying strata before and after roof cutting and the stress changes of the surrounding rock in gob-side roadways. According to the research equipment and research objectives, the geometric similarity ratio of the experimental model was 1:120, the density similarity ratio was 1:1.5, and the stress similarity ratio was 1:180. The density of the strata (γ_m) was approximately 25 kN/m³.

With material loss taken into account, a material loss coefficient of 1.1 was taken, and the total amount of material required for each layer was calculated by Equation (5):

$$G_{mi}=1.1{\gamma }_{mi}lb{h}_{mi},$$

(5)

where G_mi is the quantity of material used in the ith layer of the model; h_mi is the thickness of the ith stratum; l is the length of the model table; and b is the width of the model table. The uncut top model and the cut top model are shown in Figure 5.

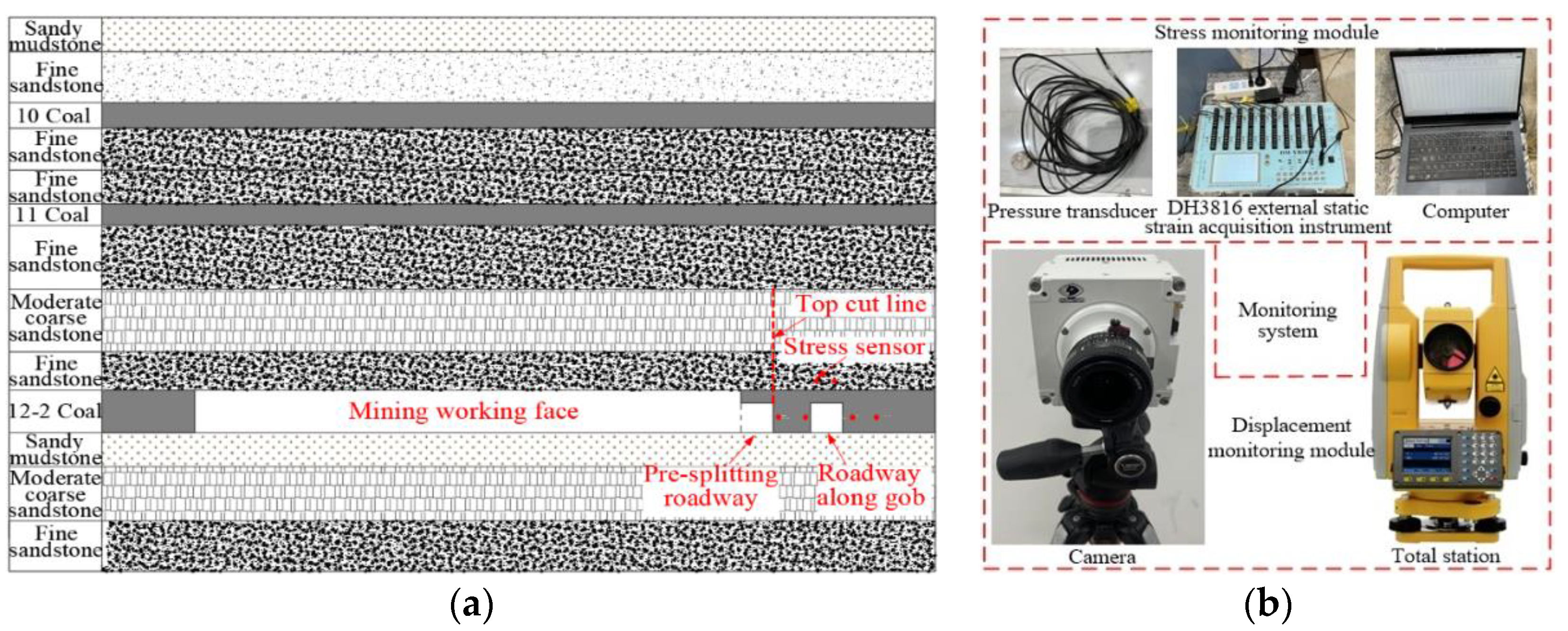
3.3. Model Monitoring and Excavation

(1)

Layout of monitoring points

The monitoring points were mainly used to monitor the stress changes in the surrounding rock of a gob-side roadway. A total of six monitoring points were arranged in the model, placed on both sides of the roadway and the roof, as shown in Figure 6a.

The monitoring system is divided into two parts: stress monitoring module and displacement monitoring module, as shown in Figure 6b. The stress monitoring module is mainly composed of a computer, a DH3816 external static strain acquisition instrument, and a pressure sensor. The displacement monitoring is to record the surface movement of the model through the camera, and to monitor the position change of the surface displacement monitoring point of the model with the total station.

(2)

Design of excavation scheme

Two model tests were conducted: with and without roof cutting. The comparison of the two tests reveals the influence of roof cutting on the lateral fracture of the roof on the surrounding rock in the gob-side roadway. To reduce the impact of boundary effects, 300 mm of boundary coal pillars were left on both sides of the model. The gob-side roadway was 50 mm wide; a coal pillar was 60 mm wide; and the excavation length of the model was 1190 mm. Taking the actual situation of the working face into account, the model was excavated by 50 mm at a time, with an interval of 30 min.

During the excavation process of the model, the DH3816 external static strain acquisition instrument was used to collect the stress data. At the same time, the total station was used to record the change of the displacement measuring point, and the graphic sketch method and the shooting method were used to record the rock caving movement in each stage of the mining process.

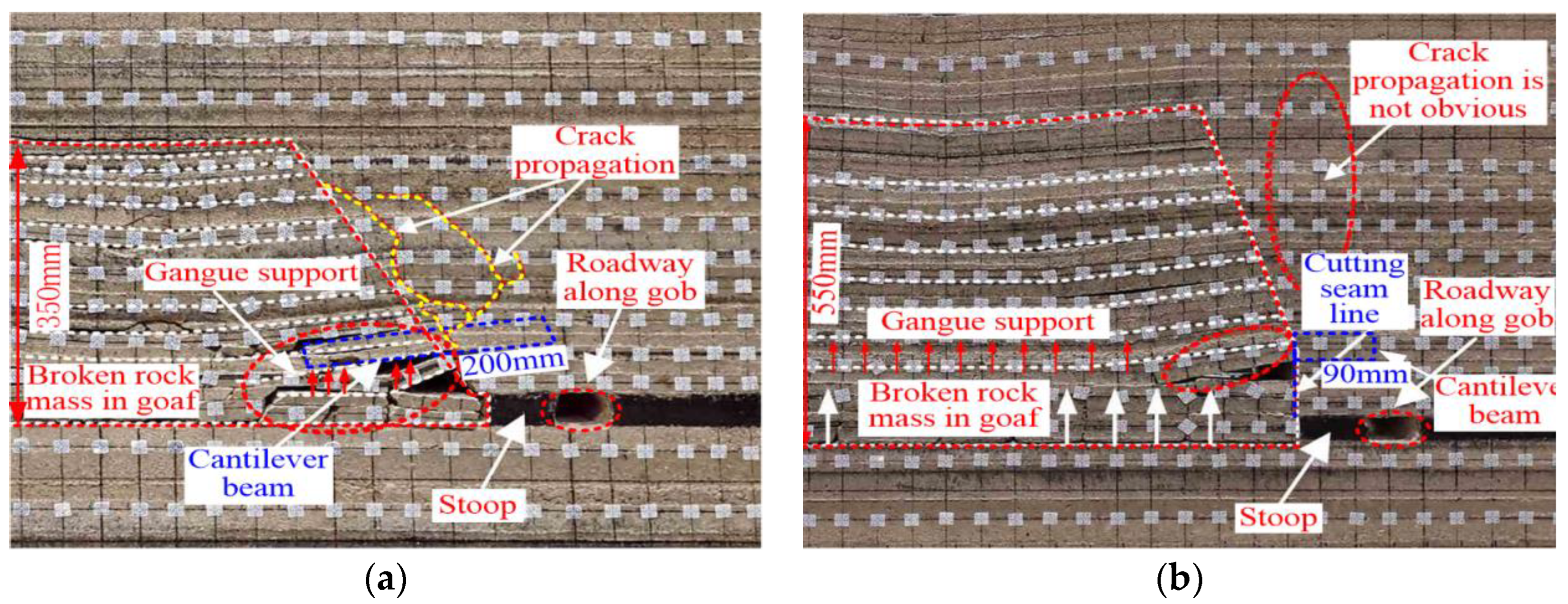
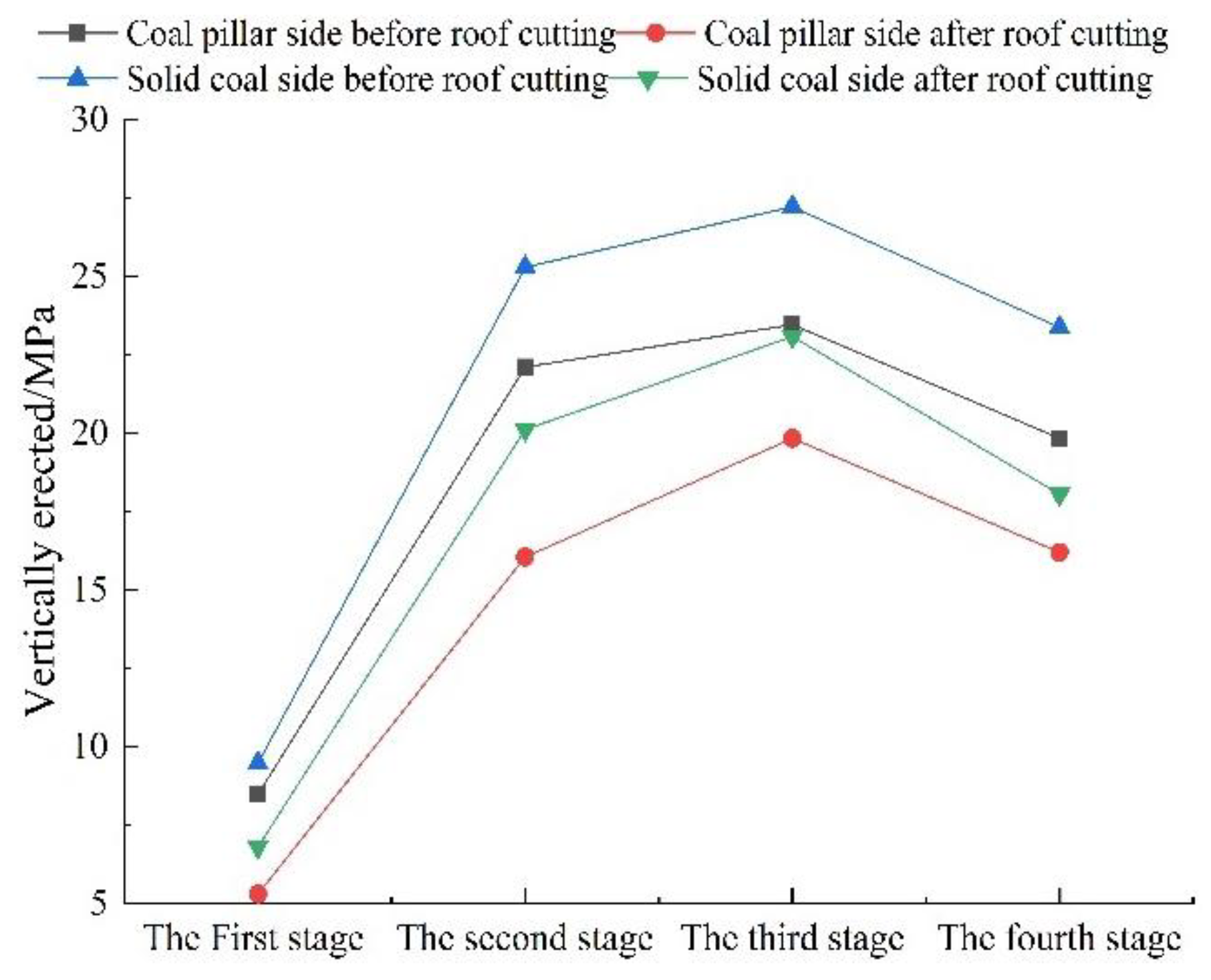
3.4. Analysis of Experimental Results

(1)

Comparison and analysis of the movement the overlying strata before and after roof cutting

Figure 7 shows the model with and without roof cutting after excavation. As shown in Figure 7a (without roof cutting), the upper overlying strata collapsed after excavation. After the movement of the upper overlying strata ended, the lower strata thoroughly collapsed, and the upper strata underwent bending and subsidence. The collapsed gangue gradually compacted, and the transverse and longitudinal cracks extended to higher positions of the roof. The cantilevered beam was long, supported by gangue at one end, and loaded on the coal pillar along the gob-side roadway. As shown in Figure 7b, after the movement of the upper overlying strata ended, the height of the collapsed strata was increased through was increased by roof cutting. Additionally, the roof strata collapsed along the cutting plane and were compacted in the gob, which effectively supported the upper overlying strata and reduced the mine pressure behavior of the movement of the upper strata. Compared to the cantilever on the roof before roof cutting, the length of the lateral cantilever of the roof significantly reduced from 200 mm to 90 mm after roof cutting, effectively reducing the load on the coal pillar.

(2)

Comparison and analysis of the stress in the surrounding rock of a gob-side roadway before and after roof cutting

After the excavation of the working face, the stress in the surrounding rock was redistributed. The changes in the stress on the two sides of the gob-side roadway before and after roof cutting are shown in Figure 8. When the roof is not cut, the peak stress of the coal pillar is 23.5 MPa, and the peak stress of the solid coal is 27.2 MPa. After the roof is cut, the peak stress of the coal pillar is 19.8 MPa, and the peak stress of the solid coal is 23.1 MPa, which is 15.7% and 14.3% lower than that when the roof is not cut. It can be seen that the roof-cutting measures shorten the cantilever length of the lateral rock beam, and the roof cutting increases the height of the collapsed rock layer to support the upper key rock layer, which effectively reduces the load of the small coal pillar overlying rock, thus reducing the stress concentration of the surrounding rock of the roadway.

4. Determination of Key Technical Parameters for Roof Cutting and Pressure Relief

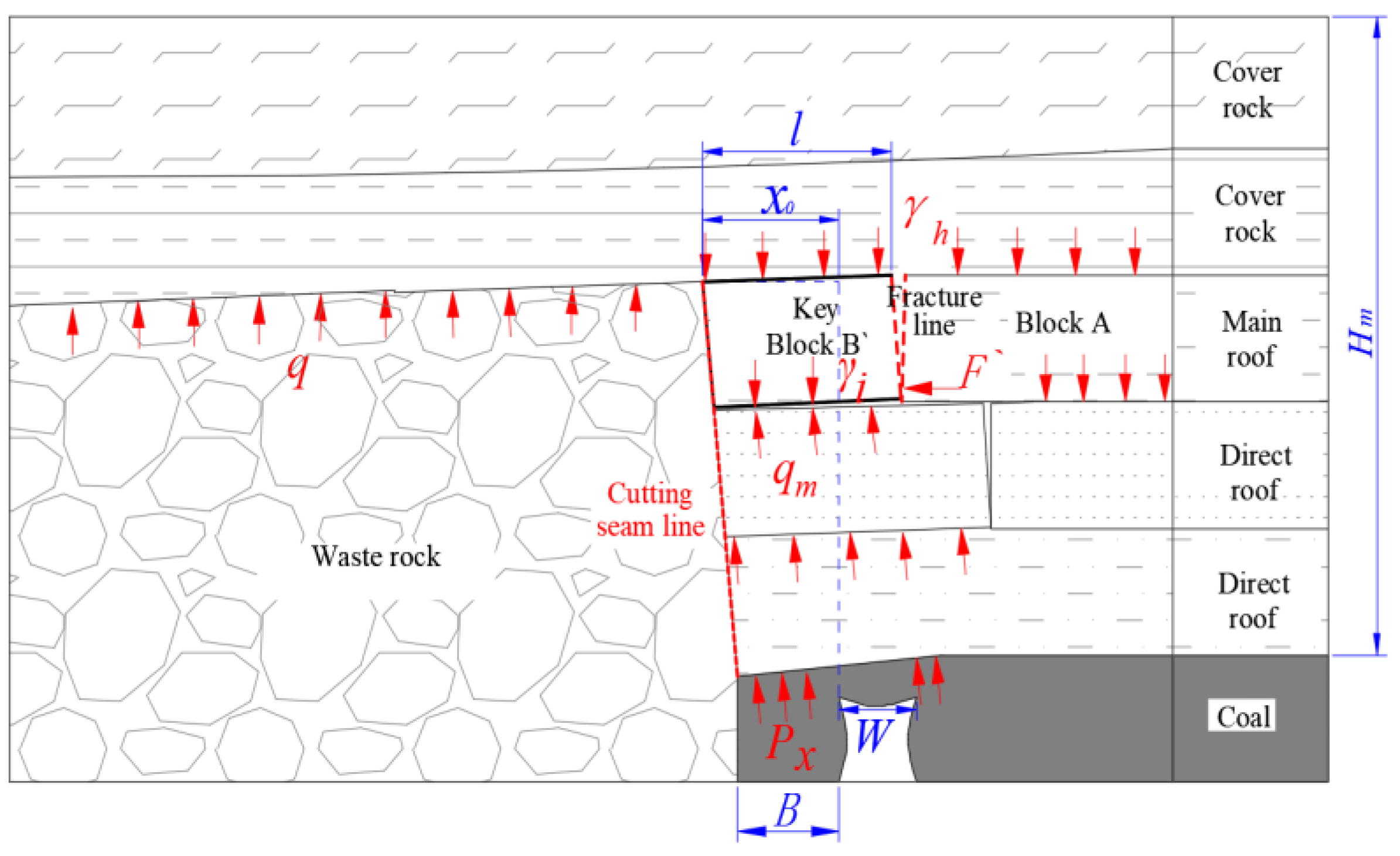
4.1. Theoretical Analysis of Roof-Cutting Parameters

(1)

Pre-splitting roof-cutting angle

After the cutting of the roof, the original key block B was divided into key blocks B‘ and D. When block D slid along the fracture surface, the stress transfer between rock beams of the main roof could be effectively cut off. At this point, the stress on key block B‘ is shown in Figure 9.

The sliding of block D along the fracture surface should satisfy the following conditions [33]:

$$T\sin \left(\phi -\beta \right)\le R\cos \left(\phi -\beta \right),$$

(6)

$$T=\frac{q{l}^2}{2\left(h-\Delta S\right)},$$

(7)

$$R=ql,$$

(8)

where T is the lateral horizontal thrust; $\phi$ is the internal friction angle of the rock block, and $\phi =40°~47°$; R is the shear stress on the rock block during the instability process in the sliding of the block; q is the concentrated load; h is the thickness of the main roof; $\Delta S$ is the subsidence of the rock block; and l is the length of the cantilevered beam.

Thus, the optimal range of roof-cutting angle for unstable sliding is [33] as follows:

$$\beta \ge \phi -\arctan \frac{2\left(h-\Delta S\right)}{l},$$

(9)

where

$$\Delta S=M\eta -H_1\left(K_1-1\right),$$

(10)

$$l=h\sqrt{\frac{R_t}{3q}}.$$

(11)

According to field measurements, the mining height (h) was 6.81 m, and the recovery ratio of the working face ($\eta$) was set to 93%. $K_1$ is the broken rock bulking coefficient (1.3–1.5); $H_1$ is the thickness of the collapsed rock layer; and $R_t$ is the tensile strength of the rock.

The optimal range of the roof-cutting angle ($\beta$) was calculated as $6°\le \beta \le 13°$.

(2)

Pre-splitting roof-cutting height

The roof-cutting height H_cut refers to the maximum vertical height of the borehole. With a reasonable roof-cutting height, the overlying strata collapse along the cutting plane after the first weighting. The bulking coefficient of the collapsed rock increases, which, to some extent, supports the rotating and subsiding overlying strata, thereby improving the stress environment in the gob-side roadway. The roof-cutting height is related to the thickness of the rock layer, and its relationship with the depth of the pre-splitting borehole (H_crack) is $H_{cut}=H_{crack}\cos \beta$. to ensure that the rock layer cut off can support the overlying strata of the gob area after fracture and bulking, the roof-cutting height also needs to satisfy the following condition: $H_{cut}\ge H_{carved}$ (is the height of the caved zone) [34]. The height of the pre-splitting borehole is calculated as follows [34,35]:

$$H_{crack}\ge H_{coal}/\left[\left(k_0-1\right)\cos \beta \right],$$

(12)

where k₀ is the initial bulking coefficient of the collapsed gangue, ranging from 1.3 to 1.5.

In this study, according to field measurements, k₀ = 1.35, the roof-cutting angle β = 12°, H_coal = 6.81 m, and the calculated cutting depth was 13.6 m. To ensure that the entire rock layer could be cut off, the roof-cutting height was determined to be 14 m (i.e., the top part of the 9.73-m-thick medium-coarse sandstone), with the position of the rock layer at the bottom of the borehole taken into account.

4.2. Numerical Analysis of Roof-Cutting Parameters

The UDEC numerical simulation software was used to compare and analyze the deformation and stress distribution of the surrounding rock in gob-side roadways under different conditions and determine the reasonable roof-cutting angle and height. A numerical model with dimensions of 300 m × 75 m was established according to the geological conditions of the 8101 working face in the Jinhuagong Coal Mine. In addition, the coal seam thickness was 6 m, and the haulage roadway of the 8101 working face had dimensions of 5.5 m × 3.5 m, while the goaf drift of the 8103 working face was 5.0 m × 3.8 m, with 6-meter-wide coal pillars for roadway protection. To reduce the impact of boundary effects on the simulation, boundary coal pillars with a width of 50 m were left on both sides of the model. The side of the model is limited to horizontal movement, which can be moved in the x-axis direction. The y-axis is fixed hinge seat, the bottom is fixed, and the upper surface is the stress boundary. The vertical load is applied to simulate the self-weight stress of the overlying strata. Through calculation, the equivalent load applied on the upper part of the model is as follows: $\sigma =\gamma h=25\times 1000\times 256.02=6.4\mathrm{MPa}$. The numerical calculation model is shown in Figure 10, and the major physical and mechanical parameters of the rock mass in the model are shown in

Table 1. Major physical and mechanical parameters of the numerical model.

Lithology	Density/kg·m3	Bulk Modulus/GPa	Shear Modulus/GPa	Internal Friction Angle/°	Cohesion/MPa	Tensile Strength/MPa
Fine sandstone	2580	7.1	2.97	37	5.45	7.3
Coal	1400	7.5	1.82	28	2.82	1.2
Sandy shale	2420	6.2	2.91	35	4.53	2.5
Medium-coarse sandstone	2580	9.4	6.76	40	6.62	8.0

.

(1)

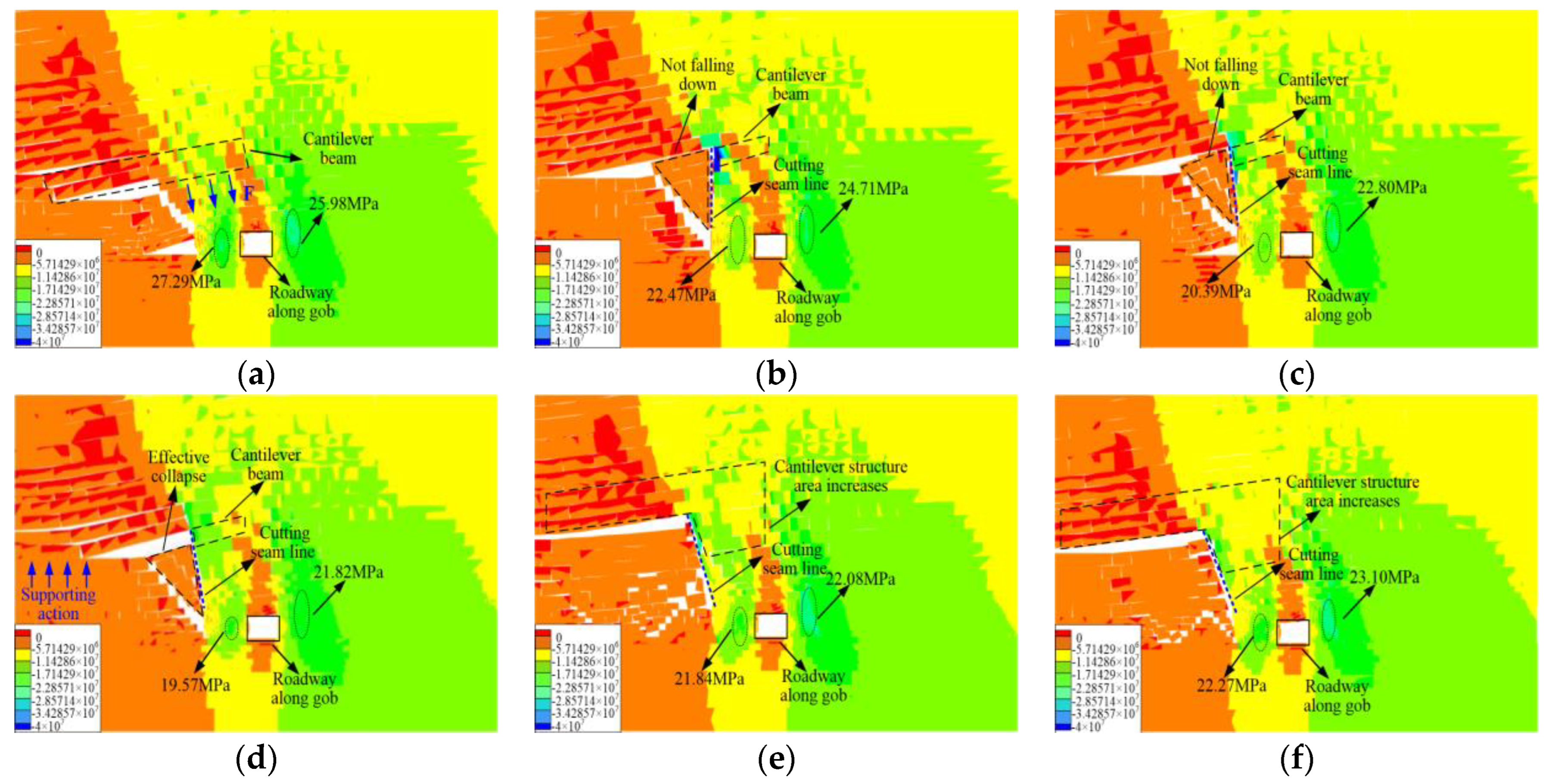
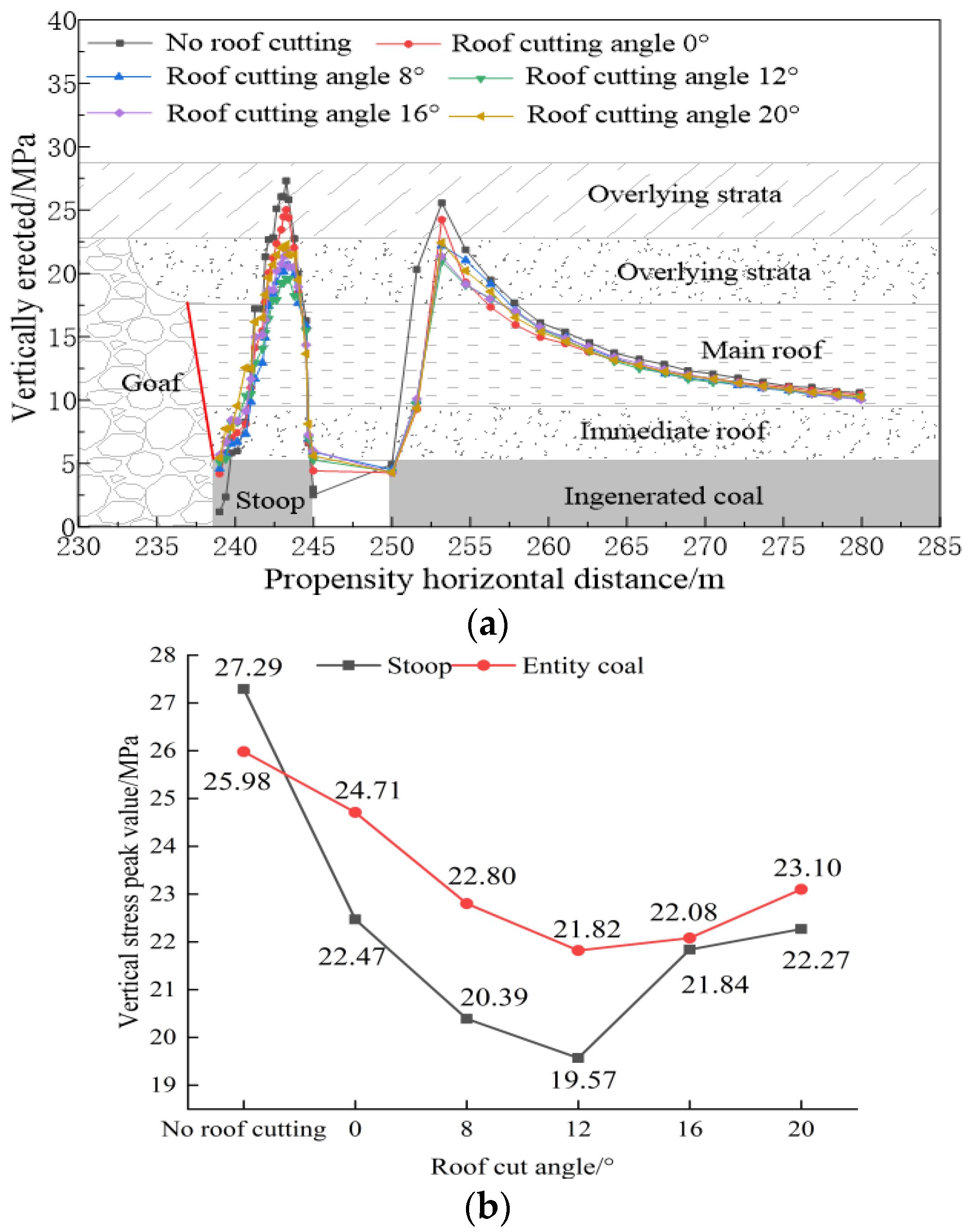
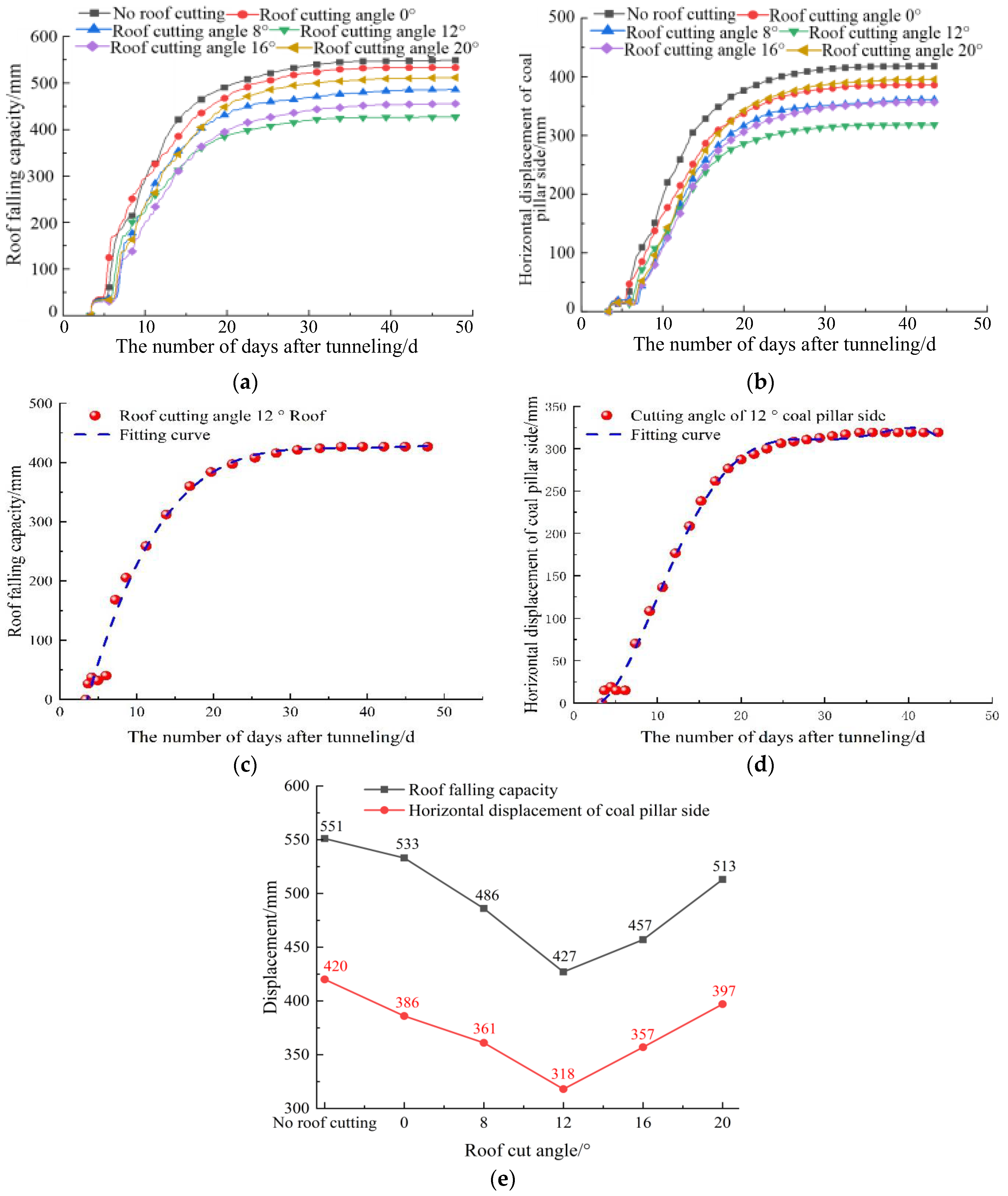
Determination of the pre-splitting roof-cutting angle

Six roof-cutting plans were designed in numerical simulation, including no roof-cutting and pre-splitting roof-cutting angles of 0°, 8°, 12°, 16°, and 20°, respectively. Figure 11 shows the fractures and vertical stress distribution of the roof surrounding rock of the roadway with different roof-cutting angles. According to Figure 11a, without roof-cutting, the immediate roof collapses and forms a cantilever beam structure above the coal pillar. The beam rotates and subsides, compressing the coal pillar. As a result, the coal pillar bears a great load, forming a high-stress concentration zone. When the roof-cutting angle is 0° (Figure 11b) and 8° (Figure 11c), the collapsed rock cannot fill up the gob area since the roof layer does not completely collapse along the cutting plane. Therefore, the overlying strata cannot be effectively supported. When the roof-cutting angle is 12° (Figure 11d), the collapsed rock fills up the gob area and provides some support for the overlying strata, effectively reducing the load on the surrounding rock in the roadway. When the roof-cutting angle is 16° (Figure 11e) and 20° (Figure 11f), the roof layer collapses relatively completely, but the contact area between the cantilever beam structure above the coal pillar and the overlying strata also increases as the roof-cutting angle becomes larger, with the weight of the overlying strata transferred via the beam structure to the coal beam. As a result, the coal pillar undergoes severe deformation due to the stress concentration on it.

Figure 12 shows the vertical stress distribution on the rocks surrounding the roadway and the peak values of vertical stress with different roof-cutting angles. The peak stresses on both sides of the roadway decrease and then increase as the roof-cutting angle increase. When the roof-cutting angle is 0° and 8°, the peak stresses on both sides of a coal pillar and the ribs of solid coal decrease compared to the case without roof-cutting, from 22.47 MPa to 20.39 Mpa and 24.71 MPa to 22.80 MPa, respectively. The peak stresses on both sides of a coal pillar and that on the ribs of solid coal are the smallest, 19.57 MPa and 21.82 MPa, respectively, when the roof-cutting angle is 12°. When the roof-cutting angle is 16° and 20°, the peak stresses on both sides of a coal pillar are 2.27 MPa and 2.7 MPa higher than when the roof-cutting angle is 12°, and those on the ribs of solid coal are 0.26 MPa and 1.28 MPa higher than when the roof-cutting angle is 12°.

To study the impact of the roof-cutting angle on the deformation of the roof and coal pillar of a gob-side roadway, displacement measurement points were arranged along the roof and on both sides of the coal pillar, as shown in Figure 13. Without roof-cutting, the cantilever of the lateral roof is long, resulting in a large load on the surrounding rock of the roadway. Under these conditions, the maximum subsidence of the roof and the maximum horizontal displacement of the coal pillar are 551 mm and 420 mm, respectively. As the roof-cutting angle increases, both figures decrease and then increase, which reach the lowest points, 427 mm, and 318 mm, respectively, when the roof-cutting angle is 12°. According to the vertical stress distribution on the rocks surrounding the roadway and the deformation characteristics of the roadway with different roof-cutting angles, the optimal pre-splitting roof-cutting angle is 12°.

According to the monitoring curve when the pre-splitting angle is 12°, it is found that the deformation of the surrounding rock of the roadway has a significant functional relationship with the roadway excavation time during the fitting process, as shown in Figure 13c,d. In order to facilitate the long-term deformation and prediction of roadway surrounding rock, the fitting equations of roof deformation and coal pillar deformation are as follows:

$$y_1=60.43x-2.22x^2+0.36x^3-2.135E^{-4}{x}^4-189.6(R^2=98.91\%),$$

(13)

$$y_2=-22.97x_1+5.88x^2-0.33x^3+0.0073x^4+23.94(R^2=99.67\%).$$

(14)

(2)

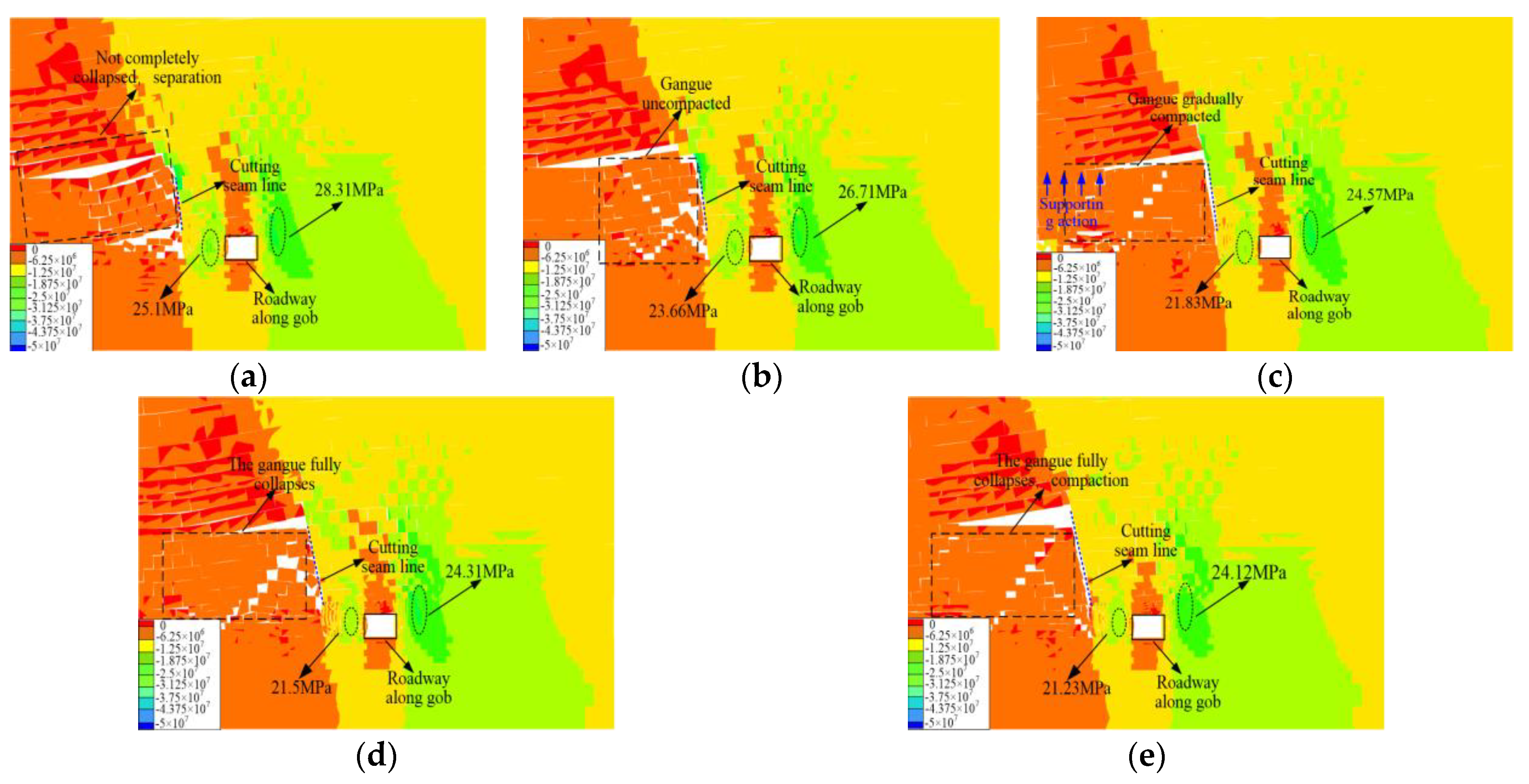
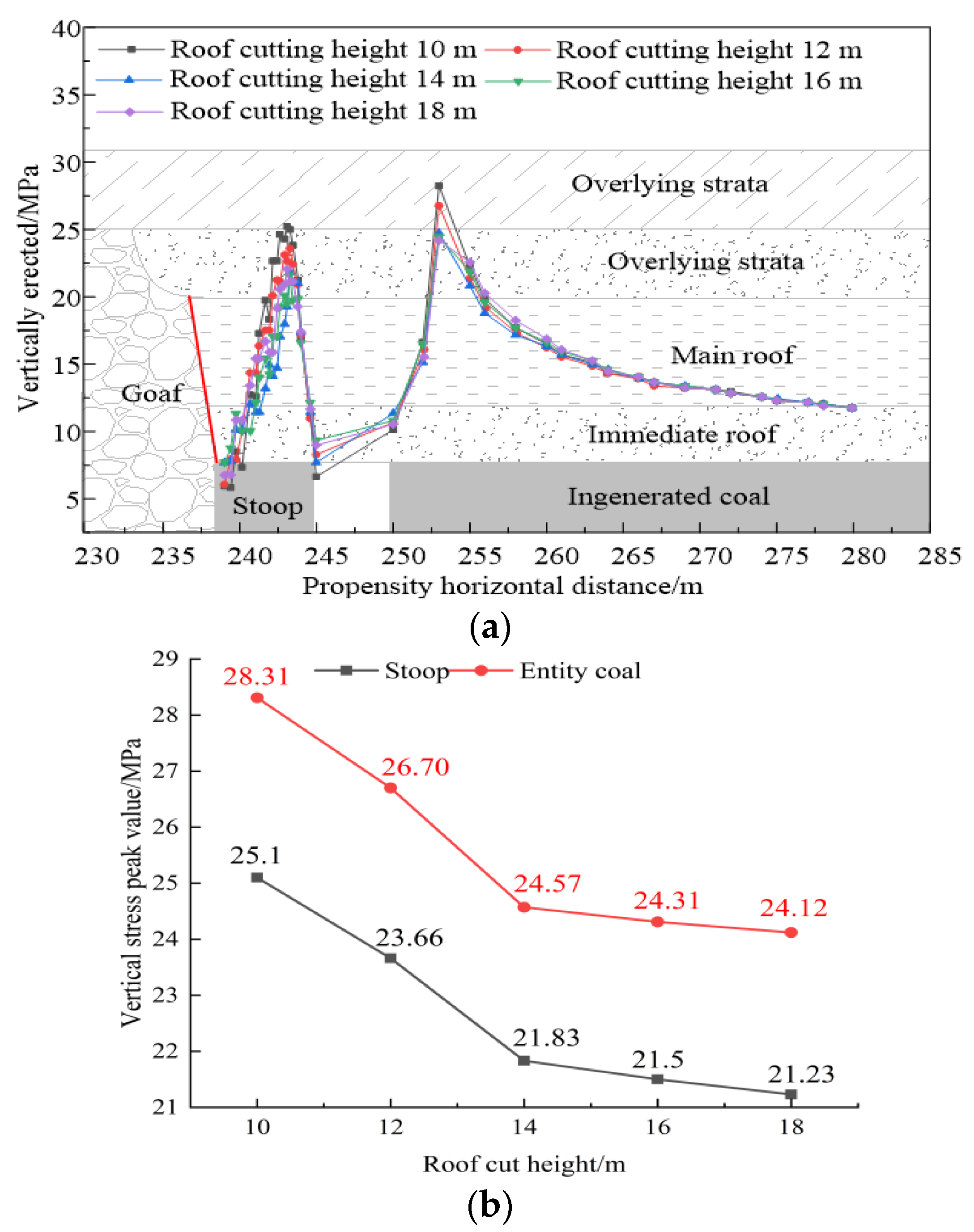
Determination of the pre-splitting roof-cutting height

The roof-cutting height determines the degree of collapsing of the overlying rock in the gob, thereby affecting the support provided by the collapsed rock to the upper strata. To investigate the pressure-relieving effect of different roof-cutting heights on a gob-side roadway, the roof-cutting angle was set to 12° in the numerical model. Five roof-cutting plans were analyzed, with heights of 10 m, 12 m, 14 m, 16 m, and 18 m, respectively.

Figure 14 shows the fractures and vertical stress distribution of the roof surrounding rock of the roadway with different roof-cutting heights. When the roof-cutting height is 10 m (Figure 14a), some rock layers are in contact with the cutting plane, and the height of the collapsed rock is small. The collapsed gangue does not fill up the gob, resulting in separation in overlying strata. When the roof-cutting height is 12 m (Figure 14b), the cantilever rock layers collapse along the cutting plane, but the collapsed gangue does not fill the gob and the overlying strata cannot be effectively supported. When the roof-cutting height is 14 m (Figure 14c), the collapsed gangue does not fill the gob and is gradually compacted, providing some support for the upper strata and reducing the concentrated stresses on both sides of the coal pillar and ribs of solid coal. When the roof-cutting height is 12 m (Figure 14d) and 18 m (Figure 14e), as the roof-cutting height increases, the range of the roof layers being cut off gradually expands, and the collapsed gangue provides effective support for the continuous bending and subsiding of the upper strata.

Taking the 2130 working face [34] of Chengjiao Coal Mine as an example, the numerical simulation results shown in Figure 14 are basically consistent with the numerical simulation results of roof cutting and pressure relief in other parts of the world. The greater the height of roof cutting, the smaller the peak value of stress concentration, and the farther the stress concentration area is from the roadway, the more favorable it is for the stability of the roadway. However, with the increase in the cutting height to a certain extent, the effect of increasing the cutting height on the stress reduction is not obvious, and with the increase in the cutting height, the construction is more difficult.

Figure 15 shows the vertical stress distribution on the rocks surrounding the roadway and the peak values of vertical stress with different roof-cutting heights. The peak stresses on both sides of the roadway increase and then decrease as the roof-cutting height increases. When the roof-cutting height is 10 m and 12 m, the peak stresses on the ribs of solid coal are 25.1 MPa and 28.31 MPa, respectively, and those on both sides of the roadway are 23.66 MPa and 26.71 MPa, respectively, showing a decreasing trend. When the roof-cutting height is 14 m, the peak stresses on the ribs of solid coal and both sides of the roadway drop significantly to 21.83 MPa and 24.57 MPa, respectively. When the roof-cutting height is 16 m and 18 m, the peak stresses on the ribs of solid coal are 21.5 MPa and 21.23 MPa, respectively, and those on both sides of the roadway are 24.31 MPa and 24.12 MPa, respectively. When the roof-cutting height is 18 m, stresses on the surrounding rock on both sides of the roadway decrease, but less significantly than when the height is 14 m. Therefore, when the roof-cutting height reaches a certain value, a further increase can continue to reduce the load on the roadway, but the stresses are not significantly reduced.

To study the impact of the roof-cutting height on the deformation of the roof and coal pillar of a gob-side roadway, displacement measurement points were arranged along the roof and on both sides of the coal pillar, as shown in Figure 16. As the roof-cutting height increases, both the maximum subsidence of the roof and the maximum horizontal displacement of the coal pillar show a decreasing trend, with the extent of the decrease becoming smaller. When the roof-cutting height is 14 m, the subsidence of the roof and the horizontal displacement of the coal pillar see the most significant decreases, by 402 mm and 271 mm, respectively. Subsequently, with the further increase in the roof-cutting height, the changes in the subsidence of the roof and the horizontal displacement of the coal pillar are not significant compared to when the roof-cutting height is 14 m, indicating that the pressure-relieving effect is not significant. According to the vertical stress distribution on the rocks surrounding the roadway and the deformation characteristics of the roadway with different roof-cutting heights, the pre-splitting roof-cutting height was 14 m.

According to the monitoring curve when the pre-splitting height is 14 m, it is found that there is a clear functional relationship between the deformation of roadway surrounding rock and the excavation time during the fitting process, as shown in Figure 16c,d. In order to facilitate the long-term deformation and prediction of roadway surrounding rock, the fitting equations of roof deformation and coal pillar deformation are as follows:

$$y_3=81.95x-4.28x^2+0.097x^3-8.034E^{-4}{x}^4-184.06(R^2=99.03\%),$$

(15)

$$y_4=56.99x-2.92x^2+0.066x^3-5.528E^{-4}{x}^4-148(R^2=99.73\%).$$

(16)

4.3. Determination of Pre-Splitting Blast Hole Spacing

Based on the above results, pre-splitting blasting was conducted 50 m ahead of the haulage roadway in the 8101 working face. The energy-gathering pre-splitting blasting technology [36] is adopted in the field. The energy-gathering device is used to gather the energy of the explosion products, and the energy-gathering flow is formed in the specified direction, and the tensile stress concentration is generated, thus forming the pre-splitting surface in the predetermined direction. The optimal pre-splitting blast hole spacing was determined by comparing the effects of different hole spacings.

(1)

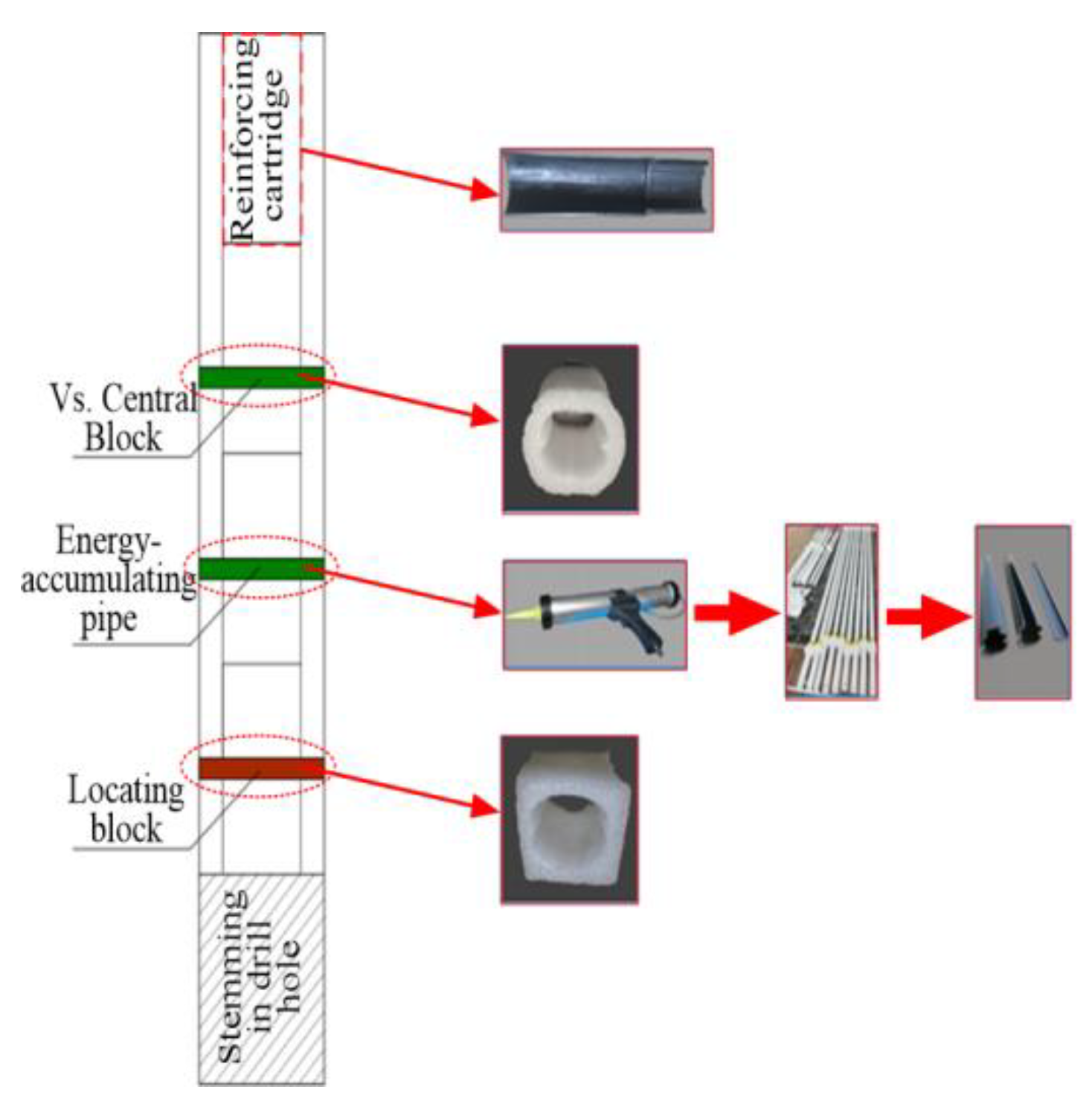
Pre-splitting blasting design parameters

Blast holes were drilled near the coal pillar, 1.2 m from the roof. The drilling angle was 12°, and the depth was 14 m. Binding energy tubes with an outer diameter of 42 mm, an inner diameter of 36.5 mm, and a length of 1500 mm were installed in the holes, and the holes were sealed using water stemming, with a length no shorter than 1500 mm. Then, pre-splitting blasting was conducted. The charging structure and blasting equipment are shown in Figure 17 [37].

(2)

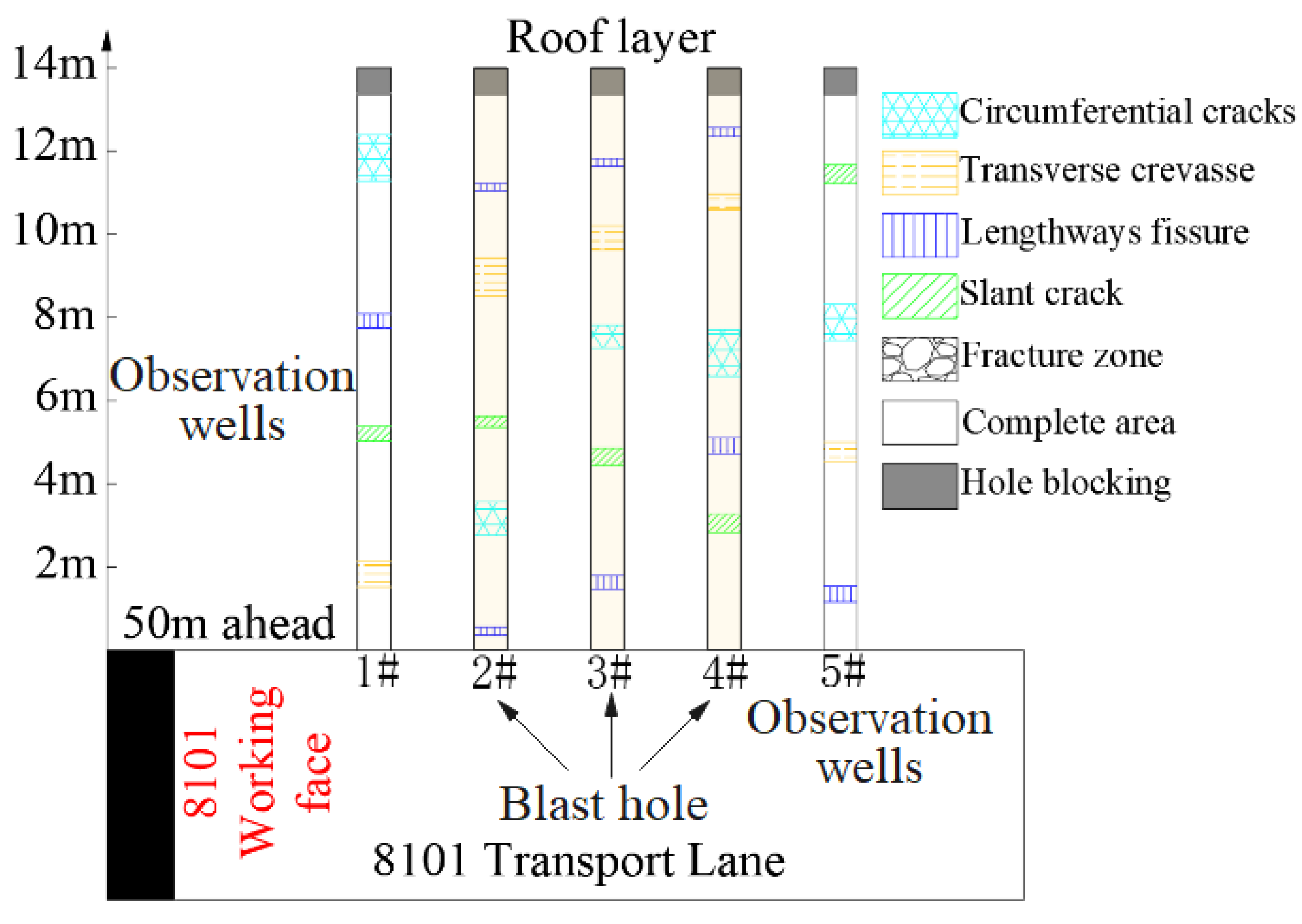
Monitoring of pre-splitting blasting effects

To observe the pre-splitting blasting effects on the lateral roof of the gob-side roadway, a borehole camera was used to inspect how the cracks generated by pre-splitting blasting expanded. The sketches of the positions of the holes and the cracks are shown in Figure 18. According to the calculation formula of pre-splitting blasting hole spacing [36,38], the hole spacing is $B=(7~12)d$, the hole diameter d is 45 mm, and the hole spacing is $B=315~540\mathrm{mm}$. Take 500 mm on site, two radial cracks appear on the borehole wall within the range of 5–14 m on the blasting section, with a width of about 2–4 m. No cracks are generated in other parts of the hole. After the field test, the peep map of the pre-splitting blasting effect is shown in Figure 19. Under the action of cumulative blasting, the roof of the goaf basically falls with mining, and there is no obvious hanging roof phenomenon. The cumulative blasting has a good pre-splitting effect on the roof strata.

5. Engineering Application

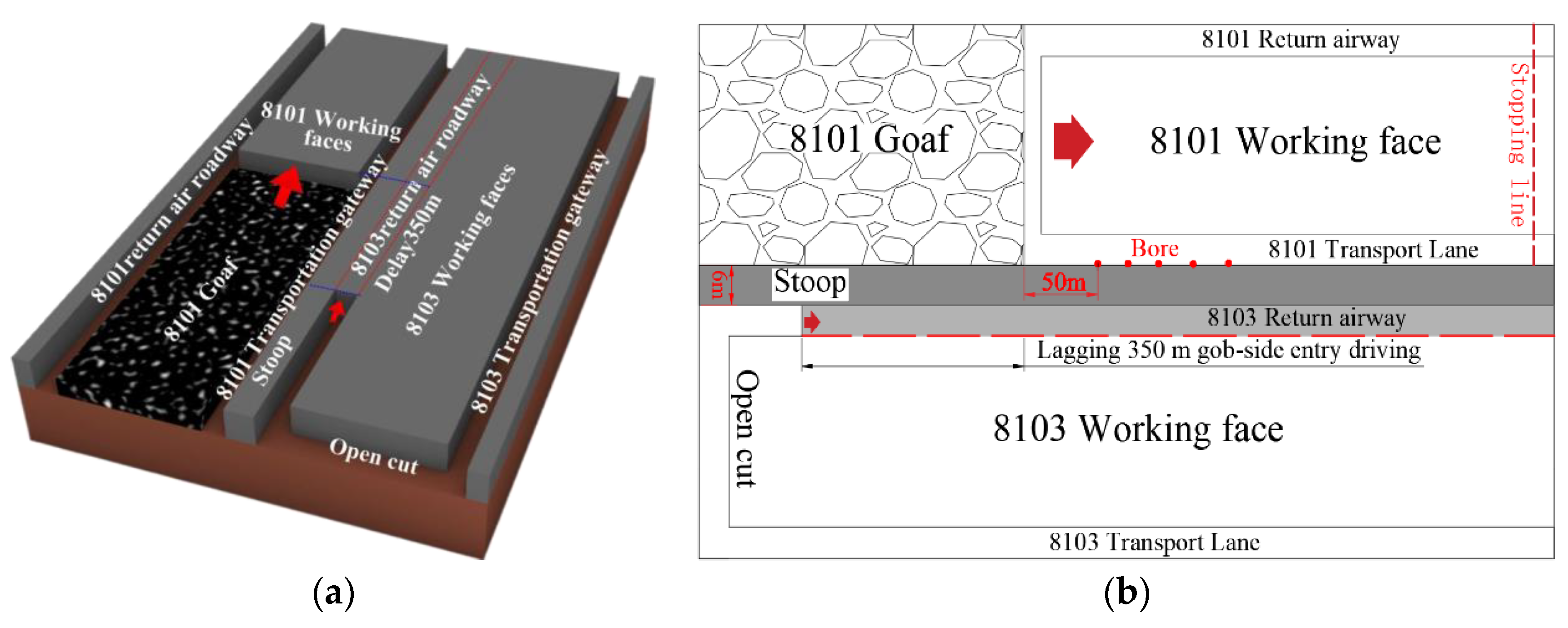
5.1. Excavation Scheme

According to the above results and the conditions on site, an excavation scheme (Figure 20) was adopted in which the 8303 return airway lags behind the 8101 working face to reduce the waiting time for excavation on the 8103 working face and ensure the stability of the surrounding rock in the gob-side roadway. After the 8101 working face advanced for a certain distance, the 8103 return airway was cut open and excavated via the 8103 haulage roadway. To mitigate the impact of roof movement in the 8101 working face on the 8103 return airway, holes were drilled by pre-splitting blasting in the 8101 haulage roadway in advance during the excavation process, and the cantilever length of the lateral rock was reduced.

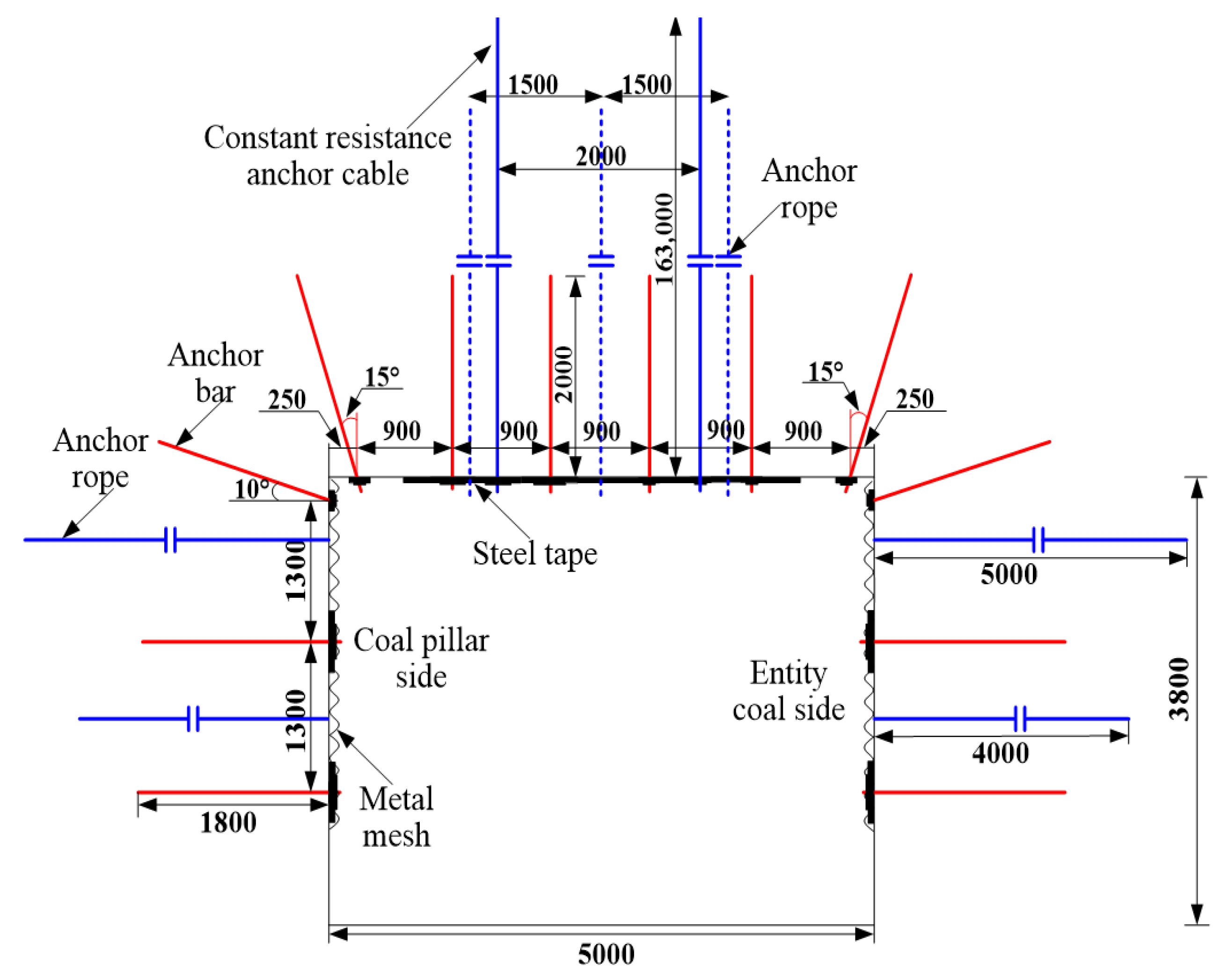
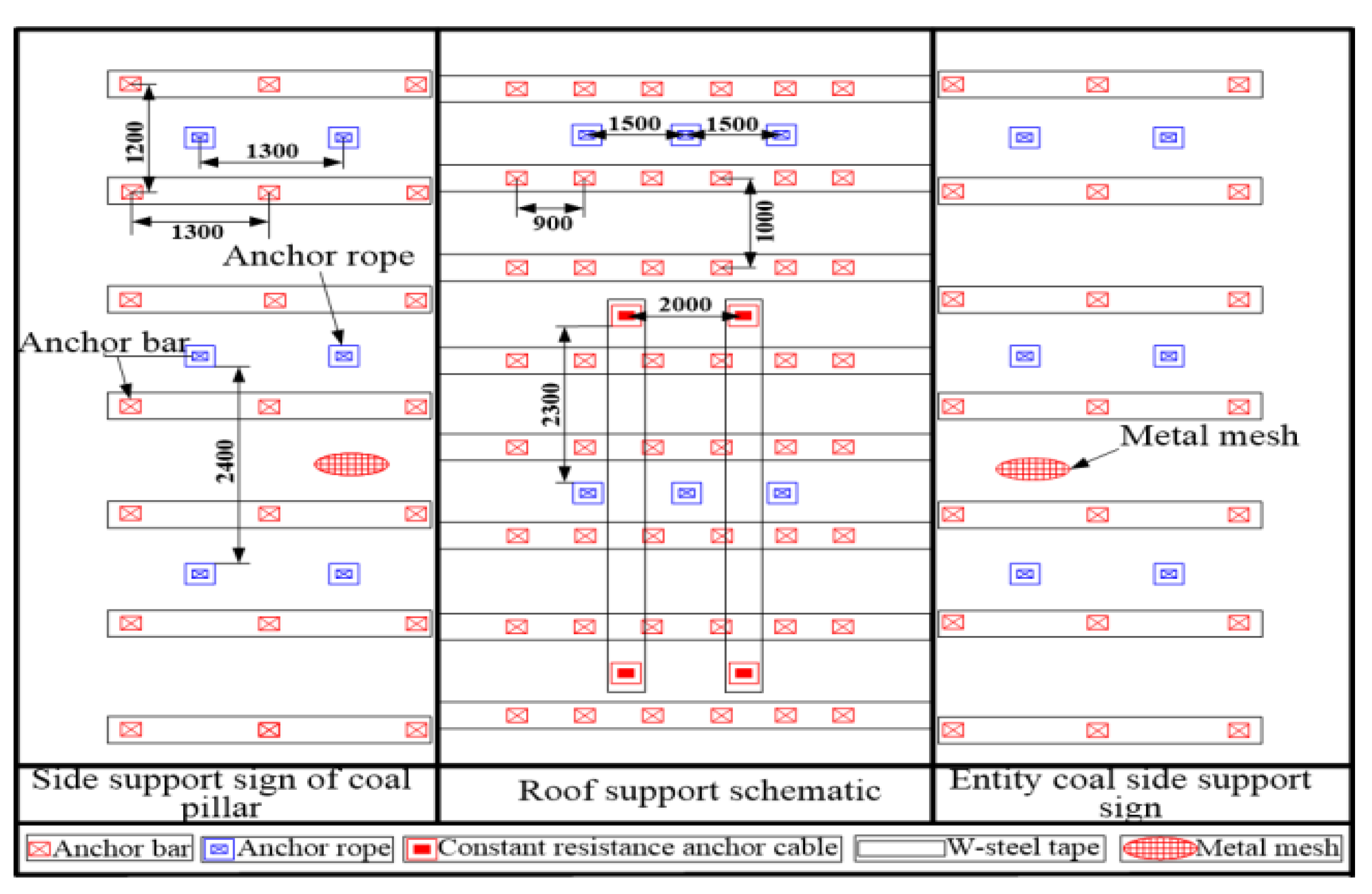
5.2. Roadway Support Scheme

The numerical simulation results show that both sides of the coal side undergo severe deformation before roof cutting. After roof-cutting measures are taken, the stress concentration in the surrounding rock of the gob-side roadway is relieved. However, the deformation is still significant because of the unstable movement of the roof layers. To improve the stability of the surrounding rock in the gob-side roadway, stronger support measures are taken during excavation to enhance the load-bearing capacity of the surrounding rock.

According to the deformation characteristics of the gob-side roadway after roof cutting and pressure relief, a comprehensive support scheme was proposed, the use of constant-resistance anchor cables with great deformation capacity was considered, and a comprehensive support scheme combining “steel strip + bolt + anchor cable + roof cutting” was also proposed. The support design of the 8103 roadway is shown in Figure 21 and Figure 22.

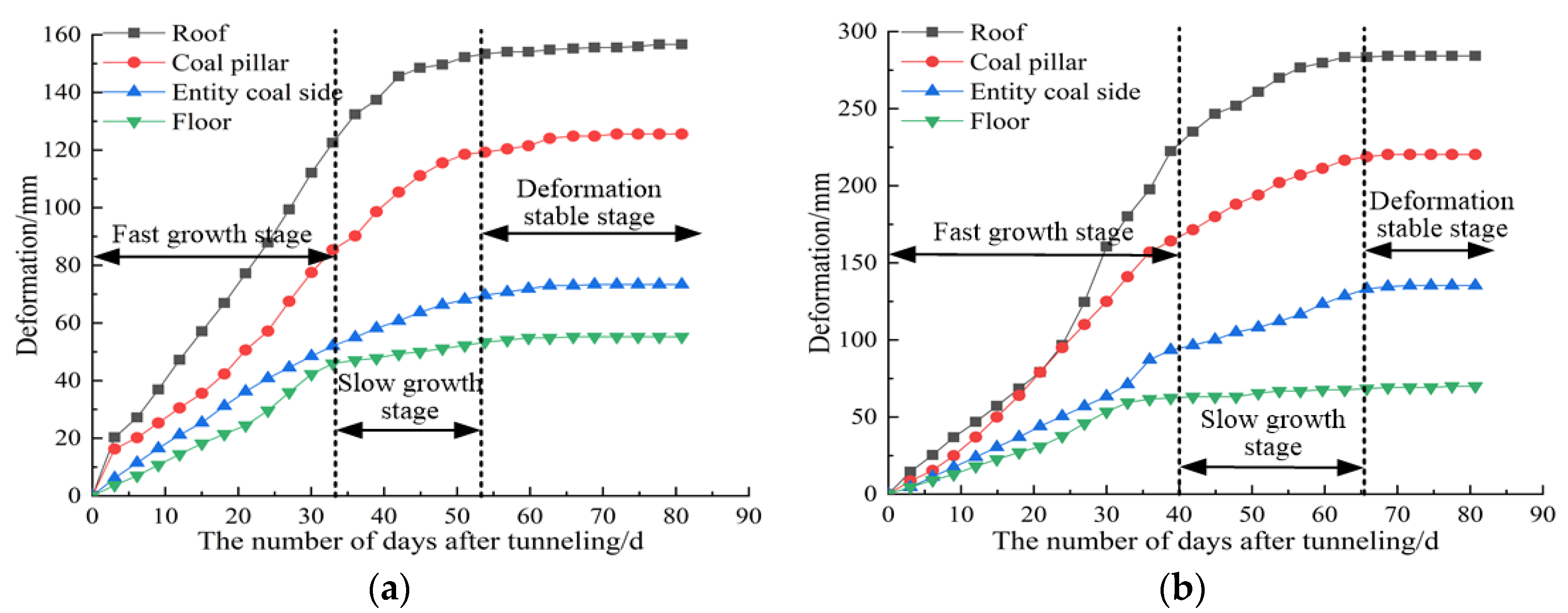
5.3. Application Effect Analysis

To test the applicability of roof-cutting and pressure-relieving techniques in gob-side entry driving with small coal pillars when the roof is under stable conditions, displacement monitoring points were arranged in the 8103 gob-side roadway. The 1# station in the test section was compared with the 2# station in the non-test section. The deformation of the roadway can be divided into three stages: the stage of rapid growth, the stage of slow growth, and the stage of stable deformation. Figure 23 shows the monitoring of the surrounding rock during the excavation of the 8103 gob-side roadway.

The deformation of surrounding rock in the non-test section (Figure 23b) is in a rapid growth stage within the first 40 days, and the change rate is fast. When the deformation of the roof and floor is 225 mm and 60 mm, respectively, and the displacement of the coal pillar and the solid coal side reaches 163 mm and 87 mm, the deformation of the surrounding rock enters a slow growth stage. The deformation of surrounding rock in the test section (Figure 23a) changed rapidly in the first 33 days and was in a rapid growth stage, which was about 7 days shorter than that in the non-test section. At this time, the deformation of the roof and floor of the test section is 122 mm and 45 mm, respectively, and the displacement of the coal pillar side and the solid coal side reaches 85 mm and 50 mm and then enters the slow growth stage.

The deformation of surrounding rock in the non-test section (Figure 23b) is in a slow growth stage within 40~65 d. When the deformation of roof and floor is 273 mm and 68 mm, respectively, and the displacement of coal pillar side and solid coal side reaches 220 mm and 134 mm, the deformation of surrounding rock enters the stable stage of deformation. The deformation of roadway surrounding rock in the test section (Figure 23a) is in a slow growth stage within 33~53 d, which is about 5 d shorter than that in the non-test section. At this time, the deformation of the roof and floor of the test section is 155 mm and 55 mm, respectively, and the displacement of the coal pillar side and the solid coal side reaches 125 mm and 73 mm. After that, it entered the stage of deformation stability.

After the surrounding rock tends to be stable, the roof subsidence of the roadway with roof-cutting measures is about 156 mm, the floor heave is about 55 mm, and the coal pillar side and solid coal side are about 125 mm and 73 mm, respectively, which are 43%, 19%, 43%, and 45% lower than those without roof cutting. It shows that roof cutting and pressure relief can indeed improve the stress environment of surrounding rock and reduce the deformation of roadway. The roof cutting and roadway protection of gob-side entry driving with small coal pillars has achieved the expected effect.

The results of this study are recommended for the design of coal mine pressure-relief schemes to reduce the stress of surrounding rock in gob-side entry. However, roof cutting parameters under different geological conditions are not universally applicable. It is necessary to explore the roof pressure-relief effect under different influencing factors, such as buried depth, mining height, and dip angle, in combination with geological conditions. At the same time, in further research, the roof-cutting method of hydraulic fracturing or expansion fracturing can be considered for roadways with different geological conditions to explore the universal applicability of different pressure-relief methods.

6. Conclusions

• Roof-cutting and pressure-relieving techniques used in gob-side entry driving with small coal pillars can alleviate the tight succeeding problem between mining and excavation in mines and save time. These techniques can change the path of stress transfer of the main roof, reduce the pressure on coal pillars, and mitigate coal pillar deformation, thereby controlling the stability of surrounding rocks in roadways.
• A mechanical model for roof cutting was constructed and theoretical analysis methods were adopted to investigate the impact of different roof-cutting parameters on the roof collapse in the gob area. It is concluded that a reasonable roof-cutting angle (β) should reduce the friction between the collapsed rock and the cutting plane, and a reasonable roof-cutting height (H_cut) should provide some support for the overlying strata after the collapsed rock is compacted.
• A simulation experiment with similar materials was performed. After pre-splitting cutting, the roof in the gob area collapsed along the cutting plane. The collapsed gangue filled the gob area well, reducing the disturbance of the instability of the upper rock layers to the lower layers and alleviating stress concentration in the surrounding rock of the roadway.
• A mechanical model for roof cutting was constructed using theoretical analysis methods. It reveals that a reasonable roof-cutting angle should reduce the friction between the collapsed rock and the cutting plane, and a reasonable roof-cutting height should provide some support for the overlying strata after the collapsed rock is compacted.
• The UDEC numerical simulation method was used to find that when the roof-cutting angle is 12° and height is 14 m, the roof layers in the gob area collapse along the pre-splitting cutting plane, and the collapsed gangue can support the upper layers, effectively reducing the disturbance of the sudden instability of the upper rock layers to the gob-side roadway.
• The roof-cutting and pressure-relieving technique realized the control of the surrounding rock in the excavation of the 8103 roadway of Panel 8103. The UDEC numerical simulation method and comparative analysis helped propose the support method combining “steel strip + bolt + constant-resistance anchor cable + roof cutting”, which can control the stability of surrounding rocks in roadways and ensure safe and efficient production in mines.