The Effect of a Three-Blade Tube on the Pneumatic Transport of Pebble Particles
Abstract
:1. Introduction
2. Numerical Methods
2.1. Governing Equations for Particle
2.2. Governing Equations for the Gas Phase
3. Numerical Simulation Setup
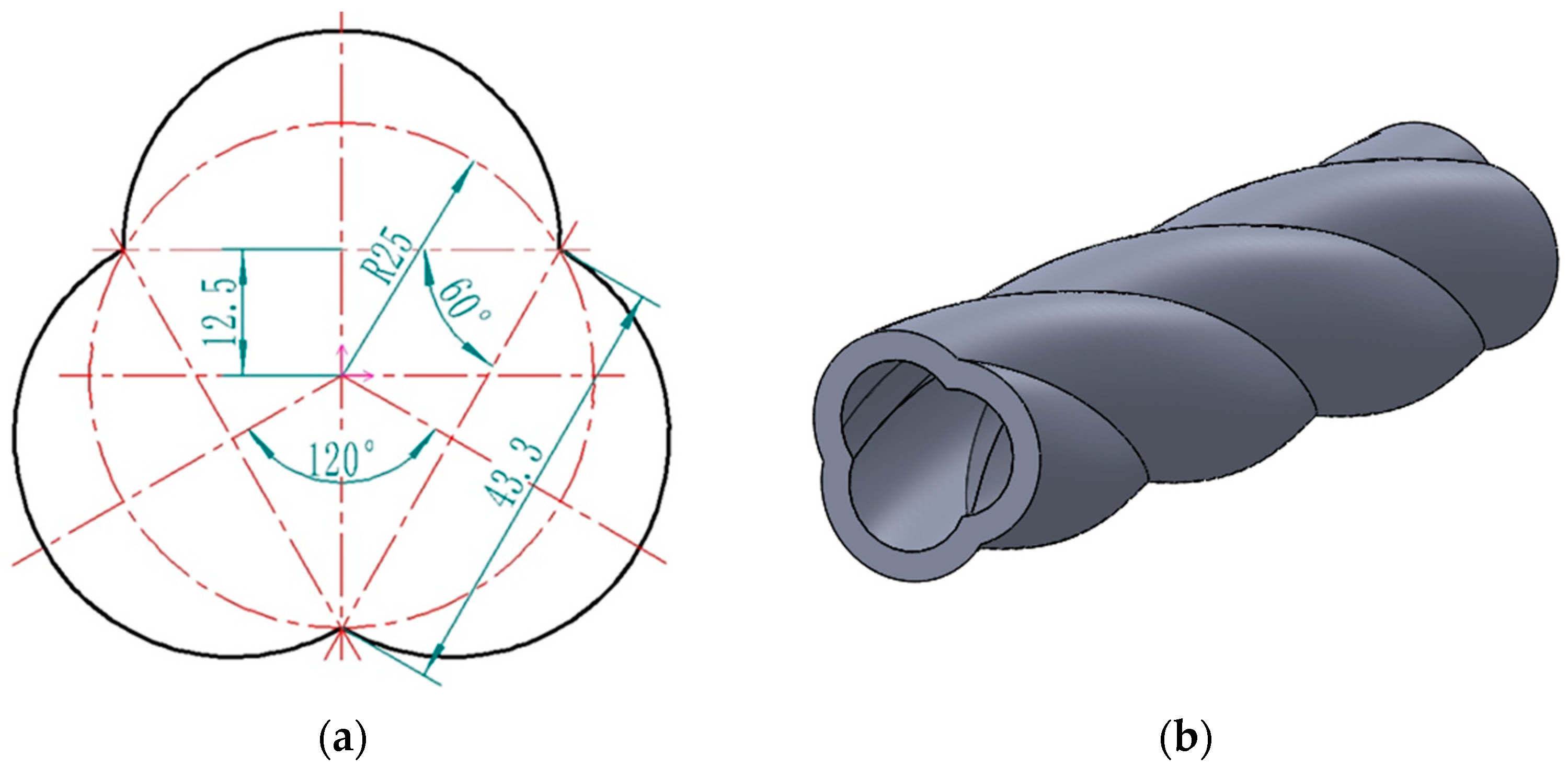
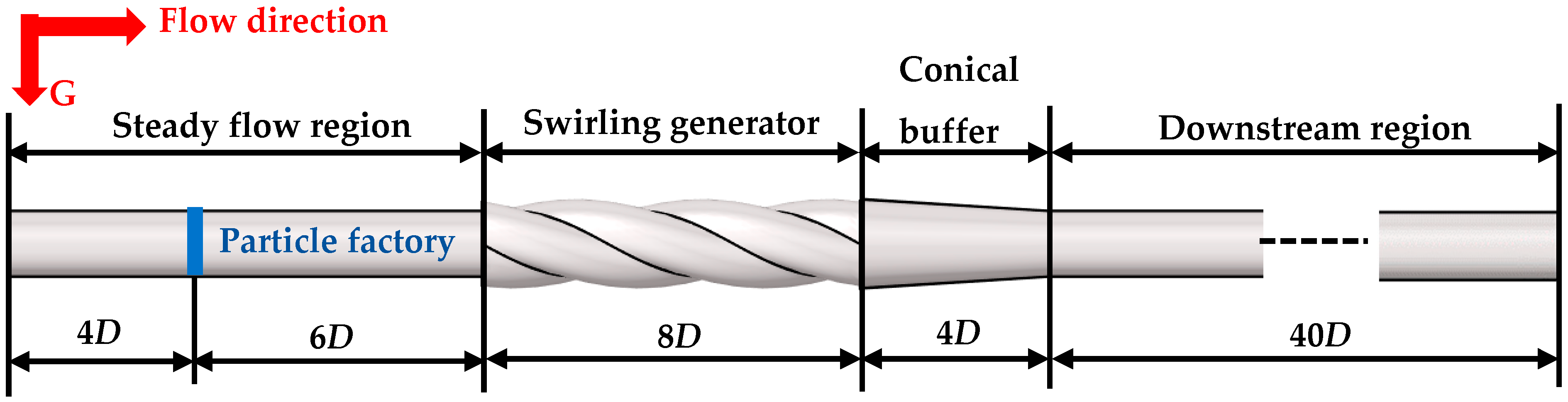
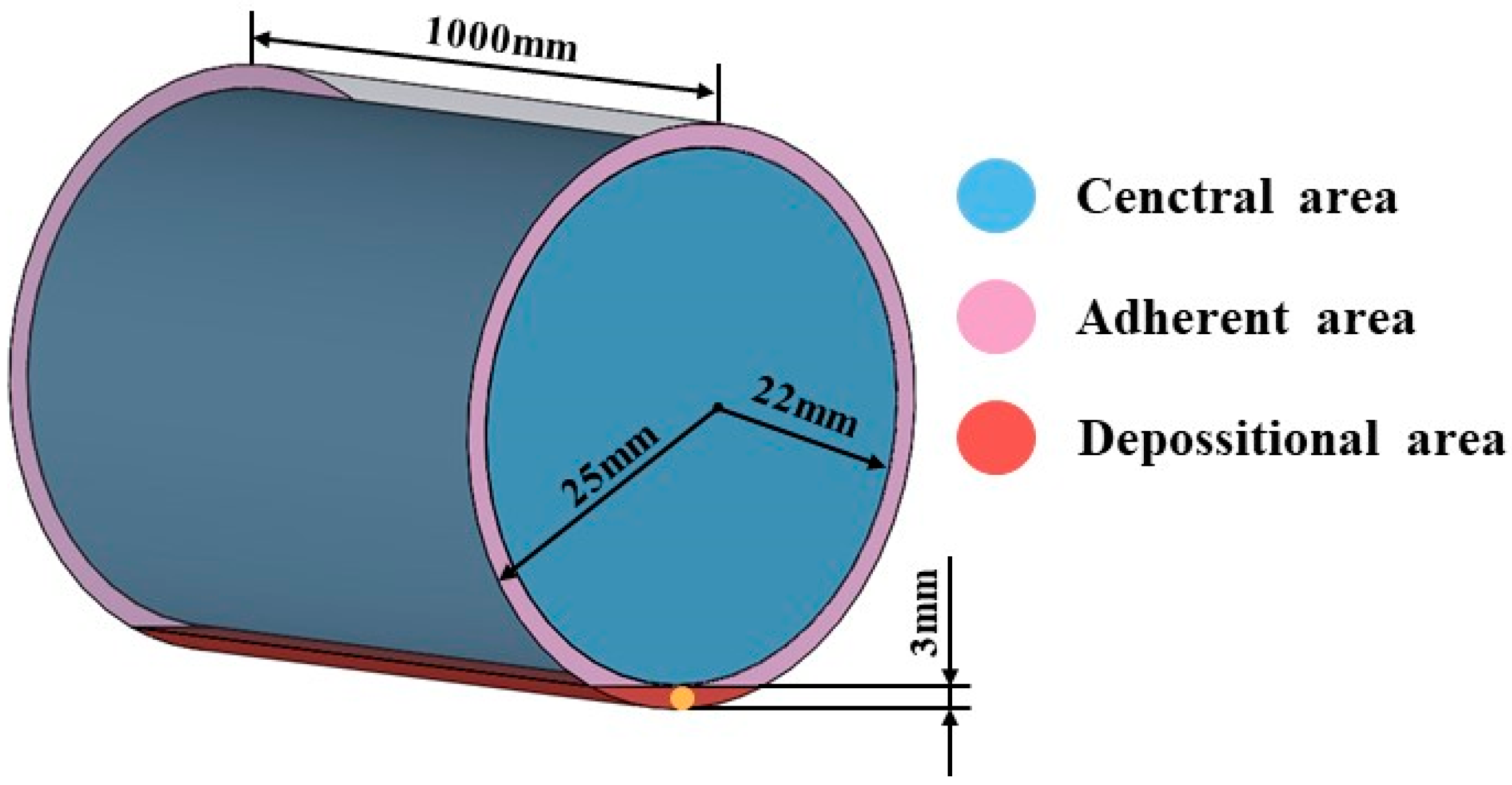
3.1. Model Setting
3.2. Numerical Simulation Boundary Conditions
4. Results and Discussion
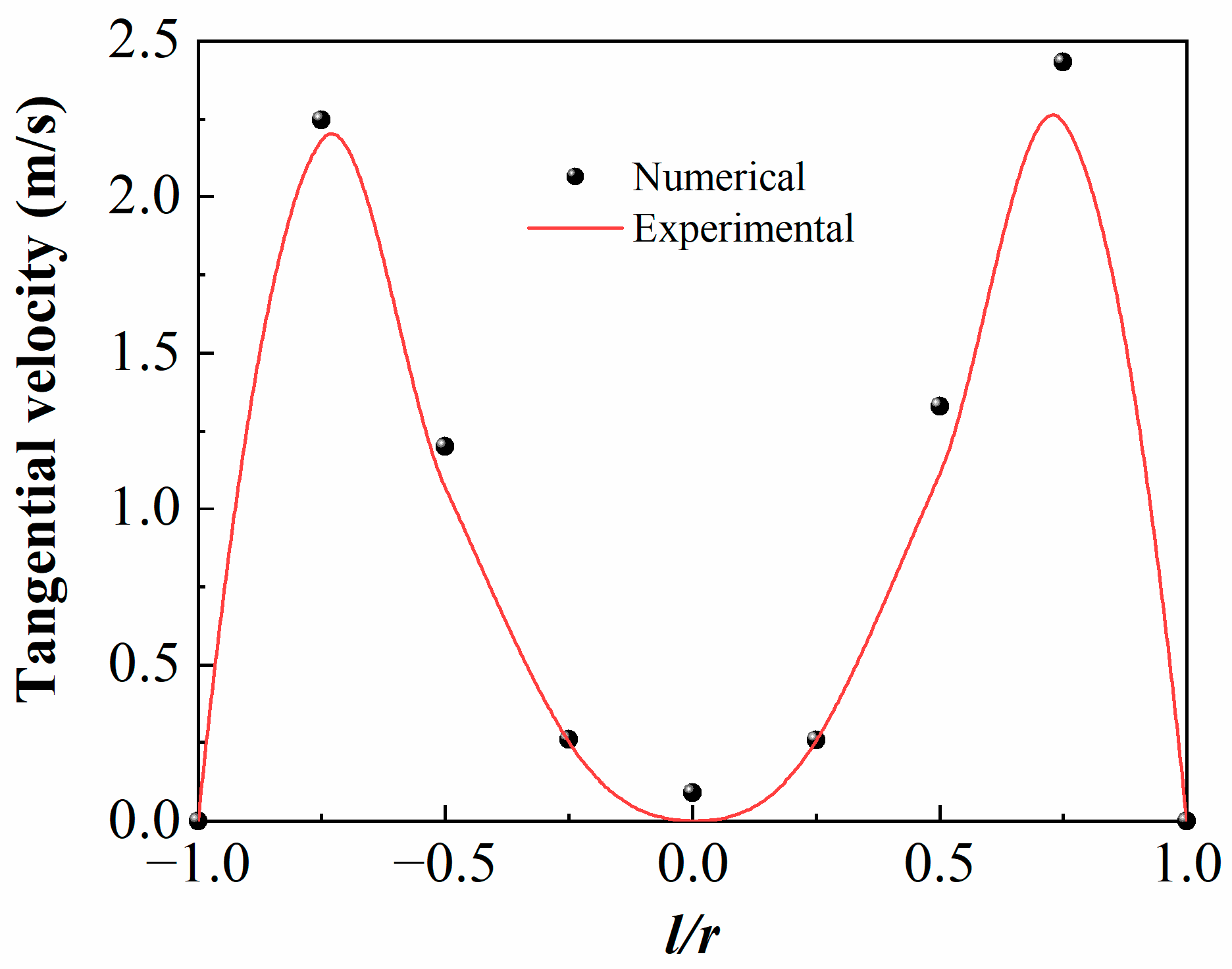
4.1. Model Validation
4.2. Flow Field Characteristics
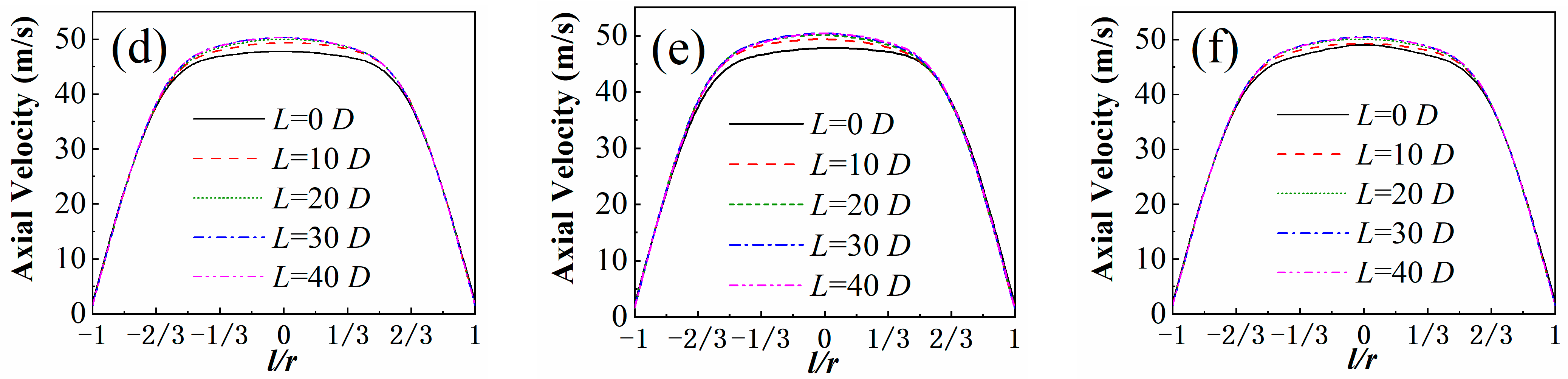
4.2.1. Axial Velocity
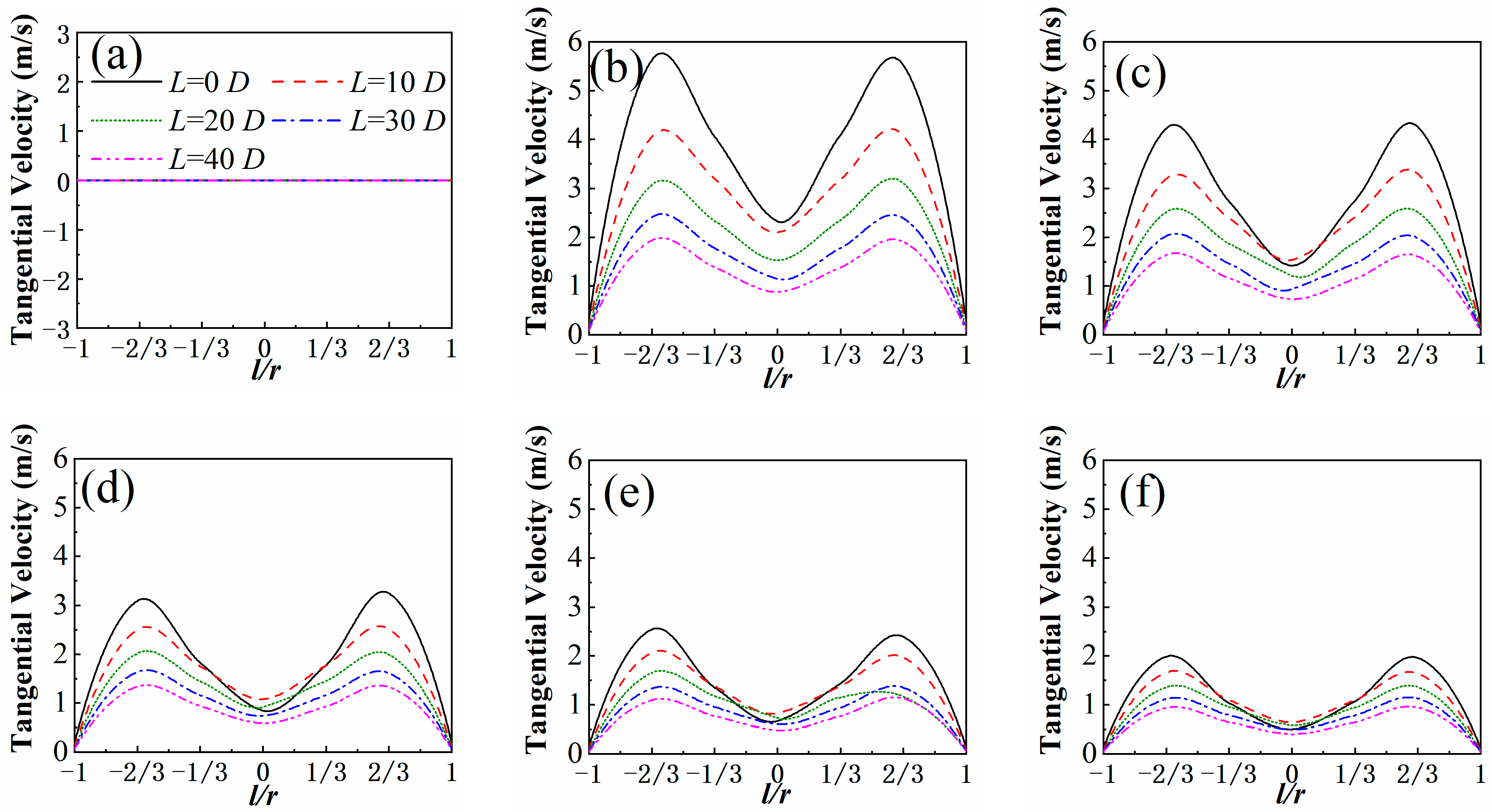
4.2.2. Tangential Velocity
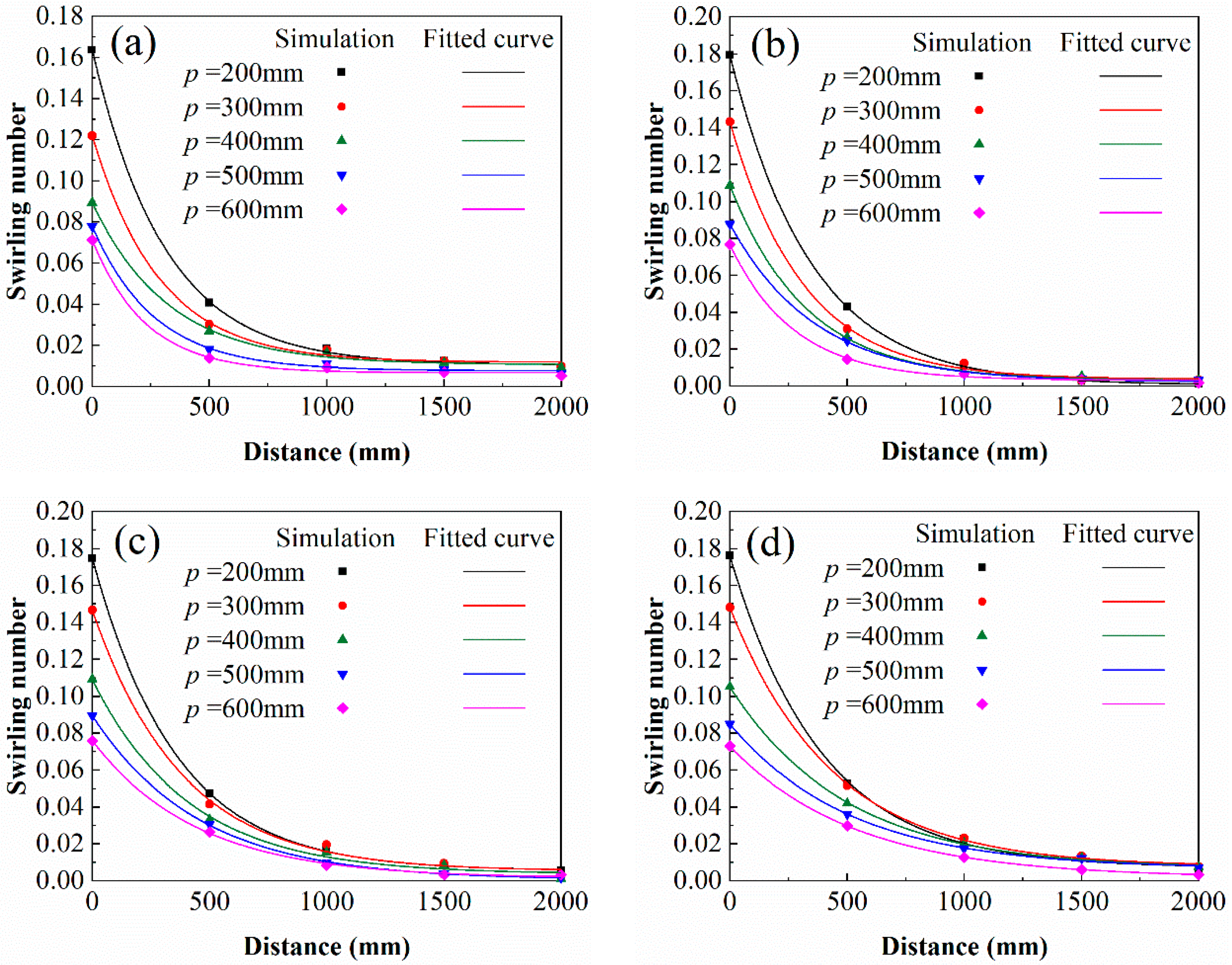
4.2.3. Swirling Number
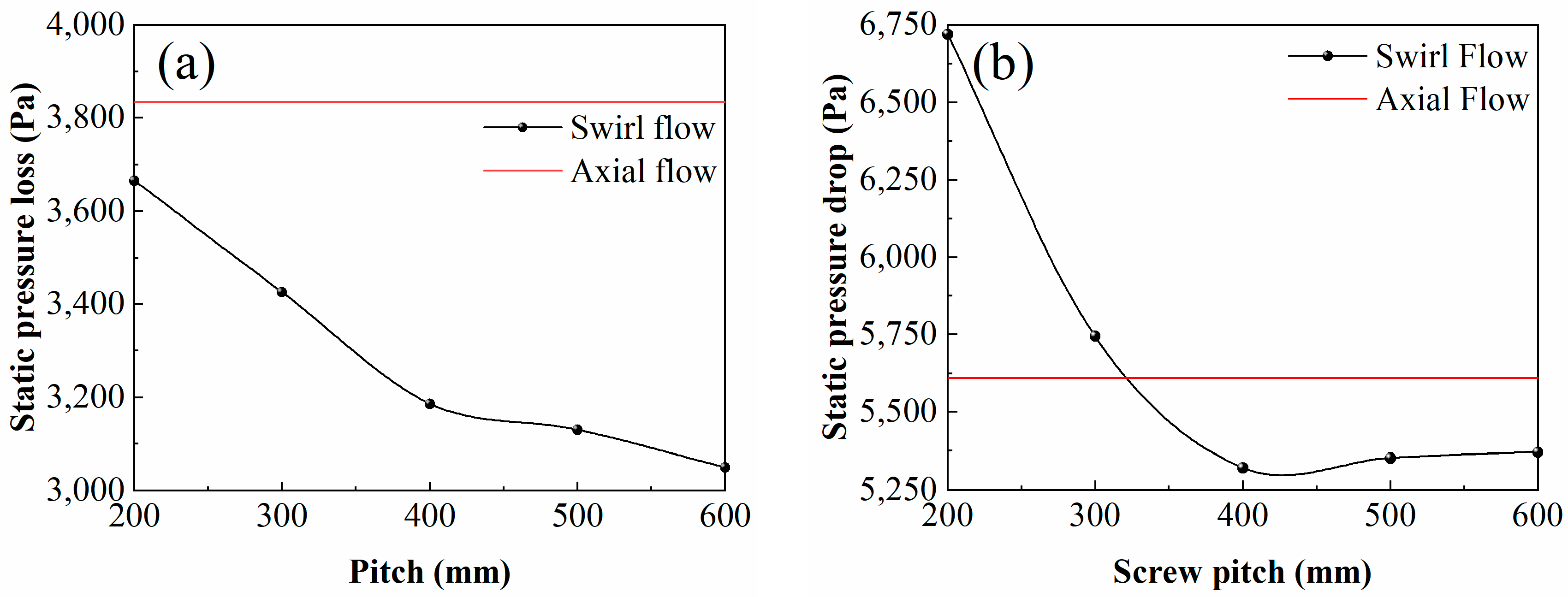
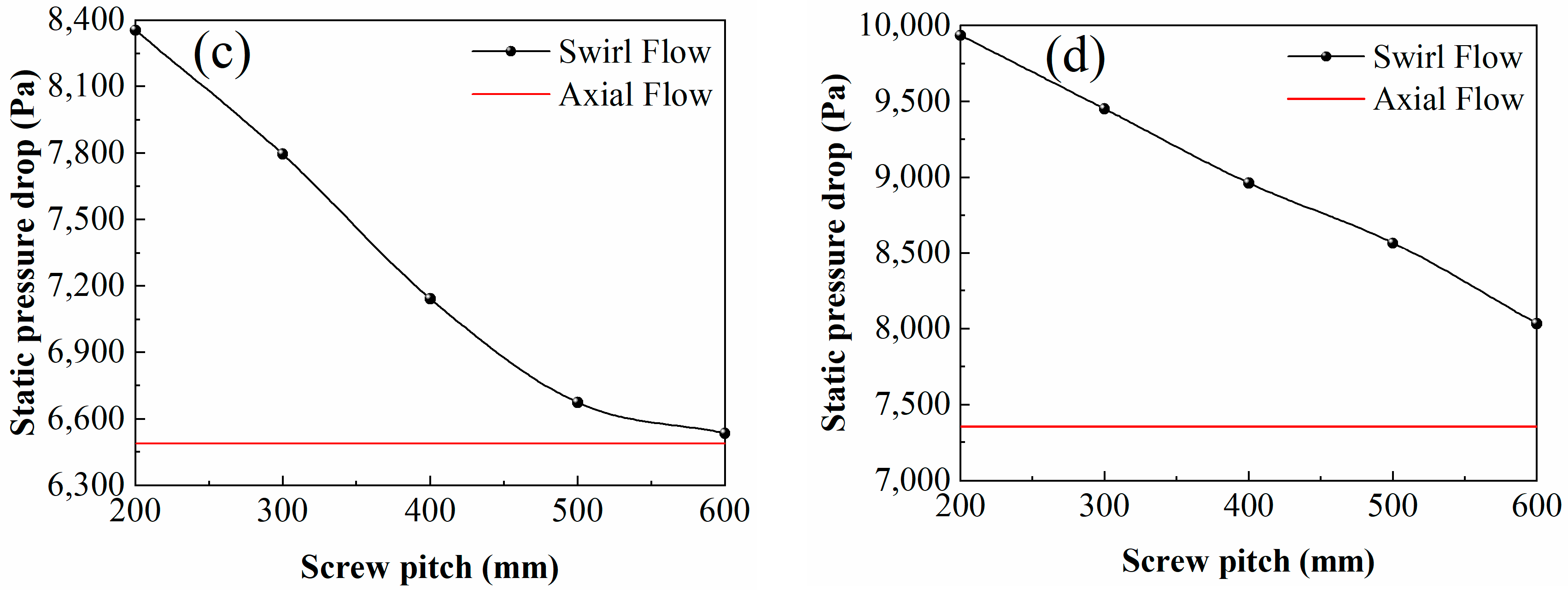
4.2.4. Static Pressure Drop
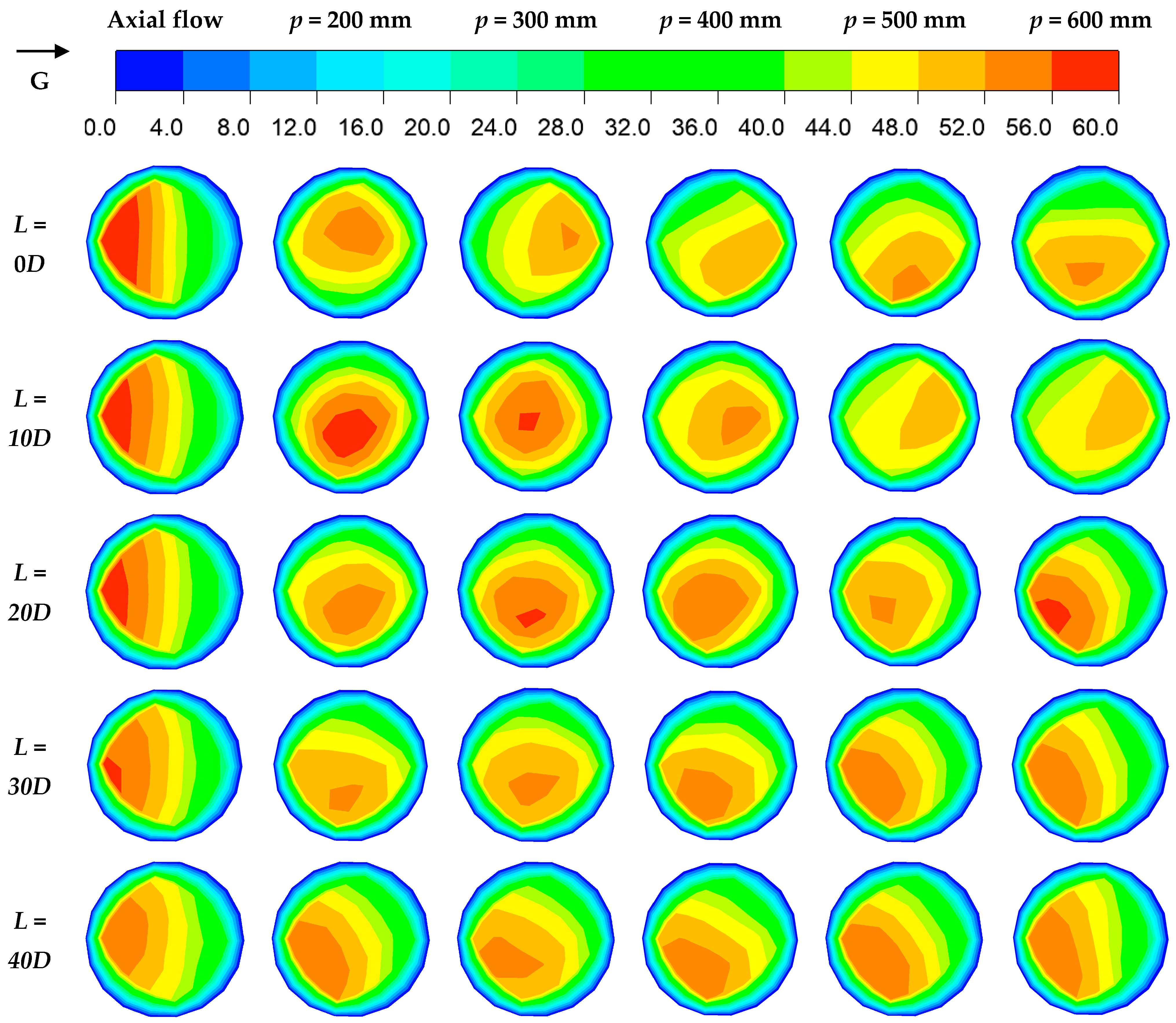
4.3. Particle Characteristics
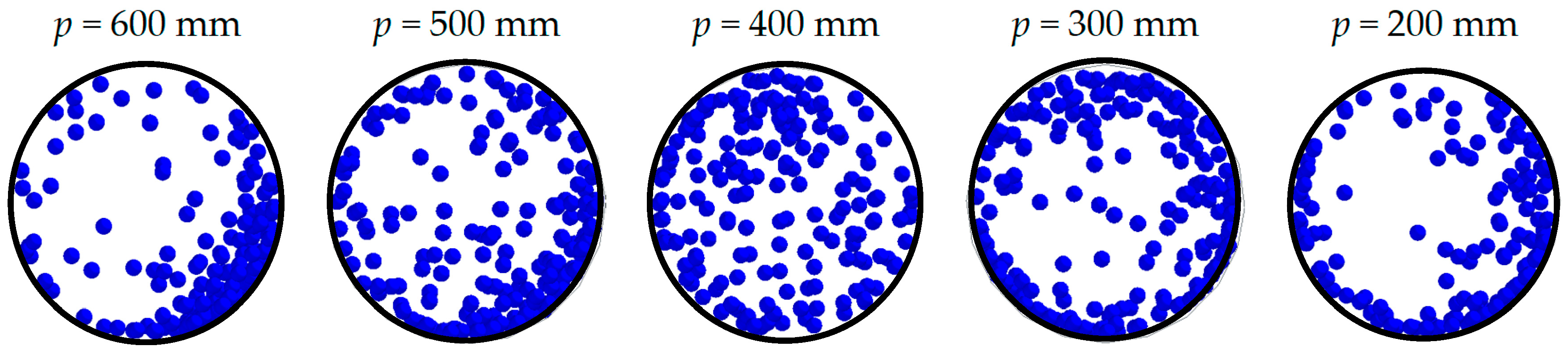
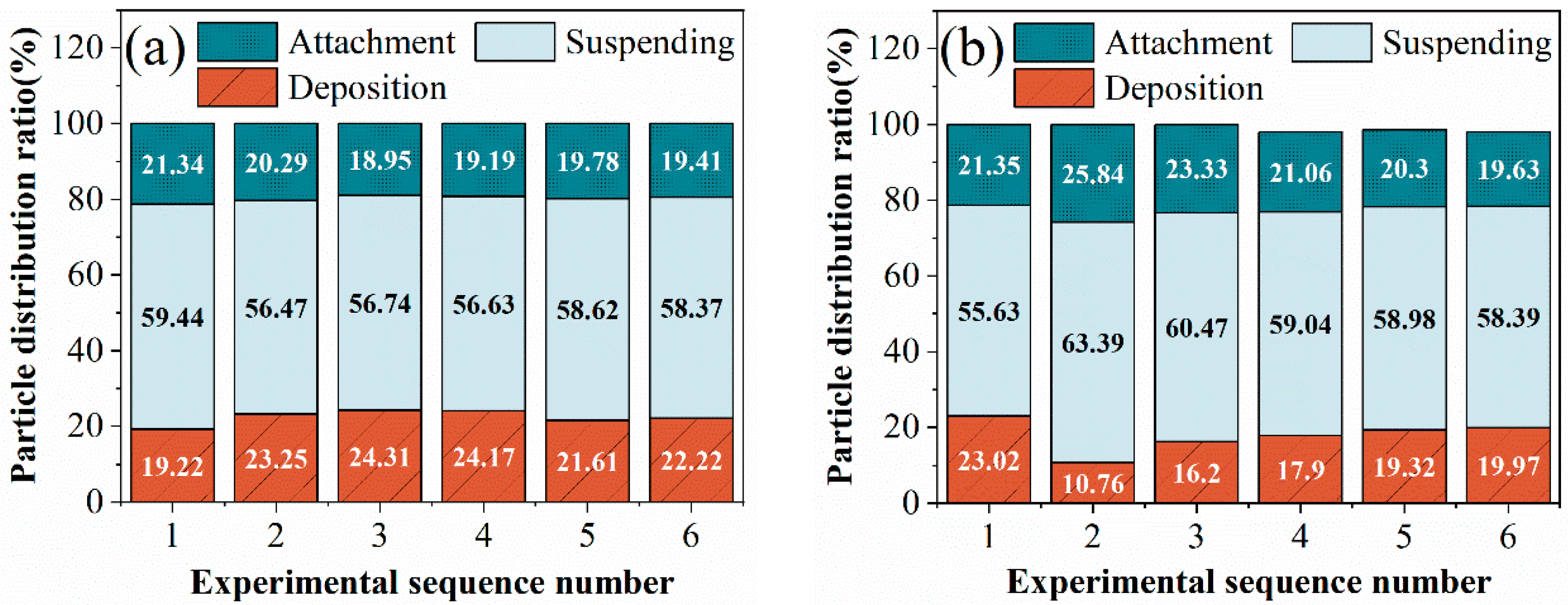
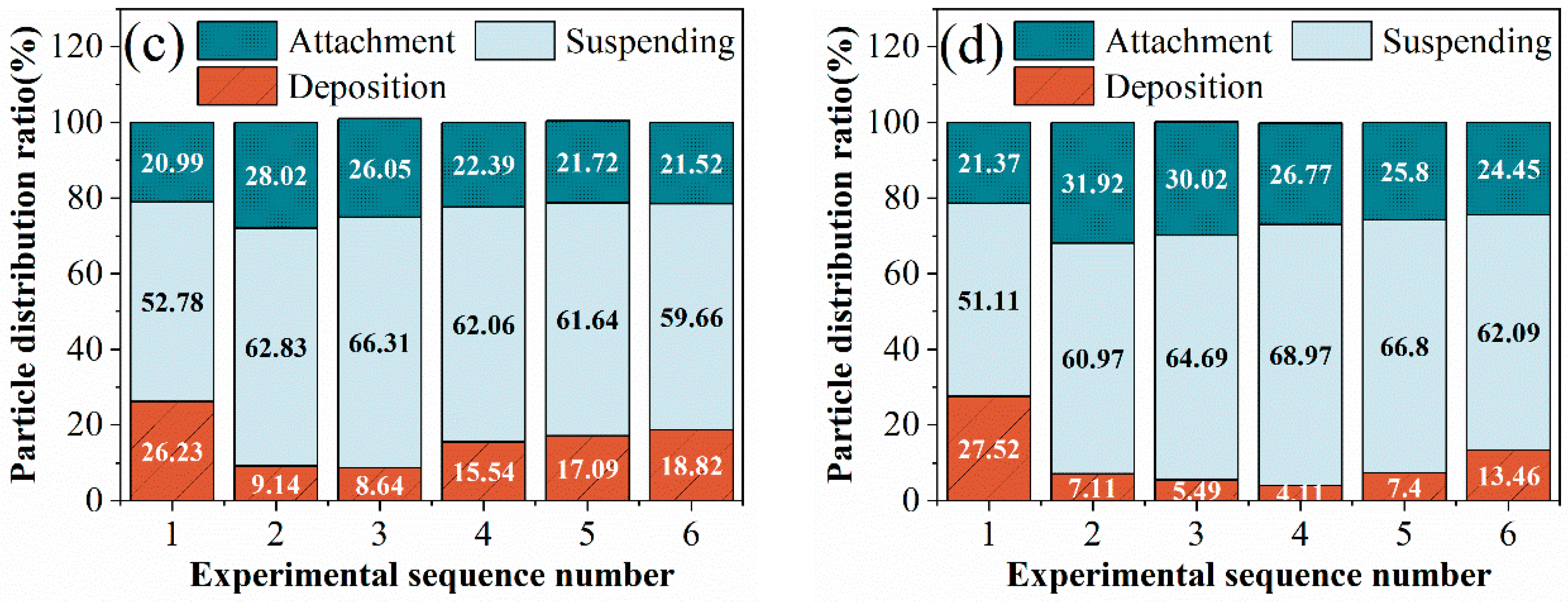
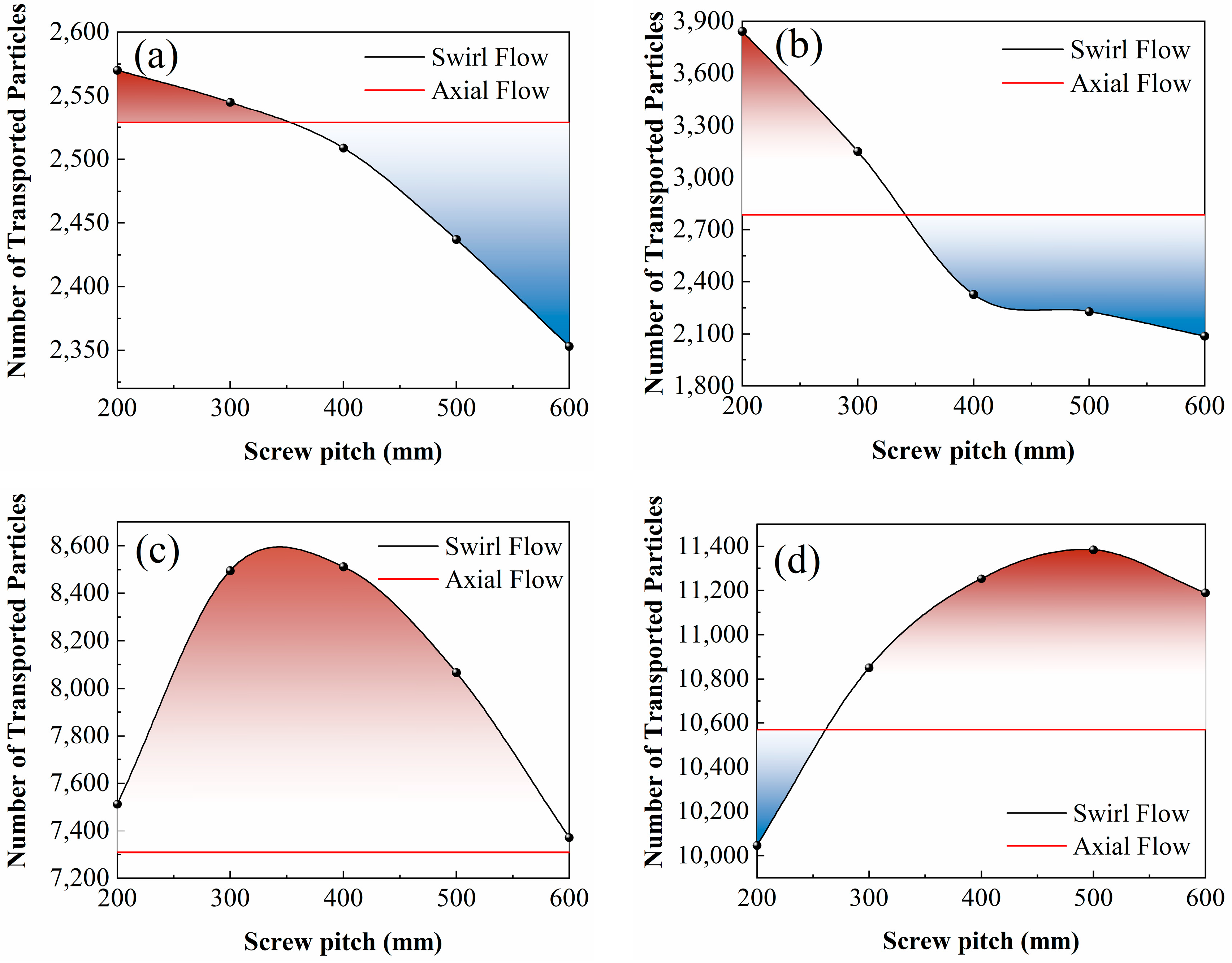
4.3.1. Particle Flow State
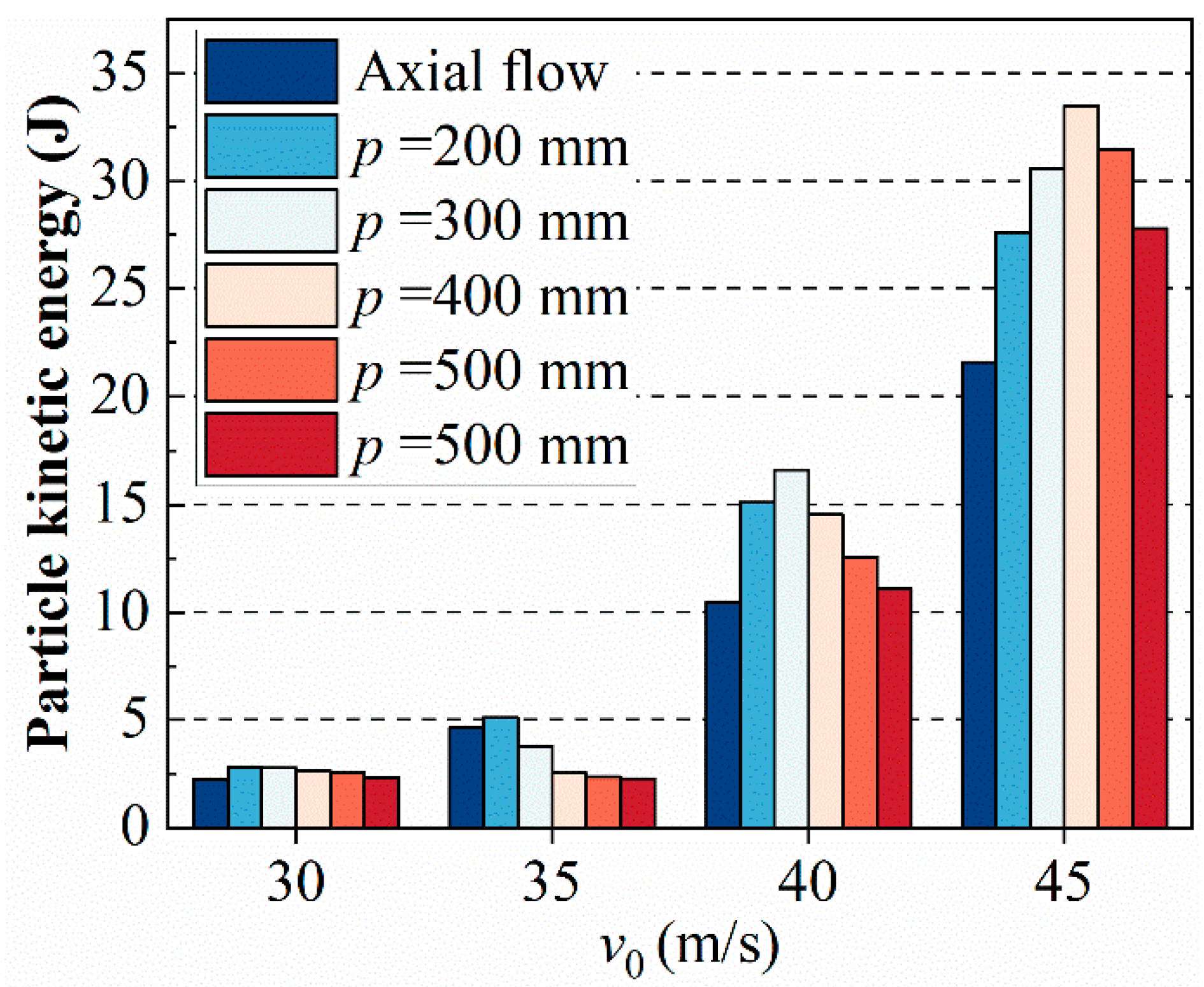
4.3.2. Energy Efficiency
5. Conclusions
- (1)
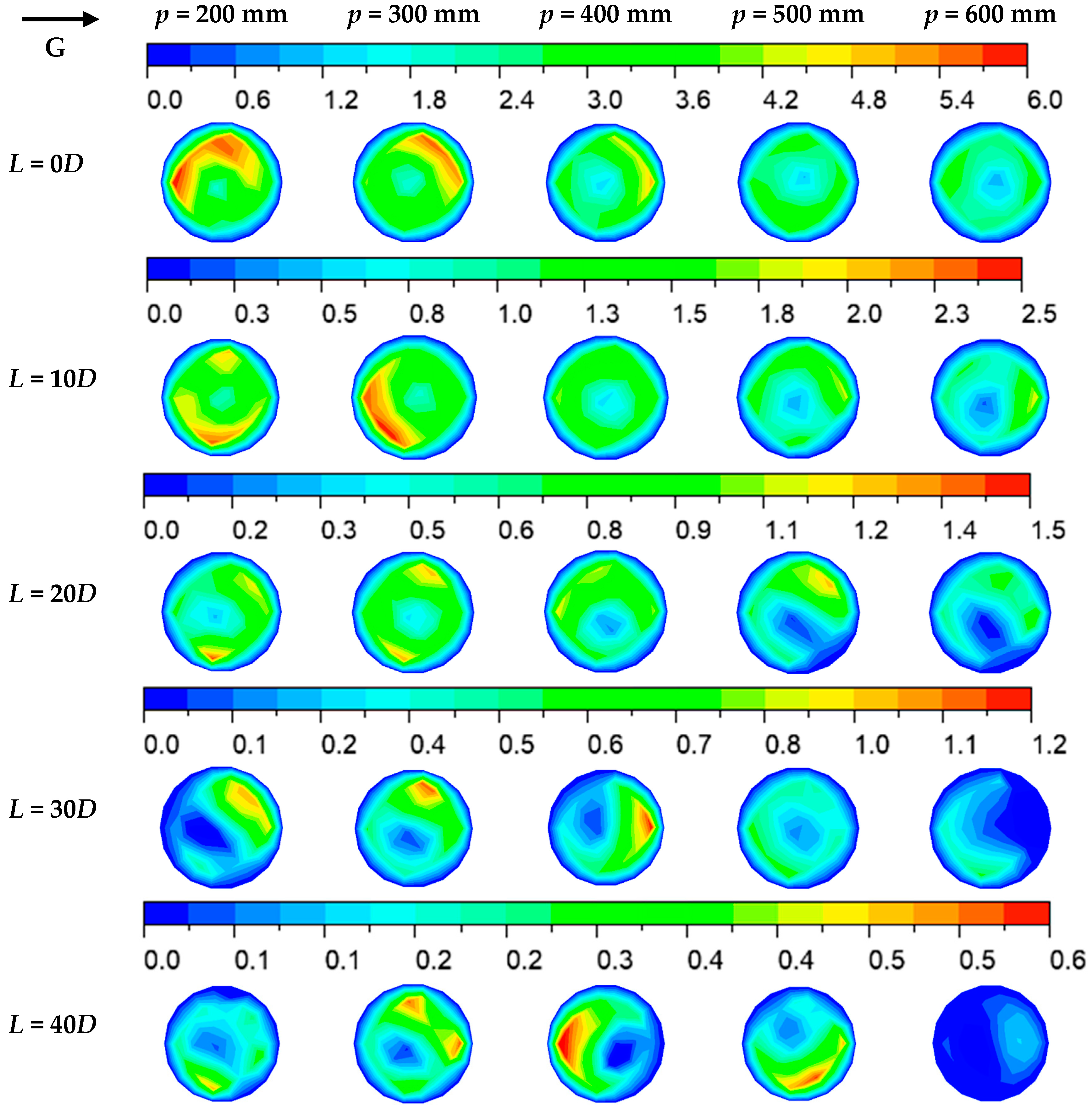
- When unloaded, the axial and tangential velocities of the airflow exhibited a symmetrical distribution. As the pitch of the three-blade tube increased, the former was almost unaffected, while the latter showed a significant decreasing trend. After loading, the rotation of particles hindered the movement of airflow. The two velocity distributions were no longer symmetrical but showed a trend of maximum rotation along the circumference. The smaller the pitch of the three-blade tube, the more pronounced the rotation trend.
- (2)
- After v0 reached 35 m/s, the swirl intensity reached saturation. After that, the increase in airflow velocity did not affect the swirl intensity. The pitch of a three-blade tube could directly change the ratio of axial airflow to tangential airflow. The smaller the pitch, the greater the swirling intensity of the flow field. The saturation value of swirling intensity at the 200 mm pitch was about 2.25 times that at the 600 mm pitch.
- (3)
- The static pressure loss reflects the energy consumption of the system. There was a choking velocity of 35 m/s. When v0 was larger than it, the static pressure drop in the swirling pipe was gradually larger than that in the straight pipe. The static pressure loss increased with the decrease in the pitch of the three-blade tube. The swirling flow would promote particle fluidization only when v0 was larger than the choking velocity.
- (4)
- Increasing the airflow velocity could significantly improve the dispersion of particles. After v0 exceeds the choking velocity, as the pitch of the three-blade tube increases, the deposition of particles first decreased and then increased. The suspension first increased and then decreased. The adhesion rate gradually decreased due to the effect of centrifugal force. There was an optimal parameter combination: v0 = 40 m/s with p = 300 mm and v0 = 45 m/s with p = 400 mm, resulting in the highest proportion of particles at the center of the flow field.
- (5)
- When v0 was the same, the particle velocity at the outlet was also similar. Before reaching the choking speed, the smaller the pitch, the higher the kinetic energy of the particles. After reaching the choking speed, an excessive swirl would increase the ineffective stroke of the particles, and the kinetic energy of the particles first increased and then decreased with the increase in the pitch. The combined effect of airflow velocity and swirl intensity should be considered to achieve the optimal tangential velocity of 5.87 m/s.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Diameter of conveying pipeline, mm | Distance between the measuring point and the axis, mm | ||
| Particle diameter, mm | L | Distance of the measured section from the cone outlet, mm | |
| Particle kinetic energy, J | Mass of particle i, kg | ||
| Basset force, N | Torque caused by tangential force, N·m | ||
| Particle–particle force including elastic force, N | Rolling friction torque, N·m | ||
| Drag force, N | Screw pitch, mm | ||
| The viscous damping force, N | R | Radius of conveying pipeline, mm | |
| Magnus lift force, N | Distance of the integral point from the axis of the pipe in the radial direction, mm | ||
| Particle–fluid interaction force on particle i, N | S | Swirling number | |
| Particle–fluid interaction force, N | Velocity of fluid, m/s | ||
| Saffman lift force, N | v0 | Initial airflow velocity, m/s | |
| Virtual mass force, N | Translational velocity of particle i, m/s | ||
| Pressure gradient force, N | Angular velocity of particle i, rad/s | ||
| Viscous force, N | Volume fraction of fluid | ||
| Domain force of particle–fluid on particle i, N | Viscous stress tensor | ||
| Moment of inertia of particle i, kg·m2 | The volume of the calculated unit, m3 | ||
| Gravitational acceleration, m/s | Hamiltonian differential operator |
References
- Zhou, J.; Liu, Y.; Du, C.; Liu, S.; Li, J. Numerical study of coarse coal particle breakage in pneumatic conveying. Particuology 2018, 38, 204–214. [Google Scholar] [CrossRef]
- Setia, G.; Mallick, S.; Pan, R.; Wypych, P. Modeling minimum transport boundary for fluidized dense-phase pneumatic conveying systems. Powder Technol. 2015, 277, 244–251. [Google Scholar] [CrossRef]
- Ji, Y.; Hao, Y.; Yi, N.; Guan, T.; Gao, D. Particle flow regime in a swirling pneumatic conveying system. Powder Technol. 2022, 401, 117328. [Google Scholar] [CrossRef]
- Shukri, E.-S.; Wirachman, W. Thermal Uniformity Study in a Circular Divergent Diffuser with Swirl Flow Generator. Energy Procedia 2019, 156, 249–253. [Google Scholar] [CrossRef]
- Kim, Y.-B.; Lee, H.-S.; Francis, L.; Kim, Y.D. Innovative swirling flow-type microbubble generator for multi-stage DCMD desalination system: Focus on the two-phase flow pattern, bubble size distribution, and its effect on MD performance. J. Membr. Sci. 2019, 588, 117197. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, P.; Xiao, H.; Liu, Z.; Liu, W. Design and optimization on symmetrical wing longitudinal swirl generators in circular tube for laminar flow. Int. J. Heat Mass Transf. 2022, 193, 193122961. [Google Scholar] [CrossRef]
- Hangi, M.; Rahbari, A.; Wang, X.; Lipiński, W. Hydrothermal characteristics of fluid flow in a circular tube fitted with free rotating axial-turbine-type swirl generators: Design, swirl strength, and performance analyses. Int. J. Therm. Sci. 2022, 173, 107384. [Google Scholar] [CrossRef]
- Wu, M.; Song, H.; Liang, X.; Huang, N.; Li, X. Generation of micro-nano bubbles by self-developed swirl-type micro-nano bubble generator. Chem. Eng. Process.-Process Intensif. 2022, 181, 109136. [Google Scholar] [CrossRef]
- Rao, Y.-C.; Ding, B.-Y.; Wang, S.-L.; Wang, Z.W.; Zhou, S.D. Flow pattern and pressure drop of gas-liquid two-phase swirl flow in a horizontal pipe. J. Cent. South Univ. 2019, 26, 2528–2542. [Google Scholar] [CrossRef]
- Yilmaz, M.; Comakli, O.; Yapici, S.; Sara, O.N. Heat transfer and friction characteristics in decaying swirl flow generated by different radial guide vane swirl generators. Energy Convers. Manag. 2003, 44, 283–300. [Google Scholar] [CrossRef]
- Bali, T.; Sarac, B.-A. Experimental investigation of decaying swirl flow through a circular pipe for binary combination of vortex generators. Int. Commun. Heat Mass Transf. 2014, 53, 174–179. [Google Scholar] [CrossRef]
- Zhou, J.-W.; Du, C.-L.; Liu, S.-Y.; Liu, Y. Comparison of three types of swirling generators in coarse particle pneumatic conveying using CFD-DEM simulation. Powder Technol. 2016, 301, 1309–1320. [Google Scholar] [CrossRef]
- Zhou, J.-W.; Du, C.-L.; Ma, Z.-L. Influence of swirling intensity on lump coal particle pickup velocity in pneumatic conveying. Powder Technol. 2018, 339, 470–478. [Google Scholar] [CrossRef]
- Zhou, J.; Han, X.; Jing, S.; Liu, Y. Efficiency and stability of lump coal particles swirling flow pneumatic conveying system. Chem. Eng. Res. Des. 2020, 157, 92–103. [Google Scholar] [CrossRef]
- Wannassi, M.; Monnoyer, F. Numerical simulation of the flow through the blades of a swirl generator. Appl. Math. Model. 2016, 40, 1247–1259. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, D. Experimental and numerical investigation on the blade angle of axial-flow swirling generator and drainage structure for supersonic separators with diversion cone. Chem. Eng. Res. Des. 2018, 133, 155–167. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, W.; Wu, Y.; Zhang, Y.; Zhang, M.; Yang, H.; Lyu, J. Effects of the inlet duct length on the flow field and performance of a cyclone separator with a contracted inlet duct. Powder Technol. 2021, 393, 12–22. [Google Scholar] [CrossRef]
- Li, H.; Tomita, Y. Particle velocity and concentration characteristics in a horizontal dilute swirling flow pneumatic conveying. Powder Technol. 2000, 107, 144–152. [Google Scholar] [CrossRef]
- Pashtrapanska, M.; Jovanović, J.; Lienhart, H.; Durst, F. Turbulence measurements in a swirling pipe flow. Exp. Fluids 2006, 41, 813–827. [Google Scholar] [CrossRef]
- Chang, T.-H.; Doh, D.-H.; Oh, K.-J. Velocity profiles with swirling flow in a vertical circular tube. J. Vis. 2012, 16, 53–64. [Google Scholar] [CrossRef]
- Zhou, J.-W.; Liu, Y.; Du, C.-L.; Liu, S.Y. Effect of the particle shape and swirling intensity on the breakage of lump coal particle in pneumatic conveying. Powder Technol. 2017, 317, 438–448. [Google Scholar] [CrossRef]
- Escue, A.; Cui, J. Comparison of turbulence models in simulating swirling pipe flows. Appl. Math. Model. 2010, 34, 2840–2849. [Google Scholar] [CrossRef]
- Chu, K.-W.; Wang, B.; Xu, D.-L.; Chen, Y.X.; Yu, A.B. CFD–DEM simulation of the gas–solid flow in a cyclone separator. Chem. Eng. Sci. 2011, 66, 834–847. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Liu, S.; Wang, K.; Gu, H. Decay law and swirl length of swirling gas-liquid flow in a vertical pipe. Int. J. Multiph. Flow 2021, 137, 137103570. [Google Scholar] [CrossRef]
- Wan, Z.; Yang, S.; Tang, D.; Yuan, H.; Hu, J.; Wang, H. CFD-DEM investigation of gas–solid swirling flow in an industrial-scale annular pipe. Chem. Eng. J. 2023, 461, 141975. [Google Scholar] [CrossRef]
- Wan, Z.; Yang, S.; Tang, D.; Yuan, H.; Hu, J.; Wang, H. Particle-scale modeling study of coaxial jets of gas-solid swirling flow in an industrial-scale annular pipe via CFD-DEM. Powder Technol. 2023, 419, 118307. [Google Scholar] [CrossRef]
- Wang, B.; Xu, D.-L.; Chu, K.-W.; Yu, A.B. Numerical study of gas–solid flow in a cyclone separator. Appl. Math. Model. 2006, 30, 1326–1342. [Google Scholar] [CrossRef]
- Li, Z.; Tong, Z.; Zhang, H.; Chu, K.; Li, R.; Miao, H.; Zhao, J.; Yu, A. CFD-DEM simulation of the supercritical water-solid flow in cyclone. Powder Technol. 2023, 418, 118261. [Google Scholar] [CrossRef]
- Feng, Y.-Q.; Yu, A.-B. Comments on “Discrete particle-continuum fluid modelling of gas–solid fluidised beds” by Kafui et al. [Chemical Engineering Scinece 57 (2002) 2395–2410]. Chem. Eng. Sci. 2004, 59, 719–722. [Google Scholar] [CrossRef]
- Feng, Y.-Q.; Yu, A.-B. Microdynamic modelling and analysis of the mixing and segregation of binary mixtures of particles in gas fluidization. Chem. Eng. Sci. 2007, 62, 256–268. [Google Scholar] [CrossRef]
- Zhou, Z.-Y.; Kuang, S.-B.; Chu, K.-W.; Yu, A. Discrete particle simulation of particle–fluid flow: Model formulations and their applicability. J. Fluid Mech. 2010, 661, 482–510. [Google Scholar] [CrossRef]
- Fokeer, S.; Lowndes, I.-S.; Hargreaves, D.-M. Numerical modelling of swirl flow induced by a three-lobed helical pipe. Chem. Eng. Process. Process Intensif. 2010, 49, 536–546. [Google Scholar] [CrossRef]
- Li, J.; Feng, Z.; Yang, D.; Yu, B.; Li, Y. Effect of swirling flow on large coal particle pneumatic conveying. Powder Technol. 2020, 362, 745–758. [Google Scholar] [CrossRef]

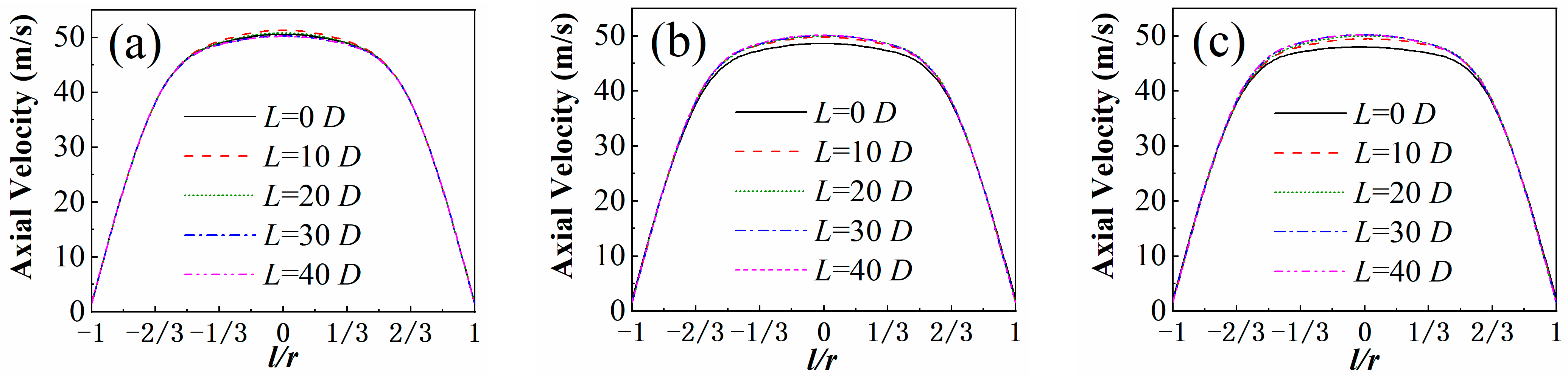

| Control Parameters | Value Range |
|---|---|
| The pitch of the three-leaf spiral tube (p), mm | 200, 300, 400, 500, 600, Axial |
| The initial velocity of airflow (v0), m/s | 30, 35, 40, 45 |
| Item | Detailed Information | Index | Value Size | |
|---|---|---|---|---|
| CFD | Material Properties | Air | Density (kg/m3) | 1.225 |
| Kinematic viscosity (kg/(m·s)) | 1.978 × 10−5 | |||
| Tube wall | Slip type | No slip | ||
| Roughness height (mm) | 0.001 | |||
| Roughness constant | 0.5 | |||
| Boundary | Velocity inlet | Velocity (m/s) | 30~45 | |
| Turbulence intensity (%) | 3.87~4.1 | |||
| Hydraulic pipe diameter (mm) | 50 | |||
| Initial gauge pressure (MPa) | 0 | |||
| Pressure outlet | Gauge pressure (Pa) | 0 | ||
| Time step | Time step size (s) | 0.001 | ||
| Total time steps | 800 | |||
| DEM | Material Properties | Particle | Density (kg/m3) | 2300 |
| Poisson’s ratio | 0.25 | |||
| Shear modulus (Pa) | 1 × 1010 | |||
| Diameter (mm) | 5 | |||
| Wall surface | Density (kg/m3) | 7861 | ||
| Poisson’s ratio | 0.3 | |||
| Shear modulus (Pa) | 7.98 × 1010 | |||
| Collision | Particles–particles | Restitution | 0.55 | |
| Static friction coefficient | 0.68 | |||
| Coefficient of rolling friction | 0.15 | |||
| Collision model | Hertz–Mindlin | |||
| Particle wall surface | Restitution | 0.5 | ||
| Static friction coefficient | 0.5 | |||
| Coefficient of rolling friction | 0.05 | |||
| Collision model | Hertz–Mindlin | |||
| Numerical Simulation Settings | Time step | Time step size (s) | 1 × 10−6 | |
| Mesh Size (mm × mm × mm) | Number of Nodes | Number of Elements |
|---|---|---|
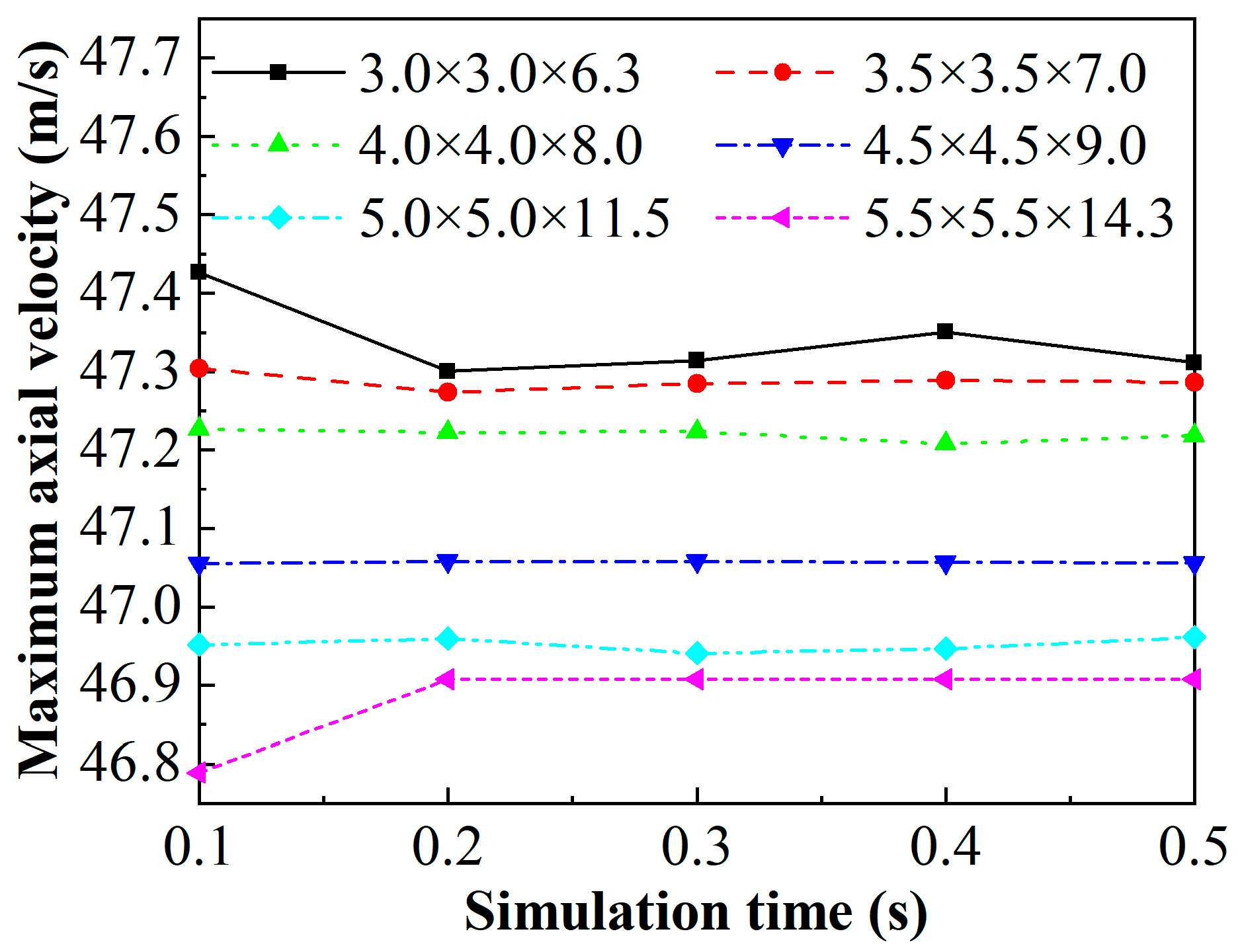
| 3.0 × 3.0 × 6.3 | 287,315 | 304,005 |
| 3.5 × 3.5 × 7.0 | 188,332 | 201,049 |
| 4.0 × 4.0 × 8.0 | 135,770 | 145,578 |
| 4.5 × 4.5 × 9.0 | 88,899 | 96,502 |
| 5.0 × 5.0 × 11.5 | 57,762 | 63,072 |
| 5.5 × 5.5 × 14.3 | 42,579 | 46,593 |
| p (mm) | Fitting Function | p (mm) | Fitting Function |
|---|---|---|---|
| v0 = 30 m/s | v0 = 35 m/s | ||
| 200 | 200 | ||
| 300 | 300 | ||
| 400 | 400 | ||
| 500 | 500 | ||
| 600 | 600 | ||
| v0 = 40 m/s | v0 = 45 m/s | ||
| 200 | 200 | ||
| 300 | 300 | ||
| 400 | 400 | ||
| 500 | 500 | ||
| 600 | 600 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Chen, H.; Ji, Y. The Effect of a Three-Blade Tube on the Pneumatic Transport of Pebble Particles. Energies 2023, 16, 7884. https://doi.org/10.3390/en16237884
Hao Y, Chen H, Ji Y. The Effect of a Three-Blade Tube on the Pneumatic Transport of Pebble Particles. Energies. 2023; 16(23):7884. https://doi.org/10.3390/en16237884
Chicago/Turabian StyleHao, Yating, Hongyu Chen, and Yun Ji. 2023. "The Effect of a Three-Blade Tube on the Pneumatic Transport of Pebble Particles" Energies 16, no. 23: 7884. https://doi.org/10.3390/en16237884
APA StyleHao, Y., Chen, H., & Ji, Y. (2023). The Effect of a Three-Blade Tube on the Pneumatic Transport of Pebble Particles. Energies, 16(23), 7884. https://doi.org/10.3390/en16237884






