Comprehensive Research on Construction and Stability of Horizontal-Well Cavity Natural Gas Storage in Thinly Bedded Salt Rocks in China
Abstract
:1. Introduction
2. Horizontal-Well Cavity Leaching Test
2.1. Similarity Simulation Test Design
2.2. Experiments Design
2.2.1. Test Procedure
- Select a salt brick with few impurities and no obvious cracks, clean the surface and absorb the moisture. A uniform surface is selected as the front face, and the surface is hand polished to meet the flatness requirements of the test.
- Lay the salt block flat with the selected face upwards, and mark the slot position on the cavity surface with a line. Drill a slot with a 6 mm diameter drill bit at the slot position on the cavity surface so that the slot width is the same, approximately 15 mm, with the top of the slot being slightly wider. A thinner layer of clear epoxy adhesive is applied evenly around the slots of the cavity surface and covered with a transparent plastic paper for sealing and bonding. It is necessary to control the dosage when applying the thin layer of adhesive to prevent the colloid from entering the slot. After slotting and sealing, due to the fluidity of the adhesive, it is necessary to keep the surface of the slotting cavity placed horizontally and wait for the epoxy resin adhesive to dry in order to avoid displacement of the adhesive before drying.
- The salt brick cavity face is erected, the side-by-side casing and gas tubing are secured with volcanic mud, the casing tube is inserted into the upper end of the wellhead, and the upper surface of the volcanic mud is covered with a layer of AB adhesive to further seal the wellhead.
- Place the salt brick as a whole into the transparent acrylic box. The length, width and height of the internal dimensions of the acrylic are 1 cm more than the length, width and height of the salt brick, and the thickness of the acrylic plate is 5 mm. After placing the salt brick, adjust the position of the salt brick so that it is roughly in the centre and the cavity surface is parallel to the acrylic box. Pour in a well-mixed clear epoxy resin adhesive from the top, filling the gap between the salt brick and the box to complete the overall seal. Glue scale strips to both sides and underneath the front of the acrylic box. After the adhesive has solidified, place the salt brick on a horizontal table with a high load-bearing capacity. Connect the water tank, flow meter and water injection tubes in turn with rubber hoses and place the end port of the drainage pipe in a beaker. Check and confirm the sealing of the connections and the test system. After opening the water tank valve and setting the flow meter to the design flow rate, the appropriate test can be carried out according to the design test parameters.
- After the start of the test, the brine concentration and the brine volume at the brine discharge port are measured every 10 min, and the shape of the cavity at this time is recorded using a video camera; after the concentration is stabilized, the measuring interval is changed to 30 min; after the completion of a certain stage of the cavity leaching phase, the position of the water injection pipe, the drainage pipe and the liquid level are adjusted according to the test program, and the next cavity leaching phase is carried out.
2.2.2. Horizontal-Well Cavity Leaching Test with Nitrogen Cushion in Large-Size Salt Rock
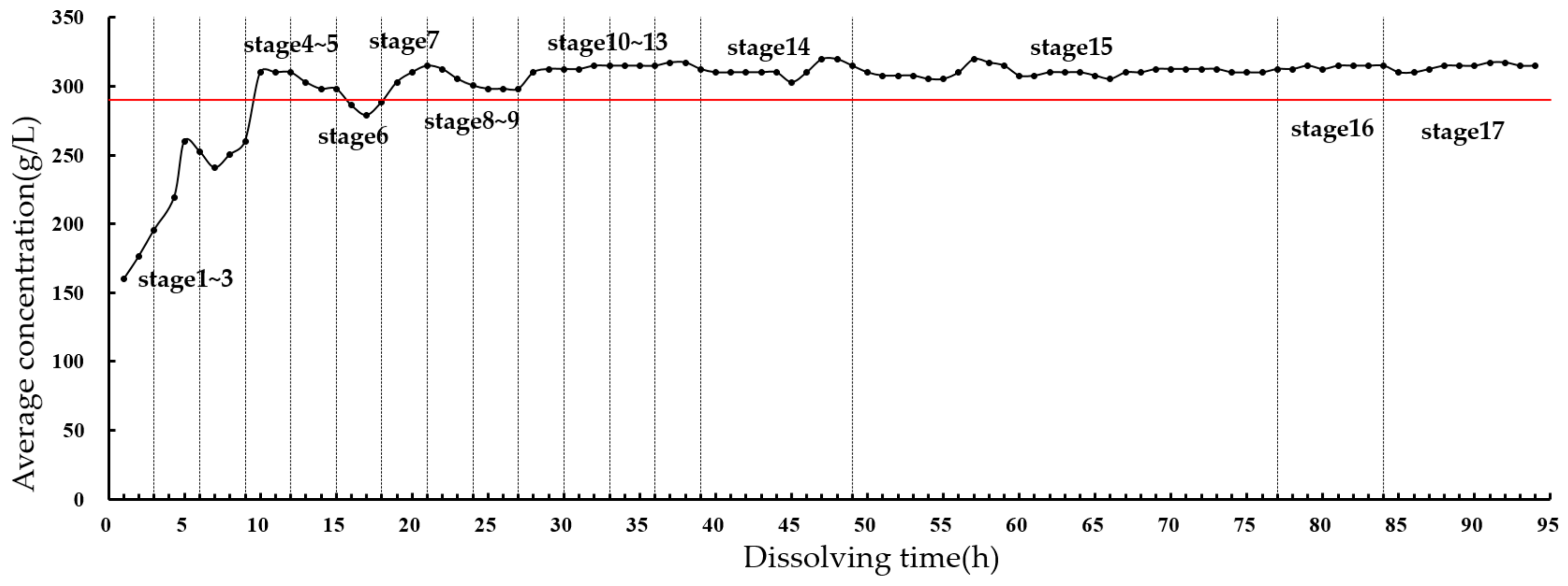
2.3. Analysis of Test Results
- Extension of cavity morphology
- Brine discharge concentration
3. Numerical Analysis
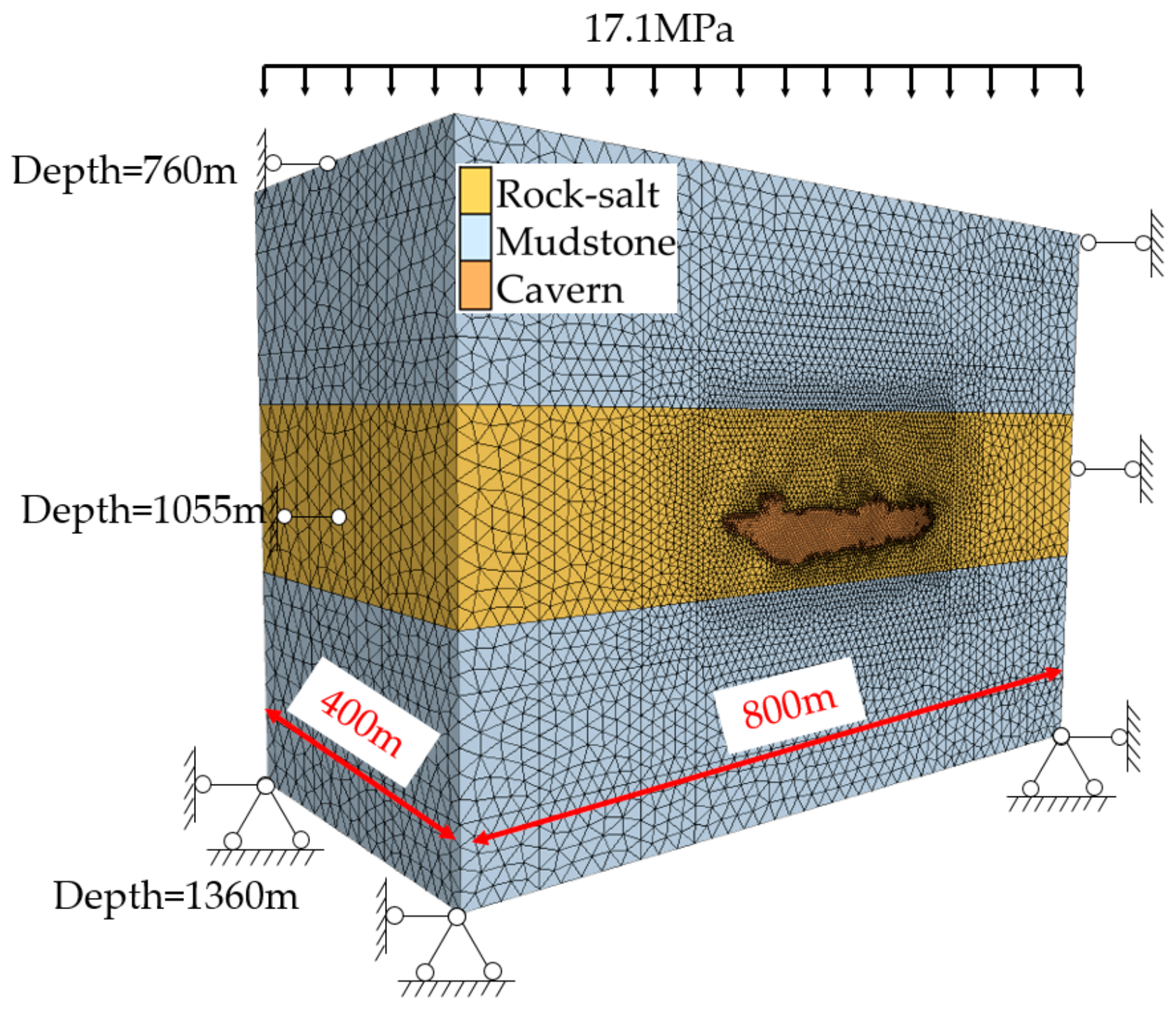
3.1. Numerical Modelling
3.2. Analysis of Simulation Results
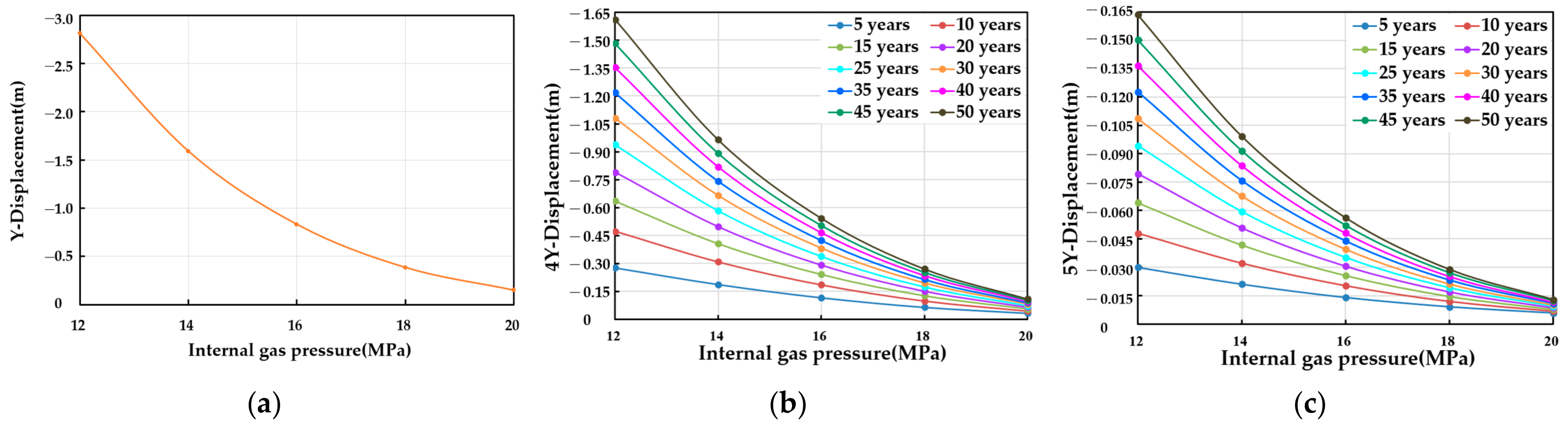
3.2.1. Displacement Analysis of Horizontal-Well Cavity
3.2.2. Relative Volume Loss of Horizontal-Well Cavity
3.2.3. Plastic Zone Volume of Horizontal-Well Cavity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, D.S.; El-Hiti, G.A.; Yousif, E.; Hameed, A.S.; Abdalla, M. New Eco-Friendly Phosphorus Organic Polymers as Gas Storage Media. Polymers 2017, 9, 336. [Google Scholar] [CrossRef]
- Hadi, A.G.; Jawad, K.; Yousif, E.; El-Hiti, G.A.; Alotaibi, M.H.; Ahmed, D.S. Synthesis of Telmisartan Organotin(IV) Complexes and their use as Carbon Dioxide Capture Media. Molecules 2019, 24, 1631. [Google Scholar] [CrossRef]
- Capros, P.; Zazias, G.; Evangelopoulou, S.; Kannavou, M.; Fotiou, T.; Siskos, P.; De Vita, A.; Sakellaris, K. Energy-system modelling of the EU strategy towards climate-neutrality. Energy Policy 2019, 134, 110960. [Google Scholar] [CrossRef]
- Rodrigues, R.; Pietzcker, R.; Fragkos, P.; Price, J.; McDowall, W.; Siskos, P.; Fotiou, T.; Luderer, G.; Capros, P. Narrative-driven alternative roads to achieve mid-century CO2 net neutrality in Europe. Energy 2022, 239, 121908. [Google Scholar] [CrossRef]
- Wang, T.; Yan, X.; Yang, H.; Yang, X.; Jiang, T.; Zhao, S. A new shape design method of salt cavern used as underground gas storage. Appl. Energy 2013, 104, 50–61. [Google Scholar] [CrossRef]
- Yang, C.; Wang, T. Advance in deep underground energy storage. Chin. J. Rock Mech. Eng. 2022, 41, 1729–1759. [Google Scholar]
- Li, Z.; Suo, J.; Fan, J.; Fourmeau, M.; Jiang, D.; Nelias, D. Damage evolution of rock salt under multilevel amplitude creep–fatigue loading with acoustic emission monitoring. Int. J. Rock Mech. Min. Sci. 2023, 164, 105346. [Google Scholar] [CrossRef]
- Malyukov, V.P.; Shepilev, A.A. Innovative Technologies for Construction of Horizontal and Double-Deck Underground Tanks in Rock Salt. In Processes in GeoMedia—Volume IV; Springer Geology; Chaplina, T., Ed.; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Shi, X.; Chen, Q.; Ma, H.; Li, Y.; Wang, T.; Zhang, C. Geomechanical investigation for abandoned salt caverns used for solid waste disposal. Bull. Eng. Geol. Environ. 2021, 80, 1205–1218. [Google Scholar] [CrossRef]
- Wang, J.; Wang, N.; Xu, K.; Xia, J. Calculation method for effective cavity volume of salt cavern gas storage. Oil Gas Storage Transp. 2021, 40, 909–913. [Google Scholar]
- Yu, P. An optimization mass-balance method for calculating the leaching volume of salt-cavern underground gas storage. Petrochem. Ind. Appl. 2020, 39, 4. [Google Scholar]
- Jiang, D.; Wang, Y.; Liu, W.; Li, L.; Qiao, W.; Chen, J.; Li, D.; Li, Z.; Fan, J. Construction simulation of large-spacing-two-well salt cavern with gas cushion and stability evaluation of cavern for gas storage. J. Energy Storage 2022, 48, 103932. [Google Scholar] [CrossRef]
- Jiang, D.; Li, Z.; Liu, W.; Ban, F.; Chen, J.; Wang, Y.; Fan, J. Construction simulating and controlling of the two-well-vertical(TWV) salt caverns with gas cushion. J. Nat. Gas Sci. Eng. 2021, 96, 104291. [Google Scholar] [CrossRef]
- Wang, T.; Yang, C.; Li, J.; Li, J.; Shi, X.; Ma, H. Failure Analysis of Overhanging Blocks in the Walls of a Gas Storage Salt Cavern: A Case Study. Rock Mech. Rock Eng. 2016, 50, 125–137. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, H.; Shi, X.; Yin, H.; Zhang, S. Position design of the casing shoe of an abandoned horizontal salt cavern to be used for gas storage. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 45, 2651–2665. [Google Scholar] [CrossRef]
- Gronefeld, P.; Pape, T. Simulation of Horizontal Solution Mining Processes. In Proceedings of the Solution Mining Research Institute Spring Meeting, Hannover, Germany, 25 September–1 October 1994. [Google Scholar]
- Zhang, G.; Zhang, H.; Liu, Y.; Wang, T.; Wang, Z. Surrounding rock stability of horizontal cavern reconstructed for gas storage. J. Energy Storage 2023, 59, 106534. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; He, M.; Song, Z.; Feng, S.; Liu, X.; Zhang, Y. Long-term stability analysis and evaluation of horizontal salt cavern gas storage. J. Energy Storage 2023, 66, 107413. [Google Scholar] [CrossRef]
- Yuan, G.; Wan, J.; Li, J.; Li, G.; Xia, Y.; Ban, F.; Zhang, H.; Jurado, M.J.; Peng, T.; Liu, W. Stability analysis of a typical two-well-horizontal saddle-shaped salt cavern. J. Energy Storage 2021, 40, 102763. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Z.; Liu, J.; Li, Y.; Cui, Z.; Zhang, H.; Wang, H.; Sui, L. Stability of the bedded key roof above abandoned horizontal salt cavern used for underground gas storage. Bull. Eng. Geol. Environ. 2020, 79, 4205–4219. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Shi, X.; Zhao, A.; Hao, S.; Gong, X.; Jiang, S.; Liu, Y. Stability analysis of U-shaped horizontal salt cavern for underground natural gas storage. J. Energy Storage 2021, 38, 102541. [Google Scholar] [CrossRef]
- Xing, W.; Zhao, J.; Hou, Z.; Were, P.; Li, M.; Wang, G. Horizontal natural gas caverns in thin-bedded rock salt formations. Environ. Earth Sci. 2015, 73, 6973–6985. [Google Scholar] [CrossRef]
- Cristescu, N.D.; Paraschiv, I. The optimal shape of rectangular-like caverns. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 285–300. [Google Scholar] [CrossRef]
- Xiao, N.; Liang, W.; Yu, Y.; Zhang, S.; Li, L. Shape prediction and parameter optimization of single-well retreating horizontal salt cavern for energy storage. J. Energy Storage 2023, 59, 106557. [Google Scholar] [CrossRef]
- Peng, T.; Wan, J.; Liu, W.; Li, J.; Xia, Y.; Yuan, G.; Jurado, M.J.; Fu, P.; He, Y.; Liu, H. Choice of hydrogen energy storage in salt caverns and horizontal cavern construction technology. J. Energy Storage 2023, 60, 106489. [Google Scholar] [CrossRef]
- Jinlong, L.; Wenjie, X.; Jianjing, Z.; Wei, L.; Xilin, S.; Chunhe, Y. Modeling the mining of energy storage salt caverns using a structural dynamic mesh. Energy 2019, 193, 116730. [Google Scholar] [CrossRef]
- Li, J.; Zhang, N.; Xu, W.; Naumov, D.; Fischer, T.; Chen, Y.; Zhuang, D.; Nagel, T. The influence of cavern length on deformation and barrier integrity around horizontal energy storage salt caverns. Energy 2022, 244, 123148. [Google Scholar] [CrossRef]
- Yang, J.; Li, H.; Yang, C.; Li, Y.; Wang, T.; Shi, X.; Han, Y. Physical simulation of flow field and construction process of horizontal salt cavern for natural gas storage. J. Nat. Gas Sci. Eng. 2020, 82, 103527. [Google Scholar] [CrossRef]
- Wang, J.; An, G.; Wang, W.; Jia, J.; Liu, C.; Miao, S.; Wang, D.; Chen, C. Solution-mining-under-nitrogen technology for salt-cavern gas storage and field test. Oil Gas Storage Transp. 2021, 40, 802–808. [Google Scholar]
- Li, J.; Shi, X.; Yang, C.; Li, Y.; Wang, T.; Ma, H.; Shi, H.; Li, J.; Liu, J. Repair of irregularly shaped salt cavern gas storage by re-leaching under gas blanket. J. Nat. Gas Sci. Eng. 2017, 45, 848–859. [Google Scholar] [CrossRef]
- Liu, W.; Jiang, D.; Chen, J.; Daemen JJ, K.; Tang, K.; Wu, F. Comprehensive feasibility study of two-well-horizontal caverns for natural gas storage in thinly-bedded salt rocks in China. Energy 2018, 143, 1006–1019. [Google Scholar] [CrossRef]
- Li, J.L.; Yang, C.H.; Shi, X.L.; Xu, W.J.; Li, Y.P.; Daemen, J.J.K. Construction modeling and shape prediction of horizontal salt caverns for gas/oil storage in bedded salt. J. Petrol. Sci. Eng. 2020, 190, 107058. [Google Scholar] [CrossRef]
- Malyukov, V. Studies of the Construction of Horizontal Underground Workings-Tanks Under the Impact of Solution on Rock Salt. In PMMEEP 2022: Physical and Mathematical Modeling of Earth and Environment Processes—2022; Springer: Berlin/Heidelberg, Germany, 2023; pp. 387–393. [Google Scholar]
- Wan, J. Influence of tubing/oil-blanket lifting on construction and geometries of two-well-horizontal salt caverns. Tunn. Undergr. Space Technol. 2020, 108, 103688. [Google Scholar] [CrossRef]
- Saberian, A. A Preliminary Model Horizontal Well Leaching; SMRI Library: San Antonio, TX, USA, 1995. [Google Scholar]
- Wang, J.; Wang, Z.; Zeng, Q.; Ding, G.; Li, K.; Wanyan, Q.; Wang, Y. Simulation of Flow Field of Solution Mining Salt Cavities for Underground Gas Storage. J. Energy Resour. Technol. 2022, 145, 022001. [Google Scholar] [CrossRef]
- Li, Q.; Ning, Z.; Liu, J.; Xu, W.; Zhan, L.; Liu, J.; Chen, Y.; Shi, X.; Chen, X.; Li, J. Stability and economic evaluation of multi-step horizontal salt caverns with different step distances in bedded salt formations. J. Energy Storage 2023, 57, 106192. [Google Scholar] [CrossRef]









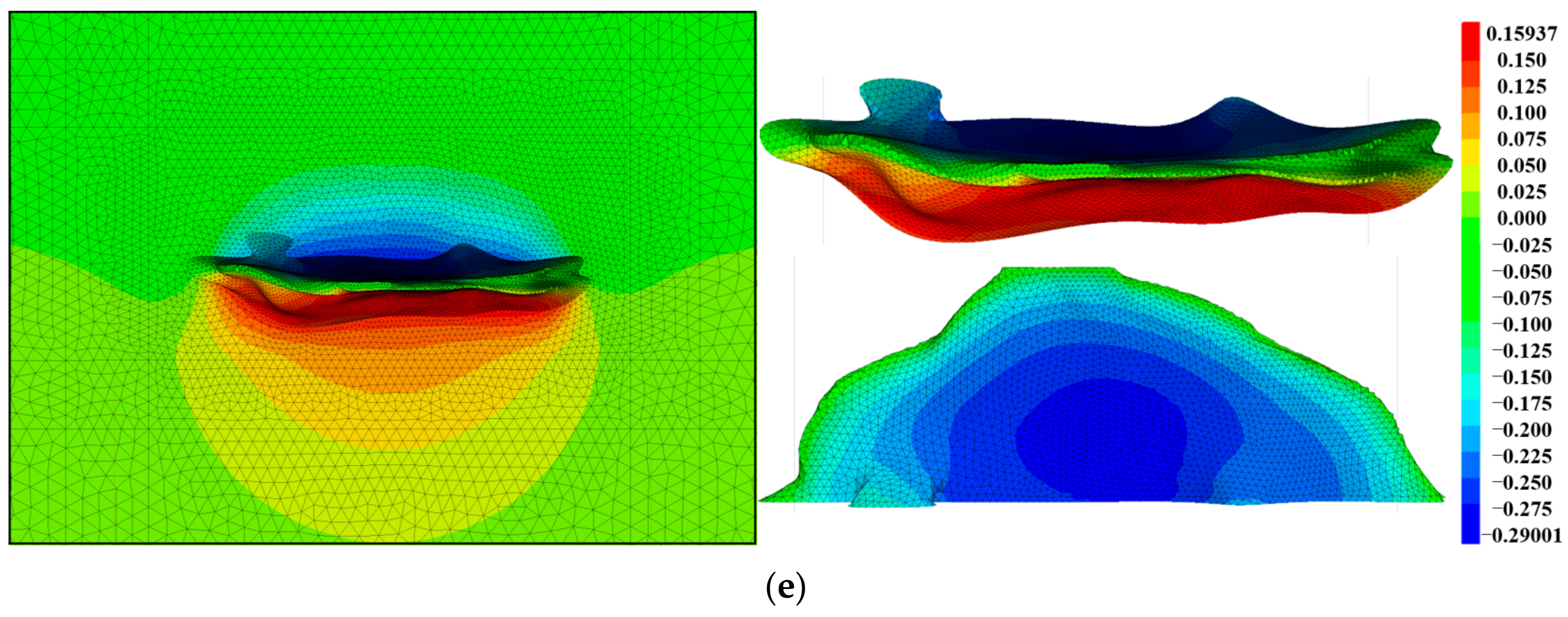


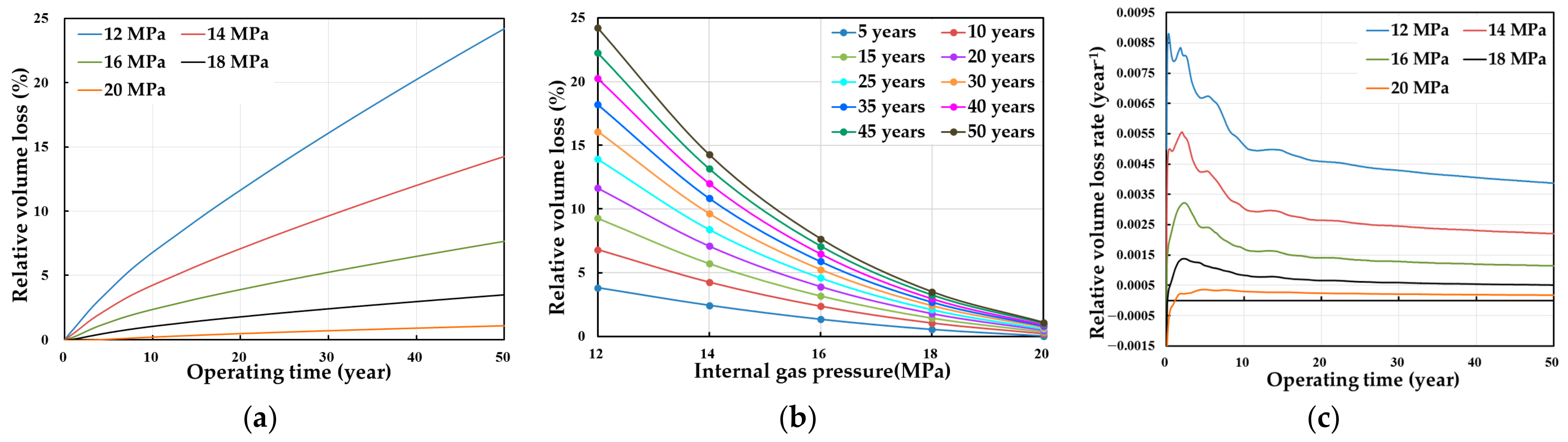
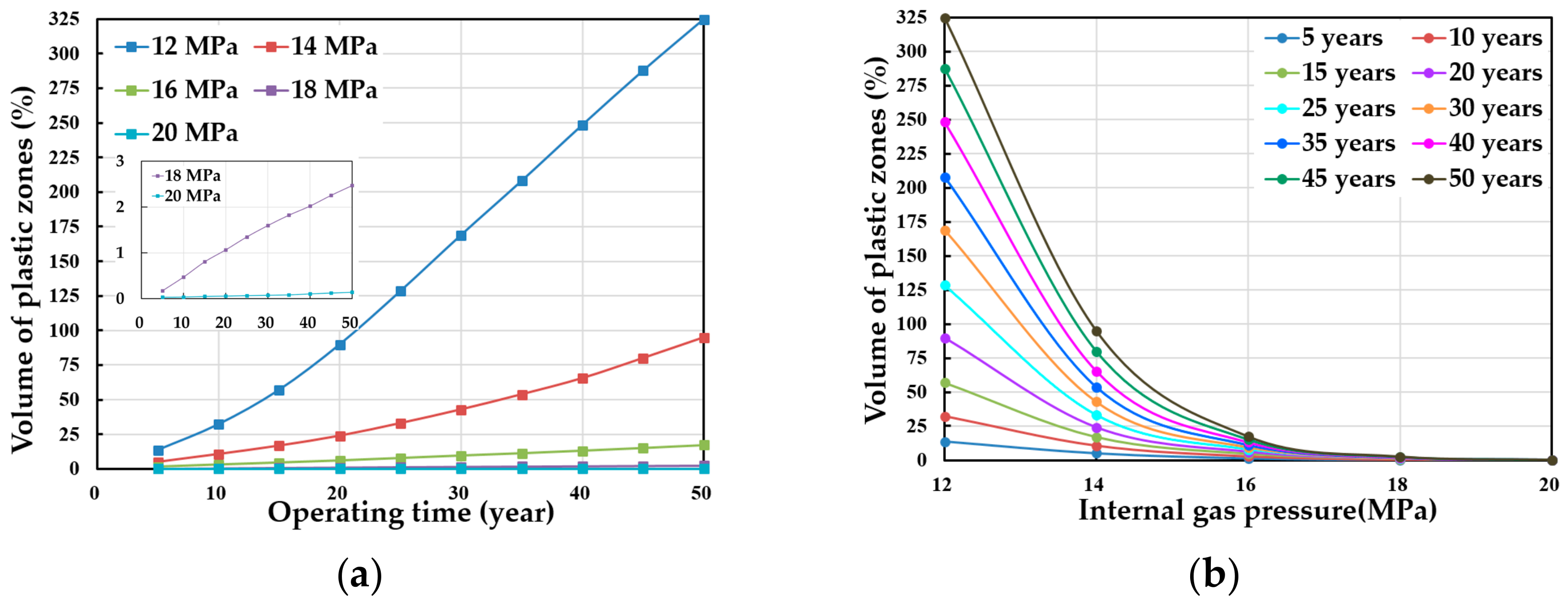

| Parameters | Dimension (Unit) | Parameters | Dimension (Unit) |
|---|---|---|---|
| l | L | c | ML−3 |
| T | T | T | Θ |
| ρ | ML−3 | q | L3T−1 |
| ω | ML−2T−1 |
| Parameters | Cavity Diameter /m | Density of Salt Rock/kg·m−3 | Dissolution Rate of the Brine/g·cm−2·h−1 | Mining Time/h | Brine Concentration/g·L−1 | Flow Rate/ mL·min−1 |
|---|---|---|---|---|---|---|
| Prototype | 125 | 2176 | 3.68 | - | - | 50 m3/h |
| Model | 0.25 | 2117 | 1.42 | - | - | 10 mL/min |
| Similarity Ratio | 500 | 1 | 2.59 | 1500 | 1 | 83,333 |
| Tubes | Inner Diameter (mm) | Outer Diameter (mm) | Wall Thickness (mm) | Tube Length (mm) | Notes |
|---|---|---|---|---|---|
| Casing | 5 | 6 | 0.5 | 60 | Fixed with volcanic clay and AB adhesive at the upper end of the slot on both sides for inserting the injection tube and drainage tube |
| Stainless Tube—Nitrogen Injection Pipe | 3.6 | 4 | 0.2 | 130 | Fixed with volcanic mud and AB adhesive on the upper end of the slot on both sides |
| Stainless Pipe-Drainage Pipe | 3.6 | 4 | 0.2 | 240 | Inserted into the casing at the right, straight-well end and wrapped with waterproof tape on the outer layer |
| Rubber Hose 1# | 3 | 5 | 1 | - | Water injection tube inserted into the casing in the inclined well, sealing tube at the upper end of the nitrogen injection tube |
| Rubber Hose 2# | 4 | 6 | 1 | 6 | Wrapped around the outside of the casing to seal the wellhead on both sides |
| Rubber Hose 3# | 4 | 8 | 2 | - | Externally connected to the flow meter and indirectly connected to the tap |
| Rubber Hose 4# | 7 | 9 | 1 | - | Externally connected to the water tap and connected to rubber hose 4# |
| Stage | Duration (h) | Flow Rate (mL/min) | Wellhead Distance (mm) |
|---|---|---|---|
| 1 | 3 | 3 | 5 |
| 2 | 3 | 6 | 5 |
| 3 | 3 | 9 | 5 |
| 4 | 3 | 3 | 35 |
| 5 | 3 | 6 | 35 |
| 6 | 3 | 9 | 35 |
| 7 | 3 | 3 | 65 |
| 8 | 3 | 6 | 65 |
| 9 | 3 | 9 | 65 |
| 10 | 3 | 3 | 95 |
| 11 | 3 | 3 | 125 |
| 12 | 3 | 6 | 125 |
| 13 | 3 | 9 | 125 |
| 14 | 10 | 12 | 125 |
| 15 | 28 | 12 | 155 |
| 16 | 7 | 12 | 155 |
| 17 | 10 | 15 | 155 |
| Lithology | Modulus of Elasticity (GPa) | Poisson’s Ratio | Cohesive Force (MPa) | Internal Friction Angle (°) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| Mudstone | 10 | 0.27 | 2.5 | 35 | 1.5 |
| Rock salt | 15 | 0.3 | 1.75 | 37.5 | 1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, D.; Chen, J.; Wu, F.; Jiang, D.; Liu, W.; Ding, B.; Luo, X.; Kang, Y.; He, Y. Comprehensive Research on Construction and Stability of Horizontal-Well Cavity Natural Gas Storage in Thinly Bedded Salt Rocks in China. Energies 2023, 16, 7877. https://doi.org/10.3390/en16237877
Lu D, Chen J, Wu F, Jiang D, Liu W, Ding B, Luo X, Kang Y, He Y. Comprehensive Research on Construction and Stability of Horizontal-Well Cavity Natural Gas Storage in Thinly Bedded Salt Rocks in China. Energies. 2023; 16(23):7877. https://doi.org/10.3390/en16237877
Chicago/Turabian StyleLu, Dan, Jie Chen, Fei Wu, Deyi Jiang, Wei Liu, Bowen Ding, Xinyu Luo, Yanfei Kang, and Yi He. 2023. "Comprehensive Research on Construction and Stability of Horizontal-Well Cavity Natural Gas Storage in Thinly Bedded Salt Rocks in China" Energies 16, no. 23: 7877. https://doi.org/10.3390/en16237877
APA StyleLu, D., Chen, J., Wu, F., Jiang, D., Liu, W., Ding, B., Luo, X., Kang, Y., & He, Y. (2023). Comprehensive Research on Construction and Stability of Horizontal-Well Cavity Natural Gas Storage in Thinly Bedded Salt Rocks in China. Energies, 16(23), 7877. https://doi.org/10.3390/en16237877








