Seismic Anisotropy Estimation Using a Downhole Microseismic Data Set in a Shale Gas Reservoir

Abstract

Shale anisotropy has a significant impact on the data processing and interpretation of microseismic monitoring in shale gas reservoirs. A geology- and rock-physics-constrained approach to estimating shale anisotropy using down-hole microseismic data sets is proposed in this study and is applied to the case of Horn River shale. A priori knowledge of shale anisotropy is obtained by integrating geological analyses and rock physics studies. This knowledge serves as an important constraint when building the initial model, minimizing the uncertainties and evaluating the results. The application to Horn River shale shows that the optimized anisotropic velocity model reduces the time misfit by about 65% compared to the originally provided velocity model. As the relocated perforation shot indicates, the event locations are significantly improved. The results also show that a high fraction of clay mineral results in strong fabric anisotropy in the Fort Simpson formation, whereas the quartz-rich shale gas reservoirs (Muskwa and Otter Park formations) show weaker fabric anisotropy. The percentage of velocity anisotropy in Horn River shale can be up to 40%. The fabric anisotropy of shale derived from the downhole microseismic data set is comparable with that of laboratory experiments. This demonstrates that downhole microseismic monitoring, as a quasi in situ experiment, has the potential to contribute to a better understanding of subsurface anisotropy beyond the laboratory. In addition, microseismic measurements of shale anisotropy are conducted in the seismic frequency band and are thus more applicable for further seismic applications.

1. Introduction

With the increasing development of shale gas and tight gas reservoirs, microseismic technology has been increasingly widely applied [1,2]. The basic application of microseismic monitoring is to map the spatial and temporal distributions and the mechanisms of hydraulically induced events [3,4]. Shale formations usually exhibit transverse isotropic and azimuth anisotropic properties due to the bedding-parallel fabric and the preferred oriented fracture set [5,6]. Shale anisotropy has a strong impact on microseismic data processing and interpretation, including the locations of microseismic events, as well as the inversion and interpretation of source mechanisms [7,8,9]. This can further affect the characterization of the fracture network, the fracture geometry and the stimulated volume. This paper focuses on estimating the fabric anisotropy (i.e., the intrinsic anisotropy) of shale using a downhole microseismic data set from a shale gas reservoir.

Although working with anisotropy has been widely acknowledged by the microseismic community, there are only a few studies on extracting the velocity anisotropy from a microseismic data set. Grechka et al. (2011, 2013, 2014) extended passive seismic tomography to simultaneously estimate the triclinic anisotropy and locations of microseismic events and applied this method to the case of Bakken shale [10,11,12]. Li et al. (2013) extended the double-difference tomography to jointly invert the microseismic location and VTI (Vertically Transversely Isotropic) model [13]. Verdon et al. (2009, 2011) and Wuestefeld et al. (2011) developed an approach to imaging sedimentary fabrics and fracture characteristics using shear-wave splitting in microseismic observations [14,15,16]. Michel et al. (2014, 2015) attempted to use waveform inversion to derive the VTI model and the source parameters of microseismic events [17,18]. These approaches are mainly adapted from the techniques developed for regional seismic monitoring or reflection seismic surveys. In microseismic applications, the spatial scale of the target area is relatively small and detailed geological and geophysical investigations around the reservoir have already been carried out prior to hydraulic fracturing operations. Large amounts of geological data are available for the estimation of anisotropy using a microseismic data set. However, the geological data have not been fully used in previous studies. Developing a practical approach specifically for microseismic applications by integrating all the available geological data is a promising direction [19].

The fabric anisotropy of shale is usually characterized by the transversely isotropic (TI) model and has the strongest impact on seismic applications. In recent decades, there have been many laboratory measurements of the fabric anisotropy of shale and further studies on the relationships between the fabric anisotropy and the mineral compositions or organic matter in shale. At the scale of a core sample, the fabric anisotropy of shale is caused by the alignment and lamination of softer and platy clay minerals and kerogen [5,20,21]. In contrast, the stiffer and non-platy quartz grains can prevent fabric alignment and significantly weaken the fabric anisotropy of shale [22]. However, these rock physics studies on the fabric anisotropy of shale have not been extensively integrated into velocity model building in microseismic applications, as is commonly being performed in reflection seismic cases.

In this paper, we propose a geology- and rock-physics-oriented approach to estimating shale anisotropy using a downhole microseismic data set and applying it to a real data set acquired from the Horn River shale gas reservoir. Geological analyses and experimental studies are deeply involved and highlighted in the working flow. They play crucial roles in building the initial model, minimizing the uncertainties and evaluating the results. The seismic responses of shale anisotropy are analyzed using seismograms and the inversion methodology is introduced. Then, we show the process of estimating the fabric anisotropy of Horn River shale and compare the time misfits and microseismic event locations before and after the optimization. Finally, we compare the shale anisotropy obtained via microseismic and laboratory measurements, and discuss the implications for the development of shale gas reservoirs.

2. Geological Analyses

Since hydraulic fracturing is usually carried out after geological and geophysical borehole investigations, a full package of geological data is available for microseismic data processing and interpretation. Geological analyses of Horn River shales help to define a reasonable initial model of fabric anisotropy for further optimization. Stratigraphic setting separates the layers of different properties and provides a frame for model geometry. Sonic logs give the elastic parameters in the vertical direction. Lithological characteristics reveal the fundamental information, such as regarding the mineral compositions and organic content, which are extremely important for rock physics modeling and the interpretation of the results. Unfortunately, the first-hand geological data from the operator are not available to us. Most of the content in this section is based on the information collected from publications and open documents.

2.1. Stratigraphic Setting

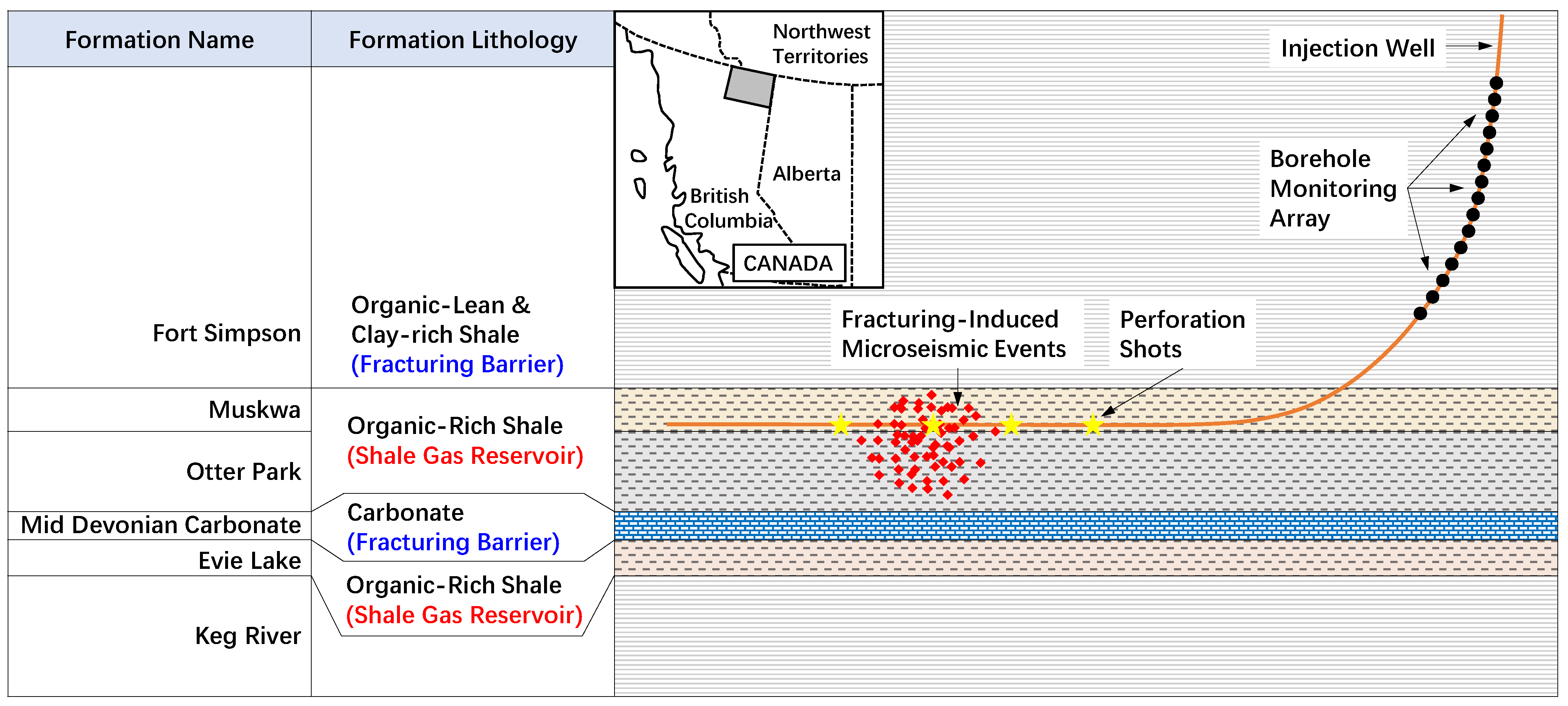
The microseismic data set under consideration was acquired during the hydraulic fracturing operation carried out in the Horn River Basin, Northeastern British Columbia, Canada. The targets of the fracturing operation are the organic-rich shale formations (Muskwa, Otter Park and Evie) with TOC (Total Organic Carbon) of up to 6 wt.% [23,24]. The fractured reservoirs are overlain by about 800 m thick clay-rich and organic-lean shales of the Fort Simpson Formation [25], exactly where the receiver arrays are deployed (Figure 1). All the formations are near-horizontal within the spatial scale of downhole microseismic monitoring. For the three-stage microseismic data set provided by the operator, the event clouds are mainly restricted within the Muskwa and upper-middle Otter Park formations. The overlying Fort Simpson shale and underlying lower Otter Park shale, with higher clay content as well as a thin carbonate layer, serve as fracture barriers [26].

2.2. Sonic Logs

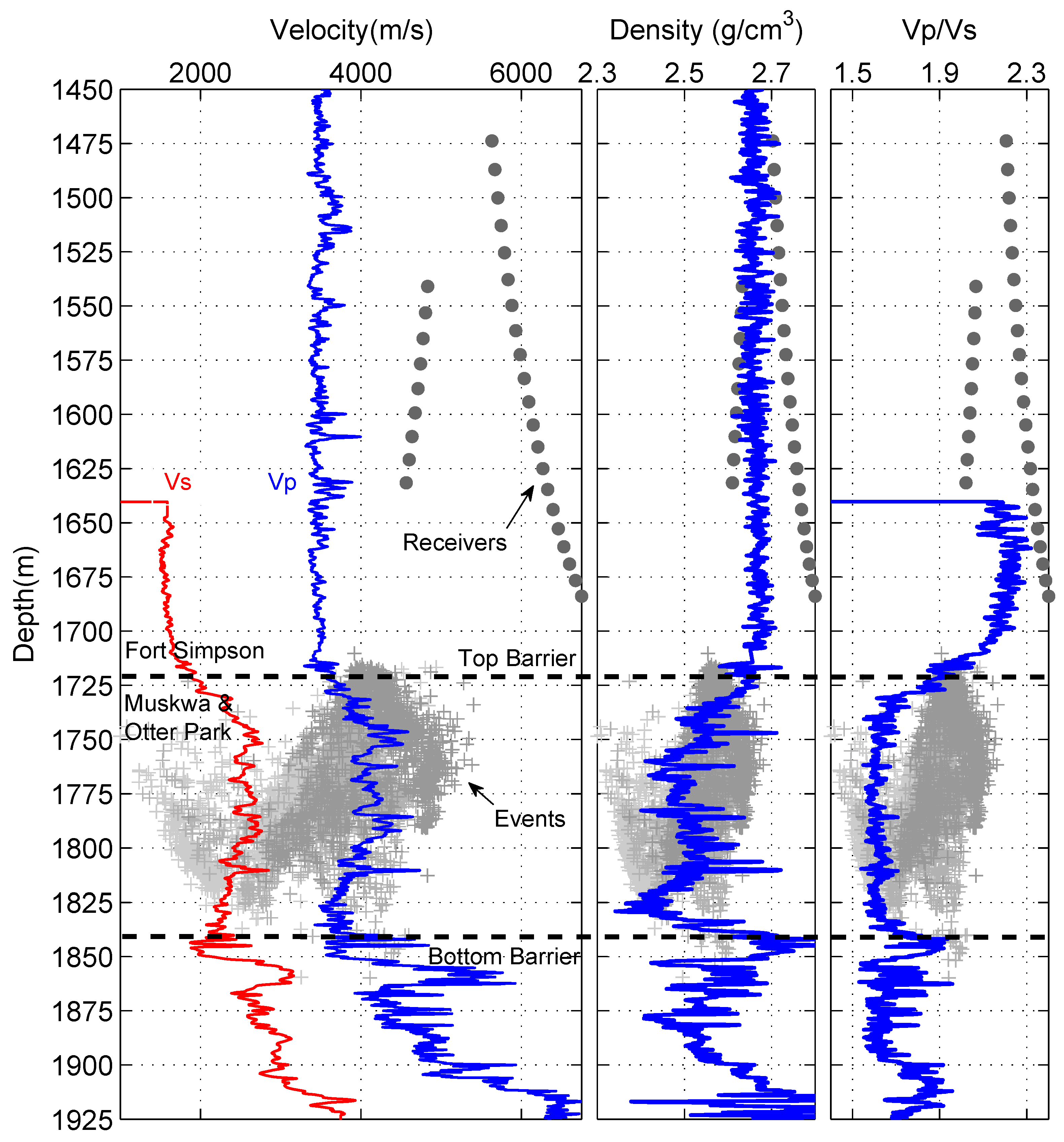
Figure 2 shows the sonic logs from an offset well in the study area. To illustrate the elastic properties of different layers, the receiver arrays and event clouds are projected on the depth axis. The shale gas reservoir (Muskwa and Otter Park formations) is characterized by a high velocity of the P- and S-wave (Vp and Vs), a low Vp/Vs ratio and a low density, which is completely opposite to the upper and lower shale formations serving as fracture barriers. The overlying thick clay-rich formation (Fort Simpson) within which the receiver arrays are deployed shows near-constant Vp, Vs and density, which implies that it is relatively homogeneous in terms of depth compared to the underlying reservoir. The wide-ranging variations in the elastic properties are closely related to the mineral composition of shale. With the constraint of the stratigraphic setting, an isotropic velocity model can be established by using the sonic logs, which is the basis of anisotropic velocity model inversion.

2.3. Lithological Characteristics

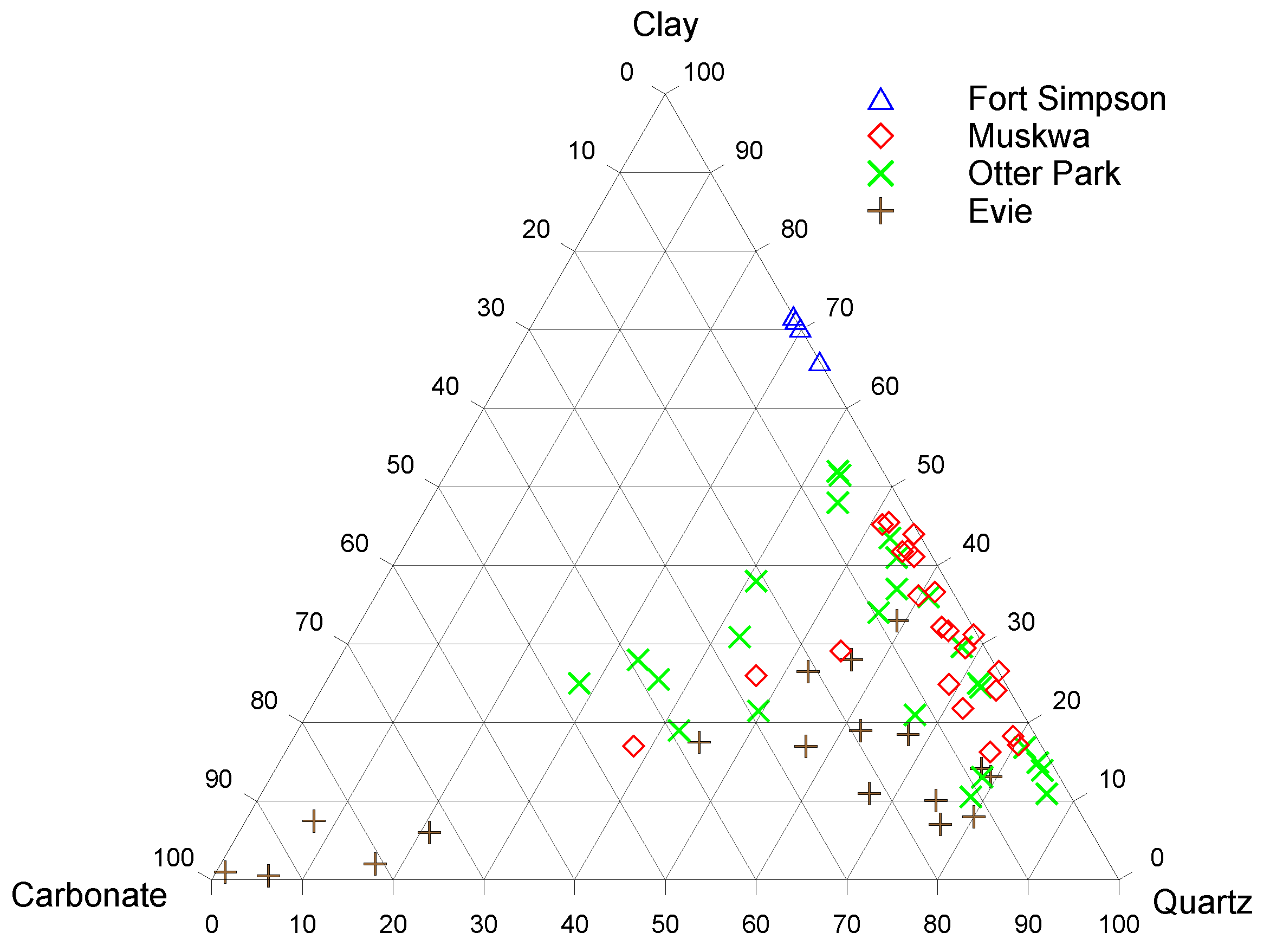
Lithological characteristics provide fundamental information on shale, such as its mineral compositions and organic content. Clay, quartz and carbonate are three major minerals of shale, the relative contents of which vary greatly for different shale samples. Since the core data of the target wells are unavailable, we collected the published core data of Horn River shale samples from different surveys and created a ternary plot of the clay, quartz and carbonate contents (Figure 3). The most notable and distinct points are the dominant clay content in Fort Simpson shale (average 70%) and the quartz content in Muskwa shale (up to 87%), and the extremely low carbonate content for both formations. The upper Otter Park shale is slightly more argillaceous and the lower Otter Park shale contains even more clay and less quartz [23]. The underlying Evie shale is more calcareous than the other two formations. The mineral composition is the geological source of the distinct elastic properties and this can be used to predict the elastic parameters via experimental studies and rock physics models.

2.4. Summary

For clarity in understanding its further applications, the geological information of Horn River shale is summarized in

Table 1. Summary of the geological information on Horn River shales. The values of mineral contents and TOC are the weight fractions.

	Formation	Clay	Quartz	TOC	Vp (m/s)	Vp/Vs	Density (g/cc)
Upper Fracture Barrier	Fort Simpson	70%	28%	<1%	3500	2.20	2.65
Fractured Reservoir	Muskwa	25%	70%	5%	4100	1.65	2.50
	Upper Otter Park	30%	60%	4%	3900	1.65	2.45
Lower Fracture Barrier	Lower Otter Park	40%	50%	2%	3600	1.8	2.70
	Thin Carbonate	/	/	/	5500	1.75	2.65

. This information provides important guidance for the definition of the anisotropic velocity model. Considering the wide ranging variations in the elastic properties observed in well logs, a piecewise continuous velocity model is used, within which the vertical gradients of the elastic parameters are kept, rather than using a step-model with constant elastic properties in each layer. The thick clay-rich shale formation, which serves as the upper fracture barrier, is assumed to be a homogeneous layer because of the near-constant elastic properties, as shown in sonic logs (Figure 2). The mineral compositions, as shown in Table 1, directly control the fabric anisotropy of shale and play a crucial role when building the initial model and evaluating the optimization results.

3. Fabric Anisotropy of Shale

The primary source of shale anisotropy is the bedding-parallel alignments of clay minerals, as well as kerogen particles, in organic-rich shales, which usually causes the fabric anisotropy (i.e., the intrinsic anisotropy) of shale [6,20]. Another important source of shale anisotropy is the preferred oriented fractures at scales much larger than grains or pores. These fractures are generally induced by the local stress field and mainly result in azimuthal anisotropy. The fine-scale lamination of shales with different stiffnesses can also introduce a layering anisotropy, which is much weaker than the first two types of anisotropy. This paper only focuses on the fabric anisotropy of shale, which is usually represented by the transverse isotropic (TI) model and has the strongest impact on microseismic applications. Laboratory measurements of the fabric anisotropy and its relationship with the mineral compositions and organic matter in shale are reviewed in this section. The experimental knowledge is used to build the initial model, constrain the inversion and evaluate the results.

3.1. Fabric Anisotropy vs. Clay and Kerogen

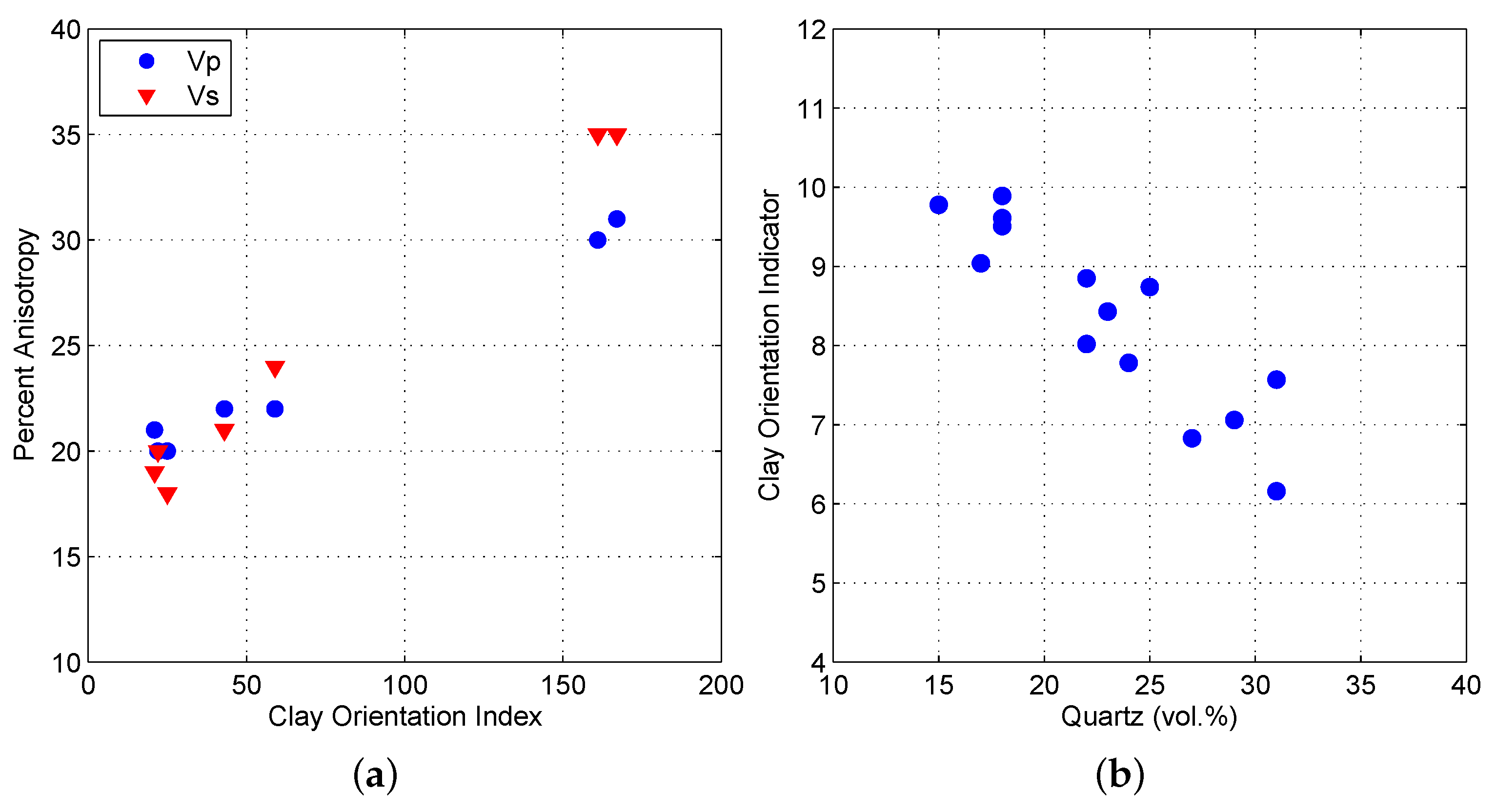
Clay minerals can be well organized via strain-induced rotation during compaction because of the low aspect ratio [22]. Using X-ray diffraction techniques, it has been quantitatively demonstrated that a strong positive correlation exists between the degree of clay mineral alignment and the fabric anisotropy of shale (Figure 4a). The electron and optical microscope images of shale fabric also support this point in a qualitative manner [20,21]. Under the condition of similar compaction histories, the fabric anisotropy of shale increases with the relative content of clay minerals.

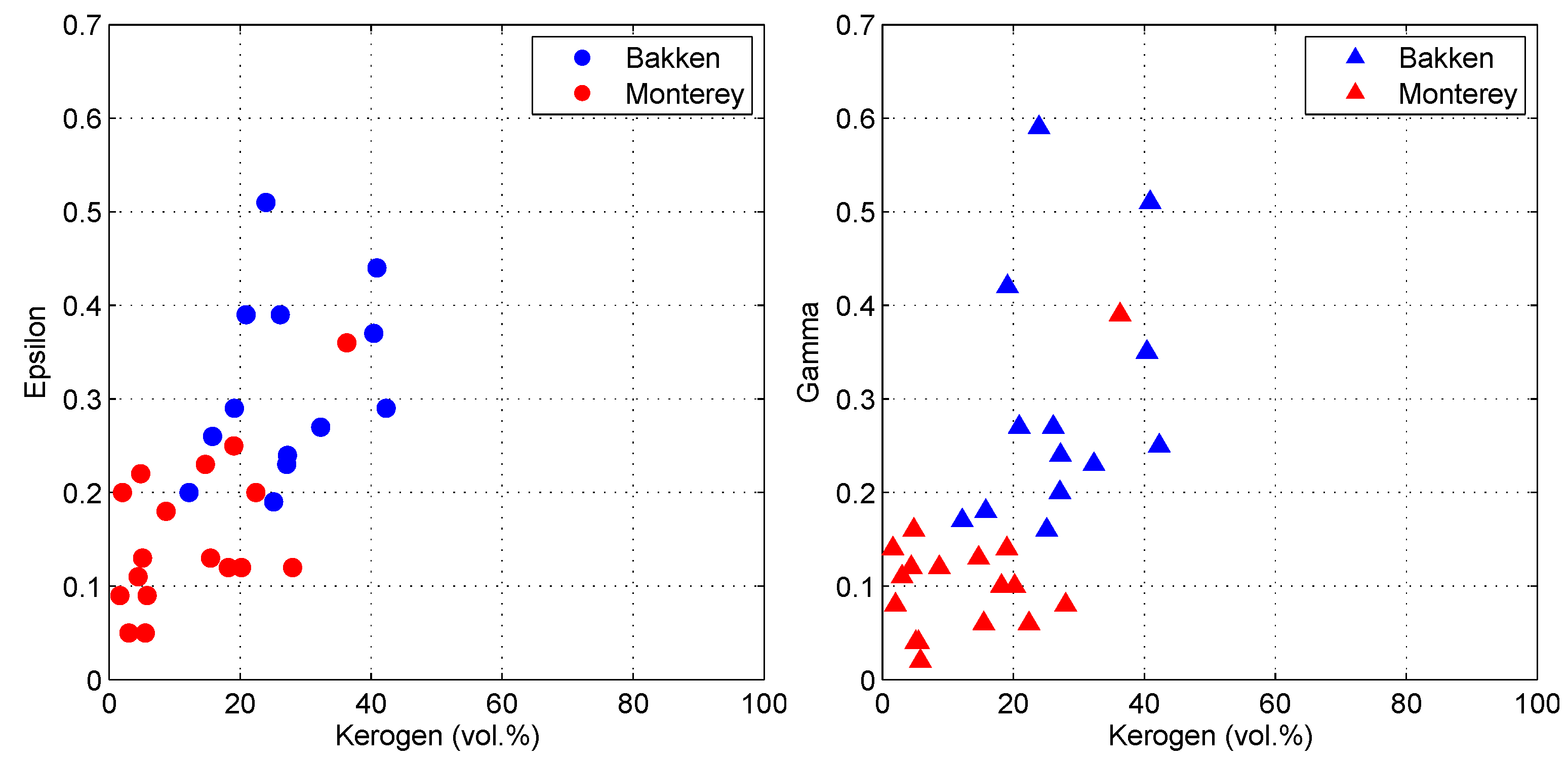
Studies by Vernik and Nur (1992), Vernik and Liu (1997) and Sondergeld et al. (2000) suggest a strong correlation between the elastic anisotropy of shale and organic richness (Figure 5) [5,29,30]. In organic-rich shale, kerogen manifests as lenticular microlayers dispersed amongst the clay matrix and with sporadic lamination in the bedding-parallel direction, as shown in the petrographic and SEM (Scanning Electron Microscopy) observations [29,31]. The extremely compliant elastic properties of kerogen result in a much larger decrease in seismic velocity in the bedding-normal direction than in the bedding-parallel direction, and thus cause strong transverse isotropy. In addition, the hydrocarbon-generation-induced microcracks further enhance the velocity anisotropy of organic-rich shales [32].

As summarized by Hall (2010), most of North America’s prospective gas shales, as well as non-source shales, do not have as high TOC contents and as low clay contents as the Bakken shale samples (TOC 4.9∼21%, Clay ∼ 5%) presented in Vernik and Nur (1992) and Vernik and Liu (1997) [5,29,33]. In the general cases, both clay mineral and organic matters contribute to the fabric anisotropy of shale and it is difficult to distinguish their influences. An alternative method is to investigate the correlations between velocity anisotropy and the soft components of shale. As shown in Figure 6, the anisotropy of P- and S-waves is strongly correlated with the sum of clay and kerogen contents.

3.2. Fabric Anisotropy vs. Quartz

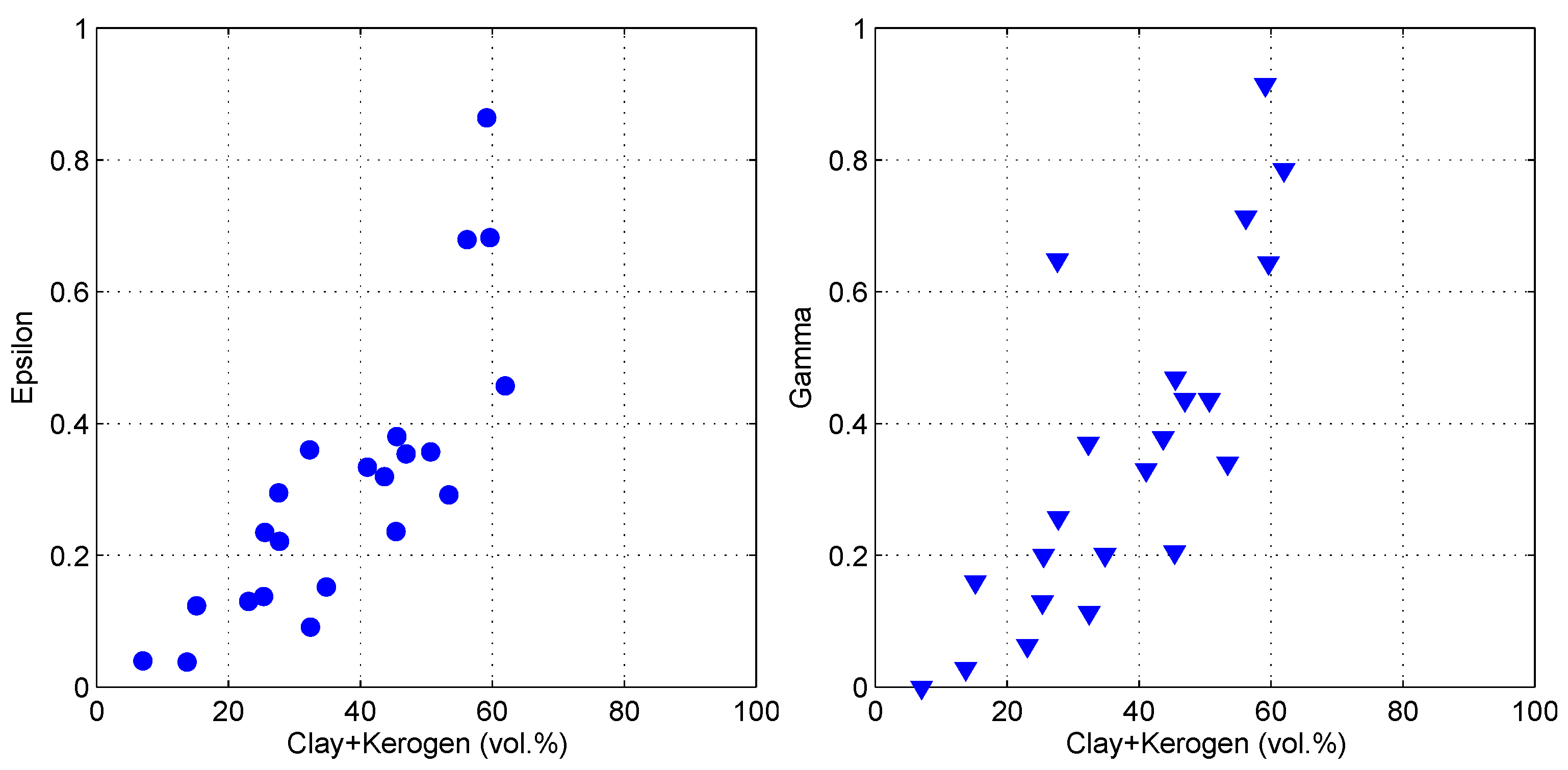
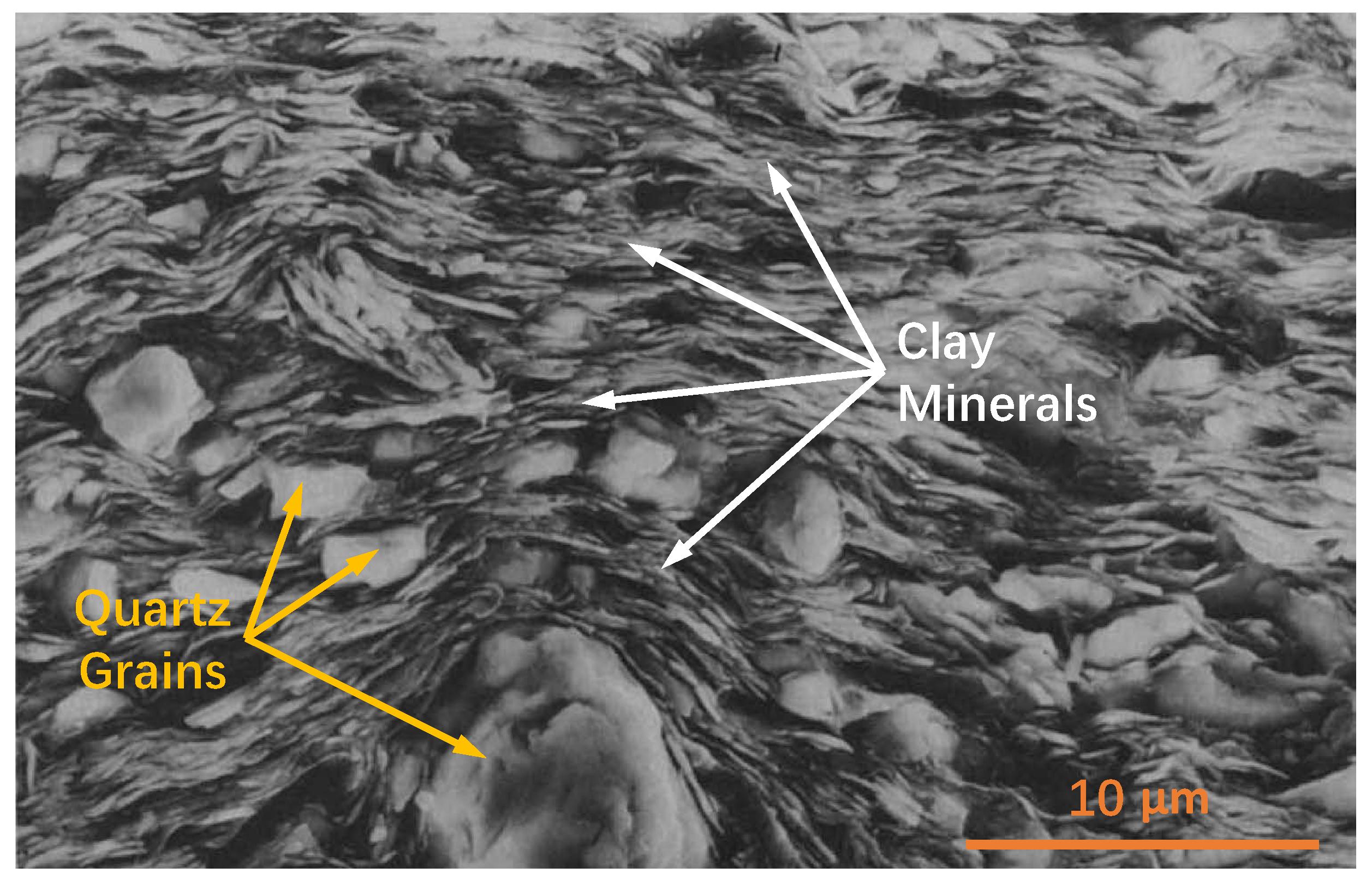
Curtis et al. (1980) measured the degree of clay mineral alignments in fine-grained sediments using X-ray techniques and found that there was a strong negative correlation with the quartz content (Figure 4b) [22]. Through observations of thin section images it was also found that the preferred clay orientation vanishes when the clay content is too low [21]. It can be interpreted that the quartz minerals with much stiffer and non-platy grains prevent the fabric alignment and disrupt the spatial continuity of compliant components (Figure 7), ultimately weakening the fabric anisotropy of shale. Therefore, the shale gas reservoir with high quartz content in the Horn River Basin is expected to show much weaker fabric anisotropy.

3.3. Thomsen Parameters of Shale

The fabric anisotropy of shale is usually represented using the transversely isotropic model, which is described using Thomsen parameters and defined as

$$\epsilon =\frac{c_{11}-c_{33}}{2c_{33}}\gamma =\frac{c_{66}-c_{55}}{2c_{55}}\delta =\frac{{(c_{13}+c_{55})}^2-{(c_{33}-c_{55})}^2}{2c_{33}(c_{33}-c_{55})}$$

(1)

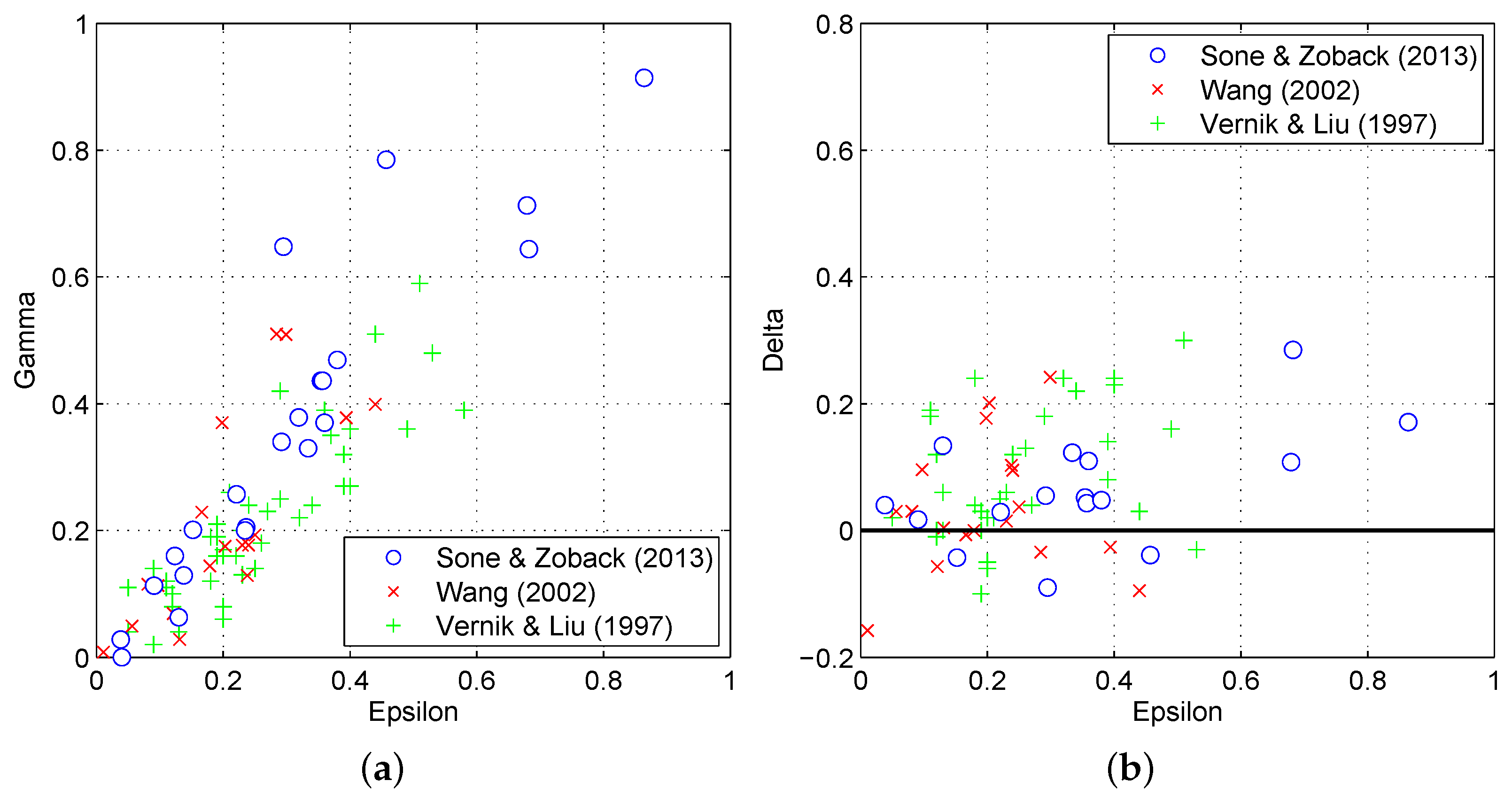
The Thomsen parameters $\epsilon$ and $\gamma$ reflect the differences of elastic parameters in the horizontal and vertical directions. $\epsilon$ controls the P-wave response and $\gamma$ controls the SH-wave response. The similarities between $\epsilon$ and $\gamma$ in terms of mathematical and physical forms implies a possible correlation between them. Thomsen parameter $\delta$, with a complex mathematical form, has no clear physical meaning. It dominates the near-vertical P wave response in the weak anisotropy case and controls the complexity of the wavefronts of P- and SV-waves, such as the cusps or triplications in the wavefront of SV-wave [35]. Laboratory measurements of the fabric anisotropy of shale show that the Thomsen parameters $\epsilon$ and $\gamma$ are almost always positive and have a correlation with each other, while $\delta$ can be either positive or slightly negative and scatter in a narrow range with no correlations with $\epsilon$ and $\gamma$ (Figure 8). Vernik and Liu (1997) and Sayers (2005) attribute the sign variation of $\delta$ to the inter-particle microcracks or to the degree of disorder in the orientations of clay minerals [5,6].

3.4. Initial Estimate of Fabric Anisotropy in Shale

Based on the geological analyses, Horn River shales have relatively simple mineral compositions which are dominated by clay and quartz minerals, and with minimal carbonate. This makes it possible to predict the fabric anisotropy according to experimental and theoretical studies. Shale gas reservoirs (Muskwa, Upper Otter Park) with extremely high quartz contents and low clay contents are expected to exhibit much weaker fabric anisotropy than the overlying and underlying clay-rich fracture barriers. The lithological characteristics also support this point, with observations showing that Horn River gas-bearing shales are weakly laminated at the core scale [23,24].

According to the semi-quantitative relationships between the fabric anisotropy of shale and the clay and kerogen contents revealed via laboratory studies (Figure 6), we can preliminarily estimate the Thomsen parameters of Horn River Shales based only on the volume fractions of clay and kerogen (

Table 2. Initial estimates of the Thomsen parameters for Horn River shales. The values of clay and kerogen volume fractions are approximately calculated according to Table 1.

	Formation	Clay and Kerogen	$\mathit{\epsilon }$	$\mathit{\gamma }$
Upper Fracture Barrier	Fort Simpson	65 vol.%	0.4	0.5
Fractured Reservoir	Muskwa and Upper Otter Park	35 vol.%	0.2	0.2
Lower Fracture Barrier	Lower Otter Park	45 vol.%	0.3	0.3

). This preliminary model, entirely derived from the geological and experimental analyses, is used as the initial model for further optimization.

4. Data and Methodology

4.1. Microseismic Data Set

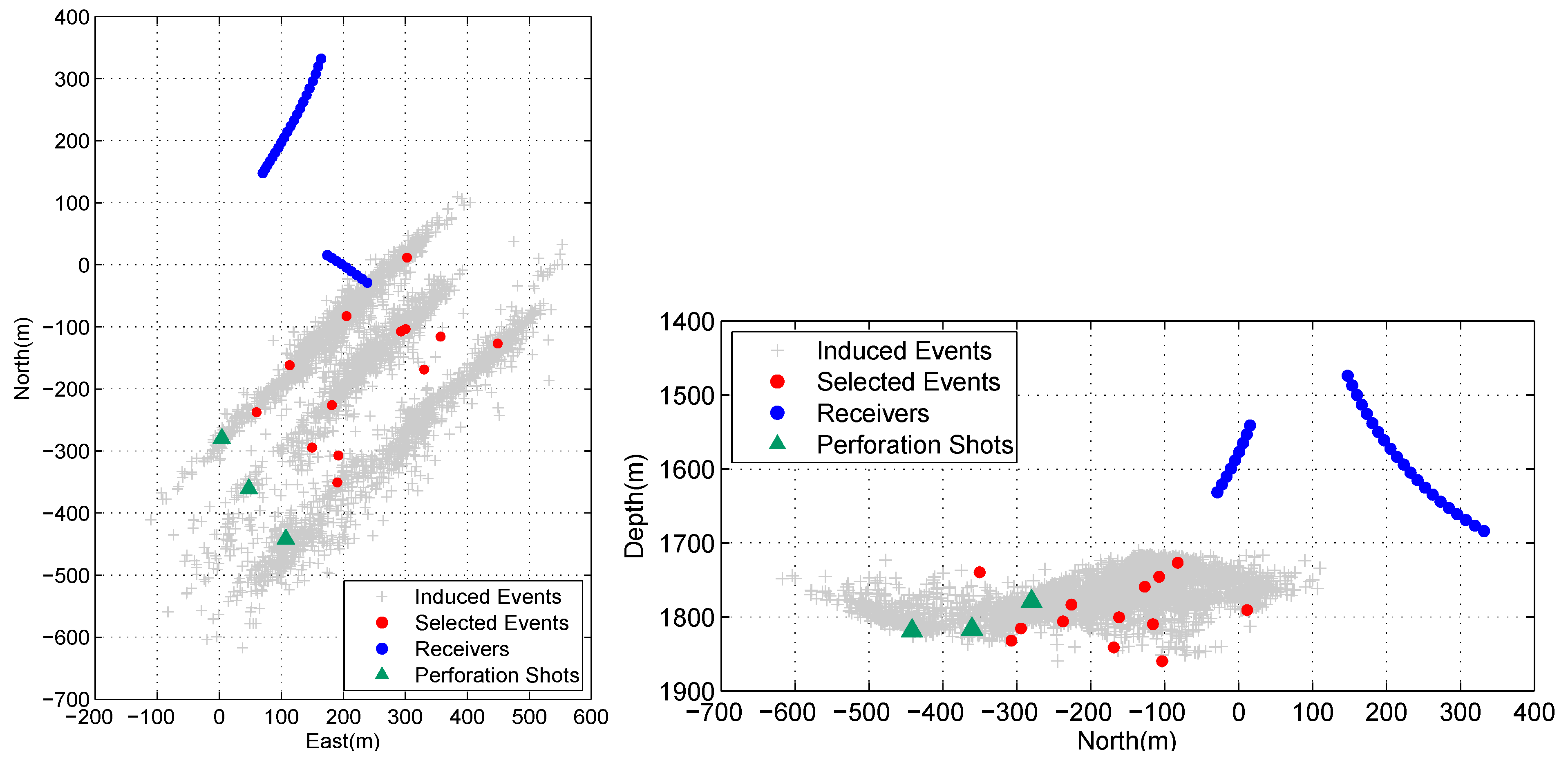
The microseismic data set originates from a 143-stage, 8-well hydraulic fracturing project, among which 3 stages were provided for this study (Figure 9). Two downhole receiver arrays with 10 and 21 geophones were deployed above the fractured reservoir at the deflecting segments of two horizontal injection wells. A total number of 3646 events were located for the three-stage treatment. Additionally, three perforation shots were provided for calibrating the velocity model. The configuration of this monitoring system was not perfect because the azimuth aperture of the receiver arrays was a bit narrow. To minimize the uncertainties, we did not take all the events as the input of the inversion. In addition to the three perforation shots, 13 events of high signal-to-noise ratio were manually selected from 10% of the events with the largest moment magnitude as the candidates for anisotropic velocity inversion.

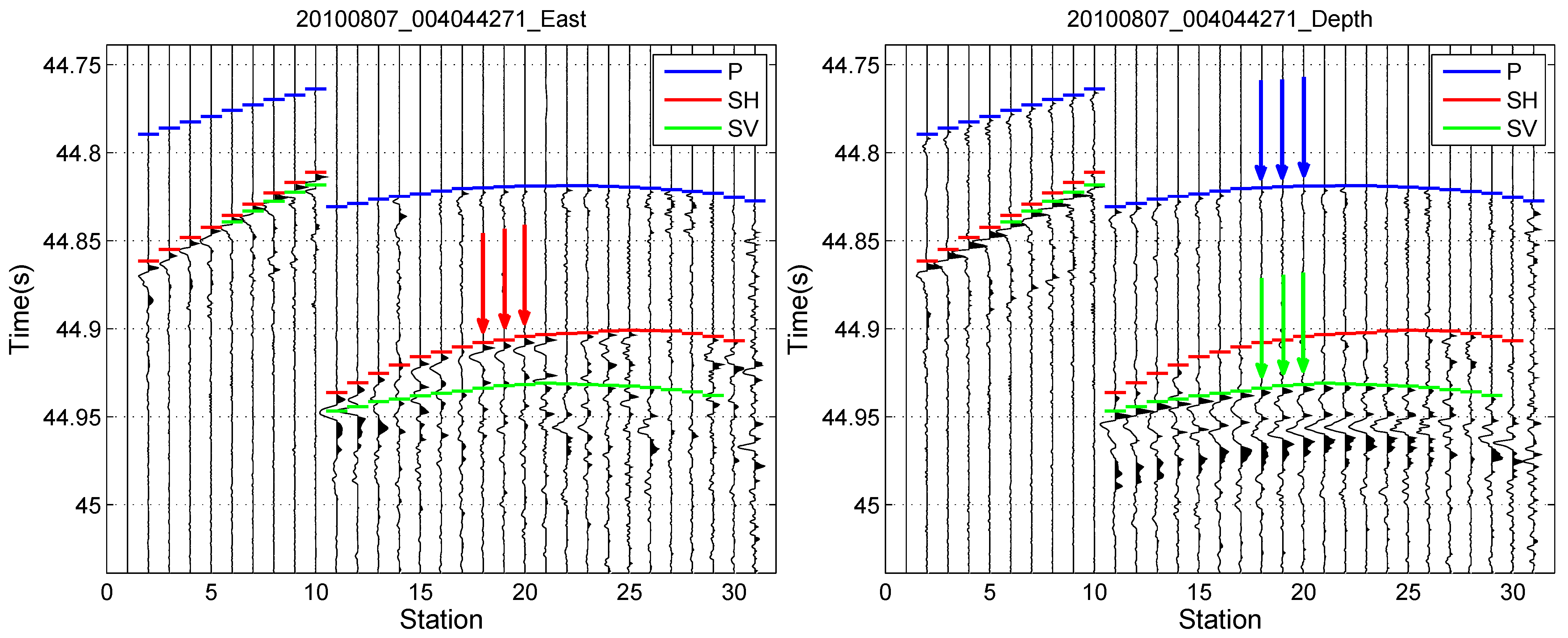
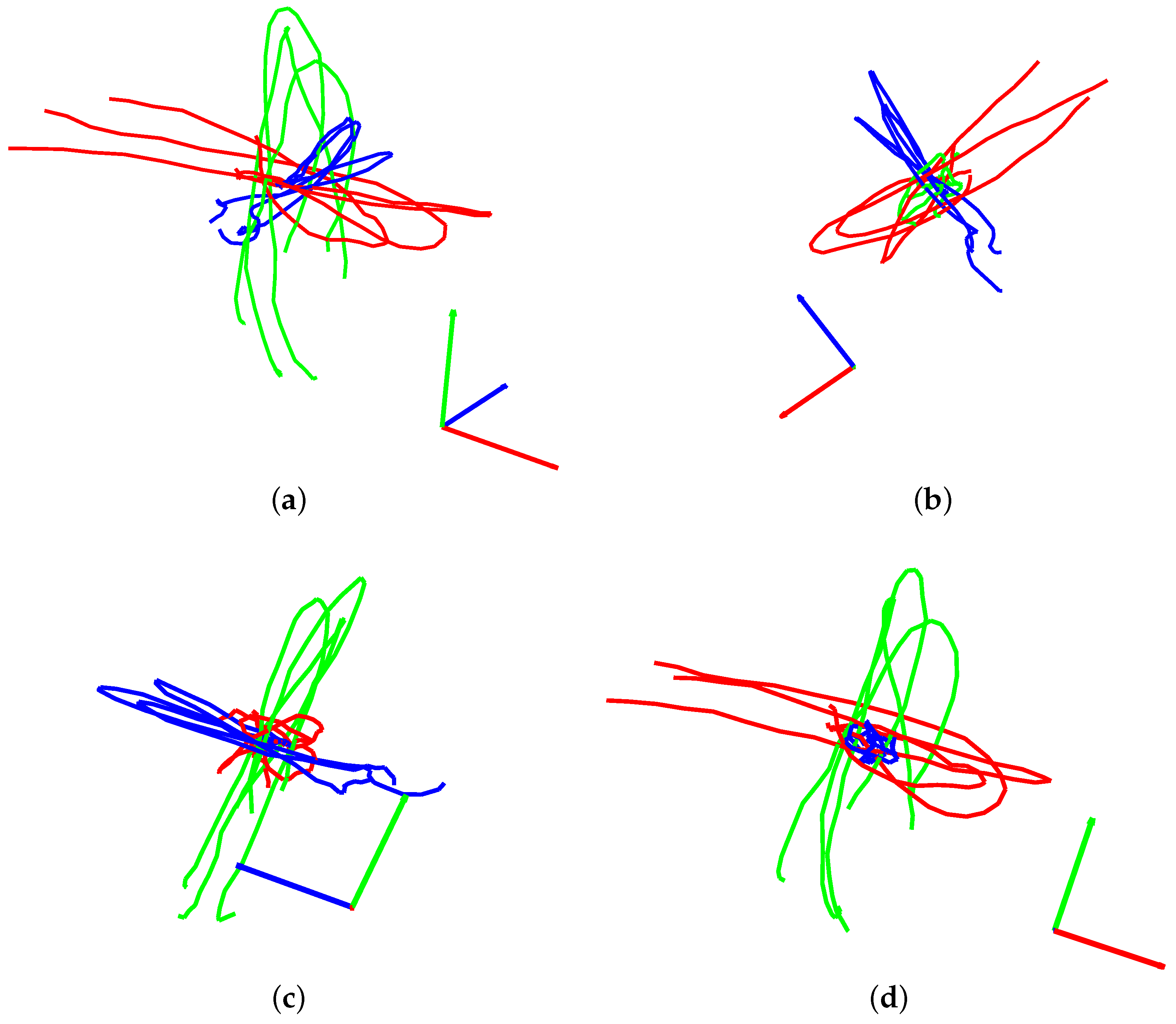
All 13 of the events presented extremely clear first arrivals, which were manually picked via seismograms. Due to the strong anisotropy of shale, shear wave splitting was clearly observed in the seismograms (Figure 10). The polarizations of the P-, SH- and SV-waves were analyzed using the method proposed by Jurkevics (1988) [37]. Figure 11 shows the polarizations and hodograms of the three traces marked in Figure 10. The dominant polarizations of the SH-wave were within a near-horizontal plane, while the polarizations of the P- and SV-waves were within a near-vertical plane. The polarizations of the three waves were nearly orthogonal to each other. According to the seismic responses of transversely isotropic media and orthorhombic media, these features imply that seismic responses in the monitoring system of this study were dominated by the vertical transverse isotropy resulting from the horizontal fabric alignments, rather than from the fracture-induced anisotropy.

4.2. Methodology

Microseismic inversion for the anisotropic velocity model can be expressed as a nonlinear least-square problem with the misfit function

$$C\left(\mathbf{m}\right)=\frac{1}{2}\sum _{i=1}^N{\left(T_i^{cal}\left(\mathbf{m}\right)-T_i^{obs}\right)}^2$$

(2)

where $T^{obs}$ is the observed arrival times, $T^{cal}$ is the synthesized arrival times and N is the number of recorded arrivals. The synthesized travel time is calculated using an anisotropic ray-tracing algorithm, which is highly modified from Gajewski and Psencik (1987) [38]. The inversion problem is solved using the Gauss–Newton method. The model vector $\mathbf{m}$ is updated iteratively by

$${\mathbf{m}}_{n+1}={\mathbf{m}}_n-\alpha {(\lambda \mathrm{diag}\left({\mathbf{H}}_a\right)+{\mathbf{H}}_a)}^{-1}\nabla C\left({\mathbf{m}}_n\right),$$

(3)

where $\lambda$ is the damping factor, ${\mathbf{H}}_a$ is the approximated Hessian matrix, $\nabla C\left({\mathbf{m}}_n\right)$ is the first order derivative (or Fréchet derivative) of the misfit function, $\alpha$ is the step length along the updating direction and diag(H_a) represents the diagonal matrix consisting of the diagonal elements of H_a. The approximated Hessian matrix ${\mathbf{H}}_a$ and the damping factor $\lambda$ are used to precondition the searching direction, which remarkably accelerates the convergence of the misfit function and stabilizes the multi-parameter inversion. The damping factor $\lambda$ is empirically derived via trials and the step length $\alpha$ is determined using a parabolic searching procedure.

A 1D VTI model is used, considering the limited spatial scale of the downhole microseismic system and the sedimentary background of shale gas reservoirs. The lateral heterogeneities within the layers are dismissed, while the vertical gradients of transverse isotropic parameters are kept when calculating the synthesized traveltime. The originally provided isotropic velocities $v_{p0}$ and $v_{s0}$ are derived from the VSP survey and fit the sonic logs very well. To minimize the complexity of the inversion problem, $v_{p0}$ and $v_{s0}$ are not optimized further in the inversion, but fixed as given parameters. The model vector being iteratively updated only consists of the Thomsen parameters of each layer [${\epsilon }^{\left(l\right)}$, ${\delta }^{\left(l\right)}$, ${\gamma }^{\left(l\right)}$]. Considering the coupling between the hypocenter parameters and the velocity model, the source location (x, y, z) and the triggering time T₀ are not inverted simultaneously with Thomsen parameters, but updated at the beginning of each iterative step using the new velocity model.

5. Results

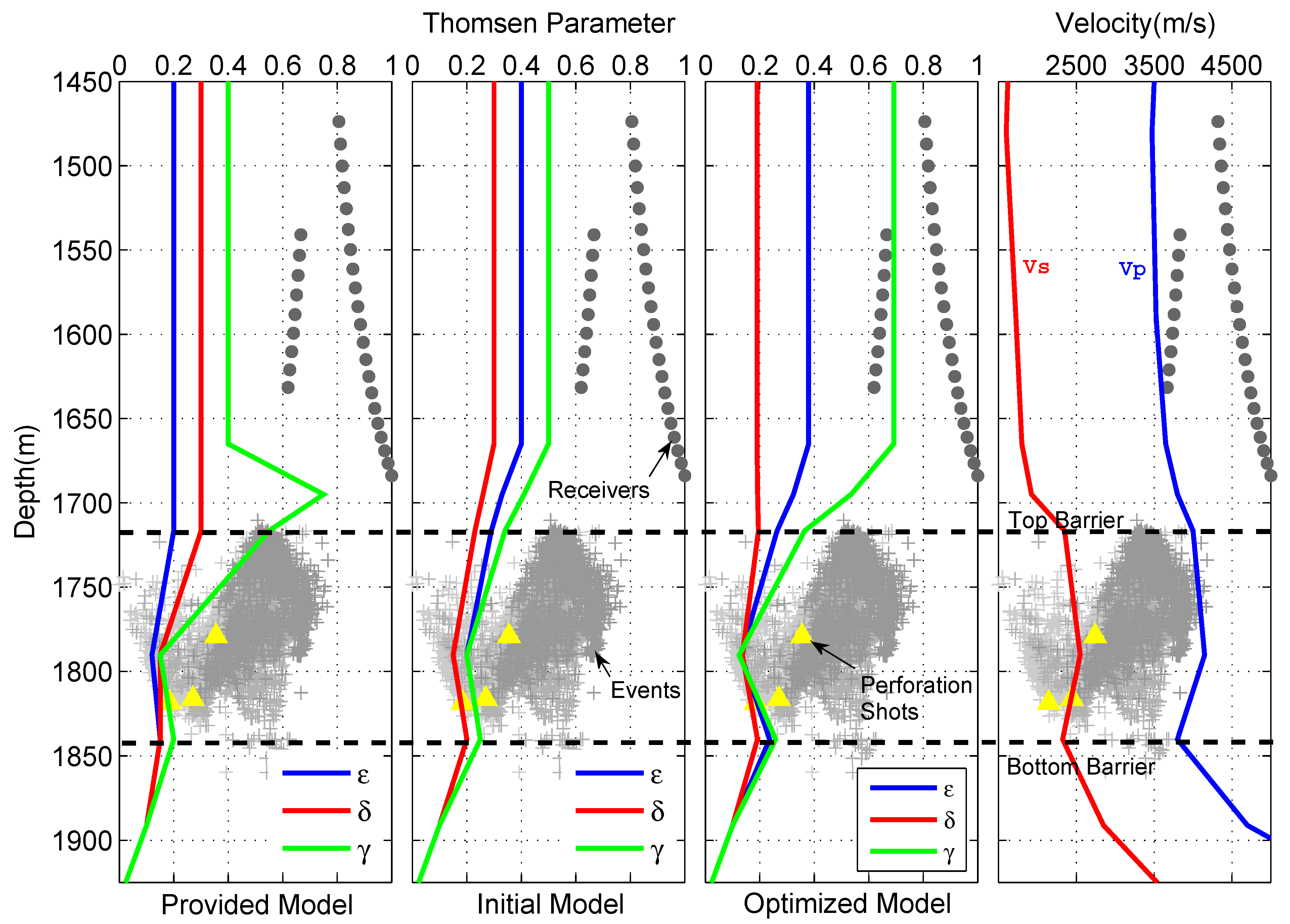
5.1. Optimization of Fabric Anisotropy

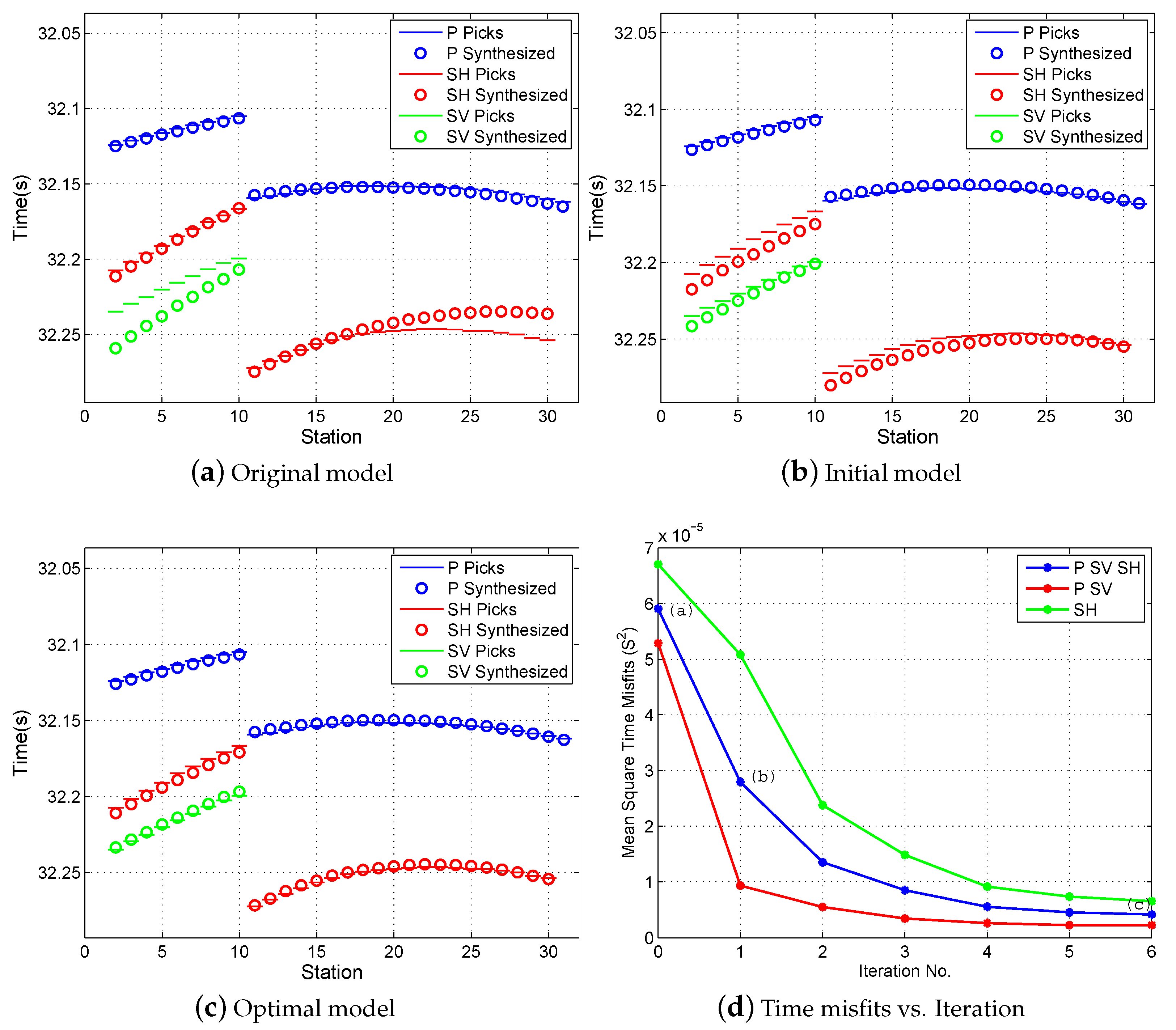
Figure 12 shows the process of optimizing the Thomsen parameters, from the originally provided model to the finally optimized model. Firstly, the original model is assessed according to the experimental knowledge of the fabric anisotropy in shale, as discussed in the section on the Fabric anisotropy of shale.

In the original model, the Thomsen parameters $\epsilon$ seem too small compared with $\delta$, especially in the upper clay-rich shale formation, which is expected to express strong fabric anisotropy. As the experimental studies show, the Thomsen parameters $\delta$ scatter within a narrow range around zero and are generally smaller than $\epsilon$, especially in the strong anisotropy range (Figure 8b). In addition, there is a sharp increase of $\gamma$ within a narrow depth interval, but no increase of $\epsilon$, which is not physically reasonable considering the correlation between $\epsilon$ and $\gamma$ (Figure 8a).

Then, the initial model was constructed for further optimization according to the semi-quantitative relationships between the fabric anisotropy of shale and clay and kerogen contents, as revealed via experimental studies (see Table 2). With the geological and physical constraints, the unreasonable aspects in the originally provided model do not exist in the initial model. An accurate initial model is essential in solving the nonlinear seismic inversion problem.

Finally, an iterative gradient-based inversion was implemented to obtain the optimal Thomsen parameters. As expected, the optimized model showed a large contrast in terms of fabric anisotropy between the clay-rich and quartz-rich shales. High fractions of clay result in a strong fabric anisotropy in the upper shale formation, whereas the quartz-rich shale gas reservoirs show a much weaker fabric anisotropy. The Thomsen parameter $\gamma$ in the overlying shale formation seems to have been somewhat overestimated. The percentage of velocity anisotropy in Horn River shales can be up to 40%.

The optimization can also be illustrated by the decrease in the time misfit between the observed and synthesized arrival times (Figure 13). The originally provided model leads to the poorest match of first arrivals compared with the initial and optimal models, especially the mismatch of SV and SH arrivals due to the large $\delta$ and the unreasonable perturbation in the $\gamma$ curve (Figure 13a–c). With the geological and physical constraints, the initial model remarkably reduces the time misfit, even without further optimization (Figure 13d). The optimal velocity model produces a good match of first arrivals and reduces the time misfit by about 65% compared to the original model.

5.2. Time and Location Misfits

To evaluate the optimized fabric anisotropy of Horn River shales, the microseismic events of one stage are located using the grid searching method. Figure 14 shows the event locations corresponding to the initial model and the optimized model. The perforation shot is also relocated to assess how it fits the true location. In the map view, the event cloud shows a typical long, narrow ellipse with the perforation shot at one end. In the section view, the events are sorted in two layers, probably due to the mechanical stratigraphy of the reservoir. When the initial model is used, the relocated perforation shot deviates greatly from the true location, either in the horizontal or depth directions. After optimization, the relocated perforation shot is shifted much closer to the correct position, which means a significant improvement in the event locations.

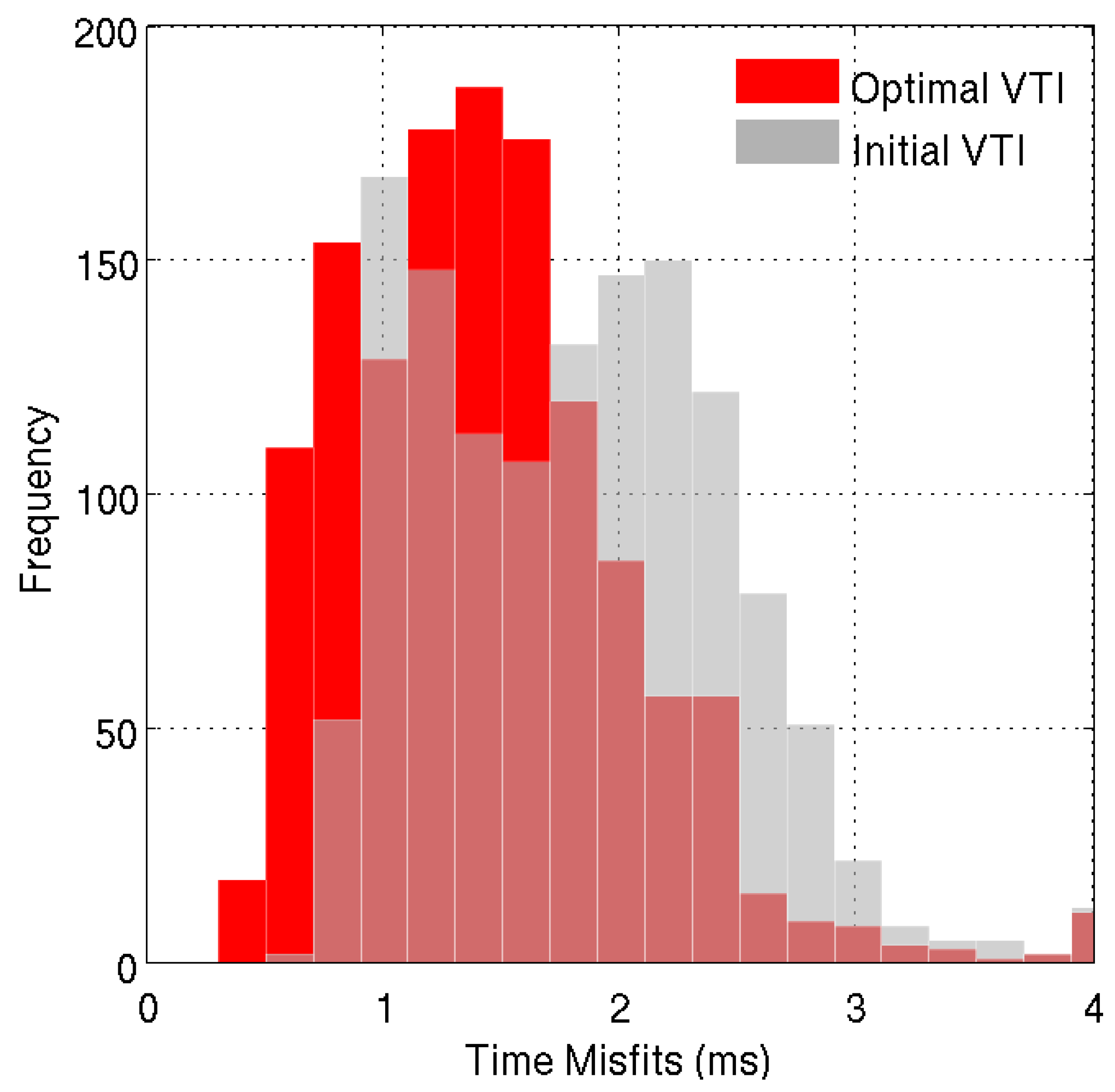
The statistic distributions of time misfits also demonstrate improvements in the event locations (Figure 15). The average time misfit of event clouds is reduced by about 0.4 ms after the optimization. The histogram of time misfits corresponding to the optimal model shows a more reasonable log-normal distribution, which means time errors are randomly distributed around the average value.

6. Discussion

6.1. Comparison with Laboratory Measurements

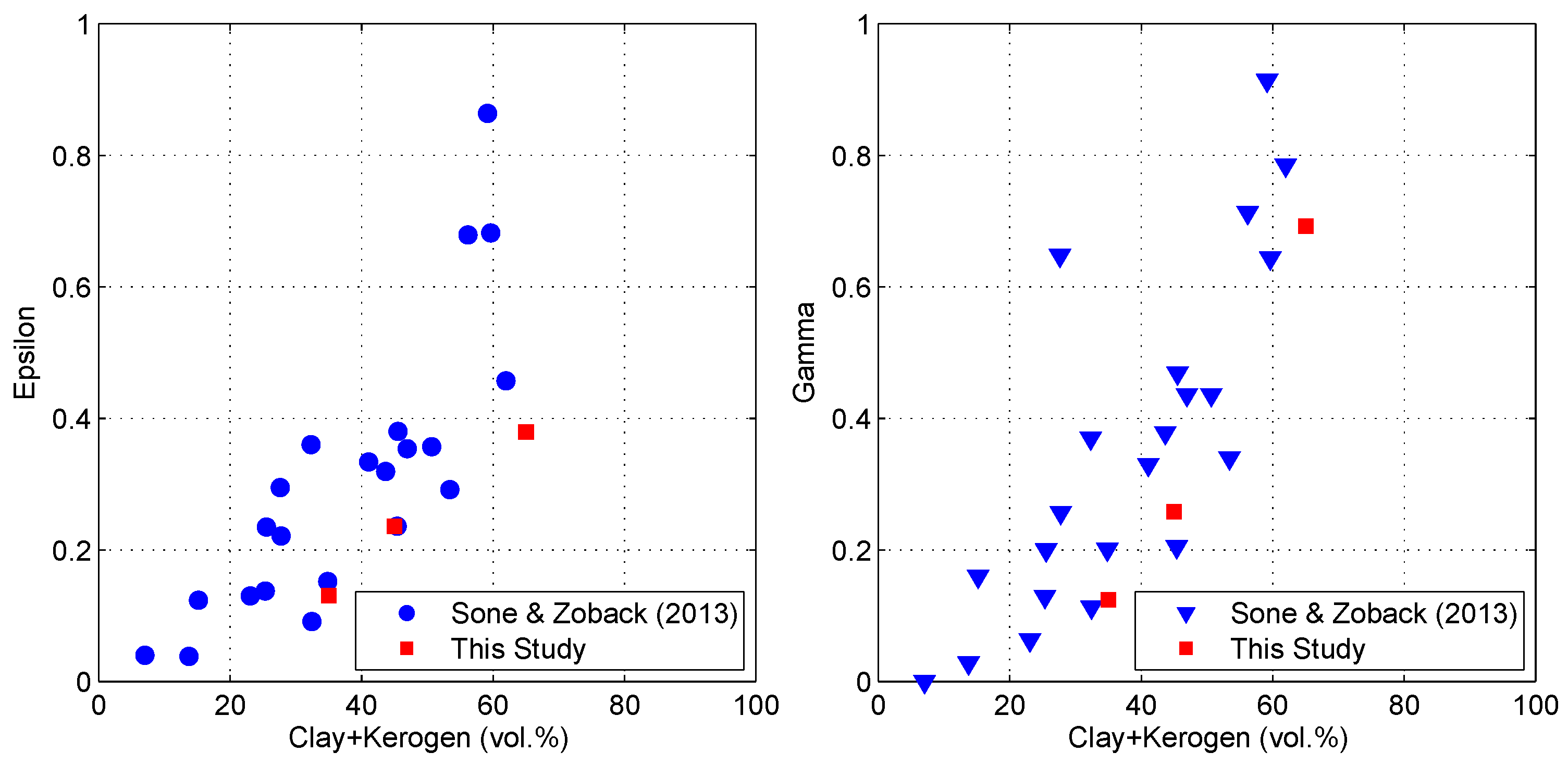
The fabric anisotropy derived from the downhole microseismic data set in this study is compared with the laboratory measurements of shale anisotropy published in previous studies (Figure 16 and Figure 17). The Thomsen parameters $\epsilon$ and $\gamma$ of Horn River shales show a strong positive correlation, which is consistent with laboratory measurements. The values of $\epsilon$ and $\gamma$ are exactly within the narrow fan-shape area that is outlined by the experimental data, except the $\gamma$ of the overlying shale formation, which seems to be slightly overestimated. The Thomsen parameters $\delta$ of Horn River shales are all positive and have no correlations with $\epsilon$ and $\gamma$. The values of $\delta$ scatter within a narrow range defined by the experimental data and are generally smaller than $\epsilon$, especially in the strong anisotropy range.

As observed in laboratory measurements, the degree of the fabric anisotropy in Horn River shales strongly depends on the clay and kerogen volume content. Although the values of the clay and kerogen contents are approximately estimated using the published data (see Table 2), the positive correlations between $\epsilon$, $\gamma$ and the clay and kerogen content are surprisingly consistent with the experimental measurements (Figure 17).

In spite of the similar features of fabric anisotropy in both the microseismic and laboratory measurements, several disagreements can be observed in the comparisons. The values of the Thomsen parameters $\epsilon$ and $\gamma$ obtained using microseismic data are slightly smaller than the laboratory results for the same contents of clay and kerogen (e.g., Figure 17). In addition, the negative values of the Thomsen parameter $\delta$ are not observed in microseismic measurements (e.g., Figure 16). Such discrepancies may reflect the influences of the frequency gap between the microseismic and laboratory measurements. Because of the limit scale of the rock sample, the measurements in the laboratory can only be conducted in the ultrasonic frequency band (MHz) [39], while the microseismic frequency can reach hundreds of Hz at most. The propagation of ultrasonic waves is affected by the fine-scale mineral fabric more strongly than by the microseismic wave, and thus can produce higher anisotropy. Microseismic measurements of shale anisotropy are conducted in the seismic frequency band in situ. Therefore, the obtained results are more reasonable for further seismic applications.

6.2. Implications for the Development of Shale Gas Reservoirs

The spatio-temporal distribution of microseismic events is the primary information used to depict the propagation of an artificial fracture network during hydraulic fracturing operation and to determine the parameters of the stimulated volume [40,41,42]. According to the study of Horn River shale, the percentage of velocity anisotropy can be up to 40% for P-wave. This would result in a large misfit of microseismic event locations if the shale anisotropy is not taken into account in data processing. As a consequence, ignoring shale anisotropy can bias the spatio-temporal distribution of microseismic events and mislead the hydraulic fracturing strategy.

In addition, shale anisotropy has a strong impact on the interpretation of the source mechanisms of microseismic events. The geometry and shear-tensile types of individual hydraulic fracture can be derived from the source mechanism of microseismic events [43]. Numerical modeling studies show that only 10% anisotropy around the source region can artificially change the observed fracture type from pure shear type to tensile shear type [44]. The optimized VTI model obtained in this study shows that the minimum fabric anisotropy of the shale gas reservoir in the Horn River basin is about 17%. Therefore, the fabric anisotropy of shale should be taken into account when investigating the source mechanisms of microseismic events in shale gas reservoirs.

Besides the intrinsic fabric of shale, the preferred oriented fracture set is another source of shale anisotropy, which usually causes azimuth anisotropy [45]. Shale formation with the horizontal fabric and vertical fracture set can be represented using the orthorhombic (ORT) model instead of the VTI model [46]. Although the magnitude of the fracture-induced anisotropy is much weaker than the fabric anisotropy in shale, its impact on microseismic data processing and interpretation should be evaluated and eliminated if necessary. Based on the results of this study, we will further develop the method to address the issue of fracture-induced azimuth anisotropy in shale gas reservoirs.

7. Conclusions

In this paper, we propose a geology- and physics-constrained approach to estimating shale anisotropy using a downhole microseismic data set and apply it to the real data acquired during the hydraulic fracturing of the Horn River shale gas reservoir.

The geological analyses and rock physics experiments on the fabric anisotropy of shale play crucial roles in building the initial model, minimizing the uncertainties and evaluating the results. In the Horn River basin, the geological analyses show that the mineral compositions of gas-bearing shales are dominated by quartz (up to 87%), while the overlying shale serving as the fracture barrier is clay-rich (an average of 70%). By integrating the geological information and experimental studies, the fabric anisotropy can be initially estimated for Horn River shale. This preliminary model is used as the initial model in further gradient-based optimizations.

The optimized model shows the expected large contrast in the fabric anisotropy between clay-rich and quartz-rich shale. A high fraction of clay mineral results in strong fabric anisotropy in the upper Fort Simpson shale, whereas the quartz-rich shale gas reservoirs (Muskwa and Otter Park shales) show much weaker fabric anisotropy. The percentage of velocity anisotropy in Horn River shales can be up to 40%. The optimized VTI model reduces the time misfit remarkably, by about 65% compared to the originally provided VTI model. The time misfits corresponding to the optimal model clearly show a more reasonable log-normal distribution, which means randomly distributed errors. The event locations are significantly improved, as indicated by the relocated perforation shot.

The fabric anisotropy of shale obtained from the downhole microseismic data set is comparable with laboratory measurements. This demonstrates that downhole microseismic monitoring, as a quasi in situ experiment, has the potential to contribute to better understanding subsurface anisotropy beyond laboratory measurements. Since the microseismic measurement of shale anisotropy is conducted in the seismic frequency band, the obtained results are more applicable to further seismic applications.