Abstract
Renewable energy sources (RESs) and electric vehicles (EVs) have been introduced as efficient technologies to address environmentally friendly and sustainable energy sources. However, the widespread integration of distributed renewable sources into the power grid and the growing adoption of EVs pose new challenges for distribution network operators. These challenges necessitate careful management to mitigate their impacts, particularly in meeting the additional demand arising from EV charging. To achieve these targets, it is necessary to strategically integrate RESs and EVs. This study focuses on the optimal allocation and energy management of distributed energy resources (DERs) and electric vehicle parking lots (EVPLs), taking into account the inherent uncertainty in the output power of these resources. Notably, parking lots (PLs) utilize vehicle-to-grid (V2G) technology of EVs and aggregate and inject their power into the distribution system. Therefore, EVs as a motion type of energy storage system play a significant role, especially in the on-peak hours. The optimization problem is addressed using the salp swarm algorithm (SSA) while adhering to operational constraints related to the power system, as well as both DERs and EVPLs. The main goal is to simultaneously enhance the technical, economic, and environmental performance of the system, by solving a multi-objective optimization problem. The effectiveness of this approach is evaluated using the IEEE 33-bus distribution system, with the study considering five different scenarios. The simulation results reveal that the planned deployment of DERs, given their proximity to the load centers, has effectively mitigated the overload impacts resulting from EVs’ charging. Furthermore, the implementation of a demand response program (DRP), cooperatively with the aforementioned resources, has significantly improved all key operating indicators of the system.
1. Introduction
In recent years, global progress, government policies to reduce environmental pollution, and limitations on fossil fuels have led to the recognition of renewable energy sources (RESs) and electric vehicles (EVs) as new active energy sources in the power system [1]. Unscheduled utilization of RESs and EVs may bring new challenges for the distribution network, such as the reduction of power quality, increasing power losses, and voltage variations, in addition to an increase in the operation cost. So, the negative impacts of these sources on the network performance are unavoidable, while effective integration of them is essential in the sustainable development of the power distribution networks [2].
Based on research findings, EVs are parked for about 90% of the day [3], making them readily available as motion energy storage devices. This utilization of EVs for energy storage aligns with the concept known as vehicle-to-grid (V2G). With V2G capabilities, EVs can actively manage the flow of power, either injecting it into or receiving it from the distribution network. Consequently, this introduces new opportunities for integrating EVs into the power network through effective power management strategies [4].
The increase in EVs’ production, driven by their remarkable efficiency, has led to an increased demand for the installation of parking lots (PLs) [5]. Also, the growing recognition of the technical, economic, and environmental benefits of renewable power plants has prompted extensive efforts to integrate them into the grid [6]. Thus, their optimal allocation holds a significant impact on enhancing the quality of the electrical grid parameters. On the other side, the coordinated utilization of microgeneration resources, wind turbines (WTs), and photovoltaic (PV) arrays alongside EVs has emerged as a fundamental strategy for achieving decarbonization, restructuring energy systems, and accelerating power system development [7].
This integration equips the distribution system operator (DSO) with two adaptable units for power generation and storage, offering profitable opportunities. To fully obtain the benefits of these resources, it becomes imperative for the DSO to determine the optimal sizes and locations of EV parking lots (EVPLs) and RESs. This decision-making process forms a crucial aspect of efficient energy management, facilitating the realization of the potential advantages that these resources bring to the system. Consequently, the challenge of strategically allocating EVPLs and RESs falls objectively into the scope of the DSO [8,9].
Moreover, demand response programs (DRPs), serving as a viable technology to use the consumers’ efficiency in optimal network management, provide the context that encourages active consumer participation in enhancing power system performance. These programs have the capability to reduce the required demand, especially during critical situations. Therefore, due to its benefits for both customers and networks, different types of this program, namely price-based and incentive-based, have gained more attention in this area [10].
A few scholars have directed their focus toward the coordinated integration of EVs and DERs into distribution systems, as evident from references [11,12,13,14,15,16,17,18,19,20,21,22]. Ref. [13] specifically addressed the optimal placement of distributed generation (DG) and PLs to minimize distribution network power losses, regardless of the uncertainty concerning these resources’ output power. In references [11,12,14,18], a single-objective optimization approach was employed for the allocation of PLs and RESs by considering the main aim of reducing the system’s voltage fluctuations and power losses. In [15], an enhancement was made by incorporating a reliability index into the existing objective set of references [11,12,14,18]. This was achieved through a more precise EV model that took into account the inherent uncertainty related to the power output of these resources.
Ref. [16] opted to use a real urban area in China as the test system for the deployment of DGs and EVPLs. To achieve a more ideal convex optimization model, they employed linearized Distflow equations with the objective of cost minimization. A hybrid optimization approach is proposed in [17] to determine the best placement and capacity of RESs and fast-charging EVPLs. The primary goal of this research is to minimize energy losses and voltage fluctuations in the power system network. Additionally, it aims to reduce land costs while maximizing the capacity to serve a maximum number of EVs with minimal installation costs for the PLs.
Ref. [19] introduces an integrated framework to optimize the allocation of plug-in electric vehicles (PEVs) charging stations, RESs, and distributed energy storage systems (DESS) within distribution networks. The formulation covers an objective function aimed at maximizing the overall annual cost of energy. The variables driving decision making within the model include the placements and capacities of PEV charging stations, RESs, and DESS. Furthermore, the formulation addresses the inherent uncertainties associated with both PEV charging demand and RES unit output generation. A DSO-oriented strategy was designed in [20] to assess the hosting capacity of renewable-based DGs and EVs within distribution systems. This strategy involved a multi-period formulation to account for the impact of EVs, DG power generation, and demand consumption variability. In order to maximize the size of DGs and EVs, operational resources were optimized. This process focused on optimizing the generation curtailment and charging patterns of EVs, aiming to prevent technical limit violations and minimize energy losses.
A model for the rearrangement of distribution networks concerning PEVs and wind power generation sources is proposed in [21]. The presented model is characterized as a stochastic model employing the Monte Carlo method to simulate scenarios associated with vehicle uncertainties. The objective function of the problem is the switching cost, purchasing electricity from the transmission network, and generating electricity through distributed sources. In [22], a two-stage model was developed to evaluate the management of PEV parking and RESs. The examination analyzed the effects of size, site, and type of RESs on the effectiveness of the PL and distribution network, aiming to maximize the profit of the PEVs.
So far, all of the articles have defined a single-objective function, by just focusing on one of the economic or technical parameters; however, it is undeniable that both techno-economic objectives are of paramount significance. Moreover, deploying demand-side management approaches in this area has remained a huge research gap. Therefore, the main contribution of the current research will be focused on bridging these research gaps.
This paper aims to simultaneously identify the optimal location and capacity of DERs and EVPLs within the distribution system considering DRPs. This approach considers the uncertainties related to RESs, EVs’ owners’ behavior, and the power output from PLs. Needless to say, the EVs under study possess V2G capabilities in addition to grid-to-vehicle (G2V) technology.
The objective functions of the problem are classified into two major categories including technical and economic. The technical objective function consists of the energy losses and voltage deviation reduction, while the economic objective comprises the cost of providing energy by DGs, the cost of energy transported from the upstream network, the cost of energy trading from/to the EVs in PLs, and the cost of greenhouse gas emissions. Therefore, in this paper, an attempt is made to improve all the system’s technical, economic, and environmental criteria.
The multi-objective optimization problem is solved using the salp swarm algorithm (SSA), taking into consideration the operational constraints arising from the power system, DERs, and EVs, all in the presence of time-varying loads and prices. To achieve this, the paper also considers optimal charging/discharging patterns for EVs, enabling them to provide network support during on-peak load periods. The proposed methodology is assessed using the IEEE 33-bus distribution system under five noticeable scenarios. The results demonstrate that integrating DRPs into the simultaneous management of EVs and DERs leads to improvements across all operational parameters of the system.
2. Modeling Formulation
2.1. EV Modeling
To effectively capture the integration of EVs into power systems, it is imperative to account for four key components that need to be determined. These components include the anticipated mileage, energy consumption during distance traveled, expected duration of EVs’ occupancy in parking facilities, and the initial state of charge (SOC) of the EVs. It is important to note that these parameters exhibit variability and lack constant values. To apply this uncertainty, the modeling of EVs was undertaken using probabilistic functions, a topic that will be developed in the subsequent sections, as referenced in [15,23,24].
2.1.1. EVs’ Expected Mileage
Utilizing the log-normal distribution function enables the modeling of anticipated vehicle mileage. Consequently, the random variable denoted as N must be determined using the following equation, which adheres to the Box–Muller technique.
In Equation (1), the variables u1 and u2 represent two distinct and independent random variables originating from a uniform distribution that spans the interval (0, 1). The expected mileage’s stochastic value can be obtained by referencing statistical data by Equation (2).
Within Equation (2), µm and σm denote the mean and standard deviation parameters associated with the specific probability distribution function. Additionally, Md represents the expected mileage achieved by EVs. The values of µm and σm can be derived by investigating the historical statistical data on EVs’ travel distances, as outlined in Equation (3).
In Equation (3), µmd and σmd signify the statistical record-derived mean and standard deviation for EV mileage, with assumed values of 40 miles and 20 miles, respectively.
2.1.2. EVs’ Energy Consumption
The energy consumption of EVs is another crucial parameter in the modeling process, as it helps determine the energy demand for EV charging and the subsequent increase in the network’s load compared to its prior state. This calculation is facilitated through Equation (4).
In the aforementioned context, Em signifies the energy consumption of the EVs. Additionally, α and β represent fixed coefficients associated with the specific EV type, while KEV denotes the portion of electrical energy directed into the EV’s battery. The highest attainable mileage of an EV when its battery is fully charged is denoted as Mdmax and can be determined through the following calculation:
In Equation (5), BCAP is the ultimate battery capacity, while the demand for charging each EV can be clarified through Equation (6).
2.1.3. Expected Availability Time of EVs in the PL
The third parameter concerns the expected duration of EV availability in a PL, which is dependent on the behaviors of the EVs’ owners. To simulate the arrival and departure times of EVs parked in a PL, a probabilistic function established in Gaussian distribution has been utilized. The estimation of arrival and departure times is determined by the following probabilistic function:
In the equation mentioned earlier, N1 and N2 denote random variables generated as per Equation (1), while µarrival and σarrival indicate the mean and standard deviation characterizing the arrival times of EVs, as derived from historical data. Furthermore, µdeparture and σdeparture correspond to the mean and standard deviation associated with the departure times, respectively. The constraint in this relation is that tdeparture must be greater than tarrival. If this requirement is not fulfilled, the times are generated from the beginning as probabilities. After constructing the probabilities of these times, the probability duration of EVs stopping in the PL is calculated according to the following relationship:
2.1.4. Initial SOC of EVs
In numerous research, the initial charge of EVs is typically examined as a constant value expressed as a percentage of the battery capacity. Nonetheless, there is uncertainty regarding the actual initial charge values for EVs. In the current investigation, we adopted an approach by modeling the SOC of EVs independently for charging and discharging modes within PLs. This modeling is achieved through the utilization of the normal distribution function. Needless to say, that are, respectively, the standard deviation and mean of the normal distribution function related to the initial charging state of the EVs.
To this extent, by correctly choosing the parameters of the probability distribution function, it is possible to estimate the initial charge of the EVs in such a way that the EVs entering the PL to sell electricity have a random initial charge level close to the total battery capacity, and the EVs that arrive in the PL to be charged have a low and initial charge level close to the minimum allowed battery level.
By obtaining the above parameters, the expected charge level will be calculated according to the following equation:
Within Equation (10), Rch denotes the charging rate of the EV, while SOCinit signifies the initial SOC for the EV during either charging or discharging states.
Based on the preceding discussion regarding EV modeling, the trend of the ultimate energy level within the EV battery can be depicted, as illustrated in Figure 1 [14].
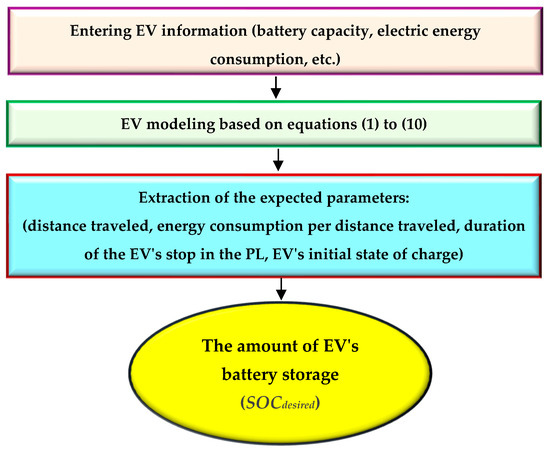
Figure 1.
The steps of EV modeling.
2.2. PL Modeling
In the subsequent section, we provide an initial explanation of the modeling process for PLs. The goal of this modeling is to ascertain the most favorable assessment of power consumption and generation in PLs. The power consumption or generation within each PL depends on factors such as the number of EVs in the network, the characteristics of their batteries, and the methodology used for modeling the presence of EVs in the PL.
2.2.1. The Predicted Percentage of EVs in the PL at Different Hours
Determining the precise number of EVs present in the PL every hour is unattainable, thus applying uncertainty to this parameter. The forecasted proportion of EVs within PL i at hour t can be described using the equation below:
In Equation (11), λi,t represents a stochastic variable employed to estimate the occurrence of EVs in the i-th PL at the time t. This variable is made to follow a normal distribution function. Meanwhile, µi,t denotes the expected percentage of EV presence at varying hours throughout the study’s time horizon, as indicated by the data in Figure 2.
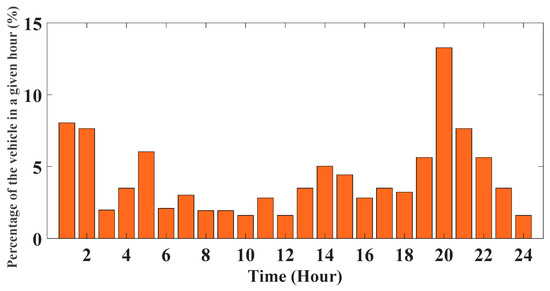
Figure 2.
The proportion of EV integration within the PLs for various periods.
2.2.2. The Consumption/Generation Power of the PL
Considering the parameters outlined, it becomes possible to compute the power consumption or generation by a PL at a given time as described in Equation (12) [10].
In the above relationship, BCAP is the capacity of j-th EV, Mi,t is the predicted percentage of EVs in i-th PL at hour t, and SOCj is the rate of energy exchange by EVs that is proportional to the initial and final charging level of the EV or in another word SOCdesired. It should be noted that to calculate the power consumed in the PL, SOCj will be determined according to what was stated in Section 2.1.4 by the EV charging scenario, and to calculate the power produced in the PL, SOCj will be determined according to the discharge scenario. By determining the production or consumption capacity of the PL, which depends on the number of EVs in the network and the type of batteries of these EVs, the allocation will be performed.
The total required PL capacity is calculated based on the number of EVs, and three PLs are considered for installation in the network. In addition to determining the location of these PLs, the optimizer algorithm will also determine the capacity of each PL based on the total power required by the EVs.
2.3. Modeling Distributed Generations
The network consists of three distributed generation varieties, each of which will be concisely introduced, followed by an exploration of the mathematical expressions forming their power generation in the following.
2.3.1. Wind Turbine and Wind Speed Uncertainty Modeling
The output power of a WT varies in response to changes in wind speed. Previous studies have indicated that the wind speed pattern at a specific location frequently conforms to a Weibull distribution. Consequently, we presume that wind speed adheres to the Weibull distribution, and its anticipated value is represented by the mean. The probability density function describing wind speed is expressed through the following Equation [25]:
In the context, v corresponds to wind speed, k denotes the shape factor, and c represents the scale factor. The Figure 3 below illustrates the Weibull wind speed distribution.
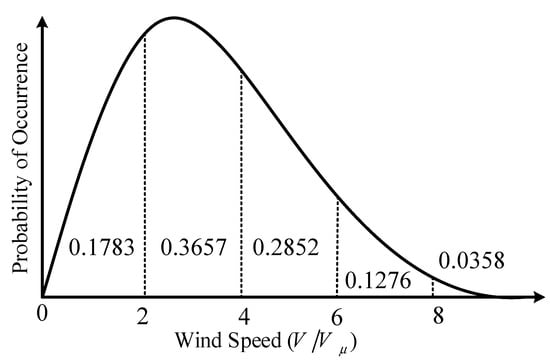
Figure 3.
The probability distribution of wind speed [26].
Using the particular wind speed distribution with the wind speed-to-power conversion function, we can derive the power distribution for the WT, in which the wind speed-to-power conversion function is as follows:
where Pw, Prated, vci, vr, and vco signify the wind turbine output power in kW, the rated power output, the cut-in wind speed, the rated wind speed, and the cut-out wind speed, respectively.
2.3.2. Solar Cell and Solar Radiation Uncertainty Modeling
Essentially, the photovoltaic power output depends on solar radiation. The hourly radiation distribution at a specific location is often characterized by a bi-exponential distribution, which can be conceptualized as a combination of two separate exponential distribution functions. This exponential distribution can be approximated using either Weibull or log-normal probability density functions. In this context, the Weibull distribution is employed, as detailed in [27].
where g symbolizes the solar radiation measured in kW/m2, w stands for the weighting factor, k denotes the shape factor, and c1 and c2 represent the scale factors. A bi-exponential radiation distribution is illustrated in the following Figure 4:
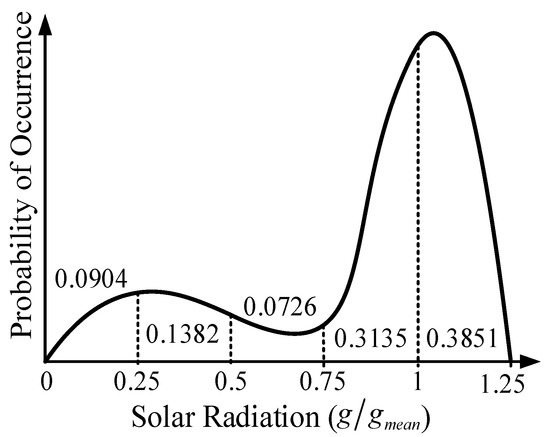
Figure 4.
The probability distribution of solar radiation [26].
By the specific radiation distribution and the radiation-to-power conversion function, the photovoltaic power distribution can be obtained. The radiation-to-power conversion function used in this research is defined as follows:
where Ppv represents photovoltaic output power in kW, ηpv corresponds to the efficiency expressed as a percentage, and spv represents the overall photovoltaic surface area in m2.
2.3.3. Microturbines
Microturbines (MTs) are small combustion turbines that can be more efficient than diesel generators by using the heat of exhaust gases. These rapid generators possess the capability to adapt to fluctuations in power demand within their designated power range, spanning from minimum to maximum power output. Furthermore, MTs can serve as standby generators when required. To incorporate the costs associated with the fuel consumption of MTs, a quadratic function is employed, and its formal expression will be provided in the section that addresses the objective function.
2.4. DRP Modeling
The DRP utilized in this research is a time-oriented model designed to optimize energy consumption by shifting it from on-peak hours to off-peak hours, resulting in decreased operational costs for the system. Figure 5 [28] illustrates this time-of-use (TOU) DRP. As depicted in Figure 5, consumers who engage in the selected DRP can transfer a specific portion of their loads to other times [26].
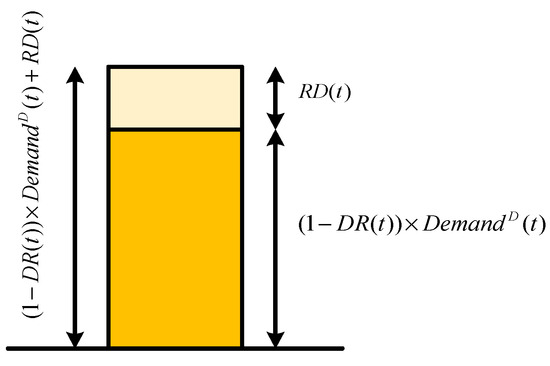
Figure 5.
The load model of the proposed time-based DRP.
The mathematical formulation of this concept is described in Equations (17) and (18), as shown below [26]:
As defined by Equations (19)–(22), the demand remains unchanged but is transferred to a different time. Equation (20) specifies that the increase in demand should not surpass a certain fraction of the base load. Furthermore, the percentage decrease or increase should not exceed a predefined value, as defined by Equations (21) and (22). This research assumes a 15% threshold.
In the context above, DemandD(t) signifies the predicted load at hour t, while DRmax and inmax denote the maximum percentage by which demand can be decreased or increased. RD(t) represents the rate of demand reduction, and Demandin(t) is the maximum permissible demand level. Moreover, in(t) represents the proportion of the maximum allowable increase in demand, and DemandDRP(t) signifies the demand after applying the DRP. Additionally, DR(t) refers to the actual demand reduction amount.
3. Problem Formulation
The aim is to simultaneously determine the capacity and optimal placement of PLs and DGs to provide energy for the electric loads consumed by consumers in the network while meeting both technical and economic objectives. The technical objectives include minimizing energy losses and voltage deviation. Additionally, the economic objectives involve assessing various costs such as charging EVs, procuring energy from EVs as mobile energy sources, purchasing energy from the main grid to meet network demands, sourcing energy from DG units, and accounting for pollution-related costs (emission of polluting gases).
3.1. Objective Function
As mentioned, the objective function in this study comprises both technical and economic components, to simultaneously minimize both while considering the essential constraints in problem solving. The variables in this problem are the optimal placement and capacity of DGs and PLs, as well as the power outputs of the DGs and the charging and discharging power of EVs. The multi-objective optimization function is defined below:
3.1.1. Technical Objective
This study examines two technical indicators within the system, specifically focusing on energy losses and the voltage profile of the system. The suggested technical objective function for this problem is presented and formulated in Equation (24), with the target of minimizing it. The technical objective function is mathematically expressed as a weighted sum of two different objectives:
The weighting coefficients, denoted as α and β, are customized to reflect the significance of each objective function. It is important to mention that before the optimization process, each objective function within Equation (24) is normalized via dividing it by its base value. This normalization serves two purposes: it avoids the dimensionless objective function and mitigates any scaling issues.
- Energy Loss (f1)
One of the primary goals in the installation of PLs and DGs within the entire network is to minimize energy losses. Consequently, the quantity of energy losses within the network is regarded as the initial component of the technical objective function, as outlined in Equation (25):
where nbr, Ri, and Ii(t) are the number of branches, the resistance of branch i, and the current flowing through the branch i at time t, respectively.
- Voltage Profile (f2)
The integration of EVPLs into the network has an impact on the current levels in the bus lines and voltage levels. In this context, the calculation of the overall voltage profile index for the network, denoted as f2, can be carried out as follows:
In Equation (45), Vn,t is the voltage of the bus n at time t.
3.1.2. Economic Objective
As explained, the economic objective function consists of cost functions associated with each generation unit, costs of energy storage and interactions, and emission costs, which are modeled by Equation (27):
- The Cost of Providing Energy by DGs (f1)
The function f1 represents the overall operational cost associated with DGs, comprising three different components. The initial part pertains to the MT’s operational costs, while the following two parts correspond to the operational costs of wind and solar power plants, respectively.
In the above-mentioned equations, PMT(t), PWind(t), and PPV(t) are the generation power of the MT, WT, and PV, respectively. The parameters a, b, and c pertain to the cost coefficients of the MT. Also, the operating cost coefficients of the WT and PV are λWind(t) and βPV(t), respectively.
- The Cost of Energy Transported from the Upstream Network (f2)
This cost of energy supply depends on the hourly price of electricity and can be calculated using the following formula:
where CGrid(t) and PGrid(t) are the grid energy price at time t and the power purchased from the upstream grid, respectively.
- Energy Trading Cost from/to the EVs in PLs (f3)
The amount of these costs depends on both the charging and discharging activities of EVs, as well as the time spent during these processes. The difference between these two costs, as described in Equation (33), represents the overall cost caused by the network due to PLs.
In the aforementioned equations, Cdch(t) and Cch(t) refer to the costs associated with discharging and charging EVs at time t, while also considering the power generation and consumption of the j-th PL at the same time t.
- The Cost of Greenhouse Gas Emissions (f4)
The emission model employed in this paper is a result of the existence of non-renewable resources and the interconnection with the primary network. This model comprises two components: the pollution cost arising from the MT and the cost associated with connecting the distribution network to the main grid [26,28].
where , , and are the weight coefficients related to the emission of pollution. Moreover, EMT(t) and EGrid(t) are the emissions of the MT and upstream grid, respectively.
3.2. Constraints
To solve the problem defined by the optimization algorithm, we require compliance with the operational restrictions that will be discussed further [15,23,24].
3.2.1. Network Equality and Inequality Constraints
- ▪
- Power balance constraint
To maintain the power balance within the analyzed system, the power generation must be equivalent to the power consumption for each hour.
where PDGi (t), PPLj (t), PGrid (t), PDemand (t), and PLoss (t) refer to the power generated by DGs, the power either generated or consumed by PLs, the electricity purchased from the primary network, the overall system demand, and power losses, respectively.
3.2.2. System Security Constraints
- ▪
- Distribution line capacity limit
Due to the thermal capacity of each transmission line, the power flowing through these lines must not exceed their allowed power limits.
where Si (t) represents the power passing through the transmission line i at time t, while Simax indicates the maximum capacity for power transmission through line i.
- ▪
- Voltage drop limit
To avoid the voltage drop, the bus voltage should be within the minimum and maximum bus voltage range.
where Vi (t) is the voltage of bus i, while Vimin and Vimax are the minimum and maximum voltage of bus i, respectively.
3.2.3. EVPL Constraints
- ▪
- Maximum EV charging and discharging power
At any time, the amount of charge and discharge of EVs’ batteries should not exceed their maximum amount.
In this context, Pch(i,t) and Pdch(i,t) represent the i-th EV’s charging and discharging power at time t. Additionally, Pch,limit(i,t) and Pdch,limit(i,t) denote the maximum allowable charging and discharging capacities for i-th EV at that moment. X(i,t) and Y(i,t) are binary variables that indicate whether the i-th vehicle is currently in a charging or discharging state.
- ▪
- Non-simultaneity of EV charging and discharging
In every scheduling period, the charging and discharging of an EV should not be performed simultaneously.
- ▪
- The limit of energy stored in the EV battery
Every hour, the storage capacity of the battery must be within the allowed range.
So that SOCimin and SOCimax are the minimum and maximum energy of the i-th EV battery, respectively.
- ▪
- Parking lot capacity constraint
Considering various factors, including the number of EVs in the analyzed region, the parking capacity must not surpass a predetermined threshold.
where CPi is the i-th PL capacity, and CPimax refers to the maximum capacity of the ith PL.
3.2.4. DG Constraints
- ▪
- Generation power capacity constraint
The constraint set for the DG units pertains to the utilization of their energy resources. This constraint defines the minimum and maximum permitted range of power generation, ensuring that all DG units operate within the prescribed power range. This condition can be formally represented by Equation (46).
where PiDG(t) represents the generated power from DG resources at time t, while PminDG and PmaxDG denote the lower and upper limits for power generation from these resources, respectively.
4. Problem-Solving Method
Heuristic optimization methods, characterized as experimental approaches, are described as efficient techniques for rapidly attaining optimal solutions to optimization problems [29]. These optimal solutions are typically unobtainable within a limited timeframe using mathematical approaches. The challenge of recognizing the locations and determining the sizes of DERs and EVPLs essentially involves a non-linear objective function subject to numerous equality and inequality constraints. Conventional optimization techniques struggle to tackle such problems while ensuring convergence to a globally optimal solution. Hence, various innovative optimization methods introduced to date can be viewed as alternative optimization approaches. In this paper, the salp swarm algorithm is adopted as an optimizer algorithm, and a concise overview of it is provided below.
4.1. Salp Swarm Optimization Algorithm
The salp swarm algorithm is classified as a social search algorithm, drawing inspiration from the social interactions observed in salps [30]. To establish a mathematical representation of the salp chain, the population is initially divided into two categories: the leader and the followers. The leader corresponds to the salp positioned at the front of the chain, while all other salps are considered followers. As the terminology suggests, the leader assumes the role of guiding the entire group, and the followers, as the name implies, trail behind each other (either directly or indirectly following the leader).
The position of the salp chain and the movement process of each salp are shown in Figure 6, where salps are randomly placed with a fixed or moving food source in a search space. It should be noted that the blue star in the figure represents food sources, and the fully shaded circles represent the leader’s salps. Salps following the leader are grayed out based on their position in the salp chain concerning the leader.
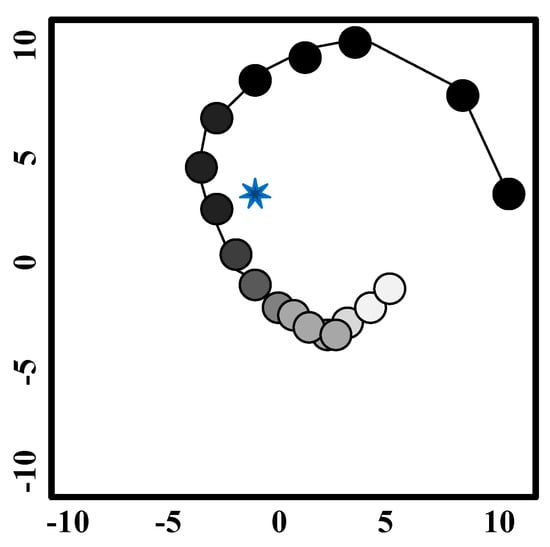
Figure 6.
Search history around food source.
Similar to other swarm-based methodologies, the salps’ positions are defined within an n-dimensional search space, where n corresponds to the number of variables inherent to the problem at hand. Consequently, the positions of all salps are stored within a two-dimensional matrix denoted as ‘x’. Additionally, it is assumed that within this search space exists a target, designated as ‘F’, which serves as the objective for the salp group. The leader’s position update is determined by the following formula:
where represents the position of the initial salp (leader) along the j-th dimension, signifies the position of the food source within the j-th dimension, while ‘ubj’ and ‘lbj’, respectively, denote the upper and lower bounds of the j-th dimension, outlining the allowable range. It should be noted that c1, c2, and c3 are random variables.
Equation (48) demonstrates that the leader’s position is exclusively updated based on the food source. The coefficient c1 holds paramount significance within the SSA, as it controls the equilibrium between exploration and exploitation, as illustrated by the following equation:
where xji is the salp position of the i-th follower in the j-th dimension, and i ≥ 2. l is the current iteration, and L corresponds to the algorithm’s maximum iteration. Parameters c2 and c3 are random numbers generated uniformly in the range [0, 1]. In fact, they determine whether the next position in the j-th dimension should trend toward positive/negative infinity or adhere to the step size. The update of the followers’ positions is likewise determined by the following formula:
Here, t denotes time, and v0 is the initial velocity and is considered equal to zero. Also, , while . Since time intervals are consistent in the optimization process, and the difference between these repeated time intervals is considered to be 1, this equation can be summarized as follows:
Therefore, by the above equations, the salp chain can be simulated.
Multi-Objective Salp Swarm Algorithm
The optimal solution for multi-objective problems is a set of solutions called the Pareto optimal set. The SSA algorithm can move salps toward food sources and update their positions during iterations. This algorithm is well-suited to solve multi-objective problems for the following reasons:
- The SSA has the ability to store multiple solutions as the best choices for multi-objective problems.
- The SSA updates the food source with the most exceptional solution so far obtained in each iteration, and for multi-objective optimization problems, there is only one best solution.
To circumvent non-local responses, the SSA can be enhanced by incorporating a storage or food source repository. This repository retains the best non-dominated solutions achieved throughout the optimization process and is similar to the multi-objective particle swarm optimization method. An illustration of the repository update mechanism is shown in Figure 7, and additional details can be found in reference [30]:
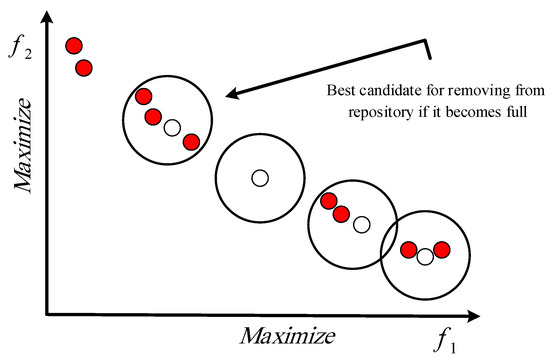
Figure 7.
Update mechanism of the repository.
The multi-objective SSA algorithm is initialized with a population of salps according to the upper and lower bands of the variables. Subsequently, this algorithm calculates target values for each salp and identifies the non-dominated response. If the repository is not at maximum capacity, the non-dominant solutions are added to the archive. However, when the archive reaches its limit, a process is initiated to eliminate solutions within a crowded neighborhood. This involves ranking and selecting solutions through a roulette wheel mechanism. Following the removal of a sufficient number of repository members, non-dominated salps can be introduced into the repository. After the repository update, a food source is chosen from the non-dominant responses in the repository with the least or the most isolated neighbors.
Similar to repository maintenance, this process involves evaluating the solutions and employing the roulette wheel technique. The next step entails the update of c1 as well as updating the positions of both leader and follower salps based on the provided formulas. If during the update process, a salp’s position falls outside the specified boundary range, it is repositioned within the range. Ultimately, all these steps are repeated, except for the initial setup phase, to satisfy the specified criteria.
4.2. Fuzzy Method
After determining the Pareto points, the optimal solution selection process involves employing the fuzzy decision making (FDM) method [31]. In this approach, each objective function (indexed as i) is expressed as a linear membership function, as specified in Equation (52):
Subsequently, the normalized membership function value denoted as μk, for solving the k-th Pareto point, is determined through the application of the following equation:
Ultimately, the most substantial membership value (μk) is selected as the optimal solution. The performance of this optimal compromise selection is depicted in Figure 8 for determining the best solution.
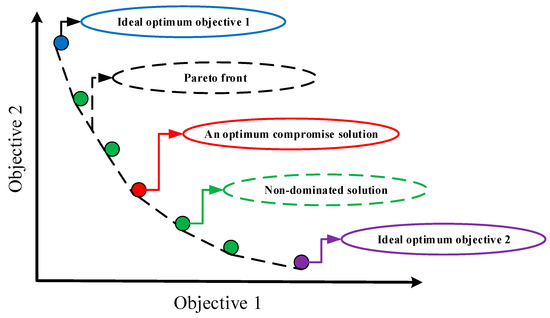
Figure 8.
Optimal compromise outline.
5. The Process of Implementing the Proposed Plan
In line with the content outlined, the process of determining both the location and the simultaneous size of PLs and DG resources in the network follows a structured procedure. Initially, essential data regarding the network, load, hourly energy prices, EV quantities, DG resources, and parameters associated with potential distribution functions are inputs. Subsequently, following the modeling of the DRP within the initial population, the SSA algorithm randomly selects the optimal positions and capacities. After simulating the demand distribution, it calculates the multi-objective function as defined in the relevant scenario. Based on the derived objective function, scores are assigned to the existing population, and the population is updated accordingly. Employing the fuzzy method and accounting for problem constraints, this iterative process continues until the optimal solution is reached. The implementation of this proposed plan is depicted in Figure 9.
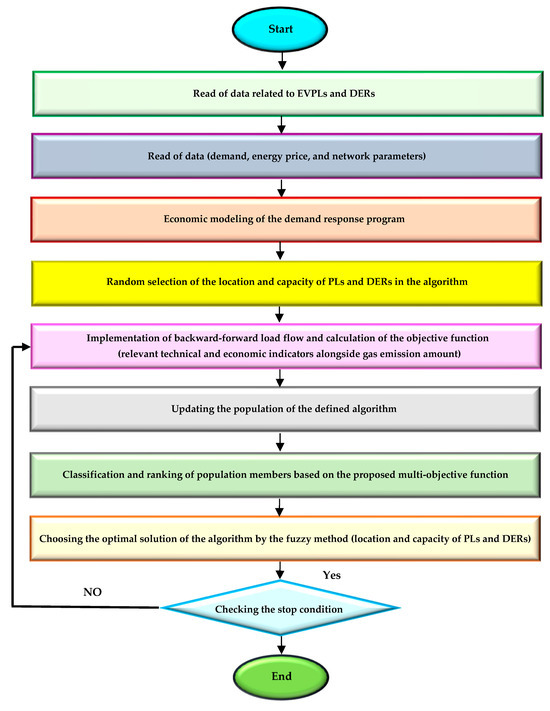
Figure 9.
Flowchart of the proposed approach.
6. Case Study
In this research, the suggested methodology is put to the test using the IEEE 33-bus distribution system to assess its effectiveness. The system under study is a radial system, whose data are shown in Table A1. To facilitate a more comprehensive assessment of the outcomes, five different scenarios were defined as follows:
- Scenario 1: Supplying the total consumption power of the distribution network by the upstream network.
- Scenario 2: Allocation of DG resources and coordinated exploitation of DG units and the network.
The resource generation limits, pollution pricing, and the selling power of DG resources are detailed in Table A2. Additionally, the parameters incorporated into the equations of MTs, wind power generation, and solar power plants align with experimental and historical data provided in Table A3 and Table A4.
- Scenario 3: Allocation of PLs and their operation alongside the network (without DGs).
As mentioned in the process of EV and PL modeling, there are several uncertainties where the parameters of these functions are according to Table A5.
To create a model for EVs, apart from the data provided in Table A5, additional factors such as the EV’s energy consumption and battery capacity are necessary, and these values depend on the EV’s specific type. In this study, four various EV models are employed in equal proportions, and their respective parameters are detailed in Table A6. It is important to note that the β index remains constant since these EVs solely rely on batteries and do not utilize fossil fuels. Lastly, the charging rate of EVs plays a significant role in the charging and discharging process.
- Scenario 4: Coordinated exploitation of DERs, PLs, and the network to optimize the multi-objective function (without considering the DRP).
- Scenario 5: Coordinated operation of DERs, PLs, and the network to minimize the multi-objective function (taking into account the DRP).
The single-line schematic of this network is depicted in Figure 10, while Figure 11 illustrates the power consumption of the network for each hour. Additionally, the electricity market price is shown in Figure 12.
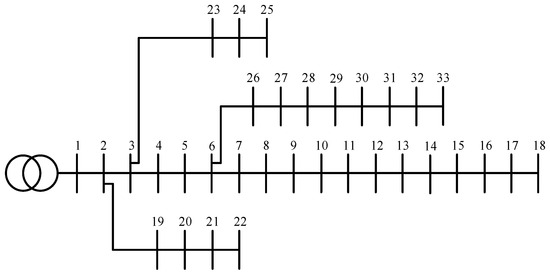
Figure 10.
Single line diagram of IEEE 33-bus distribution system.
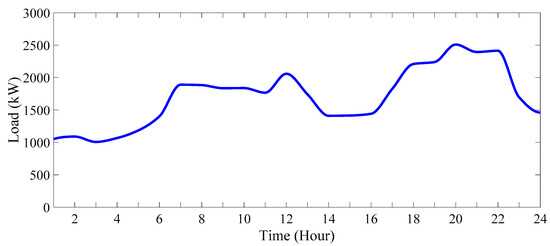
Figure 11.
Daily power curve of load.
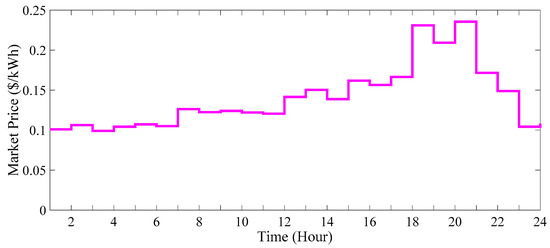
Figure 12.
Daily market price curve.
7. Simulation Results
7.1. Results of Scenario 1
In scenario 1, all the electricity required by consumers in the network is sourced from the main grid. In this case, the overall cost of supplying energy to consumers over 24 h amounts to USD 6410.1706. Of this sum, USD 6023.4041 is attributed to the cost of procuring energy from the main grid, while USD 386.7665 is associated with the cost of pollution emissions. In this scenario, a total of 9.4717 tons of CO2, 0.0250 tons of SO2, and 0.2848 tons of NOX were generated throughout the study period. The system losses and voltage deviation are equal to 4061.6 kW and 1.8283 p.u, respectively. Figure 13, Figure 14, Figure 15 and Figure 16 illustrate the status of the system buses’ voltage, power supply and balance, system operational costs, and electricity price consumption by consumers over the period of 24 h.
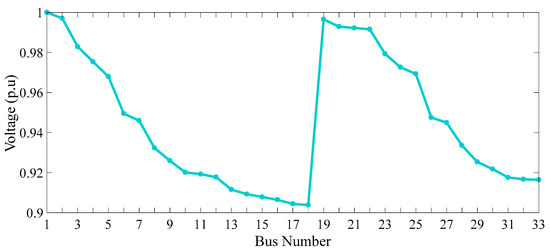
Figure 13.
Voltages of the system’s buses (scenario 1).
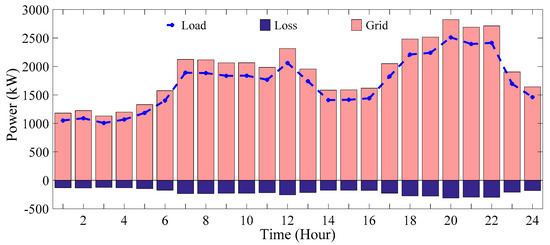
Figure 14.
The participation state of power supply sources and power balance (scenario 1).
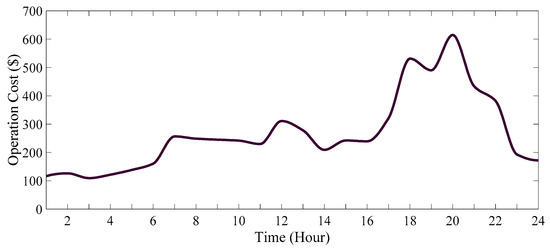
Figure 15.
The operation cost of the system in 24 h (scenario 1).
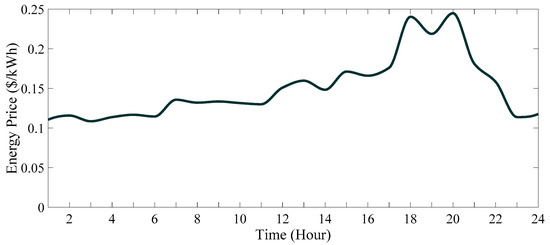
Figure 16.
The price of each kW of electricity consumed by the consumers in 24 h (scenario 1).
7.2. Results of Scenario 2
Figure 17 illustrates the placement arrangement of DG resources within the examined test network. Furthermore, the location and capacity of resources can be seen in Table 1.
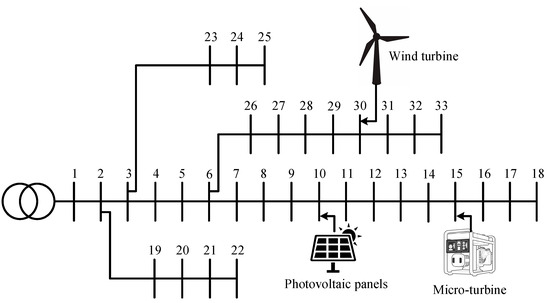
Figure 17.
The location status of DERs on the IEEE 33-bus system (scenario 2).

Table 1.
Location and capacity of DERs (scenario 2).
According to the problem’s objective function, wind and solar units are anticipated to generate USD 1,495,542 and USD 916,209 in revenue, respectively, from selling energy within the network. Additionally, the income from the sale of MT energy is projected to amount to USD 640,116. The remaining energy required by the network is provided by the main grid, incurring a cost of USD 2942.218. The pollution emissions caused by energy generation within the network result in environmental costs totaling USD 222,677. In this scenario, the overall cost of supplying energy to consumers over 24 h is USD 6,216,762. Throughout this scenario, a total of 7.0023 tons of CO2, 0.02257 tons of SO2, and 0.2453 tons of NOX are generated. The amount of system power losses and voltage deviation are calculated to be 3002.41 kW and 1.3006 p.u, respectively.
As a result of exclusively deploying DERs, operational costs are diminished by 3.0172% in comparison to the base case. Furthermore, this operational strategy has concurrently mitigated power losses by approximately 26.0781% and voltage deviation by 28.8628%. Additionally, the quantities of pollution emissions arising from both the MT and the primary grid in this scenario have decreased by around 23.2419%.
The output power of distributed renewable generation units is regarded solely as active power, and as a result, they will not inject reactive power into the network. Thus, their effect is treated as a form of negative load at the installation sites. Next, after determining the value and location of the DG for load distribution, the algorithm adjusts the power value of the DG bus (the i-th bus) according to the relationship below:
In the equation provided above, Pnewi represents the revised power consumption at the i-th bus after the incorporation of the distributed renewable generation unit. Poldi corresponds to the load power at the i-th bus before the deployment of the distributed renewable generation, while PDG signifies the active power generated by the DG. Figure 18, Figure 19, Figure 20 and Figure 21 provide visual representations of the system’s bus voltage changes, power supply and equilibrium, system operational costs, and the electricity price per kW consumed by users over a 24 h duration.
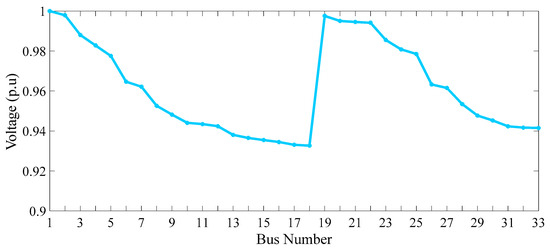
Figure 18.
Voltages of the system’s buses (scenario 2).
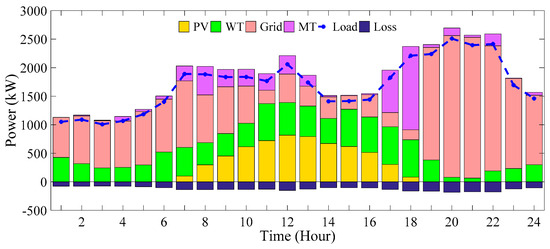
Figure 19.
The participation state of power supply sources and power balance (scenario 2).
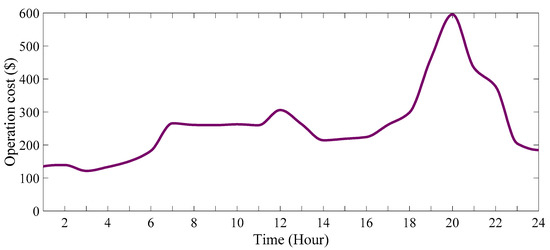
Figure 20.
The operation cost of the system in 24 h (scenario 2).
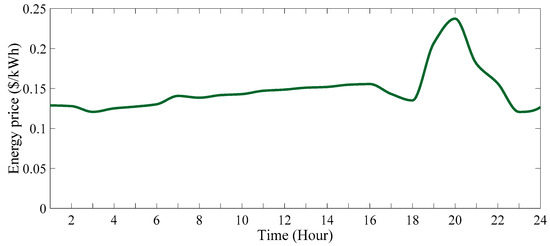
Figure 21.
The price of each kW of electricity consumed by the consumers in 24 h (scenario 2).
7.3. Results of Scenario 3
Figure 22 shows the parking lot placements within the examined test network, while the details regarding the location and capacity of resources can be found in Table 2.
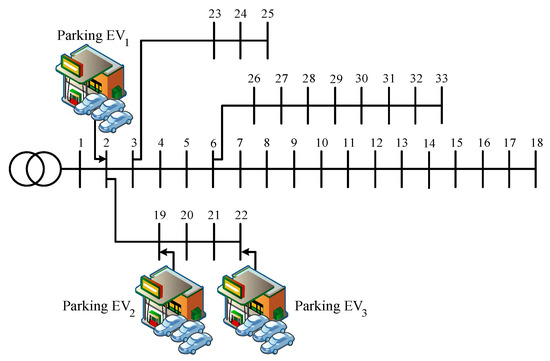
Figure 22.
The location status of PLs on the IEEE 33-bus system (scenario 3).

Table 2.
Location and capacity of PLs (scenario 3).
Within scenario 3, the EVs parked in the lots actively engage in the network’s energy management program by charging and discharging at various times. Figure 23 provides an illustrative representation of the involvement and presence of PLs and EVs in the network’s energy management program.
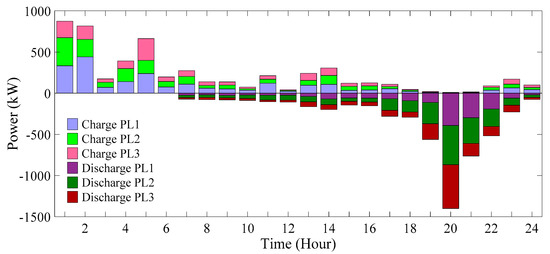
Figure 23.
Participation trend of EVPLs in 24 h (scenario 3).
As depicted in Figure 23, EV owners strategically choose their charging and discharging times based on the electricity market prices and the prevailing incentive policy. They opt to charge their vehicles during off-peak hours when electricity costs are low and discharge or sell excess energy to the grid during peak hours when prices increase. This behavior leads to an overall energy cost of USD 6757.3056 over a 24 h period. Within this cost, USD 5884.2696 corresponds to energy purchase costs from the main grid, USD 1130.6158 reflects either the cost incurred by the network due to vehicle discharging or the revenue earned by EVs’ owners and PLs, and USD 376.7547 accounts for costs tied to pollution emissions. In this particular scenario, a total of 9.1486 tons of CO2, 0.02390 tons of SO2, and 0.2761 tons of NOX are produced. Moreover, system losses reach 3752.24 kW, and voltage deviation is equal to 1.6808 p.u.
As a result of operating EVPLs, operational costs experience a 5.4154% increase relative to the base case. However, power losses and voltage deviation have reduced by about 7.6167% and 8.0676%, respectively. Furthermore, the pollution emission index has decreased by around 3.4112%.
To influence the capacity of PLs within the network, the following process is implemented:
PLs inject active power into the desired bus load based on the hourly EV charging rate and reduce the active power of the bus load in proportion to the EV discharging rate per hour.
In the above relationship, Pnewi and Poldi refer to the power consumed by the i-th bus after and before the installation of the PL, respectively. PPLch is the power used for charging EVs, and PPLdch is the power injected into the grid by the discharge of EVs.
The hourly power injection or consumption will correlate with the number of EVs present in the PL and the hourly energy prices, all while remaining below the total PL capacity. Figure 24, Figure 25, Figure 26 and Figure 27 illustrate the system’s bus voltage variation, power supply and power equilibrium, system operating costs, and per kWh electricity prices, respectively. These figures provide insight into electricity consumption by consumers over 24 h.
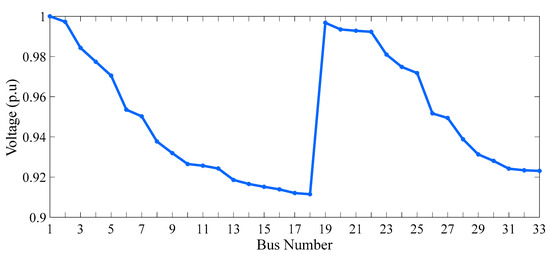
Figure 24.
Voltages of the system’s buses (scenario 3).
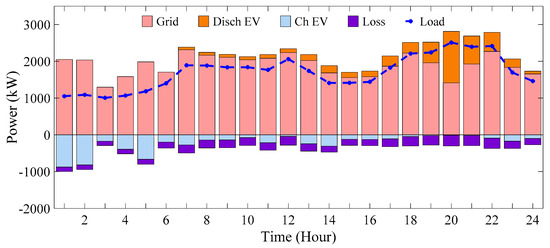
Figure 25.
The participation state of power supply sources and power balance (scenario 3).
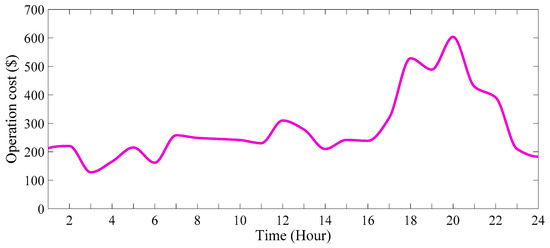
Figure 26.
The operation cost of the system in 24 h (scenario 3).
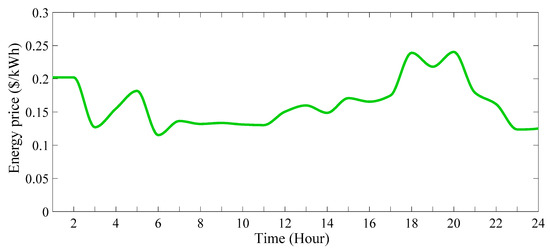
Figure 27.
The price of each kW of electricity consumed by the consumers in 24 h (scenario 3).
7.4. Results of Scenario 4
Figure 28 represents the positioning of PLs and DERs within the examined test network. Furthermore, the specific details regarding resource locations and capacities are available in Table 3.
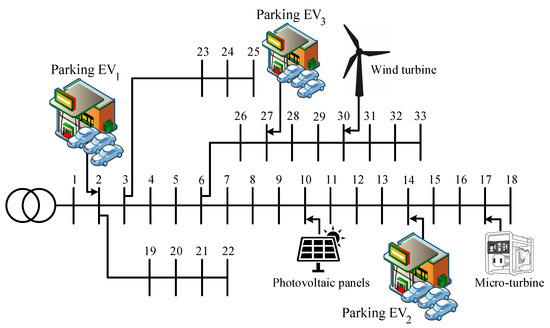
Figure 28.
The location status of DERs and PLs on the IEEE 33-bus system (scenario 4).

Table 3.
Location and capacity of DERs and PLs (scenario 4).
The trend of PL and EV participation, alongside the power generation status of distributed generation sources, is depicted in Figure 29 and Figure 30.
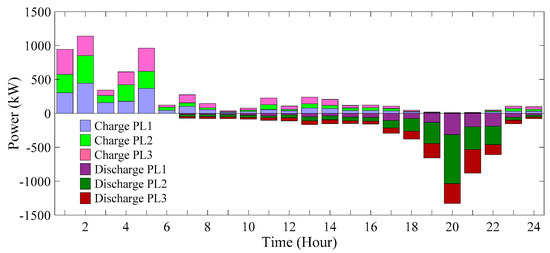
Figure 29.
Participation trend of EVPLs in 24 h (scenario 4).
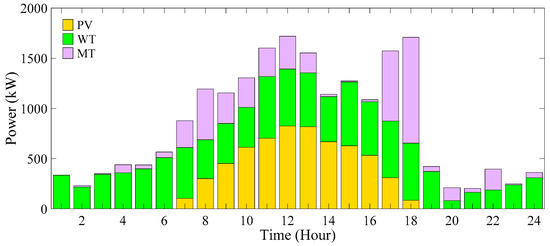
Figure 30.
Power generation changes of DERs (scenario 4).
Additionally, Figure 31 outlines the allocation of power generation from the existing resources within the network to meet power demands in scenario 4.
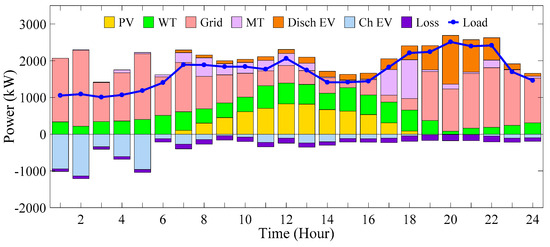
Figure 31.
The participation state of power supply sources and power balance (scenario 4).
Based on the findings, the overall energy cost and pollution-related costs have both decreased in comparison to previous scenarios, amounting to USD 5894.2688 and USD 211.9482, respectively. In this particular scenario, the emissions include 6.8004 tons of CO2, 0.02191 tons of SO2, and 0.2382 tons of NOX produced during the study period. The system power losses stand at 2737.6368 kW, and the amount of voltage deviation is equal to 0.9966 p.u.
Therefore, with the simultaneous integration of DERs and EVPLs, the overall operation cost has been reduced by 8.0482% compared to the base case. Furthermore, this framework has simultaneously alleviated power loss by 32.5971% and voltage deviation by 45.4903%. Additionally, the quantities of pollution emissions originating from both the MT and the primary grid in this scenario have decreased by around 25.4569%.
Figure 32, Figure 33 and Figure 34 provide visual representations of the system bus voltage status, system operating costs, and the price per kW of electricity consumed by consumers in 24 h.
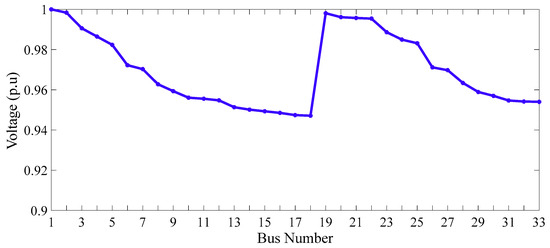
Figure 32.
Voltages of the system’s buses (scenario 4).
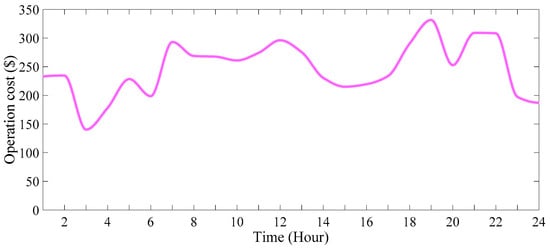
Figure 33.
The operation cost of the system in 24 h (scenario 4).
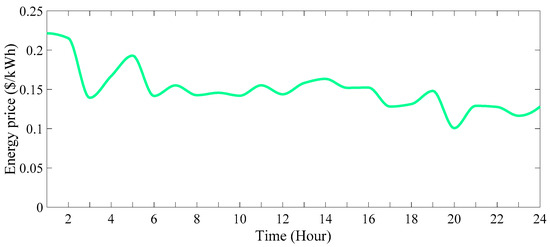
Figure 34.
The price of each kW of electricity consumed by the consumers in 24 h (scenario 4).
7.5. Results of Scenario 5
Figure 35 represents the location of PLs and DERs on the studied test network for scenario 5.
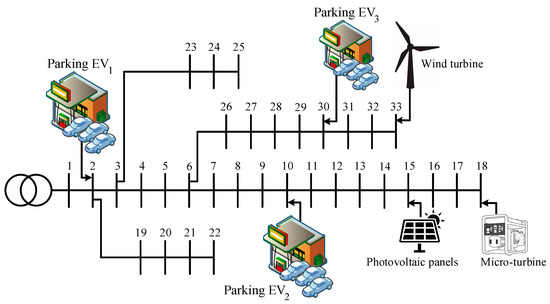
Figure 35.
The location status of DERs and PLs on the IEEE 33-bus system (scenario 5).
Figure 36 depicts the network load curve, illustrating changes before and after implementing the DRP. Additionally, Figure 37 and Figure 38 provide insights into the involvement and presence of parking facilities and EVs, and the power generation status of distributed resources. The participation strategy of units and the production power levels of DGs and PLs in the studied network under scenario 5 are presented in Figure 39. Furthermore, the location and capacity details of these resources are available in Table 4.
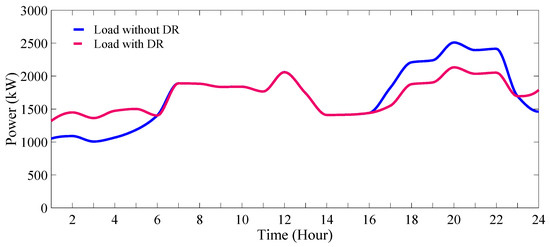
Figure 36.
System load curve before and after the implementation of the demand response program (scenario 5).
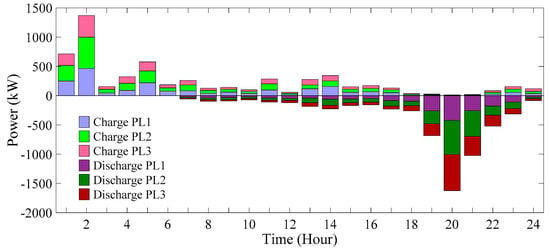
Figure 37.
Participation trend of EVPLs in 24 h (scenario 5).
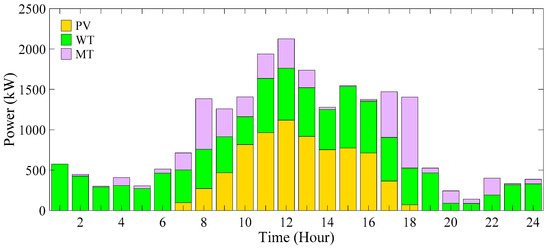
Figure 38.
Power generation changes of DERs (scenario 5).
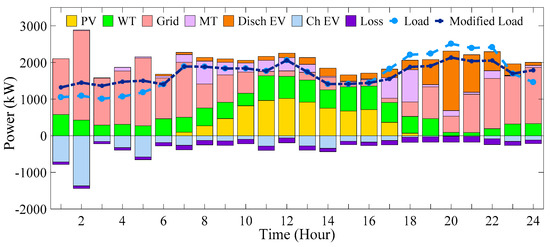
Figure 39.
The participation state of power supply sources and power balance (scenario 5).

Table 4.
Location and capacity of DERs and PLs (scenario 5).
In this particular scenario, wind and solar units are expected to generate revenues of USD 1456.5853 and USD 1056.5549 from selling energy within the network. The MT unit in the network will receive USD 572.8952 as the income for energy sales. The cost incurred from purchasing energy from the upstream network amounts to USD 2058.1914. Additionally, there is an environmental cost of USD 204.7329 associated with energy pollution within the network. Consequently, the overall cost of supplying energy to consumers over 24 h in this scenario reaches USD 5692.865. It is noteworthy that during this scenario, the network generates 5.4529 tons of CO2, 0.0144 tons of SO2, and 0.1639 tons of NOX as emissions. In addition, the system experiences losses of 2658.7104 kW and voltage deviation of 0.8244 p.u.
Therefore, by utilizing DERs and EVPLs, accounting for the DRP, the overall system cost has reached an 11.1901% reduction relative to the base case. Furthermore, this scenario due to the technologies applied has reduced power losses by 34.5403% and voltage deviation by an impressive 54.9089%. Moreover, the total pollution emission has undergone a substantial reduction of about 42% as compared to scenario 1.
Figure 40, Figure 41 and Figure 42 show the voltage changes of the system buses, system operational costs, and the price per kW of electricity consumed by consumers in 24 h.
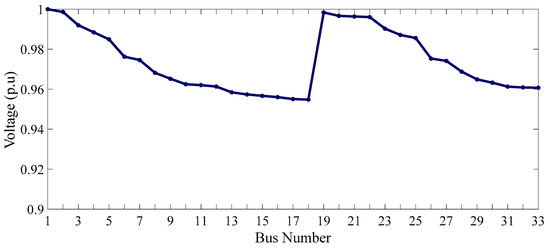
Figure 40.
Voltages of the system’s buses (scenario 5).
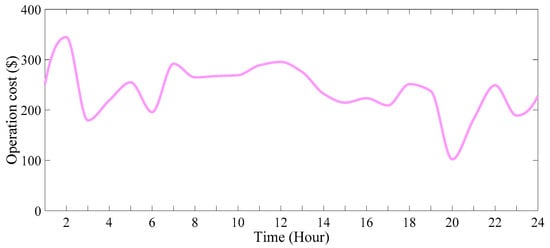
Figure 41.
The operation cost of the system in 24 h (scenario 5).
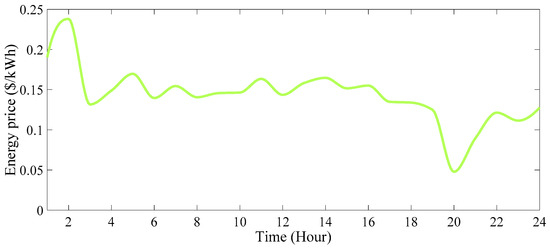
Figure 42.
The price of each kW of electricity consumed by the consumer in 24 h (scenario 5).
7.6. Scenario Comparison
Figure 43 and Figure 44 depict the changes in the average system operation cost and energy price over the studied period. Moreover, the voltage fluctuations in system buses across different scenarios are represented in Figure 45. As expected, scenario 5 is the one that has the best result of all scenarios.
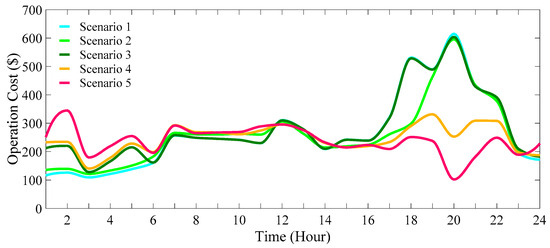
Figure 43.
The operation cost of the system during 24 h in different scenarios.
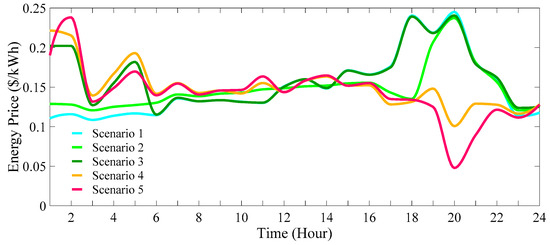
Figure 44.
The price of each kW of electricity consumed by the consumers during 24 h in different scenarios.
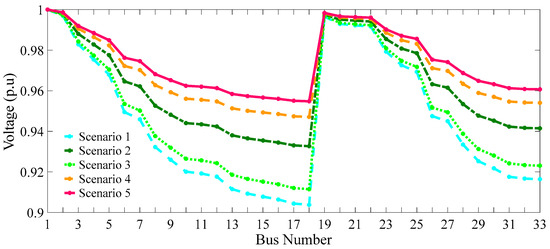
Figure 45.
Voltages of the system’s buses in different scenarios.
To gain a comprehensive understanding of the simulation conducted across the five examined scenarios, the results are summarized in Table 5. As indicated in this table, the scenario with the largest system losses, standing at 4061.6 kW, is scenario 1, while the scenario with the smallest system losses, which is 2658.7104 kW, is related to scenario 5. As expected, the voltage deviation in different scenarios has a similar trend to the power losses. As it turns out, the amounts of power losses and voltage deviation in scenario 3 are larger than in scenario 2, and it is because of the charging state of the EVs (G2V). This table also illustrates that the scenario with the high-rise average hourly system operation cost is scenario 3, amounting to USD 281.5544, while the scenario with the most economical average system operation cost is scenario 5, totaling USD 237.2027. Furthermore, the scenario with the highest average price of consumed electricity is scenario 3 with 0.162714 (USD/kWh). Conversely, scenario 5 has the lowest average price of consumed electricity, which is USD 0.14306 (USD/kWh). In summary, EVPLs can improve the technical and environmental criteria of the system in comparison to the base case (scenario 1). However, the optimal operation of DERs and EVPLs simultaneously can also reduce the operation cost of the system alongside significantly reducing the power losses and voltage deviation. To sum up, scenario 5, characterized by the coordinated utilization of EVs and DERs considering DRPs, emerges as the most favorable system performance option from both technical and economic perspectives.

Table 5.
Results of the simulation performed in 5 scenarios.
8. Conclusions
The current research assessed the efficient management and allocation of different energy resources within the IEEE 33-bus distribution test system considering the DRP. The effects of various DERs, EVPLs, and DRPs on the technical, economic, and environmental indicators of the system were evaluated by analyzing different scenarios. The salp swarm algorithm was employed to optimize the multi-objective function, determining both the optimal capacity and placement of DERs and EVPLs. Once the Pareto points have been identified, the process of selecting the optimal solution entails the utilization of the FDM method. The simulation results indicate that the proposed scheme could lead to a dramatic enhancement in the operational aspects of the system based on its design and the technologies applied.
In other words, EVPLs have the potential to enhance both technical and environmental aspects of the system compared with the base case (scenario 1). Moreover, the simultaneous utilization of DERs and EVPLs can effectively decrease the system’s operational costs, substantially reducing power losses and voltage deviation. In addition, scenario 5 which incorporates the coordinated integration of EVPLs and DERs, taking into account DRPs, presents as the most advantageous choice for system performance, considering all techno-economic and environmental indexes. Consequently, with the simultaneous operation of DERs and EVPLs, considering the DRP, the operation cost is reduced by 11.1901% compared to the base case. Moreover, this operating plan, in addition to a smoother demand curve, has reduced power losses and voltage deviation by about 34.5403% and 54.9089%, respectively. Moreover, the amounts of pollution emissions produced through the MT and main grid in the last case have reduced by about 42% in comparison to the base case.
The remarkable results can be summarized as follows:
- ➢
- The presence of EVPLs solely has improved technical and environmental indexes.
- ➢
- With the optimal allocation of DERs and EVPLs, in addition to the appropriate scheduling of EVs, all the techno-economic and environmental criteria of the network have been significantly improved.
- ➢
- The integration of the DRP alongside DERs and EVPLs can have an efficient effect on reducing the operation cost of the system and improving the power quality parameters of the network. Also, the implementation of the DRP can provide the basis for increasing the use of DERs and, as a result, reducing pollution emissions.
- ➢
- In addition to flattening the load profile, charging EVs during off-peak periods and discharging them during on-peak hours will result in economic benefits for owners of EVs.
Future work will be conducted to create novel paths in this matter including the following:
- ▪
- Investigating the effects of EVs and DGs on reactive power losses.
- ▪
- Considering the precise traffic model of EVs in the EVPL allocation and management area.
- ▪
- Determining the framework of the contract provisions between the PLs and the EVs, such as the penalty for the EV’s early departure from the PL or failure to provide the requested power by the PL, etc.
- ▪
- Allocation of PLs and DERs simultaneously with capacitors and other reactive power compensator devices such as static VAR compensators (SVC).
- ▪
- PL and DER energy management by considering the effect of different seasons on the technical and economic parameters of the studied issue.
- ▪
- Solving the problem of allocating PLs and DERs by considering the possibility of injecting reactive power into the network by EVs’ batteries, as well as RESs, and participating them in the reactive power management market.
Author Contributions
Conceptualization, L.B.; methodology, L.B.; software, L.B.; validation, I.K.; formal analysis, I.K.; investigation, L.B.; resources, L.B.; data curation, L.B.; writing—original draft preparation, L.B.; writing—review and editing, I.K.; visualization, L.B.; supervision, I.K.; project administration, I.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Canada National Sciences and Engineering Research Council through the Laval University, Grant ALLRP567550-21.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
IEEE 33-bus system parameters.
Table A1.
IEEE 33-bus system parameters.
| Transmitter Bus | Receiver Bus | R(Ω) | X(Ω) | P (kW) | Q(kVar) |
|---|---|---|---|---|---|
| 1 | 2 | 0.0922 | 0.0470 | 100 | 60 |
| 2 | 3 | 0.4930 | 0.2511 | 90 | 40 |
| 3 | 4 | 0.3660 | 0.1864 | 120 | 80 |
| 4 | 5 | 0.3811 | 0.1941 | 60 | 30 |
| 5 | 6 | 0.8190 | 0.7070 | 60 | 20 |
| 6 | 7 | 0.1872 | 0.6188 | 200 | 100 |
| 7 | 8 | 0.7114 | 0.2351 | 200 | 100 |
| 8 | 9 | 1.0300 | 0.7400 | 60 | 20 |
| 9 | 10 | 1.0440 | 0.7400 | 60 | 20 |
| 10 | 11 | 0.1966 | 0.0650 | 45 | 30 |
| 11 | 12 | 0.3744 | 0.1238 | 60 | 35 |
| 12 | 13 | 1.4680 | 1.1550 | 60 | 35 |
| 13 | 14 | 0.5416 | 0.7129 | 120 | 80 |
| 14 | 15 | 0.5910 | 0.5260 | 60 | 10 |
| 15 | 16 | 0.7463 | 0.5450 | 60 | 20 |
| 16 | 17 | 1.2890 | 1.7210 | 60 | 20 |
| 17 | 18 | 0.7320 | 0.5740 | 90 | 40 |
| 2 | 19 | 0.1640 | 0.1565 | 90 | 40 |
| 19 | 20 | 1.5042 | 1.3554 | 90 | 40 |
| 20 | 21 | 0.4095 | 0.4784 | 90 | 40 |
| 21 | 22 | 0.7089 | 0.9373 | 90 | 40 |
| 3 | 23 | 0.4512 | 0.3083 | 90 | 50 |
| 23 | 24 | 0.8980 | 0.7091 | 420 | 200 |
| 24 | 25 | 0.8960 | 0.7011 | 420 | 200 |
| 6 | 26 | 0.2030 | 0.1034 | 60 | 25 |
| 26 | 27 | 0.2842 | 0.1447 | 60 | 25 |
| 27 | 28 | 1.0590 | 0.9337 | 60 | 20 |
| 28 | 29 | 0.8042 | 0.07006 | 120 | 70 |
| 29 | 30 | 0.5075 | 0.2584 | 200 | 600 |
| 30 | 31 | 0.9744 | 0.9630 | 150 | 70 |
| 31 | 32 | 0.3105 | 0.3619 | 210 | 100 |
| 32 | 33 | 0.3410 | 0.5302 | 60 | 40 |

Table A2.
Values of generation restrictions, pollution price, and selling power of DERs.
Table A2.
Values of generation restrictions, pollution price, and selling power of DERs.
| Pmax (kW) | Pmin (kW) | Selling Price (USD/kWh) | CO2 (kg/MWh) | SO2 (kg/MWh) | NOx (kg/MWh) | DG Type |
|---|---|---|---|---|---|---|
| 1500 | 10 | 0.125 | 720 | 0.0054 | 0.23 | Microturbine |
| 1000 | 0 | 0.153 | 0 | 0 | 0 | Wind turbine |
| 1500 | 0 | 0.153 | 0 | 0 | 0 | Photovoltaic |

Table A3.
Values of microturbine parameters.
Table A3.
Values of microturbine parameters.
| Cost Coefficients | Power Plant | ||
|---|---|---|---|
| c | b | a | Microturbine |
| 0.002 | 0.0133 | 10 | |

Table A4.
Wind turbine and photovoltaic parameters along with distribution function parameters.
Table A4.
Wind turbine and photovoltaic parameters along with distribution function parameters.
| C= 5/2 | K= 5/8 | vr = 12 m/s | vci = 3 m/s, vco = 25 m/s | Wind Turbine |
| Ꞃpv = 18 | Spv= 8000 m2 | K1 = 5.5, K2 = 6.8 | C1= 8/1, C2 = 2.6 | Photovoltaic |
In these tables, the values of MT cost coefficients (a,b,c), the minimum wind speed required to produce power (vi), the maximum wind speed at which the turbine can generate power (vo), the rated speed of the wind turbine (vr), the area of the solar power plant (Spv), and the shape and scale coefficients for the distribution function related to wind and solar power plants are stated in detail.

Table A5.
Values of EV modeling parameters.
Table A5.
Values of EV modeling parameters.
| Value | Parameter | Value | Parameter |
|---|---|---|---|
| 26 | The mean of the normal distribution function of the initial charge (charge mode) | 20 | The standard deviation of the log-normal function () |
| 1/7 | The standard deviation of the normal distribution function of the initial charge (charge mode) | 40 | Mean of the log-normal function () |
| 72 | The mean of the normal distribution function of the initial charge (discharge mode) | 1 | The electric energy input to the battery |
| 2/6 | The standard deviation of the normal distribution function of the initial charge (discharge mode) | 7 | EV arrival time mean ( |
| 13/7 | The mean of the normal distribution function of the EV presence in the PLs | 1/73 | EV arrival time standard deviation () |
| 4/5 | The standard deviation of the normal distribution function of the EV’s presence in the PLs | 18 | EV departure time mean ( |
| 1 | The constant of EV energy consumption (β) | 1/73 | EV departure time standard deviation () |

Table A6.
Specifications of different EV classes.
Table A6.
Specifications of different EV classes.
| EV Type | Market Share (Percent) | BCAP (kWh) | α (kWh/mile) |
|---|---|---|---|
| 1 | 25 | 10 | 0/3790 |
| 2 | 25 | 12 | 0/4288 |
| 3 | 25 | 16 | 0/5740 |
| 4 | 25 | 21 | 0/8180 |
References
- Ravi, S.S.; Aziz, M. Utilization of Electric Vehicles for Vehicle-to-Grid Services: Progress and Perspectives. Energies 2022, 15, 589. [Google Scholar] [CrossRef]
- Ray, S.; Kasturi, K.; Patnaik, S.; Nayak, M.R. Review of electric vehicles integration impacts in distribution networks: Placement, charging/discharging strategies, objectives and optimisation models. J. Energy Storage 2023, 72, 108672. [Google Scholar] [CrossRef]
- Osório, G.J.; Gough, M.; Lotfi, M.; Santos, S.F.; Espassandim, H.M.; Shafie-Khah, M.; Catalão, J.P. Rooftop photovoltaic parking lots to support electric vehicles charging: A comprehensive survey. Int. J. Electr. Power Energy Syst. 2021, 133, 107274. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Shayeghi, H.; Pirouzi, S.; Shafie-Khah, M.; Catalão, J.P.S. Coordinated flexible energy and self-healing management according to the multi-agent system-based restoration scheme in active distribution network. IET Renew. Power Gener. 2021, 15, 1765–1777. [Google Scholar] [CrossRef]
- Afshar, S.; Macedo, P.; Mohamed, F.; Disfani, V. Mobile charging stations for electric vehicles—A review. Renew. Sustain. Energy Rev. 2021, 152, 111654. [Google Scholar] [CrossRef]
- Barman, P.; Dutta, L.; Bordoloi, S.; Kalita, A.; Buragohain, P.; Bharali, S.; Azzopardi, B. Renewable energy integration with electric vehicle technology: A review of the existing smart charging approaches. Renew. Sustain. Energy Rev. 2023, 183, 113518. [Google Scholar] [CrossRef]
- Vahidinasab, V.; Mohammadi-Ivatloo, B. Energy Systems Transition: Digitalization, Decarbonization, Decentralization and Democratization; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Zhao, B.; Duan, P.; Fen, M.; Xue, Q.; Hua, J.; Yang, Z. Optimal operation of distribution networks and multiple community energy prosumers based on mixed game theory. Energy 2023, 278, 128025. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Kamwa, I. Coupling Economic Energy Management and Flexibility Regulation of Power Systems with Renewable Energy Hubs Through Tso-Dso Coordination. Available online: https://ssrn.com/abstract=4508787 (accessed on 13 July 2023).
- Kamwa, I.; Bagherzadeh, L.; Delavari, A. Integrated Demand Response Programs in Energy Hubs: A Review of Applications, Classifications, Models and Future Directions. Energies 2023, 16, 4443. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M.; Tousi, S.R.; Hosseinian, S.M. Optimal siting and sizing of renewable energy sources and charging stations simultaneously based on Differential Evolution algorithm. Int. J. Electr. Power Energy Syst. 2015, 73, 1015–1024. [Google Scholar] [CrossRef]
- Amini, M.H.; Moghaddam, M.P.; Karabasoglu, O. Simultaneous allocation of electric vehicles’ parking lots and distributed renewable resources in smart power distribution networks. Sustain. Cities Soc. 2017, 28, 332–342. [Google Scholar] [CrossRef]
- Moradijoz, M.; Ghazanfarimeymand, A.; Moghaddam, M.P.; Haghifam, M.R. Optimum placement of distributed generation and parking lots for loss reduction in distribution networks. In Proceedings of the 2012 17th Electrical Power Distribution Conference (EPDC), Tehran, Iran, 2–3 May 2012; pp. 1–5. [Google Scholar]
- Mozafar, M.R.; Moradi, M.H.; Amini, M.H. A simultaneous approach for optimal allocation of renewable energy sources and electric vehicle charging stations in smart grids based on improved GA-PSO algorithm. Sustain. Cities Soc. 2017, 32, 627–637. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Shayeghi, H.; Shenava, S.J.S. Optimal Allocation of Electric Vehicle Parking lots and Renewable Energy Sources Simultaneously for Improving the Performance of Distribution System. In Proceedings of the 2019 24th Electrical Power Distribution Conference (EPDC), Khoramabad, Iran, 20 June 2019; pp. 87–94. [Google Scholar]
- Luo, L.; Wu, Z.; Gu, W.; Huang, H.; Gao, S.; Han, J. Coordinated allocation of distributed generation resources and electric vehicle charging stations in distribution systems with vehicle-to-grid interaction. Energy 2019, 192, 116631. [Google Scholar] [CrossRef]
- Vijayalakshmi, V.J.; Arumugam, P.; Christy, A.A.; Brindha, R. Simultaneous allocation of EV charging stations and renewable energy sources: An Elite RERNN-m2MPA approach. Int. J. Energy Res. 2022, 46, 9020–9040. [Google Scholar] [CrossRef]
- Dharavat, N.; Sudabattula, S.K.; Velamuri, S.; Mishra, S.; Sharma, N.K.; Bajaj, M.; Elgamli, E.; Shouran, M.; Kamel, S. Optimal Allocation of Renewable Distributed Generators and Electric Vehicles in a Distribution System Using the Political Optimization Algorithm. Energies 2022, 15, 6698. [Google Scholar] [CrossRef]
- Kandil, S.M.; Farag, H.E.; Shaaban, M.F.; El-Sharafy, M.Z. A combined resource allocation framework for PEVs charging stations, renewable energy resources and distributed energy storage systems. Energy 2018, 143, 961–972. [Google Scholar] [CrossRef]
- da Silva, E.C.; Melgar-Dominguez, O.D.; Romero, R. Simultaneous Distributed Generation and Electric Vehicles Hosting Capacity Assessment in Electric Distribution Systems. IEEE Access 2021, 9, 110927–110939. [Google Scholar] [CrossRef]
- Tabatabaei, J.; Moghaddam, M.S.; Baigi, J.M. Rearrangement of Electrical Distribution Networks with Optimal Coordination of Grid-Connected Hybrid Electric Vehicles and Wind Power Generation Sources. IEEE Access 2020, 8, 219513–219524. [Google Scholar] [CrossRef]
- Shafie-Khah, M.; Siano, P.; Fitiwi, D.Z.; Mahmoudi, N.; Catalao, J.P. An innovative two-level model for electric vehicle parking lots in distribution systems with renewable energy. IEEE Trans. Smart Grid 2017, 9, 1506–1520. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Shayeghi, H.; Seyed-Shenava, S.-J. Optimal Allocation of Electric Vehicle Parking Lots for Minimizing Distribution System Costs Considering Uncertainties. In Proceedings of the 2019 Iranian Conference on Renewable Energy & Distributed Generation (ICREDG), Tehran, Iran, 11–12 June 2019; pp. 1–6. [Google Scholar]
- Shayanfar, H.; Shayeghi, H.; Bagherzadeh, L. Optimal Allocation of Electric Vehicle Parking Lots for Improving the Efficiency of Distribution System. In Proceedings of the 2019 International Conference on Artificial Intelligence (ICAI), Xuzhou, China, 22–23 August 2019; pp. 116–122. [Google Scholar]
- Aljeddani, S.M.; Mohammea, M. A novel approach to Weibull distribution for the assessment of wind energy speed. Alex. Eng. J. 2023, 78, 56–64. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Shahinzadeh, H.; Shayeghi, H.; Gharehpetian, G.B. A short-term energy management of microgrids considering renewable energy resources, micro-compressed air energy storage and DRPs. Int. J. Renew. Energy Res. 2019, 9, 1712–1723. [Google Scholar]
- Afridi, M.; Tatapudi, S.; Flicker, J.; Srinivasan, D.; Tamizhmani, G. Reliability evaluation of DC power optimizers for photovoltaic systems: Accelerated testing at high temperatures with fixed and cyclic power stresses. Eng. Fail. Anal. 2023, 152, 107484. [Google Scholar] [CrossRef]
- Bagherzadeh, L.; Shahinzadeh, H.; Gharehpetian, G.B. Scheduling of Distributed Energy Resources in Active Distribution Networks Considering Combination of Techno-Economic and Environmental Objectives. In Proceedings of the 2019 International Power System Conference (PSC), Tehran, Iran, 30 December 2019; pp. 687–695. [Google Scholar]
- Rizvi, M.; Pratap, B.; Singh, S.B. Demand-side management in microgrid using novel hybrid metaheuristic algorithm. Electr. Eng. 2023, 105, 1867–1881. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Chinchanikar, S.; Shinde, S.; Shaikh, A.; Gaikwad, V.; Ambhore, N.H. Multi-objective Optimization of FDM Using Hybrid Genetic Algorithm-Based Multi-criteria Decision-Making (MCDM) Techniques. J. Inst. Eng. India Ser. D 2023, 1–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).